Physiology-based kinetic modeling of neuronal energy metabolism unravels the molecular basis of NAD(P)H fluorescence transients

Abstract

Imaging of the cellular fluorescence of the reduced form of nicotinamide adenine dinucleotide (phosphate) (NAD(P)H) is one of the few metabolic readouts that enable noninvasive and time-resolved monitoring of the functional status of mitochondria in neuronal tissues. Stimulation-induced transient changes in NAD(P)H fluorescence intensity frequently display a biphasic characteristic that is influenced by various molecular processes, e.g., intracellular calcium dynamics, tricarboxylic acid cycle activity, the malate–aspartate shuttle, the glycerol-3-phosphate shuttle, oxygen supply or adenosine triphosphate (ATP) demand. To evaluate the relative impact of these processes, we developed and validated a detailed physiologic mathematical model of the energy metabolism of neuronal cells and used the model to simulate metabolic changes of single cells and tissue slices under different settings of stimulus-induced activity and varying nutritional supply of glucose, pyruvate or lactate. Notably, all experimentally determined NAD(P)H responses could be reproduced with one and the same generic cellular model. Our computations reveal that (1) cells with quite different metabolic status may generate almost identical NAD(P)H responses and (2) cells of the same type may quite differently contribute to aggregate NAD(P)H responses recorded in brain slices, depending on the spatial location within the tissue. Our computational approach reconciles different and sometimes even controversial experimental findings and improves our mechanistic understanding of the metabolic changes underlying live-cell NAD(P)H fluorescence transients.

Introduction

Experimental information about short-term dynamics of energy metabolism of individual neuronal cells is low compared with other, nonexcitatory cell types. This deficit is mainly because of the fact that in excitable cells metabolic adaptations to varying energetic needs occur in a time window of a few seconds and thus are virtually inaccessible to invasive experimental techniques usually applied to trace temporal changes of metabolites and enzymatic flux rates. Therefore, metabolic studies of neuronal tissue require metabolic readouts, which can be noninvasively and continuously monitored. One important readout is the (auto)fluorescence of the reduced pyridine nucleotides, nicotinamide adenine dinucleotide (NADH) and nicotinamide adenine dinucleotide phosphate (NADPH), collectively termed NAD(P)H. Changes in NAD(P)H fluorescence primarily reflect changes in the mitochondrial redox state as showed 40 years ago in pioneering publications.¹ Activation of individual cells or neuronal cell populations in brain slices results in characteristic changes in NAD(P)H fluorescence intensity: the initial ‘dip' is followed by the ‘overshoot' component, both of which reflect enhanced oxidation and reduction of the pyridine nucleotides, respectively.^{2, 3, 4} Interpretation of such transient changes in NAD(P)H fluorescence in terms of the underlying biochemical and biophysical processes is difficult for several reasons. First, in most experimental studies, NAD(P)H fluorescence represents the aggregate response of a certain population of cells, which may respond differentially to an activating stimulus depending on their specific cell types and their spatial position in the tissue. For example, spatially resolved two-photon fluorescence imaging in neuronal tissue suggested the stimulus-induced NAD(P)H response to result from the superposition of two spatially separated signals generated by enhanced oxidative metabolism in the neurons and enhanced glycolytic activity in astrocytes, respectively.⁵ Second, regional differences in the preferred energy substrates, glucose or lactate, influence the strength and shape of NAD(P)H responses,⁶ as well as does the basal level of NAD(P)H fluorescence before stimulation. Third, the pyridine nucleotides, NAD and NADP are ‘metabolic hubs' that function as cofactors in several pathways, which all may contribute to the observed changes of NAD(P)H fluorescence. For example, the dip of the NAD(P)H response typically observed immediately after onset of neuronal activation may result from an increase in oxidative phosphorylation (OXPHOS) but it may also be caused by enhanced uptake of calcium into mitochondria without a significant increase in the adenosine triphosphate (ATP) consumption rate.²

Because NADH and NADPH are spectrally identical most available live-cell fluorescence studies do not distinguish between these two reduced pyridine nucleotides. Generally, NADPH is an important cofactor in biosynthetic pathways and reactive oxygen species (ROS) detoxification, while NADH is the main substrate for mitochondrial energy metabolism. Therefore, and because the cellular NADP/NADPH pool is about one order of magnitude lower than the NAD/NADH pool, the present study is based on the well-justified assumption that the short-term variation in experimentally determined NAD(P)H responses accounts for variations in NADH (see also the discussion in Mayevsky and Rogatsky⁷).

Mathematical modeling is a promising strategy to fill the experimentally unapproachable gaps of knowledge about the relative contribution of various molecular processes to observe aggregate NAD(P)H responses. To this end, we developed a detailed kinetic model of the energy metabolism of neuronal cells encompassing glycolysis and OXPHOS as central ATP-producing pathways, the generation of the mitochondrial transmembrane potential by the gradient of protons and other anions and the exchange of calcium ions between the cytosol and mitochondrial matrix. We used the model to simulate metabolic changes in various experimental settings for which NAD(P)H responses have been monitored. This way, it was possible to decipher the relative contribution of various metabolic pathways to stimulus-induced NAD(P)H responses as recorded from individual neurons and brain slices.

Methods

Metabolism

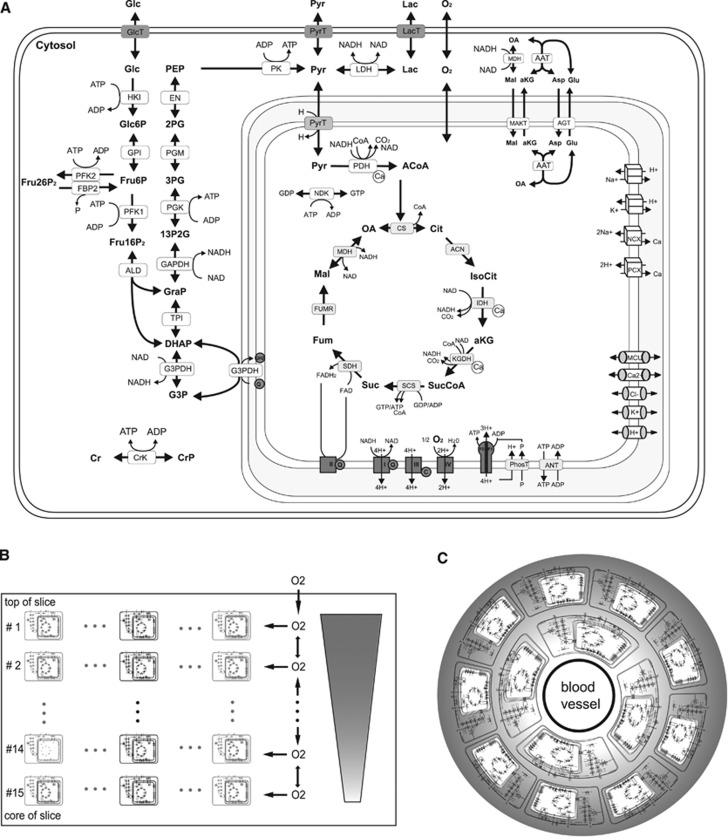
The biochemical and biophysical processes included into the kinetic model are depicted in Figure 1A. The two central ATP-producing pathways are glycolysis (the decomposition of glucose to pyruvate and NADH or lactate, respectively) and mitochondrial OXPHOS. Glycolysis and OXPHOS are coupled and mutually regulated by a number of shared metabolites. The purine nucleotides, adenosine diphosphate (ADP) and ATP, function as substrates as well as allosteric regulators of some glycolytic enzymes and are also substrates of the mitochondrial adenine nucleotide transporter and the F₀F₁-ATPase (ATP synthase). Adenosine monophosphate (AMP) formed from ADP in the adenylate kinase reaction is a sensitive indicator of the energy status of the cell because the AMP concentration rises in a super-linear manner with decreasing ATP concentration. AMP activates the AMP-dependent kinase, which among other inconvertible enzymes phosphorylates phosphofructokinase-2 and thus elevates the concentration of fructose 2,6-bisphosphate, the strongest allosteric activator of phosphofructokinase-1. The pyridine nucleotide NAD is the cytosolic cofactor of the glycolytic enzymes glyceraldehyde phosphate dehydrogenase and lactate dehydrogenase. In the mitochondrion, NAD is the cofactor of the pyruvate dehydrogenase reaction, three reactions of the tricarboxylic acid (TCA) cycle and of complex I of the respiratory chain. The cytosolic and mitochondrial NAD/NADH pools are connected through two shuttle systems for NAD and NADH in the inner mitochondrial membrane, the malate–aspartate shuttle and the glycerol phosphate shuttle. Pyruvate is the main source of mitochondrial acetyl coenzyme A (acetyl-CoA) required for the formation of citrate. Pyruvate may either be formed from glucose in the glycolytic pathway or from lactate that is imported from the external space.

Figure 1.

(A) Reactions and transport processes included in the single-cell kinetic model. The model comprises the following subsystems: conversion of glucose to pyruvate/lactate in glycolysis including the formation of fructose 2,6-bisphosphate (Fru26P₂), a potent activator of phosphofructokinase-1 (PFK1), shuttles of electrons (NAD-bound hydrogen) between the cytosol and the mitochondrial matrix combining the activities of the malate/α-ketoglutarate carrier (MAC), the mitochondrial aspartate amino transferase (AAT), the antitransport of glutamate (Glu) and aspartate (Asp) by the aspartate/glutamate carrier (AGC), the glycerol-3-phosphate (G3P) shuttle comprising mitochondrial and cytosolic G3P dehydrogenases (G3PDH), the TCA cycle starting with the formation of citrate (Cit) from oxaloacetate (OA) and acetyl-CoA (ACoA) and replenishing OA in a circular chain of reactions yielding electrons in terms of ubiquinol (QH2) and NADH and two molecules CO₂; the respiratory chain composed of four complexes of which complexes I, III, and IV function as proton pumps. The resulting proton gradient and mitochondrial membrane potential (V_mm) determine the rate of proton-assisted ion transport of Na⁺, K⁺, Ca²⁺, and phosphate (P) across the inner mitochondrial membrane, the rate of the adenine nucleotide exchanger (NE) exchanging mitochondrial ATP against cytosolic ADP and the rate of F₀F₁-ATPase using three protons per generation per ATP. The membrane potential V_mm is also influenced by the exchange of cations and anions across the inner mitochondrial membrane through ion channels. Lactate is exchanged with the external space by the monocarboxylate transporter, MCT2. Within the cell, it is reversibly converted into pyruvate by the lactate dehydrogenases LDHA and LDHB. (B) Schematic representation of the slice model used to simulate spatial oxygen gradients within a brain slice. The slice model dissects the slice from the top to the slice core into a series of 15 thin layers. Assuming spatial isotropy in cell layers parallel to slice surface, all neuronal cells present in a given layer are represented by a single ‘representative' cell (marked black) so that the three-dimensional slice can be approximated by a one-dimensional row of cells, which are diffusively coupled. The metabolism of the cell representing one layer of cells is described by the cellular metabolic model used in the single-cell simulations of the preceding sections. Oxygen diffuses from the top to the bottom of the slice. The same model architecture was used in our previous work.¹⁴ (C) Schematic representation of the tissue model used to simulate in vivo NADH transients. The tissue model dissects the tissue in 10 concentric hollow cylinders around a central blood vessel with a wall thickness of 3.5 μm giving a total tissue of 35 μm corresponding to half of the average intercapillary distance.¹⁵ Oxygen supply is modeled by diffusional exchange between these cylinders and each hollow cylinder is equipped with the single-cell metabolic system. In contrast to the slice model, the discretization size is smaller than a single cell and a single cell comprises multiple discretization layers. This is necessary as the gradient across the length of one cell is not negligible.

Calcium Transport

Besides their role in the maintenance of cellular energy levels, mitochondria also serve as calcium buffer. A stimulus-induced increase of cytosolic Ca²⁺ is accompanied by a rapid Ca²⁺ uptake driven by the inside-negative mitochondrial membrane potential and mediated by the calcium uniporter Mcu. Considerable amounts of Ca²⁺ can be sequestered inside mitochondria by unspecific binding to proteins/phosphate. The bound calcium is in exchange with the free ion, which activates three enzymes of TCA cycle and thus enhances the generation of NAD(P)H. During the resting phase, mitochondrial Ca²⁺ can be extruded to the cytosol by a sodium/calcium exchanger and a calcium/proton exchanger and finally released to the extracellular space. Activation-induced changes in the cytosolic calcium concentration result from the operation of a large number of transport processes exchanging calcium with the extracellular space, the endoplasmic reticulum as well as mitochondria are also affected by calcium binding to proteins and membranes (for a comprehensive model of cellular Ca²⁺ dynamics encompassing all these processes see Tiveci et al⁸). As detailed modeling of the cytosolic calcium dynamics was not within the scope of our study, we included time variations in the cytosolic calcium concentration by a phenomenological function, which relates the activation-induced transient of the cytosolic calcium level to the temporal profile of the activating stimulus. The basal cytosolic calcium concentration of the nonactivated cell was set to depend on the cytosolic ATP concentration⁹ as ATP depletion causes both a depolarization of the outer cell membrane and thus enhanced inward-directed calcium flux through voltage-dependent channels as well as a reduction in the capacity of secondary active and ATP-dependent pumps removing calcium from the cytosol.

Substrate Supply

Neuronal cells cover their ATP demand to >90% by the utilization of glucose.¹⁰ The uptake of glucose into the cell is modeled as facilitated diffusion mediated by the glucose transporter GLUT3. Lactate may also serve as oxidizable substrate as showed with slice preparations.¹¹ As lactate enters the TCA cycle by conversion into pyruvate with subsequent oxidative decarboxylation of pyruvate to acetyl-CoA, pyruvate is an oxidizable substrate as well.¹²

Oxygen Supply

O₂ reaches the respiratory chain by diffusion through a number of different membranes. Hence, the O₂ concentration sensed by complex IV of the respiratory chain is much lower than the O₂ concentration in the extracellular space. To account for this gradient, we modeled oxygen uptake in the cell via an effective diffusion process with an overall diffusion constant being lower than that for the free diffusion of oxygen in water.

Slice Model

To understand the impact of differential oxygen availability on the metabolic state of neurons in brain slice preparations a single-cell model is not sufficient since an oxygen concentration gradient exists between the surface and the depth of the slice so that cells in different layers of the slice experience different oxygen concentrations.^{13, 14} To account for spatially inhomogeneous oxygen availability in brain slices, we expanded the cell model to a tissue model. Assuming spatial isotropy in cell layers parallel to slice surface, all neurons present in a given layer are represented by a single ‘representative' cell so that the three-dimensional slice is approximated by a one-dimensional row of diffusively coupled cells (details of the slice model are outlined in the legend of Figure 1B). In total, the slice model encompasses 15 cells whereby cell #1 at the surface is exposed to the ambient oxygen concentration and cell #15 at the bottom experiences the lowest oxygen concentration.

Tissue Model

To apply the model to in vivo situations, we used a simple two-dimensional tissue model (Figure 1C). The model is represented as a cylinder constituted by a central supporting capillary surrounded by neuronal tissue. Tissue thickness is assumed to be 35 μm corresponding to half of the average intercapillary distance.¹⁵ Oxygen diffusion is modeled by a discrete compartment model subdividing the cylinder in a vessel compartment and 10 concentric tissue compartments around the vessel. It is assumed that no oxygen leaves the cylinder, which is equivalent to the assumption that the outflow of oxygen from the represented region is equal to the inflow from neighboring regions.

Mathematical Modeling of Kinetics

Time-dependent changes of metabolites and ion species are described by a system of ordinary differential equations comprising in their right-hand sides a linear combination of rate equations for the associated elementary processes. The rate equation establishes a quantitative relationship between the rate (either mass conversion or mass transport per time unit) of an elementary process and the concentration of the reactants and effectors (see Model Equations in Supplementary Information). Electrodiffusion of ions through the inner mitochondrial membrane is described by kinetic equations of the Goldman-Hodgkin-Katz type similar as outlined in Berndt et al.¹⁶ With metabolic and ion transport processes together, the model is given by a set of 66 nonlinear differential equations governing the dynamics of the network (see Supplementary Information). All rate laws and the related kinetic parameters have been chosen as reported for neurons or, if the information for neurons was not available, for neuronal tissue, respectively.

NADH Transients

The model predicts cytosolic and mitochondrial NADH concentrations that can be compared with experimentally determined NAD(P)H autofluorescence data. To this end, we assume that there is a linear relationship between the reduction state and NADH fluorescence. In the cell, NAD and NADH can either be bound to different proteins or exist in a free form. On binding, NADH changes its relative fluorescence by 50%.¹⁷ This, in principle, would make the interpretation of the NAD(P)H fluorescence signal difficult if there are significant changes in the fraction of bound to unbound changes. However, according to Vishwasrao et al,¹⁷ the relative fraction of bound to free NADH remains virtually unchanged (44% to 45%) even in hypoxia although the total amount of reduced NADH doubles in all fractions. Therefore, there are good reasons to assume a linear dependence between NADH concentration and NADH fluorescence intensity.

Flavin Adenine Dinucleotide (FAD) Transients

FAD is a prosthetic group of several metabolic enzymes where it functions as electron carrier. The reduction state of FAD can also be measured fluorometrically and shows typically an inverse relationship compared with NADH. To compare our model predictions to experimental FAD autofluorescence traces, we explicitly modeled the FAD reduction state. In contrast to NADH, FAD cannot be treated as a pool variable but each enzyme bound moiety has to be considered as independent from the other. FAD-containing enzymes occurring in the model comprise the pyruvate dehydrogenase complex (PDHC), α-ketogluterate dehydrogenase complex (KGDHC), glycerol-3-phosphate (G3P) dehydrogenase, and the succinate dehydrogenase. The catalytic mechanism of theses enzymes can be split into two elementary steps: the first step describes the oxidation of the substrate and the accompanying reduction of FAD to FADH₂. The second step describes the oxidation of FADH₂ to FAD and the transfer of the electrons to the final electron acceptor, e.g., NAD for PDHC and KGDHC and ubiquinone for G3P dehydrogenase and succinate dehydrogenase. Naturally, kinetic properties in terms of K_m values do not exist, but one can assume that the substrate concentration is always saturating because of the targeted supply of reduction equivalents to the bound FAD. Furthermore, the midpoint potentials of the different FAD/FADH₂ moieties have been taken into account. As a side constraint, the product of the equilibrium constants for the individual reactions has to be equal to the equilibrium constant of the whole reaction.

Parts of the model focusing mainly on mitochondrial ATP production and the generation of ROS by the respiratory chain have already been used in previous work with the aim to relate changes in the energy and redox metabolism of neurons to the development of neurodegenerative diseases.^{18, 19}

The model was implemented in MATLAB R2011b, The MathWorks (Natick, MA, USA).

Results

Calibration and Validation of the Model: Definition of the Reference State

Metabolic measurements in brain tissues reflect aggregate responses of different populations of neurons and glial cells, such as astrocytes. As the specific metabolic endowment and activation state of individual cells may vary, we defined a ‘generic' neuronal cell (=model neuron), the metabolism of which is thought to represent the average behavior of the whole cell population in the tissue. We calibrated the model such that the following key metabolic features reported for the whole brain or tissue slices of the brain are correctly reproduced: (1) the oxygen–glucose uptake ratio is ~5.^{20, 21, 22} (2) Ten percent of glucose is converted into lactate.²³ (3) Relative shares of the proton leak, the pumping of potassium ions and ATP synthesis (including F₀F₁-ATPase and phosphate uptake) in the utilization of the proton gradient amount to 24%, 16%, and 60%, respectively.^{24, 25, 26} (4) The mitochondrial transmembrane potential has a value of −140 mV.²⁷ (5) The concentration of free calcium (Ca²⁺) in the cytosol is 0.04 μmol/L.²⁸ Moreover, the model correctly recapitulates concentration values of glycolytic metabolites and intermediates of the TCA cycle measured in different activity states of cell cultures and brain slices (see Supplementary Figure S1).

Model Simulation of Different Experimental Settings

In the following, we used the model to simulate time-dependent changes of cytosolic and mitochondrial NADH in response to transient changes of either the cytosolic calcium concentration or the ATP consumption rate. The latter represents a global measure for the total energetic challenge elicited by the activation of the neuron, which is associated with an increased rate of various ATP-consuming membrane transporters (e.g., Na⁺-K⁺-ATPase, Ca²⁺ transporters, neurotransmitter reuptake), the relative contribution of which will not be further specified in the model. The computed NADH profiles were compared with experimentally determined NAD(P)H fluorescence transients, thereby neglecting a possible (but small) contribution of NADPH.

Calcium-Triggered NADH Changes Without Changes in the ATP Demand

A sufficiently strong sudden increase in cytosolic-free calcium alone is able to elicit biphasic NAD(P)H transients. This was showed more than 20 years ago in a pioneering study of Duchen² for single, freshly dissociated mammalian neurons. He used microfluorimetric techniques to measure the cytosolic Ca²⁺, the mitochondrial membrane potential (rhodamine 123 fluorescence), NAD(P)H/NAD(P)⁺ fluorescence, and FAD fluorescence in combination with whole-cell voltage-clamp recordings. Brief depolarization of the cell membrane (100 to 500 ms) was accomplished by nonphysiologically, very high K⁺ application (50 mmol/L) or by voltage commands.

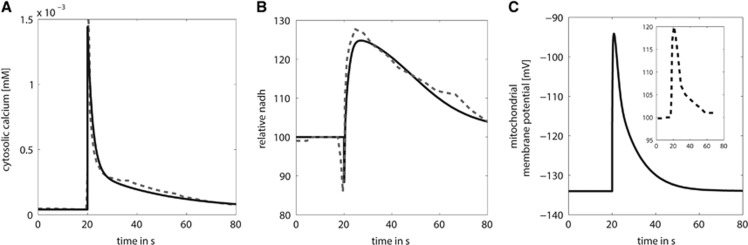
We modeled this experiment by simulating the time-dependent metabolic response to a brief cytosolic calcium transient having the same magnitude and temporal profile than the transients elicited in the Duchen experiment (Figure 2). In these simulations, the mitochondrial membrane potential exhibited a transient depolarization, while the mitochondrial NADH showed a sharp dip followed by a long-lasting overshoot. Inspecting the simulated time courses of the model variables it became evident that the depolarization of the mitochondrial membrane potential was elicited by the rapid Ca²⁺ uptake mediated by the Ca²⁺ uniporter because this uptake is an electrogenic process. Instantaneous repolarization of the mitochondrial transmembrane potential through proton pumping by the respiratory chain oxidizes some fraction of mitochondrial NADH and causes the initial dip. The Ca²⁺ taken up by the mitochondria is first sequestered by calcium-binding proteins and with some delay delivered to the mitochondrial matrix where it activates the mitochondrial dehydrogenases PDHC, isocitrate dehydrogenase, and KGDHC. Oxidation of NADH by the respiratory chain is enhanced only a short time span during the restoration of the transmembrane potential whereas the Ca²⁺-mediated activation of the TCA cycle prevails and increases the mitochondrial NADH level (overshoot) until a new quasi-stationary state at an elevated mitochondrial NADH/NAD ratio has been reached. The slow reversal of the NADH/NAD ratio toward the initial value reflects the slow release of mitochondrial Ca²⁺ to the cytosol and the associated attenuation of the TCA cycle activation.

Figure 2.

Calcium-induced biphasic NADH response. (A) The simulations were performed by using the time course of cytosolic calcium as model input described by an empirical function (see Model Equations in Supplementary Information) fitting the measured cytosolic calcium profile from Duchen.² (B) Rapid calcium uptake into the mitochondria elicited a biphasic temporal change of mitochondrial NADH. (C) Transient increase in the mitochondrial transmembrane potential. The gray dashed lines in A and B show the experimental data,² the small insert in C shows the observed fluorescence signal of the dye used to monitor the mitochondrial membrane potential.

Impact of Calcium on the NADH Response to an Energetic Challenge

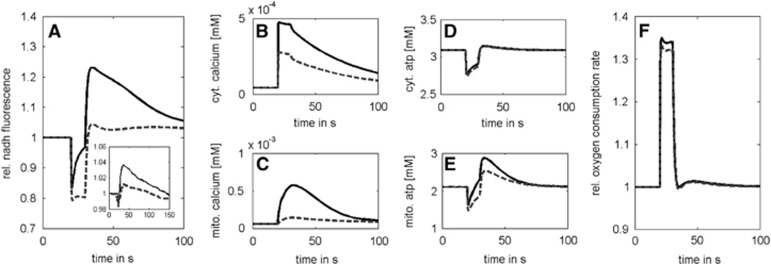
Neuronal activation modulates also the shape of the transient NAD(P)H response elicited by increase in the ATP demand. Kann et al⁴ reported that in nominally calcium-free medium the overshoot of the NAD(P)H response as elicited in hippocampal slice cultures by short-term electrical stimulation was significantly reduced. In contrast to the Duchen experiment,² the rise in extracellular free potassium concentration remained moderate (<3 mmol/L from baseline) in this experiment. We simulated this experiment by coupling the activation-induced increase in the ATP utilization rate with a transient increase in cytosolic calcium. In case of physiologic extracellular calcium concentration, the cytosolic calcium transient was calibrated to a peak value of 0.4 μmol/L according to measurements.^{28, 29} To account for a lack of calcium in the extracellular space, the peak value of the cytosolic calcium transient was lowered to a peak maximum of 0.2 μmol/L according to findings in Llinas et al.³⁰ The mitochondrial NADH responses obtained with normal and low cytosolic calcium concentrations are shown in Figure 3. In both cases, the NADH response showed an initial dip, but the overshoot was significantly higher at normal extracellular calcium concentration. As in the Duchen experiment, the overshoot is accounted for by a persistent Ca²⁺-dependent activation of the TCA cycle. However, here, the dip is primarily caused by the activation-induced increase in the ATP consumption rate and not by the mitochondrial Ca²⁺ uptake because the increase in the cytosolic calcium level up to maximal values of ~0.4 μmol/L is significantly smaller than in the Duchen experiment (reaching peak values of 1.4 μmol/L). The dominance of the transiently increased energetic load over the transiently increased calcium level in the generation of the NADH response is reflected by practically identical oxygen consumption rates for both situations (Figure 3F). The abrupt increase in the energy demand decreases the cytosolic ATP/ADP ratio. This activates the mitochondrial adenine nucleotide antiporter, which in turn decreases the mitochondrial ATP/ADP ratio. Depletion of mitochondrial ATP stimulates F₀F₁-ATPase activity, thus decreasing the proton-motive force, activating the respiratory chain and resulting in an enhanced oxidation of NADH (initial dip of NAD(P)H response).

Figure 3.

Lack of calcium diminishes the NADH overshoot. The model simulations were performed by coupling the activation with an increase in cytosolic calcium up to a maximal value of 0.4 μmol/L (bold curves) and 0.2 μmol/L (dotted curves). (A) NADH transients elicited by a 10-second electric stimulus with concomitant increase in cytosolic calcium concentration. (B and C) Cytosolic and mitochondrial calcium transients. (D and E) Cytosolic and mitochondrial ATP transients. (F) Relative oxygen consumption rate. For comparison, the small insert in A shows the experimental data from Kann et al.⁴

The Size of the Initial Dip of the NAD(P)H Response at Varying Energetic Challenges

A transient initial decline of mitochondrial NAD(P)H, the so-called dip, is commonly observed in experiments stimulated either by electric pulses⁴ or administration of excitatory neurotransmitters.³¹ The dip reflects the decrease in mitochondrial NADH caused by a sudden, activation-induced increase in the ATP utilization rate and mitochondrial Ca²⁺ uptake whereby the accompanying enhanced oxidation of NADH by the respiratory chain exceeds transiently the reduction rate in the TCA cycle. A close correlation between the magnitude of the additional ATP consumption entailed by the activating stimulus and the size of the NAD(P)H dip has been showed.¹³ In these experiments, successive blocking of major ATP-consuming processes related to pre- and postsynaptic processes as well as the uptake and metabolization of neurotransmitters resulted in a progressively diminished size of the dip (see small inserts in Figure 4A).

Figure 4.

The depth of the mitochondrial NADH dip depends on the magnitude of the excitation-induced energetic load. (A) Cells were stimulated with varying activation strengths over a constant stimulation period of 10 seconds. (B) Cytosolic NADH transients. (C) Mitochondrial NADH transients. (D) Relative changes in mitochondrial (solid line) and cytosolic (dashed line) NADH concentrations. (E) Cytosolic NAD/NADH ratios. (F) Mitochondrial NAD/NADH ratios. (G) FAD transients (dotted line, dashed line, solid line, and dash-dotted line) are almost identical in shape but differ in magnitude depending on the midpoint potential of the binding enzyme moiety. (H) Mitochondrial NADH transient (solid black line) and average NADH transients (gray dashed line) obtained by weighing the transients shown in B and D by the relative volumes of mitochondria and cytosol and the fluorescence efficiency of NADH in these compartments. The inlet in A shows experimentally determined dip sizes:¹³ (1) control, (2) inhibition of postsynaptic currents and postsynaptic action potentials by the drugs 2,3-dihydroxy-6-nitro-7-sulfamoyl-benzo[f]quinoxaline-2,3-dione and D-(-)-2-Amino-5-phosphonopentanoic acid (NBQX+AP5), (3) inhibition of presynaptic transmitter release and downstream postsynaptic events by Cd²⁺, and (4) complete blocking of excitability by tetrodotoxin (TTX).

To better understand how the magnitude of the energetic load evoked by the electrical stimulus is reflected in the size of the initial dip in NAD(P)H response, we performed a series of simulations where the magnitude of the additional energetic load was varied. The time course of the energetic load, i.e., the increase in the ATP utilization rate associated with the activating stimulus was described by activation functions with stepwise declining amplitudes (Figure 4A). In these simulations, the size of the NADH dip correlated well with the magnitude of the additional energetic load exerted by the stimulus. Figure 4G shows the traces of the FAD concentrations for the various bound species. Since the relative fluorescence efficiency of the different FAD moieties is unknown, we do not average, but show each FAD transient separately. Although the shape (overshoot and long-lasting dip) is identical for all four moieties and mirrors the mitochondrial NADH concentration, the sizes of overshoot and dip depend on the midpoint potentials, which are not identical for the PDHC, KGDHC, G3P dehydrogenase, and succinate dehydrogenase.

Of note, our simulations revealed also significant changes in the concentration of cytosolic NADH (Figure 4B). However, in contrast to mitochondrial NADH, the cytosolic changes in NADH displayed only an overshoot during the whole activation period and thereafter. The model predicts cytosolic (Figure 4E) and mitochondrial NAD/NADH ratios (Figure 4F) that can be compared with experimental data. In the unperturbed state, the cytosolic NAD/NADH ratio is ~700, while the mitochondrial NAD/NADH is ~2.25. This is in agreement with experimental data reviewed, for example, by Dienel³² who reports a cytosolic ratio of 670 to 715 and a mitochondrial ratio of ~2. During excitation, the reduction state in the cytosol increases, while the mitochondrial reduction state first decreases (dip) and then increases (overshoot; Figures 4E and 4F).

The increase in cytosolic NADH during enhanced ATP utilization is due to the reduced cytosolic phosphorylation potential, which activates the key glycolytic enzymes hexokinase, phosphofructokinase-1, and pyruvate kinase. In principle, a contribution of cytosolic NADH to the observed NAD(P)H response cannot be excluded. However, this cytosolic component of NADH fluorescence should be small for several reasons. First, given that the observed NAD(P)H fluorescence is proportional to the total NADH concentration, [NADH_tot]=Ω_cyt [NADH_cyt]+Ω_mito [NADH_mito], with Ω denoting the volume fraction of the respective compartment, the contribution of mitochondrial NAD(P)H should account for >80% of the total signal.³³ Second, the cytosolic NAD/NADH ratio is reported to lie somewhere between 1/100 and 1/1,000 and is thus much smaller than the mitochondrial NADH/NAD ratio of ~1 to 10.³⁴ Third, the fluorescence yield of mitochondrial NAD(P)H is sixfold to eightfold stronger than that of the cytosolic NAD(P)H.⁷ Taking these factors into account, the contribution of the cytosolic NADH response to the measured NADF(P)H remains negligibly small (Figures 4C and 4H).

The Influence of Oxygen Supply on the Basal and the Activation-Induced Mitochondrial NADH Response

For the modeling of slice preparations, we used a simplified one-dimensional slice model (Figure 1B). In all experiments simulated, the ambient glucose concentration was high enough to exclude limitation of glucose supply to any part of the slice. The aggregate NADH response was calculated by averaging across the simulated NADH responses of the individual slice layers, which all contribute to the measured NAD(P)H fluorescence.⁹

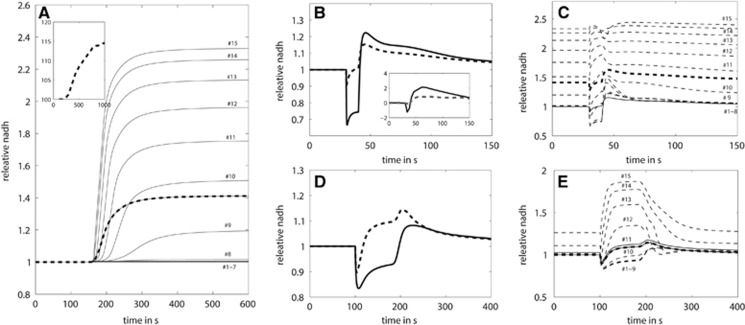
First, we calculated the stationary metabolic state of the slice model at 95% ambient oxygen for a nonstimulated slice where all cells have the same basal ATP consumption rate. Although there is a remarkable decline from the surface to the bottom of the slice, the O₂ level at the bottom is still above the oxygen affinity of complex IV of the respiratory chain. Hence, the ATP levels of all cells are identical. The situation changes if the ambient oxygen level is abruptly decreased to 20%. The decrease in O₂ propagates from the top to the bottom of the slice, i.e., there occurs a time-dependent decline in the O₂ level in all layers of the slice. As soon as the actual oxygen level in a layer falls below the oxygen affinity of complex IV of the respiratory chain, the ATP level of the cells in this layer starts to decline owing to the oxygen-limited respiratory activity. This holds true in particular for those cells that are at the bottom of the slice whereas cells close to the top are not affected as the reduced oxygen level is still high enough to saturate the respiratory chain. The stronger the respiratory chain is inhibited by the decrease in O₂ level the less NADH is oxidized and the higher the mitochondrial NADH level rises. This scenario is illustrated in Figure 5A. In the time course of successive O₂ depletion, the cells present in the bottom layer are the first ones to experience hypoxia and thus starting to elevate their mitochondrial NADH fluorescence intensity. These cells show strongest decrease in O₂ and increase in mitochondrial NADH. The imbalance between reduced NADH oxidation by the respiratory chain and ongoing NADH delivery by the TCA cycle is additionally amplified by the accumulation of mitochondrial Ca²⁺. The increase in mitochondrial Ca²⁺ is caused by both an increase in the cytosolic Ca²⁺ level with decrease in cytosolic ATP and a decrease in the Ca²⁺ release from the mitochondria to the cytosol at declining activity in the respiratory chain. In contrast to the cells present in the deeper layers of the slice, cells close to the top of the slice receive still enough O₂ to keep the respiratory chain saturated. These cells do not contribute to the increase in the baseline of aggregate NADH fluorescence.

Figure 5.

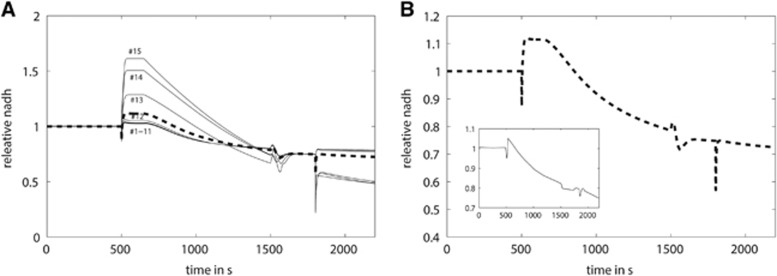
The impact of changes in the oxygen supply on the basal and excitation-induced mitochondrial NADH levels. (A) At time t=400 seconds, the ambient oxygen level was abruptly decreased to 20%. The dashed curve represents the average NADH concentration change in the slice. The solid lines mark the time-dependent increase in NADH in different layers of the slice. At 95% ambient oxygen, the mitochondrial oxygen concentration within all layers is above the O₂ affinity of the respiratory chain, which entails identical stationary NADH levels in all layers. After changing the ambient oxygen concentration, there is a time-dependent increase in the mitochondrial NADH level in different layers of the slice. The small insert shows the measured NAD(P)H fluorescence reported in Huchzermeyer et al.³⁵ (B) At time t=40 seconds, all cells in the slice were exposed to a threefold increase in the activation function for 10 seconds mimicking the extra ATP consumption induced by an electrical stimulation. Cumulative concentration profile of mitochondrial NADH of the whole slice normalized to the preexcitation state. At 95% ambient oxygen (solid line), the initial dip and the overshoot are substantially larger than at 20% oxygen (dashed line). The insert shows the measured NAD(P)H fluorescence profile at 95% and 20% ambient oxygen saturation reported in Huchzermeyer et al.³⁵ (C) Concentration profile of NADH in different layers of the slice at 20% ambient oxygen. All concentration values were normalized to the NADH concentration in the first layer during the preexcitation state. Even in the absence of the electrical stimulus, the NADH concentration increases from the top to the bottom of the layer. With increasing distance from the top of the slice, the stimulation-induced dip is decreasing and virtually disappears in cell layers at the bottom of the slice. (D) At time t=100 seconds, all cells in the slice were exposed to a twofold increase in the energetic load for 80 seconds. NADH transients averaged over the whole slice at 95% ambient oxygen (solid line) and 50% ambient oxygen (dashed line). The insert shows the measured NAD(P)H fluorescence profile at 95% and 50% ambient oxygen saturation reported in Galeffi et al.³ (E) Heterogeneous contribution of the different cell layers to the NADH profile at 50% ambient oxygen.

Next, we studied the impact of varying oxygen availability on the characteristics of the activation-induced NADH response. We simulated NADH fluorescence responses in brain slices monitored in the presence of either high (95%) or low (20%) ambient oxygen levels. Figure 5B shows simulations of an experiment with brain slices where the NAD(P)H fluorescence was elicited by a short electrical stimulation of 10 seconds.³⁵ It shows the aggregate mitochondrial NADH response for the two different ambient oxygen concentrations applied, while Figure 5C shows the contribution of the individual layers to the aggregate NADH response for an ambient oxygen fraction of 20%. At low ambient oxygen of 20%, cells close to the top remain still well supplied with O₂ and their NADH response is the same as at 95% O₂, characterized by an initial dip and a subsequent overshoot. Cells in the middle of the slice (layers #9 to 12), which receive just sufficient oxygen before the energetic challenge now experience a decrease in O₂ below the oxygen affinity constant of complex IV of the respiratory chain (hypoxia). Because of this O₂ limitation, respiratory oxidation of NADH is outperformed by the increase in NADH owing to the calcium stimulation of the TCA cycle. Hence, the NADH response in these cells does not exhibit a dip but only an overshoot. Cells present in the deep layers (cells #13 to 15) are already hypoxic before the stimulus. As these cells have already elevated baseline NADH fluorescence they show only a marginal further increase in NADH. In summary, in cells residing in the deeper layers of the slice the overall NADH response at 20% ambient oxygen shows a smaller dip and overshoot compared with the NADH response at 95% ambient oxygen. Because of the heterogeneous oxygen concentration, a smaller number of cells shows the biphasic response. This leads to smaller amplitudes at 20% ambient oxygen compared with 95% ambient oxygen (Figure 5C).

As can be seen in Figure 5C, the fraction of cells that are driven into hypoxia during activation and thus display only an overshoot entails that the recovery of the overall NADH response from the initial dip starts already during activation. This characteristic of the NAD(P)H response was even more pronounced in another experiment where oxygen concentration was decreased to 50% and neuronal activation period lasted 80 seconds.³ This experiment was also perfectly recapitulated by model simulations (Figures 5D and 5E).

The computational recapitulation of the attenuated biphasic NAD(P)H response at low oxygen levels was only possible by using a spatial slice model because the observed response is the resultant of heterogeneous contributions from different layers of the slice. Note that Galeffi et al³ also show a clear relationship between metabolic load (i.e., intensity of stimulus), NADH initial dip and O₂ requirements, similar to that shown in Figure 4. Figure 5 shows an excellent recapitulation of measured NADH transient changes in lowered O₂ environment.

The Influence of a High Pyruvate Challenge on the NADH Response

An important observation reported in a groundbreaking paper of Lipton³⁶ is that a high extracellular pyruvate concentration significantly decreases the NAD(P)H fluorescence baseline. Since pyruvate and lactate couple with cytosolic NADH and NAD through the action of the lactate dehydrogenase, an increase in cytosolic pyruvate greatly decrease the cytosolic redox state (NADH/NAD). From this, Lipton concluded that the cytosolic contribution to the overall NAD(P)H response is significant and not negligible. To check the validity of his conclusion, we included the uptake of pyruvate into the model and simulated the experiments where cortical slices were electrically stimulated for several minutes and a large amount of pyruvate was added to the slice preparation at the onset of the electrical stimulation as reported by Lipton.³⁶ The model correctly predicted the experimentally observed three-phasic NADH response: an initial dip followed by an overshoot followed by a decline in NADH below the original baseline (Figure 6). Also in agreement with the experiment, a second electrical stimulation at already much lower basal NADH showed a greatly diminished overshoot. In contrast to Lipton's interpretation, the diminished overshoot in our simulation can be exclusively attributed to a decline in the mitochondrial NADH pool. The extreme redox shift toward oxidation in the cytosol (one to two orders of magnitude corresponding to the increase in cytosolic pyruvate compared with normal physiologic concentration) results in a significant slower transport of reducing equivalents from the cytosol to the mitochondrial matrix by the G3P shuttle and even prompts an outward transport of redox equivalents from the mitochondrion to the cytosol by the malate–aspartate shuttle. This leads to a more oxidized mitochondrial redox potential and accounts for the shift in mitochondrial NADH fluorescence.

Figure 6.

The impact of pyruvate infusion on the NADH response. (A) At time t=500 seconds, all cells in the slice were exposed to a 1.75-fold increase in the activation function for 1,000 seconds mimicking the extra ATP consumption induced by an electrical stimulation. At the same time, the extracellular pyruvate concentration was successively increased from 0.2 to 6 mmol/L. At t=1,800 seconds, a second increase in the activation function was applied mimicking a second electrical stimulation. The relative NADH transients from different cells in the slice are depicted. (B) Cumulative concentration profile of mitochondrial NADH in the whole slice normalized to the preexcitation state. The insert shows the measured NAD(P)H fluorescence profile measured by Lipton.³⁶

Influence of Alternative Carbohydrate Substrates on the Stimulation-Induced Mitochondrial NADH Response

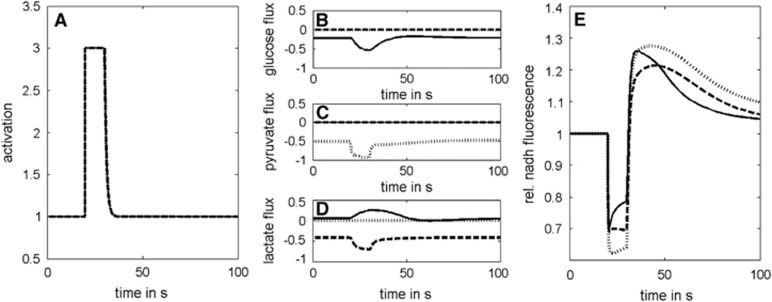
There is evidence that glucose, lactate, and pyruvate can be oxidized by neurons.^{11, 12} Here, we addressed the problem whether differences in the metabolic response of our model neuron to an energetic challenge may arise from the preferred usage of either of these possible carbohydrate substrates. To this end, we simulated metabolic changes elicited by a short energetic challenge under conditions where either glucose, lactate, or pyruvate are available as the only energy-delivering substrate and their uptake (mediated by the glucose transporter or the monocarboxylate transporter 2) is not rate limiting (Figure 7). In all three cases, the stimulation-induced changes in mitochondrial NADH produced the typical biphasic response. Dip and overshoot were more pronounced with pyruvate compared with lactate. The reason is that lactate has to be first converted to pyruvate by the reaction of lactate dehydrogenase. The additional NADH formed in this reaction can be shuttled into the mitochondrion, which alleviates the need for NADH formed by the TCA cycle or by PDHC. This not only attenuates the dip during neuronal activation but also reduces the overshoot during the postexcitation period. The additionally formed cytosolic NADH is also the reason why (at fixed energetic load) the lactate consumption is ~20% lower than the pyruvate consumption. Hence, cytosolic NADH shuttled to the mitochondria appears to play a substantial role as electron donor for the respiratory chain.

Figure 7.

The impact of the alternative carbohydrate substrates glucose, lactate, and pyruvate on the excitation-induced mitochondrial NAD(P)H response. (A) Activation function representing a stimulation-induced threefold increase in the energetic load for a time span of 10 seconds. (B, C, and D) Changes in substrate uptake fluxes with either glucose (solid lines), pyruvate (dotted lines), or lactate (dashed lines) as sole substrate. Note that with glucose as substrate, an increase in the lactate release occurs during the stimulus. (E) Response of mitochondrial NADH. The uptake rate of the three alternative carbohydrate substrates glucose, lactate, and pyruvate was not restricted in these simulations.

Glycolytic conversion of 1 mole of glucose to pyruvate as well as the conversion of 2 moles of lactate to pyruvate both yield 2 moles of NADH. However, glycolytic conversion of glucose to pyruvate yields on top 2 moles of cytosolic ATP. It is this extra production of two moles of cytosolic ATP with glucose as substrate, which slightly reliefs the ATP production by OXPHOS and thus attenuates the initial dip of NADH and intensifies the subsequent overshoot compared with the use of lactate. However, ~10% of the lactate derived from glucose is exported out of the cell.

In Vivo Application of the Model

Neuronal activity in the brain relies on sufficient supply of nutrients and oxygen in the active brain regions. This is achieved by increasing the regional blood flow in response to an increased energy demand. To show the importance of the hemodynamic response for the efficient nutrient and oxygen supply to neuronal tissue in larger distance from the supporting vessel, we used a two-dimensional tissue model (see Methods section). The blood flow rate within the capillary was put to 0.5 mm/s.³⁷ Arterial oxygen pressure (pO₂) was set to 50 mmHg. The mean oxygen concentration in the vessel (neglecting the oxygen pressure gradient along the capillary) is determined by the pO₂, blood flow rate, and rate of oxygen consumption in the tissue. The model was calibrated such that in the basal, nonactivated state the resulting oxygen pressure in the blood was ~40 mmHg. In our simulations, we assumed that the activation-dependent increase in the ATP consumption rate was the same across the whole tissue.

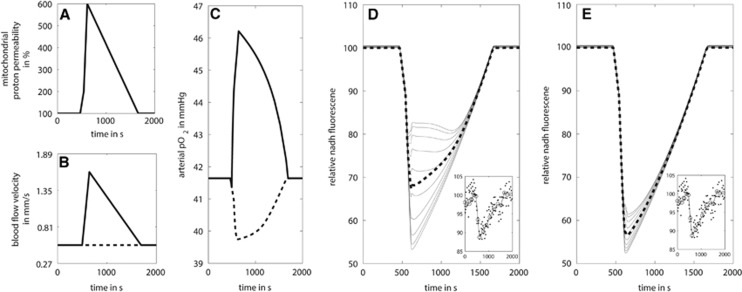
With this tissue model, we simulated an experiment by Rex et al³⁸ where the NAD(P)H fluorescence was measured after administration of the decoupling agent dinitrophenol. Dinitrophenol acts as protonophore resulting in an increase in the mitochondrial proton permeability over time and decoupling of the mitochondrial proton gradient from OXPHOS. In our simulation, the decoupling effect was modeled by a rapid increase in proton permeability to a sixfold higher value compared with the normal and subsequent decline to the original permeability within 1,000 seconds (Figure 8A). In the first simulation, we assumed that there was no change in the regional blood flow (dotted line in Figure 8B). In this case, addition of the decoupler resulted in a persistent decrease in oxygen concentration in the vessel (dotted line in Figure 8C). As a consequence, tissue regions in larger distance to the vessel run into hypoxia, i.e., oxygen pressure becomes rate limiting for the respiratory chain and this limits the respiratory NADH consumption. Therefore, with increasing distance from the vessel, the contribution of the tissue to the overall decline in NADH becomes larger (Figure 8D). In a second simulation, we included the hemodynamic response by increasing the blood flow to ~1.5 mm/s.³⁷ The simulation shows a short and weak initial decline in pO₂ followed by a pronounced increase in blood pO₂ over the baseline value, i.e., the elevated supply of oxygenated blood even overcompensates the surplus demand of the tissue (solid line in Figure 8C). Note that the shape and size of the initial decrease in plasma pO₂ (which is related to the blood-oxygen-level dependent (BOLD) effect) depend on the temporal profiles of the used load function (here decoupling of the respiratory chain; Figure 8A) and the blood flow response (Figure 8B). The transient increase in the plasma pO₂ prevents tissue regions in larger distance from the vessel to run into hypoxia and the alterations in NADH fluorescence are marginal (Figure 8E). Overall, the hemodynamic response ensures that the oxygen supply to the whole tissue remains above a threshold value that allows an adequate stimulation of ATP synthesis on an activating stimulus.

Figure 8.

The impact of blood flow response on the NADH response during dinitrophenol-induced mitochondrial uncoupling. (A) Increase in mitochondrial proton permeability over time mimicking the action of the protonophore dinitrophenol. (B) Blood flow velocity over time with (solid) and without (dashed) blood flow response. (C) Resulting arterial oxygen pressure (pO₂) in the central blood vessel with (solid) and without (dashed) blood flow response. (D) Resulting NADH transients in the tissue without blood flow response. (E) Resulting NADH transients in the tissue with blood flow response. The small inserts in D and E depict the NADH fluorescence signal observed by Rex et al.³⁸

Discussion

Strengths and Limitations of the Model

The large body of scientific work devoted to the origin and physiologic interpretation of NAD(P)H responses in cells and neuronal tissues prompted us to decipher the relative contribution of various metabolic processes to the size and shape of this signal. To this end, we developed a comprehensive kinetic model that includes central pathways of carbohydrate-fueled energy production in neuronal cells, a detailed description of ion transport processes across the inner mitochondrial membrane and the regulatory impact of free calcium on enzymatic reactions and membrane transport processes. In contrast to previous metabolic models of neuronal cells,^{39, 40, 41} the rate equations for the individual enzymatic reactions were constructed and parameterized in best possible concordance with kinetic and regulatory features reported for neuronal cells. Moreover, we put emphasis on a detailed modeling of mitochondrial energy production.^{18, 19} This is indispensable for a model-based analysis of signals that are linked to mitochondrial NADH, which is tightly coupled to the activity of the respiratory chain and the TCA cycle. All simulations were performed with the same mathematical model and recapitulated a variety of NAD(P)H responses measured in cells and brain slices under quite different experimental settings. The small differences between simulations and experiments may partially be explained by the fact that the shape of NAD(P)H responses is influenced by model parameters that have rarely been measured. For example, we assumed an instantaneous onset and termination of additional energy demand during the activation period. However, it cannot be excluded that an elevated energy demand may persist longer than the duration of the actual activating stimulus. The finding that the stimulus-induced increase in the extracellular potassium level is not only reversed during the resting phase but also even transiently falls below the initial baseline level⁴ points to an ongoing increased activity of the Na⁺-K⁺-ATPase. Another critical point is the lacking knowledge of the actual shape of activation-induced cytosolic and mitochondrial calcium transients. Hence, except for the simulations where experimental data could be used as model input (Figure 2), we were forced to make plausible guesses on the temporary profile of the cytosolic calcium transient.

A possible share of NADPH in the observed autofluorescence of the total cellular NAD(P)H pool has been discussed by Mayevsky and Chance⁴² and Shuttleworth.⁴³ These authors arrived at the conclusion that the contribution of NADPH should be small as this pyridine nucleotide is not involved in electron transfer to the respiratory chain, the main driver of changes in the mitochondrial redox state. It has been reported that oxidative stress increases the flux through the oxidative pentose phosphate pathway in a concentration-dependent manner.⁴⁴ Hence, sudden onset of oxidative stress should result in significant changes in cytosolic NADPH because the regulatory enzyme of the pentose phosphate pathway, the glucose-6-phosphate dehydrogenase (G6PD), responds immediately to changes in cytosolic NADP/NADPH. Whether such changes in cytosolic NADP could be monitored is not certain given the weak fluorescence signal of this moiety.

The first model-based interpretation of NAD(P)H fluorescence transients in neurons and astrocytes was provided by Aubert et al.⁴⁵ In these simplistic models, whole metabolic pathways were lumped into single overall reactions to illustrate the metabolic basis linking changes in the cellular energy demand to changes in cellular NADH levels. However, the proclaimed purpose of these models to serve as a computational framework for the interpretation of NADH transients elicited by various stimuli in vivo or in vitro fell short because essential factors have not been included: differential changes in the redox state in the cytosol and mitochondrion, and their coupling through shuttle systems; the central pathways of mitochondrial energy metabolism (TCA cycle including its regulation by calcium, the respiratory chain, and OXPHOS); and the kinetic properties of tissue-specific isoforms of metabolic enzymes and their allosteric regulation. All these missing details have been included in our model, which thus can be rightly stated to serve as a general modeling framework for in silico studies of the energy metabolism of neuronal cells and tissues.

Factors Influencing the NAD(P)H Response

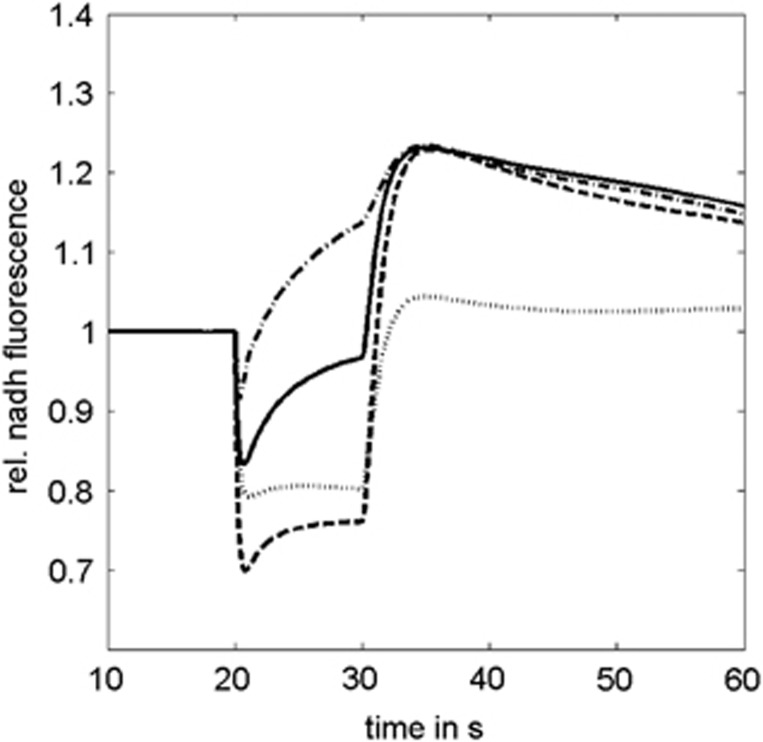
The results of our model simulations are summarized in Figure 9. A dip of mitochondrial NADH after onset of the stimulus indicates that consumption of the reduced nucleotide by the respiratory chain outweighs its reproduction by the dehydrogenases of the TCA cycle and import of cytosolic NADH. The size of the dip correlates with strength and abruptness of the energetic challenge associated with the stimulus (Figure 4). A rapid accumulation of calcium in the mitochondria attenuates the dip and causes a partial recovery of NADH fluorescence already during stimulation. Conversely, weak Ca²⁺ stimulation of the TCA cycle dehydrogenases increases the dip size and decreases the size of the overshoot. In principle, an overshoot of NADH might also occur if the use of ATP in the cell after cessation of the stimulus is lower than before stimulation, whereas the capacity of the TCA cycle has already returned to the normal level. However, the necessity to restore ion gradients, to pump calcium out of the mitochondria, and to replenish the short-term energy store, creatine phosphate renders such a scenario highly improbable.

Figure 9.

Effect of various metabolic processes on the shape of the excitation-induced mitochondrial NAD(P)H response. Solid line: typical NAD(P)H response (reference case). Dashed line: higher energetic load. Dotted line: weak Ca²⁺ stimulation of the tricarboxylic acid cycle dehydrogenases. Dash-dotted line: hypoxia during stimulation.

An overshoot of mitochondrial NADH fluorescence indicates that its production by dehydrogenases of the TCA cycle and its transfer from the cytosol by the malate–aspartate shuttle outweighs NADH oxidation by the respiratory chain. Two entirely different metabolic situations may account for such a scenario. The long-lasting overshoot commonly observed after neuronal activation may be due to an ongoing activation of the dehydrogenases of the TCA cycle: the more calcium enters the mitochondria during activation, the higher and longer the NADH overshoot. Alternatively, a stimulation-induced decrease in mitochondrial oxygen below the affinity of complex IV of the respiratory chain for oxygen may result in a transient hypoxic metabolic state where the NADH oxidation rate becomes lower than the rate of NAD⁺ reduction by the TCA cycle. In this case, the dip is shorter because the rise of NADH already starts during neuronal activation.

A low uptake rate of calcium into the mitochondria during the neuronal activation⁴⁶ may completely abolish the overshoot of the NAD(P)H response. However, a strong overshoot may solely result from a massive calcium uptake into the mitochondria without a notable increase in the energetic load. Mitochondria from one cell fulfill different functions depending on their relative spatial position with regard to the plasma membrane: they either serve primarily as calcium buffer or as the main producer of ATP.⁴⁷ Thus, it seems not unlikely that Ca²⁺ activated but energetically ‘passive' mitochondria may massively contribute to a large NADH overshoot.

Biphasic Versus Monophasic NADH Responses

Several experiments have reported monophasic NAD(P)H responses that may lack either the dip⁵ or the overshoot.⁴⁸ As discussed above, the absence of the overshoot should indicate a lacking or very weak Ca²⁺ stimulation of the TCA cycle. This may have several reasons: first, depletion of Ca²⁺ in the extracellular space diminishes its uptake into the cytosol and thus into mitochondria (Figure 9, dotted line). Second, if neurons have already experienced a longer activation period the accompanying increase in mitochondrial Ca²⁺ may have reached saturating levels with regard to the Ca²⁺-sensitive dehydrogenases of the TCA cycle. Third, impairment of key regulatory enzymes of the TCA cycle may prevent a Ca²⁺-dependent increase in the TCA cycle flux.¹⁸ In particular, KGDHC was shown to be susceptible to impairment by ROS. Elevated ROS formation is one of the major deleterious events in the epileptic brain.⁴⁹ Hence, ROS-mediated impairment of TCA cycle enzymes might account for the small NADH overshoot in acute hippocampal slices from epileptic rats and humans.⁴⁸

FAD Responses

Our model simulations confirmed the view that the NADH fluorescence transient is mirrored by the FAD fluorescence transient. Contrary to the NADH pool, FAD is a bound prosthetic group associated with specific metabolic enzymes. Although the final acceptor of the electrons from the bound FAD moieties is different among the various FAD-containing enzymes, the shape of the FAD transient is similar. This is a consequence of the similarity in the reduction state of ubiquinol and NADH as both moieties are coupled through complex 1 of the respiratory chain. A decoupling of the NADH and FAD signals might occur if the majority of reducing equivalents were to enter the respiratory chain at complex 2 or via the G3P shuttle. However, this is not the case under physiologic conditions as the first three complexes of the respiratory chain operate near equilibrium, while the irreversible step associated with a large decrease in enthalpy occurs in complex IV.⁵⁰ Furthermore, it was shown that under normal conditions the malate–aspartate shuttle is more important than the G3P shuttle in transporting reducing equivalents from the cytosol to the mitochondrion.⁵¹

Astrocytic Versus Neuronal NADH Responses

Besides neuronal cells, astrocytes comprise a major fraction of brain tissue. In contrast to neurons, it is estimated that around one third of the ATP used in astrocytes in their basal state is derived from the glycolytic pathway.⁵² To investigate potential differences in NADH transients between these two cell types, we set up a generic astrocyte model by increasing the pathway capacity of glycolysis threefold and decreasing the capacity of OXPHOS to 60%. With these changes, 34% of the total ATP in the basal reference state is generated by the glycolytic pathway. With identical energetic challenge and cytosolic calcium transients, the ‘astrocytic' NADH response is very similar to the ‘neuronal' NADH response (see Supplementary Figure S2). The relative increase in cytosolic NADH is higher in the neuron than in the astrocyte because of the lower basal NADH level, but the overall NADH response would be very similar. This is in agreement with experiments,³¹ where a biphasic response of a pure astrocyte culture in response to an energetic stimulus elicited by neurotransmitter uptake was observed. However, the in vivo response between adjacent neurons and astrocytes might be very different (as reported by Kasischke et al),⁵ since the metabolic responses (ATP demand and calcium transients) might be profoundly different in the two cell types. Although neuronal calcium transients arise to a large part from voltage-gated channels and are directly coupled to increased energy demand, the origin of astrocytic cytosolic calcium is much more heterogeneous arising from extracellular signaling via ATP or neurotransmitters, gap junctions, cell–cell contacts, and others.⁵³ Therefore, the strict coupling of calcium entry into mitochondria to the increase of energy demand may not be present in astrocytes. To clarify this point, simultaneous measurements of oxygen consumption rates and calcium transients in astrocytes or astrocyte cultures are needed to unambiguously interpret the molecular origin of astrocytic NADH transients.

Predictive Value of the NAD(P)H Responses

The simulations using the brain slice model (Figure 5) revealed that under conditions of an insufficient tissue oxygenation the observed integral NAD(P)H fluorescence signal is composed of quite different contributions of the various cells depending on their individual oxygen supply. Moreover, tissue samples comprise different types of neuronal cells differing in their calcium dynamics and expression levels of energy-producing pathways. These aspects hamper the unambiguous interpretation of this signal in terms of metabolic changes. Despite the ambiguity of metabolic changes underlying the observed size and shape of the stimulation-induced NADH responses monitored in a specific brain region, we propose from our simulations at least the following two rules: (1) if a significant increase in mitochondrial NADH occurs during the stimulation it is likely that a hypoxic metabolic state was either present before the stimulus or was reached during the time course of stimulation. Such a characteristics was indeed persistently observed in a recent study that used two-photon fluorescence lifetime microscopy to image the cerebral energy metabolism in vivo.⁵⁴ (2) Monitoring NADH fluorescence in one brain region at varying strength of the stimulus, variations in the size of the initial dip should correlate with the strength of the additional energetic load associated with the stimulus.

The model was also used to show the importance of an increased regional blood flow in response to an increased energy demand. In the simulated in vivo experiments, mitochondrial uncoupling by dinitrophenol leads to a partial breakdown of the proton gradient across the inner mitochondrial membrane. Respiratory activity increases to compensate for this extra drainage of the proton gradient. Increased respiratory activity leads to increased utilization of mitochondrial NADH, resulting in a decreased NADH reduction state. The extent of this reduction depends on sufficient supply of oxygen to the affected brain region. If this is ensured by local increase in regional blood, the decrease in NADH concentration is nearly homogenous. If, however, the blood flow response is absent (or insufficient) local hypoxia results in heterogeneous NADH consumption and NADH concentrations are higher in regions further away from the supplying blood vessel (Figure 8). An increase in NADH fluorescence with increased distance from the blood vessel during different degrees of hypoxia has been observed by Baraghis et al.⁵⁵

Conclusion and Outlook

Kinetic modeling is a powerful integrative method for the simulation of the dynamic behavior of complex systems whose molecular components have been characterized in isolation. One major objective of the model is to test whether our current understanding of the molecular interactions is consistent with the observable behavior of the system. To meet this goal the model simulations must be performed in an unbiased manner, e.g., strictly avoiding a simple fitting of simulation results to experimental data. Adopting this rule, we constructed a kinetic model, which recapitulates a wide range of experimental findings on temporal characteristics of the NAD(P)H responses. We conclude that our model indeed captures correctly central features of the energy metabolism of neurons. The model may thus represent a convenient starting point for further investigations on the energy metabolism of various neuronal cells differing in a range of properties. In future, some extensions of the model will be necessary, e.g., inclusion of glycogen synthesis and degradation, coupling of the TCA cycle with the synthesis of neurotransmitters, or the salvage of adenine nucleotides. It is our conviction that only such an often disparagingly termed ‘reductionist' modeling approach is able to meet the requirements challenged by the high level of experimentation in the field of neurobiologic research.

The authors declare no conflict of interest.