Significance
Brain–computer interface (BCI) technology provides a new communication channel. However, current applications have been severely limited by low communication speed. This study reports a noninvasive brain speller that achieved a multifold increase in information transfer rate compared with other existing systems. Based on extremely precise coding of frequency and phase in single-trial steady-state visual evoked potentials, this study developed a new joint frequency-phase modulation method and a user-specific decoding algorithm to implement synchronous modulation and demodulation of electroencephalograms. The resulting speller obtained high spelling rates up to 60 characters (∼12 words) per minute. The proposed methodological framework of high-speed BCI can lead to numerous applications in both patients with motor disabilities and healthy people.
Keywords: brain–computer interface, electroencephalogram, steady-state visual evoked potentials, joint frequency-phase modulation
Abstract
The past 20 years have witnessed unprecedented progress in brain–computer interfaces (BCIs). However, low communication rates remain key obstacles to BCI-based communication in humans. This study presents an electroencephalogram-based BCI speller that can achieve information transfer rates (ITRs) up to 5.32 bits per second, the highest ITRs reported in BCI spellers using either noninvasive or invasive methods. Based on extremely high consistency of frequency and phase observed between visual flickering signals and the elicited single-trial steady-state visual evoked potentials, this study developed a synchronous modulation and demodulation paradigm to implement the speller. Specifically, this study proposed a new joint frequency-phase modulation method to tag 40 characters with 0.5-s-long flickering signals and developed a user-specific target identification algorithm using individual calibration data. The speller achieved high ITRs in online spelling tasks. This study demonstrates that BCIs can provide a truly naturalistic high-speed communication channel using noninvasively recorded brain activities.
Brain–computer interfaces (BCIs), which can provide a new communication channel to humans, have received increasing attention in recent years (1, 2). Among various applications, BCI spellers (3–9) are especially valuable because they can help patients with severe motor disabilities (e.g., amyotrophic lateral sclerosis, stroke, and spinal cord injury) communicate with other people. Currently, electroencephalogram (EEG) is the most popular method of implementing BCI spellers due to its noninvasiveness, simple operation, and relatively low cost. However, low signal-to-noise ratio (SNR) of the scalp-recorded EEG signals and lack of computationally efficient solutions in EEG modeling limit the information transfer rates (ITRs) of EEG-based BCI spellers to ∼1.0 bits per second (bps) (1, 4). For example, the well-known P300 speller proposed by Farwell and Donchin (5) can spell up to five letters per minute (∼0.5 bps). Until recently few studies using visual evoked potentials (VEPs) demonstrated higher ITRs of 1.7–2.4 bps (6, 7). In contrast, the invasive BCI spellers in humans and monkeys show higher performance. For example, the P300 speller with electrocorticogram recordings obtained a peak ITR of 1.9 bps in a human subject (8). A recent monkey study on keyboard neural prosthesis using multineuron recordings reported an ITR up to 3.5 bps (9). Although communication speed of the EEG-based spellers has been significantly improved in the past decade (4), it still remains a key obstacle to real-life applications in humans.
Recently, the BCI speller using steady-state VEPs (SSVEPs) has attracted increasing attention due to its high communication rate and little user training (4, 10, 11). An SSVEP speller typically uses SSVEPs to detect the user’s gaze direction to a target character (10). Although the SSVEP speller has achieved relatively high ITRs (e.g., 1.7 bps in ref. 6), the ultimate performance limit still remains unknown. In principle, the theoretical performance limit of the SSVEP speller highly depends on temporal coding precision in the visual pathway, which can be reflected by visual latency in SSVEPs [i.e., apparent latency (12)]. Previous studies show that grand-average SSVEPs can accurately encode the frequency and phase of the stimulation signals, showing a constant latency across different stimulation frequencies (12). However, visual latencies in single-trial SSVEPs, especially when the stimulation duration is short (e.g., 0.5 s), are generally difficult to quantify due to the interference from spontaneous EEG activities. Here we hypothesize that the visual latency of single-trial SSVEPs, which represent activities of neuronal populations over the stimulation time, can be very stable across trials. If this is true, frequency and phase of the stimulation signals can be precisely encoded in single-trial SSVEPs. Much better performance can be expected in the SSVEP speller using a synchronous modulation and demodulation paradigm, which has been widely used in telecommunications (13).
The goal of this study is to implement a high-speed BCI speller using SSVEPs. Based on the assumption of a stable visual latency in single-trial SSVEPs, this study proposed a new joint frequency-phase modulation (JFPM) method to enhance the discriminability between SSVEPs with a very narrow frequency range, the most challenging conditions in frequency coding (10). To address the difficulty in parameter selection due to nonlinearity [i.e., SSVEP harmonics (14)], a data-driven grid-search method was developed to optimize stimulation duration and phase interval in the JFPM method. Considering individual difference of visual latency in target identification, this study adopted an improved user-specific decoding algorithm that incorporated individual SSVEP calibration data in feature extraction. In addition, a filter bank analysis method was developed to extract additional features from the harmonic SSVEP components. Together, these methods resulted in a high-speed BCI speller (up to 60 characters per minute) in multiple online spelling tasks. The methodological framework of the proposed high-speed BCI technology will potentially lead to a truly practical and naturalistic high-speed communication channel for patients with motor disabilities and healthy people.
Results
Spelling with an SSVEP-Based BCI.
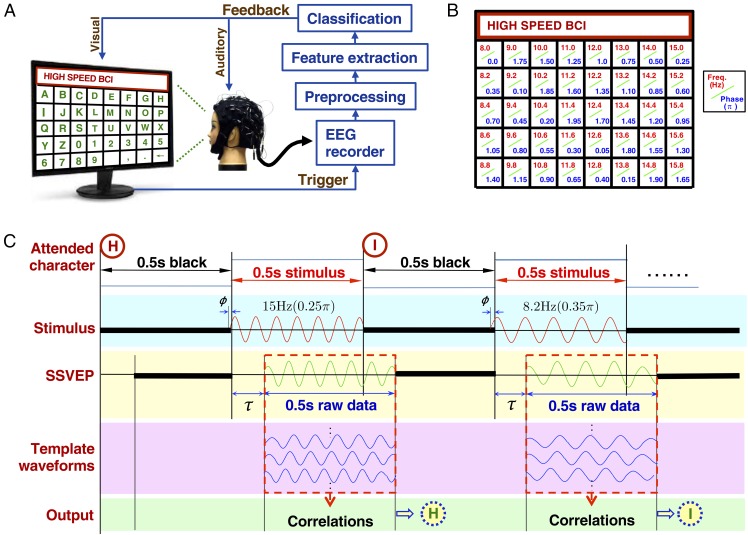
The closed-loop BCI speller consists of three major components: a 5 × 8 stimulation matrix resembling an alphanumerical keyboard, an EEG recording device, and a real-time program for target identification and feedback presentation (Fig. 1A). The system determines the user-attended target by analyzing the elicited SSVEPs, which encode the frequency and phase information of the target stimulus. The 40 characters in the stimulation matrix are tagged with different flickering frequencies and phases (Fig. 1B), which are determined by the joint JFPM method (discussed in detail below). Fig. 1C shows the procedures of spelling two example characters, “H” and “I,” consecutively with the system. For each target, the 0.5-s SSVEP epoch time-locked to the stimulus (with a visual latency ) is extracted for target identification with the SSVEP template-based decoding algorithm (see details in Materials and Methods). With this configuration, the BCI speller has a spelling rate of 60 characters per minute, which corresponds to an ITR up to 5.32 bps.
Fig. 1.
Closed-loop system design of the SSVEP-based BCI speller. (A) System diagram of the BCI speller, which consists of four main procedures: visual stimulation, EEG recording, real-time data processing, and feedback presentation. The 5 × 8 stimulation matrix includes the 26 letters of the English alphabet, 10 numbers, and 4 symbols (i.e., space, comma, period, and backspace). Real-time data analysis recognizes the attended target character through preprocessing, feature extraction, and classification. The image of the stimulation matrix was only for illustration. Parameters of the stimulation matrix can be found in Materials and Methods. (B) Frequency and phase values used for encoding each character in the stimulation matrix. These values are determined by the joint frequency-phase modulation method (Eq. 4). The frequencies range from 8.0 to 15.8 Hz with an interval of 0.2 Hz. The phase interval between two neighboring frequencies is 0.35π. (C) Examples of spelling characters “H” (15.0 Hz, 0.25π) and “I” (8.2 Hz, 0.35π) with the BCI speller. An intertrial interval of 0.5 s is used for directing gaze to a target before the stimulation matrix starts to flash for 0.5 s. The 0.5-s-long EEG epoch with a delay of (∼140 ms) to the stimulation is extracted for target identification. The target character can be determined by the decoding algorithm based on the correlations between the single-trial SSVEP and individual SSVEP templates (details are given in Materials and Methods).
Stimulation Signal and Elicited SSVEPs.
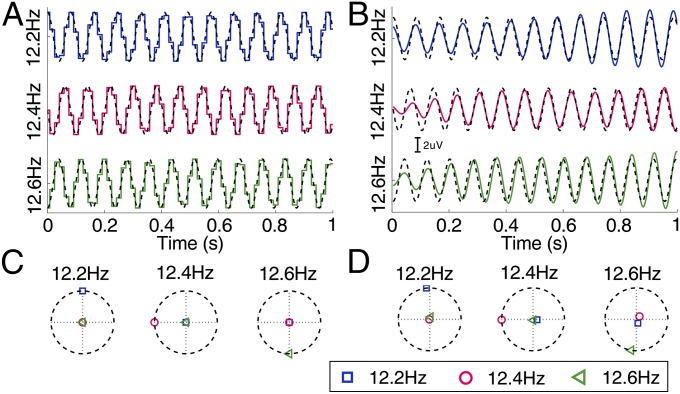
In this study, the 40 stimulation signals are generated by a sampled sinusoidal stimulation method based on the monitor’s refresh rate (6). Fig. 2 A and B show waveforms of the first 1-s stimulation signals and averaged SSVEPs (the fundamental component) at three selected frequencies (12.2, 12.4, and 12.6 Hz) from an example subject. In time domain, the real stimulation signals and SSVEPs are both precisely synchronized to the theoretical stimulation signals. Fig. 2 C and D illustrate the complex spectra of the stimulation signals and elicited SSVEPs. As shown in Fig. 2C, the angle of the stimulation signal in the complex spectra was exactly the same as the initial phase of each sinusoidal stimulation signal (12.2 Hz: 0.5π, 12.4 Hz: π, and 12.6 Hz: 1.5π). The estimated phase of SSVEPs was highly consistent with the phase of the stimulation signal (12.2 Hz: 0.53π, 12.4 Hz: 1.00π, and 12.6 Hz: 1.45π; Fig. 2D). These results proved the robustness of the sampled sinusoidal stimulation method in generating stimulation signals for both frequency and phase modulation of SSVEPs. Furthermore, the SSVEPs show nearly constant latencies across different frequencies, which is consistent with a previous study (15). The detection of SSVEPs can therefore be implemented using a synchronous demodulation method.
Fig. 2.
Examples of stimulation signals and elicited SSVEPs at 12.2, 12.4, and 12.6 Hz. (A) Temporal waveforms of stimulation signals (solid lines) using the sampled sinusoidal stimulation method (6) based on the monitor’s refresh rate (60 Hz). The dynamic range of the stimulation signal is from 0 to 1, where 0 represents dark and 1 represents the highest luminance. The initial phases of the three frequencies are 0.5π, π, and 1.5π, respectively. The dashed lines indicate the theoretical sinusoidal stimulation signals. (B) Temporal waveforms of average SSVEPs (solid lines) at electrode O1 from one sample subject after applying a time delay of 128 ms to the theoretical stimulation signals (dashed lines). The maximal amplitude of the stimulation signals was set to 3 μV for illustration. A band-pass filter of [11.5 Hz 13.5 Hz] was applied to only retain the fundamental frequency component of the SSVEP signals. The stimulation duration was 5 s in the offline experiment (Materials and Methods). Only the first second of the stimulation signals and SSVEPs is shown in A and B. (C) Complex spectral values for real stimulation signals at the three stimulation frequencies. (D) Complex spectral values for averaged SSVEPs. In each subfigure in C and D, horizontal and vertical axes (dotted lines) indicate the real and imaginary parts of the complex spectral data at each specified frequency (12.2, 12.4, and 12.6 Hz, respectively). Dashed circles indicate spectral values with the maximal amplitude at the specified frequency. The whole 5-s segment was used for calculating the complex spectrum.
Fundamental and Harmonic Components of SSVEPs.
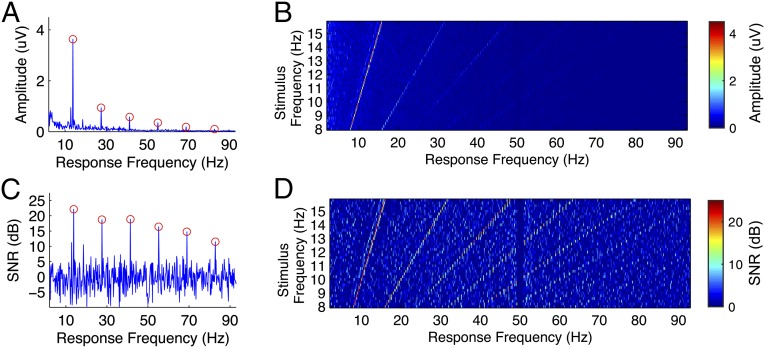
SSVEPs can be characterized by sinusoidal-like waveforms at the stimulation frequency and its harmonic frequencies (12). The advantage of combining harmonic components in frequency detection has been demonstrated in previous BCI studies (10, 16). However, a detailed analysis on the SNR of SSVEP harmonics is still missing in BCI studies. As shown in Fig. 3A, for an example subject, the fundamental component showed the highest amplitude in the mean amplitude spectrum of SSVEPs at 13.8 Hz. The amplitude of SSVEP components showed a sharp decrease as the response frequency increased (fundamental: 3.63 μV, second harmonic: 0.94 μV, third harmonic: 0.57 μV, fourth harmonic: 0.34 μV, fifth harmonic: 0.18 μV, and sixth harmonic: 0.09 μV). Because the amplitude of background EEG activities also decreased as the frequency increased, the harmonics showed a much slower decline of SNRs, compared with the amplitude. As shown in Fig. 3C, the SNRs of SSVEP components decreased slowly and steadily as the response frequency increased (fundamental: 22.11 dB, second harmonic: 18.70 dB, third harmonic: 18.89 dB, fourth harmonic: 16.37 dB, fifth harmonic: 14.74 dB, and sixth harmonic: 11.48 dB). Fig. 3 B and D show the amplitude and SNR images for all stimulation frequencies (8–15.8 Hz) as functions of stimulation frequency and response frequency. For all of the 40 stimulation frequencies, the fundamental and harmonic frequencies of SSVEPs are exactly the same as those of the stimulation signals. The SSVEP harmonics at frequencies up to 90 Hz are clearly visible in the SNR image. This study thus adopted a filter bank analysis method (17) to extract frequency and phase information from both the fundamental and harmonic SSVEP components (details are given in Materials and Methods).
Fig. 3.
Amplitude spectra and SNRs of fundamental and harmonic SSVEP components. Averaged amplitude spectrum of SSVEPs at (A) 13.8 Hz and (B) all stimulation frequencies (8–15.8 Hz) for an example subject (S12). For each stimulation frequency, six trials were first averaged for improving the SNR of SSVEPs. The amplitude spectrum was calculated by fast Fourier transform. The amplitude of spectrum was the mean of all nine channels. Averaged SNR (in decibels) of SSVEPs at (C) 13.8 Hz and (D) all stimulation frequencies (8–15.8 Hz). SNR was defined as the ratio of SSVEP amplitude to the mean value of the 10 neighboring frequencies (i.e., five frequencies on each side). SNR was calculated using the mean amplitude spectrum from A and B. The circles in A and C indicate the fundamental and harmonic frequencies of 13.8 Hz (i.e., 13.8, 27.6, 41.4, 55.2, 69, and 82.8 Hz). In B and D, amplitude spectra and SNRs were depicted as functions of stimulation frequency and response frequency. The frequency interval in the images was 0.2 Hz. The sudden drop at 50 Hz was caused by the notch filter used for removing power line noise in data recording.
JFPM.
To realize a large number of targets, the frequency coding method in SSVEP-based BCIs typically encodes multiple targets with equally spaced frequencies (18):
| [1] |
where is the lowest frequency, is the frequency interval, n is the index of the target, and N is the total number of targets. According to communication technology, to facilitate the detection of frequency-coded targets, a data length of is required so that all stimulation signals are orthogonal to each other (13). Therefore, to implement a frequency-coded system with a large number of targets, the orthogonality generally requires a long data length. For example, the 40-target speller developed in the study requires a data length of 5 s () to meet the orthogonality condition. However, toward a high ITR, a high-speed BCI speller can only use a short data length (e.g., 0.5 s) for each target. In this case, the interference from the spontaneous background EEG activities makes it very difficult to recognize SSVEPs with the existing frequency-detection methods (10).
In Eq. 1, the phase information is ignored in target coding, and therefore does not provide useful information for frequency detection. This study proposed to incorporate phase coding into frequency coding to realize a JFPM paradigm. Specifically, equally spaced phases are introduced to enhance the differentiation between frequency-coded targets:
| [2] |
where is the initial phase of the target at and is the phase interval between two adjacent frequencies. For a data length less than , an optimal phase interval can maximize the differentiation between SSVEP waveforms at the adjacent frequencies and thereby facilitate target identification. In practice, this study aimed to minimize the correlation coefficient between SSVEPs at the adjacent frequencies (i.e., toward a negative correlation value of −1).
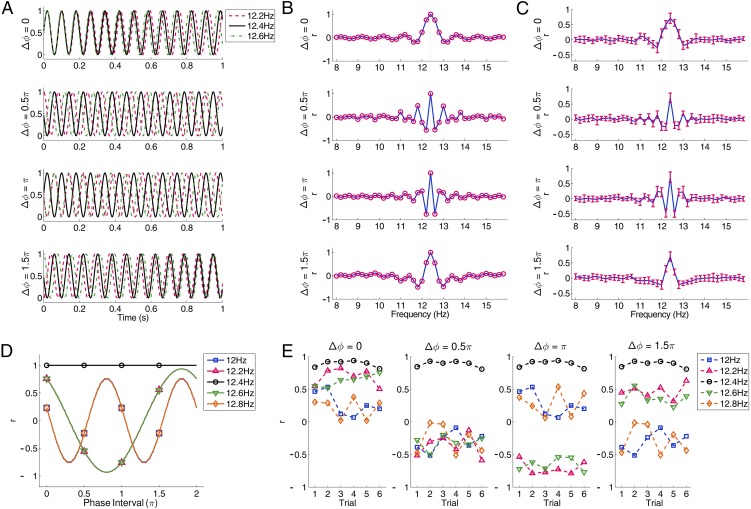
Fig. 4A illustrates temporal waveforms of the theoretical 1-s stimulation signals at 12.2, 12.4, and 12.6 Hz using four different phase interval values (0, 0.5π, π, and 1.5π). Fig. 4B shows correlation coefficients of the stimulation signals between 12.4 Hz and all 40 stimulation frequencies. The four phase interval values result in very different correlation patterns across all stimulation frequencies. The correlation coefficients between 12.4 Hz and its nearest neighbors (12.2 and 12.6 Hz) differ largely with different phase interval values (0: 0.75 and 0.75, 0.5π: −0.55 and −0.54, π: −0.75 and −0.75, and 1.5π: 0.55 and 0.54). These results suggest that the discriminability of SSVEPs can be significantly improved by introducing an appropriate phase interval value (e.g., 0.5π or π) into the stimulation signals. The phase interval of 0.5π also resulted in negative correlation values at the second-nearest neighboring frequencies (12.0 Hz: −0.22 and 12.8 Hz: −0.22). In contrast, positive correlations are obtained at the second-nearest neighboring frequencies (12.0 Hz: 0.22 and 12.8 Hz: 0.22) when the phase interval value is π. In practice, the optimal phase interval value can be determined through maximizing the BCI performance in an offline analysis (the grid-search method, discussed below). Fig. 4C shows the mean correlation values between 1-s single-trial SSVEPs at 12.4 Hz and SSVEP template signals (i.e., the average of multiple SSVEP trials from a training set; details are given in Materials and Methods) at all stimulation frequencies across subjects. The correlation coefficient was calculated with the projection of nine-channel SSVEPs using canonical correlation analysis (CCA) (details are given in Materials and Methods). The patterns of correlation values using SSVEP template signals are highly consistent with those of the stimulation signals (Fig. 4B). For example, when using a phase interval value of π, a maximum correlation value was obtained at the target frequency (12.4 Hz: 0.70). Negative and positive correlation values were obtained at the first- and second-nearest neighbors, respectively (12.2 Hz: −0.48, 12.6 Hz: −0.50, 12.0 Hz: 0.21, and 12.8 Hz: 0.21). This finding applies to single-trial SSVEPs for each individual. The correlation values of single-trial SSVEPs from one sample subject (Fig. 4E) are highly consistent with the theoretical patterns calculated from the stimulation signals (Fig. 4D).
Fig. 4.
JFPM. (A) Temporal waveforms of 1-s sinusoidal stimulation signals at 12.2, 12.4, and 12.6 Hz corresponding to four different phase interval values (0, 0.5π, π, and 1.5π). (B) Correlation coefficients between the 12.4-Hz stimulation signal and the stimulation signals at all stimulation frequencies (8–15.8 Hz with an interval of 0.2 Hz, marked by circles). The dotted lines indicate the stimulation frequency at 12.4 Hz. (C) Mean correlation coefficient between the resulting 1-s-long SSVEPs at 12.4 Hz and SSVEP template signals at all stimulation frequencies across trials and subjects. Correlation coefficient was calculated with the projection of nine-channel SSVEPs using CCA-based spatial filtering. The error bars indicate SDs across subjects. (D) Correlation coefficients between the stimulation signal at 12.4 Hz and the frequencies from 12 to 12.8 Hz (i.e., 12.4 Hz and four neighboring frequencies). Phase interval values range from 0 to 2π. The markers indicate the phase interval values at 0, 0.5π, π, and 1.5π. Note that the two curves corresponding to the same frequency distance to 12.4 Hz on both sides (12.2 and 12.6 Hz, 12 and 12.8 Hz) coincide with each other. (E) Correlation coefficients between single-trial SSVEPs at 12.4 Hz and SSVEP template signals from 12 to 12.8 Hz for one sample subject with four phase interval values (0, 0.5π, π, and 1.5π). The dataset included six trials. The SSVEP template signals were calculated using a leave-one-out method. The method to generate the data epochs with different phase interval values can be found in Materials and Methods.
Optimization of Phase Interval and Stimulation Duration.
The optimization of parameters in the JFPM method should consider the joint contribution from the fundamental and harmonic SSVEP components. However, the nonlinear modulations of SSVEP amplitudes and SNRs pose challenges in finding the theoretically optimal parameters based on the stimulation signals. To address this problem, this study developed a practical grid-search approach to determine phase interval and stimulation duration for optimizing BCI performance. The same target identification method used in the online system (details are given in Materials and Methods) was used to estimate the BCI performance (i.e., accuracy and ITR). To simulate SSVEP data corresponding to different stimulation parameters (i.e., phase interval value and data length), data epochs were extracted from the 5-s offline data epochs by adding different time shifts determined by frequency and phase (details are given in Materials and Methods).
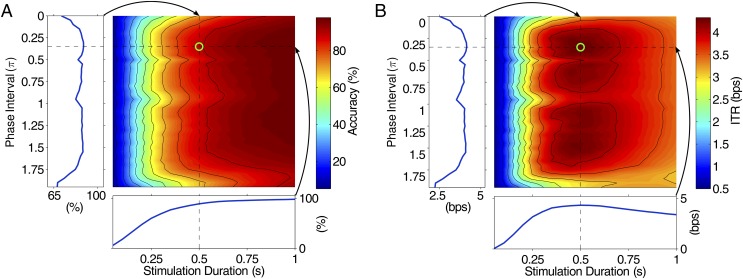
Fig. 5A shows the classification accuracy corresponding to different phase intervals and stimulation durations. The corresponding ITRs are shown in Fig. 5B. The maximal ITR (4.32 bps) was reached by a stimulation duration of 0.5 s and a phase interval of 0.35π. For a given data length of 0.5 s, the accuracy and ITR were highly related to the phase interval values (subplots along the left side in Fig. 5 A and B). For example, the phase interval of 0.35π significantly improved the classification accuracy compared with the phase interval of 0 (88.92% vs. 71.04%, paired t test: P < 10−5). For a given phase interval value of 0.35π, the accuracy increased when stimulation duration (i.e., data length) increased. The ITR increased to a peak value at 0.5 s and then decreased. These results suggest that a 0.5-s stimulation duration and a 0.35π phase interval value in the JFPM method can lead to high ITRs in a high-speed BCI speller. These parameters were therefore adopted in the online BCI speller.
Fig. 5.
Grid parameter search for optimizing phase interval and stimulation duration. (A) Group-averaged classification accuracy (percent) and (B) ITR (bps) as functions of stimulation duration and phase interval. The classification results were obtained from the offline simulation (six blocks, leave-one-out analysis) with the decoding algorithm used in the online system. The stimulation durations range from 0.05 to 1 s with a step of 0.05 s. The phase interval values range from 0 to 1.95π with a step of 0.05π. The contours in A indicate accuracies from 10 to 90% with a step of 10%. The contours in B indicate ITRs from 0.5 to 4.0 bps with a step of 0.5 bps. The green circle indicates the location with a maximal ITR (ITR: 4.32 bps; accuracy: 88.92%; stimulation duration: 0.5 s; phase interval: 0.35π). Accuracy and ITR corresponding to the 0.5 s stimulation duration and the 0.35π phase interval (indicated by the arrows) were plotted separately in A and B.
Online Spelling Performance.
This study tested the BCI speller using two online spelling tasks (i.e., cued-spelling and free-spelling tasks; details are given in Materials and Methods). Table 1 lists the accuracy and ITR for all subjects in the cued-spelling tasks where the system spelled at a speed of 1 s per character. The average accuracy in the testing session was 91.04 ± 6.73%, resulting in an ITR of 4.45 ± 0.58 bps across all subjects. Across individuals, the minimal and maximal ITR was 3.33 bps (S4) and 5.25 bps (S11) respectively. Paired t tests indicated that there was no significant difference in accuracy and ITR between the training stage and the testing stage (accuracy: 89.76% vs. 91.04%, P = 0.27; ITR: 4.35 bps vs. 4.45 bps, P = 0.31). The online accuracy and ITR were slightly higher than those obtained in the offline experiments (accuracy: 88.92%, ITR: 4.32 bps; Fig. 5). The increase of BCI performance in the online experiment could be explained in part by the increase of the number of training trials (12 trials vs. 5 trials).
Table 1.
Classification accuracy and ITR in the cued-spelling tasks
| Subject | Accuracy, % | ITR, bps | ||
| Training | Testing | Training | Testing | |
| S1 | 97.71 | 98.00 | 5.04 | 5.07 |
| S2 | 92.71 | 87.00 | 4.56 | 4.08 |
| S3 | 97.50 | 95.50 | 5.02 | 4.82 |
| S4 | 77.08 | 77.00 | 3.33 | 3.33 |
| S5 | 89.58 | 89.50 | 4.29 | 4.28 |
| S6 | 86.88 | 95.00 | 4.06 | 4.77 |
| S7 | 88.33 | 91.50 | 4.19 | 4.45 |
| S8 | 86.04 | 87.50 | 4.00 | 4.12 |
| S9 | 99.38 | 98.50 | 5.23 | 5.13 |
| S10 | 83.33 | 90.00 | 3.79 | 4.32 |
| S11 | 99.58 | 99.50 | 5.26 | 5.25 |
| S12 | 78.96 | 83.50 | 3.47 | 3.80 |
| Mean ± SD | 89.76 ± 7.77 | 91.04 ± 6.73 | 4.35 ± 0.67 | 4.45 ± 0.58 |
Each trial lasted 1 s including 0.5 s for stimulation and 0.5 s for gaze shifting. The training and testing data consisted of 12 blocks and 5 blocks (40 trials each), respectively. Results of the training data were estimated using a leave-one-out paradigm.
Table 2 illustrates the results of the free-spelling tasks. After some practice sessions (∼1 h) for familiarizing with the speller layout, all subjects successfully completed the free-spelling tasks. Eleven subjects completed the tasks without errors. One subject (S8) made seven errors and cleared the errors using “backspace.” For subjects S2 and S4, the stimulation duration was increased to 1 s to improve the accuracy. For three subjects (S5, S8, and S10), a 1-s gaze-shifting time was used due to the difficulty in fast gaze switching reported by these subjects. The mean spelling rate was 50.83 ± 11.64 characters per minute (cpm), leading to an ITR of 4.50 ± 1.03 bps (range: 2.66–5.32 bps) across all subjects. There was no significant difference of ITRs between the cued-spelling and free-spelling tasks (4.45 bps vs. 4.50 bps, paired t test: P = 0.81).
Table 2.
Results of the free-spelling tasks
| Subject | Trial length, s | Total no. of trials (correct/incorrect trials) | Spelling rate, cpm | ITR, bps |
| S1 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| S2 | 1.5 (1.0 + 0.5) | 42 (42/0) | 40 | 3.55 |
| S3 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| S4 | 1.5 (1.0 + 0.5) | 42 (42/0) | 40 | 3.55 |
| S5 | 1.5 (0.5 + 1.0) | 42 (42/0) | 40 | 3.55 |
| S6 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| S7 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| S8 | 1.5 (0.5 + 1.0) | 56 (49/7) | 30 | 2.66 |
| S9 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| S10 | 1.5 (0.5 + 1.0) | 42 (42/0) | 40 | 3.55 |
| S11 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| S12 | 1.0 (0.5 + 0.5) | 42 (42/0) | 60 | 5.32 |
| Mean ± SD | — | — | 50.83 ± 11.64 | 4.50 ± 1.03 |
The subjects were asked to input “HIGH SPEED BCI” three times without visual cues (42 characters in total). “Backspace” was used to remove an incorrect input (subject S8). For trial length, the two values in brackets correspond to stimulation duration and gaze shifting time respectively, which could vary between subjects (i.e., 0.5 or 1 s).
Discussion
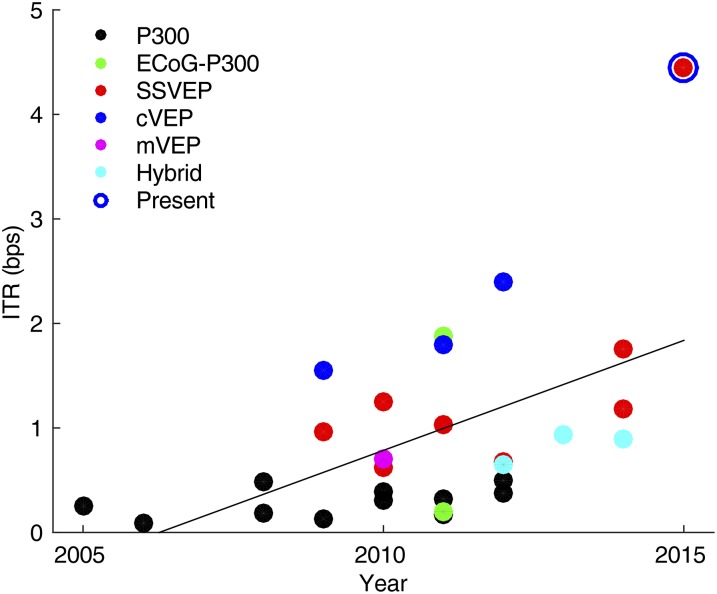
The low communication speed remains the key obstacle of practical applications of BCI spellers. The present BCI speller achieved a high spelling speed of 60 cpm in the cued-spelling task and ∼50 cpm in the free-spelling task. To our knowledge, the resultant ITRs (cued spelling: 4.45 bps; free spelling: 4.50 bps) represent the highest ITR reported in BCI spellers (4). For a direct performance comparison, this study summarizes the ITRs of online BCI spellers during the past decade (Fig. 6). It is clearly shown that the study of BCI spellers has become more popular in recent years and there is a clear trend in increase of ITRs. The mean ITR of all systems is 0.94 bps. Specifically, the mean ITR for code-modulated VEP (cVEP)-, SSVEP-, and P300-based systems is 1.91, 1.44, and 0.29 bps, respectively. Note that the ITR of the present system shows a multifold increase compared with the previous SSVEP-based systems (4.45 bps vs. 1.06 bps). The large performance improvement can be attributed to the present stimulation presentation, target coding, and target identification methods in the synchronous modulation and demodulation paradigm.
Fig. 6.
Information transfer rates of current BCI spellers. The data points indicate BCI studies characterized by “online” and “speller” from Thomson Reuters Web of Science and the present study. To emphasize practicality, the studies without online spelling tasks were not included. The line shows a linear fit for all data points, indicating a significant increase of ITR during the past decade (P < 0.01, r = 0.53). ”mVEP” indicates motion VEP and ”hybrid” indicates systems using multiple EEG signals (e.g., SSVEP and P300).
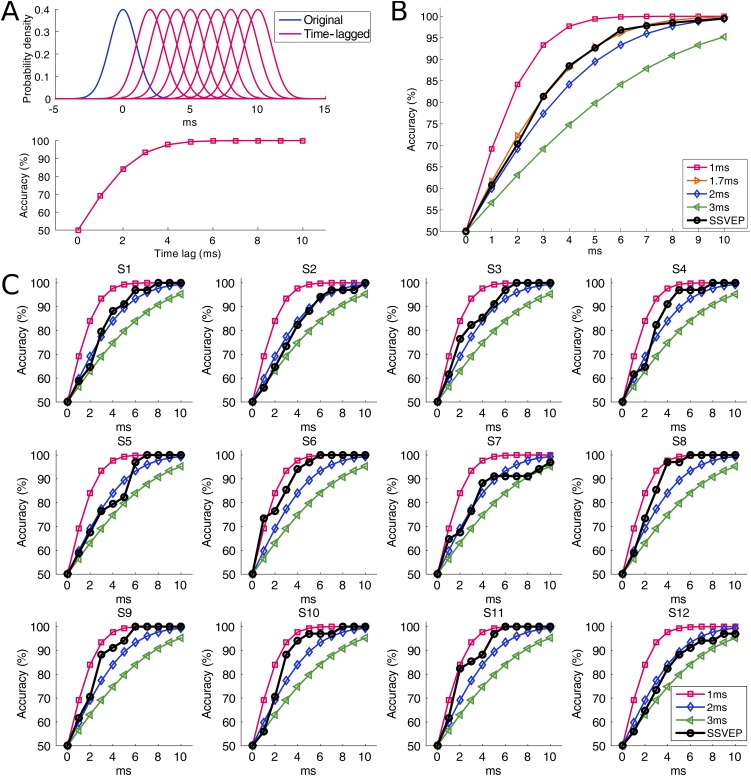
Theoretically, the performance of classifying SSVEPs using frequency-phase coding depends on the precision of the visual latency in single trials. This study hypothesizes that the visual latency of single-trial SSVEPs is very stable across trials. However, the visual latency for single-trial SSVEPs with such a short duration (i.e., 0.5 s) is difficult to measure due to the interference from spontaneous EEG activities. To solve this problem, this study developed a classification-based approach to estimate the variance of visual latency in single-trials SSVEPs by measuring the classification performance (details are given in Materials and Methods). The classification results between SSVEPs (0.5-s data epochs from the online cued-spelling tasks) and their time-lagged signals suggest that the mean SD of the visual latency is 1.7 ms across all subjects (Fig. S1B). The value for each individual is within 1–2 ms (Fig. S1C). By further considering an estimated timing error (with an SD of ∼0.6 ms) in data recording (i.e., synchronization between stimulation and EEG using event triggers) and the fact that the classification performance is generally lower than the theoretical maximum, the real SD of the visual latency in single-trial SSVEPs could be even smaller. These results suggest that the visual latency in SSVEPs is very stable across trials during fast BCI operations. Therefore, for the same stimulus, the elicited SSVEP component in multiple trials can be considered to exhibit the same frequency and phase.
Fig. S1.
Estimation of the SD of visual latency in single-trial SSVEPs. (A) Illustration of the relationship between theoretical classification accuracy and time lags (0–10 ms) for visual latencies that follow a normal distribution (mean: 0, SD: 1 ms). (B) Estimation of the mean SD of visual latency across all subjects. The accuracy curve fits well with the theoretical accuracy curve corresponding to a SD of 1.7 ms. (C) Estimation of the SD of visual latency for each subject. The estimated values are within 1–2 ms. In B and C, the 0.5-s data epochs from the online cued-spelling tasks (including both training and testing data, 17 blocks) were used for estimating the classification accuracy. Time lags from 0 to 10 ms were added to extract time-lagged epochs. The SSVEP epochs corresponding to the highest accuracy (13.4 Hz) among all stimulation frequencies were used in the analysis.
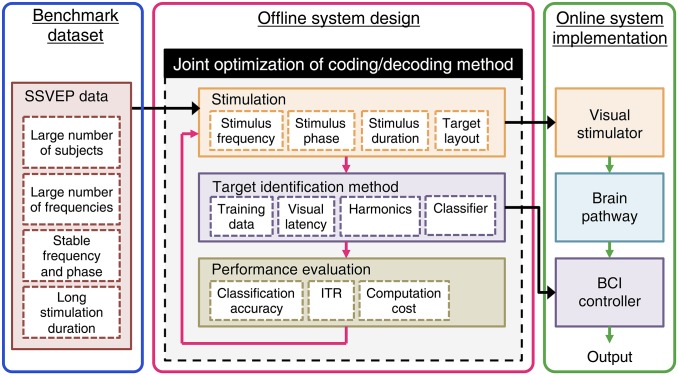
The present study further suggests a general framework for the design and implementation of an SSVEP-based BCI. A systematic framework for the design of SSVEP-based BCIs is still missing due to the lack of a computationally efficient model of single-trial SSVEPs. As shown in Fig. 7, the present study proposed a framework with three main procedures: benchmark dataset recording, offline system design, and online system implementation. The offline and online demonstrations in the present study showed comparable BCI performance (offline: 4.32 bps; online: 4.45 bps), suggesting a simple and efficient way to design an SSVEP-based BCI with a benchmark dataset. By adopting the approach in extracting SSVEP epochs from an offline dataset (Materials and Methods), various parameters in target coding (e.g., frequency, phase, and stimulation duration) can be simulated without the requirement of new data recording. The stable visual latency in single-trial SSVEPs (described above) makes it possible to translate advanced multiple access methods from the telecommunication technologies (13) to the SSVEP-based BCI. More importantly, under this framework, the coding and decoding methods can be jointly tested so that the decoding methods can be further optimized for different coding methods. The customized stimulation and target identification methods derived from offline system design can be easily transferred to operate the online BCI system for practical applications. By simplifying the system design using offline simulations, this framework can significantly facilitate the design of a new SSVEP-based BCI.
Fig. 7.
A general framework for designing an SSVEP-based BCI. The design of a new SSVEP BCI can be simplified by three procedures: (i) data collection for a benchmark dataset with a group of subjects, (ii) offline simulation, and (iii) online implementation. In this framework, offline simulation plays an important role in facilitating system design. Both coding and decoding methods can be jointly evaluated by the offline analysis with the benchmark dataset. The customized stimulation and target identification methods derived from offline system design can then be transferred to implement an SSVEP-based BCI system comprising visual stimulator, brain pathway, and BCI controller.
The present study shows a high-speed BCI speller that can spell at a speed up to 60 cpm. Note that many of the subjects in this study were experienced in using the SSVEP-based BCI speller and familiar with the layout of the targets. The spelling speed of 1 character per second seems close to the speed limit of human gaze control. The 0.5-s intertrial interval includes the visual latency (∼140 ms), online computation time (∼80 ms), and the time required for gaze switching. However, the stimulation duration can be further reduced if the classification performance can be improved. There are several directions to improve the classification performance. First, the optimization of stimulation duration (Fig. 5) can be performed separately for each individual. For example, the highest simulated ITR for single subjects reached 6.51 bps with a 0.3-s stimulation duration (subject S10, phase interval: 0.7π). Second, increasing the number of subbands (e.g., five subbands) in the filter bank analysis can improve the classification accuracy. Third, the robustness of the SSVEP templates can be improved by increasing the number of trials in the training data (19). Fourth, the variation of visual latency in single-trial SSVEPs could be reduced (e.g., by reducing the timing error in synchronization). Finally, there is still room for improving the coding and decoding approaches. The proposed JFPM method, which uses fixed frequency and phase intervals, proves to be a simple and efficient way to combine frequency and phase modulation in target coding. However, the combination strategy might be further improved (e.g., using unfixed frequency and phase intervals). By addressing these problems, the spelling rate of the present BCI speller could be as fast as 0.8 s per character (e.g., stimulation duration: 0.3 s and gaze shifting time: 0.5 s), which corresponds to a theoretical ITR up to 6.65 bps.
In two recent studies, we demonstrated the prototype systems of SSVEP-based BCI spellers with ITRs around 2.5 bps (17, 19). In ref. 17, a filter bank CCA algorithm was developed to implement a BCI speller based on the frequency coding method. In ref. 19, an offline BCI speller was proposed using a mixed frequency and phase coding method. Compared with these studies, the present study achieved significant improvements in several aspects. First, the present study implemented a fully closed-loop online system and achieved much higher ITRs (4.45 bps vs. 2.52 bps in ref. 17 and 2.76 bps in ref. 19) with cued-spelling and free-spelling tasks. Note that the data length for each trial in the present study was largely reduced (0.5 s vs. 1.25 s in ref. 17 and 1 s in ref. 19), whereas the classification accuracy was comparable (91.04% vs. 91.95% in ref. 17 and 91.35% in ref. 19). The new JFPM method incorporated phase coding into frequency coding, leading to significantly enhanced discriminability between very close frequencies. The efficiency of phase coding was further optimized by a grid-search approach. In addition, the calibration data-based target identification method was significantly improved by integrating filter bank analysis and a new feature of similarity between spatial filters (Fig. S2). Second, as described above, the present study proposed a new system framework based on a joint optimization of coding and decoding methods. This system framework can significantly facilitate the design and implementation of SSVEP-based BCIs. Third, the present study further demonstrated that the visual latency of SSVEPs is stable across trials, providing the neurophysiological basis for introducing the synchronous modulation and demodulation technique from telecommunications to BCIs. Together, these important improvements resulted in the present high-speed BCI speller with record-breaking ITR.
Fig. S2.
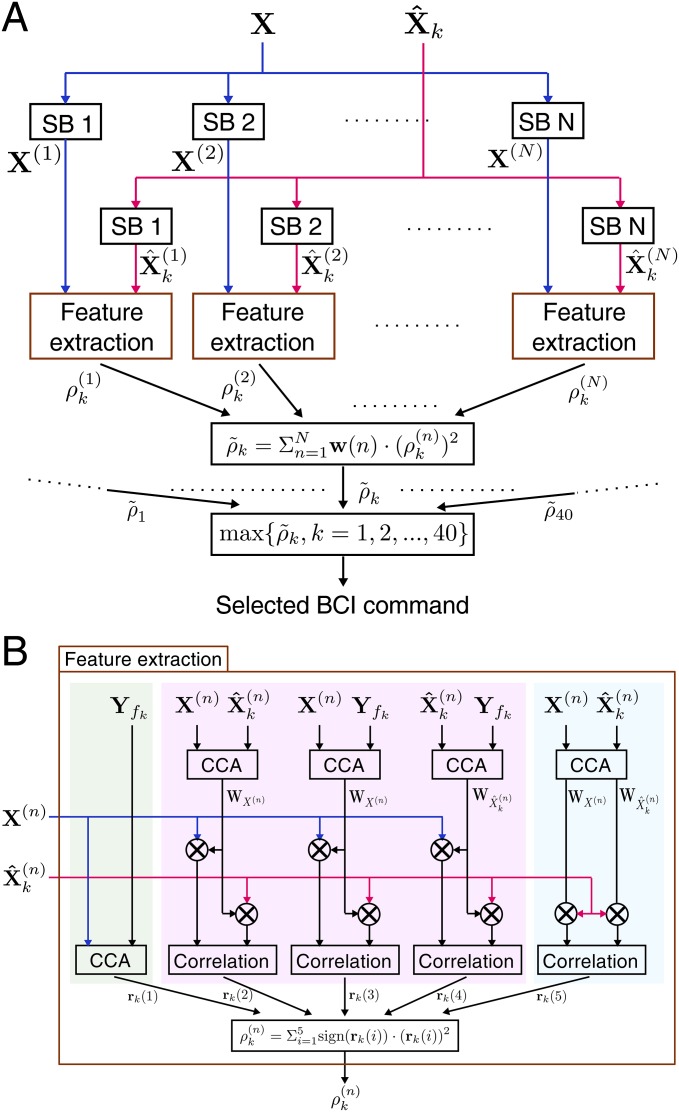
Flowchart of the improved target identification method. (A) Diagram of the filter bank-based target identification method (see details of notations in Eqs. 9 and 10). The same feature extraction procedure was applied to each subband signal obtained in the filter bank analysis. is the nth subband component for test set . is the nth subband component for the kth SSVEP template signals . (B) Diagram of the SSVEP template-based feature extraction method (see details of notations in Eqs. 7 and 8). Three types of features (marked with different background colors) were included in feature extraction: (i) the correlation coefficient from the standard CCA process, (ii) the correlation coefficients between single-trial SSVEP and SSVEP templates, and (iii) the similarity between CCA-based spatial filters corresponding to single-trial SSVEP and SSVEP templates. All features from the two-level feature extraction approach were combined together to perform target identification.
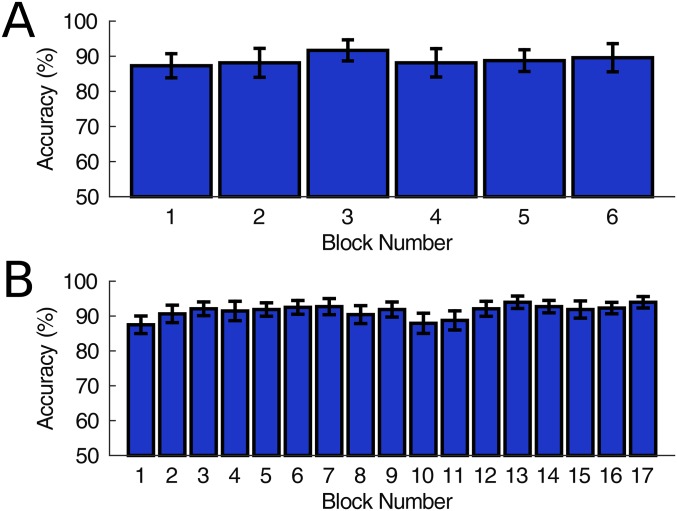
The spelling tasks in this study required fast switching between different visual targets (i.e., 1 s per character), which might lead to a high workload in system use. In addition, the training procedure in the online experiments might also increase the workload. The leave-one-out classification of the six offline blocks (Fig. S3A) and 17 online blocks (Fig. S3B) indicated that the BCI performance was stable across blocks. There was no clear drop of classification performance over time. These results suggest that the workload in the present system is within an acceptable range. This study demonstrated the visual latency is stable across 17 blocks in the online experiments (Fig. S1C). However, the stability of visual latency in long-time system use still remains unknown. Therefore, the feasibility of the high-speed speller in routine use requires further investigation. To reduce mental workload, the spelling rate can be adjusted by increasing the stimulation duration and the gaze switching time. In addition, more comfortable stimulation parameters [e.g., high-frequency stimulation above 40 Hz (20)] can be used to reduce visual fatigue. Furthermore, the calibration time for collecting training data can be reduced by adopting session-to-session transfer methods (21).
Fig. S3.
Classification accuracy for each block in offline and online experiments. (A) Simulated classification accuracy for the six blocks from the offline dataset. To simulate the phases with a phase interval of 0.35π, data segments were extracted from the 5-s-long data by adding time shifts according to Eqs. 11 and 12. (B) Leave-one-out classification accuracy for the 17 blocks from the online dataset.
The present high-speed BCI speller requires gaze control. Conventional eye-tracking approaches have been widely used to implement visual spellers (22). The reported typing speed of eye-tracking-based spellers has typically been from 5 to 10 words per minute. The BCI speller developed in this study achieved a spelling rate up to 60 cpm (i.e., ∼12 words per minute). This study therefore demonstrates that the communication speed of BCI could be comparable to that of eye-tracking systems, providing an alternative way for gaze tracking. In addition, the BCI technology can be less restricted by user environment (e.g., viewing distance and viewing angle). However, user comfortableness of the SSVEP-based BCIs requires further improvement toward practical applications. Owing to loss of gaze control, totally locked-in patients cannot use the present speller. For those patients, visual spellers need to be implemented with gaze-independent BCIs, which can be operated by covert attention (23). For SSVEP, a gaze-independent BCI speller can be realized based on spatial attention (24) and feature attention (25). The coding and decoding approaches and the system design framework developed by the present study can still benefit the design and implementation of an independent SSVEP-based BCI. For example, the joint frequency and phase modulation method and the template-based target identification method have potential to improve the speed and accuracy of attention detection.
Materials and Methods
Participants.
Eighteen healthy subjects (10 females, aged 22–29 years, mean age 25 years) with normal or corrected-to-normal vision participated in the experiment. This study designed an offline experiment and an online experiment using the SSVEP-based BCI speller. Two groups of 12 subjects participated in the two experiments respectively. Among all subjects, six participated in both experiments on two different days. Thirteen subjects had experience using the SSVEP-based BCI speller in previous studies. Five subjects in the online experiments (S3, S5, S6, S7, and S9) were naïve to the BCI speller. Each participant was asked to read and sign an informed consent form approved by the Research Ethics Committee of Tsinghua University before the experiment.
Visual Stimulus Presentation.
This study used the sampled sinusoidal stimulation method (6) to present visual flickers coded by the proposed JFPM method on a liquid-crystal display monitor. In general, the stimulus sequence s corresponding to frequency and phase can be generated by modulating the luminance of the screen using the following equation:
| [3] |
where generates a sine wave and i indicates the frame index in the stimulus sequence. The dynamic range of the stimulation signal is from 0 to 1, where 0 represents dark and 1 represents the highest luminance. Theoretically, the stimulation signal at any frequency (up to half of the refresh rate) and phase can be realized using this method.
BCI Speller.
This study designed a 40-target BCI speller using the proposed JFPM approach. As shown in Fig. 1A, the user interface is a 5 × 8 stimulation matrix containing 40 characters (26 English alphabet letters, 10 digits, and 4 other symbols). Specifically, 40 targets are tagged with linearly increasing frequencies and phases, of which the increments are both proportional to target index. The frequency and phase values for each target in the matrix can be obtained by
| [4] |
where and indicate the row (1–5) and column (1–8) index, respectively. In this study, and was 8 Hz and 0.2 Hz respectively. For the offline experiment, and were 0 and 0.5π, respectively. For the online experiment, was set to 0.35π toward high ITRs (Fig. 5B). Fig. 1B illustrates the frequency and phase values used for each character in the online experiment.
EEG Data Recording.
EEG data were acquired using a Synamps2 system (Neuroscan, Inc.) at a sampling rate of 1,000 Hz. Nine electrodes over parietal and occipital areas (Pz, PO5, PO3, POz, PO4, PO6, O1, Oz, and O2) were used to record SSVEPs. The reference electrode was placed at the vertex. Electrode impedances were kept below 10 kΩ. Event triggers generated by the stimulus program were sent from the parallel port of the computer to the EEG amplifier and recorded on an event channel synchronized to the EEG data. In the online experiment, EEG data and trigger signals were recorded and analyzed by the online data analysis program in real time. The online data analysis program was developed under MATLAB (MathWorks, Inc.).
The stimulation matrix was presented on a 23.6-inch liquid-crystal display screen with a resolution of 1,920 × 1,080 pixels and a refresh rate of 60 Hz. Each stimulus was rendered within a 140- × 140-pixel square. The character was presented within a 32- × 32-pixel square at the center of the stimulus. The vertical and horizontal distances between two neighboring stimuli were 50 pixels. The stimulus program was developed under MATLAB using the Psychophysics Toolbox Version 3 (26). During the experiment, subjects were seated in a comfortable chair in a dimly lit soundproof room at a viewing distance of ∼70 cm from the monitor.
Offline BCI Experiment.
The offline experiment consisted of six blocks. Each block contained 40 trials corresponding to all 40 characters indicated in a random order. Each trial lasted 6 s. Each trial started with a visual cue (a red square) indicating a target stimulus. The cue appeared for 0.5 s on the screen. Subjects were asked to shift their gaze to the target as soon as possible within the cue duration. Following the cue offset, all stimuli started to flicker on the screen concurrently and lasted 5 s. After stimulus offset, the screen was blank for 0.5 s before the next trial began. To facilitate visual fixation, a red triangle appeared below the flickering target during the stimulation period. In each block, subjects were asked to avoid eye blinks during the stimulation period. To avoid visual fatigue, there was a rest for several minutes between two consecutive blocks.
Online BCI Experiment.
In the online experiment, each trial only lasted 1 s including 0.5 s for visual stimulation and 0.5 s for gaze shifting. The online experiment was divided into a training stage and a testing stage. The training stage consisted of 12 blocks, each including 40 trials. The training blocks were used to derive SSVEP templates and spatial filters for each individual (details of the target identification method are given below). The testing stage included a cued-spelling and a free-spelling task. The cued-spelling task included five blocks (40 trials each). The cue for the next target appeared right after the stimulus offset. Visual and auditory feedbacks were provided to the subjects in real time. A short beep was sounded after a target was correctly identified by the online data analysis program. At the same time, the target character was typed in the text input field on the top of the screen. The free-spelling task required subjects to input a 14-character sequence (“HIGH SPEED BCI”) without visual cues. The task was repeated three times for each subject. The auditory feedback in the cued-spelling task was replaced by a visual feedback (a red square at the location of the identified target). There was a 1-min break between two consecutive blocks.
Data Preprocessing.
In offline and online experiments, data epochs comprising nine-channel SSVEPs were extracted according to event triggers generated by the stimulus program. Considering a latency delay in the visual system (27), the data epochs for offline and online experiments were extracted in [0.14 s 5.14 s] and [0.14 s 0.64 s], respectively (time 0 indicated stimulus onset). In this study, the 140-ms delay was selected toward the highest classification accuracy across all subjects. All epochs were first down-sampled to 250 Hz and then band-pass-filtered from 7 Hz to 70 Hz with an infinite impulse response (IIR) filter. Zero-phase forward and reverse filtering was implemented using the filtfilt() function in MATLAB.
CCA-Based Target Identification.
CCA has been widely used to detect the frequency of SSVEPs (28). CCA is a statistical way to measure the underlying correlation between two multidimensional variables. Considering two multidimensional variable , and their linear combinations and , CCA finds the weight vectors, and , which maximize the correlation between and by solving the following problem:
| [5] |
The maximum of with respect to and is the maximum canonical correlation. In frequency detection of SSVEPs, indicates multichannel SSVEPs and refers to reference signals. To detect the frequency of SSVEPs in an unsupervised way, sinusoidal signals are used as the reference signals (28):
| [6] |
where is the stimulation frequency and is the number of harmonics. To recognize the frequency of SSVEPs, CCA calculates the canonical correlation between multichannel SSVEPs and the reference signals corresponding to each stimulation frequency. The frequency of the reference signals with the maximal correlation is considered as the frequency of SSVEPs.
CCA with Individual Calibration Data.
Recently, individual calibration data have been incorporated into target identification approaches to improve the performance of SSVEP-based BCIs (29–32). By incorporating individual difference of SSVEPs in target identification, these methods all achieved significantly improved classification performance. This study adopted an improved SSVEP template-based method to incorporate individual SSVEP calibration data in target identification (19). Fig. S2B shows the flowchart of the method. In addition to the standard CCA method, this method combined correlation analysis between single-trial SSVEPs and SSVEP template signals in feature extraction. Furthermore, this study proposed a new type of feature that measured the similarity between CCA-based spatial filters derived from training and testing data. For the kth target, the training SSVEP template signals can be obtained by averaging multiple SSVEP trials in a training set. Correlation coefficients between projections of test set and training SSVEP template signals using CCA-based spatial filters can be used as features. Specifically, the following three weight vectors were used as spatial filters to enhance the SNR of SSVEPs: (i) between test set and training SSVEP template signals , (ii), between test set and sine-cosine reference signals , and (iii) between training SSVEP template signals and sine-cosine reference signals . The similarity between and was indirectly measured by calculating the correlation coefficient between the projections of SSVEP templates ( using the two spatial filters. For the kth template signal, a correlation vector was defined as follows (Fig. S2B):
| [7] |
where indicated the correlation coefficient between and . In the standard CCA method, the number of harmonics was set to five to include the fundamental and harmonic components of SSVEPs. The five correlation values described in Eq. 7 were combined as the feature for target identification:
| [8] |
where was used to remain discriminative information from negative correlation coefficients between test set and training SSVEP template signals . The training SSVEP template signal that maximized the weighted correlation value was selected as the SSVEP template signal corresponding to the target.
Filter Bank Analysis.
The goal of filter bank analysis (33) is to decompose SSVEPs into subband components so that independent information embedded in the harmonic components can be extracted more efficiently for enhancing the detection of SSVEPs. Fig. S2A shows the flowchart of the proposed method. The filter bank method consists of three major procedures (17): (i) subband decomposition, (ii) feature extraction for each subband signal, and (iii) target identification. First, a filter bank analysis performed subband decompositions with multiple filters that have different pass bands. The frequency range within [7 Hz 70 Hz] was selected for the filter bank. This study designed subbands covering multiple harmonic frequency bands with the same high cutoff frequency at the upper-bound frequency of SSVEP components (i.e., the nth subband started from the frequency at Hz and ended at 70 Hz). The band-pass filters for extracting subband components () from original EEG signals were zero-phase Chebyshev Type I IIR filters. The filtering was implemented using the filtfilt() function in MATLAB. After the filter bank analysis, the feature extraction method (Eqs. 7 and 8) was applied to each of the subband components separately. A weighted sum of squares of the correlation values corresponding to all subband components (i.e., ) was calculated as the feature for target identification:
| [9] |
where n was the index of the subband. According to the finding that the SNR of SSVEP harmonics decreases as the response frequency increases (Fig. 3C), the weights for the subband components were defined as follows:
| [10] |
where a and b were constants that maximized the classification performance. In practice, a and b can be determined with a grid-search method using an offline analysis. In this study, the value of a and b was set to 1 and 0 respectively. Finally, corresponding to all stimulation frequencies (i.e., ) was used for determining the frequency of SSVEPs. The frequency of the reference signals with the maximal was considered as the frequency of SSVEPs. The offline analysis indicated that a larger number of subbands resulted in higher performance. However, to satisfy the requirement of real-time processing, only two subbands ( [8 Hz 70 Hz] and [16 Hz 70 Hz]) were used in this study.
Simulation of Stimulation Duration and Phase Interval Value.
To optimize BCI performance for the speller, different phase intervals and stimulation durations were used to extract data epochs from the 5-s offline data epochs by adding different time shifts determined by frequency and phase. For each stimulation frequency, the 5-s data epochs were first shifted circularly to the left with a time shift to generate SSVEPs with a zero initial phase:
| [11] |
where n was the index of data sample and was the sampling rate. The time shifts were obtained based on the stimulation frequency and the initial phase value described in Eq. 4. The zero-phase epochs were further shifted circularly with a time shift to generate simulated SSVEPs corresponding to different phase interval values:
| [12] |
where was obtained by applying different phase interval () values in Eq. 4.
Performance Evaluation.
Classification accuracy and ITR were calculated for the offline and online experiments separately. The method for calculating ITR (in bits per second) was as follows (1):
| [13] |
where M is the number of classes (i.e., 40 in this study), P is the accuracy of target identification, and T (seconds per selection) is the average time for a selection. For the offline experiments, this study used a leave-one-out cross-validation to estimate simulated online BCI performance. Individual training SSVEP template signals were obtained from the training data in cross-validation. To estimate the optimal BCI performance in the offline experiment, this study calculated accuracy and ITR with different stimulation duration and phase intervals (Fig. 5). For the online experiment, classification accuracy and ITR were calculated based on the results obtained from the online data-analysis program in the testing stage. For the estimation of ITR in offline and online experiments, the gaze-shifting time was included in the calculation.
Estimation of the SD of Visual Latency in Single-Trial SSVEPs.
The variation of visual latency in single-trial SSVEPs can be measured by phase difference between different trials. However, the SSVEPs in single trials are typically interfered by strong spontaneous EEG activities, making it difficult to measure the phase of SSVEPs directly. This study developed a classification-based approach to estimate the variation of the visual latency in single-trial SSVEPs. The basic idea is to estimate the distribution of visual latencies by quantifying the classification accuracy between SSVEPs and their time-lagged signals. Suppose the visual latency follows a normal distribution, binary classification accuracy between data samples from the distribution and its time-lagged distributions can reflect the stand deviation of the distribution (Fig. S1A). The classification accuracy increases when the time lag increases, resulting in a smaller overlap area between the two distributions. Therefore, given an accuracy curve with respect to different time lags, the SD of visual latencies can be estimated. In practice, the accuracy curve can be calculated by classifying single-trial SSVEPs and their time-lagged signals. This study used the 0.5-s epochs from the cued-spelling tasks (17 blocks in total) and their time-lagged epochs as the two classes for estimating the classification accuracy (Fig. S1 B and C). The time lags ranged from 0 to 10 ms. To fully extract the information of SSVEPs from single trials, the classification approach was the same as the target identification method used in the BCI speller. Note that the theoretical classification accuracy should be higher than the estimations due to the interference from EEG background activities. Therefore, the real SD of visual latencies in single-trial SSVEPs should be smaller than the estimations.
Acknowledgments
This work is supported by National Basic Research Program (973) of China Grant 2011CB933204, National Natural Science Foundation of China Grants 61431007 and 91220301, National High-Tech R&D Program (863) of China Grant 2012AA011601, and the Recruitment Program for Young Professionals. This work was also supported in part by US Office of Naval Research Grant N00014-08-1215, Army Research Office Grant W911NF-09-1-0510, Army Research Laboratory Grant W911NF-10-2-0022, and Defense Advanced Research Projects Agency Grant USDI D11PC20183 (to Y.W., M.N., and T.-P.J.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1508080112/-/DCSupplemental.
References
- 1.Wolpaw JR, Birbaumer N, McFarland DJ, Pfurtscheller G, Vaughan TM. Brain-computer interfaces for communication and control. Clin Neurophysiol. 2002;113(6):767–791. doi: 10.1016/s1388-2457(02)00057-3. [DOI] [PubMed] [Google Scholar]
- 2.Lebedev MA, Nicolelis MA. Brain-machine interfaces: Past, present and future. Trends Neurosci. 2006;29(9):536–546. doi: 10.1016/j.tins.2006.07.004. [DOI] [PubMed] [Google Scholar]
- 3.Cecotti H. Spelling with non-invasive brain-computer interfaces—current and future trends. J Physiol Paris. 2011;105(1–3):106–114. doi: 10.1016/j.jphysparis.2011.08.003. [DOI] [PubMed] [Google Scholar]
- 4.Gao S, Wang Y, Gao X, Hong B. Visual and auditory brain-computer interfaces. IEEE Trans Biomed Eng. 2014;61(5):1436–1447. doi: 10.1109/TBME.2014.2300164. [DOI] [PubMed] [Google Scholar]
- 5.Farwell LA, Donchin E. Talking off the top of your head: Toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr Clin Neurophysiol. 1988;70(6):510–523. doi: 10.1016/0013-4694(88)90149-6. [DOI] [PubMed] [Google Scholar]
- 6.Chen X, Chen Z, Gao S, Gao X. A high-ITR SSVEP-based BCI speller. Brain-Comp Interfaces. 2014;1(3–4):181–191. [Google Scholar]
- 7.Spüler M, Rosenstiel W, Bogdan M. Online adaptation of a c-VEP brain-computer Interface (BCI) based on error-related potentials and unsupervised learning. PLoS One. 2012;7(12):e51077. doi: 10.1371/journal.pone.0051077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brunner P, Ritaccio AL, Emrich JF, Bischof H, Schalk G. Rapid communication with a ‘P300’ matrix speller using electrocorticographic signals (ECoG) Front Neurosci. 2011;5:5. doi: 10.3389/fnins.2011.00005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nuyujukian P, Fan JM, Kao JC, Ryu SI, Shenoy KV. A high-performance keyboard neural prosthesis enabled by task optimization. IEEE Trans Biomed Eng. 2015;62(1):21–29. doi: 10.1109/TBME.2014.2354697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang Y, Gao X, Hong B, Jia C, Gao S. Brain-computer interfaces based on visual evoked potentials - Feasibility of practical system designs. IEEE EMB Mag. 2008;27(5):64–71. doi: 10.1109/MEMB.2008.923958. [DOI] [PubMed] [Google Scholar]
- 11.Vialatte FB, Maurice M, Dauwels J, Cichocki A. Steady-state visually evoked potentials: Focus on essential paradigms and future perspectives. Prog Neurobiol. 2010;90(4):418–438. doi: 10.1016/j.pneurobio.2009.11.005. [DOI] [PubMed] [Google Scholar]
- 12.Regan D. Human Brain Electrophysiology: Evoked Potentials and Evoked Magnetic Fields in Science and Medicine. Elsevier; New York: 1989. [Google Scholar]
- 13.Rappaport TS. Wireless Communication, Principle and Practice. 2nd Ed Prentice Hall; Upper Saddle River, NJ: 2001. [Google Scholar]
- 14.Herrmann CS. Human EEG responses to 1-100 Hz flicker: Resonance phenomena in visual cortex and their potential correlation to cognitive phenomena. Exp Brain Res. 2001;137(3–4):346–353. doi: 10.1007/s002210100682. [DOI] [PubMed] [Google Scholar]
- 15.Regan D. Some characteristics of average steady-state and transient responses evoked by modulated light. Electroencephalogr Clin Neurophysiol. 1966;20(3):238–248. doi: 10.1016/0013-4694(66)90088-5. [DOI] [PubMed] [Google Scholar]
- 16.Müller-Putz GR, Scherer R, Brauneis C, Pfurtscheller G. Steady-state visual evoked potential (SSVEP)-based communication: Impact of harmonic frequency components. J Neural Eng. 2005;2(4):123–130. doi: 10.1088/1741-2560/2/4/008. [DOI] [PubMed] [Google Scholar]
- 17.Chen X, Wang Y, Gao S, Jung TP, Gao X. Filter bank canonical correlation analysis for implementing a high-speed SSVEP-based brain-computer interface. J Neural Eng. 2015;12(4):046008. doi: 10.1088/1741-2560/12/4/046008. [DOI] [PubMed] [Google Scholar]
- 18.Wang Y, Wang R, Gao X, Hong B, Gao S. A practical VEP-based brain-computer interface. IEEE Trans Neural Syst Rehabil Eng. 2006;14(2):234–239. doi: 10.1109/TNSRE.2006.875576. [DOI] [PubMed] [Google Scholar]
- 19.Nakanishi M, Wang Y, Wang YT, Mitsukura Y, Jung TP. A high-speed brain speller using steady-state visual evoked potentials. Int J Neural Syst. 2014;24(6):1450019. doi: 10.1142/S0129065714500191. [DOI] [PubMed] [Google Scholar]
- 20.Sakurada T, Kawase T, Komatsu T, Kansaku K. Use of high-frequency visual stimuli above the critical flicker frequency in a SSVEP-based BMI. Clin Neurophysiol. 2015;126(10):1972–1978. doi: 10.1016/j.clinph.2014.12.010. [DOI] [PubMed] [Google Scholar]
- 21.Krauledat M, Tangermann M, Blankertz B, Müller KR. Towards zero training for brain-computer interfacing. PLoS One. 2008;3(8):e2967. doi: 10.1371/journal.pone.0002967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Majaranta P, Räihä KJ. Text entry by gaze: utilizing eye-tracking. In: MacKenzie IS, Tanaka-Ishii K, editors. Text Entry Systems: Mobility, Accessibility, Universality. Morgan Kaufmann; San Francisco: 2007. pp. 175–187. [Google Scholar]
- 23.Treder MS, Blankertz B. (C)overt attention and visual speller design in an ERP-based brain-computer interface. Behav Brain Funct. 2010;6:28. doi: 10.1186/1744-9081-6-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kelly SP, Lalor EC, Finucane C, McDarby G, Reilly RB. Visual spatial attention control in an independent brain-computer interface. IEEE Trans Biomed Eng. 2005;52(9):1588–1596. doi: 10.1109/TBME.2005.851510. [DOI] [PubMed] [Google Scholar]
- 25.Zhang D, et al. An independent brain-computer interface using covert non-spatial visual selective attention. J Neural Eng. 2010;7(1):16010. doi: 10.1088/1741-2560/7/1/016010. [DOI] [PubMed] [Google Scholar]
- 26.Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10(4):433–436. [PubMed] [Google Scholar]
- 27.Di Russo F, Spinelli D. Electrophysiological evidence for an early attentional mechanism in visual processing in humans. Vision Res. 1999;39(18):2975–2985. doi: 10.1016/s0042-6989(99)00031-0. [DOI] [PubMed] [Google Scholar]
- 28.Lin Z, Zhang C, Wu W, Gao X. Frequency recognition based on canonical correlation analysis for SSVEP-based BCIs. IEEE Trans Biomed Eng. 2007;54(6 Pt 2):1172–1176. doi: 10.1109/tbme.2006.889197. [DOI] [PubMed] [Google Scholar]
- 29.Chen X, Wang Y, Nakanishi M, Jung TP, Gao X. Hybrid frequency and phase coding for a high-speed SSVEP-based BCI speller. Conf Proc IEEE Eng Med Biol Soc. 2014;2014:3993–3996. doi: 10.1109/EMBC.2014.6944499. [DOI] [PubMed] [Google Scholar]
- 30.Zhang Y, Zhou G, Jin J, Wang X, Cichocki A. SSVEP recognition using common feature analysis in brain-computer interface. J Neurosci Methods. 2015;244:8–15. doi: 10.1016/j.jneumeth.2014.03.012. [DOI] [PubMed] [Google Scholar]
- 31.Zhang Y, Zhou G, Jin J, Wang X, Cichocki A. Frequency recognition in SSVEP-based BCI using multiset canonical correlation analysis. Int J Neural Syst. 2014;24(4):1450013. doi: 10.1142/S0129065714500130. [DOI] [PubMed] [Google Scholar]
- 32.Tong J, Zhu D. Multi-phase cycle coding for SSVEP based brain-computer interfaces. Biomed Eng Online. 2015;14(5):5. doi: 10.1186/1475-925X-14-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Vetterli M, Herley C. Wavelets and filter banks: Theory and design. IEEE Trans Signal Process. 1992;40(9):2207–2232. [Google Scholar]