Clique topology reveals intrinsic geometric structure in neural correlations

Significance

Detecting structure in neural activity is critical for understanding the function of neural circuits. The coding properties of neurons are typically investigated by correlating their responses to external stimuli. It is not clear, however, if the structure of neural activity can be inferred intrinsically, without a priori knowledge of the relevant stimuli. We introduce a novel method, called clique topology, that detects intrinsic structure in neural activity that is invariant under nonlinear monotone transformations. Using pairwise correlations of neurons in the hippocampus, we demonstrate that our method is capable of detecting geometric structure from neural activity alone, without appealing to external stimuli or receptive fields.

Abstract

Detecting meaningful structure in neural activity and connectivity data is challenging in the presence of hidden nonlinearities, where traditional eigenvalue-based methods may be misleading. We introduce a novel approach to matrix analysis, called clique topology, that extracts features of the data invariant under nonlinear monotone transformations. These features can be used to detect both random and geometric structure, and depend only on the relative ordering of matrix entries. We then analyzed the activity of pyramidal neurons in rat hippocampus, recorded while the animal was exploring a 2D environment, and confirmed that our method is able to detect geometric organization using only the intrinsic pattern of neural correlations. Remarkably, we found similar results during nonspatial behaviors such as wheel running and rapid eye movement (REM) sleep. This suggests that the geometric structure of correlations is shaped by the underlying hippocampal circuits and is not merely a consequence of position coding. We propose that clique topology is a powerful new tool for matrix analysis in biological settings, where the relationship of observed quantities to more meaningful variables is often nonlinear and unknown.

Neural activity and connectivity data are often presented in the form of a matrix whose entries, $C_{ij},$ indicate the strength of correlation or connectivity between pairs of neurons, cell types, or imaging voxels. Detecting structure in such a matrix is a critical step toward understanding the organization and function of the underlying neural circuits. In this work, we focus on neural activity, whose structure may reflect the coding properties of neurons, rather than their physical locations within the brain. For example, place cells in rodent hippocampus act as position sensors, exhibiting a high firing rate when the animal’s position lies inside the neuron’s “place field,” its preferred region of the spatial environment (1). Without knowledge of the coding properties, however, it is unclear whether such a geometric organization could be detected purely from the pattern of neural correlations. Alternatively, a correlation or connectivity matrix could be truly unstructured, such as the connectivity pattern observed in the fly olfactory system (2), indicating random network organization.

Can we distinguish these possibilities, using only the intrinsic features of the matrix $C_{ij}$? The most common approach is to use standard tools from matrix analysis that rely on quantities, such as eigenvalues, that are invariant under linear change of basis. This strategy is natural in physics, where meaningful quantities should be preserved by linear coordinate transformations. In contrast, measurements in biological settings are often obtained as nonlinear transformations of the underlying “real” variables, whereas the choice of basis is meaningful and fixed. For example, basis elements might represent particular neurons or genes, and measurements (matrix elements) could consist of pairwise correlations in neural activity, or the coexpression of pairs of genes. Instead of change of basis, the relevant structure in these data should be invariant under matrix transformations of the following form:

$$C_{ij}=f\left(A_{ij}\right),$$ [1]

where f is a nonlinear monotonic function (Fig. 1A). In the case of hippocampal place cells, f captures the manner in which pairwise correlations $C_{ij}$ decrease with distance between place field centers (3). In less studied contexts, the represented stimuli—and the function f—may be completely unknown.

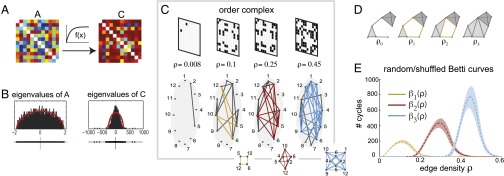
Fig. 1.

Order-based analysis of symmetric matrices. (A) A symmetric matrix A is related to another matrix C via a nonlinear monotonically increasing function $f\left(x\right)$, applied entrywise. (B, Left) Distribution of eigenvalues for a random symmetric $N\times N$ matrix $A,$ whose entries were drawn independently from the normal distribution with zero mean and variance $1/\sqrt{N}$ ($N=500$). (Right) Distribution of eigenvalues for the transformed matrix with entries $C_{ij}=f\left(A_{ij}\right)$, for $f\left(x\right)=1-e^{-30x}$. Red curves show Wigner’s semicircle distribution with matching mean and variance. (C, Top) The order complex of A is represented as a sequence of binary adjacency matrices, indexed by the density ρ of nonzero entries. (Bottom) Graphs corresponding to the adjacency matrices. Minimal examples of a 1-cycle (yellow square), a 2-cycle (red octahedron), and a 3-cycle (blue orthoplex) appear at $\rho =0.1,0.25,$ and 0.45, respectively. (D) At edge density ${\rho }_0$, there are no cycles. Cliques of size 3 and 4 are depicted with light and dark gray shading. As the edge density increases, a new 1-cycle (yellow) is created, persists, and is eventually destroyed at densities ${\rho }_1,{\rho }_2,$ and ${\rho }_3$, respectively. (E) For a distribution of 1,000 random $N\times N$ symmetric matrices ($N=88$), average Betti curves ${\beta }_1\left(\rho \right),{\beta }_2\left(\rho \right),$ and ${\beta }_3\left(\rho \right)$ are shown (yellow, red, and blue dashed curves), together with 95% confidence intervals (shaded areas).

Unfortunately, eigenvalues are not invariant under transformations of the form (Eq. 1) (Fig. 1B and SI Appendix, Fig. S1). Although large random matrices have a reliable eigenvalue spectrum [e.g., Wigner’s semicircle law (4)], it is possible that a random matrix with independent and identically distributed (i.i.d.) entries could be mistaken as structured, purely as an artifact of a monotonic nonlinearity (Fig. 1B).* The results of eigenvalue-based analyses can thus be difficult to interpret, and potentially misleading.

Here, we introduce a new tool to reliably detect signatures of structure and randomness that are invariant under nonlinear monotone transformations of the form (Eq. 1). Using pairwise correlations of hippocampal place cells recorded during both spatial and nonspatial behaviors, we demonstrate that our method is capable of detecting geometric structure from neural activity alone. To our knowledge, this is the first example of a method that detects geometric organization intrinsically from neural activity, without appealing to external stimuli or receptive fields.

Results

The only feature of a matrix that is preserved under the transformations (Eq. 1), for monotonically increasing f, is the relative ordering of its entries, as $C_{ij}<C_{k\ell }$ whenever $A_{ij}<A_{k\ell }$ (SI Appendix, Supplementary Text). We refer to this combinatorial information as the “order complex,” $\text{ord}\left(C\right)$. It is convenient to represent the order complex as a nested sequence of graphs, where each subsequent graph includes an additional edge $\left(ij\right)$ corresponding to the next-largest matrix entry $C_{ij}$ (Fig. 1C). Any quantity computed from the order complex is automatically invariant under the transformations (Eq. 1), because $\text{ord}\left(A\right)=\text{ord}\left(C\right)$. We found that the arrangement of “cliques” (all-to-all connected subgraphs) in the order complex of a matrix can be used in lieu of eigenvalues to detect random or geometric structure.

“Clique topology” provides a systematic measure of how cliques fit together and overlap across the entire order complex. The topological structure of cliques in a graph can be quantified by first “filling in” all cliques, and then counting noncontractible cycles, i.e., arrangements of cliques which bound “holes.” Minimal examples of 1-, 2-, and 3-cycles are shown in Fig. 1C (Inset). A 1-cycle bounds a 2D area, a 2-cycle bounds a 3D volume, and a 3-cycle bounds a 4D region (SI Appendix, Supplementary Text). As the edge density ρ increases, new cycles are created, modified, and eventually destroyed (Fig. 1D). One can track these changes by computing a set of Betti numbers (6, 7), ${\beta }_m$, which count the independent m-cycles in each graph after all cliques have been filled in. The Betti numbers across all graphs in an order complex yield “Betti curves,” ${\beta }_m\left(\rho \right)$ (Materials and Methods and SI Appendix, Supplementary Text).

Detection of Random Organization.

Although the details of individual graphs in the order complex may be sensitive to noise in the matrix entries, we found that clique topology provides robust signatures that can be used to distinguish structure from randomness. In the case of a random symmetric matrix with i.i.d. entries, the corresponding order complex is a sequence of Erdős–Rényi random graphs. We found that the Betti curves ${\beta }_m\left(\rho \right)$ are remarkably reliable for such matrices (Fig. 1E), and display a characteristic unimodal shape with peak values that increase with m ($m\ll N$). This reliability has been theoretically predicted (8, 9) and makes it possible to robustly distinguish random from nonrandom structure in the presence of a monotone nonlinearity (Eq. 1). Unsurprisingly, correlation matrices obtained from finite samples of N independent random variables display the same characteristic Betti curves as random symmetric $N\times N$ matrices (SI Appendix, Fig. S2). Note that computing low-dimensional $\left(m\le 3\right)$ Betti curves for matrices of size N ∼ 100 is numerically tractable due to recent advances in computational topology (7, 10, 11).

Detection of Geometric Organization.

If a correlation or connectivity matrix is not random, what kind of structure can one detect? Uncovering “geometric” structure is especially important in neuroscience, because it indicates that neurons encode geometrically organized stimuli. For example, orientation-tuned neurons (12) and hippocampal place cells (1) have correlations that decrease with distance between represented angles or locations in the environment, respectively. This is easy to see by correlating neural responses directly to the relevant stimuli. However, it is unclear whether it is even possible to detect such an organization from pairwise correlations among neurons alone—without a priori knowledge of the represented stimulus space. A further difficulty is to detect geometric organization that is invariant under nonlinear monotone transformations of the matrix entries.

To our surprise, we found that the ordering of matrix entries encodes geometric features, such as dimension (Fig. 2A). For larger matrices, the precise dimension may be difficult to discern in the presence of noise. Nevertheless, the organization of cliques in the order complex carries signatures of an underlying Euclidean geometry, irrespective of dimension. For example, the triangle inequality, $\Vert x-z\Vert \le \Vert x-y\Vert +\Vert y-z\Vert$, implies that if two edges of a triangle are present in the order complex at some edge density ρ, there is a higher probability of the third edge also being present. Intuitively, this means that cliques in the order complex will be more prominent for geometric compared with random matrices, and cycles will be comparatively short-lived, as cliques cause holes to be more readily filled in (13).

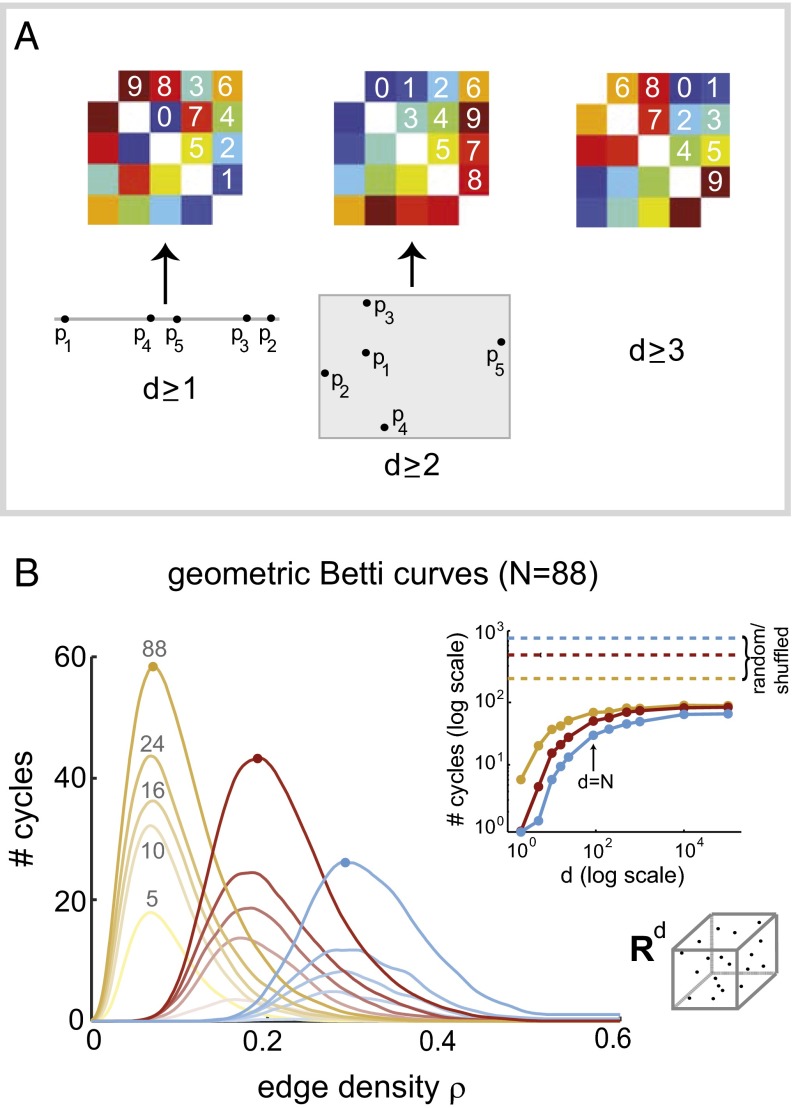
Fig. 2.

Geometric structure is encoded in the ordering of matrix entries. (A) Three $5\times 5$ symmetric matrices with distinct order complexes; the 10 off-diagonal matrix values in each are ordered from 0 to 9. An ordering of matrix values can be obtained from an arrangement of points, $p_i,$ in d-dimensional Euclidean space if $A_{ij}<A_{k\ell }$ whenever $\Vert p_i-p_j\Vert <\Vert p_k-p_{\ell }\Vert$. (Left) A matrix ordering that arises from points on a line. (Middle) An ordering that arises from points in the plane, but cannot be obtained from points on a line. (Right) An ordering that cannot arise from distances between points in one or two dimensions. (B) Betti curves for distributions of geometric matrices ($N=88$) in dimensions $d=$ 5, 10, 16, 24, and 88. Mean Betti curves ${\beta }_1\left(\rho \right),{\beta }_2\left(\rho \right),$ and ${\beta }_3\left(\rho \right)$ are shown (yellow, red, and blue curves), with darker (and higher) curves corresponding to larger d. Dots indicate peak values of $d=N$ curves. (Inset) Peak values of Betti curves for $N=88$ geometric matrices as a function of dimension. Beyond $d=N$, peak values increase very slowly and remain small compared with random/shuffled matrices with matching N (dashed lines). The last point on each curve corresponds to $d=$ 100,000.

To see whether clique topology can provide reliable signatures of geometric organization, we computed Betti curves for distributions of geometric matrices ($N=88$), generated from random points uniformly sampled from unit cubes of dimensions $d=\mathrm{5,10,16,24},$ and $88,$ and having entries that decrease with distance (Materials and Methods). We then computed average Betti curves ${\beta }_1\left(\rho \right),{\beta }_2\left(\rho \right),$ and ${\beta }_3\left(\rho \right)$ for each d, and found that they are stratified by dimension but retain characteristic features that are independent of dimension. In particular, the peak values of geometric Betti curves are considerably smaller than those of random symmetric matrices with matching parameters ($p<0.001$), and decrease with increasing m (Fig. 2B). This pattern remains over the full range of tested dimensions (Fig. 2B, Inset). We conclude that Betti curves can, in principle, be used to distinguish geometric from random structure.

Signatures of Intrinsic Geometric Structure in Neural Activity.

Can clique topology be used to detect geometric organization from pairwise correlations in noisy neural data? To answer this question, we examined correlations of hippocampal place cells in rodents during spatial navigation in a 2D open field environment. In this context, geometric structure is expected due to the existence of spatially localized receptive fields [place fields (1)] but has not previously been detected intrinsically using only the pattern of correlations.

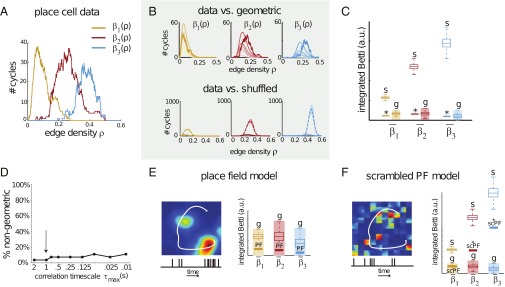
We computed correlations from spike trains of simultaneously recorded neurons in area CA1 of dorsal hippocampus (Materials and Methods). Each pairwise correlation, $C_{ij},$ was obtained from the mean of a cross-correlogram on a timescale of ${\tau }_{\text{max}}=1$ s (SI Appendix, Supplementary Methods, and Fig. S3). The resulting matrix was then analyzed using clique topology (Fig. 3A). As expected, the Betti curves from place cell data were in close agreement to those of geometric matrices (Fig. 3B, Top), up to a small rightward shift that is likely due to noise (SI Appendix, Fig. S4A).

Fig. 3.

Geometric structure of correlations for neurons with spatial receptive fields. (A) Betti curves of the pairwise correlation matrix for the activity of $N=88$ place cells in hippocampus during open-field spatial exploration. (B, Top) Betti curves from A (bold lines) overlaid on the mean geometric Betti curves from Fig. 2B. (Bottom) Comparison of Betti curves from A to those of shuffled correlation matrices (note the change in vertical scale). (C) Integrated Betti values ${\overline{\beta }}_m$ for the curves in A (solid lines), compared with standard box plots of integrated Betti values for the 1,000 shuffled [s] and geometric [g] controls displayed in B. The geometric box plots are shown for the highest dimension, $d=88$, whereas the shaded area indicates the confidence interval across all dimensions $d\le 88$. Betti values for the place cell data are significantly nonrandom (*P < 0.001), and appear consistent with those of geometric matrices. (D) Percentage of nongeometric Betti values ${\overline{\beta }}_1$, ${\overline{\beta }}_2$, ${\overline{\beta }}_3$ for a range of correlation timescales ${\tau }_{\text{max}}$. Each point is an average over nine open-field recordings. The arrow indicates the timescale considered in A–C. (E, Left) A place field together with a cartoon trajectory (white) and simulated spike train (bottom). (Right) Integrated Betti values for correlations in the place field model (bold lines, labeled PF) lie within the geometric regime. (F, Left) A scrambled version of the place field in E. (Right) Integrated Betti values for the scrambled PF model (bold lines) are significantly nongeometric (*P < 0.05) for ${\overline{\beta }}_2$ and ${\overline{\beta }}_3$, whereas ${\overline{\beta }}_1$ is in the geometric regime. The Betti values are also significantly smaller than those of shuffled controls (*P < 0.05). Box plots for geometric and shuffled controls in E and F are the same as in C.

Although we found that qualitative geometric structure is robustly detectable, the precise dimension is sensitive to noise and currently difficult to estimate, even for low dimensions. For example, a geometric matrix in dimension $d=2$ exhibits higher-dimensional nonzero Betti curves if a fraction of the neurons have nongeometric correlations with the rest (SI Appendix, Fig. S4B). A post hoc analysis of the recorded place cells showed that 5–10% exhibited nonconvex place fields; this alone could account for the higher dimensions we observed. On the other hand, Betti curves of $d=2$ geometric matrices with up to 10% of the neurons having random correlations still lie in the $d\le N$ geometric regime (SI Appendix, Fig. S4B).

We next compared the data Betti curves to shuffled controls, obtained by randomly permuting the matrix entries (SI Appendix, Fig. S5 A and B). Shuffling completely destroys any structure in the order complex, yielding distributions of Betti curves identical to those of random matrices (Fig. 1E). We found that the Betti curves from place cell data were an order of magnitude smaller than the mean Betti curves of the shuffled matrices, and well outside the 95% confidence intervals (Fig. 3B, Bottom). To quantify the significance of nonrandom structure, we used integrated Betti values as follows:

$${\overline{\beta }}_m={\displaystyle \underset{0}{\overset{1}{\int }}{\beta }_m\left(\rho \right)d\rho },$$

and verified that they were significantly smaller than those obtained from 1,000 trials of the shuffled controls (P < 0.001), but well within the confidence intervals for geometric controls (Fig. 3C).

To test whether the observed geometric organization was consistent across animals and recording sessions, we repeated these analyses for eight additional datasets from three different animals during spatial navigation (SI Appendix, Fig. S6). All but one of the nine datasets were consistent with the corresponding geometric controls, suggesting that geometric structure of correlations is a robust phenomenon during spatial navigation. We also repeated the analyses for different choices of the correlation timescale, ${\tau }_{\text{max}}$, ranging from 10 ms to 2 s, and observed similar results (Fig. 3D). As a further test of geometric organization, we computed the distribution of “persistence lifetimes” from the order complex of the open field correlation matrix (SI Appendix, Supplementary Text). The lifetime measures how long a hole persists as it evolves from one graph to the next in the order complex (Fig. 1D). Again, the data exhibited topological signatures that were far from random, but consistent with geometric organization (SI Appendix, Fig. S7).

To ensure that the observed correlation structure could not be explained by the differences in interactions of individual neurons with the “mean field” activity of the network, we performed an additional random control that preserves row and column sums of pairwise correlation matrices. Specifically, we computed Betti curves for matrices drawn from a weighted maximum entropy (WME) distribution, subject to the constraint that expected row sums match the original pairwise correlation matrix (SI Appendix, Fig. S5 C and D). The Betti curves and persistence lifetimes of the WME controls were similar to those of random symmetric matrices (SI Appendix, Fig. S8), showing that the nonrandom structure in the data does not arise from the fact that some neurons have higher levels of correlation with the population as a whole.

Scrambled Place Fields Yield Nongeometric Correlations.

Are the spatial coding properties of place cells sufficient to account for the observed geometric organization of correlations during spatial navigation? Or, alternatively, does this structure reflect finer features of the correlations, beyond what is expected from place fields alone? To address this question, we computed place fields $F_i\left(\mathbf{x}\right)$ for each place cell from the same data used in Fig. 3A, together with the animal’s 2D spatial trajectory $\mathbf{x}\left(t\right)$ (SI Appendix, Supplementary Methods). We then generated synthetic spike trains for each neuron as inhomogeneous Poisson processes, with rate functions $r_i\left(t\right)$ given by the simple place field model as follows:

$$r_i\left(t\right)=F_i\left(\mathbf{x}\left(t\right)\right),$$ [2]

where $\mathbf{x}\left(t\right)$ is the animal’s actual trajectory (Fig. 3E). By design, the synthetic spike trains preserved the influence of place fields, but discarded all other features of the data, including precise spike timing and any nonspatial correlates. Perhaps unsurprisingly, Betti curves derived from the place field model reproduced all of the signatures of geometric organization (Fig. 3E and SI Appendix, Fig. S9 B and C), indicating that place fields alone could account for the results observed in the open field data.

We next asked whether the geometry of place fields was necessary, or whether the Betti curves during spatial navigation could be attributed to an even more basic feature of the data, which is that each neuron is driven by the same global signal, $\mathbf{x}\left(t\right),$ filtered by a cell-specific function $F_i\left(\mathbf{x}\right)$. To answer this question, we scrambled each place field by permuting the values of $F_i\left(\mathbf{x}\right)$ inside “pixels” of a $100\times 100$ grid, creating nongeometric receptive fields ${\tilde{F}}_i\left(\mathbf{x}\right)$ (SI Appendix, Fig. S9D; a $10\times 10$ scrambling is shown in Fig. 3F for clarity). We then generated spike trains from the actual trajectory, as in Eq. 2, but using the scrambled place fields ${\tilde{F}}_i\left(\mathbf{x}\right)$. For this model, we found that the second and third Betti curves were far outside of the geometric regime, whereas the first Betti curve ${\beta }_1\left(\rho \right)$ was insufficient to rule out geometric organization (Fig. 3F and SI Appendix, Fig. S9 E–H). We obtained similar results after scrambling on a $10\times 10$ grid (SI Appendix, Fig. S10). We conclude that the geometric signatures observed during spatial navigation reflect the geometry of place fields and are not simply a consequence of neurons being driven by the same global signal, $\mathbf{x}\left(t\right).$ Nevertheless, each of the Betti curves for the scrambled place field model was also significantly smaller than those of random controls (Fig. 3F; P < 0.001), suggesting that neurons controlled by a global signal via nongeometric receptive fields do exhibit nonrandom structure in their pairwise correlations.

Evidence of Geometric Organization During Nonspatial Behaviors.

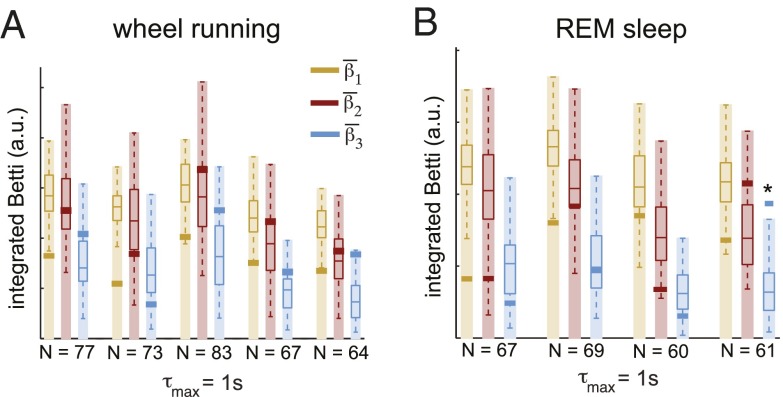
The above results suggest that geometric structure in place cell correlations is a consequence of position coding and is not necessarily expected during nonspatial behaviors. To see whether this is true, we repeated our analyses on neural activity recorded during two nonspatial conditions: wheel running and rapid eye movement (REM) sleep. Surprisingly, we found that the Betti curves were again highly nonrandom (SI Appendix, Fig. S11), and consistent with geometric organization across all five wheel running recordings and three out of four sleep recordings (Fig. 4). These findings suggest that geometric organization on a timescale of ${\tau }_{\text{max}}\sim 1$ s is a property of the underlying hippocampal network, and not merely a byproduct of spatially structured inputs. At much finer timescales, however, geometric features appear to deteriorate in both REM sleep and wheel-running conditions (SI Appendix, Fig. S12), in contrast to the open-field data (SI Appendix, Fig. S13).

Fig. 4.

Geometric organization in hippocampus during nonspatial behaviors. (A) Integrated Betti values ${\overline{\beta }}_1$, ${\overline{\beta }}_2$, and ${\overline{\beta }}_3$ (bold yellow, red, and blue lines) for five recordings from two animals, during wheel running. N indicates the number of neurons in each recording. Box plots indicate the distributions of Betti values for 100 geometric controls with matching N and dimension $d=N$. Shaded regions indicate confidence intervals for the full geometric regime, with $d\le N$. (B) Integrated Betti values for four recordings from two animals, during REM sleep. One Betti value was significantly nongeometric (*P < 0.05).

Discussion

We have developed a novel tool for detecting structural features of symmetric matrices that are invariant under the transformations most commonly observed in neural systems. We have shown that this method can reliably detect both geometric and random structure in the presence of an unknown nonlinearity. Our approach exploits the little-known fact that the ordering of matrix entries, irrespective of their actual values, carries significant information about the underlying matrix organization. Unlike eigenvalues, which can be badly distorted by monotone nonlinearities, the information encoded in the order complex is invariant.

Applying techniques from computational topology, relevant features can be extracted from the order complex that enable robust detection of geometric (or random) structure. In contrast to previous instances of topological data analysis (14–20), our method relies on the statistical properties of cycles, as captured by Betti curves and persistence lifetime distributions, and is used as a generic tool for matrix analysis, rather than the analysis of point cloud data. Although the precise dimension associated to geometric data is currently difficult to estimate, this situation should improve once we gain a better understanding of how Betti curves and persistent cycles are distorted by different types of noise.

In this work, we have emphasized two extremes: geometric vs. random. In many cases, however, correlations may be structured in a nonrandom, but also nongeometric, manner. One example of this is the scrambled place field model. Here, the existence of a global signal controlling the firing of all neurons introduced nonrandom relationships among the entries of the pairwise correlation matrix, and the Betti curves were able to distinguish this case from both the geometric and random controls. It is likely that many kinds of structure leave their fingerprints on the ordering of matrix elements and can thus in principle be detected with our methods.

In summary, we found that geometric organization of hippocampal place cell activity—a prerequisite for the existence of spatial receptive fields—can be detected from pairwise correlations alone, without any a priori knowledge about the nature of receptive fields. Using simulated data from a model, we confirmed that such geometric structure would be observed as a result of realistic place fields, but would not arise from nongeometric (“scrambled”) place fields. Perhaps surprisingly, we also found geometric organization in correlations during wheel running and REM sleep. We suggest that clique topology is a powerful new tool for matrix analysis, and one that is especially useful in biological settings, to detect relevant structure in the presence of unknown nonlinearities.

Materials and Methods

Experimental Data.

All procedures were approved by the Janelia Research Campus Institutional Animal Care and Use Committee. Spike trains of neurons in area CA1 of rodent hippocampus were recorded during three behavioral conditions: (i) spatial navigation in a familiar, 2D, 1.5 m $\times$ 1.5-m square box environment; (ii) wheel running in the context of a delayed alternation task, as described in refs. 21 and 22; and (iii) REM sleep. Experimental procedures have been previously described in refs. 21 and 23. SI Appendix, Supplementary Methods, contains further details related to the data, the computation of pairwise correlations, and the place field (PF) and scrambled PF models.

Clique Topology.

We performed topological data analysis on pairwise correlation matrices (SI Appendix, Supplementary Methods) as well as random and geometric “control” matrices (below). Here, we describe the general procedure; for more detailed explanations, see SI Appendix, Supplementary Text.

Random and Geometric Matrices.

For each symmetric matrix C we considered three types of controls: shuffled (or “random”) control matrices, WME control matrices, and geometric matrices. “Shuffled matrices” were created by randomly permuting the $\left(\begin{array}{c}N\\ 2\end{array}\right)$ off-diagonal elements of C. Because only the ordering of matrix elements is considered in the subsequent topological analyses, this is equivalent to considering random symmetric matrices with i.i.d. entries, whose corresponding order complex is a sequence of nested Erdős–Rényi random graphs. “WME matrices” were obtained by sampling the maximum entropy distribution on weighted graphs with constrained mean degree sequence induced by C. This distribution was previously described in ref. 24 (SI Appendix, Fig. S5).

“Geometric matrices” were obtained by sampling a set of N i.i.d. points uniformly distributed in the d-dimensional unit cube ${\left[\mathrm{0,1}\right]}^d\subset {\mathrm{ℝ}}^d,$ for $d\le N$. The matrix entries were then given by $C_{ij}=-\Vert p_i-p_j\Vert$, where the minus sign ensures that they monotonically decrease with distance, as expected for geometrically organized correlations.

Order Complex.

For any $N\times N$ symmetric matrix A with distinct entries, the order complex $\text{ord}\left(A\right)$ is a sequence of graphs:

$$G_0\subset G_1\subset ···\subset G_{\left(\begin{array}{c}N\\ 2\end{array}\right)},$$

where $G_0$ is the graph having N vertices and no edges, $G_1$ has a single edge $\left(ij\right)$ corresponding to the highest off-diagonal matrix value $A_{ij}$, and each subsequent graph has an additional edge for the next-highest off-diagonal matrix entry. The graphs $\left\{G_k\right\}$ can also be indexed by the edge density, $\rho =k/\left(\begin{array}{c}N\\ 2\end{array}\right)\in \left[\mathrm{0,1}\right],$ where k is the number of edges in the graph $G_k$.

Betti Curves.

A clique in a graph is an all-to-all connected set of vertices. For each graph G in the order complex $\text{ord}\left(A\right)$, we compute simplicial homology groups $H_m\left(X\left(G\right),{\mathrm{\mathbb{Z}}}_2\right)$ for $m=\mathrm{1,2}$, and 3, where $X\left(G\right)$ is the clique complex of G. We call this the clique topology of G, to distinguish it from the usual graph topology. The dimensions of the homology groups $H_m\left(X\left(G\right),{\mathrm{\mathbb{Z}}}_2\right)$, yield the Betti numbers ${\beta }_m$. Indexing the graphs by edge density ρ, we organize the Betti numbers across all graphs in the order complex into Betti curves ${\beta }_1\left(\rho \right),{\beta }_2\left(\rho \right),$ and ${\beta }_3\left(\rho \right)$.^† The Betti curves provide a summary of the topological features of the matrix A.

Computations.

All software for computing clique topology is freely available in our Matlab package CliqueTop (26). To compute Betti curves for a matrix A, we begin by finding all maximal cliques of up to five vertices (those are needed to compute ${\beta }_3$) for each graph $G_{\rho }$, with $\rho \le 0.6$. The resulting lists are then input into Perseus, a computational topology software package implemented by Vidit Nanda (27); this software builds on work by Mischaikow and Nanda (28) using discrete Morse theory to reduce the sizes of simplicial complexes before performing persistent homology computations.

Integrated Betti Values.

To facilitate the comparison of Betti curves to control matrices, we integrate the Betti curves with respect to graph density: ${\overline{\beta }}_m={\displaystyle {\int }_0^1{\beta }_m\left(\rho \right)\hspace{0.17em}\text{d}\rho }.$ The values ${\overline{\beta }}_1$, ${\overline{\beta }}_2$, and ${\overline{\beta }}_3$ were computed for each dataset. For distributions of shuffled and geometric control Betti curves, the resulting integrated Betti values are summarized in box-and-whisker plots. We used standard box plots in Matlab, with bottom, middle, and top horizontal lines on the boxes denoting first quartile ($Q_1$, 25th percentile), median (50th percentile), and third quartile ($Q_3$, 75th percentile) boundaries in the distributions of integrated Betti values; whereas the bottom and top whiskers denote $Q_1-1.5\left(Q_3-Q_1\right)$ and $Q_3+1.5\left(Q_3-Q_1\right)$, respectively.

Significance Threshold.

Our threshold for rejecting the geometric hypothesis for a given integrated Betti value was obtained from the box-and-whisker plot for a distribution of 100 geometric matrices with matching N and dimension $d=N$. Specifically, we used the top whisker value, $Q_3+1.5\left(Q_3-Q_1\right)$, as the significance threshold. The bottom whisker was not used, as Betti values lower than this are consistent with geometric matrices with smaller dimension d. In a normal distribution, 99.3% of the data lie within the whiskers, so that less than 0.4% of data points lie above the top whisker. Our integrated Betti values ${\overline{\beta }}_m$ for geometric controls, however, are not normally distributed. In the case of ${\overline{\beta }}_1$ and ${\overline{\beta }}_2$, the top whisker corresponds, on average, to the 98th percentile of the distribution. In the case of ${\overline{\beta }}_3$, the top whisker is just under the 97th percentile value. A data point above the top whisker is thus inconsistent with geometric controls with P < 0.05. For comparisons against shuffled/random control distributions, we computed the P value directly from the distribution, as in these cases we built the distributions from 1,000 trials, rather than just 100. Note that clique topology computations are much faster for matrices with random structure than for geometric matrices, because of differences in the statistics of the cliques.