Tomography of a Cryo-immobilized Yeast Cell Using Ptychographic Coherent X-Ray Diffractive Imaging

Abstract

The structural investigation of noncrystalline, soft biological matter using x-rays is of rapidly increasing interest. Large-scale x-ray sources, such as synchrotrons and x-ray free electron lasers, are becoming ever brighter and make the study of such weakly scattering materials more feasible. Variants of coherent diffractive imaging (CDI) are particularly attractive, as the absence of an objective lens between sample and detector ensures that no x-ray photons scattered by a sample are lost in a limited-efficiency imaging system. Furthermore, the reconstructed complex image contains quantitative density information, most directly accessible through its phase, which is proportional to the projected electron density of the sample. If applied in three dimensions, CDI can thus recover the sample's electron density distribution. As the extension to three dimensions is accompanied by a considerable dose applied to the sample, cryogenic cooling is necessary to optimize the structural preservation of a unique sample in the beam. This, however, imposes considerable technical challenges on the experimental realization. Here, we show a route toward the solution of these challenges using ptychographic CDI (PCDI), a scanning variant of coherent imaging. We present an experimental demonstration of the combination of three-dimensional structure determination through PCDI with a cryogenically cooled biological sample—a budding yeast cell (Saccharomyces cerevisiae)—using hard (7.9 keV) synchrotron x-rays. This proof-of-principle demonstration in particular illustrates the potential of PCDI for highly sensitive, quantitative three-dimensional density determination of cryogenically cooled, hydrated, and unstained biological matter and paves the way to future studies of unique, nonreproducible biological cells at higher resolution.

Introduction

Coherent (x-ray) diffractive imaging (CDI) is a relatively new microscopic technique that allows nanoscale imaging with very high spatial and contrast sensitivity (1, 2, 3). CDI and its variants share the common characteristic that the conventional objective lens between sample and detector is replaced by a numerical reconstruction scheme. Without the constraints imposed by the use of a specific optical element to form an image on the detector, the method is inherently only diffraction-limited in resolution. Furthermore, if extended to three dimensions, CDI yields quantitative density information from the reconstructed volume (4, 5, 6).

Nevertheless, classical CDI, which is based on the application of a planar wave field to an isolated sample and the observation of the resulting diffraction in the optical far field, is limited to samples significantly smaller than the lateral extent of the illuminating wave field (the probe). Ptychographic coherent x-ray diffractive imaging (PCDI) has overcome this limitation by combining the reconstruction of the sample exit wave field and the probe simultaneously, thus extending conventional CDI to a scanning technique (7, 8, 9, 10, 11). Shortly after its introduction, PCDI has also been extended to three dimensions (12, 13, 14, 15, 16).

As a highly sensitive (17, 18, 19, 20) and quantitative (12, 13, 14, 20, 21, 22) lensless imaging technique, PCDI offers great potential—especially in application to biological materials from subcellular structures (22), single or a few cells (15, 18, 20, 21, 23, 24), multicellular complexes (13), and tissue (25), to fractions of mammalian bone (12). For a review of applications using CDI, particularly in the context of biological imaging, see Larabell and Nugent (2) and Mancuso et al. (26).

Despite its advantages, (ptychographic) CDI is subject to limitations due to radiation damage (27). Radiation damage can be observed as structural changes due to molecular reordering processes arising from the interaction of an intense x-ray wave field with biological matter. Changes first appear for lower dose at higher spatial frequencies (smaller features) and then proceed with increasing dose to lower spatial frequencies (larger features). This structural damage is usually accompanied by a significant mass loss in the specimen (28), and ultimately limits the resolution to which structural details may be resolved.

Several methods exist to circumvent the radiation damage problem. One of the most anticipated realizations of CDI applied to biological samples is the use of ultrabright x-ray free electron laser radiation to collect many diffraction measurements from identical copies of a sample to compose a three-dimensional (3D) representation (29, 30). Here the diffraction pattern is collected before the structural disintegration of the sample due to the very short and intense x-ray pulses (30, 31, 32). The limitation of this method is that the sample must be available in many copies that are identical, or near-identical. While biological samples may be sorted into categories (e.g., into identifiable cell lines or physiological state), they display—to different extents—a structural diversity that can further complicate such experiments.

Alternatively, CDI experiments at (quasi-)continuous sources (e.g., synchrotrons) rely on techniques to prevent or at least limit reordering, i.e., radiation damage (18, 20, 33, 34, 35). It thus becomes possible to obtain 3D structural insight from a single, unique object by imaging it over a series of projection angles (tomography).

A minimum alteration of the sample structure can be achieved by fixing the object under study in its closest-to-natural state. For biological samples in an aqueous environment, this can be performed merely by cooling to cryogenic temperatures (36). Here, the method of vitrification, i.e., rapid cooling of an aqueous sample into an amorphous phase, combines the goal of minimal structural or chemical alteration with that of a fixed and radiation-protected environment (36, 37).

While imaging under cryogenic conditions has now become standard in lens-based (soft) x-ray tomography (38, 39) and has been demonstrated for two-dimensional (2D) CDI in plane wave (33, 34, 35) and ptychographic mode (18, 20), it has not yet been routinely established for 3D coherent imaging techniques. As a first demonstration, 3D imaging of a cryogenically cooled hydrated biological cell using plane-wave CDI has been reported very recently (40). We present here a quantitative 3D PCDI experiment on a single, unstained, and unsliced yeast cell (Saccharomyces cerevisiae) that has been immobilized and imaged at cryogenic temperature (100 K) in its aqueous environment. In particular, we describe how a quantitative (electron) density reconstruction may be obtained for a flat sample geometry. This resembles the geometry used in cryo-electron tomography (41) and is ideal for cryo-immobilization by rapid injection into a liquid coolant, as it offers a direct interaction surface between the coolant and the sample, facilitating the vitrification process (37).

Materials and Methods

Sample preparation

Diploid Saccharomyces cerevisiae (Baker’s yeast, strain CEN.PK; type: MATa ura3-52 his3-D1, leu2-3, 112 tryp1-289, MAL2-8 SUC2) cells were grown in a shaking incubator at 37°C and 200 rpm in YPD medium, pH 7, supplemented with Carbenicillin (100 μg/mL) to avoid bacterial growth. To increase the sample complexity with respect to the resting state, cells were harvested in the exponential phase when >80% of the cells were budding. A quantity of 30 mL was centrifuged at 4000 rpm, 4°C, for 5 min and washed with 5 mL PBS (phosphate-buffered saline) buffer (10 mM Na₂HPO₄ × 7 H₂O, 1.8 mM KH₂PO₄, 137 mM NaCl, 2.7 mM KCl, pH 7.4). After further centrifugation the cells were resuspended in 20 mL PBS, pH 7.5, and refrigerated until usage for rapid freezing (see below). To suppress the formation of crystalline ice during cryo-fixation the cells were finally resuspended in PBS supplemented with 10% (vol/vol) glycerol, yielding a final concentration of 5% (vol/vol) of glycerol.

Cryo-immobilization was carried out in a commercial plunging device (EM-GP; Leica Microsystems, Wetzlar, Germany) that allowed for a controlled environment before injection (relative humidity >95%; temperature (T) ∼21°C). A microfabricated polyimide foil (MiTeGen, Ithaca, NY) with a thickness of 12.5 μm, mounted on a steel pin, was used as a sample holder (see Fig. 1). The foil was hydrophilized using an air plasma cleaner (Harrick Plasma, Ithaca, NY), then mounted in the plunger, and a small amount of cell suspension (<1 μL) was deposited onto it. After a resting period of a few minutes the majority of liquid was soaked away using a fine paper wick (MiTeGen), followed by rapid injection into the cryogenic liquid (ethane/propane at 38:62 vol % ratio (42), T = ∼−193°C) and subsequent transfer into liquid nitrogen for storage.

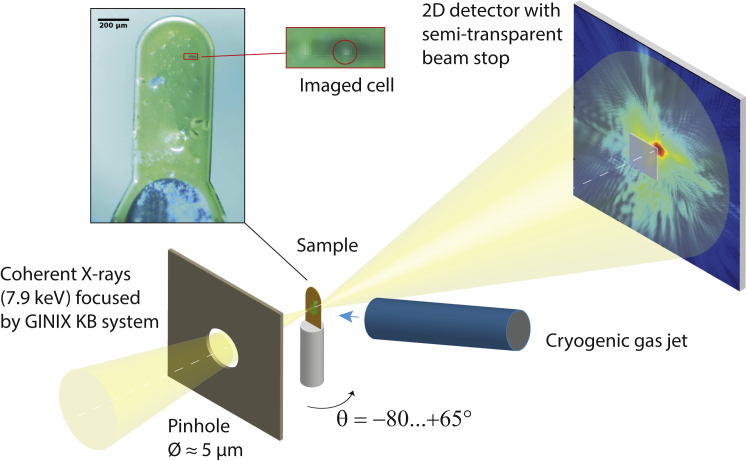
Figure 1.

Schematic of the experimental setup. The aqueous cell suspension was kept on a thin polyimide foil attached to a steel pin that was surrounded by a cryogenic nitrogen stream. The direct beam was attenuated by a semitransparent beam stop placed in front of the two-dimensional detector. The sample was scanned in a plane perpendicular to the optical axis (dashed white line). The tomographic rotation axis about the angle θ was oriented parallel to the steel pin of the sample holder, with θ = 0° corresponding to the substrate being roughly perpendicular to the optical axis. (Inset, upper-left) Optical image of the sample holder obtained using an in situ microscope. (Red circle) The cell imaged in this work, within the magnified region.

At the beamline the sample was transferred manually into a cryogenic gas stream (100 K; Oxford Cryosystems, Long Harborough, Oxon, UK). This process required some manual readjustment to optimize the position of the sample in the cryogenic stream. Note that in ultrastructural studies by soft x-ray microscopy, S. cerevisae cells have been cryo-immobilized by direct insertion into a cryogenic gas stream, rather than liquid ethane, and no structural damage due to ice formation was observed (43). A video showing the sample holder at different orientations in the cryogenic stream is attached as Movie S1 in the Supporting Material.

Experimental setup

The experiment presented here was performed at the P10 beamline of the PETRA III storage ring at DESY, Hamburg, Germany, using the Göttingen Instrument for Nano-imaging with X-rays (GINIX). Detailed descriptions of this device can be found in Kalbfleisch et al. (44) and Salditt et al. (45). A schematic of the setup is given in Fig. 1.

The photon energy was set to 7.9 keV, monochromatized by a double-crystal Si (111) monochromator. The focal size of the GINIX setup was adjusted by slits opened to 50 μm in horizontal and vertical direction, located at ∼3.3 m upstream of its Kirkpatrick-Baez focusing mirrors. A tungsten pinhole (diameter ∼5 μm; thickness 40 μm) placed 6 mm upstream of the focal plane was used to confine and optimize the focus (46). As a result, we obtained a nearly fully coherent focus with a diameter of ∼0.5 μm.

The yeast sample was mounted onto a 3D piezo-electric translation stage (Physik Instrumente, Karlsruhe, Germany) and was placed at ∼2.8 mm downstream of the focal plane. This allowed for sufficient distance of the cryogenic gas jet, cooling the sample, to the pinhole further upstream. The translation stages rested on top of an air-bearing high-precision rotation stage (PI miCos, Eschbach, Germany), which provided the tomographic rotation axis (θ). For visualization and locating the sample, an in situ optical microscope with a drilled objective lens (Research Instruments, Bergisch Gladbach, Germany, formerly Accel Instruments) was mounted downstream of the sample, aligned coaxially with the x-ray beam.

A 2D detector (Pilatus 300K; Dectris, Baden, Switzerland) with a pixel size of 172 × 172 μm² was placed 5.11 m downstream of the focal plane. In contrast to a more standard setup for ptychographic CDI (8), a semitransparent beam stop (47) was installed in front of the detector. We could thus exploit the high coherent flux of the GINIX instrument (48), using a low overall attenuation factor of ∼3 with an incident coherent flux >10⁹ photons/s. By using a detector with even higher dynamic range, this experiment could be carried out without any global attenuation (49).

For the collection of the tomographic data, the biological sample was first positioned into the instrument’s center of rotation using the in situ optical microscopy and subsequently, for better resolution, online scanning transmission x-ray microscopy in differential phase contrast mode (50, 51).

Data collection

Ptychography is a scanning variant of CDI where the sample is illuminated by a beam considerably smaller than the sample’s spatial extent at multiple, overlapping regions (7, 8, 9, 10, 11). Typically, the sample is scanned in a plane perpendicular to the direction of the beam propagation, while at each scan point a diffraction pattern is recorded on a 2D detector. The common information in diffraction data from overlapping points is exploited, and leads to an improved stability and robustness of the ptychographic algorithm compared with traditional plane wave CDI (10).

In this experiment, ptychographic scans were taken at projection angles separated by 2.5°, covering a range from θ = −80° to θ = 65°, resulting in a missing wedge of 35°. Each ptychographic scan used 540 scan points, placed on a non-Cartesian grid to suppress the formation of artifacts from the scanning grid (17). Each scan covered a rectangular area of 11 μm × 9 μm (horizontal × vertical). For the first three out of the fifty-nine covered projection angles, an illumination time of 0.15 s per frame was applied. To optimize the signal on the detector, the illumination time was then increased to 0.2 s per scan point for the remaining scans.

The net illumination time was ∼1.8 min per ptychographic scan and ≤1.8 h for the whole dataset. This fast scanning is very beneficial for optimum ptychographic imaging using a cryogenic stream (18, 34), as effects of thermal drifts on the sample and motor positions are minimized.

To assess potential structural changes due to radiation damage, an image at θ = 0° (i.e., with the optical axis oriented perpendicular to the sample support) was taken before and at the end of the tomographic data collection process (see below).

To assist the reconstruction of the tomographic data from the weakly scattering biological sample, the probe wave field was precharacterized in a first experiment on a strongly scattering test sample (17).

Ptychographic reconstruction of projections

For all diffraction data, the central 128 × 128 pixels were selected for further analysis from each diffraction pattern, resulting in a real-space pixel width of 36.4 nm. The pixels covered by the semitransparent beam stop were rescaled according to the expected transmission factor for 300 μm of silicon (density 2.33 g/cm³) at 7.9 keV, 1.145 × 10⁻² (52). One horizontal line of pixels, 18 pixels long, was masked out from the data and left unconstrained in the algorithm, as here the beam stop was only partially covering the pixels, so that the theoretical transmission factor could not be applied.

Each projection from the biological sample was then reconstructed using the predetermined probe as a starting point for the illumination function and a random array for the object. For reconstruction, we applied the so-called ptychographical iterative engine (11). For further details on the ptychographic reconstruction, see Section S1.1 in the Supporting Material.

Alignment of projections

The ptychographic reconstruction process yielded 59 2D reconstructions at different projection angles. A necessary step before tomographic reconstruction is the lateral alignment of the projections. This involves two steps, firstly the intrinsic alignment of projections with respect to each other, yielding a fixed global rotation axis, and secondly, the alignment of the global rotation axis with respect to the numerical field of view.

Without fiducial markers, such as gold nanoparticles, the lateral alignment of projections must be based on intrinsic properties of the projections themselves (41). One common method is based on the center of mass of the projections (53). This, however, can only be applied as long as the total mass in the field of view is constant for all projections. In principle, this is also true for the case of a plane-parallel slab of material surrounding and supporting a cell, after a correction for the background density of that substrate is made (see below). However, if, e.g., the sample substrate varies in thickness, the background density is no longer constant and an alignment approach based on the center of mass may become inaccurate, even after empirical correction of the background in each projection (see below).

We therefore followed another well-known approach that is based on correlations between neighboring projections (41). Due to the high degree of cylindrical symmetry in the sample, we omitted a geometric scaling factor that is usually required for flat samples (41). As the phase reconstructions themselves provided a correlation signal too small for reliable alignment, we used the support masks of the cell at each projection angle as input to the calculation of correlation values. These masks were determined by visual inspection of each phase projection and manual definition of a polygon enclosing the cell body.

Once the dataset is internally aligned, the lateral position of the common axis of rotation must be identified. Within experimental accuracy, the center of mass of the support at projection at θ = 0 coincided with the horizontal position of the axis of rotation. As we did not observe significant “tuning-fork”-type artifacts in resulting tomographic slices we did not further optimize this selection (54). The so-determined center of rotation was then used as the horizontal center of the selected region of interest (221 × 221 pixels) around the support in each projection. The second (vertical) center coordinate for the region of interest, whose absolute position does not influence the (parallel-beam) tomographic reconstruction, was simply chosen such that the whole cell was covered by the field of view.

Modeling of background contributions

The subtraction of background contributions can dramatically improve reconstructions, as the sample contribution can then be clearly differentiated. The subtraction of modeled background has been considered in coherent x-ray microscopy, using a glass capillary as a sample holder (55). This background structure is rotationally symmetric, which is advantageous for tomographic applications, but due to its high density may contribute much more to the diffraction signal than a biological cell inside. This leads to additional effects such as phase wrapping, which need to be corrected for separately.

The yeast cell imaged here is embedded within a thin aqueous layer on a flat supporting substrate. This geometry has two important implications for tomographic (phase) microscopy. Firstly, the flat shape of the sample support imposes a missing wedge of inaccessible projection angles, as well known from, e.g., (cryo-)electron microscopy (41). Secondly, in general, the absolute electron density of the slab material cannot be determined from the phase reconstructions alone; the reconstructed object phase is only known up to an arbitrary offset and furthermore, if the edges of the support structure never enter the field of view, there is no absolute reference (such as air surrounding the sample holder) to which the phase offset could be calibrated. Instead, the reconstructions are sensitive only to the excess density of the cell relative to its surrounding. As seen below, this does not generally prevent a quantitative reconstruction and can be even advantageous from an experimental point of view, as the signal of interest (from the cell) is not buried in a potentially much larger background signal (from, e.g., the sample holder).

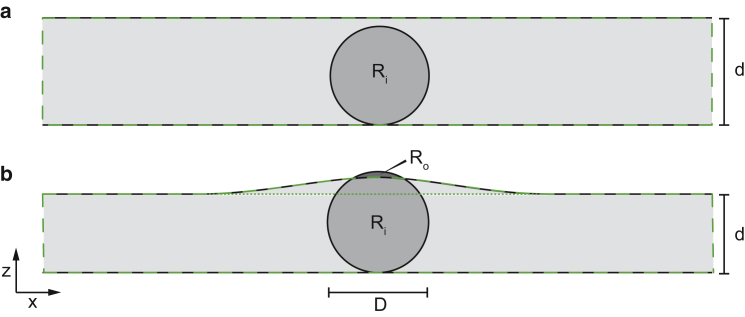
As depicted in Fig. 2 a, we consider a slice through a plane-parallel slab that is oriented parallel to the x,y plane in a right-handed Cartesian coordinate system, with an overall width L along the x axis. The x-ray beam propagates along the z direction, with the tomographic rotation axis (θ) oriented parallel to the y axis. The cell (region R_i) of diameter D << L is assumed to be totally immersed into the slab. In the slice the cell and the surrounding medium may then be described by density functions ρ_c(x,z) and ρ_m(x,z), respectively. ρ_c(x,z) has a compact support with diameter D. Let ρ_m(x,z) = ρ₀χ_m(x,z) denote the density of the medium. Here χ_m denotes the characteristic function of the medium (including the area of the cell), which is equal to 1 inside the medium and vanishes outside, as indicated by the areas enclosed by a dashed green line in Fig. 2, a and b. In analogy to buoyant density (56), let ρ_c⁽⁺⁾(x,z) = ρ(x,z) − ρ₀χ_m(x,z) denote the excess cell density, i.e., the difference of the absolute (cell) density and the density contribution of the medium. The total density function of cell and medium is then given as

$$\rho \left(x,z\right)={\rho }_c^{(+)}\left(x,z\right)+{\rho }_0{\chi }_m\left(x,z\right).$$ (1)

Now let ${\Re }_{\theta }\left[f\left(x,z\right)\right]\left(t\right)$ denote the Radon transform of a 2D density function f(x,z), with t denoting the coordinate along the axis perpendicular to the projection direction (within the x,z plane). Due to the linearity of the Radon transform (57), the projections may be separated into background and cell contributions, i.e.

$${\Re }_{\theta }\left[\rho \right]={\Re }_{\theta }\left[{\rho }_c^{(+)}\right]+{\Re }_{\theta }\left[{\rho }_m\right].$$ (2)

For a plane-parallel slab, the background term ${\Re }_{\theta }\left[{\rho }_m\right]$ on the right-hand side of Eq. 2 is constant, as long as the field of view is smaller in the horizontal direction than the projected width L × cosθ of the slab for all applied projection angles.

Figure 2.

Slice through a simplified model for a cell within a plane-parallel slab of material, e.g., amorphous ice. (a) A biological cell (region R_i, medium gray, diameter D) is immersed into a plane-parallel slab of material (light gray, thickness d). The width L of the slab in the x direction is assumed to be much larger than D and thus extends outside the figure area. (b) With d < D, a large fraction of the cell (region R_i, medium gray) is still contained within the slab, but a small fraction protrudes from it (region R_o, dark gray). Slices are shown parallel to the x,z plane. (Dashed green line in a and b) Extension of the modeled slab, i.e., the support of ρ_m(x,z). (Dotted horizontal line in b) Separation between the homogeneous and inhomogeneous component of ρ_m(x,z).

In phase tomography the projected density ${\Re }_{\theta }\left[\rho \right]\left(t\right)$ is proportional to the obtained phase change due to the material in the beam, ${\overline{\Phi }}_{\theta }\left(t\right)\propto {\Re }_{\theta }\left[\rho \right]\left(t\right)$. As ${\overline{\Phi }}_{\theta }\left(t\right)$ is only defined up to an arbitrary offset, the reference can always be set such that ${\overline{\Phi }}_{\theta }\left(t\right)=\kappa \times {\Re }_{\theta }\left[{\rho }_c^{(+)}\right]\left(t\right)$ for all θ, i.e., ${\overline{\Phi }}_{\theta }\left(t\right)=0$ for t outside the support S of the cell. The value κ here denotes a constant scaling factor. The integral ${\int }_S{\overline{\Phi }}_{\theta }\left(t,y\right)\text{d}t\text{d}y$ then remains constant for all θ, after setting the offset for each of the obtained ${\overline{\Phi }}_{\theta }\left(t,y\right)$ to zero outside the cell support.

The projections thus contain nonconstant density variations due to the cell only, reduced in contrast by the constant (projected) density contribution of the surrounding medium. If known, the constant density ρ₀ can be added after inverting the Radon transform numerically, in order to obtain the absolute density ρ_c(x,z) of the cell.

Consider now a case that differs from the previous case in two aspects: the cell is not completely immersed into the slab and, due to surface tension, the surface of the water layer is slightly curved surrounding the cell, as depicted in Fig. 2 b. Nevertheless, Eq. 2 remains valid and ρ_m may now be divided into several parts that additively form the total background arising from the medium surrounding the cell. If the functional form of these components is known, they may each be corrected for individually by subtraction—before inverting the tomographic projections.

The total density of cell and water may now be written as

$$\rho \left(x,z\right)=\left[{\rho }_{c,\text{in}}^{(+)}\left(x,z\right)+{\rho }_{c,\text{out}}\left(x,z\right)\right]+\left[{\rho }_{m,\text{hom}}\left(x,z\right)+{\rho }_{m,\text{inh}}\left(x,z\right)\right],$$ (3)

where ρ_c,in⁽⁺⁾(x,z) = (ρ(x,z) − ρ₀)χ_m(x,z) denotes the (excess) density of the cell inside the medium (region R_i) and ρ_c,out(x,z) = ρ(x,z) × (1 − χ_m(x,z)) is the (absolute) cell density outside the medium (region R_o). Furthermore, the medium (indicated by a dashed green line in Fig. 2 b) is composed of a homogeneous component ρ_m,hom with constant thickness d (as per our earlier example) and an (additional) inhomogeneous component ρ_m,inhom with varying thickness, delineated by the dotted green line in Fig. 2 b. As before, all of the background material is assumed to have a constant density ρ₀. Again, due to the linearity of the Radon transform, each component on the right side of Eq. 3 can be transformed individually. For small enough projection angles, the term ρ_m,hom leads to a constant phase offset that can be set to zero at each projection (as above). After further subtraction of a modeled phase background due to the inhomogeneous component ρ_m,inhom, the reconstructed density only has contributions from the cell itself, with excess density

$${\rho }_c^{(+)}\left(x,z\right)={\rho }_{c,\text{in}}^{(+)}\left(x,z\right)+{\rho }_{c,\text{out}}\left(x,z\right).$$ (4)

Eq. 4 illustrates that a protrusion of the cell from a (nearly) plane parallel slab leads to a pronounced region of higher phase retardation in the projections (caused by ρ_c,out), compared with the remaining areas in the cell. This is because the protruding fraction is not surrounded by the slab medium, and hence exhibits a higher contrast to its background than the volume inside the slab. Such an effect was confirmed by simulation as shown in Section 1.2.1 in the Supporting Material.

Experimental background subtraction

As described by the theoretical model, we have corrected the ptychographic phase projections by subtraction of an inhomogeneous component and the subsequent offset equalization (to a vanishing phase outside the cell area). While the latter corresponds to the correction for the homogeneous component, the former accounts for a fraction with a curved surface in the vicinity of the cell. This fraction was modeled by fitting a 2D Gaussian height distribution function with a full width at half-maximum of 8 μm to the background around the cell at projection at θ = 0°. The resulting phase contribution, assuming a water density of 1.0 g/mL, was then calculated for all projection angles and subtracted from the projections. Here an angular deviation α = 5° and translational offset Δz = 1 μm of the inhomogeneous water layer from the axis of rotation were also taken into account, as determined by exploring the residual between modeled and experimental background within a small range of values for α and Δz.

To correct for remaining inhomogeneity in the horizontal direction, arising mainly for projection angles θ < −65°, a further correction step was applied. The vertical mean of the lowermost 12 and the uppermost 10 rows in each projection was formed and the result smoothed by convolution with a Gaussian (standard deviation of 5 pixels). The result was then subtracted from each row in the projection. This inhomogeneity in the horizontal direction, which is not accounted for in the analytical model of the water surface, may be caused by inaccuracies in the model and by additional material that enters the field of view for very high projection angles and thus eludes modeling here, based on the projection at θ = 0°. This last correction step also accounts for equalizing the arbitrary phase offset in the background to nearly the same level for all projection angles.

To suppress high-frequency artifacts in the tomographic reconstruction, the projections were finally low-pass-filtered by a Gaussian with a standard deviation of 1.5 pixels. This value is below the spatial resolution as determined here (see below).

The full series of all projections, after alignment and background correction, can be seen in Fig. 3. An elliptically shaped area of locally increased phase change can be observed in all projections. As discussed previously, this region is attributed to the small fraction of the cell that protrudes the water layer surrounding it, thus leading to a higher apparent contrast (against air) than in the remainder of the cell (against water). This effect was also confirmed by reconstruction of a simulated dataset (see Fig. S1 in the Supporting Material).

Figure 3.

Overview of the experimentally obtained tomographic projections at angles θ = −80° to θ = +65° (left to right and top to bottom), with increments of 2.5°. Each of these projections represents a ptychographic reconstruction, aligned and background-corrected. Note that, for the projections at −80° and −77.5°, another cell becomes visible on the right side of the field of view.

The effect of the background subtraction procedure on the overall phase sum in the background area of each projection is illustrated in Fig. S2.

Tomographic reconstruction and determination of the 3D electron density distribution

A tomographic reconstruction was performed by standard filtered back projection using linear interpolation and a Shepp-Logan filter as provided by the built-in MATLAB (Ver. R2012a; The MathWorks, Natick, MA) routine iradon.m. The voxel side length was fixed by the experimental geometry and the selected detector field of view to Δr = 36.4 nm. The excess electron density, i.e., the difference to the density of the surrounding medium, is given here by

$${\rho }_{\mathrm{c}}^{\left(\mathrm{+}\right)}\left(x,y,z\right)=\frac{2\pi }{r_{\mathrm{e}}{\mathit{\lambda }}^2}\mathrm{\cdot }{\mathit{\delta }}_{\mathit{c}}^{(+)}\left(x,y,z\right),$$ (5)

with

$${\mathit{\delta }}_{\mathit{c}}^{\left(\mathrm{+}\right)}\left(x,y,z\right)=-\frac{\mathit{\lambda }}{2\pi \Delta \mathit{r}}{\mathrm{\Phi }}_c^{(+)}\left(x,y,z\right),$$ (6)

where Φ_c⁽⁺⁾(x,y,z) denotes the background-corrected reconstructed phase contribution of the cell for each pixel, λ is the photon wavelength, δ_c⁽⁺⁾(x,y,z) is the refractive index profile (beyond the background level), and r_e is the classical electron radius. Here the relations outlined, e.g., in Dierolf et al. (12), were adapted to the considered sample geometry and ρ_c⁽⁺⁾(x,y,z) is defined in 3D analogously to Eq. 4 in two dimensions. If the accurate density of the water that surrounds the sample is known, it may be added to the excess density within the medium, yielding absolute density. Note that for partial immersion, the value ρ_c⁽⁺⁾, as defined in Eq. 4, has a contribution both in and outside the medium. Ideally, they differ in density only by the constant water background density.

After the tomographic reconstruction, a 3D support for the 3D density distribution was generated from the manually obtained supports of the 2D projections. To this end, the manually determined 2D support maps were low-pass filtered by Gaussian convolution with a standard deviation of 3 pixels and afterwards reconstructed by filtered back projection. To form the final 3D support, the resulting volume was first thresholded such that values ≥ 0.006 were set to 1 and others to 0. Afterwards, the resulting support volume was filtered by a 3D Gaussian with standard deviation of 3 pixels.

Results and Discussion

Computed tomography

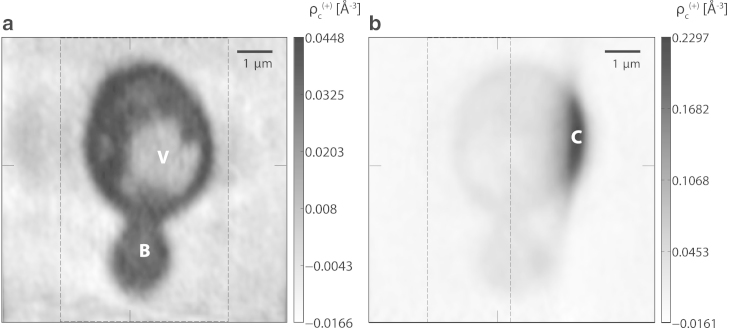
A tomographic slice in the plane perpendicular to the optical axis (at θ = 0°) is shown in Fig. 4 a. The cell is clearly visualized with high contrast against the background, and a bud (B) at the bottom of the mother cell can be easily identified. Here the excess electron density with respect to the surrounding medium is shown, which varies around zero outside the cell. Inside the cell, the excess density is ∼5–15% times the electron density of water at ambient conditions (${\rho }_e^{\left({\text{H}}_2\text{O}\right)}=0.3361$ Å⁻³, as obtained by elemental conversion from a refractive index value of ${\delta }_e^{\left({\text{H}}_2\text{O}\right)}=3.7126\times {10}^{-6}$ (52), assuming pure water with a mass density of 1.0 g/mL and a photon energy of 7.9 keV).

Figure 4.

(a) Tomographic slice (voxel sidelength 36.4 nm) perpendicular to the optical axis at θ = 0°. Considerable internal cell structure becomes apparent, including a low-density region (V) that is interpreted as a vacuole inside the cell. The bud (B) is clearly visible. (Black markers at the bottom and top of the frame) Position of the slice shown in (b). (b) Tomographic slice in a plane perpendicular to the slice shown in (a). An area of higher excess density (C) becomes apparent where the cell protrudes from the water layer surrounding it (see main text). The corresponding perpendicular slice shown in (a) is indicated (markers at the bottom and top) as before. For both subfigures, the volume used for quantitative density analysis (see main text) is indicated (dashed rectangle). (Horizontal markers) Position of the slice shown in Fig. S3 in both subfigures. (Grayscale in a and b) Excess electron density (see main text).

The internal structure of the cell becomes more apparent in the tomographic slice than in the projections (see Figs. 3 and 4). For example, a region with lower nominal electron density (V) is clearly visible in the center of the cell, while it is less easily identified in the projections. Based on its density and shape, this region is attributed to a vacuole inside the mother cell. Other density variations on smaller lateral length scales start to become visible as well. Most of the cell’s interior is more dense than pure water by a small, but significant relative density offset of ∼0.03 Å⁻³.

A slice in a perpendicular plane is shown in Fig. 4 b. Here the region of higher excess electron density (C) at the edge of the cell becomes visible. The form of this region resembles a spherical cap protruding outside a 2D surface, consistent with its interpretation as the cell protruding from the aqueous layer (see above and Sections S1.2 and S1.3 in the Supporting Material). This protrusion qualitatively explains the higher excess density in region C, which is caused by the different offset densities in- and outside the medium surrounding the cell. Its exact density value is not considered to be quantitative, as it could be influenced by the unmeasured missing wedge of projections and unknown factors such as components of the sample not modeled in the correction, but coming into the beam at high projection angles. The region of higher excess density is also visible in a plane perpendicular to the rotation axis as shown in Fig. S3.

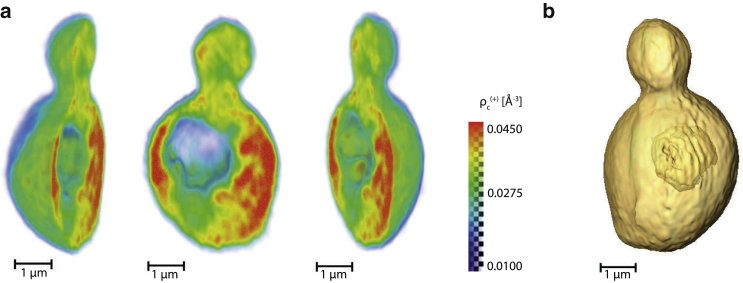
In contrast to the region protruding from the water layer, the density in the opposite half of the reconstructed volume remains essentially unaffected by the water surface after background correction. Therefore, a half-cylindrical section R_q around the rotation axis, with a radius of 0.3 times the field of view, was selected from this volume for quantitative analysis. The region R_q is indicated by dashed lines in Figs. 4, a and b, and S3 a. Using this region and a density threshold $\ge 0.04{\rho (}_{\text{e}}^{{\text{H}}_2\text{O}})$ a cellular region R_c ⊂ R_q was obtained whose density is illustrated in Fig. 5 a. Before rendering the density distribution (Amira Ver. 5.4.2; Visage Imaging, Berlin, Germany), isolated regions below the threshold within the cell were added to the cell support using morphological image processing (function imfill, MATLAB; The MathWorks). The region identified as a vacuole in the tomographic slices is clearly visible, with additional small density fluctuations inside the cell.

Figure 5.

Three-dimensional (3D) renderings of the obtained tomographic reconstructions. (a) The 3D electron density distribution, used for obtaining the overall density mean (see main text and dashed rectangles in Fig. 4), is visualized. The colorscale, which also indicates corresponding levels of transparency, has been clipped to values between 0.010 and 0.045 Å⁻³. (b) Isosurface representation of the cell density (threshold value 0.015 Å⁻³), after multiplication with the 3D support function (see main text).

The outline of the 3D shape of the budding cell can be seen in Fig. 3 b, which shows an isosurface representation of the cell density. The cell volume was defined here by multiplication of the reconstructed 3D density distribution by a 3D support function (see above). The volume corresponding to this 3D support is ∼52 μm³, a value well in accordance with the expected range of volumes in the early budding state (56, 58).

Mean cell electron density and sensitivity

The mean excess electron density value within the volume R_c amounts to $\langle {\rho }_c^{(+)}\rangle =$ 0.027(0.010) Å⁻³, where the standard deviation of 0.010 Å⁻³ is a measure of the natural density variation inside the cell. Its statistical or measurement uncertainty can be determined by the standard deviation of density values in the region outside the cell (12), i.e., the complement of R_c within R_q. This is amounts to 0.005 Å⁻³. This is an upper bound for the very high sensitivity of the method, as in general peak locations in density distributions may be discriminated with lower uncertainty than given by the peak width (12).

To assess the accuracy of $\langle {\rho }_c^{(+)}\rangle$ within the cell on an absolute scale, we consider a reference value of 1.1049(0.0024) g/mL for the mass density of a yeast cell at the start of the budding process (the so-called S-phase) (56), as determined on an ensemble of many hundreds of cells. With respect to water with a density of 1.0 g/mL, this corresponds to an excess electron density of 0.030(0.001) Å⁻³, assuming a water mass fraction of 78%, and a protein mass fraction of 22% with a protein molar composition H₅₀C₃₀N₉O₁₀S₁ (18).

The deviation between the value derived from the literature and the value obtained in this experiment may be explained by natural variations from cell to cell, differences in used strains and a decrease in water mass (and electron) density due to the freezing process. This can be as high as ∼7% for pure water (37). In addition, the conversion of the reference mass-density value into electron density depends on the chemical composition of the yeast cells, which is not exactly known. Nevertheless, with respect to the absolute electron density of the reference sample at room temperature, the deviation between the value as determined here and the reference is on the level of only 1%. The determined excess electron density value strongly suggests that the nonprotruding volume of the cell was fixed and imaged in its natural frozen-hydrated state.

Dose and resolution

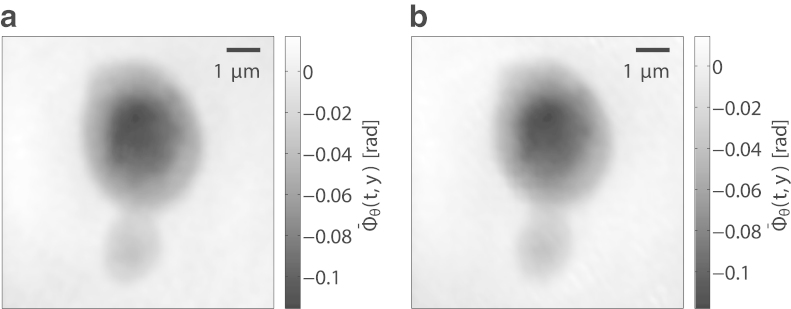
To assess the radiation damage effects in this experiment, a projection at θ = 0° was obtained before and after recording the tomographic dataset. The two resulting phase projections (after background correction and filtering as described above) are shown in Fig. 6. There is no significant change in overall structure and the total phase sums in both images deviate by as little as 2.5%, indicating a high level of cell mass preservation during the experiment. It is noted that remaining differences, e.g., in the background structure surrounding the cell, are on the uncertainty level of the iterative reconstruction.

Figure 6.

Ptychographic projections (phase) before (a) and after (b) collection of the tomographic dataset. Differences between the two images are very small, and there is no obvious sign of radiation damage visible.

The total fluence delivered to the sample during tomographic data collection was ∼8.0 × 10¹⁰ photons per μm², resulting in an average fluence of 1.4 × 10⁹ photons per μm² per projection. For a mass density of 1.094(0.031) g/mL, as determined from the mean electron density within one half of the cell, and assuming a chemical composition as described in Lima et al. (18), the resulting average dose per projection is ∼1.8 × 10⁶ Gy. This results in a relatively low total applied dose of ∼1.1 × 10⁸ Gy for the whole dataset, which is only expected to damage structures in the sample on length scales shorter than 10 nm (27).

The (half-period) resolution of the 3D density distribution was determined by using Fourier shell correlation (FSC), a standard method in 3D electron microscopy (59), which has become increasingly common in coherent imaging applications (16, 60). More specifically, the FSC curve was determined from two independent tomographic reconstructions, each using only every second projection. Before correlating them, the two 3D reconstructions were aligned with respect to each other using subpixel correlation (61). Note that, to yield the most accurate representation of the resolution, no low-pass filtering was performed on the phase reconstructions used here. The resulting FSC curve is presented in Fig. S4.

The (half-period) resolution as determined from the FSC curve is 234 nm. It is noted that, compared to other measures, this global measure of resolution is relatively conservative as it summarizes all internal correlations within the sample, rather than referring to a single feature, e.g., a sharp edge in the sample. Therefore, in comparing resolution values in coherent x-ray microscopy, the applied method of resolution determination should always be taken into account. Given a total dose of ∼1.1 × 10⁸ Gy, a value of 234 nm is well above the feature-destroying limit (27). In fact, for cryo-cooled samples as used here, a considerably higher dose could be used in future work to explore similar samples to higher resolutions, without concern for radiation damage.

Conclusions

We have quantitatively demonstrated the experimental combination of hard x-ray ptychographic coherent diffractive imaging with computed tomography on a cryogenically cooled, single yeast cell. Using cryo-cooling, no significant radiation damage was observed, using a total dose of ∼1.1 × 10⁸ Gy.

We have further shown that the GINIX and P10 experimental apparatus, including a semitransparent beam stop, allowed for the rapid and convenient acquisition of the diffraction data—which is essential to minimize drifts and yield a successful interpretation of the ptychographic data sets. We have demonstrated both experimental and computational tools that account for a sample mounted on a flat sample holder—which is an ideal mount for vitrification of samples.

A partial protrusion of the cell from the surrounding water was concluded from a careful interpretation of the data. It was shown that this in general does not prevent a quantitative electron density analysis for large fractions of the cell. It is expected that such an effect can be mitigated in future experiments by increasing the water layer thickness before injecting the sample into the freezing medium.

The reconstructed 3D electron excess density distribution demonstrates that the method is capable of imaging unstained cryo-immobilized biological cells with enough contrast to visualize structures within the cell, based on their natural difference in electron density. The resulting mean excess cell electron density obtained from the tomogram is in overall agreement with literature values for hydrated yeast cells and could be readily extended to an absolute density scale by inserting accurately characterized reference samples (37). In addition, these could also serve the alignment process as fiducial markers.

An upper bound of 0.005 Å⁻³ to the high sensitivity of the experiment was determined here. This shows that hard x-ray ptychographic cryo-tomography of biological specimens is a viable tool for quantitative electron density determination of unstained cells that simultaneously provides a detailed view of their 3D structure. In this respect, the method complements emerging trends in optical phase microscopy (62), with a more general applicability due to its penetrating power and a potential for higher resolution.

Author Contributions

K.G., A.P.M., C.H., M.R.G., and R.J. planned/devised the experiment; K.G., R.J., R.N.W., A.Z., and M.S. provided tools/protocols; C.H. and K.G. prepared the sample; K.G., R.N.W., A.A., G.B., A.P.M., K.S., and A.Z. performed the experiment; K.G. analyzed the data; and K.G., C.H., M.R.G., V.S.L., and A.P.M. wrote/edited the article.

Editor: Lois Pollack.

Supporting Citations

Refs. (63, 64) appear in the Supporting Material.

Supporting Material

Movie S1. Optical view on sample holder in cryogenic stream

Sample holder in cryogenic gas flow as visualized using the in-situ microscope at the beamline. Projection angles from –90 to +90 degrees are shown. The imaged cell is indicated by the black ellipse.