Abstract
We investigate computationally the self-organization and contraction of an initially random actomyosin ring. In the framework of a detailed physical model for a ring of cross-linked actin filaments and myosin-II clusters, we derive the force balance equations and solve them numerically. We find that to contract, actin filaments have to treadmill and to be sufficiently cross linked, and myosin has to be processive. The simulations reveal how contraction scales with mechanochemical parameters. For example, they show that the ring made of longer filaments generates greater force but contracts slower. The model predicts that the ring contracts with a constant rate proportional to the initial ring radius if either myosin is released from the ring during contraction and actin filaments shorten, or if myosin is retained in the ring, while the actin filament number decreases. We demonstrate that a balance of actin nucleation and compression-dependent disassembly can also sustain contraction. Finally, the model demonstrates that with time pattern formation takes place in the ring, worsening the contractile process. The more random the actin dynamics are, the higher the contractility will be.
Introduction
Among dynamic cytoskeletal structures, contractile networks are especially prominent (1). The prime example is the stable sarcomere structure of the muscle cells (2), but dynamic stress fibers (3), and cytokinetic rings (4) are equally important, playing crucial roles in cytokinesis, cell motility, and mechanosensation. Both in vivo and in vitro assays showed that four molecular players—actin filaments, myosin-II motors pulling polar actin filaments together, actin cross-linking proteins, and actin nucleation and/or branching factors—are essential for contraction (4), but gaps in our understanding of contraction in disordered cytoskeletal assemblies remain. A number of experimental studies used model systems such as fission yeast, Caenorhabditis elegans, and filamentous fungus Neurospora crassa. They established that actin, myosin, and actin accessory proteins are dynamic and turning over in cytokinetic rings, and measured respective kinetic rates, geometry, and contraction force (5, 6, 7, 8). Mathematical models are instrumental for mechanistic understanding of the actomyosin contraction as they test whether hypothesized mechanisms of the contraction reproduce these experimental results.
First we have to solve the fundamental puzzle: what is the microscopic mechanics of contraction of disordered actin arrays (9, 10, 11)? This is clear in principle in muscle sarcomere, where actin filaments are arranged in a perfect crystalline array optimal for contraction: pointed ends of actin filaments are at the center, where myosin-II moves to the outward-pointing barbed ends, thereby pulling filaments inward. It is easy to see, however, that in random arrays, where a filament pair could have pointed ends outward with the same probability as barbed ends outward, the filaments would be under compression with the same probability as being under tension (Fig. 1 B). In vitro experiments have shown that random actomyosin networks contract (12, 13, 14, 15), so the question is: What is the hidden asymmetry in them that discriminates against expansion in favor of contraction?
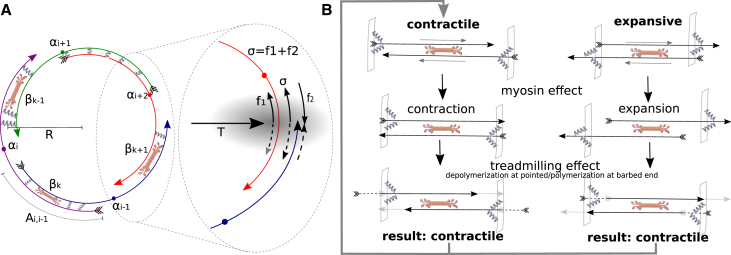
Figure 1.
(A) Schematic representation of the actomyosin ring model. The model describes a ring of radius R composed of N actin filaments and M myosin clusters. The center of filament i is located at the angular position αi and it has length li and polarity ni = ±1. Myosin clusters (rods with multiple motor heads at the ends) are treated as point objects with angular positions βk, 1 ≤ k ≤ M. Cross links are shown as springs; in the model, with one exception, we treat them not as discrete objects, but as effective viscous drag distributed along filament pair overlaps (i.e., overlap length Ai,i−1 is shown). (Inset) Pressure of the cytoplasm and cortical tension T are balanced by the contractile stress σ divided by the ring radius R. The stress σ at the cross section shown by shadowing is equal to the sum of forces acting on the cross section of two bisected filaments. In the example shown, f1 is the tensile force, and f2 is the compressive force. (B) (Top) If actin filaments are positioned randomly, myosin action causes contraction as often as expansion. (Middle and bottom) Intuitive explanation of the contraction mechanism we propose: first, myosin converges the barbed ends of the antiparallel filaments (middle), but then treadmilling moves the barbed ends apart (newly polymerized ends are shown with dashed lines) and converges the pointed ends (newly depolymerized ends are shown with shaded lines). This keeps contractile configuration (left) contractile, and converts expansive configuration into the contractile one. To see this figure in color, go online.
Clever models have been formulated to hypothesize about the microscopic mechanism generating such asymmetry (reviewed in Mendes Pinto et al. (11)). First, actin filaments could be nucleated at and grow with their barbed ends anchored at the membrane, so that respective pointed ends can overlap and interact with myosin (16). This mechanism is supported by the experiment in fission yeast (16). Second, another possibility is for mini-sarcomeres to emerge when myosin clusters do not slide off the barbed ends, but hang onto them (17, 18); such a possibility is yet to be experimentally confirmed. Third, actin filaments under compression in pairs, which are trying to expand, could buckle while filaments under tension in pairs, which are trying to contract, are stable, so a net contraction could develop (19), which was indeed observed in vitro (20). Fourth, and last but not least, actin filaments’ disassembly at the pointed ends together with tricky deformations of cross links could lead to net contraction (7). The last two models also emphasized the importance of cross links for developing contraction, which was confirmed in vitro (13, 21).
The additional difficulty in understanding contraction of random actomyosin arrays is that the very same dynamics that generates contraction leads to self-organization into patterned structures with actin filaments sorted out by polarity into periodic arrays. This was predicted computationally (22, 23, 24, 25, 26, 27, 28), as well as observed in reconstituted actomyosin bundles (25). How these emerging patterns affect the proposed mechanisms is unclear, so it is crucial for understanding the contraction mechanism not to limit the model to static structures, but to examine the self-organization of the actomyosin arrays coupled with mechanics.
The aim of this study is to propose another mechanism for the actomyosin contraction based on actin treadmilling—simultaneous barbed-end growth and pointed-end shortening. We hypothesize that this mechanism can generate asymmetry in the random actomyosin arrays that results in contraction. To prove this, we formulate a detailed microscopic physical model, which takes into account both mechanical interactions among actin, myosin, and cross links, and their movements. We demonstrate that this mechanism, indeed, leads to contraction, which is worsened with time by pattern formation in the actomyosin array. Throughout the article we use the ring geometry of the actomyosin array, which makes it easier to compare the model predictions with the rich literature on the mechanics of cytokinesis. However, as the model addresses the fundamental basic question about the nature of microscopic contraction mechanism, model applicability is more general: most of the results are valid for linear arrays characteristic of stress fibers in adherent and migrating cells. In this article, for brevity, we use term “myosin” for myosin-II, and myosin “clusters” instead of “mini-filaments” to avoid confusion with actin filaments.
Materials and Methods
Mathematical model
We use the microscopic model illustrated in Fig. 1. The actomyosin array is on the ring of variable radius R(t). The ring consists of N actin filaments marked by index 1 ≤ i ≤ N. Each filament is characterized by its length l, polarity ni = ±1 (plus/minus if the pointed end is pointing in the anticlockwise/clockwise direction, respectively), and angular position αi(t) of the filament center. The ring includes M myosin clusters marked with index 1 ≤ k ≤ M and angular positions βk(t). The velocities of given actin filaments and myosin clusters along the ring of a variable radius are and , respectively. In the periodic setting, the difference between two actin filament angular positions is defined as
where τij = 0 unless the difference is evaluated across the imaginary plane at angle 0, in which case τij is either −1 or +1. Relative velocities within the ring are , so ; the differences between angular positions of actin filaments αi and myosin clusters βk are defined in the same way.
In the model, each myosin cluster is characterized by two actin-binding sites. A cluster can be detached from actin completely, and then each of the two binding sites can attach to any actin filament, passing through the cluster’s location. One binding site of a cluster can be attached to a filament, and another site detached, in which case the cluster glides toward the barbed end of a respective filament with constant load-free velocity Vm; meanwhile, another site attaches to any available actin filament. Both binding sites of a cluster can be attached to an overlapping filament pair. When any of the two binding sites reaches a respective filament end, it slides off without delay and becomes unbound. A myosin cluster completely detached reattaches to any filament at the same location at random with the rates specified in respective sections of the article. As these rates tend to be fast, we did not simulate myosin diffusion. Actin treadmilling is modeled by simultaneous elongation and shortening of the barbed and pointed ends, respectively, with rate vp.
The velocities of actin and myosin are determined by the force balance equations. Following many previous models (7, 18, 27, 29), we consider a balance of two types of forces: active myosin and passive cross-linking forces (30). Actomyosin interactions are specified by coefficients ∈ {0,1} (1 if the ith filament is bound to the kth cluster, zero otherwise). In the model, an active force exerted by the kth myosin cluster on the ith filament is given by the linear force-velocity relation: fki = Fs (ni + (Vk − vi)/Vm), where Fs is the myosin stall force (30). Effective drag force due to the cross linking originates from protein friction that stems from continuous turnover, attachment, detachment, and stretching of elastic cross-linking proteins. Many models and much data point out that such dynamics lead to effective viscous drag characterized by the coefficient η (31, 32, 33, 34, 35) proportional to the number of the cross links per unit length of actin, to the cross-link elasticity and to the inverse rate of cross-link dissociation from actin. The effective viscous force between the ith and jth filaments is equal to the product of coefficient η; the difference of the cross-linked filament velocities, (vi – vj); and the filaments’ overlap length Aij. Effective coarse-grained mean-field treatment of cross linkers significantly simplifies the simulations. Note, however, that in one instance we employ a more detailed model of cross linkers as discrete elastic springs (for the results reported in Fig. 2 C and Fig. S2 in the Supporting Material). In the latter case, the cross linkers are fixed in space, therefore we do not explicitly model diffusion of detached cross linkers. Indirectly, the mean-field approach assumes such rapid diffusion.
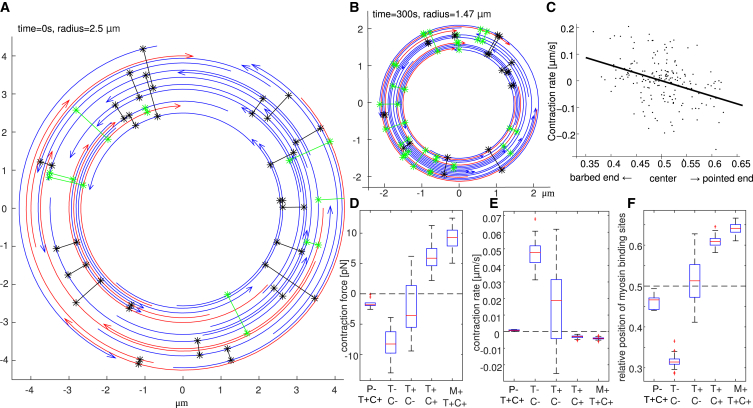
Figure 2.
(A) A randomly generated initial ring. Arcs are actin filaments, with arrowheads marking the pointed ends. Radial connections are myosins linking actin filament pairs. (B) The ring contracted after 5 min from the initial state shown in (A). Note that the rings in (A) and (B) are shown on the same scale. (C) The contraction rate of randomly generated actomyosin rings is correlated to the average relative position of myosin on antiparallel actin filament pairs (slope of the regression line is −0.37 with p = 6 × 10−6 %). Rings with a bias of myosin bindings sites toward the pointed (barbed) ends of actin filaments tend to contract (expand). The position along a filament is scaled so that 0, +0.5, and +1 correspond to the barbed end, center, and pointed end, respectively. (D–F) Contraction force (D), rate (E), and myosin position (F) in the presence and absence of treadmilling (T+: with, T−: without), cross linking (C+: strong, C−: weak), processivity (P−: myosin nonprocessive), and disassembly under mechanical load (M+: increased rate of disassembly of filaments under tension). For each condition, the statistics consists of 20–40 simulations, each averaged between t = 40 s and t = 120 s. To see this figure in color, go online.
The system of force balance equations has the form:
| (1) |
| (2) |
| (3) |
Each of the first set of N equations (Eq. 1) describes the balance of forces acting on the ith actin filament. The first sum in Eq. 1 is the sum of forces from myosins interacting with this filament, and the second sum is the sum of cross-linking forces from all other filaments interacting with the ith filament. Each of the second set of M equations (Eq. 2) is responsible for the balance of forces applied to the kth myosin cluster; each force in this sum is the counter-force applied to the kth myosin cluster from the ith actin filament.
Note that there are N + M equations (Eqs. 1 and 2) for N + M variables—actin and myosin velocities vi, 1 ≤ i ≤ N, and Vk, 1 ≤ k ≤ M, respectively—so at first glance, this is a self-consistent system. Strictly speaking, any equation is a linear combination of the remaining equations, but also the system is invariant with respect to rotations, so a constant can be added to all velocities. Thus, one of the filament velocities can be considered to be zero, so there are (N + M − 1) variables and (N + M − 1) equations. However, there is one more variable, ring radius R. Indeed, and . The final equation (Eq. 3) mathematically closes the system. Mechanically, this equation defines the force-velocity relation between the tensile stress σ in the ring and the rate of change of the ring radius. In the general case, explicit algebraic solution of this equation is prohibitive, but the numerical solution is straightforward: we have a large system of algebraic equations with one of the variables being the rate of change of radius R at a given tensile stress. Alternatively, one of the variables is the tensile stress at a given radius. This notion is illustrated in Fig. 1 and it is the generalization of the conventional mechanical stress: if an imaginary plane dissects the ring, the sum of all forces applied by the dissected actin filaments to the cross section divided by the cross-section area is the stress. In our one-dimensional model, σ has the dimension of force, and in the remainder of the article we call it a contraction force. A useful way to think about it is to consider the fact that in dividing cells the contractile ring is compressing the cell interior and cortex against pressure T (force per unit length of the ring) (36) (Fig. 1). Then, by Laplace’s Law, σ = TR. In the Supporting Material, we demonstrate that σ is constant in space. Numerical simulations are described in the Supporting Material.
Results
Conditions for contraction
Spatial bias of myosin to pointed ends and of cross links to barbed ends on antiparallel actin filaments are correlated with contractility
We investigated the model Eqs. 1–3 in which the effective drag between actin filaments is replaced by a finite number of cross links, each modeled as a linear elastic spring at a random location connecting two random actin filaments at this location (see the Supporting Material). We generated 500 random actomyosin rings of N = 34 actin filaments connected randomly by Mcl = 40 cross links and M = 28 myosin clusters. For every configuration, we recorded the average position of myosin and cross links on the actin filaments represented by a rescaled coordinate between 0 and 1, corresponding to the barbed and pointed ends, respectively. We simulated such random arrays for just one discrete time step, computed the contraction rate , and analyzed the correlation between this rate and the spatial bias of myosin and cross links.
In Figs. 2 C and S2, each point corresponds to one random ring. As both myosin and cross links connect actin filament pairs, we distinguish whether each protein connects antiparallel or parallel filaments. Figs. 2 C and S2 show that the contraction rate and average relative positions of myosin and cross links are correlated: the ring contracts when the positions of myosin connecting antiparallel filaments are biased toward the pointed ends, and when cross links connecting antiparallel filaments have a bias toward the barbed ends. The relative positions of myosin and cross links connecting parallel filaments are not correlated to expansion/contraction.
These results make perfect intuitive sense: we want myosin at the pointed ends’ overlaps because myosin action there increases the antiparallel filaments’ overlap, as opposed to unwanted myosin at the barbed ends’ overlap, which decreases this overlap expanding the system. We also want cross links away from myosin, hence at the barbed ends’ overlap, to transmit the stress to the rest of the system and resist simple reshuffling of the filaments. However, how can such organization be an emerging property of the self-organizing system? We demonstrate that treadmilling is one possible answer.
Without treadmilling, actomyosin rings typically expand
In fact, without actin treadmilling, the ring not only does not contract, it actually expands. To demonstrate this, we simulated the model without filament dynamics (treadmilling rate set to zero). We observed that the average position of myosin clusters between pairs of antiparallel filaments shifts toward the barbed ends. This shift is caused by the myosin gliding toward the barbed ends. As a result, the actomyosin ring without actin turnover, or structural or mechanical asymmetries, typically expands (Figs. S3 and 2, scenarios T−C−). Simulations of the model without actin treadmill under isometric conditions give the same result: stress generated by random actomyosin arrays (Fig. 2, scenario T−C−) is typically expansive.
Indeed, with time, myosin clusters tend to maximally segregate the overlapping antiparallel actin filaments, so in the end the distances between the centers of initially overlapping filaments increase on the average. This microscopic effect translates into divergence of the filaments in the ring and expansion. This happens even in the absence of external pressure on the ring.
The combined effect of treadmilling and cross linking promotes contraction
If we consider a myosin cluster in the framework of the treadmilling filament, then the elongating barbed end moves away from myosin, while the shortening pointed end moves toward the cluster (37). Thus, actin treadmilling biases myosin to the pointed ends, which could cause overall contraction. To prove that, we repeated the simulations, now including treadmilling—each actin filament polymerizes at the barbed and depolymerizes at the pointed end with rate 0.1 μm/s. The computed evolution of the radius for 30 random arrays is plotted in Fig. S3 and the mean values of contraction rate and stress are in Fig. 2, scenario T+C−.
Compared to the no-treadmilling case, the shift of myosin toward the barbed ends is diminished by treadmilling (Fig. 2). One observes that a few rings contract while others expand, yet slower than without treadmilling (Fig. S3 D). In the simulations, we observed that the relative velocities of antiparallel actin filaments were of the same magnitude as the polymerization rate, so treadmilling was able to compensate approximately the effect of myosin gliding toward the barbed ends, but was not fast enough to shift myosin toward the pointed ends.
We examined consequences of increasing cross-linking density and magnitude of the drag friction by increasing the value for drag friction coefficient η by the factor 8. The average relative position of myosin attached to antiparallel actin filaments shifts toward the pointed ends of actin filaments within the first seconds (Fig. 2). As a consequence, all actomyosin rings contract (Figs. 2, B and C, and S3 E).
Myosin processivity is necessary for contraction
Myosin clusters have to stay on the same actin filament in order for treadmilling to bias their positions toward the pointed ends. If they detach frequently and attach at random positions to new filaments, then the biasing effect of treadmilling would be cancelled. In other words, to generate contraction in our model, myosin has to be processive. To test this, we performed numerical simulations where rapid association and dissociation of myosin is modeled by disconnecting all myosin clusters at every time-step and reconnecting them randomly to actin filaments.
Simulations with nonprocessive myosin shows rings expanding slowly, while the average position of myosin does not have a clear spatial bias (Fig. 2). Simulations with the same parameters but processive myosin show contraction (Fig. 2).
Buckling of filaments under compression promotes contraction
Actin filaments under compression are prone to buckling (38, 39) and/or severing (20). In Lenz et al. (19), it has been proposed that the mechanical asymmetry—filament buckling under compression, and filament mechanical stability under tension—can generate actomyosin contraction. However, this hypothesis has only been tested in random static arrays. In the Supporting Material we confirm that in the dynamic random arrays, the mechanism proposed in Lenz et al. (10, 19) promotes contraction.
Mechanical scaling in the actomyosin ring
The model allows us to see how the contraction force and rate scale with key protein densities and filament lengths. We simulate the evolution of initially random actomyosin rings under isometric conditions at the fixed radius R0 = 2.5 μm to compute the contraction force as a function of time, and under zero external force to obtain the contraction rate as a function of time. We investigate how the contraction force and rate depend on myosin density, ring width (proportional change of actin, cross linking, and myosin content), coarseness (length of actin filaments), and cross linking.
Both contraction force and rate are proportional to the myosin density
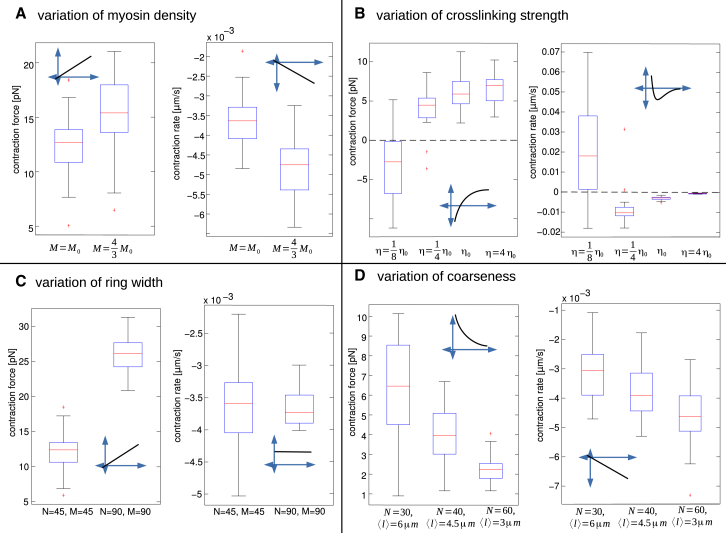
We ran simulations in the rings where the amount of myosin was increased by 33%. As expected, both the isometric contraction force and the rate of contraction (Fig. 3 A) increase by the same factor, because the ring contracting by the proposed mechanism does so in the regime of strong cross linking, and so myosin works close to stall, and both force and rate are proportional to the active myosin force.
Figure 3.
Contraction force (left) and rate (right) from 20 to 50 simulations averaged in time between t1 = 60 s and t1 = 100 s before and after modifying a single parameter of a reference parameter set. (A) Effect of increasing the total number of myosin clusters by one-third. (B) Effect of modifying cross-linking drag η by factors 1/8, 1/4, and 4. (C) Effect of doubling the thickness (both numbers of actin and myosin filaments, with appropriately scaled cross linking) of the ring. (D) Effect of changing filament length and number while keeping total filament length constant. (Insets) Schematic view of the approximate dependence of the force and rate on scaled parameters. To see this figure in color, go online.
As the thickness of the ring increases, the contraction force increases, while the contraction rate stays constant
To test the dependence on ring thickness, we generated random rings increasing the number of both actin filaments and myosin clusters by 2. We simultaneously decrease η by 2 to keep the cross-linking drag per filament unchanged, as the drag per filament scales linearly with actin density. Doubling the ring thickness increases the contraction force by the factor 2 whereas the rate of contraction remains invariant (Fig. 3 C). Indeed, increasing the thickness means adding effective contractile units in parallel, which should increase the force without changing the contraction rate.
Stronger cross linking increases contraction force and slows down contraction
We simulated the rings where the value for cross-linking drag is either reduced by the factor 1/8 or 1/4 or increased by the factor 4. A decrease in η led to a decrease in the contraction force (Fig. 3 B). Actomyosin rings simulated with the lowest amount of cross linking (η = 1/8 η0) actually expanded, as expected from the simulations reported above.
Increasing cross linking affected the contraction force very little due to the saturation as illustrated for a simple two-filament model in Eq. S6 in the Supporting Material. As far as the contraction rate is concerned (Fig. 3 B), the cross linking has to be fine-tuned to a certain range to allow for contraction. Increasing the cross linking essentially freezes the ring slowing down the rate of contraction to almost zero. This agrees with Eq. S6 in the Supporting Material for the two-filament model. The contraction rate increases as the cross linking is reduced (η = 1/4 η0), but with cross linking reduced further (η = 1/8 η0), the filament sliding cancels the effect of treadmilling, and the contraction slows down. To summarize, there is an optimal level of cross linking for fast contraction, but the isometric contraction force increases to saturation at increasing cross linking.
Shorter actin filaments accelerate contraction, longer filaments generate greater force
We simulated the evolution of the rings where the number of actin filaments was changed with simultaneous change of the filament lengths, so that the total F-actin length remained constant. As a result, the isometric contraction force scales almost linearly with the filament length, while the force-free contraction rate scales almost linearly with the filament number (Fig. 3 D). Small deviations from linearity are due to effective scaling of cross-linking strength. Longer filaments mean greater average overlaps between neighboring filaments, and so more myosin clusters working in series, with additive forces, while greater number of shorter filaments means more contractile units in series, leading to a faster contraction. By the same logic, increasing the ring radius without changing its architecture should not affect the isometric force but increase the rate of contraction proportionally to the radius. The model simulations indeed confirmed this prediction (Fig. 4 B).
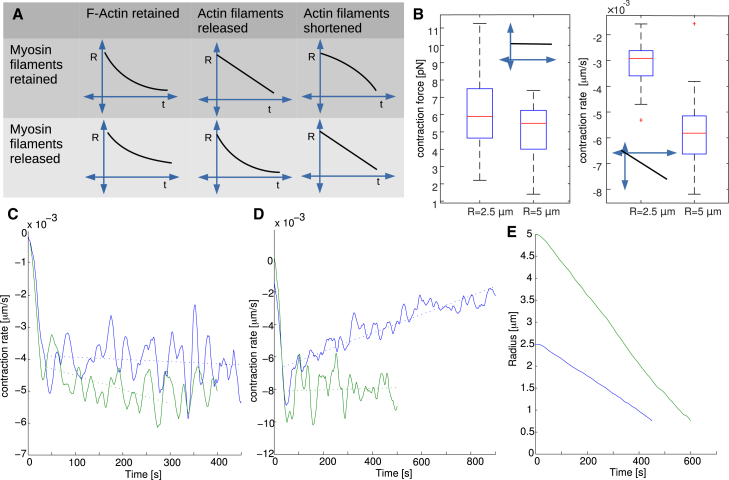
Figure 4.
(A) Schematic representation of the ring radius decrease at six various scenarios combining either myosin retention or release in the ring with three different models for how the content of actin changes during contraction (retention, release, or shortening). (B) Effect on contraction force and rate of doubling the radius of actomyosin rings. For the ring with radius 2.5 μm, N = 45, M = 45, and η = η0; for the ring with radius 5 μm, N = 90, M = 90, and η = η0/2. Statistics from 30 simulations, with data from averaging between t = 40 s and t = 200 s. (C) Contraction rate as a function of time for simulations combining filament shortening with either myosin release (not changing in time, on average) or myosin retention (decreasing fast on average). (D) Contraction rate as a function of time for simulations combining filament number decrease with either myosin release (gradually changing in time) or myosin retention (not changing in time, on average). (E) Comparison of contraction dynamics for two different initial ring radii, R0 = 2.5 μm and R0 = 5 μm, when actin disassembly is driven by shortening of actin filaments and myosin release. We obtain the same result by combining myosin retention with actin disassembly by decreasing the number of constant-length filaments. To see this figure in color, go online.
Scaling of the contraction in the presence of ring disassembly
In cytokinesis, an incompletely understood part of contraction is the observed decrease of the amount of actin and myosin in the ring, which depends on the cell type. In fission yeast, it was found that actin filaments shorten as the ring contracts (40), while in C. elegans embryos the width and the thickness of the constriction ring, and also the concentration of actin-related proteins such as cross links, remain constant during contraction (6). In C. elegans and budding yeast, a constant myosin concentration was reported implying a release of myosin during contraction (6, 7). In other experimental systems, such as fission yeast and filamentous fungus N. crassa, myosin is retained during cytokinesis, resulting in an increase of its concentration (5, 8). In all these experimental systems, it was generally observed that the contraction rate remained constant during most of the contraction process (5, 6, 7, 8).
Here we investigate the ability of our model to reproduce maintenance of the constant contraction rate. We scale parameter η to maintain the ratio of cross links to F-actin of the reference parameter set (Table S1 in the Supporting Material). The scaling result concerning changes in ring size, Fig. 4 B, allows us to infer the dynamics of ring contraction in the absence of actin disassembly. In this case, concentration of actin would grow and, if myosin is retained, the actin/myosin would not change. The scaling implies that the contraction rate would decrease proportionally to ring size, because the number of effective contractile units decreases. Exponential decay of the radius with respect to time would be the consequence, whereas myosin release during contraction would slow down contraction even more, as sketched in Fig. 4 A (first column).
Actin concentration in experimentally observed rings, however, is constant and therefore we examined two strategies to release actin. One is removing filaments randomly one by one. Another is keeping the filament number constant, but shortening the filaments keeping a greater depolymerization rate of pointed ends compared to the polymerization rate of barbed ends. In both cases, we choose the rates of removal and disassembly so that average actin concentration is constant and total actin length is proportional to the ring radius. This implies the assumption of a feedback between the ring geometry and actin density, the molecular nature of which is unknown. We also test the difference between retaining all myosin in the ring, as observed in fission yeast and filamentous fungus N. crassa, and releasing myosin from the ring at the same rate as actin decreases, maintaining a fixed ratio between myosin and actin density, corresponding to the observations made in C. elegans and budding yeast.
Myosin retention in combination with actin decrease by random filament removal maintains a constant contraction rate
In the simulations, actin decreases by removal of whole filaments picked at random. In the first scenario, myosin is released from the ring at the same rate as actin. The contraction rate (Fig. 4 D, blue) decreases as the ring contracts because the local structure of the ring remains the same, and, effectively, when the radius of the ring decreases, the number of contractile units decreases, while the rate of contraction per unit remains constant. In the second scenario (Movie S1 in the Supporting Material), all myosin remains in the ring, but the number of actin filaments decreases at the constant rate. In this case, both contraction rate (Fig. 4 D, green) and ring thickness are constant because the increase of the myosin density compensates for the decrease of the number of the contractile units in series.
Actin filament shortening in combination with myosin release also maintains a constant rate of contraction
Another possible way of F-actin disassembly is shortening actin filaments. We model this by increasing the rate by which a constant number of filaments shorten at the pointed end. In this case, when the number of myosin clusters is constant during contraction, the contraction rate increases (Fig. 4 C, green) because the myosin density, and hence the force per effective contractile unit, increases. However, when myosin is released from the ring proportionally to actin, the contraction rate becomes constant (Fig. 4 C, blue, Movie S2).
The duration of contraction does not depend on the initial ring size
In C. elegans (6), filamentous fungus N. crassa (8), and budding yeast (7), the constant in time contraction rate scales with the initial radius of the ring, so that the total duration of the contraction does not depend on the initial ring size. Our model exhibits the same feature in both scenarios (releasing myosin together with shortening actin filaments (Fig. 4, B and E)).
Pattern formation in the ring worsens the contraction
A number of models predicted polarity sorting in filament-motor systems (26, 27, 28). This phenomenon is simple: a small local aggregate of myosin tends to slide actin filaments of opposite orientations into opposite directions, so that the barbed ends of all filaments end up close to the myosin aggregate, and the filaments with barbed ends at the left/right accumulate to the right/left. As myosin glides toward the actin barbed ends, this actin polarity segregation causes even greater myosin aggregation, and this positive feedback leads to the pattern. To examine whether this mechanism works in the presence of treadmilling and cross linking, we investigated myosin and actin polarity distributions in simulations.
We defined the actin polarity as a position-dependent counting measure in which actin filaments whose pointed ends point in anticlockwise (clockwise) direction are counted positively (negatively). An isotropic ring is characterized by zero polarity. Fig. 5 shows snapshots from a characteristic simulation (Movie S3) and evolution of the actin polarity and myosin density, from which it is clear that the predicted pattern forms.
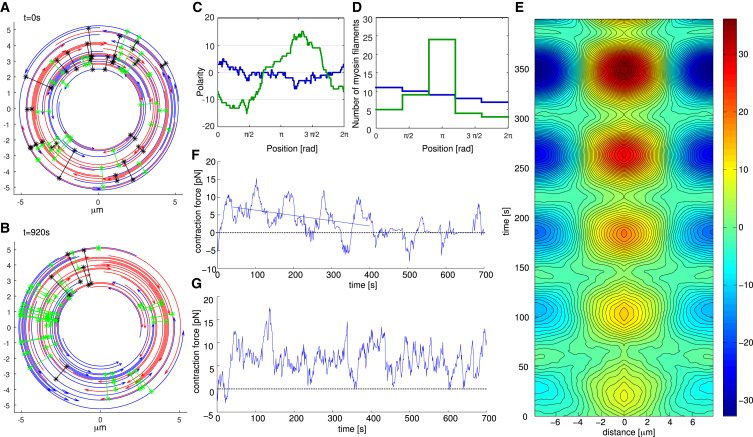
Figure 5.
(A) Early stage of a simulation under isometric conditions. (B) Later snapshot of the same simulation reveals pronounced polarity sorting of actin filaments. (C) Polarity (sum of anticlockwise filaments counted as +1 and clockwise filaments counted as −1) as a function of position for the two snapshots visualized in (A) and (B) illustrates polarity sorting. (D) Histograms of myosin distribution for these two snapshots reveal increased aggregation of myosin in the ring that has undergone polarity sorting. (E) Contour plot of the polarity autocorrelation function reveals formation of the pattern in space, oscillations of polarity due to rotation of actin filaments driven by treadmilling, and a long time trend toward higher polarization. (F) The contraction force shows the same frequency oscillations as the polarity autocorrelation function, and a long time trend of contractility decay. (G) Simulation of an actomyosin ring under isometric conditions with random reshuffling of actin filaments shows that random actin turnover makes the contraction force, on average, constant in time. To see this figure in color, go online.
A contour plot of the time-dependent polarity autocorrelation function (Fig. 5 E) reveals not only overall polarity increase with time, but also periodic behavior in time. This pattern is a consequence of the rotating dynamics of clockwise- and anticlockwise-oriented filaments due to their treadmilling. The separation of clockwise and anticlockwise filaments to the two opposing halves of the ring slowly grows in time. Approximately every t = 80 s the polarity profile becomes almost homogeneous because two filament groups overlap due to rotation in the opposite directions, and every other t = 80 s the two groups of actin filaments separate at opposing halves of the ring. The length of the time period is approximately equal to the time necessary to treadmill at the rate vp = 0.1 μm/s across half of the actomyosin ring with radius 2.5 μm.
Intuitively, the pattern formation should worsen contractility: myosin bias to the barbed ends is associated with expansion. This is, indeed, what the simulations reveal: the contraction force (Fig. 5 F) exhibits oscillations as well as the long-term trend toward decrease. Besides the decrease of the contractility, there is another potential danger of the pattern formation for contraction: simulated actomyosin rings sometimes disrupt (Fig. S3 F): There is a finite probability that polarity sorting reaches a degree where gaps in the actomyosin array appear, at which point the force drops to zero (Fig. 5 F).
Randomness of actin dynamics improves contractility
We expect therefore that the actin turnover (random removal and nucleation of actin filaments) in the ring hinders the pattern formation and disruption of the ring and maintains contraction. To confirm this, we simulated a random actomyosin ring in which every actin filament is removed randomly at the rate 0.005 s−1, and simultaneously another filament appears at a random location. Importantly, the turnover diminished spatial concentration of both myosin and filaments of the same polarity, which caused the average polarity to remain steady and kept myosin at a steady level. As a result, contractility stabilized at a steady level and did not decrease (Fig. 5 G). The simulated ring did not disrupt.
Discussion
Actin treadmilling combined with myosin processivity and cross linking generates conditions for contraction of random actomyosin arrays
We found that a disordered actin ring can be contracted if myosin has a bias toward the filament pointed ends. We demonstrate that such asymmetry can emerge in the presence of actin treadmilling, which, in the framework of an actin filament, effectively biases myosin to the pointed end. We further predict that this mechanism can only work if myosin is processive, and cross linking is strong enough; otherwise rapid filament sliding overcomes the effect of treadmilling. Effectively, the treadmilling biases the actomyosin array structure toward having a more sarcomere-like architecture on the microscopic scale, although we emphasize that the mechanism we propose by no means is based on emergence of stable sarcomeres; actin filaments are always in flux in our simulated arrays. It is worth noting, however, that an effective degree of sarcomericity, discussed in Stachowiak et al. (16), is a very useful general notion that correlates with contractility.
Contraction force is predicted to increase and saturate with increasing cross linking, while the rate of contraction is maximal at an intermediate level of cross linking: heavy cross linking stalls the decrease of the ring radius. In agreement with Lenz et al. (10, 19), we show that severing of actin filaments under compression helps the contraction, and could even be the standalone mechanism of contraction, without the treadmilling, but only if it is coupled with actin turnover keeping the ring interconnected. Importantly, we demonstrate this in the dynamic ring.
We investigate the scaling of the contraction and find that if the ring is made of shorter filaments, it can contract faster, but if stalled, it generates a smaller contraction force. The reason is that actin filaments combine with myosin and cross linkers into effective contractile units, connected in series in the ring. Shorter filaments make smaller units, but their number in the effective chain around the ring is greater. Thus, contractions of each unit add together, summing up to a faster net rate. However, the force of units in series is not additive, and the force developed by an average unit is roughly proportional to a number of myosins working in parallel along a characteristic actin overlap, which becomes small if the filaments are short. One of the model predictions is that the contraction rate is independent of the ring width, which is in agreement with measurements reported in Bourdages et al. (41).
Actin polarity sorting worsens the contraction, while actin turnover improves it
The simulations predict that, with time, polarity sorting will take place. Two filament subbundles start rotating in opposite directions, gradually dampening average contractility and disrupting the ring. Interestingly, experiments indeed suggest that parallel actin bundles are less contractile than the antiparallel ones (42). We demonstrate that increased randomness of actin array, i.e., by frequent random nucleation and disassembly, improves the contractile properties.
Two actomyosin disassembly mechanisms maintain a constant contraction rate that scales with the initial ring radius
It was observed that the contraction rate remains constant during most of the contractile process in a number of systems (5, 6, 7, 8). Moreover, in a number of organisms (6, 8) the constant in time contraction rate scales with the initial radius of the constriction ring. Two strategies regarding myosin are employed in these experimental systems: myosin is released from the bundle maintaining a constant concentration within the constriction ring in C. elegans (6), while it is accumulated in filamentous fungus N. crassa (8). Actin appears to be lost progressively from the ring during constriction in filamentous fungus and fission yeast (8, 40). In budding yeast, both myosin and actin were released from the contracting ring (7).
Within the framework of the myosin end-tracking model, it was illustrated that actomyosin disassembly is the key for contraction rate constancy and scalability (18). For our proposed mechanism, we identified two mechanisms that provide this feature of contraction. One is the removal of actin filaments combined with the conservation of myosin. Another is conservation of the total number of actin filaments while shortening them, and, at the same time, releasing myosin. In both cases, there has to be some unidentified feedback keeping the actin density constant. The second mechanism has some conceptual similarity to the model proposing functional contractile units in series (6). It is argued in that study that the number of these units scales proportionally to the initial radius of the ring, and that they contract at an equal rate, which should coincide with the shortening rate for actin filaments. Note that our model simulations relying on actin filament shortening reproduce the same behavior without imposing a specific structure of the actomyosin meshwork. Finally, note that in some organisms, i.e., Dictyostelium discoideum, the ring radius decreases exponentially rather than linearly (36), which could be the case predicted by our model in a number of actomyosin disassembly scenarios.
Contraction efficiency
One of the key questions about the contraction mechanism is efficiency: what fraction of the myosin motor force is converted into the contraction force. In the numerical experiments with the reference parameter set, the sum of myosin stall forces is M × Fs = 30 × 5 = 150 pN, while the average contraction force generated was ∼10 pN (see Fig. 2, scenario T+C+), which implies efficiency of the proposed mechanism of ∼7%. Note that the effect of filament curvature in the ring can be safely ignored: the estimate for the bending force per filament is equal to the effective spring constant of the filament, 10 kBT λ/l3, where kBT = 0.004 pN × μm is the thermal energy, λ = 10 μm is the filament persistence length, and l = 6 μm is the filament length, times the filament deformation, which is ∼l2/R, where R ≈ 1 μm is the ring radius. Such force is ∼0.01–0.1 μm/s, which is too small compared to average myosin and cross-linking force per filament, which in our simulation was in the picoNewton range.
Comparison with published experimental data
The initial radius of the ring is of order of a few microns for a number of organisms (fission yeast (5), D. discoideum (43), C. elegans (6), and fungus N. crassa (8)). The contraction rate is ∼0.001–0.1 μm/s (C. elegans (6), fission yeast (44), and fungus N. crassa (8)). The duration of cytokinesis is hundreds of seconds in D. discoideum (43), C. elegans (6), fission yeast (5), and fungus N. crassa (8), in agreement with the ratio between the initial ring radius and the contraction rate. Our model uses the same order of magnitude radius, and predicts a similar contraction rate and duration to those observed.
In fission yeast, the ratio of actin filaments of both orientations is 1:1 (40), as in our model. In this organism, actin filaments are ∼0.1 μm long, i.e., the same order of magnitude as we use. The number of filaments in fission yeast is estimated to be 200 filaments, and the number of myosin molecules is 3000. Assuming ∼15 myosin molecules per cluster (45), this gives 200 myosin clusters, so the ratio of the actin and myosin observed in this organism is similar to that used in our model. For computational speed, we simulate the ring, which is ∼5 times thinner than the ring in the fission yeast, but our scaling results allow estimates for any ring width. If all myosin in fission yeast ring were active, they would produce 1500 pN of force (5). The study (16) estimates a contraction force of 250 pN, so the efficiency of the mechanism of contraction in the fission yeast is ∼25%, 3–4 times higher than in the mechanism we propose. This is not surprising because the fission yeast mechanism relies on actin filaments arranged by formins, proteins that stay at growing barbed ends and clusters of that could effectively bring barbed ends close together so that overlapping filament pairs are highly contractile.
It is hard to compare our predictions to the contractile ring in D. discoideum, because the actin and myosin dynamics there are less studied. It is known, however, that actin filaments in the contractile ring in D. discoideum are only ∼0.1 μm long (46), which, according to our model, could mean a small contraction force. Interestingly, the minimal force required for contraction in this organism is estimated to be approximately a few nanoNewtons (36, 43). The estimated maximal myosin force is ∼50 pN. Consequently, conversion efficiency in D. discoideum is only ∼2.5%.
Finally, let us reiterate that actin being randomly dynamic is the key for the contraction mechanism we propose. Highly dynamic actin in the fission yeast ring was reported in Pelham and Chang (44). The study (16) reached the same conclusion about beneficial character of actin turnover and disorder for the contraction.
Conclusions
In this study, we focused on the one-dimensional actin array. The problem in two and three dimensions remains the same: how is the symmetry of actin broken (47)? Stochastic simulations (24) showed that the mechanical symmetry break mechanism similar to that proposed in Lenz et al. (19) could also work in two dimensions. It remains to be seen how the mechanism we propose performs in higher dimension, but, qualitatively, it is clear that it leads to contraction for some parameter values. Another promising model extension would be its application to one-dimensional stress fiber geometry. The equations for the fiber interior would remain unchanged, but highly nontrivial boundary conditions for actomyosin array interactions with dynamic force-sensing adhesions will have to be added. As of this writing, we have to consider theoretically every conceivable mechanism of actomyosin contraction, because it is likely that complex cells use a combination of redundant mechanisms. A future lofty modeling goal is to investigate which contraction mechanisms are combined, and how mechanical processes are coupled to biochemical feedbacks.
Author Contributions
D.B.O., B.Y.R., and A.M. designed research; D.B.O. and A.M. wrote the article; D.B.O. performed research and analyzed data; and B.Y.R. contributed analytic tools.
Acknowledgments
We thank M. Lenz for useful discussions.
This work was supported by National Institutes of Health grant No. GM068952 to A.M. and by the Erwin Schrödinger Fellowship No. J3463-N25 of the Austrian Science Fund to D.B.O.
Editor: Charles Wolgemuth.
Footnotes
Supporting Materials and Methods, four figures, one table, and three movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00950-9.
Supporting Material
Actin filaments are removed at the rate that approximately maintains a constant actin concentration during contraction. Note that the ring in the movie occasionally bounces to a larger size, but this is not an actual size increase: at these moments we simply change the length scale to represent the shrinking ring in detail. Actin filaments with their pointed ends marked (arrow) in the anticlockwise (clockwise) direction are blue (red). (Stars on actin filaments) Myosin binding sites and myosin clusters connecting them are shown as transversal lines. These are drawn in green (black) if the connected actin filaments are antiparallel (parallel).
Actin filaments shorten at the rate that approximately maintains a constant actin concentration during contraction. Myosin is also released during contraction at the rate that approximately maintains a constant myosin concentration during contraction. Note that the ring in the movie occasionally bounces to a larger size, but this is not an actual size increase: at these moments we simply change the length scale to represent the shrinking ring in detail. Actin filaments with their pointed ends marked (arrow) in the anticlockwise (clockwise) direction are blue (red). (Stars on actin filaments) Myosin binding sites and myosin clusters connecting them are shown as transversal lines. These are drawn in green (black) if the connected actin filaments are antiparallel (parallel).
The degree of polarity sorting increases as anticlockwise and clockwise actin filaments gradually concentrate at the same position while they keep treadmilling around the ring. Actin filaments with their pointed ends marked (arrow) in the anticlockwise (clockwise) direction are blue (red). (Stars on actin filaments) Myosin binding sites; (transversal lines) myosin clusters connecting them. These are drawn in green (black) if the connected actin filaments are antiparallel (parallel). (Blue stars) Myosin filaments detached from actin filaments. The polarity graph (top right) shows the sum of anticlockwise filaments counted as +1 and clockwise filaments counted as −1. Over time, the amplitude of polarity fluctuations increases, illustrating the tendency of the ring to polarize. In synchrony with periodic polarity increase, the distribution of myosin clusters becomes increasingly inhomogeneous as shown in the histogram (bottom right), with a greater fraction of myosin accumulating to fewer spots.
References
- 1.Vignaud T., Blanchoin L., Théry M. Directed cytoskeleton self-organization. Trends Cell Biol. 2012;22:671–682. doi: 10.1016/j.tcb.2012.08.012. [DOI] [PubMed] [Google Scholar]
- 2.Gautel M. The sarcomeric cytoskeleton: who picks up the strain? Curr. Opin. Cell Biol. 2011;23:39–46. doi: 10.1016/j.ceb.2010.12.001. [DOI] [PubMed] [Google Scholar]
- 3.Naumanen P., Lappalainen P., Hotulainen P. Mechanisms of actin stress fibre assembly. J. Microsc. 2008;231:446–454. doi: 10.1111/j.1365-2818.2008.02057.x. [DOI] [PubMed] [Google Scholar]
- 4.Pollard T.D. Mechanics of cytokinesis in eukaryotes. Curr. Opin. Cell Biol. 2010;22:50–56. doi: 10.1016/j.ceb.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wu J.-Q., Pollard T.D. Counting cytokinesis proteins globally and locally in fission yeast. Science. 2005;310:310–314. doi: 10.1126/science.1113230. [DOI] [PubMed] [Google Scholar]
- 6.Carvalho A., Desai A., Oegema K. Structural memory in the contractile ring makes the duration of cytokinesis independent of cell size. Cell. 2009;137:926–937. doi: 10.1016/j.cell.2009.03.021. [DOI] [PubMed] [Google Scholar]
- 7.Mendes Pinto I., Rubinstein B., Li R. Actin depolymerization drives actomyosin ring contraction during budding yeast cytokinesis. Dev. Cell. 2012;22:1247–1260. doi: 10.1016/j.devcel.2012.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Calvert M.E., Wright G.D., Balasubramanian M.K. Myosin concentration underlies cell size-dependent scalability of actomyosin ring constriction. J. Cell Biol. 2011;195:799–813. doi: 10.1083/jcb.201101055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hatano S. Actin-minding proteins in cell motility. Int. Rev. Cytology. 1994;156:199–273. doi: 10.1016/s0074-7696(08)62255-x. [DOI] [PubMed] [Google Scholar]
- 10.Lenz M., Gardel M.L., Dinner A.R. Requirements for contractility in disordered cytoskeletal bundles. New J. Phys. 2012;14:033037. doi: 10.1088/1367-2630/14/3/033037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mendes Pinto I., Rubinstein B., Li R. Force to divide: structural and mechanical requirements for actomyosin ring contraction. Biophys. J. 2013;105:547–554. doi: 10.1016/j.bpj.2013.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Takiguchi K. Heavy meromyosin induces sliding movements between antiparallel actin filaments. J. Biochem. 1991;109:520–527. doi: 10.1093/oxfordjournals.jbchem.a123414. [DOI] [PubMed] [Google Scholar]
- 13.Bendix P.M., Koenderink G.H., Weitz D.A. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys. J. 2008;94:3126–3136. doi: 10.1529/biophysj.107.117960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thoresen T., Lenz M., Gardel M.L. Reconstitution of contractile actomyosin bundles. Biophys. J. 2011;100:2698–2705. doi: 10.1016/j.bpj.2011.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Soares e Silva M., Depken M., Koenderink G.H. Active multistage coarsening of actin networks driven by myosin motors. Proc. Natl. Acad. Sci. USA. 2011;108:9408–9413. doi: 10.1073/pnas.1016616108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stachowiak M.R., Laplante C., O’Shaughnessy B. Mechanism of cytokinetic contractile ring constriction in fission yeast. Dev. Cell. 2014;29:547–561. doi: 10.1016/j.devcel.2014.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kruse K., Jülicher F. Actively contracting bundles of polar filaments. Phys. Rev. Lett. 2000;85:1778–1781. doi: 10.1103/PhysRevLett.85.1778. [DOI] [PubMed] [Google Scholar]
- 18.Zumdieck A., Kruse K., Jülicher F. Stress generation and filament turnover during actin ring constriction. PLoS One. 2007;2:e696. doi: 10.1371/journal.pone.0000696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lenz M., Thoresen T., Dinner A.R. Contractile units in disordered actomyosin bundles arise from F-actin buckling. Phys. Rev. Lett. 2012;108:238107. doi: 10.1103/PhysRevLett.108.238107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Murrell M.P., Gardel M.L. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc. Natl. Acad. Sci. USA. 2012;109:20820–20825. doi: 10.1073/pnas.1214753109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Abu Shah E., Keren K. Symmetry breaking in reconstituted actin cortices. eLife. 2014;3:e01433. doi: 10.7554/eLife.01433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kruse K., Jülicher F. Self-organization and mechanical properties of active filament bundles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;67:051913. doi: 10.1103/PhysRevE.67.051913. [DOI] [PubMed] [Google Scholar]
- 23.Recho P., Putelat T., Truskinovsky L. Contraction-driven cell motility. Phys. Rev. Lett. 2013;111:108102. doi: 10.1103/PhysRevLett.111.108102. [DOI] [PubMed] [Google Scholar]
- 24.Dasanayake N.L., Carlsson A.E. Stress generation by myosin minifilaments in actin bundles. Phys. Biol. 2013;10:036006. doi: 10.1088/1478-3975/10/3/036006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stachowiak M.R., McCall P.M., O’Shaughnessy B. Self-organization of myosin II in reconstituted actomyosin bundles. Biophys. J. 2012;103:1265–1274. doi: 10.1016/j.bpj.2012.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Friedrich B.M., Fischer-Friedrich E., Safran S.A. Sarcomeric pattern formation by actin cluster coalescence. PLOS Comput. Biol. 2012;8:e1002544. doi: 10.1371/journal.pcbi.1002544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zemel A., Mogilner A. Motor-induced sliding of microtubule and actin bundles. Phys. Chem. Chem. Phys. 2009;11:4821–4833. doi: 10.1039/b818482h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Craig E.M., Dey S., Mogilner A. The emergence of sarcomeric, graded-polarity and spindle-like patterns in bundles of short cytoskeletal polymers and two opposite molecular motors. J. Phys. Condens. Matter. 2011;23:374102. doi: 10.1088/0953-8984/23/37/374102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oelz D. A viscous two-phase model for contractile actomyosin bundles. J. Math. Biol. 2014;68:1653–1676. doi: 10.1007/s00285-013-0682-6. [DOI] [PubMed] [Google Scholar]
- 30.Letort G., Politi A.Z., Blanchoin L. Geometrical and mechanical properties control actin filament organization. PLOS Comput. Biol. 2015;11:e1004245. doi: 10.1371/journal.pcbi.1004245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tawada K., Sekimoto K. Protein friction exerted by motor enzymes through a weak-binding interaction. J. Theor. Biol. 1991;150:193–200. doi: 10.1016/s0022-5193(05)80331-5. [DOI] [PubMed] [Google Scholar]
- 32.Bormuth V., Varga V., Schäffer E. Protein friction limits diffusive and directed movements of kinesin motors on microtubules. Science. 2009;325:870–873. doi: 10.1126/science.1174923. [DOI] [PubMed] [Google Scholar]
- 33.Sabass B., Schwarz U.S. Modeling cytoskeletal flow over adhesion sites: competition between stochastic bond dynamics and intracellular relaxation. J. Phys. Condens. Matter. 2010;22:194112. doi: 10.1088/0953-8984/22/19/194112. [DOI] [PubMed] [Google Scholar]
- 34.Milišić V., Oelz D. On the asymptotic regime of a model for friction mediated by transient elastic linkages. J. Math. Pures Appl. 2011;96:484–501. [Google Scholar]
- 35.Oelz D., Schmeiser C. Derivation of a model for symmetric lamellipodia with instantaneous cross-link turnover. Arch. Ration. Mech. Anal. 2010;198:963–980. [Google Scholar]
- 36.Zhang W., Robinson D.N. Balance of actively generated contractile and resistive forces controls cytokinesis dynamics. Proc. Natl. Acad. Sci. USA. 2005;102:7186–7191. doi: 10.1073/pnas.0502545102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Carlsson A.E. Contractile stress generation by actomyosin gels. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:051912. doi: 10.1103/PhysRevE.74.051912. [DOI] [PubMed] [Google Scholar]
- 38.Berro J., Michelot A., Martiel J.-L. Attachment conditions control actin filament buckling and the production of forces. Biophys. J. 2007;92:2546–2558. doi: 10.1529/biophysj.106.094672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tang H., Laporte D., Vavylonis D. Actin cable distribution and dynamics arising from cross-linking, motor pulling, and filament turnover. Mol. Biol. Cell. 2014;25:3006–3016. doi: 10.1091/mbc.E14-05-0965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kamasaki T., Osumi M., Mabuchi I. Three-dimensional arrangement of F-actin in the contractile ring of fission yeast. J. Cell Biol. 2007;178:765–771. doi: 10.1083/jcb.200612018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bourdages K.G., Lacroix B., Maddox A.S. Quantitative analysis of cytokinesis in situ during C. elegans postembryonic development. PLoS One. 2014;9:e110689. doi: 10.1371/journal.pone.0110689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Reymann A.-C., Boujemaa-Paterski R., Blanchoin L. Actin network architecture can determine myosin motor activity. Science. 2012;336:1310–1314. doi: 10.1126/science.1221708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Robinson D.N., Cavet G., Spudich J.A. Quantitation of the distribution and flux of myosin-II during cytokinesis. BMC Cell Biol. 2002;3:4. doi: 10.1186/1471-2121-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pelham R.J., Jr., Chang F. Actin dynamics in the contractile ring during cytokinesis in fission yeast. Nature. 2002;419:82–86. doi: 10.1038/nature00999. [DOI] [PubMed] [Google Scholar]
- 45.Stam S., Alberts J., Munro E. Isoforms confer characteristic force generation and mechanosensation by myosin II filaments. Biophys. J. 2015;108:1997–2006. doi: 10.1016/j.bpj.2015.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Reichl E.M., Ren Y., Robinson D.N. Interactions between myosin and actin crosslinkers control cytokinesis contractility dynamics and mechanics. Curr. Biol. 2008;18:471–480. doi: 10.1016/j.cub.2008.02.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ronceray P., Lenz M. Connecting local active forces to macroscopic stress in elastic media. Soft Matter. 2015;11:1597–1605. doi: 10.1039/c4sm02526a. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Actin filaments are removed at the rate that approximately maintains a constant actin concentration during contraction. Note that the ring in the movie occasionally bounces to a larger size, but this is not an actual size increase: at these moments we simply change the length scale to represent the shrinking ring in detail. Actin filaments with their pointed ends marked (arrow) in the anticlockwise (clockwise) direction are blue (red). (Stars on actin filaments) Myosin binding sites and myosin clusters connecting them are shown as transversal lines. These are drawn in green (black) if the connected actin filaments are antiparallel (parallel).
Actin filaments shorten at the rate that approximately maintains a constant actin concentration during contraction. Myosin is also released during contraction at the rate that approximately maintains a constant myosin concentration during contraction. Note that the ring in the movie occasionally bounces to a larger size, but this is not an actual size increase: at these moments we simply change the length scale to represent the shrinking ring in detail. Actin filaments with their pointed ends marked (arrow) in the anticlockwise (clockwise) direction are blue (red). (Stars on actin filaments) Myosin binding sites and myosin clusters connecting them are shown as transversal lines. These are drawn in green (black) if the connected actin filaments are antiparallel (parallel).
The degree of polarity sorting increases as anticlockwise and clockwise actin filaments gradually concentrate at the same position while they keep treadmilling around the ring. Actin filaments with their pointed ends marked (arrow) in the anticlockwise (clockwise) direction are blue (red). (Stars on actin filaments) Myosin binding sites; (transversal lines) myosin clusters connecting them. These are drawn in green (black) if the connected actin filaments are antiparallel (parallel). (Blue stars) Myosin filaments detached from actin filaments. The polarity graph (top right) shows the sum of anticlockwise filaments counted as +1 and clockwise filaments counted as −1. Over time, the amplitude of polarity fluctuations increases, illustrating the tendency of the ring to polarize. In synchrony with periodic polarity increase, the distribution of myosin clusters becomes increasingly inhomogeneous as shown in the histogram (bottom right), with a greater fraction of myosin accumulating to fewer spots.