Abstract
One of four overarching goals of Healthy People 2020 (HP2020) is to achieve health equity, eliminate disparities, and improve the health of all groups. In health disparity indices (HDIs) such as the mean log deviation (MLD) and Theil index (TI), disparities are relative to the population average, whereas in the index of disparity (IDisp) the reference is the group with the least adverse health outcome. Although the latter may be preferable, identification of a reference group can be affected by statistical reliability. To address this issue, we propose a new HDI, the Rényi index (RI), which is reference-invariant. When standardized, the RI extends the Atkinson index, where a disparity aversion parameter can incorporate societal values associated with health equity. In addition, both the MLD and TI are limiting cases of the RI. Also, a symmetrized Rényi index (SRI) can be constructed, resulting in a symmetric measure in the two distributions whose relative entropy is being evaluated. We discuss alternative symmetric and reference-invariant HDIs derived from the generalized entropy (GE) class and the Bregman divergence, and argue that the SRI is more robust than its GE-based counterpart to small changes in the distribution of the adverse health outcome. We evaluate the design-based standard errors and bootstrapped sampling distributions for the SRI, and illustrate the proposed methodology using data from the National Health and Nutrition Examination Survey (NHANES) on the 2001–04 prevalence of moderate or severe periodontitis among adults aged 45–74, which tracks Oral Health objective OH-5 in HP2020. Such data, which uses a binary individual-level outcome variable, are typical of HP2020 data.
Keywords and phrases: Epidemiological methods, Health inequalities, Alpha-gamma divergence, Survey data, Taylor series linearization, Rescaled bootstrap
1. Background and introduction
The measurement, tracking, and elimination of health disparities are central to the U.S. Healthy People initiative; see Green and Fielding (2011). One of two overarching goals of Healthy People 2010 (HP2010) was to “eliminate health disparities” (U.S. Department of Health and Human Services, 2000, 2006; National Center for Health Statistics, 2011), and one of four overarching goals of Healthy People 2020 (HP2020) is to “achieve health equity, eliminate disparities, and improve the health of all groups” (http://healthypeople.gov). There are several concepts and definitions associated with the terms health disparities and health equity, which are reviewed in Braveman (2006). In this paper, we do not discuss how to measure or assess health equity. Instead, we restrict our attention to the measurement of health disparities, although, as seen below, measures of health disparities are inevitably tied to normative or societal values associated with health equity. Our working definition of health disparity is that of Keppel, Pearcy and Klein (2004), who state that “in the context of public health, a disparity is the quantity that separates a group from a reference point on a particular measure of health that is expressed in terms of a rate, proportion, mean, or some other quantitative measure.”
When there are three or more population groups, e.g., population breakdown by race and ethnicity, education, or income, the differences among those groups in the magnitude of their disparities relative to the reference point can be summarized using a between-group index. Such between-group health disparity indices (HDIs) have been reviewed in Wagstaff, Paci and van Doorslaer (1991), Mackenbach and Kunst (1997), and Pearcy and Keppel (2002). Their characteristics and limitations have been investigated in Keppel, Pearcy and Klein (2004), Keppel et al. (2005), Levy, Chemerynski and Tuchmann (2006), and Harper et al. (2008, 2010).
For a population that is partitioned into m mutually exclusive groups of sizes n1, n2, ···, nm, with , we study the distribution of a particular adverse health outcome, which, at the individual level, is given by yij, say, for individual i in group j. Specifically, our goal is to compare the aggregate health outcomes , j = 1, 2, ···, m, across groups. When the variable yij is a binary variable, indicating presence or absence of the adverse health outcome for individual i, the aggregate y·j is simply the frequency count of the number of individuals in group j with the adverse health outcome.
We look upon (between-group) HDIs as measures of generalized relative entropy (or divergence) between two nonnegative mass functions p = (p1, p2, ···, pm) and q = (q1, q2, ···, qm). In the analysis of health disparities, the quantities pj can be weights that the analyst assigns to each population group j. The groups are said to be ‘equally-weighted’ if they are assigned equal weights (e.g., 1/m) and ‘population-weighted’ if they are assigned weights that are proportional to their size (e.g., nj/n). On the other hand, the qj can quantify the disease burden in group j. Various HDIs differ in the specification of the qj. Entropy-based HDIs commonly specify qj as a function of the ratio between the group average (ȳ·j) and a fixed reference for measuring disparities. The reference can be the population average (ȳ··), the least adverse health outcome (min1≤k≤m ȳ·k), a Healthy People target, or any other reference.
In this paper, we introduce a new class of HDIs, the Rényi index (RI), which is based on a generalized Rényi (or alpha-gamma) divergence. Generalized Rényi divergence was considered by Fujisawa and Eguchi (2008) in the context of robust parameter estimation in the presence of outliers and is reviewed in Cichocki and Amari (2010). The RI is a class of HDIs that are invariant to the choice of the reference used for evaluating disparities. This invariance property—also known as ‘strong scale-invariance’—is relevant to Healthy People, as well as to other initiatives that monitor health disparities, because the identification of a reference group can be affected by statistical reliability; see National Center for Health Statistics (2011). Reference-invariance is not unique to the RI. As discussed in section 3, the well-known generalized entropy (GE) class, for one, can be modified for strong scale-invariance. Nonetheless, the robustness of the RI makes it less sensitive than its GE-based counterpart to small changes in the distribution of the adverse health outcome.
Looking at HDIs as measures of generalized relative entropy (or divergence) between two nonnegative mass functions p and q—not necessarily probabilities—provides a common mathematical framework within which various HDIs can be compared. In particular, this unified framework enables a sensitivity analysis for the effect of changing the reference used for evaluating disparities (e.g., average versus best group rate) as well as the effect of modifying the weighting distribution pj (equally-weighted versus population-weighted), which are issues of concern; see Harper et al. (2010).
The RI is a class of HDIs, {RIα : α ∈ ℝ}. When the parameter α > 0 increases, the rescaled index αRIα is nondecreasing; therefore, α can be interpreted as a disparity aversion parameter in a manner akin to the Atkinson index (Atkinson, 1970). Indeed, for α > 0, the Atkinson index simply is obtained via the standardizing exponential transformation 1 − e−αRIα. The disparity aversion parameter can reflect a range of societal values attached to inequality. In Levy, Chemerynski and Tuchmann (2006), the Atkinson index is shown to fulfill some of the core axioms of health benefits analysis, e.g., Pigou-Dalton transfer principle and subgroup decomposability. The authors also argue that, unlike some indices in the GE class, the Atkinson index avoids a value judgment about the relative importance of transfers at different percentiles of the distribution of the adverse health outcome.
In this paper, we illustrate the proposed methodology using data from the National Health and Nutrition Examination Survey (NHANES) on the 2001–04 prevalence of moderate or severe periodontitis among U.S. adults aged 45–74. These binary individual-level data track Oral Health objective OH-5 in HP2020. NHANES is the data source for approximately 1 in 7 population-based objectives in HP2020. Close to half of the (approximately) 1,200 objectives in HP2020 are population-based, and most, though not all, such objectives track a proportion or a rate where the underlying individual-level variable has a binary outcome. See http://healthypeople.gov. The supplement to this article in Talih (2012a) provides further illustration of the proposed methodology with continuous individual-level data on total blood cholesterol levels among adults aged 20 and over, from NHANES 2005–08. These data track Heart Disease and Stroke objective HDS-8 in HP2020.
1.1. Common practice
The most commonly used between-group HDIs are weighted sums of the form , where rj = qj/pj, for some function f(r); see Firebaugh (1999).
Population average as reference
When the distributions p and q are given by pj = nj/n, qj = pjrj, and rj is the ratio of the average ȳ·j of the adverse health outcome in group j relative to the population average ȳ··,
| (1.1) |
the resulting class of HDIs, with f(r) = fα(r) := (1 − r1−α)/[α(1− α)], is the generalized entropy (GE) class, which extends the mean log deviation (MLD; f1(r) = −ln r) and the Theil index (TI; f0(r) = r ln r); see Haughton and Khander (2009; chapter 6).
That the GE HDIs are nonnegative, that equal zero only when rj = 1 for all j, follows from the convexity of the function fα(r) specified above and the fact that the pj and qj sum to one—GE is a class of Csiszár f-divergences; see Ali and Silvey (1966). However, the requirement that the distributions p and q be probability mass functions can be restrictive.
Least adverse health outcome as reference
Keppel et al. (2005) recommend measuring disparities relative to the group with the least adverse health outcome. Instead of (1.1), this would result in rj’s of the form
| (1.2) |
Clearly, with the rj as in (1.2) and the pj = 1/m or nj/n, the qj = pjrj no longer define a probability mass function.
The health inequality paradox
There are two essentially distinct approaches to evaluating health disparities overall, each of which makes an explicit value judgment regarding the trade-off between an individual’s burden of disease and a group’s burden of disease. Used in the GE class, which includes the MLD and TI, the population-weighted distribution pj = nj/n is consistent with individuals in the population being equally-weighted—with weights 1/n—regardless of their group membership. In contrast, the equally-weighted distribution pj = 1/m, which is used in the index of disparity (IDisp) of Keppel et al. (2005), results in more weight being given to individuals in smaller population groups than in larger ones. [Keppel et al. use weights 1/(m − 1) instead of 1/m, since there are only m − 1 comparisons relative to the group with the least adverse health outcome.]
Because of this trade-off between the individual’s burden of disease and the group’s burden of disease, potential impact of public health interventions is modified by the specific measure of health disparities used. When all groups are equally-weighted, an intervention that targets a relatively small group with a relatively large burden of disease can prove very effective in reducing overall disparity. On the other hand, when groups are population-weighted, that same intervention will not have as much impact on reducing overall disparity, and other interventions might be desired; see Harper et al. (2010), Frohlich and Potvin (2008), and Rose (1985). The aforementioned trade-off between individual’s health and population’s health is, perhaps, what differentiates most strikingly analyses of health disparities from studies of wealth inequalities—the latter having provided the impetus for the development of the GE and related families of inequality indices. When possible, methods used for comparing health outcomes should similarly be differentiated from those used for comparing income distributions.
1.2. Organization of the paper
The paper is organized as follows.
In section 2, we introduce the generalized Rényi divergence as the basis for developing the RI. A critical property of the generalized Rényi divergence is its invariance to scaling of either of the two distributions whose divergence is being evaluated; see section 2.1. Thus, when monitoring health disparities, the RI remains the same, regardless of whether we use: the population average as the denominator for the relative disparities rj, as in (1.1); the group with the least adverse health outcome as the denominator, as in (1.2); or use a Healthy People or some other target as the denominator.
The RI extends the MLD and TI. The MLD is mostly influenced by groups with large population shares pj = nj/n, whereas the TI is mostly influenced by groups where the adverse health outcome is more frequent or severe (qj = y·j/y··); see section 2.2. In section 2.3, we show that the RI can be symmetrized, which yields a symmetric measure in the two distributions whose relative entropy is being evaluated. Thus, when pj = nj/n, qj = pjrj, and the rj are as in (1.1), the resulting symmetrized Rényi index (SRI) generalizes the symmetrized Theil index (STI) of Borrell and Talih (2011).
In section 2.4, we show that, for α > 0, the Atkinson index simply is obtained via the standardizing exponential transformation 1 − e−αRIα. Hence, the parameter α > 0 is a disparity aversion parameter for αRIα and it can reflect a range of societal values attached to inequality.
Because of scale invariance, the RI and SRI only depend on the relative disparities rj in (1.1) or (1.2) through the numerator ȳ·j. Thus, in section 2.5, we express the between-group RI and SRI as functions of the group sizes nj and means ȳ·j, both when groups are population-weighted (pj = nj/n) and when groups are equally-weighted (pj = 1/m).
In section 3, we discuss two potential alternatives to the RI based on the GE (section 3.1) and Bregman class (section 3.2). In section 3.3, we compare the (reference-invariant) SRI with a symmetrized reference-invariant GE under simple hypothetical scenarios and argue that the SRI is less sensitive to small changes in the distribution of the adverse health outcome.
In section 4, we proceed as in Borrell and Talih (2011) and Biewen and Jenkins (2006) to derive design-based standard errors for the (between-group) RI and SRI using Taylor series linearization. To validate our derivation, we implement in the supplemental R code the balanced repeated replication and bootstrap methods, introduced by McCarthy (1969) and Rao and Wu (1988), respectively; see Talih (2012b). Rescaled bootstrap enables the design-based estimation of the sampling distribution of the RI and SRI. Further, we examine the effect of the weighting distribution p, comparing the population-weighted (pj = nj/n) to the equally-weighted case (pj = 1/m).
In section 5, we illustrate the proposed methodology using periodontal disease data from NHANES. Section 6 concludes.
The technical appendix includes a detailed discussion of the decomposability of the RI and SRI; see Talih (2012c). Decomposability is the separation of the total or aggregate HDI into between- and within-group components; see Bourguignon (1979). Just like for the GE class of HDIs, decomposability allows for multiple predictors of individual-level disparities to be considered in succession, as in multi-way analysis of variance. We examine the decomposition of the total RI and SRI when groups are population-weighted (e.g., pj = nj/n)—which, as mentioned earlier, is consistent with individuals being equally-weighted—as well as when groups are equally-weighted (e.g., pj = 1/m). In the latter case, only a weak decomposition of the aggregate RI and SRI holds. The technical appendix also contains the derivation of the designed-based standard errors for the total or aggregate RI and SRI and their within-group components; see Talih(2012c).
2. An Entropy-based reference-invariant health disparity index
Consider two nonnegative (yet, not necessarily probability) mass functions p and q. Suppose they are defined on a common set of integers {1, 2, ···, m}, which we take to be group membership indicators for different socioeconomic and demographic groups in a larger population. In analyses of health disparities, pj typically denotes the relative population share of group j, whereas qj denotes its relative disease burden (or, inversely, the relative health advantage). However, as discussed in section 1, other choices for the quantities pj and qj may be desired. From the mathematical point of view, investigating health disparities within the population amounts to ascertaining the discrepancy between the two distributions p and q.
Definition
Based on a divergence proposed by Fujisawa and Eguchi (2008) for robust parameter estimation in the presence of outliers, and for rj = qj/pj and a scalar α ≠ 0, 1, Cichocki and Amari (2010) define the generalized Rényi (or alpha-gamma) divergence as
| (2.1) |
Remark
Our approach, reflected in (2.1) and throughout the paper, differs from the standard information theoretic approach in that we introduce dependence between the distributions p and q. The former is a weighting distribution—typically, the pj are the relative sizes of groups in the population. The latter is constructed from qj = pjrj. Each rj specifies the disparity for group j relative to a common reference point, as explained in section 1.1.
2.1. Scale invariance and relation to Rényi divergence
Due to the form of the argument of the logarithm in (2.1), the generalized Rényi divergence Rα(p||q) is invariant to re-scaling of either the p or the q distributions. Indeed, for any positive scalars c1 and c2,
In particular, for p̄j = pj/Σp, q̄j = qj/Σq, and r̄j = q̄j/p̄j we have
| (2.2) |
When α > 0, the divergence αRα(p̄||q̄) is the Rényi divergence between two probability mass functions—here, p̄ and q̄—introduced by Rényi (1960).
Nonnegativity
When α > 0 and α ≠ 1, Jensen’s inequality ensures that Rα(p̄||q̄) ≥ 0, with equality if and only if p = cq for some positive scalar c; see, for example, van Erven (2010; chapter 6). By skew-symmetry, see (2.5) below, it follows that Rα(p||q) ≥ 0 for all α ≠ 0, 1.
Monotonicity
Jensen’s inequality also ensures that the Rényi divergence αRα(p||q) is nondecreasing when α > 0 increases, see van Erven (chapter 6). Thus, when α > 0, α can be looked upon as an inequality (or divergence) aversion parameter for the Rényi divergence.
Practical relevance of scale invariance
Henceforth, we refer to the HDI that is derived from (2.2) as the Rényi index (RIα, or RI, for short). Scale invariance is appropriate when it is believed that uniform proportional changes across the population should leave the HDI unchanged; see Levy, Chemerynski and Tuchmann (2006). Scale invariance is especially desirable when seeking HDIs that are invariant to the choice of the reference for evaluating disparities, because, as seen in the Healthy People 2010 Final Review, identification of a reference group can be affected by statistical reliability. In this respect, the RI remains the same, whether we use the population average as the denominator for the relative disparities rj, as in (1.1), the group with the least adverse health outcome, as in (1.2), or take any pre-set (positive) target, e.g., a HP2010 or HP2020 target.
2.2. Limiting cases
The generalized Rényi divergence is extended by continuity to the limiting cases α → 1 and α → 0 (l’Hôpital’s rule):
| (2.3) |
When pj = nj/n, qj = pjrj, and the rj are as in (1.1), these special limiting cases of the RI with α → 1 and α → 0 are the MLD and the TI, respectively; see Borrell and Talih (2011).
Interpretation of the MLD and the TI
The MLD and the TI were originally proposed as measures of income inequality by Theil (1967). Both the MLD and the TI are well-established measures of relative entropy between two probability distributions, due to Kullback and Leibler (1951). The general form of the Kullback-Leibler (K-L) divergences is
| (2.4) |
When pj = nj/n, qj = pjrj, and the rj are as in (1.1), MLD = KL(p||q) whereas TI = KL(q||p). Thus, the MLD and the TI summarize the disproportionalities between the relative sizes of groups in the population and those groups’ shares of an adverse health outcome. In this regard, from (2.3), the MLD is seen as a log-likelihood ratio test statistic for the null hypothesis that group shares of the adverse health outcome have been “allocated” according to the relative sizes of the groups in the population. Similarly, the TI tests the null hypothesis that group shares of the total population have been “allocated” according to the groups’ shares of the adverse health outcome. This interpretation of the MLD and TI as log-likelihood ratio tests will be revisited in the case-study of section 5 to assess the statistical significance of the symmetrized Rényi index.
2.3. Symmetrized Rényi index
Generalized Rényi divergence in (2.2) is asymmetric in the two distributions whose generalized relative entropy is being evaluated: Rα(p||q) will be mostly influenced by groups with large values of pj, whereas Rα(q||p) will be mostly influenced by groups with large values of qj. Borrell and Talih (2011) discuss this issue of lack of symmetry in the context of the special cases R1(p̄||q̄) = KL(p̄||q̄) (MLD) and R0(p̄||q̄) = KL(q̄||p̄) (TI), with pj = nj/n, qj = pjrj, and the rj as in (1.1). Yet,
| (2.5) |
Thus, a symmetrized generalized Rényi divergence, SRα(p, q), is obtained from [Rα(p||q) + R1−α(p||q)]/2. For p̄j = pj/Σp, q̄j = qj/Σq, and r̄j = q̄j/p̄j, SRα(p, q) is given by
| (2.6) |
We refer to the HDI that is derived from (2.6) as the Symmetrized Rényi index (SRI).
Limiting case
As in section 2.2, SRα(p, q) is extended by continuity to the cases α → 1, 0:
| (2.7) |
The divergence in (2.7) is a symmetrized Kulback-Leibler divergence, also known as half the Jeffrey’s divergence; see, for example, Pollard (2002). When pj = nj/n is the population share for group j, the rj are as in (1.1), and qj = pjrj is the disease share y·j/y··, Borrell and Talih (2011) coin the symmetrized divergence in (2.7) the symmetrized Theil index (STI).
2.4. Standardization and relation to the Atkinson index
For α > 0, a standardized generalized Rényi divergence, with values between 0 and 1, and which we denote by Aα(p||q), can be defined for any nonnegative (not necessarily probability) distributions p and q:
| (2.8) |
Thus, when α > 0, we have
For pj = nj/n, qj = pjrj, and the rj as in (1.1), this is the (between-group) Atkinson index, introduced by Atkinson (1970) for measuring income inequalities, with parameter α > 0 quantifying society’s aversion to inequality.
Standardized SRI
Applying a standardizing exponential transformation similar to the one in (2.8), we construct a standardized SRI, with values between 0 and 1, as follows:
| (2.9) |
This construction preserves symmetry of the SRI around the parameter value α = 1/2. Since αSRα(p, q) is nondecreasing for α ≥ 1/2, α is a disparity aversion parameter for the standardized SRI. By symmetry, 1 − α is a disparity aversion parameter when α < 1/2. The value α = 1/2 can be interpreted as the most conservative choice for disparity aversion in the standardized SRI, in that it gives a lower bound for the index.
2.5. The RI and SRI as between-group HDIs
By construction, we have qj = pjrj and, from (1.1) or (1.2), rj ∝ ȳ·j. From (2.1) and (2.6), we have expressions for the between-group RI and SRI in terms of the group sizes nj and means ȳ·j, which we list next for α ≠ 0, 1. Henceforth, to distinguish the between-group RI (respectively, SRI) from the within-group RI (respectively, SRI) and the aggregate or total RI (respectively, SRI) that are discussed in the technical appendix (Talih, 2012c), we use the notation [RI]B (respectively, [SRI]B).
- Population-weighted group contributions pj = nj/n
(2.10) (2.11) - Equally-weighted group contributions pj = 1/m
(2.12) (2.13)
Limiting cases
The expressions for the RI and SRI when α → 1 or α → 0 are obtained by taking limits in (2.10–2.13) above. We list them here for ease of reference. (2.10) with α → 1 yields the MLD,
whereas α → 0 yields the TI,
As well, (2.11) with either α → 1 or α → 0 yields the STI,
On the other hand, taking the limit when α → 1 in (2.12) results in
while the limit when α → 0 is
Thus, the limit in (2.13) when α → 1 or 0 is
3. Alternatives to the Rényi index
3.1. Generalized entropy class
A class of measures that originate in the measurement of income inequalities is the generalized entropy (GE) class, which specifies pj = nj/n and the ratios rj as in (1.1); see Biewen and Jenkins (2006), Elbers et al. (2008), and references therein. The GE class is a special case of alpha divergence. The latter was introduced by Chernoff (1952) to evaluate the asymptotic efficiency of likelihood ratio tests. Cressie and Read (1984) also discuss such measures for multinomial goodness-of-fit tests. Using the parameterization in Cichocki and Amari (2010), alpha divergence is defined for any nonnegative mass functions p and q and any real number α, α ≠ 0, 1, as
| (3.1) |
where, as before, the rj are the ratios rj = qj/pj. Just like the generalized Rényi divergence, Dα(p||q) can be extended by continuity to the limiting cases α → 1 and α → 0, yielding the K-L divergences in (2.4). It is well known that alpha divergence Dα(p||q) remains nonnegative, Dα(p||q) ≥ 0, with equality if and only if pj = qj for each j in 1, 2, ···, m. When p and q are probability mass functions, i.e., and , alpha divergence is a Csiszár f-divergence; see Ali and Silvey (1966).
We refer to the index that is derived from (3.1) as the GE index. Just like with the Rényi index, a symmetrized GE index is obtained simply by taking the arithmetic average of Dα(p||q) and D1−α(p||q):
| (3.2) |
In addition, the symmetrized GE index in (3.2) can be standardized to take values between 0 and 1 using the exponential transformation in (2.9).
Further, whereas alpha divergence is not scale-invariant,—it only holds that, for a positive scalar c, Dα(cp||cq) = cDα(p||q),—a reference-invariant GE index Dα(p̄||q̄) can be constructed easily using the normalized distributions p̄ and q̄, because and for any positive scalars c1 and c2. (As before, p̄j = pj/Σp, q̄j = qj/Σq, and r̄j = q̄j/p̄j.) Thus,
| (3.3) |
We refer to this HDI as the symmetrized reference-invariant GE index.
Proposition
For nonnegative mass functions p and q on {1, 2, ···, m}, let p̄j = pj/Σp, q̄j = qj/Σq, and r̄j = q̄j/p̄j. For SRα(p̄, q̄) in (2.6) and SDα(p̄, q̄) in (3.3):
| (3.4) |
| (3.5) |
with equality when α → 1 or α → 0.
Proof
Without loss of generality, let α > 1. The proof follows from the application of the arithmetic-geometric mean inequality and the fact that x−1 ≥ ln x for all x > 0.
In section 3.3, we show not only that the SRI is more conservative than the symmetrized reference-invariant GE index for α > 1, as implied by (3.4), but also that the SRI is more robust to small changes in the disease distribution q, which renders it a more desirable HDI.
The GE class is well-studied in the economics literature. The GE class is consistent with a certain set of axiomatic properties that are relevant for income distributions; see, for example, Cowell, Davidson and Flachaire (2011), Cowell and Kuga (1980), and Shorrocks (1980). Even though such axioms are not sufficient for health benefits analyses, the GE class remains a widely used class for constructing HDIs; see Levy, Chemerynski and Tuchmann (2006). In addition to the K-L divergences (α → 1 or 0), special cases of alpha divergence in (3.1) are the Pearson (α =−1) and Neyman (α = 2) chi-squared statistics and the squared Hellinger distance (α = 0.5).
3.2. Bregman class
Bregman divergences are generated from any twice differentiable and strictly convex function Φ as follows:
A common choice for the generating function Φ, for β ≠ 0,1, is
which yields the beta divergence, defined for β ≠ 0,1 and rj = qj/pj,
| (3.6) |
and appropriate extensions by continuity when β → 0 or 1; see Cichocki and Amari (2010). As before, the limiting case β → 0 reduces to the Kulback-Leibler divergence KL(q||p) in (2.4). However, the case β → 1 is no longer KL(p||q), but, instead, the so-called Itakura-Saito (IS) divergence, given by
Beta divergence in (3.6) provides a class of HDIs that are worth investigating in future work. For instance, a symmetrized reference-invariant beta divergence is obtained from [Bβ(p||q) + Bβ(q||p)]/2, resulting in
However, as explained in section 1, the pj are weights that are assigned by the analyst to each population group j, commonly using either equal weights (e.g., 1/m) or size-based weights (e.g., nj/n). Therefore, in the context of this paper, the analyst would need to provide additional justification for the logarithmic rescaling of the pj in (3.6) by the factor 1 − β, which is not the case for alpha divergence (3.1) or generalized Rényi divergence (2.2).
Magdalou and Nock (2011) derive the Bregman class as the unique class of measures that are consistent with certain inequality measurement principles, including the transfer principle (albeit modified) and decomposability. By the authors’ own assessment, the key to their derivation is a new principle of “judgment separability” that they introduce for the analysis of income inequalities. In this paper, we restrict attention to reference-invariant HDIs (i.e., strong scale-invariant measures), whereby judgment separability is not necessary, because it reduces to the weaker principle of “indiscernability of identicals. ” The latter postulates simply that an inequality measure D satisfy D(p||p) = 0 for any distribution p.
For those reasons, we do not discuss beta divergence in section 3.3; we compare the SRI only with the symmetrized reference-invariant GE index.
3.3. SRI and changes therein
To illustrate the robustness of the SRI (2.6) to small changes in the distribution q = pr, for a fixed p, and in comparison with the symmetrized reference-invariant GE index in (3.3), we examine the SRI under simple scenarios borrowed from Harper et al. (2010).
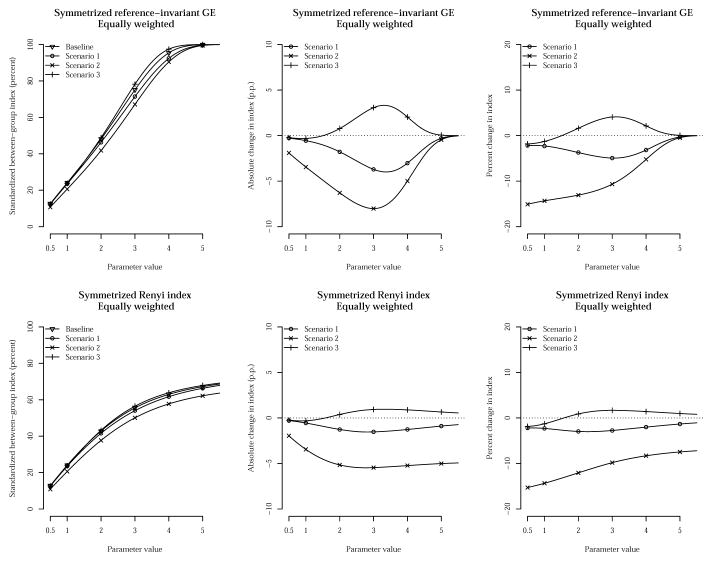
In Table 1, we consider a population that is divided into four groups of equal size, so that the population-weighted distribution pj = nj/n is the same as the equally-weighted distribution pj = 1/4. At baseline, group D has the least adverse health outcome, with a rate of 10%, whereas group A has the most adverse outcome, with a rate of 50%. Groups B and C have rates of 40% and 30%, respectively. In scenarios 1 and 3, the groups with the least and most adverse outcomes remain the same, but, in scenario 1 the rate for group B decreases 10 percentage points from baseline, whereas in scenario 3 the rate for group C increases 10 percentage points from baseline, in both scenarios achieving equal rates for groups B and C. In scenario 2, the rate for group A decreases 10 percentage points while the other group rates remain unchanged. Because in scenario 3 group D (the “best-off” group) is further separated from the other groups, with a 30 percentage points difference from the next best (group C), compared to a 20 percentage points difference at baseline, we expect that disparities will increase overall. In scenario 2, the gap between the best-off group (group D) and the worst-off group (group A) has decreased; therefore we expect an overall decrease in disparities. In scenario 1, we similarly expect a decrease in disparities because the rate for group B has moved closer to the best rate.
Table 1.
Baseline and three hypothetical scenarios to examine changes in the SRI and its GE-based counterpart
| Group (j) | A | B | C | D |
|---|---|---|---|---|
| Relative size nj/n | 25% | 25% | 25% | 25% |
| Baseline | ||||
| Group rate ȳ·j | 50% | 40% | 30% | 10% |
| Scenario 1 | ||||
| Group rate ȳ·j | 50% | 30% | 30% | 10% |
| Scenario 2 | ||||
| Group rate ȳ·j | 40% | 40% | 30% | 10% |
| Scenario 3 | ||||
| Group rate ȳ·j | 50% | 40% | 40% | 10% |
The top- and bottom-left panels in Figure 1 compare the symmetrized reference-invariant GE and the symmetrized Rényi indices under the above scenarios for different values of the disparity aversion parameter α. Only values of α ≥ 0.5 are shown due to symmetry. As confirmed in (3.4), the standardized SRI is seen to be more conservative for values of α> 1; moreover, the SRI is seen to better discriminate between the different scenarios in Table 1 for large values of α. Indeed, observe how the symmetrized reference-invariant GE can no longer distinguish between the various scenarios for large values of α, whereas the SRI still can. This is observed both in the absolute scale, in the top- and bottom-center panels, as well as the relative scale, in the top- and bottom-right panels. Furthermore, for α ≤ 3 (approximately), the change in the SRI is considerably smaller than the change in the symmetrized reference-invariant GE, both in the absolute as well as in the relative scales, which illustrates the robustness of the SRI to small changes in the distribution of the adverse health outcome.
Fig 1.
Comparison of the symmetrized Rényi index (SRI) with the symmetrized reference-invariant GE index. The top- and bottom-left panels show the symmetrized reference-invariant GE and the SRI, respectively, under the scenarios described in Table 1 for different values of the disparity aversion parameter α. Only values of α ≥ 0.5 are shown due to symmetry. As confirmed in (3.4), the standardized SRI is more conservative for parameter values α > 1. In addition, the SRI is seen to better discriminate between the different scenarios in Table 1 for large values of α. Furthermore, for α ≤ 3 (approximately), the change in the SRI is considerably smaller than the change in the symmetrized reference-invariant GE, both in the absolute as well as the relative scales, which illustrates the robustness of the SRI to small changes in the distribution of the adverse health outcome.
4. Design-based standard errors
Martinez-Camblor (2007) establishes a central limit theorem for the total TI under simple random sampling. Cowell, Davidson and Flachaire (2011) use similar empirical processes techniques to analyze the asymptotic distribution of goodness-of-fit statistics that are derived from the GE class. Using Taylor series linearization, Biewen and Jenkins (2006) derive the sampling variances for both the total TI and MLD—as well as the GE class of total HDIs—for complex survey data. Borrell and Talih (2011) extend the Taylor series linearization method to the case of grouped complex survey data to obtain the sampling variance of the total STI and its between-group and within-group components. Borrell and Talih (2011) validate the sampling variances obtained via linearization by comparing them to the ones obtained via balanced repeated replication and rescaled bootstrap, which are developed in McCarthy (1969), Fay (1989), Judkins (1990), Rao and Wu (1988), Rao, Wu and Yue (1992), and discussed in the context of health inequality measures in Harper et al. (2008) and Cheng, Han and Gansky (2008). In this paper, we adopt a strategy similar to the one in Borrell and Talih (2011), using Taylor series linearization, balanced repeated replication, and the rescaled bootstrap to evaluate and validate the design-based standard errors for the RI (and, by extension, the SRI) and its between- and within- group components. Below, we only show the calculations for the between-group component [RIα]B. The calculations for the sampling variance for the within-group component [RIα]W are shown in the technical appendix; see Talih (2012c). Also, because SRIα = (RIα +RI1−α)/2, the sampling variance for the SRI and its between-and within-group components easily follows. R code for computing the total RI and SRI, together with their group-specific, between-, and within-group components in grouped complex survey data, as well as their design-based standard errors, is provided as a supplement; see Talih (2012b).
Define, for any real number a :
| (4.1) |
| (4.2) |
In the above, S is the number of strata; Cs is the number of PSU’s in stratum s; lcs is the number of sample observations in the PSU-stratum pair (c, s); wics is the sampling weight for sample observation i in the PSU-stratum pair (c, s); yics is the severity of the adverse health outcome for sample observation i in the PSU-stratum pair (c, s); δicsj = 1 when observation i [in PSU-stratum pair (c, s)] belongs to group j and δicsj = 0 otherwise; and j ranges from 1 to m, where m is the number of groups in the population. With the notation introduced in (4.1) and (4.2), we have n = U0,·, nj = U0,j, y·· = U1,·, y·j = U1,j, ȳ·· = U1,·/U0,·, and ȳ·j = U1,j/U0,j.
4.1. Population-weighted groups: pj = nj/n
From (2.10), we see that the between-group component [RIα]B can be written as a function solely of the sufficient statistics Ua,k in (4.1). Thus, when α ≠ 0,1, the partial derivatives with respect to U0,k and U1,k are:
| (4.3) |
| (4.4) |
The partial derivatives for the between-group component for the SRI, which is given by [SRIα]B = [RIα]B + [RI1−α]B/2, easily follow.
Limiting cases
When pj = nj/n, rj ∝ ȳ·j, and qj = pjrj, the distributions p̄ = p/Σpj and q̄ = q/Σqj are given by p̄j = nj/n and q̄j = p̄jr̄j, respectively, with r̄j = ȳ·j/ȳ··, as in (1.1). Thus, the limiting cases when α → 1 or 0 in (4.3–4.4) reduce to the partial derivatives of the between-group MLD and TI, respectively; see (2.3). These were computed in Borrell and Talih (2011). We group them here for completeness:
Introduce an artificial variable σicsk that represents the variance contribution from each sample observation. The σicsk are obtained by taking the dot product of the vector of partial derivatives from (4.3–4.4) with the vector of summands in the sufficient statistics in (4.1):
| (4.5) |
Thus, an estimate of the sample variance of [RIα]B is given by the sampling variance of the total statistic . The latter is readily available, e.g., using the command for survey estimation of variances of totals (‘svytotal’) in the R package ‘survey’; see Lumley (2004, 2011) and R Development Core Team (2011).
4.2. Equally-weighted groups: pj = 1/m
From (2.12) and (4.1), when α ≠ 0,1, the partial derivatives with respect to U0,k and U1,k are given by:
| (4.6) |
| (4.7) |
The partial derivatives for the between-group component for the SRI, which is given by , also follow.
Limiting cases
Limiting expressions for the partial derivatives in (4.6–4.7) of the between-group component are obtained as follows.
- When α→ 1 :
- When α→ 0 (l’Hôpital’s rule):
5. Case study from NHANES
HP2020 objective OH-5 in the Oral Health Topic Area aims to reduce the proportion of U.S. adults aged 45–74 with moderate or severe periodontitis. Table 2 presents estimated prevalence (and standard errors) from NHANES 2001–04. The gradient associated with socioeconomic status and the differences by sex and by race/ethnicity are well documented; see, for example, Borrell and Talih (2012).
Table 2.
Prevalence (in percent) of moderate or severe periodontitis among U.S. adults aged 45–74, 2001–04.1
| Percent | SE2 | 95% | CI3 | |
|---|---|---|---|---|
| Total | 12.8 | 0.755 | 11.2 | 14.3 |
| Sex | ||||
| Male | 16.3 | 0.941 | 14.3 | 18.2 |
| Female | 9.4 | 0.882 | 7.6 | 11.2 |
| Race/Ethnicity | ||||
| White only, non-Hispanic | 10.5 | 0.861 | 8.8 | 12.3 |
| Black only, non-Hispanic | 22.1 | 1.863 | 18.3 | 25.9 |
| Mexican-American | 18.1 | 2.829 | 12.3 | 23.9 |
| Other4 | 20.3 | 3.637 | 12.9 | 27.8 |
| Educational attainment | ||||
| Less than high school | 26.8 | 1.974 | 22.8 | 30.9 |
| High school graduate | 14.6 | 1.811 | 10.9 | 18.3 |
| Some college or AA degree | 11.3 | 0.899 | 9.5 | 13.2 |
| College graduate or above | 6.5 | 1.191 | 4.0 | 8.9 |
| Family income (percent FPL5) | ||||
| Less than 100 | 28.2 | 3.305 | 21.4 | 34.9 |
| 100–199 | 24.1 | 2.134 | 19.7 | 28.4 |
| 200–399 | 10.8 | 1.413 | 8.0 | 13.7 |
| 400–499 | 8.4 | 1.504 | 5.3 | 11.4 |
| 500 or above | 8.5 | 1.089 | 6.3 | 10.7 |
| N/A6 | 13.3 | 3.362 | 6.5 | 20.2 |
| Country of birth | ||||
| U.S. | 11.8 | 0.713 | 10.4 | 13.3 |
| Outside U.S. | 19.2 | 2.622 | 13.9 | 24.6 |
Data are from the National Health and Nutrition Examination Survey (NHANES) 2001–02 and 2003–04. The case definitions adopted by the CDC working group for use in population-based surveillance of periodontitis are as follows: for severe periodontitis, it is required that two or more interproximal sites have clinical attachment loss (CAL) ≥ 6mm, not on the same tooth, and one or more interproximal sites have pocket depth (PD) ≥ 5mm; for moderate periodontitis, it is required that either two or more interproximal sites have CAL ≥ 4mm, not on the same tooth, or two or more interproximal sites have PD ≥ 5mm, not on the same tooth. Page and Eke (2007) explain the rationale for those cutoff values.
Designed-based standard errors (SE) obtained via Taylor linearization (e.g., SUDAAN or R ‘survey’ package).
Lower and upper confidence limits, respectively, for a 95 percent confidence interval (CI).
The category Other consists of Hispanic or Latino other than Mexican-American and non-Hispanic of races other than black and white, including multiracial adults. The category Other is listed to provide a complete partition of the population into mutually exclusive groups, but it is not part of the HP2020 population template for objectives monitored using NHANES 1999 and later.
Family income as a percent of the federal poverty level (FPL), also known as the poverty income ratio (PIR).
Adults whose family PIR is not available (N/A), listed to maintain a complete partition of the population.
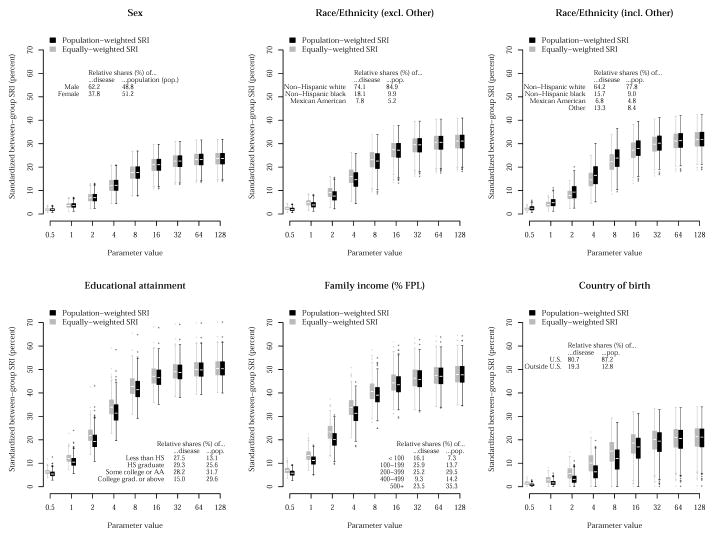
Figure 2 compares the standardized SRI for values of the parameter α when groups are population-weighted and when groups are equally-weighted. As seen in section 2.5, the population-weighted SRI uses the estimated distributions (displayed in the table within each figure panel) for the relative shares of population (pj = nj/n) and of disease (qj = y·j/y··) in the symmetrized Rényi divergence Sα(p, q), whereas the equally-weighted SRI uses pj = 1/m. Due to symmetry of the SRI around the parameter value 0.5, only values of α ≥ 0.5 are shown. For values of α ≥ 0.5, the parameter α is a disparity aversion parameter for the standardized SRI: the standardized SRI is nondecreasing in α for α ≥ 0.5. The rescaled bootstrap method allows the design-based estimation of the sampling distribution of the index. The box plots in Figure 2 represent the bootstrapped sampling distributions for the different values of α and types of indices shown.
Fig 2.
Standardized between-group SRI by population characteristic for the prevalence of moderate or severe periodontitis among U.S. adults aged 45–74, 2001–04. Due to symmetry of the SRI around the parameter value 0.5, only values of α ≥ 0.5 are shown. For values of α ≥ 0.5, the parameter α is a disparity aversion parameter for the standardized SRI: the standardized SRI is nondecreasing in α for α ≥ 0.5; see (2.9). The population-weighted SRI uses the estimated distributions (displayed in the table within each figure panel) for the relative shares of population (pj = nj/n, restricting to individuals with valid periodontal data) and of disease (qj = y·j/y··) in the symmetrized Rényi divergence Sα(p, q), whereas the equally-weighted SRI uses pj = 1/m. The box plots are design-based, obtained via rescaled bootstrap with 500 replications.
As mentioned earlier, design-based standard errors obtained via Taylor series linearization can be validated against—and are generally in agreement with—the ones that are obtained via balanced repeated replication and rescaled bootstrap, as shown in Table 3 for the analysis by race/ethnicity.
Table 3.
Standardized between-group SRI (in percent) for the analysis by race/ethnicity of moderate or severe periodontitis prevalence among U.S. adults aged 45–74, 2001–04: Comparison of standard error (SE) for various design-based estimation methods.
| Parameter value (α) | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|---|---|---|---|---|---|---|---|---|---|
| Population weighted | |||||||||
| Index | 1.85 | 3.67 | 7.25 | 13.82 | 21.76 | 26.56 | 28.84 | 29.93 | 30.45 |
| Taylor linearization SE | 0.711 | 1.395 | 2.662 | 4.509 | 5.244 | 4.738 | 4.349 | 4.063 | 3.846 |
| Balanced repeated replication SE | 0.678 | 1.330 | 2.530 | 4.188 | 4.704 | 4.388 | 4.224 | 4.142 | 4.098 |
| Rescaled bootstrap SE | 0.728 | 1.428 | 2.707 | 4.393 | 4.838 | 4.449 | 4.234 | 4.137 | 4.091 |
| Equally weighted | |||||||||
| Index | 2.19 | 4.33 | 8.34 | 14.87 | 21.96 | 26.47 | 28.78 | 29.90 | 30.43 |
| Taylor linearization SE | 0.822 | 1.604 | 3.013 | 4.948 | 5.783 | 5.412 | 5.003 | 4.560 | 4.060 |
| Balanced repeated replication SE | 0.665 | 1.297 | 2.420 | 3.888 | 4.495 | 4.331 | 4.206 | 4.137 | 4.096 |
| Rescaled bootstrap SE | 0.693 | 1.352 | 2.516 | 3.981 | 4.532 | 4.355 | 4.200 | 4.122 | 4.084 |
Notice how the two indices in Figure 2 agree perfectly for the analysis by sex, since males and females are represented almost equally in the population. On the other hand, when the ‘Other’ category is taken into account in the analysis by race/ethnicity, the population-weighted SRI tends to be larger than the equally-weighted SRI for all values of the parameter α, whereas when ‘Other’ is excluded, this ordering is reversed. This suggests that the analyst should carefully assess the interaction between the groups’ weighting scheme and the partitioning of the population. Still, unlike in Harper et al. (2010), where the effect of weighting relative to population size versus weighting equally was examined using different classes of indices—the MLD for the former (a GE-based HDI with the average health outcome as the reference), but the IDisp for the latter (a non-entropy based HDI with the least adverse health outcome as the reference)—, the SRI class of HDIs introduced in this paper provides a unified framework for such comparative analyses, controlling more effectively for other characteristics of the index. However, we concur with Harper et al. (2010) that researchers should recognize that relying on only one HDI inevitably endorses normative judgments of one nature or another. Though they are mostly in agreement, here, it is clear from Figure 2 that it is incumbent on researchers to consider both the population-weighted and equally-weighted SRIs, as well as the gradient that corresponds to increasing values of the disparity aversion parameter.
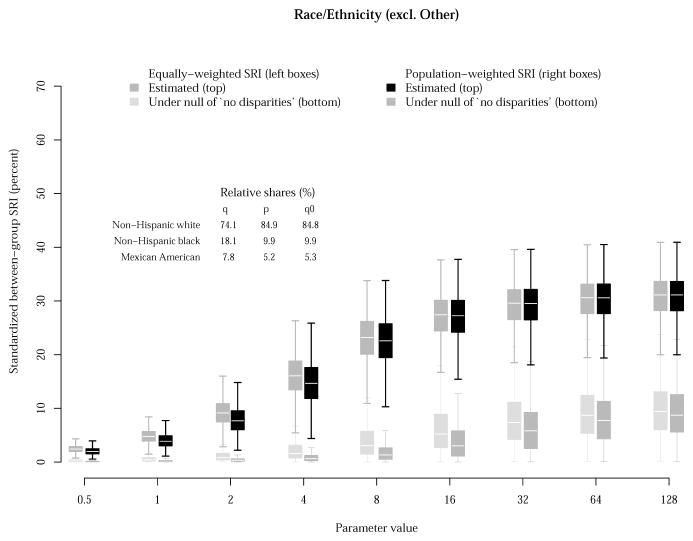
In Figure 3, the sampling distribution of the index is compared to one that is obtained under a null hypothesis of ‘no disparities.’ For the analysis by race/ethnicity, and without disrupting the survey design structure, a dummy disease indicator variable is simulated such that the relative shares of disease, qj = y·j/y··, are (approximately) equal to the given relative population shares, pj = nj/n. As seen in Figure 3, the resulting null and alternative distributions using the population-weighted SRI are well separated, indicating that the null hypothesis of ‘no disparities’ would be rejected for all values of the parameter α. Further, even if we were to use the equally-weighted SRI instead (i.e., pj = 1/m instead of p0j = nj/n), we would still reject the null; the overlap between the null and alternative distributions remains minimal.
Fig 3.
Standardized between-group SRI for the analysis of moderate or severe periodontitis prevalence by race/ethnicity among U.S. adults aged 45–74, 2001–04. The population-weighted SRI uses the estimated distributions (displayed in the offset table) for the relative shares of population (pj = nj/n) and of disease (qj = y·j/y··) in the symmetrized Rényi divergence Sα(p, q), whereas the equally-weighted SRI uses pj = 1/m. The box plots are design-based, obtained via rescaled bootstrap with 500 replications. The null hypothesis of ‘no disparities’ is tested with simulated data for which the null distribution q0j of disease burden is (approximately) equal to the population shares pj = nj/n.
The case-study in section 5 illustrates how the SRI can help examine disparities in the prevalence of moderate or severe periodontitis among adults aged 45–74 with data from NHANES 2001–04. This case-study is relevant to HP2020 because, as stated in section 1, most population-based objectives in HP2020 track a proportion or a rate where the underlying individual-level variable has a binary outcome, and because NHANES is the data source for approximately 1 in 7 population-based objectives in HP2020. The supplementary case-study in Talih (2012a) provides further illustration of the proposed methodology with continuous individual-level data on total blood cholesterol levels among adults aged 20 and over from NHANES 2005–08. These data track Heart Disease and Stroke objective HDS-8 in HP2020.
Caveat
The stratified multistage probability sampling design structure of NHANES is well-documented; see http://www.cdc.gov/nchs/nhanes.htm. While the sample weights provided in the NHANES public-use data files reflect the unequal probabilities of selection, they also reflect non-response adjustments and adjustments to independent population controls. Therefore, strictly speaking, they are not the true sampling weights wics in (4.1).
6. Conclusion
In this paper, we introduce a new class of HDIs, the Rényi index (RI), which is based on a generalized Rényi divergence. When standardized, the RI generalizes the Atkinson index; thus, a disparity aversion parameter can incorporate societal values associated with health equity. In addition, both the MLD and TI, which belong to the GE class of HDIs, are limiting cases of the RI. Like the MLD and TI, the RI can be symmetrized, resulting in the symmetrized Rényi index (SRI). We use Taylor series linearization, balanced repeated replication, and rescaled bootstrap to examine the design-based standard errors and bootstrapped sampling distributions for the between-group RI and SRI in complex survey data such as NHANES. A critical property of the RI and SRI is their invariance to the choice of the reference used for evaluating disparities, which implies that the index remains the same, regardless of whether we use the population average as the reference, the group with the least adverse health outcome, a Healthy People target, or some other reference. This invariance property is critical to initiatives that monitor health disparities because the identification of a reference group can be affected by statistical reliability. An important property of the SRI is its robustness when compared with its GE-based counterpart.
Unlike in past comparative studies, the SRI class of HDIs introduced here provides a unified framework for ascertaining the effect of weighting groups relative to population size versus weighting groups equally, while controlling more effectively for other characteristics of the index. Nonetheless, we concur with past studies that relying on only one HDI inevitably endorses some normative judgments. Thus, it is incumbent on the analyst who would use the SRI to consider both population- and equally-weighted values, together with the disparity aversion gradient. This would enable sensitivity analyses that support development of policy recommendations that are more robust to the numerous value judgments, both implicit and explicit, in the measurement of health disparities. Further, although the disparity aversion parameter α in the standardized SRI is treated in this paper as a “tuning” parameter, future work could, instead, determine the parameter α from global variables such as cost of treatment, availability of health care resources, and other structural factors discussed in Fleurbaey and Schokkaert(2009).
Supplementary Material
Acknowledgments
The author thanks Luisa Borrell (CUNY) and Elizabeth Jackson (NCHS) for a discussion of the periodontitis case definitions in HP2020 objective OH-5, and Kimberly Rosendorf (NCHS) for input on findings on total blood cholesterol levels (HP2020 objective HDS-8). Jeff Pearcy (NCHS) and Yukiko Asada (Dalhousie University, Canada) discussed the interpretation of the parameter α as a disparity aversion parameter for the standardized SRI. Comments received from Van Parsons (NCHS) helped improve the section on variance estimation. The support and input received from Rebecca Hines, Chief of the Health Promotion Statistics Branch at NCHS, are gratefully acknowledged. Comments from Richard Klein, Jennifer Madans (NCHS), the journal editors, and anonymous reviewers have vastly improved the presentation of the material in the paper.
Footnotes
Technical Appendix: Decomposability
(http://lib.stat.cmu.edu/aoas/???/???;.pdf). Expressions and variance calculations for the total or aggregate RI and SRI and their within-group components when individual-level data are continuous.
Additional Case Study from NHANES
(http://lib.stat.cmu.edu/aoas/???/???;.pdf). Disparities in mean total blood cholesterol levels (μg/dL) in U.S. adults aged 20 and over, 2005–08.
(http://lib.stat.cmu.edu/aoas/???/???;.zip). Syntax and output from case-studies comparing the equally-weighted and population-weighted RI and SRI; their group-specific, between-, and within-group components; and their design-based standard errors and sampling distributions, obtained via Taylor series linearization, balanced repeated replication, and rescaled bootstrap. Syntax is reverse-compatible with that in Borrell and Talih (2011, 2012).
References
- Ali SM, Silvey SD. A General class of coefficients of divergence of one distribution from another. Journal of the Royal Statistical Society, Series B (Methodological) 1966;28:131–42. [Google Scholar]
- Atkinson AB. On the measurement of inequality. Journal of Economic Theory. 1970;2:244–63. [Google Scholar]
- Biewen M, Jenkins SP. Variance estimation for generalized entropy and Atkinson inequality indices: The Complex survey data case. Oxford Bulletin of Economics and Statistics. 2006;68:371–83. [Google Scholar]
- Borrell LN, Talih M. A Symmetrized Theil index measure of health disparities: An Example using dental caries in U.S. children and adolescents. Statistics in Medicine. 2011;30:277–90. doi: 10.1002/sim.4114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borrell LN, Talih M. Examining periodontal disease disparities among U.S. adults 20 years of age and older: NHANES III (1988–1994) and NHANES 1999–2004. Public Health Reports. 2012;127:497–506. doi: 10.1177/003335491212700505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourguignon F. Decomposable income inequality measures. Econometrica. 1979;47:901–20. [Google Scholar]
- Braveman P. Health disparities and health equity: Concepts and measurement. Annual Review of Public Health. 2006;27:167–94. doi: 10.1146/annurev.publhealth.27.021405.102103. [DOI] [PubMed] [Google Scholar]
- Cheng NF, Han PZ, Gansky SA. Methods and software for estimating health disparities: the case of childrens oral health. American Journal of Epidemiology. 2008;168:906–14. doi: 10.1093/aje/kwn207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernoff H. A Measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Annals of Mathematical Statistics. 1952;23:493–507. [Google Scholar]
- Cichocki A, Amari S. Families of alpha- beta- and gamma-divergences: Flexible and robust measures of similarities. Entropy. 2010;12:1532–68. [Google Scholar]
- Cowell FA, Davidson R, Flachaire E. Goodness of fit: An Axiomatic approach. Groupement de Recherche en Economie Quantitative d’Aix-Marseille (GREQAM) DT 2011-50. 2011 http://halshs.archives-ouvertes.fr/docs/00/63/90/75/PDF/DTGREQAM2011_50.pdf.
- Cowell FA, Kuga K. Additivity and the entropy concept: An Axiomatic approach to inequality measurement. Journal of Economic Theory. 1980;25:131–43. [Google Scholar]
- Cressie N, Read TRC. Multinomial goodness-of-fit tests. Journal of the Royal Statistical Society, Series B (Methodological) 1984;46:440–64. [Google Scholar]
- Elbers C, Lanjouw P, Mistiaen JA, Özler B. Reinterpreting between-group inequality. Journal of Economic Inequality. 2008;6:231–45. [Google Scholar]
- Fay RE. Theoretical application of weighting for variance calculation. Proceedings of the Section on Survey Research Methods of the American Statistical Association. 1989:212–17. [Google Scholar]
- Firebaugh G. Empirics of world income inequality. American Journal of Sociology. 1999;104:1597–1630. [Google Scholar]
- Fleurbaey M, Schokkaert E. Unfair inequalities in health and health care. Journal of Health Economics. 2009;28:73–90. doi: 10.1016/j.jhealeco.2008.07.016. [DOI] [PubMed] [Google Scholar]
- Frohlich KL, Potvin L. The Inequality paradox: The Population approach and vulnerable populations. American Journal of Public Health. 2008;98:216–21. doi: 10.2105/AJPH.2007.114777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujisawa H, Eguchi S. Robust parameter estimation with a small bias against heavy contamination. Journal of Multivariate Analysis. 2008;99:2053–81. [Google Scholar]
- Green LW, Fielding J. The U.S. Healthy People initiative: Its Genesis and its sustainability. Annual Review of Public Health. 2011;32:451–70. doi: 10.1146/annurev-publhealth-031210-101148. [DOI] [PubMed] [Google Scholar]
- Harper S, Lynch J, Meersman SC, Breen N, Davis WW, Reichman ME. An overview of methods for monitoring social disparities in cancer with an example using trends in lung cancer incidence by area-socioeconomic position and race-ethnicity, 1992–2004. American Journal of Epidemiology. 2008;167:889–99. doi: 10.1093/aje/kwn016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper S, King NB, Meersman SC, Reichman ME, Breen N, Lynch J. Implicit value judgments in the measurement of health inequalities. Milbank Quaterly. 2010;88:4–29. doi: 10.1111/j.1468-0009.2010.00587.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haughton J, Khander SR. Handbook on Poverty and Inequality. The World Bank; Washington, DC: 2009. [Google Scholar]
- Judkins DR. Fay’s method for variance estimation. Journal of Official Statistics. 1990;6:223–39. [Google Scholar]
- Keppel K, Pearcy J, Klein R. Statistical Notes. Vol. 25. National Center for Health Statistics; 2004. Measuring progress in Healthy People 2010. [PubMed] [Google Scholar]
- Keppel K, Pamuk E, Lynch J, Carter-Pokras O, Kim I, Mays V, Pearcy J, Schoenbach V, Weissman JS. Vital and Health Statistics, Series 2. Vol. 141. National Center for Health Statistics; 2005. Methodological issues in measuring health disparities. [PMC free article] [PubMed] [Google Scholar]
- Kullback S, Leibler RA. On information and sufficiency. Annals of Mathematical Statistics. 1951;22:79–86. [Google Scholar]
- Levy JI, Chemerynski SM, Tuchmann JL. Incorporating concepts of inequality and inequity into health benefits analysis. International Journal of Equity in Health. 2006;5 doi: 10.1186/1475-9276-5-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lumley T. Analysis of complex survey samples. Journal of Statistical Software. 2004;9:1–19. [Google Scholar]
- Lumley T. R package version 3.26. 2011. ‘survey’: Analysis of complex survey samples. [Google Scholar]
- Mackenbach JP, Kunst AE. Measuring the magnitude of socioeconomic inequalities in health: An Overview of available measures illustrated with two examples from Europe. Social Science and Medicine. 1997;44:757–71. doi: 10.1016/s0277-9536(96)00073-1. [DOI] [PubMed] [Google Scholar]
- Magdalou B, Nock R. Income distributions and decomposable divergence measures. Journal of Economic Theory. 2011;146:2440–54. [Google Scholar]
- Martinez-Camblor P. Central limit theorems for s-Gini and Theil inequality coefficients. Revista Colombiana de Estadisticas. 2007;30:287–300. [Google Scholar]
- McCarthy PJ. Pseudo-replication: half samples. Revue de l’Institut International de Statistique—Review of the International Statistical Institute. 1969;37:239–64. [Google Scholar]
- National Center for Health Statistics. Healthy People 2010 Final Review. National Center for Health Statistics; Hyattsville, MD: 2011. [Google Scholar]
- Page RC, Eke PI. Case definitions for use in population-based surveillance of periodontitis. Journal of Periodontology. 2007;78:1387–99. doi: 10.1902/jop.2007.060264. [DOI] [PubMed] [Google Scholar]
- Pearcy JN, Keppel KG. A Summary measure of health disparity. Public Health Reports. 2002;117:273–80. doi: 10.1016/S0033-3549(04)50161-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard DE. A User’s Guide to Measure Theoretic Probability. Cambridge University Press; Cambridge, UK: 2002. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2011. http://www.R-project.org. [Google Scholar]
- Rao JNK, Wu CFJ. Resampling inference with complex survey data. Journal of the American Statistical Association. 1988;83:231–41. [Google Scholar]
- Rao JNK, Wu CFJ, Yue K. Some recent work in resampling methods. Survey Methodology. 1992;18:209–17. [Google Scholar]
- Rényi A. On Measures of entropy and information. Fourth Berkeley Symposium on Mathematics, Statistics and Probability. 1960:547–61. [Google Scholar]
- Rose G. Sick individuals and sick populations. International Journal of Epidemiology. 1985;14:32–8. doi: 10.1093/ije/14.1.32. [DOI] [PubMed] [Google Scholar]
- Shorrocks AF. The Class of additively decomposable inequality measures. Econometrica. 1980;48:613–25. [Google Scholar]
- Talih M. Supplement to: A Reference-invariant health disparity index based on Rényi divergence—additional case study from NHANES. 2012a doi: 10.1214/12-AOAS621. Under Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talih M. Supplement to: A Reference-invariant health disparity index based on Rényi divergence—R syntax and output files. 2012b doi: 10.1214/12-AOAS621. Under Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talih M. Supplement to: A Reference-invariant health disparity index based on Rényi divergence—technical appendix. 2012c doi: 10.1214/12-AOAS621. Under Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theil H. Economics and Information Theory. North Holland; Amsterdam, Netherlands: 1967. [Google Scholar]
- U.S. Department of Health and Human Services. Healthy People 2010 2nd ed. With Understanding and Improving Health and Objectives for Improving Health. Vol. 2. U.S. Government Printing Office; Washington, DC: 2000. [Google Scholar]
- U. S. Department of Health and Human Services. Healthy People 2010 Midcourse Review. U.S. Government Printing Office; Washington, DC: 2006. [Google Scholar]
- van Erven TAL. PhD thesis. Leiden University—CWI; the Netherlands: 2010. When Data Compression and Statistics Disagree: Two Frequentist Challenges for the Minimum Description Length Principle. http://hdl.handle.net/1887/15879. [Google Scholar]
- Wagstaff A, Paci P, van Doorslaer E. On the measurement of inequalities in health. Social Science and Medicine. 1991;33:545–57. doi: 10.1016/0277-9536(91)90212-u. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.