Highly adaptive tests for group differences in brain functional connectivity

Abstract

Resting-state functional magnetic resonance imaging (rs-fMRI) and other technologies have been offering evidence and insights showing that altered brain functional networks are associated with neurological illnesses such as Alzheimer's disease. Exploring brain networks of clinical populations compared to those of controls would be a key inquiry to reveal underlying neurological processes related to such illnesses. For such a purpose, group-level inference is a necessary first step in order to establish whether there are any genuinely disrupted brain subnetworks. Such an analysis is also challenging due to the high dimensionality of the parameters in a network model and high noise levels in neuroimaging data. We are still in the early stage of method development as highlighted by Varoquaux and Craddock (2013) that “there is currently no unique solution, but a spectrum of related methods and analytical strategies” to learn and compare brain connectivity. In practice the important issue of how to choose several critical parameters in estimating a network, such as what association measure to use and what is the sparsity of the estimated network, has not been carefully addressed, largely because the answers are unknown yet. For example, even though the choice of tuning parameters in model estimation has been extensively discussed in the literature, as to be shown here, an optimal choice of a parameter for network estimation may not be optimal in the current context of hypothesis testing. Arbitrarily choosing or mis-specifying such parameters may lead to extremely low-powered tests. Here we develop highly adaptive tests to detect group differences in brain connectivity while accounting for unknown optimal choices of some tuning parameters.

The proposed tests combine statistical evidence against a null hypothesis from multiple sources across a range of plausible tuning parameter values reflecting uncertainty with the unknown truth. These highly adaptive tests are not only easy to use, but also high-powered robustly across various scenarios. The usage and advantages of these novel tests are demonstrated on an Alzheimer's disease dataset and simulated data.

Highlights

• •Rigorous testing for genuinely altered functional networks between two groups
• •The proposed tests are high powered and general across a wide range of scenarios.
• •Data-driven penalized network estimation
• •Data-driven choice between correlations and partial correlations to describe association
• •Some key differences between network estimation and testing are highlighted.

1. Introduction

Previous studies have shown that neurological illnesses such as Alzheimer's disease and autism are related to altered brain functional networks, or functional connectivity, among distinct and distant brain regions (Greicius et al., 2004, Supekar et al., 2008). However, group-level statistical inference on functional connectivity is both challenging and necessary due to the high dimensionality of the parameters in a network model and the high noise level in neuroimaging data. Even though recent advances in neuroimaging technologies, such as rs-fMRI, offer great potentials for studying brain functional networks (Biswal, 2012), most statistical methods are for point estimation while only few exist in drawing inference for group comparisons in brain networks (Varoquaux and Craddock, 2013). In particular, many studies examined possible differences between two covariance or precision matrix estimates; however, whether there were any genuine differences between the corresponding population matrices was never or inadequately addressed. Without rigorous statistical testing, it is unknown whether any estimated network differences are simply due to estimation errors. In practice, we recommend to first test for differences of the networks between two groups; only if it is confirmed that the differences exist, then proceed to the next step to examine how they are different, possibly in an exploratory analysis.

Functional brain connectivity can be described as a network or graph (Bullmore and Sporns, 2009, Habeck and Moeller, 2011, He and Evans, 2010), in which a set of nodes are linked by edges. Nodes stand for brain regions, and brain connectivity (or edges) refer to pairwise associations between every two nodes (Varoquaux and Craddock, 2013). Yet, what measure of association should be used for the weights of network edges remains to be an open question. Currently the two most popular choices are Pearson's correlations and partial correlations. A correlation represents the marginal relationship between two brain regions, while a partial correlation quantifies the conditional association between the two, conditioning on other brain regions' activities. Pearson's (full or marginal) correlations have been adopted in many functional connectivity studies (Azari et al., 1992, Horwitz et al., 1987, Kim et al., 2014, Stam et al., 2007, Supekar et al., 2008). Partial correlations also have been advocated (Marrelec et al., 2006, Salvador et al., 2005, Smith et al., 2011), especially when one is interested in seeking conditional independence between any two regions. However, as shown by Kim et al. (2015), the choice of the association measure would influence statistical power in subsequently detecting group-level network differences. Moreover, since brain networks can be reasonably assumed to be sparse, they can be thus estimated via regularized sparse covariance or precision matrices, which however pose some challenges in the choice of a suitable regularization or tuning parameter. In addition, there may be other tuning parameters to be determined in an analysis. In general, the choice of such parameters may be difficult, and at the same time critical. We propose highly adaptive testing procedures that automatically search over and thus take account of these parameter values to maintain high power across various situations.

Kim et al. (2014) reviewed and compared many statistical methods, and concluded that the Network Based Statistic (NBS) (Zalesky et al., 2012) and an adaptive sum of powered score (aSPU) test (Pan et al., 2014) showed great performance, often complementary to each other, for testing group differences in brain functional connectivity. In particular, mass-univariate testing on each edge and testing on some network summary statistics is in general low-powered: for the former, in addition to possibly small differences on the edges, the stringent significance level after multiple testing adjustment is often too high to achieve; for the latter, it largely depends on the choice of the network summary statistics, which may be too mildly altered to be detected. NBS was originally developed to identify changed subnetworks in the neuroimaging research, but could be employed for global testing as considered here. By assuming that changed network edges form subnetworks, NBS can be potentially powerful when the assumption holds. However, since it is based on mass univariate testing to detect altered edges, it may miss some edges and thus connected subnetworks, leading to loss of power. As an alternative, the aSPU test does not impose any assumption on the structure of altered edges or networks while data-adaptively accumulating evidence against a null hypothesis, and thus yields high power under various situations. These are two representative and state-of-the-art tests we consider here. In particular, we propose two versions of highly adaptive aSPU and NBS tests respectively. The proposed tests utilize and data-adaptively choose multiple parameter values reflecting uncertainty with unknown true data structures, while adjusting for multiple testing automatically. At the end, we obtain two adaptive tests that can maintain high power more robustly across many situations; being data-adaptive to unknown true association patterns, the proposed tests are robust in the sense that they can achieve high power across many situations, in contrast to a possibly high powered test in only one or few situations that may lose much power in many other situations. We will apply the proposed adaptive tests to simulated data and an Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset.

The remainder of the paper is organized as follows. We first review sparse estimation of brain connectivity, then present highly adaptive versions of aSPU and NBS in Section 2. Section 3 is devoted to the analysis of ADNI data. In Section 4, we conduct simulation studies with realistic set-ups mimicking the ADNI data. We end with some discussions on a few technical aspects and comparisons with the literature in Section 5.

2. Methods

2.1. Data and notation

We focus on a case–control study design with covariates. Suppose there are n unrelated subjects, either healthy or having a disease.

We denote a group indicator Y_l = 0 for controls, Y_l = 1 for cases, and Z_i = (Z_i1, …, Z_il)′ for the covariates for subject i. We consider N brain regions of interests (ROIs), which define the nodes in a network or graph. For each node, fMRI BOLD signals are measured at t = 1,2,…,M time points. The BOLD signals from N nodes at time point t, D_t = (D_t1, ····, D_tN)′, are assumed to be distributed as multivariate Gaussian N(μ, Σ) with the mean vector μ ∈ ℝ^N and the positive definite covariance matrix Σ.

The next step is to estimate the pairwise association between any two nodes. This measure is stored in a symmetric N × N adjacency matrix with its (i,j)th element as the association between the ith and jth nodes (Bullmore and Sporns, 2009). Hence a total of k = N × (N − 1)/2 unique pairwise associations are estimated for each subject, and these k continuous measures are called brain connectivity or network edges to be used for testing group differences. In our study, both Pearson's correlations and partial correlations were considered. As usual, the correlations (or partial correlations) are normalized via Fisher's z-transformation to generate subject i's brain connectivity, X_i = (X_i1,⋯, X_ik)′. Fisher's transformation is used to alleviate the effects of skewed distributions and outliers, which may negatively influence the power of a subsequent test.

In the following, we use matrix notation: Y_n × 1 as a vector for disease indicators, X_n × k as a matrix of pairwise associations between nodes (with each element as a z-transformed correlation or partial correlation), and Z_n × l as a covariate matrix.

2.2. Estimating covariance and precision matrices via graphical lasso

Building on the work of Banerjee et al. (2008), Friedman et al. (2008) proposed a graphical lasso (glasso) algorithm to estimate sparse (or non-sparse) covariance and precision matrices, given M observations of dimension N, which are distributed as multivariate Gaussian N (μ, Σ). Let subject i have a possibly subject-specific true precision matrix Θ_i = Σ_i^− 1, and S_i be its empirical covariance matrix of the BOLD signals extracted from N nodes; the problem is to maximize the penalized log-likelihood,

$$L_{P,i}\left({\mathrm{\Theta }}_i;\lambda \right)=L_i\left({\mathrm{\Theta }}_i\right)-P\left({\mathrm{\Theta }}_i;\lambda \right)=logdet\left({\mathrm{\Theta }}_i\right)-\mathrm{t}\mathrm{r}\left(S_i{\mathrm{\Theta }}_i\right)-{\lambda }_i{‖{\mathrm{\Theta }}_i‖}_1$$

over the semi-positive definite Θ_i, where tr denotes the trace. ‖Θ_i‖₁ = ∑_p ≠ q|θ_i,pq| is the L₁ norm for non-diagonal elements; λ_i ≥ 0 is a regularization parameter to be determined. The graphical lasso finds the estimate, satisfying ${\widehat{\mathrm{\Theta }}}_i={{\widehat{\mathrm{\Theta }}}_i}_i\left({\lambda }_i\right)=arg{max}_{{\mathrm{\Theta }}_i}{L}_{P,i}\left({\mathrm{\Theta }}_i;{\widehat{\lambda }}_i\right)\text{.}$ Here ${\widehat{\mathrm{\Theta }}}_i$ is a function of λ_i, from which we also obtain a regularized estimate for the covariance matrix ${\widehat{\mathrm{\Sigma }}}_i={\widehat{\mathrm{\Theta }}}_i^{-1}$. Full correlations and partial correlations can be estimated with ${\widehat{\mathrm{\Sigma }}}_i$ and ${\widehat{\mathrm{\Theta }}}_i$ respectively.

In this paper, the graphical lasso was employed to estimate brain connectivity at various sparsity levels. Denote c as the connection density (or proportion of nonzero elements) in a precision matrix estimate ${\widehat{\mathrm{\Theta }}}_i$. Using a grid search, λ_i can be chosen to generate the precision matrix estimate at a predefined connection density c, namely ${\widehat{\mathrm{\Theta }}}_i\left(c\right)={\widehat{\mathrm{\Theta }}}_i\left({\lambda }_i\left(c\right)\right)$. Again ${\widehat{\mathrm{\Sigma }}}_i\left(c\right)$ is obtained by inverting ${\widehat{\mathrm{\Theta }}}_i\left(c\right)$; we note that, c is the connection density of the precision matrix estimate, not of the corresponding covariance matrix estimate.

For testing between-group differences in brain connectivity, recent studies have chosen λ_i at the group level so that each group should have the same or similar connection density in their estimated precision matrices (Huang et al., 2010, Stam et al., 2007, Supekar et al., 2008). Hence, at a low estimated connection density, only strong connectivity would show up as non-zeros in the resulting estimates, based on which we compare the two groups by focusing on their strong connectivity; as the connection density increases, mild connectivity will also show up in the network estimates ($\widehat{\mathrm{\Theta }}$), and a two-group test would utilize both mild and strong connectivity. Consequently considering multiple estimated connection densities (c) allows one to vary the strength of connectivities to be tested, possibly boosting the power. In addition, since it is hard to choose the best regularization parameter value, considering multiple values of c could be a useful strategy for exploring group differences in brain connectivity. Furthermore, as to be shown, a chosen regularization parameter value that is optimal in estimating networks may not be optimal for testing, leading to low statistical power.

We imposed the group level regularization to estimate a subject level precision matrix at a predefined connection density c: for any subject i in group j (i.e., i ∈ G_(j)), λ_i(c) = λ_(j)(c) and ${\widehat{\mathrm{\Theta }}}_i\left(c\right)={\widehat{\mathrm{\Theta }}}_i\left({\lambda }_i\left(c\right)\right)={\widehat{\mathrm{\Theta }}}_i\left({\lambda }_{\left(j\right)}\left(c\right)\right)$. It is possible that the group-level regularization may not result in exactly the same connection density across all subject-level network estimates at the specified connection density, but the differences were observed to be minor in our numerical studies. For subject i ∈ G_(j), we estimated ${\widehat{\mathrm{\Theta }}}_i\left(c\right)$ and ${\widehat{\mathrm{\Sigma }}}_i\left(c\right)$ by applying the group-level λ_(j)(c) to the graphical lasso. These ${\widehat{\mathrm{\Theta }}}_i\left(c\right)$ and ${\widehat{\mathrm{\Sigma }}}_i\left(c\right)$ were normalized to estimate the partial correlations and full correlations respectively, to which we applied Fisher's z-transformation to generate brain connectivity data X_i(c) = (X_i1(c), ⋯, X_ik(c))′. To distinguish the brain connectivity estimated by partial correlations and that by correlations, we use $\mathrm{\Omega }\in \left\{\widehat{\mathrm{\Theta }},\widehat{\mathrm{\Sigma }}\right\}$ to indicate; in the following, we use $\widehat{\mathrm{\Theta }}$ for partial correlations and $\widehat{\mathrm{\Sigma }}$ for correlations. Hence, with given BOLD time series data, brain connectivity can be estimated as X_i(c, Ω) = (X_i1(c, Ω), ⋯, X_ik(c, Ω))′, based on an estimated connection density c and the type of association measures Ω.

To demonstrate the benefits of considering multiple estimated connection densities (c), we considered a cross-validation (CV) selected group-level regularization parameter value in one of our simulation examples. 10-fold CV was performed to choose the best group-level regularization parameter value. For each group, the original sample was partitioned into 10 equal size subsamples. The training data was formed with 9 sets while the remaining one was retained as the validation data. A candidate group-level regularization value λ_(j), j = 1,2 was applied to the training set and the optimal ${\widehat{\lambda }}_{\left(j\right)}$ was found to maximize the total predictive log likelihood using a grid search on λ_(j). Denote an estimate with the fth fold training set as ${\widehat{\mathrm{\Theta }}}_{\left(j\right)}^{\mathrm{train}\left(f\right)}=\widehat{\mathrm{\Theta }}{\left({\lambda }_{\left(j\right)}\right)}^{\mathrm{train}\left(f\right)}$, and n_(j) as the number of subjects in the group j. The optimal group-level regularization parameter value was defined as

$${\widehat{\lambda }}_{\left(j\right)}=\underset{{\lambda }_{\left(j\right)}}{argmax}{\displaystyle \sum _{f=1}^{10}}{\displaystyle \sum _{i=1}^{n_{\left(j\right)}}}logdet\left({\widehat{\mathrm{\Theta }}}_{\left(j\right)}^{\mathrm{train}\left(f\right)}\right)-\mathrm{t}\mathrm{r}\left(S_i^{\mathrm{test}\left(f\right)}{\widehat{\mathrm{\Theta }}}_{\left(j\right)}^{\mathrm{train}\left(f\right)}\right)\text{.}$$

${\widehat{\lambda }}_{\left(j\right)}$ was imposed to estimate subject level precision and covariance matrices: ${\widehat{\mathrm{\Theta }}}_i\left({\widehat{\lambda }}_{\left(j\right)}\right)$ and ${\widehat{\mathrm{\Sigma }}}_i\left({\widehat{\lambda }}_{\left(j\right)}\right)={\left\{{\widehat{\mathrm{\Theta }}}_i\left({\widehat{\lambda }}_{\left(j\right)}\right)\right\}}^{-1}$. Then the brain connectivity was estimated as discussed before.

2.3. Adaptive tests for group comparisons in brain functional connectivity

In practice it is in general unknown which association measure to use to yield the highest power in testing for group differences in two functional networks. In addition, statistical power may depend on the specified density level of the estimated brain networks. The proposed tests consider both the type of association measures (Ω) and the density level of estimated networks (c).

Either the aSPU or NBS test includes one tuning parameter that incorporates unknown features of given data, to maximize power of the test, as to be discussed. We propose two versions of highly adaptive SPU or NBS to accommodate two new tuning parameters (c,Ω) in addition to their original tuning parameters. The main idea is similar to, but generalizes, that of the aSPU test (Pan et al., 2014).

2.3.1. Highly adaptive SPU tests

The sum of powered score (SPU) tests are a family of global tests for assessing overall differences across groups, applicable to small samples with high dimensions, such as brain connectivity data (Kim et al., 2014, Pan et al., 2014). Any SPU test includes a γ parameter, whose choice depends on the unknown data distribution to yield high power. Since the true data distributions are unknown, we specify a set of the γ parameter values, then apply the adaptive SPU (aSPU) test to the results of the SPU(γ) tests across various γ′ values: for any given non-negative integer set Γ, an odd γ ∈ Γ might be more suitable when all brain connectivity changes are in the same direction; otherwise an even γ would be favored; furthermore, if only a small portion of edges are changed, a larger γ could yield higher power. In addition to these features, we add more flexibility on the SPU tests in the following way.

We briefly comment on the connections of the SPU tests with γ = 1,2 and ∞ with other tests used in the neuroimaging studies. As Kim et al. (2014) pointed out, the SPU(1) test is equivalent to an fMRI network test proposed in Meskaldji et al. (2011); the SPU(2) test is equivalent to MDMR employed by Shehzad et al. (2014) and Reiss et al. (2010), and to kernel machine regression with a linear kernel (Hua and Ghosh, 2014, Liu et al., 2007, Pan, 2011); the SPU(∞) test can be regarded as mass-univariate testing (Nichols and Holmes, 2001).

We extend the SPU(γ) test to SPU(γ,c,Ω) to incorporate two more parameters, the estimated connection density and the type of association measures used. The SPU(γ,c,Ω) test is based on the score vector from a generalized linear model with estimated brain connectivity X_i(c, Ω) = (X_i1(c, Ω), ⋯, X_ik(c, Ω))′. For a case–control study, a logistic regression model is applied with k functional network connections and l covariates as predictors:

$$\mathrm{Logit}\left[\mathit{Pr}\left(Y_i=1\right)\right]={\beta }_0+{\displaystyle {\sum }_{j=1}^k{X}_{ij}\left(c,\Omega \right)}\cdot {\beta }_j+{\displaystyle {\sum }_{m=1}^l{Z}_{im}{\delta }_m}\text{.}$$ (1)

We would test the null hypothesis of no group differences in functional brain connectivity: H₀ : β = (β₁, …, β_k)′ = 0. Under the null hypothesis H₀, the full model (1) reduces to

$$\mathrm{Logit}\left[\mathit{Pr}\left(Y_i=1\right)\right]={\beta }_0+{\displaystyle \sum _{m=1}^l{Z}_{im}{\delta }_m\text{.}}$$ (2)

Suppose ${\widehat{\beta }}_0$ and ${\widehat{\delta }}_m$'s are the maximum likelihood estimates under the null model (2), and ${\widehat{Y}}_i=1/\left[1+exp\left(-{\widehat{\beta }}_0-{\displaystyle {\sum }_{m=1}^l{Z}_{im}{\widehat{\delta }}_m}\right)\right]$. Denote a residual res_i = Y_i − Ŷ_i for i = 1,⋯n. Based on the data {X_i(c,Ω), Z_i, Y_i}, the score vector for β is defined as

$$U\left(c,\mathrm{\Omega }\right)={\displaystyle \sum _{i=1}^n\left(Y_i-{\widehat{Y}}_i\right)\cdot X_i\left(c,\mathrm{\Omega }\right)={\displaystyle \sum _{i=1}^{n}re{s}_i\cdot X_i\left(c,\mathrm{\Omega }\right)\text{,}}}$$

which will be used for obtaining the test statistic of SPU(γ,c,Ω). Given a candidate integer γ ≥ 1, c and Ω, the test statistic is defined as

$$T_{\mathrm{S}\mathrm{P}\mathrm{U}\left(\gamma ,c,\mathrm{\Omega }\right)}={{\displaystyle \sum _{j=1}^k\left[U_j\left(c,\mathrm{\Omega }\right)\right]}}^{\mathrm{\gamma }}\text{.}$$

Note that U_j(c,Ω) is the jth component of U(c, Ω) = (U₁, …, U_k)′. For an extreme case, as an even number γ → ∞, we have T_{SPU(∞,c,Ω)} ∝ max _j = 1^k|U_j(c, Ω)|. To draw statistical inference, as Pan et al. (2014) proposed, we permute the original set of residuals res = {res₁⋯res_n} to create a new set of residuals res^(b) = {res₁^(b), ⋯ res_n^(b)}. Based on res^(b), we calculate the score vector U(c, Ω)^(b) = ∑_i = 1ⁿres_i^(b) ⋅ X_i(c, Ω) and the null statistic T_SPU(γ,c,Ω)^(b) = ∑_j = 1^k[U_j(c, Ω)^b]^γ; with b = 1,…,B permutations, we compute the p-value as P_SPU(γ,c,Ω) = ∑_b = 1^B[I(|T_SPU(γ,c,Ω)ⁿ| ≥ [T_SPU(γ,c,Ω)]) + 1]/(B + 1). The SPU test is computationally efficient, since it only requires permuting residuals to calculate U(c, Ω)^(b) for drawing inference.

An adaptive SPU test, called aSPU(γ,Ω), combines the p-values of multiple SPU(γ,c,Ω) tests across various connection density c's, and its test statistic can be stated as

$$T_{\mathrm{aSPU}\left(\gamma ,\mathrm{\Omega }\right)}=\underset{c\in C}{min}{P}_{\mathrm{S}\mathrm{P}\mathrm{U}\left(\gamma ,c,\mathrm{\Omega }\right)}\text{.}$$

To estimate the null distribution of T_aSPU(c,Ω), we first generate an empirical null distribution of the p-values for $\mathrm{S}\mathrm{P}\mathrm{U}\left(\gamma ,c,\Omega \right):p_{\mathrm{S}\mathrm{P}\mathrm{U}\left(\gamma ,c,\Omega \right)}^{\left(b\right)}={\displaystyle {\sum }_{b_1\ne b}I\left(T_{\mathrm{S}\mathrm{P}\mathrm{U}\left(\gamma ,c,\Omega \right)}^{b_1}\ge T_{\mathrm{S}\mathrm{P}\mathrm{U}\left(\gamma ,c,\Omega \right)}^{\left(b\right)}\right)/\left(B-1\right)}$ for b = 1,…,B. Then the null distribution of T_aSPU(γ,Ω) can be estimated as the empirical distribution of T_aSPU(γ,Ω)^(b) = min_c ∈ Cp_SPU(γ,c,Ω)^(b). Finally the p-value of the aSPU(γ,Ω) test is computed as P_aSPU(γ,Ω) = ∑_b = 1^B[I(T_aSPU(γ,Ω)^(b) ≤ T_aSPU(γ,Ω)) + 1]/(B + 1) for γ ∈ Γ. In our study, for possible γ's, we considered Γ = {1,2,3,…,8,∞} as in Pan et al. (2014) and Kim et al. (2014). The analyses with γ = 1,2 and ∞ will be presented as representatives.

A doubly adaptive SPU (daSPU(Ω)) test across double parameters (γ,c) simply combines the p-values of multiple aSPU tests with various values of γ. Similar to the aSPU test, the combining procedure is to take the minimum p-value:

$$T_{\mathrm{daSPU}\left(\Omega \right)}=\underset{\gamma \in \Gamma }{min}{P}_{\mathrm{aSPU}\left(\gamma ,\Omega \right)}\text{.}$$

To construct the null distribution of T_daSPU(Ω), we calculate $p_{\mathrm{aSPU}\left(\gamma ,\Omega \right)}^{\left(b\right)}={\displaystyle {\sum }_{b_i\ne b}I\left(T_{\mathrm{aSPU}\left(\gamma ,\Omega \right)}^{\left(b_1\right)}\ge T_{\mathrm{aSPU}\left(\gamma ,\Omega \right)}^{\left(b\right)}\right)}/\left(B-1\right)$ for b = 1,…,B and the null distribution can be generated with T_daSPU(Ω)^(b) = min_γ ∈ Γp_aSPU(γ,Ω)^(b), from which the p-value of the daSPU test is computed.

Finally, we propose a triply adaptive SPU (taSPU) test across all three parameters (γ,c,Ω), which combines the results of the daSPU(Ω) tests with Ω for correlations and partial correlations respectively. The test statistic of taSPU is the minimum p-value of daSPU(Ω)'s:

$$T_{\mathrm{taSPU}}=\underset{\mathrm{\Omega }\in \left\{\widehat{\mathrm{\Theta }},\widehat{\mathrm{\Sigma }}\right\}}{min}{P}_{\mathrm{daSPU}\left(\mathrm{\Omega }\right)}\text{.}$$

The procedure for p-value calculation is similar to those of the aSPU and daSPU tests: an empirical null distribution of T_taSPU can be obtained from $T_{\mathrm{taSPU}}^{\left(b\right)}={min}_{\mathrm{\Omega }\in \left\{\widehat{\mathrm{\Theta }},\widehat{\mathrm{\Sigma }}\right\}}{p}_{\mathrm{daSPU}\left(\mathrm{\Omega }\right)}^{\left(b\right)}$, for b = 1,…,B, where $p_{\mathrm{daSPU}\left(\mathrm{\Omega }\right)}^{\left(b\right)}={\displaystyle {\sum }_{b_1\ne b}I\left(T_{\mathrm{daSPU}\left(\mathrm{\Omega }\right)}^{\left(b_1\right)}\ge T_{\mathrm{daSPU}\left(\mathrm{\Omega }\right)}^{\left(b\right)}\right)}/\left(B-1\right)$ The p-value of taSPU test is estimated as P_taSPU = ∑_b = 1^B[I(T_taSPU^(b) ≤ T_taSPU) + 1]/(B + 1).

2.3.2. Highly adaptive NBS tests

Zalesky et al. (2010) proposed the Network Based Statistic (NBS) to identify altered subnetworks across groups, providing topological clusters as evidence of group differences. Originally NBS was not developed for global testing, but depending on its threshold NBS provides small to large subnetworks as evidence of group differences: at a low threshold, NBS detects large-scale subnetworks, but not intense and small-sized subnetworks; with a high threshold, only small and substantially altered subnetworks will be detected. Most of all, in practice it is unknown which threshold to use, while using different threshold values may lead to quite different results; trying multiple values of the threshold requires an adjustment to multiple testing. Our proposed methods overcome this shortcoming and further improve its performance via an adaptive choice of other two parameters (c,Ω).

Suppose we apply the NBS test on brain connectivity data X_i(c, Ω) = (X_i1(c, Ω), ⋯, X_ik(c, Ω))′. NBS fits a linear model on each edge separately. For each edge j = 1,…k,

$$X_{ij}\left(c,\mathrm{\Omega }\right)=a_0+Y_i{a}_1+{\displaystyle \sum _{m=1}^l{Z}_{im}{\delta }_m+{\mathrm{e}}_{ij}i=1,\dots ,n}$$

where the errors ${\mathrm{e}}_{ij}\stackrel{iid}{~}N\left(0,{\sigma }^2\right)$. To test the null hypothesis H₀: a₁ = 0, we can derive a t-statistic (ψ) at each edge j individually, which quantifies the edge-wise difference between two groups, i.e.,

$$\begin{array}{ll}{\psi }_j=\frac{{\widehat{a}}_1}{se\left({\widehat{a}}_1\right)}\hfill & j=1,\dots ,k\hfill \end{array}$$

where â₁ is an OLS estimate and se(â₁) is the standard error of the estimate â₁. Let a predetermined threshold parameter nbs(t) represent the tth percentile in absolute values of ψ_j's, satisfying P(|ψ_j| ≤ nbs(t)) = t (Kim et al., 2014). For possible thresholds t ∈ H, we chose H = {0.10,0.25,0.50,0.75,0.9,0.95} to cover small to large-scale subnetworks as evidence of group-differences.

We denote NBS(t,c,Ω) as the NBS test that evaluates group differences with brain connectivity measures Ω, at estimated connection density c, and with the threshold nbs(t). The test statistic of the NBS(t,c,Ω) can be defined as the maximum size (i.e. number of edges) of the connected edges comprising supra-thresholded edges. Here supra-thresholded edges represent the edges with weights exceeding the predetermined threshold. Denote the test statistics of NBS(t,c,Ω) as T_NBS(t,c,Ω). To make inference, permutation is used (Nichols and Holmes, 2001); for each permutation b = 1,…,B, group memberships are randomly permuted, and calculate the size of the largest identified components T_NBS(t,c,Ω)^(b). This yields an empirical null distribution of maximal suprathresholded component size. The p-value of NBS(t,c,Ω) can be obtained by P_NBS(t,c,Ω) = ∑_b = 1^BI(|T_NBS(t,c,Ω)|^(b) ≥ |T_NBS(t,c,Ω)|)/B.

An adaptive NBS (aNBS(t,Ω)) adjusts for multiple testing with NBS(t,c,Ω) being conducted at multiple connection densities. The test statistic of aNBS(t,Ω) is the minimum p value of NBS(t,c,Ω)'s:

$$T_{\mathit{aNBS}\left(t,\mathrm{\Omega }\right)}=\underset{c\in C}{min}{P}_{\mathit{N}\mathit{B}\mathit{S}\left(t,c,\mathrm{\Omega }\right)}\text{.}$$

The null distribution of T_aNBS(t,Ω)^(b) can be generated with T_NBS(t,c,Ω)^(b) in a way that $p_{\mathrm{N}\mathrm{B}\mathrm{S}\left(t,c,\mathrm{\Omega }\right)}^{\left(b\right)}={\displaystyle {\sum }_{b_1\ne b}I\left(T_{\mathrm{N}\mathrm{B}\mathrm{S}\left(t,c,\mathrm{\Omega }\right)}^{\left(b_1\right)}\ge T_{\mathrm{N}\mathrm{B}\mathrm{S}\left(t,c,\mathrm{\Omega }\right)}^{\left(b\right)}\right)/\left(B-1\right)}$ for b = 1,…,B; and defined as T_aNBS(t,Ω)^(b) = min_c ∈ Cp_NBS(t,c,Ω)^(b). The final p-value of aNBS(t,Ω) is P_aNBS(t,Ω) = ∑_b = 1^B[I(T_aNBS(t,Ω)^(b) ≤ T_aNBS(t,Ω) + 1]/(B + 1).

A doubly adaptive NBS (daNBS(Ω)) takes the minimum p-value of aNBS(t,Ω)'s as its test statistic:

$$T_{\mathit{daNBS}\left(\mathrm{\Omega }\right)}=\underset{t\in H}{min}{P}_{\mathit{aNBS}\left(t,\mathrm{\Omega }\right)}\text{.}$$

Its p-value is calculated as P_daNBS(Ω) = ∑_b = 1^B[I(T_daNBS(Ω)^(b) ≤ T_daNBS(Ω)) + 1]/(B + 1) with T_daNBS(Ω)^(b) = min_t ∈ Hp_aNBS(t,Ω)^(b) and $p_{\mathrm{aNBS}\left(t,\mathrm{\Omega }\right)}^{\left(b\right)}={\displaystyle {\sum }_{b_1\ne b}I\left(T_{\mathrm{aNBS}\left(t,\mathrm{\Omega }\right)}^{\left(b_1\right)}\ge T_{\mathrm{aNBS}\left(t,\mathrm{\Omega }\right)}^{\left(b\right)}\right)/\left(B-1\right)}$.

With the same logic and inference procedure, a triply adaptive NBS test (taNBS) can be applied to combine the results of daNBS($\widehat{\mathrm{\Theta }}$) and daNBS($\widehat{\mathrm{\Sigma }}$), which are based on partial correlations and on correlations respectively:

$$T_{\mathit{taNBS}}=\underset{\mathrm{\Omega }\in \left\{\widehat{\mathrm{\Theta }},\widehat{\mathrm{\Sigma }}\right\}}{min}{P}_{\mathit{daNBS}\left(\mathrm{\Omega }\right)}\text{.}$$

3. Application to the ADNI data

Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a 60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California — San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow-up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

3.1. Data acquisition and preprocessing

Data used in this study were obtained from the ADNI-2 dataset. The raw images of 30 Alzheimer's disease (AD) patients and 38 cognitively normal (CN) controls were downloaded from the ADNI website http://www.adni-info.org. We applied automated anatomical labeling (AAL) of 116 anatomical volumes of interest (AVOIs). The AVOIs represent different regions of the whole brain and N = 116 of whole brain regions were included in our analyses. The resting-state fMRI signals were measured at 140 timepoints.

Preprocessing was performed utilizing a combination of the Statistical Parametric Mapping (SPM8) software (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) (Wellcome Department of Cognitive Neurology, University College London, UK), the Resting-State fMRI Data Analysis Toolkit (REST) version 1.8 (http://www.restfmri.net) (Song et al., 2011), and Data Processing Assistant for Resting-State fMRI (DPARSF) version 2.3 (http://www.restfmri.net) (Yan and Zang, 2010). All subjects were scanned with the same scanning protocol using 3.0 T Philips medical systems with the following parameters: TR/TE = 3000/30 ms, flip angle = 80°, imaging matrix = 64 pixels × 64 pixels, 6720 slices in total (48 slices × 140 volumes), and slice thickness = 3.3 mm. The 140 images were processed with the standard preprocessing procedure using the SPM8 and DPARSF package. These rs-fMRI images were corrected for the acquisition time delay before they were realigned to the first volume of the remaining images to primarily remove movement artifact in rs-fMRI time series. Since there were a total of 48 slices, we chose slice 2 as the temporal reference slice. Functional images were normalized to the MNI space with resolution 3 × 3 × 3 mm³. The images were then smoothed with 8 mm FWHM. The processed rs-fMRI images were parcellated into 116 regions of interest (ROIs) according to the automated anatomical labeling atlas with template size 61 × 73 × 61. The mean rs-fMRI time series of each ROI was band-pass filtered (0.01 ≤ f ≤ 0.08 Hz). Note that we did not correct for head motion mainly because it is still a highly debatable point: according to Power et al. (2014), “Motion-related signal changes are not removed by a variety of motion-based regressors, but are effectively reduced by global signal regression”, while Saad et al. (2012) argued against the use of global signal regression.

3.2. ADNI data analysis

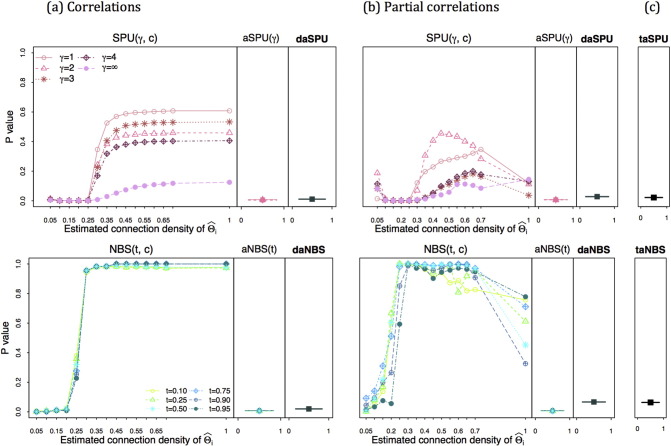
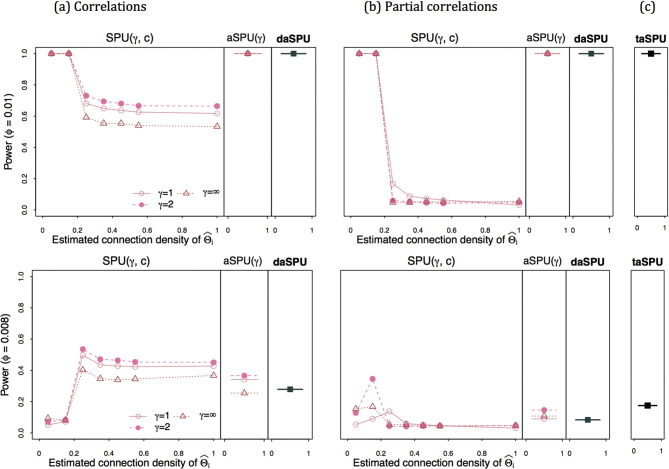
We applied the proposed methods to test network differences between 30 Alzheimer's disease (AD) patients and 38 cognitively normal (CN) controls after adjusting for covariates age, gender and education. Both correlations and partial correlations were considered for k = 116 × (116 − 1)/2 = 6670 edges. Demographic information of the participants is reported in Table 1. There was no significant difference in any covariate between AD and CN. 15 different regularization values were applied to generate various connection densities. Fig. 1 illustrates how the p-values changed with the group-level connection density. The p-values are color-coded by statistical tests and sorted by plotting symbols for each parameter. The top row of Fig. 1 illustrates the p-values of SPU tests (only the results of a subset of the γ values are reported), and in the bottom row, the p-values of NBS tests are reported. The left column (a) shows the p-values when using correlations, while the middle column (b) shows the p-values with the use of partial correlations; the last column (c) gives the p-values for the triply adaptive tests, taSPU and taNBS. With no or only moderate regularization, neither SPU nor NBS could find any significant group differences. As regularization increased, the p-values tended to decrease when using correlations (a). Using partial correlations (b), the p-values were unstable when small regularization was imposed. The p-value of taSPU was 0.02, more significant than that of taNBS, 0.06.

Table 1.

Demographic information of the participants in the ADNI data.

Group	No. of subjects	Gender (F/M)	Age	Years of education
AD	30	16F/14M	72.33 ± 7.38	15.46 ± 2.64
CN	38	20F/18M	75.22 ± 6.12	16.23 ± 2.29
Two sample test p-Value	–	0.955	0.090	0.212

Fig. 1.

p-Values for testing brain network differences between the AD group and CN group in the ADNI data. The left column (a) shows the p-values using correlations. The middle column (b) shows the p-values with using partial correlations. The last column (c) taSPU and taNBS shows the p-values by combining two inferences evaluated with correlations or partial correlations.

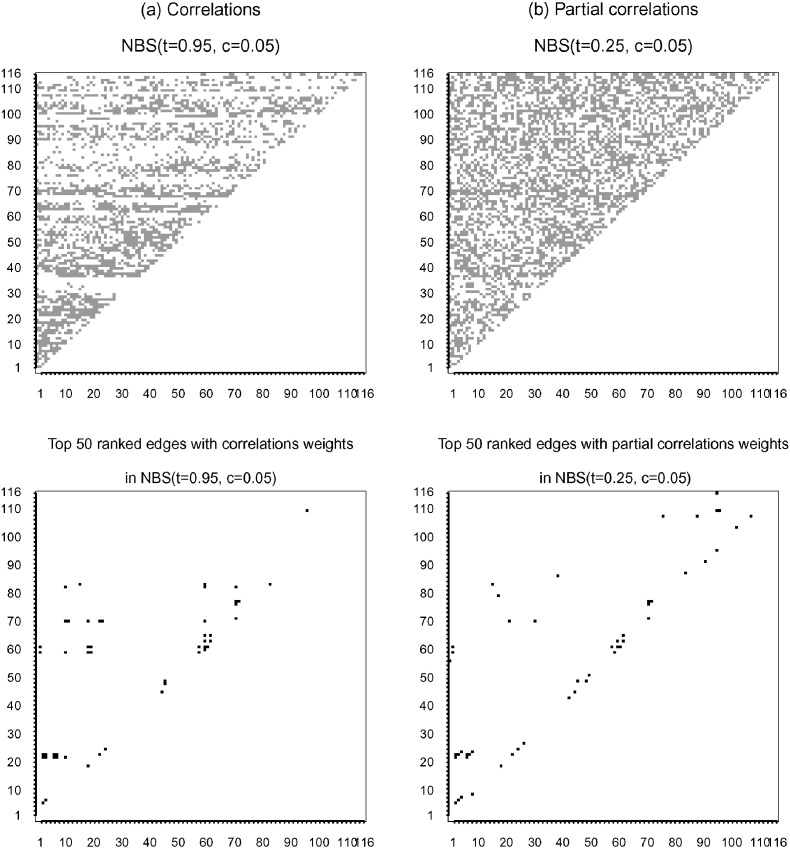
As discussed, NBS is useful for identifying changed subnetworks between the two groups. Fig. 2 illustrates the two subnetworks identified to be different between the two groups by the two individual NBS tests with two most significant p-values: NBS(t = 0.25,c = 0.05, $\widehat{\mathrm{\Theta }}$) for partial correlations, and NBS(t = 0.95,c = 0.05, $\widehat{\mathrm{\Sigma }}$) for correlations. Each changed subnetwork was represented in an N × N indicator matrix; each row/column of the indicator matrix corresponds to a distinct node, i.e. a brain region of interest. The (i,j)th element of the indicator matrix was marked out if the edge linking the ith and jth nodes was detected as significantly changed by the two NBS tests.

Fig. 2.

Altered network edges selected by the most significant NBS tests and the top 50 ranked by univariate score components.

Note that, although NBS (or any global test) identified a large subnetwork, it does not mean that all the edges from the subnetwork were genuinely altered. To facilitate interpretation, we further ranked the detected edges by their absolute scores in the score vector as used by the SPU tests, thus identifying the top 50 edges as presented at the bottom row of Fig. 2.

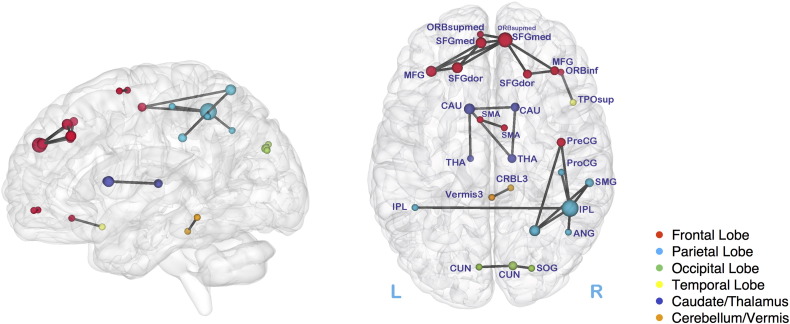
The two association measures (partial correlations and correlations) answer somewhat different questions, but we found 27 common altered connectivity edges for both correlations and partial correlations. The 27 edges in Fig. 3, BrainNet Viewer (Xia et al., 2013) were mainly located within the frontal and parietal regions classified as the salient mode network. Beyond the frontal and parietal regions, the proposed tests identified the subcortical structures caudate (CAU) and thalamus (THA), and cerebellum (CRBL3 and Vermis3); Table 2 lists some regions and their abbreviations. In this analysis, right frontal superior medial (SFGmed) and parietal inferior (IPL) showed the highest node degree; 5 and 6 respectively. The proposed tests detected altered interhemispheric functional connectivity in ADs, linking the left and right sides of the supplementary motor area (SMA), frontal superior medial (SFGmed), Superior frontal gyrus, medial orbital (ORBsupmed), cuneus (CUN), parietal inferior (IPL), and caudate (CAU) respectively. We will discuss the results by comparing with the literature in the Discussion section.

Fig. 3.

Altered brain connectivity for Alzheimer's disease: Left side shows the brain in sagittal view and right side is for axial view; brain areas are color coded; the node size is proportional to the degree of the node size; abbreviations for brain regions are in Table 2.

Table 2.

Anatomical parcellation of the brain and their abbreviations used for the ADNI data.

Region	Abbreviation	Region	Abbreviation
Precentral	PreCG	Frontal inf orb	ORBinf
Frontal sup	SFGdor	Cuneus	CUN
Supp motor area	SMA	Occipital sup	SOG
Frontal sup medial	SFGmed	Postcentral	PoCG
Frontal mid	MFG	Parietal sup	SPG
Frontal med orb	ORBsupmed	Parietal inf	IPL
Supramarginal	SMG	Angular	ANG
Caudate	CAU	Thalamus	THA
Temporal pole sup	TPOsup	Cerebellum3	CRBL3
		Vermis3	Vermis3

4. Simulations

We further investigated the performance of the proposed tests based on realistic simulations mimicking the ADNI data. Since brain connectivity networks were found sparse in previous studies (Oh et al., 2014, Hilgetag et al., 2002), we assumed either true precision matrices or covariance matrices to be sparse.

In our simulations, we assumed the true brain connection density to be 0.20, and 1% of the total brain network edges to be possibly altered. The BOLD signals (D_t) of the 116 regions were simulated from multivariate Gaussian distribution with mean 0 and group-level covariance matrices, Σ_(j) for j = 1 or 2.

4.1. True parameters Σ_(j)

4.1.1. Set-up 1

This simulation set-up assumes that the true precision matrix is sparse. First, group-level sample covariance matrices were obtained from the ADNI data, to which the graphical lasso was applied to generate sparse precision matrices (${\tilde{\mathrm{\Theta }}}_{\left(1\right)}$ and ${\tilde{\mathrm{\Theta }}}_{\left(2\right)}$), both with connection density 0.20. To specify altered brain network, we defined edges comprising a connected subnetwork as the truth, which was identified by NBS for the ADNI data. In this set-up, the changed edges were detected with the weights of partial correlations. Denote Δ as an N × N indicator matrix for the altered connectivity between the groups. The true parameters Θ₍₁₎ and Θ₍₂₎ were stated as

$$\begin{array}{cc}\hfill {\mathrm{\Theta }}_{\left(1\right)}={\tilde{\mathrm{\Theta }}}_{\left(1\right)},\hfill & \hfill {\mathrm{\Theta }}_{\left(2\right)}={\mathrm{\Theta }}_{\left(1\right)}+\varphi \cdot \left({\tilde{\mathrm{\Theta }}}_{\left(2\right)}-{\tilde{\mathrm{\Theta }}}_{\left(1\right)}\right)\circ \mathrm{\Delta }\hfill \end{array}$$

where ϕ is a scalar parameter to control the group differences and ○ is the Hadamard (i.e. matrix element-wise) product. For type I error rates, ϕ = 0, and for power analyses, ϕ = 0.008, 0.009 and 0.01 were considered. The true group-level covariance matrices were obtained as Σ_(j) = Θ_(j)^− 1 for j = 1 or 2.

4.1.2. Set-up 2

We also considered a case where the true covariance matrix is sparse. Applying the graphical lasso to the group-level sample covariance matrices of the ADNI data, we generated sparse covariance matrices (${\tilde{\mathrm{\Sigma }}}_{\left(1\right)}$ and ${\tilde{\mathrm{\Sigma }}}_{\left(2\right)}$), each of which had connection density 0.20. In set-up 2, the true altered brain connectivity (Δ) was defined with the measures of correlations. Similar to set-up 1, the true parameters Σ₍₁₎ and Σ₍₂₎ were defined as ${\mathrm{\Sigma }}_{\left(1\right)}={\tilde{\mathrm{\Sigma }}}_{\left(1\right)}$ and ${\mathrm{\Sigma }}_{\left(2\right)}={\mathrm{\Sigma }}_{\left(1\right)}+\varphi \cdot \left({\tilde{\mathrm{\Sigma }}}_{\left(2\right)}-{\tilde{\mathrm{\Sigma }}}_{\left(1\right)}\right)\circ \mathrm{\Delta }\text{.}$

We set ϕ = 0 for calculating type I error rates, and ϕ = 0.45 for power analysis.

4.2. Generating simulated data

At any time point t, the BOLD signals for N = 116 brain regions were generated independently as

$$\begin{array}{ll}{D}_t={\left(D_{t1},\cdots ,D_{tN}\right)}^{\prime }~N\left(0,{\mathrm{\Sigma }}_{\left(j\right)}\right),\hfill & t=1,\dots ,M\text{,}\hfill \end{array}$$

for each subject in group j. We mimicked the ADNI data by setting the number of time points at M = 140, and generating data of 30 subjects for AD or CN group respectively.

4.3. Estimating networks

The following procedure was used to estimate networks (${\widehat{\mathrm{\Sigma }}}_i\left(c\right)$ and ${\widehat{\mathrm{\Theta }}}_i\left(c\right)$) with the time-series data. First we tried to find the group level λ_(j)(c) so that estimated connection density of ${\widehat{\mathrm{\Theta }}}_i\left(c\right)$ is close to the target density c, for subject i in a group j. Applying the graphical lasso with λ_(j)(c) to each subject's time course data, we would estimate each subject-specific covariance (or precision) matrix, from which correlations (or partial correlations) were estimated. In the simulation study, the estimated connection density of the precision matrix was predefined at c ∈ {0.05,0.15,0.25,0.35,0.45,0.55,1}.

In one of the simulation set-ups, we also estimated networks by applying 10-fold CV-selected regularization parameter values, ${\widehat{\lambda }}_{\left(j\right)}$.

4.4. Type I error and power for testing

In the procedure of applying the adaptive tests, brain connectivity X_i(c,Ω) was estimated at various sparsity levels and with different association measures. Given X_i(c,Ω), the SPU(γ,c,Ω), aSPU(γ,Ω), daSPU(Ω) and taSPU tests were sequentially applied while adjusting for multiple testing results over each parameter c, γ and Ω. Similarly, the NBS(t,c,Ω), aNBS(γ,Ω), daNBS(Ω) and taNBS test were consecutively implemented to test group-level network differences.

The test significance level was fixed at a = 0.05 throughout the simulations. The empirical type I errors and power were based on 1000 independent replicates for each set-up. The permutation number used for all tests was 1000.

4.5. Errors in estimating networks

Suppose that subject i has a network estimate ${\widehat{\mathrm{\Sigma }}}_i$ (or ${\widehat{\mathrm{\Theta }}}_i$) for the true Σ_i (or Θ_i) and Σ_iΘ_i = I. Estimation errors in the assessment of networks (${\widehat{\mathrm{\Sigma }}}_i$ and ${\widehat{\mathrm{\Theta }}}_i$) were quantified with an entropy loss (EL) and a quadratic loss (QL). EL and QL from estimating ${\widehat{\mathrm{\Sigma }}}_i$ were computed as

$$\mathrm{EL}\left({\widehat{\mathrm{\Sigma }}}_i,{\mathrm{\Sigma }}_i\right)=\mathrm{t}\mathrm{r}\left({\widehat{\mathrm{\Sigma }}}_i{\mathrm{\Theta }}_i\right)-log\left|{\widehat{\mathrm{\Sigma }}}_i{\mathrm{\Theta }}_i\right|-N$$

$$\mathrm{Q}\mathrm{L}\left({\widehat{\mathrm{\Sigma }}}_i,{\mathrm{\Sigma }}_i\right)=\mathrm{t}\mathrm{r}{\left({\widehat{\mathrm{\Sigma }}}_i{\mathrm{\Theta }}_i-I\right)}^2\text{.}$$

Here Σ_i = Σ_(j) and Θ_i = Θ_(j) for subject i in a group j i.e. i ∈ G_(j), since we assumed the true networks at the group level. Similarly errors in estimating ${\widehat{\mathrm{\Theta }}}_i$ were obtained with

$$\mathrm{EL}\left({\widehat{\mathrm{\Theta }}}_i,{\mathrm{\Theta }}_i\right)=\mathrm{t}\mathrm{r}\left({\widehat{\mathrm{\Theta }}}_i{\mathrm{\Sigma }}_i\right)-log\left|{\widehat{\mathrm{\Theta }}}_i{\mathrm{\Sigma }}_i\right|-N$$

$$\mathrm{Q}\mathrm{L}\left({\widehat{\mathrm{\Theta }}}_i,{\mathrm{\Theta }}_i\right)=\mathrm{t}\mathrm{r}{\left({\widehat{\mathrm{\Theta }}}_i{\mathrm{\Sigma }}_i-I\right)}^2\text{.}$$

In one of the simulation studies, EL and QL were obtained for each group at different connection density c's and averaged out based on 1000 replicates.

4.6. Results

4.6.1. Type I error rates

Type I error rates in each simulation are reported in Table 3, Table 4, where all tests had empirical type I error rates close to the nominal level of 0.05.

Table 3.

Type I error rates of the various SPU-based tests for testing network differences.

	Set-up 1
	Correlations			Partial correlations
SPU(γ,c)	γ = 1	γ = 2	γ = ∞	γ = 1	γ = 2	γ = ∞
c = 0.05	0.033	0.030	0.032	0.046	0.044	0.050
0.15	0.049	0.039	0.031	0.044	0.049	0.033
0.25	0.054	0.041	0.033	0.042	0.041	0.059
0.35	0.054	0.041	0.035	0.038	0.041	0.056
0.45	0.054	0.041	0.039	0.038	0.043	0.057
0.55	0.053	0.041	0.037	0.041	0.043	0.052
1	0.056	0.046	0.037	0.041	0.046	0.042
	Correlations			Partial correlations
aSPU(γ)	γ = 1	γ = 2	γ = ∞	γ = 1	γ = 2	γ = ∞
	0.026	0.022	0.021	0.013	0.042	0.040
	Correlations			Partial correlations
daSPU	0.040			0.021
taSPU	0.033
	Set-up 2
	Correlations			Partial correlations
SPU(γ,c)	γ = 1	γ = 2	γ = ∞	γ = 1	γ = 2	γ = ∞
c = 0.05	0.033	0.030	0.050	0.046	0.044	0.050
0.15	0.048	0.040	0.031	0.043	0.049	0.033
0.25	0.053	0.042	0.033	0.042	0.042	0.059
0.35	0.053	0.042	0.034	0.038	0.042	0.056
0.45	0.053	0.042	0.039	0.038	0.043	0.057
0.55	0.052	0.042	0.036	0.041	0.043	0.052
1	0.055	0.046	0.037	0.042	0.046	0.043
	Correlations			Partial correlations
aSPU(γ)	γ = 1	γ = 2	aSPU(γ)	γ = 1	γ = 2	aSPU(γ)
	0.029	0.024	0.025	0.036	0.040	0.039
	Correlations			Partial correlations
daSPU	0.017			0.026
taSPU	0.015

Table 4.

Type I error rates of the various NBS-based tests for testing network differences.

	Set-up 1
	Correlations	Partial correlations
NBS(t,c)	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95
c = 0.05	0.050	0.040	0.032	0.036	0.036	0.036	0.052	0.052	0.052	0.052	0.046	0.049
0.15	0.057	0.060	0.062	0.064	0.055	0.055	0.047	0.047	0.047	0.048	0.037	0.040
0.25	0.053	0.051	0.053	0.053	0.055	0.058	0.039	0.061	0.054	0.052	0.046	0.044
0.35	0.058	0.051	0.053	0.053	0.048	0.048	0.058	0.063	0.052	0.048	0.037	0.029
0.45	0.060	0.058	0.053	0.053	0.053	0.060	0.058	0.045	0.044	0.047	0.031	0.042
0.55	0.055	0.053	0.053	0.055	0.053	0.051	0.052	0.047	0.043	0.045	0.040	0.033
1	0.053	0.048	0.053	0.046	0.051	0.057	0.047	0.049	0.052	0.039	0.037	0.036
	Correlations	Partial correlations
aNBS(t)	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95
	0.014	0.016	0.016	0.009	0.012	0.007	0.049	0.045	0.040	0.043	0.036	0.030
	Correlations	Partial correlations
daNBS	0.012	0.044
taNBS	0.042
	Set-up 2
	Correlations	Partial correlations
NBS(t,c)	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95
c = 0.05	0.048	0.055	0.055	0.053	0.062	0.059	0.048	0.055	0.055	0.053	0.062	0.059
0.15	0.15	0.063	0.063	0.057	0.066	0.060	0.050	0.063	0.063	0.057	0.066	0.060
0.25	0.25	0.060	0.062	0.065	0.054	0.061	0.050	0.060	0.062	0.065	0.054	0.061
0.35	0.35	0.060	0.056	0.056	0.054	0.047	0.051	0.060	0.056	0.056	0.054	0.047
0.45	0.45	0.062	0.057	0.047	0.049	0.049	0.049	0.062	0.057	0.047	0.049	0.049
0.55	0.55	0.067	0.062	0.053	0.047	0.052	0.039	0.067	0.062	0.053	0.047	0.052
1	1	0.059	0.059	0.053	0.054	0.055	0.049	0.059	0.059	0.053	0.054	0.055
	Correlations	Partial correlations
aNBS(t)	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95	t = 0.10	t = 0.25	t = 0.50	t = 0.75	t = 0.90	t = 0.95
	.047	0.050	0.052	0.047	0.055	0.046	0.028	0.031	0.030	0.031	0.031	0.029
	Correlations	Partial correlations
daNBS	0.049
taNBS	0.038

4.6.2. Power for set-up 1

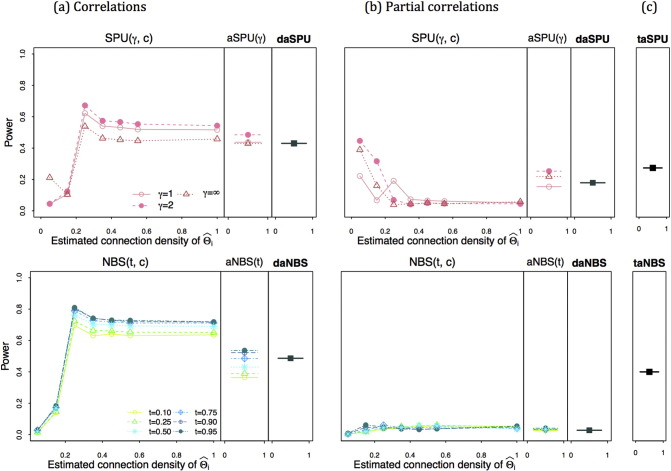
Fig. 4, Fig. 5 show the power for testing group-level network differences when the true precision matrices were set sparse and the group-differences were created with the partial correlations. High regularization led to a low estimated connection density at ${\widehat{\mathrm{\Theta }}}_i$. The left column (a) of Fig. 4 shows the power when using correlations while the middle column (b) with using partial correlations; in the last column (c), the power of taSPU and taNBS is presented. When assuming true sparse precision matrices, using correlations gave higher power than employing partial correlations. The estimated connection density of ${\widehat{\mathrm{\Theta }}}_i$ was influential on the power for testing group differences. When using correlations (a), the power of SPU(γ,c,Ω) and NBS(t,c,Ω) was low at estimated connection density less than 0.25; but with using partial correlations (b), the power of SPU(γ,c,Ω) test was higher at lower estimated connection density. The aSPU(γ,Ω) and the aNBS (t,Ω) maintained high power robustly across different estimated connection density c's. It is emphasized that the power of SPU(γ,c,Ω) and NBS(t,c,Ω) largely depended on the sparsity level of estimated networks. As expected, the daSPU and daNBS tests showed the power between the lowest and the highest power of aSPU(γ,Ω)'s and aNBS(t,Ω)'s respectively, while the power of the taSPU test was between those of the two daSPU(Ω) tests applied to correlations (a) and partial correlations (b), and taNBS gave the power between those of two daNBS(Ω)'s with correlation and partial correlations.

Fig. 4.

Simulation set-up 1: power for testing network differences with true sparse precision matrices when ϕ = 0.009; the left panel (a) shows the power using correlations; the middle panel (b) for the power with using partial correlations; in the last panel (c), is the power of taSPU and taNBS.

Fig. 5.

Simulation set-up 1: power of SPUs for testing network differences with true sparse precision matrices; in the top row, ϕ = 0.01, and in the bottom ϕ = 0.008. The left panel (a) shows the power using correlations; the middle panel (b) for the power with using partial correlations; in the last panel (c), is the power of taSPU.

Fig. 5 shows how effect size (ϕ) of the group differences is related to the statistical power. To illustrate the possible patterns of the power, we only presented the power of SPU tests. In the top row, ϕ = 0.01, and in the bottom ϕ = 0.008. In both cases, testings with correlations (a) outperformed those using partial correlations (b). When ϕ = 0.01, lower estimated connection density gave higher statistical power; possible causes for this are the dimension of edges to be tested was reduced due to the high regularization. However with ϕ = 0.008 where effect size was too small, lower estimated connection density could not show high power, since only with small number of edges of weak effects, the group differences were hard to be detected. The aSPU(γ,Ω), aSPU(Ω), and taSPU tests showed the power between the lowest and the highest of each previous stage respectively, as expected.

Overall, since the true precision matrices were sparse (and hence the true covariance matrices were not sparse), a test based on using correlations seemed to be more stable and more powerful than that using partial correlations.

4.6.3. CV-selected regularization parameter in set-up 1

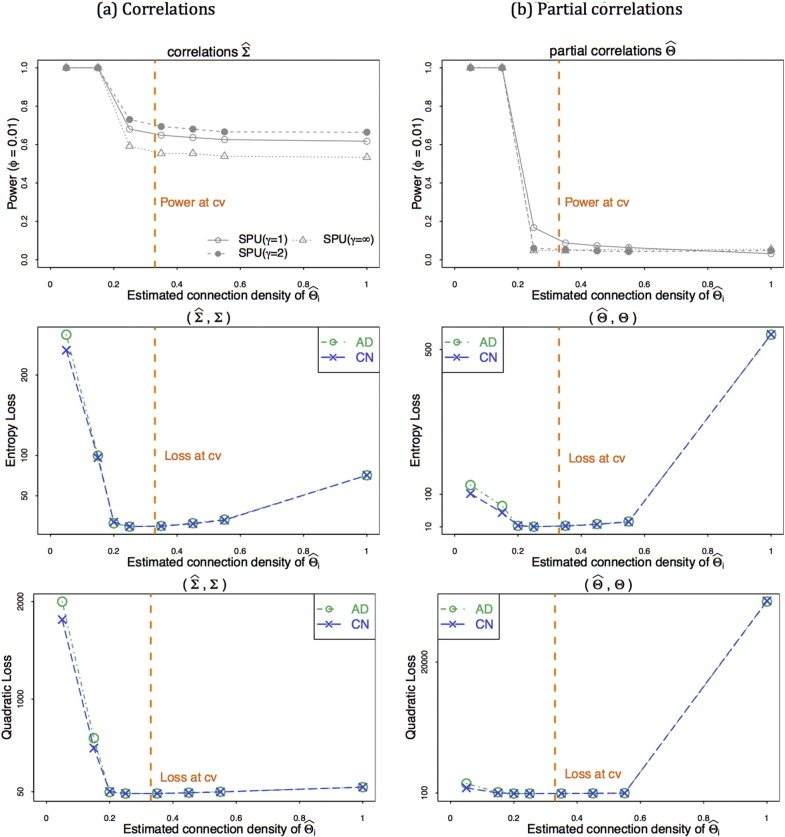
Fig. 6 illustrates the power for testing network-differences and network estimation errors when CV-selected regularization was applied in estimating networks. The simulation setting was the same as that for the top row of Fig. 5, where the true sparse precision matrices were assumed and ϕ = 0.01. The vertical lines in Fig. 6, represent the results when CV-selected parameter values were imposed. When CV-selected regularization was imposed, the estimated connection density at ${\widehat{\mathrm{\Theta }}}_i$ was 0.33 for both groups, close to the true value of 0.2. As shown by the top row of Fig. 6, the CV-selected regularization did not give the highest statistical power for testing network differences when using correlations (a) or partial correlations (b).

Fig. 6.

Simulation set-up 1: CV-selected regularization for testing network differences and estimation errors with true sparse precision matrices and ϕ = 0.01.

For testing group-differences, imposing higher regularization than the CV-selected parameter value was preferred. The middle and bottom rows of Fig. 6 show network estimation errors using the entropy loss and the quadratic loss. It is interesting to note that CV was successful for estimating networks ($\widehat{\mathrm{\Sigma }}$ and $\widehat{\mathrm{\Theta }}$), yielding nearly the minimal entropy loss and quadratic loss. This numerical example clearly suggests that testing group-differences differs from network estimation; a good procedure (like CV) for the latter does not necessarily guarantee high performance in testing.

4.6.4. Power for set-up 2

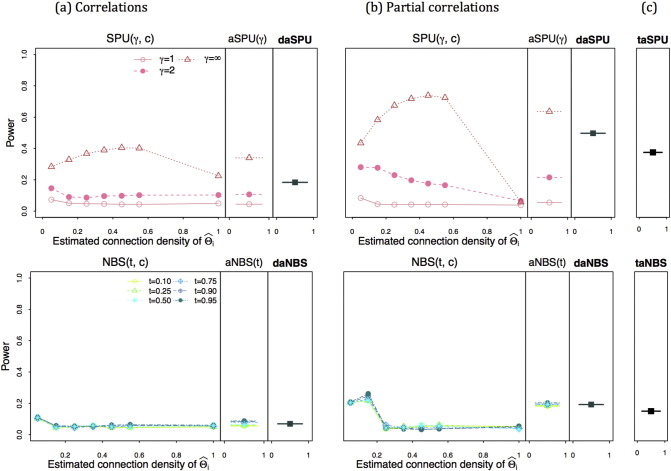
Fig. 7 describes power for testing network differences when true covariance matrices are sparse. The proposed adaptive tests were successful in combining multiple testing results over parameters c, γ (or t) and Ω. The patterns of the relative power between using correlations and partial correlations were switched compared to Fig. 4, Fig. 5, Fig. 6, presumably because the true covariance matrices, not true precision matrices, were sparse, highlighting the necessity of data-adaptively choosing an association measure.

Fig. 7.

Simulation set-up 2: power for testing network differences with true sparse covariance matrices; the left panel (a) shows the power using correlations; the middle panel (b) for the power with using partial correlations; in the last panel (c), is the power of taSPU and taNBS.

5. Discussion

We have proposed two highly adaptive tests for group differences in brain connectivity, building on two existing tests, aSPU and NBS (Pan et al., 2014, Zalesky et al., 2010, Zalesky et al., 2012), which appeared to be high powered and complementary to each other in a previous study (Kim et al., 2014). In practice, one has to specify a few parameters, such as the estimated connection density and type of association measures, which will critically influence the corresponding brain functional network estimates, and thus the subsequent group comparison of networks. On the other hand, it is in general unknown how to choose these parameters to maximize the power of group comparison. These issues have not been carefully considered in the current practice of two-group testing, for example, is based on some arbitrarily chosen parameters, e.g. unpenalized sample covariance matrices or some penalized precision matrices. As shown in our numerical examples, in addition to possible power loss with the use of sample covariance matrices, the commonly used model selection method, cross-validation, may not be able to choose an appropriate value of such a parameter for hypothesis testing, though it may perform well for network estimation (Kim et al, 2015). Motivated by these observations, we have developed the highly adaptive tests aiming to automatically and optimally choose these parameters to maximize power, in contrast to the current practice of using some ad hoc parameters. Specifically, among multiple candidate tests, each based on a set of specified tuning parameter values, we take the minimum p-value of these tests. Due to the unavailability of a closed-form expression for the power of a test, we use a p-value as a (negative) surrogate for its power; ideally we would choose a test based on its power (Fan, 1996, Kulasekera and Wang, 1997). The idea of using p-values to approximate statistical power is both simple and proven useful in practice. For example, Zou and Qiu (2010) proposed choosing the maximum of a set of (normalized) test statistics with each test being constructed based on a specific value of the regularization parameter in lasso, which is equivalent to our choosing of the minimum p-value. Our proposed tests generalize the idea of Zou and Qiu (2010) to the case with more than one tuning parameter. We also note that other p-value combining methods (Pan et al., 2010) are possible and worth further investigation. Through both simulated and real data applications, we have demonstrated the easy use, flexibility and possible power gain of the proposed highly adaptive tests over non-adaptive tests.

In the following, we highlight a few of our technical choices, illustrating our major innovations and/or contributions, and then discuss the ADNI data application and how to apply the proposed tests in practice.

5.1. How does network testing differ from network estimation?

Since brain networks are known to be highly clustered and sparse (Achard and Bullmore, 2007, He et al., 2007), it is presumably better to incorporate the sparsity of networks into both estimation and testing. For example, many studies, including the current one, have employed the graphical lasso with a group-level regularization parameter value to estimate the networks at a given sparsity (or density) level. However, it is difficult to choose an appropriate value of the regularization parameter (or the sparsity/density level) to maximize the power of a test. Existing model selection criteria, such as CV, are developed for estimation, not for testing. As we have shown, although CV-selected tuning parameter (nearly) minimized the estimation error, it led to loss of power in the subsequent testing (Fig. 6). This clearly demonstrates that an optimal procedure for estimation may no longer be optimal for hypothesis testing, highlighting the need for further investigation on testing.

Another example is which association measure, the (full) correlation or the partial correlation, should be preferred. For network estimation, the answer largely depends on what is the question of interest, though often the partial correlation, and hence the precision matrix, are preferred due to the connection with conditional independence and thus easy interpretation of the latter (Smith et al., 2011). For testing, since two unequal covariance matrices imply the inequality of the two corresponding precision matrices, and vice versa, the choice between the two should depend on the power of the resulting test. Perhaps surprisingly, in agreement with Kim et al. (2015), we confirmed that the question of which one is preferred depends on which of the true covariance and precision matrices is sparse. For example, if two different true precision matrices are sparse, then using the full correlations based on the covariance matrix estimates (with suitable regularization) gives higher power; otherwise the conclusion is the opposite (see Fig. 4, Fig. 7). A possible explanation is that, by definition of sparsity, there are only few different elements between two different and sparse matrices; on the other hand, since the inverse of a sparse matrix is in general non-sparse, there will be more different elements between the inverses of the two sparse matrices, leading to higher power of a test.

The sparsity of a matrix may also influence the power of some non-adaptive test. For example, if the two different precision matrices are sparse, then as shown in Fig. 4, NBS may have much lower power to detect their differences. The reason is that NBS is based on identifying the largest altered (and connected) subnetwork; however, with sparse matrices and weak signals, it is much harder to detect a large and connected disrupted subnetwork, because missing one or two key edges may split the altered subnetwork into a few much smaller subnetworks.

We note that, due to space limit, we only present a few examples here; we have obtained similar results based on a different real dataset (as used in Kim et al., 2014) and more simulated datasets.

5.2. Why to ignore temporal correlations?

While BOLD signals are in general correlated across time, we ignore the correlations when estimating a spatial covariance or precision matrix for a set of ROIs. This is largely for simplicity, but theoretical support exists. It is sufficient to consider only one group here. As before, suppose D_t = (D_t1, …, D_tN)′ is the vector of BOLD signals for N ROIs at time t, t = 1,…,M. Now write D = (D₁,…,D_M) as the data matrix. If we assume that D ~ MN(0, Σ, V) has a matrix Normal variate distribution, i.e. vec (D) = (D₁′, …, D_M′)′ ~ N(0, Σ ⊗ V) with ⨂ as the Kronecker product, then a penalized spatial correlation matrix R can be estimated by the glasso:

$$\tilde{R}\left(\lambda \right)=arg\underset{R}{max}\left\{log\left|R^{-1}\right|-\mathrm{t}\mathrm{r}\left(\widehat{R}{R}^{-1}\right)-\lambda {‖R^{-1}‖}_1\right\}\text{,}$$

where R = (R_ij) is the population correlation matrix derived from ∑ = (∑_ij) with $R_{ij}={\mathrm{\Sigma }}_{ij}/\sqrt{{\mathrm{\Sigma }}_{ii}{\mathrm{\Sigma }}_{jj}}$, and $\widehat{R}$ is the sample correlation matrix of D₁, …, D_M under the working assumption that D₁, …, D_M are independent (i.e. by ignoring the temporal correlations). Some theoretical justifications and good finite-sample performance of such an estimate were studied in Zhou (2014). Note that $\tilde{R}$ and its (generalized) inverse are used in our proposal to obtain correlations and partial correlations for a brain network. Furthermore, under more general conditions (e.g. without the matrix variate normal assumption and without assuming a common temporal covariance matrix V across the ROIs), the theoretical validity of some penalized (spatial) covariance and correlation matrices for ∑ and R, based on the sample covariance or correlation matrix $\widehat{R}$ obtained by ignoring temporal correlations, is established in Shu and Nan (2014).

More intuitively, the validity of using the sample covariance matrix

$$S=\frac{1}{M}{\displaystyle \sum _{t=1}^M\left(D_t-\overline{D}\right){\left(D_t-\overline{D}\right)}^{\prime }\text{,}}$$

with $\overline{D}={\displaystyle {\sum }_{t=1}^M{D}_t}/M$, (or using the sample correlation matrix $\widehat{R}$,) is due to its unbiasedness, no matter whether D_t's are correlated or not across time t, because of the simple fact of $E\left[\left(D_t-\overline{D}\right){\left(D_t-\overline{D}\right)}^{\prime }\right]=\mathrm{\Sigma }$. This is analogous to the fact that the sample mean is unbiased for the population mean even if we have a correlated sample. More generally, the normal likelihood based on assuming independent D_t's can be regarded as a pseudo-likelihood or composite likelihood (Lindsay, 1988). In fact, for the normal likelihood under the working independence assumption,

$$log{L}_I=log\left|R^{-1}\right|-\mathrm{t}\mathrm{r}\left(\widehat{R}{R}^{-1}\right)\text{,}$$

it is easy to verify that

$$\frac{\partial log{L}_I}{\partial R^{-1}}=R-\widehat{R}\text{.}$$

By the unbiasedness of the sample correlation matrix $\widehat{R}$, we have $E\left(\widehat{R}\right)=R$ and thus E(∂ log L_I/∂R^− 1) = 0. By the theory of estimating functions (e.g. Liang and Zeger, 1986, Lindsay, 1988), using log L_I is equivalent to using an unbiased estimating function, leading to some nice asymptotic properties, e.g. consistency, of the resulting estimator under some regularity conditions. However, we acknowledge that ignoring temporal correlations may lead to an inefficient estimate of a covariance or precision matrix (Zhou, 2014) and thus possible loss of power in subsequent testing. How to incorporate temporal correlations while maintaining the simplicity and robustness in estimating a covariance or precision matrix warrants further investigation.

5.3. Why to use penalized covariance and precision matrix estimates?

By striking a better bias–variance trade-off, penalization may lead to a better estimate. In the current context of testing the equality of two large group-level covariance (or precision) matrices, there are a large number of parameters (i.e. element-wise differences between the two matrices). Because usually many elements are equal but their estimates may not be equal (due to estimation errors), using all non-penalized element-wise differences will simply contribute noises to the test statistic, and thus reduce the power of the resulting test. By penalization, some or all of these elements may be shrunk to be (nearly) zero, thus effectively eliminating (or reducing) their negative influences on the power; on the other hand, the shrinkage of those elements that are unequal between the two population matrices may also lead to loss of power (by reducing the element-wise differences). In the end, it is a trade-off between the two effects. As shown in Fig. 1, Fig. 4, a proper shrinkage or penalization (with the corresponding connection density) will yield higher power than no shrinkage or over-shrinkage.

A potential problem of penalization is its introducing biased parameter estimates, which in the current context is not critical, because our goal is to maintain a correct Type I error rate while maximizing the power. This is why we propose choosing the penalization (or connection density) at the group level: under the null hypothesis H₀, the two group-level covariance or precision matrices are equal, implying that they have the same connection density; enforcing an equal connection density between the two groups ensures that under H₀, no differences between the two groups would arise simply due to the artifact of imposing different connection densities between the two groups. The effectiveness of our proposal was confirmed in our simulations with properly controlled Type I error rates (e.g. Table 3, Table 4). Of course, under an alternative hypothesis, if the two groups have different covariance matrices with different connection densities, then our method may lose power, though it is unclear to us what is a better alternative.

We also note that, we do not assume that all the subjects in the same group have the same covariance matrix (and connection density); it is possible that each individual has his/her own covariance matrix, and their mean is the corresponding group-level covariance matrix. This is analogous to testing for differences of blood pressure between two populations; within each population, the individuals may have different blood pressures. Through our proposed group-level penalty parameter selection, we aim to penalize the individual covariance matrices by a similar amount so that the between-group equality (or differences) can be maintained, leading to a correct Type I error rate (or high power). Note that, we do not assume that an estimated covariance (or precision) matrix for each individual is exact; we treat them as observations with random errors, which are then used in the subsequent two-sample testing.

5.4. How do our proposed methods differ from existing two-sample tests for covariance matrices?

Two new tests have been proposed recently for high-dimensional covariance matrices (Cai et al., 2013, Li and Chen, 2012). A key difference between the two tests and ours is the lack of replicates in the former; that is, only one sample covariance matrix is observed from each of the two groups. Because of this difference, no penalization is applied in the two tests, both of which are based on the sample covariance matrices. Specifically, the two tests are based on the sum of the squared element-wise differences and the most significant element-wise difference between the two sample covariance matrices respectively, hence they are similar to our proposed SPU(γ = 2, c = 1, S) and SPU(γ = ∞, c = 1, S) tests, respectively. In particular, the test of Cai et al. (2013) is similar to a mass-univariate testing procedure, which has been shown by Kim et al. (2014) to be low-powered for non-sparse alternatives. Accordingly, the two tests are not adaptive: they will not be powerful unless under their desired alternatives with appropriately dense and sparse element-wise differences respectively.

For simplicity, we used the popular glasso to estimate both a covariance matrix and a precision matrix; other penalization methods can be equally applied.

5.5. More on the ADNI data application

Independent component analysis (ICA) is a popular method for analysis of functional connectivity. Zhou et al. (2010) applied ICA to each single subject's estimated brain networks and then test for their group differences. Here we compare our results with theirs and others' for differential functional connectivity between patients with Alzheimer's disease and controls. For our methods, we focus on the 27 edges and related ROIs in Fig. 3.

Zhou et al. (Supplementary Table 1) revealed connectivity alternations in the salience network of ADs, including the pregenual anterior cingulate cortex (ACC), right subgenual ACC, right dorsal anterior insula, left putamen, left pallidum, left caudate, right pulament, thalamus, midbrain periaqueductal gray, and brainstem, among which the caudate and thalamus were overlapped with those identified by our methods (Fig. 3). Furthermore, Jiji et al. (2013) found a significant reduction in the caudate volume in Alzheimer's patients when compared to normal controls, while reduction in thalamus volume in Alzheimer's disease was pointed out by de Jong et al. (2008). For the regions included in the default mode network (DMN), our proposed tests indicated altered connectivity linked to the cuneus (CUN), temporal pole (TPOsup), and inferior parietal gyrus; Zhou et al. (Supplementary Table 2) reported the left lingual gyrus, cuneus, left precuneus, right dorsolateral prefrontal cortex, left middle temporal gyrus, left parahippocampa, right precuneus, right angular gyrus, right posterior MCC, left hippocampus, right putamen, and brainstem.

Our proposed tests also identified connectivity differences in clusters in the frontal, temporal, and subcortical (CAU and THA) regions, which were also uncovered by Zhang et al. (2009) and Allen et al. (2007).

5.6. How to apply the proposed tests?

As a global test, the primary goal of each proposed method is to achieve high power in detecting any differences of connectivity, rather than localizing such differences. The main reason is that, with often a small sample size and a large number of parameters (i.e. edges) to be tested, even the power of a global test can be low while that of a localization test (e.g. a mass-univariate test) is much worse. Our proposed strategy is to first apply a high-powered global test to assess whether there are any genuine differences of connectivity; if so, then explore and localize the differences. Since our proposed global tests build on univariate tests on individual edges, in practice the results of the uniavraite tests can be examined to help identify possible differences. For example, at each c, t and Ω, NBS(t,c,Ω) provides subnetworks with the strongest evidence against the null hypothesis H₀, thus allowing one to visualize possible connectivity differences.

To apply our proposed tests, one has to specify some ranges for several tuning parameters, which may influence the performance of the tests: searching a too wide or too narrow range than necessary may lead to loss of power. One effective way is to incorporate prior knowledge. For example, since brain structural networks are known to be sparse with a connection density c around 17–20% (Oh et al, 2014), one may specify the range of c around 0.20. However, such prior knowledge may not exist or may not be reliable. In practice, to be conservative, one may choose to specify a full range of a tuning parameter, e.g. 0 < c < 1 as done before. An advantage of our proposed tests is that they will search for an optimal tuning parameter (e.g. c) automatically.

5.7. Future work

The main idea of our construction of adaptive tests over multiple tuning parameters is general and can be equally applied to other tests (e.g. Lin et al., 2012, Sun et al., 2015). Our proposed tests may be also extended to other cases. For example, they can be extended to comparison among three or more groups. For adaptive SPU tests, a multinomial logistic regression (for a categorical group indicator) or a proportional odds model (POM) (for an ordinal group indicator such as NC, MCI and AD groups in the ADNI data) can be employed in lieu of the binomial logistic model, from which we derive the score vector and thus the SPU tests. The score vector of the POM has a closed-form solution (McCullagh, 1980, Zhang et al., 2014b). Since the NBS tests are based on linear regression on each connectivity edge, it is easy to incorporate a multi-categorical group indicator as several binary dummy variables as covariates in a linear model and test the significance of group-edge association by an F-test (instead of the t-test). In this way it is straightforward to apply the highly adaptive NBS test to more than two groups. In addition, rather than using the graphical lasso, other methods (Eavani et al., 2014) can be used to estimate the undirected networks, or dynamic/directional networks (Ou et al., 2014, Zhang et al., 2014a, Zhang et al., 2015), based on which of our proposed tests can be applied. Furthermore, instead of Pearson's correlations or partial correlations as considered here, other association measures (Lindquist et al., 2014, Varoquaux and Craddock, 2013) may be also used. These are all interesting topics to be pursued in the future.

Appendix A. Supplementary data

Supplementary Materials.