Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2015 Sep 16;201(3):1189–1200. doi: 10.1534/genetics.115.182550

Extent of QTL Reuse During Repeated Phenotypic Divergence of Sympatric Threespine Stickleback

Gina L Conte *,1, Matthew E Arnegard *,†, Jacob Best *, Yingguang Frank Chan ‡,2, Felicity C Jones ‡,2, David M Kingsley ‡, Dolph Schluter *,3, Catherine L Peichel †,3
PMCID: PMC4649644  PMID: 26384359

Abstract

How predictable is the genetic basis of phenotypic adaptation? Answering this question begins by estimating the repeatability of adaptation at the genetic level. Here, we provide a comprehensive estimate of the repeatability of the genetic basis of adaptive phenotypic evolution in a natural system. We used quantitative trait locus (QTL) mapping to discover genomic regions controlling a large number of morphological traits that have diverged in parallel between pairs of threespine stickleback (Gasterosteus aculeatus species complex) in Paxton and Priest lakes, British Columbia. We found that nearly half of QTL affected the same traits in the same direction in both species pairs. Another 40% influenced a parallel phenotypic trait in one lake but not the other. The remaining 10% of QTL had phenotypic effects in opposite directions in the two species pairs. Similarity in the proportional contributions of all QTL to parallel trait differences was about 0.4. Surprisingly, QTL reuse was unrelated to phenotypic effect size. Our results indicate that repeated use of the same genomic regions is a pervasive feature of parallel phenotypic adaptation, at least in sticklebacks. Identifying the causes of this pattern would aid prediction of the genetic basis of phenotypic evolution.

Keywords: genetics of adaptation, genetic parallelism, parallel evolution, repeated evolution, QTL mapping

WE still have a poor understanding of the predictability of the genetic basis of phenotypic adaptation (Stern and Orgogozo 2008; Conte et al. 2012; Martin and Orgogozo 2013; Stern 2013). One way to make progress is to quantify the repeatability of the genetic changes that underlie repeated phenotypic evolution. When organisms independently evolve similar phenotypes in response to similar selection pressures (a reliable signature of adaptive evolution (Endler 1986; Harvey and Pagel 1991; Schluter 2000; Losos 2011), we can ask: How similar are the genetic “solutions” underlying those phenotypes? Many features may influence similarity of genetic solutions, including availability of standing genetic variation, mutational biases, and functional constraints. The extent to which the genetic basis of repeatedly evolved phenotypes is shared indicates the extent to which the genetic basis of adaptation is predictable.

Although there is some evidence indicating that gene reuse during repeated phenotypic evolution is common, current estimates of the frequency of gene reuse in adaptive evolution might not be accurate because of methodological limitations. A recent metaanalysis of studies of natural populations estimated that the average probability of gene reuse is 0.32–0.55 (depending on the type of data used to calculate it) across a diversity of taxa spanning divergence times from hundreds of years to hundreds of millions of years (Conte et al. 2012). The probability of gene reuse was highest among closely related species and it declined with increasing divergence time between the taxa being compared. This estimate of gene reuse was based on published cases in which a repeatedly evolved phenotype had either been genetically mapped in multiple populations or in which the role of a specific candidate gene on a given trait had been tested in different populations (Conte et al. 2012). However, caution is warranted when interpreting estimates based on both approaches. Candidate gene studies of repeated phenotypic evolution are prone to publication bias and have focused mainly on a small number of genes with mostly unknown effect sizes. Mapping studies of repeated phenotypic evolution have tended to focus on a small number of traits controlled by genes of apparently large effect. Few studies to date have mapped the genetic basis of a large number of repeatedly evolved phenotypes to quantitatively estimate the repeated use of the same loci.

To help remedy this gap, we investigated the genetic basis of repeated evolution in a large number of traits in two sympatric species pairs of threespine stickleback (Gasterosteus aculeatus species complex) from two isolated lakes in British Columbia, Canada. Both species pairs consist of a limnetic ecotype that specializes on zooplankton in the open water zone of the lake and a benthic ecotype that feeds on invertebrates from the littoral and benthic zones of the lake (McPhail 1984, 1992, 1994; Schluter and McPhail 1992). The species pairs appear to have originated independently in the past 10,000–12,000 years, following double invasions by ancestral marine populations into postglacial lakes (Schluter and McPhail 1992; McPhail 1994; Taylor and McPhail 2000; Jones et al. 2012a). Phenotypic divergence between species within each pair has occurred largely in parallel among the replicate pairs [that is, the phenotypes evolved in the same direction from a common ancestral species (Conte et al. 2012), and individuals of the same ecotype from different lakes strongly resemble one another (Schluter and McPhail 1992; Schluter and Nagel 1995; McKinnon and Rundle 2002; Gow et al. 2008)].

Here, we used a quantitative trait locus (QTL) approach to map many continuously varying, quantitative traits, as well as a few discrete traits that have diverged in parallel in the species pairs. This approach is a necessary first step in our effort to determine the frequency of gene reuse in this system because it provides the requisite locations of genetic factors underlying repeated phenotypic evolution, and the phenotypic effect sizes of these loci (Lynch and Walsh 1998; Broman and Sen 2009; Conte et al. 2012). Subsequent studies will address whether chromosomal regions that repeatedly underlie parallel phenotypic evolution in the two populations are due to mutations in at the same genes or different linked genes. However, our QTL results provide an interim estimate of gene reuse based on a large number of traits. We discuss the potential effects of this limitation on the interpretation of our results in Discussion.

In contrast to most previous studies, we used identical methods to simultaneously cross, raise, phenotype, and genotype fish, as well as to conduct linkage and QTL mapping. In both cases, we raised the F2 hybrids in controlled, seminatural ponds, which allowed natural expression of the focal phenotypes. To measure QTL reuse, we implemented an Akaike information criterion (AIC) model selection approach to distinguish among alternative models of the effects of individual chromosomal regions on phenotypic divergence in the two species pairs. This allowed us to determine whether a QTL had parallel effects, an effect in one of the pairs but not the other, or effects in opposite directions in the two pairs. As a second measure of QTL reuse during parallel evolution, we calculated similarity between species pairs in the proportional contributions of QTL to trait differences, using the method of Conte et al. (2012). Finally, we tested whether the frequency of QTL reuse increases with their phenotypic effect sizes, as predicted by theory (Orr 2006).

Materials and Methods

Ethics statement

G.L.C. is certified by the Canadian Council on Animal Care (CCAC)/National Institutional Animal User Training (NIAUT) Program; certificate number 4061-11. Permission for collections of wild threespine sticklebacks used herein was granted by the following permits: British Columbia Ministry of the Environment permit numbers NA/SU08-42033 and NA/SU09-51805; Fisheries and Oceans Canada SARA permit number SECT 08 SCI 002 and SARA-116. Permission to care for and use threespine sticklebacks for the studies herein was granted by the University of British Columbia (UBC) Animal Care Certificate A07-0293 and the Fred Hutchinson Cancer Research Center Institutional Care and Use Committee protocol 1797.

Genetic crosses and experimental ponds

In 2009, we used wild-caught adult fish to make two in vitro interspecific crosses, one using fish from Paxton Lake and the other using fish from Priest Lake. Both crosses involved a limnetic female and a benthic male. We stored their bodies in 95% ethanol for DNA analysis. We reared the resulting F1 hybrids in the laboratory. On May 2, 2010 we randomly selected 35 F1 hybrid adults (19 female and 16 male) from the Paxton cross and 25 F1 hybrid adults (12 female and 13 male) from the Priest cross. We took a sample of caudal fin tissue from each individual F1 hybrid for DNA analysis and then released them into two separate experimental ponds (one for the Paxton cross and one for the Priest cross) at the UBC pond facility. These ponds (25 × 15 m surface area) were designed to harbor both benthic and limnetic habitat and contained a sloping shallow zone and a deep open-water zone (6 m deep) (Arnegard et al. 2014). To establish a natural prey base, we inoculated the ponds with macrophytes, sediments, and water full of aquatic insects, mollusks, and plankton from Paxton Lake. We did this once in the spring of 2009 (a year before releasing our F1 hybrids) and once in the spring of 2011. We additionally added 1.25 kg of a 25.5:1 mix of 50% pure KNO3:KH2PO4 in the spring of 2009 and again in the spring of 2010. After release, the F1 hybrids were allowed to mate freely with their full siblings in the ponds throughout the breeding season. The following year, on September 14, 2011, we collected 407 adult F2 hybrids from the Paxton Lake cross and 324 adult F2 hybrids from the Priest Lake cross. We euthanized F2 hybrids using buffered MS222 and then took a sample of caudal fin tissue from each individual F2 for DNA analysis. Then, we fixed each F2 hybrid body in 10% formalin for morphological measurements. During the same summer, we collected an additional 230 F2 hybrids from the Paxton Lake cross and 92 F2 hybrids from the Priest Lake cross for a separate study. These F2 hybrids were not included in the QTL mapping stage of this study but were used to construct the linkage map.

Wild-caught benthic and limnetic samples

To enable us to determine whether or not our focal phenotypes diverged in parallel, we obtained high-quality photos of Alizarin-Red–stained, wild-caught benthic and limnetic specimens from Paxton and Priest lakes. From these collections, made in the spring of 2005 (Ingram et al. 2012), we used 25 benthics and 21 limnetics from Paxton Lake and 36 benthic and 22 limnetics from Priest Lake. Since the Priest limnetic sample contained no females, we supplemented the collection with 23 additional Alizarin-Red–stained wild-caught Priest limnetics (10 female) that were collected, stained, and photographed in 1999 by J. Gow.

Phenotype measurements

We stained the F2 specimens with Alizarin Red, following the methods of Peichel et al. (2001) and then took high-resolution lateral photographs, with a ruler in each photograph for scale. All of the following steps were done separately for the wild-caught benthic and limnetic collection and for the F2 hybrid collection. Using tpsDig (Rohlf 2010), we digitized and scaled 26 morphological landmarks (Supporting Information, Figure S1) on the photos of the specimens. Photos were analyzed in random order. We measured centroid size as the square root of the sum of squared distances of the 26 landmarks from their centroid. We then performed generalized Procrustes superimposition on the x- and y-coordinates of the scaled landmarks using the R package “shapes” (Dryden 2013), resulting in 52 landmark coordinates that we analyzed as distinct traits. To correct for specimen bending, we followed the approach of Albert et al. (2008).

We scored five skeletal meristic traits (i.e., countable quantitative traits: number of lateral plates along the right side of the body; presence/absence of first and second dorsal spines; the number of long and short gill rakers on the first gill arch on the left side of the body) (Figure S1) using the fixed and stained F2 specimens. In the absence of the wild-caught reference fish specimens, we scored meristic traits using their photos. However, since photos do not show the gill rakers, we could not count the long and short gill rakers on the first gill arch for the wild-caught benthic and limnetic samples, as was done for the F2 hybrids. Instead we used counts taken by Ingram et al. (2012) of the total gill raker number on the first gill arch for the same individuals. For the 23 additional Priest limnetic fish, no gill raker counts were available, and thus, they were left out of the test of parallelism in gill raker divergence.

We tested for and removed significant outlier data points for all traits using the function “outlierTest” in the R package “car” (Fox et al. 2013). F2 hybrids that were standard length outliers were dropped from the study (four Paxton individuals and one Priest individual).

Identifying parallel phenotypic evolution

We classified divergence in a trait as “parallel” when the ecotype difference in the trait was in the same direction in both lakes (i.e., benthics had a higher mean than limnetics in both lakes, or vice versa), though not necessarily of the same magnitude. We classified divergence in a trait as “opposite” when the ecotype difference was in opposite directions in the two lakes (i.e., benthics had a higher mean than limnetics in one lake and a lower mean than limnetics in the other). If the ecotypes differed in a trait in only one of the two lakes, we classified divergence in the trait as “single lake.” Finally, if the species did not differ in a trait in either lake, we classified divergence in the trait as “neither lake.” For each trait, we tested these scenarios by fitting five linear models to phenotypes of our wild-caught benthics and limnetics from both lakes and then deciding which fit the data best (Table S1). The models were as follows.

Model 1, “same effect,” was a linear model that fitted the given trait to the explanatory variable ecotype (benthic vs. limnetic). Model 2, “different effect,” included the ecotype variable and its interaction with lake (Paxton vs. Priest). Including the interaction allowed the detection of a difference between lakes in the magnitude and direction of the difference between the two ecotypes. In model 3, “effect in Paxton only,” an explanatory variable was fitted that constrained the benthic and limnetic species of Priest Lake to the same mean, while allowing the means to differ in Paxton Lake. The reverse was done in model 4, “effect in Priest only.” Finally in model 5, “no effect,” the given trait was fitted to a constant, which constrained benthics and limnetics from both lakes to have the same mean. All five models included sex as a covariate.

We used the AICc value to determine the best model for each trait and then grouped the traits accordingly into the four divergence categories. Trait divergence was classified as parallel either if model 1 was the best or if model 2 was the best and the trait difference between the two ecotypes was in the same direction in the two lakes. Traits were classified as single lake if either model 3 or 4 was the best. Trait divergence was classified as opposite if model 2 was the best and the effect of species was in opposite directions in the two lakes. Finally, a trait was classified as divergent in neither lake if model 5 was the best.

For 15 traits, more than one trait divergence category fit the data nearly equally well. That is, the ΔAICc value between the best and second best models was <2 (Burnham and Anderson 2002) and the second best model represented a different trait divergence category than the best model (Table S1). These 15 traits were left out of all calculations and analyses in which trait divergence category was a variable. Finally, because the gill raker counts for the wild-caught reference fish were of the total number on the first gill arch, rather than the subdivided counts of long and short rakers on the first arch, as was scored in our F2 hybrids, the trait divergence category determined for the total number of gill rakers was inferred to be the trait divergence category of the subdivided counts as well. However, when calculating the proportion of traits in each trait divergence category (parallel, single lake, or opposite), only the total gill raker count was considered (therefore, N = 57 rather than N = 58 traits for those calculations).

Single nucleotide polymorphism genotyping

We isolated genomic DNA from caudal fin tissue of the 4 F0 progenitors, 60 F1 hybrids and 1057 F2 hybrids (407 + 230 from the Paxton cross and 324 + 92 from the Priest cross) using either Proteinase K digestion, phenol-chloroform extraction, ethanol precipitation, and resuspension of the precipitated DNA in 30 μl of TE buffer (10 mM Tris, 1 mM EDTA, pH 8.0), or the DNeasy 96 Blood and Tissue Kit (Qiagen), using only 30 μl of buffer AE for the first elution. We then diluted an aliquot of each sample using TE buffer to a DNA concentration between 3 ng/μl and 150 ng/μl, based on the PicoGreen assay (Life Technologies).

We genotyped all F0, F1, and F2 individuals using Illumina’s GoldenGate assay and a custom multiplex oligonucleotide pool developed for a recently published collection of single nucleotide polymorphisms (SNPs) (Jones et al. 2012a). We found 430 of these SNPs to be polymorphic in at least one of our crosses (246 were polymorphic in the Paxton cross and 318 were polymorphic in the Priest cross, 134 of which were polymorphic in both). See Table S2 for the identities, genomic locations, and National Center for Biotechnology Information (NCBI) identification numbers for all 430 SNP markers. The Illumina Sentrix Array Matrices used for genotyping were processed at the Genomics Shared Resource of the Fred Hutchinson Cancer Research Center. We scored genotypes from the raw data using GenomeStudio software (Illumina).

Linkage mapping

We created a linkage map with JoinMap ver. 3.0 (Ooijen and Voorrips 2002), coding F2 hybrid genotypes according to the “cross-pollinator” population code for outbred crosses between two diploid parents. To determine F1 parentage of each F2 hybrid, we used the R package “MasterBayes” (Hadfield 2013) to reconstruct pedigrees based on the full SNP dataset. When creating the linkage map, we only included F1 × F1 families containing at least 10 F2 hybrids. This included 268 F2 hybrids from the Paxton cross and 261 F2 hybrids from the Priest cross, some of which were not part of the QTL mapping study, as noted above.

To estimate a linkage map based on all families, we used JoinMap ver. 3.0 to compute all obtainable pairwise recombination fractions and associated base 10 logarithm of odds (LOD) scores between SNP markers for each F1 × F1 family (hereafter “family”) separately. We then combined the pairwise recombination fractions from the different families into a single data file and used JoinMap to produce a single combined Paxton–Priest linkage map. Using a similar procedure, we also created separate linkage maps for each lake. We detected all the same QTL in each lake whether we used the combined map or the separate map for that lake (data not shown). Therefore, we proceeded with the use of the combined map for the remaining analyses. Our combined linkage map had a total genetic length of 876.68 cM. It contained SNP markers every 2.15 cM on average, which translates to ∼1.14 Mb of physical distance based on the reference stickleback genome assembly (Broad S1, February 2006) (Jones et al. 2012b).

Identifying candidate QTL

To identify a set of chromosomal regions at which to conduct tests of genetic parallelism, we carried out three QTL scans to identify those chromosomal regions that had a phenotypic effect on a given trait in at least one of the lakes. These we termed “candidate QTL.” Only parallel phenotypic traits were used in these analyses. Each of the three scans involved interval mapping using Haley–Knott regression via the “scanone” function in R/qtl and included family identity and sex as covariates. We used F2 genotype coding (Broman and Wu 2013), in which case scanone detects additive and/or dominance components of genotypes when testing for QTL. The first scan used only the F2 hybrids from the Priest Lake cross (N = 323). The second scan used only the F2 hybrids from the Paxton Lake cross (N = 403). The third scan used the F2 hybrids from both crosses and included a genotype × cross interaction as a covariate. For simplicity, we grouped all F2 hybrids from singleton families into a single pseudofamily. This pseudofamily consisted of 20 F2 hybrids from the Priest Lake cross and 24 F2 hybrids from the Paxton Lake cross. Results did not change when we coded F2 hybrids from singleton families into their own family instead. For each trait, we performed 10,000 permutations to determine the genome-wide LOD thresholds for significant QTL at the α = 0.05 and α = 0.01 levels. We present detailed results below for the 0.05 level and then describe how they are modified when we use the 0.01 level instead. We did not employ more stringent thresholds to account for multiple traits because our goal was to determine the frequency of gene reuse on a per-trait basis with conventional significance levels.

Thirty-nine of 40 candidate QTL discovered in the combined scan were also detected in one or both of the single-lake scans, as indicated by overlapping 1.5 LOD confidence intervals. In this case, we used the QTL position from the combined scan as our candidate QTL as it offered a fixed position at which to test for parallelism. Ten additional candidate QTL were detected in the Paxton Lake scan and 8 were detected in the Priest Lake scan. All detected candidate QTL are shown in Table S3, Table S4, and Table S5.

Genetics of parallel evolution

We classified the effects of a QTL as parallel when its phenotypic effect was in the same direction in both lakes (i.e., F2 hybrids with two benthic alleles at the QTL had a higher mean than F2 hybrids with two limnetic alleles in both lakes, or vice versa), though not necessarily of the same magnitude. We classified the effects of a QTL as opposite when its phenotypic effect was in opposite directions in the two lakes (i.e., F2 hybrids with benthic genotypes had a higher mean than F2 hybrids with limnetic genotypes in one lake and the opposite in the other lake). If the phenotypic effect of a QTL was present in only one of the lakes, we classified the effect of the QTL as single lake. We tested these scenarios for each candidate QTL and corresponding trait, by fitting five linear models to the trait values of F2 hybrids from both lakes combined, and then deciding which fit the data best (Table S6).

To fit the linear models, we first converted genotype information to additive and dominance scores, reflecting the additive and dominance components of genotype effects on the trait. The additive score varied between 0 and 1 and reflected the estimated proportion of the genotype inherited from the benthic grandparent. The additive score was calculated as 0.5 – P(AA)/2 + P(BB)/2, where P(AA) is the probability that the genotype at a chromosome position is homozygous limnetic, and P(BB) is the probability it is homozygous benthic. The dominance score varied between 0 and 0.5 and reflects half the estimated probability that the genotype is heterozygous. The dominance score was calculated as P(AB)/2, where P(AB) is the probability the genotype is a heterozygote. QTL effects were evaluated with linear models that included both additive and dominant genotype variables as main effects. Genotype probabilities were calculated using the R/qtl function “calc.genoprob” (Broman and Wu 2013).

In model 1, “same effect,” we fitted the trait measurements with a linear model that included the additive and dominance effects of QTL genotype. Model 2, different effect included both the main effects of QTL genotype and the interaction between the additive score and lake. The presence of the interaction fits a different effect of the additive component in the two lakes. In model 3, “effect in Paxton only,” the data were fitted to a modified genotype variable that allowed for differences in trait means between QTL genotypes in Paxton Lake but constrained different Priest Lake genotypes to have the same mean. The reverse was done in model 4, “effect in Priest only.” Finally in model 5, “no effect,” the effects of QTL genotype were dropped completely. All models included family and sex as covariates.

We then grouped the 58 candidate QTL into the three QTL effect categories based on which model had the lowest AICc value, which we term the “best model.” QTL were classified as parallel if either model 1 was the best or model 2 was the best and the effect of the QTL was in the same direction in the two lakes. QTL were classified as single lake if either model 3 or 4 was the best. QTL were classified as opposite if model 2 was the best and the effect of the QTL was in opposite directions in the two lakes. Model 5 was never the best, so all QTL were accounted for by the first 4 models. For 15 of the candidate QTL, more than one QTL effect category fit the data nearly equally well, as judged by an AICc difference <2 (Table S6). These 15 candidate QTL were left out of all calculations and analyses in which QTL effect category was a variable.

QTL reuse and pleiotropy

The proportion of traits whose QTL are parallel may be a biased estimate of genetic parallelism if the underlying genetic changes are pleiotropic, affecting multiple traits. We carried out three additional procedures to minimize such bias. First, we inspected correlations between traits in the F2 individuals to assess the extent to which traits vary independently (Figure S2 and Figure S3). Second, we conservatively treated all QTL on the same chromosome as though they represented a single QTL and measured parallelism between lakes as the proportion of traits mapping to that chromosome whose QTL had parallel, single lake, or opposite phenotypic effects. This procedure counts each chromosome and QTL only once when calculating the genome-wide average proportion of parallel QTL and eliminates bias if each chromosome indeed has just one causative gene. Third, we repeated our phenotypic and genetic model selection analyses on uncorrelated principal components of phenotypic variation in the F2 hybrids rather than the original traits. Although the total number of principal components must equal the number of traits, any suite of traits affected by the same underlying pleiotropic gene or genes should covary in the F2 hybrids. In this case, the majority of genetic variation in the F2 hybrids will be captured by a reduced number of principal components that map to detectable QTL.

Our principal component analysis (PCA) was conducted on the 32 parallel phenotypic traits in F2 individuals from Paxton and Priest lakes using the correlation matrix. Here we used total number of gill rakers rather than the subdivided counts. F2 values were first corrected for mean differences between sexes and lakes. Only individuals with no missing phenotype data were included in the PCA (396 Paxton F2 hybrids; 317 Priest F2 hybrids). We first determined whether each of these 32 principal component phenotypes diverged in parallel in the pure-species fish from the two lakes using the model selection technique described above in the Identifying parallel phenotypic evolution subsection. To obtain the principal component phenotypes for pure-species fish, we corrected for differences between sexes and lakes as was done for F2 hybrids, and we also corrected for differences between the means of pure-species and F2 fish. We then projected the pure-species fish onto the F2 principal components. Only individuals with no missing phenotype data were included in the PCA (30 Paxton individuals; 55 Priest individuals). For the 17 parallel principal components, we then obtained a set of 25 candidate QTL (Table S7) using the methods described in the Identifying candidate QTL subsection above. Finally, we used the model selection technique described in the Genetics of parallel evolution subsection above to classify principal component QTL effects as parallel, single lake, or opposite. In a modification of this third approach, we also carried out the model selection analysis only on the first 18 principal components (rather than all 32), which cumulatively accounted for 89.3% of the phenotypic variation in the F2 cross (Table S7). This approach should reduce bias by reducing redundancy caused by pleiotropy, and it also ignores QTL underlying principal components having little phenotypic variation in the F2 hybrids.

Proportional similarity of QTL use

In a separate approach to measuring genetic parallelism, we estimated the proportional similarity of QTL use (Conte et al. 2012) underlying each trait represented in our candidate QTL dataset (N = 26 traits) by first fitting multiple QTL models to parallel phenotypic traits using the R/qtl function “fitqtl” (Broman and Wu 2013) (multiple QTL mapping, MQM; Table S8). We did this separately for the two lakes. We first retested each candidate QTL and its corresponding trait one at a time and dropped any QTL that were not significant at α = 0.05. These models included family and sex as covariates. The effects of surviving QTL were then estimated by entering them into a multiple QTL model that included the main effects of those QTL genotypes, as well as family and sex as covariates. Nonsignificant QTL were assumed to have zero effect.

We calculated the proportional similarity of QTL use underlying each trait following the methods of Conte et al. (2012). For each lake separately, the percent of the phenotypic variance explained by QTL (PVE) of all QTL included in the multiple QTL model for a given trait were scaled so that their sum was equal to 1, resulting in proportional contributions of each QTL to the phenotype (Table S8). We then calculated proportional similarity as the overlap in the distribution of proportional contributions; PS = Σimin(pi1, pi2), where pi1 and pi2 are the proportional contributions of QTLi in the two lakes. Because this approach focuses on the extent to which the same loci are repeatedly involved, overlaps in the proportional contributions of loci are counted regardless of whether their phenotypic effects are in the same direction or not.

QTL reuse and effect size

To test the relationship between effect size and QTL reuse, first we extracted the largest effect QTL for a given phenotypic trait in each lake (traits without at least one QTL in both lakes were not considered). We used PVE as our measure of effect size. We then scored the trait according to whether the QTL was the same (occurred at the same genomic location) or different in the two lakes. This was repeated for every phenotypic trait that had diverged in parallel between the Priest and Paxton lake pairs (15 traits in total fit the criteria). We determined PVE for each candidate QTL in each lake separately by fitting each QTL to its corresponding trait in linear models as described above. These models included family and sex as covariates. We calculated PVE as the absolute value of the difference in the residual sum of squares explained by the full model and a reduced model from which the QTL was dropped divided by the total sum of squares explained by the full model. The PVEs of candidate QTL that were not significant at α = 0.05 were assumed to be 0. For each parallel phenotypic trait that had at least one significant QTL in each lake, we then asked whether the largest effect QTL underlying that trait was the same in both lakes or not.

QTL reuse and genotype information

We tested whether genotype information explained any variation in QTL results. We used entropy to measure the proportion of missing genotype information, obtained using the function “plot.info” in R/qtl (Broman and Wu 2013) (Figure 1). Lower entropy indicates greater genotype information. Entropy was calculated directly for QTL occurring at SNP markers, and using interpolation when QTL occurred between two SNPs. We then asked whether single-lake QTL were associated with larger differences in entropy between the lakes than QTL with an effect in both lakes (parallel or opposite), using a Wilcoxon rank-sum test. Fifteen candidate QTL were left out of this analysis because more than one QTL effect category fit the data nearly equally well. The analysis included the remaining 43 candidate QTL underlying traits that evolved in parallel.

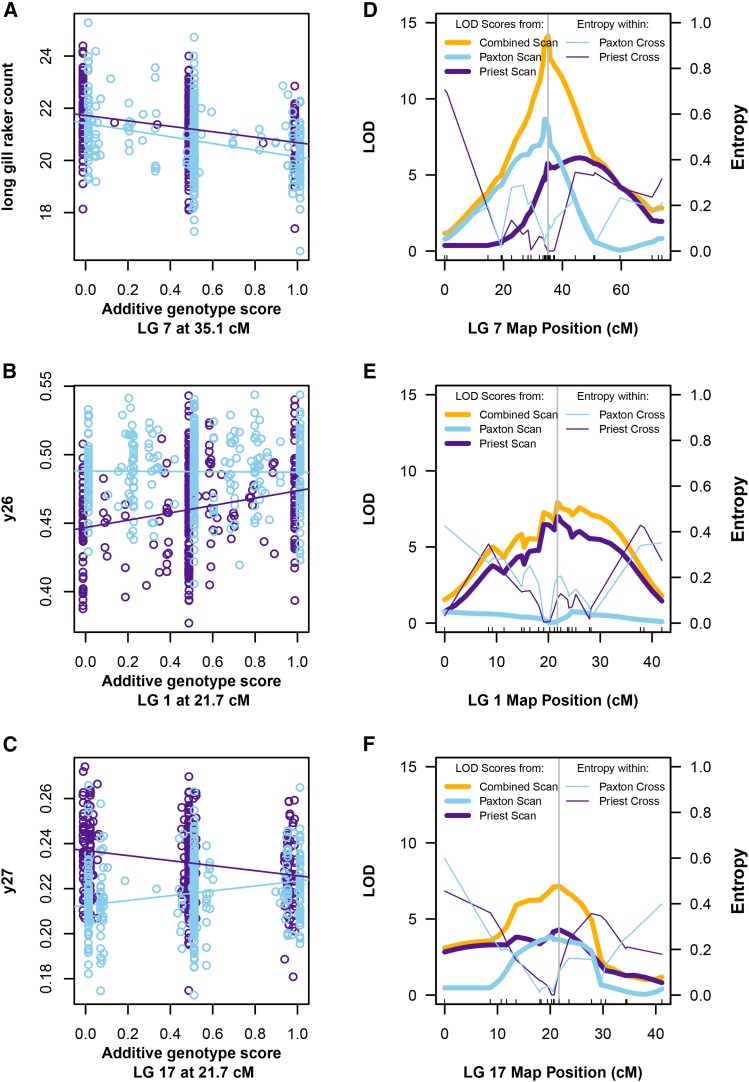
Figure 1.

Figure 1

Open in a new tab

Examples of QTL with parallel, single-lake, and opposite effects. (A–C) F2 phenotypes from the Paxton Lake cross (light blue) and the Priest Lake cross (purple) are shown on the vertical axes. Additive genotype scores at candidate QTL are shown on the horizontal axes, with 0 indicating two limnetic alleles, 1 indicating two benthic alleles, and 0.5 the heterozygote. Values in between these categories indicate uncertain genotypes (see Materials and Methods). Lines represent the fitted values of linear models fitted to the phenotype and genotype data for each lake (light blue, Paxton Lake cross; purple, Priest Lake cross). F2 family identity and sex were covariates in fitted models. Phenotypic measurements shown here are corrected for family identity. (D–F) For the same three QTL (one QTL per row), the plots in the right column show the LOD profiles (left vertical axis and bold lines) from the three distinct QTL scans across the entire linkage group on which the QTL was detected (horizontal axis). They also show the entropy scores (an index of missing genotype information) for each lake’s cross across the entire linkage group (right vertical axis and nonboldface lines). The positions of SNPs markers in the combined Paxton and Priest linkage map are depicted by tick marks. The vertical gray line represents the position of the peak marker in the combined scan (gold).

Data availability

File S1 contains phenotype data for all F2 hybrids, all pure benthics and all pure limnetics from Paxton and Priest Lakes. File S2 contains all F0, F1 and F2 SNP genotypes for all families in the Paxton Lake cross. File S3 contains all F0, F1 and F2 SNP genotypes for all families in the Priest Lake cross.

Results

Parallel phenotypic evolution

We found that of 42 traits assigned to a divergence category, 32 (76.2%) diverged in parallel in the two pairs. Divergence in the other 10 traits was nonparallel, with 5 (11.9%) divergent in only a single pair and 5 divergent in opposite directions in the two pairs (Table S1). Thus, the majority of morphological traits diverged in parallel between the species pairs, though evolution in a substantial number of traits has been nonparallel. For the remainder of the study we focused on the genetic basis of the traits that diverged in parallel, thereby allowing us to estimate the repeatability of the genetics of adaptation.

Genetics of parallel evolution

We performed QTL mapping of the 33 phenotypic traits that diverged in parallel (33 traits rather than 32 due to separation of gill raker counts into long and short gill raker counts). We detected a total of 58 QTL that had an effect in one or both pairs underlying 26 of the 33 traits (Figure 1 and Figure 2; Table S3, Table S4, and Table S5). These 58 QTL represent candidate chromosomal positions at which we subsequently tested for parallel QTL effects.

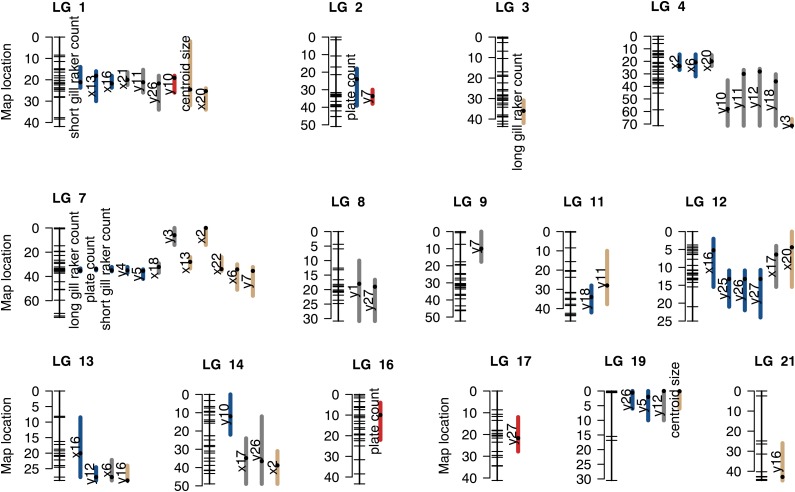
Figure 2.

Figure 2

Open in a new tab

Map of candidate QTL. Map of 58 candidate QTL (i.e., QTL with an effect in one or both lakes). Linkage groups on which QTL were detected are shown. For each, the positions of SNPs markers in the combined Paxton and Priest linkage map are depicted by tick marks on the left. Colored bars span the 1.5-LOD confidence intervals of candidate QTL. Black dots within bars represent the peak marker position. The phenotype affected by each candidate QTL is indicated to the left of its bar. Colors of bars represent the “QTL effect” category, as follows: parallel effects, blue; effect in only one lake, gray; and opposite effects, red. Tan colored bars represent the candidate QTL for which more than one QTL effect category fit the data nearly equally well.

Figure 1 shows examples of classified QTL and traits illustrating the three model selection outcomes: parallel, single lake, and opposite. The number of long gill rakers in F2 hybrids decreases with an increasing number of benthic alleles at a candidate QTL on linkage group (LG) 7 in parallel in both species pairs (Figure 1A). The trait “landmark y26” (the y-coordinate of a landmark placed on the dorsum of the trunk over the pectoral fin midpoint) increases with an increasing number of benthic alleles at a candidate QTL on LG 1 in Priest Lake but not in Paxton Lake (Figure 1B). The trait “landmark y27” (the y-coordinate of a landmark placed at the posterior insertion of the dorsal fin at the first soft ray) changes with the genotype at a candidate QTL on LG 17 in both pairs, but in opposite directions (Figure 1C).

Of the 43 candidate QTL classified into QTL effect categories, representing 23 parallel phenotypic traits, 21 (48.8%) had parallel effects in the two pairs (Figure 2; Table S6). That is, almost half of these QTL that underlie parallel phenotypic evolution had phenotypic effects in the same direction in crosses from both lakes, though not necessarily of identical magnitudes. A slightly smaller fraction (41.9%, N = 18) had an effect in one lake but not the other. Finally, a minority (9.3%, N = 4) had phenotypic effects in opposite directions in the two pairs (Figure 2; Table S6). Using a more stringent significance threshold of α = 0.01 revealed similar proportions of QTL (N = 18) with parallel (67%; N = 12;), single lake (22%; N = 4), and opposite effects (11%; N = 2;), suggesting that the results are robust to significance threshold.

QTL reuse and pleiotropy

Many classified QTL were located in clusters on the same chromosomal regions (Figure 2). It is possible that multiple phenotypes map to the same locations because of the pleiotropic effects of a smaller number of loci. We carried out three checks to ensure that overcounting of QTL did not bias our results. First, we found that most, but not all, correlations between parallel traits in the F2 hybrids were low (Figure S2 and Figure S3). Second, when we reduced the data to 13 QTL groups by combining all QTL on the same chromosome, we found that the average proportions of parallel, single lake, and opposite effects per chromosome were similar to the proportions based on the separate QTL (41.5% ± 9.6% SE parallel, 38.1% ± 10.1% SE single lake, and 20.3% ± 10.5% SE opposite effects; Figure S4). Third, we repeated our genetic analysis using uncorrelated principal components rather than the original traits. Of the 32 principal components, we mapped the 17 principal components that were found to be phenotypically parallel in the two lakes, which is fewer than the original number of parallel traits (N = 32). This analysis identified 25 candidate QTL, of which 16 could be classified using our model selection technique (Table S7). Of these, the majority had parallel effects (62.5%, N = 10), a minority had an effect in one lake but not the other (37.5%, N = 6), and no QTL had effects in opposite directions. Interestingly, we were able to identify QTL for principal components that explained relatively little of the phenotypic variance in the F2 crosses (Table S7). However, in a modification of this procedure, we considered only the 18 principal components that accounted for the first 90% of cumulative phenotypic variance in F2’s. Of the 18, only 13 were phenotypically parallel and they mapped to 15 QTL that could be classified using model selection. The results were similar to the previous analysis: most QTL had parallel effects (66.7%, N = 10), a minority had single lake effects (33.3%, N = 5), and none had opposite effects (Figure S5). The similarity of the results of these varied approaches suggest that trait correlations caused by pleiotropy have not greatly biased the results based on single traits.

Proportional similarity of QTL use

Across the 26 traits that had undergone parallel phenotypic evolution, and for which QTL were detected (Table S8), average proportional similarity of QTL use was 0.38 ± 0.07 SE. Whereas the frequency of QTL with parallel effects reflects how commonly QTL have phenotypic effects in the same direction in both pairs, proportional similarity of QTL use measures the similarity of the full distribution of QTL effects of a trait in the two pairs (Conte et al. 2012).

QTL reuse and effect size

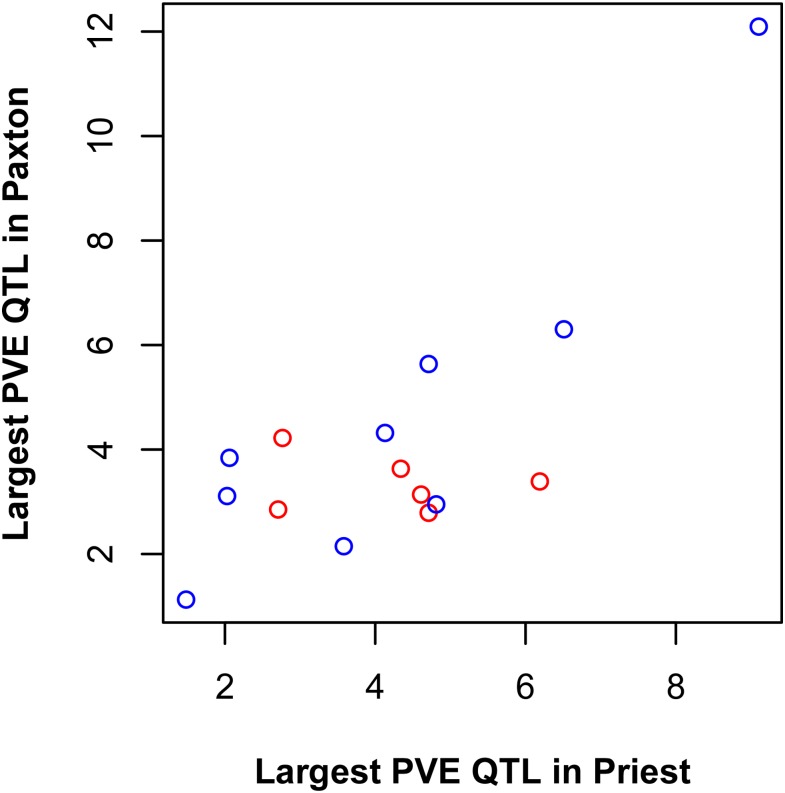
To test the relationship between effect size and parallelism of QTL effects, we asked whether the largest effect QTL was in the same or different genomic locations in the two pairs for each parallel phenotypic trait having at least one QTL in each pair (N = 15). We assumed that phenotypic effect sizes of QTL are positively correlated with fitness effect sizes (Orr 2006) and used PVE as our measure of effect size. We predicted that the two QTL should be the same QTL (occur at the same location) more often when their effects are both large than when their effects are both small. However, we found that the largest effect QTL for individual phenotypic traits were no more likely to be the same in both pairs when the mean of their effect sizes was relatively large than when the mean of their effect sizes was relatively small (t = −0.69, d.f. = 9.31, P = 0.51) (Figure 3). We did, however, observe a tantalizing trend, whereby the two traits with the largest-effect QTL in both pairs indeed mapped to the same genomic location (Figure 3).

Figure 3.

Figure 3

Open in a new tab

QTL effect size and genetic parallelism. The horizontal axis shows the percent of the phenotypic variance explained (PVE) by the largest effect QTL in Priest Lake underlying each trait having at least one QTL in both lakes (N = 15 traits). The same for Paxton Lake is shown on the vertical axis. Blue dots represent cases where the QTL is the same (maps to the same genomic location) in both lakes. Red dots represent cases where the QTL is different (maps to different genomic locations) in the two lakes.

QTL reuse and genotype information

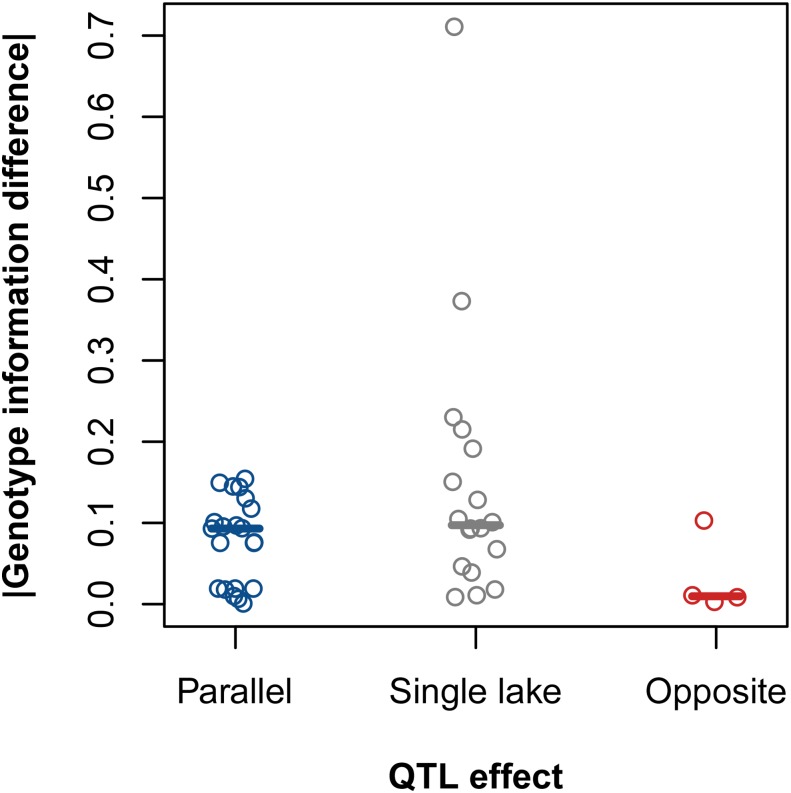
We tested whether classification of QTL as single lake was associated with a difference between species pairs in genotype information, as measured using entropy, compared with QTL detected in both lakes (parallel or opposite) (Broman and Wu 2013). Genotype information may be lower in one pair than the other if, for example, a marker is informative in the grandparents of the cross from one lake but not the other, or if the frequency of missing genotypes at a marker differs between F2 hybrids from the two crosses. This alone could cause differences in apparent QTL effects in the two lakes. We found that differences in the proportion of missing genotype information between the crosses were generally small (0–0.2), and there were no significant overall differences in missing genotype information between QTL detected in both pairs vs. in only one pair (Wilcoxon rank-sum test, W = 293.5, d.f. = 1, P = 0.09) (Figure 4). However, a few large entropy values occurred in the single-lake QTL category; such effects might have caused us to slightly overestimate the frequency of QTL in the single-lake category and underestimate the frequencies of QTL in the other two categories.

Figure 4.

Figure 4

Open in a new tab

Difference in proportion of missing genotype information between crosses by QTL effect category. The absolute value of the difference in genotype information between the Paxton Lake cross and the Priest Lake cross at candidate QTL that were determined to have parallel effects (N = 21; blue), an effect in only a single lake (N = 18; gray), and opposite effects (N = 4; red). Solid lines represent medians for each group.

Discussion

We found that almost half of genomic regions underlying parallel phenotypic differences between the Paxton and Priest lake species pairs themselves had parallel effects. That is, in approximately half the cases, the phenotypic effects of QTL alleles inherited from a given ecotype were in the same direction in the crosses from both pairs. We also found that the average proportional similarity of QTL use underlying parallel phenotypic traits was 0.38 between the two pairs. Because our focal phenotypes have repeatedly evolved in correlation with the environment and are therefore likely to be adaptive (Endler 1986; Harvey and Pagel 1991; Schluter 2000; Losos 2011), these values estimate the repeatability of the QTL underlying parallel phenotypic adaptation. Our study is one of the first to use simultaneous mapping to measure the repeatability of the genetics of adaptation using a large number of parallel traits in wild species.

What explains the prevalence of QTL reuse found to underlie parallel phenotypic evolution between the stickleback species pairs? First, the pairs are recently derived from a common ancestral population (∼10,000–12,000 years ago) (Schluter and McPhail 1992; McPhail 1994; Taylor and McPhail 2000; Jones et al. 2012a). Genetic constraints (e.g., the number and identity of loci capable of producing a particular phenotype), and genetic biases (e.g., beneficial mutation rates, negative pleiotropic consequences, etc.) are likely to be very similar between them, increasing the probability that the same genes will underlie adaptive evolution (Conte et al. 2012). Second, in the case of threespine stickleback, prevalent QTL reuse may be due at least in part to the use of a shared pool of standing genetic variation. Previous evidence suggests that the repeated evolution of many traits in freshwater threespine stickleback populations after colonization by the same marine ancestral form involved natural selection on shared standing genetic variation (Colosimo et al. 2005; Miller et al. 2007; Kitano et al. 2010; Jones et al. 2012b). On the other hand, definitive evidence for de novo mutations at the same locus underlying the independent evolution of similar phenotypes has also been observed in freshwater sticklebacks (Chan et al. 2010). However, we do not yet know the extent to which selection on standing variation vs. de novo mutation contributes to phenotypic evolution in the benthic–limnetic species pairs, in other stickleback populations, or in other species. The population genomic analyses of Jones et al. (2012b) found that ∼35% of divergent genomic regions between a single marine-freshwater stickleback pair occurred at the same loci in multiple marine-freshwater population pairs. In the future, it will be crucial to investigate the relative importance of shared standing variation vs. de novo mutations to repeated phenotypic evolution in three-spine sticklebacks, as well as across independent natural populations in many systems.

Our quantitative, simultaneous-mapping approach using many morphological traits and including many small-effect QTL estimated surprisingly similar levels of gene reuse to those reported in the metaanalysis by Conte et al. (2012). Average proportional similarity of QTL use underlying parallel traits was 0.38 ± 0.07 SE in the current study, which is only slightly lower than the estimate of 0.47 ± 0.15 SE obtained in Conte et al. 2012) calculated from parallel traits mapped in young independent populations belonging to the same species. The metaanalysis estimate is based on multiple study systems, but only one or a few traits per system, in contrast to the present study of a large number of traits in a single system. The similarity of these estimates of QTL reuse based on different approaches suggests that gene reuse may be a robust and pervasive feature of adaptation in natural populations.

Nevertheless, our estimates might also be affected by several biases. First, QTL are relatively large genomic regions containing many genes, and some instances of parallel phenotypic evolution associated with QTL reuse might actually be caused by mutations in different, linked genes. Shared local mutation and recombination rates (Renaut et al. 2014) in addition to clustering of loci involved in local adaptation (Yeaman 2013) may cause different genes within the same genomic regions to sometimes underlie parallel phenotypic evolution. Consistent with this potential bias, other studies have found the highest repeatability of genetic evolution between independently diverged populations when large genomic regions are compared, moderate repeatability when individual genes are compared, and low repeatability when individual nucleotides are compared (Tenaillon et al. 2012; Renaut et al. 2014). However, in those studies it is not known whether the phenotypic effects of genomic changes are parallel. Second, our QTL analysis is based on only one cross per lake and therefore one individual per species. If QTL are polymorphic within species in one or both lakes, we may by chance find a QTL in one lake and not the other due to sampling error. This should occur inversely in relation to degree of allele fixation within each pair and the difference in QTL allele frequency between sympatric species. Nevertheless, our results should give an accurate picture of the probability of QTL reuse when averaged over many QTL. Third, pleiotropic effects of a single genetic change might have caused us to overestimate the number of independent QTL used in our analyses. Indeed, when we conducted QTL mapping of principal components rather than traits, we detected fewer QTL, yet they occurred in largely the same locations in the genome. This suggests that pleiotropy might indeed be present. Nevertheless, several uncorrelated principal components mapped to overlapping genomic locations, suggesting that multiple genetic changes might be present on some chromosomes. Furthermore, despite the possible effects of pleiotropy, accounting for it in our analyses did not greatly change our estimates of QTL reuse. Fourth, we may have missed some QTL with parallel and opposite effects if there was too little genotype information at a locus in one of the crosses but not the other. We found that the single-lake category included a small number of QTL having a large difference between the crosses in the proportion of missing genotype information (entropy differences). It is therefore possible that some parallel QTL have been classified as single-lake QTL in our analysis because of missing genotype information in a given chromosomal region in one of the two crosses. However, based on the range of values observed for QTL with parallel and opposite effects, entropy differences corresponding to single-lake QTL appeared large enough to potentially mislead us in a relatively small number of cases (Figure 4). Fifth, the traits we mapped were mostly continuously varying, quantitative traits, underlain by mostly small effect loci. The closer the effect of a QTL is to a given detection threshold (either slightly above or below it), the less likely it is to be detected twice, because of sampling error. For this reason, small-effect QTL may have a tendency to be miscategorized as having an effect in only a single lake and we may have underestimated proportional similarity of QTL use between lakes. However, if this were the case, we would have expected an enrichment of small effect QTL in the single-lake QTL effect category, which we did not see.

We predicted that the probability of QTL reuse would depend on its effect size, assuming that phenotypic effect size is indicative of fitness effect size. Under fairly broad assumptions, if a new beneficial mutation independently fixes in two identical populations experiencing the same selection pressures, the probability it is the same mutation depends on the number of beneficial mutations available (Orr 2005). The number of available beneficial mutations of large effect is generally small compared with the number of beneficial small-effect mutations (Orr 2006). It follows that when a mutation fixes in two populations, the probability it is the same mutation should be higher when the effect size is relatively large than when it is relatively small. Although Orr (2005, 2006) explicitly considered de novo mutation, the qualitative expectation should still hold when beneficial mutations fix from standing variation as long as large effect beneficial mutations are rarer than those of small effect (Albert et al. 2008). We found no evidence in support of this prediction (Figure 3). However, we observed a tantalizing trend: the two traits having the largest QTL effects in both lakes indeed mapped to the same QTL (Figure 3). Small sample size, a small range of QTL effect sizes, and a noisy relationship between phenotypic and fitness effect sizes might explain why we found no evidence for the predicted effect.

Looking ahead, it will be important to combine forward genetic approaches that link genotypes to phenotypes (i.e., QTL and association mapping) with population genomics studies to identify the specific genetic changes underlying parallel phenotypic changes. Such an approach will also allow use of phylogenetics to determine how often shared standing genetic variation is the cause of genetic parallelism. To date, relatively few population genomic studies provide quantitative estimates of parallel genomic changes, and these find somewhat lower estimates than we have observed. For example, 20% of genes experiencing mutations are shared across independent lines of experimentally evolved Escherichia coli populations adapting to similar environmental conditions (Tenaillon et al. 2012), 17% of divergent SNPs are shared across independent population pairs of stick insects (Soria-Carrasco et al. 2014), and 35% of the divergent genomic regions found in a single freshwater–marine comparison of threespine sticklebacks are shared across multiple freshwater–marine pairs (Jones et al. 2012b). However, while our approach addresses how often and to what extent the same loci underlie parallel adaptive evolution of specific phenotypes, the population genomic studies measure how often the same loci have acquired mutations in association with adaptation to a shared type of environment regardless of the specific phenotypic effects of mutations. A combination of the two approaches will enable fine-scale resolution of the genetics underlying parallel phenotypic evolution.

As we obtain more and better estimates of the repeatability of the genetics of adaptation across many systems, we will be able to ask what factors influence repeatability. For example, future studies should aim to estimate the actual number of genes in which mutations may lead to a particular phenotype, and then begin to dissect the genetic biases that will cause the effective number to be lower (Streisfeld and Rausher 2011). As our understanding of these factors improves, so will our ability to predict the genetics of adaptation.

Supplementary Material

Supporting Information
supp_201_3_1189__index.html (2.9KB, html)

Acknowledgments

We thank N. Bedford and T. Ingram for their assistance in the collection of F2 hybrid fish and C. Sather for performing the SNP genotyping. We are also grateful to R. Svanback and J. Gow for providing wild-caught benthic and limnetic specimens (or photographs of specimens) from their collections. We thank Leonie Moyle and two anonymous reviewers for comments that greatly improved the manuscript. This work was supported by the National Science and Engineering Research Council (NSERC) CREATE training program and a University of British Columbia Zoology Graduate Fellowship (to G.L.C.), as well as grants from the National Institutes of Health (F32 GM086125 to M.E.A., P50 HG002568 to D.M.K. and C.L.P., and R01 GM089733 to D.S. and C.L.P.) and NSERC (D.S.).

Footnotes

Communicating editor: L. Moyle

Supporting information is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.115.182550/-/DC1.

Literature Cited

  1. Albert A. Y. K., Sawaya S., Vines T. H., Knecht A. K., Miller C. T., et al. , 2008.  The genetics of adaptive shape shift in stickleback: pleiotropy and effect size. Evolution 62: 76–85. [DOI] [PubMed] [Google Scholar]
  2. Arnegard M. E., McGee M. D., Matthews B., Marchinko K. B., Conte G. L., et al. , 2014.  Genetics of ecological divergence during speciation. Nature 511: 307–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Broman K. W., Sen S., 2009.  A Guide to QTL Mapping with R/qtl, Springer-Verlag, New York. [Google Scholar]
  4. Broman, K. W., and H. Wu, 2013 QTL: Tools for Analyzing QTL Experiments CRAN: Comprehensive R Archive Network. Available at: http://www.r-project.org.
  5. Burnham K. P., Anderson D. R., 2002.  Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, Springer-Verlag, New York. [Google Scholar]
  6. Chan Y. F., Marks M. E., Jones F. C., Villarreal G., Shapiro M. D., et al. , 2010.  Adaptive evolution of pelvic reduction in sticklebacks by recurrent deletion of a Pitx1 enhancer. Science 327: 302–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Colosimo P. F., Hosemann K. E., Balabhadra S., Villarreal G., Dickson M., et al. , 2005.  Widespread parallel evolution in sticklebacks by repeated fixation of ectodysplasin alleles. Science 307: 1928–1933. [DOI] [PubMed] [Google Scholar]
  8. Conte, G. L., M. E. Arnegard, C. L. Peichel, and D. Schluter, 2012 The probability of genetic parallelism and convergence in natural populations. Proc. R. Soc. B Biol. Sci. 279: 5039–5047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dryden, I. L., 2013 Shapes: Statistical Shape Analysis CRAN: Comprehensive R Archive Network. Available at: http://www.r-project.org.
  10. Endler J. A., 1986.  Natural Selection in the Wild, Princeton University Press, Princeton, NJ. [Google Scholar]
  11. Fox, J., S. Weisberg, D. Adler, D. Bates, G. Baud-Bovy et al., 2013 car: Companion to Applied Regression CRAN: Comprehensive R Archive Network. Available at: http://www.r-project.org.
  12. Gow J. L., Rogers S. M., Jackson M., Schluter D., 2008.  Ecological predictions lead to the discovery of a benthic–limnetic sympatric species pair of threespine stickleback in Little Quarry Lake, British Columbia. Can. J. Zool. 86: 564–571. [Google Scholar]
  13. Hadfield, J., 2013 Masterbayes: ML and MCMC methods for pedigree reconstruction and analysis CRAN: Comprehensive R Archive Network. Available at: http://www.r-project.org.
  14. Harvey P. H., Pagel M. D., 1991.  The Comparative Method in Evolutionary Biology, Oxford University Press, Oxford. [Google Scholar]
  15. Ingram T., Svanbäck R., Kraft N. J. B., Kratina P., Southcott L., et al. , 2012.  Intraguild predation drives evolutionary niche shift in threespine stickleback. Evolution 66: 1819–1832. [DOI] [PubMed] [Google Scholar]
  16. Jones F. C., Chan Y. F., Schmutz J., Grimwood J., Brady S. D., et al. , 2012a A genome-wide SNP genotyping array reveals patterns of global and repeated species-pair divergence in sticklebacks. Curr. Biol. 22: 83–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Jones F. C., Grabherr M. G., Chan Y. F., Russell P., Mauceli E., et al. , 2012b The genomic basis of adaptive evolution in threespine sticklebacks. Nature 484: 55–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kitano J., Lema S. C., Luckenbach J. A., Mori S., Kawagishi Y., et al. , 2010.  Adaptive divergence in the thyroid hormone signaling pathway in the stickleback radiation. Curr. Biol. 20: 2124–2130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Losos J. B., 2011.  Convergence, adaptation, and constraint. Evolution 65: 1827–1840. [DOI] [PubMed] [Google Scholar]
  20. Lynch M., Walsh B., 1998.  Genetics and Analysis of Quantitative Traits, Sinauer Associates, Sunderland, MA. [Google Scholar]
  21. Martin A., Orgogozo V., 2013.  The loci of repeated evolution: a catalog of genetic hotspots of phenotypic variation. Evolution 67: 1235–1250. [DOI] [PubMed] [Google Scholar]
  22. McKinnon J. S., Rundle H. D., 2002.  Speciation in nature: the threespine stickleback model systems. Trends Ecol. Evol. 17: 480–488. [Google Scholar]
  23. McPhail J. D., 1984.  Ecology and evolution of sympatric sticklebacks (Gasterosteus): morphological and genetic evidence for a species pair in Enos Lake, British Columbia. Can. J. Zool. 62: 1402–1408. [Google Scholar]
  24. McPhail J. D., 1992.  Ecology and evolution of sympatric sticklebacks (Gasterosteus): evidence for a species pair in Paxton Lake, Texada Island, British Columbia. Can. J. Zool. 70: 361–369. [Google Scholar]
  25. McPhail J. D., 1994.  Speciation and the evolution of reproductive isolation in the sticklebacks (Gasterosteus) of south-western British Columbia, pp. 399–437 in The Evolutionary Biology of the Threespine Stickleback, edited by Bell M. A., Foster S. A. Oxford University Press, Oxford. [Google Scholar]
  26. Miller C. T., Beleza S., Pollen A. A., Schluter D., Kittles R. A., et al. , 2007.  Cis-regulatory changes in kit ligand expression and parallel evolution of pigmentation in sticklebacks and humans. Cell 131: 1179–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ooijen, J. W., and R. E. Voorrips, 2002 JoinMap: Version 3.0: Software for the Calculation of Genetic Linkage Maps, Plant Research International, Wageningen, The Netherlands. [Google Scholar]
  28. Orr H. A., 2005.  The probability of parallel evolution. Evolution 59: 216–220. [PubMed] [Google Scholar]
  29. Orr H. A., 2006.  The distribution of fitness effects among beneficial mutations in Fisher’s geometric model of adaptation. J. Theor. Biol. 238: 279–285. [DOI] [PubMed] [Google Scholar]
  30. Peichel C. L., Nereng K. S., Ohgi K. A., Cole B. L. E., Colosimo P. F., et al. , 2001.  The genetic architecture of divergence between threespine stickleback species. Nature 414: 901–905. [DOI] [PubMed] [Google Scholar]
  31. Renaut S., Owens G. L., Rieseberg L. H., 2014.  Shared selective pressure and local genomic landscape lead to repeatable patterns of genomic divergence in sunflowers. Mol. Ecol. 23: 311–324. [DOI] [PubMed] [Google Scholar]
  32. Rohlf, F. J., 2010 tpsDig. Department of Ecology and Evolution, State University of New York at Stony Brook, Stony Brook, NY. [Google Scholar]
  33. Schluter D., 2000.  The Ecology of Adaptive Radiation, Oxford University Press, Oxford. [Google Scholar]
  34. Schluter D., McPhail J. D., 1992.  Ecological character displacement and speciation in sticklebacks. Am. Nat. 140: 85–108. [DOI] [PubMed] [Google Scholar]
  35. Schluter D., Nagel L. M., 1995.  Parallel speciation by natural selection. Am. Nat. 146: 292–301. [Google Scholar]
  36. Soria-Carrasco V., Gompert Z., Comeault A. A., Farkas T. E., Parchman T. L., et al. , 2014.  Stick insect genomes reveal natural selection’s role in parallel speciation. Science 344: 738–742. [DOI] [PubMed] [Google Scholar]
  37. Stern D. L., 2013.  The genetic causes of convergent evolution. Nat. Rev. Genet. 14: 751–764. [DOI] [PubMed] [Google Scholar]
  38. Stern D. L., Orgogozo V., 2008.  The loci of evolution: How predictable is genetic evolution? Evolution 62: 2155–2177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Streisfeld M. A., Rausher M. D., 2011.  Population genetics, pleiotropy, and the preferential fixation of mutations during adaptive evolution. Evolution 65: 629–642. [DOI] [PubMed] [Google Scholar]
  40. Taylor E. B., McPhail J. D., 2000.  Historical contingency and ecological determinism interact to prime speciation in sticklebacks, Gasterosteus. Proc. R. Soc. Lond. B Biol. Sci. 267: 2375–2384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Tenaillon O., Rodríguez-Verdugo A., Gaut R. L., McDonald P., Bennett A. F., et al. , 2012.  The molecular diversity of adaptive convergence. Science 335: 457–461. [DOI] [PubMed] [Google Scholar]
  42. Yeaman S., 2013.  Genomic rearrangements and the evolution of clusters of locally adaptive loci. Proc. Natl. Acad. Sci. USA 110: E1743–E1751. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_201_3_1189__index.html (2.9KB, html)
supp_115.182550_182550SI.pdf (4.1MB, pdf)
supp_115.182550_FigureS1.pdf (2.8MB, pdf)
supp_115.182550_FigureS2.pdf (387.3KB, pdf)
supp_115.182550_FigureS3.pdf (387.4KB, pdf)
supp_115.182550_FigureS4.pdf (58.4KB, pdf)
supp_115.182550_FigureS5.pdf (62.9KB, pdf)
supp_115.182550_TableS1.pdf (88.6KB, pdf)
supp_115.182550_TableS2.pdf (146.2KB, pdf)
supp_115.182550_TableS3.pdf (89.1KB, pdf)
supp_115.182550_TableS4.pdf (71.9KB, pdf)
supp_115.182550_TableS5.pdf (89.5KB, pdf)
supp_115.182550_TableS6.pdf (92.1KB, pdf)
supp_115.182550_TableS7.pdf (63.2KB, pdf)
supp_115.182550_TableS8.pdf (84.8KB, pdf)
supp_115.182550_FileS1.csv (252.2KB, csv)
supp_115.182550_FileS2.zip (283.4KB, zip)
supp_115.182550_FileS3.zip (233.4KB, zip)

Data Availability Statement

File S1 contains phenotype data for all F2 hybrids, all pure benthics and all pure limnetics from Paxton and Priest Lakes. File S2 contains all F0, F1 and F2 SNP genotypes for all families in the Paxton Lake cross. File S3 contains all F0, F1 and F2 SNP genotypes for all families in the Priest Lake cross.

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES