The Double-Reduction Landscape in Tetraploid Potato as Revealed by a High-Density Linkage Map

Abstract

The creation of genetic linkage maps in polyploid species has been a long-standing problem for which various approaches have been proposed. In the case of autopolyploids, a commonly used simplification is that random bivalents form during meiosis. This leads to relatively straightforward estimation of recombination frequencies using maximum likelihood, from which a genetic map can be derived. However, autopolyploids such as tetraploid potato (Solanum tuberosum L.) may exhibit additional features, such as double reduction, not normally encountered in diploid or allopolyploid species. In this study, we produced a high-density linkage map of tetraploid potato and used it to identify regions of double reduction in a biparental mapping population. The frequency of multivalents required to produce this degree of double reduction was determined through simulation. We also determined the effect that multivalents or preferential pairing between homologous chromosomes has on linkage mapping. Low levels of multivalents or preferential pairing do not adversely affect map construction when highly informative marker types and phases are used. We reveal the double-reduction landscape in tetraploid potato, clearly showing that this phenomenon increases with distance from the centromeres.

POLYPLOID species constitute a very important group among cultivated crops. Polyploids themselves can be further divided into auto- and allopolyploids, with autopolyploids showing random association between homologous chromosomes and allopolyploids showing nonrandom or preferential pairing during meiosis. Linkage mapping in autopolyploid species remains a challenging exercise despite recent advances in genotyping technology and mapping methodology. Breeding work in many autopolyploid crops has yet to benefit from the use of markers in breeding programs. This is partly due to the lack of software to perform linkage mapping and QTL analysis in polyploids but is also due to the complicated nature of autopolyploid genomes and genetics. The software program TetraploidMap (Hackett and Luo 2003) is a notable exception to this but is constrained by the relatively low numbers of markers it can handle (currently 800 is the maximum) and the need to manually assign marker phase, which may become infeasible with large data sets.

One autopolyploid species in which large advances in genetic analysis have been made is tetraploid potato (Solanum tuberosum L.), in terms of the availability of a high-quality reference sequence (Potato Genome Sequencing Consortium 2011), many published linkage maps (Meyer et al. 1998; van Os et al. 2006; Felcher et al. 2012; Hackett et al. 2013) as well as methods for performing linkage mapping at the polyploid level (Luo et al. 2001; Bradshaw et al. 2004; Hackett et al. 2013). In comparison with other economically important autotetraploid species such as alfalfa, rose, and leek, the pairing behavior of potato is thought to be relatively well understood, with random bivalent pairing during prophase I of meiosis being generally assumed (Swaminathan and Howard 1953; Milbourne et al. 2009). Although a certain proportion of multivalents is known to occur, these are not deemed to occur at a sufficient frequency to merit their inclusion in a pairing model (Bradshaw 2007).

The simplest marker segregation type to map in a tetraploid cross is the simplex × nulliplex marker type, which is expected to segregate in a 1:1 fashion. In a tetraploid, we employ the term simplex × nulliplex to collectively refer to 1 × 0, 3 × 0, 3 × 4, and 1 × 4 markers (with 0 × 1, 0 × 3, 4 × 3, and 4 × 1 markers being nulliplex × simplex). A relabeling of allele dosages is sufficient to convert all these markers to their simpler form. These have traditionally been the markers most favored in tetraploid mapping because of their simple segregation, reliability in genotype calling, and high information content in coupling phase. One important practical advantage is that these markers can be mapped using advanced mapping software developed for diploids such as JoinMap (Van Ooijen 2006), which can efficiently map large numbers of markers as well as providing many checks on map and data quality. Simplex × nulliplex markers also provide the clearest linkage information to cluster markers into separate homologous chromosomes, forming the basis of homolog maps. In our population, simplex × nulliplex markers were also the most abundant marker segregation type. We therefore restricted our analysis to simplex × nulliplex markers, which nevertheless allowed us to map a total of 3273 markers across both parents.

Simplex × nulliplex markers are also the most useful markers to provide direct evidence of one of the observable consequences of multivalent formation, namely, double reduction (DR). In autopolyploid species, pairing may occur between all homologous chromosomes, which can lead to complicated pairing structures during the first meiotic division (Milbourne et al. 2009). In cases where a crossover occurs between two sets of sister chromatids that subsequently migrate to the same pole, it is possible for a chromatid and its recombinant copy (segment) to end up in the same gamete, a situation that can never occur in diploids. For a simplex × nulliplex marker with the segregating allele on the recombinant segment in question, this can lead to a duplex score in that offspring.

By simulating comparable mapping populations genotyped with the same mapped markers, we were able to estimate the rate of multivalent formation that would account for the observed levels of DR. We also performed a simulation study using populations with different rates of multivalent formation and preferential pairing to investigate the effect that the assumption of random bivalent formation has on the estimation of recombination frequency and marker phase.

Materials and Methods

Plant material

An F₁ mapping population of 237 individuals was created from the cross between two tetraploid potato varieties, cultivars Altus (hereafter referred to as parent one, P₁) and Colomba (P₂).

DNA extraction and genotyping

DNA was extracted from leaf material using KingFisher Flex according to the manufacturer’s instructions (Thermo Scientific). The concentration of DNA was measured using a NanoDrop ND-1000 Spectrophotometer (Thermo Scientific), and the DNA concentration was adjusted to ∼50 ng/µl (Vos et al. 2015). For DNA concentrations in the range of 25–50 ng/µl, the sample also was used; samples having concentrations lower than 25 ng/µl were discarded, and DNA isolation was performed again.

The samples were genotyped on the SolSTW Infinium SNP array, which assayed 17,987 SNPs, as described by Vos et al. (2015). Of these SNPs, 4179 also form part of the SolCap SNP array (Felcher et al. 2012). The arrays were processed according to the manufacturer’s protocol at ServiceXS, Leiden, The Netherlands. Each parent was genotyped in duplicate using two biological replicates. A total of 1662 other tetraploid accessions were sampled in a similar fashion, as well as 516 diploid accessions (for use in another study as well as helping marker dosage fitting).

Assignment of dosages

The X and Y allele signal intensities were imported from the Illumina data output into the R programming environment (R Core Team 2015). SNPs were initially filtered so that the average of their total signal intensity (the sum of the X and Y allele signal intensities) over all samples was greater than 0.2. The marker intensities were converted into allele dosages using the fitTetra package for R (Voorrips et al. 2011). Changes to the default settings of the saveMarkerModels function of fitTetra were as follows: p.threshold was decreased from 0.99 to 0.95; peak.threshold was increased from 0.85 to 0.99; and sd.target was set to 0.04, where p.threshold is the minimum P-value required to assign a genotype to a sample; peak.threshold is the maximum allowed fraction of the scored samples that are in one peak; and sd.target is used to specify the maximum nonpenalized SD of the fit on a transformed scale (Voorrips et al. 2011). All diploid and tetraploid samples were included in the fitting because this generally results in a better fit of the dosage classes.

Following fitting with fitTetra, the marker dosage scores were screened to ensure consistency between parental and offspring genotypes. Markers with up to 3% invalid scores (scores that were not expected based on the parental genotypes and bivalent chromosome pairing) were allowed. A high frequency of many invalid scores suggests that either the marker performed poorly, there was some consistent error in dosage assignment, or one or both of the parents had been incorrectly genotyped. Highly skewed markers (P < 0.001) were also removed at this stage.

Marker conversion

Markers that segregated in a 1:1 fashion were relabeled as simplex × nulliplex (or nulliplex × simplex) for mapping and DR analysis. Considering markers whose segregating allele is inherited from P₁, these consisted of triplex × nulliplex, triplex × quadruplex, and simplex × quadruplex markers. For example, a triplex × nulliplex marker is expected to produce 50% dosage 1 and 50% dosage 2 among the offspring, with observable DR scores appearing as dosage 0 (a double copy of the 0 allele from P₁). Relabeling 2 as 0 and 0 as 2 (with the parents relabeled as simplex and nulliplex) achieves the desired result of marker conversion.

Linkage-map construction

Simplex × nulliplex marker data were recoded to JoinMap 4.1 cross-pollinator format (lm × ll). “Impossible” genotypes (invalid scores) were removed before importation into JoinMap. One pair of identical individuals was identified in the data set (similarity of 0.9922); therefore, we removed individual 202. Markers were assigned to linkage groups with a minimum LOD score of 4 (a higher LOD score was used if clusters broke into large subclusters at a higher LOD score). Marker clusters were assigned to physical chromosomes based on the position of markers on the physical sequence (Potato Genome Sequencing Consortium 2011). Mapping was first performed using the groupings from the groupings tree using maximum likelihood (ML). Homologs then were identified by large gaps in the estimated map distances (≥60 cM), which also were often accompanied by a transition in estimated marker phase. Marker data for separate homologs were exported from JoinMap in .loc files and reimported for creation of the homolog maps. After an initial mapping of the homologs, individual 067 was found to contribute unrealistic numbers of recombinations in many linkage groups across both parents and therefore was removed, resulting in a final mapping population of 235 individuals. Mapping was performed using ML with three rounds of map optimization using the default settings for spatial sampling thresholds. Haldane’s mapping function was used to convert recombination frequency estimates to map distances, as has been used previously for linkage-map construction in tetraploid potato (Meyer et al. 1998; Hackett et al. 2013). In a number of cases, we used linkage information from the duplex × nulliplex and simplex × simplex markers to connect subhomolog linkage groups that had poor internal linkage among simplex × nulliplex markers. Map data were exported from JoinMap as text files and imported into MapChart 2.3 (Voorrips 2002) for further plotting.

Comparison of genetic and physical maps

The genetic positions of markers were compared with their physical positions, as defined in Vos et al. (2015). It was found that some markers did not map to the same chromosome as expected from the physical map; a list of such markers is included in Supporting Information, Table S1. The physical position of the centromere boundaries was initially adopted from previously published values (Sharma et al. 2013). These were not found to coincide precisely with the points of inflection on the genetic physical map, following which the approximate centromere bounds were redefined by examinating the aligned genetic physical plots [also referred to as Marey maps (Chakravarti 1991)] and calculating an approximate physical position between marker pairs flanking the points of inflection on these plots (Figure S2). The order of the genetic map was reversed in cases where the genetic maps were found to be inversely ordered with respect to the physical map.

Conversion rate of physical-to-genetic distance

The conversion rate between genetic and physical distance was determined by regressing the genetic positions on the physical positions per homolog arm. The slopes of the regression lines for each homolog arm were tested for equality in an analysis of covariance by introducing, where necessary, up to three dummy variables (to code for the presence or absence of a homolog) per chromosome arm per parent (Andrade and Estévez-Pérez 2014). An average genome-wide estimation of the genetic-to-physical conversion rate was calculated after excluding a single outlying value from the northern arm of homolog 2 of chromosome 1 in parent 1. This genome-wide recombination rate was used to convert the physical map to a pseudointegrated genetic map for use in the simulation studies.

Rates of DR

After recoding the 1:1 segregating marker data, duplex marker scores in the offspring were taken as possible evidence for DR. Duplex scores also can arise as a result of genotyping errors. Therefore, we used a relatively strict criterion to decide whether such scores were evidence of DR: a string of three consecutive duplex-scored markers on a homolog map was required to be considered strong enough evidence for DR. This theoretically could lead to some underestimation of the rates of DR, but the simplex marker density was sufficient that in most cases a DR region would contain at least three (segregating) simplex × nulliplex markers.

A routine was written in R to identify strings of three or more duplex scores. The rate of DR was determined for each marker by counting the number of times it formed part of a DR segment and dividing this by the number of nonmissing values scored for that marker across the population. We then derived the average rate of DR per homologue for 1-Mb windows north and south of the centromeric bounds by calculating the mean rate of DR over all markers within that window. These means were aggregated to give a single average rate of DR per homologue for each 1-Mb window distance from the centromeres across all chromosomes and both parents. The average rate per chromosome was estimated by multiplying the homologue rates by a factor of four.

Simulation of DR and prediction of quadrivalent formation

An approximate “integrated” genetic linkage map was produced using the average cM/Mb conversion rate and physical positions of the simplex markers. Only markers for which the assigned linkage group and physical chromosome corresponded were considered. Marker phase was determined according to the homolog assignment of all markers. Phased marker genotypes and a consensus genetic map position are the basic inputs for the simulation software PedigreeSim (Voorrips and Maliepaard 2012), which simulates (diploid or) polyploid populations with specified levels of multivalents and/or preferential pairing. One thousand separate populations of 235 individuals were generated using the same simplex marker data and approximated map under a range of different fractions of quadrivalents. The algorithm for estimating DR was applied to the simulated data sets, allowing us to deduce the relationship between the rate of DR and the frequency of multivalents underlying meiosis.

Estimation of the rate of preferential pairing

Repulsion-phase simplex marker data can be used to investigate whether preferential pairing occurs because the estimates for recombination frequency in repulsion are expected to differ under disomic and tetrasomic inheritance (Qu and Hancock 2001). We have adapted the approach of Qu and Hancock (2001) to correct for multiple testing using the false-discovery rate (FDR) (Benjamini and Hochberg 1995), confining our analysis to within chromosomes to reduce the overall number of tests (coupling or repulsion linkage has no meaning when marker pairs from separate linkage groups are considered).

For two markers A and B, we define $n_{00}$ as the number of individuals with dosage 0 at both markers, $n_{01}$ as the number of individuals with dosage 0 at marker A and dosage 1 at marker B, and so on. The explicit ML estimator for the recombination frequency r in coupling phase under both disomic and tetrasomic inheritance is invariant, i.e.,

$$\frac{n_{01}+n_{10}}{n_{00}+n_{01}+n_{10}+n_{11}}$$

whereas in repulsion phase the ML estimator under disomic inheritance is

$$r_{\text{disom}}=\frac{n_{00}+n_{11}}{n_{00}+n_{01}+n_{10}+n_{11}}$$

and under tetrasomic inheritance is

$$r_{\text{tetra}}=\frac{2\left(n_{00}+n_{11}\right)-\left(n_{01}+n_{10}\right)}{n_{00}+n_{01}+n_{10}+n_{11}}$$

If the mode of inheritance is tetrasomic, $r_{\text{disom}}$ should never fall below the value of 1/3, whereas in the case of disomic inheritance, $r_{\text{disom}}\in \left[0,0.5\right)$. This forms the basis of an exact binomial test with $H_0:r_{\text{disom}}=1/3$ and $H_1:r_{\text{disom}}<1/3$. Correction for multiple testing was performed using the FDR procedure with α = 0.05, as described in Benjamini and Hochberg (1995).

Simulation of mapping under different rates of quadrivalent formation and preferential pairing

One of the hypotheses we wanted to test was whether bivalent formation predominates in tetraploid potato, as is commonly assumed. We also wanted to see the effect that deviations from this assumption could have on recombination frequency estimates that are based on a bivalent model. In this study, we limited our focus to 1:1 segregating markers. We used PedigreeSim to simulate new mapping populations of 250 individuals, with the fraction quadrivalents varying from 0 to 1 in increments of 0.1. For each setting, 1000 simulated populations were generated. The simulated genome had a single chromosome of 100 cM with 51 simplex × nulliplex markers randomly distributed at positions no closer than 0.1 cM apart and the centromere at 25 cM. The true and estimated recombination frequencies between the first marker and the other 50 markers on the chromosome were recorded, as well as the LOD score and assigned phase (“coupling” or “repulsion”). Recombination frequencies between marker pairs were estimated using ML, for which explicit estimators can be derived in the case of simplex marker pairs (see the preceding section). Phase was determined by choosing the lowest estimate for the recombination frequency in the range $\left[0,0.5\right)$, which we term phasing by the minimum recombination frequency (MINR). This differs from previous studies, where the maximum of the log likelihood (MLL) was used to assign the most likely phase (Luo et al. 2001; Hackett et al. 2013). Negative estimates for r can occur owing to Mendelian sampling variation under weak repulsion linkage. For strongly negative values (r < −0.05), a recombination frequency of 0.499, a LOD score of 0, and phase “unknown” were assigned, and in the case −0.05 ≤ r < 0, the recombination frequency was set to 0, and the LOD score and phase were left unchanged. The recombination frequency estimates were regressed on their true values for both coupling and repulsion phase to evaluate how close to the true value the estimates fell for each pairing scenario. The proportion of correctly assigned phases for coupling- and repulsion-phase markers was also recorded.

Data availability

Genotype data of the 1:1 segregating markers used in this study are provided as supplementary data (Table S5). The genetic map positions of these markers are also provided (Table S6).

Results

Genotyping and dosage assignment

Of the 17,987 SNPs assayed, only 40% were found to be acceptable and segregating in this population (Table 1). Acceptable markers were those for which dosages could be assigned by fitTetra, for which parental dosages were scored consistently between replicates, and for which parental dosages and offspring segregation patterns were consistent. Approximately 85% of the markers could be assigned dosages by fitTetra, after which a further 5% were rejected for having inconsistent parental-offspring dosages or for being too highly skewed (χ² test with P < 0.001). Markers that segregated 1:1 formed the largest group among the 7214 segregating markers in our population (Table 2), accounting for over 45% of usable markers.

Table 1. Breakdown of SNP marker numbers after quality filtering.

Steps in SNP filtering	No. of SNPs	Percent
SolSTW Infinium array total number of SNPs	17,987	100.0
Dosages assigned by fitTetraa	15,266	84.9
Both parents assigned	15,137	84.2
F1 pattern acceptableb	13,767	76.4
F1 monomorphic	6,553	36.4
F1 polymorphic	7,214	40.0

^aMarkers not scored were either monomorphic or not clearly resolved.

^bCriteria for lack of F₁ fit: presence of null alleles, >3% invalid scores, highly skewed segregation (P < 0.001).

Table 2. Tetraploid marker segregation types by number.

Parental dosage	Segregation	No. of SNPa
Simplex × nulliplex	1:1	1549
Nulliplex × simplex	1:1	1733
Duplex × nulliplex	1:4:1	466
Nulliplex × duplex	1:4:1	421
Simplex × simplex	1:2:1	949
Simplex × triplex	1:2:1	441
Duplex × simplex	1:5:5:1	714
Simplex × duplex	1:5:5:1	640
Duplex × duplex	1:8:18:8:1	303
Total	—	7214

^aNumber of SNP markers after simplifying marker conversions have been performed.

Mapping of the 1:1 segregating markers

Almost no simplex × nulliplex markers dropped out during the mapping stage. Of the 1549 simplex × nulliplex markers in P₁, 1544 were mapped (Table 3), and 1729 of the 1733 P₂ markers were mapped. The unmapped markers were lost owing to poor linkage (either no chromosome assignment or extremely weak linkage within a linkage group) or large numbers of missing values.

Table 3. Composition of parental homolog maps.

Chromosome	h1a	h2	h3	h4	Totalb
Parent 1
1	98.4 (44)	60.8 (34)	67.3 (26)	89.9 (54)	158
2	71.5 (44)	76.7 (34)	56.0 (31)	46.0 (46)	155
3	91.5 (17)	59.0 (23)	56.4 (12)	86.0 (57)	109
4	20.3 (5)	95.1 (98)	91.9 (21)	69.4 (20)	144
5	75.1 (32)	74.3 (101)	114.7 (9)	66.3 (50)	192
6	67.7 (12)	76.6 (35)	75.4 (15)	69.9 (14)	76
7	72.4 (21)	60.0 (36)	57.3 (13)	55.4 (35)	105
8	61.2 (40)	58.1 (99)	58.6 (20)	56.1 (27)	186
9	97.0 (8)	78.8 (62)	86.9 (24)	101.8 (23)	117
10	66.4 (22)	64.8 (18)	58.2 (13)	64.0 (30)	83
11	59.7 (34)	50.3 (37)	61.1 (22)	56.4 (44)	137
12	33.9 (15)	77.6 (27)	73.1 (20)	52.2 (20)	82
Total	—	—	—	—	1544
Parent 2
1	72.1 (25)	48.7 (61)	87.5 (60)	94.5 (37)	183
2	76.6 (74)	71.7 (17)	76.7 (55)	62.9 (89)	235
3	53.7 (110)	26.6 (26)	60.2 (47)	62.0 (42)	225
4	52.9 (32)	70.6 (37)	113.2 (19)	66.3 (46)	134
5	60.4 (69)	68.6 (34)	74.0 (78)	83.7 (15)	196
6	61.3 (24)	59.8 (51)	53.2 (28)	66.1 (50)	153
7	51.2 (12)	55.8 (48)	66.8 (28)	50.5 (46)	134
8	60.0 (12)	69.9 (37)	48.8 (31)	66.3 (24)	104
9	72.6 (15)	71.8 (39)	70.9 (12)	68.1 (41)	107
10	45.7 (5)	45.3 (4)	75.1 (11)	55.9 (23)	43
11	44.5 (23)	59.0 (34)	77.5 (21)	53.4 (51)	129
12	54.1 (8)	61.1 (39)	11.9 (19)	23.6 (20)	86
Total	—	—	—	—	1729

h1, homolog 1; h2, homolog 2; etc.

^aHomolog map lengths in centimorgans using Haldane’s mapping function, with number of mapped markers in brackets.

^bTotal number of mapped markers.

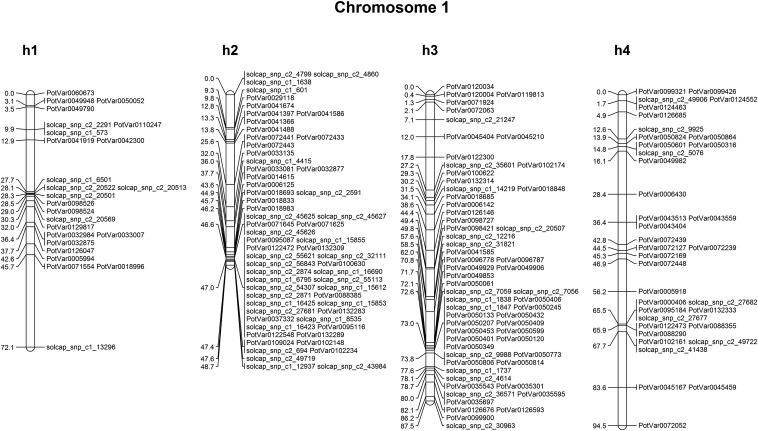
Marker coverage over all chromosomes was well spaced, with, on average, over 270 markers per chromosome. Only chromosomes 10 and 12 had fewer than 200 mapped markers (126 and 168 markers, respectively), with chromosomes 2 and 5 having the highest marker coverage (390 and 388 markers mapped, respectively). A number of homologs were split up over more than one linkage group as a result of insufficient linkage information. In these cases, duplex × nulliplex and simplex × simplex markers were used to provide linkage information between homolog fragments. An example of the four homolog maps of chromosome 1 in parent 2 is shown in Figure 1. In total, 30 mapped markers were found to have a discrepancy between their assignment to a linkage group in this population and their assigned chromosome on the physical sequence (Felcher et al. 2012; Vos et al. 2015). Of these, two SolCAP markers (solcap_snp_c2_42265 and solcap_snp_c2_32337) were found to have positions at two physical locations but mapped to a single genetic position. A further 25 mapped markers were found to have an unknown physical position from the published data sets of marker positions (Felcher et al. 2012; Vos et al. 2015). We provide a list of these markers with their mapped positions in Table S1. None of the 30 markers that showed linkage group discrepancies were included in the analysis of cM/Mb conversion rates or DR, but they were included on the final genetic maps because of their unambiguous genetic position.

Figure 1.

Homolog linkage maps of potato chromosome 1 for parent 2.

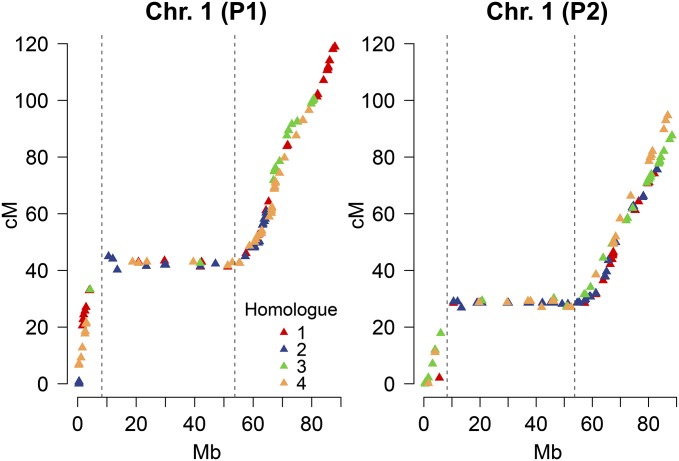
Position of the centromeres

A graphical comparison of the aligned genetic and physical maps allowed an estimation of the centromeric bounds (Figure 2). When compared to previously published centromere boundaries (Sharma et al. 2013), the results do not correspond precisely for chromosomes 4, 5, 7, 9, 10, 11, and 12. It is possible that the discrepancies are due to the fact that our estimates are based on a tetraploid population rather than a diploid one (Felcher et al. 2012; Sharma et al. 2013) because the method used to determine the boundaries was essentially the same. Table S2 provides our estimates for the centromere bounds used in the calculation of relative distance from the centromere for the DR analysis.

Figure 2.

Comparison of genetic-to-physical distance with homolog maps of potato chromosome 1. Approximate centromere bounds are shown as dashed lines, corresponding to the inflection points in the curve (averaged over P₁ and P₂). Homolog maps were aligned prior to graphing by redefining the 0-cM positions, if necessary.

Conversion rate between genetic and physical distance

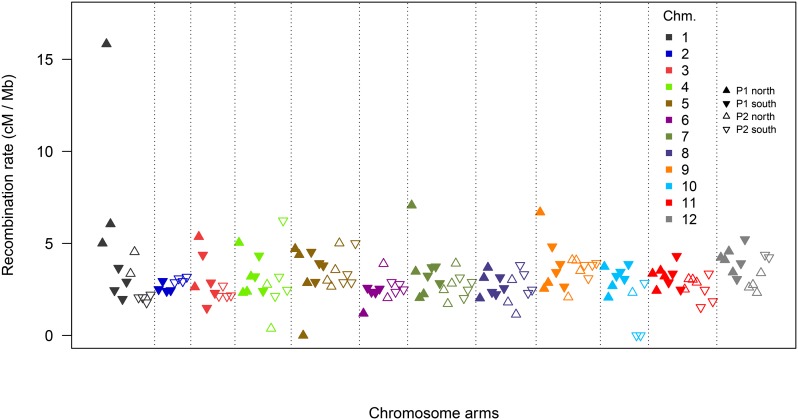
The cM/Mb conversion rate was determined per homolog arm across all chromosomes in both parents by linear regression of genetic distance on the physical distance (Figure 3). Apart from one clearly outlying value (owing to insufficient marker coverage), the recombination rate was found to be relatively constant across all chromosomes, with an average value of 3.07 ± 0.09 (SEM).

Figure 3.

Average recombination rate across homologous chromosome arms. Rates calculated per homolog arm (north or south of the centromere) by linear regression of marker positions on the physical vs. genetic distance plots. Points are colored by chromosome, with upward-pointing triangles denoting north (p) arms and downward denoting south (q) arms. P₁ data are shown by filled triangles, P₂ data by empty triangles.

Double reduction

DR events were identified on all 12 chromosomes, suggesting that multivalent pairing structures can form among all potato chromosomes. Of the 235 individuals in the mapping population, 112 (47.7%) showed evidence of DR coming from P₁ meioses, and 89 (37.9%) showed DR segments from P₂. Forty-six individuals showed evidence of having inherited a DR segment from both parents (but not necessarily from the same chromosome), which corresponds well with the 42.5 individuals expected under independence of parental meioses. The distribution of duplex string lengths shows that singleton duplex scores predominate in this data set (Figure S1). Here we have chosen to consider singleton duplex scores as unsupported evidence for DR that cannot be distinguished from errors in dosage estimation. We also use an algorithm that allows for possible missing scores within a string of duplex values.

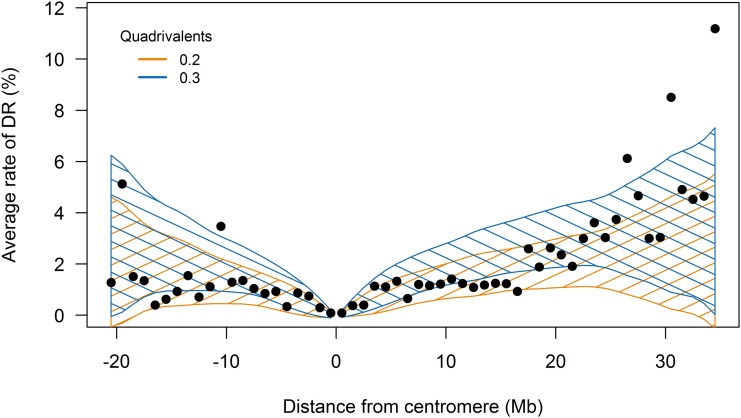
Using this approach, we were able to reveal the relationship between DR and the average distance from the centromere (Figure 4) by pooling the estimates from all 96 homolog maps, giving the average rate of DR as a function of distance from the centromere. The rate of DR close to the centromeres approaches zero, while toward the telomeres it increases substantially. Within the centromeres themselves, there were 22 P₁ markers and 5 P₂ markers with duplex scores in the offspring. Of these, 18 were single occurrences that were probable errors. (For example, the centromeric marker PotVar0014900, which mapped to chromosome 1, homolog 4 in P₁, gave five separate duplex scores. This marker also was found to have 16.2% missing values, suggesting a lower reliability. Other isolated cases would require a double recombination at both sides of the markers, which is highly unlikely to have occurred.) There remained five cases of longer strings of duplex scores that partially entered the boundaries of the centromeric regions (Table S3), suggesting that recombination may occur within what is considered to be a nonrecombining region in a very limited number of cases.

Figure 4.

Average rate of DR vs. distance from the centromeres. Shaded areas represent 95% confidence regions around the simulated mean rate of DR arising from fraction quadrivalents 0.2 and 0.3. The SD of the simulated mean rate of DR increases toward the telomeres, coinciding with greater fluctuations in the true rate of DR in these regions.

PedigreeSim has been used previously to determine the rate of DR in simulated populations and to visualize the relationship between (genetic) distance from the centromere and DR (Voorrips and Maliepaard 2012). In this study, we simulated phased marker data and a mapping population size of 235 to empirically fit a pairing model to the observed data. The observed rates of DR and those predicted by simulation overlap well when the fraction of quadrivalents was simulated in the range 0.2–0.3. Toward the telomeres, the average rate of DR exceeded the expected rates (within a 95% confidence interval), although the confidence intervals were found to widen greatly in these regions. This may be due to the limited number of markers at these distances from the centromeres, causing greater uncertainty in the estimates.

Evidence for preferential pairing

Using the repulsion-phase marker data, we investigated whether there was any evidence for preferential pairing in this population. We found almost no evidence for preferential pairing (correcting for multiple testing using the FDR correction). On chromosomes 5 and 8 in P₁, there were four marker pairs (of 18,336 and 17,205 pairs, respectively) that did show possible evidence of disomic pairing, but this was not considered strong enough evidence to support a hypothesis of preferential pairing. In P₂, no markers displayed disomic-like behavior. It was therefore concluded that potato follows tetrasomic inheritance, as is generally assumed.

Effect of quadrivalents on mapping of simplex markers

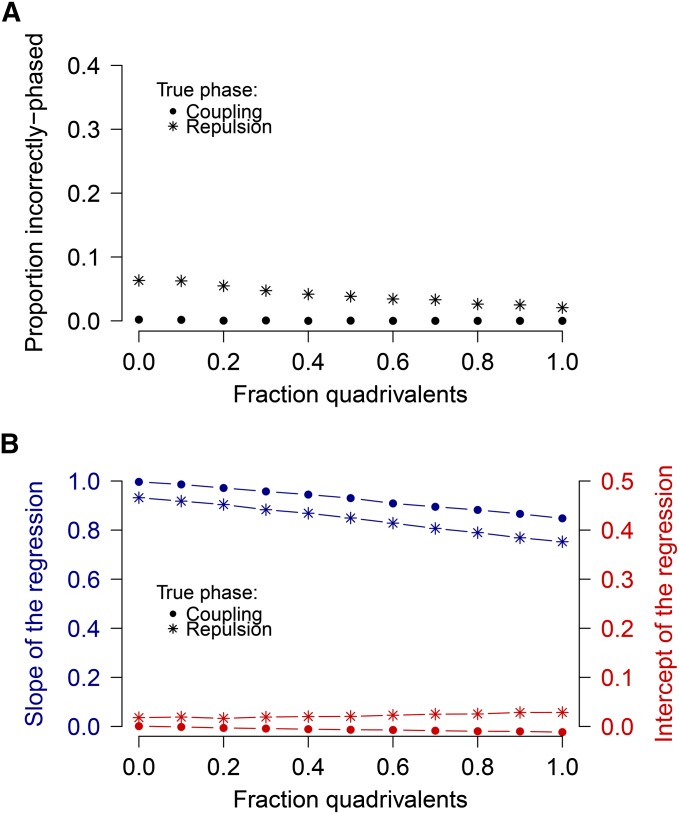
Our analysis of DR suggests that quadrivalents may account for between 20 and 30% of all meiotic pairing configurations in this population. Given that previous mapping studies in potato have assumed that the rate of quadrivalent formation is negligible, we wanted to examine what effect quadrivalents have on recombination frequency estimates (and hence on linkage mapping). We compared pairwise ML estimators for r to their true underlying values (Figure 5) for different rates of quadrivalents. Overall, the effect of quadrivalents on coupling-phase estimates for simplex marker pairs was relatively minor, as shown by the gradual decrease in the slope of the regression between the true and estimated values (Figure 6B). Correct phasing in the coupling phase also was unaffected by quadrivalents (Figure 6A). For a quadrivalent rate between 0.2 and 0.3, the effect on coupling-phase estimates likely can be ignored. For repulsion-phase marker pairs, a greater effect was found, although, remarkably, the assignment of marker phasing actually improves slightly with higher numbers of quadrivalents (Figure 6A). Of the 2374 incorrect repulsion-phase assignments in the purely bivalent situation, only 14 had an associated LOD score greater than 1. This suggests that as a precaution against incorrect phase assignment within a linkage group, an “unknown” phase should be assigned in cases where the LOD score falls below a certain threshold (e.g., a LOD score of 1).

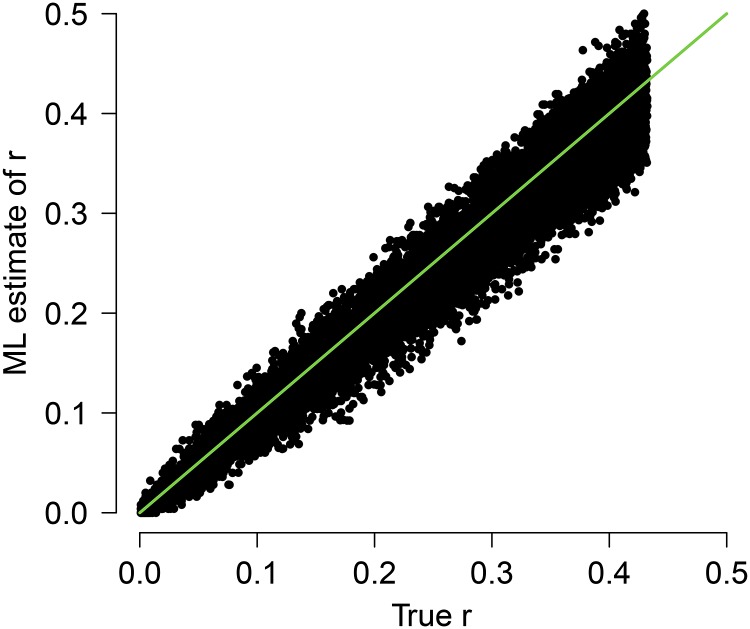
Figure 5.

True vs. estimated r (using ML) for coupling-phase simplex markers with fraction quadrivalents 0.2. The green line (y = x) shows the line of perfect correspondence between true and estimated values.

Figure 6.

(A) Proportion of incorrectly phased markers pairs under different levels of quadrivalent formation. (B) Effect of quadrivalents on accuracy of r ML estimates for coupling- and repulsion-phase simplex marker pairs

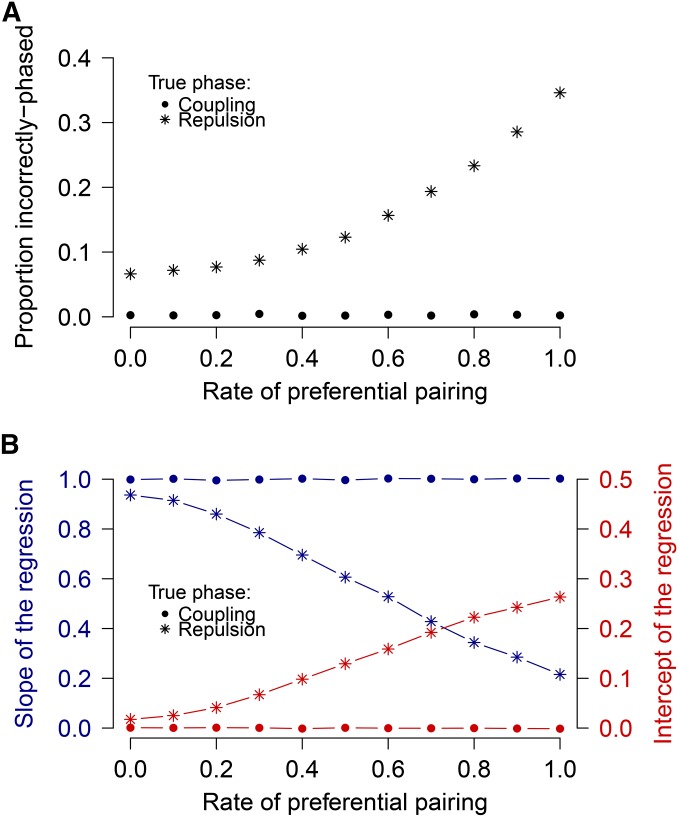
Effect of preferential pairing on mapping of simplex markers

Our study on the effect of preferential pairing on estimates of r revealed that preferential pairing has no effect on these estimates in coupling phase but has a dramatic impact in repulsion phase (Figure 7B). This fact has already been reported (Qu and Hancock 2001; Koning-Boucoiran et al. 2012) and forms the basis for a test of preferential pairing that we also exploit in this study. It is evident that preferential pairing can have a severe impact on the correct assignment of repulsion phase (Figure 7A) regardless of whether MINR or MLL is used for phase assignment (data not shown). Because we found no evidence to suggest that any systematic preferential pairing occurred, we can be fairly confident that the estimates for recombination frequency and phase were performed accurately, as confirmed by the simulation study.

Figure 7.

(A) Proportion of incorrectly phased marker pairs with different levels of preferential pairing. (B) Effect of preferential pairing on accuracy of r ML estimates for coupling- and repulsion-phase simplex marker pairs

Discussion

Linkage maps

A recent publication describes the methods used to produce a high-density SNP linkage map of a well-studied tetraploid mapping population (Hackett et al. 2013) using the Infinium 8300 SolCAP Array (Felcher et al. 2012). Although we have not attempted to include all marker types in the current linkage maps, we have mapped a large number of markers (3273) in a tetraploid population that to the best of our knowledge is the highest-yet reported marker density of a tetraploid potato map. This has given us adequate coverage to recover all homologous chromosomes and develop an accurate picture of the DR landscape in this tetraploid species. We have presented separate homolog maps rather than a single consensus integrated map per chromosome, as achieved by Hackett et al. (2013). Separate homolog maps give one the ability to infer the phasing of markers directly from the map (long-range haplotyping) without recourse to hidden Markov models (Hackett et al. 2013), although, ultimately, integrated maps and genotype probabilities estimated using the integrated map will lead to greater power in subsequent QTL studies. Our finding that the large-scale conversion rate between genetic and physical distance is essentially constant outside the centromeric regions (genome-wide recombination rate) has shown that the prospects for integrating maps across homologs and between parents are good and should not impose undue stress on the underlying homolog maps. We also found little evidence of recombination hot or cold spots outside the centromeres, as evidenced by the high R² values associated with our genetic-physical distance regressions (Table S4).

Potato cytology

Information on the pairing behavior of polyploids traditionally has been generated from cytological studies. One of the more influential publications on potato cytology has been the early review of Swaminathan and Howard (1953), who summarized the findings of previous researchers such as Cadman (1943), Lamm (1945), and Bains (1951) for the mean number of multivalents per cell at diakinesis and first metaphase in tetraploid S. tuberosum as ranging from 1.70 to 5.24. This cytological evidence has been used to support the use of a simplified pairing model in potato mapping and QTL analysis since then (Hackett et al. 2001, 2003, 2013; Luo et al. 2001; Bradshaw et al. 2008). In our study, we have used marker data to estimate the rate of DR and from this to extrapolate the likely frequency of multivalents involved (we only consider quadrivalents). A fraction of 20–30% quadrivalents translates to between 2.4 and 3.6 quadrivalents per cell, consistent with the original cytologic findings of Lamm (1945) performed on the cultivar Deodara and the line 36/209 from the cross Greta × Fürstenkrone.

General polyploid model

Attempts have been made previously to develop a general theory of linkage mapping in tetraploids that simultaneously considers the possibility of preferential pairing and multivalent formation (Wu et al. 2004). According to these authors, if the preferential pairing factor is set to 0 (for the case of random pairing), their model implies that the fraction of quadrivalents will equal 2/3 and that of bivalents 1/3. This is consistent with the random-end pairing model, which assumes that pairing initiation occurs at one set of telomeres, with probability of 1/3 that the pairing at the other telomeres will result in a separation into bivalents (John and Henderson 1962). Our data show that preferential pairing does not occur in potato, yet we have not found a fraction of quadrivalents as high as 2/3. Our findings on quadrivalent pairing are in line with a previous review of autopolyploid meiosis that found a mean multivalent frequency (trivalents and quadrivalents) of 28.8% over 93 different studies (Ramsey and Schemske 2002). It also has been shown that low numbers of multivalents do not necessarily suggest that preferential pairing behavior occurs (Sybenga 1992, 1994).

Identification of DR

We decided to take a more stringent approach than studies that consider two or even a single locus as sufficient evidence for DR (Luo et al. 2006; Hackett et al. 2013). This is likely to have led to an underestimation of DR on our part. However, all quantification of DR using marker data are likely to underestimate the true rate of DR to some extent. For instance, DR segments can be hidden (no segregating allele carried on the segment), or owing to limited numbers of markers, one might recover only part of a DR segment. Higher-density linkage maps (where all homolog parts are covered by segregating markers) will lead to more accurate estimates of the rate of DR unless a strong bias exists in how markers are distributed or where DR occurs. In this study, with over 3000 well-distributed simplex × nulliplex markers, we feel that we have sufficient marker coverage for a detailed understanding of the DR landscape.

Simplex × nulliplex markers give the most unambiguous information about the presence of DR when compared with other marker segregation types. Other marker classes could have been used as well (e.g., simplex × simplex markers, which are expected to show triplex scores in 50% of the cases of DR involving one of the simplex alleles). However, no marker class other than simplex × nulliplex allow DR scores to be distinguished directly as a DR product. ML approaches that estimate the rate of DR, such as that described in Luo et al. (2006), may be useful for the identification of DR in cases where it is not clear, although we feel that flanking simplex × nulliplex marker information that supports the duplex score should be used, as we have done here.

DR increases toward the telomeres

It has been widely reported that the rate of DR is expected to increase toward the telomeres (Mather 1936; Fisher 1947; Butruille and Boiteux 2000; Stift et al. 2008; Nemorin et al. 2012; Zielinski and Scheid 2012), given that the probability of a crossover occurring between the centromere and a locus should increase as that locus is situated further from the centromere. Nevertheless, this has been experimentally verified only rarely. The clearest evidence we found in the literature came from an analysis of tetraploid potato using isozyme markers, although the number of markers used was rather limited, with fewer than 50 loci considered (Haynes and Douches 1993). In our study, we have clearly shown, using high-density marker data of over 3000 markers, that the rate of DR steadily increases with distance from the centromere. We have furthermore been able to visualize this phenomenon, which has not been reported previously.

The fact that the frequency of DR increases toward the telomeres is perhaps cause for some concern because this could be considered a systematic source of error in the marker data. Nevertheless, with dense marker data, it is now possible to accurately estimate the rate of DR in a mapping population. In cases where the rate of DR is low and marker number high, it is questionable whether highly complicated models with many parameters to be estimated are actually useful, particularly if they do not distinguish between singleton DR scores and genotyping errors. Our simulations have shown that even with fully quadrivalent pairing, pairwise estimators for recombination frequency between coupling-phase simplex × nulliplex markers under a bivalent pairing model are close to being exact (and because these constitute the most informative pairing scenario, they are the most important estimates for linkage-map construction). We look forward to comparing our estimates for DR in tetraploid potato with other polyploid species and in gaining a deeper understanding of why these rates differ in what are otherwise classified collectively as autopolyploids.

DR in mapping

Some authors claim that DR should be included in map estimation and QTL analysis to increase the power and accuracy of the analysis (Li et al. 2011). Our findings show that quadrivalents have little effect on the mapping of simplex markers in the highly informative coupling phase. In potato at least, our data show that the level of quadrivalent formation (and preferential pairing) is very low and therefore is not likely to be of serious worry for linkage mapping. However, confirmation of this finding for other marker types is still needed.

It is also worth pointing out that quadrivalent formation not only leads to DR but also can result in the formation of homolog combinations of more than two parental homologs (Sved 1964), which can result from pairing-partner switches (Jones and Vincent 1994) along the chromosome. The fact that this is already part of the simulation process in PedigreeSim (Voorrips and Maliepaard 2012) increases the accuracy of our approach not only in terms of modeling DR but also in our study of the effect of quadrivalents on map estimation.

DR in breeding

DR has many implications for polyploid breeding. One consequence that has been described is its potential to lead to a higher inbreeding coefficient in dihaploids derived from tetraploid lines (Haynes and Douches 1993). Given the efforts currently underway toward hybrid potato breeding (Lindhout et al. 2011), DR may have unwanted impacts on genetic diversity at the diploid level if future diploid founder material is derived from tetraploid lines. However, hybrid breeding depends on the production of highly homozygous inbred lines. Tetraploid potato breeding might welcome greater levels of homozygosity in a crop that is often complicated by high heterozygosity (Uitdewilligen et al. 2013), as well as the potential purging effect that DR can have by exposing deleterious alleles to selection (Butruille and Boiteux 2000). DR also could speed up the accumulation of rare but favorable alleles through marker-assisted selection. Here we have developed the tools for the identification of DR in a segregating population that could be applied by breeders in the selection of founder parents for subsequent crossings or for confirmation studies of QTL positions.

Conclusions

In this study, we constructed 96 separate homolog linkage maps of tetraploid potato using 1:1 segregating simplex markers. We estimated the approximate rate of DR (6% or more at the distal regions) and predicted by simulation that a fraction of quadrivalents of 20–30% is required to account for this level of DR. We found no evidence of preferential pairing in our data, consistent with previous reports on the mode of inheritance in potato. Simulation studies using simplex × nulliplex markers revealed that marker phasing and recombination-frequency estimation under a simplifying bivalent-pairing model are relatively robust, even when some level of multivalent pairing occurs.