Abstract
Diffusion of molecules is simulated stochastically by letting them jump between voxels in a Cartesian mesh. The jump coefficients are first derived using finite difference, finite element, and finite volume approximations of the Laplacian on the mesh. An alternative is to let the first exit time for a molecule in random walk in a voxel define the jump coefficient. Such coefficients have the advantage of always being non-negative. These four different ways of obtaining the diffusion propensities are compared theoretically and in numerical experiments. A finite difference and a finite volume approximation generate the most accurate coefficients.
Keywords: stochastic simulation, diffusion, Cartesian mesh, 65C05, 65C35, 92C05
1. Introduction
Small copy numbers of many molecular species in biological cells require stochastic models of the chemical reactions between the molecules and their diffusive motion. One example is gene expression where the number of molecules involved is small and only stochastic models can explain observations in experiments [1, 2]. Continuum models for the concentrations of the chemical species based on partial differential equations (PDEs) capture neither the randomness in the chemical reactions nor the fact that the number of molecules is integer.
In a well stirred system, there is no space dependence of the distribution of the species. Gillespie [3] invented an algorithm to simulate such chemical systems, the Stochastic Simulation Algorithm (SSA). The efficiency of the algorithm is improved in [4]. It is extended in [5, 6] to space-dependent systems where the diffusion of the molecules cannot be neglected.
The domain of interest is Ω with boundary ∂Ω. It is partitioned by a Cartesian mesh into compartments or voxels
 i with volume |
i with volume |
 i| and a node xi in the center in [5]. The molecules jump between the voxels (or between the nodes in the lattice) with a certain probability. The time until a molecule jumps from
i| and a node xi in the center in [5]. The molecules jump between the voxels (or between the nodes in the lattice) with a certain probability. The time until a molecule jumps from
 i to the adjacent
i to the adjacent
 j is assumed to be exponentially distributed with parameter λij. With ni neighbours, the total jump propensity out of
j is assumed to be exponentially distributed with parameter λij. With ni neighbours, the total jump propensity out of
 i is
i is
| (1) |
The diffusion propensity is λimi with mi molecules in
 i. Then the SSA for the diffusion in the molecular system is:
i. Then the SSA for the diffusion in the molecular system is:
Initialize the number of molecules mk, k = 1, …, K, in the K voxels at t = 0.
Sample the exponentially distributed time Δtk with rate λkmk to the first diffusion event in all K voxels and let tk = Δtk.
Determine the smallest tk. Let ti be the minimum of all tk in voxel
 i.
i.For the jump from
 i, sample a jump to
i, sample a jump to
 j with probability θij = λij/λi.
j with probability θij = λij/λi.Update t := ti and molecule numbers mi := mi − 1 and mj := mj + 1.
Sample Δti and Δtj with rates λimi and λjmj and let ti = t + Δti and tj = t + Δtj and go to 3.
In the algorithm, the number of molecules mi in each voxel is updated if it has changed after an event and a new time ti is determined for the next event in the same voxel. The SSA generates one realization of a continuous time, discrete space Markov process. We will compare different ways of determining non-negative jump coefficients λij for a Cartesian mesh where all voxels have equal size assuming that the rates to jump from
 i to
i to
 j and back again are equal, λij = λji.
j and back again are equal, λij = λji.
Let ui(t) be the numerical approximation at xi on the Cartesian mesh of the concentration u(x, t) satisfying the diffusion equation in the domain Ω
| (2) |
with Neumann boundary condition n · ▽u = 0 at the boundary ∂Ω with the outward normal n. Choose the λij coefficients such that they approximate the Laplacian in node i at xi
| (3) |
The node at xi has ni adjacent nodes at xj used in the approximation. In the limit of a large total number of molecules
, the time dependent expected values of the concentrations ũi = mi/(M|
 i|) in the voxels in SSA with the jump coefficients in (3) converge to the deterministic concentrations ui solving the discretized diffusion equation (2) using (3), see [7]. The distribution for the difference between ũi and ui is given in [8].
i|) in the voxels in SSA with the jump coefficients in (3) converge to the deterministic concentrations ui solving the discretized diffusion equation (2) using (3), see [7]. The distribution for the difference between ũi and ui is given in [8].
In an equidistant Cartesian mesh, the Laplacian is discretized with a finite difference method (FDM) in [5, 6, 9]. Unstructured triangular meshes in 2D and tetrahedral meshes in 3D are better suited to represent complicated geometries inside the cell effectively. The coefficients for these unstructured meshes are derived from a finite element method (FEM) for the Laplacian in [10, 11] and with a finite volume method (FVM) in [12].
The jump propensities λij have to be non-negative to be meaningful in the SSA. The standard 5-point (2D) and 7-point (3D) approximations of the Laplace operator in (2) with FDM on a Cartesian mesh yield positive λij for the neighbouring voxels but the FEM coefficients for an unstructured mesh may be negative for a poor mesh [11]. The numerical discretization of the diffusion equation (2) by a common FVM method may be inconsistent [13] and not converge to the analytical solution on a general unstructured mesh but the coefficients are non-negative.
If the jump coefficients are negative, the numerical solution of (2) will in general not be monotone and not satisfy the discrete maximum principle. For the discrete maximum principle to hold the coefficients must satisfy the following conditions, see [14]: (1) is valid for interior nodes; λij ≥ 0; and λi is greater than the sum of the off-diagonal elements for at least one boundary node. Thus, the two first conditions apply for both the diffusion coefficients in the SSA and the spatial discretization of the diffusion equation.
Many papers are devoted to the derivation of consistent FEM and FVM approximations fulfilling the discrete maximum principle for triangular and quadrilateral meshes in 2D and tetrahedral meshes in 3D, e.g. [15, 16, 17, 18, 19]. They are nonlinear and the coefficients in (3) depend on the solution ui making them less suitable as jump propensities in the SSA or rely on meshes with geometrical properties that may be difficult to achieve with a mesh generator. In [20, 21] it has been shown that it is impossible to construct a linear method, i.e. λij is constant in (3), satisfying the discrete maximum principle for a linear elliptic equation on general quadrilateral meshes in 2D.
As an alternative, we solve the diffusion equation on a local domain and use the solution to calculate the mean first exit time (FET) from that domain for a molecule in Brownian motion. The molecule is released at xi at t = 0 and after a random walk it leaves a subdomain defined by the convex hull of the adjacent nodes xj, j = 1, …, ni, for the first time at t = τ. The expected value of τ from this subdomain is the inverse of the rate λi. The mesh is Cartesian in 2D with different mesh sizes hx and hy in the x and y directions, respectively. Jumps are allowed in the coordinate directions and along the diagonals, see Fig. 1. The probability to exit from
 i to
i to
 j depends on the distance between the nodes xi and xj i.e. hx and hy. The FET coefficients are always non-negative. They are compared with the methods above for approximations of the Laplacian. The coefficients derived with FDM, FEM, and FVM also depend only on hx and hy in the mesh. The jump coefficients obtained by the FET and the systematic comparison with the coefficients from numerical discretizations are the main contributions of this paper. The analysis is extended to the fully unstructured case in [22].
j depends on the distance between the nodes xi and xj i.e. hx and hy. The FET coefficients are always non-negative. They are compared with the methods above for approximations of the Laplacian. The coefficients derived with FDM, FEM, and FVM also depend only on hx and hy in the mesh. The jump coefficients obtained by the FET and the systematic comparison with the coefficients from numerical discretizations are the main contributions of this paper. The analysis is extended to the fully unstructured case in [22].
Figure 1.
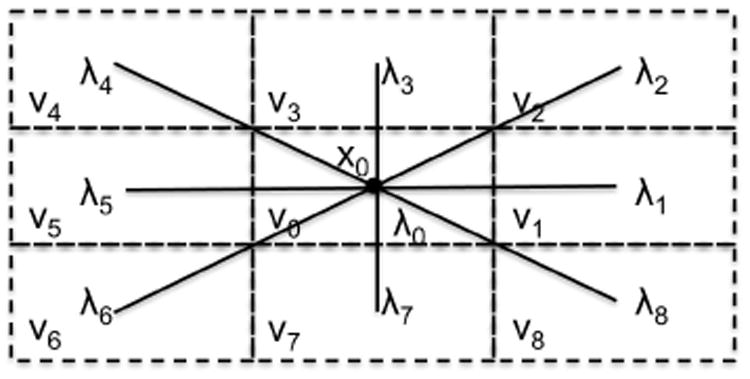
The reference nine point stencil in 2D for the voxel
 0 with midpoint x0 and its neighbours.
0 with midpoint x0 and its neighbours.
The expected FET can be utilized in a different way to solve (2), see [23] and the references therein. Stochastic simulations determine the FET in polygonal domains with general boundary and initial conditions in a Monte Carlo method suitable for high dimensions. Here we are interested in using FET to find the probabilities of the motion of molecules on a discrete lattice.
In the next section, we present the FDM, FEM, and FVM discretizations of the Laplacian and how to derive the jump coefficients from them. We compute expressions for the FET in Sect. 3 to derive new jump coefficients from the exit behavior of a diffusing molecule. In Sect. 4, we compare the four methods to obtain λi, λij, and θij in SSA. We perform numerical experiments in Sect. 5 and draw conclusions in the final section.
2. FDM, FEM, and FVM coefficients
The primal mesh is Cartesian in 2D and has nodes at xi = (xi1, xi2) and the dual mesh consists of voxels
 i with xi in the center. The distance is hx between the nodes in the x direction and hy in the y direction. In the following, we consider the reference voxel
i with xi in the center. The distance is hx between the nodes in the x direction and hy in the y direction. In the following, we consider the reference voxel
 0 with midpoint x0 and area hxhy, see Fig. 1, and introduce the aspect ratio κ, such that hx = κh and hy = h. As we will only work on this reference voxel from now on, the notation is simplified by letting λ0i → λi and θ0i → θi in the remainder of the paper.
0 with midpoint x0 and area hxhy, see Fig. 1, and introduce the aspect ratio κ, such that hx = κh and hy = h. As we will only work on this reference voxel from now on, the notation is simplified by letting λ0i → λi and θ0i → θi in the remainder of the paper.
2.1. FDM
Discretize the Laplacian Δ with the FDM as in [24] to obtain the weights λi in the difference stencil for the mesh in Fig. 1. By symmetry, λ1 = λ5, λ3 = λ7, and λ2 = λ4 = λ6 = λ8 and by consistency, the weight in the center point is . The following coefficients obtained after Taylor expansion give a second order approximation of Δ
| (4) |
where α is a free parameter. If α = 0 then we have the usual 5-point stencil. We wish all λi to be non-negative to fulfill the discrete maximum principle and to be useful as jump coefficients requiring
| (5) |
The weight in the center is
| (6) |
with a negative sign. If κ → ∞ then α → 0 in (5) for positive coefficients and
. For a large κ, almost all jumps out of
 0 will be in the y direction with the same rate as in 1D. Accordingly, if κ → 0, then α → 0 by (5) and
and the diffusion behaves as one-dimensional in the x direction. The jump rate to node i is λi and the relative rates θi = λi/λ0 between the nodes are
0 will be in the y direction with the same rate as in 1D. Accordingly, if κ → 0, then α → 0 by (5) and
and the diffusion behaves as one-dimensional in the x direction. The jump rate to node i is λi and the relative rates θi = λi/λ0 between the nodes are
| (7) |
With α = 0 and κ = 1, the non-zero relative rates are θ1 = θ3 = θ5 = θ7 = 1/4, the 5-point stencil for the Laplacian.
2.2. FEM
We approximate the Laplacian by bilinear basis functions on a rectangular element, see [14, 25]. The lumped mass matrix has hxhy on the diagonal. After division by hxhy, the coefficients corresponding to λi in (4) and (6) are
| (8) |
The free parameter α in (4) is here (κ2+1)/(3κ) with the following constraints on the mesh for non-negative coefficients
| (9) |
The relative rates are
| (10) |
cf. (7).
2.3. FVM
The Laplacian in the FVM is approximated by (see [13, 26]):
| (11) |
in voxel
 0 of area |
0 of area |
 0| = hxhy = κh2 and with outward normal n(x) at the boundary
. We now approximate the outward fluxes n · ∇u across the edges. Suppose that uj is the solution in
0| = hxhy = κh2 and with outward normal n(x) at the boundary
. We now approximate the outward fluxes n · ∇u across the edges. Suppose that uj is the solution in
 j, j = 1, …, 8, surrounding
j, j = 1, …, 8, surrounding
 0 in Fig. 1 and u0 is the solution in
0 in Fig. 1 and u0 is the solution in
 0. The straightforward approximation of the outward flux on the edge ν01 in (11) is (u1 − u0)/hx. Similar approximations on the other edges yield the coefficients
0. The straightforward approximation of the outward flux on the edge ν01 in (11) is (u1 − u0)/hx. Similar approximations on the other edges yield the coefficients
| (12) |
corresponding to the case α = 0 in (4). There is no problem with negative jump propensities here. The relative rates in Step 4 in the SSA in Sect. 1 are
| (13) |
In another gradient approximation involving the diagonal voxels, let ∂u/∂x ≈ (u1+u2-(u0+u3))/2hx in the corner to
 2, see Fig. 1. With the same kind of approximation for ∂u/∂y and in the other corners of
2, see Fig. 1. With the same kind of approximation for ∂u/∂y and in the other corners of
 0 and a linear variation of the gradient along v0j, the coefficients are
0 and a linear variation of the gradient along v0j, the coefficients are
| (14) |
These are non-negative only if κ = 1. Then they are the same as for the FDM with α= 1 in Sect. 2.1.
The jump coefficients derived here are defined by FDM (4), FEM with bilinear basis functions (8) as in [14], and a standard FVM (12). Additional constraints for non-negativity are necessary for FDM (5) and FEM (9).
3. First exit time
Let x0 be a node inside a simply connected domain ω with boundary ∂ω. The FET of a molecule from ω initially at x0 at t = 0 is denoted by the random variable τ. The mean value Eτ = E[τ] and the location on ∂ω where the molecule left ω can be computed from the probability density function (PDF) p(x, t) for the position x of the molecule at time t. Then p(x, t) satisfies the following PDE with diffusion coefficient D in ω:
| (15) |
Then p(x, t) is the probability density for the position x of a diffusing molecule provided that it has not left ω until time t [27, 28, 29, 30]. The probability that the molecule is still inside ω at t is the survival probability
| (16) |
Here dω denotes integration over the domain ω. Let further n(x) be the outward normal of ∂ω. The PDF pω(t) for a molecule to exit at time t is then derived from (15), (16), and Gauss' formula
| (17) |
Here ds denotes integration over the boundary ∂ω. The expected value of the exit time is obtained from pω(t)
| (18) |
For the Markov property to hold in the SSA simulations, the exit time distribution has to be exponential. Since S(0) = 1, limt→∞ S(t) = 0, and S(t) decays monotonically it can be approximated by an exponential S(t) ≈ S̃(t) = exp(–λt) and we can e.g. choose λ such that the two distributions have the same mean value in (18). With this S̃, by (18) Eτ = 1/λ and by (17) the approximate PDF of the exit time τ is
| (19) |
i.e. τ is exponentially distributed. The diffusion propensity λ0 in the SSA in Sect. 1 to jump out of
 0 is then 1/Eτ with the corresponding domain ω0 embedding
0 is then 1/Eτ with the corresponding domain ω0 embedding
 0, see Fig. 2a.
0, see Fig. 2a.
Figure 2.
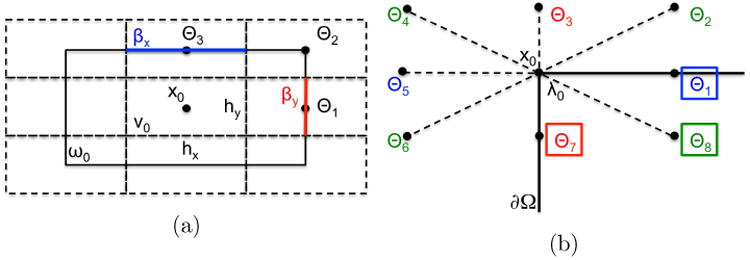
(a) The voxel
 0 embedded in the rectangle ω0. (b) Boundary treatment for a corner.
0 embedded in the rectangle ω0. (b) Boundary treatment for a corner.
The flux of molecules out of ω0 at a point on ∂ω0 is −D▽p · n. Let ∂ω0 consist of non-overlapping sections ∂ωj such that ∂ω0 = ∪j∂ωj. The probability that the molecule leaves ω0 through ∂ωj of the boundary at t is
| (20) |
Given that the exit time out of ω0 is t, the conditional probability for the molecule to exit along the edge ∂ωj is
| (21) |
The probability in the SSA to leave ω0 through ∂ωj at time τ is then the expected value
| (22) |
and by (21) Σjθj = 1. No matter how we choose ω0, the θj are always non-negative.
The time to leave
 0 and enter a neighbouring voxel
0 and enter a neighbouring voxel
 i, i = 1, …, n0, is exponentially distributed in (19). The rate at which a molecule reaches
i, i = 1, …, n0, is exponentially distributed in (19). The rate at which a molecule reaches
 i is λi = θiλ and the time for the jump to occur is exponentially distributed with rate λi. The SSA algorithm in Sect. 1 defines a continuous time, discrete Markov process [27] with these jump coefficients.
i is λi = θiλ and the time for the jump to occur is exponentially distributed with rate λi. The SSA algorithm in Sect. 1 defines a continuous time, discrete Markov process [27] with these jump coefficients.
The coefficients for the voxel in Fig. 1 are calculated by choosing ω0 to be the rectangle defined by the surrounding nodes x1, …, x8, see Fig. 2a. By this choice, we arrive at jump coefficients that are comparable to the FDM, FEM, and FVM coefficients. We compute the jump rate λ0 by (16) and (18). The boundary ∂ω0 is partitioned into ∂ωj, j = 1, …,8, centered around the nodes xj. We choose two parameters 0 ≤ βx,βy ≤ 1 such that |∂ω1| = |∂ω5| = 2βyhy and |∂ω3| = |∂ω7| = 2βxhx, where | · | is the length of an edge. Consequently, the length of ∂ω2, ∂ω4, ∂ω6, and ∂ω8 is (1 − βx)hx + (1 − βy)hy. Then θj follows from (21) and (22).
The analytical solution of (15) with x0 = (hx,hy) in the rectangular domain ω = [0, 2hx] × [0, 2hy] is obtained by separation of variables and an expansion in the eigenfunctions
| (23) |
This formula converges rapidly when D·t is not too small. A different formula is available when D · t is small, cf. [23, 31].
Choosing βx = βy = 1 corresponds to α = 0 in the FDM in Sect. 2.1. In that case, jumps only happen along the coordinate axes of the mesh and coordinate splitting allows us to simulate two one dimensional diffusions instead. The choice βx = βy = 0 corresponds to α = 1 in Sect. 2.1 with only the nodes in the corners involved.
By (16), (18) and (23) the jump rate from x0 out of ω0 is
| (24) |
There are two parameters in the definition of the FET coefficients, βx and βy. They determine ∂ωj and θj in (21) and (22). At the edge where x = 2κh, p∂ω1 is given by (20)
| (25) |
Hence, θ1 in (22) depends nonlinearly on βy and κ, and accordingly for θ3 and βx.
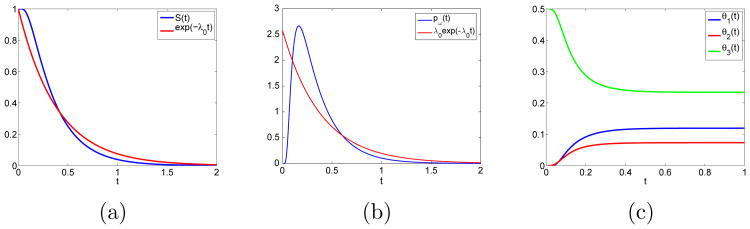
Henceforth, the diffusion coefficient D is taken to be 1. Examples of time dependent solutions to (16), (17) and (21) using (23) are found in Fig. 3 for κ = 1.4 and h = 1. We approximate the cumulative survival time distribution S(t) by an exponential distribution with the same mean value to preserve the Markov property in the SSA. In this way, the average waiting time for a jump sampled from e–λ0t is the same as from the accurate S(t). The higher order moments are for the exponential distribution and can be computed from (16) and (17). In Table 1, we see that the second moments agree well between the approximation by an exponential and the exact S(t). The products of the infinite sums in (23) to compute S(t) and (24) to compute λ0 are rewritten as Cauchy products and truncated after 103 terms.
Figure 3.
FET quantities calculated for κ = 1.4, h = 1, D = 1 and βx = βy = 0.5: (a) S(t) and approximation by an exponential with λ0 = 2.5841 as in (24) and Table 2. (b) Exit time distributions pω(t) = −∂S(t)/∂t. (c) θj(t) calculated by (21) and (25).
Table 1.
Higher order moments for the exact exit time distribtuion S(t) and the approximating exponential exp(−λ0t).
| S(t) | exp(−λ0t) | |
|---|---|---|
|
| ||
 [t] [t] |
0.3870 | 0.3870 |
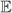 [t2] [t2] |
0.2267 | 0.2995 |
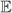 [t3] [t3] |
0.1866 | 0.3477 |
The jump coefficients θj are computed for a t > 0 in Fig. 3c. For small t and κ > 1 jumps are more likely to occur in the y direction, i.e. to x3 and x7 since θ3 > θ1, θ2. When t is large, it follows from (25) that the sums are well approximated by their first term, cj exp(−γt), where γ = π2D(1 + κ2)/4κ2h2, resulting in
| (26) |
the constant behaviour for large times we see in Fig. 3b.
4. Comparison of the coefficients
The FEM, FVM, and FET define the coefficient λ0 without any parameter. We can then choose the free parameter α such that the FDM coefficient corresponds to either of them:
| (27) |
The values of λ0 and α for k = 1 and k = 1.4 are found in Table 2.
Table 2.
The jump coefficients for different methods when κ = 1 and κ = 1.4 and α is such that the FDM has the same λ0.
| FEM | FVM | FET | ||
|---|---|---|---|---|
| κ = 1 | λ0·h2 | 2.6667 | 4 | 3.3934 |
| α | 0.6667 | 0 | 0.3033 | |
|
| ||||
| κ = 1.4 | λ0·h2 | 2.0136 | 3.0204 | 2.5841 |
| α | 0.7048 | 0 | 0.3054 | |
By choosing α as in (27) we obtain the same relative jump coefficients θj as the FEM (10) and the FVM (13). The relative jump coefficients in FET depend on βx and βy in Sect. 3. By solving
| (28) |
numerically for βx and βy and using that by symmetry
| (29) |
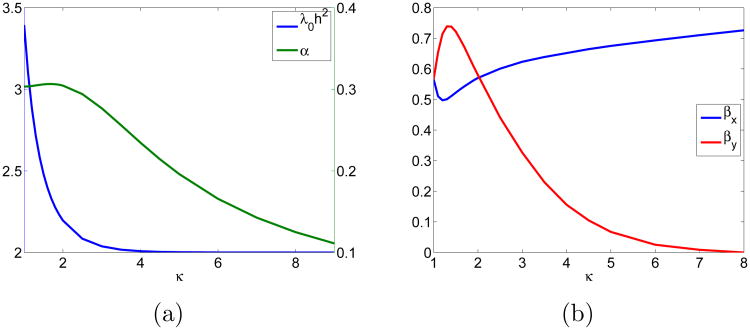
the FET jump coefficients agree with those from FDM. With κ = 1.4, the values of βx and βy are 0.511 and 0.738, respectively. With this choice of βx and βy, the FET coefficients define a second order approximation of the Laplacian. In Fig. 4, we see the behaviour of βx, βy, λ0 and the appropriate α for different κ. as κ increases, λ0h2 → 2 converging again to the one-dimensional case, cf. (24). In Fig. 4b, we find that an increase in κ affects βy - regulating the contribution from the shorter edge - more than βx, which only slightly depends on κ.
Figure 4.
(a) The α parameter (right) in FDM to achieve the same h2λ0 as in FET in (27) and the corresponding λ0h2. (b) The β coefficients in FET in (28) to achieve the same relative jump coefficients θj for the same λ0 as in FDM.
5. Numerical results
We will now examine the performance of the coefficients in SSA simulations of the diffusion of molecules. A square Ω = [0, 20] × [0, 20] is discretized in the experiments into nx nodes or grid points in the x-direction and ny = κ(nx – 1) + 1 in the y-direction. The boundary is defined by the first and the last nodes in the x and y directions. We choose κ = 1 and κ = 1.4. The molecules are reflected as they reach the boundary.
The methods are compared for high copy numbers where there are convergence results due to Kurtz [7, 8]. This approach is similar to the comparison of methods for the numerical solution of PDEs. Their convergence to the analytical solution is usually measured when the step length vanishes. To validate a stochastic method one can examine the moments of the solution. Here we focus on the first moment. According to Kurtz [7, 8] the mean value of the concentrations of molecules computed by the SSA converges to the deterministic solution of the diffusion equation in the limit of large molecule numbers. In an example with low copy numbers, the variance is compared for different approximations at the steady state.
The distribution of molecules is compared to the analytical solution of the diffusion equation with Neumann boundary conditions in (2) with u(x, 0) = δ(x – x0). To implement the reflecting boundary condition, we add the contributions θj from the standard voxel at the boundary, which are outside the domain, to θj in the interior, see Fig. 2b.
Let M be the number of molecules and the final time T = 5. The molecules are released at t = 0 at the center x0 = (10, 10) of the domain. The error e in the simulations is defined by
| (30) |
where mij is the copy number in voxel (i, j), |
 ij| = κh2 is the volume of voxel
ij| = κh2 is the volume of voxel
 ij and xij is the node coordinate. As the FDM, the FEM, and the FVM are second order accurate, their errors will behave as
because of the space discretization and the statistical error.
ij and xij is the node coordinate. As the FDM, the FEM, and the FVM are second order accurate, their errors will behave as
because of the space discretization and the statistical error.
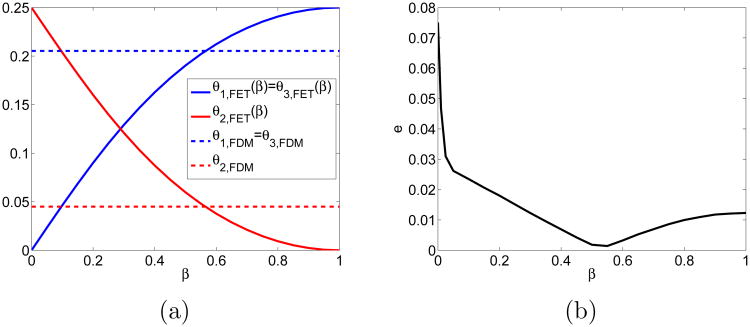
In the case κ = 1, we have βx = βy = β. The β value is chosen such that θi,FET = θi,FDM with α = 0.3033. The relative jump coefficients vary with β in Fig. 5a. At β ≈ 0.56 they agree with the FDM coefficients in (7), see also Fig. 4b. We calculate the error on a grid with nx = ny = 21 grid points and M = 5 · 106 and see that the accuracy varies with β in Fig. 5b. The minimum is at β ≈ 0.56 where the FET is equal to an FDM in Fig. 5a and is second order accurate in h.
Figure 5.
Comparison between FDM with α = αFET and FET at κ = 1: (a) Relative jump propensities depending on parameter β in FET and the constant FDM coefficients. (b) Error e for different values of β.
In Fig. 5b, the error increases monotonically when β decreases from 0.56 to 0, which corresponds to α = 1 in the FDM. Then the molecules only jump along the diagonals, which means - if they are released in one voxel - they do not reach all voxels in the domain but only half of them in a checkerboard pattern. If the molecule starts in the voxel above, then it will reach the other half of the voxels. This particular distribution of the diffusing molecules explains the high error.
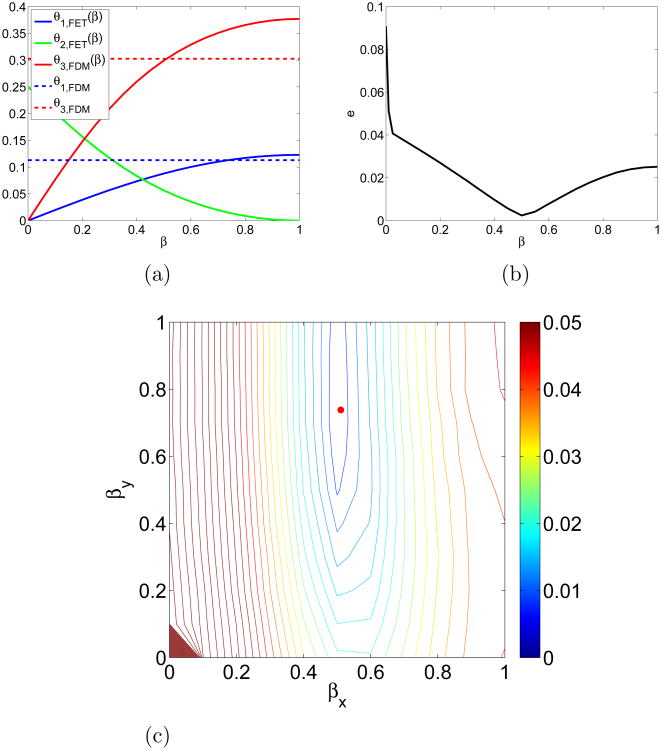
The FET jump coefficients for different β = βx =βy are compared to FDM coefficients for κ = 1.4 in Fig. 6a. The absolute error for the same parameters as before is displayed in Fig. 6b with a minimum at β ≈ 0.5. The behaviour is similar in both Fig. 5b (κ = 1) and Fig. 6b (κ =1.4). The isolines of the error for combinations of βx and βy are found in Fig. 6c.
Figure 6.
Comparison between FDM with α = αFET and FET at κ = 1.4: (a) Relative jump propensities for FET depending on parameter β and the constant FDM coefficients. (b) Absolute error for different values of β = βx = βy. (c) Level curves of the error for different values of βx and βy with the red dot indicating the minimum.
We observe in Fig. 6a that the match with the FDM coefficients occurs for βx = 0.511 and βy = 0.738, which coincides with the minimum - indicated by the red dot - in Fig. 6c. The FET viewed as an approximation to the Laplacian is second order accurate there. The simplification β = βx = βy has its minimum at β ≈ 0.5 in Fig. 6b. This value corresponds to integration in (25) and in Fig. 2a between the boundaries of the adjacent voxels
 1,
1,
 2, and
2, and
 3 to obtain θ1, θ2, and θ3, respectively.
3 to obtain θ1, θ2, and θ3, respectively.
In Figs. 6b, c, the error increases again when βx and βy approach 0 as in Fig. 5, which corresponds to the particular diffusion explained earlier where the molecules only reach half of the domain.
We measure the relative error e/‖u‖ in Fig. 7a for the four different methods where e is calculated as in (30) and
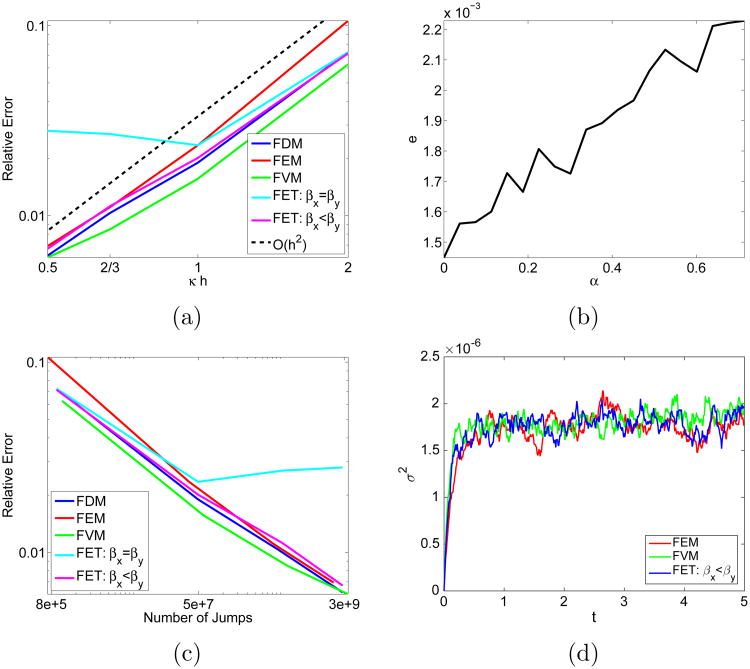
Figure 7.
Performance on a square domain with κ = 1.4 (a) Convergence for the FDM with α = 0.3054, the FVM, the FEM, and the FET with βx = βy= 0.5 and βx = 0.511 and βy = 0.738. The reference curve decays as h2 (b) Absolute error for the FDM method for different parameters α. (c) Relative error versus the number of jumps needed in each simulation. (d) Variance around steady state.
| (31) |
We discretize the square into nx = 11, 21, 31 and 41 nodes and choose κ = 1.4, such that ny = 15,29,43 and 57 and κh = 2,1,0.67 and 0.5. We set in order to keep the statistical error smaller than the spatial error. In Fig. 7b, we display the error in the FDM for α ≤ 1/κ, where κ = 1.4, M = 5 · 106 and n = 21. The error increases slightly with increasing α and the fluctuations indicate the size of the statistical error. Furthermore, we count the number of jumps for each simulation. This number is proportional to the number of generated random numbers and the administration of an event in the system - and therefore the computational work - and we plot the error against it in Fig. 7c. To examine the behaviour for low copy numbers we distribute M = 2240 molecules evenly across all voxels for nx = 21 and ny = 29. We compare the fluctuating molecule numbers mij to the spatially constant steady state concentration μ = 0.0025 in three realizations in the time interval [0, 5]. In Fig. 7d the sample variances
| (32) |
for FEM, FVM and FET with βx = 0.511 and βy = 0.738 agree well.
The three methods FDM, FVM, and FEM converge to the analytical solution of the diffusion equation with rate 2 in Fig. 7a, as expected. There is a unique choice of βx and βy such that the FET corresponds to the FDM and becomes second order, too. With βx = βy = 0.5, the FET is not a consistent approximation of Δ and no reduction in e/‖u‖ is observed when h is lowered from 1 to 0.5. The relative error stagnates at 0.02 − 0.03 which is sufficiently low for most problems. The minimum error for the FDM is obtained for α = 0 in Fig. 7b. This method is the standard five point approximation and is equal to the FVM in (12) and (13). In Table 2, the FEM has the smallest λ0. As the exit time is distributed exponentially, that means that the FEM has the longest expected time between events, corresponding to fewer jumps being simulated in [0, T]. For a given error, the number of jumps should be as low as possible for the best efficiency. As the FEM corresponds to a mixed FDM with α = 0.7048 it generates a higher error than the standard five point FDM with α = 0, see Fig. 7b. The FET or the FDM with α = 0.3054 on the other hand results in a smaller error while still jumping less than the FVM or the FDM with α = 0. In the comparison in Fig. 7c, the difference between the methods is small. In Fig. 7d, the three methods show similar fluctuations around steady state in low copy number simulations.
6. Conclusions and discussion
We evaluate four different ways of computing jump coefficients between voxels for stochastic simulation of diffusion in a Cartesian mesh; as a distinctive feature we include jumps along the diagonals in the mesh. The method based on the first exit time (FET) is equivalent to a finite difference method (FDM) of second order accuracy if the parameters are chosen appropriately. The most accurate and efficient method compared to the solution of the diffusion equation on a square is to use the coefficients of the finite volume method (FVM) or equivalently a FDM with jumps in the coordinate directions without including the diagonals. If we count the number of jumps to obtain a certain relative error, the differences between the methods are minor. The FVM and FET coefficients are always non-negative. There are restrictions on the mesh for the finite element method (FEM) to generate non-negative coefficients and for a given mesh there are restrictions on the FDM for non-negativity.
A generalization of these methods to an unstructured mesh consisting of triangles and tetrahedra as in [11] is desirable for improved geometrical flexibility. The straightforward FVM in Sect. 2.3 is easily adapted to a triangulated domain. A FEM with linear basis and test functions will generate jump coefficients as in [11]. A FDM consistent with the Laplacian on such a mesh is not easily derived analytically. However, the FVM may not be consistent and the jump coefficients of the FEM may be negative. On a triangular mesh, FVM is consistent if the mesh is of Delaunay type derived from a Voronoi tessellation [32]. A Cartesian mesh has the properties of a Delaunay mesh making FVM consistent there. The FET is easily transformed to an unstructured mesh. The analytical solution of (15) is no longer possible but p(x, t), λ0, and θj can be computed numerically. The jump coefficients are non-negative but there is no FDM to help us determine β. Taking β = 0.5 works fairly well in Sect. 5 for reasonable error levels. The inconsistency with the Laplacian plays a role only for very small errors in the numerical experiments. Hence, this would be the natural choice for an unstructured mesh. The generalization to triangular and tetrahedral meshes of the calculation of the diffusion jump coefficients is the subject of [22].
Acknowledgments
This work has been supported by the Swedish Research Council and the NIH grant for StochSS with number 1R01EB014877-01.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Lina Meinecke, Email: lina.meinecke@it.uu.se.
Per Lötstedt, Email: perl@it.uu.se.
References
- 1.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 2.Raj A, van Oudenaarden A. Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell. 2008;135:216–226. doi: 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. 1976;22:403–434. [Google Scholar]
- 4.Gibson MA, Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J Phys Chem. 2000;104:1876–1889. [Google Scholar]
- 5.Elf J, Ehrenberg M. Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Syst Biol. 2004;1:230–236. doi: 10.1049/sb:20045021. [DOI] [PubMed] [Google Scholar]
- 6.Hattne J, Fange D, Elf J. Stochastic reaction-diffusion simulation with MesoRD. Bioinformatics. 2005;21:2923–2924. doi: 10.1093/bioinformatics/bti431. [DOI] [PubMed] [Google Scholar]
- 7.Kurtz TG. Solutions of ordinary differential equations as limits of pure jump Markov processes. J Appl Prob. 1970;7:49–58. [Google Scholar]
- 8.Kurtz TG. Limit theorems for sequences of jump Markov processes approximating ordinary differential processes. J Appl Prob. 1971;8:344–356. [Google Scholar]
- 9.Gardiner CW, McNeil KJ, Walls DF, Matheson IS. Correlations in stochastic theories of chemical reactions. J Stat Phys. 1976;14:307–331. [Google Scholar]
- 10.Drawert B, Engblom S, Hellander A. URDME: a modular framework for stochastic simulation of reaction-transport processes in complex geometries. BMC Syst Biol. 2012;6:76. doi: 10.1186/1752-0509-6-76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Engblom S, Ferm L, Hellander A, Lötstedt P. Simulation of stochastic reaction-diffusion processes on unstructured meshes. SIAM J Sci Comput. 2009;31:1774–1797. [Google Scholar]
- 12.Hepburn I, Chen W, Wils S, Schutter ED. STEPS: efficient simulation of stochastic reaction-diffusion models in realistic morphologies. BMC Syst Biol. 2012;6:36. doi: 10.1186/1752-0509-6-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Svärd M, Gong J, Nordström J. An accuracy evaluation of unstructured node-centred finite volume methods. Appl Numer Math. 2008;58:1142–1158. [Google Scholar]
- 14.Christie I, Hall C. The maximum principle for bilinear elements. Int J Numer Meth Eng. 1984;20:549–553. [Google Scholar]
- 15.Burman E, Ern A. Stabilized Galerkin approximation of convection-diffusion-reaction equations: Discrete maximum principle and convergence. Math Comp. 2005;74:1637–1652. [Google Scholar]
- 16.Horváth R. Sufficient conditions of the discrete maximum-minimum principle for parabolic problems on rectangular meshes. Comp Math Appl. 2008;55:2306–2317. [Google Scholar]
- 17.Lipnikov K, Svyatskiy D, Vassilevski Y. A monotone finite volume scheme for advection-diffusion equations on unstructured polygonal meshes. J Comput Phys. 2010;229:4017–4032. [Google Scholar]
- 18.Sheng Z, Yuan G. An improved monotone finite volume scheme for diffusion equation on polygonal meshes. J Comput Phys. 2012;231:3739–3754. [Google Scholar]
- 19.Thomée V, Wahlbin L. On the existence of maximum principles in parabolic finite element equations. Math Comp. 2008;77:11–19. [Google Scholar]
- 20.Nordbotten JM, Aavatsmark I, Eigestad GT. Monotonicity conditions for control volume methods. Numer Math. 2007;106:255–288. [Google Scholar]
- 21.Keilegavlen E, Nordbotten JM, Aavatsmark I. Sufficient criteria are necessary for monotone control volume methods. Appl Math Lett. 2009;22:1178–1180. [Google Scholar]
- 22.Lötstedt P, Meinecke L. Dept of Information Technology. Uppsala University; Uppsala, Sweden: 2014. Simulation of stochastic diffusion via first exit times, Technical Report 2014-012. Available at http://www.it.uu.se/research/publications/reports/ [Google Scholar]
- 23.Deaconu M, Lejay A. Simulation of diffusions by means of importance sampling paradigm. Ann Appl Probab. 2010;20:1389–1424. [Google Scholar]
- 24.Strikwerda JC. Finite Difference Schemes and Partial Differential Equations. 2nd. SIAM; Philadelphia: 2004. [Google Scholar]
- 25.Larson MG, Bengzon F. The Finite Element Method Theory, Implementation and Applications. Springer; Berlin: 2013. [Google Scholar]
- 26.LeVeque RJ. Finite Volume Methods for Hyperbolic Problems. Cambridge University Press; Cambridge, UK: 2002. [Google Scholar]
- 27.Gillespie DT, Seitaridou E. Simple Brownian Diffusion. Oxford University Press; Oxford: 2013. [Google Scholar]
- 28.Øksendal B. Stochastic Differential Equations. 6th. Springer; Berlin: 2003. [Google Scholar]
- 29.Opplestrup T, Bulatov VV, Gilmer GH, Kalos MH, Sadigh B. First-passage Monte Carlo algorithm: diffusion without all the hops. Phys Rev Lett. 2006;97:230602. doi: 10.1103/PhysRevLett.97.230602. [DOI] [PubMed] [Google Scholar]
- 30.Redner S. A Guide to First-Passage Processes. Cambridge University Press; Cambridge: 2001. [Google Scholar]
- 31.Oppelstrup T, Bulatov VV, Donev A, Kalos MH, Gilmer GH, Sadigh B. First-passage kinetic Monte Carlo method. Phys Rev E. 2009;80:066701. doi: 10.1103/PhysRevE.80.066701. [DOI] [PubMed] [Google Scholar]
- 32.Eymard R, Gallouët T, Herbin R. A cell-centred finite-volume approximation for anisotropic diffusion operators on unstructured meshes in any dimension. IMA J Numer Anal. 2006;26:326–353. [Google Scholar]