Health, Height, Height Shrinkage, and SES at Older Ages: Evidence from China

Abstract

In this paper, we build on the literature that examines associations between height and health outcomes of the elderly. We investigate the associations of height shrinkage at older ages with socioeconomic status, finding that height shrinkage for both men and women is negatively associated with better schooling, current urban residence, and household per capita expenditures. We then investigate the relationships between pre-shrinkage height, height shrinkage, and a rich set of health outcomes of older respondents, finding that height shrinkage is positively associated with poor health outcomes across a variety of outcomes, being especially strong for cognition outcomes.

The rapid aging of the population places health at older ages among the top public health priorities in recent years, as the fraction of the population that is elderly has been rising. In countries such as China, rapid aging has occurred at much lower levels of national income and worse health conditions than was the case in industrial countries. The elderly in such countries were children when economic development and health conditions were far worse than today, and their health as adults is likely to have been affected by such past conditions, more so than the elderly in industrial countries.

The effects of early-life health and environment on cognitive function, health, well-being, and mortality have been documented by researchers across a range of disciplines, using data from many countries over the world (Elo and Preston 1992; Barker 1994; Nystrom, Peck, and Lundberg 1995; Godfrey and Barker 2000; Finch and Crimmins 2004; Case and Paxson 2005; Case and Paxson 2008b, 2009b, 2010a, 2010b; Alderman and Behrman 2006; Yi, Gu, and Land 2007; Van den Berg, Lindeboom, and Portrait 2006; Smith 2009; Huang and Elo 2009; Almond and Currie 2011).

There are several literatures that have used height to proxy for past health. In the large historical literature, adult height is taken to be an indicator of population health (Fogel 1986, 2004; Steckel 1995, 2009). The nutrition literature long ago established that child height is a very good summary measure of overall health of children (e.g., Martorell and Habicht 1986). Adult height, while reflective of the adolescent growth spurt, is also highly correlated with height during childhood.

A strong association has been found to exist among the elderly between measured height and cognitive ability including dementia, self-reported health, illness status, and measures of depression (e.g., Abbott et al. 1998; Schnaider Beeri et al. 2005; Case and Paxson 2008a, 2010a; Deaton and Arora 2009; Heineck 2009; Maurer 2010; Smith et al. 2012). Most of this literature is from industrial countries (Maurer 2010 and Smith et al. (2012), are exceptions). The exact mechanisms are not completely known, as these studies are not structural, nor causal. Some of the pathways are likely to be through better health during the fetal period and childhood and prime-aged adulthood (e.g., Case and Paxson 2008b or Smith 2009), but other pathways exist as well, such as taller people having more schooling and consequently making better health behavior decisions (e.g., Cutler and Lleras-Muney 2010).

However, older people suffer height shrinkage during aging. Aging is associated with several physiological and biological changes, including body composition, such as an increase in body fat, a decrease in lean body mass and bone mass. Through such mechanisms as certain kinds of arthritis (such as ankylosing spondylitis), inflammation of spine joints, herniated disks, or kyphosis, these changes can lead to vertebral deformity, which can contribute to a reduction in height, or shrinkage (Kwok, Lau, and Woo 2002; Prothro and Rosenbloom 1993; Roubenoff and Wilson 1993). One health condition that can influence shrinkage directly and through many of these other proximate causes is osteoporosis. Early osteoporosis can be caused by mechanisms such as early menopause, diet, exercise, smoking, excess drinking and exposure to certain heavy metals such as lead. Some of these conditions may have their origins in childhood. Height shrinkage may thus be more severe in those with current health problems or problems from early childhood, or even be correlated with pre-shrinkage height itself. This suggests a potential relationship between shrinkage and different SES factors that are associated with current health and early childhood health problems. Furthermore, estimates of the impacts of height on other health measures, as we see in the current literature, may miss some important insights because shrinkage is not considered.

In this paper, we construct estimates of height shrinkage using techniques from the nutrition/human biology literature. We examine the SES correlates of shrinkage and use both estimated pre-shrinkage height and shrinkage as covariates in OLS regressions of health on height. The first step is to estimate the pre-shrinkage height of the seniors. This issue has a long history in the nutrition and human biology literature, even, especially, using cross-section data. Measured height is regressed on limb length(s) and the resultant prediction is used as a measure of pre-shrinkage height. This works because the limbs used in this literature do not generally shrink as people age. Lower leg length (Chumlea, Roche, and Steinbaugh 1985; Chumlea and Guo 1992; Protho and Rosenbloom 1993; Myers, Takiguchi, and Yu 1994; Zhang, Hsu-Hage, and Wahlqvisl 1998; Bermúdez, Becker, and Tucker 1999; Li et al. 2000; Cheng, See, and Shieh 2001; Pini et al. 2001; Knous and Arisawa 2002), arm span from roughly the shoulder to the wrist (Kwok and Whitelaw 1991; Kwok, Lau, and Woo 2002), total arm length (Mitchell and Lipschitz 1982; Haboubi, Hudson, and Pathy 1990; Auyeung and Lee 2001), upper arm or humeral length, tibia length (Haboubi, Hudson, and Pathy 1990) and fibula length (Auyeung and Lee 2001) have all been employed to estimate pre-shrinkage stature.

Most of this literature simply uses lower leg or arm length to predict height using older populations. In some cases, a younger population that should not have shrunk yet, is used to estimate the function relating height to limb length(s), and the parameters used to predict height for an older population that has been shrinking, assuming that the parameters are the same for the two age groups (e.g., Reeves, Varakamin, and Henry 1996). Rarely is an attempt made to actually estimate shrinkage, and generally no attempt is made to relate shrinkage to socioeconomic variables. Likewise, very little literature exists that relates height shrinkage to other health variables, although see Hillier et al. (2012) for a recent interesting exception relating shrinkage in older women to subsequent hip fractures and mortality. In contrast, there is some literature, though not large, that relates limb lengths to different health outcomes. The idea is that limb lengths are a proxy for childhood health influences. For instance, Huang et al. (2008) use leg length and arm span to predict dementia in an older population. More interesting for our purposes is a recent paper by Zhang, Gu, and Hayward (2010) that uses another survey of Chinese elderly, the Chinese Longitudinal Healthy Longevity Survey, to relate arm length and knee height to cognitive impairment at older ages, finding strong negative associations between limb lengths and cognition among this older population. They do not, however, examine the correlations between height shrinkage and cognition or the SES correlates of shrinkage.

Based on the national baseline data from the China Health and Retirement Longitudinal Study (CHARLS), this paper investigates the correlates of shrinkage with current SES and indicators of childhood health, and whether shrinkage is correlated with pre-shrinkage height and, separately, with limb lengths. We find strong negative associations between shrinkage and current measures of SES, such as level of education, log of household per capita expenditure (pce), and urban residence, as well as strong correlations with county of current residence and province of birth. However, the correlation between height shrinkage and nonlocation measures of childhood background are weak.

We then replace measured height by our pre-shrinkage height estimates, plus our estimates of height shrinkage, as covariates in regressions to investigate their associations with a rich set of later-life health variables: measures of cognitive functioning, hypertension, lung capacity, grip strength, balance, walking speed, self-reported general health, measures of physical functioning, activities of daily living (ADLs), instrumental activities of daily living (IADLs), the Center for Epidemiologic Studies Depression Scale (CES-D) and expectation of surviving to age 75 (for respondents under 65). We find that even controlling for SES and early-life health conditions, that pre-shrinkage height and especially height shrinkage have significant associations with these later-life health conditions. In general, height shrinkage is negatively correlated with good health outcomes and pre-shrinkage height positively so. For many of our health variables, height shrinkage has considerably larger coefficients (in absolute value), which are more likely to be statistically significant, than for pre-shrinkage height.

Given our shrinkage results, height shrinkage is more a marker for later-life health problems than for early-life health conditions, in contrast to pre-shrinkage height, which is a marker of early-life health. Hence, this evidence means that it is not only early life events that are associated with late life health outcomes (childhood background variables are jointly significant in these health regressions), but health insults in later life as well. Had we only examined the correlations between measured height and these health variables, we would have missed this important insight. By providing evidence of whether and how height shrinkage is correlated with SES, this paper also validates the concern raised, but not tested, by Case and Paxson (2008a), that individuals with poor health tend to shrink more than healthy ones.

This paper is organized as follows. In Section I, we discuss our model and econometric framework to estimate height shrinkage and pre-shrinkage height. Section II discusses the data used in this paper and summary statistics. Section III shows how we estimate the pre-shrinkage height function from a sample of “young” respondents and height shrinkage for our “older” sample. Section IV discusses the evidence on the association between height shrinkage and SES and pre-shrinkage height. Section V provides further evidence on the association between height shrinkage, pre-shrinkage height and our health measures of this older population. Section VI concludes.

I. Theoretic Framework

In previous studies, what has interested many researchers is the association between height and health status. A prototypical regression is

$$y={\mathbf{x}}^{\prime }\mathbf{\theta }+p\alpha +u,$$ (1)

in which y stands for health variables such as self-reported health, ADL disability, or cognitive ability; p is respondents’ pre-shrinkage height; x is short for a set of covariates, such as demographic variables, possibly SES, or perhaps other childhood health variables; u is the error term, which is assumed in the literature to be mean independent of height and control variables. We also assume that it is mean independent of the predictors of pre-shrinkage height.¹ Most researchers are interested in the coefficient α. However, in most situations, pre-shrinkage height is unobserved and the interviewers have available only measured height (h), which might have been contaminated by height shrinkage (s). The regression thus estimated is

$$y={\mathbf{x}}^{\prime }\stackrel{\sim }{\theta }+h\stackrel{\sim }{\alpha }+\stackrel{\sim }{u},$$ (2)

and for the older population measured height (h), as an identity equals pre-shrinkage height (p) minus height shrinkage (s) (in the younger sample, in principle, measured height equals pre-shrinkage height):

$$h\equiv p-s.$$ (3)

Height shrinkage may be independent of pre-shrinkage height, which is easier to handle, but this may not be the case. On the one hand, pre-shrinkage height is a marker of early-life health status, and healthier people might shrink less with aging, have less osteoporosis, for example. On the other hand, taller people may lose more height if they suffer kyphosis or some other related diseases. In these situations, the coefficients on height and x in (2) are a biased estimate of the coefficients on preshrinkage height and x in (1) because the error in (2) will contain shrinkage that is correlated with pre-shrinkage height and x.²

Maurer (2010) assumed that lower leg length was correlated with pre-shrinkage height and not correlated with height shrinkage, and used lower leg length as an instrument for measured height, using data from Latin America and the Caribbean. Then he argued that the 2SLS estimation would give consistent results. However, if pre-shrinkage height is correlated with height shrinkage conditional on control variables and error term, this suggests that lower leg length may be correlated with the error term as well, then this 2SLS estimate will also be inconsistent. We will test this directly.

In this paper, we use lower leg length and upper arm length to predict pre-shrinkage height using different data on a younger population, instead of taking them as instruments directly. We use estimates of this height function to predict pre-shrinkage height and height shrinkage for respondents from an older population, aged 60 and over. Of course in doing so we have to assume that the relationships between limb lengths and heights are the same for the two age groups. There is not much literature on this, what there is we discuss below, along with limited evidence from CHARLS that we can provide.

Firstly, we estimate the following equation for the younger group:

$$h_y={\mathbf{z}}_y^{\prime }\mathbf{\gamma }+{\eta }_y,$$ (4)

where z is a vector representing lower leg length, upper arm length (as an adult), and a Han ethnic dummy. The variables in x and z overlap because of the Han dummy, but there are variables (the limb lengths) in z that are excluded from x. We assume

$$\mathbb{E}({\eta }_y\mid {\mathbf{z}}_y,{\mathbf{x}}_y)=0.$$

We then apply the estimated γ coefficients to the older age group to estimate their pre-shrinkage height:

$$\widehat{p_o}={\mathbf{z}}_o^{\prime }\widehat{\mathbf{\gamma }}.$$ (5)

Height shrinkage is defined as the difference between pre-shrinkage height and measured height, as in (3).

After estimating pre-shrinkage height and height shrinkage, we estimate the association between height shrinkage and SES variables, i.e., education levels; per capita pce; age dummies; living in an urban area; marital status; and childhood background variables, such as having an urban childhood upbringing, schooling of each parent, whether each parent had died before the respondent was 18, a self-reported general health measure of the respondent’s health before age 16, and dummies for province of birth.³ To test potential bias in an IV specification using limb lengths as instruments, we add limb lengths as x covariates and test their association with shrinkage. In a second specification, we add pre-shrinkage height. That is,

$$s={\mathbf{x}}^{\prime }\mathbf{\beta }+p\delta +\epsilon ,$$ (6)

with 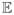(ε | x, p, z) = 0. Finally, we estimate (1) and (2), along with (7), to examine the associations between height and health:⁴

$$y={\mathbf{x}}^{\prime }\mathbf{\theta }+p\alpha +s\kappa +u.$$ (7)

Separate OLS estimation of (4) and (6), or (4) and (7), is the optimal two-step GMM estimator. Our standard errors for (1), (6), and (7) are corrected for the fact that we use predicted variables as dependent and/or independent variables. We derive the asymptotic variances in Appendix 1.

II. Data

CHARLS was initiated to study the elderly population of China. It is designed to be complementary to the Health and Retirement Study (HRS) in the United States and similar surveys around the world. CHARLS covers 150 counties randomly chosen across China. Twenty-eight provinces are represented in the data.⁵ Counties were grouped into eight geographic regions and stratified by rural/urban status and by per capita county GDP.⁶ Counties were then sampled and stratified, with probability proportional to population (PPS).⁷ Within counties we sampled three administrative villages or urban neighborhoods (resident committees) as our primary sampling units (PSU), again using PPS.⁸

The sampling goal within primary sampling units was 24 households with an age eligible member, defined as a person aged 45 or older. Sampling rates varied by PSU. We first mapped all of the dwellings in the PSU, using Google Earth maps, adjusted from the ground by our mapping teams.⁹ From this we obtained a sampling frame of dwelling doors. We then randomly sampled 80 doors, and obtained information on the age of the oldest person and whether the dwelling was vacant (which some were). Using this information, we calculated age eligibility rates. From this information we determined PSU-specific sampling rates to ensure, in expectation, 24 age-eligible households and re-sampled from the initial dwelling list. If a dwelling had multiple households living in it, we randomly sampled one with an age-eligible person. Households were defined as living together, sharing meals and at least some other expenses. After sampling our final list of households, we again checked for age eligibility and then randomly sampled one person age 45 or over, and their spouse (no matter the age), as our respondents.

The national baseline was fielded from late summer 2011 until March 2012 (see Zhao et al. 2012, for details). Among all households, the age eligibility rate was 62 percent and the response rate among eligible households was 85 percent, 91 percent among rural households, and 79 percent for urban households.¹⁰ These rates compare very well with other HRS surveys in their initial waves. Sample size is 17,705 individuals with nonmissing ages.

We use two samples for this paper. We estimate our pre-shrinkage height prediction equation using a “young” sample of respondents and spouses aged 45–49, who have presumably not started to shrink yet, or if so, have only shrunk a very small amount on average. We then use respondents and spouses aged 60 and over to predict pre-shrinkage heights, calculate shrinkage, and estimate our models. Of the 17,705 observations, 3,451 are between 45 and 49 years old and 7,736 are 60 years old and over. Approximately 25 percent of “young” respondents did not get their biomarkers taken, usually because they were busy at work and unavailable. Among the “old” sample, 18 percent did not get any biomarkers taken, usually because they were too frail to be measured. Nonmeasurement rates were higher among those over 80 years. In addition, some observations were dropped because they had missing heights or other key variables missing or out of reasonable range. We are left with 1,101 men and 1,508 women in the “young” sample and 2,953 men and 2,935 women in the “old” sample, who have complete height and limb measurements (fewer with all of the other health variables complete).

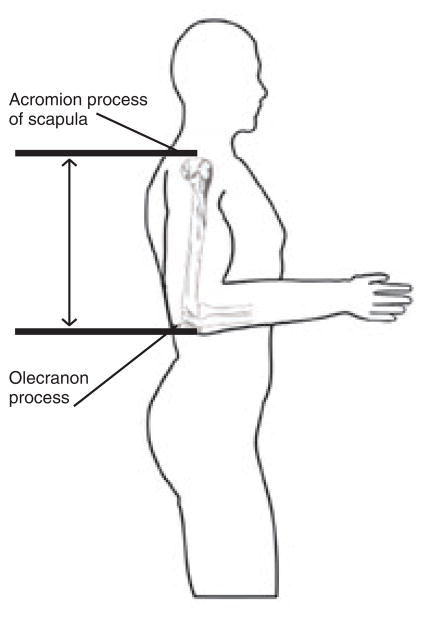
Anthropometric measures included respondent’s standing height, upper arm length, and lower leg length, all measured in millimeters. The summary statistics of these variables are shown in panels A and B of Table 1 for the “young” and “old” samples, respectively. Height was measured using a stadiometer directly from the heel to the top of the head, with the elders standing upright. Upper arm length was measured with a Martin caliper with the respondent standing and holding the left or right arm at a right angle. We measured from the acromion process of the scalpula to the olecranon process. Lower leg length was also measured using a Martin caliper from the right knee joint to the ground (pictures of how limb lengths are measured, used in the CHARLS training, are provided in Appendix 2). Measured heights are smaller for the older group, by some 4.0 cm for men and 4.6 cm for women. Much of this difference could be due to shrinkage, although it could also be that older birth cohorts were less tall. Comparing upper arm lengths, they are very close between the 45–49 and 60 and over age groups, suggesting that shrinkage may be the more important explanation. On the other hand, lower leg lengths are about 0.6 cm smaller for the over 60 group for both men and women, suggesting some possible cohort effects. Indeed, our estimates of shrinkage for the older population are 3.3 cm for men and 3.8 cm for women, a bit less than the differences in measured heights between the two age groups, consistent with part of the height differences being birth cohort differences.

Table 1.

Summary Statistics

Variable	Male sample			Female sample
	Obs.	Mean	SD	Obs.	Mean	SD
Panel A. Younger sample (45 < = Age < = 49)
Height (cm)	1,101	166.35	6.16	1,508	155.20	5.86
Upper arm length (cm)	1,101	35.20	2.37	1,508	32.60	2.20
Lower leg length (cm)	1,101	50.00	3.09	1,508	46.52	2.98
Age	1,101	47.31	1.31	1,508	47.25	1.35
Han race	1,101	0.94	0.24	1,508	0.92	0.27
Panel B. Older sample (Age > = 60)
Biological measures and demographics
Height (cm)	2,953	162.33	6.79	2,935	150.65	6.50
Upper arm (cm)	2,953	35.22	2.39	2,935	32.49	2.20
Lower leg (cm)	2,953	49.45	2.92	2,935	45.89	2.97
Pre-shrinkage height (cm)	2,953	165.62	4.32	2,935	154.44	4.05
Height shrinkage (cm)	2,953	3.30	5.05	2,935	3.80	5.02
Age	2,953	68.06	6.41	2,935	68.11	6.93
Han race	2,953	0.94	0.23	2,935	0.93	0.25
Cognitive abilities
TICS (0–5)	2,941	7.17	2.72	2,915	5.26	3.15
Words recall (0–10)	2,720	3.10	1.67	2,619	2.85	1.74
Draw a figure successfully (0–1)	2,941	0.64	0.48	2,915	0.40	0.49
Biomarkers
Hypertension (0–1)	2,939	0.48	0.50	2,921	0.57	0.50
Lung capacity	2,799	263.96	113.48	2,673	195.17	79.39
Grip strength	2,903	32.70	9.04	2,847	21.67	7.34
Balance (0–1)	2,850	0.75	0.43	2,767	0.60	0.49
Walk time	2,780	4.42	2.10	2,714	5.01	2.68
General health
Poor general health (0–1)	2,953	0.29	0.46	2,934	0.36	0.48
Physical function (0–7)	2,741	1.13	1.40	2,500	1.64	1.59
ADLs (0–6)	2,931	0.39	0.99	2,907	0.56	1.16
IADLs (0–5)	2,937	0.49	1.09	2,913	0.75	1.27
CESD (0–30)	2,773	8.04	5.98	2,669	10.26	6.77
Life expectation pessimistic (0–1)	2,599	0.33	0.47	2,451	0.38	0.49
Adulthood socioeconomic status
Education levels
Illiterate	2,953	0.20	0.40	2,935	0.54	0.50
Primary	2,953	0.56	0.50	2,935	0.35	0.48
Junior	2,953	0.16	0.37	2,935	0.07	0.26
Senior and above	2,953	0.08	0.27	2,935	0.03	0.18
Log (expenditure per capita)	2,953	8.35	0.91	2,935	8.29	0.93
Married	2,953	0.86	0.34	2,935	0.71	0.46
Urban	2,953	0.18	0.38	2,935	0.21	0.41
Childhood socioeconomic status
Urban before 16	2,953	0.08	0.28	2,935	0.08	0.27
Childhood health fair and better	2,953	0.93	0.25	2,935	0.90	0.30
Childhood health poor	2,953	0.06	0.24	2,935	0.09	0.29
Childhood health missing	2,953	0.01	0.08	2,935	0.01	0.09
Father illiterate	2,953	0.66	0.48	2,935	0.70	0.46
Father literate	2,953	0.29	0.46	2,935	0.24	0.43
Father education missing	2,953	0.05	0.22	2,935	0.06	0.24
Mother illiterate	2,953	0.91	0.28	2,935	0.93	0.26
Mother literate	2,953	0.05	0.22	2,935	0.04	0.19
Mother education missing	2,953	0.04	0.18	2,935	0.03	0.18
Father alive before 18	2,953	0.87	0.34	2,935	0.89	0.31
Father dead before 18	2,953	0.12	0.33	2,935	0.10	0.30
Father death missing	2,953	0.01	0.10	2,935	0.01	0.08
Mother alive before 18	2,953	0.91	0.29	2,935	0.93	0.25
Mother dead before 18	2,953	0.07	0.26	2,935	0.06	0.23
Mother death missing	2,953	0.01	0.12	2,935	0.01	0.10

Source: CHARLS 2011

As mentioned above, this study examines the associations between pre-shrinkage height and height shrinkage on different measures of health of older people. We start with cognition questions, which are grouped into three categories, following McArdle (2010) and Smith, McArdle, and Willis (2010). The first component is the Telephone Interview of Cognitive Status (TICS). There are ten questions in this part, from awareness of the date (using either solar or lunar calendar), the day of the week and season of the year, to successively subtracting 7 from 100. An index is formed using the number of correct answers. This is a measure of the mental intactness of the respondent (Smith, McArdle, and Willis 2010). A second set of questions asks a respondent to recall a series of ten simple nouns and to recall them again after approximately ten minutes. Following McArdle (2010), we average the number of correct answers as our dependent variable. This is a measure of episodic memory, and is a component of fluid intelligence (Smith, McArdle, and Willis 2010). Finally, respondents are shown a picture of two overlapping pentagons and asked to draw it. We score the answer as one if the respondent successfully performs this task.

We have several biomarker variables available. We measure blood pressure three times. We create a dummy variable equal to one if a respondent has hypertension. For this case, we take means of systolic and diastolic measurements and assign a hypertensive status equal to 1 if mean systolic is 140 or greater or if mean diastolic is 90 or greater. In addition, respondents self-report if they have been diagnosed by a doctor with hypertension, and we include those cases as being hypertensive. Respondents blow into a peak flow meter three times to measure lung capacity and we take the average. Respondents have their grip strength measured by a dynamometer. Two measurements are taken from each hand. We use average measurement from the self-reported dominant hand. Respondents are given a balance test, whether they can stand semi-tandem or full tandem. Because most can stand full tandem, we create a dummy equal to one if they can do so.¹¹ Finally we conduct a timed walk of four meters, asking the respondent to walk at a “normal” speed.

The remaining health measures are self-reported. General health is reported on a scale: very good, good, fair, poor, and very poor. We construct a binary variable equal to one if health is reported as very poor or poor, zero otherwise. Respondents are asked about whether they have difficulty in performing certain classes of activities: physical functioning, ADLs, and IADLs.¹² We count the number of items in each group that the respondent claims having difficulty performing or cannot perform. The expected survival question asks respondents to rank their expectation of surviving to a specific older age on a five point scale, from almost impossible to almost certain. We group the bottom two answers, almost impossible and not very likely. Because different age groups are asked survival chances at different ages, we standardize by only using those respondents under age 65 who are asked their survival chances to age 75. Similarly, respondents answered a Chinese version of CES-D 10 questionnaire in the survey, which contained ten questions about the respondents’ depression status. Based on that, we constructed a CES-D scale a with range from 0 to 30.

Mean values and standard deviations of all the health variables are provided in panel B of Table 1 for the “old” sample. As is generally the case, health measures for older women are worse than for men. This is true both for self-reported measures, such as poor general health, difficulties with physical functioning or ADLs, and the CES-D depression scale, and for biomarkers, such as hypertension, the cognition measures, grip strength, and lung capacity.

Panel B also reports summary statistics of demographic variables like education level, log of household per capita expenditure (pce),¹³ marital status, and type of areas (urban/rural) where respondents lived at the time of the survey. The current generation of elderly population in China has only a small amount of schooling, particularly among women. Fifty-four percent of women 60 and over are illiterate, and 20 percent of men are illiterate. Only 8 percent of older men and 3 percent of women have completed senior high school or more. However, 56 percent of men have completed primary school, while 35 percent of women completed primary school. When we compare these numbers to the parents of these elderly, some progress had been made, since 70 percent of fathers and over 90 percent of mothers are reported to be illiterate (no schooling or less than primary school completion, see panel B). The preponderance of our respondents are still married, more so among men, since their spouses tend to be younger. An overwhelming majority, roughly 80 percent of older men and women, live in rural areas.

Childhood background variables are also reported in panel B. An even larger percent, over 90 percent, have a rural background as a child. About 10–12 percent of fathers and about 6–7 percent of mothers died before the respondent was age 18. CHARLS has a retrospective question about general health before the respondent turned 16 (an average over that period), with categories excellent, very good, good, fair, or poor. This has been successfully used by HRS and other aging surveys, including the CHARLS pilot, and has been linked to later-life health outcomes (e.g., Smith 2009). In the CHARLS sample, 6 percent of men and 9 percent of women report that their childhood health was poor. Finally, CHARLS also elicits province of birth. Evidence on public health infrastructure for prerevolutionary China is scant, but some evidence exists that in Beijing better water and sanitation facilities were built between 1910 and 1920 (Campbell 1997) and that led to a rapid decline in infant mortality there. This would have affected our cohorts. For other major cities there is some, but not much, evidence that public health infrastructure was being built during that time period (Campbell 1997).

III. Estimation of Pre-shrinkage Height

Following the methodology in the medical literature, we use lower leg length and upper arm length and estimate gender-specific equations using measured height as the dependent variable. Additionally, we add quadratics in both limb lengths and interactions to allow for nonlinearities. We also add a Han dummy variable to pick up potential ethnic differences.¹⁴

The steps to estimate pre-shrinkage height are as follows. First, we use data from the “young” group, aged 45–49, and regress measured height on lower leg length, upper arm length, their squares and interaction, and the Han dummy. These coefficients are then applied in the “older” sample, those aged 60 and above, and the predicted value is the estimated pre-shrinkage height for this group. Some medical studies have used this approach, separating “young” and “old” groups, including Steele and Mattox (1987) and Reeves, Varakamin, and Henry (1996).¹⁵ A strong assumption is required that any secular changes in height across birth cohorts (which are important in China) do not change the relationship between height and limb length (see Leung et al. 1996 and Kwok, Lau, and Woo 2002).¹⁶ While we cannot test this restriction directly, we provide some indirect evidence for the 5-year age group, 45–49. We add individual age dummies plus interactions between the age dummies and each of the limb lengths. We then test the joint significance of the age dummies plus limb interactions to examine whether the coefficients vary by age. While this is suggestive, it does not rule out possible change of coefficients across a wider age gap. The regressions are shown in Table 2.

Table 2.

Pre-shrinkage Height Prediction

Variables	Measured height (cm)
	Male sample			Female sample
	(1)	(2)	(3)	(4)	(5)	(6)
Upper arm length	0.694*** (0.115)	−0.0819 (1.712)	0.563 (0.381)	0.776*** (0.0946)	−1.993* (1.169)	0.498* (0.276)
Lower leg length	0.996*** (0.105)	−6.689*** (1.245)	0.952*** (0.325)	0.931*** (0.0735)	−4.116*** (1.107)	0.938*** (0.182)
Upper arm length square		0.00268 (0.0240)			0.0561** (0.0226)
Lower leg length square		0.0761*** (0.0122)			0.0632*** (0.0149)
Interaction of arm length and leg length		0.00982 (0.0330)			−0.0196 (0.0221)
Han race	0.397 (0.564)	0.716 (0.589)	0.367 (0.587)	1.056** (0.426)	1.260*** (0.408)	0.896** (0.430)
Age dummies
45 (Reference)
46			1.678 (15.93)			−11.56 (10.30)
47			−7.384 (17.57)			−15.77 (11.73)
48			−15.24 (16.26)			−9.856 (9.858)
49			−12.63 (16.60)			−13.19 (10.15)
Age dummies interacting upper arm length
45 and arm (reference)
46 and arm			−0.146 (0.417)			0.217 (0.311)
47 and arm			0.0730 (0.462)			0.402 (0.337)
48 and arm			0.0520 (0.433)			−0.0234 (0.323)
49 and arm			0.708 (0.446)			0.732** (0.353)
Age dummies interacting lower leg length
45 and leg (reference)
46 and leg			0.0703 (0.363)			0.0828 (0.221)
47 and leg			0.102 (0.420)			0.0468 (0.252)
48 and leg			0.258 (0.374)			0.220 (0.225)
49 and leg			−0.243 (0.397)			−0.246 (0.239)
Constant	91.78*** (4.536)	291.4*** (47.90)	98.59*** (13.81)	85.63*** (3.263)	243.2*** (19.51)	94.92*** (8.104)
Observations	1,101	1,101	1,101	1,508	1,508	1,508
R2	0.443	0.518	0.458	0.452	0.513	0.465
f-test for all limbs	140.3	136.5	12.14	228.6	180.3	30.56
p-value	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]
f-tests–Limbs quadratic terms		16.90			23.25
p-value		[0.000]			[0.000]
f-test–Age dummies plus interactions with limbs			1.182			1.242
p-value			[0.291]			[0.248]

Source: CHARLS 2011. Sample used are those aged between 45 and 49. Coefficients in columns 2 and 5 are used to predict pre-shrinkage height in older sample (60 +).

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level.

Columns 1–3 in Table 2 show the coefficients of the pre-shrinkage height function for the male sample, and columns 4–6 show the coefficients of the pre-shrinkage height function for the female sample. We first show a linear specification in limb lengths and the Han dummy, then add quadratics and an interaction, and finally add the age dummies and limb interactions. In the linear models, an increase of 1 cm in lower leg length is associated with an increase of 1 cm in measured height for men and 0.93 for women,¹⁷ as one would expect if shrinkage has not yet begun. The coefficients on upper arm length are 0.69 and 0.78 for men and women, respectively, each significant at 0.001. The Han dummy is positive for both men and women, but significant (at 5 percent) only for women. The quadratics and interaction are always jointly significant at under 0.001, while the age dummies and limb interactions are not jointly significant at standard levels. Hence, we use columns 2 and 5 as our preferred estimates. The marginal effects on height of both lower leg and upper arm lengths are positive over the entire distribution, and convex. The R²s are over 0.51 for both men and women.¹⁸

After we obtain our pre-shrinkage height estimates for the 60 and older group, height shrinkage is defined as the estimated pre-shrinkage height less the current measured height. The summary of our estimates are shown in panel B of Table 1. Mean height shrinkage is 3.3 cm for men and 3.8 cm for women, which is consistent with findings in the human biology literature that women have more problems with vertebral deformity (see Kwok, Lau, and Woo 2002).

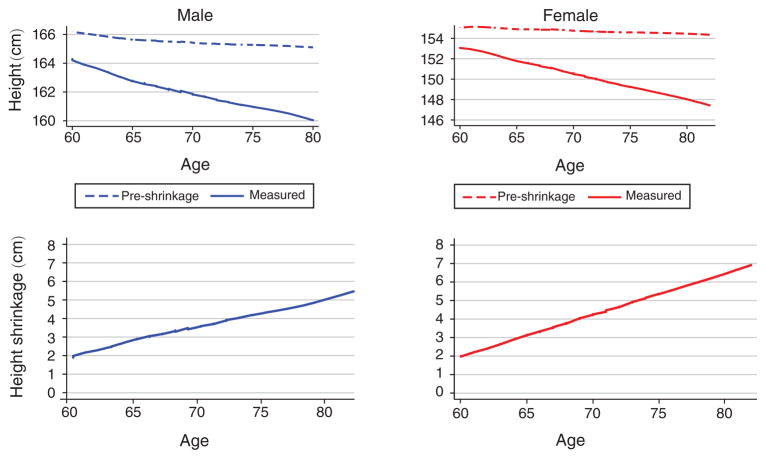
Figure 1 shows the age pattern of measured height, pre-shrinkage height, and height shrinkage by gender. The top two figures show nonparametric graphs of measured height and pre-shrinkage height as a function of age. And the bottom two graphs show the pattern of height shrinkage and age for males and females, respectively. ¹⁹ From the top two graphs, estimated pre-shrinkage height does not decline much with age, a little more for men than for women. However, measured height does decline with age, indicating that height shrinkage increases, as shown in the bottom two figures. Our pre-shrinkage height estimates do not correct for mortality selection. If we assume that respondents who survived to older ages are those who were taller and less frail, then adding those who died back would result in preshrinkage heights declining with age. This is what we would expect if older birth cohorts faced worse health conditions at birth, and in early life.

Figure 1.

Measured Height, Pre-shrinkage Height, and Height Shrinkage

Source: CHARLS 2011

As a check on our pre-shrinkage height estimates, we compare our CHARLS pre-shrinkage heights for the sample aged 60–69 in 2011, by year of birth, to measured heights in another data source, the China Health and Nutrition Survey (CHNS). We use the same birth year cohorts in both datasets, but in the CHNS data we can measure heights of these cohorts 20 years earlier, in 1991, when they would be aged 40–49, and so should not have begun to shrink much yet. We thus expect their measured heights in 1991 to be close to our estimated pre-shrinkage heights in the CHARLS data for the same birth year cohort.²⁰ The CHNS data in 1991 only covers eight provinces, not 28 provinces as in CHARLS. To make the comparisons cleaner, we restrict the CHARLS data to the same eight provinces as covered in CHNS. The results are shown in Table 3. Comparing mean heights by birth year cohort between being measured in 1991 in CHNS and in 2011 in CHARLS, heights in 1991 are higher, by, generally, between 1.5–3.2 cm for men, depending on the age, and 1.3–5.3 cm for women. These differences are consistent with shrinkage. Comparing mean heights in 1991 with estimated pre-shrinkage heights from CHARLS, the results show a close correspondence. For women, the differences between the CHARLS estimated pre-shrinkage heights and the CHNS measured heights is very small, generally under 0.7 cm in absolute value and often less than 0.5 cm. For men, aged 60–64 in 2011 (40–44 in 1991), the differences are very small as well; they increase some for those aged 63–69 in 2011, which may indicate that there is some shrinkage that has begun in this age group.²¹

Table 3.

Height Comparison with CHNS 1991

Age in 2011	CHNS 1991			CHARLS 2011			Differences
	MH	Obs.	Age in 1991	MH	PH	Obs.	MH 2011–MH 1991	PH 2011–MH 1991
Panel A. Male sample
60	165.64 [5.667]	106	40	163.05 [6.048]	165.50 [5.119]	91	−2.59	−0.14
61	166.71 [5.819]	84	41	164.85 [5.947]	166.58 [4.627]	85	−1.86	−0.13
62	165.66 [6.391]	82	42	162.66 [5.992]	165.70 [3.398]	114	−3.00	0.04
63	165.43 [5.609]	75	43	163.94 [6.568]	166.35 [5.261]	82	−1.50	0.92
64	164.81 [7.259]	79	44	163.39 [7.350]	165.57 [4.422]	97	−1.41	0.76
65	163.76 [6.708]	98	45	163.69 [7.135]	165.90 [4.766]	76	−0.06	2.14
66	164.16 [6.396]	62	46	162.52 [6.664]	164.95 [4.103]	61	−1.64	0.79
67	163.36 [5.885]	57	47	161.47 [7.655]	164.50 [5.381]	63	−1.90	1.13
68	163.94 [6.415]	59	48	161.50 [6.462]	164.76 [3.829]	70	−2.45	0.82
69	163.77 [6.453]	63	49	160.59 [6.530]	165.58 [4.361]	63	−3.17	1.81
Panel B. Female sample
60	154.60 [5.886]	104	40	151.90 [5.801]	154.57 [4.125]	123	−2.71	−0.03
61	153.98 [5.899]	101	41	151.68 [6.051]	154.47 [3.639]	105	−2.29	0.50
62	154.19 [4.964]	97	42	152.93 [5.596]	154.71 [3.753]	94	−1.27	0.52
63	154.03 [5.859]	89	43	151.97 [6.942]	154.93 [4.140]	74	−2.06	0.90
64	155.49 [6.032]	80	44	152.04 [6.080]	154.17 [3.636]	98	−3.45	−1.31
65	152.16 [6.189]	86	45	150.09 [6.471]	153.72 [4.056]	76	−2.08	1.56
66	153.61 [5.869]	61	46	150.50 [7.179]	154.17 [4.315]	69	−3.11	0.55
67	153.28 [4.554]	58	47	148.84 [5.879]	154.44 [4.391]	60	−4.44	1.16
68	153.49 [5.383]	69	48	148.23 [5.558]	153.67 [4.207]	51	−5.26	0.18
69	153.96 [6.537]	67	49	150.39 [5.903]	153.94 [4.024]	59	−3.57	−0.03

Notes: MH-Measured Height; PH-Pre-shrinkage Height. Standard deviations are in brackets. Unit of heights is centimeters. CHNS 1991 was fielded in eight provinces: Liaoning, Jiangsu, Shandong, Henan, Hubei, Hunan, Guangxi, and Guizhou. The CHARLS data are from the same provinces.

IV. Height Shrinkage, Pre-shrinkage Height and SES

Very few studies have been able to measure height shrinkage and we know precious little about the correlations between shrinkage and later life SES, early-life health conditions, and family background. Further, as noted, any correlations between height shrinkage and upper arm and lower leg length are important since they determine whether an IV estimator using lower leg and upper arm lengths as IVs for measured height in health equations is consistent. Table 4 shows the gender-specific results of the association between SES, early life conditions, upper arm and lower leg length, and height shrinkage. All regressions control for basic demographic variables, including dummy variables for age, Han ethnicity, marital status, urban residence, and current residential county. We also include covariates measuring early life conditions, including dummies for province of birth, urban upbringing before age 16, for schooling of the father and mother, for whether the father and mother died by respondent’s age 18, and for whether the respondent reported being in poor health, on average, before age 16. In columns 2 and 5, we add pre-shrinkage height. In columns 3 and 6, we replace pre-shrinkage height with lower leg and upper arm lengths in order to test for bias with an IV estimator of (2). All estimates correct standard errors for the fact that we predict shrinkage and pre-shrinkage heights (see Appendix 1 for detailed derivations).

Table 4.

Pre-shrinkage Height and SES

Variables	Height shrinkage (cm)
	Male sample			Female sample
	(1)	(2)	(3)	(4)	(5)	(6)
Pre-shrinkage height (cm)		0.007 (0.0275)			0.044 (0.0283)
Lower leg length			−0.104** (0.0466)			0.066 (0.0467)
Upper arm length			0.053 (0.0576)			−0.033 (0.0622)
Education level: Illiterate (reference)
Primary	−0.928*** (0.2375)	−0.925*** (0.2376)	−0.939*** (0.2373)	−0.594*** (0.2044)	−0.603*** (0.2043)	−0.599*** (0.2044)
Junior	−1.597*** (0.3144)	−1.597*** (0.3145)	−1.589*** (0.3141)	−0.976** (0.3866)	−1.012*** (0.3865)	−0.996** (0.3866)
Senior and above	−1.922*** (0.4042)	−1.920*** (0.4042)	−1.948*** (0.4038)	−1.728*** (0.5571)	−1.743*** (0.5568)	−1.749*** (0.5569)
Log expenditure per capita	−0.217** (0.1045)	−0.218** (0.1046)	−0.204* (0.1045)	−0.086 (0.1018)	−0.091 (0.1017)	−0.090 (0.1017)
Married	−0.334 (0.2547)	−0.335 (0.2547)	−0.321 (0.2544)	−0.024 (0.2041)	−0.032 (0.2040)	−0.022 (0.2040)
Urban	−0.858** (0.3487)	−0.862** (0.3488)	−0.835** (0.3483)	−1.099*** (0.3159)	−1.118*** (0.3158)	−1.119*** (0.3159)
Han race	−0.141 (0.6594)	−0.142 (0.6583)	−0.148 (0.6590)	0.641 (0.5853)	0.589 (0.5802)	0.636 (0.5851)
Urban area before 16-year-old	−0.347 (0.4020)	−0.347 (0.4021)	−0.344 (0.4016)	−0.384 (0.3880)	−0.411 (0.3879)	−0.404 (0.3880)
Childhood health poor	0.031 (0.3555)	0.034 (0.3556)	0.006 (0.3552)	0.513* (0.2939)	0.526* (0.2937)	0.534* (0.2938)
Father’s literate	0.074 (0.2023)	0.072 (0.2023)	0.095 (0.2020)	0.074 (0.2145)	0.064 (0.2144)	0.064 (0.2145)
Mother’s literate	−0.062 (0.4065)	−0.061 (0.4066)	−0.070 (0.4061)	0.160 (0.4676)	0.174 (0.4673)	0.199 (0.4678)
Father’s dead before 18	0.163 (0.2651)	0.162 (0.2652)	0.187 (0.2649)	0.423 (0.2896)	0.445 (0.2896)	0.434 (0.2896)
Mother’s dead before 18	0.424 (0.3288)	0.421 (0.3289)	0.450 (0.3282)	0.211 (0.3742)	0.198 (0.3740)	0.214 (0.3741)
Age categories: 60–64 (reference)
65–69	0.760*** (0.2156)	0.763*** (0.2156)	0.737*** (0.2154)	1.085*** (0.2159)	1.103*** (0.2159)	1.093*** (0.2160)
70–74	0.886*** (0.2418)	0.887*** (0.2418)	0.877*** (0.2415)	1.653*** (0.2488)	1.656*** (0.2487)	1.662*** (0.2488)
75–79	1.606*** (0.2956)	1.612*** (0.2958)	1.581*** (0.2954)	3.180*** (0.3031)	3.210*** (0.3031)	3.204*** (0.3032)
80–84	2.335*** (0.4253)	2.338*** (0.4253)	2.326*** (0.4248)	3.336*** (0.4124)	3.362*** (0.4122)	3.366*** (0.4124)
85 +	3.087*** (0.7180)	3.091*** (0.7181)	2.984*** (0.7176)	5.646*** (0.5770)	5.658*** (0.5767)	5.677*** (0.5770)
Constant	2.927 (3.1213)	1.749 (5.5651)	6.295* (3.8560)	2.391 (2.12437)	−4.240 (4.8218)	0.484 (2.9550)
Observations	2,953	2,953	2,953	2,935	2,935	2,935
R2	0.274	0.274	0.276	0.285	0.286	0.286
Birth province dummies	Yes	Yes	Yes	Yes	Yes	Yes
Current county dummies	Yes	Yes	Yes	Yes	Yes	Yes
Wald tests
Adult SES variables	58.384	58.491	57.288	36.154	37.561	37.342
p-value	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]
Age category dummies	61.127	61.339	59.321	192.519	194.947	195.057
p-value	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]
Childhood SES variables	7.118	7.057	7.441	10.456	10.894	11.050
p-value	[0.789]	[0.794]	[0.762]	[0.490]	[0.452]	[0.439]
Birth province dummies	30.290	30.286	30.377	39.145	39.955	40.479
p-value	[0.065]	[0.065]	[0.064]	[0.006]	[0.005]	[0.004]
Current county dummies	448.144	446.369	455.192	376.873	368.428	370.915
p-value	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]	[0.000]
Upper arm and lower leg			5.058			2.076
p-value			[0.080]			[0.354]

Notes: Missing dummies are added if available. Standard errors adjusted for predicted variables are in parentheses. In Wald tests, adult SES variables include urban, married, education levels and income per capita; childhood SES variables include living in urban area before 16 years old, childhood health status, parents’ education, parents’ death before 18 years old.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level.

From these estimates, we find that the SES variables are very important predictors of height shrinkage. The Wald tests are all highly significant. Dummy coefficients of level of education are negative, monotonically declining with higher education and jointly significant. For men, having primary schooling, compared to being illiterate, is associated with shrinkage of 0.9 cm less. This is a large difference when compared to mean shrinkage for men of 3.3 cm. For women, the difference is smaller, 0.6 cm, but still large compared to the mean female shrinkage of 3.8 cm. For men or women with senior high school or more, the additional shrinkage compared to people with primary schooling is 1 cm for men, or slightly more for women. So these regression coefficients are large. One potential explanation can be that people with higher education levels are more likely to have had better health behaviors when younger. They are also likely to have had better health during childhood, perhaps in ways not measured by our childhood general health variable.

Household log pce is negatively associated with height shrinkage, especially for men. A 1 standard deviation on log pce is approximately 0.9, so a 2 standard deviation increase in log pce would be associated with a reduction in shrinkage of 0.4 cm, a much lower difference than we see for schooling. It is likely that higher income people may be able to purchase better medical care and nutritious food for themselves, although there is likely to exist reverse causality as well, which may explain why the coefficients are more negative for men.

Being currently married is associated with less shrinkage for men, but not significant. Marriage is often found to be correlated positively with better health and more happiness, and is associated with better labor market outcomes for men, so this is not surprising, though, again, we must remember that these estimates are not necessarily causal. Not surprisingly, there are very strong positive associations between shrinkage and age. Currently living in an urban area is significantly associated with less shrinkage for both men and women, on the order of 1 cm less for women, and almost that much for men. These effects are similar to the schooling differences from illiterate to primary school. The county dummies are jointly significant at under the 0.001 level. This is consistent with results such as Strauss et al. (2010), who find very strong community effects on health outcomes for the elderly in China, using the CHARLS Pilot data. Early childhood background and health are not jointly significant in these regressions. However, having had poor childhood health is associated with more shrinkage for women, significant at 10 percent, although the magnitude of the difference is only half of the difference between those currently living in urban versus rural areas (and of the difference between those who are illiterate and those with primary schooling). Dummies for birth provinces are jointly significant, for both men and women.

Table 4 also demonstrates joint significance of lower leg and upper arm lengths for men at the 10 percent level, though they are not significant for women. A 1 standard deviation increase in lower leg length for men is associated with shrinkage of 0.3 cm less. Preshrinkage height is positively associated with shrinkage for women, although not quite significant at 10 percent, and the magnitude of the coefficient is small. The evidence for men is consistent with IV estimates of measured height using limb lengths as instruments, shown below, being inconsistent.

V. Results: Impact of Estimated Height on Health Outcomes

Since there is a growing literature, cited above, that investigates how height is associated with other adult health outcomes, it is of interest to explore this with our estimates of pre-shrinkage heights and height shrinkage. We do not claim causality from these regressions because of the usual problem of omitted variables, but also because in some instances reverse causality is possible.²² The procedure is to regress our health measures first on measured height and control variables to get our baseline estimates. Then we replace measured height by predicted pre-shrinkage height and then add height shrinkage. Standard errors are again corrected for predicted shrinkage and pre-shrinkage heights. We also use an IV estimator for -measured height using limb lengths, their quadratics, and interaction as instruments to compare to our OLS estimates. Since some health outcomes are missing for some observations, the number of observations differs by outcome.

Tables 5.1–5.3 show the results from the regressions of our health measures on height.²³ The same demographic and SES controls, and controls for early life conditions that we use in Table 4 are added in all the regressions. We start with the cognition outcomes in Table 5.1. Measured height is positively and significantly associated with all of the cognition measures for both men and women. Case and Paxson (2008a) find such relationships among the older population in the United States using the Health and Retirement Study (HRS) when they do not include current SES measures, notably schooling, in their regressions. However, when they add schooling height many times becomes insignificant, unlike our results for cognition (also, see Smith et al. (2012) for evidence on China of height associations with health measures of the elderly, also when current SES variables are not included). A likely mechanism for this relationship is the positive association between childhood height and childhood and later cognition. There exists a large literature on early child height impacts on later child cognition. Case and Paxson (2008b) is a recent example (see Glewwe and Miguel 2008 and Strauss and Thomas 2008 for reviews). Since childhood heights are strongly related to adult heights and cognition skills persist from childhood through adulthood, it is not surprising to see this relationship among older persons. However, the magnitude of the estimated changes in cognition associated with a one or even two standard deviation increase in height is smaller than estimated change associated with increasing the level of education from illiteracy to completing primary school. This is consistent with the results in Case and Paxson (2008a).

Table 5.1.

Height Shrinkage, Pre-shrinkage Height, and Cognitive Abilities

Dependent variable	TICS (0–10)				Words recall (0–10)
	OLS (1)	2SLS (2)	OLS (3)	OLS (4)	OLS (5)	2SLS (6)	OLS (7)	OLS (8)
Panel A. Male sample
Measured height	0.0368*** (0.00660)	0.0332*** (0.01018)			0.0187*** (0.00474)	0.0127* (0.00727)
Pre-shrinkage height			0.0310*** (0.01030)	0.0312*** (0.01025)			0.0105 (0.00724)	0.0107 (0.00722)
Height shrinkage				−0.0414*** (0.00930)				−0.0254*** (0.00665)
Observations	2,941	2,941	2,941	2,941	2,720	2,720	2,720	2,720
R2	0.305	0.305	0.300	0.305	0.184	0.183	0.180	0.184
Wald tests
Adult SES variables			636.733	600.097			194.206	175.390
p-value			0.000	0.000			0.000	0.000
Age category dummies			91.500	79.902			128.313	115.236
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			48.030	48.129			29.533	29.182
p-value			0.000	0.000			0.002	0.002
Birth province dummies			22.137	19.854			13.688	12.789
p-value			0.333	0.467			0.846	0.886
Current county dummies			253.984	245.744			258.094	256.117
p-value			0.000	0.000			0.000	0.000
Panel B. Female sample
Measured height	0.0440*** (0.00758)	0.0417*** (0.01259)			0.0138** (0.00571)	0.0094 (0.00870)
Pre-shrinkage height			0.0387*** (0.01223)	0.0407*** (0.01218)			0.0089 (0.00823)	0.0096 (0.00823)
Height shrinkage				−0.0463*** (0.01041)				−0.0167*** (0.00699)
Observations	2,915	2,915	2,915	2,915	2,619	2,619	2,619	2,619
R2	0.336	0.336	0.331	0.336	0.208	0.208	0.207	0.208
Wald tests
Adult SES variables			623.868	601.217			176.355	169.520
p-value			0.000	0.000			0.000	0.000
Age category dummies			111.676	84.939			130.266	107.223
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			43.673	45.053			23.725	24.295
p-value			0.000	0.000			0.014	0.012
Birth province dummies			44.782	44.196			36.093	36.260
p-value			0.001	0.001			0.015	0.014
Current county dummies			324.447	321.329			354.749	351.004
p-value			0.000	0.000			0.000	0.000

Dependent variable	Draw a figure successfully (0–1)
	OLS (9)	2SLS (10)	OLS (11)	OLS (12)
Panel A. Male sample
Measured height	0.0049*** (0.00130)	0.0020 (0.00191)
Pre-shrinkage height			0.0018 (0.00195)	0.0018 (0.00195)
Height shrinkage				−0.0074*** (0.00176)
Observations	2,941	2,941	2,941	2,941
R2	0.199	0.197	0.195	0.200
Wald tests
Adult SES variables			364.191	338.556
p-value			0.000	0.000
Age category dummies			49.160	41.184
p-value			0.000	0.000
Childhood SES variables			25.231	24.794
p-value			0.008	0.010
Birth province dummies			19.613	17.694
p-value			0.482	0.608
Current county dummies			301.732	303.959
p-value			0.000	0.000
Panel B. Female sample
Measured height	0.0045*** (0.00148)	0.0056*** (0.00211)
Pre-shrinkage height			0.0052*** (0.00204)	0.0054*** (0.00203)
Height shrinkage				−0.0038*** (0.00174)
Observations	2,915	2,915	2,915	2,915
R2	0.224	0.224	0.223	0.225
Wald tests
Adult SES variables			386.200	375.602
p-value			0.000	0.000
Age category dummies			40.433	31.892
p-value			0.000	0.000
Childhood SES variables			30.168	30.613
p-value			0.001	0.001
Birth province dummies			27.982	26.282
p-value			0.110	0.157
Current county dummies			401.491	397.046
p-value			0.000	0.000

Source: CHARLS 2011. Columns 1, 5, and 9 show OLS results with robust standard errors are in parentheses. Columns 2, 6, and 10 show 2SLS results with instrumental variables being upper arm length, lower leg length, quadratics and the interaction between upper arm and lower leg length. Robust standard errors are in parentheses. In other columns, standard errors adjusted for predicted variables are in parentheses. All regressions include adult SES variables, age category dummies, childhood SES variables, birth province dummies and current county dummies. Missing dummies are added, if available. In Wald tests, adult SES variables include urban, married, education levels, and log expenditure per capita; childhood SES variables include living in urban area before 16 years old, childhood health status, parents’ education, and parents’ death before 18 years old.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level.

Table 5.3.

Height Shrinkage, Pre-shrinkage Height, and Health

Dependent variable	Poor health (0–1)				Physical function (0–7)
	OLS (1)	2SLS (2)	OLS (3)	OLS (4)	OLS (5)	2SLS (6)	OLS (7)	OLS (8)
Panel A. Male sample
Measured height	−0.0019 (0.00155)	0.0007 (0.00208)			−0.0048 (0.00423)	0.0085 (0.00677)
Pre-shrinkage height			0.0008 (0.00211)	0.0008 (0.00211)			0.0092 (0.00652)	0.0090 (0.00652)
Height shrinkage				0.0042** (0.00191)				0.0164*** (0.00596)
Observations	2,953	2,953	2,953	2,953	2,741	2,741	2,741	2,741
R2	0.027	0.025	0.026	0.028	0.055	0.052	0.055	0.058
Wald tests
Adult SES variables			22.242	19.940			37.739	33.346
p-value			0.001	0.003			0.000	0.000
Age category dummies			7.169	6.035			50.890	44.943
p-value			0.208	0.303			0.000	0.000
Childhood SES variables			9.722	9.633			5.837	5.936
p-value			0.556	0.564			0.884	0.878
Birth province dummies			20.810	21.084			14.331	14.329
p-value			0.408	0.392			0.813	0.813
Current county dummies			168.569	165.423			208.101	210.692
p-value			0.013	0.019			0.000	0.000
Panel B. Female sample
Measured height	0.0009 (0.00158)	0.0040* (0.00243)			−0.0042 (0.00505)	0.0141* (0.00850)
Pre-shrinkage height			0.0039 (0.00240)	0.0038 (0.00240)			0.0147 (0.00854)	0.0139 (0.00856)
Height shrinkage				0.0011 (0.00204)				0.0174** (0.00734)
Observations	2,934	2,934	2,934	2,934	2,500	2,500	2,500	2,500
R2	0.029	0.027	0.029	0.030	0.052	0.048	0.053	0.055
Wald tests
Adult SES variables			5.567	5.351			11.733	10.054
p-value			0.473	0.500			0.068	0.122
Age category dummies			7.692	6.997			26.091	20.330
p-value			0.174	0.221			0.000	0.001
Childhood SES variables			24.612	24.522			29.028	28.599
p-value			0.010	0.011			0.002	0.003
Birth province dummies			32.981	32.826			25.055	24.908
p-value			0.034	0.035			0.199	0.205
Current county dummies			197.339	197.540			262.430	264.937
p-value			0.000	0.000			0.000	0.000

Dependent variable	ADLs (0–6)				IADLs (0–5)
	OLS (9)	2SLS (10)	OLS (11)	OLS (12)	OLS (13)	2SLS (14)	OLS (15)	OLS (16)
Panel A. Male sample
Measured height	−0.0022 (0.00311)	0.0006 (0.00452)			−0.0046 (0.00349)	−0.0023 (0.00483)
Pre-shrinkage height			0.0012 (0.00454)	0.0011 (0.00454)			−0.0015 (0.00490)	−0.0016 (0.00490)
Height shrinkage				0.0049 (0.00411)				0.0070 (0.00444)
Observations	2,931	2,931	2,931	2,931	2,937	2,937	2,937	2,937
R2	0.039	0.039	0.039	0.039	0.077	0.077	0.076	0.077
Wald tests
Adult SES variables			14.191	12.934			29.733	27.379
p-value			0.028	0.044			0.000	0.000
Age category dummies			49.994	46.526			108.138	102.167
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			11.724	11.905			18.271	18.436
p-value			0.385	0.371			0.075	0.072
Birth province dummies			15.433	15.282			15.626	15.638
p-value			0.751	0.760			0.740	0.739
Current county dummies			188.294	189.114			224.101	226.600
p-value			0.001	0.001			0.000	0.000
Panel B. Female sample
Measured height	−0.0037 (0.00395)	0.0108* (0.00582)			−0.0064 (0.00429)	0.0122* (0.00649)
Pre-shrinkage height			0.0105 (0.00564)	0.0098* (0.00566)			0.0120* (0.00611)	0.0111* (0.00612)
Height shrinkage				0.0135*** (0.00480)				0.0190*** (0.00520)
Observations	2,907	2,907	2,907	2,907	2,913	2,913	2,913	2,913
R2	0.045	0.040	0.046	0.049	0.087	0.080	0.087	0.092
Wald tests
Adult SES variables			12.612	10.930			19.537	16.870
p-value			0.050	0.091			0.003	0.010
Age category dummies			50.781	38.930			122.448	98.581
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			8.456	8.205			20.864	21.271
p-value			0.672	0.695			0.035	0.031
Birth province dummies			17.612	17.705			21.959	21.197
p-value			0.613	0.607			0.343	0.386
Current county dummies			296.722	301.227			253.470	257.616
p-value			0.000	0.000			0.000	0.000

Dependent variable	CESD (0–30)				Life expectation pessimistic (0–1)
	OLS (17)	2SLS (18)	OLS (19)	OLS (20)	OLS (21)	2SLS (22)	OLS (23)	OLS (24)
Panel A. Male sample
Measured height	−0.0456** (0.01748)	−0.0409 (0.02681)			−0.0023 (0.00147)	−0.0002 (0.00215)
Pre-shrinkage height			−0.0337 (0.02731)	−0.0346 (0.0273)			−0.0005 (0.00223)	−0.0006 (0.00223)
Height shrinkage				0.0547** (0.02480)				0.0037* (0.00202)
Observations	2,773	2,773	2,773	2,773	2,599	2,599	2,599	2,599
R2	0.046	0.046	0.045	0.046	0.078	0.077	0.077	0.078
Wald tests
Adult SES variables			63.839	58.753			31.081	27.999
p-value			0.000	0.000			0.000	0.000
Age category dummies			7.206	6.341			94.309	87.783
p-value			0.206	0.274			0.000	0.000
Childhood SES variables			7.357	7.132			10.608	10.563
p-value			0.770	0.788			0.477	0.481
Birth province dummies			23.468	23.301			23.580	23.670
p-value			0.266	0.274			0.261	0.257
Current county dummies			301.109	300.828			225.756	224.294
p-value			0.000	0.000			0.000	0.000
Panel B. Female sample
Measured height	−0.0018 (0.02144)	0.0396 (0.03317)			−0.0009 (0.00180)	0.0034 (0.00265)
Pre-shrinkage height			0.0379 (0.03358)	0.0362 (0.03365)			0.0035 (0.00255)	0.0032 (0.00256)
Height shrinkage				0.0297 (0.02901)				0.0038* (0.00218)
Observations	2,669	2,669	2,669	2,669	2,451	2,450	2,451	2,451
R2	0.041	0.040	0.042	0.042	0.065	0.062	0.066	0.067
Wald tests
Adult SES variables			28.776	27.606			13.282	11.460
p-value			0.000	0.000			0.039	0.075
Age category dummies			1.881	1.569			72.261	62.713
p-value			0.865	0.905			0.000	0.000
Childhood SES variables			20.490	20.241			15.126	14.956
p-value			0.039	0.042			0.177	0.185
Birth province dummies			29.943	29.884			22.615	22.588
p-value			0.071	0.072			0.308	0.309
Current county dummies			343.272	342.989			239.585	237.877
p-value			0.000	0.000			0.000	0.000

Notes: Columns 1, 5, 9, 13, 17, and 21 show OLS results with robust standard errors are in parentheses. Columns 2, 6, 10, 14, 18, and 22 show 2SLS results with instrumental variables being upper arm length, lower leg length, quadratics and the interaction between upper arm and lower leg length. Robust standard errors are in parentheses. In other columns, standard errors adjusted for predicted variables are in parentheses. All regressions include adult SES variables, age category dummies, childhood SES variables, birth province dummies and current county dummies. Missing dummies are added, if available. In Wald tests, adult SES variables include urban, married, education levels and log expenditure per capita; childhood SES variables include living in urban area before 16 years old, childhood health status, parents’ education, and parents’ death before 18 years old.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level.

Source: CHARLS 2011

When we replace measured heights by pre-shrinkage heights and height shrinkage, pre-shrinkage height has the same positive, significant association for women with the TICS and draw a picture variables, though not for the word recall. For men, pre-shrinkage height is positive and significantly associated with the TICS and word recall. Height shrinkage is, however, strongly, negatively correlated with all of these measures and for both men and women, suggesting that a part, perhaps a large part, of the association between measured height and cognition occurs through height shrinkage. Indeed, for men, the magnitude of the shrinkage coefficients is substantially larger, compared to the coefficients on measured height. As is true for measured height, the associated differences in cognition from height shrinkage is much smaller than the associated difference between levels of schooling.²⁴ Furthermore, the shrinkage coefficients are often larger in magnitude than the coefficients on pre-shrinkage height, which are only significant in half of the six cases. Hence, if we had used only measured height as our measure of height, we might have wrongly concluded that it is height from childhood, as proxied by pre-shrinkage height, that was correlated with these later-life health variables, instead of height shrinkage.

Shrinkage in turn, as is clear from results in Table 4, is more strongly associated with current SES covariates than with childhood background variables. In contrast, both current and childhood SES and childhood health variables are each jointly significantly associated with the cognition outcomes, as are the current county of residence dummies and, for women, the birth provinces. So these results imply that later life cognition and health are associated with health events throughout the life cycle and in later life, not just from early childhood, and that the association with height is more with shrinkage than preshinkage height.²⁵ We also see in Tables 5.1–5.3 that using the Maurer IV approach for measured height results in coefficients that are fairly close to the coefficients on pre-shrinkage height when we include both pre-shrinkage height and shrinkage. However, the comparison of pre-shrinkage height and shrinkage coefficients are not forthcoming from the IV results.

In Table 5.2, we show results for the biomarkers. Preshrinkage height is significantly, positively related to lung capacity and grip strength, and height shrinkage is significantly, negatively related to both outcomes. In contrast to the cognition results, the size of the shrinkage coefficients are larger for these outcomes. The difference in lung capacity or grip strength for men if there was no shrinkage is predicted to be only a little less than the predicted difference between illiterate and literate men.²⁶ Men who have shrunk more take more time to do the timed walk, but for women, shrinkage and pre-shrinkage heights are not related to walk time. Hypertension and ability to balance are also unrelated to both pre-shrinkage height and shrinkage. Current and childhood SES are related to many of these outcomes, as are current county of residence and province of birth.

Table 5.2.

Height Shrinkage, Pre-shrinkage Height, and Biomarkers

Dependent variable	Hypertension (0–1)				Lung capacity
	OLS (1)	2SLS (2)	OLS (3)	OLS (4)	OLS (5)	2SLS (6)	OLS (7)	OLS (8)
Panel A. Male sample
Measured height	0.0009 (0.00136)	−0.0003 (0.00229)			2.7058*** (0.36493)	2.5538*** (0.44079)
Pre-shrinkage height			−0.0007 (0.00231)	−0.0007 (0.00231)			2.3014*** (0.46938)	2.3561*** (0.46325)
Height shrinkage				−0.0021 (0.00210)				−2.9885*** (0.41716)
Observations	2,939	2,939	2,939	2,939	2,799	2,799	2,799	2,799
R2	0.035	0.034	0.035	0.035	0.176	0.176	0.160	0.176
Wald tests
Adult SES variables			24.107	23.324			32.148	22.433
p-value			0.000	0.001			0.000	0.001
Age category dummies			39.088	40.011			249.914	222.555
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			9.846	9.903			15.895	16.334
p-value			0.544	0.539			0.145	0.129
Birth province dummies			18.906	18.759			65.187	69.276
p-value			0.528	0.538			0.000	0.000
Current county dummies			188.634	188.329			593.088	612.090
p-value			0.001	0.001			0.000	0.000
Panel B. Female sample
Measured height	−0.0004 (0.00165)	0.0011 (0.00249)			1.7369*** (0.27666)	1.8764*** (0.37590)
Pre-shrinkage height			0.0012 (0.00246)	0.0011 (0.00247)			1.8020*** (0.34908)	1.8860*** (0.34587)
Height shrinkage				0.0015 (0.00211)				−1.6234*** (0.30366)
Observations	2,921	2,921	2,921	2,921	2,673	2,673	2,673	2,673
R2	0.045	0.045	0.045	0.046	0.153	0.153	0.144	0.154
Wald tests
Adult SES variables			15.405	15.563			36.316	30.802
p-value			0.017	0.016			0.000	0.000
Age category dummies			39.200	35.380			151.600	117.621
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			6.044	5.962			7.326	7.649
p-value			0.870	0.876			0.772	0.744
Birth province dummies			45.006	45.035			47.926	43.932
p-value			0.001	0.001			0.000	0.002
Current county dummies			198.785	199.240			929.699	933.195
p-value			0.000	0.000			0.000	0.000

Dependent variable	Grip strength				Balance (0–1)
	OLS (9)	2SLS (10)	OLS (11)	OLS (12)	OLS (13)	2SLS (14)	OLS (15)	OLS (16)
Panel A. Male sample
Measured height	0.3641*** (0.02122)	0.3578*** (0.03461)			−0.0011 (0.00145)	−0.0017 (0.00194)
Pre-shrinkage height			0.3500*** (0.03580)	0.3543*** (0.03436)			−0.0013 (0.00198)	−0.0013 (0.00198)
Height shrinkage				−0.3723*** (0.03141)				0.0008 (0.00181)
Observations	2,903	2,902	2,903	2,903	2,850	2,850	2,850	2,850
R2	0.262	0.262	0.224	0.262	0.047	0.047	0.047	0.047
Wald tests
Adult SES variables			50.380	31.335			8.721	8.874
p-value			0.000	0.000			0.190	0.181
Age category dummies			402.132	345.473			56.926	56.727
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			4.798	4.864			20.374	20.416
p-value			0.941	0.938			0.040	0.040
Birth province dummies			42.826	46.774			19.624	19.222
p-value			0.002	0.001			0.482	0.507
Current county dummies			591.974	645.679			282.516	279.810
p-value			0.000	0.000			0.000	0.000
Panel B. Female sample
Measured height	0.2191*** (0.02733)	0.2646*** (0.03450)			−0.0010 (0.00187)	−0.0014 (0.00252)
Pre-shrinkage height			0.2511*** (0.03147)	0.2590*** (0.03088)			−0.0015 (0.00247)	−0.0015 (0.00247)
Height shrinkage				−0.1907*** (0.02620)				0.0007 (0.00214)
Observations	2,847	2,847	2,847	2,847	2,767	2,767	2,767	2,767
R2	0.185	0.184	0.170	0.186	0.052	0.052	0.052	0.052
Wald tests
Adult SES variables			41.395	33.655			8.630	8.703
p-value			0.000	0.000			0.195	0.191
Age category dummies			177.411	126.617			68.687	66.582
p-value			0.000	0.000			0.000	0.000
Childhood SES variables			13.989	14.482			6.696	6.662
p-value			0.234	0.207			0.823	0.826
Birth province dummies			64.672	71.609			21.609	21.458
p-value			0.000	0.000			0.362	0.371
Current county dummies			903.208	928.378			250.165	250.048
p-value			0.000	0.000			0.000	0.000

Dependent variable	Walk time
	OLS (17)	2SLS (18)	OLS (19)	OLS (20)
Panel A. Male sample
Measured height	−0.0142** (0.00621)	−0.0148* (0.00785)
Pre-shrinkage height			−0.0117 (0.00852)	−0.0118 (0.00852)
Height shrinkage				0.0164** (0.00788)
Observations	2,780	2,780	2,780	2,780
R2	0.093	0.093	0.092	0.093
Wald tests
Adult SES variables			35.320	31.917
p-value			0.000	0.000
Age category dummies			113.240	104.349
p-value			0.000	0.000
Childhood SES variables			4.409	4.213
p-value			0.956	0.963
Birth province dummies			27.691	27.537
p-value			0.117	0.121
Current county dummies			936.804	941.687
p-value			0.000	0.000
Panel B. Female sample
Measured height	−0.0154 (0.00947)	−0.0220* (0.01234)
Pre-shrinkage height			−0.0198 (0.01240)	−0.0202 (0.01240)
Height shrinkage				0.0119 (0.01062)
Observations	2,714	2,714	2,714	2,714
R2	0.107	0.107	0.107	0.107
Wald tests
Adult SES variables			14.527	13.490
p-value			0.0242718	0.0358841
Age category dummies			157.251	142.195
p-value			0.000	0.000
Childhood SES variables			18.072	18.265
p-value			0.080	0.076
Birth province dummies			29.289	29.601
p-value			0.082	0.077
Current county dummies			709.213	708.750
p-value			0.000	0.000

Notes: Columns 1, 5, 9, 13, and 17 show OLS results with robust standard errors in parentheses. Columns 2, 6, 10, 14, and 18 show 2SLS results with instrumental variables being upper arm length, lower leg length, quadratics and the interaction between upper arm and lower leg length. Robust standard errors are in parentheses. In other columns, standard errors adjusted for predicted variables are in parentheses. All regressions include adult SES variables, age category dummies, childhood SES variables, birth province dummies and current county dummies. Missing dummies are added, if available. In Wald tests, adult SES variables include urban, married, education levels and log expenditure per capita; childhood SES variables include living in urban area before 16 years old, childhood health status, parents’ education, and parents’ death before 18 years old.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level.

Source: CHARLS 2011

Table 5.3 has results for self-reported health outcomes. As can be seen, shrinkage is generally related to worse outcomes, and more strongly and significantly so than pre-shrinkage height is positively correlated with these outcomes. Examining the OLS or IV results for measured height would, again, not provide this result. For men, this is so for the CES-D depression index, the self-assessed likelihood of not surviving to age 75 (for those 65 and younger), the number of measures of physical functioning that the respondent reports having difficulty with, and having poor or very poor general health. For women, shrinkage is significantly associated with having more difficulties with measures of physical functioning: ADLs, IADLs and the likelihood of not surviving to age 75. What is surprising about these results is that pre-shrinkage height has positive, significant at the 10 percent level, associations with bad outcomes for ADLs and IADLs for women, although not for men. This is very unlike the results for cognition and the biomarkers. Mortality selection could be partly causing this, but we cannot be more than speculative on this point.

VI. Conclusions

According to Barker (1994), childhood health in uterus has a lasting impact on health, including at old ages. Height has been used widely as an indicator in part of childhood health. However, because height shrinks with aging, it suffers a measurement error problem when studying its impact on health outcomes at older ages.

Based on unique data of Chinese aged 45 and older, we address this problem by making use of upper arm and lower leg lengths to construct estimates of the relationship between these limb lengths and measured height on a population aged 45–49, and then use these estimates to estimate pre-shrinkage height and height shrinkage on a population 60 years and older. We then investigate the association between height shrinkage, SES variables, and variables measuring different dimensions of childhood health. We follow this exercise by examining the associations between measured height on the one hand, or pre-shrinkage height and shrinkage on the other, and a rich set of health variables including measures of cognition, biomarkers, as well as various self-reported health measures.

The results in this paper show that shrinkage and socioeconomic variables, such as schooling, household per capita expenditure, and current urban residence are negatively correlated for both men and women. Differences are largest across levels of schooling and urban/rural residence. Childhood background factors are much more weakly associated with shrinkage, excepting province of birth, which is highly significant. These results are consistent with the concerns raised in Case and Paxson (2008a).

Height shrinkage, and to a lesser extent pre-shrinkage height, are also correlated with many later-life health outcomes, particularly cognition and biomarker measures. The shrinkage coefficients tend to be larger than for pre-shrinkage height, suggesting that current health issues are important in understanding the health of the elderly, not just events in early childhood. In general, the more the shrinkage the worse are these other health outcomes.

Appendix 1: Asymptotic Variances

Table 4 uses a constructed dependent variable, height shrinkage, while Tables 5.1–5.3 use predicted pre-shrinkage height and, in some specifications, height shrinkage, as right-hand side variables. Furthermore, the predicted pre-shrinkage height coefficients are derived from a different sample. This suggests that a two sample GMM procedure might be appropriate (e.g., Ridder and Moffitt 2007), however, we are not using the standard setup because we do not use all of the variables in the second stage to predict pre-shrinkage height. We derive the asymptotic variances here.

Shrinkage as Dependent Variable

The regression with shrinkage as the dependent variable is

$$s={\mathbf{x}}^{\prime }\mathbf{\beta }+p\delta +\epsilon ,$$

with 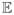(ε | x, p, z) = 0. Substitution of (4) gives

$${\mathbf{z}}^{\prime }\mathbf{\gamma }-h={\mathbf{x}}^{\prime }\mathbf{\beta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }\delta +(\delta -1)\eta +\epsilon ={\mathbf{x}}^{\prime }\mathbf{\beta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }\delta +\zeta ,$$

with ζ = (δ − 1)η + ε. Rearranging gives

$$-h={\mathbf{x}}^{\prime }\mathbf{\beta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }(\delta -1)+\zeta ={\mathbf{x}}^{\prime }\mathbf{\beta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }\alpha +\zeta .$$

Note that α = −1 if pre-shrinkage height is not in the relation.

This equation is estimated on the older sample with γ being estimated on the younger sample. The unconditional moment restrictions are

$$\begin{array}{ll}\hfill {\mathbb{E}}_O\left[\left(\begin{array}{c}\mathbf{x}\\ \mathbf{z}\end{array}\right)(-h-{\mathbf{x}}^{\prime }\mathbf{\beta }-{\mathbf{z}}^{\prime }\mathbf{\gamma }\alpha )\right]& =0\hfill \\ \hfill {\mathbb{E}}_Y[\mathbf{z}(p-{\mathbf{z}}^{\prime }\mathbf{\gamma })]& =0.\hfill \end{array}$$

Define

$$\begin{array}{ll}{m}_O(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =\left(\begin{array}{c}\mathbf{x}\\ \mathbf{z}\end{array}\right)(-h-{\mathbf{x}}^{\prime }\mathbf{\beta }-{\mathbf{z}}^{\prime }\mathbf{\gamma }\alpha )\hfill \\ m_Y(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =\mathbf{z}(p-{\mathbf{z}}^{\prime }\mathbf{\gamma }).\hfill \end{array}$$

We have

$${\mathbb{E}}_O[{\mathbf{m}}_O({\mathbf{\beta }}_0,{\alpha }_0,{\mathbf{\gamma }}_0){\mathbf{m}}_Y{({\mathbf{\beta }}_0,{\alpha }_0,{\mathbf{\gamma }}_0)}^{\prime }]=0,$$

so that the variance matrix of the moment conditions is

$$\mathbf{W}=\left(\begin{array}{ccc}{\sigma }_{\zeta }^2{\mathbb{E}}_O(\mathbf{x}{\mathbf{x}}^{\prime })& {\sigma }_{\zeta }^2{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })& 0\\ {\sigma }_{\zeta }^2{\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime })& {\sigma }_{\zeta }^2{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })& 0\\ 0& 0& {\sigma }_{\eta }^2{\mathbb{E}}_Y(\mathbf{z}{\mathbf{z}}^{\prime })\end{array}\right),$$

with estimator

$$\widehat{\mathbf{W}}=\left(\begin{array}{ccc}{\widehat{\sigma }}_{\zeta }^2\frac{{\mathbf{X}}_O^{\prime }{\mathbf{X}}_O}{N_1}& {\widehat{\sigma }}_{\zeta }^2\frac{{\mathbf{X}}_O^{\prime }{\mathbf{Z}}_O}{N_1}& 0\\ {\widehat{\sigma }}_{\zeta }^2\frac{{\mathbf{Z}}_O^{\prime }{\mathbf{X}}_O}{N_1}& {\widehat{\sigma }}_{\zeta }^2\frac{{\mathbf{Z}}_O^{\prime }{\mathbf{Z}}_O}{N_1}& 0\\ 0& 0& {\widehat{\sigma }}_{\eta }^2\frac{{\mathbf{Z}}_Y^{\prime }{\mathbf{Z}}_Y}{N_2}\end{array}\right),$$

where X_O, Z_O are the matrices with covariates for the old sample and Z_Y is the matrix with covariates of the young sample.

The inverse of Ŵ is block diagonal and that implies that the optimal GMM estimator with weighting matrix Ŵ⁻¹ is the solution to

$$\begin{array}{ll}\hfill {\mathbf{X}}_O^{\prime }(-h_O-{\mathbf{X}}_O\mathbf{\beta }-{\mathbf{Z}}_O\mathbf{\gamma }\alpha )& =0\hfill \\ \hfill {\mathbf{Z}}_O^{\prime }(-h_O-{\mathbf{X}}_O\mathbf{\beta }-{\mathbf{Z}}_O\mathbf{\gamma }\alpha )& =0\hfill \\ \hfill {\mathbf{Z}}_Y^{\prime }(p_Y-{\mathbf{Z}}_Y\mathbf{\gamma })& =0.\hfill \end{array}$$

Therefore the optimal GMM estimator regresses p on z in the young sample and uses these estimates in the old sample. We can therefore rewrite the moment function for the old sample as (we use the same notation for the moment function)

$$m_O(\mathbf{\beta },\alpha ,\mathbf{\gamma })=\left(\begin{array}{c}\mathbf{x}\\ {\mathbf{z}}^{\prime }\mathbf{\gamma }\end{array}\right)(-h-{\mathbf{x}}^{\prime }\mathbf{\beta }-{\mathbf{z}}^{\prime }\mathbf{\gamma }\alpha )$$

and use unweighted GMM.

To obtain the asymptotic variance, we first compute

$$\begin{array}{ll}\frac{\partial {\mathbf{m}}_O}{\partial {\mathbf{\beta }}^{\prime }}(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =-\left(\begin{array}{c}\mathbf{x}\\ {\mathbf{z}}^{\prime }\mathbf{\gamma }\end{array}\right){\mathbf{x}}^{\prime }\hfill \\ \frac{\partial {\mathbf{m}}_O}{\partial \alpha }(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =-\left(\begin{array}{c}\mathbf{x}\\ {\mathbf{z}}^{\prime }\mathbf{\gamma }\end{array}\right){\mathbf{z}}^{\prime }\mathbf{\gamma }\hfill \\ \frac{\partial {\mathbf{m}}_O}{\partial {\mathbf{\gamma }}^{\prime }}(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =-\left(\begin{array}{c}\mathbf{x}\\ {\mathbf{z}}^{\prime }\mathbf{\gamma }\end{array}\right)\alpha {\mathbf{z}}^{\prime }+\left(\begin{array}{c}\mathbf{0}\\ {\mathbf{z}}^{\prime }\end{array}\right)(-h-{\mathbf{x}}^{\prime }\mathbf{\beta }-{\mathbf{z}}^{\prime }\mathbf{\gamma }\alpha )\hfill \\ \frac{\partial {\mathbf{m}}_Y}{\partial {\mathbf{\beta }}^{\prime }}(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =\mathbf{0}\hfill \\ \frac{\partial {\mathbf{m}}_Y}{\partial \alpha }(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =\mathbf{0}\hfill \\ \frac{\partial {\mathbf{m}}_Y}{\partial {\mathbf{\gamma }}^{\prime }}(\mathbf{\beta },\alpha ,\mathbf{\gamma })\hfill & =-\mathbf{z}{\mathbf{z}}^{\prime }.\hfill \end{array}$$

The variance matrix of

$$\left(\begin{array}{c}\widehat{\mathbf{\beta }}\\ \widehat{\alpha }\\ \widehat{\mathbf{\gamma }}\end{array}\right)$$

is

$${({\mathbf{A}}^{\prime }{\mathbf{W}}^{-1}\mathbf{A})}^{-1},$$

with

$$\mathbf{A}=\left(\begin{array}{ccc}-{\mathbb{E}}_O(\mathbf{x}{\mathbf{x}}^{\prime })& -{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\mathbf{\gamma }& -{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\alpha \\ -{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime })& -{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\mathbf{\gamma }& -{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\alpha \\ 0& 0& -{\mathbb{E}}_Y(\mathbf{z}{\mathbf{z}}^{\prime })\end{array}\right),$$

and (using the same notation for the variance of the new moment conditions)

$$\mathbf{W}=\left(\begin{array}{ccc}{\sigma }_{\zeta }^2{\mathbb{E}}_O(\mathbf{x}{\mathbf{x}}^{\prime })& {\sigma }_{\zeta }^2{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\mathbf{\gamma }& \mathbf{0}\\ {\sigma }_{\zeta }^2{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime })& {\sigma }_{\zeta }^2{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\mathbf{\gamma }& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\sigma }_{\eta }^2{\mathbb{E}}_Y(\mathbf{z}{\mathbf{z}}^{\prime })\end{array}\right).$$

Now,

$${\mathbf{A}}^{\prime }{\mathbf{W}}^{-1}\mathbf{A}=\left(\begin{array}{ccc}{\sigma }_{\zeta }^{-2}{\mathbb{E}}_O(\mathbf{x}{\mathbf{x}}^{\prime })& {\sigma }_{\zeta }^{-2}{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\mathbf{\gamma }& {\sigma }_{\zeta }^{-2}{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\alpha \\ {\sigma }_{\zeta }^{-2}{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime })& {\sigma }_{\zeta }^{-2}{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\mathbf{\gamma }& {\sigma }_{\zeta }^{-2}{\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\alpha \\ {\sigma }_{\zeta }^{-2}{\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime })\alpha & {\sigma }_{\zeta }^{-2}{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime }){\mathbf{\gamma }}^{\prime }\alpha & {\sigma }_{\eta }^{-2}{\mathbb{E}}_Y(\mathbf{z}{\mathbf{z}}^{\prime })+{\sigma }_{\zeta }^{-2}\mathbf{C}\end{array}\right)$$

with

$$\mathbf{C}={\alpha }^2\left({\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime }){\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime }){\mathbf{\gamma }}^{\prime }\right){\left(\begin{array}{cc}{\mathbb{E}}_O(\mathbf{x}{\mathbf{x}}^{\prime })& {\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\mathbf{\gamma }\\ {\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime })& {\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\mathbf{\gamma }\end{array}\right)}^{-1}\left(\begin{array}{c}{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime })\\ {\mathbf{\gamma }}^{\prime }{\mathbb{E}}_O(\mathbf{z}{\mathbf{z}}^{\prime })\end{array}\right).$$

If pre-shrinkage height is excluded, i.e., α = −1, the second row and column in A′W⁻¹A are removed, we substitute α = −1, and

$$\mathbf{C}={\mathbb{E}}_O(\mathbf{z}{\mathbf{x}}^{\prime }){({\mathbb{E}}_O(\mathbf{x}{\mathbf{x}}^{\prime }))}^{-1}{\mathbb{E}}_O(\mathbf{x}{\mathbf{z}}^{\prime }).$$

The resulting variance matrix is for

$$\left(\begin{array}{c}\widehat{\mathbf{\beta }}\\ \widehat{\mathbf{\gamma }}\end{array}\right).$$

We estimate 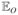(xx′) by

$$\frac{{\mathbf{X}}_O^{\prime }{\mathbf{X}}_O}{N_1},$$

and same for other moments for the older population. For the younger population we estimate 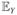(zz′) by

$$\frac{{\mathbf{Z}}_Y^{\prime }{\mathbf{Z}}_Y}{N_2}.$$

The variances ${\sigma }_{\eta }^2$ and ${\sigma }_{\zeta }^2$ are estimated in the usual way. Note that we do not have to make an assumption on the correlation of η and ε for the older population (which would not be identified).

Pre-shrinkage Height and Shrinkage as Independent Variables

The basic regression is now

$$y={\mathbf{x}}^{\prime }\mathbf{\theta }+p\alpha +s\kappa +u,$$

with 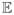(u | x, p, s) = 0. Substitution of the prediction equation gives

$$\begin{array}{l}y={\mathbf{x}}^{\prime }\mathbf{\theta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }\alpha +({\mathbf{z}}^{\prime }\mathbf{\gamma }-h)\kappa +(\alpha +\kappa )\eta +u\\ ={\mathbf{x}}^{\prime }\mathbf{\theta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }(\alpha +\kappa )-h\kappa +(\alpha +\kappa )\eta +u\\ ={\mathbf{x}}^{\prime }\mathbf{\theta }+{\mathbf{z}}^{\prime }\mathbf{\gamma }\mu +h\nu +\zeta ,\end{array}$$

with μ = α + κ and ν = −κ and ζ = μη + u.

If we read for x′ the vector (x′ h) and for β′ the vector (θ′ ν) and for δ the parameter μ, then we see that the variance matrix in the previous section applies with these changes (if we use the same estimator). This gives us the variance matrix of

$$\left(\begin{array}{c}\widehat{\mathbf{\theta }}\\ \widehat{\nu }\\ \widehat{\mu }\\ \widehat{\mathbf{\gamma }}\end{array}\right)$$

From this we easily obtain the variance matrix of the original parameters.

Appendix 2. Measurement of Upper Arm and Low Leg Lengths

Figure A1.

Upper Arm Length Measurement

Figure A2.

Lower Leg Measurement