Longitudinal Functional Data Analysis

Abstract

We consider dependent functional data that are correlated because of a longitudinal-based design: each subject is observed at repeated times and at each time a functional observation (curve) is recorded. We propose a novel parsimonious modeling framework for repeatedly observed functional observations that allows to extract low dimensional features. The proposed methodology accounts for the longitudinal design, is designed to study the dynamic behavior of the underlying process, allows prediction of full future trajectory, and is computationally fast. Theoretical properties of this framework are studied and numerical investigations confirm excellent behavior in finite samples. The proposed method is motivated by and applied to a diffusion tensor imaging study of multiple sclerosis.

1. Introduction

Longitudinal functional data consist of functional observations (such as profiles or images) observed at several times for each subject of many. Examples of such data include the Baltimore Longitudinal Study of Aging (BLSA), where daily physical activity count profiles are observed for each subject at several consecutive days (Goldsmith et al., 2014; Xiao et al., 2015) and the longitudinal diffusion tensor imaging (DTI) study, where modality profiles along well-identified tracts are observed for each multiple sclerosis (MS) patient at several hospital visits (Greven et al., 2010). As a result of an increasing number of such applications, longitudinal functional data analysis has received much attention recently; see for example Morris et al. (2003); Morris & Carroll (2006); Baladandayuthapani et al. (2008); Di et al. (2009); Greven et al. (2010); Staicu et al. (2010); Li & Guan (2014).

Our motivation is the longitudinal DTI study, where the objective is to investigate the evolution of the MS disease as measured by the dynamics of a common DTI modality profile - fractional anisotropy (FA) - along the corpus callosum (CCA) of the brain. Every MS subject in the study is observed over possibly multiple hospital visits and at each visit the subject's brain is imaged using DTI. In this paper we consider summaries of FA at 93 equally spaced locations along the brain's CCA, which we refer to as CCA-FA profile. The change over time in the CCA-FA profiles is informative of the progression of the MS disease, and thus a model that accounts for all the dependence sources in the data has the potential to be a very useful tool in practice. We propose a modeling framework that captures the process dynamics over time and provides prediction of a full CCA-FA trajectory at a future visit.

Existing literature in longitudinal functional data can be separated into two categories, based on whether or not it accounts for the actual time T_ij at which the profile Y_ij(·) is observed; here i indexes the subjects and j indexes the repeated measures of the subject. Moreover, most methods that incorporate the time T_ij focus on modeling the process dynamics (Greven et al., 2010) and only few can do prediction of a future full trajectory. Chen & Müller (2012) considered the latter issue and introduced an interesting perspective, but their method is very computationally expensive and its application in practice is limited as a result. We propose a novel parsimonious modeling framework to study the process dynamics and prediction of future full trajectory in a computationally feasible manner.

In this paper we focus on the case where the sampling design of T_ij's is sparse (hence sparse longitudinal design) and the subject profiles are observed at fine grids (hence dense functional design). We propose to model Y_ij(·) as:

$$Y_{ij}\left(s\right)=\mu (s,T_{ij})+X_i(s,T_{ij})+{∊}_{ij}\left(s\right);X_i(s,T_{ij})=\sum _{k\ge 1}{\xi }_{ik}\left(T_{ij}\right){\varphi }_k\left(s\right)\text{for}s\in \mathcal{S}\text{and}{T}_{ij}\in \mathcal{T}$$ (1)

where $\mathcal{S}$ and $\mathcal{T}$ are closed compact sets, μ(·, T_ij) is an unknown smooth mean response corresponding to T_ij, X_i(·, T_ij) is a smooth random deviation from the mean at T_ij, and ε_ij(·) is a residual process with zero-mean and unknown covariance function to be described later. The bivariate processes X_i(·, ·)'s are independent and identically distributed (iid), the error processes ε_ij's are iid and furthermore are independent of X_i's. For identifiability we require that X_i comprises solely the random deviation that is specific to the subject; the repeated time-specific deviation is included in ε_ij. Here {ϕ_k(·)}_k is an orthogonal basis in $L^2\left(\mathcal{S}\right)$ and ξ_ik(T_ij)'s are the corresponding basis coefficients that have zero-mean, are uncorrelated over i, but correlated over j. We assume that the set of visit times of all subjects, {T_ij : i, j}, is dense in $\mathcal{T}$. Full model assumptions are given in Section 2.

The class of model (1) is rich and includes many existent models, as we illustrate now. (i) If ξ_ik(T_ij) = ζ₀,_ik + T_ijζ₁,_ik for appropriately defined random terms ζ₀,_ik and ζ₁,_ik, model (1) can be represented as in Greven et al. (2010). (ii) If cov(ξ_ik(T), ξ_ik(T′)) = λ_kρ_k(|T – T′|; ν) for some unknown variance λ_k, known correlation function ρ_k(·; ν) with unknown parameter ν, and n = 1, model (1) resembles to Gromenko et al. (2012) and Gromenko & Kokoszka (2013) for spatially indexed functional data. (iii) If ξ_ik(T_ij) = ${\sum }_{l\ge 1}{\zeta }_{ikl}{\psi }_{ikl}\left(T_{ij}\right)$ with orthogonal basis functions ψ_ikl(T)'s and the corresponding coefficients ζ_ikl's, then model (1) is similar to Chen & Müller (2012) who used time-varying basis functions ϕ_k(·|T) instead of our proposed ϕ_k(·) in model (1) and assumed a white noise residual process ε_ij.

The use of time-invariant orthogonal basis functions is one key difference between the proposed framework and Chen & Müller (2012); another important difference is the flexible error structure that our approach accommodates. The key difference leads to several major advantages of the proposed method. First, by using a time-invariant basis functions, the basis coefficients, ξ_ik(T_ij)'s extract the low dimensional features of these massive data. The longitudinal dynamics is emphasized only through the time-varying coefficients ξ_ik(T_ij)'s of (1) and, thus, this perspective makes the study of the process dynamics easier to understand. Second, our approach involves at most two dimensional smoothing and as a result is computationally very fast; in contrast, the time-varying basis functions {ϕ_k(·|T)}_k at each T, require three dimensional smoothing which is not only complex but also computationally intensive and slow.

Nevertheless, selecting the time-invariant basis is nontrivial. One option is to use a pre-specified basis; Zhou et al. (2008) considered this approach in modeling paired of sparse functional data. Another option is to use data-driven basis functions, such as eigenbasis of some covariance. The challenge is: what covariance to use ? We take the latter direction and propose to determine {ϕ_k(·)}_k using an appropriate marginal covariance. In this regard, let c((s, T), (s′, T′)) be the covariance function of X_i(s, T) and g(T) be the density of T_ij's. Define Σ(s, s′) = ${\int }_{\mathcal{T}}c((s,T),(s^{\prime },T))g\left(T\right)dT$ for s, s′ ∈ $\mathcal{S}$: we show that this bivariate function is a proper covariance function (Horváth & Kokoszka, 2012). Section 2 shows that the proposed basis {ϕ_k(·)}_k has optimal properties with respect to some appropriately defined criterion. From this view point, the model representation (1) is optimal. The idea of using the eigenbasis of the pooled covariance can be related to Jiang & Wang (2010) and Pomann et al. (2013), who considered independent functional data.

The rest of paper is organized as follows. Section 2 introduces the proposed modeling framework. Section 3 describes the estimation methods and implementation. The methods are studied theoretically in Section 4 and then numerically in Section 5. Section 6 discusses the application to the tractography DTI data.

2. Modeling longitudinal functional data

Let [{T_ij, Y_ij(s_r) : r = 1, . . . , R} : j = 1, . . . , m_i,] be the observed data for the ith subject, where Y_ij(·) is the jth profile at random time T_ij for subject i, and each profile is observed at the fine grid of points {s₁, . . . , s_R}. For convenience we use the generic index s instead of s_r. The number of ‘profiles’ per subject, m_i is relatively small to moderate and the set of time points of all subjects, {T_ij : for all i, j}, is dense in $\mathcal{T}$. Without loss of generality, we set $\mathcal{S}=\mathcal{T}=[0,1]$. We model the response Y_ij(·) using (1), where we assume that ε_ij(s) is the sum of independent components ε_ij(s) = ε₁,_ij(s) + ε₂,_ij(s). Here ε₁,_ij(·) is a random square integrable function which has smooth covariance function Γ(s, s′) = cov{ε₁,_ij(s),ε₁,_ij(s′)} and ε₂,_ij(s) is white noise with covariance cov{ε₂,_ij(s), ε₂,_ij(s′)} = σ² if s = s′ and 0 otherwise.

Let c((s, T), (s′, T′)) = E[X_i(s, T)X_i(s′, T′)] be the covariance function of the process X_i(·,·) and let Σ(s, s′) = ∫ c((s, T), (s′, T))g(T)dT, where g(·) is the sampling density of T_ij. In Section 4 we show that Σ(s, s′) is a proper covariance function (Horváth & Kokoszka, 2012); due to its definition we call Σ as the marginal covariance function induced by X_i. The unpublished work Chen et al. (2015) independently considered a similar marginal covariance in a related setting. Denote by W_i(s, T_ij) = X_i(s, T_ij) + ε₁,_ij(s); W_i is a bivariate process defined on [0, 1]² and its induced marginal covariance is Ξ(s, s′) = Σ(s, s′) + Γ(s, s′). Let {ϕ_k(s), λ_k}_k be the eigencomponents of Ξ(s, s′), where {ϕ_k(·) : k} forms an orthogonal basis in L²[0, 1] and λ₁ ≥ λ₂ ≥ . . . ≥ 0. Using arguments similar to the standard functional principal component analysis (FPCA), the eigenbasis functions {ϕ_k(·) : k = 1, . . . , K} are optimal in the sense that they minimize the following weighted mean square error: MSE(θ₁(·), . . . , θ_K(·)) = ${\int }_0^1\mathsf{E}{\Vert W_i(\cdot ,T)-{\sum }_{k=1}^K<W_i(\cdot ,T),{\theta }_k(\cdot )>{\theta }_k(\cdot )\Vert }^{2}g\left(T\right)dT$, where $<f_1(\cdot ),f_2(\cdot )>={\int }_0^1{f}_1\left(s\right)f_2\left(s\right)ds$ is the usual inner product in L²[0, 1].

Using the orthogonal basis in L²[0, 1] {ϕ_k(·)}_k, we can represent the square integrable smooth process W_i(·, T) as W_i(s, T_ij) = ${\sum }_{k=1}^{\infty }{\xi }_{W,ijk}{\varphi }_k\left(s\right)$, where ξ_W,ijk = ∫W_i(s, T_ij)ϕ_k(s)ds = ξ_ik(T_ij) + e_ijk, and ξ_W,ijk are not necessarily uncorrelated over k. Here ξ_ik(T_ij) = ∫X_i(s, T_ij)ϕ_k(s)ds and e_ijk = ∫ ε_1,ij(s)ϕ_k(s)ds are specified by the definition of W_i; for fixed k these terms are mutually independent due to the independence of the processes X_i and ε₁,_ij. For each k, one can easily show that, ξ_ik(·) is a smooth zero-mean random process in L²[0, 1] and is iid over i. Furthermore e_ijk are zero-mean iid random variables over i, j; denote by ${\sigma }_{e,k}^2$ their finite variance.

One way to model the dependence of the coefficients, ξ_ik(T_ij)'s, is by using common techniques in longitudinal data analysis; for example by assuming a parametric covariance structure. As we discussed in Section 1, this leads to models similar to Greven et al. (2010); Gromenko et al. (2012); Gromenko & Kokoszka (2013). We consider this approach in the analysis of the DTI data, Section 6. Another approach is to assume a nonparametric covariance structure and employ a common functional data analysis technique. We detail the latter approach in this section.

For each k ≥ 1 denote by G_k(T, T ′) = cov{_,ik(T), _,ik(T′)} the smooth covariance function in [0, 1] × [0, 1]. Mercer's theorem provides the following convenient spectral decomposition $G_k(T,T^{\prime })={\sum }_{l\ge 1}{\eta }_{kl}{\psi }_{kl}\left(T\right){\psi }_{kl}\left(T^{\prime }\right)$, where η_k1 ≥ η_k2 ≥ . . . ≥ 0 and {ψ_kl(·)}_l≥₁ is an orthogonal basis in L²[0, 1]. Using the Karhunen-Loève (KL) expansion, we represent ξ_ik(·) as: ξ_ik(T_ij) = ${\sum }_{l=1}^{\infty }{\zeta }_{ikl}{\psi }_{kl}\left(T_{ij}\right)$, where ζ_ikl = ∫ ξ_ik(T)ψ_kl(T)dT, have zero-mean, variance equal to η_kl, and are uncorrelated over l. By collecting all the components, we represent the model (1) as Y_ij(s) = μ(s, T_ij) + ${\sum }_{k=1}^{\infty }{\sum }_{l=1}^{\infty }{\zeta }_{ikl}{\psi }_{kl}\left(T_{ij}\right){\varphi }_k\left(s\right)+{∊}_{ij}\left(s\right)$, for ${∊}_{ij}\left(s\right)={\sum }_{k=1}^{\infty }{e}_{ijk}{\varphi }_k\left(s\right)+{∊}_{2,ij}\left(s\right)$. In practice we truncate this expansion. Lek K and L₁,...,L_K such that Y_ij(s) is well approximated by the following truncated model based on the leading K and ${\sum }_k{L}_k$ respective basis functions

$$Y_i(s,T_{ij})=\mu (s,T_{ij})+\sum _{k=1}^K\sum _{l=1}^{L_k}{\zeta }_{ikl}{\psi }_{kl}\left(T_{ij}\right){\varphi }_k\left(s\right)+{∊}_{ij}\left(s\right),$$ (2)

where ${∊}_{ij}\left(s\right)\approxeq {\sum }_{k=1}^K{e}_{ijk}{\varphi }_k\left(s\right)+{∊}_{2,ij}\left(s\right)$. The truncated model (2) gives a parsimonious representation of the longitudinal functional data. It allows to study its dependence through two sets of eigenfunctions: one dependent solely on s and one solely on T_ij. This approach involves two main challenges: first, determining consistent estimator of the marginal covariance and second determining consistent estimators of the time-varying coefficients ξ_ik(·).

3. Estimation of model components

We discuss estimation of all model components. The mean estimation is carried out using existing methods (Chen & Müller, 2012; Scheipl et al., 2014); here we briefly describe it for completeness. Our focus and novelty is the estimation of the marginal covariance function and of the eigenfunctions ϕ_k(·)'s (see Section 3.2), as well as the the estimation of the time-varying basis coefficients ξ_ik(·)'s (see Section 3.3). Prediction of Y_i(s, T) is detailed in Section 3.4.

3.1. Step 1: Mean function

As in Scheipl et al. (2014) we estimate the mean function, μ(s, T), using bivariate smoothing via bivariate tensor product splines (Wood, 2006) of the pooled data Y_ijr = Y_ij(s_r)'s. Consider two univariate B-spline bases, {B_s,1(s), . . . , B_s,ds(s)} and {B_T,1(T), . . . , B_T,dT(T)}, where d_s and d_T are their respective dimensions. The mean surface is represented as a linear combination of a tensor product of the two univariate B-spline bases μ(s, T ) = ${\sum }_{q_1=1}^{d_s}{\sum }_{q_2=1}^{d_T}$ B_s,q1(s)B_T,q2(T)β_q1q2 = B(s, T)^Tβ, where B(s, T) is the known d_sd_T-dimensional vector of B_s,q1(s)B_T,q2(T)'s, and β is the vector of unknown parameters, β_q1q2's. The bases dimensions, d_s and d_T, are set to be sufficiently large to accommodate the complexity of the true mean function, and the roughness of the function is controlled through the size of the curvature in each direction separately, i.e. $\int \int {\{{\partial }^2\mu (s,T)∕\partial s^2\}}^{2}dTds={\beta }^T({\mathbf{p}}_{\mathrm{s}}\otimes {\mathbf{I}}_{{\mathrm{d}}_{\mathsf{T}}})\beta$ in direction s, and $\int \int {\{{\partial }^2\mu (s,T)∕\partial T^2\}}^{2}dTds={\beta }^T({\mathbf{I}}_{{\mathrm{d}}_{\mathrm{s}}}\otimes {\mathbf{P}}_{\mathsf{T}})\beta$ in T. The penalized criterion to be minimized is ${\sum }_{i,j,r}{[Y_{ijr}-\mathbf{B}{(s_r,T_{ij})}^T\beta ]}^2+{\beta }^T({\lambda }_s{\mathbf{P}}_{\mathrm{s}}\otimes {\mathbf{I}}_{{\mathrm{d}}_{\mathsf{T}}}+{\lambda }_T{\mathbf{I}}_{{\mathrm{d}}_{\mathrm{s}}}\otimes {\mathbf{P}}_{\mathsf{T}})\beta$,, where λ_s and λ_T are smoothing parameters that control the trade-off between the smoothness of the fit and the goodness of fit. The smoothing parameters can be selected by the restricted maximum likelihood (REML) or generalized cross-validation (GCV). The estimated mean function is $\widehat{\mu }(s,T)$ = $\mathbf{B}{(s,T)}^T\widehat{\beta }$. This method is a very popular smoothing technique of bivariate data.

Other available bivariate smoothers can be used to estimate the mean μ(s, T): for example, kernel-based local linear smoother (Hastie et al., 2009), bivariate penalized spline smoother (Marx & Eilers, 2005) and the sandwich smoother (Xiao et al., 2013). The sandwich smoother (Xiao et al., 2013) is especially useful in the case of very high dimensional data for its appealing computational efficiency, in addition to its estimation accuracy.

3.2. Step 2: Marginal covariance. Data-based orthogonal basis

Once the mean function is estimated, let ${\tilde{Y}}_{ijr}=Y_{ijr}-\widehat{\mu }(s_r,T_{ij})$ be the demeaned data. We use the demeaned data to estimate the marginal covariance function induced by W_i(s, T_ij), Ξ(s, s′) = Σ(s, s′) + Γ(s, s′). The estimation of Ξ(s, s′) consists of two steps. In the first step, a raw covariance estimator $\tilde{\Xi }(s,s^{\prime })$ is obtained; the pooled sample covariance is a suitable choice, if all the curves are observed on the same grid of points:

$$\tilde{\Xi }(s_r,s_{r^{\prime }})=\sum _{i=1}^n\sum _{j=1}^{m_i}{\tilde{Y}}_{ijr}{\tilde{Y}}_{ij{r}^{\prime }}∕\left(\sum _{i=1}^n{m}_i\right).$$ (3)

As data Y_ijr's are observed with white noise, ε_2,ij(s_r), the ‘diagonal’ elements of the sample covariance, $\tilde{\Xi }(s_r,s_r)$, are inflated by the variance of the noise, σ². In the second step, the preliminary covariance estimator is smoothed by ignoring the ‘diagonal’ terms; see also Staniswalis & Lee (1998) and Yao et al. (2005) who used similar technique for the case of independent functional data. In our simulation and data application we use the sandwich smoother (Xiao et al., 2015). To ensure the positive semi-definiteness of the estimator the negative eigenvalues are zero-ed. The resulting smoothed covariance function, $\widehat{\Xi }(s,s^{\prime })$, is used as an estimator of $\Xi (s,s^{\prime })$. In Section 4, we show that $\widehat{\Xi }(s,s^{\prime })$ is an unbiased and consistent estimator of $\Xi (s,s^{\prime })$ in two settings: 1) the data are observed fully and without noise, i.e. ∈_ij(s) ≡ 0 and 2) the data are observed fully and with measurement error of type ∈_1,ij(s), i.e ∈_ij(s) ≡ ∈_1,ij(s).

Let ${\{{\widehat{\varphi }}_k\left(s\right),{\widehat{\lambda }}_k\}}_k$ be the pairs of eigenvalues/eigenfunctions obtained from the spectral decomposition of the estimated covariance function, $\widehat{\Xi }(s,s^{\prime })$. The truncation value K is determined based on pre-specified percentage of variance explained (PVE); specifically, K can be chosen as the smallest integer such that $({\sum }_{k=1}^K{\widehat{\lambda }}_k∕{\sum }_{k=1}^{\infty }{\widehat{\lambda }}_k)$ is greater than the pre-specified PVE (Di et al. 2009; Staicu et al., 2010).

3.3. Step 3: Covariance of the time-varying coefficients

Let ${\tilde{\xi }}_{W,ijk}=\int {\tilde{Y}}_{ij}\left(s\right){\widehat{\varphi }}_k\left(s\right)ds$ be the projection of the jth repeated demeaned curve of the ith subject onto the direction ${\widehat{\varphi }}_k(\cdot )$ for k = 1, . . . , K. Since ${\tilde{Y}}_{ij}(\cdot )$ is observed at dense grids of points {s_r : r = 1, . . . , R} in [0, 1] for all i and j, ${\tilde{\xi }}_{W,ijk}$ is approximated accurately through numerical integration. It is easy to see that the version of ${\tilde{\xi }}_{W,ijk}$ that uses μ(s, T_ij) in place of $\widehat{\mu }(s,T_{ij})$ and ϕ_k(s) in place of ${\widehat{\varphi }}_k\left(s\right)$ converges to ξ_W,ijk with probability one, as R diverges. The time-varying terms ${\tilde{\xi }}_{W,ijk}$ are proxy measurements of ξ_ik(T_ij); they will be used to study the temporal dependence along the direction ϕ_k(·), G_k(T, T′) = cov{_,ik(T), _,ik(T′)}, and furthermore to obtain prediction for all times T ∈ [0, 1].

Consider now ${\{(T_{ij},{\tilde{\xi }}_{W,ijk}):j=1,\dots ,m_i\}}_i$ as the ‘observed data’. One viable approach is to assume a parametric structure for G_k(·, ·) such as AR(1) or a random effects model framework; this is typically preferable when m_i is very small and the longitudinal design is balanced. We discuss random effects model for estimating the longitudinal covariance in the data application. Here we consider a more flexible approach and estimate the covariance G_k(·,·) nonparametrically, by employing FPCA techniques for sparse functional data (Yao et al., 2005).

Let ${\{{\psi }_{kl}(\cdot ),{\eta }_{kl}\}}_l$ be the pairs of eigenfunctions and eigenvalues of the covariance G_k; we model the proxy observations as ${\tilde{\xi }}_{W,ijk}$ = ${\sum }_{l=1}^{\infty }{\zeta }_{ikl}{\psi }_{kl}\left(T_{ij}\right)+{\tilde{e}}_{ijk}$ where ζ_ikl's are random variables with zero mean and variances equal to η_kl, ${\tilde{e}}_{ijk}$'s are iid with zero-mean and variance equal to ${\tilde{\sigma }}_{e,k}^2$ and independent of ζ_ikl. Following Yao et al. (2005), we first obtain the raw sample covariance, ${\tilde{G}}_{ik}(T_{ij},T_{i{j}^{\prime }})$ = ${\tilde{\xi }}_{W,ijk}{\tilde{\xi }}_{W,i{j}^{\prime }k}$. Then the estimated smooth covariance surface, ${\widehat{G}}_k(T,T^{\prime })$, is obtained by using bivariate smoothing of $\{(T_{ij},T_{i{j}^{\prime }}),{\tilde{G}}_{ik}(T_{ij},T_{i{j}^{\prime }}):i,j\ne j^{\prime }\}$. Kernel-based local linear smoothing (Yao et al., 2005) or penalized tensor product spline smoothing (Wood, 2006) can be used at this step. The diagonal terms $\{{\tilde{G}}_{ik}(T_{ij},T_{i{j}^{\prime }}):i,j=j^{\prime }\}$ are removed because the noise ${\tilde{e}}_{ijk}$ leads to inflated variance function. Let ${\{{\widehat{\psi }}_{kl}(\cdot ),{\widehat{\eta }}_{kl}\}}_l$ be the pairs of eigenvalues/eigenfunctions of the estimated covariance surface, ${\widehat{G}}_k(T,T^{\prime })$. The truncation value, L_k, is determined based on pre-specified PVE; using similar ideas as in Section 3.2. The variance ${\tilde{\sigma }}_{e,k}^2$ is estimated as the average of the difference between a smooth estimate of the variance based on $\{T_{ij},{\tilde{\xi }}_{W,ijk}^2\}$ and ${\widehat{G}}_k(T,T)$; Yao et al. (2005) discusses an alternative that dismisses the terms at the boundary when estimating the error variance.

Once the eigenbasis functions ${\left\{{\psi }_{kl}(\cdot )\right\}}_{l=1}^{L_k}$, eigenvalues η_kl's, and error variance ${\tilde{\sigma }}_{e,k}^2$ are estimated, the above model framework can be viewed as a mixed effects model and the random components ζ_ikl can be predicted using conditional expectation and a jointly Gaussian assumption for ζ_ijk's and e_ijk's. In particular, ${\widehat{\xi }}_{ikl}$ = $\mathsf{E}\left[\widehat{{\zeta }_{ikl}\mid {\tilde{\xi }}_{W,ik}}\right]$ = ${\widehat{\eta }}_{kl}{\widehat{\psi }}_{ikl}^T{\widehat{\Sigma }}_{{\xi }_{W,ik}}^{-1}{\tilde{\xi }}_{W,il}$, where ${\widehat{\psi }}_{ikl}={\{{\widehat{\psi }}_{kl}\left(T_{i1}\right),\dots ,{\widehat{\psi }}_{kl}\left(T_{i{m}_i}\right)\}}^T$ is the m_i-dimensional column vector of the evaluations of ${\widehat{\psi }}_{kl}(\cdot )$ at {T_ij : j = 1, . . . , m_i}, ${\widehat{\Sigma }}_{{\xi }_{W,ik}}$ is a m_i × m_i - matrix with (j, j′)th element equal to ${\widehat{G}}_k(T_{ij},T_{i{j}^{\prime }})+{\widehat{\tilde{\sigma }}}_{e,k}^2$, for j = j′ and ${\widehat{G}}_k(T_{ij},T_{i{j}^{\prime }})$ otherwise, and ${\tilde{\xi }}_{W,ik}$ is the m_i - dimensional column vector of ${\tilde{\xi }}_{W,ijk}$'s. The predicted time-varying coefficients corresponding to a generic time T are obtained as ${\widehat{\xi }}_{ik}\left(T\right)={\sum }_{l=1}^{L_k}{\widehat{\zeta }}_{ikl}{\widehat{\psi }}_{kl}\left(T\right)$. Yao et al. (2005) proved the consistency of the eigenfunctions and predicted trajectories when ξ_W,ijk's are observed. In Section 4 we extend these results to the case when the proxy ${\tilde{\xi }}_{W,ijk}$'s are used instead and when the profiles Y_ij(·) are fully observed and the noise is of the type ε_ij(s) = ε_1,ij(s); i.e. the data Y_ij(·) are observed with smooth error.

3.4. Step 4: Trajectories reconstruction

We are now able to predict the full response curve at any time point T ∈ [0, 1] by: ${\widehat{Y}}_i(s,T)=\widehat{\mu }(s,T)+{\sum }_{k=1}^K{\widehat{\xi }}_{ik}\left(T\right){\widehat{\varphi }}_k\left(s\right)$, where s ∈ [0, 1]. In Section 4 we show the consistency of ${\widehat{Y}}_i(s,T)$.

4. Theoretical properties

Next we discuss the asymptotic properties of the estimators and the predicted trajectories. Our setting - sparse longitudinal design and dense functional design - requires new techniques than the ones commonly used for theoretical investigation of repeated functional data such as Chen & Müller (2012). Since the mean estimation has been studied previously, we assume that the response trajectories, Y_ij(·)'s, have zero-mean and focus on the estimation of the model covariance. Throughout this section we assume that Y_ij(·) is observed fully as a function over the domain, $\mathcal{S}=[0,1]$. Section 4.1 discusses the main theoretical results when data are observed without error, i.e. ε_ij(s) ≡ 0 for s ∈ [0, 1]. Section 4.2 extends the results to the case when the data are corrupted with smooth error process ε_ij(s)≡ ε_1,ij(s). The proofs are detailed in the Supplementary Material; also in the Supplementary Material we include a discussion on how to relax some of the assumptions. Throughout this section we use $\mathcal{S}$ and $\mathcal{T}$ to distinguish between the domains.

We assume that the bivariate process X_i(s, T) is a realization of a true random process, X(s, T), with zero-mean and smooth covariance function, c((s, T),(s′, T ′)), which satisfies some regularity conditions:

• (A1.)X = {X(s, T) : (s, T) ∈ $\mathcal{S}\times \mathcal{T}$ is a square integrable element of the $L^2(\mathcal{S}\times \mathcal{T})$, i.e. $\mathsf{E}[\int \int X^2(s,T)dsdT]<\infty$, where $\mathcal{S}$ and $\mathcal{T}$ are compact sets.
• (A2.)The sampling density g(T) is continuous and sup_T∈T|g(T)| < ∞.

Under (A1.) and (A2.), the function Σ(s, s′) defined above (i) is symmetric, (ii) is positive definite, and (iii) has eigenvalues λ_k's with ${\sum }_{k=1}^{\infty }{\lambda }_k<\infty$. Thus Σ(·, ·) is a proper covariance function (Horváth & Kokoszka, 2012, p.24).

4.1. Response curves measured without error

Assume ε_ij(s) ≡ 0 and thus Y_ij(s) = X_i(s, T_ij) for s ∈ $\mathcal{S}$. The sample covariance of Y_ij(s) is $\widehat{\Sigma }(s,s^{\prime })={\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{Y}_{ij}\left(s\right)Y_{ij}\left(s^{\prime }\right)∕\left({\sum }_{i=1}^n{m}_i\right)$. The following assumptions regard the moment behavior of X and are commonly used in functional data analysis (Yao et al., 2005; Chen & Müller, 2012); we require them in our study.

• (A3.)E[X(s, T)X(s′, T)X(s, T′)X(s′, T′)] < ∞ for arbitrary s, s′ ∈ $\mathcal{S}$ and T, T′ ∈ $\mathcal{T}$.
• (A4.)E[[∥X(·, T)∥⁴] < ∞ for each T ∈ $\mathcal{T}$.

Theorem 1

Assume (A1.) - (A3.) hold. Then $\mid \widehat{\Sigma }(s,s^{\prime })-\Sigma (s,s^{\prime })\mid \stackrel{p}{\to }0$ as n diverges. If in addition (A4.) holds, then

$${\Vert \widehat{\Sigma }(\cdot ,\cdot )-\Sigma (\cdot ,\cdot )\Vert }_s\stackrel{p}{\to }0asn\to \infty ,$$ (4)

where ∥k(·,·)∥_s = ${\{\int \int k^2(s,s^{\prime })dsd{s}^{\prime }\}}^{1∕2}$ is the Hilbert-Schmidt norm of k(·,·).

(A5.) Let $a_1=({\lambda }_1-{\lambda }_2)$ and $a_k=\max [({\lambda }_{k-1}-{\lambda }_k),({\lambda }_k-{\lambda }_{k+1}))]$ for k ≥ 2, where _k is the kth largest eigenvalues of Σ(s, s′). Assume that $0<a_k<\infty$ and λ_k > 0 for all k (no crossing or ties among eigenvalues).

Using Theorem 4.4 and Lemma 4.3 of Bosq (2000, p.104), the consistency result (4) implies that, if furthermore (A5.) holds, the eigen-elements of $\widehat{\Sigma }(s,s^{\prime })$ are consistent estimators of the corresponding eigen-elements of Σ(s, s′).

Corollary 1

Under the assumptions (A1.)-(A5.), for each k we have $\mid {\widehat{\lambda }}_k-{\lambda }_k\mid \stackrel{p}{\to }0$, and ${\Vert {\widehat{\varphi }}_k(\cdot )-{\varphi }_k(\cdot )\Vert }_s\stackrel{p}{\to }0$ as n diverges.

Next, we focus on the estimation of the covariance G_k(T, T′), which describes the longitudinal dynamics. We first show the uniform consistency of ${\widehat{\xi }}_{W,ijk}$; the result follows if sup_j,s|Y_i(s, T_ij)| is bounded almost surely. which is ensured if (A6.) holds. Then, we use this result to show that the estimator of G_k(T, T′) based on ${\widehat{\xi }}_{W,ijk}$'s is asymptotically identical to that based on ${\xi }_{W,ijk}$. Consistency results of the remaining model components follow directly from Yao et al. (2005). The Gaussian assumption (A8.) is needed to show the consistency of ${\widehat{\zeta }}_{ikl}$.

• (A6.)E[sup_s,T|X(s, T)|^a] ≤ M^a for a constant, M > 0, and an arbitrary integer, a ≥ 1; This is equivalent to assume that X(s, T) is absolutely bounded almost surely.
• (A7.)Let b_k1 = (η_k1 − η_k2) and b_kl = max[(η_k(l–1) – η_kl), (η_kl – η_k(l+1)))] for l ≥ 2, where η_kl is the lth largest eigenvalues of G_k(T, T′). Assume that 0 < b_kl < ∞ and η_kl > 0 for all k and l.
• (A8.)ζ_ikl and e_ijk are jointly Gaussian.

Theorem 2

Under the assumptions (A1.) - (A6.), for each k $su{p}_j\mid {\tilde{\xi }}_{W,ijk}-{\xi }_{W,ijk}\mid \stackrel{p}{\to }0$ and ${\Vert {\widehat{G}}_k(\cdot ,\cdot )-G_k(\cdot ,\cdot )\Vert }_s\stackrel{p}{\to }0$ as n diverges. In fact a stronger result also holds, namely $su{p}_{T,T^{\prime }}\mid {\widehat{G}}_k(T,T^{\prime })-G_k(T,T^{\prime })\mid \stackrel{p}{\to }0$ as n diverges.

Corollary 2

Assume (A1.) - (A8.) hold for each k and l. Then the eigenvalues ${\widehat{\eta }}_{kl}$ and eigenfunctions ${\widehat{\psi }}_{kl}(\cdot )$ of ${\widehat{G}}_k(\cdot ,\cdot )$ satisfy $\mid {\widehat{\eta }}_{kl}-{\eta }_{kl}\mid \stackrel{p}{\to }0$, and ${\Vert {\widehat{\psi }}_{kl}(\cdot )-{\psi }_{kl}(\cdot )\Vert }_s\stackrel{p}{\to }0$ as n diverges. Uniform convergence of ${\widehat{\psi }}_{kl}(\cdot )$ also holds: $su{p}_T\mid {\widehat{\psi }}_{kl}\left(T\right)-{\psi }_{kl}\left(T\right)\mid \stackrel{p}{\to }0$. Furthermore, as n diverges, we have $\mid {\widehat{\tilde{\sigma }}}_{e,k}^2-{\sigma }_{e,k}^2\mid \stackrel{p}{\to }0$ and $\mid {\widehat{\zeta }}_{ikl}-{\tilde{\zeta }}_{ikl}\mid \stackrel{p}{\to }0$, where ${\tilde{\zeta }}_{ikl}=E[{\zeta }_{ikl}\mid {\xi }_{W,ik}]$ and ${\xi }_{W,ik}$ is the m_i-dimensional column vector of ${\xi }_{W,ijk}$'s.

The consistency results for all model components imply prediction consistency.

Thorem 3

Assume (A1.) - (A8.), for each (s, T) ∈ $\mathcal{S}\times \mathcal{T}$, Then ${\widehat{Y}}_i(s,T)\stackrel{p}{\to }{\sum }_{k=1}^{\infty }{\sum }_{l=1}^{\infty }{\tilde{\zeta }}_{ikl}{\psi }_{kl}\left(T\right){\varphi }_k\left(s\right)$ as n, K and L_k's → ∞.

4.2. Response curves measured with smooth error

Assume next that Y_ij(s) are observed with smooth error ε_ij(s) ≡ ε_1,ij(s) and thus Y_ij(s) = X_i(s, T_ij) + ε_1,ij(s) for s ∈ $\mathcal{S}$ and ε_1,i (·) ∈ L² ($\mathcal{S}$). The main difference from Section 4.1 is that the sample covariance of Y_ij(s) is an estimator of Ξ(s, s′) = Σ(s, s′) + Γ(s, s′), not of (Σs, s′); we denote the sample covariance of Y_ij(s) by $\widehat{\Xi }(s,s^{\prime })$ = ${\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{Y}_{ij}\left(s\right)Y_{ij}\left(s^{\prime }\right)∕\left({\sum }_{i=1}^n{m}_i\right)$. Using similar arguments as earlier, we show that $\widehat{\Xi }(s,s^{\prime })$ is an unbiased estimator of Ξ(s, s′). Moreover similar arguments can be used to show the pointwise consistency as well as the Hilbert-Schmidt norm consistency of $\widehat{\Xi }(s,s^{\prime })$. Additional assumptions are required.

• (A9.)Assume ε_ij(·) is realization of ε = {ε(s) : s ∈ $\mathcal{S}$}, which is square integrable process in L²($\mathcal{S}$).
• (A10.)$\mathsf{E}\left[{\Vert ∊(\cdot )\Vert }^4\right]<\infty$
• (A11.)$\mathsf{E}\left[{\sup }_s{\mid ∊\left(s\right)\mid }^a\right]\le M^a$ for a constant, M > 0, and an arbitrary integer, a ≥ 1.

Corollary 3

Under the assumptions (A1.) - (A3.), and (A9.), for each(s, s′) – $\mid \widehat{\Xi }(s,s^{\prime })-\Xi (s,s^{\prime })\mid \stackrel{p}{\to }0$ as n diverges. And under the assumptions (A1.)-(A4.), (A9.)-(A11.), ${\Vert \widehat{\Xi }(\cdot ,\cdot )-\Xi (\cdot ,\cdot )\Vert }_s\stackrel{p}{\to }0$ and $su{p}_j\mid {\tilde{\xi }}_{W,ijk}-{\xi }_{W,ijk}\mid \stackrel{p}{\to }0asn\to \infty$.

The proofs of these results are detailed in the Supplementary Material. As the smooth error process ε_1,ij(s) is correlated only along the functional argument, s, and ε_1,ij(s) are iid over i, j, it follows that the theoretical properties of the predictions - of the time-varying coefficients and the response curve - hold without any modification.

The theoretical results are based on the assumptions that data Y_ij(s)'s are observed fully, without white noise, ε_2,ij(s) ≡ 0 for all s, and have mean zero. Some of these assumptions are quite common in theoretical study involving functional data; Cardot et al. (2003, 2004); Chen & Müller (2012). They are discussed in the Supplementary Material.

5. Simulation study

We study our approach in finite samples and compare its performance with Chen & Müller (2012) denoted by CM. We generate N_sim = 1000 samples from model (1) with K = 2, Y_ij(s) = μ(s, T_ij) + ξ_i1(T_ij)ϕ₁(s) + ξ_i2(T_ij)ϕ₂(s) + ε_ij(s), where μ(s, T) = 1 + 2s + 3T + 4sT, and ϕ₁(s) = 1 and ϕ₂(s) = $\sqrt{2}\sin (2ß\mathrm{s})$. The grid of points for s is the set of 101 equispaced points in [0, 1]. For each i, there are m_i profiles associated with visit times, {T_ij : j = 1, . . . , m_i}; T_ij's are randomly sampled from 41 equally spaced points in [0, 1]. ξ_ik(T) are generated from various covariance structures: (a) non-parametric covariance (NP) where ξ_ik(T) = ζ_ik1 ψ_k1(T) + ζ_ik2 ψ_k2(T); (b) random effects model (REM) ξ_ik(T) = b_ik0 + b_ik1T, and (c) exponential autocorrelation (Exp) $\mathrm{cov}{\{}_{,\mathrm{ik}}\left(\mathsf{T}\right),{}_{,\mathrm{ik}}\left({\mathsf{T}}^{\prime }\right)\}=\check{\mathrm{k}}{\ae }_{\mathrm{k}}^{\mid \mathsf{T}-{\mathsf{T}}^{\prime }\mid }$. Errors are generated from ε_ij(s) = e_ij1ϕ₁(s) + e_ij2ϕ₂(s) + ε_2,ij(s), where e_ij1, e_ij2 and ε_2,ij(s) are mutually independent with zero- mean and variances equal to ${\sigma }_{e,1}^2,{\sigma }_{e,2}^2$ and σ², respectively; the white noise variance, σ², is set based on the signal to noise ratio (SNR). The details of the models are specified in the Supplementary Material. For each sample of size n we form a training set and a test set. The test set contains 10 profiles and is obtained as follows: randomly select 10 subjects from the sample and collect the subjects’ last profile. The remaining profiles for the 10 subjects and the data corresponding to the rest (n – 10) of the subjects form the training set. Our model is fitted using the training set and the methods of Section 3. The mean function, μ(s, T), is modeled using 50 cubic spline basis functions obtained from the tensor product of d_s = 10 basis functions in direction s and d_T = 5 in T . The smoothing parameters are selected via REML. The finite truncations K and L_k's are all estimated using the pre-specified level PVE = 0.95.

Estimation accuracy for the model components is evaluated using integrated mean squared errors (IMSE), while prediction performance is assessed through in-sample integrated prediction errors (IN-IPE) and out-of-sample IPE (OUT-IPE). Table 1 shows the results for different covariance models for ξ_ik(T), different number of repeated curve measurements per subject, different SNRs, complex error process, and varying sample sizes. The performance of the proposed estimation (see columns for μ, ϕ₁, and ϕ₂ of this table) is slightly affected by the covariance structure of ξ_ik(T)'s and m_i, but in general is quite robust to the factors we investigated. As expected the estimation accuracy improves with larger sample size; see the 3 × 3 top left block of IMSE results corresponding to n = 100, n = 300, and n = 500. Moreover both the prediction of ξ_ik(T )'s and that of Y_ij(·) are considered; see columns labeled ξ₁, ξ₂, IN-IPE and OUT-IPE of Table 1. The underlying covariance structure of ξ_ik(T)'s affects the prediction accuracy. Furthermore increasing the number of repeated curve measurements m_i improves the accuracy more than increasing the sample size n. This observation should not be surprising, as with larger number of repeated measurements the estimation of the covariance of the longitudinal process ξ_ik(T)'s improves and as a result it yields superior prediction. We compared our results with another, rather naïve approach: predict a subject's profile by the average of all previously observed profiles for that subject. The naïve approach (see columns IN-IPE_naive and OUT-IPE_naive) is very sensitive to the covariance structure of ξ_ik(T). In all the cases studied the prediction accuracy is inferior to the proposed method.

Table 1.

Estimation and prediction accuracy results based on N_sim = 1000 simulations

$m_i\stackrel{\mathrm{iid}}{\sim }\{8,\dots ,12\}\text{and}\mathrm{SNR}=1$
		μ	ϕ 1	ϕ 2	ξ 1	ξ 2	IN-IPE	IN-IPEnaive	OUT-IPE	OUT-IPEnaive
NP (a)	n = 100	0.092	0.003	0.011	0.338	0.224	0.406	7.790	0.988	11.478
	n = 300	0.031	0.001	0.009	0.226	0.138	0.313	7.773	0.559	11.349
	n = 500	0.019	0.001	0.009	0.199	0.117	0.288	7.779	0.455	11.262
REM (b)	n = 100	0.114	0.027	0.033	0.376	0.314	0.328	1.199	1.011	2.160
	n = 300	0.040	0.008	0.013	0.216	0.162	0.265	1.197	0.675	2.160
	n = 500	0.024	0.005	0.010	0.181	0.133	0.247	1.197	0.571	2.150
Exp (c)	n = 100	0.095	0.022	0.030	0.399	0.540	0.554	1.528	1.426	2.520
	n = 300	0.031	0.007	0.015	0.289	0.412	0.508	1.531	1.143	2.498
	n = 500	0.019	0.004	0.013	0.266	0.383	0.494	1.530	1.074	2.492

$m_i\stackrel{\mathrm{iid}}{\sim }\{15,\dots ,20\}\text{and}\mathrm{SNR}=1$
		μ	ϕ 1	ϕ 2	ξ 1	ξ 2	IN-IPE	IN-IPEnaive	OUT-IPE	OUT-IPEnaive
NP (a)	n = 100	0.076	0.002	0.010	0.180	0.101	0.238	7.807	0.477	10.666
	n = 300	0.026	< 0. 001	0.009	0.120	0.065	0.183	7.796	0.282	10.728
	n = 500	0.016	< 0. 001	0.009	0.108	0.058	0.173	7.797	0.242	10.772
REM (b)	n = 100	0.097	0.025	0.031	0.272	0.252	0.232	0.897	0.612	1.833
	n = 300	0.034	0.008	0.013	0.156	0.132	0.201	0.896	0.462	1.841
	n = 500	0.020	0.005	0.010	0.135	0.110	0.194	0.897	0.440	1.836
Exp (c)	n = 100	0.080	0.022	0.030	0.308	0.417	0.467	1.240	1.048	2.147
	n = 300	0.026	0.006	0.015	0.233	0.309	0.444	1.245	0.938	2.155
	n = 500	0.016	0.004	0.012	0.221	0.285	0.438	1.246	0.886	2.129

$m_i\stackrel{\mathrm{iid}}{\sim }\{8,\dots ,12\}\text{and}\mathrm{SNR}=5$
		μ	ϕ 1	ϕ 2	ξ 1	ξ 2	IN-IPE	IN-IPEnaive	OUT-IPE	OUT-IPEnaive
NP (a)	n = 100	0.092	0.005	0.005	0.328	0.213	0.363	7.184	0.958	10.795
	n = 300	0.031	0.001	0.002	0.213	0.124	0.268	7.170	0.506	10.662
	n = 500	0.019	0.001	0.001	0.187	0.103	0.242	7.178	0.402	10.585
REM (b)	n = 100	0.114	0.037	0.037	0.404	0.355	0.293	0.594	0.958	1.478
	n = 300	0.040	0.010	0.011	0.218	0.167	0.235	0.595	0.627	1.476
	n = 500	0.024	0.006	0.007	0.180	0.135	0.219	0.596	0.529	1.467
Exp (c)	n = 100	0.095	0.033	0.033	0.420	0.573	0.513	0.922	1.419	1.838
	n = 300	0.031	0.010	0.010	0.290	0.412	0.466	0.929	1.109	1.814
	n = 500	0.019	0.006	0.006	0.264	0.378	0.453	0.929	1.033	1.807

$m_i\stackrel{\mathrm{iid}}{\sim }\{15,\dots ,20\}\text{and}\mathrm{SNR}=5$
		μ	ϕ 1	ϕ 2	ξ 1	ξ 2	IN-IPE	IN-IPEnaive	OUT-IPE	OUT-IPEnaive
NP (a)	n = 100	0.076	0.003	0.003	0.174	0.095	0.205	7.462	0.441	10.300
	n = 300	0.026	0.001	0.001	0.113	0.057	0.147	7.453	0.239	10.359
	n = 500	0.016	< 0. 001	0.001	0.101	0.050	0.136	7.454	0.200	10.406
REM (b)	n = 100	0.097	0.035	0.035	0.300	0.293	0.205	0.552	0.568	1.464
	n = 300	0.034	0.010	0.010	0.160	0.140	0.178	0.552	0.426	1.473
	n = 500	0.020	0.006	0.007	0.136	0.114	0.172	0.554	0.405	1.470
Exp (c)	n = 100	0.080	0.033	0.033	0.330	0.451	0.434	0.895	1.012	1.779
	n = 300	0.027	0.009	0.010	0.236	0.313	0.410	0.902	0.901	1.785
	n = 500	0.016	0.005	0.006	0.221	0.284	0.403	0.902	0.851	1.763

Table 2 shows the comparison with CM, when the kernel bandwidth is fixed to h = 0.1 for both mean and covariance smoothing. The prediction using CM is more sensitive to the covariance structure of the underlying time-varying coefficients ξ_ik(T) and its accuracy can be improved by up to 50% using our proposed approach. Computation-wise, there is an order of magnitude difference in the computational cost between the methods: when n = 100 CM takes over 16 minutes, while our approach takes about 7 seconds. The overall conclusion is that the proposed approach provides an improved prediction performance over the existing methods in a computationally efficient manner.

Table 2.

Comparison between the proposed method and Chen & Muller (2012) in the presence of correlated errors. Results based on N_sim = 1000 simulations

$m_i\stackrel{\mathrm{iid}}{\sim }\{8,\dots ,12\}\text{and}\mathrm{SNR}=1$
		Chen & Muller (2012)			Proposed method (from Tables 1 and S2)
		IN-IPE	OUT-IPE	time (seconds)	IN-IPE	OUT-IPE	time (seconds)
NP (a)	n = 100	0.880	2.221	983.872	0.406	0.988	7.369
	n = 300	0.622	1.468	1659.611	0.313	0.559	15.892
	n = 500	0.556	1.298	2502.462	0.288	0.455	21.418
REM (b)	n = 100	0.424	1.359	1084.753	0.328	1.011	9.282
	n = 300	0.289	0.729	1955.193	0.265	0.675	11.347
	n = 500	0.257	0.614	2947.126	0.247	0.571	22.559
Exp (c)	n = 100	0.634	1.642	1556.182	0.554	1.426	7.514
	n = 300	0.549	1.251	1959.219	0.508	1.143	16.229
	n = 500	0.531	1.155	2865.041	0.494	1.074	17.109

6. DTI application

DTI is a magnetic resonance imaging technique, which provides different measures of water diffusivity along brain white matter tracts; its use is instrumental especially in diseases that affect the brain white matter tissue, such as MS (see Alexander et al. (2007), Basser et al. (1994), Basser et al. (2000), Basser & Pierpaoli (2011)). In this paper we consider the DTI measure called FA along CCA; specifically we consider one-dimensional summaries of FA along CCA (CCA-FA). The DTI study involves 162 MS patients, which are observed at between one and eight hospital visits, with a total of 421 visits and a median of two visits per subject. At each visit, FA profile is recorded at 93 locations along the CCA. The measurements are registered within and between subjects using standard biological landmarks identified by an experienced neuroradiologist (Scheipl et al., 2014).

Our main objective is twofold: (i) to understand the dynamic behavior of the CCA-FA profile in MS patients over time and (ii) to make accurate predictions of the CCA-FA profile of a patient at their next visit. Various aspects of the DTI study have been also considered in Goldsmith et al. (2011), Staicu et al. (2012), Pomann et al. (2013), and Scheipl et al. (2014). Greven et al. (2010) used an earlier version of the DTI study consisting of data from fewer and possibly different patients and obtained through a different registration technique. They studied the dynamic behavior of CCA-FA over time in MS; however, their method cannot provide prediction of the entire CCA-FA profile at the subject's next visit. By being able to predict the full CCA-FA profile at the subject's future visit, our approach has the potential to shed lights on the understanding of the MS progression over time as well as its response to treatment.

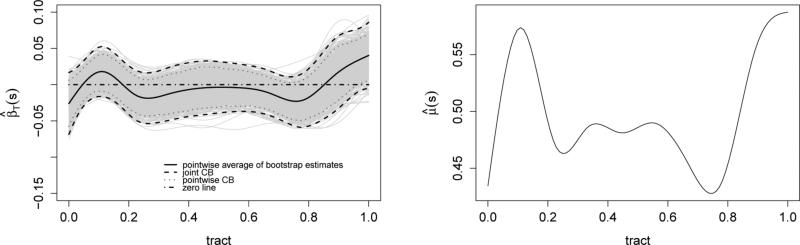
To start with, for each subject we define the hospital visit time T_ij by the difference between the reported visit time and the subject's baseline visit time; thus T_i1 = 0 for all subjects i. Then the resulting values are scaled by the maximum value in the study so that T_ij ∈ [0, 1] for all i and j. The sampling distribution of the visit times is right-skewed with rather strong skewness; for example there are only few observations T_ij's close to 1. The strong skewness of the sampling distribution of T_ij's has serious implications on the estimation of the bivariate mean μ(s, T); a completely nonparametric bivariate smoothing would results in unstable and highly variable estimation. This is probably why Greven et al. (2010) first centered the times for each patient i, {T_ij : j = 1, . . . , m_i}, and then standardized the overall set {T_ij : i, j} to have unit variance. However, such subject-specific transformation of T_ij's loses interpretability and it is not suited for prediction at unobserved times - which is crucial in our analysis. One way to bypass this issue is to assume a simpler parametric structure along the longitudinal direction, T, for the mean function; based on exploratory analysis we assume linearity in T . Specifically we consider μ(s, T_ij) = μ₀(s) + β_T(s)T_ij, where μ₀(·) and β_T(·) are unknown, smooth functions of s. We estimate μ₀(·) and β_T(·) using a penalized univariate cubic spline regression with 10 basis functions; the smoothing parameters are estimated using REML. The estimates $\widehat{\mu }(s,T)$ and ${\widehat{\beta }}_T\left(s\right)$ are displayed in Figure S1 of the Supplementary Material. Using the bootstrap of subjects - based methods of Park et al. (2015) and B = 1000 bootstrap samples we construct 95% joint confidence bands for ${\widehat{\beta }}_T\left(s\right)$; see Figure 1. The confidence band contains zero for all s, indicating evidence that a mean model μ(s, T_ij) = μ₀(s) is more appropriate.

Figure 1.

Left panel: 95% pointwise and joint confidence bands of the slope function β_T(s) of μ(s, T) using bootstrap; Right: final mean estimate, $\widehat{\mu }(s,T)={\widehat{\mu }}_0\left(s\right)$

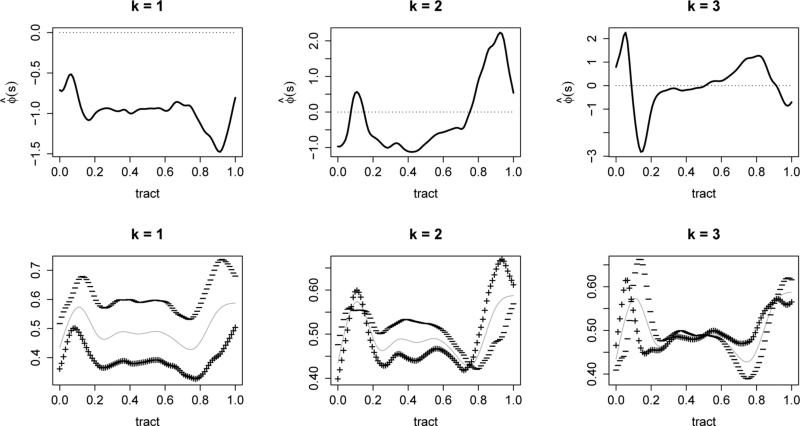
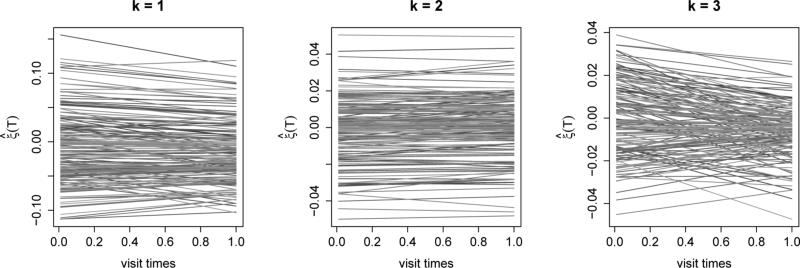
Next we demean the data and estimate the marginal covariance; using a preset level PVE = 0.95 we obtain K = 10 eigenfunctions. Figure 2 shows the leading 3 eigenfunctions that explain in turn 62.69%, 8.37% and 6.77% of the total variance; the rest of the estimated eigenfunctions are given in Figure S3 of the Supplementary Material. Preliminary investigation (not shown here) indicates a simpler model for the longitudinal covariance: a random effects model ξ_ik(T_ij) = b_0ik + b_1ikT_ij, where var(b_lik) = ${œ}_{\mathrm{lk}}^2$ for l = 0, 1 and cov(b_0ik, b_1ik) = œ_01k. This resulting model is similar to Greven et al. (2010). The fitted time-varying coefficient functions, ${\widehat{\xi }}_{ik}\left(T\right)$, for k = 1, 2 and 3 are shown in Figure 3, and the rest are shown in Figure S4 of the Supplementary Material. The estimated ${\widehat{\xi }}_{i1}\left(T\right)$ suggest some longitudinal changes, but the signs generally remain constant across time. The results imply that a subject mean profile tends to stay lower than the population mean, if the first eigenfunction corresponding to that individual is positively loaded at baseline, and vise versa. In contrast, ${\widehat{\xi }}_{i2}\left(T\right)$, are mostly constant across visit times and imply little changes over time.

Figure 2.

Top: First three eigenfunctions of the estimated marginal covariance; Bottom: estimated mean function ${\widehat{\mu }}_0\left(s\right)$ (gray line) ± $2\sqrt{{\widehat{\lambda }}_k}{\widehat{\varphi }}_k\left(s\right)$ (+ and − signs, respectively)

Figure 3.

Estimated time-varying coefficients ${\widehat{\xi }}_{ik}\left(T\right)$ for k = 1, 2 and 3 using REM

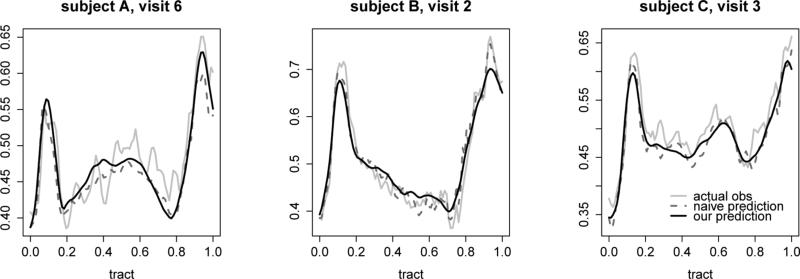
Finally, we assess the goodness-of-fit and prediction accuracy of our final model. For the goodness-of-fit we use the in-sample integrated prediction error (IN-IPE): IN-IPE= ${\sum }_{i=1}^{162}{\sum }_{j=1}^{m_i}\int {\{Y_{ij}\left(s\right)-{\widehat{Y}}_{ij}\left(s\right)\}}^{2}ds∕\left\{{\sum }_{i=1}^{162}{m}_i\right\}$, where ${\widehat{Y}}_{ij}\left(s\right)={\widehat{\mu }}_0\left(s\right)+{\sum }_{k=1}^K({\widehat{b}}_{0ik}+{\widehat{b}}_{1ik}{T}_{ij}){\widehat{\varphi }}_k\left(s\right)$, and Y_ij(·)'s are the observed curve data. The square root of the IN-IPE is 2.31 × 10⁻² for our model; for comparison Greven et al. (2010) yields 2.66 × 10⁻² and Chen & Müller (2012) gives 3.76 × 10⁻². For prediction accuracy we use leave-the last-curve-out integrated prediction error (OUT-IPE) calculated for the 106 subjects observed at two hospital visits or more: OUT-IPE = ${\sum }_{i=1}^{106}\int {\{Y_{i{m}_i}\left(s\right)-{\widehat{Y}}_{i{m}_i}^{[-i{m}_i]}\left(s\right)\}}^{2}ds∕106$, where ${\widehat{Y}}_{i{m}_i}^{[-i{m}_i]}\left(s\right)$ is the predicted curve at time T_imi for the ith subject using the fitted model based on all the data less the m_ith curve of the ith subject. Figure 4 shows such predicted curves ${\widehat{Y}}_{i{m}_i}^{[-i{m}_i]}\left(s\right)$ obtained using our model and the naive model for three randomly selected subjects at their last visit. The square root of OUT-IPE is 3.48 × 10⁻² for our model; for comparison Chen & Müller (2012) gives 8.71 × 10⁻² and the naïve approach gives 3.52 × 10⁻². These results suggest that, in this short term study of MS, there is a small variation of CCA-FA profiles over time.

Figure 4.

Predicted values of FA for the last visits of three randomly selected subjects; actual observations (gray); predictions using our model (black solid) and using the naive approach (black dashed)