Significance
The hydrodynamic forces within bursting bubbles are of interest for their relevance to small-scale fluid mechanics, bioreactor efficiency, pollutant degradation, and the origin of life. However, despite the 150-year history of their study, the strengths of flows within bursting bubbles are only hypothetically known. Here, we show that DNA nanotubes––architecturally similar to biological microtubules—are fragmented during the bubble bursting process. Further, by analyzing the resulting fragment lengths, we characterize the spectrum of elongational flow rates, revealing that surprisingly strong tensile forces can be generated––in principle sufficient to fragment filamentous cyanobacterial chains, lipid vesicle protocells, genomic DNA, and other long polymeric molecules residing within or near the disintegrating liquid film.
Keywords: DNA nanotechnology, polymer dynamics, hydrodynamics
Abstract
Quantifying the mechanical forces produced by fluid flows within the ocean is critical to understanding the ocean’s environmental phenomena. Such forces may have been instrumental in the origin of life by driving a primitive form of self-replication through fragmentation. Among the intense sources of hydrodynamic shear encountered in the ocean are breaking waves and the bursting bubbles produced by such waves. On a microscopic scale, one expects the surface-tension–driven flows produced during bubble rupture to exhibit particularly high velocity gradients due to the small size scales and masses involved. However, little work has examined the strength of shear flow rates in commonly encountered ocean conditions. By using DNA nanotubes as a novel fluid flow sensor, we investigate the elongational rates generated in bursting films within aqueous bubble foams using both laboratory buffer and ocean water. To characterize the elongational rate distribution associated with a bursting bubble, we introduce the concept of a fragmentation volume and measure its form as a function of elongational flow rate. We find that substantial volumes experience surprisingly large flow rates: during the bursting of a bubble having an air volume of 10 mm3, elongational rates at least as large as s−1 are generated in a fragmentation volume of . The determination of the elongational strain rate distribution is essential for assessing how effectively fluid motion within bursting bubbles at the ocean surface can shear microscopic particles and microorganisms, and could have driven the self-replication of a protobiont.
Functioning like a giant heat engine between the high-temperature heat bath of the sun and the low-temperature heat bath of outer space, the earth’s atmosphere generates wind and rain with intense fluid flows. The mechanical stresses produced by these hydrodynamic flows are among the environmental stresses that biological organisms must cope with. Organisms often exploit these stresses and fluid flows, most notably to aid reproduction. A well-known example at the macroscopic scale is the wind dispersal of spores, seeds, and pollen. Less well-known, fragmentation resulting from fluid-flow-induced stress is used by a number of marine organisms as a means of vegetative reproduction, such as macrophyte algae (1) and sponge and coral colony (2, 3) propagation by storm-induced fragmentation. Can analogous mechanical forces facilitate vegetative reproduction at the microscale? Current evidence is at best indirect: Filamentous cyanobacteria are known to fragment under environmental stress (4, 5), suggesting that prokaryotes may use fluid-flow-induced fragmentation as a means of clonal reproduction and dispersal as well.
Several origin-of-life hypotheses invoke processes in which environmentally produced microscale mechanical forces drive self-replication through fragmentation. Oparin proposed that fragmentation of coacervates may have constituted a primitive form of self-replication allowing for Darwinian evolution by natural selection (6). More concretely, Cairns-Smith proposed that life arose from mineral crystals that replicated by fragmentation into new seed crystals, thereby propagating genetic information consisting of the patterns of defects within the mother crystal (7–9). Szostak’s group also proposed that division of protocells (having a lipid bilayer) can be driven by fluid flow (10–12). Inspired by Cairns-Smith’s proposal, Schulman, Yurke, and Winfree used DNA tile self-assembly to construct a self-replicating system in which fragmentation was induced by intense elongational flow at a constriction in a flow channel (13). This synthetic system is analogous to an in vitro system in which exponential growth of prions is driven via fragmentation by mechanical shearing of amyloid fibrils (14). Similarities between regeneration (self-healing) and asexual reproduction in modern organisms have led some to postulate fragmentation-and-regeneration as a primordial form of reproduction (15).
To effectively shear microscopic objects such as bacteria or protobionts, fluid flows must exhibit high-velocity gradients over the length scale of the object. Such small-scale high-velocity-gradient flows occur naturally in breaking ocean waves that produce whitecaps (16). Within these waves, the highest velocity gradients are expected to occur in the films of bursting bubbles due to the rapid acceleration produced by surface tension forces acting on the small fluid mass. Moreover, bursting bubbles can generate mechanical stresses of sufficient intensity to be biologically relevant to organisms living in the sea surface microlayer (neuston) (17). As a technological example, cell death at the air–liquid interface during the sparging of bioreactors to enhance oxygen diffusion has been attributed to bubble bursting (18).
The fluid flows most effective at shearing small free-floating objects are those that exhibit strain deformation. In such flows, a rod-shaped object will tend to align itself along the direction of maximum fluid extension. In this orientation the rod experiences the greatest tensile stress and is most susceptible to fragmentation. In a given fluid element, the rate of fluid extension––i.e., the rate at which two points in the fluid separate, divided by the distance between them––has a maximum that is referred to as the elongational rate and is here denoted by . A useful way to conceptualize the meaning of is to consider the case when it is constant. In this case, the time it takes for the fluid element to double its length is .
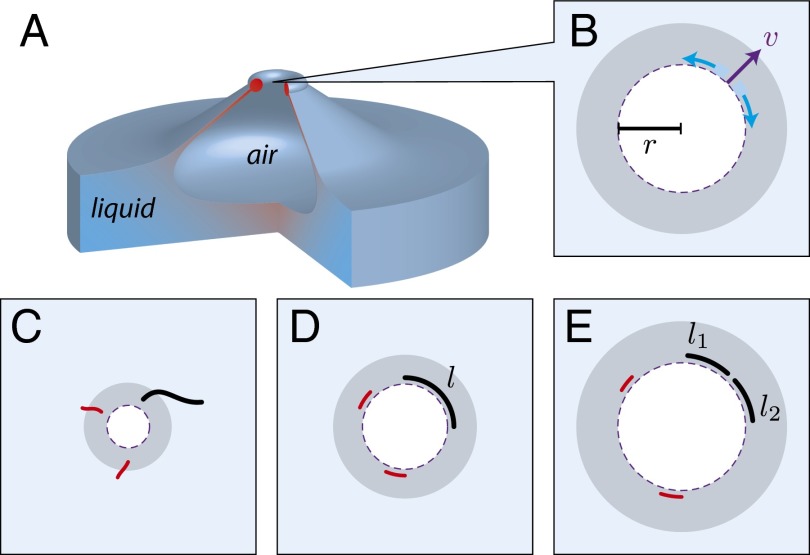
Fig. 1 shows a mechanism by which rod-shaped objects within bursting fluid films can be fragmented. As the hole produced in the bubble film expands, its circumference increases (Fig. 1B). Due to this, fluid elements near the hole’s edge will experience elongation in the direction perpendicular to the velocity of the hole edge. As shown in Fig. 1 C and D, rod-shaped structures within the bubble film will align along the circumference of the expanding hole. If the tension generated along the length of the structure exceeds its tensile strength, the structure will fragment (Fig. 1E).
Fig. 1.
DNA nanotubes fragmentation by bursting bubbles. Side (A) and top (B) views of a bubble filled with air bursting on a water surface. Color gradient loosely corresponds to the expected magnitude of the hydrodynamic forces. (B–E) As the hole travels outward driven by surface tension, the liquid film is accumulated into a growing toroidal rim (gray rings). The enlargement of the hole produces elongational flow, with rate , which is tangential to the perimeter where r is the hole radius and v is the outward velocity of the hole perimeter. The two blue arcs are the two volume elements of the bursting film. (C and D). As the hole expands, the fluid flow orients DNA nanotubes (black, red). (D and E) The elongational flow breaks sufficiently long DNA nanotubes (black) of length l into fragments of length and due to tension applied to the nanotube by the elongational fluid flow. Short nanotubes (red) are not fragmented due to insufficient build-up of tension.
The elongational rates generated by this mechanism can be estimated using a model of film hole dynamics, for a film of uniform thickness. Initially considered by Dupré (19), Rayleigh (20), and Ranz (21), then corrected by Culick (22) and Taylor (23), the model treats the rupture as a circular hole that propagates outward with the film fluid accumulating in a toroid at the hole perimeter. From momentum balance, the hole propagates outward with a constant speed , where σ is the surface tension of the film, ρ is the fluid density, and δ is the film thickness. The elongational rate of the circumference is given by , where r is the hole radius. The volume of fluid subjected to elongational rates greater than , in this simple model, is given by , which is, surprisingly, independent of film thickness. Such volumes provide a natural way to characterize the ability of a bursting bubble to fragment objects suspended within the bubble film that will shear under given elongational rate . Importantly, can be defined in a model-independent way as the volume of fluid that experiences elongational rates greater than during the course of bubble bursting. We will refer to such volumes as fragmentation volumes.
Although easiest to explain, the Culick and Taylor model does not describe the only type of elongational flow that can be generated within a bursting bubble; therefore the estimate for based on this model should be considered a loose lower bound for the true value. In fact, only half the surface-tension energy released is converted into the kinetic energy of the outward motion of the fluid (24). This suggests that the other half of the surface-tension energy must be dissipated within the film near the edge of the hole. For fluids with low viscosity, such as water, this implies that there are intense small-scale fluid flows near the edge of the hole (18) in addition to those illustrated in Fig. 1. Hydrodynamic instabilities, particularly with larger bubbles, can occur along the perimeter, resulting in fingering and the formation of droplets (25). Also, particularly for small bubbles, the expanding hole produces an inward propagating wave at the bottom surface of the bubble that forms a jet that may launch droplets (26, 27). High-flow gradients are expected in the region where these jets pinch to form droplets. A recent discussion of droplet production during bubble bursting in ocean-like (i.e., not soapy) water was given by Lhuissier and Villermaux (28).
As discussed by Lhuissier and Villermaux, at the instant the bubble bursts it possesses a cap of uniform thickness that, at a well-defined edge, joins with the bulk fluid in a region where the thickness rapidly increases with distance from the center of the bubble (Fig. 1A). The critical thickness at which bubble films spontaneously burst depends on the bubble radius (28), increasing from 0.05 to 30 μm as the bubble radius increases from 1 to 20 mm. For an object such as a microorganism to be fully impacted by the mechanical stresses produced by bubble bursting, it would have to reside in the cap film or close to the cap boundary; that is, its thinnest dimension would have to be smaller than the film thickness. Nevertheless, mechanical stresses produced by bursting bubbles are among the stresses that microorganisms, particularly those that occupy the niche consisting of the neuston or sea surface microlayer (29–31), must cope with. We hypothesize that protobionts, small enough to be suspended within the bubble film, also occupied this niche and used these stresses to facilitate replication. However, little work seems to have been done to characterize the elongational rates produced during the bursting of a bubble that would facilitate assessing whether forces of sufficient magnitude are generated.
In this study the fragmentation of DNA nanotubes is used to characterize both the magnitude of the elongational rates produced and the volume of fluid subjected to these elongational rates during bubble bursting. These nanotubes are constructed from short DNA oligomers referred to as single-stranded tiles, which each have four sequence domains by which a given oligomer binds with four neighboring oligomers via Watson–Crick base pairing. Thus, whereas each DNA oligomer is held together by covalent bonds, the entire tube assembly is held together by the supramolecular interactions that enable two complementary single-stranded oligomers to form duplex DNA. Base sequences of the oligomers are designed so that the axes of the duplex DNA are parallel to the long axis of the tube. The supramolecular Watson–Crick bonds between neighboring single-stranded tiles are much weaker than the covalent bonds of the phosphate backbone of a single-stranded tile (32). Under sudden tension along the axis of the duplex DNA (33), the tensile force at which the supramolecular bonding fails is referred to as the overstretching force , which has a value of about 65 pN (34, 35). For a tube in which there are n duplex strands in cross-section, the tensile force will be . For the tubes used in the experiments reported here, (SI Appendix, Fig. S1) and consequently the tubes fragment when subjected to tensile forces in excess of 455 pN. The tubes have a radius of 4 nm, a persistence length of 5 μm (36), and a length distribution that peaks at 5 μm at the start of the experiment (SI Appendix, Fig. S2; see Fig. 3 B and G).
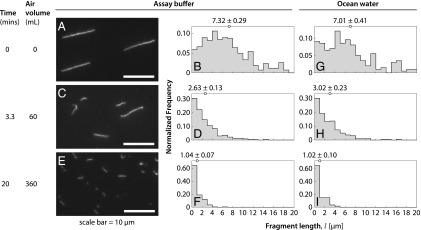
Fig. 3.
Nanotube length distributions for bubble bursting experiments in assay buffer or in ocean water. Fluorescence microscopy images and fragment length distributions of DNA nanotubes withdrawn from a sample with an initial volume of 100 μL after 0 mL (A and B), 60 mL (C and D), and 360 mL (E and F) of air had passed through the sample at a flow rate of 18 mL/min. The mean tube length for each distribution is given at the top of each histogram. Nanotube length distribution in bubble bursting experiment with ocean water after 0 mL (G), 60 mL (H), and 360 mL (I) of air.
Some of these tubes will be trapped in the bubble film and will be subjected to elongational forces in the manner illustrated in Fig. 1. Although nanotubes will necessarily also be subject to compressive fluid flows, they are not fragile under compression. The junctions at which a given single-stranded tile connects with two neighboring tiles are flexible, allowing the tube to crumple and then straighten when the compressive forces are relieved. This collapse into a coil configuration followed by stretching has been studied for other stiff linear biopolymers and synthetic fibers in hydrodynamic flows near stagnation points (33, 37, 38). Generally, the tubes will crumple under the compressive flow and reorient and stretch along the axis of the elongational flow (Movie S1 and SI Appendix, section 10). A further complication is that Brownian motion will tend to counteract the alignment produced by the elongational flow. However, as will be shown, under the conditions in which our DNA nanotubes break, the Péclet number––which is the ratio of the active transport rate to the diffusive transport rate––is in excess of , indicating that diffusive misalignment of the nanotubes plays a negligible role in our experiments. Due to the viscous stresses exerted on the DNA nanotube as it reorients along the direction of maximum extension flow, the tension experienced by the tube will be greatest at the center of the tube and will be greater for longer tubes, scaling as , where l is the tube length and R the tube radius (34). If the tensile force is exceeded, the tube will break into two fragments of nearly equal length. If the elongational flow continues to intensify so that the two fragments experience a tension at their centers that exceeds the tensile force, each of these in turn will fragment into two shorter pieces of equal length. This cascading process will continue until the elongational rate reaches its maximum value.
DNA nanotubes are well-suited to serve as probes of hydrodynamic flows within bubble films for three reasons. First, their fragmentation in elongational flows has already been extensively characterized (34). Second, they are highly soluble in water and do not exhibit a surfactant-like tendency to stick to the air–water interface, unlike many proteins. Third, it is straightforward to measure histograms of nanotube lengths using fluorescence microscopy. Here, from the evolution of the DNA nanotube fragment length during the course of bubbling, we were able to determine the fragmentation volumes for elongational rates over five orders of magnitude, although our experimental techniques were not able to distinguish where the DNA nanotubes were broken within the bubble. Our findings suggest that, via bubbles, ocean waves provide a source of strong mechanical forces at the micron-scale mechanical stresses that ocean surface-dwelling microbes must cope with, that may be involved in the natural breakdown of pollutants, and that would have been available for protobionts to use as a means of driving self-replication.
Results
Fig. 2 shows the experimental setup and molecular design.
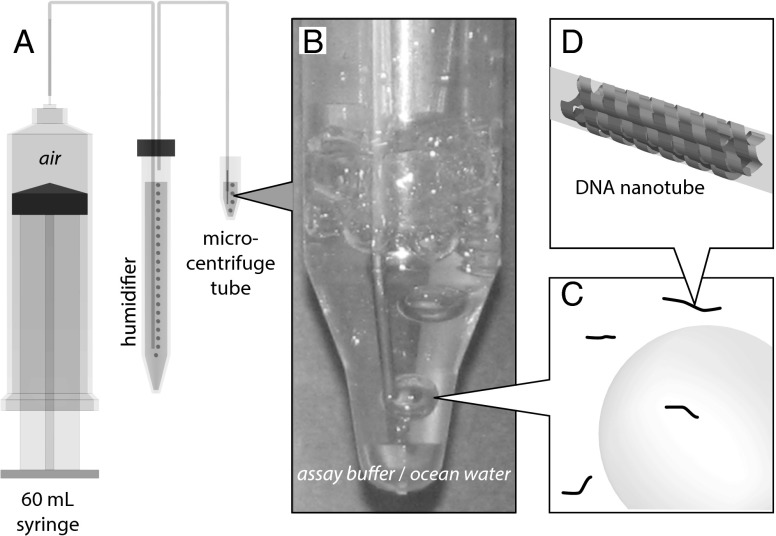
Fig. 2.
Bubbles production apparatus. (A) Schematic of apparatus. (B) Sample, housed in a microcentrifuge tube, to which air is being delivered. For scale, the OD of the upper section of the microcentrifuge tube is 1.1 cm. (C) Bubbles and 7-helix nanotubes (not to scale) are in the solution. (D) Schematic of the 7-helix nanotube used in this experiment (SI Appendix, Fig. S1 and Table S1).
DNA Nanotubes.
For the experiments, DNA nanotubes with monodisperse diameter and bond strength were used (32, 34). These tubes were self-assembled from 7 DNA oligomers (Fig. 2D and SI Appendix, Fig. S1), as described in Materials and Methods. The tubes seldom grow longer than 20 μm and have a persistence length of over 5 μm (36), making them more amenable to theoretical analysis than a reptating polymer. For the experiments here, they can be regarded as rigid rods that break when an axial tensile force of 455 pN is applied (34).
Bubble Production at Constant Rate and Precise Bubble Size.
Bubbles were generated by flowing air through buffer solution containing DNA nanotubes (Fig. 2). Air was supplied via a motorized syringe pump equipped with a 60-mL syringe [26.70-mm inner diameter (ID)]. To minimize evaporation, the air was delivered via polyethylene tubing, 0.58-mm ID, and was bubbled through a humidifier consisting of a 15-mL centrifuge tube filled to 13.5 mL with the assay buffer [1 TAE (40 mM Tris-acetate and 1 mM EDTA) with 12.5 mM MgCl2]. Two stainless steel capillaries, passing through the cap and cemented with silicone aquarium sealant, served as feedthroughs for air to and from the airtight humidifier chamber. The bubbles were generated at the end of a stainless steel capillary, 0.635-mm outer diameter (OD) and 0.432-mm ID, connected to the end of the polyethylene tubing that was pointed downward into the sample fluid (Fig. 2B). To minimize the amount of synthetic DNA used, the sample, typically consisting of 100 μL of fluid, was housed in a 2.0-mL microcentrifuge tube (Fig. 2B). The nose of the tube has a 4-mm ID and a depth of 6 mm. The tapered region flares out to a 1-cm ID.
Bubbles of different size were obtained by varying the airflow rate. Two airflow rates, 1.8 and 18 mL/min, were used in the experiments. A bubble volume of 5.32 mm3 at the slower airflow rate (1.8 mL/min) was determined from photographs of bubble production at the end of the capillary tube in a flat-walled flask containing assay buffer. The height and width of the bubbles were measured and the volumes were computed under the assumption that the bubbles are oblate spheroids. At the slower flow rate, individual bubbles reached the surface and burst before the arrival of subsequent bubbles. Larger bubbles were produced at the higher flow rate. By counting the number of bubbles produced over a known time interval at a given airflow rate, the ratio of the volume of the bubbles produced at 18 and 1.8 mL/min was measured to be . From this ratio, a bubble volume of 9.26 mm3 was inferred for the higher flow rate (18 mL/min). At this bubbling rate, the sample chamber contained multiple bubbles at any one time, i.e., a foam, as shown in Fig. 2B. A mean bubble lifetime of 2 s was determined for both buffer and ocean water based on an estimate of the number of bubbles in the sample chamber divided by the rate of bubble production. This lifetime is intermediary between that of pure (distilled) water and saturated soap bubbles, indicating the presence of surfactant in highly dilute amounts, typical of tap water or water found in nature, such as river water, ocean water, and rain puddles (28). Due to drainage, bubble lifetime is related to the film thickness at bursting; for similar-sized bubbles bursting individually in tap water, Lhuissier and Villermaux (28) report thickness on the order of 100 nm.
Bubble Bursting Driven Fragmentation of DNA Nanotubes in Assay Buffer or in Ocean Water.
To follow the fragmentation of the DNA nanotubes by bubbling, two experiments were performed in assay buffer and in ocean water at the 18-mL/min airflow rate. For the experiment in ocean water, a control sample was left undisturbed to assess the stability of the DNA nanotubes in ocean water (SI Appendix, Fig. S3 A and B). At the beginning of the run, the mean fragment length of the DNA nanotube control sample was determined to be μm. At the end of 1 h, the mean fragment length in the undisturbed sample was measured to be μm, which is statistically indistinguishable from the initial value.
The experiment in assay buffer consisted of two runs. In the first run, 1-μL volumes were drawn at time points when = 0, 60, and 240 mL of air had passed through the sample. In the second run, the data were acquired at = 0, 9, 18, 36, 72, 180, and 360 mL. Representative total internal reflection fluorescence (TIRF) microscopy images taken from the second run samples are shown in Fig. 3 A, C, and E along with the corresponding length histograms (Fig. 3 B, D, and F). The data of both runs were treated as a homogeneous set (SI Appendix, Fig. S2). For the experiment in ocean water, samples were withdrawn at = 0, 60, 120, and 360 mL (Fig. 3 G–I and SI Appendix, Fig. S3).
The evolution of DNA nanotube length distributions was quantified by measuring individual nanotube lengths in fluorescence images (34). DNA nanotubes were covalently labeled with Cy3 fluorophores at uniform density (1 Cy3 every 7 nm, SI Appendix, Fig. S1). As a consequence, the relation between emitted photons and fragment length is expected to be linear. By measuring the photons emitted by each nanotube and the contour length of the longest nanotube in each image, the length of each nanotube can be inferred directly from the photon counts, even for nanotubes whose length is less than the diffraction-limited resolution of the microscope (Materials and Methods).
The length distributions (Fig. 3 and SI Appendix, Figs. S2 and S3) show a decrease in mean fragment length with increasing bubble bursting. After 20 min, when 360 mL of air had been bubbled through the sample, the mean fragment length was measured to be μm and μm for the experiments in assay buffer and ocean water, respectively. The decrease in mean fragment length showed that a substantial amount of tube fragmentation had occurred. Moreover, the assay buffer and ocean water histograms indicated that DNA nanotube fragmentation proceeds similarly in the two fluids.
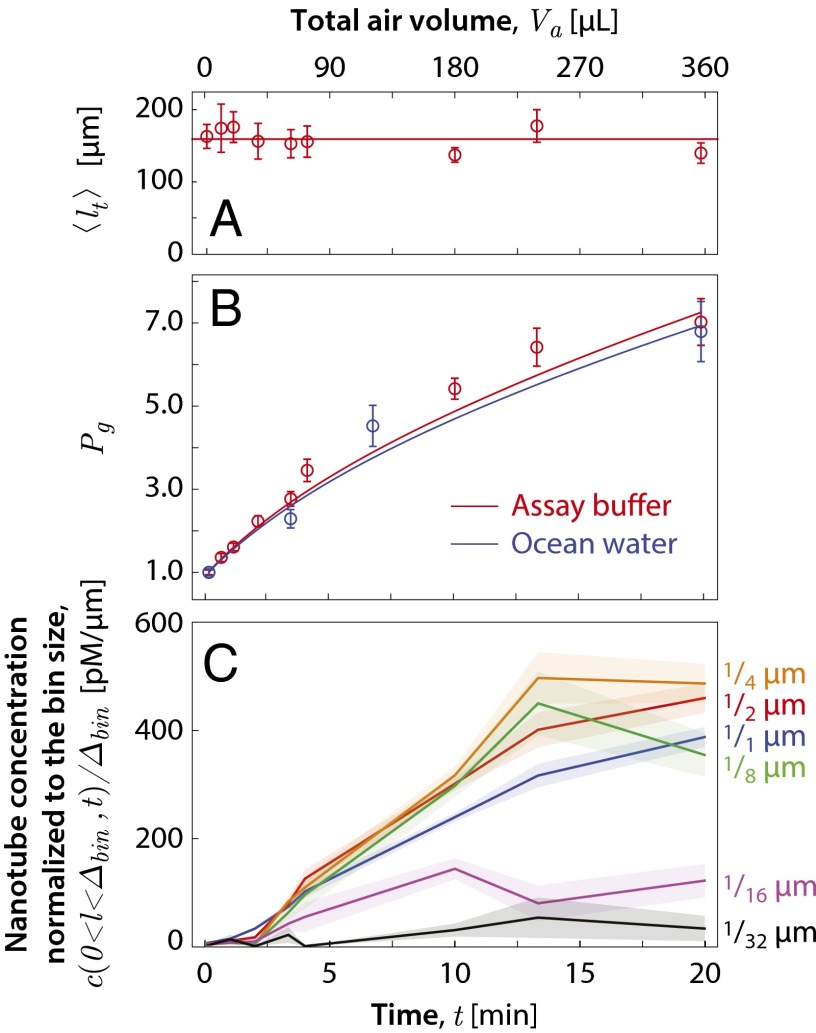
Under shearing, the sum of tube lengths should remain conserved. This was tested by measuring the total tube length per image for the samples extracted during the run in assay buffer at different time points. Fig. 4A shows that remains constant as a function of the air volume that has passed through the sample, . Because , where N is the total number of nanotubes and is the mean tube length, the time independence of allows one to infer the population ratio , where is the initial number of nanotubes, via , where is the initial mean tube length. , inferred by this method, is plotted as a function of in Fig. 4B. There is a sevenfold increase in the number of nanotubes by the time an air volume of 360 mL has passed through the sample. The curves are the result of a global best fit of the theory presented in the Model for Extracting the Fragmentation Volume section to the experimentally measured tube length distributions.
Fig. 4.
DNA-nanotube fragmentation data as a function of the bubbling exposure time at a flow rate of 18 mL/min. (A) Total tube length per microscope field of view. The horizontal line represents a constant total tube length of 159 μm per image. Error bars show the SEM. (B) Plot of the population ratio for experiments in assay buffer (red) and in ocean water (blue). The lines are the Bayesian fit to the experiments in assay buffer (red) and in ocean water (blue) based on the theory described in the model section. (C) Plot of the nanotube concentration per tube length in the length range for , , , , , and μm. (See SI Appendix, Fig. S2 for detailed histograms.)
To determine the smallest tube fragments that were produced, the concentration of tubes in the length range for , , , , , and μm was tabulated at different . In Fig. 4C, we plotted , which is the observed nanotube concentration normalized to the bin of size . For μm and larger, this quantity grows substantially with , whereas for μm the data remain relatively fixed, indicating that fragments as short as μm are produced. A comparison of the curves of Fig. 4C with that of the results of a global best fit of the theory presented in the model section to the experimentally measured tube length distributions is given in SI Appendix, Fig. S7.
In previously reported experiments (34), we have shown that the suddenly applied fluid elongational rate required for midpoint scission of an initial nanotube of length l to produce two fragments that have identical length of is
| [1] |
where R is the tube radius, η is the viscosity of the fluid, and the tension required to break the tube is given by , where n is the number of duplex DNA strands along the circumference of the tube (SI Appendix, Fig. S1) and pN is the critical force to overstretch a DNA helix (35). Note that the tension required to break the tube does not depend on the length of the duplex DNA segments that link successive tiles along the tube axis. This is because when stress is applied on a time scale that is short compared with that over which base pairs disassociate due to Brownian fluctuations, the strain will distribute uniformly along the linker duplex segments. All base pairs will break at once when this strain reaches the value where overstretching occurs. For our tubes, and nm. The observation of -μm tube fragments implies that tubes as short as μm are broken in two via the hydrodynamic flows generated within the bubbles of the experiment of Figs. 3 and 4. Taking Pa⋅s, Eq. 1 indicates that elongational flow rates at least as large as s−1 are generated during bubble rupture.
Fragmentation Is Little Affected by the Bubble Production Rate.
To show that fluid flow associated with bubble inflation and transport was not primarily responsible for the tube fragmentation, we repeated the experiment in assay buffer at an order of magnitude slower flow rate of 1.8 mL/min (SI Appendix, Fig. S4). The mean tube length when 60 mL of air had passed through the sample was μm. If, as presumed by our simple theoretical estimate based on film hole dynamics, a fixed amount of fragmentation occurs each time a bubble bursts, then the same amount of fragmentation should be apparent in samples that experienced the same number of bubbles. Because of the different size bubbles at the two flow rates, 60 mL of air at the slower flow rate generates the same number of bubbles as 104 mL of air at the faster flow rate. Interpolating between measured values for the faster flow rate of 18 mL/min (Fig. 3 and SI Appendix, Fig. S2) yields a mean fragment length of 1.88 μm. This is only 20% shorter than found at the slower airflow rate, despite the 10-fold faster airflow rate, supporting a dominant role for bubble bursting rather than other hydrodynamic flows in the observed fragmentation processes. Furthermore, the similar degree of fragmentation in bubbles bursting individually at the surface (as for the slower flow rate) or in the context of a foam (as for the higher flow rate) suggests that the relevant hydrodynamic effects are similar for these two contexts.
Eliminating Bubble Bursting on the Water–Air Interface Suppresses Fragmentation.
The assumption that fluid flows associated with bubble bursting are primarily responsible for tube breakage was confirmed by the suppression of tube fragmentation through the addition of 200 μL of heptane to the sample vial to form a fluid layer on top of the assay buffer. Air bubbles rising through this layer would leave the hydrophilic DNA in the aqueous phase. The aqueous fluid flows associated with this process are also reduced because of viscous coupling of the buffer with the heptane at the interface (39–41). The mean tube length when 60 mL of air was bubbled through the sample at 18 mL/min was μm (SI Appendix, Fig. S5), which is similar to the initial mean tube length μm and large compared with the mean tube length μm measured at mL for the experiment of Fig. 3 and SI Appendix, Fig. S2.
Decreasing Surface Tension also Suppresses Fragmentation.
Finally, we demonstrated that fluid flows associated with bubble bursting are primarily responsible for tube breakage by reducing tube fragmentation through the addition of 2 mM of the surfactant SDS to the assay buffer. The surfactant reduces the surface tension, increases surface viscosity effects (42), and increases the bubble lifetime. These effects inhibit nanotube breakage by reducing surface-tension–driven flow velocities and by reducing the film fluid volume through film drainage. The foam produced during this experiment necessitated using a 300-μL sample volume. Even then it was necessary to periodically stop the airflow to allow the foam to subside. Because of the 3 greater volume, the mean tube length μm at mL for this experiment (SI Appendix, Fig. S6) should be compared with the μm at mL for the experiment of Fig. 3 and SI Appendix, Fig. S2. Reducing the surface tension suppresses the breakage of the nanotubes. In agreement with previously published reports (43, 44), we verified that DNA nanotubes are stable in SDS buffer by constructing a length histogram of a control sample that was incubated in SDS buffer for 30 min without airflow. The final mean tube length μm was found to be statistically indistinguishable from the initial mean tube length μm, indicating the stability of DNA nanotubes in SDS buffer (SI Appendix, Fig. S6).
Model for Extracting the Fragmentation Volume.
The results we have presented show that bursting bubbles will fragment DNA nanotubes and document how the fragment distribution in a fixed volume of fluid changes as a function of time as the fluid is cycled through the bursting bubbles. To apply these results more generally, one would like to know the number N of objects of a particular type that would be broken in a bubble if they are present in the fluid at concentration c and if an elongational rate of was required to break them. The proportionality factor between N and c is the fragmentation volume ; that is, . The fragmentation volume is the sum of all of the fluid volume elements whose elongational rate has exceeded at some point during the bubble rupture process. The fragmentation volume characterizes the fragmentation process for a single pass through a bubble. However, during the course of our experiments, a given nanotube or its fragments will have passed through bubbles multiple times. This complicates the determination of from the data. We will now describe how the time evolution of the DNA nanotube length distribution can be processed to extract .
Let denote the concentration distribution of tubes of length l as a function of time t, such that in the limit , is the concentration of tubes having lengths in the interval from to at a given time. The time evolution of the experimentally determined contains information on how effectively a bubble can break a tube of length l. To extract the fragmentation volume from these data, a model is crafted for the case where the bubbles all have the same volume , are produced a constant rate γ, and the sample volume remains sufficiently well mixed that can be regarded as constant over the sample volume. For the experiments reported here, is expected to be uniform because the sample volume is small and well mixed by the fluid motion produced as the bubbles rise to the surface.
Let be the rate with which tubes of length l are fragmented upon bursting of a bubble and let be the rate per unit tube length that tubes of length l are produced from tubes of length upon bursting of a bubble. Then, the rate of change of is given by
| [2] |
where γ is the rate at which bubbles are produced (i.e., ). Note that the lower limit of integration could have been set to l because for because producing a new fragment of length l requires breakage of a tube longer than l. Because the total tube length per unit volume remains constant as the tubes are broken into shorter sections, one must have
| [3] |
The rate is inversely proportional to because this determines the frequency with which a given tube of length l will be within the vicinity of a bursting bubble. We thus write
| [4] |
where the fragmentation volume characterizes the effectiveness with which a bursting bubble breaks a tube of length l. Here, is used as shorthand for , where indicates the minimum elongational rate required to break tubes of length l. Similarly, we write
| [5] |
where is the mean number of tubes of length l per unit tube length produced by the fragmentation of a tube of length .
In principle, the functions and could be obtained through numerical calculation of the hydrodynamic flows of bursting bubbles and numerical calculation of the breakage of tubes within these hydrodynamic flows. To our knowledge, the requisite hydrodynamical calculations to determine and have not been carried out. The aim of the analysis here is to determine using a plausible model for in conjunction with our experimental data.
Imagine a small tube in the vicinity of a bubble that has begun to burst. The elongational flow rate of the fluid element the tube is imbedded in will increase over time. When the tension at the center of the tube exceeds the tensile strength of the tube, the tube will break into two fragments of equal length. If the elongational rate continues to increase so that the tension at the center of the two shorter tubes exceeds the tube tensile strength, then again each of these two shorter tubes will break into two smaller tubes of equal length. At long times the fluid motions produced by the bursting bubble will dissipate, the bifurcation cascade will terminate, and the elongational flow rates within the fluid element containing the tube fragments will return to zero. One thus expects the fragmentation process to be a cascade of bifurcations. In the model for this case, which we call the “full cascade model,” is given by
| [6] |
where is the conditional probability that a tube of length l has broken into fragments given that it has broken, the delta function ensures that , and the multiplier in front of the delta function is the number of fragments produced by a cascade of m bifurcations.
This is, of course, an idealization. Because of microscopic disorder, tubes are not expected to break exactly in half. However, our experience in modeling imperfections in tube breakage by hydrodynamic flows in another context indicates that the results are insensitive to the inclusion of such disorder in the modeling (34). More seriously, the assumption that the tube lengths are small compared with the length scale over which the elongational flow rate varies is likely to be violated in our experiments. Our longest tubes exceed 20 μm, which is likely to be substantially greater than the bubble film thickness. In this case, we expect a long tube to fragment into tubes having a distribution of lengths rather than into tubes of equal length. As an extreme case one might imagine that the tubes only break in two. This choice results in the “single bifurcation model,” which uses
| [7] |
We show in SI Appendix, Figs. S7–S9 and sections 3–6 that the single bifurcation model does not fit the data as well as the full cascade model. This indicates that the data have the power to distinguish between models of and suggests that Eq. 6 is a satisfactory approximation for our experiments.
As shown in SI Appendix, section 3, Eq. 2, using Eqs. 4–6, yields the full cascade model:
| [8] |
Note that because shorter tubes require higher fluid elongational rates to break and very short tubes require a very high elongational rate to break, is a monotonically increasing function
| [9] |
and
| [10] |
Eqs. 8–10 define the model of tube breaking used in the analysis.
It has been experimentally observed that DNA nanotubes can join end-to-end (45). To assess the effect end-joining might have on attempts to extract from the data, a more complete model incorporating end-joining of DNA nanotubes was considered. This “end-to-end joining model” considers the full cascade of bifurcations and is given by
| [11] |
where is the second-order rate constant for the joining of two tubes, one of length l, the other of length to a tube of length . The first integral on the right-hand side gives the rate of loss of tubes of length l due to joining with another tube. The second integral on the right-hand side gives the rate of production of tubes of length l due to the joining of a tube of length with a tube of length . It is straightforward to show that total tube length is conserved in this more complete model, that is,
| [12] |
The full cascade model also satisfies this condition because condition 3 was imposed in building the model.
There are few data available on the rate constant . Using the expression for the Stokes drag on a rod of length l and radius r, the relationship between mobility and diffusion, and the relation between diffusion constants and reaction rates for diffusion-controlled reactions (46, 47), we modeled this rate constant as
| [13] |
where R is the tube diameter, accounts for the fraction of productive collisions, is the Boltzmann constant, and T is the absolute temperature [see SI Appendix, section 7 for details, including a comparison with the result of Hill (48)]. With , this expression is an upper bound for diffusion-controlled end-joining.
However, it is known that DNA hybridization is not diffusion-controlled, i.e., the majority of collisions are unproductive (49). Based on hybridization rate constants measured for 10-mers (50), we estimated a reference value of (SI Appendix, section 7). Using the methods described below to extract from the experimental data, and assuming various values for κ, we found that there was minimal change in the quality of fit () and in the inferred fragmentation volumes ( for μm μm and 10-fold for μm) for , but the quality of fit was 3.3-fold worse for . From this we concluded both that is a reasonable estimate and that neglecting end-joining is satisfactory for analysis of the experiment. Consequently, most of the data analysis was carried out using the full cascade model rather than the end-to-end joining model. The analysis was facilitated by the fact that Eq. 8 can be solved analytically given in look-up table form and knowledge of . The solutions are presented in SI Appendix, section 4.
Data Analysis for Extracting the Fragmentation Volume.
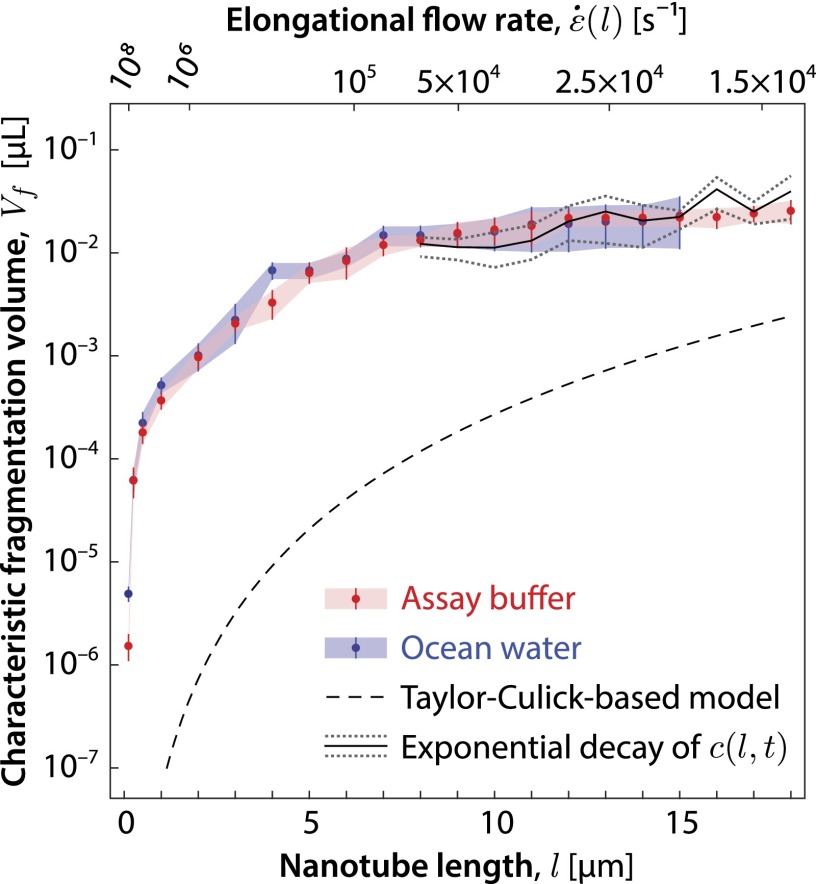
The experimentally measured tube length distribution at obtained by partitioning the measured tube lengths in -μm-wide bins served as the initial value data (SI Appendix, Fig. S2). A stochastic search method was used to find a piecewise linear and continuous , constrained to start at zero and to be monotonic so as to satisfy Eqs. 9 and 10, which resulted in the best fit (weighted mean-squared error) between the measured concentration distribution and the computed concentration distribution . The fitness function, as well as other details of the data analysis process, is given in SI Appendix, section 6. For the full cascade model, Eqs. 8–10, the best-fit computed concentration distribution compared with the measured concentration distribution is shown in SI Appendix, Figs. S7 and S8 for the assay buffer and in SI Appendix, Fig. S10 for the case of ocean water. The results of extracting from the buffer and ocean water data using the full cascade model are shown in Fig. 5. One sees that the fragmentation volume functions for the buffer and ocean water overlap within the uncertainty of the fit. Using Eq. 1, can be expressed as a function of the elongational flow rate , as indicated by the x-axis labels above the figure.
Fig. 5.
Characteristic fragmentation volume for tubes in the length bin interval μm for assay buffer (red) and ocean water (blue) data. The best-fit function for assay buffer is similar to the best-fit function for ocean water, which indicates that DNA nanotube fragmentation occurs in a similar fashion in the two liquids. The simple theoretical estimate of using the Culick and Taylor model of film hole dynamics (black dashed line) falls below our data, as expected, due to the neglect of hydrodynamic effects within bursting bubbles that are not easily modeled. For sufficiently long nanotubes ( μm), the best-fit for assay buffer data (blue) is similar to the values (solid black line gray dotted lines) extracted from the exponential decay of (SI Appendix, Fig. S11). Error bars represent SEM (SI Appendix, section 6.4).
In the large l region (as defined below), the plot of Fig. 5 does not depend on and is thus model independent, making the values for extracted in this region particularly robust. This follows from the fact that our initial tube length distributions fall off rapidly for large l so that the distribution effectively cuts off at a maximum tube length . Consequently, new tubes with lengths in the region will not be produced, and the change in as a function of time will only be due to loss of tubes from this part of the distribution through tube breakage. In this region, the length distribution simply decays exponentially with the decay constant , as per the first term of Eq. 8. Hence, in this interval a fit to the exponential decay of suffices to extract , as is shown in Fig. 5 and SI Appendix, Fig. S11. The theory we have presented is necessary to extract in the region because here the dynamics is complicated by the addition of new tubes from the breakage of tubes of length .
As an aside, note that rod-like DNA nanostructures could be fabricated with well-defined lengths (43, 51) and designed to split exactly in the middle by introducing a “weak spot” with fewer helices in the cross-section. Such structures could be used to determine for the length l of the structure simply by monitoring the exponential decay due to breakage, because the possibility of breakage at multiple locations can be discounted. However, compared with using tile-based DNA nanotubes that have a broad length distribution, this approach has the disadvantage that, for a given nanostructure, can only be determined at one l.
Some insight into where most of the fragmentation is occurring can be obtained by considering the size of . The data of Fig. 5 suggest that approaches an asymptotic value of μL for large l. The bubbles in this experiment have an air volume equivalent to a sphere of radius 1.3 mm. For bubbles of this size, surface tension rather than gravity dominates in determining the bubble shape. These bubbles in isolation rest largely below the water surface and maintain a nearly spherical shape with a small cap protruding above the water surface that is 100 nm thick as measured by Lhuissier and Villermaux (28). The depth of the bubble foam formed under the fast bubbling rate is roughly three bubble diameters thick (Fig. 2B). Pushed up by the buoyancy of the bubbles below, the bubbles near the top of the film can be expected to protrude higher and have cap films and foam facet films with areas somewhat larger than that of an isolated bubble. However, one expects the film thickness to be comparable to that of an isolated bubble due to similar surface-tension–driven film draining. A generous overestimate of μL for the film volume per bubble is obtained by multiplying half the bubble surface area by 100 nm. The 20-fold discrepancy with the measured fragmentation volume implies either that the film is considerably thicker than 100 nm––perhaps due to the context of the foam––or that substantial fragmentation occurs outside the cap region, i.e., in the meniscus where the film thickness increases, in the interstices between bubbles of a foam, or in the bulk.
As indicated in the Introduction, a crude estimate for associated with fluid stretching along the length of the perimeter can be obtained from the Taylor–Culick model of film hole dynamics, where the volume of fluid swept up by the hole before the elongational rate falls below a particular value is given by . Using Eq. 1, one obtains , where we have used g/cm3 and dyn/cm for the density and surface tension of water, and l is the nanotube length. This relationship is plotted as a dashed line in Fig. 5.
As we have already mentioned, within this model, energy conservation requires that half the surface-tension energy released must be dissipated within the toroid, suggesting the existence of additional microscale fluid flows within the toroid (18, 24) that must be taken into account to accurately predict . In addition, an accurate calculation would require taking into account the geometry of a bubble contacting a water surface (26), which differs from that of a planar film of uniform thickness, and mechanisms that give rise to instabilities and droplet spray along the hole perimeter (28, 52). In summary, the of the Taylor–Culick-based model, plotted in Fig. 5, is a loose lower bound above which the data must lie.
By computing the Péclet number , we can now confirm that misalignment of the nanotube from the direction of the elongational flow due to Brownian motion is not significant. In the present case, Pe can be taken to be the ratio of the elongational rate to the rotational diffusion constant (53), where the rotational diffusion constant is given by (54) and l is the length of the tube before scission. Therefore, the Pe number for nanotubes that experience midpoint scission can be estimated based on the experimentally measured length-dependent (Eq. 1), from which we see that Pe increases monotonically with tube length l. For the range of nanotubes in Figs. 4 and 5 that experience substantial fragmentation ( μm), Pe was estimated to be . By analyzing torques within the fluid (47, 55), we showed that Pe is the inverse of the mean-squared angular deviation of the nanotube axis from the elongational direction and therefore rad (SI Appendix, Eq. S88 and section 8). Taken together, the high Pe number and small indicate that the effects of diffusional reorientation are expected to be negligible.
Discussion
Our experiments indicate that DNA nanotube fragmentation can serve as a probe of elongational flows generated at small scales in time-varying complex fluid flows, where imaging of tracer particles would be impractical. We have used DNA nanotube fragmentation to probe the elongational rates in the fluid flows generated by bursting bubbles in aqueous solutions, including ocean water. The DNA nanotube fragment distributions we have measured indicate more intense elongational flow rates than those predicted using the Culick (22) and Taylor (23) model. A more accurate model will have to take into account small-scale hydrodynamic flows occurring within the bubble film. The ability of a bursting bubble to fragment objects suspended within the bubble film has been characterized by the fragmentation volume , which is the volume of fluid subject to elongational rates in excess of . Although our data for two different bubble sizes did not reveal a strong size dependence of the fragmentation volume, further exploration using a wider range of bubbles sizes could be illuminating. In addition, it will depend on surface tension, viscosity, and the presence of surfactants. The exploration of these dependencies is left to future work. However, when these dependencies are sufficiently well known, the fragmentation volume can be used to determine the rate with which small objects will be broken, by passage through bubbles, in bodies of water ranging from oceans to bioreactors, provided the concentration of the objects, their susceptibility to elongational flows [i.e., ], and the size spectrum rate for the bubble production are known.
Whether biological organisms use the energy available in bursting bubbles to aid clonal reproduction and dispersal is not known. However, measurements of the tensile strength of microorganisms suggest that this is a possibility. For example, Stocks and Thomas (56) have measured a tensile strength of for the filamentous bacterium Saccharopolyspora erythraea grown in a fermentation tank. A hypha diameter of 180 nm and a mean hypha length of 60 μm was reported for this organism. Using these numbers, Eq. 1 yields s−1 for the elongational rate needed to break these hypha in two. This is two orders of magnitude below the maximum elongational rates inferred from DNA nanotube breakage (Fig. 5).
Protobionts may have used the energy available in bursting bubbles to induce cell division without the need for complicated molecular machinery. In SI Appendix, section 9, we present a calculation [using the tensile strength of an analogous substance (57)] that estimates that the tubular vesicle investigated by Szostak’s group (10–12) can be broken into 1-μm sections under an elongational rate of , where n is the number of lamella in the vesicle. This is also well within the range of that we have inferred for bursting bubbles. Bursting bubbles therefore provide ample hydrodynamic forces to drive this protocell division process.
Bursting bubbles are also capable of fragmenting covalently linked polymers such as duplex DNA. Using 6 nN as the suddenly applied force needed to break a covalent bond (58–60) and 1 nm as the radius for duplex DNA, one finds from Eq. 1 that an elongational rate of s−1 is able to fragment duplex DNA into sections 0.33 μm long. Long-chain synthetic polymers, in which the monomer units are covalently linked together by a single bond, have a radius that is typically less than half that of duplex DNA and can thus be fragmented into segments as small as those of duplex DNA. It is conceivable that bursting bubbles may play some role in degrading plastics and biomaterials within the ocean (61) and may aid in the dispersal of natural and man-caused oil slicks (62).
Our use of self-assembled DNA nanostructures to probe hydrodynamic flows within bursting bubbles suggests that DNA nanotechnology can provide tools to explore hydrodynamics at short length scales and fast time scales that would be difficult to investigate by other means. Among the other intense transient ocean fluid flows that are effective in shearing small objects in modern oceans and that may have aided reproduction of the protobiont are those associated with rain impacts on the ocean surface and with whitecap formation during wave breaking. DNA-based probes may serve as useful tools to characterize the fragmentation potential of these fluid flows as well, particularly because, as our experiments have shown, such probes can function in ocean water.
Materials and Methods
DNA Nanotubes.
The design and characterization of the nanotubes is discussed in ref. 32. A stock solution of DNA nanotubes was prepared by mixing 7 DNA strands (Integrated DNA Technologies, Inc.; SI Appendix, Table S1 and Fig. S1) at equimolar concentration of 3.50 μM in a buffer consisting of 1 TAE (40 mM Tris-acetate and 1 mM EDTA), pH 8.3 with 12.5 mM Mg-acetate and then slowly annealing from 90 °C to room temperature (25 °C) over the course of a day in a Styrofoam box. The nanotube stock solution was then diluted by a factor of 20 for the experiments, which were performed at room temperature.
Imaging.
The images were acquired with a custom-built prism-based TIRF upright microscope, as described in refs. 32, 34. A solid-state green laser (GCL-025, 25 mW, CrystaLaser) equipped with an adjustable power supply (CL2005, CrystaLaser) provides the excitation beam at 532 nm. The excitation light was filtered with a 532-nm laser filter (Z532/10×, Chroma). The filtered excitation beam passed through a quarter-wave plate (Thorlabs) to produce a circularly polarized light wave, which effectively has uniform polarization to counter the fluorescence dependence on the relative orientation between fluorophore and the polarization of excitation light. Two mirrors (Thorlabs) were used to guide the illumination beam to the field of view below the imaging optics. Another mirror (Thorlabs) and a 15-cm focusing lens (CVI Laser Optics) steered the excitation beam onto a Suprasil 1 right-angle prism (CVI Laser Optics) at ∼0 ° from the horizon to produce a weakly focused illumination spot directly below the objective. We calculated that the incoming angle between the incoming laser and the normal vector of the microscope slide is sufficiently larger than critical angle for evanescent wave to occur at the interface between glass and liquid, where the sample and focal plane of the objective are located.
DNA nanotubes resided inside a glass capillary tube that was optically coupled with the prism by a thin layer of immersion oil. The emitted photons were captured by a 60× 1.2-N.A. water immersion objective (Nikon) and focused to the electron multiplier CCD camera (C9100-02, Hamamatsu) by a 20-cm lens tube (double achromat, CVI Laser Optics). The combination of the high brightness and photostability of Cy3-labeled DNA nanotubes, low background from RCA-cleaned microscope slides, and efficient light collection produce images with high signal-to-noise ratio.
Nanotube Length Measurement.
Following a procedure previously reported (32, 34) for the microscopy assay, a 1-μL volume of fluid was withdrawn and immediately diluted by a factor of 40 in buffer. A 5-μL volume of this diluted sample was then deposited between an RCA-cleaned (63) microscope slide and RCA-cleaned coverslip and then imaged. We found that DNA nanotubes stuck readily to this surface.
Contour lengths of Cy3-labeled DNA nanotubes were analyzed using ImageJ (64). Nanotube detection was performed manually. The maximum pixel intensity in each detected feature was used to exclude aggregates of DNA nanotubes and colocalized DNA nanotube fragments. Moreover, all features whose maximum pixel intensities were above the saturation level of the camera were excluded from the length measurement. For each detected nanotube, the number of emitted photons was measured as a proxy for the contour length l. Briefly, two rectangular region of interests and were selected manually to satisfy these criteria: (i) the nanotube of interest was the only detected feature inside and (ii) was well inside . Then, the mean local background was calculated by , where and are the sum of all pixel intensities in and , respectively, and and are the areas of regions and , respectively. The number of photons emitted by a nanotube was determined to be . Finally, in each image, the contour length and photon numbers of the longest nanotube (whose length, μm, could be easily measured) provided a calibration factor for the linear conversion of to l. This technique is robust to the curvature of DNA tubes and to the image sharpness. Moreover, the photon-counting method allows for the determination of nanotube lengths even for fragments that are not optically resolved.
In other experiments, our prism-based TIRF microscope proved capable of detecting single Cy3 molecules. Despite this sensitivity, here we obtained very low false-positive detection rates with our experimental procedure, as indicated by the counts of short nanotubes at early times (before 2 min of bubbling) that are plotted in Fig. 4C. On the other hand, we cannot exclude the possibility that some DNA nanotubes, e.g., those shorter than μm, did not stick as readily to the RCA-cleaned glass, or were not counted due to photobleaching. However, the constancy of total measured tube length (Fig. 4A) suggests that this effect was not significant. Furthermore, if our experimental methods undercounted short nanotubes, then an even larger maximal elongational rate could be inferred than what we have reported here, making our reported value a lower bound.
Ocean Water.
The ocean water was collected from a rock breakwater in San Buenaventura State Beach in Ventura, California. For use in the experiments, a 1-mL sample of ocean water was filtered through a Millex-GP filter unit (Millipore, 0.22-μm pore size) using a syringe.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge Rebecca Schulman, Damien Woods, Paul Rothemund, Carter Swanson, Manu Prakash, John O. Dabiri, and Sandra Troian for helpful discussions. This work was supported by the National Science Foundation through Grants EMT-0622254, NIRT-0608889, CCF-0832824 (The Molecular Programming Project), and CCF-0855212.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1424673112/-/DCSupplemental.
References
- 1.Khou M, Paul NA, Wright JT, Steinberg PD. Intrinsic factors influence the attachment of fragments of the green alga Caulerpa filiformis. J Exp Mar Biol Ecol. 2007;352(2):331–342. [Google Scholar]
- 2.Highsmith RC. Reproduction by fragmentation in corals. Mar Ecol-Prog Ser. 1982;7(2):207–226. [Google Scholar]
- 3.Coffroth MA, Lasker HR. Population structure of a clonal gorgonian coral: The interplay between clonal reproduction and disturbance. Evolution. 1998;52(2):379–393. doi: 10.1111/j.1558-5646.1998.tb01639.x. [DOI] [PubMed] [Google Scholar]
- 4.Adamec F, Kaftan D, Nedbal L. Stress-induced filament fragmentation of Calothrix elenkinii (cyanobacteria) is facilitated by death of high-fluorescence cells. J Phycol. 2005;41(4):835–839. [Google Scholar]
- 5.Bennett A, Bogorad L. Complementary chromatic adaptation in a filamentous blue-green alga. J Cell Biol. 1973;58(2):419–435. doi: 10.1083/jcb.58.2.419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Oparin AI, Morgulis S. The Origin of Life. Dover; New York: 1953. p. 193. [Google Scholar]
- 7.Cairns-Smith AG. The origin of life and the nature of the primitive gene. J Theor Biol. 1966;10(1):53–88. doi: 10.1016/0022-5193(66)90178-0. [DOI] [PubMed] [Google Scholar]
- 8.Cairns-Smith AG. Chemistry and the missing era of evolution. Chemistry. 2008;14(13):3830–3839. doi: 10.1002/chem.200701215. [DOI] [PubMed] [Google Scholar]
- 9.Bullard T, Freudenthal J, Avagyan S, Kahr B. Test of Cairns-Smith’s ‘crystals-as-genes’ hypothesis. Faraday Discuss. 2007;136(1-2):231–245. doi: 10.1039/b616612c. [DOI] [PubMed] [Google Scholar]
- 10.Budin I, Debnath A, Szostak JW. Concentration-driven growth of model protocell membranes. J Am Chem Soc. 2012;134(51):20812–20819. doi: 10.1021/ja310382d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Budin I, Szostak JW. Expanding roles for diverse physical phenomena during the origin of life. Annu Rev Biophys. 2010;39:245–263. doi: 10.1146/annurev.biophys.050708.133753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhu TF, Szostak JW. Coupled growth and division of model protocell membranes. J Am Chem Soc. 2009;131(15):5705–5713. doi: 10.1021/ja900919c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schulman R, Yurke B, Winfree E. Robust self-replication of combinatorial information via crystal growth and scission. Proc Natl Acad Sci USA. 2012;109(17):6405–6410. doi: 10.1073/pnas.1117813109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Collins SR, Douglass A, Vale RD, Weissman JS. Mechanism of prion propagation: Amyloid growth occurs by monomer addition. PLoS Biol. 2004;2(10):e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Alvarado AS. Regeneration in the metazoans: Why does it happen? BioEssays. 2000;22(6):578–590. doi: 10.1002/(SICI)1521-1878(200006)22:6<578::AID-BIES11>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 16.Deane GB, Stokes MD. Scale dependence of bubble creation mechanisms in breaking waves. Nature. 2002;418(6900):839–844. doi: 10.1038/nature00967. [DOI] [PubMed] [Google Scholar]
- 17.Cunliffe M, et al. Sea surface microlayers: A unified physicochemical and biological perspective of the air–ocean interface. Prog Oceanogr. 2013;109:104–116. [Google Scholar]
- 18.Cherry RS, Hulle CT. Cell death in the thin films of bursting bubbles. Biotechnol Prog. 1992;8(1):11–18. doi: 10.1021/bp00013a003. [DOI] [PubMed] [Google Scholar]
- 19.Dupré A. Sixième mémoire sur la théorie méchanique de la chaleur. Ann Chim Phys. 1867;4(11):194–220. [Google Scholar]
- 20.Rayleigh L. Some applications of photography. Nature. 1891;44(1133):249–254. [Google Scholar]
- 21.Ranz WE. Some experiments on the dynamics of liquid films. J Appl Phys. 1959;30(12):1950–1955. [Google Scholar]
- 22.Culick FEC. Comments on a ruptured soap film. J Appl Phys. 1960;3(6):1128–1129. [Google Scholar]
- 23.Taylor G. The dynamics of thin sheets of fluid. III. Disintegration of fluid sheets. Proc R Soc Lond A. 1959;253(1274):313–321. [Google Scholar]
- 24.Pandit AB, Davidson JF. Hydrodynamics of the rupture of thin liquid films. J Fluid Mech. 1990;212:11–24. [Google Scholar]
- 25.Spiel DE. On the births of film drops from bubbles bursting on seawater surfaces. J Geophys Res. 1998;103(C11):24907–24918. [Google Scholar]
- 26.Boulton-Stone JM, Blake JR. Gas bubbles bursting at a free surface. J Fluid Mech. 1993;254:437–466. [Google Scholar]
- 27.Dey D, Boulton-Stone JM, Emery AN, Blake JR. Experimental comparisons with a numerical model of surfactant effects on the burst of a single bubble. Chem Eng Sci. 1997;52(16):2769–2783. [Google Scholar]
- 28.Lhuissier H, Villermaux E. Bursting bubble aerosols. J Fluid Mech. 2012;696:5–44. [Google Scholar]
- 29.Franklin MP, et al. Bacterial diversity in the bacterioneuston (sea surface microlayer): The bacterioneuston through the looking glass. Environ Microbiol. 2005;7(5):723–736. doi: 10.1111/j.1462-2920.2004.00736.x. [DOI] [PubMed] [Google Scholar]
- 30.Gladyshev M. Biophysics of the Surface Microlayer of Aquatic Ecosystems. IWA; London: 2002. [Google Scholar]
- 31.Liss PS, Duce RA. The Sea Surface and Global Change. Cambridge Univ Press; Cambridge, UK: 1997. [Google Scholar]
- 32.Yin P, et al. Programming DNA tube circumferences. Science. 2008;321(5890):824–826. doi: 10.1126/science.1157312. [DOI] [PubMed] [Google Scholar]
- 33.Smith DE, Chu S. Response of flexible polymers to a sudden elongational flow. Science. 1998;281(5381):1335–1340. doi: 10.1126/science.281.5381.1335. [DOI] [PubMed] [Google Scholar]
- 34.Hariadi RF, Yurke B. Elongational-flow-induced scission of DNA nanotubes in laminar flow. Phys Rev E. 2010;82(4):046307. doi: 10.1103/PhysRevE.82.046307. [DOI] [PubMed] [Google Scholar]
- 35.Wenner JR, Williams MC, Rouzina I, Bloomfield VA. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys J. 2002;82(6):3160–3169. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schiffels D, Liedl T, Fygenson DK. Nanoscale structure and microscale stiffness of DNA nanotubes. ACS Nano. 2013;7(8):6700–6710. doi: 10.1021/nn401362p. [DOI] [PubMed] [Google Scholar]
- 37.Kantsler V, Goldstein RE. Fluctuations, dynamics, and the stretch-coil transition of single actin filaments in extensional flows. Phys Rev Lett. 2012;108(3):038103. doi: 10.1103/PhysRevLett.108.038103. [DOI] [PubMed] [Google Scholar]
- 38.Wandersman E, Quennouz N, Fermigier M, Lindner A, Du Roure O. Buckled in translation. Soft Matter. 2010;6:5715–5719. [Google Scholar]
- 39.Reyssat É, Quéré D. Bursting of a fluid film in a viscous environment. Europhys Lett. 2006;76(2):234–242. [Google Scholar]
- 40.Martin P, Buguin A, Brochard-Wyart F. Bursting of a liquid film on a liquid substrate. Europhys Lett. 1994;28(6):421–426. [Google Scholar]
- 41.Goodall DG, Gee ML, Stevens G, Perera J, Beaglehole D. An investigation of the critical thickness of film rupture and drainage phenomena using dual wavelength ellipsometry. Colloid Surface A. 1998;143(1):41–51. [Google Scholar]
- 42.Boulton-Stone JM. The effect of surfactant on bursting gas bubbles. J Fluid Mech. 1995;302:231–257. [Google Scholar]
- 43.Douglas SM, Chou JJ, Shih WM. DNA-nanotube-induced alignment of membrane proteins for NMR structure determination. Proc Natl Acad Sci USA. 2007;104(16):6644–6648. doi: 10.1073/pnas.0700930104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Graugnard E, et al. Kinetics of DNA and RNA hybridization in serum and serum-SDS. IEEE T Nanotechnol. 2010;9(5):603–609. doi: 10.1109/TNANO.2010.2053380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ekani-Nkodo A, Kumar A, Fygenson DK. Joining and scission in the self-assembly of nanotubes from DNA tiles. Phys Rev Lett. 2004;93(26):268301. doi: 10.1103/PhysRevLett.93.268301. [DOI] [PubMed] [Google Scholar]
- 46.Calef DF, Deutch JM. Diffusion-controlled reactions. Annu Rev Phys Chem. 1983;34:493–524. [Google Scholar]
- 47.Riseman J, Kirkwood JG. The intrinsic viscosity, translational and rotatory diffusion constants of rod-like macromolecules in solution. J Chem Phys. 1950;18(4):512–516. [Google Scholar]
- 48.Hill TL. Length dependence of rate constants for end-to-end association and dissociation of equilibrium linear aggregates. Biophys J. 1983;44(2):285–288. doi: 10.1016/S0006-3495(83)84301-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wetmur JG, Davidson N. Kinetics of renaturation of DNA. J Mol Biol. 1968;31(3):349–370. doi: 10.1016/0022-2836(68)90414-2. [DOI] [PubMed] [Google Scholar]
- 50.Morrison LE, Stols LM. Sensitive fluorescence-based thermodynamic and kinetic measurements of DNA hybridization in solution. Biochemistry. 1993;32(12):3095–3104. doi: 10.1021/bi00063a022. [DOI] [PubMed] [Google Scholar]
- 51.Wei B, Dai M, Yin P. Complex shapes self-assembled from single-stranded DNA tiles. Nature. 2012;485(7400):623–626. doi: 10.1038/nature11075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lhuissier H, Villermaux E. Soap films burst like flapping flags. Phys Rev Lett. 2009;103(5):054501. doi: 10.1103/PhysRevLett.103.054501. [DOI] [PubMed] [Google Scholar]
- 53.Manhart M. Visco-elastic behaviour of suspensions of rigid-rod like particles in turbulent channel flow. Eur J Mech B-Fluid. 2004;23(3):461–474. [Google Scholar]
- 54.Tsyboulski DA, Bachilo SM, Kolomeisky AB, Weisman RB. Translational and rotational dynamics of individual single-walled carbon nanotubes in aqueous suspension. ACS Nano. 2008;2(9):1770–1776. doi: 10.1021/nn800364r. [DOI] [PubMed] [Google Scholar]
- 55.Broersma S. Rotational diffusion constant of a cylindrical particle. J Chem Phys. 1960;32(6):1626–1631. [Google Scholar]
- 56.Stocks SM, Thomas CR. Viability, strength, and fragmentation of Saccharopolyspora erythraea in submerged fermentation. Biotechnol Bioeng. 2001;75(6):702–709. doi: 10.1002/bit.10017. [DOI] [PubMed] [Google Scholar]
- 57.DeSain JD, Brady BB, Metzler KM, Curtiss TJ, Albright TV. AEROSPACE REPORT NO. ATR-2009(8268)-1. The Aerospace Corporation; El Segundo, CA: 2009. Tensile tests of paraffin wax for hybrid rocket fuel grains; pp. 1–20. [Google Scholar]
- 58.Beyer MK, Clausen-Schaumann H. Mechanochemistry: The mechanical activation of covalent bonds. Chem Rev. 2005;105(8):2921–2948. doi: 10.1021/cr030697h. [DOI] [PubMed] [Google Scholar]
- 59.Bustamante C, Smith SB, Liphardt J, Smith D. Single-molecule studies of DNA mechanics. Curr Opin Struct Biol. 2000;10(3):279–285. doi: 10.1016/s0959-440x(00)00085-3. [DOI] [PubMed] [Google Scholar]
- 60.Vanapalli SA, Ceccio SL, Solomon MJ. Universal scaling for polymer chain scission in turbulence. Proc Natl Acad Sci USA. 2006;103(45):16660–16665. doi: 10.1073/pnas.0607933103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Law KL, et al. Plastic accumulation in the North Atlantic subtropical gyre. Science. 2010;329(5996):1185–1188. doi: 10.1126/science.1192321. [DOI] [PubMed] [Google Scholar]
- 62.Feng J, et al. Nanoemulsions obtained via bubble-bursting at a compound interface. Nat Phys. 2014;10(8):606–612. [Google Scholar]
- 63.Braslavsky I, Hebert B, Kartalov E, Quake SR. Sequence information can be obtained from single DNA molecules. Proc Natl Acad Sci USA. 2003;100(7):3960–3964. doi: 10.1073/pnas.0230489100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nat Methods. 2012;9(7):671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.