Abstract
Personalized neuromusculoskeletal (NMS) models can represent the neurological, physiological, and anatomical characteristics of an individual and can be used to estimate the forces generated inside the human body. Currently, publicly available software to calculate muscle forces are restricted to static and dynamic optimisation methods, or limited to isometric tasks only. We have created and made freely available for the research community the Calibrated EMG-Informed NMS Modelling Toolbox (CEINMS), an OpenSim plug-in that enables investigators to predict different neural control solutions for the same musculoskeletal geometry and measured movements. CEINMS comprises EMG-driven and EMG-informed algorithms that have been previously published and tested. It operates on dynamic skeletal models possessing any number of degrees of freedom and musculotendon units and can be calibrated to the individual to predict measured joint moments and EMG patterns. In this paper we describe the components of CEINMS and its integration with OpenSim. We then analyse how EMG-driven, EMG-assisted, and static optimisation neural control solutions affect the estimated joint moments, muscle forces, and muscle excitations, including muscle co-contraction.
Keywords: EMG-driven, EMG-informed, Neuromusculoskeletal modelling, static optimisation
2. Introduction
Estimation of individual muscle forces and their contribution to joint moments is essential for understanding how humans solve the dynamics of movement. Different methods have been developed to estimate muscle forces (Erdemir et al., 2007). These methods include static and dynamic optimisation (Anderson and Pandy, 2001; Crowninshield et al., 1978), which involve the use of inverse dynamics to track external joint moments and/or joint kinematics and estimation of muscle activations and forces to satisfy pre-selected objective criteria. However, optimisation methods cannot account for variations in muscle activation patterns (Buchanan and Shreeve, 1996) between tasks (Buchanan and Lloyd, 1995; Tax et al., 1990) and individuals (Lloyd and Buchanan, 2001), even when joint angles and moments are the same. Furthermore, optimisation methods cannot predict the muscle co-contraction evident in the electromyography (EMG) patterns of different tasks (Colby et al., 2000; Lloyd and Buchanan, 2001; Neptune et al., 1999) and different patient populations (Bryant et al., 2008; Heiden et al., 2009; Schmitt and Rudolph, 2007).
An alternative to optimisation is to use EMG-driven neuromusculoskeletal (NMS) models, in which EMG signals and three-dimensional (3D) joint angles are used to calculate individual muscle forces (Buchanan et al., 2004; Lloyd and Besier, 2003; Lloyd and Buchanan, 1996). EMG-driven models overcome the limitations of static and dynamic optimisation; however, they are not without shortcomings (Chèze et al., 2012), such as limited muscles from which EMG data can be acquired and errors in EMG measurement and normalisation (De Luca, 1997; Sartori et al., 2014).
While optimisation methods are easily accessible (Delp et al., 2007), EMG-driven methods have been developed by different research groups (Amarantini and Martin, 2004; Buchanan et al., 2004; Langenderfer et al., 2005; Lloyd and Besier, 2003; Thelen et al., 1994) and they are not publicly available (Fregly et al., 2012b), or are limited to isometric tasks (Menegaldo et al., 2014). Also, software developed for research is often tuned to a particular project, data acquisition protocol, or laboratory, which makes it difficult to share. Furthermore, implementations of the same algorithm may be inconsistent among different software, with subsequent difficulties to compare results across research groups. Additionally, comparison between EMG-driven and static optimisation has not been possible. For example, comparison of the mechanical consequences of muscle co-contraction has not been possible, as it is unclear whether different muscle force outputs are due to the different neural control solution methods or musculoskeletal models.
We have created and released the Calibrated EMG-informed NMS Modelling Toolbox (CEINMS, simtk.org/home/ceinms), an OpenSim (Delp et al., 2007) plug-in which enables investigators to implement EMG-informed algorithms that have been previously published and validated (Lloyd and Besier, 2003; Sartori et al., 2014; Sartori et al., 2012a). While EMG-informed methods encapsulate all algorithms that use EMG as inputs, EMG-driven models specifically use EMG to derive muscle excitation patterns. CEINMS covers neural control solutions from EMG-driven (Lloyd and Besier, 2003), to hybrids between EMG-driven (Sartori et al., 2014) and static optimisation, to full static optimisation (Lenaerts et al., 2008). Additionally, CEINMS can use a set of excitation primitives and weighting factors as inputs rather than estimating muscle excitations directly from EMG (Sartori et al., 2013). Finally, CEINMS can operate with OpenSim musculoskeletal models possessing any number of degrees of freedom (DOF) and musculotendon units (MTU) and can be calibrated to the individual to predict joint moments (Lloyd and Besier, 2003; Sartori et al., 2012a). In this paper we describe CEINMS and its structure and integration with OpenSim. We then provide examples of using CEINMS to explore how different neural control solutions affect predicted joint moments, muscle forces, muscle excitations, and muscle co-contraction using the same NMS model and motion data.
3. Methods
3.1. CEINMS overview
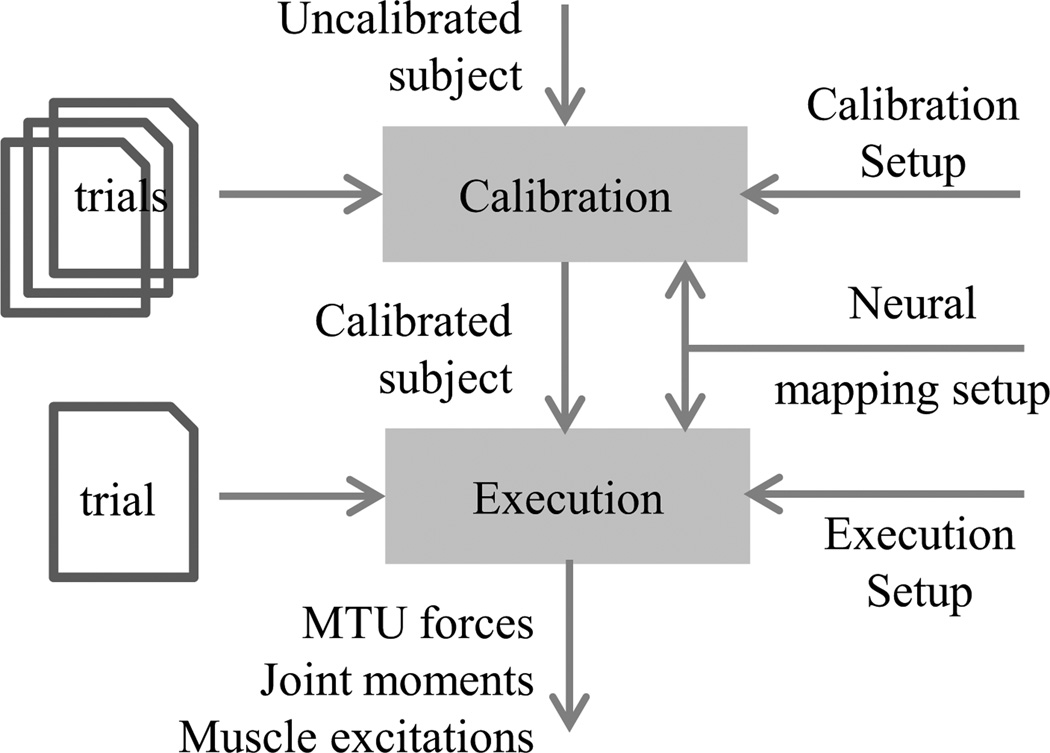
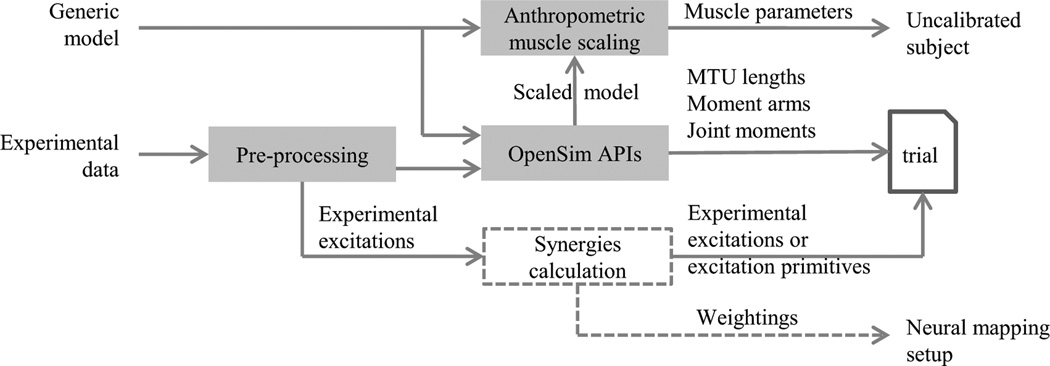
CEINMS is an open-source (Apache License, Version 2.0) software written in C++, which can be compiled and optimised on different operating systems and processor architectures. CEINMS use involves three steps: calibration, execution, and validation (Fig. 1). Execution inputs are MTU kinematics and external joint moments calculated with OpenSim (Fig. 1), and either muscle excitations or muscle excitation primitives and weightings extracted from experimental EMG data (Fig. 2), to estimate MTU forces and joint moments. Calibration refines the NMS model parameter values for a specific subject by including the execution step in an optimisation loop that minimises error between estimated and experimental joint moments (Fig. 3). Following calibration, execution (Fig. 4) estimates MTU forces and joint moments for trials that have not been used in calibration. Results are validated comparing CEINMS outputs to experimental data, such as joint moments (Lloyd and Besier, 2003; Sartori et al., 2012a) and joint contact forces (Gerus et al., 2013).
Figure 1.
The muscle parameters in the uncalibrated subject are used as the initial conditions for CEINMS calibration. The calibration setup defines the parameters to calibrate and their relative boundaries, while the association between experimental muscle excitations (or excitation primitives and weightings) and MTUs is defined by the neural mapping. The output of the calibration is the set of calibrated parameters (calibrated subject) that is used as input for the execution of CEINMS to predict MTU forces, joint moments, and adjusted muscle excitations of trials not used for the calibration. The execution setup defines the neural algorithm to be used for the CEINMS execution.
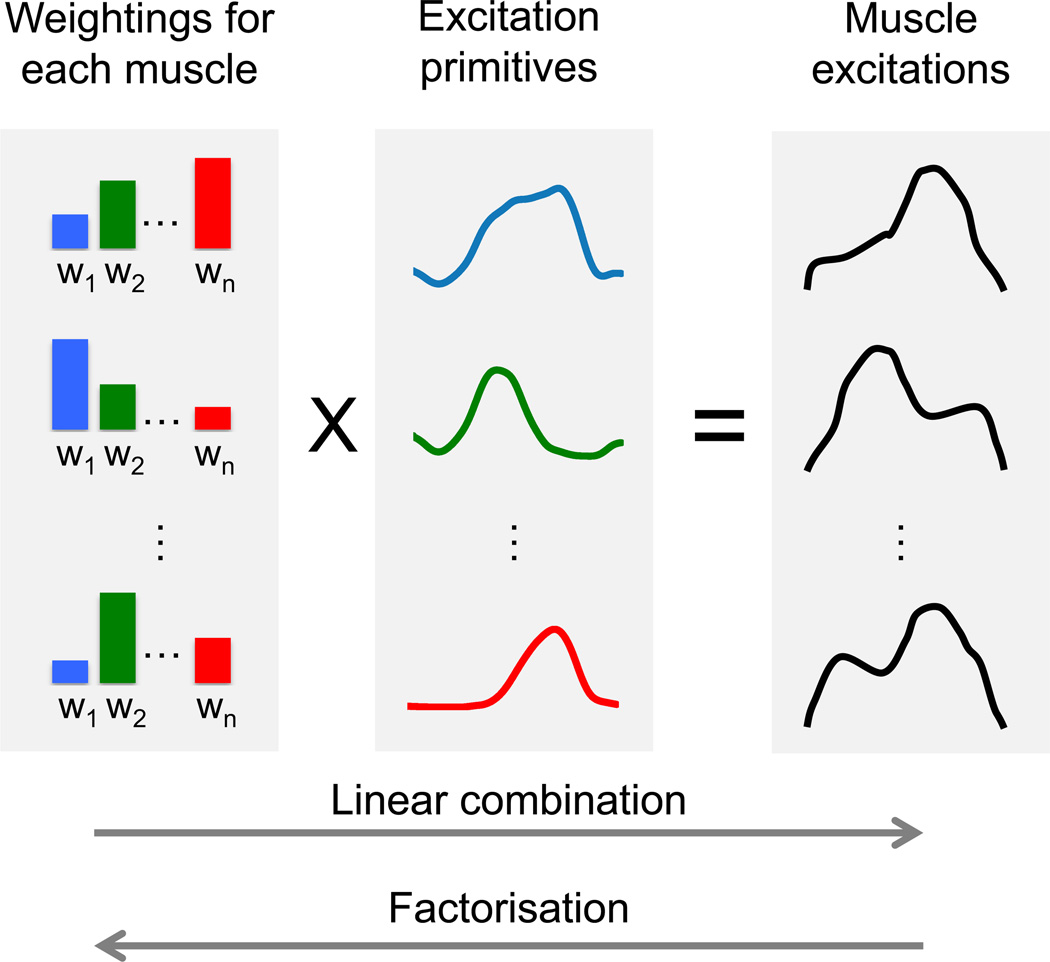
Figure 2.
Excitation primitives and weighting factors from factorisation of experimental excitations can be used as input for CEINMS. CEINMS neural mapping is integrated in the software and can be configured to linearly combine excitation primitives and weightings.
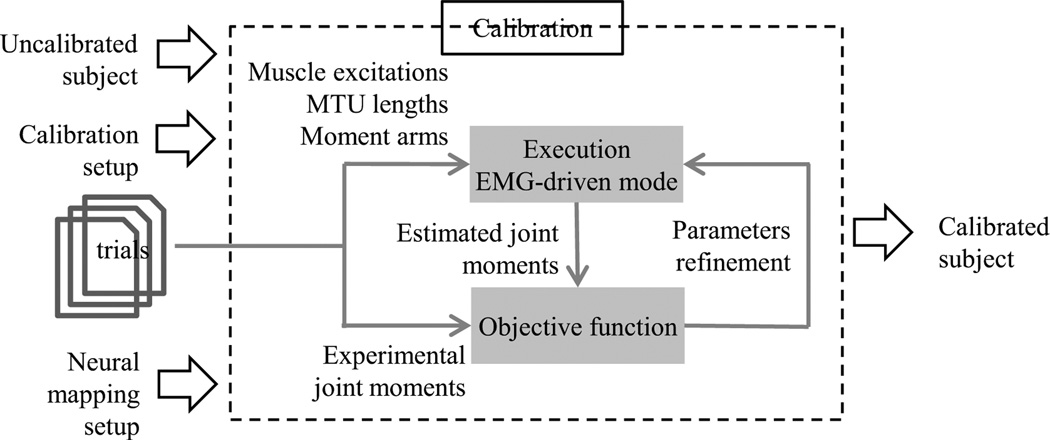
Figure 3.
The calibration refines the subject’s neuromuscular parameters to reduce the error between experimental joint moments and joint moments predicted by the CEINMS EMG-driven open-loop mode.
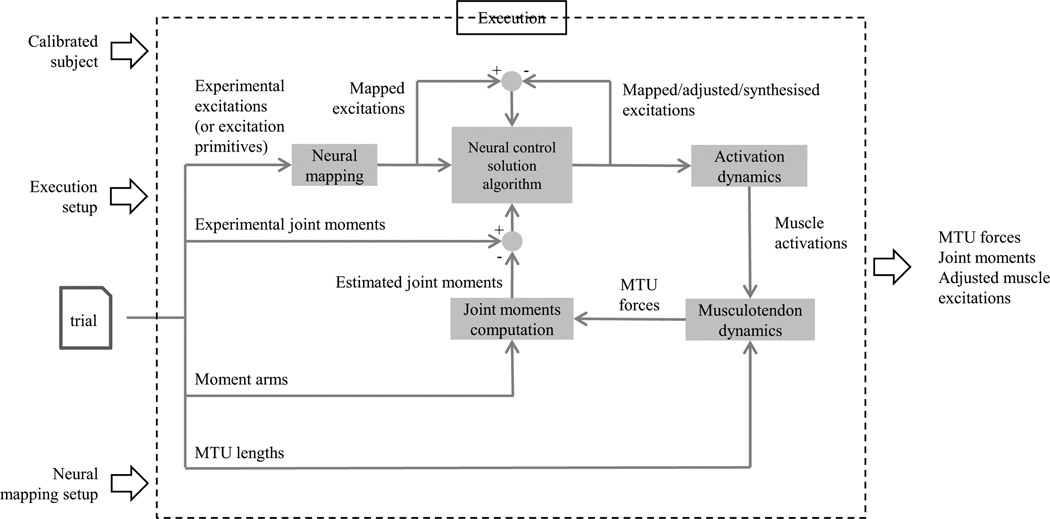
Figure 4.
In CEINMS execution the adjusted muscle excitations in conjunction with MTU lengths and moment arms from OpenSim are used as inputs to estimate MTU forces and joint moments from a single experimental trial. For each timeframe the neural control solution algorithm uses the mapped excitations, the error between mapped and adjusted excitations, and the joint moments tracking error to minimise a weighted objective function. The weighting factor values and the choice of muscle excitations to adjust determine the final muscle excitations produced by the neural control solution algorithm (i.e. EMG-driven, EMG-assisted or static optimisation).
CEINMS comprises six components; (1) data preparation, (2) neural mapping, (3) neural solution, (4) activation dynamics, (5) musculotendon dynamics, and (6) calibration.
3.2 Data preparation
CEINMS requires three setup files, one each for: calibration, neural mapping, and execution. It also needs an initial set of model parameter values and experimental trials (Fig. 1). The calibration and execution setup files enable the user to select the neural control algorithm (described below) and tune the behaviour of CEINMS, while the subject’s scaled musculoskeletal model derived from OpenSim and the input trials are created from experimental data using a MATLAB pipeline.
The pre-processing block (Fig. 5) is a MATLAB toolbox (MOtoNMS, simtk.org/home/motonms) that converts raw EMG data, marker trajectories, and ground reaction forces (GRF) from a C3D file to .trc and .mot files compatible with OpenSim. Experimental muscle excitations were calculated from raw EMG signals that were high-pass filtered (30Hz), full-wave-rectified, and low-pass filtered (6Hz) using a zero-lag fourth-order recursive Butterworth filter. Experimental muscle excitations were normalised using data from multiple maximum voluntary contraction trials. A similar low-pass filter was applied to marker trajectories and GRF using a cutoff frequency of 8 Hz.
Figure 5.
CEINMS data preparation pipeline in MATLAB. Experimental data, including marker trajectories, ground reaction forces, and EMG signals, are first conditioned in the pre-processing block which performs filtering, rotation of coordinate systems, calculation of hip, knee, and ankle joint centres, calculation and normalisation of experimental excitations from EMG signals, and file conversions in OpenSim format. OpenSim APIs are then used to first scale a generic OpenSim model, then inverse kinematics, muscle analysis, and inverse dynamics tools are used to calculate MTU lengths, moment arms, and joint moments. The muscle parameters in the scaled OpenSim model are anthropometrically scaled to maintain the same operation range of the generic model (Winby et al 2008), which are then used as the initial conditions for the calibration process in CEINMS. Synergies and weighting factors can be also used in place of experimental muscle excitations as input for CEINMS.
It is also possible to extract muscle synergies and weighting factors (Fig. 3) from experimental muscle excitations using factorisation algorithms (Fig. 2) (d'Avella and Tresch, 2002; Neptune et al., 2009; Sartori et al., 2013; Tresch et al., 2006).
CEINMS also requires as inputs MTU lengths, moment arms, and external joint moments. OpenSim muscle analysis and inverse dynamics tools are used to calculate these variables.
3.3. Neural mapping
Previous studies have mapped experimental muscle excitations to muscles from which EMG data were unavailable (Lloyd and Besier, 2003; Sartori et al., 2012a). For example, vastus intermedius excitation was calculated as average of vastus medialis and vastus lateralis excitations. Alternatively, as in Neptune et al. (2009) and Sartori et al. (2013), muscle excitation primitives and weightings can be used as input. CEINMS has a generalised method for creating muscle excitations by linearly combining any number of time varying input signals. This method can be used to create new muscle excitations from existing experimental excitations and/or derive muscle excitations from pre-calculated muscle synergies (Sec 3.2). The resulting muscle excitations are input to a neural control solution algorithm (Fig. 4).
3.4. Neural control solution algorithms
The neural control solution algorithm adjusts muscle-specific excitations to improve the tracking of experimental joint moments (Sartori et al., 2014) (Fig. 4). For each time frame, a simulated annealing algorithm (Corana et al., 1987) minimises an objective function, which can be customised to target specific DOF and MTUs. Therefore, using the same objective function (Eq. 1), one can access several neural control algorithms, grouped into three classes:
EMG-driven mode. No optimisation is performed (Lloyd and Besier, 2003; Sartori et al., 2012a).
EMG-assisted mode. Optimisation adjusts existing excitations determined from experimental EMG signals and synthetise excitations for muscles with no experimental EMGs available (Sartori et al., 2014).
Static optimisation mode. Without the use of experimental EMG data, an optimisation synthesises all muscle excitations.
Modes 2–3 minimise the objective function (Sartori et al., 2014):
| (1) |
where M̄d and Md are experimental and estimated joint moment for the dth DOF, ē and e are experimental and estimated muscle excitations, MTUsynth is the list of MTUs with excitations to synthesise, MTUadj the list of MTUs with excitations to adjust, and α, β, γ are positive weighting factors (Sartori et al., 2014). Importantly, different modes can be executed on the same motion data and musculoskeletal geometry.
3.5. Activation dynamics
Neural activation is derived from muscle excitations by modelling the muscle’s twitch response. This improves muscle force predictions (Buchanan et al., 2004; Lloyd and Besier, 2003; Lloyd et al., 2008) and is represented by a critically-damped linear second-order differential system (Milner et al., 1973; Thelen et al., 1994) in a discrete form (Lloyd and Besier, 2003):
| (2) |
where e(t) is a muscle excitation at the time t, u(t) the neural activation, α the muscle gain, C1 and C2 recursive coefficients, and d the electromechanical delay. The relation between neural and muscle activation is non-linear, and CEINMS provides two different solutions. The first is that of Lloyd and Besier (2003),
| (3) |
where a(t) is the muscle activation, and A is the non-linear shape factor, constrained in the interval (−3, 0). The second model is described by Manal and Buchanan (2003) as a piecewise function:
| (4a) |
| (4b) |
For each muscle, αact, βact, m, c depend only on the shape factor A, constrained in the interval (0, 0.12].
3.6. Musculotendon dynamics
MTU kinematics and muscle activation are used as input for a Hill-type muscle model with a compliant tendon, which is implemented in CEINMS in accordance with (Buchanan et al., 2004; Lloyd and Besier, 2003; Schutte, 1993). Musculotendon dynamics can be solved using three computational methods. The first integrates a set of ordinary differential equations (ODE) with a Runge-Kutta-Fehlberg algorithm. The second uses a Wijngaarden-Dekker-Brent optimisation routine (Brent, 1973) to find the root of the equilibrium equation between the force produced by the muscle fibres and the tendon. The third considers the tendon as an element of infinite stiffness (Sartori et al., 2012b).
While the stiff tendon has been shown to produce large force errors for increasing ratios of optimal fibre length and tendon slack length (Millard et al., 2013), the integration of ODEs can be unsuccessful due to high system stiffness when a muscle is inactive and muscle damping is small or absent. Also, MTUs with short tendons may lead to stiff ODEs that are unstable for explicit integration solvers. The equilibrium model is more robust to variations in and and hence more suitable for the calibration step, where these two parameters are optimised.
3.7. Calibration
CEINMS can be calibrated to experimental data collected from an individual subject (Lloyd and Besier, 2003; Sartori et al., 2012a). Initial muscle parameter values for the subject are tuned using simulated annealing (Corana et al., 1987), which minimises the error between experimental joint moments and those estimated by the EMG-driven mode of CEINMS (Fig. 3). A number of trials, encompassing static and/or dynamic tasks (Lloyd and Besier, 2003; Sartori et al., 2012a), are used for calibration.
The calibration objective function fcal is defined as:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
To reduce length and magnitude differences between trials, we normalise the sum of squared differences between predicted (Mt,d,r) and experimental joint moments by trial variance and number of data points (Nrows) for each tth trial. The penalty function P(r, j) discourages the adoption of non-physiological solutions corresponding to values of l̃m outside its operative range (0.5, 1.5).
Following calibration, the optimised parameters are used to execute CEINMS using a novel set of trials as inputs and any of the neural control solution algorithms (Sec. 3.4).
3.8 Example Application
To demonstrate CEINMS’s different modes of operation, we collected gait data from five healthy subjects (30.6 ± 6.7 years; 77.8 ± 9.9 kg). The study was approved by Griffith University Human Research Ethics Committee and participants provided written informed consent. Ten walking trials (1.5 ± 0.23 m/s) were collected using a 10-camera motion-capture system (Vicon, Oxford, UK) and two force plates (Kistler, Amherst, NY). Surface EMG (Zerowire, Aurion, Milan, IT) signals were acquired from 16 muscles from a single leg: gluteus maximus, gluteus medius, tensor fasciae latae, rectus femoris, sartorius, vastus lateralis, vastus medialis, adductor group, gracilis, medial and lateral hamstring, semimembranosus, gastrocnemius medialis, gastrocnemius lateralis, soleus, tibialis anterioris, and peroneus group.
A generic OpenSim model (gait2392) was scaled to each subject. The hip joint centres were calculated using regression equations (Harrington et al., 2007), while markers on the femoral condyles and ankle malleoli were used to establish knee and ankle joint centres. This was followed by the anthropometric scaling of and parameters using method number 9 in (Winby et al., 2008), which were then used as input for the calibration step (Fig 3). Inverse kinematics, muscle analysis, and inverse dynamics tools in OpenSim were used to calculate 3D joint angles, MTU lengths, moment arms, and external joint moments of each dynamic trial.
A total of 34 MTUs and 3 DOFs (hip and knee flexion-extension and ankle plantar-dorsi flexion (FE)) were analysed in CEINMS. The 16 channels of EMG data were mapped to 32 MTUs (Sec. 3.3), as described by Sartori et al. (2012a). CEINMS was configured to use the equilibrium elastic tendon for musculotendon dynamics (Sec. 3.6) and equation 3 for activation dynamics (Sec. 3.5). For each subject, calibration was performed using four walking trials, which were not the walking trials used for CEINMS execution. During the calibration, and of each MTU were constrained within ±5% from their initial values, while activation dynamics parameters A, C1, and C2 were calibrated globally (Lloyd and Besier, 2003). The shape factor A was bounded between −3 and 0 and the coefficients C1 and C2 between −1 and 1. MTUs were divided into 11 groups based on being posteriorly or anteriorly located on each lower limb segment. A strength coefficient bounded between 0.5 and 2.5 was then assigned to each group (Sartori et al., 2012a). These coefficients were used to scale peak isometric force of the different muscle groups. After calibration, CEINMS was used to predict hip, knee, and ankle FE moments using the EMG-driven, EMG-assisted, and static optimisation modes. In the EMG-assisted mode, the weighting parameters α, β, and γ (equation 1) were calculated through an automatic procedure aimed at finding the lowest tracking errors for both muscle excitations and external joint moments (Sartori et al., 2014).
Root mean square error (RMSE) and coefficient of determination (R2) were used to compare prediction of external joint moments and muscle excitations between neural solutions.
To examine the effect of different neural control solutions on the muscle co-contraction, co-contraction ratios (CCR) of FE moments (Mf and Me respectively) for hip, knee, and ankle were calculated as follows (Heiden et al., 2009):
| (6) |
This ratio provides an indication of relative final mechanical action of muscle co-contraction between flexors and extensors, where being close to 0 indicates a higher level of co-contraction, and 1 or −1 no effective co-contraction but a moment directed to flexion or extension respectively.
4. Results
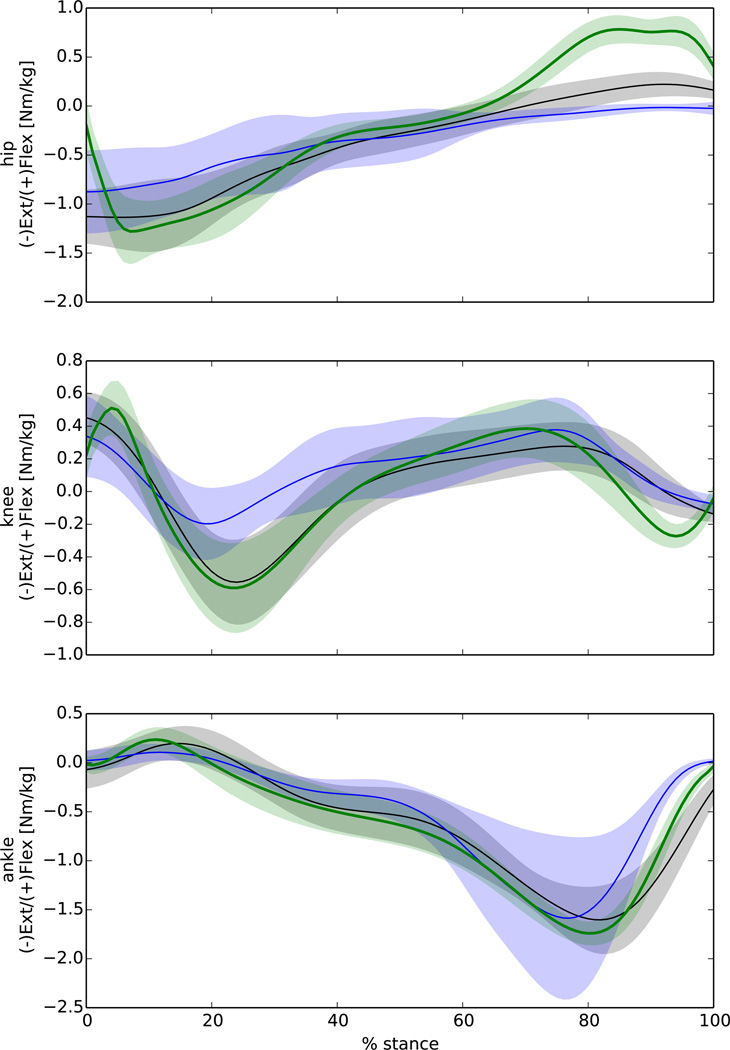
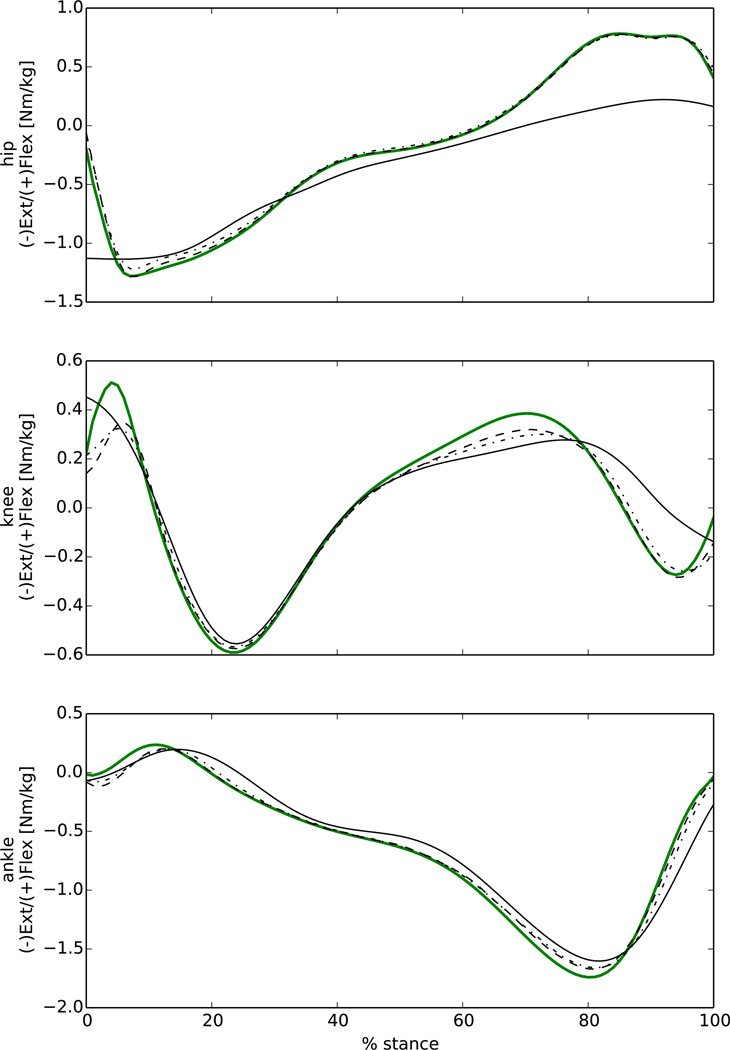
The calibration procedure improved the estimation of hip, knee, and ankle FE moments for the EMG-driven mode (Fig. 6). The calibrated EMG-driven mode well predicted the knee and ankle FE moments (RMSE 0.18 Nm/kg and 0.24 Nm/kg respectively) but underestimated the hip flexion moment in the second half of stance phase due to a missing contribution from iliopsoas MTUs (Fig. 7). These muscles were accounted for in the EMG-assisted and the static optimisation modes, which matched the experimental joint moments well for all three DOFs (Table 1).
Figure 6.
External joint moments from OpenSim inverse dynamics (green), calibrated EMG-driven (black), and uncalibrated EMG-driven (blue). The curves represent the ensemble average (shaded area 1 SD) of 30 walking trials from 5 different individuals. These results were from trials different to those used to calibrate CEINMS.
Figure 7.
Comparisons between experimental joint moments from OpenSim inverse dynamics (solid green) and joint moments predicted by EMG-driven (solid black), EMG-assisted (dash-point), and static optimisation (dashed) modes for hip, knee and ankle flexion extension during stance phase.
Table 1.
External joint moment predictions of the uncalibrated EMG-driven, and the calibrated EMG-driven, EMG-assisted, and the static-optimisation modes.
| Uncalibrated EMG-driven | EMG-driven | EMG-assisted | Static optimisation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (Nm/kg) |
SD | R2 | SD | RMSE (Nm/kg) |
SD | R2 | SD | RMSE (Nm/kg) |
SD | R2 | SD | RMSE (Nm/kg) |
SD | R2 | SD | |
| hip FE | 0.56 | 0.12 | 0.65 | 0.13 | 0.39 | 0.1 | 0.84 | 0.07 | 0.07 | 0.05 | 0.99 | 0.03 | 0.04 | 0.04 | 0.99 | 0.01 |
| knee FE | 0.28 | 0.08 | 0.67 | 0.12 | 0.18 | 0.05 | 0.80 | 0.11 | 0.09 | 0.04 | 0.93 | 0.07 | 0.08 | 0.04 | 0.95 | 0.05 |
| ankle FE | 0.44 | 0.19 | 0.86 | 0.17 | 0.24 | 0.13 | 0.88 | 0.14 | 0.10 | 0.07 | 0.97 | 0.04 | 0.06 | 0.04 | 0.99 | 0.01 |
RMSE (Nm/kg) = root mean square error normalised to body mass. R2 = coefficient of determination
When compared to the static optimisation mode, the EMG-assisted mode consistently estimated muscle excitations closer to the experimental excitations (Table 2), presenting both higher R2 and lower RMSE for each muscle.
Table 2.
Comparison between experimental muscle excitations and muscle excitations estimated using the EMG-assisted and static-optimisation modes.
| EMG-assisted | Static optimisation | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | STD | RMSE | STD | R2 | STD | RMSE | STD | |
| Adductor magnus | 0.36 | 0.34 | 0.061 | 0.047 | 0.11 | 0.15 | 0.104 | 0.063 |
| Bicep femoris long head | 0.64 | 0.23 | 0.079 | 0.044 | 0.42 | 0.19 | 0.127 | 0.068 |
| Gluteus maximus | 0.41 | 0.33 | 0.083 | 0.054 | 0.19 | 0.14 | 0.111 | 0.038 |
| Gluteus medius | 0.61 | 0.33 | 0.035 | 0.039 | 0.06 | 0.07 | 0.068 | 0.029 |
| Gracilis | 0.62 | 0.31 | 0.033 | 0.031 | 0.13 | 0.13 | 0.091 | 0.035 |
| Gastrocnemius lateralis | 0.88 | 0.15 | 0.040 | 0.039 | 0.49 | 0.26 | 0.136 | 0.071 |
| Gastrocnemius medialis | 0.79 | 0.20 | 0.060 | 0.039 | 0.58 | 0.24 | 0.120 | 0.055 |
| Peroneus longus | 0.89 | 0.18 | 0.022 | 0.019 | 0.31 | 0.23 | 0.108 | 0.043 |
| Rectus femoris | 0.15 | 0.26 | 0.032 | 0.014 | 0.04 | 0.07 | 0.048 | 0.015 |
| Sartorius | 0.75 | 0.32 | 0.014 | 0.014 | 0.02 | 0.03 | 0.069 | 0.064 |
| Semimembranosus | 0.43 | 0.32 | 0.089 | 0.047 | 0.23 | 0.16 | 0.145 | 0.045 |
| Soleus | 0.60 | 0.30 | 0.079 | 0.041 | 0.59 | 0.26 | 0.097 | 0.038 |
| Tensor fasciae latae | 0.64 | 0.29 | 0.013 | 0.012 | 0.05 | 0.05 | 0.046 | 0.018 |
| Tibialis anterioris | 0.62 | 0.21 | 0.092 | 0.048 | 0.37 | 0.22 | 0.128 | 0.052 |
| Vastus lateralis | 0.60 | 0.22 | 0.036 | 0.018 | 0.44 | 0.18 | 0.060 | 0.026 |
| Vastus medialis | 0.60 | 0.29 | 0.026 | 0.018 | 0.41 | 0.20 | 0.046 | 0.027 |
RMSE = root mean square error. R2 = coefficient of determination
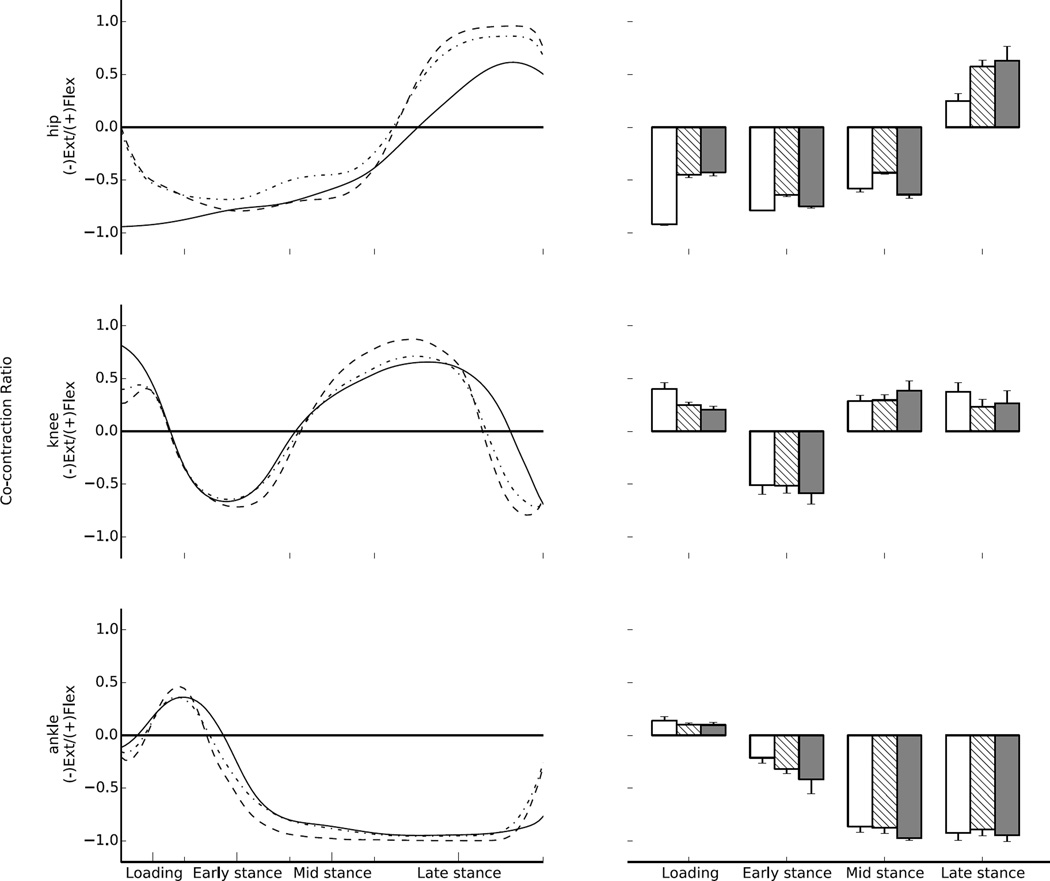
When compared to the EMG-driven mode, EMG-assisted and static optimisation presented a co-contraction ratio closer to 0 for the loading phase of hip and knee and closer to 1 for the late stance of the hip (Fig. 8). Conversely, compared to static optimisation the EMG-assisted mode predicted co-contraction ratios closer to 0 during early, mid, and late stance for the hip, knee, and ankle (Fig. 8).
Figure 8.
Effective mechanical co-contraction ratios between flexion and extension muscle moments at the hip, knee, and ankle of 30 walking trials from 5 different individuals. Zero represents maximum co-contraction, and 1 or −1 minimum co-contraction. On the left data is presented as mean time series for EMG-driven (solid), EMG-assisted (dash-point), and static optimisation (dashed) modes. On the right mean (1 SD) on co-contraction ratios of the muscle moments for each stage of stance, for EMG-driven (white), EMG-assisted (crosshatch), and static optimisation (grey). Loading first 15% of stance, early stance from 15% to 40%of stance, mid stance from 40% to 60% of stance, late stance from 60% to 100% of stance.
5. Discussion
We created and released CEINMS, an OpenSim toolbox to explore the effect of different neural control solution algorithms using consistent musculoskeletal geometry. Although software for EMG-driven modelling have been released in the past (Menegaldo et al., 2014), CEINMS is the first that can be configured to work with any number of MTUs and DOFs. CEINMS comprises a calibration procedure, includes state-of-the-art EMG-informed algorithms, and can be used with dynamic tasks.
In line with previous studies (Gerus et al., 2013; Lloyd and Besier, 2003; Sartori et al., 2012a), calibration of CEINMS improved joint moment estimations for the knee and ankle (Fig. 6 and Table 1). While not employed in the current study, some muscle parameters can be measured using medical imaging. CEINMS allows the user to define the MTU and associated parameters included in the calibration, facilitating concurrent use of measured and calibrated parameters. The use of measured parameters and inclusion of additional criteria in the calibration function (equation 5), such as the minimisation of joint contact loads (Gerus et al., 2013), is expected to improve muscle force predictions.
Similar to the findings of Sartori and colleagues (Sartori et al., 2014; Sartori et al., 2012a) the calibrated EMG-driven mode poorly estimated the hip flexion moment (Fig. 7) due to the lack of experimental EMG data for the iliacus and psoas MTUs, which only contributed passively to the hip moment. Conversely, EMG-assisted mode predictions of joint moments were consistent with the experimental data (Tables 1 and 2).
It could be argued that our implementation of static optimisation does not perfectly track the external joint moments from inverse dynamics (Table 1). This observation is attributable to the inclusion of the activation dynamics (Se c. 3.5) in the optimisation loop, making muscle activation depend on past values of neural excitation (equation 2), therefore limiting the MTU force solution space. However, our implementation enables the direct comparison of estimated and experimental muscle excitations (Table 2), which would not possible otherwise.
To describe CEINMS and its possible applications, we used consistent musculoskeletal geometry to perform an example study that compared effective mechanical co-contraction for EMG-informed and static optimisation modes. Even during walking in normal healthy individuals, the mechanical effect of co-contraction was clearly different between EMG-informed methods and pure static optimisation (Fig. 8). While co-contraction ratios estimated by the EMG-driven mode cannot be considered reliable for the hip joint, EMG-assisted and EMG-driven modes predicted similar co-contractions for knee and ankle. Also, the EMG-assisted mode consistently predicted higher co-contractions for the three DOFs when compared to static optimisation. Furthermore, we expect to observe greater differences in co-contraction during different tasks (e.g. running, sidestepping) or patient populations (e.g. osteoarthritis, anterior cruciate ligament reconstruction) that need to employ greater levels of joint stabilisation than during healthy walking (Bryant et al., 2008; Colby et al., 2000; Heiden et al., 2009; Neptune et al., 1999; Schmitt and Rudolph, 2007). However, such evaluation goes beyond the scope of the paper and should be investigated in further studies.
Future users of CEINMS may benefit from the following guidance. The quality of EMGs affects the EMG-informed solutions, therefore it is recommended following best-practice procedures for EMG collection, as per the SENIAM guidelines (Hermens et al., 2000). Since CEINMS uses amplitude-normalised EMG it is recommended normalizing to maximum EMGs recorded from a variety of maximum exertion isometric and dynamic tasks. Selecting which muscles to record EMG from depends on the application. It is suggested choosing muscles with the largest cross-sectional areas as these have the greatest mechanical effect on the joint contact forces and motion. Furthermore, when recording EMGs from a limited number of muscles, it is important to select at least one muscle from each neuro-anatomical group of interest to enable mapping of the other muscle excitations (Lloyd and Besier, 2003; Sartori et al., 2012a). Additionally, when using the EMG-assisted mode it is recommended to record EMG from the gracilis, sartorius, vastus medialis, gastrocnemius medialis, and peroneus group as Sartori et al. (2014) showed that these muscles were poorly predicted. Finally, selection of which EMG-informed mode to use depends on the application and EMG availability. The EMG-assisted mode potentially compensates for the inability to access deep muscles, as well as cross-talk and noisy EMGs, (Sartori et al., 2014), making it appropriate for hip joint investigations. Alternatively, the multiple-DOF EMG-driven mode (Sartori et al., 2012a) is adequate for investigating knee and ankle joints, where most EMGs are easily recorded. Finally, EMG-informed modes should be preferred over static optimisation, as EMG-informed methods will reflect an individual’s neural solution to generate movement, and better predict knee joint contact forces, particularly in the lateral tibiofemoral joint, measured using instrumented prostheses (Fregly et al., 2012a; Gerus et al., 2013; Walter et al., 2014; Winby et al., 2009).
When using CEINMS a number of factors must be considered. The neural mapping (Lloyd and Besier, 2003; Sartori et al., 2012a) is a simplification of muscle recruitment strategies and may result in suboptimal model calibration and inaccurate force predictions. This is exemplified by larger discrepancies in measured and predicted excitations in the muscles surrounding the hip compared to the knee and ankle (Table 2). This may be caused by the iliacus and psoas excitations not being included in the calibration, resulting in the other hip muscles’ parameters being less-than ideally calibrated in their absence. Thus, the prediction of hip muscles excitations using EMG-assisted mode may have contained some errors. Possible solutions include multiple iteration between calibration and prediction of excitations (Walter et al., 2014) or the simultaneous calibration of muscle parameters and prediction of excitations, for all trails from an individual, using dynamic optimization. However, further research is required to develop these processes.
In line with previous research (Barrett et al., 2007; Gerus et al., 2013) we performed both model calibration and execution using the same task. Other investigations (Shao et al., 2011; Winby et al., 2013; Winby et al., 2009) used a range of additional tasks for calibration, which improved prediction of walking, while Lloyd and Besier (2003) also predicted tasks not included in the calibration. Nevertheless, a systematic investigation is needed on how to best calibrate in regard to types of trials, which muscles to record EMG from, neural mapping, and how to attain true maximum excitations in some populations. This is a large undertaking and beyond the scope of the current study and a much needed area of future research. Finally, we used CEINMS in combination with MOtoNMS, an easy-to-use self-contained software package written in MATLAB. While MOtoNMS simplifies data pre-processing, it is not essential for the use of CEINMS and researchers may perform data pre-processing using freely available alternatives to MATLAB, such as Octave (www.gnu.org/software/octave) and Scilab (www.scilab.org).
This study describes the new CEINMS toolbox and how it can be configured to obtain different neural control solutions for the same NMS model and motion data. While the current research only provides a little insight into how the different neural control solutions estimate MTU forces and muscle excitations, CEINMS enables investigators to further explore these differences with their own datasets. Although each EMG-informed algorithm has been described and validated previously (Barrett et al., 2007; Gerus et al., 2013; Lloyd and Besier, 2003; Manal and Buchanan, 2013; Sartori et al., 2014; Sartori et al., 2013; Sartori et al., 2012a; Shao et al., 2011; Winby et al., 2013; Winby et al., 2009), direct comparisons between all these different neural control solutions have not been possible before. The availability of CEINMS source code will enable the larger biomechanics community to explore, extend, and improve the methods of calibration and the neural control solutions currently implemented. It is our hope that CEINMS will facilitate and promote the comparison of different neural solutions deriving physiologically relevant data, such as MTU forces, joint contact forces, and muscle co-contraction, across different research groups and projects, allowing more comprehensive insight in biomechanics of health and pathology.
Acknowledgements
The authors would like to thank Dr Nicole Grigg for her assistance with data collection and manuscript preparation, A/Prof Jonas Rubenson for his contribution to the implementation of the elastic tendon model, and Dr Alice Mantoan for the development of MOtoNMS. This work was funded by the Australian National Health and Medical Research Council (628850), Royal Society of NZ Marsden Fund (12-UOA-1221), the US National Institutes of Health grant R01EB009351, EU-F7 grant BioMot (project no. 611695), and PhD scholarship from Griffith University and Menzies Health Institute Queensland.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement
The authors have no conflicts of interest concerning the publication of the results of this study.
References
- Amarantini D, Martin L. A method to combine numerical optimization and EMG data for the estimation of joint moments under dynamic conditions. Journal of biomechanics. 2004;37:1393–1404. doi: 10.1016/j.jbiomech.2003.12.020. [DOI] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG. Dynamic optimization of human walking. Journal of biomechanical engineering. 2001;123:381–390. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- Barrett RS, Besier TF, Lloyd DG. Individual muscle contributions to the swing phase of gait: and EMG based forward dynamics model. Simulation Modelling Practice and Theory. 2007;15:1146–1155. [Google Scholar]
- Brent RP. Some Efficient Algorithms for Solving Systems of Nonlinear Equations. Siam J Numer Anal. 1973;10:327–344. [Google Scholar]
- Bryant AL, Kelly J, Hohmann E. Neuromuscular adaptations and correlates of knee functionality following ACL reconstruction. Journal of Orthopaedic Research. 2008;26:126–135. doi: 10.1002/jor.20472. [DOI] [PubMed] [Google Scholar]
- Buchanan TS, Lloyd DG. Muscle-Activity Is Different for Humans Performing Static Tasks Which Require Force Control and Position Control. Neurosci Lett. 1995;194:61–64. doi: 10.1016/0304-3940(95)11727-e. [DOI] [PubMed] [Google Scholar]
- Buchanan TS, Lloyd DG, Manal K, Besier TF. Neuromusculoskeletal modeling: estimation of muscle forces and joint moments and movements from measurements of neural command. Journal of applied biomechanics. 2004;20:367–395. doi: 10.1123/jab.20.4.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchanan TS, Shreeve DA. An evaluation of optimization techniques for the prediction of muscle activation patterns during isometric tasks. Journal of biomechanical engineering. 1996;118:565–574. doi: 10.1115/1.2796044. [DOI] [PubMed] [Google Scholar]
- Chèze L, Moissenet F, Dumas R. State of the art and current limits of musculoskeletal models for clinical applications. Movement & Sport Sciences - Science & Motricité. 2012 [Google Scholar]
- Colby S, Francisco A, Yu B, Kirkendall D, Finch M, Garrett W. Electromyographic and kinematic analysis of cutting maneuvers - Implications for anterior cruciate ligament injury. Am J Sport Med. 2000;28:234–240. doi: 10.1177/03635465000280021501. [DOI] [PubMed] [Google Scholar]
- Corana A, Marchesi M, Martini C, Ridella S. Minimizing Multimodal Functions of Continuous-Variables with the Simulated Annealing Algorithm. Acm T Math Software. 1987;13:262–280. [Google Scholar]
- Crowninshield RD, Johnston RC, Andrews JG, Brand RA. A biomechanical investigation of the human hip. Journal of biomechanics. 1978;11:75–85. doi: 10.1016/0021-9290(78)90045-3. [DOI] [PubMed] [Google Scholar]
- d'Avella A, Tresch MC. Modularity in the motor system: decomposition of muscle patterns as combinations of time-varying synergies. Adv Neur In. 2002;14:141–148. [Google Scholar]
- De Luca CJ. The use of surface electromyography in biomechanics. Journal of applied biomechanics. 1997;13:135–163. [Google Scholar]
- Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54:1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- Erdemir A, McLean S, Herzog W, van den Bogert AJ. Model-based estimation of muscle forces exerted during movements. Clin Biomech (Bristol, Avon) 2007;22:131–154. doi: 10.1016/j.clinbiomech.2006.09.005. [DOI] [PubMed] [Google Scholar]
- Fregly BJ, Besier TF, Lloyd DG, Delp SL, Banks SA, Pandy MG, D'Lima DD. Grand challenge competition to predict in vivo knee loads. Journal of Orthopaedic Research. 2012a;30:503–513. doi: 10.1002/jor.22023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fregly BJ, Boninger ML, Reinkensmeyer DJ. Personalized neuromusculoskeletal modeling to improve treatment of mobility impairments: a perspective from European research sites. Journal of neuroengineering and rehabilitation. 2012b;9:18. doi: 10.1186/1743-0003-9-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerus P, Sartori M, Besier TF, Fregly BJ, Delp SL, Banks SA, Pandy MG, D'Lima DD, Lloyd DG. Subject-specific knee joint geometry improves predictions of medial tibiofemoral contact forces. Journal of biomechanics. 2013;46:2778–2786. doi: 10.1016/j.jbiomech.2013.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington ME, Zavatsky AB, Lawson SE, Yuan Z, Theologis TN. Prediction of the hip joint centre in adults, children, and patients with cerebral palsy based on magnetic resonance imaging. Journal of biomechanics. 2007;40:595–602. doi: 10.1016/j.jbiomech.2006.02.003. [DOI] [PubMed] [Google Scholar]
- Heiden TL, Lloyd DG, Ackland TR. Knee joint kinematics, kinetics and muscle co-contraction in knee osteoarthritis patient gait. Clin Biomech. 2009;24:833–841. doi: 10.1016/j.clinbiomech.2009.08.005. [DOI] [PubMed] [Google Scholar]
- Hermens HJ, Freriks B, Disselhorst-Klug C, Rau G. Development of recommendations for SEMG sensors and sensor placement procedures. Journal of Electromyography and Kinesiology. 2000;10:361–374. doi: 10.1016/s1050-6411(00)00027-4. [DOI] [PubMed] [Google Scholar]
- Langenderfer J, LaScalza S, Mell A, Carpenter JE, Kuhn JE, Hughes RE. An EMG-driven model of the upper extremity and estimation of long head biceps force. Computers in biology and medicine. 2005;35:25–39. doi: 10.1016/j.compbiomed.2003.12.002. [DOI] [PubMed] [Google Scholar]
- Lenaerts G, De Groote F, Demeulenaere B, Mulier M, Van der Perre G, Spaepen A, Jonkers I. Subject-specific hip geometry affects predicted hip joint contact forces during gait. Journal of biomechanics. 2008;41:1243–1252. doi: 10.1016/j.jbiomech.2008.01.014. [DOI] [PubMed] [Google Scholar]
- Lloyd DG, Besier TF. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. Journal of biomechanics. 2003;36:765–776. doi: 10.1016/s0021-9290(03)00010-1. [DOI] [PubMed] [Google Scholar]
- Lloyd DG, Besier TF, Winby CR, Buchanan TS. Neuromusculoskeletal modelling and simulation of tissue load in the lower extremities. In: Hong Y, Bartlett R, editors. Routledge Handbook of Biomechanics and Human Movement Science. Oxford, UK: Taylor & Francis Books Ltd; 2008. pp. 3–17. [Google Scholar]
- Lloyd DG, Buchanan TS. A model of load sharing between muscles and soft tissues at the human knee during static tasks. Journal of biomechanical engineering. 1996;118:367–376. doi: 10.1115/1.2796019. [DOI] [PubMed] [Google Scholar]
- Lloyd DG, Buchanan TS. Strategies of muscular support of varus and valgus isometric loads at the human knee. Journal of biomechanics. 2001;34:1257–1267. doi: 10.1016/s0021-9290(01)00095-1. [DOI] [PubMed] [Google Scholar]
- Manal K, Buchanan TS. A one-parameter neural activation to muscle activation model: estimating isometric joint moments from electromyograms. Journal of biomechanics. 2003;36:1197–1202. doi: 10.1016/s0021-9290(03)00152-0. [DOI] [PubMed] [Google Scholar]
- Manal K, Buchanan TS. An Electromyogram-Driven Musculoskeletal Model of the Knee to Predict in Vivo Joint Contact Forces During Normal and Novel Gait Patterns. J Biomech Eng-T Asme. 2013;135 doi: 10.1115/1.4023457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menegaldo LL, de Oliveira LF, Minato KK. EMGD-FE: an open source graphical user interface for estimating isometric muscle forces in the lower limb using an EMG-driven model. Biomed Eng Online. 2014;13:37. doi: 10.1186/1475-925X-13-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millard M, Uchida T, Seth A, Delp SL. Flexing computational muscle: modeling and simulation of musculotendon dynamics. Journal of biomechanical engineering. 2013;135:021005. doi: 10.1115/1.4023390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner HS, Stein RB, Yemm R. Changes in Firing Rate of Human Motor Units during Linearly Changing Voluntary Contractions. J Physiol-London. 1973;230:371–390. doi: 10.1113/jphysiol.1973.sp010193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neptune RR, Clark DJ, Kautz SA. Modular control of human walking: A simulation study. Journal of biomechanics. 2009;42:1282–1287. doi: 10.1016/j.jbiomech.2009.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neptune RR, Wright IC, Van den Bogert AJ. Muscle coordination and function during cutting movements. Med Sci Sport Exer. 1999;31:294–302. doi: 10.1097/00005768-199902000-00014. [DOI] [PubMed] [Google Scholar]
- Sartori M, Farina D, Lloyd DG. Hybrid neuromusculoskeletal modeling to best track joint moments using a balance between muscle excitations derived from electromyograms and optimization. Journal of biomechanics. 2014;47:3613–3621. doi: 10.1016/j.jbiomech.2014.10.009. [DOI] [PubMed] [Google Scholar]
- Sartori M, Gizzi L, Lloyd DG, Farina D. A musculoskeletal model of human locomotion driven by a low dimensional set of impulsive excitation primitives. Frontiers in computational neuroscience. 2013;7:79. doi: 10.3389/fncom.2013.00079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sartori M, Reggiani M, Farina D, Lloyd DG. EMG-driven forward-dynamic estimation of muscle force and joint moment about multiple degrees of freedom in the human lower extremity. PloS one. 2012a;7:e52618. doi: 10.1371/journal.pone.0052618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sartori M, Reggiani M, Pagello E, Lloyd DG. Modeling the human knee for assistive technologies. IEEE transactions on bio-medical engineering. 2012b;59:2642–2649. doi: 10.1109/TBME.2012.2208746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt LC, Rudolph KS. Influences on knee movement strategies during walking in persons with medial knee osteoarthritis. Arthritis Rheum. 2007;57:1018–1026. doi: 10.1002/art.22889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schutte LM. Ph.D. Thesis. Stanford University; 1993. Using musculoskeletal models to explore strategies for improving performance in electrical stimulation-induced leg cycle ergometry. [Google Scholar]
- Shao Q, MacLeod TD, Manal K, Buchanan TS. Estimation of ligament loading and anterior tibial translation in healthy and ACL-deficient knees during gait and the influence of increasing tibial slope using EMG-driven approach. Annals of biomedical engineering. 2011;39:110–121. doi: 10.1007/s10439-010-0131-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tax AAM, Vandergon JJD, Gielen CCAM, Kleyne M. Differences in Central Control of M-Biceps-Brachii in Movement Tasks and Force Tasks. Exp Brain Res. 1990;79:138–142. doi: 10.1007/BF00228882. [DOI] [PubMed] [Google Scholar]
- Thelen DG, Schultz AB, Fassois SD, Ashtonmiller JA. Identification of Dynamic Myoelectric Signal-to-Force Models during Isometric Lumbar Muscle Contractions. Journal of biomechanics. 1994;27:907–919. doi: 10.1016/0021-9290(94)90263-1. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Cheung VCK, d'Avella A. Matrix factorization algorithms for the identification of muscle synergies: Evaluation on simulated and experimental data sets. Journal of neurophysiology. 2006;95:2199–2212. doi: 10.1152/jn.00222.2005. [DOI] [PubMed] [Google Scholar]
- Walter JP, Kinney AL, Banks SA, D'Lima DD, Besier TF, Lloyd DG, Fregly BJ. Muscle synergies may improve optimization prediction of knee contact forces during walking. Journal of biomechanical engineering. 2014;136:021031. doi: 10.1115/1.4026428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winby CR, Gerus P, Kirk TB, Lloyd DG. Correlation between EMG-based coactivation measures and medial and lateral compartment loads of the knee during gait. Clinical biomechanics (Bristol, Avon) 2013 doi: 10.1016/j.clinbiomech.2013.09.006. [DOI] [PubMed] [Google Scholar]
- Winby CR, Lloyd DG, Besier TF, Kirk TB. Muscle and external load contribution to knee joint contact loads during normal gait. Journal of biomechanics. 2009;42:2294–2300. doi: 10.1016/j.jbiomech.2009.06.019. [DOI] [PubMed] [Google Scholar]
- Winby CR, Lloyd DG, Kirk TB. Evaluation of different analytical methods for subject-specific scaling of musculotendon parameters. Journal of biomechanics. 2008;41:1682–1688. doi: 10.1016/j.jbiomech.2008.03.008. [DOI] [PubMed] [Google Scholar]