Abstract
In mammals, a network of coupled neurons within the hypothalamus coordinates physiological rhythms with daily changes in the environment. In each neuron, delayed negative transcriptional feedbacks generate oscillations, albeit noisy and unreliable ones. Coupling mediated by diffusible neuropeptides lends precision and robustness to circadian rhythms. The double knockout of Cryptochrome Cry turns adult mice arrhythmic. But, remarkably, double knockout neonates continue to show robust oscillation much like wild-type neonates and appear to lose rhythmicity with development. We study quantitatively dispersed neurons and brain slices from wild-type and Cry double knockout mice to understand the links between single cell rhythmicity and intercellular coupling. We quantify oscillator properties of dispersed cells using nonlinear regression and study bifurcations diagrams of network models. We find that varying just three parameters—oscillator strength, strength of coupling, and timing of coupling—can reproduce experimentally observed features. In particular, modeling reveals that minor changes in timing of coupling can destroy synchronization as observed in adult slices from knockout mice.
Introduction
A network of neurons in the suprachiasmatic nucleus (SCN) in the brain is primarily responsible for orchestrating temporal organization of most physiological processes in mammals (1). Using light inputs from the retina, this master circadian timekeeper adapts to diurnal and seasonal environmental changes (2). The network lends precision (3) and robustness (4) against certain genetic perturbations to this collection of ∼20,000 noisy neuronal oscillators. The rhythms in gene transcription and firing in each neuron are generated by a delayed negative feedback involving certain clock genes, whose protein products repress their own transcription. It was, therefore, understood that clock genes accounted for rhythmicity in each neuron, while the intercellular signaling mediated by diffusible neuropeptides (5, 6, 7), synapses (8), and gap junctions worked to synchronize the network.
However, a recent study (9) revealed that a double knockout of clock genes, Cry1 and Cry2, disrupted synchrony in adult mice, while maintaining rhythmicity in single neurons. Remarkably, neonatal double knockout mice showed robust synchronized rhythms that appeared to deteriorate with development. These results question the current theory on the essential mechanisms necessary to achieve synchrony in the SCN, and leave the relative roles of single cell rhythmicity and intercellular coupling open. We address this question by comparing SCNs from Cry1,2 knockout background (10) against wild-type (WT) SCN using an oscillator network modeling approach.
Modeling can help to identify generic mechanisms of synchronization from a wide variety of experimental data ranging from dispersed single cells and neonatal and adult SCN slice cultures, to perturbation of coupling and restoration of rhythm by coculturing. Date analysis highlights the high degree of heterogeneity in the periods, amplitudes, and degree of synchronization of different neurons within the SCN. Here, we study quantitatively six types of datasets: WT SCN (dispersed cells, neonatal and adult slices) and Cry double knockout (dispersed cells, neonatal and adult slices). Furthermore we perturb synchronization pharmacologically using TTX (tetrodotoxin). We find that the diversity of empirically observed behaviors can be reproduced in simulations by varying only three parameters. In addition, we can classify SCNs as strong and weak based on how easily they are synchronized to a global signal (11). Finally, we show that the timing of coupling is essential and provides a likely explanation of the changes in synchrony during development.
Materials and Methods
Animals
Cry double-deficient (Cry1−/−Cry2−/−) mice were bred with PER2::LUC mice carrying a PER2 luciferase reporter (12). WT (Cry1+/+Cry2+/+) PER2::LUC transgenic mice on the C57BL/6J background were used as the control. Mice were reared in the animal quarters in Hokkaido University where environmental conditions were controlled (lights-on, 6–18 h; light intensity, ∼100 l× at the bottom of cage; humidity, 60 ± 10%). Experiments were conducted in compliance with the rules and regulations established by the Animal Care and Use Committee of Hokkaido University.
SCN slice and dispersed cell culture
For measurement of PER2::LUC bioluminescence from a cultured SCN slice, mice of 8–16 weeks or 2–5 days old kept under light-dark (LD) conditions were euthanized between 8 and 16 h by cervical dislocation and decapitated. The brain was rapidly removed and a coronal SCN slice of 100-μm thick for adults and 200 μm thick for neonates was made by a DTK-1000 D.S.K. microslicer (Dosaka EM, Kyoto, Japan) and a McIlwain tissue chopper (Ted Pella, Redding, CA), respectively. The brain slice containing the middle portion of the SCN was selected and trimmed ∼2 × 2 mm square. The slice was cultured in air at 36.5°C with 1.2 mL Dulbecco’s modified Eagle’s medium (Invitrogen, Carlsbad, CA) with 0.2 mM D-luciferin K and 5% supplement solution, the composition of which was described previously in Ono et al. (9).
For the measurement of PER2::LUC from dispersed SCN cells, the SCNs from 4 to 8 neonatal pups (2–5 days old) were dissected from hypothalamic slices of 400-μm thick and dissociated using trypsin. Dispersed cells were plated on a 35-mm Petri dish precoated with 0.01% poly-L-ornithine. The cell density was 1100 ± 500 cells/mm2. Medium composition was the same as that for slice culture, except for 5% fetal bovine serum in dispersed cell culture.
Bioluminescence imaging
Bioluminescence at the SCN cell level in cultured slices or in dispersed cells was obtained by a DM IRB (Leica Microsystems, Wetzlar, Germany), a Luminoview 200 (Olympus, Melville, NY), or a Cellgraph (Atto, Tokyo, Japan) equipped with an electron-multiplying charge-coupled device camera cooled at −80°C. Bioluminescence was measured every 60 min with an exposure time of 59 min for 7–14 days. The pixel size was 2.3 × 2.3 μm for the DM IRB, 2.0 × 2.0 μm for the Luminoview 200 (Olympus), and 1.6 × 1.6 μm for the Cellgraph (Atto). Bioluminescence signals were analyzed in terms of a region of interest (ROI). The mean area of a single ROI was ∼100 μm2, almost equivalent to the size of a single SCN cell. The intensity of bioluminescence was expressed as an average intensity of pixels involved in a ROI.
Actogram
Wheel-running activity was measured in a cage with a running-wheel (10 cm in diameter). Mice were individually housed in a polycarbonate cage placed in a light-proof box where environmental conditions were the same as in the animal quarters except for the light intensity in the light phase s (∼300 1 ×). Wheel revolutions were fed into a computer every 1 min by computer software (The Chronobiology Kit; Stanford Software Systems, Stanford, CA).
Parameter estimation of single cell models
As a generic model for self-sustained oscillators, we introduce the following stochastic amplitude-phase oscillator (13):
| (1) |
| (2) |
The system is described in polar coordinates of radius r and angle φ, and has a limit cycle with amplitude A and frequency ω. Any perturbation away from the limit cycle will relax back with a damping rate λ. The model has two noise intensities, one for amplitude fluctuations (〈ξr〉 = 0, 〈ξr (t + τ)ξr (t)〉 = 2Drδ(τ)) and the other for phase noise (〈ξφ〉 = 0, 〈ξφ (t + τ)ξφ (t)〉 = 2Dφδ(τ)). This model provides one of the simplest mathematical systems to generate limit cycle oscillations. Winfree (14) has studied this model in the context of circadian rhythms. It has been shown analytically that the stochastic system has an autocorrelation function in the following form (13):
| (3) |
The single cell model has five unknown parameters {A, ω, λ, Dr, Dφ} to be fitted to a dispersed cell culture data. The data fitting is performed as follows. First, the bioluminescence signal was detrended using a least-square fitting of a second-degree polynomial. The polynomial was then subtracted from the signal and the signal was mean centered. Next, the autocorrelation function was calculated from the detrended bioluminescence signal. We used only 40% of the autocorrelations representing the shortest time lags, because estimates of autocorrelations for larger time lags become poor. Then, the five parameters were optimized so that the autocorrelation function (Eq. 3) of the single cell model is fitted to that of the bioluminescence signal. We used the lsqcurvefit subroutine of the MATLAB Statistical Toolbox (The MathWorks, Natick, MA) to optimize the parameters. It should be noted that the fitting of Eq. 3 is an ill-conditioned problem, because the function involves a summation of two exponentials. To avoid misfitting, initial guesses are used as described in detail in Westermark et al. (13). From the estimated parameters, the coefficient of variation (CV = σr/A = ) can be computed, which represents the ratio of the standard deviation of the amplitude fluctuations to the fit amplitude of a single cell oscillator. Note that the amplitude fluctuations can be directly computed as a function of the fitted parameters. Detailed steps of the parameter estimation, e.g., detrended bioluminescence signals, fitted autocorrelation functions, and simulated cellular signals, are shown in Fig. S1 in the Supporting Material. The effect of detrending on the estimation results is examined in Fig. S2.
Coupled amplitude-phase oscillators
We constructed a cellular network model of the SCN by coupling the amplitude-phase oscillators that were fitted previously to the single cell data. By studying synchronization property of the cellular network, we examined whether the dynamical characteristics of slice data can be reproduced. The single cell amplitude-phase model of Eqs. 1 and 2 was first transformed to Cartesian (x,y) coordinates (see Eqs. S1 and S2), whereupon interneuronal connections were introduced through x and y variables to obtain a network of SCN cells,
| (4) |
| (5) |
where xi and yi represent dynamical variables of the ith cell (i = 1, 2,…, N), ξx,i and ξy,i are independent Gaussian noises, and . Ai, ωi, and λi are the parameters estimated previously. A global and diffusive coupling K with a coupling delay ψ is introduced with mean field coupling and .
The degree of synchrony was quantified by means of the synchronization index R,
| (6) |
where 〈⋅⋅⋅〉 denotes the average over time, and is the average of the variable of interest among oscillators.
Network model of biochemical oscillators
To evaluate the generality of our results beyond a network of coupled amplitude-phase oscillators, we constructed a network of more detailed biomechanical oscillators describing the individual cellular rhythms. We slightly modified a previously published model of coupled circadian oscillators that was used to study synchronization-induced rhythmicity (15). The intracellular model is composed of transcriptional/translational feedback loops of the core clock genes in the mammalian circadian system (16). The intercellular coupling in the SCN network is considered to be due to the circadian release of a neuropeptide. It is also assumed (15) that the release of the neuropeptide is induced quickly after the cytosolic PER/CRY protein complex. In the connected cells, the neuropeptide activates a signaling cascade of PKA and CREB, which then leads to activation of Per/Cry mRNA transcription. The dynamics of the single-cell oscillator is described by the following set of differential equations:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
The nonlinear transcription functions are given by
| (17) |
| (18) |
The variables represent the following species: Y1, Per/Cry mRNA; Y2, PER/CRY cytosolic complex; Y3, nuclear PER/CRY complex; Y4, Bmal1 mRNA; Y5, cytosolic BMAL1; Y6, nuclear BMAL1; Y7, transcriptionally active BMAL1∗; V, neuropeptide; X1, PKA; and X2, CREB.
Parameter configurations in biochemical models are usually not known in detail. To cope with such ambiguity, parameter values for the single cell model were chosen from two published studies: one as a model of a self-sustained oscillator (16) and the other as a model of a damped oscillator (15). There two parameter sets varied only in the parameters representing P = {p, k2t, k4b, k1d, k2d, k3d, k4d, k5d, k6d, k7d} and the corresponding parameter values are termed P1 for the self-sustained oscillator (16) and P2 for the damped oscillator (15) with values listed in Table S2. The remaining model parameters were held at fixed values listed in Table S3.
By introducing a parameter representing oscillator strength α (0 ≤ α ≤ 1) that linearly interpolates between the two oscillatory regimes as
| (19) |
we simulate the effect of Cry1 and Cry2 double deficiency. The cells of knockout mice can be characterized by α = 0, which gives rise to a strongly damped oscillation. On the other hand, a larger value of α leads to a regime of self-sustained oscillation (see Fig. S4 a). It should be noted that there is no direct biochemical interpretation of the parameter variation of α, because the intracellular models are not quantitative in all details.
To simulate a network of N cellular oscillators, the single cell model was replicated N times (for readability, the indices i = 1,…,N for X and Y variables were omitted). To add heterogeneity, each set of equations is scaled by a factor ei = 0.92/gi to generate a distribution of periods, where gi is generated from a Gaussian distribution centered at 1 with a standard deviation of 0.05. This 5% period spread was arrived at as a consensus of our estimated period variability from single cell analysis and several published estimates (3, 17, 18).
The coupling function Q, which activates two-step signaling cascade leading to Per/Cry mRNA transcription, is given by Q = KF(t − ψ), where F is a mean field of the neuropeptide, K determines the coupling strength, and ψ represents the coupling delay. As an average concentration of the neuropeptide released by the SCN cells, the mean field is given by . Among a variety of SCN network topologies that have been considered (15, 19, 20, 21, 22), only the case of global coupling was considered as the simplest yet reasonable representation based on the globally diffusive nature of the neuropeptide.
To take into account the effect of molecular noise, stochastic dynamics of the circadian system was simulated based on the chemical Langevin equation (23).The light input was simulated by the following clipped sine wave,
| (20) |
where L0 is the Zeitgeber intensity and T is the Zeitgeber period.
Results
Oscillator network modeling requires appropriate single cell models (16, 24, 25) together with reasonable assumptions on network topology and coupling mechanisms (15, 26, 27). As a first step, we extract from the dispersed cell cultures single cell parameters (periods, amplitudes, and noise strength) using regression analysis. The distributions of these single cell parameters allow suitable parameterization of previously published gene regulatory network models. WT cells are identified as self-sustained oscillators, whereas Cry1−/−/Cry2−/− cells are well represented by noise-driven damped oscillators. By comprehensively varying coupling strength and coupling delay, we can specify parameter regions with synchronized rhythms. It turns out that varying just three parameters—oscillator strength α, coupling strength K, and coupling delay ψ—can reproduce experimentally observed features. Next, we describe our results in detail.
Extracting single cell parameters
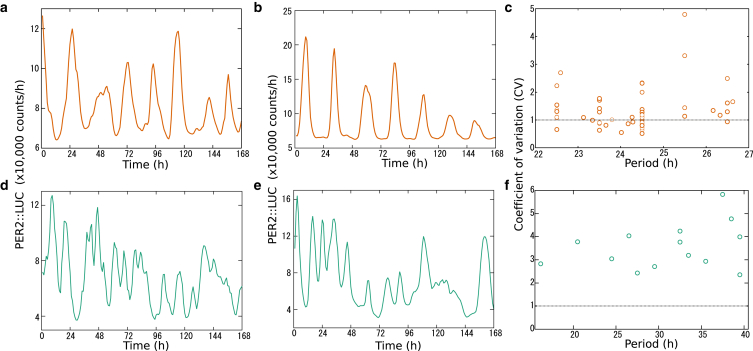
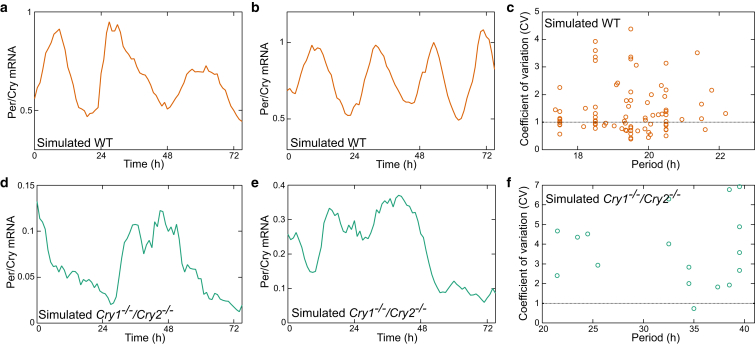
Data for single cell parameter estimation was drawn from PER2::LUC bioluminescence recordings of plated SCN slices as described in Nakamura et al. (28) (see Materials and Methods). In total, we analyzed N = 74 WT cells and N = 48 cells from double knockout Cry1−/−/Cry2−/− mice, each measured every 60 min for 7–14 days (Figs. 1, S8, and S9). Using nonlinear regression, introduced by Westermark et al. (13) and outlined in the Materials and Methods, we estimated for each cell a period T, amplitude A, relaxation rate λ, and fluctuation strength Dr by fitting a stochastic amplitude-phase model. Representative traces of the fits to individual cells and their reproduction by our stochastic model are shown in Fig. S1. N = 66 WT cells and N = 14 knockout Cry1−/−/Cry2−/− cells fit the model reasonably well. Of particular interest is the coefficient of variation (CV) representing fluctuations in the amplitude relative to the mean amplitude. For CV > 1, the associated stationary probability densities are unimodal and the cells can be regarded as noise-driven damped oscillators (13).
Figure 1.
Analysis of oscillations in dispersed SCN cell cultures. Sample bioluminescence traces from dispersed SCN cell culture from WT (a and b) and knockout (Cry1−/−/Cry2−/−) mice (d and e). Single cell analyses of biolumninescene traces from dispersed cell culture of WT (N = 66) (c) and knockout (N = 14) SCNs (f). Abscissa and ordinate represent estimated period and coefficient of variation CV, respectively. To see this figure in color, go online.
Fig. 1 and Table 1 show key results of our regression: the periods of WT cells center at ∼24 h and almost half of them exhibit CV < 1. This implies that these cells are relatively reliable oscillators and can be classified theoretically as noisy limit-cycle oscillators. On the contrary, the estimated periods of Cry1−/−/Cry2−/− cells vary in the range from 20 to 40 h and all CV values exceed 1. Consequently, cells from knockout mice are much less reliable oscillators and can be regarded as noise-driven damped oscillators. These findings were robust to the use of raw or detrended bioluminescence data for single cell parameter estimation (see Fig. S2).
Table 1.
Results of the single cell analysis for dispersed culture data of WT (N = 74) and double knockout mice (Cry1−/−/Cry2−/−, N = 48)
| Mouse | Period (h) | Cells with CV < 1 (%) | |
|---|---|---|---|
| Experiment | WT | 24.3 ± 1.1 | 36.4 |
| Cry1−/−/Cry2−/− | 31.1 ± 7.3 | 0 | |
| Model | WT | 19.6 ± 1.6 | 39.5 |
| Cry1−/−/Cry2−/− | 32.7 ± 6.7 | 6.7 |
The estimated values are compared with those of the simulation data. Average and standard deviation of the estimated period T = 2π/ω are indicated and the percentage of rhythmic cells having a CV < 1 is shown.
In summary, there is a spectrum of oscillators from limit-cycle oscillators that are reliable and have continued rhythmicity without stimulation to damped oscillators that lose rhythm amplitude. This spectrum can be parameterized by the CV under our regression approach (13) and allows us to classify cells from different genotypes. These findings serve as constraints on more complex simulations of gene regulatory networks presented next.
Simulations of coupled amplitude-phase oscillators
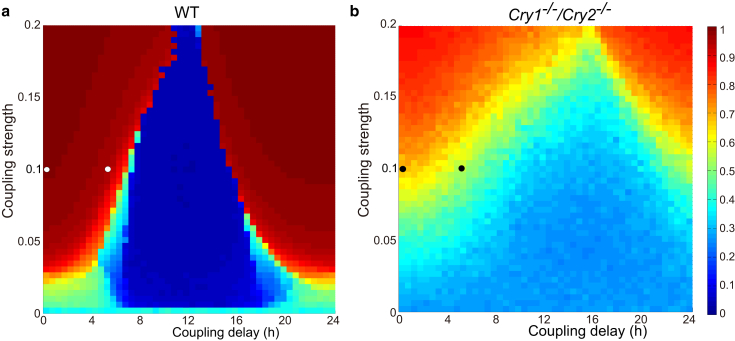
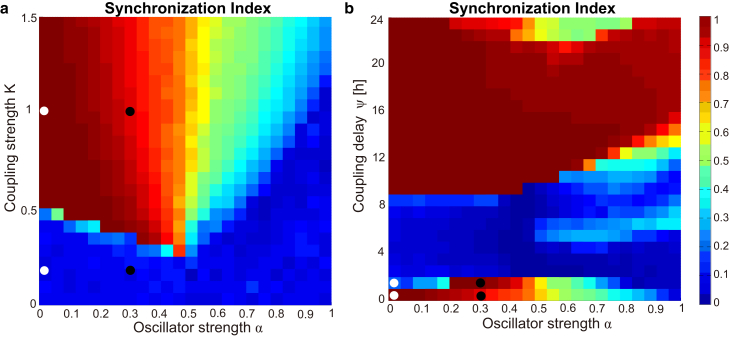
We next coupled the amplitude-phase oscillators fit to the dispersed cell data from the previous section according to Eqs. 4 and 5 to study the network dynamics of this simple SCN model. The network consisted of N = 66 and N = 14 parameterized cells with reasonable fits to dispersed cells in WT and double knockout Cry1−/−/Cry2−/− mice, respectively. Fig. 2 shows dependencies of the network synchrony on the coupling strength K and coupling delay ψ for WT and double knockout cell networks. For the coupled oscillators constructed from WT cells, synchrony clearly appears as the coupling strength is increased. Interestingly, the synchronization depends upon the coupling delay ψ. Although a small coupling delay enhances the synchronization, a medium coupling delay at ∼ψ = 12 h destroys the synchronization. It has been known in coupled phase oscillators that the effect of coupling can easily turn from attractive to repulsive by a coupling delay of half of the intrinsic period (29). The observed desynchrony can be understood as a result of such repulsive (or negative) coupling. A similar basic structure can be observed in the synchronization diagram of the network constructed from knockout cells (Fig. 2 b). Compared to the network of WT cells, the region of synchronization in the network of Cry1−/−/Cry2−/− cells is smaller and, moreover, the level of synchrony (measured by the synchronization index) is not as high even with a strong coupling and a small coupling delay. This is likely due to the increased heterogeneity and higher noise in the double knockout cells that therefore necessitate stronger coupling to induce global synchrony.
Figure 2.
Dependence of the synchronization index R of the coupled amplitude-phase model on the coupling strength K and coupling delay ψ. (Open and solid points) Where the simulated Cry1−/−/Cry2−/− and WT SCN mice in Fig. S3, respectively, lie. The models were parameterized using fits to dispersed WT (a) and Cry1−/−/Cry2−/− SCN cells (b). To see this figure in color, go online.
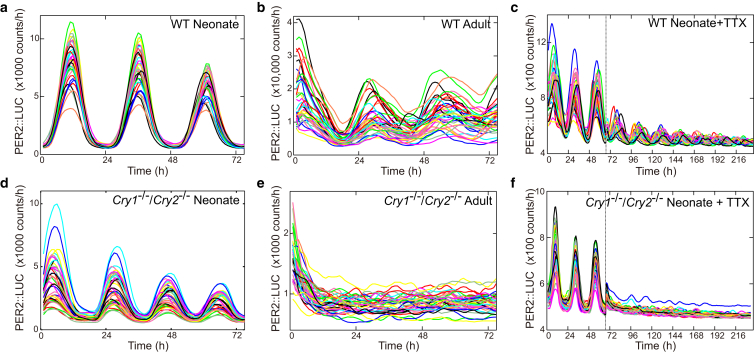
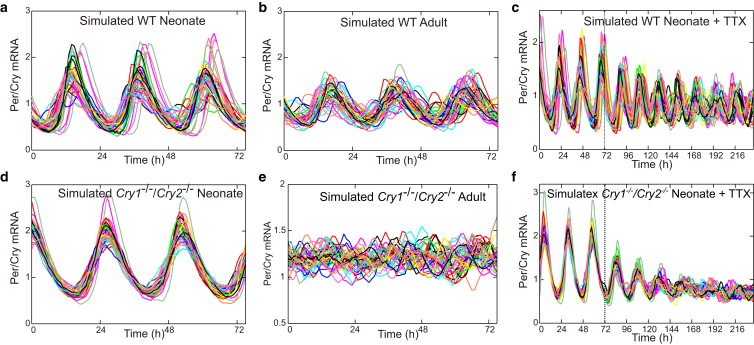
As a possible default situation for neonate slices, the coupling strength and delay were set as K = 0.1 and ψ = 0 h and for adult slice, the delay was increased to ψ = 5.5 h. Under these conditions, the model simulations (Fig. S3) capture essential features of the bioluminescence data seen later in Fig. 5. In other words, the coupling was strong enough to synchronize both WT and knockout cells in neonate slice. Introduction of the coupling delay of ψ = 5.5 h in the adult slice maintained the synchrony in the WT cells, whereas it destroyed the synchrony in the knockout cells. Next, administration of TTX to adult slice was simulated by reducing the coupling strength from K = 0.1 to 0.04 at time t = 72 h (see Fig. S3, c and f). Whereas the WT cells maintained the synchronized oscillations even after the TTX administration, the phases of the double knockout cells started to move apart from each other, resulting in desynchronized oscillations during TTX administration.
Figure 5.
Comparison of single cell bioluminescence signals from SCN slice culture across genotype, age, and pharmacological perturbation. Bioluminescence signals from SCN slice culture of WT mouse from neonate (a and c) and adult (b). (Dashed line in c) Timing at which TTX was administered to a neonate slice. The corresponding bioluminescent signal traces for the knockout mouse are shown in (d)–(f). To see this figure in color, go online.
Simulations of gene-regulatory circadian oscillators
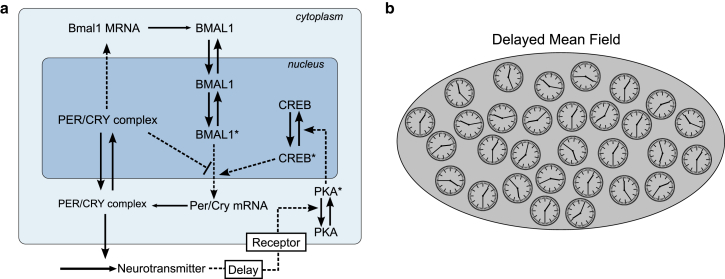
The simulations of coupled amplitude-phase oscillators revealed that coupling strength and delay have major effects on the synchronization properties of the network. Moreover, clear differences between WT and knockout mice were visible. Next, we examined whether these observations are valid also in a more detailed gene-regulatory network model developed in earlier studies (15, 16). The model is based on transcriptional-translational feedback loops involving the transcription factor BMAL1 and the PER/CRY complex (see Fig. 3 a). The effects of light input and coupling are included via the upregulation of transcription. It has been shown that the diffusible neuropeptide VIP plays an essential role in synchronizing SCN neurons (5, 7, 30). Therefore, we implemented global coupling of all SCN neurons in our model using a mean field representing the average neuropeptide level in the extracellular medium (Fig. 3 b).
Figure 3.
Schematic of the single cell oscillator and the coupled SCN network. (a) The intracellular model consists of transcriptional/translational feedback loops of clock genes, modified from Bernard et al. (15). Clock genes induce the release of a neuropeptide that acts as a coupling agent. Feedback of the neuropeptide activates PKA and CREB, leading to Per/Cry mRNA transcription. (b) The individual cellular oscillators are coupled through a mean field of the released neuropeptide in the intercellular medium with a time delay to account for different phases of neuropeptide release. To see this figure in color, go online.
To keep the number of adjusted parameters small, we introduce, in addition to the coupling strength and its delay, to our knowledge, a novel parameter α that characterizes the strength of an oscillator in the network. The gene-regulatory network model was originally developed to describe self-sustained single cell oscillations (16). A modified version was used subsequently to generate damped single cell oscillations (15). Our single cell analyses have shown that many WT cells exhibit self-sustained rhythms, whereas Cry1−/−/Cry2−/− appear to be damped. As a parameter to control such single cell property, the oscillator strength α interpolates between the two parameter sets published earlier (15, 16). The corresponding bifurcation diagram shows a smooth transition from damped to self-sustained oscillations in Fig. S4. For knockout cells, we chose α = 0 and for WT cells α = 0.3. The omnipresent molecular noise, for example, induced by transcriptional bursts (31), is taken into account by stochastic simulation based on the chemical Langevin equation (23).
We then examined ability of the resulting simulations in Fig. 4 to reproduce qualitatively the bioluminescence SCN dispersed cell data in Fig. 1. The simulated traces in Fig. 4 represent noisy signals with no clear periodicity as observed in the bioluminescence data. For a quantitative comparison of experimental data and simulations, we applied our nonlinear regression approach also to the simulated data. Table 1 and Fig. 4, c and f (compare Fig. 1, c and f), demonstrate that simulations reproduce the most essential properties of dispersed WT and knockout Cry1−/−/Cry2−/− SCN cells.
Figure 4.
Analysis of oscillations in simulated SCN dispersed cell cultures. Sample simulated signals for dispersed SCN cells from WT (a and b) (α = 0, K = 0.2, ψ = 0) and knockouts (d and e) (α = 0.3, K = 0.2, ψ = 0). Single cell characteristics of simulated dispersed cells for WT (c) and knockout (f) are shown. Abscissa and ordinate represent estimated period and coefficient of variation CV, respectively. To see this figure in color, go online.
Strength and timing of coupling control synchronization
Our SCN slice data from WT and Cry1−/−/Cry2−/− mice show different degrees of synchronization depending on the degree of development of the mice (see Figs. 5 and S10–S13 and Table S1). For example, neonatal knockout mice exhibit robust synchronization that deteriorates with development. To find possible explanations for this variability, we employ network simulations of our gene-regulatory model. We systematically vary the single cell oscillator strength α, coupling strength K, and its coupling delay ψ. The timing of coupling, parameterized by ψ, depends on the expression profiles of neuropeptides and their receptors. There are reports of oscillating levels of VIP and its receptor VPAC2 (32, 33). These observations suggest that intracellular regulation can control cell-to-cell coupling. Consequently, clock knockout mice or mice at different developmental stages might exhibit different coupling strengths and timing.
We quantify the degree of synchrony by the synchronization index R (see Eq. 6). Fig. 6, a and b and show the index R for comprehensive variations of the core model parameters α, K, and ψ. To clarify the regime of damped oscillations, periodicity is drawn for the same parameter variations in Fig. S5. Oscillator strength α and coupling parameters K and ψ have profound effects on the degree of synchronization, as observed for the amplitude-phase oscillator networks. Interestingly, damped single cell oscillators (small α) are particularly easy to synchronize with each other as described earlier (15, 26). As expected, large coupling strength K increases the synchronization index. More surprisingly, the timing of coupling described by ψ also has a very strong effect on synchronization, as shown in Ananthasubramaniam et al. (34).
Figure 6.
Oscillator synchrony in the simulated SCN for different choices of system parameters. (a) Dependence of the synchronization index R of the cellular network model on the oscillator strength α and coupling strength K. (Open and solid points) Conditions for simulating Cry1−/−/Cry2−/− and WT mice, respectively, in Fig. 7. (b) Dependence of the synchronization index R on single cell oscillator strength α and the coupling delay ψ (coupling strength was set to K = 1). To see this figure in color, go online.
We mark in Fig. 6, a and b, specific parameter configurations that reproduce qualitative experimental findings. That is, the simulated neonate WT and Cry1−/−/Cry2−/− network display synchrony, while on development to an adult, the WT network remains synchronous, whereas the double knockout is desynchronous. Oscillator strength α = 0.3 and α = 0 represent WT and double knockout mice, respectively. K = 1 describes slice data well, whereas very small K values, such as K = 0.2, mimic dispersed cultures better. While there is no evidence that coupling strength changes with development, preliminary data indicate that VIP expression profiles vary with age (32). Our simulations show that an increase of ψ from zero to 12 h can deteriorate synchronization.
Comparison of network simulations in Fig. 7 with experimental data presented in Fig. 5 demonstrate that by varying just three parameters—oscillator strength α, coupling strength K, and coupling delay ψ—we can mimic complex experimental findings.
Figure 7.
Comparison of SCN cellular network model across genotype, age, and pharmacological perturbation (corresponding to Fig. 5). (a–c) Simulated clock mRNA levels in the SCN network of WT mouse (α = 0.3, K = 1). (a and c) Neonates (ψ = 0); (b) adults (ψ = 1). (Dashed line in c) Time at which the coupling was lowered from K = 1 to K = 0.4 simulating administration of tetrodotoxin. (d–f) The corresponding clock mRNA levels in the SCN network of a Cry1−/−/Cry2−/− mouse (α = 0, K = 1). The neonate (ψ = 0) is shown in (d) and (f) and adults (ψ = 1) in (f). To see this figure in color, go online.
Weak oscillator networks have a wide entrainment range
So far, we studied synchronization in the absence of external LD cycles. Under natural conditions, Zeitgebers entrain endogenous circadian rhythms allowing adaptation to environmental cycles. Entrainment of WT mice is illustrated in Fig. 8 a. There is a precise onset of activity at the beginning of the dark phase. After release in continuous darkness (DD) the onset of activity is shifted to an earlier time every day, indicating an intrinsic period below 24 h.
Figure 8.
Comparison of behavioral rhythms in mice from both genotypes against simulated predictions. (a) Actogram of WT mouse, which was initially put under LD condition and then exposed to DD condition. (b) Actogram of knockout mouse (Cry1−/−/Cry2−/−), which was initially put under LD condition and then exposed to DD condition. (c) Simulated actogram corresponding to the WT mouse in (a). (d) Simulated actogram corresponding to the knockout mouse in (b). To see this figure in color, go online.
Interestingly, knockout mice can also be entrained by LD cycles (10, 35) as shown in Fig. 8 b. These features can be reproduced by our network simulation as illustrated in Fig. 8, c and d. The agreement of experiments and simulations is illustrated by periodograms in Figs. S6 and S7.
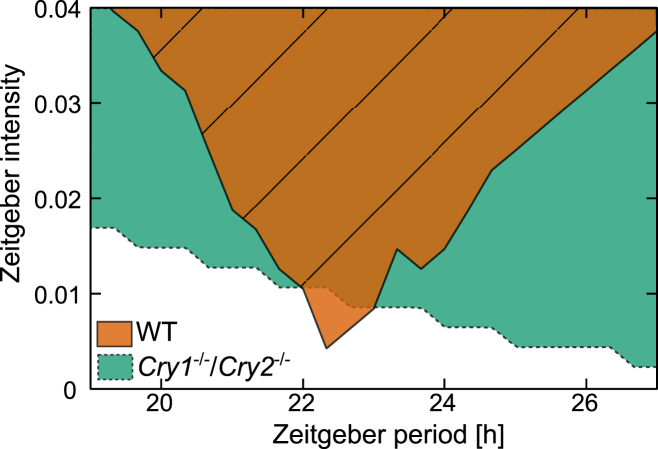
It was suggested in the preceding section that adult Cry1−/−/Cry2−/− mice have impaired coupling. It has been shown previously (36) that weak coupling increases the range of entrainment, i.e., the range of external periods to which entrainment can be achieved. Fig. 9 demonstrates that our network simulations of knockout mice have indeed a much larger range of entrainment. These modeling results have been confirmed by experimental observations (37). Consequently, the SCN of knockouts can be regarded as a weak oscillator (see Granada et al. (11) for mathematical classifications of weak and strong oscillators), which is characterized by a large range of entrainment.
Figure 9.
Dependence of the entrainment range of the network model to Zeitgeber parameters. The combinations of Zeitgeber period T and intensity L0 for which the network model entrains to the Zeitgeber is shown for WT and Cry1−/−/Cry2−/−. To see this figure in color, go online.
Discussion
Our study was motivated by the inability of current theories based on compartmentalized mechanisms for rhythm generation and intercellular coupling to explain the complex phenotypes displayed by dispersed cells and SCN slices in WT and knockout mice. In particular, the robust synchronous rhythms of neonatal slices with disrupted rhythm generation components in Cry1−/−/Cry2−/− mice and the subsequent loss of synchrony in adult slices, while maintaining single cell rhythms, was difficult to interpret. Our data-driven modeling connects rhythmicity of single cells to synchronous rhythms in a population of cells via intercellular coupling.
As a starting point, we applied regression techniques based on Westermark et al. (13) to dispersed neurons from WT and double knockout mice from Ono et al. (9). We thus quantified cellular oscillators from different genotypes as damped or self-sustained based on rhythm regularities. Consistent with earlier analyses (13, 18, 38) using different data, we concluded that there are, in fact, a continuum of single cell oscillator characteristics between self-sustained and damped oscillators. These results guided our parameter determination in more complex models capable of connecting single cell rhythmicity and the release of coupling agents, such as the neuropeptide VIP, to the SCN network.
Because single cell data do not support a strict classification into damped and self-sustained oscillators, we varied systematically a system parameter α quantifying the strength of the single cell oscillators. This allowed us to distinguish weak oscillators and strong oscillators along the lines of Granada et al. (11) and Abraham et al. (36). Interestingly, damped oscillators that are considered weak can be more easily synchronized and exhibit wide entrainment ranges. Varying coupling strength K and coupling delay ψ in a network with reasonable single cell characteristics, we find that both parameters govern the synchrony of the network. Even minor changes in timing of the neuropeptide release led to complete loss of synchrony. Our findings allowed us to reproduce the complexity of observations by varying just three parameters: oscillator strength α, coupling strength K, and coupling delay ψ. Because both coupled amplitude-phase oscillators and coupled gene regulatory oscillators showed essentially the same results, our findings appeared to be model-independent.
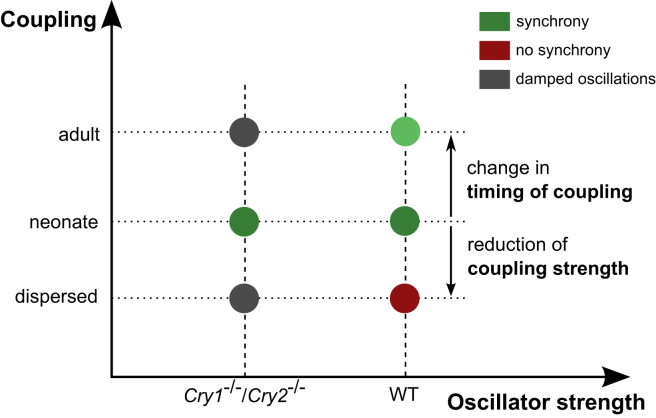
In particular, our results suggest that the observed loss of synchrony from neonates to adults in knockout mice can be explained by changes in just these three system properties. As seen in Fig. 10, the experimental data (WT versus Cry1−/−/Cry2−/−, neonate versus adult, dispersed cells versus slice culture) can be located in a space spanned by the three parameters. Our data-driven analysis showed that the strength of oscillators is weaker in knockout than in WT mice. Reduction of the coupling strength in slices produced desynchronized oscillators as observed in dispersed cells (compare Fig. 4 and Fig. 6 a). While the amplitude and period of the SCN appears to change with age (39), there is no direct evidence of implicating changes in strength of coupling.
Figure 10.
Schematic illustration of the mechanism of coupling-induced rhythmicity. Abscissa represents system parameter that controls the single oscillator properties (WT versus knockout). Ordinate represents developmental stage (adult versus neonate), in which the coupling properties (e.g., coupling strength K or coupling delay ψ) are changed. To see this figure in color, go online.
A novel model-based suggestion is that the coupling delay (or timing of coupling) ψ changes with age. Along with changes in the timing of neuropeptide release with age, knockout of two core clock components Cry1,2 possibly affects the phase of neuropeptide release, which is under clock control (40). Therefore, the knockout SCN having weak single oscillators is severely disrupted with development, whereas the WT is not. There is indeed evidence in rats that shows that circadian phase of VIP mRNA changes with age (32).
This hypothesis is the explanation of other counterintuitive observations described recently in Evans et al. (41). Many studies suggest that GABA acts in the SCN as a desynchronizer opposing the synchronization via VIP and gap junctions (42). However, in the case of SCN regions being out of phase, GABA contributes to resynchronization (41). A plausible explanation of these seemingly contradictory facts might be the distinct phase of GABA release.
Network simulations discussed in this article provide a framework to integrate details of intracellular dynamics with coupling mechanisms including relative timing of coupling. The predicted phenotype with a small change in the timing of coupling points to the need for empirically measuring the timing (or phase) of important coupling agents, such as VIP and AVP, under in vitro or in vivo conditions in both neonates and adults, building on the work of Ban et al. (32). Moreover, this marked phenotype might cause the timing to be evolutionarily selected. Based on the predicted role of timing of coupling, we propose experimental investigation of the effect of time-of-day dependent perturbation of coupling agents and their receptors. Finally, circadian changes in coupling might play a role in seasonal adaptation of the circadian system (20, 43, 44) and tuning the phase angle of entrainment (11, 45).
Author Contributions
H.P.H., B.A., I.T.T., S.H., and K.I.H. designed the study; D.O. performed the experiments; I.T.T. analyzed the data and simulated models; and I.T.T., B.A., D.O., and H.P.H. wrote the text.
Acknowledgments
The authors thank Ute Abraham, Pål Westermark, and Grigory Bordyugov for useful discussions on the analysis of data and model development.
The authors acknowledge financial support from the Deutsches Forschungsgemeinschaft (DFG SPP InKomBio), the Bernstein Center for Computational Neuroscience Berlin (grant No. 01GQ1001C), the Alexander von Humboldt Foundation (research fellowships), the Japan Society for the Promotion of Science (Outline of Grants-in-Aid for Scientific Research KAKENHI grant Nos. 20249010, 24390055, and 24890001), and the Ministry of Education, Culture, Sports, Science and Technology of Japan (Creation of Innovation Centers for Advanced Interdisciplinary Research Areas Program).
Editor: Ewa Paluch.
Footnotes
Isao T. Tokuda, Daisuke Ono, and Bharath Ananthasubramaniam contributed equally to this work.
Supporting Materials and Methods, thirteen figures, and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00995-9.
Supporting Citations
References (46, 47) appear in the Supporting Material.
Supporting Material
References
- 1.Welsh D.K., Takahashi J.S., Kay S.A. Suprachiasmatic nucleus: cell autonomy and network properties. Annu. Rev. Physiol. 2010;72:551–577. doi: 10.1146/annurev-physiol-021909-135919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Herzog E.D. Neurons and networks in daily rhythms. Nat. Rev. Neurosci. 2007;8:790–802. doi: 10.1038/nrn2215. [DOI] [PubMed] [Google Scholar]
- 3.Herzog E.D., Aton S.J., Tei H. Temporal precision in the mammalian circadian system: a reliable clock from less reliable neurons. J. Biol. Rhythms. 2004;19:35–46. doi: 10.1177/0748730403260776. [DOI] [PubMed] [Google Scholar]
- 4.Liu A.C., Welsh D.K., Kay S.A. Intercellular coupling confers robustness against mutations in the SCN circadian clock network. Cell. 2007;129:605–616. doi: 10.1016/j.cell.2007.02.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Aton S.J., Colwell C.S., Herzog E.D. Vasoactive intestinal polypeptide mediates circadian rhythmicity and synchrony in mammalian clock neurons. Nat. Neurosci. 2005;8:476–483. doi: 10.1038/nn1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maywood E.S., Reddy A.B., Hastings M.H. Synchronization and maintenance of timekeeping in suprachiasmatic circadian clock cells by neuropeptidergic signaling. Curr. Biol. 2006;16:599–605. doi: 10.1016/j.cub.2006.02.023. [DOI] [PubMed] [Google Scholar]
- 7.Maywood E.S., Chesham J.E., Hastings M.H. A diversity of paracrine signals sustains molecular circadian cycling in suprachiasmatic nucleus circuits. Proc. Natl. Acad. Sci. USA. 2011;108:14306–14311. doi: 10.1073/pnas.1101767108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yamaguchi S., Isejima H., Okamura H. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science. 2003;302:1408–1412. doi: 10.1126/science.1089287. [DOI] [PubMed] [Google Scholar]
- 9.Ono D., Honma S., Honma K. Cryptochromes are critical for the development of coherent circadian rhythms in the mouse suprachiasmatic nucleus. Nat. Commun. 2013;4:1666. doi: 10.1038/ncomms2670. [DOI] [PubMed] [Google Scholar]
- 10.van der Horst G.T., Muijtjens M., Yasui A. Mammalian Cry1 and Cry2 are essential for maintenance of circadian rhythms. Nature. 1999;398:627–630. doi: 10.1038/19323. [DOI] [PubMed] [Google Scholar]
- 11.Granada A.E., Bordyugov G., Herzel H. Human chronotypes from a theoretical perspective. PLoS One. 2013;8:e59464. doi: 10.1371/journal.pone.0059464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yoo S.-H., Yamazaki S., Takahashi J.S. PERIOD2:LUCIFERASE real-time reporting of circadian dynamics reveals persistent circadian oscillations in mouse peripheral tissues. Proc. Natl. Acad. Sci. USA. 2004;101:5339–5346. doi: 10.1073/pnas.0308709101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Westermark P.O., Welsh D.K., Herzel H. Quantification of circadian rhythms in single cells. PLOS Comput. Biol. 2009;5:e1000580. doi: 10.1371/journal.pcbi.1000580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Winfree A.T. Springer; New York: 2001. The Geometry of Biological Time. [Google Scholar]
- 15.Bernard S., Gonze D., Kramer A. Synchronization-induced rhythmicity of circadian oscillators in the suprachiasmatic nucleus. PLOS Comput. Biol. 2007;3:e68. doi: 10.1371/journal.pcbi.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Becker-Weimann S., Wolf J., Kramer A. Modeling feedback loops of the mammalian circadian oscillator. Biophys. J. 2004;87:3023–3034. doi: 10.1529/biophysj.104.040824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Welsh D.K., Logothetis D.E., Reppert S.M. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron. 1995;14:697–706. doi: 10.1016/0896-6273(95)90214-7. [DOI] [PubMed] [Google Scholar]
- 18.Webb A.B., Angelo N., Herzog E.D. Intrinsic, nondeterministic circadian rhythm generation in identified mammalian neurons. Proc. Natl. Acad. Sci. USA. 2009;106:16493–16498. doi: 10.1073/pnas.0902768106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fukuda H., Tokuda I., Hayasaka N. Quantitative analysis of phase wave of gene expression in the mammalian central circadian clock network. PLoS One. 2011;6:e23568. doi: 10.1371/journal.pone.0023568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bodenstein C., Gosak M., Perc M. Modeling the seasonal adaptation of circadian clocks by changes in the network structure of the suprachiasmatic nucleus. PLOS Comput. Biol. 2012;8:e1002697. doi: 10.1371/journal.pcbi.1002697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hafner M., Koeppl H., Gonze D. Effect of network architecture on synchronization and entrainment properties of the circadian oscillations in the suprachiasmatic nucleus. PLOS Comput. Biol. 2012;8:e1002419. doi: 10.1371/journal.pcbi.1002419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vasalou C., Herzog E.D., Henson M.A. Small-world network models of intercellular coupling predict enhanced synchronization in the suprachiasmatic nucleus. J. Biol. Rhythms. 2009;24:243–254. doi: 10.1177/0748730409333220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gillespie D.T. The chemical Langevin equation. J. Chem. Phys. 2000;113:297–306. [Google Scholar]
- 24.Leloup J.-C., Goldbeter A. Toward a detailed computational model for the mammalian circadian clock. Proc. Natl. Acad. Sci. USA. 2003;100:7051–7056. doi: 10.1073/pnas.1132112100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Forger D.B., Peskin C.S. A detailed predictive model of the mammalian circadian clock. Proc. Natl. Acad. Sci. USA. 2003;100:14806–14811. doi: 10.1073/pnas.2036281100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gonze D., Bernard S., Herzel H. Spontaneous synchronization of coupled circadian oscillators. Biophys. J. 2005;89:120–129. doi: 10.1529/biophysj.104.058388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.To T.-L., Henson M.A., Doyle F.J., 3rd A molecular model for intercellular synchronization in the mammalian circadian clock. Biophys. J. 2007;92:3792–3803. doi: 10.1529/biophysj.106.094086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nakamura W., Honma S., Honma K. Clock mutation lengthens the circadian period without damping rhythms in individual SCN neurons. Nat. Neurosci. 2002;5:399–400. doi: 10.1038/nn843. [DOI] [PubMed] [Google Scholar]
- 29.Kuramoto Y. Springer; Berlin, Germany: 1984. Chemical Oscillations, Waves, and Turbulence. [Google Scholar]
- 30.Reed H.E., Meyer-Spasche A., Piggins H.D. Vasoactive intestinal polypeptide (VIP) phase-shifts the rat suprachiasmatic nucleus clock in vitro. Eur. J. Neurosci. 2001;13:839–843. doi: 10.1046/j.0953-816x.2000.01437.x. [DOI] [PubMed] [Google Scholar]
- 31.Suter D.M., Molina N., Naef F. Mammalian genes are transcribed with widely different bursting kinetics. Science. 2011;332:472–474. doi: 10.1126/science.1198817. [DOI] [PubMed] [Google Scholar]
- 32.Ban Y., Shigeyoshi Y., Okamura H. Development of vasoactive intestinal peptide mRNA rhythm in the rat suprachiasmatic nucleus. J. Neurosci. 1997;17:3920–3931. doi: 10.1523/JNEUROSCI.17-10-03920.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.An S., Tsai C., Herzog E.D. Spatiotemporal distribution of vasoactive intestinal polypeptide receptor 2 in mouse suprachiasmatic nucleus. J. Comp. Neurol. 2012;520:2730–2741. doi: 10.1002/cne.23078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ananthasubramaniam B., Herzog E.D., Herzel H. Timing of neuropeptide coupling determines synchrony and entrainment in the mammalian circadian clock. PLOS Comput. Biol. 2014;10:e1003565. doi: 10.1371/journal.pcbi.1003565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ono D., Honma S., Honma K. Postnatal constant light compensates Cryptochrome1 and 2 double deficiency for disruption of circadian behavioral rhythms in mice under constant dark. PLoS One. 2013;8:e80615. doi: 10.1371/journal.pone.0080615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Abraham U., Granada A.E., Herzel H. Coupling governs entrainment range of circadian clocks. Mol. Syst. Biol. 2010;6:438. doi: 10.1038/msb.2010.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Honma S., Ono D., Honma K. Cellular oscillators in the suprachiasmatic nucleus for behavior rhythm expression in the mouse lacking cryptochrome. In: Honma K., editor. Dynamics of Circadian Oscillation in the SCN. Hokkaido University Press; Sapporo, Hokkaido, Japan: 2014. pp. 85–96. [Google Scholar]
- 38.Rougemont J., Naef F. Dynamical signatures of cellular fluctuations and oscillator stability in peripheral circadian clocks. Mol. Syst. Biol. 2007;3:93. doi: 10.1038/msb4100130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yamazaki S., Straume M., Block G.D. Effects of aging on central and peripheral mammalian clocks. Proc. Natl. Acad. Sci. USA. 2002;99:10801–10806. doi: 10.1073/pnas.152318499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shinohara K., Honma S., Honma K. Circadian rhythms in the release of vasoactive intestinal polypeptide and arginine-vasopressin in organotypic slice culture of rat suprachiasmatic nucleus. Neurosci. Lett. 1994;170:183–186. doi: 10.1016/0304-3940(94)90269-0. [DOI] [PubMed] [Google Scholar]
- 41.Evans J.A., Leise T.L., Davidson A.J. Dynamic interactions mediated by nonredundant signaling mechanisms couple circadian clock neurons. Neuron. 2013;80:973–983. doi: 10.1016/j.neuron.2013.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Freeman G.M., Jr., Krock R.M., Herzog E.D. GABA networks destabilize genetic oscillations in the circadian pacemaker. Neuron. 2013;78:799–806. doi: 10.1016/j.neuron.2013.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pfeuty B., Thommen Q., Lefranc M. Circadian clocks in changing weather and seasons: lessons from the picoalga Ostreococcus tauri. BioEssays. 2012;34:781–790. doi: 10.1002/bies.201200012. [DOI] [PubMed] [Google Scholar]
- 44.Azzi A., Dallmann R., Brown S.A. Circadian behavior is light-reprogrammed by plastic DNA methylation. Nat. Neurosci. 2014;17:377–382. doi: 10.1038/nn.3651. [DOI] [PubMed] [Google Scholar]
- 45.Bordyugov G., Abraham U., Herzel H. Tuning the phase of circadian entrainment. J. R. Soc. Interface. 2015;12:20150282. doi: 10.1098/rsif.2015.0282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Halberg F., Tong Y., Johnson E. Circadian system phase, an aspect of temporal morphology; procedures and illustrative examples. In: von Mayersbach H., editor. The Cellular Aspects of Biorhythms. Springer; Berlin, Germany: 1967. pp. 20–48. [Google Scholar]
- 47.Sokolove P.G., Bushell W.N. The χ2 periodogram: its utility for analysis of circadian rhythms. J. Theor. Biol. 1978;72:131–160. doi: 10.1016/0022-5193(78)90022-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.