Kymographic Imaging of the Elastic Modulus of Epithelial Cells during the Onset of Migration

Abstract

Epithelial cell migration during wound repair involves a complex interplay of intracellular processes that enable motility while preserving contact among the cells. Recent evidence suggests that fluctuations of the intracellular biophysical state of cells generate traction forces at the basal side of the cells that are necessary for the cells to migrate. However, less is known about the biophysical and structural changes throughout the cells that accompany these fluctuations. Here, we utilized, to our knowledge, a novel kymographic nanoindentation method to obtain spatiotemporal measurements of the elastic moduli of living cells during migration after wounding. At the onset of migration, the elastic modulus increased near the migration front. In addition, the intensity of fluctuations in the elastic modulus changed at the migration front, and these changes were dependent upon f-actin, one of the major components of the cytoskeleton. These results demonstrate the unique biophysical changes that occur at the onset of migration as cells transition from a stationary to a migratory state.

Introduction

Collective cell migration is an essential component of wound repair, embryonic morphogenesis, and cancer (1). Sprouting in the vasculature and 2D migration of epithelial cells as a sheet are only two variants of the complex process in which cells remodel and regenerate their surrounding tissue. Recent advances in imaging methods and in silico modeling have led to increasing evidence that mechanics plays a role in epithelial social behavior (2, 3) through processes such as intercellular load sharing (4, 5), the formation of free edges (6), and friction with the substrate (7). It is evident that the cytoskeleton mediates these processes (8) and more research is needed to uncover the underlying biophysical role of the cell cytoskeleton in collective cell migration, which leads to the complex behaviors observed in experiments.

Epithelial cell migration during wound repair involves a complex interaction of intracellular processes that enable motility while preserving contact among the cells (8, 9). Neighboring and distant cells share or transmit mechanical cues (4, 10, 11, 12), and the cells near the leading edge experience relatively higher traction forces. Another characteristic of this type of collective migration is that the cells at the wound edge migrate faster than the distant cells in the monolayer (13). Prior studies that focused primarily on single-cell migration showed that cells undergo cytoskeletal remodeling in a cyclic manner, enabling them to crawl into denuded regions (10, 14, 15). These cycles are characterized by the transient formation of focal adhesions in the cell front, contraction of the cytoskeleton, and detachment in the rear of the cell. These processes generate traction forces on the substrate, which then lead to intracellular stresses (4, 5, 11). In this study, we aimed to demonstrate that these remodeling processes also cause localized changes in the stiffness of the cells at the migration front that can be detected by nanoindentation.

We developed, to our knowledge, a novel method in which we measured the mechanical response of epithelial cells, i.e., the elastic modulus (E), at the onset of migration as a function of time. We utilized nanoindentation and developed a code that extracted the E of cells at the migration front in a height-adjusted manner. We examined the E using either 1) high-spatial-resolution and low-temporal-resolution (HS/LT) maps, or 2) high-temporal-resolution and low-spatial-resolution (HT/LS) maps. Our results show that at the onset of migration, epithelial cells exhibit an increase in E during normal migration that is dependent on one of the major components of the cytoskeleton, f-actin. Moreover, we found that migrating epithelial cells undergo larger fluctuations in E than stationary cells.

Materials and Methods

Cell culture

Mouse lung alveolar epithelial (MLE-12) cells were cultured on 60 mm plastic dishes with MLE-12 culture medium (Dulbecco’s modified Eagle’s medium with 10% heat-inactivated fetal bovine serum (FBS), 4 mM glutamine, 1% penicillin/streptomycin, 0.02 M HEPES, 1.0 × 10⁶ cells/m). Cells reached >90% confluence at ∼48 h on average. All experiments were conducted 48–60 h from the time of seeding. Unwounded cells were used as controls. Each experiment was repeated a minimum of three to six times from at least three individual cell-seeding events.

Wound assays

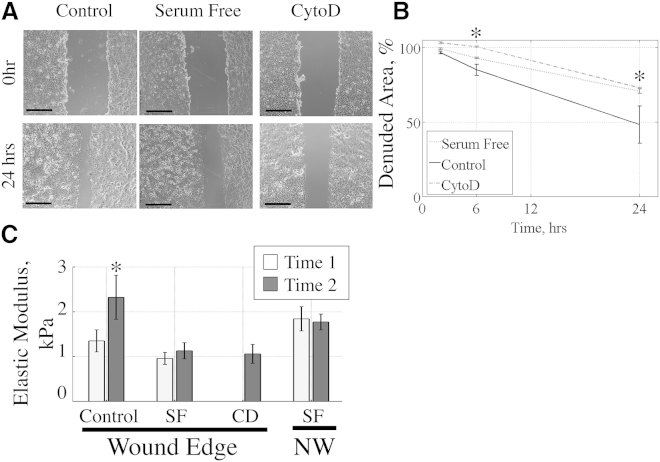
Confluent MLE-12 monolayers were wounded with a pipette tip, creating an ∼1-mm-wide area of denuded cells. The cells were washed twice with PBS and fresh medium with or without serum was added. Cytochalasin D (cytoD, 1 μg/mL; Tocris) treatment in medium with serum was also provided at the time of wounding, but only for 30 min, after which time the cells were washed to completely remove the cytoD and provided with fresh medium including serum. Phase-contrast images were recorded at 0, 2, 6, and 24 h time points to measure the remaining denuded area as a ratio of the total denuded area at the time of wounding.

Kymographic measurements of E

To measure the spatial and temporal variations in the E of cells by atomic force microscopy (AFM), we used an atomic force microscope (Asylum MFP3D; Oxford Instruments, Abingdon, Oxfordshire) mounted on an Olympus IX71 IO microscope, and obtained E-maps by using the force-volume mode and indenting live cells at each pixel of the grid (Fig. 1 A). For AFM indentation, the cantilever beam (Si-Ni; Budget Sensors, Sofia, Bulgaria) was lowered onto the cells to cause an indentation. The force required to indent the cell was related to the E of the cell, the nominal stiffness of the cantilever beam (spring constant), and the geometry of the tip. Because the structure of a cell below the indented location is heterogeneous, the resulting force-deflection (F-d) curve is an average resistance of the nearby affected cytoskeletal structure. To capture the time-dependent changes that occurred in the mechanical response of the cells near the migration front, we recorded two specific types of E-maps: HS/LT and LS/HT. We repeated these measurements on multiple 60 mm dishes from multiple cell-seeding events.

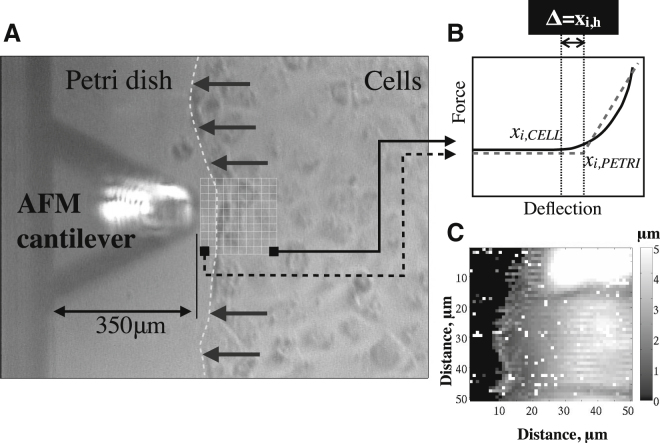
Figure 1.

(A) Photomicrograph of the AFM tip and the cell migration front, and the grid for a representative HS/LT map. (B) Two F-d curves, with the nonlinear one representing the cell and the linear one representing contact with the petri dish. (C) Example of a height map that was obtained by registration of the difference between the contact point of the petri dish (x_i,PETRI) and cell (x_i,CELL).

AFM nanoindentation analysis

At each location, we recorded F-d curves (see Fig. 1 B) on the petri dish and the cells. This allowed us to obtain the reference contact height, x_i,PETRI, of the petri dish for our AFM analysis with height correction (discussed below). We utilized pyramidal tips with a 35° opening angle and a nominal stiffness of 0.050–0.200 pN/nm. To determine the actual stiffness of each cantilever beam, we measured its resonant frequency peaks using the thermal-noise method and the slope of an F-d curve obtained on a relatively stiff cell-free substrate. Both of these methods are available tools in the AFM system used in these studies. This pyramidal tip geometry allowed the resolution necessary for measurements at the migration front. We recorded HS/LT and LS/HT maps over 50 μm × 50 μm and 30 μm × 30 μm areas, respectively. To examine spatial changes in E at the onset of migration, we recorded HS/LT maps over 50 μm × 50 μm areas with 1 μm resolution. For the HS/LT maps, we recorded three E-maps (each requiring ∼45 min) in a series beginning at the time of wounding. To examine the temporal changes in E that occurred during cell migration, we recorded LS/HT E-maps over a 30 μm × 30 μm area with a 30 × 4 grid (requiring ∼2 min each) in a repetitive manner. In other words, we recorded ∼30 E-maps on the same area over 60 min. These LS/HT temporal E-maps were initiated 2 h after wounding.

Analysis of AFM indentation data

We used a MATLAB (The MathWorks, Natick, MA) code developed in our group to batch process the F-d curves and determine the E from those curves. We read the raw F-d results files in a sequential manner, identified the approach portion of the F-d curve and the contact point (δ_i), and eliminated the portion of the curve that belonged to indentations greater than a preset value (see below) limiting the indentation depth. We then computed the E using the following relationship:

$$\text{E}=\text{F}\left[2\left(1\text{-}{v}^2\right)\right]/\left[1.4906{\delta }^2\tan \mathit{\theta }\right],$$ (1)

where ν is Poisson’s ratio, θ is the tip half-opening angle, and δ is the indentation (16, 17). In this analysis, Poisson’s ratio is assumed to be 0.49. We utilized the fminsearch minimization function in MATLAB and computed a goodness-of-fit (R²) value for each computed versus experimental pair of F-d curves. Once the E_i, x_i, and R² values were computed for a given E-map, a results file was written for the particular map that was being analyzed. We conducted this type of analysis three times for each E-map with three different indentation depths (0.150 μm, 0.250 μm, and 0.500 μm).

Postprocessing

A postprocessing code was written to collect and report the desired plots from previously analyzed E-maps. First, a specific results file belonging to a given E-map was called, and the E values from locations of the petri dish and with a poor fit (R² > 0.95) were set equal to zero. Because the contact point (x_i) on each F-d curve was identified in the analysis of the AFM data, the contact point of a given location over cells (x_i,CELL) was subtracted from the average contact point of all petri dish locations (x_i,PETRI). This computation generated cell height (x_i,HEIGHT) maps such as the one shown in Fig. 1 C. Once the cell height at each pixel was known, the E for a given pixel from the appropriate results file was selected based on criteria shown in Fig. 2. When all of the pixels in a map were analyzed, the results of the E-maps were averaged or E-maps were plotted.

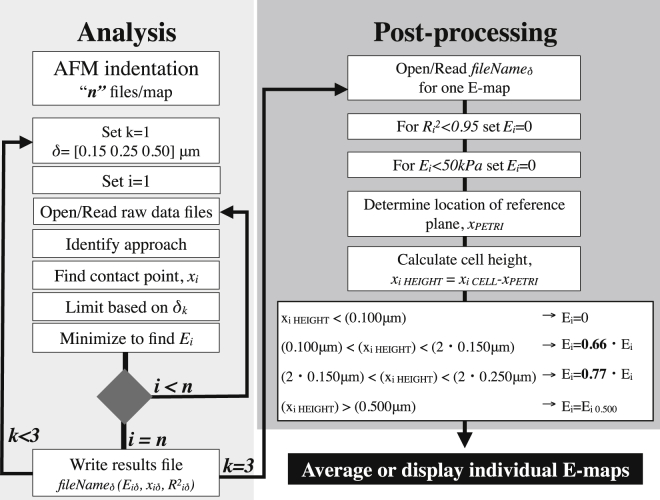
Figure 2.

Flowchart of the data analysis used to obtain E at various indentation depths and postprocessing with height correction of E for a given E-map. The raw data files were analyzed three times at three different indentation depths. The analysis ended when all data points in the E-map were analyzed and three results files were written for a given E-map. Postprocessing utilized these three results files and selected the proper results file for a given pixel based on cell height information, and then corrected this value by multiplying with the factors shown depending on the specific tip geometry.

Height correction

Mechanical evaluation of thin structures with an indenter can be affected by the underlying substrate properties. A height-to-indentation depth ratio of 10 is needed to obtain accurate estimates of E of thin soft films on rigid substrates (e.g., as shown experimentally by Gavara and Chadwick (18)). However, in biological materials such as live cells, it is challenging to attain a large height-to-indentation depth ratio. For example, near the migration front, cells form lamellipodial regions that spread to thicknesses of <0.5 μm. On the other hand, to obtain a reasonable average of the local mechanical response at a given point on the cell, it is necessary to generate an indentation that is multiple times the thickness of structures such as the plasma membrane (∼0.05 μm). Moreover, the geometry of the tip also dictates the optimum depth of the indentation. For example, one of the most commonly used cantilever beam tips, a pyramidal tip with an opening angle of 35°, necessitates a depth of ≥0.3 μm for accurate measurements of E with a sufficient cross-sectional area (16). Any indentation of <0.3 μm would provide an artificially high E based on the geometrical factors.

To improve the accuracy of our results, especially near the migration front where cell thickness is low, we took these limitations into consideration. We developed, to our knowledge, a novel analysis technique to accurately compute the E near the wound edge, where the low thickness of the cell becomes a limitation in AFM indentation. Instead of analyzing all of our force-indentation data at a constant depth, in our algorithm we altered the depth of analysis at each location based on the local cell height. We developed a practical approach to eliminate potential artifacts due to the varying thickness of the samples. We utilized previously published results for a pyramidal tip with an opening angle of 35°, which showed the dependence of the E of agarose (E∼1.38 kPa at plateau) on the indentation depth (see Fig. 4 a in Rico et al. (16)). Using the experimental results obtained for agarose, we calculated that the apparent E should be adjusted by a factor of 0.66 when analyzed at 0.150 μm, and by a factor of 0.77 when analyzed at 0.250 μm. We utilized these factors in the postprocessing of our experimental results to multiply the computed E at a given location with a known cell height (as depicted in red in the criterion section of the flowchart). For example, if the height of a given location at which the F-d curve was recorded was greater than 0.150 μm but less than 0.300 μm, we multiplied the E that was computed by a factor of 0.66. This again is due to the fact that a sharp tip leads to an overestimation of the E due to its geometry.

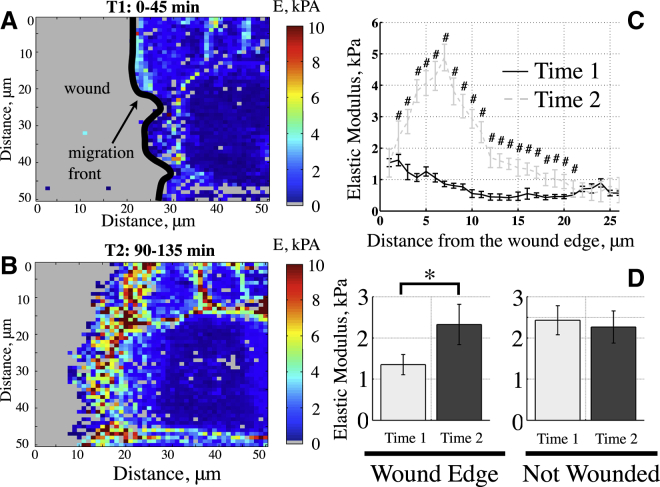
Figure 4.

(A and B) Changes in E in the same field of cells using HS/LT E-maps at two consecutive time points: T1 (A, 0–45 min) and T2 (B, 90–135 min). (C) Change in the average E of epithelial cells as a function of the distance from the migration front for the E-maps from two time points. (D) There was a significant increase in the average E within the first 15 μm from the later time map (T2) compared with the initial time map (T1). Unwounded control cells from separate dishes did not display changes in E over time (n = 3–6, ^∗paired t-test, p < 0.05).

Results

Height correction eliminates artificially high E measurements

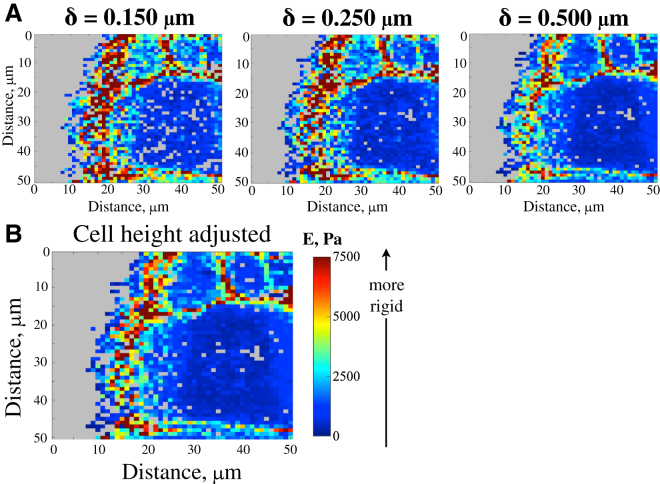
To improve the quality of indentation measurements recorded at the migration front, where cells are thin, we developed and implemented a height correction in the analysis of the nanoindentation. The benefits of our height-corrected analysis and postprocessing can be seen in the maps displaying the distribution of E across multiple cells near the migration front (Fig. 3). The petri dish is shown in gray on the left side of the maps. The E-maps in Fig. 3 demonstrate the differences in artifacts obtained from the same field depending on the indentation depth used in the analysis. Fig. 3 B shows the height-corrected E-map for this field with fewer artifacts. For example, for the E-map with a 0.50 μm indentation depth, fewer data were analyzed near the migration front. This is because the cells were thin in this region and the R² values of this region were lower than the minimum accepted 0.95 due to the cantilever beam potentially touching the substrate and resulting in a linear F-d curve. In addition, the artificially high E that was observed in the analysis of a 0.15 μm indentation near the wound edge was also apparent when the analysis was carried out with a low indentation depth. These artifacts were eliminated by the height-correction procedure in our code, as shown in Fig. 3 B.

Figure 3.

Display of the height-adjusted E-maps. (A) E-maps without height correction, displaying artifacts near the migration front. (B) Cell-height-corrected E-map in which the artificial E increase near the migration front was eliminated.

The E increases near the migration front during the development phase

We quantified the spatial changes in the E of cells between the time of wounding and ∼2 h after wounding in the presence of FBS using HS/LT E-maps, and found that there was an increase in the E during this development phase of migration (Fig. 4). We measured the E near the migration front during the first 45 min (T1) after wounding and compared it with the E profile obtained 90–135 (T2) minutes after wounding (Fig. 4, A and B). When we averaged the E values in a column-wise manner normalized to the migration front from multiple fields, we observed an increase in the E of the cells over time near the wound edge (Fig. 4 C). The average E in the first 15 μm from the wound edge increased significantly between the two time points: E_T1 = 1.35 ± 0.25 kPa and E_T2 = 2.33 ± 0.49 kPa (n = 6, standard error (STE); Fig. 4 D). These results were independent of the height of the cells in this region, since there was no significant difference in height at the two different times (data shown in Fig. S1 in the Supporting Material). When we conducted similar temporal measurements at two sequential time points with confluent monolayers of nonwounded cells, we did not observe changes in the E with time (E_T1 = 2.43 ± 0.35 kPa vs. E_T2 = 2.26 ± 0.39 kPa, n = 3, STE; Fig. 4 D). We observed that the E of the wounded cells at T2 was similar to that of the nonwounded cells.

The increase in E is associated with migration

To investigate the transient changes that occurred in the E of cells at the wound edge during cell migration, we measured wound closure and changes in the E of cells at the migration front after deprivation of FBS or after a 30 min treatment with cytoD. Our wound-closure assays confirmed that both serum deprivation and cytoD treatment delayed wound closure at 6 and 24 h (Fig. 5, A and B). CytoD treatment caused an initial increase in the wounded area. When we examined HS/LT maps on serum-free (SF) cells, we found that there was no significant increase in E near the wound edge, in contrast to what we observed in control (FBS-treated) cells (Fig. 5 C). In addition, there was no change in the E of unwounded SF cells between T1 and T2 (E_T1 = 1.84 ± 0.27 kPa vs. E_T2 = 1.77 ± 0.18 kPa, n = 3, STE). The increase in E observed near the wound edge at T2 in serum-treated control cells was abolished by the 30 min treatment with cytoD.

Figure 5.

MLE-12 cell migration and the increase in E were blocked by serum deprivation and cytoD treatment. (A) Light-microscopy images of the initial wounds and wounds after 24 h. (B) The remaining denuded area is shown as a function of time for three conditions. At time 0, the wound is 100% open. (C) Whereas control serum-treated cells showed a significant increase in E at the later time, no increase in E was observed in serum-free (SF) cells. Similarly, there was no increase in E in cytoD-treated (CD) cells compared with control cells at time 1. NW, nonwounded cells (n = 3, ^∗p < 0.05).

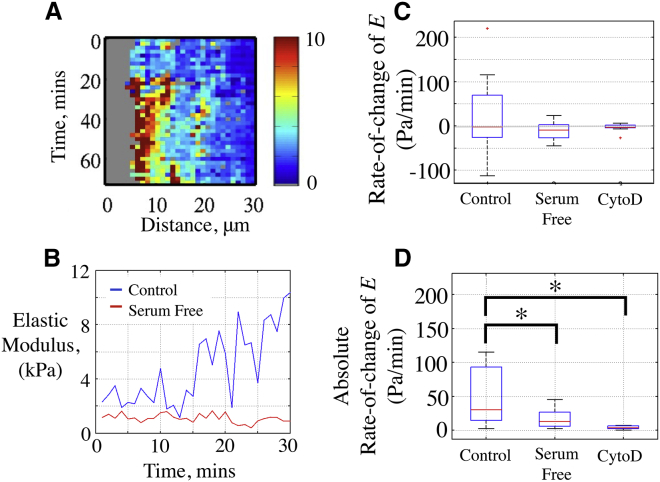
Migrating cells exhibit fluctuations in E

We then hypothesized that in addition to the long-term responses we observed (on a scale of hours), migrating cells should also undergo dynamic changes on a shorter timescale (minutes). To capture these short-term temporal changes, we made repeated measurements of E at the same location using LS/HT. We then quantified the rate of change in the E of cells near the wound edge by measuring the E at a given location every 2 min beginning 2 h after wounding (LS/HT maps) (Fig. 6). We utilized the same analysis technique to compute E as we employed for the HS/LT maps, but we then plotted E at a particular location as a function of time. Fig. 6 A shows an example of an LS/HT E-map with time on one axis and distance on the other, in which an area of high E developed near the wound edge after 20 min of scanning. To examine these fluctuations further, we plotted the average E from the same location 10 μm from the wound edge as a function of time (Fig. 6 B). Whereas there were minimal changes in E in SF cells, serum-treated cells exhibited marked variations in E with time. To quantify this further, we calculated the rate of change of E from several locations, and found that the median value was ∼0 for all treatments regardless of whether the cells were stimulated or not (Fig. 6 C), suggesting that increases in E were balanced by decreases in E over time. However, the serum-stimulated cells exhibited a significantly higher variation in the rate of change of E compared with the SF and cytoD-treated cells (Fig. 6 C). Since changes in E occurred in both positive and negative directions as the cells migrated, we also computed the absolute value of the rate of change of E. Fig. 6 D shows that the serum-stimulated cells exhibited a significantly higher rate of change of E than the SF or cytoD-treated cells.

Figure 6.

(A) Kymographic mapping of E in a field of serum-stimulated cells at the same wound-edge location using LS/HT E-maps. (B) Serum-stimulated (control) cells exhibited large variations in the median E of the first 10 μm from the wound edge, whereas SF cells showed little variation. (C) Median of the rate of change of E within the first 10 μm from the wound edge. (D) Median of the absolute value of the rate of change of E within the first 10 μm from the wound edge (n = 10–20 locations from three separate cell-seeding events, ^∗p < 0.05).

Discussion

We previously showed that bronchial epithelial cells (16HBE) displayed a decreased E at the leading edge and an elevated E 10–20 μm back from the leading edge 2 h after wounding compared with cells away from the edge (19). Mihai et al. (20) showed that inhibition of PTEN enhanced single-cell migration (invasion) in a Boyden chamber, with a corresponding global decrease in E in human transformed epithelial cells (BEAS2B), and a further decrease in E after 4 h at the migration front. In the study presented here, we again measured an increase in E close to the migration front, but in the case of MLE12 cells, it was within 15 μm of the leading edge. Our current kymographic measurements, obtained close to the time of wounding, show for the first time (to our knowledge) the development of this cell strengthening after wounding and how it is dependent on serum stimulation and intact f-actin. In addition, we found that E fluctuated at a given location in migrating cells, but these fluctuations were reduced in SF or cytoD-treated cells. Combined with studies of monolayer stress microscopy (21), traction force microscopy (5), patterned cell-removal techniques (4, 6), and spatiotemporal changes in signaling pathways (22, 23), our study provides, to our knowledge, new data about the mechanical state of migrating epithelial cells during wound healing.

With the growing interest in cell mechanobiology and mechanotransduction, as well as the increasing recognition of cells as a biophysical structure with material properties (24, 25) and applied loads (26), many experimental techniques have been developed for the measurement of cellular mechanical responses (27, 28, 29). Among these techniques, traction-force microscopy is unique in that it measures the forces exerted by cells on the extracellular matrix (30). The underlying idea of this method is that cells generate traction forces due to cytoskeletal remodeling and contraction, which are measured through the deformation of a flexible substrate. Although this approach has provided important insights into the forces exerted by cells upon the substrate, including during migration, it does not directly measure the changes in cell mechanical properties. Therefore, we conducted kymographic measurements of the E to better understand the transient response of the cell cytoskeleton near the migration front.

A previous study by Trepat et al. (11) showed a persistent positive traction force acting on the focal adhesions of cells near the migration front. Furthermore, the maximum intensity of such tractions has been shown to occur at the leading edge of migrating epithelial cells (31). Our results suggest that these traction forces may translate to the cell cytoskeleton and contribute to the substantial temporal changes in E that we measured on both timescales. It is important to note that when cell migration was inhibited by serum deprivation or cytoD treatment, the short-term fluctuations in E were also inhibited. Also, the overall rate of change of E was conserved, suggesting that although there were large changes in E as the cells remodeled, there was no overall stiffening of the cells. Given that epithelial cell migration can occur by different mechanisms (32), including lamellipodial extension, purse string contraction, and collective sheet versus individual cell migration (4), the extent to which these different mechanisms contributed to the fluctuations in E observed in this study is unclear.

A major limitation to our study, especially with regard to our measurements of E changes over short time periods, is the possibility that the indentation itself may lead to stiffening or softening of the cells. Another limitation in most AFM nanoindentation studies is that the substrate may contribute to the measured E depending on the sample thickness. This is important when one considers the fact that cells near the migration front spread and form thin structures. In our measurements, we accounted for the tip geometry based on the sample thickness to obtain more accurate measurements of the changes in E particularly near the migration front. However, we recognize that other material and geometric nonlinearities may also contribute to the very complex mechanical response that we measured with the use of AFM nanoindentation. Another important consideration is the timescale of our measurements in relation to the time dependence of cell material properties. Recent studies have utilized AFM to measure the viscoelastic properties of cells (33, 34). In our measurements, the analyzed indentation occurred within 0.5 s, during which time a cell may be considered to be less dependent on the movement of fluid within it and more dependent on the local arrangement of the cytoskeleton and porosity (35).

In our study, we aimed to understand the adaptation of cells to wounding and their subsequent transition from wounding to active migration, which required us to use a method that indeed damaged the cell monolayer. Although numerous assays have been developed to study collective cell migration (36), in studies focusing on wound repair, a scratch-wound assay is considered appropriate. As such, we chose to utilize the scratch-wound assay for our work. A limitation of the scratch assay is that the cells are actually harmed by the wounding, and the gap that is formed in general is wide and the cell front is in the shape of a line.

In summary, for the first time to our knowledge, we report that one of the mechanical properties (i.e., the E) of epithelial cells near the migration front changes after wounding as the cells strengthen, and that this increase is perturbed on a shorter timescale by fluctuations in E. Furthermore, we provide evidence that this increase in E and fluctuations in elasticity are necessary for efficient wound closure. In the closure of smaller wounds, where the onset of migration accounts for a considerable proportion of the overall time of wound closure, facilitating this transition from a stationary to a migratory phenotype may be a key factor in facilitating wound repair. Based on our study and other studies on early stages of wound closure and cytoskeletal organization (37), we propose that this initial phase in the overall process of epithelial cell migration should be identified as the strengthening phase.

Author Contributions

E.R., K.W., and C.M.W. developed the study, designed the experiments, and wrote and edited the manuscript. E.R. and K.W. conducted the experiments.

Editor: Leah Edelstein-Keshet.