Permutation and parametric tests for effect sizes in voxel-based morphometry of grey matter volume in brain structural MRI

Abstract

Permutation testing has been widely implemented in voxel-based morphometry (VBM) tools. However, this type of non-parametric inference has yet to be thoroughly compared with traditional parametric inference in VBM studies of brain structure. Here we compare both types of inference and investigate what influence the number of permutations in permutation testing has on results in an exemplar study of how grey matter proportion changes with age in a group of working age adults. High resolution T₁-weighted volume scans were acquired from 80 healthy adults aged 25–64 years. Using a validated VBM procedure and voxel-based permutation testing for Pearson product-moment coefficient, the effect sizes of changes in grey matter proportion with age were assessed using traditional parametric and permutation testing inference with 100, 500, 1000, 5000, 10000 and 20000 permutations. The statistical significance was set at P < 0.05 and false discovery rate (FDR) used to correct for multiple comparisons. Clusters of voxels with statistically significant (P_FDR < 0.05) declines in grey matter proportion with age identified with permutation testing inference (N ≈ 6000) were approximately twice the size of those identified with parametric inference (N = 3221 voxels). Permutation testing with 10000 (N = 6251 voxels) and 20000 (N = 6233 voxels) permutations produced clusters that were generally consistent with each other. However, with ≥ 1000 permutations there were approximately 20% more statistically significant voxels (N = 7117 voxels) than with 10000 permutations. Permutation testing inference may provide a more sensitive method than traditional parametric inference for identifying age-related differences in grey matter proportion. Based on the results reported here, at least 10000 permutations should be used in future univariate VBM studies investigating age related changes in grey matter to avoid potential false findings. Additional studies using permutation testing in large imaging databanks are required to address the impact of model complexity, multivariate analysis, number of observations, sampling bias and data quality on the accuracy with which subtle differences in brain structure associated with normal ageing can be identified.

1. Introduction

Brain MRI data are often analysed using parametric statistical methods, for example the general linear model (GLM) [1–3]. These methods make a number of assumptions about the generation and statistical distributions of these imaging data. Specifically, subject samples are assumed to have been acquired randomly from their population and distributions of data are assumed to be approximately statistically Normal, or “Gaussian” [4–6]. Previous seminal work in voxel-based morphometry (VBM) has used voxel-wise smoothing, i.e. averaging, to circumvent the issue of statistical Normality [1,2]. Permutation testing was proposed at a similar time [7], and has recently been widely implemented in VBM methods, for example FMRIB Software Library (FSL; http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Randomise), to address the assumptions of random samples and homoscedasticity [8,9]. Current implementations of permutation testing in VBM are optimised for t-tests and analysis of variance (ANOVA). These provide robust tools for assessing differences in, for example, the proportion of grey matter voxels between two or more groups. Reductions in grey matter volume are a commonly observed feature of normal ageing [10], and are also seen in diseases such as amyotrophic lateral sclerosis [11], epilepsy [12], Alzheimer’s disease [13] and schizophrenia [14]. However, differences in tissue structure can be subtle and difficult to identify consistently between studies [14,15].

Effect size statistics, for example Cohen’s d for two groups or Pearson product-moment coefficient (r) for continuous data such as age [16,17], may be a useful addition to imaging statistics derived from existing implementations of permutation testing. Measures of effect size provide standardised results that can be more easily compared across different studies and populations [16,17]. However, the influence of parametric versus permutation inference for effect sizes and the impact of the number of permutations on results have not yet been formally tested in VBM studies.

In the present study we therefore describe a framework for permutation testing of effect size in VBM studies of brain structural MRI data. We then compare parametric and permutation testing inference and assess the impact of the number of permutations on the latter in an exemplar study of changes in brain grey matter proportion with age in structural MRI data acquired from a cohort of healthy subjects with ages spanning normal working age adulthood.

2. Materials and Methods

2.1 Subjects

Eighty clinically normal, right-handed, healthy volunteers (40 males, 40 females) aged 25–64 (median 43, IQR 17) years were recruited by advertisement from staff working at the University of Edinburgh, the Western General Hospital and the Royal Infirmary, Edinburgh, United Kingdom. All subjects gave written informed consent. Health status was assessed using medical questionnaires and all structural MRI scans were reported by a fully qualified neuroradiologist. To aid identification of age-related differences in brain volumes, the cohort was divided into four 10-year age bands as detailed in Table 1.

Table 1.

Demographics of the cohort.

Age group (years)	Number
25–34	21
35–44	23
45–54	24
55–64	12
25–64	80

2.2 MRI acquisition

All brain MRI data were acquired using a GE Signa Horizon HDxt 1.5T clinical scanner (General Electric, Milwaukee, WI, USA) equipped with a self-shielding gradient set (33 mT m⁻¹ maximum gradient strength) and manufacturer supplied 8-channel phased-array head coil. The imaging protocol consisted of whole brain axial T₂-, T₂*- and FLAIR-weighted structural sequences, and a high resolution 3D T₁-weighted inversion-recovery-prepared fast spoiled gradient-echo (FSPGR) volume scan acquired in the coronal plane with 180 contiguous 1.3 mm thick slices resulting in voxel dimensions of 1 × 1 × 1.3 mm.

2.3 Voxel-based morphometry

The T₁-weighted volume scans were first converted from DICOM to NIfTI–1 format (http://nifti.nimh.nih.gov/nifti-1) using MRIcron’s “dcm2nii” tool (http://www.nitrc.org/projects/mricron). A modified FSL-VBM pipeline was then employed to process these imaging data and produce grey matter proportion volumes for each subject. The first step in this pipeline consisted of randomly selecting a subject for manual, slice-by-slice, brain extraction. This subject was then non-linearly registered to all other subjects to produce initial brain masks for the whole cohort [18]. These initial brain masks were manually edited slice-by-slice and applied to the raw imaging data to produce brain extracted T₁-weighted volumes for each subject. These brain extracted T₁-weighted volumes were then processed using the standard FSL-VBM pipeline [19]. Briefly, each subject’s T₁-weighted scan was segmented into grey matter, white matter and cerebrospinal fluid volumes using signal intensity and spatial information [20]. These grey matter volumes contained the proportion of grey matter tissue within each voxel in native space. No subject had white matter hyperintensities on FLAIR-weighted MRI (hypointense on T₁-weighted MRI) which might confound the grey matter segmentations. After segmenting these three tissue types, all data were aligned to Montréal Neurological Institute (MNI) standard space. A study specific atlas was created by registering all subjects to the initial average of all subjects aligned in MNI space. The grey matter proportion volumes were then smoothed using a 3 mm Gaussian kernel in standard space. There are currently no standard optimal parameters for Gaussian kernels [21], and our reasoning for choosing 3 mm smoothing was that, based on visual assessment of the imaging data, it provided a reasonable middle ground between removing noise and maintaining the underlying anatomy. Finally, a 4D volume of voxel-wise grey matter proportions was created by concatenating all individual grey matter volumes together in the axial direction in standard space; effect sizes and P-values were then calculated using this cohort 4D volume.

2.4 Permutation testing for effect sizes

We provide the Pearson product-moment coefficient (r) as a measure of effect size. This was proposed as a measure of effect size by Cohen [16] and is valid for continuous variable data. Absolute effect sizes of approximately ± 0.1 are considered small, approximately ± 0.3 medium and approximately ± 0.5 large [16]. Effect size r was calculated using Equation

$$\frac{{\displaystyle \sum _{i=1}^n}\frac{x_i-\overline{x}}{{\sigma }_x}\times \frac{y_i-\overline{y}}{{\sigma }_y}}{n-1}$$ (1)

where n is the number of pair-wise observations, x̄ is the mean of variable x, ȳ is the mean of variable y, σ_x is the standard deviation (SD) of variable x and σ_y is the SD of variable y. In the present study, x is age and y is grey matter proportion in each voxel.

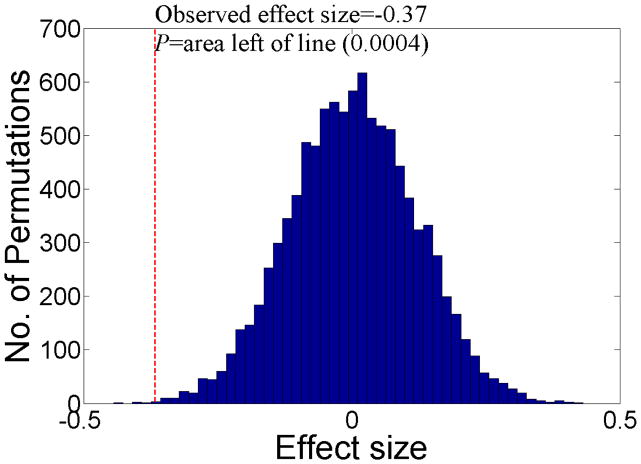
Permutation testing is a very simple concept. For i permutations (for example 1000), the order of independent variables is randomly shuffled and the test statistic of interest (in this case, effect size) is calculated in each random permutation (see Figure 1). This is supposedly equal to producing 1000 pseudo random samples and the P-value of the effect size is defined as the number of times this effect size could be produced by chance, i.e. in each random permutation of the data (see Figure 1).

Figure 1.

Permutation testing for effect sizes. The statistical significance (P) of an observed effect size is calculated by counting how many times an effect size larger than the observed effect size is found in random permutations of the data. In this case the observed effect size of −0.37 was calculated from the Pearson product-moment coefficient formula. When randomly permuting the data, effect sizes of −0.37 or larger were found 0.04% of the time, i.e. P=0.0004. This indicates that the observed effect size of −0.37 was highly statistically significant and unlikely to be due to chance.

We report both parametrically defined P-values and non-parametric permutation testing P-values for effect sizes with the latter assessed using 100, 500, 1000, 5000, 10000 and 20000 permutations. For 20000 permutations the smallest achievable P-value is 0.00005, a value twenty times smaller than that used in previous “extensive simulations” [9]. False discovery rate (FDR) was used to correct for multiple comparisons [22–24], and we provide 1-P_FDR corrected and 1-P uncorrected volumes as outputs. Alpha (P-value cut off) and lambda (FDR corrected P-value cut off) were set at 0.05.

3. Results

3.1 Observed effect sizes

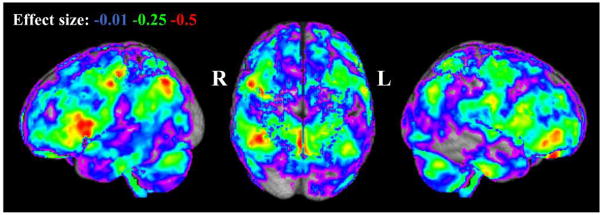
Observed effect sizes of age (25 to 64 years) versus grey matter proportion are shown in Figure 2. Reductions in grey matter proportion are seen across the brain at an effect size of −0.01 to −0.5, which become increasingly localised, in particular, to clusters in right hemisphere frontal and parietal/occipital regions as r becomes more negative.

Figure 2.

Observed effect size for reductions in grey matter proportion with age (25–64 years) across the cohort provided by the Pearson product-moment coefficient. R=right; L=left.

3.2 Parametric inference

Figure 3 provides illustrations of the statistical significance of effect sizes obtained with parametric inference, while brain regions with parametric effect sizes of P_FDR < 0.05 are displayed in Table 2. Overall, there are 3221 voxels which have significant reductions in grey matter proportion with parametric effect sizes of P_FDR < 0.05. The largest clusters of voxels with the largest effect sizes are found in the right inferior frontal gyrus, precuneous cortex, right lateral occipital cortex and right precentral gyrus. There is also a small concentration (84 voxels) of large effect sizes in the left frontal pole.

Figure 3.

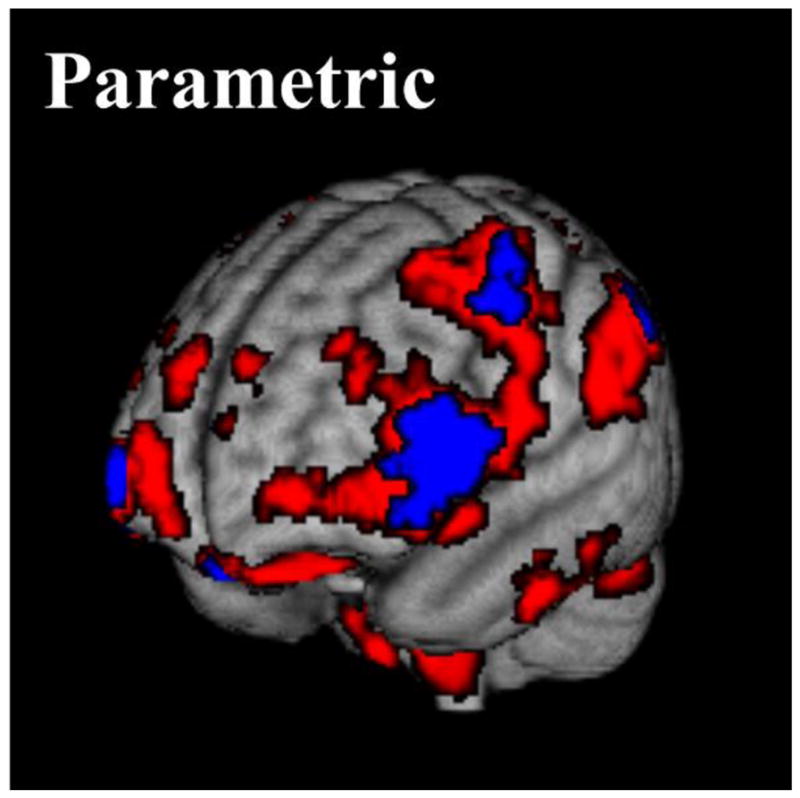
P-values for effect sizes with parametric inference showing reductions in grey matter proportion with age (25–64 years) across the cohort. The red volume shows uncorrected P-values of < 0.05, while the blue volume shows false discovery rate corrected P-values of < 0.05.

Table 2.

Brain regions with parametric effect sizes of P_FDR < 0.05.

Approximate structure	MNI coordinates of centroid of voxel cluster (mm)	Number of voxels in cluster	Effect size range (mean)
Right cerebellar VI lobule	18, −68, −28	453	−0.36 to −0.45 (−0.39)
Left inferior temporal gyrus	−56, −12, −34	58	−0.36 to −0.45 (−0.39)
Left cerebellar crus	−50, −60, −30	51	−0.36 to −0.40 (−0.38)
Left frontal pole	−12, 46, −22	84	−0.36 to −0.57 (−0.44)
Left frontal pole	−46, 50, −2	253	−0.36 to −0.49 (−0.41)
Right inferior frontal gyrus	50, 26, 10	624	−0.36 to −0.54 (−0.42)
Right caudate	12, 16, 8	153	−0.36 to −0.47 (−0.41)
Left caudate	−18, 16, 8	64	−0.36 to −0.42 (−0.38)
Left inferior frontal gyrus	−52, 22, 22	134	−0.36 to −0.49 (−0.38)
Left precentral gyrus	−60, −6, 36	90	−0.36 to −0.43 (−0.39)
Left lateral occipital cortex	−44, −68, 40	61	−0.36 to −0.42 (−0.38)
Precuneous cortex	0, −62, 46	523	−0.36 to −0.53 (−0.41)
Right lateral occipital cortex	40, −58, 48	333	−0.36 to −0.52 (−0.41)
Right precentral gyrus	40, −12, 56	289	−0.36 to −0.50 (−0.41)
Left precentral gyrus	−34, −24, 56	51	−0.36 to −0.44 (−0.39)
Total number of voxels with effect sizes of PFDR < 0.05		3221

Note: Bolded rows highlight regions with the largest effect sizes ≥ 0.50.

3.3 Permutation testing inference

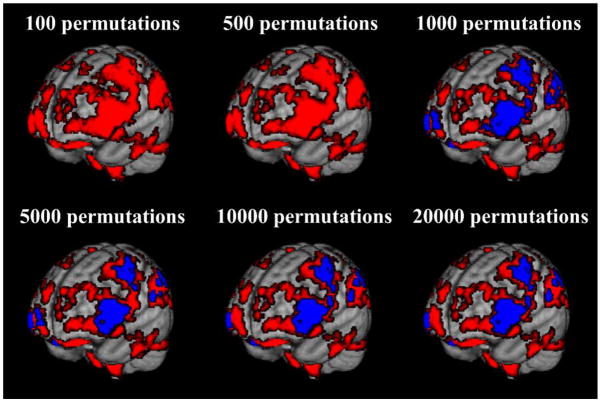
Figure 4 provides illustrations of statistically significant effect sizes with permutation testing inference from 100 to 20000 permutations. Brain regions with permutation testing effect sizes of P_FDR < 0.05 for 1000, 5000, 10000 and 20000 permutations are displayed in Tables 3 to 6, respectively. (Permutation testing with 100 or 500 permutations did not produce effect sizes with P-values sufficient to survive FDR correction.) With 1000 permutations there are 7117 voxels which have significant reductions in grey matter proportion with permutation testing effect sizes of P_FDR < 0.05, with 5000 permutations there are 6294 voxels with effect sizes of P_FDR < 0.05, while with 10000 permutations there are 6251 voxels with effect sizes of P_FDR < 0.05. Finally, with 20000 permutations, there are 6233 voxels with permutation testing effect sizes of P_FDR < 0.05.

Figure 4.

P -values for effect sizes with permutation testing inference showing reductions in grey matter proportion with age (25–64 years) across the cohort. The red volumes show uncorrected P-values of < 0.05, while the blue volumes are false discovery rate (FDR) corrected P-values of < 0.05. No P-values at 100 and 500 permutations survived FDR correction. Patterns of grey matter loss were approximately stable from ≥ 10000 permutations.

Table 3.

Brain regions with permutation testing effect sizes P_FDR< 0.05 for 1000 permutations.

Approximate structure	MNI coordinates of centroid of voxel cluster (mm)	Number of voxels in cluster	Effect size range (mean)
Right cerebellar VI lobule	18, −66, −28	1004	−0.26 to −0.45 (−0.36)
Left inferior temporal gyrus	−56, −12, −32	130	−0.29 to −0.45 (−0.36)
Left cerebellar crus	−48, −60, −30	124	−0.28 to −0.40 (−0.35)
Left frontal pole	−12, 46, −22	139	−0.28 to −0.57 (−0.40)
Left frontal pole	−46, 48, −2	401	−0.29 to −0.49 (−0.38)
Right inferior frontal gyrus	48, 26, 10	1021	−0.27 to −0.54 (−0.39)
Left frontal pole	−22, 66, 6	81	−0.29 to −0.39 (−0.33)
Right putamen	32, 8, 4	102	−0.28 to −0.42 (−0.35)
Left inferior frontal gyrus	−52, 18, 16	525	−0.28 to −0.49 (−0.35)
Left caudate	−18, 16, 8	203	−0.27 to −0.42 (−0.34)
Left thalamus	−6, −4, 6	66	−0.28 to −0.47 (−0.35)
Right caudate	12, 16, 10	253	−0.29 to −0.47 (−0.38)
Right angular gyrus	44, −52, 44	734	−0.28 to −0.52 (−0.37)
Left precentral gyrus	−58, −8, 36	200	−0.27 to −0.43 (−0.36)
Left lateral occipital cortex	−44, −66, 40	169	−0.29 to −0.42 (−0.35)
Precuneous cortex	−4, −60, 50	1125	−0.27 to −0.53 (−0.37)
Right precentral gyrus	40, −10, 54	652	−0.26 to −0.50 (−0.36)
Left precentral gyrus	−34, −24, 56	91	−0.30 to −0.44 (−0.36)
Left middle frontal gyrus	−36, −2, 64	97	−0.26 to −0.40 (−0.33)
Total number of voxels with effect sizes of PFDR < 0.05		7117

Note: Bolded rows highlight regions with the largest effect sizes ≥ 0.50.

Table 6.

Brain regions with permutation testing effect sizes P_FDR< 0.05 for 20000 permutations.

Approximate structure	MNI coordinates of centroid of voxel cluster (mm)	Number of voxels in cluster	Effect size range (mean)
Right cerebellar VI lobule	20, −66, −28	927	−0.31 to −0.45 (−0.36)
Left inferior temporal gyrus	−56, −12, −32	113	−0.31 to −0.45 (−0.36)
Left cerebellar crus	−48, −60, −30	114	−0.32 to −0.40 (−0.35)
Left frontal pole	−12, 46, −22	124	−0.31 to −0.57 (−0.41)
Left frontal pole	−46, 48, −2	376	−0.31 to −0.49 (−0.38)
Right inferior frontal gyrus	48, 26, 10	960	−0.31 to −0.54 (−0.39)
Right putamen	32, 8, 4	91	−0.31 to −0.42 (−0.36)
Left inferior frontal gyrus	−54, 20, 20	366	−0.31 to −0.49 (−0.36)
Left caudate	−18, 16, 8	177	−0.31 to −0.42 (−0.35)
Left frontal operculum cortex	−40, 12, 6	84	−0.31 to −0.39 (−0.35)
Right caudate	12, 16, 8	233	−0.32 to −0.47 (−0.38)
Right parietal operculum cortex	58, −32, 28	54	−0.31 to −0.38 (−0.34)
Left precentral gyrus	−58, −8, 36	187	−0.31 to −0.43 (−0.36)
Right angular gyrus	42, −56, 46	551	−0.31 to −0.52 (−0.38)
Left lateral occipital cortex	−46, −66, 40	152	−0.31 to −0.42 (−0.36)
Precuneous cortex	−2, −60, 50	1029	−0.31 to −0.38 (−0.53)
Right precentral gyrus	40, −12, 54	558	−0.31 to −0.50 (−0.37)
Left precentral gyrus	−34, −24, 56	84	−0.31 to −0.44 (−0.37)
Left middle frontal gyrus	−32, −4, 66	53	−0.31 to −0.40 (−0.34)
Total number of voxels with effect sizes of PFDR < 0.05		6233

Note: Bolded rows highlight regions with the largest effect sizes ≥0.50.

3.4 Comparison of parametric and permutation testing inference

Tables 2 to 6 show that clusters of statistically significant voxels identified with permutation testing inference are approximately twice the size of the corresponding clusters identified with parametric inference. The regional locations of statistically significant voxel clusters are broadly similar for both types of inference, but permutation testing reveals additional structures with significant effect size reductions in grey matter proportion with age, most notably in the right putamen. Other regions identified by permutation testing (but not parametric inference) are proximate to regions identified with parametric inference.

3.5 Effect of number of permutations on permutation testing inference

Figure 4 and Tables 3 to 6 show that the clusters of statistically significant voxels identified with 1000 permutation tests are generally 20% larger than the corresponding clusters identified with ≥5000 permutations. The statistically significant effect sizes found in the left thalamus with 1000 permutations disappear when the number of permutations is increased to ≥5000. Furthermore, permutation testing with 1000 permutations does not detect the small but statistically significant regions in the left frontal (~ 80 voxels) and right parietal operculum (~ 50 voxels) cortices identified with ≥5000 permutations. A small region (66 voxels) of statistically significant effect sizes identified in the left frontal pole with 5000 permutations also disappears with 10000 and 20000 permutations, while 5000 permutations fails to identify significant voxels found in the right inferior frontal lobe with 10000 and 20000 permutations (Figure 4). The separate regions of statistically significant effect sizes seen in the right angular gyrus and precuneous cortex with 5000 and 20000 permutations become a single continuous region with 10000 permutations. However, aside from these small differences, clusters of statistically significant effect sizes are in approximately the same location and of the same volume with 10000 and 20000 permutations.

4. Discussion

Non-parametric permutation testing inference in brain MRI studies has been proposed as a more robust alternative to traditional parametric inference [7–9,25–27]. We found in a sample of working age healthy adults, typical of samples commonly used in brain imaging studies [10,28–34], that permutation testing inference revealed approximately twice as many voxels with statistically significant reductions in grey matter proportion with age than parametric inference, albeit in approximately the same brain regions. These data therefore suggest that permutation testing inference may be useful in identifying subtle changes in brain structure which have been difficult to identify consistently with parametric inference [14,15]. The larger skews from Normal distributions in brain imaging data acquired from ageing and neurodegenerative disease cohorts further supports the use of permutation testing inference in these groups [15].

The results from permutation testing with 10000 and 20000 permutations were generally consistent. The clusters of statistically significant voxels identified with 1000 permutations were approximately 20% larger than the corresponding clusters identified with ≥10000 permutations. Although approximately the same number of statistically significant voxels were identified with 5000 permutations compared with ≥10000, there were differences in the locations of statistically significant voxels in 5000 permutations relative to ≥ 10000 permutations. For example, 5000 permutations may have produced false positive findings in the left frontal pole and false negative findings in the right inferior frontal lobe. Based on these findings, we recommend that at least 10000 permutations are used in future univariate VBM permutation testing studies investigating age related changes in grey matter to avoid potential false findings. However, it should be noted that the number of permutations required also depends on the quality of data, parameters to be examined, number of observations and sampling bias. Specifically, our results and recommendations are provided for studies investigating age related changes in grey matter and do not generalise to multivariate studies.

We performed a maximum of 20000 permutation tests for effect sizes in each voxel. This number of permutations is far less than the maximum number of permutations available in our data (80 factorial). However, 80 factorial permutations are not feasible with current computing power and not all permutations are required to produce valid results [35,36]. Twenty thousand permutations is twenty times more than that used in previous “extensive simulations” [9], and future work will determine whether using more than 20000 leads to marked improvement in the results obtained. The stability of results we show from 10000 to 20000 permutations suggests any improvement may be limited, i.e. although the number of permutations was doubled from 10000 to 20000, the resulting difference was only approximately 1%. Our sample size of 80 subjects is small relative to large image databank projects currently ongoing [15], but is typical of similar studies assessing changes in grey matter proportion with age [10,28–34]. Other nonparametric methods, for example bootstrapping [37], are available for providing confidence intervals for test statistics and these require evaluation in future work. Finally, the effect size measure we used was univariate and this limits the generalisability of our results. Future work is required to investigate the role of permutation methods in multivariate statistics, for example repeated measures regression for longitudinal studies. Additional studies into permutation testing are also required to address the impact of model complexity, number of observations, sampling bias and data quality in the plethora of potential VBM analyses.

Notwithstanding these limitations, these results provide one of the first formal investigations of permutation testing inference for effect sizes in VBM studies of grey matter proportion differences across working age adulthood. Further work is required to determine if permutation testing is truly a more robust alternative to traditional parametric inference. Large quantities of structural brain MRI data are required to determine whether this is, indeed, the case. We are collecting such data and encourage others to join our initiative (http://www.brainsimagebank.ac.uk). This work, and other large databanks currently being prepared worldwide (see, for example [38]), will determine whether the apparent increased sensitivity of permutation testing inference shown here can be used to identify subtle brain structural changes associated with normal ageing and neurodegenerative disease.

Table 4.

Brain regions with permutation testing effect sizes P_FDR < 0.05 for 5000 permutations.

Approximate structure	MNI coordinates of centroid of voxel cluster (mm)	Number of voxels in cluster	Effect size range (mean)
Right cerebellar VI lobule	18, −66, −28	909	−0.30 to −0.45 (−0.36)
Left inferior temporal gyrus	−56, −12, −32	116	−0.31 to −0.45 (−0.36)
Left cerebellar crus	−48, −60, −30	114	−0.31 to −0.40 (−0.35)
Left frontal pole	−12, 46, −22	125	−0.31 to −0.57 (−0.41)
Left frontal pole	−46, 48, −2	376	−0.30 to −0.49 (−0.38)
Right inferior frontal gyrus	48, 28, 10	909	−0.30 to −0.54 (−0.39)
Left frontal pole	−22, 66, 6	66	−0.31 to −0.39 (−0.34)
Right putamen	32, 8, 4	87	−0.32 to −0.42 (−0.36)
Left inferior frontal gyrus	−54, 20, 20	385	−0.30 to −0.49 (−0.35)
Left caudate	−18, 16, 8	174	−0.30 to −0.42 (−0.35)
Left frontal operculum cortex	−38, 12, 6	84	−0.31 to −0.39 (−0.35)
Right caudate	12, 16, 8	235	−0.31 to −0.47 (−0.38)
Right parietal operculum cortex	58, −32, 28	52	−0.31 to −0.38 (−0.34)
Left precentral gyrus	−58, −8, 36	195	−0.30 to −0.43 (−0.36)
Right angular gyrus	42, −56, 46	589	−0.30 to −0.52 (−0.38)
Left lateral occipital cortex	−46, −68, 40	157	−0.30 to −0.42 (−0.35)
Precuneous cortex	−2, −60, 50	1012	−0.30 to −0.53 (−0.38)
Right precentral gyrus	40, −12, 54	557	−0.30 to −0.50 (−0.37)
Left precentral gyrus	−34, −24, 56	85	−0.30 to −0.44 (−0.37)
Left middle frontal gyrus	−34, −4, 64	67	−0.30 to −0.40 (−0.34)
Total number of voxels with effect sizes of PFDR < 0.05		6294

Note: Bolded rows highlight regions with the largest effect sizes ≥ 0.50.

Table 5.

Brain regions with permutation testing effect sizes P_FDR < 0.05 for 10000 permutations.

Approximate structure	MNI coordinates of centroid of voxel cluster (mm)	Number of voxels in cluster	Effect size range (mean)
Right cerebellar VI lobule	18, −66, −28	931	−0.30 to −0.45 (−0.36)
Left inferior temporal gyrus	−56, −12, −32	116	−0.31 to −0.45 (−0.36)
Left cerebellar crus	−48, −60, −30	122	−0.31 to −0.40 (−0.35)
Left frontal pole	−12, 46, −22	127	−0.31 to −0.57 (−0.41)
Left frontal pole	−46, 48,−2	372	−0.31 to −0.49 (−0.38)
Right inferior frontal gyrus	48, 26, 10	955	−0.31 to −0.54 (−0.39)
Right putamen	32, 8, 4	92	−0.31 to −0.42 (−0.36)
Left inferior frontal gyrus	−54, 20, 20	377	−0.31 to −0.49 (−0.36)
Left caudate	−18, 16, 8	174	−0.31 to −0.42 (−0.35)
Left frontal operculum cortex	−38, 12, 6	86	−0.31 to −0.39 (−0.35)
Right caudate	12, 16, 8	240	−0.31 to −0.47 (−0.38)
Right parietal operculum cortex	58, −32, 28	55	−0.31 to −0.38 (−0.34)
Left precentral gyrus	−58, −8, 36	179	−0.32 to −0.43 (−0.36)
Left lateral occipital cortex	−46, −66, 40	153	−0.31 to −0.42 (−0.36)
Precuneous cortex	14, −58, 48	1573	−0.30 to −0.53 (−0.38)
Right precentral gyrus	40, −12, 54	556	−0.31 to −0.50 (−0.37)
Left precentral gyrus	−34, −24, 56	83	−0.31 to −0.44 (−0.37)
Left middle frontal gyrus	−32, −2, 64	60	−0.31 to −0.40 (−0.34)
Total number of voxels with effect sizes of PFDR < 0.05		6251

Note: Bolded rows highlight regions with the largest effect sizes ≥ 0.50.