A Bayesian semiparametric approach with change points for spatial ordinal data

Abstract

The change-point model has drawn much attention over the past few decades. It can accommodate the jump process, which allows for changes of the effects before and after the change point. Intellectual disability is a long-term disability that impacts performance in cognitive aspects of life and usually has its onset prior to birth. Among many potential causes, soil chemical exposures are associated with the risk of intellectual disability in children. Motivated by a study for soil metal effects on intellectual disability, we propose a Bayesian hierarchical spatial model with change points for spatial ordinal data to detect the unknown threshold effects. The spatial continuous latent variable underlying the spatial ordinal outcome is modeled by the multivariate Gaussian process, which captures spatial variation and is centered at the nonlinear mean. The mean function is modeled by using the penalized smoothing splines for some covariates with unknown change points and the linear regression for the others. Some identifiability constraints are used to define the latent variable. A simulation example is presented to evaluate the performance of the proposed approach with the competing models. A retrospective cohort study for intellectual disability in South Carolina is used as an illustration.

1 Introduction

Intellectual disability (ID) is a long-term disability that impacts performance in cognitive aspects of life and usually has its onset prior to birth. Many factors may cause ID, including genetic and chromosomal abnormalities, infections, chemical exposures, intentional and unintentional injuries. Chemical exposures such as arsenic (As), lead (Pb) and mercury (Hg) are developmental toxicants that have been associated with neurobehavioral dysfunctions and have been found to have adverse effects on intelligence in children, even at low levels of exposure.^1–3 Substantial evidence shows that the chemical metals cross the placenta and accumulate in fetal tissues.⁴ The exposure route for the pregnant woman has been identified as oral and dermatologic.^5–7 Previous studies demonstrate elevated soil metal concentrations in urban areas from industrial and transportation sources and elevated rural soil concentrations of metals from natural geologic sources, pesticides, and industrial facilities.^8–10 A significant association is verified between soil and blood concentrations of Pb and As in children through hand to mouth contamination.^1,3,11

Our research is motivated by a retrospective cohort study of pregnant women who were insured by South Carolina Medicaid from 1996 through 2002 and resided in one of ten residential study areas during pregnancy. In this study, we want to identify the soil chemicals as risk factors for unknown cause ID. ID is categorized in order based on intellectual quotient (IQ), containing three ordered levels: normal, mild and moderate/severe. Although some association between soil chemicals and ID has been unveiled,^12,13 it is of substantial interest to assess the elevated risk of ordinal ID associated with the detectable concentrations of soil chemicals with geographical information.

To model ordinal outcomes, cumulative logit models can be utilized.¹⁴ Particularly the proportional odds model is often adopted, which assumes an identical effect of the predictors for each cumulative probability.¹⁵ Most of the existing methods are primarily based on linking categorical data to latent continuous variables, which have an underlying normal regression structure.¹⁶ Among the methods from the Bayesian perspective, Albert and Chib¹⁷ proposed Bayesian methods for analysis of binary and polychotomous response data through the data augmentation with Gibbs sampling. The probit regression model for binary outcomes is seen to have an underlying normal regression structure on latent continuous variables. Values of the latent variables can be simulated from suitable truncated normal distributions. If the underlying continuous measurements are known, then the posterior distribution of the parameters can be computed using standard results for normal linear models. To accelerate Markov chain Monte Carlo (MCMC) convergence for the ordered probit model, one may use a multivariate Hastings-within-Gibbs update step to generate latent data and bin boundary parameters jointly, instead of individually from their respective full conditional posterior distributions.¹⁸ However, these approaches cannot be extended straightforwardly to deal with spatially correlated ordinal data.

Compared to the models for spatially correlated continuous response data, approaches for spatially correlated ordinal data are less developed. The existing methods mainly focus on binary outcomes. Diggle et al.¹⁹ modeled binary and count data by using generalized linear spatial models or generalized geostatistical models, where a spatial random effect term is included in the overall mean structure of a continuous latent variable relative to the categorical variable. To avoid nonidentifiability when estimating parameters of the underlying spatial correlation function, a unified Bayesian method²⁰ can be adopted for inference and prediction for binary spatial data. Higgs and Hoeting²¹ proposed a parametric model for a point-referenced spatially correlated ordered categorical response. This approach relies on the approach by Albert and Chib¹⁷ with incorporation of spatial correlation. However, the approach is parametric which has less flexibility. In addition, the method has potential convergence problems¹⁸ and does not consider the change-point issues.

The methods for change-point problems have drawn much attention over the past few decades. Most of the methods focused on time series related data where the change points are taken from discrete time points. Few change-point models were developed for spatial data. The most related work to our problem is the method by Majumdar et al.²² who proposed a spatio-temporal change-point model for spatio-temporal continuous outcomes, allowing one time change point to reflect the overall mean change in both temporal and spatial associations. Since we focus on the association between the elevated risk of ordinal ID and potential multiple change points in concentrations of all soil contaminants, the approach by Majumdar et al.²² cannot be directly applied.

To detect the unknown threshold concentrations of metals associated with the elevated risk of ordinal ID with spatial information, we propose a Bayesian semiparametric spatial approach with change points. The spatial continuous latent variable underlying the spatial ordinal outcome is modeled by the Gaussian process, which captures spatial variation and is centered at the nonlinear mean. The mean function is modeled by using the penalized smoothing splines for the soil metals with unknown change points and the linear regression for the demographic covariates. Some identifiability constraints are used to define the latent variable. The proposed approach provides a solution to the issues raised by the data.

The remainder of the article is organized as follows. Section 2 describes the latent variable model with change points. Prior specification, reparameterization, posterior implementation, and model comparison are also described. Section 3 evaluates the performance of the approach based on simulated examples. Section 4 illustrates the approach via an application to a retrospective cohort study of ID in South Carolina. Finally, Section 5 concludes with a summary and discussion.

2 The model

2.1 Latent variable model with change points

Let y_i (i = 1, …, n) be an ordinal outcome with L categories, y_i ∈ {1, …, L}, and x_i be the ith geographical location with x_i ∈ R² (i.e. latitude and longitude). We can model the ordinal outcome as:

$$y_i~\mathit{Categorical}({\mathbf{\pi }}_i)$$

where π_i = (π_i1, …, π_iL) denotes the vector of model probabilities that subject i is at level l, for l = 1, …, L, and ${\sum }_{l=1}^L{\pi }_{il}=1$. Since the categories of the outcome are ranked, the cumulative probability $p_{il}=Pr(y_i\le l)={\sum }_{r=1}^l{\pi }_{ir}$, for l = 1, …, L. The cumulative probability p_il can then be modeled as

$$\text{logit}(p_{il})=g_l({\mathbf{z}}_i^{\ast })+b_i,l=1,\dots ,L-1$$ (1)

where ${\mathbf{z}}_i^{\ast }={\mathbf{z}}^{\ast }({\mathbf{x}}_i)$ denotes a vector of the covariates with linear or nonlinear effects at location x_i, $g_l({\mathbf{z}}_i^{\ast })$ is a linear or nonlinear function of ${\mathbf{z}}_i^{\ast }$ at level l, and b_i = b(x_i) is the spatial random effect. However, modeling the ordinal outcome using logistic models could be complicated, especially when the linear predictor, η_il, is complex. Also, incorporating a realization from a spatial Gaussian process for each category is not straightforward. To allow for more convenient and efficient modeling on the spatial ordinal outcome, following Albert and Chib,¹⁷ we use a latent continuous variable $y_i^{\ast }$ distributed as N(η_i, 1) with ${\eta }_i=g({\mathbf{z}}_i^{\ast })+b_i$ and the variance being one for identifiability. The link between y_i and $y_i^{\ast }$ is set as y_i = 1 if $y_i^{\ast }\in ({\nu }_{l-1},{\nu }_l]$ with cut-points ν₀ < ν₁ < ··· < ν_L, where ν₀ = −∞ and ν_L = +∞, and ν₁ = 0 for ensuring identifiability.

If function $g({\mathbf{z}}_i^{\ast })$ is a linear function, the model becomes a typical linear model. In general, the outcome can be linearly associated with some covariates while nonlinearly associated with the others. Thus, we further define $<g({\mathbf{z}}_i^{\ast })={\mathbf{\alpha }}^{\prime }{\mathbf{u}}_i+f({\mathbf{z}}_i)$, where u_i = (u_i1, …, u_iq)′ denotes the vector of covariates with linear effects, α denotes the vector of coefficients for covariates u_i, z_i = z(x_i) = (z_i1, …, z_ip)′ denotes a vector of the covariates with potential nonlinear effects, and f(z_i) denotes a nonlinear function of z_i. Among different nonlinear formulations, we consider a penalized smoothing spline function for f(z_i) due to its flexibility and efficiency. Then function f(z_i) can be written as

$$f({\mathbf{z}}_i)=\sum _{j=1}^p\left({\mathit{\beta }}_j{\mathbf{z}}_{ij}^{\ast }+{\mathit{\gamma }}_j{(z_{ij}-{\mathit{\kappa }}_j)}_{+}^H\right)$$

where ${\mathbf{z}}_{ij}^{\ast }={(1,z_{ij},z_{ij}^2,\dots ,z_{ij}^H)}^{\prime }$ with H being the order of splines, β_j and γ_j denote the vectors of regression coefficients, a₊ = max(0, a) and $a_{+}^H={(a_{+})}^H$, and κ_j = (κ_j1, …, κ_jK)′ denotes the vector of fixed knots. As mentioned in the last section, it is potentially the case that some spatial covariates (e.g. soil metals) may have extraordinary positive or negative effects on the outcome beyond a certain value. To allow for such change points, we model η_i as

$${\eta }_i={\mathbf{\alpha }}^{\prime }{\mathbf{u}}_i+f({\mathbf{z}}_i)+\sum _{j=1}^p\left({\mathit{\beta }}_j^{\ast }{\mathbf{z}}_{ij}^{\ast }+{\mathit{\gamma }}_j^{\ast }{(z_{ij}-{\mathit{\kappa }}_j)}_{+}^H\right)I(z_{ij}>d_j)+b_i$$ (2)

where I(z > d) is an indicator which is 1 if z > d and 0 otherwise, d_j is a change point for covariate j, and ${\mathit{\beta }}_j^{\ast }$ and ${\mathit{\gamma }}_j^{\ast }$ denote the vectors of regression coefficients. Equation (2) provides a general model to assess the effects of spatial covariates on ordinal outcomes with inclusion of potential change points. When I(z > d) = 0, there is no change point for a covariate in terms of its effect on the outcome. The model then reduces to the nonlinear regression model. When H = 1, the model reduces to the typical linear spline model with change points. In this article, the nonlinear function is chosen as the penalized quadratic splines (i.e. H = 2).

Due to the spatial correlation, the realization of the spatial Gaussian process, b = (b₁, …, b_n)′, is assumed to be distributed as a multivariate Gaussian distribution, b ~ N_n(0, Σ(x, θ)) where Σ(x, θ) is the n × n spatial matrix with θ being certain spatial parameters of a geostatistical model that may control smoothness (σ²) and correlation decay (ρ) of the process. The spatial covariance matrix Σ(x, θ) is taken to be C(||x_i − x_j||) with ||a|| = (a′a)^1/2 and C(r) being a member of the Matérn family of covariance functions. Generally, the Matérn covariance matrix function can be written as $\frac{{\sigma }^2}{2^{\nu -1}\mathrm{\Gamma }(\nu )}{(\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert \rho )}^{\nu }{\mathcal{K}}_{\nu }(\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert \rho )$ with 𝒦_ν being a modified Bessel function of order ν (e.g. Stein,²³ p.31). For a special case of ν = 3/2, the Matérn covariance function becomes C(r) = σ²(1 + |r|ρ)exp(−|r|ρ). We use this covariance function in our analysis because this expression is the simplest sub-family of the Matérn covariance functions that results in differentiable estimates.²⁴ Since the information contained in the categorical data pertains to the probability of being in a particular category, we cannot estimate both the variance of the (potentially hypothetical) latent continuous distribution and the thresholds for the categories.²⁰ Following Higgs and Hoeting,²¹ the smoothing parameter σ² is set to be one. With the latent continuous variable y^*, the complete-data likelihood can be expressed as

$${\mathrm{N}}_n({\mathbf{y}}^{\ast };\mathit{\eta },I_n)\prod _{i=1}^{n}1\{{\nu }_{y_i-1}<y_i^{\ast }<{\nu }_{y_i}\}$$ (3)

where ${\mathbf{y}}^{\ast }={(y_1^{\ast },,y_n^{\ast })}^{\prime }$, η = (η₁, …, η_n)′ and 1(x ∈ A) denotes an indicator function. This model is much simpler and easier to be implemented. One of the advantages of the latent variable model is that for three ordinal categories (i.e. L = 3) in the outcome of our data, there is only one unknown cut-point (i.e. ν₂).

2.2 Prior specification and reparameterization

To complete the Bayesian specification of our model, we need to choose prior distributions for the parameters. We assume a priori independence for these different parameter vectors. Following the conventional choice of priors for the regression coefficients, we let α ~ N(0, R_α), β_j ~ N(0, R_β), γ_j ~ N(0, R_γ), ${\mathit{\beta }}_j^{\ast }~\mathrm{N}(\mathbf{0},R_{{\beta }^{\ast }})$, and ${\mathit{\gamma }}_j^{\ast }~\mathrm{N}(\mathbf{0},R_{{\gamma }^{\ast }})$. Since the potential change points can be any value within the range of the corresponding covariate, we assume that potential change point follow a uniform prior with its range, d_j ~ Uniform(min(z_j), max(z_j)). The prior for the decay parameter ρ is chosen as 𝒢(a, b) to ensure that it is positive. According to French and Wand,²⁴ one may also fix ρ at $1/\underset{\le i,j\le n}{max}\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert$. A 𝒢(a, b) random variable is parameterized to have expected value a/b and variance a/b².

The use of standard Gibbs sampler in the model with ordered categorical response variables suffers from the slow convergence problem. Nandram and Chen²⁵ developed an improved algorithm by using Dirichlet proposal for re-scaled cut-point parameters. Weadopt their reparameterization approach for our model with ordered categorical responses. Let $\varphi =\frac{1}{{\nu }_{L-1}}$, we define ν̃_l = ϕν_l, for l = 0, …, L. ϕ is a re-scaling parameter which transfers the cut-points, 0 = ν₁ < ··· < ν_L−1, to the values between 0 and 1. This re-scaling step reduces the correlations between the cut-points and the latent variables and thus accelerates the convergence of the algorithm. We then define the following transformations as

$${\stackrel{\sim }{y}}_i^{\ast }=\varphi y_i^{\ast },\stackrel{\sim }{\mathbf{\alpha }}=\varphi \mathbf{\alpha },{\stackrel{\sim }{\mathit{\beta }}}_j=\varphi {\mathit{\beta }}_j,{\stackrel{\sim }{\mathit{\gamma }}}_j=\varphi {\mathit{\gamma }}_j,{\stackrel{\sim }{\mathit{\beta }}}_j^{\ast }=\varphi {\mathit{\beta }}_j^{\ast },{\stackrel{\sim }{\mathit{\gamma }}}_j^{\ast }=\varphi {\mathit{\gamma }}_j^{\ast },{\stackrel{\sim }{b}}_i=\varphi b_i$$

With this reparameterization, the realization b̃ ~ N_n(0, Σ̃(x, θ)) where Σ̃(x, θ) = C̃(||x_i − x_j||) = ϕ²(1 + |r|ρ) exp(−|r|ρ). By integrating out b̃, the likelihood becomes

$${\mathrm{N}}_n({\stackrel{\sim }{\mathbf{y}}}^{\ast };{\stackrel{\sim }{\mathit{\eta }}}_{-\stackrel{\sim }{\mathbf{b}}},\mathbf{\sum }^{\sim }(\mathbf{x},\mathit{\theta })+{\varphi }^2{I}_n)\prod _{i=1}^{n}1\{{\stackrel{\sim }{\nu }}_{y_i-1}<{\stackrel{\sim }{y}}_i^{\ast }<{\stackrel{\sim }{\nu }}_{y_i}\},$$ (4)

where η̃_−b̃ is η̃ without b̃. For simplicity, we suppress the subscript −b̃ for the remainder of the article. The prior for ϕ² is chosen as ℐ𝒢(c, d). It is clear that when L = 3, it becomes ν̃₀ = −∞ < ν̃₁ = 0 < ν̃₂ = 1 < ν̃₃ = ∞ and there is no unknown threshold scale needed to be updated.

2.3 Posterior computation

The full conditional posterior distributions for all the parameters can be derived based on the likelihood, the priors and the reparameterization specified in Section 2.2. Our posterior computation relies on the Gibbs sampler and Metropolis–Hastings algorithms. After specifying initial values for the parameters and latent variables, the proposed MCMC algorithm proceeds by updating the unknown parameters sequentially as shown in the Appendix.

Samples from the joint posterior distribution of the parameters and the latent variables are generated by repeating the steps for a large number of iterations after apparent convergence. It is noticed that the full conditional posterior distributions for all the parameters except ρ are conjugate, which provides an efficient sampling scheme. For ρ, we adopt the Metropolis–Hastings algorithm. In this article, multiple chains with different initial settings are carried out, which are used for the final summary. The implementation is carried out by using R.²⁶ The code is available from the first author upon request.

2.4 Model comparison

We consider the deviance information criterion (DIC),²⁷ a widely used criterion for model selection in hierarchical Bayesian models. Similar to the Bayesian information criterion (BIC) and Akaike’s information criterion (AIC), the DIC combines a measure of fit and complexity. The measure of fit is given by the posterior mean of the deviance and the measure of complexity by the difference between the posterior mean of the deviance and the deviance based on the posterior means of the parameters. The Bayesian deviance, D(Θ), is defined as

$$D(\mathbf{\Theta })=-2\mathit{logL}(\mathbf{\Theta }\mid \mathbf{y})+2\text{log}(Q(\mathbf{y}))$$

where Θ denotes the set of all parameters in the model of interest, L(Θ|y) denotes the likelihood for the observed data y, and Q(y) denotes some specified standardizing term that is a function of the data alone and hence does not affect model comparison. The DIC is defined as $\overline{D(\mathbf{\Theta })}+p_D$, where $\overline{D(\mathbf{\Theta })}=E_{\mathbf{\Theta }\mid \mathbf{y}}(D(\mathbf{\Theta }))$ denotes the posterior expectation of the deviance, and p_D denotes the effective number of parameters which is defined by difference between the expected deviance and the deviance evaluated at the posterior expectation, $\overline{D(\mathbf{\Theta })}-D(\overline{\mathbf{\Theta }})$. The DIC can be easily calculated by taking the difference of the sample mean of the simulated values of D and the deviance based on the sample means of the simulated values of Θ obtained via MCMC.

3 A simulated example

We evaluated the performance of the proposed approach based on a simulation with 100 replications. Without loss generality, we generated 500 observations with categorical outcomes and four covariates with nonlinear effects. The response variable y_i was categorized into three categories described in Section 2.2 with ${\eta }_i={\sum }_{k=1}^4{f}_k(z_{ik})+b_i$, where z_i1 ~ Uniform(0, 1), z_i2 ~ Uniform(0, 4), z_i3 ~ Uniform(0, 10), z_i4 ~ Uniform(0, 7), and the associations between the covariates and the linear predictor follow different functions with change points,

$$\begin{array}{l}{f}_1(z)=sin(\pi z)+0.8I(z\ge 0.4),\\ f_2(z)=0.1exp(z)+5I(z\ge 2),\\ f_3(z)=0.1(0.2{(z/10)}^{11}{(10-z)}^6+10z^3{(1-z/10)}^{10})+2I(z\ge 5),\\ f_4(z)=0.2+6I(z\ge 4).\end{array}$$

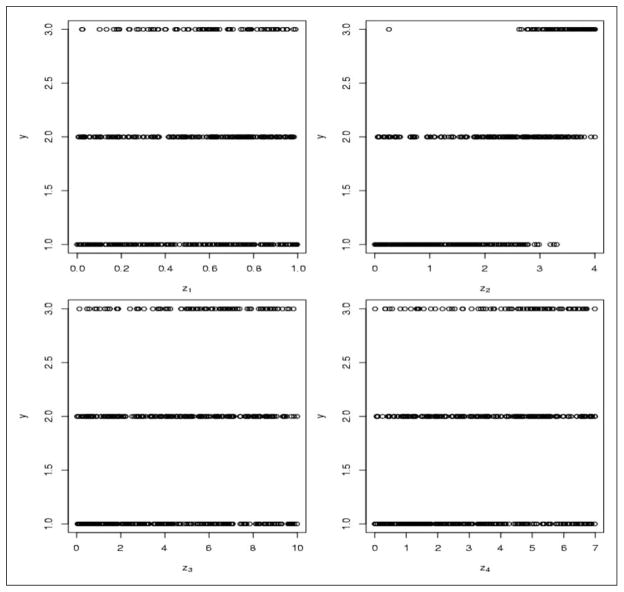
The spatial locations, x, were randomly generated from Uniform(0, 5). The realization of the spatial Gaussian process b was generated from a multivariate Gaussian distribution, N_n(0, Σ(x, θ)), where Matérn covariance function in Σ(x, θ) is described in Section 2.1 with ρ = 1. With generated b, we generated samples for the continuous variable y^* ~ N_n(ζ, I_n). The samples for the ordinal categorical response variable were then generated as y_i = 1 if $y_i^{\ast }<0$, y_i = 2 if $0<=y_i^{\ast }<1$ and y_i = 3 if $y_i^{\ast }>=1$. Figure 1 depicts the plots of covariates vs. the response variable in a simulated data set.

Figure 1.

Plots of covariates vs. the response variable in a simulated data set.

We fitted the proposed model with change points to the simulated data. We chose a flat normal prior N(0, 100) for the coefficients. The gamma prior 𝒢(2, 1) was chosen for ρ. Since the response variable has three ordered categories, ϕ is fixed as one. For each replication, we ran the Gibbs sampling algorithm described in Section 2.3 for 20,000 iterations after a burn-in of 5000 iterations. The diagnostic tests^28,29 were carried out which showed good convergence and efficient mixing.

For comparison, we also fitted the generalized additive model (GAM) and the proposed model without change points to the simulated data. The GAM model used here was proposed by Wood,³⁰ which relies on approximations to the thin plate splines. The smoothers provide optimal low rank approximations to generalized smoothing spline models that are both computationally efficient and stable. The GAM approach is available in the R package mgcv, available from www.cran.r-project.org. In the package, the smooth class ‘tp’ was used, indicating optimal low rank approximation to thin plate spline.

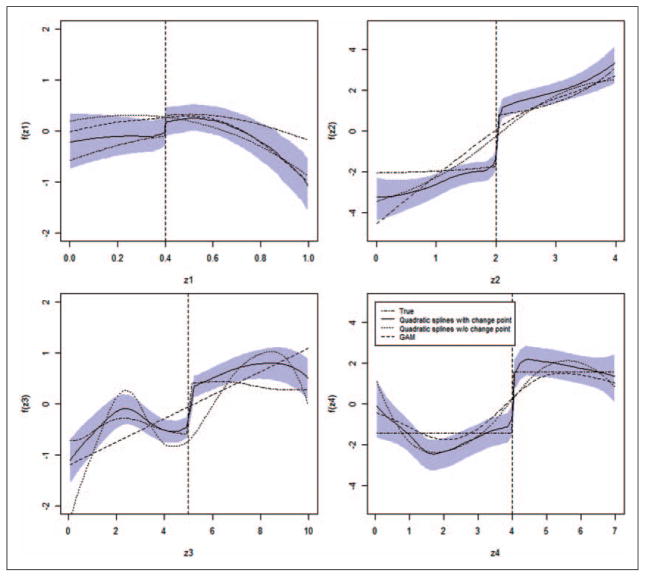
Figure 2 shows the averaged fitted nonlinear curves for the four covariates based on the proposed method with change points, the method without change points and the GAM model. The shaded band indicates the 95% pointwise credible intervals from the simulated data sets. Since the estimate of the nonlinear curves based on the proposed model without change points and the GAM could not fully reflect the true curves, the results may potentially be misleading. In contrast, the proposed semiparametric model with change points provides the best fit for the designed covariates functions. In addition, the estimate of ρ from the proposed model is 0.92 with 95% credible interval (0.58, 1.34). The estimates and 95% credible intervals of the change points for the four covariates are 0.37(0.31,0.43), 1.94 (1.46,2.40), 4.86 (4.20, 5.44) and 4.07 (3.65, 4.82), respectively. The estimated change points for the covariates are close to the true values.

Figure 2.

True and fitted curves from the different methods for simulated data. The vertical line indicates the true value of the change point. The shaded band indicates the 95% pointwise credible intervals from the simulated data sets.

To compare the goodness of fit of the proposed model with change points to that of the model without change points, we also calculated the deviance information criterion (DIC)²⁷ (there is no DIC available for the frequentist GAM model). The DICs for the model with change points and the model without change points are 130.7 and 144.6, respectively, implying that the proposed model with change points is better than the other model. For each replication of the simulation, we also assessed the sensitivity of the results to the prior specification by repeating the analysis with the different hyperparameters. We noticed that the estimates of the parameters varied slightly with different specifications of hyperparameters.

4 Application

We applied the proposed method to the ID data introduced in Section 1. The women in this study were followed through pregnancy and delivery. Then they were longitudinally followed to see if their child received a diagnosis of ID. The study areas were dispersed throughout South Carolina, in rural and urban areas and each area contained a low and high prevalence area for the outcome of ID. In order to maintain the confidentiality agreement, the soil samples were collected according to grids throughout the residential study areas. Nine chemicals were measured in soil samples collected, arsenic (As), barium (Ba), beryllium (Be), chromium (Cr), copper (Cu), mercury (Hg), manganese (Mn), nickel (Ni) and lead (Pb). Other available mother and baby covariates include mother’s age, mother’s ethnicity (white, black and other), mother’s alcohol consumption during pregnancy (yes/no), the number of prior births (parity)(0, 1, 2 and 3 or more), birth weight, child sex and weeks of gestation. Clusters of ID for each gestational month of pregnancy were identified based on maternal addresses. Ten distant geographic areas of land that included a gradient of risk of ID were then selected. Based on a unified grid system, soil samples were collected and analyzed for nine metals and a general toxicity indicator within the areas.

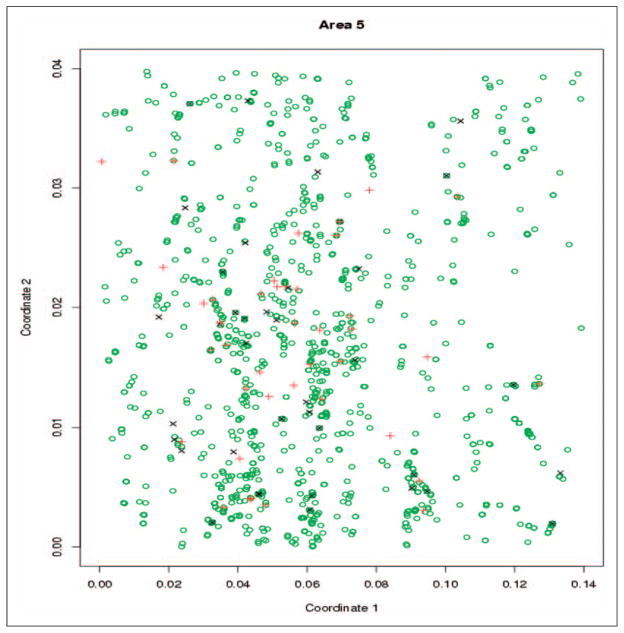
In our analysis, we included 9440 individual samples with 7 demographic covariates related to mothers and children’s information. In each area, grided soil samples were collected with 8 chemical concentrations being measured. Figure 3 shows the ID outcome locations in Area 5. In the application, the mother’s age range is from 12 to 44. Previous studies show that mothers over 35 would have higher risks of having ID babies than younger mothers. However, the percentage of mothers’ age over 35 in our data is only 2.83%. When we categorized the age into three categories, [12, 20), [20, 24) and [24, 44], the proportions of having ID for these three categories are 30%, 35% and 35% respectively, indicating that they are in slightly increasing trend. It is known that there is a dramatically increasing risk of the ID when mothers’ age is over 35 (e.g. Newberger³¹). However, the percentage of mothers’ age over 35 in our data is only 2.83%. Thus, it seems plausible to assume the linear effect of mother’s age. Preliminary analysis based on the logistic regression shows that there is no significant interactions between the demographic covariates.

Figure 3.

The ID locations in Area 5. ‘○’ denotes the non-ID case, ‘×’ denotes the mild ID case and ‘+’ denotes the moderate/severe ID case.

ID: intellectual disability.

We chose flat priors for the coefficients similar to those in the simulation. The prior for ρ was chosen as a gamma distribution 𝒢(3, 1) to allow for a reasonable range. We ran the Gibbs sampling algorithm detailed in the appendix for 40,000 iterations after a burn-in of 10,000 iterations. Convergence was deemed adequate based on the diagnostic tests used in the simulation study.

Table 1 shows the summary of regression coefficients for the demographic covariates based on the three models. The results from the three models in Table 1 show that the older mother, the black mother, male baby and lower gestational age would significantly increase the risk of children having ID. Although the three models have similar results of effects of demographic covariates, it is shown that the proposed model with change points provides narrower credible intervals.

Table 1.

Summary of regression coefficients for the demographic covariates in the ID application based on the three models

Effect	Proposed model with thresholds		Proposed model without thresholds		Generalized additive model
	Posterior Mean	95% C.I.1	Posterior Mean	95% C.I.1	Mean	95% C.I.2
Mother’s age	0.03	(0.01, 0.04)	0.03	(0.01, 0.06)	0.04	(0.02, 0.05)
Mother’s race3 (black)	0.29	(0.08, 0.49)	0.28	(0.06, 0.52)	0.28	(0.05, 0.50)
Mother’s race (other)	0.022	(−0.68, 0.92)	0.025	(−0.78, 0.80)	0.027	(−0.77, 0.82)
Female child	−0.80	(−0.95, −0.58)	−0.81	(−0.93, −0.53)	−0.73	(−0.90, −0.53)
Mother’s alcohol consumption (yes)	−0.06	(−0.81, 0.66)	−0.07	(−0.77, 0.61)	−0.07	(−0.79, 0.64)
Number of prior births =14	0.06	(−0.12, 0.27)	0.05	(−0.19, 0.33)	0.06	(−0.15, 0.28)
Number of prior births =2	0.18	(−0.08, 0.48)	0.18	(−0.10, 0.49)	0.16	(−0.12, 0.42)
Number of prior births =3 or more	0.08	(−0.20, 0.39)	0.09	(−0.23, 0.41)	0.10	(−0.23, 0.43)
Gestational age (week)	−0.07	(−0.09, −0.04)	−0.07	(−0.10, −0.04)	−0.06	(−0.11, −0.02)
Birth weight (kg)	−0.00	(−0.00, −0.00)	−0.00	(−0.00, −0.00)	−0.00	(−0.00, −0.00)

¹Credible interval.

²Confidence interval.

³Reference category: Mother’s race = white.

⁴Reference category: Number of prior births = 0.

Table 2 shows the posterior means and 95% credible intervals of the change points for the soil metals. It is observed that the 95% credible intervals for Ba, Cr, Cu, Mn, Ni and Pb are quite wide which cover most of their ranges. This implies that there is no obvious evidence of change points for the dramatic changes of ID for the six metals based on the data. We actually produced the histograms of the change-point samples for the six metals, which show fairly flat shapes. In contrast, As and Hg seem to have change points for elevated risk of ID due to much narrower 95% credible intervals compared to the other soil chemicals. Besides showing the significant impact of the two metals on children’s ID, which is consistent with that in the previous studies,^12,13 the proposed approach allows for detecting a sudden change in the effects of the metals on the risk of ID.

Table 2.

Posterior means and 95% credible intervals of change points of the soil metals

Soil metal (mg/kg)	Posterior mean	95% Credible interval
As	2.11	(1.47, 2.78)
Ba	50.25	(2.53, 155.40)
Cr	18.56	(0.81, 67.86)
Cu	32.06	(2.40, 68.47)
Hg	0.42	(0.02, 0.96)
Mn	104.0	(5.95, 286.45)
Ni	7.73	(0.03, 20.52)
Pb	105.86	(5.40, 325.67)

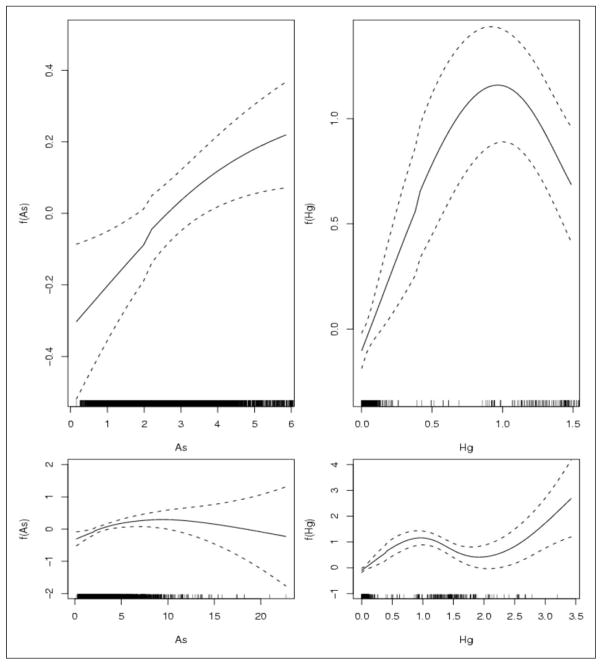
Figure 4 depicts the estimated curves and 95% pointwise intervals for As and Hg based on the proposed model with change points. The lower panel shows the fitted curves and 95% credible intervals for As and Hg across the entire observed ranges, where it is unclear if there exist the change points that accelerate the risk of ID. However, in the upper panel where the zoomed estimated curves are displayed, it is obvious that the change points exist which have accelerated risk effects on ID occurrence in short ranges. This implies that when the two soil metals reach over their thresholds, there would be a sudden increase of risk of ID. This is an interesting finding as the detected thresholds of As and Hg in the soil suggest that some interventions might be needed to reduce the accelerated risk of ID in those areas. Since no previous studies focused on the change point detection for association between ID and the soil chemicals, more investigations are needed to unveil the scenario in the future work.

Figure 4.

The estimated curves and 95% pointwise intervals for As and Hg based on the proposed model with change points. The lower panel shows the estimated curves for the entire range of As and Hg. The upper panel shows the estimated curves for the dense range of As and Hg. The rug plots on the horizontal axis represent the data points for As and Hg.

Similarly, we calculated the DICs for the model with change points and the model without change points, which are 4072.21 and 4098.58, respectively. This indicates that the model with change points has a better fit than the model without change points.

5 Discussion

In this article, we propose a Bayesian semiparametric approach with change points for spatial ordinal data, which allows to detect the unknown threshold points. By using the latent variable underlying the spatial ordinal outcome and the penalized smoothing splines for the covariates, we are able to efficiently model the ordinal outcome nonlinearly associated with the predictors. The simulation study and the application have shown the improvement of modeling and estimation from the proposed approach compared to the other two models without change points.

Although the location of the change point can be potentially found by using diagnostic methods, they often fail to provide statistical inferences about structural change. This is because searching for change points with diagnostics risks mistaking random variation for structural change. In contrast, the proposed Bayesian analysis provides statistical inferences for both regression coefficients and the location of the change point. The Bayesian change point model is shown to be feasibly estimated by stochastically sampling from the conditional posteriors for the regression coefficients. The simulation study shows that when a sudden change occurs, the proposed approach outperforms the methods without change points. However, when there is no dramatic change (e.g. for several soil chemicals in the application), the proposed method provides an estimate for the change point with a wide credible interval, implying that no important threshold effects can be effectively detected by the proposed method under this scenario.

The proposed approach can be implemented in WinBUGS³² with exponential covariance function. Conceptually WinBUGS can carry out the proposed approach with Matérn covariance matrix. However, we experienced slowness in computation time even for the model with very few latent covariates. It is noticed that there might be a potential estimation bias due to the measurement error. The occurrence of the measure error may lead to potential misleading conclusion. On-going work involves incorporating Berkson measurement error model for the latent spatial covariates³³ to reduce potential biases. In addition, although a relatively small sample size (300) was used in the simulation study which shows reasonably good performance of the proposed approach, a systematic study is needed to examine the sample size for detecting important threshold effects.

Appendix

The full conditional distributions in Section 2.3 are:

• Step 1: Update ${\stackrel{\sim }{y}}_i^{\ast }$ from its full conditional distribution,

  $$\pi ({\stackrel{\sim }{y}}_i^{\ast }\mid ·)\propto \mathrm{N}({\stackrel{\sim }{y}}_i^{\ast };{\mu }_i,{\psi }_i)1\{{\stackrel{\sim }{\nu }}_{y_i-1}<{\stackrel{\sim }{y}}_i^{\ast }<{\stackrel{\sim }{\nu }}_{y_i}\}.$$

  where ${\mu }_i=({\stackrel{\sim }{\mathbf{y}}}_{-i}^{\ast }-{\stackrel{\sim }{\mathit{\eta }}}_{-i}){({\mathbf{\sum }^{\sim }}_{-i}+{\varphi }^2{I}_{n-1})}^{-1}{\mathit{\sigma }}_{i,-i}+{\stackrel{\sim }{\eta }}_i$, Σ̃_−i is the submatrix of Σ̃(x, θ) excluding the ith row and column, σ_i,−i is the vector of covariances between ${\stackrel{\sim }{y}}_i^{\ast }$ and ${\stackrel{\sim }{\mathbf{y}}}_{-i}^{\ast }$, and ${\psi }_i={\sigma }_{ii}-{\mathit{\sigma }}_{i,-i}^{\prime }{({\mathbf{\sum }^{\sim }}_{-i}+{\varphi }^2{I}_{n-1})}^{-1}{\mathit{\sigma }}_{i,-i}$.

• Step 2: Update α̃ from its full conditional distribution,

  $$\pi (\stackrel{\sim }{\mathbf{\alpha }}\mid ·)\propto \mathrm{N}(\stackrel{\sim }{\mathbf{\alpha }};\widehat{\mathbf{\alpha }},{\widehat{R}}_{\stackrel{\sim }{\alpha }}),$$

  where α̂ = ϕ⁻² R̂_α̃U′(Σ(x, θ) + I_n)⁻¹(ỹ^* − η̃_−α̃′U) and ${\widehat{R}}_{\alpha }={\left(R_{\stackrel{\sim }{\alpha }}^{-1}+{\varphi }^{-2}{\mathbf{U}}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}\mathbf{U}\right)}^{-1}$ with U=(u₁,…, u_n)′.

• Step 3: Update d_j from its full conditional distribution. To update d_j, we first calculate the probability, $p_{ij}=\mathrm{P}(d_j=w_{ij}\mid ·)=L(d_j=w_{ij}\mid ·)/{\sum }_{r=1}^{n-1}L(d_j=w_{rj}\mid ·)$, where ${\{w_{ij}\}}_{i=1}^{n-1}$ denote the ordered {z_ij} and L(·) denotes the likelihood. Then we draw d_j from the Categorical (p_j), where p_j=(p_1j,…, p_{n−1, j}).

• Step 4: Update β̃_j from its full conditional distribution,

  $$\pi ({\stackrel{\sim }{\mathit{\beta }}}_j\mid ·)\propto \mathrm{N}({\stackrel{\sim }{\mathit{\beta }}}_j;{\widehat{\mathit{\beta }}}_j,{\widehat{R}}_{\stackrel{\sim }{\mathit{\beta }}}),$$

  where ${\widehat{\mathit{\beta }}}_j={\varphi }^{-2}{\widehat{R}}_{\stackrel{\sim }{\mathit{\beta }}}{{\mathbf{z}}_j^{\ast }}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}({\stackrel{\sim }{\mathbf{y}}}^{\ast }-{\stackrel{\sim }{\mathit{\eta }}}_{-{\stackrel{\sim }{\mathit{\beta }}}_j^{\prime }{\mathbf{z}}_j^{\ast }})$ and ${\widehat{R}}_{\stackrel{\sim }{\mathit{\beta }}}={\left(R_{\stackrel{\sim }{\mathit{\beta }}}^{-1}+{\varphi }^{-2}{{\mathbf{z}}_j^{\ast }}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}{\mathbf{z}}_j^{\ast }\right)}^{-1}$ with ${\mathbf{z}}_j^{\ast }={({\mathbf{z}}_{1j}^{\ast },\dots ,{\mathbf{z}}_{nj}^{\ast })}^{\prime }$.

• Step 5: Update γ̃_j from its full conditional distribution,

  $$\pi ({\stackrel{\sim }{\mathit{\gamma }}}_j\mid ·)\propto \mathrm{N}({\stackrel{\sim }{\mathit{\gamma }}}_j;{\widehat{\mathit{\gamma }}}_j,{\widehat{R}}_{\stackrel{\sim }{\gamma }}),$$

  where ${\widehat{\mathit{\gamma }}}_j={\widehat{R}}_{\stackrel{\sim }{\gamma }}{\mathbf{V}}_j^{\prime }({\mathrm{\sum }^{\sim }}^{-1}(\mathbf{x},\mathit{\theta })+{\varphi }^{-2}{I}_n)({\stackrel{\sim }{\mathbf{y}}}^{\ast }-{\stackrel{\sim }{\mathit{\eta }}}_{-{\stackrel{\sim }{\mathit{\gamma }}}_j^{\prime }{\mathbf{V}}_j})$ and ${\widehat{R}}_{\stackrel{\sim }{\gamma }}={(R_{\stackrel{\sim }{\gamma }}^{-1}+{\mathbf{V}}_j^{\prime }({\mathrm{\sum }^{\sim }}^{-1}(\mathbf{x},\mathit{\theta })+{\varphi }^{-2}{I}_n){\mathbf{V}}_j)}^{-1}$ with V_j=(V_1j,…,V_nj)′ and ${\mathbf{V}}_{ij}={({(z_{ij}-{\kappa }_{j1})}_{+}^H,\dots ,{(z_{ij}-{\kappa }_{jK})}_{+}^H)}^{\prime }$.

• Step 6: Update ${\stackrel{\sim }{\mathit{\beta }}}_j^{\ast }$ from its full conditional distribution,

  $$\pi ({\stackrel{\sim }{\mathit{\beta }}}_j^{\ast }\mid ·)\propto \mathrm{N}({\stackrel{\sim }{\mathit{\beta }}}_j^{\ast };{\widehat{\mathit{\beta }}}_j^{\ast },{\widehat{R}}_{{\stackrel{\sim }{\mathit{\beta }}}^{\ast }}),$$

  where ${\widehat{\mathit{\beta }}}_j^{\ast }={\varphi }^{-2}{\widehat{R}}_{{\stackrel{\sim }{\mathit{\beta }}}^{\ast }}{[{{\mathbf{z}}_j^{\ast }}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I)}^{-1}({\stackrel{\sim }{\mathbf{y}}}^{\ast }-{\stackrel{\sim }{\mathit{\eta }}}_{-{{\widehat{\mathit{\beta }}}_j^{\ast }}^{\prime }{\mathbf{z}}_j^{\ast }})]}_{z_{ij}>d_j}$ and ${\widehat{R}}_{{\stackrel{\sim }{\mathit{\beta }}}^{\ast }}={(R_{{\stackrel{\sim }{\mathit{\beta }}}^{\ast }}^{-1}+{\varphi }^{-2}{[{{\mathbf{z}}_j^{\ast }}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}{\mathbf{z}}_j^{\ast }]}_{z_{ij}>d_j})}^{-1}$.

• Step 7: Update ${\stackrel{\sim }{\mathit{\gamma }}}_j^{\ast }$ from its full conditional distribution,

  $$\pi ({\stackrel{\sim }{\mathit{\gamma }}}_j^{\ast }\mid ·)\propto \mathrm{N}({\stackrel{\sim }{\mathit{\gamma }}}_j^{\ast };{\widehat{\mathit{\gamma }}}_j^{\ast },{\widehat{R}}_{{\stackrel{\sim }{\gamma }}^{\ast }}),$$

  where ${\widehat{\mathit{\gamma }}}_j^{\ast }={\varphi }^{-2}{\widehat{R}}_{{\stackrel{\sim }{\gamma }}^{\ast }}{[{\mathbf{V}}_j^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}({\stackrel{\sim }{\mathbf{y}}}^{\ast }-{\stackrel{\sim }{\mathit{\eta }}}_{-{{\stackrel{\sim }{\mathit{\gamma }}}_j^{\ast }}^{\prime }{\mathbf{V}}_j})]}_{z_{ij}>d_j}$ and ${\widehat{R}}_{{\stackrel{\sim }{\gamma }}^{\ast }}={(R_{{\stackrel{\sim }{\gamma }}^{\ast }}^{-1}+{\varphi }^{-2}{[{\mathbf{V}}_j^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}{\mathbf{V}}_j]}_{z_{ij}>d_j})}^{-1}$.

• Step 8: Update ϕ² from its full conditional distribution,

  $$\pi ({\varphi }^2\mid ·)\propto \mathcal{I}\mathcal{G}\left(a+\frac{1}{2}(n+1),b+\frac{1}{2}{({\stackrel{\sim }{\mathbf{y}}}^{\ast }-\stackrel{\sim }{\mathit{\eta }})}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}({\stackrel{\sim }{\mathbf{y}}}^{\ast }-\stackrel{\sim }{\mathit{\eta }})\right).$$
• Step 9: Update ρ from its full conditional distribution,

  $$\frac{{\rho }^{a-1}}{\varphi {\mid \mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n\mid }^{1/2}}exp\left(-b\rho -\frac{1}{2{\varphi }^2}{({\stackrel{\sim }{\mathbf{y}}}^{\ast }-\stackrel{\sim }{\mathit{\eta }})}^{\prime }{(\mathrm{\sum }(\mathbf{x},\mathit{\theta })+I_n)}^{-1}({\stackrel{\sim }{\mathbf{y}}}^{\ast }-\stackrel{\sim }{\mathit{\eta }})\right).$$