Abstract
Hypertrophic cardiomyopathy (HCM) is a cardiovascular disease where the heart muscle is partially thickened and blood flow is (potentially fatally) obstructed. A test based on electrocardiograms (ECG) that record the heart electrical activity can help in early detection of HCM patients. This paper presents a cardiovascular-patient classifier we developed to identify HCM patients using standard 10-seconds, 12-lead ECG signals. Patients are classified as having HCM if the majority of their recorded heartbeats are recognized as characteristic of HCM. Thus, the classifier’s underlying task is to recognize individual heartbeats segmented from 12-lead ECG signals as HCM beats, where heartbeats from non-HCM cardiovascular patients are used as controls. We extracted 504 morphological and temporal features - both commonly used and newly-developed ones - from ECG signals for heartbeat classification. To assess classification performance, we trained and tested a random forest classifier and a support vector machine classifier using 5-fold cross validation. We also compared the performance of these two classifiers to that obtained by a logistic regression classifier, and the first two methods performed better than logistic regression. The patient-classification precision of random forests and of support vector machine classifiers is close to 0.85. Recall (sensitivity) and specificity are approximately 0.90. We also conducted feature selection experiments by gradually removing the least informative features; the results show that a relatively small subset of 264 highly informative features can achieve performance measures comparable to those achieved by using the complete set of features.
Keywords: Electrocardiogram, Feature selection, Hypertrophic Cardiomyopathy, Machine learning, Patient classification
I. Introduction
Hypertrophic cardiomyopathy (HCM) is a genetic cardiovascular disease that may cause sudden cardiac death in young people [1]. The most consistent characteristic of HCM is the thickening (hypertrophy) of the muscle (myocardium) at the lower left chamber of the heart (left ventricle). Fig. 1 provides the illustration of two hearts, where the left one is normal while the one on the right shows the thickened muscle typical of hypertrophic cardiomyopathy. An imaging method, two-dimensional echocardiography, is often used to identify left ventricular hypertrophy (LVH). However, this method cannot reliably identify HCM patients when the thickening of the left ventricular muscle is not clearly detectable. Moreover, early prediction of the disease in patients not yet showing muscle thickening is not possible through echocardiography [2]. Therefore, the analysis of electro-cardiogram (ECG) signals in patients with a family history of HCM and no clear muscle thickening has high diagnostic value for early detection and prediction. In a recent study we have also shown that the standard procedure of conducting ECG tests should be considered in mass pre-participation screening of young athletes [3].
Fig. 1.
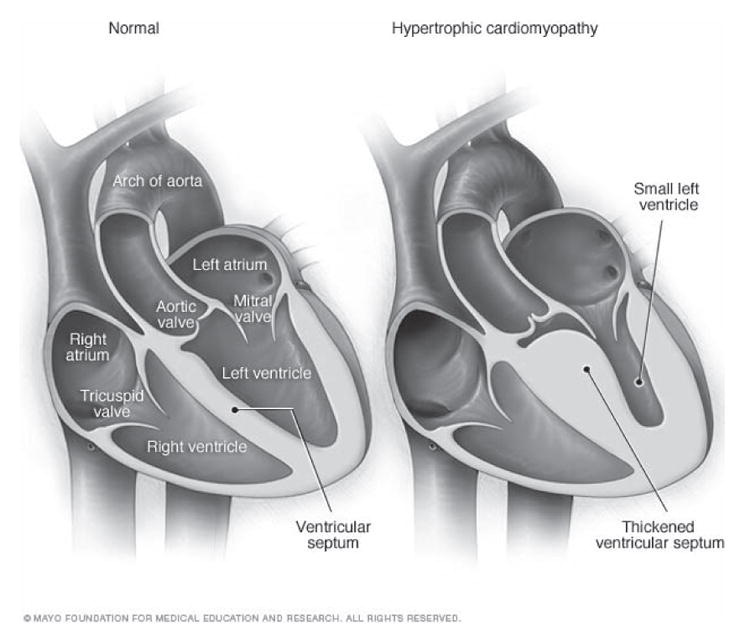
Illustrations of a normal heart (left) and a heart with hypertrophic cardiomyopathy (HCM). The heart walls (muscle) are much thicker (hypertrophied) in the HCM heart [35].
Classifiers that automatically identify cardiovascular disease in patients may help reduce both cost and time of the pre-screening process. Historically, the main focus of ECG-classification research has been on identifying arrhythmia in cardiovascular patients. Arrhythmia is a condition where the heart beats too quickly, too slowly or in an irregular pattern. Early research has been concerned with using heartbeat classification to detect life threatening types of arrhythmia such as ventricular tachycardia (fast heart rhythm that originates in one of the ventricles of the heart) and ventricular fibrillation (uncontrolled quivering of the ventricular muscle) [4]–[6]. More recent research has expanded this idea to categorizing heartbeats along all categories of arrhythmia [7]–[9]. Traditional machine learning methods such as artificial neural networks [9], support vector machines [8], random forests [10], and linear discriminants [11] have been used to detect arrhythmia. Random forests and support vector machines have been shown to perform well with accuracy greater than 95%.
As mentioned earlier, left ventricular hypertrophy is the most common indicator of the presence of HCM in cardiovascular patients. Several criteria, derived from, amplitude values of ECG waveforms have been proposed to detect cardiovascular patients with left ventricular hypertrophy (LVH) based on ECG signals. Many studies have been conducted to validate these LVH-detection criteria, which have generally achieved high specificity (approximately 100%) [12]–[14]. However sensitivity has been reported to be low (approximately 50%) across different studies [15]. Multiple linear regression and rule-based methods have also been used to detect cardiovascular patients with LVH [16], [17]. Corrado and McKenna have proposed a set of amplitude-thresholds for specifically detecting HCM patients [18]. Potter et al. have tested these thresholds on a small group of 56 HCM patients and 56 healthy control subjects [19]. The reported sensitivity and specificity from this study was approximately 90%. However, we are not aware of any previous work that employs machine learning methods for identifying HCM patients from ECG signals. Moreover, the number of HCM patients used in our classification experiment is 221, which is much higher than other previous work on HCM detection.
In this study, we aim to develop a classifier that can distinguish between ECG signals from HCM patients and those from non-HCM controls. Such a classifier will facilitate automated detection of HCM from ECG signals. However, we note that the classifier is not expected to replace extensive cardiovascular diagnosis. Rather, it is intended as an initial screening method that will hopefully detect patients that may have HCM. The automatically detected patients will be referred for further cardiovascular tests and be examined by expert cardiologists.
In order to develop a classifier for automated detection of patients with HCM, we have segmented ECG signals into individual heartbeats, extracted features from each heartbeat and then classified these heartbeats by applying machine learning methods. We assigned a patient to the HCM class if the number of heartbeats classified as HCM is equal to or greater than the number of heartbeats classified as control. For our classification experiments, we have extracted features that have been previously used, as well as some new morphological features (amplitude values of ECG waves) from ECG signals. We have applied random forests and support vector machines classifiers to distinguish between heartbeats from HCM and those from non-HCM patients. Using 5-fold and 10-fold cross validation for training and testing, we achieve high performance levels as measured in terms of precision, recall (sensitivity), specificity and F-measure. For comparison, we also applied logistic regression as a baseline classifier. We use feature selection to reduce the number of features required to achieve the same performance level as that obtained by using the complete set of features.
The rest of the paper is organized as follows: Section II describes the ECG dataset obtained from HCM patients and from control subjects, which is used in our classification experiments. In Section III, we discuss feature extraction, feature selection, and classification methods, as well as related tools. All classification results are presented in Section IV. We discuss and analyze the results and present directions for future work in Section V.
II. Data
The ECG dataset used in this study comprises standard 10-second, 12-lead ECG signals from two groups of cardiovascular patients. The first group consists of 221 hypertrophic cardiomyopathy (HCM) patients. Each HCM patient has one or more ECG recordings in the dataset. The total number of ECG signals in the HCM patients’ dataset is 754. In the second group there are 541 subjects, all of which were diagnosed with ischemic or non-ischemic cardiomyopathy, and had implantable cardioverter defibrillator (ICD) installed for primary prevention of sudden cardiac death. As none of the ICD patients was diagnosed with HCM, their ECG data is used as the control in the experiments described here. While there may be cases in which a set of healthy controls would be preferable (e.g., pre-screening for HCM among young athletes), we have chosen the ICD patients’ ECG dataset as the control because most of the patients referred for ECG tests in a hospital do not usually have a normal cardiac diagnosis; accordingly distinguishing HCM patients from other cardiovascular patients is a realistic, essential task. That said, we expect the methods used in this study to be applicable in other scenarios of distinguishing HCM patients from another group. Each patient in our control dataset has exactly one ECG recording, resulting in a total of 541 ECG signals the control set.
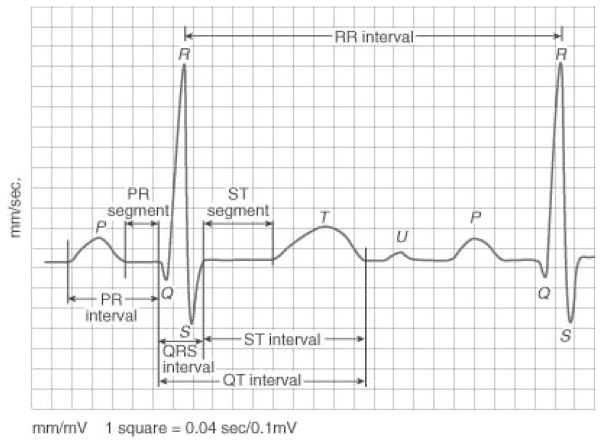
We segmented each ECG signal into individual heartbeats using the freely available ECGPUWAVE tool [20]. A heartbeat is a single cycle in which the heart’s chambers relax and contract to pump blood, where each heartbeat comprises multiple waveforms. The ECG waves are created by the electrical signal that passes through the heart chambers (atria and ventricles). Fig. 2 shows a typical heartbeat and its waves: P, Q, R, S, T and U. It also shows inter-wave segments and intervals. While identifying each heartbeat, ECGPUWAVE detects the onset and offset points of the P-wave and the QRS-complex. It also identifies the offset point of the T-wave and the peak of the QRS-complex.
Fig. 2.
A typical heartbeat comprising P, Q, R, S, T, U waveforms and inter-wave segments and intervals [36].
The segmentation of ECG signals was conducted on signals from each of the 12 leads. We then identified the heartbeats that are simultaneously detected on all 12-leads. Each of these heartbeats was classified using machine learning methods as described in Section III-B. The summary of the dataset is presented in Table I.
TABLE I.
Summary of the ECG Dataset Used in This Study. Each HCM Patient Has One or More ECG Signals, Whereas Each of the Controls Has Only One Signal in the Dataset.
| Type of patient | Number of patients | Total number of ECG recordings | Total number of Heartbeats |
|---|---|---|---|
| HCM | 221 | 754 | 6488 |
| ICD (Control) | 541 | 541 | 4442 |
III. Methods and Tools
After segmenting the 12-lead ECG signals into individual heartbeats, we extracted features from each heartbeat and represented it as a feature vector for classification. We also applied feature selection to identify highly informative features, and repeated the classification experiments using the selected features. We compared the results obtained from the different classification experiments and assessed the statistical significance of the observed differences. Finally, we identified HCM patients, by classifying each subject based on his/her respective number of heartbeats classified as HCM. The methods and tools used are discussed next.
A. Feature Extraction
As described in Section II, we utilized the ECGPUWAVE tool to detect individual waveforms from heartbeats of HCM and ICD patients. We utilized the onset and offset points of various waveforms detected by the tool for extracting temporal and morphological features from each heartbeat. The peak of the QRS-complex was used to measure the length of intervals between the R-waves of consecutive heartbeats. The temporal features and the morphological features extracted from the QRS complex and the T-wave have been used in the literature for heartbeat classification in a different context, namely, automatic detection of arrhythmia in cardiovascular patients [11], [21]. In the current study, we add morphological features of the P-wave that have not been used before. The complete list of features is shown in Table II. To represent each heartbeat, we extract all 42 features from each of the 12 leads, resulting in a total of 504 features.
TABLE II.
Complete List of the 42 Features Extracted From Each of the 12-Lead ECG Signals for Classifying Heartbeats. (The Total Number of Features is 42×12=504)
| Group | Feature | Definition | Number of features |
|---|---|---|---|
| Temporal (based on length of intervals) | Pre-RR interval | The interval between the current heartbeat and the previous heartbeat | 6 |
| Post-RR interval | The interval between the current heartbeat and the following heartbeat | ||
| Average RR-interval | The mean of the RR intervals of a recording and the it is used as the same for all the heartbeats in a recording | ||
| P-wave duration | The interval between the P-wave onset and offset | ||
| QRS interval | The interval between the QRS onset and offset | ||
| T-wave duration | The interval between QRS-offset and T-wave offset | ||
| Morphological (based on amplitude values) | QRS morphology | 10 uniformly sampled amplitude values between the QRS onset and the QRS offset. | 36 |
| Maximum and minimum of original sampled amplitude values in the QRS complex. | |||
| P and T wave morphology | 10 uniformly sampled amplitude values between the wave onset and the wave offset. | ||
| The maximum and the minimum of the original sampled amplitude values in the P and T wave. |
B. Heartbeat Classification and HCM Patient Detection
As a first step to automatically detect HCM patients from 12-lead ECG signals, we developed a classifier whose task was to assign each instance (heartbeat) into one of two possible classes: HCM or control. As noted before, in this study heartbeats from ICD patients serve as controls. We applied two standard classification methods: random forests [22] and support vector machine (SVM) [23]. We have chosen these two methods because they have been previously used and were reported to perform well when classifying heartbeats for arrhythmia detection [8], [10]. For comparison, we also conducted experiment using a logistic regression classifier [24], which is often employed in biomedicine for classification tasks [25]–[27].
Random forests form an ensemble classifier based on a collection of decision trees, learned from multiple random samples taken from the training set. Decision tree classifiers are constructed using the information content of each attribute; thus the decision-tree learning algorithms first select the most informative attributes for classification. Random samples from the training dataset are selected uniformly, with replacement, such that the total size of each random sample is the same as the size of the whole training set. To classify a new instance, each decision tree is applied to the instance, and the final classification decision is made by taking a majority vote over all the decision trees. We applied the standard random forests classification package in WEKA [28], using 500 trees in the random forests implementation. The number of features selected at random at each tree-node was set to , where n is the total number of features. We chose this number because in our classification experiments we found it to perform well compared to several alternatives proposed in the literature (e.g. log2 n, [22], [29], [30]).
The second classification method, support vector machines (SVM), is primarily a binary linear classifier. A hyperplane is learnt from the training dataset in the feature-space to separate the training instances for classification. The hyperplane is constructed such that the margin, i.e., the distance between the hyperplane and the data points nearest to it is maximized. If the training instances are not linearly separable, these can be mapped into high dimensional space to find a suitable separating hyperplane. In our experiments, we used the WEKA libsvm [31], employing the Gaussian radial basis function kernel.
Another classification method we used for comparison is logistic regression. Given a training dataset D consisting of instances X⃗1, X⃗2, …, X⃗m where each is represented as a feature vector , a linear combination of the input features for X⃗j is defined as: . The conditional probabilities of the binary class variable, C over the values {H C M, Control} given the instance X⃗j are calculated as:
where is known as the logistic function. The training dataset D is used to estimate the values of the parameter vector W⃗ =< w0, w1, …, wn > such that the conditional data likelihood is maximized. The conditional data likelihood is the conditional probability of the observed heartbeat-classes in the training dataset given their corresponding feature vector. Thus, W⃗ is estimated such that the following condition is satisfied:
An instance, X⃗j is assigned the class label C = Control if , and C = H C M otherwise.
We used the logistic package in WEKA for implementing the logistic regression classifier that estimates the parameter vector, W⃗ following the estimation method proposed by Cessie and Houwelingen [24].
In our classification experiment, we represented each heartbeat as a 504-dimensional vector of features where 42 features were extracted from each of 12-leads as described in Section III.A. We used the stratified 5-fold cross-validation procedure for training and testing.
Although we are classifying here individual heartbeats, recall that the goal of this study is to classify patients into two groups: HCM vs. control. Hence, we partitioned both HCM patients and control patients into 5 equal sized groups. Heartbeats from one group of HCM patients and from one group of control patients were included in the test set and the other four groups were used for training. We repeated the process 5 times such that each heartbeat from a HCM patient or from a control subject is tested exactly once. We also applied 10-fold cross validation in the same manner to verify the stability of the classification performance.
After classifying all heartbeats from a subject, we classified that subject as a HCM patient based on the number of heartbeats classified as HCM. If the number of heartbeats classified as HCM is equal to or higher than that of heartbeats that have been classified as control, the subject is classified as a HCM patient.
To evaluate the performance of both the heartbeat and the patient classification, we have used several standard measures, namely, precision, recall (sensitivity), and specificity. These measures are defined below, where true positives (TP) and true negatives (TN) are correctly classified HCM and control heartbeats (or patients), respectively; False positives (FP) denote control heartbeats (or patients) that are misclassified as HCM; HCM heartbeats (or patients) incorrectly classified as control are false negatives (FN);
In addition to these three measures, we also calculate the F-measure, which is the harmonic mean of precision and recall, defined as:
We compared the performance measures obtained by random forests, SVM and logistic regression, where the paired t-test was used to assess the statistical significance of the differences along each performance measure [32].
C. Feature Selection
We initially used all 504 features to classify heartbeats as HCM or control beats. Building classifiers from a large feature set can possibly lead to overfitting; moreover, including features that carry only negligible information about the heartbeat-class may incur unnecessary extra training time. To address these issues, we performed feature selection to reduce the number of features.
To select features that have high predictive value, we utilized the well-known Information Gain criterion [33]. For each feature, the information gain measures how much information is gained about the heartbeat-class when the value of the feature is obtained. It is calculated as the difference between the unconditional entropy associated with the heartbeat-class and the conditional entropy of the heartbeat-class given the value of a feature. These measures are formally defined as follows: Let C = {H C M, Control} be the set of heartbeat-classes and VF be the value of the feature F. The maximum likelihood estimate for the probability of a heartbeat to be recorded from a HCM patient, Pr (C = H C M), is calculated as:
while the same estimate for a Control heartbeat is calculated as:
Similarly, we define the conditional probability of the heartbeat-class to be HCM (or Control), given the value of feature F, as: Pr(C = U|VF = xi, 1 ≤ i ≤ k) where U is either HCM or Control and xi is one of k possible values of F. The conditional probabilities are estimated from the observed proportions; e.g., the probability of the heartbeat-class to be HCM given that the value of feature F is xi, Pr(C = H C M|VF = xi), is estimated as:
For a heartbeat-class variable, C, the entropy H(C) is defined as:
The conditional entropy associated with C given that the value of the feature F is xi is defined as:
Based on this definition, the conditional entropy associated with C given a feature F is calculated as:
The information gain associated with a feature F, I G (C, VF), is thus formally defined as:
The above formal definition of information gain is based on the assumption that the features are discrete. As all features in our study are continuous, they first must be discretized. We calculated the information gain using the feature selection package in WEKA, which first discretizes continuous features following Fayyad and Irani’s algorithm [34].
After calculating the information gain for each feature, we removed the 20 least-informative features and repeated the 5-fold cross validation experiment. We continued conducting this procedure by gradually removing 20 features at a time until we observed decline in performance. Notably, only the training dataset is used for information gain calculation and feature selection. Once the reduced feature set has been determined, the test set is represented based on the selected features.
IV. Results and Discussion
As explained in Section III.B, the first step in our experiment toward identifying HCM patients was to classify individual heartbeats such that each heartbeat is assigned to one of the two classes: HCM or control. We applied random forests and support vector machine using the complete set of 504 features for heartbeat classification. As noted earlier, we also used logistic regression for comparison. Table III shows the results from the 5-fold cross validation experiments using all three classifiers. Both random forests and SVM performed better than logistic regression. Differences in precision and specificity between logistic regression and the other two classifiers are statistically significant (p<0.05). Therefore we do not use logistic regression further in the rest of our experiments, namely, patient classification and feature selection. For both random forests and SVM classifiers, precision (0.94) and F-measure (0.91) are the same. The small differences in recall and specificity for these two classifiers are not statistically significant (p>0.35). We also conducted 10-fold cross validation experiments using the complete feature set and the results are shown in Table IV. All four performance measures are exactly the same for both 5-fold and 10-fold cross-validation. Hence we apply 5-fold cross validation for training and testing random forests and SVM classifiers using the reduced set of features as described below.
TABLE III.
Heartbeat Classification Results Using All 504 Features (5-Fold Cross Validation). Standard Deviation Is Shown in Parentheses.
| Classifier | Precision | Recall (Sensitivity) | Specificity | F-measure |
|---|---|---|---|---|
| RF (all features) | 0.94 (0.02) | 0.87 (0.03) | 0.92 (0.02) | 0.91 (0.03) |
| SVM (all features) | 0.94 (0.03) | 0.88 (0.03) | 0.91 (0.03) | 0.91 (0.02) |
| Logistic Regression (all features) | 0.90 (0.02) | 0.85 (0.02) | 0.86 (0.02) | 0.87 (0.02) |
TABLE IV.
Heartbeat Classification Results Using All 504 Features (10-Fold Cross Validation). Standard Deviation Is Shown in Parentheses.
| Classifier | Precision | Recall (Sensitivity) | Specificity | F-measure |
|---|---|---|---|---|
| RF (all features) | 0.94 (0.02) | 0.87 (0.02) | 0.92 (0.03) | 0.91 (0.02) |
| SVM (all features) | 0.94 (0.03) | 0.88 (0.02) | 0.91 (0.03) | 0.91 (0.02) |
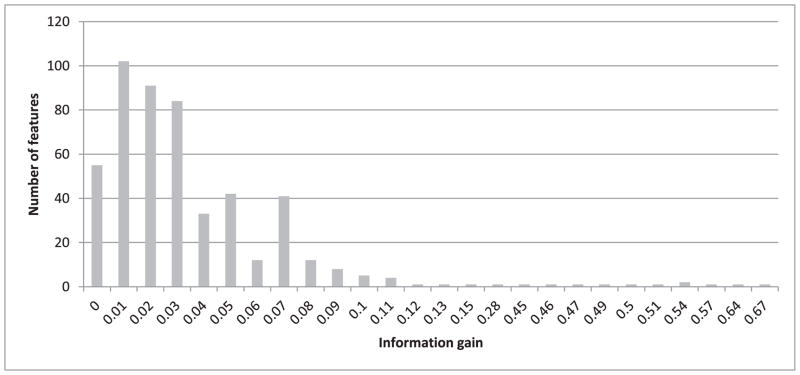
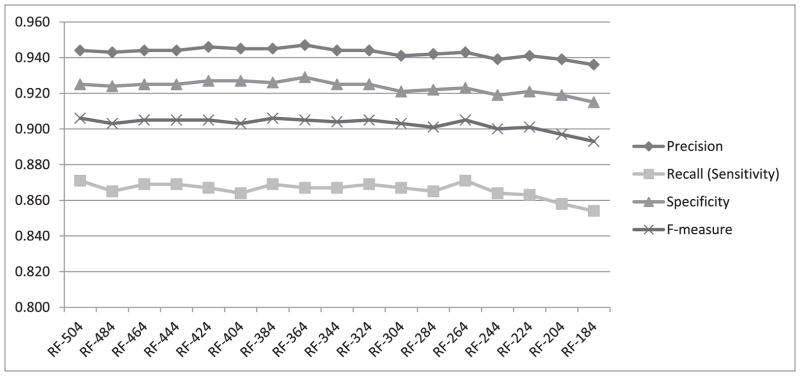
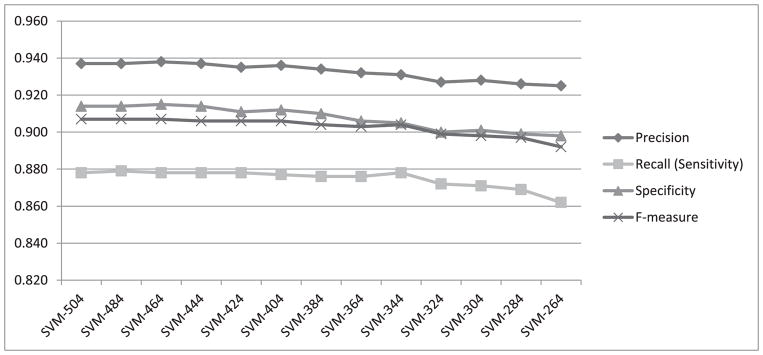
To investigate how the four performance measures change when the number of features is reduced, we first calculated information gain for each feature. The highest information gain was 0.67 and the lowest was 0.001. Fig. 3 shows a histogram of the information gain distribution across features, where the x-axis shows the information gain values and the y-axis shows the number of features associated with each information gain. As values on the x-axis are rounded to 2 decimal points, an information gain of less than 0.01 is shown as zero (the leftmost column on the graph). We observe that more than 300 features (four columns from the left) are associated with a negligible information gain (less than 0.04). We expect that removing some of these features will not lead to significant reduction in the classification performance. Therefore, as described in Section III.C, we gradually removed the least-informative features, 20 at a time, and repeated the heartbeat classification experiment using both random forests and SVM. The change in performance in terms of all four measures using random forests for classification is shown in Fig. 4. All four performance measures fluctuate slightly as we continue removing features until the number of features reaches 264. After that, the performance steadily declines as additional features are removed. All four measures, obtained when using 264 features in our representation, are exactly the same as those obtained when using the complete set of 504 features. We have also plotted the performance measures for SVM while removing 20 features at a time, as shown in Fig. 5. The performance remains almost the same when gradually reducing the number of features from 504 to 404. Beyond that, the performance declines steadily as we remove additional features.
Fig. 3.
Histogram of the information gain distribution across 504 features.
Fig. 4.
Performance measures from heartbeat classification using random forests while gradually removing 20 features at a time.
Fig. 5.
Performance measures from heartbeat classification using SVM while gradually removing 20 features at a time.
The next step in identifying HCM patients was to classify each subject as belonging to one of two classes: HCM or non-HCM. If the percentage of heartbeats classified as HCM was 50% or more, the subject was classified as an HCM patient. Table V shows results of patient classification, where the heartbeats used in the classification were represented based on all 504 features. Random forests and SVM perform almost the same and the marginal difference in performance measures is not statistically significant (p>0.85)
TABLE V.
Results From the Patient Classification Experiment, Where Heartbeats Were Classified Using the Complete Set of 504 Features. Standard Deviation Is Shown in Parentheses
| Classifier | Precision | Recall (Sensitivity) | Specificity | F-measure |
|---|---|---|---|---|
| RF (all features) | 0.84 (0.05) | 0.89 (0.04) | 0.93 (0.02) | 0.86 (0.04) |
| SVM (all features) | 0.83 (0.05) | 0.90 (0.03) | 0.92 (0.03) | 0.87 (0.03) |
As 264 features for the random forests classifier and 404 features for the SVM classifier performed the same as the complete feature set when classifying individual heartbeats, we used the respective reduced feature sets to identify HCM patients based on the number of heartbeats categorized as HCM. Patient classification results are presented in Table VI, where heartbeats were represented using 264 features for random forests and 404 features for SVM. The paired t-tests show no statistically-significant performance-difference between SVM and random forests for classifying patients, when the reduced feature-sets are used for heartbeat classification (p>0.58).
TABLE VI.
Results From the Patient Classification Experiment Where Heartbeats Were Classified Using Reduced Sets of 264 (RF) and 404 (SVM) Features. Standard Deviation Is Shown in Parentheses.
| Classifier | Precisian | Recall (Sensitivity) | Specificity | F-measure |
|---|---|---|---|---|
| RF (264 features) | 0.84 (0.05) | 0.89 (0.04) | 0.93 (0.03) | 0.86 (0.04) |
| SVM (404 features) | 0.82 (0.05) | 0.89 (0.03) | 0.92 (0.03) | 0.85 (0.03) |
The classification results described above show that we were able to achieve high performance level while identifying HCM patients from 12-lead ECG data by classifying individual heartbeats using a set of 504 features. We also demonstrate that reduced feature-sets, obtained by gradually removing the least informative features, performs equally well. The statistical tests applied show that the difference in performance obtained by random forests and by support vector machines is not statistically significant.
V. Conclusion
We have classified individual heartbeats from standard 10-second, 12-lead ECG signals to identify hypertrophic cardiomyopathy (HCM) patients. We have used ECG signals from HCM patients and from non-HCM controls to train and test heartbeat classifiers by applying random forests and support vector machines. A comprehensive set of 504 features extracted from ECG signals was used for heartbeat representation and classification. A subject was identified as a HCM patient if the majority of heartbeats for the patient were classified as HCM. The four performance measures from the patient classification experiment using random forests are: precision 0.84, recall 0.89, specificity 0.93 and F-measure 0.86; similar performance measures were obtained by using SVM, as confirmed by the paired t-test. For comparison, we have also applied the logistic regression method to classify heartbeats, which showed a diminished level of performance compared to both random forests and SVM. We have used the information-gain criterion for selecting highly informative features to represent the heartbeats in the training and in the test set. For random forests, performance measures using 264 selected features were similar to the measures obtained using the complete set of 504 features. For SVM, this was true for a set of 404 informative features.
This work is the first study of its kind, setting out to automatically identify HCM patients from 12-lead ECG signals by classifying heartbeats using machine-learning methods. We have shown that it is possible to attain high performance using random forests or SVMs. We also showed that the information-gain criterion can be effectively used to choose a reduced set of temporal and morphological features that retain a similar level of performance. While in this study we have classified patients simply based on the percentage of individual heartbeats classified as HCM, in future research we shall focus on analyzing and modeling the sequence of heartbeats using advanced machine learning methods.
Acknowledgments
This work was partially supported by HS’s NSERC Discovery Award #298292-2009, NSERC DAS #380478-2009, CFI New Opportunities Award 10437, NIH Grant #U54GM104941, and Ontario’s Early Researcher Award #ER07-04-085, and by TA’s grant HL 098046 from the National Institutes of Health, and a grant from John Taylor Babbit Foundation.
Contributor Information
Quazi Abidur Rahman, Computational Biology and Machine Learning Lab, School of Computing, Queen’s University, Kingston, ON@COMMA Canada.
Larisa G. Tereshchenko, Heart and Vascular Institute, Johns Hopkins University, Baltimore, MD@COMMA USA and Knight Cardiovascular Institute, Oregon Health & Science University, OR, USA
Matthew Kongkatong, Heart and Vascular Institute, Johns Hopkins University, Baltimore, MD@COMMA USA.
Theodore Abraham, Heart and Vascular Institute, Johns Hopkins University, Baltimore, MD@COMMA USA.
M. Roselle Abraham, Heart and Vascular Institute, Johns Hopkins University, Baltimore, MD@COMMA USA.
Hagit Shatkay, Computational Biology and Machine Learning Lab, School of Computing, Queen’s University, Kingston, ON, Canada and Dept. of Computer and Information Sciences & Center for Bioinformatics and Computational Biology, University of Delaware, Newark, DE, USA.
References
- 1.Maron BJ, Salberg L. Hypertrophic Cardiomyopathy: For Patients, Their Families and Interested Physicians. Wiley-Blackwell; 2008. [Google Scholar]
- 2.Maron BJ. The electrocargiogram as a diagnostic tool for Hypertrophic Cardiomyopathy?: Revisited. Ann Noninvasive Electrocardiol. 2001;6(4):277–279. doi: 10.1111/j.1542-474X.2001.tb00118.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rahman QA, Kanagalingam S, Pinheiro A, Abraham T, Shatkay H. What We Found on Our Way to Building a Classifier?: A Critical Analysis of the AHA Screening Questionnaire. In: Imamura K, Usui S, Shirao T, Kasamatsu T, Schwabe L, Zhong N, editors. Proc BHI 2013 LNAI. 2013. Vol. 8211. Springer; Heidelberg: 2013. pp. 225–236. [Google Scholar]
- 4.Kuo S, Dillman R. Computer detection of ventricular fibrillation. Proc of Computers in Cardiology. 1978:347–349. [Google Scholar]
- 5.Clayton RH, Murray A, Campbell RWF. Comparison of Four Techniques for Recognition of Ventricular Fibrillation from the surface ECG. Med Biol Eng Comput. 1993;(31):111–117. doi: 10.1007/BF02446668. [DOI] [PubMed] [Google Scholar]
- 6.Nygards M, Hulting J. Recognition of ventricular fibrillation utilizing the power spectrum of the ECG. Proc of Computers in Cardiology. 1977:393–397. [Google Scholar]
- 7.Llamedo M, Marte J. Heartbeat classification using feature selection driven by database generalization criteria. Biomed Eng IEEE Trans. 2010;58(99):1–1. doi: 10.1109/TBME.2010.2068048. [DOI] [PubMed] [Google Scholar]
- 8.Melgani F, Bazi Y. Classification of electrocardiogram signals with support vector machines and particle swarm optimization. IEEE Trans Inf Technol Biomed. 2008 Sep;12(5):667–77. doi: 10.1109/TITB.2008.923147. [DOI] [PubMed] [Google Scholar]
- 9.Yu S, Chou K. Integration of independent component analysis and neural networks for ECG beat classification. Expert Syst Appl. 2008 May;34(4):2841–2846. [Google Scholar]
- 10.Emanet N. ECG beat classification by using discrete wavelet transform and Random Forest algorithm. Proc. Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control; 2009. pp. 1–4. [Google Scholar]
- 11.De Chazal P, Reilly RB. patient-adapting heartbeat classifier using ECG morphology and heartbeat interval features. IEEE Trans Biomed Eng. 2006;53(12):2535–2543. doi: 10.1109/TBME.2006.883802. [DOI] [PubMed] [Google Scholar]
- 12.Savage DD, Drayer JI, Henry WL, Mathews EC, Ware JH, Gardin JM, Cohen ER, Epstein SE, Laragh JH. Echocardiographic assessment of cardiac anatomy and function in hypertensive subjects. Circulation. 1979 Apr;59(4):623–632. doi: 10.1161/01.cir.59.4.623. [DOI] [PubMed] [Google Scholar]
- 13.Cohen A, Hagan AD, Watkins J, Mitas J, Schvartzman M, Mazzoleni A, Cohen IM, Warren SE, Vieweg WVR. Clinical correlates in hypertensive patients with left ventricular hypertrophy diagnosed with echocardiography. Am J Cardiol. 1981 Feb;47(2):335–341. doi: 10.1016/0002-9149(81)90406-9. [DOI] [PubMed] [Google Scholar]
- 14.Carr AA, Prisant LM, Watkins LO. Detection of hypertensive left ventricular hypertrophy. Hypertension. 1985 Nov;7(6_Pt_1):948–954. doi: 10.1161/01.hyp.7.6.948. [DOI] [PubMed] [Google Scholar]
- 15.Schillaci G, Battista F, Pucci G. A review of the role of electrocardiography in the diagnosis of left ventricular hypertrophy in hypertension. J Electrocardiol. 2012;45(6):617–23. doi: 10.1016/j.jelectrocard.2012.08.051. [DOI] [PubMed] [Google Scholar]
- 16.Kaiser W, Faber TS, Findeis M. Automatic learning of rules. A practical example of using artificial intelligence to improve computer-based detection of myocardial infarction and left ventricular hypertrophy in the 12-lead ECG. J Electrocardiol. 1996 Jan;29(Suppl):17–20. doi: 10.1016/s0022-0736(96)80004-5. [DOI] [PubMed] [Google Scholar]
- 17.Warner RA, Ariel Y, Gasperina MD, Okin PM. Improved electrocardiographic detection of left ventricular hypertrophy. J Electrocardiol. 2002 Jan;35(Suppl):111–5. doi: 10.1054/jelc.2002.37163. [DOI] [PubMed] [Google Scholar]
- 18.Corrado D, McKenna WJ. Appropriate interpretation of the athlete’s electrocardiogram saves lives as well as money. Eur Heart J. 2007 Aug;28(16):1920–2. doi: 10.1093/eurheartj/ehm275. [DOI] [PubMed] [Google Scholar]
- 19.Potter SLP, Holmqvist F, Platonov PG, Steding K, Arheden H, Pahlm O, Starc V, McKenna WJ, Schlegel TT. Detection of hypertrophic cardiomyopathy is improved when using advanced rather than strictly conventional 12-lead electrocardiogram. J Electrocardiol. 2010 Jan;43(6):713–8. doi: 10.1016/j.jelectrocard.2010.08.010. [DOI] [PubMed] [Google Scholar]
- 20.Laguna P, Jane R, Bogatell E, Anglada D. [Accessed: 10-May-2014];ECGPUWAVE. [Online]. Available: http://www.physionet.org/physiotools/ecgpuwave/
- 21.De Chazal P, O’Dwyer M, Reilly RB. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans Biomed Eng. 2004;51(7):1196–1206. doi: 10.1109/TBME.2004.827359. [DOI] [PubMed] [Google Scholar]
- 22.Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. [Google Scholar]
- 23.Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;297:273–297. [Google Scholar]
- 24.Le Cessie S, Van Houwelingen J. Ridge estimators in logistic regression. Appl Stat. 1992;41(1):191–201. [Google Scholar]
- 25.Subasi A, Erçelebi E. Classification of EEG signals using neural network and logistic regression. Comput Methods Programs Biomed. 2005 May;78(2):87–99. doi: 10.1016/j.cmpb.2004.10.009. [DOI] [PubMed] [Google Scholar]
- 26.Eilers PHC, Boer JM, van Ommen G-J, van Houwelingen HC. Classification of microarray data with penalized logistic regression. Proc. BiOS 2001 The International Symposium on Biomedical Optics; 2001. pp. 187–198. [Google Scholar]
- 27.Liao JG, Chin KV. Logistic regression for disease classification using microarray data: model selection in a large p and small n case. Bioinformatics. 2007 May;23(15):1945–1951. doi: 10.1093/bioinformatics/btm287. [DOI] [PubMed] [Google Scholar]
- 28.Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software. ACM SIGKDD Explor Newsl. 2009 Nov;11(1):10. [Google Scholar]
- 29.Genuer R, Poggi J-M, Tuleau C. Random Forests: some methodological insights. 2008 Nov; arXiv:0811.3619v1 [stat.ML] [Google Scholar]
- 30.Genuer R, Poggi JM, Tuleau-Malot C. Variable selection using random forests. Pattern Recognit Lett. 2010 Oct;31(14):2225–2236. [Google Scholar]
- 31.El-Manzalawy Y. [Accessed: 15-Mar-2015];WLSVM: Integrating LibSVM into Weka Environment. [Online] available: http://weka.wikispaces.com/LibSVM.
- 32.Dietterich TG. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. Neural Comput. 1998 Oct;10(7):1895–1923. doi: 10.1162/089976698300017197. [DOI] [PubMed] [Google Scholar]
- 33.Mitchell TM. Machine Learning. McGraw-Hill; 1997. p. 432. [Google Scholar]
- 34.Fayyad U, Irani K. Multi-interval discretization of continuous-valued attributes for classification learning. Proc. Thirteenth International Joint Conference on Articial Intelligence; 1993. pp. 1022–1027. [Google Scholar]
- 35.Hypertrophic cardiomyopathy. Mayo Clinic; [Accessed: 20-Apr-2015]. [Online]. Available: http://www.mayoclinic.com/health/medical/IM00586. [Google Scholar]
- 36. [Accessed: 20-Apr-2015];ECG wave. [Online]. Available: http://lifeinthefastlane.com/ecg-library/basics/t-wave/