Twist-Induced Defects of the P-SSP7 Genome Revealed by Modeling the Cryo-EM Density

Abstract

We consider the consequences of assuming that DNA inside of phages can be approximated as a strongly nonlinear persistence length polymer. Recent cryo-EM experiments find a hole in the density map of P-SSP7 phage, located in the DNA segment filling the portal channel of the phage. We use experimentally derived structural constraints with coarse-grained simulation techniques to consider contrasting model interpretations of reconstructed density in the portal channel. The coarse-grained DNA models used are designed to capture the effects of torsional strain and electrostatic environment. Our simulation results are consistent with the interpretation that the vacancy or hole in the experimental density map is due to DNA strain leading to strand separation. We further demonstrate that a moderate negative twisting strain is able to account for the strand separation. This effect of nonlinear persistence length may be important in other aspects of phage DNA packing.

INTRODUCTION

The packaging of DNA genomes inside of bacteriophages is essential to their lifecycle. During the packaging process, a phage will load a single molecule of nucleic acid, here double-stranded DNA, usually on the order of several kilobasepairs (kbp) in length, into a highly condensed state within the volume enclosed by the mature phage’s protein capsid shell. This process is performed solely by the phage’s ATP-driven motor.^1,2 Many theoretical^3–7 and experimental studies^1,8 have been performed to understand the basic thermodynamic properties of DNA inside of such a confined environment. It has been proposed that DNA has a highly ordered “inverse-spool” structure inside of the phage.⁵ Within such a model, the bending energy of DNA is assumed to follow that of a linearly elastic rod. The Harvey group has proposed an alternate model that assumes that the DNA can form a somewhat less ordered, spooled toroid^7,9,10 but that still assumes that the DNA always behaves with a linearly elastic bending force. This work successfully reproduces the ring-like density map of DNA inside of the ϕ29 phage observed in the cryo-electron microscopy (cryo-EM) experiment.⁸ It is partially able to describe the force needed to load the DNA into the ϕ29 phage observed by optical tweezer experiments.¹ These previous works are all important steps in understanding the structures of the DNA inside of phages; however, some questions remain.

A recent simulation¹¹ has shown that the ring-like conformation of the density map is strongly linked to the correlation between the DNA and the inner wall of the phage capsid, rather than the polymeric structure of the DNA itself. The authors demonstrated that even unconnected pieces of DNA six base pairs (bps) in length, for the entire phage genome, reproduce the ring-like density map upon confinement. Thus, more disordered structures are not necessarily excluded from consideration by the structural data.

Whether DNA inside of the phage can be sufficiently approximated as a perfectly linearly elastic bending rod thus also needs to be re-examined. In a recent cryo-EM experiment, a hole was observed in the density map of P-SSP7 phage,¹² located within a short DNA segment filling the portal channel of the phage. There are two hypotheses that might account for the hole: (1) several bps melt, forming a bubble; (2) DNA forms a structure with extremely high curvature locally and attaches to the wall of the channel. The hole is the result of averaging many such curved conformations. Curved DNA has been observed in the portal portion of the phage ϕ29.^13,14 Clearly, the first hypothesis implies a large departure away from modeling the DNA as a perfectly linearly elastic rod; as such, defects would dramatically decrease the persistence length of DNA and the bending energy. Simulations have shown that the bending energy could account for as much as 22% of the total energy.⁷ Therefore, this could have substantial implications on the interpretation of thermodynamic properties of DNA inside of the phage.

To explore the most probable interpretation of the question, in this work, we used a constrained simulation method to reproduce the density map of P-SSP7 observed in the experiment. This type of method has been developed to fit high-resolution structures by combining simulations with experimental density maps. It has proven useful to obtain all-atom model structures of proteins and DNA complexes.^15,16

The P-SSP7 genome is more than 40 kbp long, making it inconvenient to use atomistic simulations to explore this problem. In addition, it is inefficient to explore the constrained configuration space using the all-atom simulations. Thus, coarse-grained (CG) models can be employed to represent DNA at lower resolutions,^17–19 reducing the complexity of the computation. Here, we used a previously developed CG model^20,21 extended to explicitly consider the effects of salt and torsional strain.²² Despite its relatively lower resolution compared with all-atom models, our simulation results below clearly show that the hole in the density map is due to bps being locally melted or flipped out. Given the two hypotheses above, our results support the idea that the DNA inside of the phage has structural defects.

We further explore possible reasons for nonlinear persistence length behavior such as base flipping. It has been shown experimentally that negative twist is imparted during the DNA packaging process.²³ The effect of such twist on the final structure of DNA is debatable. It has been reported that DNA could form different structures with twist and without twist.²⁴ However, others have suggested that the torsional stress may have little, if any, effect on the structure of DNA under the assumption that the twist energy is able to relax quickly.²⁵ Recently, experiments found that DNA packaging is a nonequilibrium and quite slow relaxation process.²⁶ In addition, all of the aforementioned models assumed no structural defects along the DNA under twist.

It has been found, both by simulation and experiment, that DNA under mild negative (and extreme positive) twist spontaneously forms defects such as kinks and single-stranded bubbles.^27–29 Further investigation indicates that those defects are strongly sequence-dependent and often localized.³⁰ By simulating DNA under appropriate twist (without the experimental density map fitting), here we qualitatively reproduced the density map with the hole. The location of the hole is assigned to an AT-rich tract, which qualitatively matches the prediction by an analytic thermodynamic model.²² In addition, this analytic model indicates that the hole in the density map is probably not the only defect within the DNA. There may in fact be a large number of defects distributed along the DNA inside of the capsid that are not detectable after averaging. Our results indicate a need for new models with which to further investigate the DNA packaging problems.

Below, we describe our model in relation to the experimental cryo-EM density.¹² CG models of both the DNA and the portal wall were used to represent the filling with DNA of the portal channel of the phage. The results are discussed in terms of the known nonlinear behavior of DNA under negative twisting strain.

MATERIAL AND METHODS

We focused on a small segment of the P-SSP7 ds-DNA genome close to its terminus, where the hole was observed in the density map.¹² The exact number of bps in this segment is not clear from experiment. However, the length of the visible DNA filling the channel in the entire portal vertex is roughly 250 Å (~75 bps, assuming B-form DNA). Thus, we chose the last 80 bps in the terminus of the P-SSP7 genome³¹ to investigate in this work. The detailed sequence information can be found in the Supporting Information (sequence A).

CG Model and Simulation Protocols

The CG model used to represent DNA molecules can be found in our previous work.²² In short, a Debye–Hückel potential³² was added to the original model to represent the effects of local electrostatics and salt concentration.²⁰ This model is able to represent accurate melting temperatures for DNA molecules with given sequences, which makes it powerful to explore the sequence-dependent characteristics of DNA molecules. The temperature was set to 310 K. Newtonian dynamics was applied for sampling, and the Andersen thermostat method³³ was used to maintain the temperature. Ionic strength was set to 0.1M.

Three Simulation Models Used to Reproduce the Experimental Density Map

Model A: Cryo-EM-Derived Potential Constraints

The cryo-EM map was obtained from previous experiments.¹² The bin size from the reconstructed density was 2.34 Å. To model the DNA filling the portal channel of the phage, a potential term, V_EM, was added to the Hamiltonian of the DNA model. This term, which mimics the wall and motor protein interaction, is given by

$$V_{\mathrm{E}\mathrm{M}}(x,y,z)=\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}\phi <0\hfill \\ \hfill \epsilon \times (-\phi (x,y,z))\hfill & \hfill \text{else}\hfill \end{array}$$ (1)

ε = 4.14 × 10⁻¹⁹ J. The value of density, φ, can be directly read from the cryo-EM map. All negative numbers from the deposited experimental density were screened in order to reduce the noise. Thus, the EM potential biases the DNA to the positions with the highest value of φ. However, the DNA structural Hamiltonian should prevent grossly unphysical structures. The width or diameter of constraint (from left to right in Figure 1C) is 16.4 Å, and the length (from top to bottom in Figure 1C) is 217.6 Å, which covers the region of the “hole” seen in the experimental density map. In order to mimic capping interactions and prevent the DNA drifting away from the region of V_EM, the first bp of the DNA was restrained by the harmonic potential V_first = k(z − z₀)², where z is the coordinate of the first bead in the direction of the main axis of the DNA and k = 0.114 J/m². Besides V_EM and V_first, there is no extra twisting or pulling force on the DNA in model A. The simulation was initiated from normal B-form DNA. The whole simulation time (after equilibrium) was 1.5 µs. The density map was processed for visualization using VMD.³⁴ The simulation was averaged over 10 000 different configurations.

Figure 1.

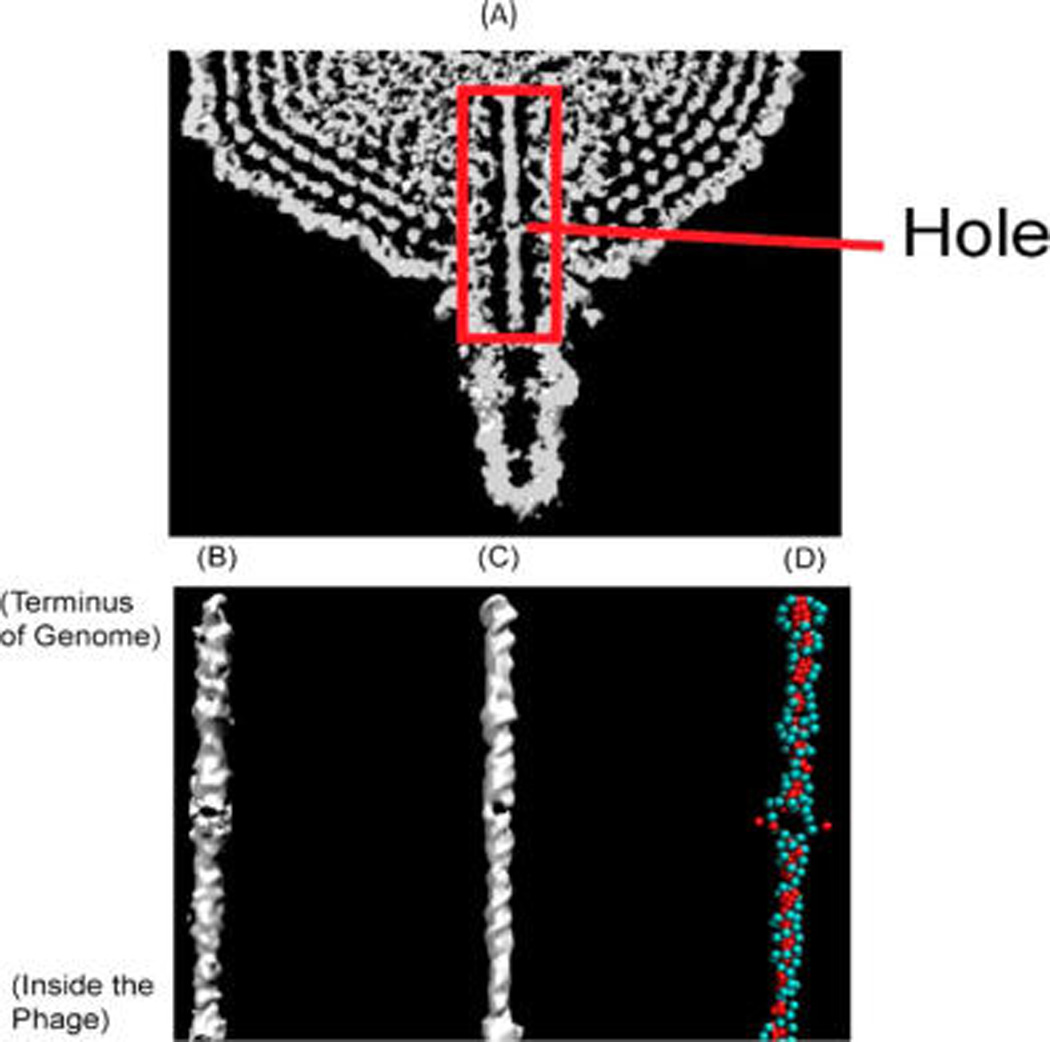
Comparison of the density map between experiment and simulation. (A) Cryo-EM density map from experiment for the phage from ref 12. The red box indicates the region investigated in this work. (B) Cryo-EM density map from the experiment for DNA in the channel (ref 12). (C) Density map produced by simulation with cryo-EM fitting. (D) Snapshot of the DNA structure from a simulation. The backbone beads are represented in cyan, and the base beads are red.

Model B: Twisted DNA without Cryo-EM Fitting

As a control, simulations were performed on the same sequence of DNA in a simple linear channel rather than the cryo-EM fitting potential. A mechanical twist for simulation was induced by using a variant of periodic boundary conditions.³⁰ The negative twist was thus not able to be released under such periodic boundary conditions, representing the “cap” effect (see more discussion about the cap effect below). Three different relative linking numbers σ were tested: −0.33, −0.2, and −0.067. The stress was initially distributed along the DNA evenly so that the resulting twist angle of each bp was 22.5, 27, and 31.5°, corresponding, respectively, to each case of the different relative linking numbers. To simulate within the portal channel, besides the twist, we added channel restraints on the linear DNA segment. The DNA segment inside of the portal channel cannot move completely freely in 3D because it is constrained by the protein channel wall. Moreover, although the details have not been fully resolved experimentally in the case of P-SSP7, there are important electrostatic interactions between the DNA and the portal proteins.²³ To simplify the problem, a harmonic potential in eq 2 was also used in this group of simulations and applied to the “backbone” beads of the model

$$V_{\text{res}}=k{(r-r_0)}^2$$ (2)

k = 0.0057 J/m², where r₀ is the initial position of DNA in the simulation. This harmonic potential roughly represents the interactions between DNA and the channel. Although this is a low-level approximation, our studies indicate that there are not only steric interactions between DNA and the channel but effective attractive forces. Electrostatic interactions between DNA and channel proteins play an important role in determining the DNA configuration inside of the channel (see the Results and Discussion section). Without knowing precise atomic-level information about the channel proteins, here we model the interaction as a harmonic potential.

Model C: Twisted and Stretched DNA without Cryo-EM Fitting

A twisted and stretched DNA model was also simulated. We first built a twisted DNA as in model B. Then, we increased the rise of each bp from 3.3 to 4.6 Å (the twisting angle remained the same). As a result, the whole 80 bp DNA was “pulled” from 266 to 368 Å. This served as the initial configuration in the simulation. To model the exteral forces, as before, we used the periodic boundary conditions.³⁰ The total length of stretched DNA (368 Å) did not change in the simulation. All simulations were repeated 240 times, initiated from different random velocity seeds. Each simulation was performed for 150 ns. The density map was calculated and processed for visualization by VMD.³⁴ The final calculation was averaged over a total of 19200 configurations from the above 240 different simulations.

RESULTS AND DISCUSSION

Fitting the Experimental Cryo-EM Density Map

An intriguing part of the experimental density map of P-SSP7 phage is the hole in the portal channel (Figure 1A and B). We first tested whether we could reproduce the hole in the density map from simulations. Using the cryo-EM constrained fitting method above (Figure 1C), a hole was clearly visible in the simulated density map. The hole forms near the middle of this DNA segment, which matches with the experiment. In addition, its dimension is similar to the experimental value of ~14 Å.

As mentioned, there are at least two possible explanations for the appearance of the hole in the refined structure: (1) a DNA strand split from local melting and (2) DNA bent and associated with the wall of the channel with high curvature and the “hole” is the result of averaging many such ring-like structures. Figure 1D is a typical snapshot of our simulations. It is clear that in the sequence position of the hole, about four adjacent bps flipped out and the strands split in this location. Because the Hamiltonian of our model has no bias toward either of the two hypotheses above, our simulation strongly supports that the hole is due to a strand split. Notice that the EM hole is not the only position that has the bp opening observed in Figure 1D. There are other places where the hydrogen bonds between complementary bps show local melting with a reasonable probability as well.

Structural Defects of DNA under Negative Twist

Although we have already reproduced the density map in the experiment, the setup of the initial conditions of the simulation is biased by the existing experimental data. Next, we probe the reason for the defect formations. It is known that during the genome packaging process, DNA is negatively twisted due to the motor-portal rotation.²³ Both experiments and simulations indicate that twisted DNA can show structural defects such as kinks and bubbles from local melting into two single strands.^28,29 Thus, control simulations on mildly twisted DNA without any extra cryo-EM fitting constraint potentials were performed in order to investigate the dependence of the defects on the torsional stress along the DNA.

We note that the density map showing the apparent strand split in the experiment was after genome packaging was complete. Therefore, a specific mechanism would need to exist in order to maintain the twist along the DNA molecule. The end toward the inner part of the phage can be approximately treated as locked in place or “capped” because DNA forms a very highly condensed state inside of the phage, for example, the osmotic pressure inside of the phage was estimated to be as high as 40 atm^4,35,36 for phage λ. In such a crowded environment, it is difficult for the entire DNA molecule to move much to fully relax the stress. As for the other end (marked as “Terminus of Genome” in Figure 1B), it has been reported that six nozzle proteins toward the central axis cap the tip of the DNA terminus.¹² On the basis of the above discussions, we assume that a restraint mechanism exists on both ends of the DNA segment, filling the portal channel. Thus, in this simulation, a permanent twist was imposed upon the DNA segment through periodic boundary conditions.³⁰

The density map produced by the control simulation qualitatively matches with the experimental result (Figure 2A). There is a clear split in the DNA segment. This hole is due to bps being flipped out, and its dimension is similar to the experimental result of 14 Å. Importantly, the existence of this hole is dependent upon both the sequence and the amount of torsional stress on the DNA. Of the three different cases of σ (relative linking number) tested, only in the case containing high twist (σ = −0.33) was the hole formed within the control simulations, while under minor twist, σ = −0.2 (Figure 2B) and −0.067 (Figure 2C), there was no hole. This result sets a lower bound on the strength of the torsional stress along the genome required to locally melt the sequence of interest.

Figure 2.

Density map produced from simulations of twisted DNA without the cryo-EM portal channel fitting potential; σ = (A) −0.33, (B) −0.2, and (C) −0.067.

We next probed the sequence dependence of the defects. Indeed, if the defect could appear in any position, the hole-like signal would be smeared in the density map by averaging images. It is known that under negative twist, the location of defects is strongly sequence-dependent. More specifically, when DNA has torsional stress, the stress will localize in the weak point along the DNA sequence rather than be distributed evenly along the whole DNA.^22,30 Roughly speaking, the “bp open” state more likely happens in the AT tract segments.

The free energy of each bp (i.e., change between the duplex and pairs of single-strand DNA) from simulation (black line) versus theory (red line)²² is shown in Figure 3. The free energies have different reference states and have been shifted vertically for comparison. The P-SSP7 channel subsequence that has the highest free energy, meaning the highest probability to open (most unstable), is ATATTA (marked with a black arrow). There are other places that have high relative probabilities to open as well. The free energies of those places are ~0.25 kcal/mol or more lower than the peak of the free-energy profile (ATATTA part). By adjusting the contour threshold when producing the density map, we can also observe holes in those places in the averaged density map. This also matches our previous simulation result that there are multiple positions having bp openings along the DNA (Figure 1D). Nevertheless, the ATATTA subsequence is the most unstable position and has six continuous bps, which makes it the dominant place where the strand splits.

Figure 3.

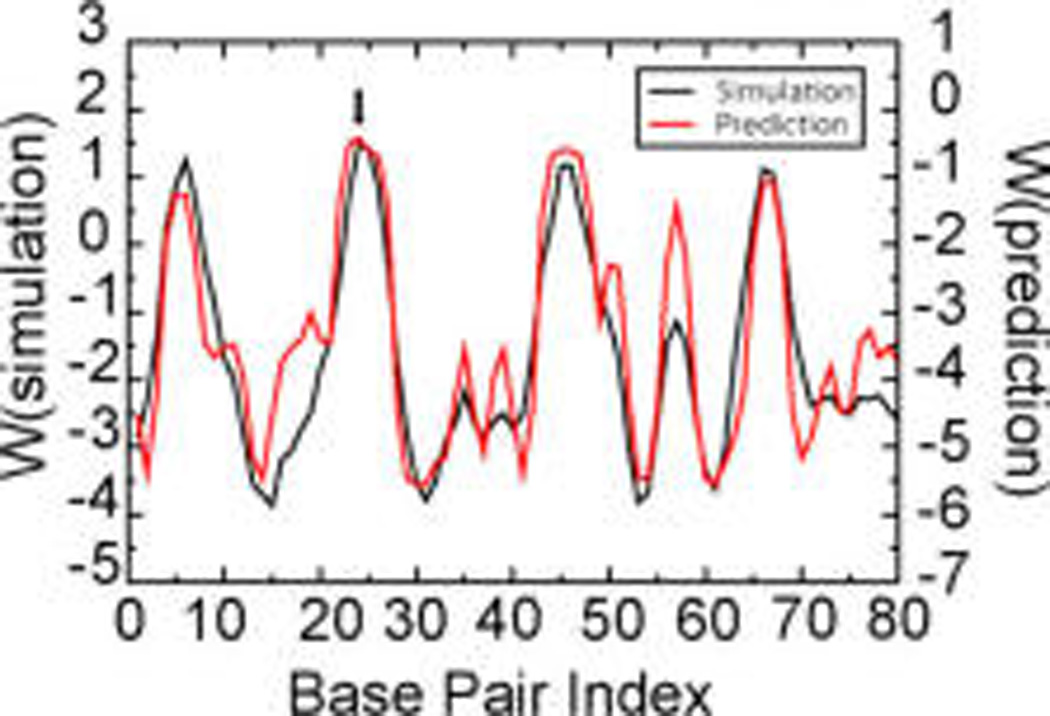
Free energy, W, of each bp to open up obtained by simulation (black line) and theoretical prediction (red line) for sequence A (see the Supporting Information). The units are kcal/mol.

We also tested a different DNA sequence (sequence B in the Supporting Information) for two reasons. First, there is little experimental evidence showing which end of the P-SSP7 genome (3′ end or 5′ end) enters the phage first. Second, it helps to check the sequence dependence of the split location. From Figure S1 (Supporting Information), we can see that this sequence is also capable of creating a clear hole in the density map. The sequence at this location is TTTA, also an-AT rich tract. Before more experimental results are available, we cannot verify the actual sequence; however, both cases support the fact that the location of the hole is strongly sequence-dependent.

We note here that mild torsional stress alone is not enough to reproduce the split in the density map. The interactions between DNA and portal proteins are necessary to reproduce the split seen for the sequences considered. The effect of confinement of DNA molecules by the portal channel is nontrivial. In addition, we hypothesize that a variety of detailed DNA–protein interactions exist. Unfortunately, due to lack of experimental data on the all-atom structures of the portal proteins, it is difficult to model the interaction between DNA and the portal atomically accurately. However, we tested two other cases: (1) twisted DNA without any other constraints and (2) twisted DNA plus a pure repulsive interaction by portal proteins. We find that there is no hole in the averaged density map in either case. Indeed, the hole in the density map indicates both a low density in the center and a higher density at the edges, and therefore, this high density at the edges implies that there should be strong correlations inducing effective attractions between DNA and portal proteins. In our simulation, we simplified the case and used position constraint to model the effective interactions. If we remove such a constraint or change to a pure repulsive interaction, the density is low at both the center and edges due to averaging, which leads to an absence of density or a “breaking layer” instead of a “hole” (Figure S2, Supporting Information). The interactions between DNA and portal proteins can be better modeled when more experimental data are available.

Although simulations of twisted DNA can reproduce the hole with similar size to the experimental result, a careful comparison of the simulation and experimental results shows that the absolute position of the hole in the simulation (Figure 4A) is slightly higher than that in the experiment (Figure 4B). In simulation, the distance between the hole and the terminus of the P-SSP7 genome is 73–90 Å. If we assume that the shift for the base stack along the main axis of DNA is around 3.3 Å, then 73–90 Å corresponds to bp 22–27. The bp 22–27 is ATATTA (setting the index of the end of P-SSP7 to 1) and happens to be a place having high probability to open, as detailed above. In contrast, the distance in the experiment between the hole to the terminus of the P-SSP7 genome is about 105–119 Å, corresponding to bp 31–36. There is a 10 bp (about one B-form turn) difference between simulation and experiment. However, bp 31–36 is GCCGAC, which should be much more stable compared to the rest AT tract position. There are several possible reasons for this difference. First, as detailed above, the position of the hole is strongly sequence-dependent. A slight change or shift in the sequence can change the position of the strand split. Second, the DNA in the portal channel may be slightly stretched from the motor proteins’ strong interactions. Theoretical models²³ have been proposed that suggest that there may be pulling forces between DNA and portal proteins by electrostatic interactions.

Figure 4.

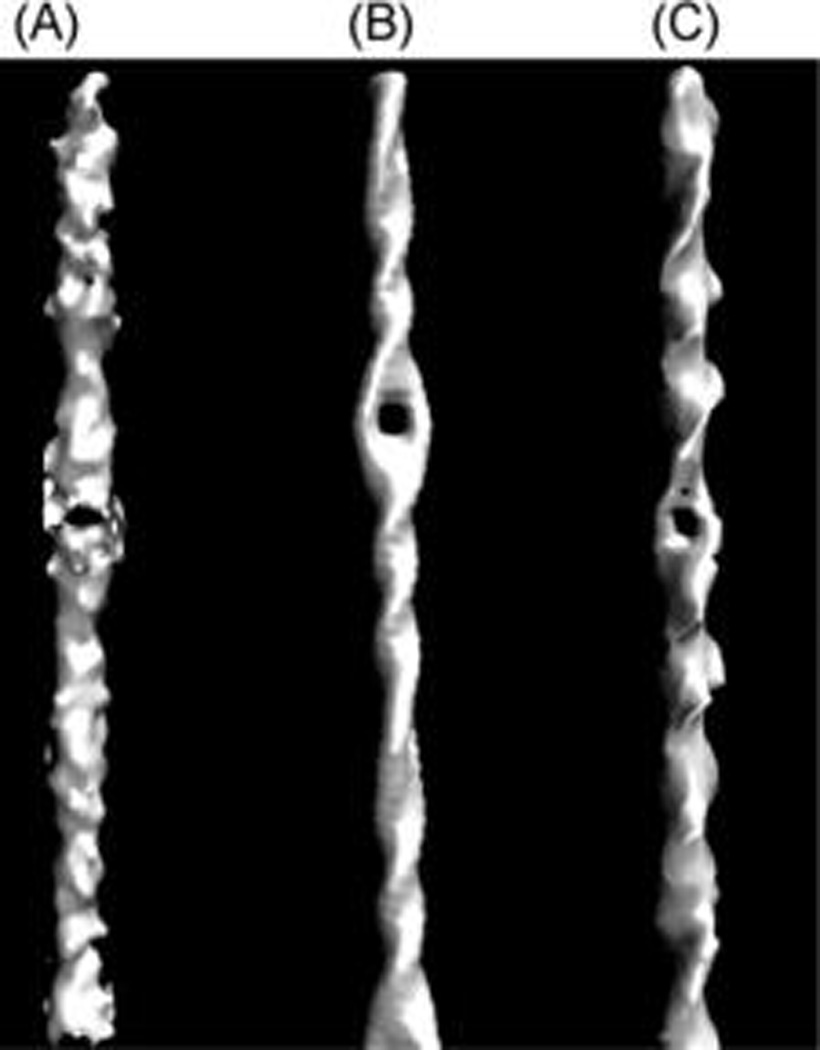
Comparison of the density map between experiment and simulation. (A) Cryo-EM map from experiment (reproduced from ref 12). (B) Density map produced from simulations on a twisted DNA without cryo-EM fitting. (C) Density map produced from simulations on a twisted and stretched DNA without cryo-EM fitting.

We performed similar simulations in which the same DNA sequence was both twisted and stretched. Without changing the overall profile of the density map, the position of the hole in the simulation becomes similar to that in the experiment (Figure 4C). The pulling force needed in the simulation is about 126 pN, comparable to the value for the packing forces obtained in other studies.^1,7

Potential Defects of the Whole P-SSP7 Genome

Although there is only one hole in the density map in the portal region, it does not mean that this is the only place in the genome that could potentially have a defect. In fact, many more potential defects may exist inside of the capsid; however, due to lack of position constraint associated with the portal channel, those defects would not show in the density map after averaging tens of thousands of structures. We applied a previously developed analytical method²² to qualitatively predict the unstable segments for the whole P-SSP7 genome. First, we tested the accuracy of this model by simulating the 80 bp DNA segment simulated in this work (Figure 3, red line). The theoretical prediction successfully shows the same unstable positions (high free energy) and stable positions (low free energy) as the simulation result. The absolute value of the prediction is 2 kcal/mol lower than the value obtained in the simulation (Figure 3, black line). This is because the parameters used in the analytical model were obtained when σ = −0.0857 and not to the level of twist (σ = −0.33) used in the simulations here. As a result, there is a shift in the free-energy profile. Given the change in reference state, the analytical result gave a successful prediction of the unstable segment, and the whole profile highly correlated with the simulation result with the correlation coefficient as high as 0.89 (Figure 5A), verifying the accuracy of the model.

Figure 5.

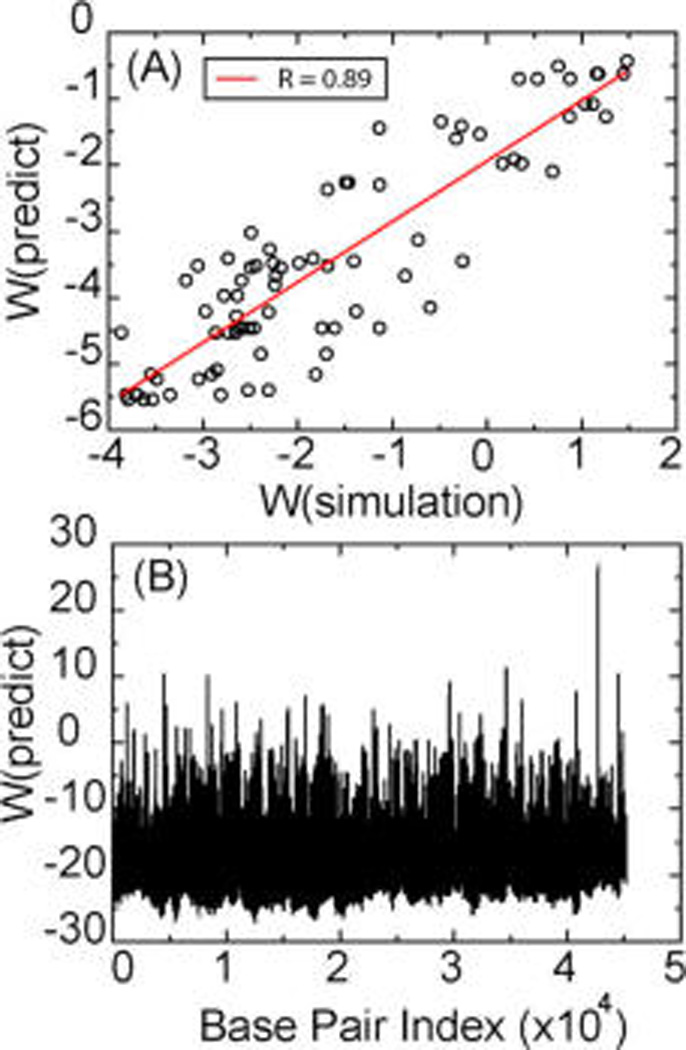
Free energy, W, of each bp to open. (A) Correlation between simulation and theoretical prediction for sequence A (See the Supporting Information). (B) Theoretical prediction of the free energy of each bp for the whole P-SSP7 genome. W is in kcal/mol.

We then applied this model to the whole P-SSP7 genome (Figure 5B), and it is clear that there are a variety of unstable segments under this amount of twist. We found that there are over 10% of the bps of the whole genome with high free energy (>2 kcal/mol), suggesting the potential to form twisting stress-induced bubbles. A continuous 20 bp segment from bp 42692 to 42714 has a very high probability for local melting. Currently, the traditional method to model DNA packaging is to assume that DNA is an elastic rod with a linear bending force. Our results indicate that the thermodynamic properties of DNA may differ from the perfectly linear elastic model due to thermodynamically accessible structural defects.

CONCLUSION

We considered the origin of the hole-like feature in the portal channel of P-SSP7 seen experimentally. Our results are consistent with the possibility that the feature is due to multiple bps melting along the DNA in the P-SSP7 phage portal. Our results are inconsistent with the hypothesis that the hole-like feature is induced by local high curvature of the DNA structure. Indeed, our simulations show that this hole is about 4 bps in length, much shorter than the dsDNA persistence length, such that it would be very difficult to bend the DNA without disrupting stacking and the hydrogen bonds between complementary bps.

Considering that the hole appears in the same average position in the phage, mechanistically, we considered two different interpretations to explain the local melting: (1) it is due to effective attractive forces between portal proteins in a specific location and any bp (nonspecific); this attraction force is large enough to pull the dsDNA apart locally; (2) it is due to the torsional stress (σ has to be larger than 0.2) induced by the rotation of motor proteins.²³ In this case, specific bps will unstack and break their hydrogen bonds, forming a bubble. Without more information about the portal proteins, we have not totally excluded hypothesis 1. However, in this article, we showed that hypothesis 2 is enough to reproduce the experimental EM density map. Clearly, the sequence dependence distinguishes these two hypotheses and thus can be used to design mutation experiments to further test possible mechanisms. In the case of the P-SSP7 genome, under torsional stress, the bps flipped out were identified as ATATTA or TTTA segments (depending on which end of the genome enters into the capsid first). If the strand split is due to the torsional stress, then mutating those positions from A/T to C/G would make the hole disappear or move to other places in the density map; otherwise, hypothesis 1 is more likely the truth. Problems in assembly could prevent a simple realization of such a change.

The models proposed are not without caveats. The channel sequence has been inferred from the genome. The actual filling direction is not experimentally well-established. Nonetheless, the model that we propose allows the DNA to relax by forming strand separations rather than be very tightly wound within phage capsids. These structural defects along the genome can greatly affect the thermodynamics within phage capsids. Previous simulation³⁷ and analytical studies^38,39 found that single-stranded bubble defects can switch the bending free energy of DNA molecules from essentially quadratic to a linear function. This predicts that because the forces change in this case, the pressure inside of the capsid will be affected. Currently, the investigation of DNA packing inside of phages focuses on elastic bending energies,⁴⁰ long-range electrostatic interactions,⁷ and DNA–DNA attractions.¹⁰ DNA sequence-dependent structure defects may serve as another important factor when studying such packing problems.