Plasmonic Nanopores for Trapping, Controlling Displacement, and Sequencing of DNA

Abstract

With the aim of developing a DNA sequencing methodology, we theoretically examine the feasibility of using nanoplasmonics to control the translocation of a DNA molecule through a solid-state nanopore and to read off sequence information using surface-enhanced Raman spectroscopy. Using molecular dynamics simulations, we show that high-intensity optical hot spots produced by a metallic nanostructure can arrest DNA translocation through a solid-state nanopore, thus providing a physical knob for controlling the DNA speed. Switching the plasmonic field on and off can displace the DNA molecule in discrete steps, sequentially exposing neighboring fragments of a DNA molecule to the pore as well as to the plasmonic hot spot. Surface-enhanced Raman scattering from the exposed DNA fragments contains information about their nucleotide composition, possibly allowing the identification of the nucleotide sequence of a DNA molecule transported through the hot spot. The principles of plasmonic nanopore sequencing can be extended to detection of DNA modifications and RNA characterization.

The past 10 years have witnessed a dramatic reduction of DNA sequencing costs enabled by the emergence of several disruptive sequencing technologies.¹ As the costs of sequencing a human genome falls below $10,000, the overall sequencing speed, genome coverage, and accuracy of the sequence detection become the priority for future technology development.¹ Nanopores have emerged as a promising platform for DNA sequencing,²⁻⁴ culminating with the reports of DNA sequence readout obtained using biological nanopore MspA^5,6 or α-hemolysin⁷ and a DNA-processing enzyme phi29 polymerase.

Despite the great achievements, sequencing methods based on biological nanopores have several intrinsic limitations. In particular, the processing enzymes and lipid bilayers used to control DNA transport are fragile at high salt conditions required for DNA sequence readout based on nanopore ionic current. The enzymes are also known to skip and backstep^5,7 along the DNA strand in a stochastic manner, introducing deletion and insertion errors in the recorded sequence. Moreover, the enzymes are difficult to synchronize, and large arrays of biological membranes are difficult to manufacture, making parallel multiplex detection with biological nanopores problematic when compared to large arrays of solid-state nanostructures that are common in electronics.

Synthetic solid-state nanopores present attractive systems for single-molecule analysis because of their potential to overcome many of the limitations of their biological counterparts while being compatible with a wide spectrum of molecular characterization techniques.⁸⁻¹² The high speed of DNA transport through conventional solid-state nanopores,¹³⁻¹⁷ however, limits the residence time of DNA nucleotides inside the nanopore to less than a few microseconds. Combined with a higher (than that in biological pores) ionic current noise,¹⁸ such residence time is too short to identify the chemical structure of the nucleotides.^3,4,17 Much effort has been placed into solving this problem, including attempts to slow transport using optical tweezers,¹⁹ magnetic beads,²⁰ and other methods.²¹⁻²⁶ None of these attempts, however, has yielded the desired level of control.

Plasmonic nanopores are conceptually a novel type of nanoscale device that combines plasmonic nanoantennas with the solid-state nanopores²⁷ (Figure 1). The key element of the plasmonic nanopore systems is metallic nanostructures that, when illuminated with light, can focus the optical field to nanometer-size hot spots.²⁸ The high local optical field produced by the plasmonic nanostructures can be used to control the nanopore resistance²⁹ and apply optical forces directly to nanoscale objects. For example, plasmonic forces were used to manipulate micrometer- and nanometer-size dielectric beads,^30,31 living cells,³² and even single proteins.³³⁻³⁵ Placement of plasmonic nanostructures in proximity of the nanopore can enable, in principle, application of optical forces directly to DNA molecules. Plasmonic nanopore systems featuring a gold bow tie structure with a nanopore in the gap of the bow tie have already been manufactured²⁷ and used for DNA translocation measurements.³⁶ Plasmonic particles have been used to control temperature inside nanopores,^27,37 the transport properties of molecules,³⁷ and to manufacture nanopores in graphene membranes.³⁸

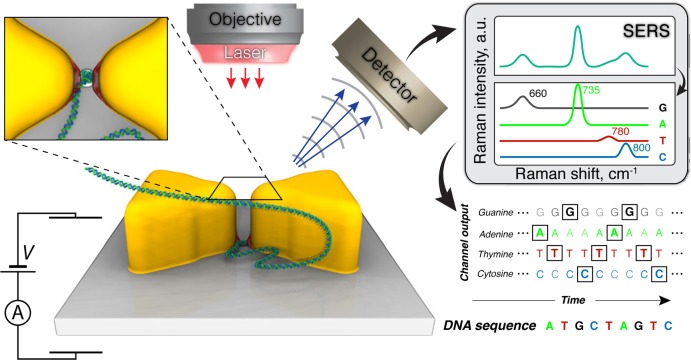
Figure 1.

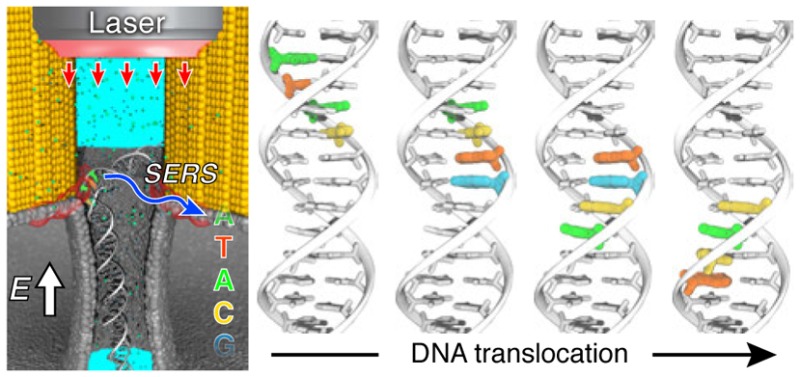
Concept of our approach to use a plasmonic nanopore device for trapping and sequencing DNA. Two gold triangular prisms form a bow tie structure on top of a solid-state membrane. A nanopore in the gap of the bow tie structure connects one side of the membrane to the other; the entire structure is submerged in an electrolyte solution. Driven by a transmembrane potential, DNA molecules travel from one side of the membrane to the other through the nanopore. The bow tie structure focuses the incident laser beam onto nanometer-size hot spots in proximity of the nanopore. The optical field of the hot spots applies a restraining force on the DNA molecule, counteracting the pull of the electrophoretic force. Switching the laser beam on and off produces stepwise displacement of DNA through the nanopore. Surface-enhanced Raman scattering (SERS) reports the nucleotide composition of the DNA fragment confined within the hot spots. The nucleotide sequence of DNA is deciphered through deconvolution of the SERS signals at the frequencies that uniquely identify each of the four DNA nucleotides.

The high density optical field produced by the plasmonic excitations dramatically increases the probability of Raman emission from the molecules in the hot spots. In 1977, the van Duyne group demonstrated enhancement of Raman signals from molecules adsorbed on a roughened metal surface.³⁹ Since then, the methodology of surface-enhanced Raman scattering (SERS) has been improved to permit detection of even single biomolecules.⁴⁰⁻⁴² Importantly, Raman spectra report the vibrational modes of the scattering molecules, providing direct information about their chemical structure. In the context of DNA sequencing, SERS signatures can directly identify the four nucleotides of DNA without any chemical labeling.^43,44 SERS detection of nanopore translocation has already been demonstrated,⁴⁵ albeit not yet at a single-molecule level.

Here we theoretically demonstrate the capabilities of plasmonic nanopores as a new platform for label-free DNA sequencing. By coupling continuum optics calculations to all-atom molecular dynamics (MD) simulations, we assess the feasibility of using plasmonic forces to trap and displace in discrete steps double-stranded DNA (dsDNA) through a solid-state nanopore. We evaluate the theoretical resolution of SERS measurement for identification of DNA nucleotides during such a stepwise displacement process, finding that determination of the nucleotide sequence of a DNA molecule transported through the hot spot may be possible.

Results and Discussion

Trapping of DNA in Plasmonic Nanopores

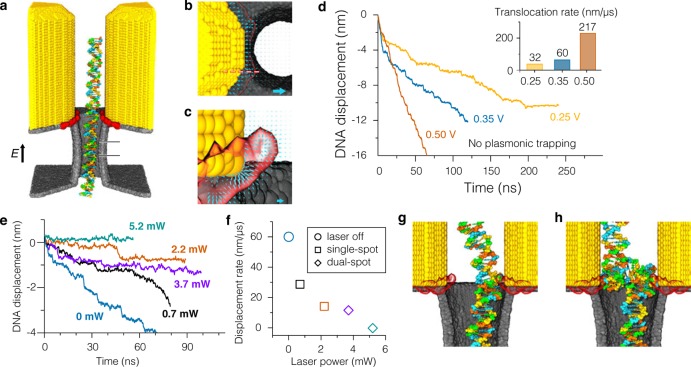
Our all-atom MD simulations demonstrated the feasibility of arresting dsDNA translocation through a solid-state nanopore by means of plasmonic excitations. To carry out the simulations, we built an all-atom model containing the tips of the gold triangular prisms, the inorganic membrane, an hourglass nanopore, a 77 base pair fragment of dsDNA prethreaded through the pore, and 1 M KCl solution (Figure 2a). A constant electric field was applied to produce a transmembrane bias of a desired voltage difference.⁴⁶ The effect of plasmonic excitations was accounted for by computing the local optical intensity enhancement factors I(r)/I₀ for a continuum model of the plasmonic nanopore system²⁷ using the finite difference time domain (FDTD) method.⁴⁷ The optical intensity map was computed for a resonant EM pulse of a 788 nm wavelength; see Methods for details. The dimensions of the gold prisms’ tips, the thickness of the membrane, and the geometry of the nanopore were identical in the FDTD and all-atom MD models. Figure 2a–c illustrates the location of the volumes of the highest optical intensity resulting from the FDTD calculations. The optical forces were applied to DNA atoms in all-atom MD simulations according to the dipole approximation: F_opt = 1/2 α∇|E(r)|², where α = 7.48 × 10^–39 C m² V^–1 is the average polarizability of non-hydrogen DNA atoms estimated assuming 1.526 and 1.33 to be the indices of refraction of DNA and the surrounding environment, respectively. Figure 2b,c illustrates the distribution of optical forces in the hot spots; Supporting Information Figure S1 shows a typical optical intensity map at a larger scale. The absolute magnitude of the optical forces is determined by the power of the incident laser beam; see the Methods section for the derivation. Our simulations did not explicitly consider the effects of local heating,^{27,36,48−50} as those can be mitigated by integration of heat sinks with the plasmonic nanopore structure (see Supporting Information).

Figure 2.

MD simulation of dsDNA trapping in plasmonic nanopores. (a) All-atom model of a plasmonic nanopore. A cut-away view reveals a 3.5 nm diameter nanopore. The surface atoms of the bow tie and of the inorganic membrane are shown as yellow and gray spheres, respectively; atoms of DNA are colored according to the nucleotide type; water and ions are not shown. Hereafter, we visualize a plasmonic hot spot by drawing an isosurface of the average intensity of the plasmonic excitation (red); panels b and c provide zoomed-in views of the hot spots. Displacement of DNA through the nanopore is measured within a 2 nm slab in the middle of the membrane, depicted by the horizontal black lines. (b,c) Distribution of optical forces within the plasmonic hot spot. The arrows indicate the magnitude and direction of the plasmonic forces on a single non-hydrogen atom of DNA within the plane perpendicular (b) and parallel (c) to the nanopore axis. The forces were evaluated on a 2.5 (b) or 1.0 (c) Å grid; only the in-plane components of the forces are shown. The cyan arrows in the bottom right corners correspond to a 10 pN force under a 3.71 mW incident laser beam. In panel b, the dashed line indicates the plane in which the forces displayed in panel c were computed. The semitransparent surfaces indicate the isosurface of the optical field intensity for an optical enhancement of 30,000. (d) Simulated translocation of dsDNA in the absence of plasmonic excitations. Steps in the translocation traces indicate the stick–slip character of dsDNA motion. The three simulations began from the conformation shown in panel a. The inset plots the average rate of dsDNA translocation versus transmembrane bias. (e) Simulated translocation of dsDNA under a voltage bias of 0.35 V in the presence of plasmonic excitations of various strengths. To simplify comparison, the first 12 ns of the MD trajectories are not shown. (f) Average translocation rate versus the laser power. Squares and diamonds indicate single and dual trapping, respectively. Single-spot (g) and dual-spot (h) trapping of dsDNA.

In the absence of plasmonic excitation, the DNA molecule was observed to translocate through the nanopore with a rate proportional to the transmembrane bias voltage. Figure 2d plots the simulated displacement of dsDNA under the transmembrane bias of 0.25, 0.35, and 0.5 V. At the beginning of the simulations, the DNA molecule is aligned with the nanopore axis and does not make direct contacts with the nanopore surface (Figure 2a). As a result, DNA translocates very fast within the first ∼10 ns of the simulations until it encounters the surface of the nanopore and slows down because of intermittent nonspecific interactions of the DNA with the surface of the nanopore.¹⁶ The average rate of DNA displacement after it comes in contact with the nanopore surface decreases with the transmembrane bias (Figure 2d). The DNA motion clearly exhibits a stick–slip character, which is particularly noticeable at low transmembrane bias voltages.

To systematically determine the effect of the plasmonic field on the dsDNA translocation rate, we repeated the DNA translocation simulations at 0.35 V transmembrane voltage for several values of the plasmonic field intensity reported here in the units of the incident laser beam power (Figure 2e). The translocation rate of dsDNA in the presence of the plasmonic field is considerably reduced in comparison to the translocation rate observed in the absence of the plasmonic field (Figure 2f). The reduction is caused by the local plasmonic forces that pull DNA toward the local maxima of the plasmonic field located at the orifice of the nanopore near the tips of the gold prisms (Figure 2b,c). At the highest illumination power (5.2 mW), the DNA could be arrested fully. Prolonged arrests of dsDNA motion were less observed for the weaker plasmonic fields. In the simulations at low powers, a portion of the dsDNA molecule was attracted toward one of the two hot spots (Figure 2g). At higher powers of the incident beam (3.7 and 5.2 mW), the translocation of dsDNA was observed to halt when the DNA molecule was pulled into the two hot spots at the same time, adopting a highly bent conformation (Figure 2h). A transition from the single to dual hot spot capture occurred spontaneously and required the trailing end of the molecule to venture into the proximity of the second hot spot by diffusion. Movie S1 and movie S2 in the Supporting Information illustrate the MD trajectories where single- and dual-spot trapping were observed. At the strongest plasmonic field (5.2 mW), plasmonic trapping disrupted the secondary structure of dsDNA, breaking the base-pairing and base-stacking pattern of the double helix.

To determine if the disruption of the dsDNA structure at high laser powers was caused by the DNA’s simultaneous binding to the two hot spots, we repeated our simulations of the plasmonic trapping for a bow tie structure that had an asymmetric distribution of the plasmonic field. Experimentally, such asymmetric distributions can, for example, be achieved using an asymmetric nanoantenna geometry like a triangle facing a circle. In our simulations, the asymmetric distribution was realized by setting the forces derived from the optical intensity variation equal to zero for a part of the system encompassing one of the triangles of the bow tie (x > 0). Such a single hot spot trapping could arrest DNA motion fully at high trapping power (up to 7.4 mW, see next section), producing minimal disruption of the DNA base-pairing.

Stepwise Displacement of dsDNA through Plasmonic Nanopores

The preferred mode of DNA translocation for sequencing applications is stepwise displacement, whereby prolonged arrests of DNA motion, required for sufficient signal-to-noise identification of the nucleotide, alternate with rapid, ideally single nucleotide or base pair displacements of the molecule. Although stepwise translocation was found to naturally occur in several nanopore systems,^5,7,51 only in a few, the character of the motion could be externally controlled.^25,52,53 Note that the optical control over DNA translocation does not have the time scale limitation associated with the capacitance response of the system and therefore can, in principle, be exercised very fast, with nanosecond precision.

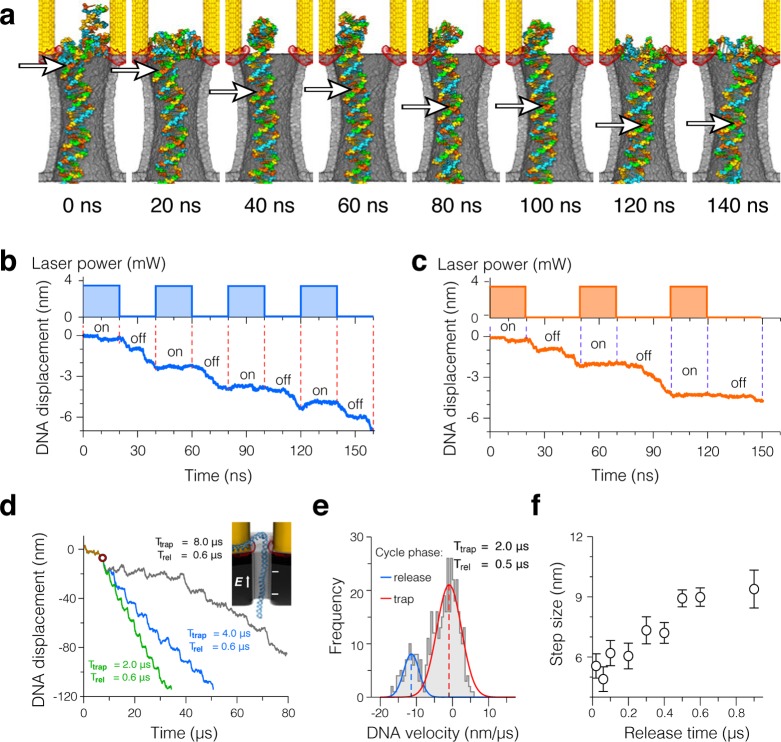
To determine if stepwise displacement of dsDNA could be realized by a periodic modulation of the plasmonic field, we continued one of our all-atom MD simulations of the plasmonic trapping (at 3.7 mW power), periodically switching the plasmonic field on and off. Figure 3a,b illustrates the outcome of this simulation. As expected, the DNA molecule does not translocate when the plasmonic field is on. Switching off the plasmonic field releases the trap, allowing the DNA to both relax its highly bent conformation and move through the nanopore. Upon switching the plasmonic field back on, a different part of dsDNA gets trapped by the two hot spots in a conformation that resembles the conformation of the molecule observed during the previous trapping phase of the plasmonic field pulse. The on/off cycle was repeated four times until no DNA was left to realize the dual-spot trapping. Changing the duty cycle of the plasmonic field pulse was observed to modulate the parameters of the stepwise motions: the longer duration of the off phase produced larger displacements of dsDNA between the trapped states (Figure 3c). However, adhesion of DNA to the nanopore surface delayed the release of the trapped conformation and caused stochastic stalls during the free translocation phase of the pulse.

Figure 3.

Controlled displacement of dsDNA through a plasmonic nanopore. (a,b) All-atom MD simulation of dsDNA displacement at a constant 0.35 V transmembrane bias and a pulsing plasmonic field. The snapshots in panel a illustrate the conformation of dsDNA at the beginning (0, 40, 80, and 120 ns) and the end (20, 60, 100, and 140 ns) of the plasmonic field pulses. The white arrows indicate the location of the same DNA base pair. The top and bottom traces in panel b show the duty cycle of the incident laser beam and the simulated displacement of the DNA molecule, respectively. Vertical dashed lines indicate the moments when the laser power was switched on or off. Movie S3 illustrates this MD trajectory. (c) Same as in panel b but for a different duty cycle of the incident beam. (d–f) Coarse-grained MD simulation of dsDNA displacement. (d) Simulated displacement of a 500 base pair dsDNA at a constant transmembrane bias (50 mV) and pulsing plasmonic field of three different duty cycles. The inset shows a part of the simulated system; the entire system is shown in Figure 1. All three simulations began with a trapping phase of 8 μs; the moment the plasmonic field was switched off for the first time is indicated by a circle. (e) Distribution of DNA translocation velocity. The histogram was constructed from nine independent trajectories at the same duty cycle using DNA velocities sampled every 4 ns and block-averaged over 0.5 μs. The average velocities of dsDNA during the trap and release phases of the plasmonic field pulse, v_trap and v_rel, were obtained from a double-Gaussian fit to the histogram. (f) Average stepwise displacement of dsDNA versus duration of the release phase of the pulse. The average step size was calculated as v_trapT_trap + v_relT_rel. Each data point was obtained from an ensemble of nine independent simulations; T_trap = 2 μs in each simulation.

With coarse-grained MD simulations, we explored the behavior of longer dsDNA molecules under pulsing plasmonic fields and in the absence of adhesive interactions between DNA and the nanopore surface. A typical simulation system, featured in Figure 1, was a cube, ∼360 nm on each side, containing a full-scale model of the plasmonic bow tie, an inorganic membrane, a nanopore, and a 500 base pair fragment of dsDNA prethreaded through the nanopore; solvent was not modeled explicitly in these coarse-grained simulations.⁵⁴ The surface of the nanopore and the bow tie was modeled as a featureless repulsive potential, offset by 2 nm from the structure used in the FDTD calculations, which corresponds to a physical situation where a layer of molecular coating is used to prevent DNA sticking to the surface of the device. Under such conditions, stable trapping of dsDNA was observed at a 50 mV bias and a 16.8 mW power of the incident beam.

Using the above trapping condition, we systematically investigated the effect of the plasmonic field duty cycle on the parameters of stepwise translocation. Figure 3d shows three typical displacement traces that characterized translocation of dsDNA for the plasmonic field pulses of the same duration of the free translocation phase T_rel = 0.6 μs and varying lengths of the trapping phase, T_trap = 2, 4, and 8 μs. After the initial 8 μs trapping phase, the DNA molecule was observed to move through the nanopore with the overall speed that was determined by the duration of the trapped phase: longer trapping resulted in slower translocation. Movie S4 illustrates a fragment of such coarse-grained MD trajectory.

With a set of coarse-grained MD simulations, we also determined the effect of the duration of the release phase on the average magnitude of the stepwise displacement. Keeping the duration of the trapping phase constant (T_trap = 2 μs), the duration of the release phase was varied from 0.02 to 0.9 μs; nine independent coarse-grained MD simulations were performed for each simulation condition. The resulting MD trajectories were analyzed via a two-Gaussian fit of the distribution of the translocation velocities (Figure 3e). The location of the peaks of the Gaussians reported the mean translocation velocities in the trapping and release phases of the pulse. Weighted with the duration of each phase, the sum of velocities yields the average step size. Figure 3f plots the dependence of this average step size on the duration of the release phase. In general, the step size decreases as the release phase of the pulse becomes shorter. For T_rel = 0.1 μs, the step size was ∼6 nm, which corresponds to approximately 17 base pairs. Further reduction of the release time did not substantially reduce the average translocation step, likely because of the lack of friction between DNA and the surface of the device in these coarse-grained model simulations.

Substantially smaller translocation steps were observed in all-atom MD simulations of single hot spot trapping. When trapped by a hot spot localized near the tip of one of the bow ties, the DNA displacement through the nanopore remained close to zero under a 500 mV transmembrane bias (Figure 4a). Switching the plasmonic field on and off produced stepwise displacements (Figure 4b–d). The amplitude of the displacement step varied with the duration of the release phase of the pulse and was 1 base pair or less at T_rel = 3 ns and 4 base pairs, on average, at T_rel = 5 ns.

Figure 4.

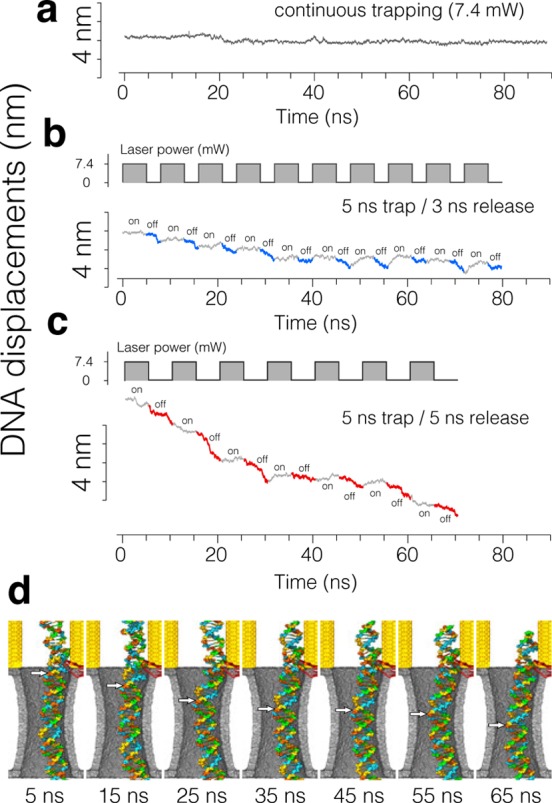
Stepwise displacement of dsDNA trapped by a single hot spot. (a–c) All-atom MD simulation of dsDNA displacement at a constant 0.5 V transmembrane bias and a pulsing plasmonic field. In panel a, a constant plasmonic field is applied for the entire duration of the simulation. In panels b and c, the top and bottom figures show the duty cycle of the incident laser beam and the simulated displacement of the DNA molecule, respectively. (d) Sequence of snapshots illustrating the conformation of dsDNA at the end of each plasmonic field pulse corresponding to the simulation performed at T_trap = 5 ns / T_rel = 5 ns duty cycle of the plasmonic field. The white arrows indicate the location of the same DNA base pair. Movie S5 illustrates this MD trajectory.

SERS Detection of DNA Sequence

The application of plasmonic nanopores to DNA sequencing is not limited to trapping and controlled displacement of DNA but can be employed for sequence determination, as well. Plasmonic hot spots are known to dramatically increase the probability of Raman emission from molecules confined to them, which may be used to identify the nucleotide sequence of a DNA molecule. Indeed, the four DNA nucleotides have already been shown to have distinct Raman spectra.^43,44 To use Raman signals for DNA sequencing, small parts of the DNA molecule should be sequentially exposed to the high-intensity plasmonic field. Below, we describe the type of signals that could be recorded in such measurements.

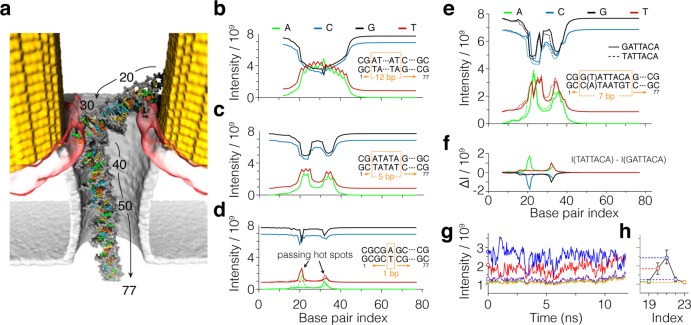
The SERS signal from a DNA molecule passing through a plasmonic nanopore is determined by both the sequence and the trapping conformation of the DNA molecule. To evaluate the potential utility of SERS for nanopore sequencing of DNA, we first consider a situation where the conformational fluctuations of the molecule are negligible, which, in practice, would correspond to trapping the DNA molecule in the same conformation for each of the translocation steps. Starting from a typical conformation of the trapped dsDNA molecule observed in our all-atom MD simulations (Figure 5a), we examine the effect of the nucleotide sequence on the SERS signal by assigning custom sequences to the trapped DNA fragment. To compute the Raman signal, we approximate the Raman spectrum of each type of DNA nucleotides by a Gaussian, centered at 800 (cytosine), 780 (thymine), 735 (adenine), and 660 (guanine) cm^–1.⁴³ The contribution of an individual nucleotide to the overall spectrum depends on the nucleotide’s location within the hot spot. Assuming that the probability of SERS emission is proportional to the square of the local field intensity⁴³ and knowing the position of all DNA bases, we can compute the spectrum of the entire DNA molecule as a superposition of the individual nucleotide’s Gaussians scaled by the local field enhancement factor I²(r)/I₀². Thus, our calculations account for the variation of the field enhancement between the triangles. Figure 1 shows a superposition of the A, C, G, and T Gaussians scaled by the same field enhancement factor. In the subsequent analyses, we characterize the spectra by plotting the intensity at the peak frequencies of the four Gaussians, referred hereafter as the four (A, C, G, and T) frequency channels.

Figure 5.

SERS detection of DNA sequence. (a) Typical conformation of dsDNA trapped between two hot spots. The base pairs are numbered in ascending order from the trailing to the leading end of the molecule. (b–d) SERS signals from a poly(AT) block in the poly(CG) background. The calculated SERS intensity in the four frequency channels is shown for different locations of the poly(AT) block. The intensities are plotted in the units of peak intensities that would have been measured in each channel under the same illumination in the absence of the plasmonic enhancement. For each substitution, the DNA molecule is assumed to have the same conformation (shown in panel a). The base pair index specifies the location of the first base pair of the poly(AT) block from the trailing end of the molecule using the base pair numbering defined in panel a. Data in panels b–d correspond to poly(AT) blocks containing 12, 5, and 1 base pairs. Dashed lines in panel d indicate the signal from a TA base pair. The TA and AT base pairs differ from one another by the strands the A and T nucleotides located in the helix. (e) SERS detection of a single nucleotide substitution. The calculated SERS signals from the GATTACA and TATTACA blocks inserted at a specified location in the poly(CG) molecule. (f) Difference between the signals from the GATTACA and TATTACA blocks. (g) Effect of thermal fluctuations on SERS signal. The SERS intensity of a thymine nucleotide is plotted for a sequence of DNA conformations obtained from the all-atom MD trajectory of dsDNA trapping (at 3.7 mW laser power). The first frame of the trajectory is shown in panel a. The DNA is assumed to be made entirely from CG base pairs with the exception of a single AT base pair inserted 19, 20, 21, 22, or 23 base pairs away from the trailing end of the molecule. The color of the lines indicates the location of the thymine nucleotide in the DNA molecule (panel h). (h) Averaged over the MD trajectory SERS signals from the thymine nucleotide at the specified location in the DNA molecule. The error bars show the standard deviation of the signal.

Figure 5b–d details the theoretical resolution of the SERS signal for identifying a block of poly(AT) nucleotides in a poly(CG) background. As a block of 12 alternating AT base pairs is placed closer toward the nanopore, the SERS intensity in the C and G channels decreases (Figure 5b). The intensity returns to its original levels as the block leaves the hot spot and reaches the middle of the membrane in the nanopore. The change of intensity in the A and T channels anticorrelates with the changes in the C and G channels, reaching a maximum when the AT block is located between the edges of the gold triangles, across the nanopore. The intensity in the T channel does not reach zero because of some bleed over from the C channel. The small but distinguishable variation in the A and T signal within the broad (∼25 bp) maximum of the intensity traces is caused by the conformation of the DNA molecule in proximity of the bow tie. Because the A and T bases alternate within the poly(AT) block, the change of the intensity corresponding to a 1 base pair displacement of the block is, neglecting the end-of-the-block effects, equivalent to moving all A and T nucleotides to the opposite strands of dsDNA. That is, the signal from an AT base pair can be, in principle, distinguished from the signal from a TA base pair if both are placed at the same location within the hot spot. In the case of a poly(AT) segment made up from five base pairs (Figure 5c), the traces of intensity in all four channels show two maxima, corresponding to the placement of the blocks in proximity to the hot spot at each of the two triangles of the bow tie. The width of each maximum is ∼5 base pairs. Even a single AT base pair gives a considerable signal in the CG background (Figure 5d). In the latter case, the two peaks have clearly different heights reflecting the difference in the conformations of dsDNA molecule near individual bow ties. Moving the A and T nucleotide to the opposite strands of the helix produces distinguishable changes in the intensity traces (Figure 5d).

Figure 5e shows an example of the signals that could be recorded under good conditions from a heterogeneous sequence dsDNA polymer. A GATTACA block, which is displaced through the poly(CG) background in single base pair steps, produces two broad maxima in the SERS signals; the finer structure within each maximum carries the information about the base pair resolution nucleotide sequence. To assess the influence of a single nucleotide substitution on the SERS signals, we repeated the calculations replacing a single CG base pair at the beginning of the block with an AT base pair. Figure 5f plots the difference in the intensity channels corresponding to the single base pair substitution. A clear well-defined peak is observed at the expected location. As in the case of Figure 5d, the signal’s width is approximately 3 base pairs, and this depends on the configuration of dsDNA in the proximity of the bow tie.

To evaluate the effect of thermal fluctuations of dsDNA on the SERS signal recorded in a trapped state, we repeated our calculations of the SERS intensities for a single AT base pair insertion in a poly(CG) DNA molecule using not the fixed DNA conformation of Figure 5a but an ensemble of conformations obtained from all-atom MD simulations of the trapped state. Figure 5g plots the SERS intensity in the T channel for AT substitution at five locations in the dsDNA molecule. Although the SERS intensity undergoes considerable fluctuations, the signal corresponding to placement of the AT base pair near the local hot spot (position 21) is clearly discernible from other placement of the base pair in the helix (Figure 5h). In the harmonic approximation, the equipartition theorem suggests that the root-mean-square displacement due to thermal fluctuations increases as a square root of temperature. Thus, modest (several degrees) increase of the local temperature that may be produced by plasmonic heating at experimental conditions is not expected to considerably increase the magnitude of thermal fluctuations.

Next, we used one of our coarse-grained MD trajectories of stepwise dsDNA translocation to evaluate the type of signals that could be recorded by a SERS detector in the presence of conformation disorder. Figure 6a shows a displacement trace of dsDNA obtained from coarse-grained simulations under a 50 mV transmembrane bias and a 2 μs on / 0.4 μs off pulse of the plasmonic field. In this trajectory, the DNA moves through the nanopores in 25 base pair steps (Movie S4). Figure 6b–d shows the SERS signals evaluated from the coarse-grained MD trajectory assuming that the nucleotide sequence of the DNA is made of blocks of AT and CG nucleotides (our coarse-grained model does not have explicit information about DNA sequence). In the case of the equal-length 25 base pair blocks, the presence of either AT and CG block in the plasmonic hot spots could be clearly identified from the SERS signal. The stepwise displacement was reproducible enough to distinguish the presence of two neighboring AT base pairs placed every 48 base pairs in the poly(CG) DNA (Figure 6c). For small AT blocks, the strength of the AT-specific signal linearly increases with the length of the block (Figure 6d), saturating for blocks greater than 10 base pairs. The relatively small variation of the signal within and between the trapping phases and the highly nonlinear dependence of the Raman emission probability on the local field enhancement factor suggests that DNA sequence detection at base pair resolution may be possible for small-amplitude stepwise displacement of dsDNA.

Figure 6.

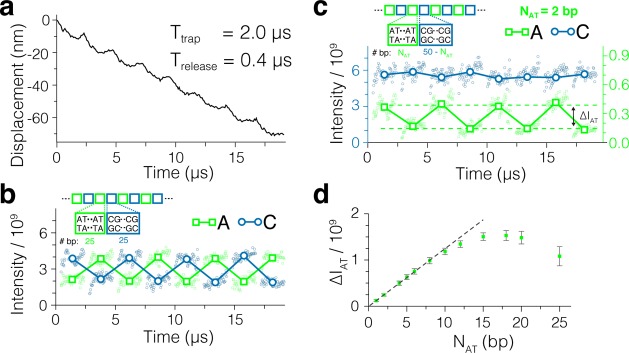
SERS signal from DNA block copolymer translocation. (a) Stepwise displacement of dsDNA simulated using the coarse-grained MD approach. The simulation was performed at a constant transmembrane bias of 50 mV; the plasmonic field was periodically switched on and off for 2.0 and 0.4 μs, respectively. (b) SERS signal from the trajectory featured in panel a. The SERS intensity in the adenine (green) and cytosine (blue) channels is plotted as a function of the simulation time. To compute the SERS intensity, the DNA molecule was assumed to comprise blocks of 25 AT and 25 CG base pairs. Solid squares indicate the SERS intensity in the adenine (green) and cytosine (blue) channels averaged over each trapping phase of the plasmonic field pulse. Lines are guides for the eyes. The temporal changes of the SERS intensity in the guanine and thymine channels follow the dependences in the cytosine and adenine channels, respectively. (c) Same as in panel b but for a DNA molecule comprising alternating blocks of 2 AT and 48 CG base pairs. SERS intensities in the cytosine and adenine channels are shown on the left and right axes, respectively. Green dashed lines indicate the average intensity of the odd (top) and even (bottom) cycles. The difference between the average intensities in the odd and even cycles is defined as ΔI_AT. (d) Dependence of ΔI_AT on the length of the AT block, N_AT. The length of the CG block is N_CG = 50 – N_AT. The dashed line illustrates a linear fit to the data in the N_AT < 8 regime.

Finally, we describe the type of SERS signals that could be obtained from a heterogeneous sequence DNA moving through a plasmonic hot spot. First, we consider the 5 ns on / 5 ns off trajectory of dsDNA stepwise displacement obtained under the single hot spot trapping condition (Figure 4c,d). Figure 7a shows the contribution of individual nucleotides to the overall SERS signal from the DNA molecule at the seven trapping phases of this all-atom MD trajectory. Figure 7b shows how the total SERS intensity in each frequency channel changes with the translocation step (which is the signal to be measured experimentally), as well as the contribution of individual nucleotides to the total intensity in each step. In each channel, the modulation of the total intensity is produced by three or less nucleotides, whereas the contribution from all other nucleotides is approximately constant (white bars in Figure 7b). As the DNA molecule is displaced through the hot spot in seven translocation steps, the contribution of the nucleotides to the overall SERS signal in each channel changes in accordance with the translocation direction prescribed by the transmembrane bias. The SERS intensity of the individual nucleotide is not a simple function of the DNA displacement because of the complex shape of the dsDNA molecule. Nevertheless, the change of the SERS intensity pattern covers without breaks the 20 base pair dsDNA fragment (base pairs 52 to 72) displaced through the hot spot.

Figure 7.

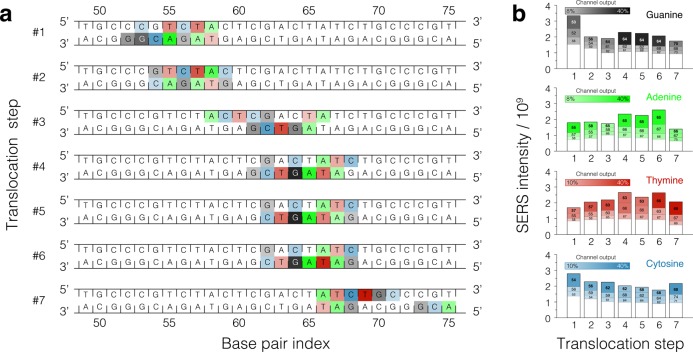
SERS signal from DNA displaced in steps through a single plasmonic hot spot. (a) Schematic representation of a DNA fragment that displaced through a plasmonic hot spot in seven translocation (trapping) steps. Each nucleotide of every base pair contributes to the SERS intensity. For each translocation step, three nucleotides contributing the largest fractions of the total intensity in each frequency channel are highlighted using colors with opacities proportional to their contribution to the signal: the greater the contribution, the more intense background color; the colors are defined in panel b. Because the total intensity varies in each channel at each translocation step (panel b), coloring of the nucleotides can be discontinuous along the DNA strands. The SERS signals were computed for the all-atom MD trajectory of stepwise displacement obtained under the 5 ns on / 5 ns off plasmonic field pulse (Figure 4c); only the parts of the trajectory that had the trapping field on were used to compute the SERS signals. (b) Partitioning of the SERS signal among nucleotides of the DNA molecule. The average SERS intensity in each of the four frequency channels is plotted for each translocation step. For a given translocation step, the total height of the bar indicates the total SERS intensity; the segments of the bar indicate the contributions from individual nucleotides. The three nucleotides having the largest contributions to the total intensity in each channel are highlighted using colors and base pair indices; the white bar indicates the contribution from all other nucleotides of the same type. The height of the white bars does not vary considerably from one translocation step to the other and thus can be considered as a background offset for sequence determination purposes.

Conversion of the SERS signals into a DNA sequence will require a deconvolution algorithm not unlike the algorithm used for decoding of the ionic current blockades.^6,55 There are, however, considerable differences with regard to deconvolution of ionic current and SERS signatures of DNA sequence. The ionic current blockade is a nontrivial function of the order in which the four or more nucleotides are presented to the pore constriction. Furthermore, the information about the nucleotide order is condensed into a single ionic current value. By contrast, SERS signals are distributed over four independent channels, hence the signal from neighboring nucleotides that are of different types do not interfere with one another and, therefore, the deconvolution problem is reduced to determining how many nucleotides of the same type contribute to the signal in each channel. The latter, however, is a very tractable problem as the SERS intensity is directly related to the distance between the nucleotide and the hot spot.

To illustrate the potential of SERS sequencing, we considered a situation where a single DNA strand is moved through a single plasmonic hot spot (Figure 8a). The practical realization of such a system would require a method to put the trailing end of the DNA strand under tension, preventing uncontrolled accumulation of DNA near the plasmonic hot spot. In this particular simulation, in addition to a strong electric field pulling the DNA strand through the nanopore and the constant plasmonic field (33.3 mW power) attracting the DNA to the hot spot, a constant force was applied to the trailing end of the DNA stand, pulling it away from the nanopore, parallel to the membrane. The SERS signals recorded from the DNA strand during the translocation exhibit a sequence of maxima that coincide with the passage of individual nucleotides through the hot spot (Figure 8b). In fact, the sequence of the DNA strand can be reconstructed by recording the times at which these peaks appear and laying them out in a chronological order.

Figure 8.

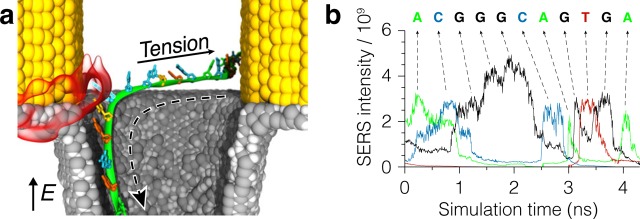
SERS sequencing of single-stranded DNA. (a) All-atom MD simulation of ssDNA translocation through a single plasmonic hot spot. A single DNA strand is pulled through the nanopore by a strong transmembrane bias, while a plasmonic hot spot (red semitransparent surface) attracts the strand toward the bow tie. To prevent ssDNA from accumulating near the bow tie, an additional force is applied to the trailing end of the DNA directed away from the nanopore. (b) SERS intensity signals recorded during the translocation of ssDNA through a single plasmonic hot spot. Signals in the adenine, guanine, cytosine, and thymine SERS channels are shown in different colors. Peaks in the intensity traces correspond to the passage of individual nucleotides through the hot spot. The nucleotide sequence of the DNA fragment and its relationship to the SERS signal is shown at the top of the figure.

Regarding experimental detection of single molecules using SERS, the major challenge typically lies in proving that a particular device can detect single molecules, whereas achieving single-molecule sensitivity has been described as more straightforward and a commonly overstated challenge.⁵⁶ Our nanopore approach is particularly helpful in this respect because, in contrast to other SERS methods, the nanopore helps to locate a single molecule right to where it needs to be, in the plasmonic hot spot. According to our theoretical estimates (see Supporting Information), SERS signals from trapped DNA bases can exceed 10⁵ photons per second, which may allow detection of single bases with subsecond acquisition time.

Conclusions

In summary, the results of our study suggest that the possibility of using plasmonic nanopores bears great potential as a novel approach to DNA sequencing. Specifically, our simulations have demonstrated the possibility of direct optical trapping and controlling displacement of DNA molecules through a solid-state nanopore as well as detection of DNA sequence by measuring Raman signals. The implementation of our concept in practice would require precise control over the interactions between DNA and the surface of the device, which ultimately will determine how slowly and precisely the DNA molecule could be displaced through the plasmonic hot spot. In that respect, an ideal nanopore material would have a friction coefficient that could be modulated by the plasmonic field pulse: high friction for the trapping phase of the cycle and low friction for the translocation. A practical realization of such an idealized nanopore material could require a molecular coating sensitive to small variations in temperature and/or plasmonic field.

Compared with non-nanopore DNA sequencing methods that are already available or in development, the proposed approach can potentially yield very long reads of DNA sequences (hundreds of thousands of nucleotides, potentially unlimited). Our method requires no labeling, and hence the reagent costs can be very low. It also uses no fragile proteins or lipid bilayers but provides a reliable solid-state platform with only physical tools for control and readout of the DNA. The method is amenable to multiplex detection by using large arrays of plasmonic nanopores and wide-field readout of scattering radiation. When produced on a mass scale, the nanofabrication costs per device can be low, as the precise control of the nanopore dimensions is not required for the DNA sequence detection. Furthermore, because Raman spectroscopy provides direct molecular information, our concept, without any change, will, in principle, be applicable to the detection of epigenetic variations in single DNA molecules, DNA damage, and, possibly, protein characterization and sequencing.

Methods

All-Atom MD Simulations

The all-atom MD simulations were performed using the program NAMD2,⁵⁷ periodic boundary conditions and 2–2–6 fs multiple time-stepping. The interatomic interactions were described using the CHARMM27 force field,⁵⁸ CHARMM-compatible parameters for silicon oxide⁵⁹ and gold⁶⁰ atoms, and custom NBFIX corrections for the description of DNA–ion interactions.⁶¹ The Lorentz–Berthelot rules applied to describe interactions between nonbonded atoms. All simulations employed SETTLE and RATTLE⁶² algorithms to keep water and other covalent bonds involving hydrogen bonds rigid, correspondingly, a 7–8 Å cutoff for van der Waals and short-range electrostatic forces, and particle mesh Ewald (PME) method⁶³ over a 1.0 Å resolution grid for long-range electrostatic interactions.

The all-atom model of a plasmonic nanopore was prepared to reproduce the design of an experimental setup.³⁶ The model featured a gold bow tie structure at the surface of an inorganic membrane with a nanopore passing through the membrane right at the center of the bow tie (Figure 2a). The surface of the membrane was modeled as amorphous SiO₂, which commonly coats Si-based membranes submerged in an electrolyte solution. Both the membrane and the bow tie were prepared using the inorganic builder plugin of VMD⁶⁴ following the procedures described elsewhere.⁵⁹ The bow tie structure consisted of two quasi-equilateral triangles (∼60 nm on a side) facing each other, with the corners that were separated by the distance equal to the pore diameter at the surface of the membrane and their angle bisectors forming a single line. The thickness of the membrane and the height of the gold triangles were 10 and 20 nm, correspondingly, both measured along the nanopore axis. The nanopore had an hourglass shape and measured 3.2 nm in diameter in the middle and 5 nm at the surface of the membrane. All atoms of the membrane and the bow tie located more than 1.2 nm away from the surface were removed, which made them hollow but still impermeable to water, ions, and DNA. Doing so significantly reduced the number of atoms in the simulation system while preserving atomistic details of DNA–membrane interactions. Simulated annealing procedure was then applied to the atoms of the membrane.⁵⁹ In production simulations, atoms of the bow tie and the membrane were restrained to their initial positions with a harmonic force, with the force constant of 20 kcal mol^–1 Å ^–2.

A 77 base pair piece of a double-stranded DNA molecule of a random sequence was then prepared using the 3D-DART server.⁶⁵ The molecule was added to the plasmonic nanopore model in such a way that it was concentric with the nanopore axis and penetrated 8 nm (about one-third of its contour length) through the nanopore. The system was then solvated and ionized using the solvate and autoionize plugins of VMD, correspondingly, producing a neutral 1 M KCl solution. Upon building, the system underwent 18,000 steps of energy minimization using the conjugate gradient method followed by equilibration in the NPT ensemble—constant number of particles N, pressure P, and temperature T = 295 K—during which a time step of 1 fs was used and Nosé–Hoover Langevin piston pressure control⁶⁶ maintained the pressure at 1 atm by adjusting the system’s dimension along the nanopore (z) axis. The final system measured approximately 13 × 18 × 38.5 nm³ and contained about 0.52 million atoms. In all production simulations, a constant electric field was applied along the z axis of the system.

Coarse-Grained MD Simulations

The coarse-grained MD simulations were performed using a custom version of NAMD2.⁵⁴ Each simulation system contained a 500 base pair fragment of dsDNA molecule described using our two beads per nucleotide coarse-grained model.⁵⁴ The persistence length of dsDNA simulated using this model was 50 ns. Subject to an external electric field, each backbone bead of coarse-grained DNA experienced an electrophoretic force equal to the product of the local electric field and 0.25 q*, where q* is the nominal charge of a DNA nucleotide. All other components of the system were represented as grid-based potentials: a grid potential representing the presence of the gold bow tie and the membrane, a grid potential representing the optical field generated by the plasmonic nanostructure, and a grid potential representing the transmembrane bias. The geometry of the device was similar to that used in our all-atom model; however, the volume explicitly modeled in the coarse-grained simulation was approximately 10 times larger than that in the all-atom model in each dimension. The gold bow tie was 60 nm on each side of the triangle face and 28 nm in height. The inorganic membrane was 20 nm thick. The cross sections of the nanopore in the middle and at the surface of the membrane were 5.4 and 6.4 nm in diameter, respectively. The grid potential representing the steric interactions of DNA with the inorganic components of the system was generated by assigning 0 and 1 to regions of space occupied by the solution and the inorganic components, respectively; the grid spacing was 1 nm in each dimension. The grid representing the optical field was obtained using the FDTD method (see below). The grid representing the transmembrane potential was obtained using the COMSOL Multiphysics program (version 4.3) using a previously described method.⁶⁷ Briefly, the steady-state numerical solution of the electric potential distribution in the system was calculated from coupled electrostatics, ion diffusion, and laminar flow equations using the PARDISO direct solver and damped Newton’s method. The solution was then converted into a grid-based potential with a grid spacing of 2 nm. Effects associated with the local heating of the bow tie were not taken into account in this calculation.

The forces on the coarse-grained beads from the grid potentials were calculated using the grid forces feature⁶⁸ of NAMD2. The simulation unit cell was a cube 360 nm on each side. The simulations employed periodic boundary conditions and a nominal time step of 40 fs. The tabulated nonbonded interactions were computed using a 34–35 Å cutoff. Stochastic forces from the solvent were introduced via a Langevin thermostat set to a temperature of 295 K and a nominal damping coefficient of 1.24 ps^–1. The trajectories were recorded every 10,000 simulation steps. The calibration of the time scale of the coarse-grained simulations was performed by matching the electrophoretic mobility of a 22 base pair DNA fragment obtained using the all-atom and coarse-grained methods.

Calculations of the Effect of Optical Field

The optical properties of the plasmonic nanopore were modeled using the finite difference time domain method^27,47,69 (FDTD Solutions, Lumerical Solutions, Inc., Canada). Two separate models for the FDTD simulation were built, matching the geometry of the systems used in the all-atom and coarse-grained MD simulations. For the all-atom MD setup, the bow tie antenna was modeled as two 17 nm thick and 40 nm long (tip to end) equilateral gold triangles, separated by a 5 nm gap on a 10 nm thick Si₃N₄ membrane. There was a 5 nm in diameter nanopore through the membrane at the gap center of the bow tie antenna. The upper corners of the triangles had a rounding of 5 nm in radius. For the coarse-grained simulations, the bow tie antenna was modeled as two 34 nm thick, 60 nm on a side equilateral gold triangles, separated by a 10 nm gap on a 22 nm thick Si₃N₄ membrane. A 10 nm in diameter nanopore parallel to the z axis was made at the gap center of the bow tie antenna.The upper corners of the triangles had a rounding of 30 nm in radius. Refractive indices of silicon nitride and surrounding medium were set to 2.0 and 1.33, respectively, and the one for gold was taken from Johnson and Christy.⁷⁰ The plasmonic antenna was excited by a pulse from a total-field scattered-field source with the optical axis perpendicular to the membrane and the polarization along the long side of the bow tie antenna.³⁶ Symmetry was used to reduce the computational time. The result of FDTD calculations was a three-dimensional distribution of the electromagnetic field intensity enhancement I(r)/I₀ at 788 nm, a wavelength close to that realized in previous experimental studies.^27,36 The distribution was exported and converted to an appropriate format using Matlab (R2011b, The MathWorks, Inc., USA).

The obtained distribution of the optical field intensity enhancement I(r)/I₀ was used in all-atom and coarse-grained MD simulations as an external potential defined on a grid⁶⁸ that applied to DNA only. In the course of an MD simulation, affected DNA atoms (or coarse-grained beads) experienced an additional force F_opt proportional to the gradient of the optical field intensity: F_opt = κ∇I(r)/I₀. The coefficient κ is directly proportional to the power of the incident laser beam and atomic polarizability. Therefore, by tuning this parameter, we could simulate plasmonic fields generated by laser beams of a particular power. In MD simulations, we assigned all affected DNA atoms (non-hydrogen atoms) with the same coefficient. By doing so, we assumed that all affected atoms have identical polarizabilities. In our coarse-grained model of DNA, the P and B beads represented 7 and 13 non-hydrogen atoms, correspondingly, and therefore, proportionally higher coefficients κ were used for each bead type.

To estimate the numerical value of κ, we recall that DNA atoms polarized by the strong electromagnetic field in the hot spot experience the force due to gradients of the optical field: F⃗_opt = 1/2α∇ |E⃗|², where α is their polarizability. Assuming the refractive indices of the surrounding medium n_e and DNA atoms n_p are both real, the polarizability can be calculated as⁷¹

, where ε₀ is the permittivity of vacuum (8.85 × 10^–12 W s V^–2 m^–1) and V_p is the volume of an atom. Substituting n_p = 1.526,⁷²n_e = 1.33, and a typical volume for an atom (estimated based on the assumptions that N_A atoms are equivalent to 1 L), we arrive at polarizability α = 7.48 × 10^–39 C m² V^–1. If laser of power P is focused to a Gaussian spot with radius R, theoretical maximum of its intensity is I = 2P/πR². The factor 2 comes from the Gaussian profile and should be removed if a flat-top beam is used. Note that the effective excitation intensity is likely smaller also for a Gaussian beam since the antenna captures light from a quite large cross sectional area. The intensity is related to the electric field amplitude through I = 1/2cε₀n_e|E|², where c is the speed of light in vacuum (3 × 10^–8 m s^–1). Therefore, the electric field amplitude is

. In MD simulations, we use F = κ∇|E/E₀|², where κ had been assigned values of 1, 3, 5, 7, and 10 × 10^–7. Equating expressions for the optical force, and assuming that the laser beam has a radius R = 250 nm, we arrive at the following relation between κ and the laser power: κ = 1 corresponds to P = 0.74 mW, κ = 3 to P = 2.22 mW, κ = 5 to P = 3.71 mW, κ = 7 to P = 5.19 mW, and κ = 10 to P = 7.4 mW. In the text, we report the intensity of the plasmonic excitation as the laser power using the above justifications.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.5b04173.

• Optical enhancement maps, simulation of the local heating effects, and estimates of the experimental SERS signals (PDF)

• Single-spot trapping of double-stranded DNA (movie S1) (AVI)

• Dual-spot trapping of double-stranded DNA (movie S2) (AVI)

• Stepwise displacement of double-stranded DNA through a plasmonic nanopore (movie S3) (AVI)

• Step-like motion of a double-stranded DNA molecule through the plasmonic nanopore (movie S4) (AVI)

• Stepwise displacement of double-stranded DNA under the single hot spot trapping conditions (movie S5) (AVI)

The authors declare no competing financial interest.