Abstract
Viruses that express reporter genes upon infection have been recently used to evaluate neutralizing antibody responses, where a lack of reporter expression indicates specific virus inhibition. The traditional model-based methods using standard outcome of percent neutralization could be applied to the data from the assays to estimate antibody titers. However, the data produced is sometimes irregular, which can yield meaningless outcomes of percent neutralization that do not fit the typical curves for immunoassays, making automated or semi-high throughput antibody titer estimation unreliable. We developed a type of new outcomes model, which is biologically meaningful and fits typical immunoassay curves well. Our simulation study indicates that the new response approach outperforms the traditional response approach regardless of the data variability. The proposed new response approach can be used in similar assays for other disease models.
Keywords: four-parameter logistic regression, nonlinear maximization, microneutralization assay, green fluorescent protein (GFP), neutralizing antibodies, influenza virus, hemagglutinin (HA), antibody-mediated virus inhibition
1 Introduction
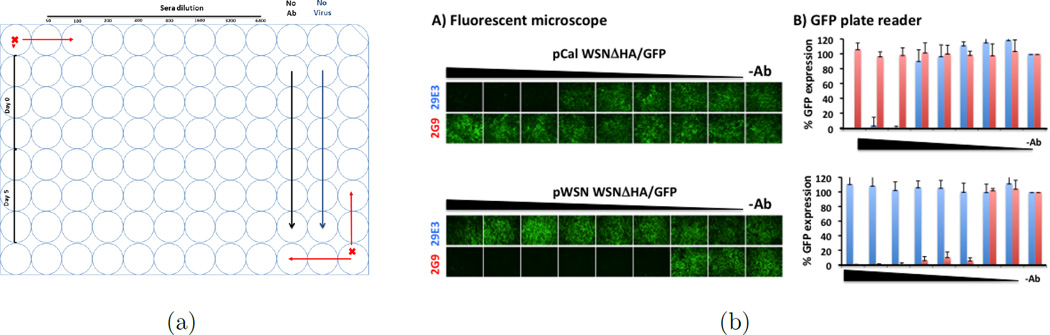
Green fluorescent protein (GFP) expressing influenza viruses have been developed to monitor virus infection by observation or quantification of GFP expression (18; 22; 1; 10; 2; 13). A common virological assay that benefits from such reporter gene expression is the microneutralization assay, or an approach to detect antibody-mediated virus inhibition (18; 1; 10; 2; 13). In this study, a GFP-expressing influenza virus was used to determine the presence and potency of influenza neutralizing antibodies in cell culture. Specifically, the GFP-based microneutralization assay evaluates a known influenza virus isolate against a test sample (antibody-containing sera) of unknown specificity or concentration. The test sample, which may be subject to pre-dilution, is two-fold serially diluted in a 96-well plate, using triplicates. Next, an equivalent amount of influenza virus is added to each well containing diluted test samples. The virus-antibody mixture is then used to infect cells and, 24 hours later, the change in GFP expression over the antibody dilution series will be evaluated by a fluorescence microscope or a fluorescence plate reader. This produces a dose-response curve. Figure 1 provides an example of a GFP-based influenza microneutralization assay using monoclonal antibodies. Figure 1(a) demonstrates the typical plate layout of the experiments, where influenza virus alone (in the absence of antibody) are used as positive controls characterizing 100% GFP expression, and cells without virus are used as negative controls providing the background auto-fluorescence of the cells within the assay. Thus the dose-response over serial dilution of neutralizing antibodies is evaluated. As strain-specific monoclonal antibodies are diluted, GFP expression is recovered which can be observed directly by fluorescence microscopy (Figure 1).
Figure 1.
(a) Typical design; (b) Identity of pCal WSNΔHA/GFP: Influenza A/California/04/09 HA-pseudotyped WSN-GP/GFP virus (pCal WSNΔHA/GFP, top) was tested in the GFP-based microneutralization assay using the influenza A/California/04/09 monoclonal neutralizing antibody 29E3 (blue). Influenza A/WSN/33 monoclonal neutralizing antibody 2G9 (red) was used as an internal control. Two-fold serial dilutions of the antibodies (starting concentration of 100 ng) were pre-incubated with the pCalE3 WSNΔHA/GFP virus for 1 hour. The antibody-virus mixture was used to infect MDCK HA-expressing cells. Virus infection was monitored under a fluorescent microscope (a) and GFP-expression was quantified under a GFP plate reader (b). Percentage of GFP expression is illustrated for the different antibody dilutions. Virus in the absence of antibody (−Ab) was used to set up 100% GFP expression. Same monoclonal antibodies were also tested with the influenza A/WSN/33 HA-pseudotyped WSNΔHA/GFP virus (pWSN WSNΔHA/GFP, bottom). As expected, monoclonal antibody 29E3 specifically neutralize the pCal WSNΔHA/GFP virus but not pWSN WSNΔHA/GFP. To the contrary, monoclonal antibody 2G9 neutralized the pWSN WSNΔHA/GFP but not the pCalE3 WSNΔHA/GFP virus.
The question becomes how to quantify neutralizing antibody titers, or the concentration at which 50% virus neutralization is achieved. This corresponds to the highest dilution at which the GFP intensity is reduced by 50%. A simple but classical way is using linear interpolation by Reed and Muench (23), assuming a linear dose-response relationship around the potential antibody titer. But the Reed-Muench method uses only information from two points around the potential titer, and thus it is inefficient in both precision and accuracy. Another way is to model the dose-response curve. Before any model is selected to depict the dose-response curve, a response has to be appropriately defined in a way that the response is not only biologically meaningful, but can precisely capture the dose-response curve, by which it either increases or decreases as test samples are diluted. Traditionally, percent neutralization has been used to depict the dose-response curves. In consideration of negative controls (no-virus) and positive controls (no-antibody), percent neutralization can be calculated as
| (1) |
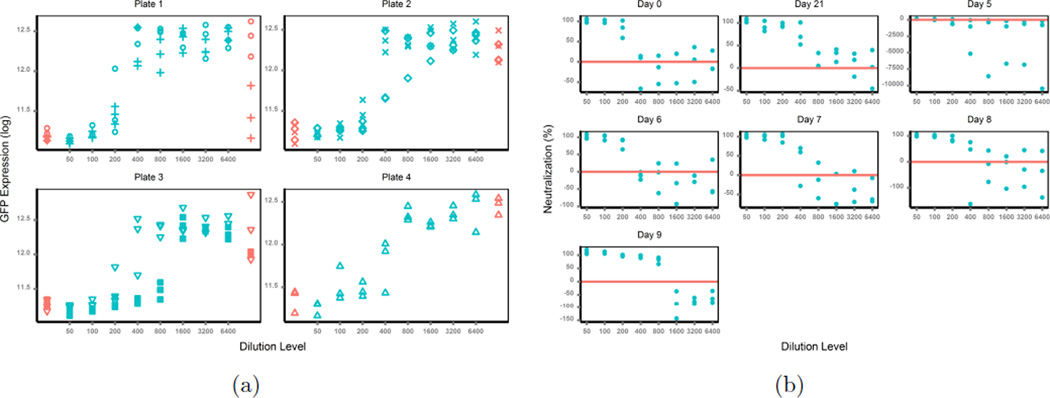
In theory, GFP intensities are maximum in no-antibody samples (positive controls) and minimum in no-virus samples (negative controls), and the signals from test antibody samples (simplified as TAS, and used thereafter) lie between the maximums and the minimums. If the data produced follow these principles, there will be no problem in the use of percent neutralization. But in reality, the data from the assays are often irregular; for example, signals from positive controls are smaller than those from TAS, or background noise from negative controls are larger than signals from TAS. As an example (Figure 2(a), different symbols represent different days), the raw GFP intensity data shows a subject’s neutralization antibody responses against influenza A/California/04/2009 (H1N1) on different days (0, 5 ~ 9 and 21) post vaccination. This intensity data can then be extrapolated as percent neutralization (described above) to generate a dose-response curve (Figure 2(b)). The test antibody samples from the subjects at different days were run on four plates, with test samples on day 0 and day 5 on plate 1, day 6 and 7 on plate 2,day 8 and 9 on plate 3 and day 21 on plate 4. Data from all four plates present the above-mentioned irregularities, especially from plate 1 and plate 3, which may be an artifact of differences in the plates themselves. The GFP intensities from the positive controls (no-test-antibody mixture) were very noisy, with a majority smaller than those from the test-antibody mixture, and 2 out of 6 values even smaller than those from the negative controls (no-virus mixture). As a reason the majority of the calculated percent neutralization was negative, which was biologically impossible and meaningless. The percent neutralization was also noisy in many cases, it neither decreased upon TAS dilution nor generated clear dose-response curves (see the subject’s responses on day 5 in Figure 2(b)). Thus the traditional use of percent neutralization to measure antibody inhibition in this assay is associated with severe problems, and any inferences from model fitting based on such responses are unreliable. Therefore, a better response approach in cases such as these with similar assays needs to be defined for a reliable estimation of antibody titers in the context of infection or vaccination.
Figure 2.
(a) Raw Data; (b) Percent Neutralization.
In response to the need characterized by the example above, we defined a new response approach, which is not only biologically meaningful, but reliably represents dose-response curves typically used in immunoassays. The performance of the new response approach compared with the traditional response approach and the point-based RM method is evaluated numerically through simulations, and illustrated by data from the example study. This new response approach can be extended to data from similar assays such as the TZM-b1 assay for detecting HIV neutralizing antibodies (4; 19; 7; 20; 17; 26).
This paper is organized as follows. In Section 2, we define the new response and the subsequent non-linear model fitting and estimation. In Section 3, we conduct extensive simulation studies to evaluate the performance of the new response approach, and illustrate its application in analysis of real data from the example study. The paper is concluded with some discussion in Section 4.
2 Methods
2.1 Dose-response Curve
For a given assay run, let (xi, yij) be observations to describe the dose-response relationship, where yij is one of mi chosen responses, j = 1, …, mi, at one of the g dilution levels, i = 1, …, g. A general dose-response model for bioassay data is the nonlinear regression model
| (2) |
where the mean function f(xi, β) is nonlinear in the p - dimensional parameter vector β, the variance function υ{f(xi, β), θ} may depend on the mean function f(xi, β) besides the q - dimensional variance parameter θ, and εij are assumed to be independent random normal variables with mean 0 and variance 1. Hence the variance for response Var(yij) = σ2υ{f(xi, β), θ} may depend on both the scale parameter σ and the mean function f(xi, β). The most common variance model for bioassays assumes that υ{f(xi, β), θ} = fθ(xi, β). When θ = 0 we end up with a constant variance, suggesting response variance is homogeneous over dilution factors.
The commonly used model for the mean response is the 4-parameter logistic regression model (25; 12),
| (3) |
where the dilution level xi is usually in log2 or log10 scale depending on serial dilution factor (2-fold or 10-fold), and the parameters are biologically meaningful, with β3 representing the maximum response, β2 being the minimum response, β4 being concentration that results in 50% response, and β1 denoting the relative slope around 50% response (β4). The 4-parameter logistic regression model has been successfully applied to radioimmunoassays, ELISA, pneunococcal opsonophagocytic killing assay and others (24; 15; 8; 3; 30; 14; 27). For simplicity, we will use this commonly used model for illustration, but other similar models such as the five-parameter logistic model (21) can be used as well.
2.2 Newly Defined Response
As mentioned earlier, percent neutralizations calculated from the readings of microneutralization assays is often non-monotonic over dilution levels, and thus the traditional use of it as response has potentially serious problem. A better response has to be defined to capture the dose-response curve (3). The new response has to be biologically meaningful, and also has to be robust to the aforementioned data irregularities which are common in practice, so that it will present a clear dose-response curve, either increasing or decreasing as TAS are diluted. Considering all the issues discussed above, we define the new response as
| (4) |
In theory the negative controls have zero GFP intensity and the positive controls have the maximum GFP intensity. Thus the newly defined response theoretically measures the percent fluorescence intensity of test antibody samples relative to the maximum. Hence it is biologically meaningful. Advantages of the newly defined response approach include:
By using the percent of GFP intensity from the test samples relative to the sum of GFP intensity of negative and positive controls, we circumvent the problems of meaningless negative values in traditional response of percent neutralization brought by common data irregularities;
For each plate, the GFP intensities are fixed for no-test-antibody (positive controls) and no-virus (negative controls), but increases as the test antibody samples are diluted. With a fixed denominator and the numerator decreasing as the dilution levels, it clearly defines a dose-response curve;
ynew = 50 ⇔ ytrad = 50. In other words, the calibration of the fitted curve at 50 using the new response approach is the exact antibody titer estimator (50% reduction of GFP intensity), consistent with the literature definition on antibody titer.
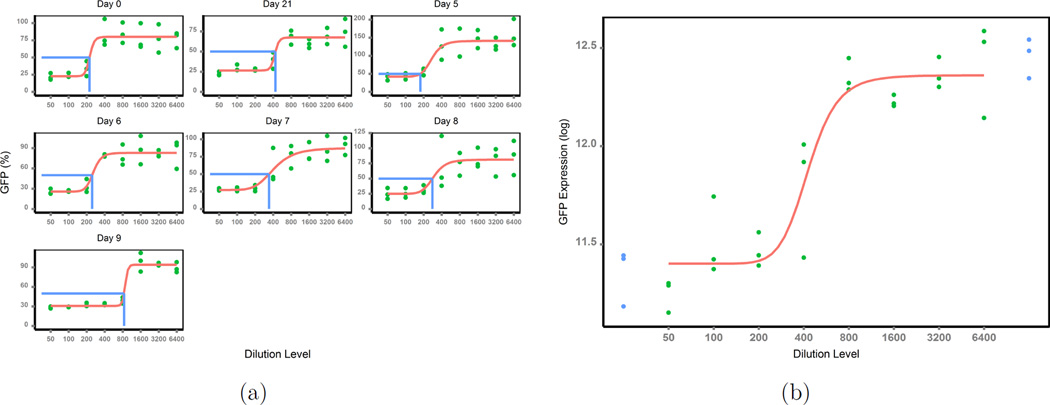
These advantages are clearly suggested by the new dose-response scatter curves (Figure 3(a)) for the same set of data, where percent neutralization was previously used as a response (Figure 2(b)). As expected, the new response increased as test samples were diluted, and it generated a clear logistic curve. In addition, the new response approach is always positive, bypassing the negative value problem brought by the classical use of percent neutralization as a response approach.
Figure 3.
(a) Response newly defined; (b) Raw GFP data at day 21.
2.3 Nonlinear Model Fitting
The methods for nonlinear model fitting were previously detailed (5; 3), and will not be discussed here. Noteworthy here is the specification of initial parameter values required by nonlinear maximization. The choice of initial values may influence the convergence of estimation algorithm, and in the worst case may yield no convergence. For the 4-parameter logistic regression model above, the initial values can be obtained by using the biological representations of the parameters and linearization:
Using the maximum response as the initial value for β3;
Using the minimum response as the initial value for β2;
- Transforming the 4-parameter logistic model as
with , x* = log x and .(5)
Then the initial values β1 and β4 can be obtained by linear regression. With a good choice of initial values, nonlinear model fitting can be processed as previously described (5; 3).
2.4 Antibody Titer Estimation & Inference
Once model fitting and parameter estimation is accomplished by the non-linear model fitting as described in section 2.3, the antibody titers x50, at which 50% neutralization is achieved, shall be obtained by inversion of the fitted curve at 50 for test samples. In the general case let h(y, β) be the inverse function of the monotonic mean function f(x, β). Then a natural estimator of x50 is x̂50 = h(50, β̂), where β̂ is the parameter estimator of β with asymptotic covariance matrix σ2V (β, θ). In the case of 4-parameter logistic regression model, we have
| (6) |
The variance estimation of x50 can be processed by the Delta method. Let h(y, β) denote the inverse function of the mean function f(x, β) in (3). In the case of the 4-parameter logistic regression model, x = h(y, β) = exp (1/β̂1 log (β̂3 − 50)/(50 − β̂2) + log β̂4). By the Delta method,
| (7) |
where hβ(y, β) represents the derivative of h with respect to β, (β̂, θ̂) are estimators for (β, θ), σ2V (β, θ) is the asymptotic covariance matrix for β, which can be obtained by standard theory.
3 Numerical Study
3.1 Monte Carlo Simulations
Monte Carlo simulations are applied to validate the good features of the new response approach over the traditional response approach. Unlike the common simulation studies where endpoints are measurements directly from experiments, the endpoints yij in this study are derived from the experiments’ measurements of GFP expressions. To mimic experimental scenarios, we need to randomly simulate the raw measurements of GFP expressions, and then use the generated data to derive model responses and apply our method. Thus the question becomes how to simulate raw data of GFP expression to mimic the real experiments. As an example of experimental GFP expression, we will use the raw GFP intensity data of the subject T11 in Figure 3(b) at day 21.
The GFP expressions (in log scale, green dots) from the serially diluted test samples also fall into a logistic regression curve over the dilution levels, and the 4-parameter logistic model fits the raw data relatively well (the solid curve). The 5-parameter logistic regression model should also fit the raw data. However, our purpose is not on the model development, but the way to define a meaningful response which clearly depicts the typical dose-response curve once data is generated. Thus it does not matter which model is used to simulate raw data as long as the generated data mimic real data examples. For simplicity, we use the 4-parameter logistic model to generate data. As suggested in (8; 11), raw data from immunoassays often present unequal variance varying with dilution factors. Hence we consider here both constant variance model and varying variance model. Specifically, the model below was used to simulate the raw data:
| (8) |
In practise there are usually 3 replicates at each dilution level, and 8 dilution levels in total, so we chose g = 8 and k = 3, to mimic the real situations. The selection of β is based on fitting the 4-parameter logistic model to the raw data (Figure 3(b)), and using the coefficient estimator β̂ = (−15.67, 11.41, 12.35, 3.08)′ to generate data. Recalling that β4 is the concentration that results in 50% response, the true antibody titer is set at 3.08.
To assess the relative performance, we first studied their numerical failure (NF) occurrence and their out-of-limit (OOL) frequency out of 1000 runs for the two model-based estimators. An out-of-limit event occurs when a model converges but the two asymptotes are either both larger than 50 or both smaller than 50, thus the titer estimator is out of the limits and can not be obtained. Next, we explored the coverage properties of the associated confidence intervals using the variance estimator (7) for the model-based estimators, by computing the coverage probabilities (CP) of the associated CIs containing the true titers. Last, we compare the three estimators by their absolute relative errors (defined below).
| (9) |
where b denotes the bth simulation run, with b = 1, …, 1000. The 10% trimmed mean of AREs is used to avoid extreme data due to random generation.
We start with the constant variance model, when θ = 0. We selected σ ranging from 0.2 to 0.5 as in (8), to explore the performance of the proposed approach over a broad range.
Table 1 presents the NF, OOL and CP of the the two model-based estimators and the ARE of all the three estimators under each σ. As indicated, the new response approach performs very stable in terms of both the NF and the OOL even when data variance is large, while the traditional response approach encounters more numerical problems in addition to much higher rate of out-of-limit problems for large data variance. Overall, both of the model-based estimators have good coverage properties when data variance is small to medium, but the new response approach has better coverage rate when data variance is large. With respect to ARE, the two model-based estimators have similar performance for small constant variance, while the RM method performs much worse, as expected. As variance increases, the AREs of the two model based estimators increase as well, but the absolute relative error of the traditional response approach increases much faster. This again proves the advantages of the new response approach. The RM keeps giving the largest AREs.
Table 1.
Constant Variance Model. ARE, average relative error; NF, numerical failure; OOL, out of limits; CP, coverage probability.
| Methods | # of NF | # of OOL | CP | ARE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σ = | 0.2 | 0.3 | 0.4 | 0.5 | 0.2 | 0.3 | 0.4 | 0.5 | 0.2 | 0.3 | 0.4 | 0.5 | 0.2 | 0.3 | 0.4 | 0.5 |
| New | 0 | 0 | 0 | 2 | 0 | 6 | 29 | 80 | 0.96 | 0.96 | 0.94 | 0.93 | 0.04 | 0.07 | 0.11 | 0.16 |
| Trad | 0 | 1 | 4 | 17 | 0 | 15 | 73 | 155 | 0.97 | 0.97 | 0.94 | 0.89 | 0.04 | 0.08 | 0.14 | 0.24 |
| RM | 0.75 | 0.68 | 0.66 | 0.62 | ||||||||||||
We also consider the varying variance model where θ ≠ 0, with the model (8) used to generate data and the coefficient β being the same as well. We let the average noise level σ be 0.05, 0.08 and and 0.1, as previously used (8). Different values of θ represent different variance model: when θ = 0, the variance model reduces to the constant variance model we studied previously; when θ = 1, the variance is proportional to mean response; when θ = 2, it is a constant coefficient variation model. Due to its effect on the generation of positive control data, θ having values greater than 1.5 often leads to irregular data and hence numerical convergence failure. Thus we let θ vary from 0.5 to 1.2.
We present the NF, OOL and CP of the two model-based estimators in Table 2, and the ARE of all three estimators in Table 3. As suggested by the tables, the traditional response method has severe numerical convergence problem under the varing variance model, with over 98% convergence failure. On the contrary, the new response method has zero convergence failure. Considering both the NF and the OOL, the new response method successfully gives estimators over 92% runs against less than 2% runs by the traditional response approach, although its OOL frequencies look worse. Furthermore, the new response method has very good coverage rates (close to 95%). The poor performance of the traditional response method is not surprising, since when data variability is large and changes with dilution levels, the responses traditionally defined are frequently irregular and biologically meaningless, and therefore do not follow any curves. As for ARE, each method performs worse as either δ or θ increases. However, the estimator using the new response approach is much more amenable to the change in data variance. As in the constant variance model, the AREs of the RM estimator are consistently the largest.
Table 2.
Varying Variance Model. NF, numerical failure; OOL, out of limits; CP, coverage probability.
| Methods | σ = 0.05 | σ = 0.08 | σ = 0.1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ = 0.5 | 0.8 | 1 | 1.2 | θ = 0.5 | 0.8 | 1 | 1.2 | θ = 0.5 | 0.8 | 1 | 1.2 | ||
| # of NF | New | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Trad | 993 | 991 | 988 | 995 | 981 | 986 | 998 | 988 | 993 | 988 | 996 | 997 | |
| # of OOL | New | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 24 | 0 | 6 | 25 | 76 |
| Trad | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 0 | 1 | 1 | 2 | |
| CP | New | 0.88 | 0.94 | 0.93 | 0.94 | 0.93 | 0.95 | 0.95 | 0.94 | 0.94 | 0.95 | 0.93 | 0.94 |
| Trad | 0.57 | 1.00 | 0.67 | 0.40 | 0.79 | 0.92 | . | 0.80 | 0.86 | 0.91 | 1.00 | . | |
Table 3.
Varying Variance Model. ARE, average relative error.
| Methods | σ = 0.05 | σ = 0.08 | σ = 0.1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ = 0.5 | 0.8 | 1 | 1.2 | θ = 0.5 | 0.8 | 1 | 1.2 | θ = 0.5 | 0.8 | 1 | 1.2 | ||
| ARE | New | 0.03 | 0.03 | 0.04 | 0.05 | 0.04 | 0.05 | 0.07 | 0.10 | 0.04 | 0.07 | 0.10 | 0.13 |
| Trad | 0.08 | 0.03 | 0.09 | 0.21 | 0.11 | 0.09 | . | 0.43 | 0.13 | 0.14 | 0.26 | . | |
| RM | 0.80 | 0.79 | 0.77 | 0.74 | 0.80 | 0.74 | 0.68 | 0.66 | 0.76 | 0.70 | 0.69 | 0.61 | |
3.2 Real Data Examples
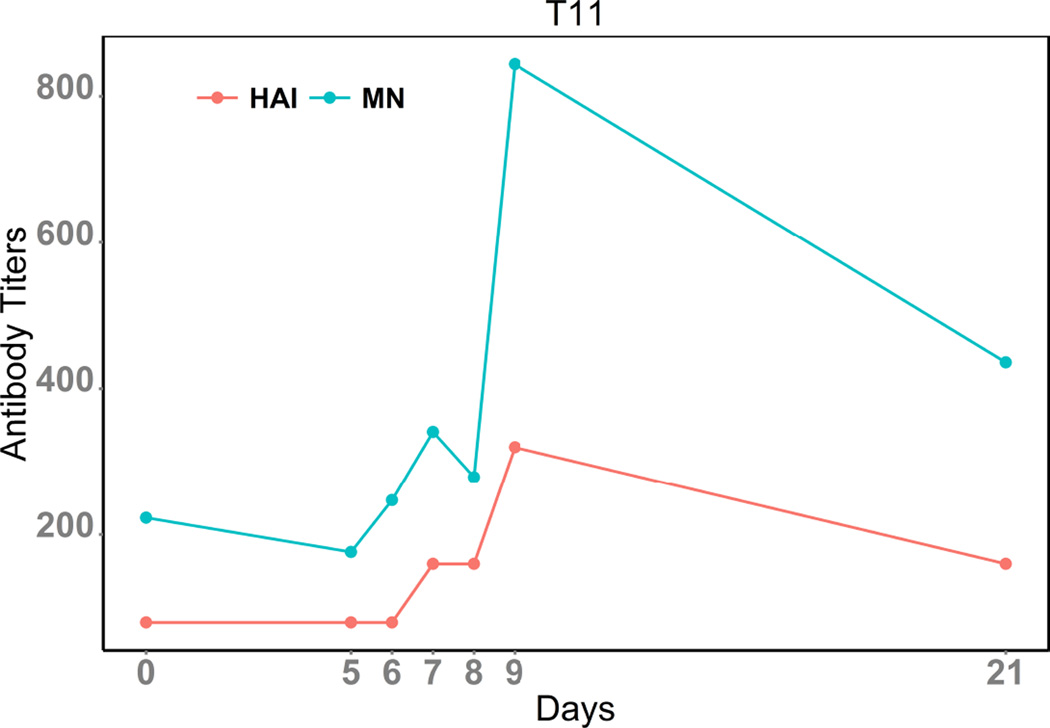
Influenza neutralizing antibodies correlate well with protection against future viral infections (9). The antigenic, but highly variable, head domain of influenza HA is a common target for neutralizing antibodies, where they aim to hinder access to the receptor binding domain (28; 6). The hemagglutination inhibition (HAI) assay strictly evaluates neutralizing antibodies that can block HA-receptor binding. However, neutralizing antibodies that bind to the more conserved stalk domain and can inhibit virus entry are similarly important, but are not detected using HAI and instead rely on other methodologies (e.g. conventional microneutralization assays or plaque reduction neutralization titer 50 assays) for detection (29). In general HAI and traditional microneutralization titers correlate well with each other, perhaps because the concentration or efficiency of inhibition of head-reactive antibodies is often saturating in sera. To address if HAI correlates with GFP-based microneutralization assays we describe here, the new response approach was used to analyze subject T11, using HAI for comparison (Figure 4). As expected, GFP-based microneutralization and HAI titers followed the same dynamic trend despite differences in magnitude, suggesting that the GFP-based microneutralization analysis is biologically relevant. The plots also suggest that after vaccination, the induction of neutralizing antibodies for this subject increases starting at day 6 and peaks around day 9, which then gradually waned for the next two weeks. Differences in magnitude between the GFP-based microneutralization and HAI approaches likely result from the amount of virus used for these assays. For the GFP-based microneutralization assay, ~ 100 – 200 viruses are pre-incubated with the tested samples (18), while, in the HAI assay, an estimated amount of ~ 1, 000 – 10, 000 viruses are used (16). Thus, in the GFP-based microneutralization assay, a lower concentration of neutralizing antibodies are required for effective neutralization as compared to traditional HAI.
Figure 4.
Dynamic Curve of MN & HAI titers for subject T11.
4 Discussion
Virus microneutralization assays using reporter gene expression as a surrogate for viral infection are relatively new (18; 22; 4; 19; 7; 20; 17; 26). The traditional model-based methods using standard outcome of percent neutralization could be, and often are, used in such assays to estimate neutralizing antibody titers. However, there can be problems with the data in practice, which yield meaningless and irregular outcomes that do not fit the typical curves for immunoassays. Thus antibody titer estimators obtained are often unreliable. We developed a new type of outcomes model that generates data that are biologically meaningful and fit the typical immunoassay curves well. The 4-parameter logistic model was used to generate raw data in our simulation study. Although the 5-parameter logistic regression model or others could be used as well, our purpose is not on the model development, but the way to define a meaningful response which clearly depicts the typical dose-response curve once data is generated. Thus it does not matter which model is used to simulate raw data as long as the generated data mimic real data examples. The simulation study indicates that the new response approach outperforms the traditional response approach regardless of the data variability. The proposed new response approach can be used in similar assays for other diseases (4; 19; 7; 20; 17; 26). Statistical software R was used for data analysis and simulation studies.
Acknowledgements
This work is supported by the NIAID Center for Biodefense Immune Modeling (HHSN272201000055C), by the NIAID Centers of Excellence for Influenza Research and Surveillance (HHSN266200700008C), by the NIAID Center for AIDS Research (Grant Number P30AI078498), and by the NIH grant R01HD071779. Research in the L.M.-S. laboratory is funded by the NIH grants RO1AI077719, R21NS075611-01, and R03AI099681-01A1, the NIAID Centers of Excellence for Influenza Research and Surveillance (HHSN266200700008C), and the University of Rochester Center for Biodefense Immune Modeling (HHSN272201000055C). SFB is currently supported by the University of Rochester Immunology Training Grant (AI 007285-26).
The authors thank the Statistical Center for HIV/AIDS Research and Prevention at Fred Hutchinson Cancer Research Center (especially Dr. George K. Lewis) for sharing us their HIV neutralizing antibodies data, and the Referees and the Editors for their detailed comments and valuable suggestions that greatly improved the presentation and contents of this paper.
References
- 1.Baker SF, Guo H, Albrecht RA, Garca-Sastre A, Topham DJ, Martnez-Sobrido L. Protection against lethal influenza with a viral mimic. J Virol. 2013;87:8591–8605. doi: 10.1128/JVI.01081-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Baker SF, Nogales A, Finch C, Tuffy KM, Domm W, Perez DR, Topham DJ, Martnez-Sobrido L. Influenza A and B Virus Intertypic Reassortment through Compatible Viral Packaging Signals. J Virol. 2014;88:10778–10791. doi: 10.1128/JVI.01440-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Belanger BA, Davidian M, Giltinan DM. The Effect of Variance Function Estimation on Nonlinear Calibration Inference in Immunoassay Data. Biometrics. 1996;52:158–175. [PubMed] [Google Scholar]
- 4.Biacchesi S, Skiadopoulos MH, Yang L, Murphy BR, Collins PL, Buchholz UJ. Rapid human metapneumovirus microneutralization assay based on green fluorescent protein expression. Journal of Virological Methods. 2005;128:192–197. doi: 10.1016/j.jviromet.2005.05.005. [DOI] [PubMed] [Google Scholar]
- 5.Carroll RJ, Ruppert D. Transformation and Weighting in Regression. New York: Chapman and Hall; 1988. [Google Scholar]
- 6.Caton AJ, Brownlee GG, Yewdell JW, Gerhard W. The antigenic structure of the influenza virus A/PR/8/34 hemagglutinin (H1 subtype) Cell. 1982;31:417–427. doi: 10.1016/0092-8674(82)90135-0. [DOI] [PubMed] [Google Scholar]
- 7.Combita A, Touze A, Bousarghin L, Christensen ND, Coursaget P. Identification of two cross-neutralizing linear epitopes within the L1 major capsid protein of human papillomaviruses. J Virol. 2002;76:6480–6486. doi: 10.1128/JVI.76.13.6480-6486.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Davidian M, Carroll RJ, Smith W. Variance Functions and the Minimum Detectable Concentration in Assays. Biometrika. 1988;75:549–556. [Google Scholar]
- 9.Dowdle WN, Kendal AP, Noble GR. Diagnostic procedures for viral, rickettsial and chlamydial infections. 5th Edition. Washington, DC: American Public Health Association; 1979. Influenza viruses; p. 6035. [Google Scholar]
- 10.Domm W, Brewer M, Baker SF, Feng C, Martnez-Sobrido L, Treanor J, Dewhurst S. Use of bacteriophage particles displaying influenza virus hemagglutinin for the detection of hemagglutination-inhibition antibodies. J Virol Methods. 2014;197:47–50. doi: 10.1016/j.jviromet.2013.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Feng F, Sales AP, Kepler TB. A Bayesian approach for estimating calibration curves and unknown concentrations in immunoassays. Bioinformatics. 2011;27:707–712. doi: 10.1093/bioinformatics/btq686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Finney DJ. Radioligand assay. Biometrics. 1976;32:721–740. [PubMed] [Google Scholar]
- 13.Guo H, Baker SF, Martnez-Sobrido L, Topham DJ. Induction of CD8 T Cell Heterologous Protection by a Single Dose of Single-cycle Infectious Influenza Virus. J Virol. 1998 doi: 10.1128/JVI.01847-14. pii: JVI.01847-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Higgins KM, Davidian M, Chew G, Burge H. The Effect of Serial Dilution Error on Calibration Inference in Immunoassay. Biometrics. 1998;54:19–32. [PubMed] [Google Scholar]
- 15.Healy MJR. Statistical Analysis of Radioimmunoassay Data. Biochem. J. 1972;130:207–210. doi: 10.1042/bj1300207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Killian ML. Hemagglutination assay for the avian influenza virus. Methods Mol Biol. 2008;436:47–52. doi: 10.1007/978-1-59745-279-3_7. [DOI] [PubMed] [Google Scholar]
- 17.Lam R, Farrell R, Aziz T, Gibbs E, Giovannoni G, Grossberg S, Oger J. Validating parameters of a luciferase reporter gene assay to measure neutralizing antibodies to IFNbeta in multiple sclerosis patients. Journal of Immunological Methods. 2008;336:113–118. doi: 10.1016/j.jim.2008.03.014. [DOI] [PubMed] [Google Scholar]
- 18.Martinez-Sobrido L, Cadagan R, Steel J, Basler CF, Palese P, Moran TM, Garcia-Sastre A. Hemagglutinin-pseudotyped green fluorescent protein-expressing influenza viruses for the detection of influenza virus neutralizing antibodies. J Virol. 2010;84:2157–2163. doi: 10.1128/JVI.01433-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Montefiori DC. Evaluating neutralizing antibodies against, HIV, and SIV, and SHIV in luciferase reporter gene assays. Curr Protoc Immunol. 2005;Chapter 12(Unit 12.11) doi: 10.1002/0471142735.im1211s64. [DOI] [PubMed] [Google Scholar]
- 20.Okuma K, Nakamura M, Nakano S, Niho Y, Matsuura Y. Host range of human T-cell leukemia virus type I analyzed by a cell fusion-dependent reporter gene activation assay. Virology. 1999;254:235–244. doi: 10.1006/viro.1998.9530. [DOI] [PubMed] [Google Scholar]
- 21.Paul G, Gottschalk JRD. The five-parameter logistic: A characterization and comparison with the four-parameter logistic. Analytical Biochemistry. 2005;343:54–65. doi: 10.1016/j.ab.2005.04.035. [DOI] [PubMed] [Google Scholar]
- 22.Rimmelzwaan GF, Verburgh RJ, Nieuwkoop NJ, Bestebroer TM, Fouchier RA, Osterhaus AD. Use of GFP-expressing influenza viruses for the detection of influenza virus A/H5N1 neutralizing antibodies. Vaccine. 2011;18:3424–3430. doi: 10.1016/j.vaccine.2011.02.082. [DOI] [PubMed] [Google Scholar]
- 23.Reed LJ, Muench H. A Simple Method OF Estimating Fifty Percent Endpoints. American Journal of Epidemiology. 1938;27:493–497. [Google Scholar]
- 24.Rodbard D. Statistical Estimation of the Minimal Detectable Concentration (Sensitivity) for Radioligand Assay. Analytical Biochemistry. 1978;90:1–12. doi: 10.1016/0003-2697(78)90002-7. [DOI] [PubMed] [Google Scholar]
- 25.Rodbard D, Frazier GR. Statistical analysis of radioligand assay data. Methods of Enzymology. 1975;37:839–841. doi: 10.1016/s0076-6879(75)37003-1. [DOI] [PubMed] [Google Scholar]
- 26.Sprangers MC, Lakhai W, Koudstaal W, Verhoeven M, Koel BF, Vogels R, Goudsmit J, Havenga MJE, Kostense S. Quantifying adenovirus-neutralizing antibodies by luciferase transgene detection: addressing preexisting immunity to vaccine and gene therapy vectors. J Clin Microbiol. 2003;41:5046–5052. doi: 10.1128/JCM.41.11.5046-5052.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang D, Soong SJ. Comparisons of titer estimation methods for multiplexed pneunococcal opsonophagocytic killing assay. Computational Statistics and Data Analysis. 2008;52:5022–5032. [Google Scholar]
- 28.Wiley DC, Wilson IA, Skehel JJ. Structural identification of the antibody-binding sites of Hong Kong influenza haemagglutinin and their involvement in antigenic variation. Nature. 1981;289:373–378. doi: 10.1038/289373a0. [DOI] [PubMed] [Google Scholar]
- 29.Wrammert J, Koutsonanos D, Li GM, Edupuganti S, Sui J, Morrissey M, McCausland M, Skountzou I, Hornig M, Lipkin WI, Mehta A, Razavi B, Del Rio C, Zheng NY, Lee JH, Huang M, Ali Z, Kaur K, Andrews S, Amara RR, Wang Y, Das SR, O’Donnell CD, Yewdell JW, Subbarao K, Marasco WA, Mulligan MJ, Compans R, Ahmed R, Wilson PC. Broadly cross-reactive antibodies dominate the human B cell response against 2011 pandemic H1N1 influenza virus infection. J Exp Med. 2011;208:181–193. doi: 10.1084/jem.20101352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zeng Q, Davidian M. Bootstrap-Adjusted Calibration Confidence Intervals for Immunoassay. Journal of the American Statistical Association. 1997;92:278–290. [Google Scholar]