From Mouth-level to Tooth-level DMFS: Conceptualizing a Theoretical Framework

Abstract

Objective

There is no dearth of correlated count data in any biological or clinical settings, and the ability to accurately analyze and interpret such data remains an exciting area of research. In oral health epidemiology, the Decayed, Missing, Filled (DMF) index has been continuously used for over 70 years as the key measure to quantify caries experience. The DMF index projects a subject’s caries status using either the DMF(T), the total number of DMF teeth, or the DMF(S), counting the total DMF teeth surfaces, for that subject. However, surfaces within a particular tooth or a subject constitute clustered data, and the DMFS mostly overlook this clustering effect to attain an over-simplified summary index, ignoring the true tooth-level caries status. Besides, the DMFT/DMFS might exhibit excess of some specific counts (say, zeroes representing the set of relatively disease-free carious state), or can exhibit overdispersion, and accounting for the excess responses or overdispersion remains a key component is selecting the appropriate modeling strategy.

Methods & Results

This concept paper presents the rationale and the theoretical framework which a dental researcher might consider at the onset in order to choose a plausible statistical model for tooth-level DMFS. Various nuances related to model fitting, selection and parameter interpretation are also explained.

Conclusion

The author recommends conceptualizing the correct stochastic framework should serve as the guiding force to the dental researcher’s never-ending goal of assessing complex covariate-response relationships efficiently.

Discrete count data abounds in a variety of scientific disciplines such as epidemiology, medicine, biology, and in a number of clinical trial settings (1,2). For example, in the epidemiology of dental caries, dental researchers exhibit unparallel fidelity to the DMFT/DMFS index, whose origin dates back to Klein, Palmer and Knutson, 1938 (3). The DMFT/DMFS index counts the total number of decayed (D), missing (M) and filled (F) tooth/surfaces for the whole mouth. A common feature of these data is the presence of ‘overdispersion’ when fitting to a Poisson (P) distribution, the default statistical distribution for count data, in the sense that the sample variance is larger than the sample mean, and hence the well-known “unit variance to mean ratio” is violated. Overdispersion might be a result of several factors, such as unobserved heterogeneity, missing covariates, or correlation among repeated, or longitudinal measures. These count responses are also sometimes characterized by excessive observations at one end of the ordering, typically zeroes (4), than what is permitted by the distribution under consideration. In caries DMFS, these zeros represent the cases where one does not observe any disease.

Modeling strategies that account for overdispersion and excess zeroes continue to remain an important area of statistical research, particularly in caries assessments. Often, one choose to use a Negative Binomial (NB) regression (5) to model full mouth DMFS to tackle overdispersion. In situations of excess zeros, the zero-inflated (ZI) model (6) is widely used in dental epidemiology (7). In the ZI framework, the probability of being an excess zero is modeled through a mixture distribution allowing greater weight to be placed on the probability of observing a zero count (8). A very nice review on applications of the ZI model to full-mouth DMFT/DMFS data, and some recommendations appear in (9).

When modeling excess zeroes, it is of utmost importance to consider the latent process from which the zeroes evolved. For example, for DMFT/DMFS in any dataset, the zeroes can appear from two separate regimes. There might be some tooth/surfaces which had remained potentially ‘disease-free’, while others are ‘disease free’ for the present, might have developed caries earlier and got cured, or are prone to develop carious lesions in the future. The zeroes arising from tooth/surfaces that are never truly at any risk are known as ‘structural zeroes’, while zeros arising from tooth/surfaces potentially at risk contributes to ‘sampling zeroes’ (4).

For many data analysis problems, one can assume a latent process that divides the entire set of zeroes into the structural and sampling components. The ZI modeling is often more advantageous if a dataset contains both these types of zeroes whose probabilities can be modeled separately (8). In cases with only an excess of sampling zeroes, Hurdle (H) models proposed in (10) are more appropriate. In contrast to the mixture setup in a ZI model, the H model is essentially a 2-part model, with the first part modeling a binary response of zero versus non-zero, and the second part modeling a truncated-at-zero distribution, such as the P, B, etc. This modeling strategy allows for differentiation between the process generating the zeroes, and that generating all other count values.

The World Health Organization has adopted the mouth-level aggregative DMF index for oral health assessments in national surveys (11). However, it comes with its own set of limitations (12). The DMF neither evaluates the number of teeth at risk, not it is useful in tracking rate of caries progression. It is not intended for root caries assessment. It provides equal weighting to missing, untreated decayed, and well-restored (filled) teeth, which might be unrealistic. There is also a lot of controversy in calculating the ‘M’ (missing) component of the DMF (12). The DMF is often invalid for elderly subjects where teeth can be lost due to a variety of other reasons other than caries. Also, with age, DMF can reach a saturation level (13) involving all teeth, and that hinders caries registration even when caries activity continues. However, the most perplexing issue are the various possible suggestions (12) in the assignment of the M component in DMF(S) for a missing tooth, which can lead to overestimation, or possible underestimation. Yet, the DMFT/DMFS has withstood the test of time as the prime index of caries assessment.

Aggregative in nature, the DMFS/DMFT provide a summary caries index for the whole mouth without going into the details at the tooth or surface level. To alleviate this, the author has earlier proposed modeling caries at the tooth-level (14), by considering the DMFS count for each tooth, clustered within a subject. However, there are some important considerations in pursuing this theoretical framework which were not discussed in details. This concept paper aims to enlighten the dental researchers and other clinical practitioners into understanding the correct theoretical premise behind such a model choice, and ways to validate such choices in real data applications and simulation studies.

Tooth-level DMFS Modeling Framework Background

With the goal of assessing covariate-response relationships efficiently at the tooth-level, the author sets forward with his tooth-level DMFS (14) proposition. Henceforth, DMFS refers to the tooth-level count. One might consider various conventions in calculating the DMFS discussed in (12), particularly in the context of assigning the ‘M’ component. Whatever be the case, it leads to ‘bounded’ counts, where the range of the count is upper-bounded. Note that, in the context of DMFT, the range is from 0 to 28 (or 32), depending on whether the third molars are included in the scoring. For DMFS, this is either 128, or 148, based on the inclusion of the third-molar surfaces (15). All these are amenable to P and NB modeling where the unbounded support of the P and NB distributions can be approximated with the upper bound values of 28 or 128.

Following the ‘DM5FS’ convention (i.e., for a missing tooth we consider all the surfaces to be missing) described in (12), the tooth-level DMFS can range from 0 to 4, or 5, depending on the tooth-location. Figure 1 presents the density plot of raw tooth-level DMFS counts packed over tooth and subjects from a dataset assessing caries status of Type-2 diabetic, Gullah-speaking African-Americans (16). With an upper bound reaching 5, a P or NB model is inappropriate here, and one can start modeling with a Binomial (B) distribution. However, there can be excess of zeroes (due to the presence of healthy teeth), and also presence of clustering because the tooth-level counts are clustered within that subject. Both can lead to heterogeneity, and overdispersion, which can be tackled via. the Beta-Binomial (BB) specification. The excess zero situation can be handled by either the ZI or H formulation of the B distribution, depending on the origin of the zeroes. To accommodate both overdispersion and excess zeroes, one can reconsider fitting a ZI or H formulation of the BB model (17). After selecting a suitable model, or a set of models, one needs to ascertain the model producing the best fit, investigate model fit diagnostics, and finally assess the covariate-response relationship by connecting the covariates to the DMFS counts through suitable link functions (18), such as the logistic, probit, or cloglog links. We now briefly sketch the theoretical framework of the models described above.

Fig. 1.

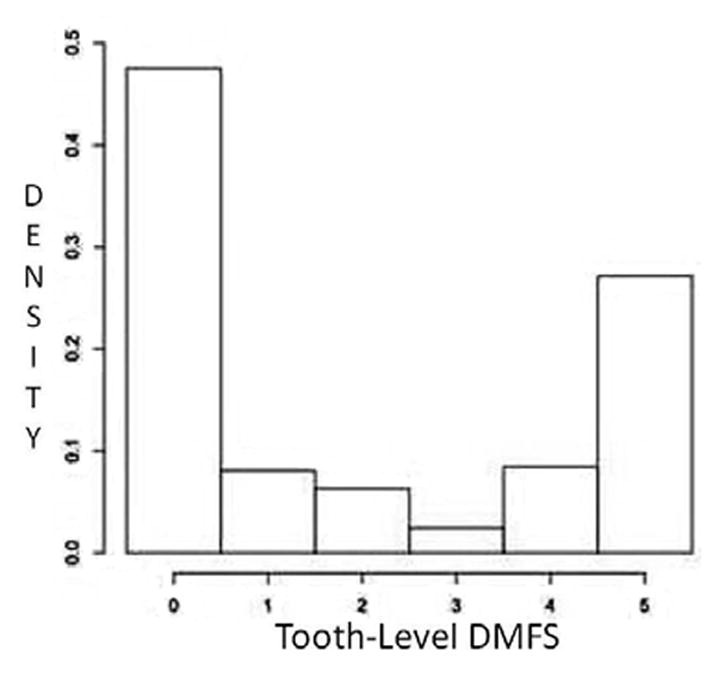
Density histogram of tooth-level DMFS counts for the Gullah dataset

The theoretical framework, model fitting and parameter interpretations

Let Y be a random variable (r.v.) representing the DMFS counts, with y being our observed value of the count. Define f(y_ij) = P(Y_ij = y_ij) to be the probability mass function of Y corresponding to the j^th tooth of the i^th subject. For our Binomial model, the distribution function of Y is represented by f(y_ij) = Bin(n_ij, θ_ij), where the parameters n_ij and θ_ij correspond to the counts (4, or 5), and the probability of experiencing a D, M or F surface for the (i, j)^th response, respectively. Note, here we assume the probabilities of occurrence of a D, M or F surface are all equal. Next, the effect of possible subject level (such as Age, gender, glycemic status, etc), and/or tooth-level (such as tooth-type, i.e., whether a tooth is either one of incisor, canine, pre-molar and molar; jaw indicator, i.e. whether tooth is located in the mandible or the maxilla, etc) covariates can be assessed via a regression function over θ_ij using the logit link, such that: $\mathit{logit}({\theta }_{ij})={\beta }_{\mathit{0}}+X_i^T\beta +U_i$, where logit(θ_ij) = log[θ_ij/(1−θ_ij)], β₀ is the model intercept, X_i is the design matrix of covariates (of appropriate dimensions) corresponding to the regression parameter vector β, and U_i is the random effect/intercept term that controls for the clustering. U_i is assigned a Normal distribution with an unknown (but estimable) variance σ², i.e. U_i ~ N(0, σ²), and parameter estimation can proceed via maximum likelihood (ML) (19), available in standard software like SAS (20), R (21), etc. The exponentiated estimate of a single parameter β₁ can be expressed in terms of increase/decrease in the odds of having an extra D, M or F surface with 1 unit increase in the covariate (for continuous ones), or a change from a 0 to 1 category (for categorical ones), conditioned on the other covariates and the clustering effect.

Next, in the Beta-Binomial (BB) specification capable of handling overdispersion, θ_ij is allowed to follow a Beta distribution, i.e. θ_ij ~ Beta (a_ij, b_ij), where a_ij, and b_ij, are the Beta parameters. For assessing covariate effects, one parameterizes a_ij, and b_ij, as a_ij = μij * φ and b_ij = (1−μ_ij) * φ and, where φ is an unknown (constant), but estimable, dispersion parameter and μ_ij = E(Y_ij). Note that 0 ≤ μ_ij ≤ 1 and φ > 0. and. Data covariates are then connected to the true response Y via the logit link on μ_ij as above. Interpretation remains the same for a single parameter β₁, however, here the odds are expressed in terms of increase/decrease in the ‘mean’ probability of having an extra D/M/F surface, conditioned on other covariates and random effects. One might also consider φ to be varying with subjects, tooth, or both subject and tooth, i.e., φ_i, φ_j, or φ_ij, and estimate those from the data, or connecting those to the covariates via. a log link, i.e. $\mathit{log}({\phi }_{ij})={\gamma }_{\mathit{0}}+Y_i^T\gamma +V_i$, where γ₀ the intercept, γ the vector of regression parameters corresponding to the design matrix of covariates Y (which may or may not be equivalent to X considered above), and V_i is another random effect term assigned a N(0, δ²), where δ² is the variance component for V_i. Covariates here are linked linearly to log (φ_ij). Similarly as above, parameter estimation follows standard ML methods utilizing available software.

With the goal of accommodating excess zeroes in our model, the choice between the ZI and H specification of a Binomial distribution is dictated by the zero-generation process. Although both the ZI and H models can be viewed as finite mixture models (22), they often produce indistinguishable fits revealed through goodness-of-fit measures. Yet, one model might be more applicable than the other based on the objectives and design of the study. Hence, a proper evaluation of the underlying clinical framework is necessary. The ZIB probability distribution (23) is given by:

$$P(Y_{ij}=y_{ij})=\{\begin{array}{ll}{p}_{ij}+(1-p_{ij})f(0),\hfill & \text{if}{y}_{ij}=0\hfill \\ (1-p_{ij})f(y_{ij}),\hfill & \text{if}{y}_{ij}>0\hfill \end{array}$$

where p_ij is the probability of excess ‘structural’ zeroes, f(y_ij) is the B distribution, with f(0) the value at y_ij = 0. The ZIB model puts greater emphasis on the probability of observing a zero, which is determined as the sum of the probabilities of observing a structural and a sampling zero (the expression corresponding to y_ij = 0 in the equation above). Thus, the ZIB has the ability to pick up two different regimes of zeroes; when p_ij equals 0, the ZIB reduces to the standard B distribution, and with p_ij approaching 1, the data exhibit greater over-dispersion. On the contrary, the HB is a modified count model (8) that conceptualizes two separate processes generating the zero and positive counts, the positive counts resulting after crossing the zero threshold or the ‘hurdle’. Thus, the HB model is defined as

$$P(Y_{ij}=y_{ij})=\{\begin{array}{ll}{p}_{ij},\hfill & \text{if}{y}_{ij}=0\hfill \\ (1-p_{ij})\frac{f(y_{ij})}{1-f(0)},\hfill & \text{if}{y}_{ij}>0\hfill \end{array}$$

where p_ij is the probability of a zero, 1−p_ij is the probability of ‘crossing the hurdle’, and f(y_ij) is the B distribution. In general, the H model is an alternative way to model zero modifications (both inflation and deflation), whereas the ZI model can handle only zero-inflations.

In a ZI framework, there is no selection process leading to a zero or non-zero values; in contrast, within the H framework, there is a clear hierarchical process leading to the choice of Y_ij = 0 vs. Y_ij > 0, and afterwards a process that follows accounting for Y_ij > 0. Once again, one can connect the covariates to θ_ij in both the ZIB and HB models via. a logit link as described above after adding the normally distributed random intercept U_i to the linear predictor. The excess zero probability p_ij in both the framework can be estimated from the dataset assuming it to be a constant, or connected to the covariates via. a similar logit link function. Another normally distributed random intercept V_i (described above) may or may not be added to the linear predictor of p_ij. Both the variance parameters associated with U_i and V_i and can be estimated from the data, or they may follow the same normal distribution with the same variance parameter, or (U_i, V_i) may be allowed to follow a bivariate normal distribution from which the covariance between the two random intercepts for both ZI and H models can be estimated. It is likely that for the H model, the covariance can be negative because a subject with a greater probability of producing zero counts will tend to have a lower binomial success probability in the truncated (Y > 0) second stage.

In order to accommodate both excess zeroes and overdispersion, one can also consider the ZI and H specification of the BB model (17, 24). This framework is straightforward, where f(y_ij) in the ZIB and HB models above is replaced with a BB distribution. Note, here the covariates can be regressed over any combination of p_ij, μ_ij, φ_ij, and via. suitable link functions, and interpretations remain the same as described in the context of BB, ZIB and HB models. Once again, parameter estimation can follow the ML estimation method in all the above specifications of the ZI and H models.

Note, instead of modeling p_ij, one can choose to model (1−p_ij) representing the probability of ‘not crossing the hurdle’, and consequently the sign of the estimated covariance is expected to reverse. However, there remain subtle differences in the interpretation of the regressions parameters on p_ij and θ_ij, for both models. For p_ij, the parameters are evaluated in terms of the odds of ‘structural zero DMFS versus a random DMFS (that includes the sampling zeroes)’ for the ZI model, and of ‘no DMFS versus a positive DMFS’ for the H model. For θ_ij, the parameters are again evaluated in terms of the odds of ‘experiencing an additional D/M/F surface among surfaces that includes sampling zeroes’ for the ZI model, and of ‘experiencing an additional D/M/F surface, given that there is at least one such surface (i.e., after crossing the hurdle)’ for the H model. Intuitively, some of the covariates (such as Age) might be predicting p_ij, and θ_ij in a completely opposite direction, which should be the case. Also note that the interpretation of regression parameters in the BB (and B) model for θ_ij, and μ_ij, are not the same as that in the H specification for θ_ij. For the BB and B models, the parameters have marginal interpretation, while for the H model the parameters are interpreted conditional on crossing the hurdle of having at least one DMFS counts, and hence they are not comparable. However, certain parameter transformations similar to (9, 24) can be adopted to render the parameters suitable for comparisons.

Post model fit, the competing models (B, BB, ZIB, HB, ZIBB and HBB) should be compared via popular model selection techniques such as Deviance, AIC, BIC, etc criteria popularly used in statistical model fitting and available in almost all software, or using the Vuong’s test (25) to arrive at the ‘best model’. Finally, goodness of fit can be assessed through visual checks by plotting the observed proportion minus the mean (expected) probability at each count for the competing models, and the best model is expected to yield values that lie close to a horizontal line passing through the origin. Inference in terms of odds from the best model can then be reported by assessing statistical significance of the parameters at a 5% level. Finally, in order to quantify the effect of model misspecification on the regression parameters (i.e., trying to understand how far away the model parameters are estimated from their true values using the wrong model under ground truth), simulation studies that uses artificially generated data under various scenarios are necessary. After generating data from one of the models, the parameter estimates obtained after fitting the above class of competing models can be compared via mean squared error (MSE), coverage probability (CP), etc. The model that closely resemble the underlying data generation will have the minimum MSE and maximum CP. However, one needs to be careful in comparing the model parameters β while comparing the BB and H models in light of the discussion above, and the recommendations in (9, 23).

Moving Forward

The analysis of clustered count data with finite upper bounds that exhibits overdispersion and excess zeroes remains a complex statistical problem. With the aim to better understand dental caries, the author proposes to model (bounded) tooth-level DMFS over the usual mouth-level (aggregative) DMFS, and sketches the theoretical framework of a set of plausible statistical models which a dental researcher might consider at the onset. Various nuances related to model fitting, selection and parameter interpretation are also explained which should serve as a guiding force to dental researchers interested in assessing complex covariate-response relationships.

In this context, the recommendations of the author are the same as described in the excellent review article on caries assessment (9), and the estimation of overall exposure effects in ZI models (24). A researcher might have at his/her disposal a rich toolbox of models with varying complexity, staring from the simple B model to the ZI and H specification of a BB model. No matter whatever the starting models are, the final model selection should always consider comparing various model fit statistics like deviance, AIC, BIC, etc. This may seem counter-intuitive, because the model fit statistics can sometimes choose a simpler model over a more complex one which seems to better explain the underlying stochastic phenomenon. Note that the ZI and H structure of the B or BB models are just some theoretical ramifications aiming to better explain the ground truth, and there remains a possibility that a much simpler model can sometimes be closer to the truth. Next, covariate choice for the two separate regressions (say, p_ij and θ_ij for the HB model) should also follow the recommendations in (9). Finally, adding a random intercept term (U_i and V_i) to these regressions is quintessential in controlling the effects of clustering as we move from mouth-level to tooth-level DMFS assessments, and ignoring these might lead to possible underestimation of true p-values and narrowing of confidence intervals of covariate effects (26).

The search for the most efficient index for caries assessment remains an open problem even today. The author contends that exploring tooth-level DMFS should throw some new light into caries assessments. The rate of caries progression is not homogenous throughout the mouth, and different regions are susceptible to different degrees of carious lesions (such as, molars can be different than incisors). The tooth-level DMFS counts can provide inference and prediction for each tooth at various locations inside the mouth, which are not possible using the popular full-mouth DMFT/DMFS measures. In light of the statistical framework described in this concept paper and other recommendations suggested in (9, 24), further studies and analysis using tooth-level DMFS are warranted.