Abstract
This paper describes a method to estimate mechanical properties of soft, anisotropic materials from measurements of shear waves with specific polarization and propagation directions. This method is applicable to data from magnetic resonance elastography (MRE), which is a method for measuring shear waves in live subjects or in vitro samples. Here, we simulate MRE data using finite element analysis. A nearly-incompressible, transversely isotropic (ITI) material model with three parameters (shear modulus, shear anisotropy, and tensile anisotropy) is used, which is appropriate for many fibrous, biological tissues. Both slow and fast shear waves travel concurrently through such a material with speeds that depend on the propagation direction relative to fiber orientation. A three-parameter estimation approach based on directional filtering and isolation of slow and fast shear wave components (directional filter inversion, or DFI) is introduced. Wave speeds of each isolated shear wave component are estimated using local frequency estimation (LFE), and material properties are calculated using weighted least squares. Data from multiple finite element simulations are used to assess the accuracy and reliability of DFI for estimation of anisotropic material parameters.
Keywords: MR elastography, shear waves, anisotropy, transversely isotropic material, inversion algorithms
1. Introduction
Magnetic resonance elastography (MRE) is an innovative method for non-invasive estimation of material parameters of living biological tissue, including in human subjects. In MRE, shear waves are introduced by external vibration at a specific frequency and the resulting displacement fields are visualized by motion-sensitive MR imaging sequences. Material parameters are estimated from the wavelengths (hence speed) of shear wave components in the tissue. Recent studies using MRE have been performed to estimate the material properties of a wide range of tissue including the liver (Klatt et al. (2010a); e.g.), skeletal muscle (Klatt et al. (2010b); Papazoglou et al. (2006); e.g.), and brain (Green et al. (2008); Clayton et al. (2011); e.g). While in many studies an isotropic material is assumed, biological tissue is often anisotropic, which requires more sophisticated material models.
Recently, researchers have proposed anisotropic material models with two (Qin et al., 2013; Sinkus et al., 2005), three (Guo et al., 2015; Feng et al., 2013; Namani and Bayly, 2009; Papazoglou et al., 2006), and five or more (Romano et al., 2012) elastic parameters. Each of these models assumes a transversely isotropic or orthotropic material undergoing small elastic or viscoelastic deformations, which are appropriate assumptions for MRE of many soft anisotropic tissues. For both two-parameter models (Qin et al., 2013; Sinkus et al., 2005), the material is assumed to be nearly incompressible, which simplifies the model so that analytical expressions for wave speed can be found. As a further simplification, only shear anisotropy is considered, in which the effect of stretching the fiber is ignored. The two-parameter model implies a single shear wave mode (slow) whose speed varies with direction.
For the three-parameter models (Guo et al., 2015; Feng et al., 2013), both shear and tensile anisotropies are taken into account. Tensile anisotropy accounts for the effect of fiber stretching and is the basis of the distinction between slow and fast shear waves. While the three-parameter model is unable to describe pressure waves in a material, for nearly incompressible materials such as many soft tissues, the assumption of incompressibility allows accurate predictions of isochoric deformations. Guo et al. (2015) have recently published a method to estimate three material parameters for an ITI material from the curl of a displacement field measured by MRE. In their material model, Guo et al. (2015) assume incompressibility, a priori, in the derivation of the equations used in the inversion. The estimation approach introduced by Guo et al. (2015) requires taking the curl of the displacement field and does not explicitly require that both slow and fast shear waves are included for inversion. The paper by Feng et al. (2013) includes the derivation of inverse equations before applying the incompressibility assumption, which can be used to determine ranges of the bulk modulus for which the approach is valid. Feng et al. (2013) demonstrate how the compliance tensor with the incompressibility approximation can be used to find expressions for Young’s moduli, shear moduli, and Poisson’s ratios.
Romano et al. (2012) introduced a spatial-spectral filter in order to identify five viscoelastic material parameters from MRE data. Combined with Helmholz Decomposition (Romano et al., 2012, 2005), shear and pressure waves are separated within a waveguide in which fibers follow a known path. Wave speeds estimated in a local reference frame relative to the waveguide are then used to estimate material properties. A nine-parameter, orthotropic material model is assumed, and the five independent components of the transversely isotropic material model are revealed through redundancies.
This material model used by Romano et al. (2012) captures both shear and pressure waves and does not require the assumption of near-incompressibility. However, the model is described in terms of the stiffness tensor rather than the compliance tensor which greatly increases the complexity of the estimation problem. In a nearly incompressible material, the speed of the pressure waves tend to be orders of magnitude larger than the speed of the shear waves; corresponding elements of the stiffness matrix may also differ by orders of magnitude.
A phenomenon specific to anisotropic elastic or viscoelastic media is the concurrent existence of slow and fast shear waves, which can be exploited to estimate material properties. The three-parameter model (Feng et al. (2013), e.g.) is the simplest approach that captures both shear waves. In this paper, we develop and demonstrate a method to identify the three incompressible, transversely isotropic (ITI) material parameters using a directional filter inversion (DFI) approach. The DFI method separates the slow and fast shear waves by projecting onto the corresponding polarization vectors and using directional filters similar to the spatial-spectral filters introduced by Romano et al. (2012). However, in the DFI approach, arbitrary propagation directions are used with the separated slow and fast shear waves to isolate specific components. The proposed method explicitly requires both slow and fast shear waves for a valid material parameter estimate and can be performed directly on the displacement field. In this study, we analyzed simulated data to assess the ability of DFI to estimate shear wave speeds and material properties.
2. Methods
We first demonstrate that, in general, harmonic excitation at frequencies typical of MRE in an ITI material results in both slow and fast shear waves. Next, we present the DFI method which uses both slow and fast shear waves to estimate the three ITI material parameters. We describe the simulation approach, based on a motivating physical experiment, and show how it is used to assess the accuracy and reliability of this approach.
2.1. Theory of Shear Waves in an Incompressible, Transversely Isotropic Elastic Material
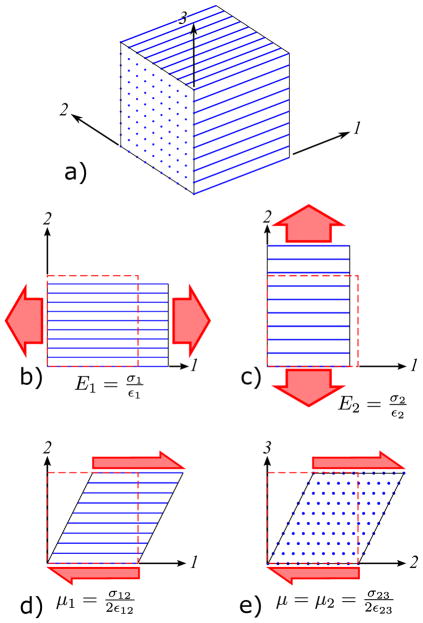
This section presents the basic concepts underlying shear wave behavior in a fibrous material. (Appendix A includes a derivation of the equations described below.) We start with a linear, elastic, ITI material model (a fiber reinforced isotropic substrate), as shown in Fig. 1. Typically, both the tensile modulus in the fiber direction and the shear modulus in planes parallel to the fibers are stiffened, as highlighted in Fig. 1b and Fig. 1d, respectively. Rather than seeking the elements of the elasticity matrix, it is convenient to use the substrate shear modulus μ, shear anisotropy ϕ = μ1/μ − 1, and tensile anisotropy ζ = E1/E2 − 1 as the three material parameters.
Figure 1.
a) Transversely isotropic material with fiber reinforcement. Tensile moduli in directions b) parallel and c) perpendicular to the fibers are given by E1 and E2, respectively. Shear moduli in planes d) parallel and c) perpendicular to the fibers are given by μ1 and μ, respectively. The 13-plane (not shown) has the same shear and tensile properties as the 12-plane. The dashed boxes indicate the undeformed case.
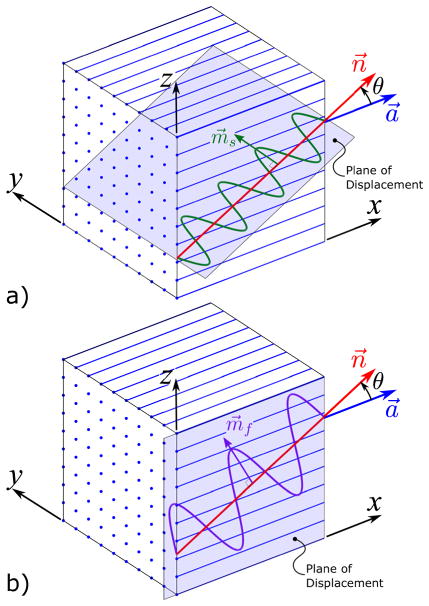
Consider a shear wave traveling in an ITI material with an arbitrary propagation direction n⃗ at an angle θ from the fiber direction a⃗ such as the one shown in Fig. 2. The displacement of this shear wave can be polarized into independent slow and fast shear wave components. The polarization direction of the slow shear wave is given by (Appendix A)
Figure 2.
A displacement field with a single propagation direction, n⃗, at an angle θ from the fiber direction, a⃗, can be decomposed into two shear waves, (a) “slow” and (b) “fast” with different polarization directions. This is illustrated for the case in which the fiber direction is aligned with the x-axis. (a) The displacements of the slow shear wave are in the m⃗s polarization direction which lies in the shaded plane. (b) The displacements of the fast shear wave are in the m⃗f polarization direction which lies in the shaded (xz) plane. Note that the wavelength of the fast shear waves is longer than that of the slow shear wave for the same frequency.
| (1) |
which occurs in a direction perpendicular to both the propagation direction and the fiber direction. The normalized vector is given by m̂s = m⃗s/|m⃗s|, which is used for all dot products. Because the slow shear wave does not stretch the fibers, the speed of the slow shear wave only depends on the shear anisotropy and is given by
| (2) |
On the other hand, from the polarization direction of the fast shear wave given by
| (3) |
and the speed of the fast shear wave given by
| (4) |
The normalized vector is given by m̂f = m⃗f/|m⃗f|, which is used for all dot products. It is clear that the fast shear wave stretches the fiber and that its speed is dependent on the tensile anisotropy. The result is two independent shear wave components traveling in the same direction at different speeds.
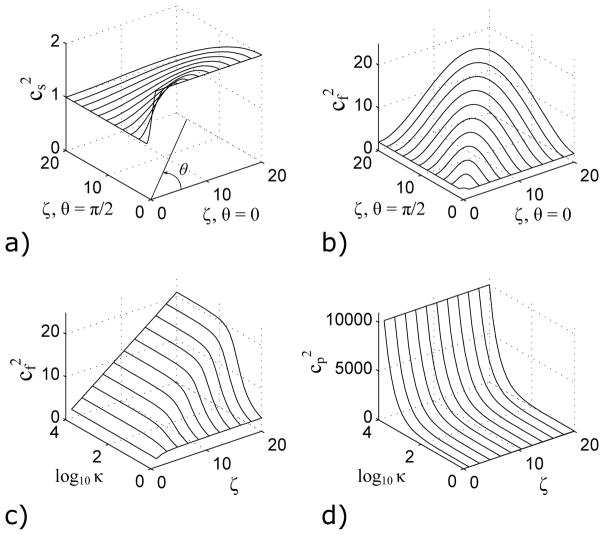
To illustrate the differences between the slow and fast shear wave speeds due to tensile anisotropy, consider the plots in Fig. 3 of wave speed versus tensile anisotropy. The slow shear wave speed in Fig. 3a is independent of ζ, since the slow shear wave speed does not depend on tensile anisotropy. However, the speed of the fast shear wave does increase for larger values of tensile anisotropy as shown in Fig. 3b. Note for the degenerate cases of θ = 0° and θ = 90°, only the slow shear wave is present.
Figure 3.
The effect of tensile modulus ζ and propagation direction θ on the a) slow cs and b) fast cf shear speeds is shown (μ = ρ = ϕ = 1 and κ → ∞). The tensile modulus increases along a radius from the origin with an angle θ from the θ = 0 axis. An increase in ζ increases cf, but has no effect on cs. The effects of ζ and bulk modulus κ on the c) fast shear speed and d) pressure wave speed cp are shown (μ = ρ = ϕ = 1 and θ = 135°). The fast shear speed approaches a constant value for finite κ.
One of the critical assumptions of an ITI material model is incompressibility, in which the bulk modulus κ approaches infinity. To see the effects of this assumption, consider Fig. 3 in which the fast shear wave and pressure wave speeds in a nearly-incompressible transversely isotropic (NITI) material are plotted versus bulk modulus, κ, and tensile anisotropy, ζ. Figure 3c shows that for even a relatively small ratio of bulk modulus to shear modulus (κ/μ = 100), the speed of the fast shear wave is already approaching the incompressible case. The slow shear wave speed is unaffected by the bulk modulus. In addition, in this nearly-incompressible material, the pressure wave speed cp is much larger than the speed of either shear wave as shown in Fig. 3d.
2.2. Directional Filter Inversion
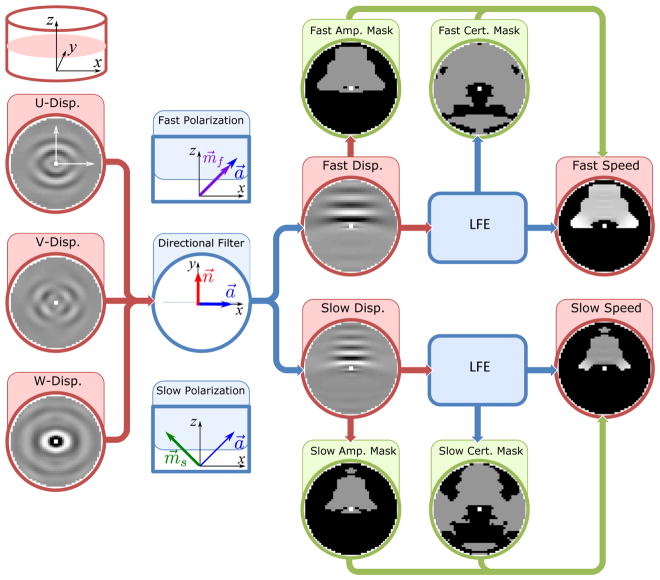
For an ITI material with a known displacement field, the three parameters can be estimated if the slow and fast shear waves in multiple directions can be isolated and the speeds of the waves estimated. This is the fundamental concept behind the DFI method. Figure 4 outlines the steps used in DFI to identify the speed of slow and fast shear waves.
Figure 4.
The process of estimating the shear wave speed for DFI begins with the 3D displacement field. The data displayed in this figure is from the cylindrical simulation shown in Fig. 5. All slices are shown in the xy-plane with the slice location and coordinate system indicated in the upper left hand corner of this figure. The U, V, and W displacement fields are in the x, y, and z directions, respectively. The total displacement field is decomposed into slow and fast shear waves and directionally filtered using the propagation and polarization directions shown, resulting in slow and fast shear wave displacement fields for each direction. Next, wave speeds are estimated from the slow and fast shear wave displacement fields using LFE. Inclusion criteria using an amplitude threshold and certainty threshold result in amplitude and certainty masks, respectively for both the slow and fast shear waves. These amplitude and certainty masks are applied to the speed estimates resulting in the slow and fast shear wave speed estimates shown at the end of the process. Outlier wave speeds (> 1 standard deviation from the mean) are not included in the subsequent parameter fitting step.
2.2.1. Isolation of wave components
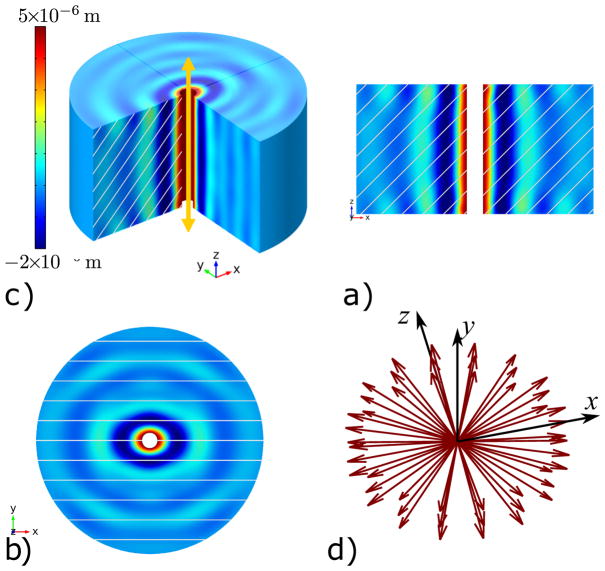
The input to DFI is a harmonic displacement field such as one generated in MRE. The first step is vector projection, in which the slow and fast shear waves are isolated by performing a dot product between the displacement field and the normalized slow and fast polarization directions, respectively. The polarization directions are determined using Eq. (1) and (3). While the arbitrary propagation direction, n⃗, may be selected, the fiber direction, a⃗, must be known a priori using diffusion tensor imaging (DTI) (Romano et al., 2012) or other suitable method. Next, the propagation direction, n⃗, is isolated by filtering the polarized data in Fourier space (Manduca et al., 2003). The resulting directionally filtered dataset consists of an independent displacement field for either the slow and fast shear wave in an arbitrary propagation direction. In principle, any arbitrary set of propagation directions may be chosen for the analysis, such as an equally spaced 3D set or a set containing directions with large amplitude contributions such as the one shown in Fig. 5d. Creating a set of propagation directions with large amplitudes typically requires an iterative approach. The process is repeated for all propagation directions in the set, for both slow and fast shear waves.
Figure 5.
Finite element (Comsol™) simulation of Case 1 with displacement in the z-direction shown. The location and direction of excitation is shown by the arrow in a), and the resulting propagation is shown in both the b) xz-plane and c) xy-plane. The lines indicate fiber direction. Note that the wavelength is longer in the direction parallel to planes containing the fibers. For all cases, the boundary conditions (BCs) include a 5 μm excitation at 200 Hz on the inner boundary radius = 1.6 mm; fixed displacement on the outer boundary radius = 23 mm; and free displacement on the top and bottom faces. For all cases, the output data was discretized to simulated images with “field of view” of 48 × 48 × 24 mm3 with a 1 mm3 voxel size. d) Propagation direction vector set used for the local and global inversion approaches.
2.2.2. Wave speed estimation
We use the well-established local frequency estimation (LFE) (Knutsson et al., 1994) method to estimate wave speeds. However, other approaches to estimate wave speeds such as wavelet analysis (Kingsbury, 2001) can also be used. In addition to wave speed, LFE also provides a measure of the variance of the speed estimate at each voxel (Okamoto et al., 2014; Knutsson et al., 1994), which they call “certainty.” This value may be useful for assessing confidence in wave speed estimates for parameter identification. We used the LFE parameters ρ0 = 1 for the center frequency and N = 11 for the number of filters (Okamoto et al., 2014).
2.2.3. Inclusion criteria
The main complication in estimating wave speeds for each direction is that a displacement field may not include significant slow and fast shear wave components at every location. For example, consider the filtered displacement fields in Fig. 4, which highlight directionally filtered wave fields that fill a subset of the domain. LFE and other techniques return wave speed estimates for the entire domain, including regions with little displacement. In addition, directional filters are not ideally narrow or selective. Therefore, wave speed estimates must be carefully selected before being included in parameter identification. In this study, we use three selection criteria: (i) amplitude of the corresponding shear wave component, (ii) LFE “certainty,” and (iii) rejection of outlying wave speed estimates.
For the amplitude threshold, the magnitude of the filtered displacement at a particular voxel must be larger than a specified fraction of the median amplitude of the unfiltered field. The resulting mask eliminates voxels in which the amplitude of the specified shear wave is too low for an accurate wave speed estimate.
The certainty threshold results in a mask in which the variance of wave speed estimates is relatively low, based on LFE. A certainty of one corresponds to a low variance, and a certainty of zero corresponds to a large variance.
The mean and standard deviation of the remaining wave speeds are then calculated in order to create a mask that eliminates wave speeds one standard deviation above and below the mean. This final step is a simple approach that is effective in removing artifacts from imperfect directional filtering.
2.2.4. Material parameter estimation
Next, material parameters can be estimated from Eq. (2), Eq. (4), and the wave speed. To estimate all three parameters, valid speed estimates for both types of shear waves must be available for a range of propagation directions. Therefore, estimates of material properties are improved by combining multiple voxels that include waves with a variety of propagation directions. For a local inversion, which results in an estimate centered at each voxel, a kernel or sphere of voxels is selected to be included in the fitting process. The estimated material properties are then assigned to the voxel at the center of the kernel. For a global inversion, all voxels within a region are assumed to have uniform material properties, and consequently, any subset of the voxels may be used for the inversion.
In this paper, we use the weighted least squares approach to estimate the material parameters for both local and global inversion methods (see Appendix B for more details). The weights are the relative displacement amplitudes at each voxel for a particular propagation direction and polarization. At least two propagation directions with different angles θ from the fiber direction are required for a valid inversion. Parameter estimates are retained using a selection criteria based on the coefficient of determination or R value. For the local inversion, voxels with a R value greater than the mean of the non-zero R values are kept. For the global inversion, only estimates above 0.95 of the mean of the non-zero R values are included in the average estimated material parameters.
It should be noted that we did not attempt to estimate dissipative viscoelastic terms (complex moduli, loss factors, or damping ratios) in this study. These terms were neglected in order to focus on the underlying relationship between transversely isotropic elastic parameters and slow and fast shear waves. This choice enabled us to use a simple, efficient wavelength estimation method: LFE. LFE-based methods are limited in that information on dissipation is not estimated without modification (Clayton et al., 2013). In principle, the directionally filtered approach could be combined with another method such as direct inversion (Oliphant et al., 2001) to estimate viscoelastic parameters in addition to μ, ϕ, and ζ.
2.3. Simulation Approach
To evaluate the DFI approach, we created four finite element (FE) simulations in Comsol™ with the four sets of parameters given in Table 1. The parameters in Case 1 were chosen to be similar to those expected in muscle tissue. Cases 1, 3, and 4 have a fiber orientation optimal for parameters estimation, while Case 2 has a less favorable fiber orientation. We chose a minimum tensile anisotropy of ζ = 0 in Case 3 and a maximum value of tensile anisotropy in Case 4 to explore the limits of DFI. Figure 5 shows the FE model which corresponds roughly to a motivating experiment presented by Schmidt et al. (2015b). For each case, the fiber direction is parallel to the xz-plane at an angle of β from the xy-plane. For all cases we used an isotropic loss factor of η = 0.2, which is similar to ranges (0.23 < η < 0.93) found for the human brain using MRE (Bayly et al., 2014), (0.11 < η < 0.23) for gelatin using MRE (Okamoto et al., 2011), and qualitatively similar in turkey breast ex vivo using MRE (Schmidt et al., 2015a,b).
Table 1.
The material properties for all four finite element simulations, where ρ is the density, μ is the substrate shear modulus, ϕ is the shear anisotropy, and ζ is the tensile anisotropy. The angle between the xy-plane and the fiber orientation is given by β.
| ρ [kg/m3] | μ [Pa] | ϕ | ζ | β | |
|---|---|---|---|---|---|
|
| |||||
| Case 1 | 1000 | 1000 | 1 | 2 | 45° |
| Case 2 | 1000 | 1000 | 1 | 2 | 15° |
| Case 3 | 1000 | 1000 | 2 | 0 | 45° |
| Case 4 | 1000 | 1000 | 0.5 | 4 | 45° |
The Young’s moduli and Poisson’s ratios in the FE simulations were calculated from E1 = μ(4ζ + 3), E2 = E1/(1 + ζ), ν12 = 0.49, ν21 = ν12E2/E1, and ν23 = 1 − ν21 − 0.01. The cylinder in the simulation had an outer diameter of 47.75 mm, an inner diameter of 3.2 mm, and was 25 mm thick. The swept mesh was equally spaced with 15 elements along the radius, 48 elements around the perimeter, and 15 elements along the vertical. The excitation amplitude was A = 5 × 10−6 m at a frequency of 200 Hz.
We added noise to the FE simulation data of all four cases, which resulted in an SNR of 10, to the simulation results of all four cases. The SNR is defined using the following relationship
| (5) |
where is the RMS of the excitation amplitude and σ is the standard deviation. The normally distributed noise was added to the total displacement.
3. Results
In this section we compare the material parameter estimates using the DFI method with known values from the four simulation cases from Table 1. First, slow and fast shear wave speeds are compared with values calculated analytically from the wave speed equations. Next, local material parameter estimates are presented for Case 1. Finally, global estimates are compared with the known values for all four cases.
3.1. Wave Propagation Speeds
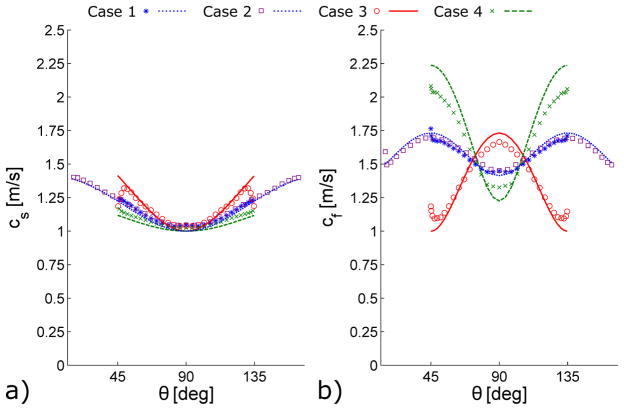
Since the material parameters are known in each simulation, the speed of both shear waves can be calculated analytically from the material parameters for any propagation direction. This allows a direct comparison between speed estimates from the DFI process and the analytical values. Figure 6 shows the comparison for slow and fast shear waves for cases 1, 3, and 4 from Table 1. The estimated wave speeds are the mean values of all selected voxels for each direction. For clarity, wave speeds are estimated from a total of 32 equally spaced propagation directions within the xy-plane.
Figure 6.
Analytical propagation speeds (lines) and mean estimated propagation speeds from simulation (symbols) of a) slow and b) fast shear waves. Parameters for Case 1 (dotted line, * symbols), Case 2 (dotted line, □ symbols), Case 3 (solid line, ○ symbols), and Case 4 (dashed line, x symbols) are given in Table 1. Mean wave speed estimates are calculated by averaging voxel estimates for each direction using the process outlined in Fig. 4. Note that Cases 1 and 2 have the same theoretical curve, but Case 2 has a wider range of angles, θ.
3.2. Local Parameter Estimates
The local inversion of the material parameters for the Case 1, which is typical of all four cases, is shown in Fig. 7. Slices 8 through 17 of the total 24 are shown. A total of 48 propagation directions, mainly near the xy-plane as shown in Fig. 5d, were used in the estimation process. Propagation directions near the xy-plane result in polarization directions with large components in the z-direction, which corresponds to the direction of excitation. We selected a fractional amplitude threshold of 0.10, a certainty threshold of 0.25, and a kernel size (radius) of 5 voxels. We accepted estimates for which R > 0.83 resulting in 33,065 voxels with parameter estimates, which is about 83% of total number of voxels in the displacement field. The mean values of the estimated parameters and their standard deviations are given by μ = 986 ± 56, ϕ = 0.92 ± 0.23, and ζ = 1.57 ± 0.23. The results highlight the effect of the typical limited number of directions in a relatively small kernel, which reduces the accuracy of the inversion. For a homogeneous region, increasing the kernel size to the total volume will typically give the best results. Great care should be taken in a local approach to ensure that both slow and fast shear waves of sufficient amplitude (good SNR) in multiple propagation directions are present. Therefore, we have chosen to focus on the global approach in this paper and have only included results for the local approach for Case 1.
Figure 7.
Local estimates of parameter values for Case 1 (see Table 1) with added noise (SNR=10) using DFI. a) W-displacement field of slice 12 without noise (SNR= ∞) above and with noise (SNR=10) below. The b) shear modulus (μsim = 1000 Pa), c) shear anisotropy (ϕsim = 1), d) tensile anisotropy (ζsim = 2), and e) R 2 are shown for slices 8 through 17. For the parameters μ, ϕ, and ζ, the range shown is ±50% of the true values (this range contains 98% of all estimated values). The full range is shown for R2.
3.3. Global Parameter Estimates
For the global inversion, we chose a Monte Carlo approach in which the material properties at every voxel are assumed to be homogeneous. The same propagation directions and threshold values used in the local inversion where applied to the global approach for all 4 cases with additive noise. For results without noise, we selected a fractional amplitude threshold of 0.25. For the Monte Carlo analysis, we picked 100 random wave speed estimates with an equal number of slow and fast shear wave speeds and repeated this process 1000 times. Estimates were taken from any voxel and direction remaining after the three selection techniques from Section 2.2 were applied. For inversions with additive noise, we repeated the Monte Carlo approach with 30 different sets of noise and averaged the mean and variance of those 30 cases. Table 2 shows the known values, mean values, and standard deviations of the estimated material parameters for all four cases with and without additive noise.
Table 2.
Global material parameter estimates and their standard deviations for the four cases from Table 1 using a Monte Carlo approach to DFI. For simulations without noise (SNR=∞), all estimated material parameters are within 25% of the known values. For the cases with additive noise (SNR=10), most estimated material parameters are within 25% of the known values, except for ζ in cases 2 and 4 and ϕ in case 3, which are within 40% of the known values.
| Case 1 | Case 2 | |||||
|---|---|---|---|---|---|---|
| Actual | SNR=∞ | SNR=10 | Actual | SNR=∞ | SNR=10 | |
| μ | 1000 | 1040±21 | 994±25 | 1000 | 1030±36 | 980±37 |
| ϕ | 1 | 1.04±0.07 | 0.91±0.08 | 1 | 1.02±0.09 | 0.95±0.10 |
| ζ | 2 | 1.76±0.06 | 1.51±0.08 | 2 | 1.60±0.10 | 1.21±0.10 |
| Case 3 | Case 4 | |||||
|---|---|---|---|---|---|---|
| Actual | SNR=∞ | SNR=10 | Actual | SNR=∞ | SNR=10 | |
| μ | 1000 | 1050±23 | 996±25 | 1000 | 1040±20 | 986±27 |
| ϕ | 2 | 1.53±0.08 | 1.32±0.09 | 0.5 | 0.59±0.06 | 0.60±0.08 |
| ζ | 0 | 0.00±0.04 | 0.01±0.04 | 4 | 3.10±0.11 | 2.47±0.11 |
4. Discussion
In materials that can be modeled as incompressible and transversely isotropic, two types of shear wave can exist and their speeds can be used to estimate material parameters. We use simulated data in this paper to assess the accuracy and reliability of a method based on directional filtering to estimate parameters of an ITI material. As an intermediate step, analytical and estimated shear waves speeds are compared in Fig. 6. This figure shows that slow and fast shear waves can be successfully separated using vector projection onto specific polarization directions and directional filtering. Estimating the fast shear wave speed is critical if the tensile anisotropy is to be estimated. For most propagation directions, excellent agreement is found between analytical and estimated wave speeds.
Two important points are highlighted by the few directions in Fig. 6, in which the wave speed comparison is inexact. First, a sufficiently wide range of propagation directions is crucial for good material parameter estimates. Such a range of directions could be achieved either by an approach that includes multiple voxels in each inversion or by adding excitations that induce shear waves with different propagation directions. Second, good selection criteria for determining which wave speed estimates to include in the inversion process is essential for accurate material parameter estimates.
Local Approach
The capabilities and limitations of the local DFI approach are highlighted by the inversion results shown in Fig. 7. Valid estimates were found for most of the central voxels, but could not be found for voxels near the vertical edges on the left and right of the cylinder. For voxels with valid estimates, there is good agreement between the estimated and known parameters. More than 99% of μ estimates, 93% of ϕ estimates, and 62% of ζ estimates are ±25% from the known values. For soft tissue, in which properties are difficult to measure, accuracy within 25% is noteworthy. Voxels in which no estimates were achieved reveals a limitation of the local approach. Namely, for a given wave field, at certain locations there may be too little information to accurately estimate all three parameters. Caution should, therefore, be used when taking the local approach. However, potentially good selection criteria can be used to eliminate a majority of poor estimates as demonstrated in the presented case.
Global Approach
The results of the global DFI approach in Table 2 indicate that DFI is quite accurate and not sensitive to the fiber direction or material parameters. Estimated material parameters are within 25% of the known values for all four cases, with the exception of ζ in cases 2 and 4 with noise added and ϕ in case 4 with noise added. For the BCs in the simulation, a fiber direction of β = 45° from the xy-plane is optimal for estimating material properties, since the amplitude of both shear waves will be similar. However, as the fiber direction approaches the xy-plane, the amplitude of the fast shear wave is also reduced. A fiber direction of β = 0° will result in only slow shear waves being excited. Case 2, which includes a fiber angle of β = 15° from the plane, is expected to be challenging for DFI, but the accuracy of the material parameter estimates for this case is similar to the other cases. Accurate estimates were obtained for both large and small values of tensile anisotropy ratio, ζ.
5. Summary and Conclusions
Material parameters of soft, anisotropic tissue can be estimated from shear wave measurements such as those acquired from MRE. The accuracy of DFI was evaluated using simulated data for both a local and global approach. Using a local approach, good estimates could be found in some but not all regions of the sample. However, using information from multiple regions in the sample, very accurate global estimates of all parameters could be obtained. Improvements to the DFI method could include incorporating more sophisticated selection criteria, and alternative inversion techniques could improve accuracy in material parameter estimates. Adding multiple experiments with different modes of excitation or fiber directions to the estimation process should increase the available information and lead to more accurate estimates especially in the local approach in which information tends to be more limited than the global approach. Future studies will explore the estimation of material properties from experimental data.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge funding from the NIH from grant no. NS055951 and the NSF from grant no. CMMI-1332433.
Appendix A Derivation of Shear Wave Speeds
In this section we derive the equations for both the speed and amplitude polarization of the slow and fast shear waves. We begin with the linear elasticity tensor of a four-parameter, nearly incompressible, transversely isotropic (NITI) material model from Feng et al. (2013), given in Voigt notation as
| (A.1) |
where ε is the linearized strain from the small strain assumption. In the derivation of the elasticity tensor, the fiber direction was assumed to be which is in the direction of x⃗1. The plane of symmetry of the ITI material (the 23-plane in Fig. 1) is perpendicular to the fiber direction. The terms in Eq.(A.1) are given by
| (A.2) |
where μ is the substrate shear modulus, κ is the bulk modulus, ϕ is the shear anisotropy, and ζ is the tensile anisotropy (Feng et al., 2013). This stiffness matrix satisfies the symmetry requirements for any linear, elastic transversely isotropic material, or if ϕ and ζ are zero, an isotropic, linear elastic material. For a nearly incompressible material, it is instructive to examine the compliance tensor, which is the inverse of the elasticity tensor ℂ−1 = 𝕊. In this case the compliance tensor is given in Voigt notation by
| (A.3) |
Note that as the ratio κ/μ increases, the effect of the bulk modulus on the compliance tensor, becomes negligible. In contrast, elements of the stiffness tensor approach infinity for an incompressible material. Once the incompressible assumption is made, we take a similar approach as Royer et al. (2011) and Rouze et al. (2013) to find the Young’s moduli E, shear moduli μ, and Poisson’s ν ratios:
| (A.4) |
where the coordinate system and fiber direction are defined by Fig. 1.
For the case of elastic, plane waves traveling in the four-parameter NITI material, the assumed solution
| (A.5) |
satisfies the equation of motion (EOM)
| (A.6) |
where σ is a second order stress tensor, div is the divergence, u0 is the amplitude of the displacement, t is time, is the polarization direction of the displacement, is the propagation direction, k is the wavenumber, ω is the excitation frequency, and ρ is the density (Holzapfel, 2000, pp. 144–145). Substituting the assumed solution into the EOM results in the eigenvalue problem:
| (A.7) |
where Q is the acoustic tensor and c is the wave speed. The solution to the eigenvalue problem defines three eigenvalues λ = ρc2 and eigenvectors m⃗.
Without loss of generality, we can specify that the propagation direction remains in the 12-plane (see Fig. (1)) and can be defined by . Substituting n⃗ from the 12-plane and the elastic tensor terms from Eq. A.2 gives the acoustic tensor the form of
| (A.8) |
where 𝔠 = cos θ and 𝔰 = sin θ. For a given set of material properties, the eigenvalue problem from Eq.(A.7) can now be solved numerically. For an incompressible material where the limit of κ → ∞ is taken, an analytical form of the eigenvalues is given by
| (A.9a) |
| (A.9b) |
| (A.9c) |
where cs is the slow shear wave speed, cf is the fast shear wave speed, and cp is the pressure wave speed. The eigenvectors are given by
| (A.10) |
and are not dependent on the value of the bulk modulus. In general, the fiber and propagation directions will be in arbitrary directions, and the slow m⃗s and fast m⃗f shear wave polarization directions are
| (A.11a) |
| (A.11b) |
Appendix B Weighted Least Squares Approach
Material parameters can be estimated using weighted least squares (WLS) from Eq. (2), Eq. (4), and the wave speed. This section follows the same approach used by Tweten et al. (2015). We start with the typical least squares equation
| (B.1) |
where H is the observation matrix, x⃗ is a vector containing the parameters to be estimated, and y⃗ is a vector containing the measurements. The wave speed equations (Eq. 2 and Eq. 4) for both wave modes can be written in the form of Eq. (B.1) as
| (B.2) |
where θ1 is the angle between the propagation direction n⃗1 and the fiber direction, cs,1 and cf,1 are the slow and fast shear wave speeds in the propagation direction n⃗1, respectively, and M and N are the total number slow and fast wave speed estimates, respectively. Each row in Eq. (B.2) comes from a different voxel (repeated for slow and fast shear waves), and the total number of rows corresponds to twice the number of voxels in the kernel for the local approach or twice the number of voxels in the volume for the global approach. At least three rows are required, and at least two different angles θ are required for a valid estimate.
The material parameters can be estimated using the WLS equation
| (B.3) |
where x̃ is a vector of the estimated material parameters and W is the weighting matrix. The weights used in this paper are the relative displacement amplitudes at each voxel for a given propagation direction and polarization.
Footnotes
Conflict of Interest Statement
None of the authors has a conflict of interest that could influence the work described in this manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bayly P, Clayton E, Genin G, Okamoto R. Magnetic resonance elastography of the brain. In: Neu C, Genin G, editors. Handbook of Imaging in Biological Mechanics. CRC Press; New York: 2014. [Google Scholar]
- Clayton E, Garbow J, Bayly P. Frequency-dependent viscoelastic parameters of mouse brain tissue estimated by MR elastography. Phys Med Biol. 2011;56:2391–2405. doi: 10.1088/0031-9155/56/8/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton E, Okamoto R, Bayly P. Mechanical properties of viscoelastic media by local frequency estimation of divergence-free wave fields. J Biomed Eng. 2013;135:0210251–0210256. doi: 10.1115/1.4023433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Y, Okamoto R, Namani R, Genin G, Bayly P. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J Mech Behav Biomed. 2013;23:117–132. doi: 10.1016/j.jmbbm.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green M, Bilston L, Sinkus R. In vivo brain viscoelastic properties measured by magnetic resonance elastography. NMR Biomed. 2008;21:755–764. doi: 10.1002/nbm.1254. [DOI] [PubMed] [Google Scholar]
- Guo J, Hirsch S, Scheel M, Braun J, Sack I. Three-parameter shear wave inversion in MR elastography of incompressible transverse isotropic media: Application to in vivo lower leg muscles. Magn Reson Med. 2015 doi: 10.1002/mrm.25740. [DOI] [PubMed] [Google Scholar]
- Holzapfel G. Nonlinear solid mechanics: a continuum approach for engineering. John Wiley & Sons, Inc; New York: 2000. [Google Scholar]
- Kingsbury N. Complex wavelets for shift invariant analysis and filtering of signals. Appl Comput Harmon A. 2001;10:234–253. [Google Scholar]
- Klatt D, Friedrich C, Korth Y, Vogt R, Braun J, Sack I. Viscoelastic properties of liver measured by oscillatory rheometry and multifrequency magnetic resonance elastography. Biorheology. 2010a;47:133–141. doi: 10.3233/BIR-2010-0565. [DOI] [PubMed] [Google Scholar]
- Klatt D, Papazoglou S, Braun J, Sack I. Viscoelasticity-based MR elastography of skeletal muscle. Phys Med Biol. 2010b;55:6445–6459. doi: 10.1088/0031-9155/55/21/007. [DOI] [PubMed] [Google Scholar]
- Knutsson H, Westin CF, Granlund G. Image Processing, 1994. Proc. ICIP-94. 1994. Local multiscale frequency and bandwidth estimation; pp. 36–40. [Google Scholar]
- Manduca A, Lake D, Kruse S, Ehman R. Spatio-temporal directional filtering for improved inversion of MR elastography images. Med Image Anal. 2003;7:465–473. doi: 10.1016/s1361-8415(03)00038-0. [DOI] [PubMed] [Google Scholar]
- Namani R, Bayly P. Shear wave propagation in anisotropic soft tissues and gels. Engineering in Medicine and Biology Society, 2009. EMBC 2009. Annual International Conference of the IEEE; 2009. pp. 1117–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamoto R, Clayton E, Bayly P. Viscoelastic properties of soft gels: comparison of magnetic resonance elastography and dynamic shear testing in the shear wave regime. Phys Med Biol. 2011;56:6379. doi: 10.1088/0031-9155/56/19/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamoto R, Johnson C, Feng Y, Georgiadis J, Bayly P. MRE detection of heterogeneity using quantitative measures of residual error and uncertainty. Proc SPIE 9038, Med Imaging. 2014:90381E. [Google Scholar]
- Oliphant T, Manduca A, Ehman R, Greenleaf J. Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation. Magn Reson Med. 2001;45:299–310. doi: 10.1002/1522-2594(200102)45:2<299::aid-mrm1039>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Papazoglou S, Rump J, Braun J, Sack I. Shear wave group velocity inversion in MR elastography of human skeletal muscle. Magn Reson Med. 2006;56:489–497. doi: 10.1002/mrm.20993. [DOI] [PubMed] [Google Scholar]
- Qin EC, Sinkus R, Geng G, Cheng S, Green M, Rae CD, Bilston LE. Combining MR elastography and diffusion tensor imaging for the assessment of anisotropic mechanical properties: A phantom study. JMRI-J Magn Reson Im. 2013;37:217–226. doi: 10.1002/jmri.23797. [DOI] [PubMed] [Google Scholar]
- Romano A, Abraham P, Rossman P, Bucaro J, Ehman R. Determination and analysis of guided wave propagation using magnetic resonance elastography. Magn Reson Med. 2005;54:893–900. doi: 10.1002/mrm.20607. [DOI] [PubMed] [Google Scholar]
- Romano A, Scheel M, Hirsch S, Braun J, Sack I. In vivo waveguide elastography of white matter tracts in the human brain. Magn Reson Med. 2012;68:1410–1422. doi: 10.1002/mrm.24141. [DOI] [PubMed] [Google Scholar]
- Rouze N, Wanga M, Palmeria M, Nightingale K. Finite element modeling of impulsive excitation and shear wave propagation in an incompressible, transversely isotropic medium. J Biomech. 2013;46:2761–2768. doi: 10.1016/j.jbiomech.2013.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Royer D, Gennisson J, Deffieux T, Tanter M. On the elasticity of transverse isotropic soft tissues. J Acoust Soc Am. 2011;129:2757–2760. doi: 10.1121/1.3559681. [DOI] [PubMed] [Google Scholar]
- Schmidt J, Tweten D, Mahoney M, Portnoi T, Okamoto R, Garbow J, Bayly P. Experimental measurement of shear and tensile moduli in anisotropic tissue using magnetic resonance elastography. Proc SB3C. 2015a doi: 10.1016/j.jbiomech.2016.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt J, Tweten D, Mahoney M, Portnoi T, Okamoto R, Garbow J, Bayly P. Magnetic resonance elastography of slow and fast shear waves illuminates differences in shear and tensile moduli in anisotropic tissue. Proc ISMRM. 2015b doi: 10.1016/j.jbiomech.2016.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinkus R, Tanter M, Catheline S, Lorenzen J, Kuhl C, Sondermann E, Fink M. Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography. Magn Reson Med. 2005;53:372–387. doi: 10.1002/mrm.20355. [DOI] [PubMed] [Google Scholar]
- Tweten D, Okamoto R, Schmidt J, Garbow J, Bayly P. Identification of anisotropic material parameters in elastic tissue using magnetic resonance imaging of shear waves. Proc. 27th ASME VIB; Boston. 2015. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.