Direct force measurements reveal that protein Tau confers short-range attractions and isoform-dependent steric stabilization to microtubules

Significance

The microtubule-associated protein Tau is known to stabilize microtubules against depolymerization in neuronal axons, ensuring proper trafficking of organelles along microtubules in long axons. Abnormal interactions between Tau and microtubules are implicated in Alzheimer’s disease and other neurodegenerative disorders. We directly measured forces between microtubules coated with Tau isoforms by synchrotron small-angle X-ray scattering of reconstituted Tau–microtubule mixtures under osmotic pressure (mimicking molecular crowding in cells). We found that select Tau isoforms fundamentally alter forces between microtubules by undergoing a conformational change on microtubule surfaces at a coverage indicative of an unusually extended Tau state. This gain of function by longer isoforms in imparting steric stabilization to microtubules is essential in preventing microtubule aggregation and loss of function in organelle trafficking.

Abstract

Microtubules (MTs) are hollow cytoskeletal filaments assembled from αβ-tubulin heterodimers. Tau, an unstructured protein found in neuronal axons, binds to MTs and regulates their dynamics. Aberrant Tau behavior is associated with neurodegenerative dementias, including Alzheimer’s. Here, we report on a direct force measurement between paclitaxel-stabilized MTs coated with distinct Tau isoforms by synchrotron small-angle X-ray scattering (SAXS) of MT-Tau mixtures under osmotic pressure (P). In going from bare MTs to MTs with Tau coverage near the physiological submonolayer regime (Tau/tubulin-dimer molar ratio; Φ_Tau = 1/10), isoforms with longer N-terminal tails (NTTs) sterically stabilized MTs, preventing bundling up to P_B ∼ 10,000–20,000 Pa, an order of magnitude larger than bare MTs. Tau with short NTTs showed little additional effect in suppressing the bundling pressure (P_B ∼ 1,000–2,000 Pa) over the same range. Remarkably, the abrupt increase in P_B observed for longer isoforms suggests a mushroom to brush transition occurring at 1/13 < Φ_Tau < 1/10, which corresponds to MT-bound Tau with NTTs that are considerably more extended than SAXS data for Tau in solution indicate. Modeling of Tau-mediated MT–MT interactions supports the hypothesis that longer NTTs transition to a polyelectrolyte brush at higher coverages. Higher pressures resulted in isoform-independent irreversible bundling because the polyampholytic nature of Tau leads to short-range attractions. These findings suggest an isoform-dependent biological role for regulation by Tau, with longer isoforms conferring MT steric stabilization against aggregation either with other biomacromolecules or into tight bundles, preventing loss of function in the crowded axon environment.

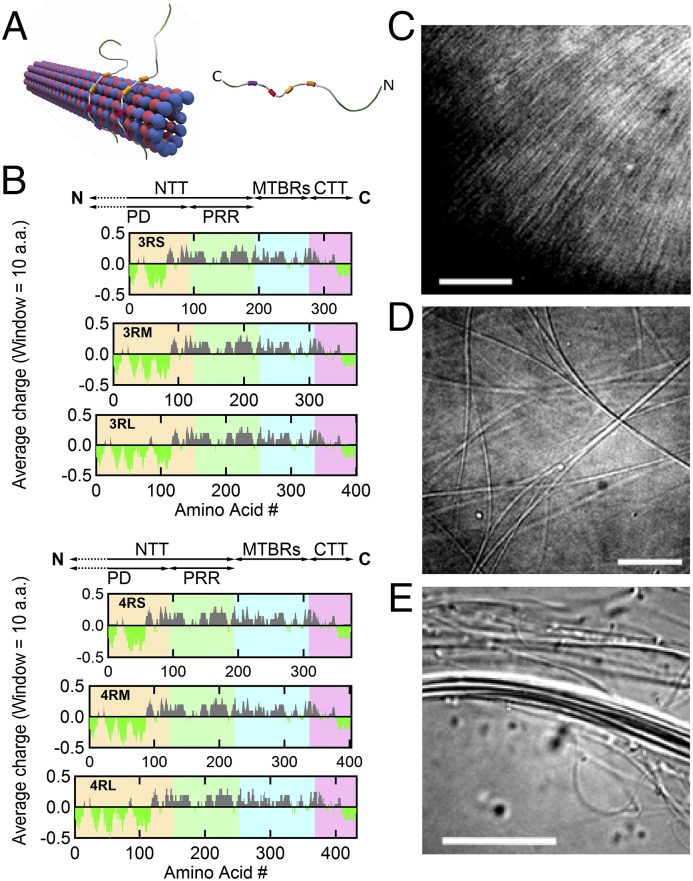
Microtubules (MTs), structural components of the eukaryotic cytoskeleton, are protein nanotubes involved in a range of cell functions, including intracellular trafficking, cell motility, segregating chromosomes, and establishing cell shape (1, 2). MTs are composed of straight protofilaments (PFs), which are head to tail assemblies of globular αβ-tubulin heterodimers that self-organize, with lateral PF–PF interactions stabilizing the hollow MT (Fig. 1A, Left) (3–5). MT structure and assembly dynamics are regulated and functionally differentiated in vivo by MT-associated proteins (1, 6). One MT-associated protein in particular, Tau (Fig. 1A, Right), is primarily localized to the axons of mature vertebrate neurons (1, 7). Although Tau is involved in numerous functions, which remain to be fully elucidated (8), a well-characterized function of Tau on binding to MTs (Fig. 1A, Left) in mature neurons is in the modulation of MT dynamic instability (i.e., cycles of slow polymerization and rapid disassembly) by enhancing tubulin assembly while suppressing MT depolymerization (9–11). This modulation of MT dynamic instability ensures proper trafficking of organelles along relatively stable MTs in axons (1, 12–15). Chemical modifications of Tau, including hyperphosphorylation and mutations leading to loss of function, have been implicated in Alzheimer’s disease and a wide range of neurodegenerative disorders, including Fronto-Temporal Dementia with Parkinsonism linked to chromosome 17, Pick’s, supranuclear palsy (16–20), and more recently, chronic traumatic encephalopathy in athletes suffering concussions (21).

Fig. 1.

MT-associated protein Tau binds to the MT surface and modulates the higher-order structure of MTs with increasing osmotic pressure. (A) Schematics of (Left) an MT with bound Tau protein and (Right) a single Tau protein (labeled with N- and C-terminal ends) with four MT-binding repeats (colored boxes). (B) Charge (averaged over 10 residues) vs. amino acid residue number for six isoforms of human Tau. The charge distribution diagram of each isoform shows the cationic (gray) nature of Tau, with the exception of the amino- and carboxyl-terminal tails, which include anionic (bright green) regions that lead to dipole-like characteristics. Data were obtained from the National Center for Biotechnology Information Protein Database (accession nos. NP_058525.1, NP_001190180.1, NP_001190181.1, NP_058518.1, NP_001116539.1, and NP_005901.2 for 3RS, 3RM, 3RL, 4RS, 4RM, and 4RL, respectively). The N-terminal tail (NTT) is made up of the PD (yellow background; first 92, 121, and 150 amino acids for -S, -M, and -L isoforms, respectively) and PRR (green background; next 94 amino acids) followed by the MT-binding region (MTBR; blue background) and ending at the carboxyl terminus (C) with the C-terminal tail (CTT; pink background). Tau isoforms have either three or four MT-binding repeats (3R- or 4R-) as a result of excluding (or including) exon 10 (33 amino acids), which contains a second MT-binding repeat and the interrepeat region between the first and second repeats. Additionally, the exclusion of exons 2 and 3 (both 29 amino acids), the exclusion of exon 2, or no exclusions in the PD result in the short (-S), medium (-M), or long (-L) isoforms, respectively. (C–E) DIC microscopy of samples at Φ_3RL = 1/40 show the presence of (C) an unbundled and (D and E) two distinct bundled phases at 0, 1, and 10 wt% 20k PEO, respectively. (Scale bars: C, 10 μm; D, 10 μm; E, 20 μm.)

The human CNS generates six Tau isoforms as a result of alternative RNA splicing (22). Tau structure is often described sequentially: the N-terminal tail (NTT) consists of a projection domain [PD; with no affinity for MTs and projecting off its surface (23, 24)] and a proline-rich region (PRR; with weak affinity for MTs), the MT-binding region (a series of three to four 18-aa-long imperfect repeats separated from one another by 13- to 14-aa-long interrepeats), and finally, a C-terminal tail (CTT) (Fig. 1B) (25–28). The number of imperfect repeats is determined by the excision or inclusion of exon 10 (leading to three-repeat Tau or four-repeat Tau, respectively), whereas the excision or inclusion of exons 2 and/or 3 determines the length of the PD (i.e., short, medium, or long) (Fig. 1B). Although all of the Tau isoforms are intrinsically disordered in solution (29), it is unclear whether the cationic domains in the repeat:interrepeat region that specifically bind to the MT surface adopt folded structures on attachment (Fig. 1A, Left). Although Tau strongly binds to the MT surface (∼1–3 µM affinity) (10, 26), recent work suggests that Tau–MT interactions are highly dynamic and that Tau can assume numerous structures (30, 31).

Previous synchrotron small-angle X-ray scattering (SAXS) work revealed that increasing coverage of paclitaxel-stabilized MTs by any of six Tau isoforms led to an increase in the average number of PFs in MTs (32). This increase in the ensemble-averaged inner radius of MTs, <R_in^MT>, indicated that MT-associated protein Tau isoforms do not just bind and stabilize MTs, for example, by enhancing PF–PF interactions but also, change the shape of αβ-tubulin and thus, PFs, leading to a change in curvature of MTs. This conclusion is consistent with recent NMR work showing that Tau binds, at least in part, between tubulin heterodimers (31).

Although Tau affects tubulin shape and inter–αβ-tubulin interactions within individual MTs, much less is known about how MT-bound Tau modifies inter-MT forces. This study focuses on elucidating the structure and interactions of paclitaxel-stabilized MTs (33–35) assembled at varying Tau/tubulin-dimer molar ratios [Φ_Tau = 1/10, 1/13, 1/20, 1/40, and 1/100, spanning the physiological range observed in axons (36)] using synchrotron SAXS in the presence of an osmotic depletant. By varying osmotic pressure [induced by 20k polyethylene oxide (PEO)] (SI Appendix, SI Note S1 and Fig. S1.3) and Tau-grafting density [Tau per MT outer surface area (32) controlled by Φ_Tau, because Tau binds stoichiometrically to MTs up to Φ_Tau ∼ 1/5], the force response of Tau-coated MTs was directly measured by SAXS line shape analysis (37). Previous literature noted the functional dependence of the MT-binding region of Tau in stabilizing individual MTs (26–28), but herein, we present data showing that inter-MT forces are functionally dependent on and regulated by the NTT PD of Tau. Specifically, at Φ_Tau = 1/10, isoforms with longer PDs suppressed MT bundling, requiring pressures an order of magnitude larger than bare MTs and MTs with short PD isoforms of Tau. This result indicates a gain of function of Tau isoforms with longer NTTs (by longer PDs) in adopting brush-like conformations at higher coverages to impart steric stabilization to individual MTs. This observed transition is in striking contrast to other neuronal cytoskeletal systems, such as the protruding charged side arms of neurofilaments, which have been found to always be in a brush-like phase with no observed subunit composition dependence on sidearm conformation (38, 39). In the high-pressure limit, where Tau chains from opposing MT surfaces are osmotically forced to interpenetrate, irreversible MT bundling was observed, which was attributed to the polyampholytic nature of Tau, leading to short-range attractions between anionic/cationic residues on neighboring Tau chains.

Results and Discussion

Phase Behavior of MT/Tau Mixtures Under Osmotic Pressure.

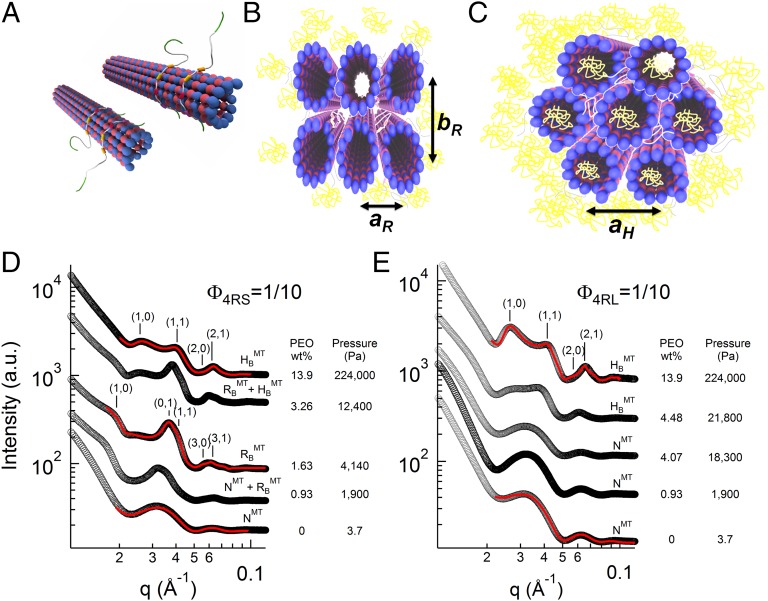
Structurally distinct higher-order phases of paclitaxel-stabilized MTs coassembled with Tau at different P were initially observed by video-enhanced differential interference contrast (DIC) microscopy (Fig. 1 C–E). Consistent with previous results without Tau (40, 41), MTs at high concentration undergo a transition from an orientationally ordered nematic state (N_MT) (Fig. 1C) to two distinct higher-ordered bundled phases (Fig. 1 D and E) as a function of increasing osmotic pressure. The bundled phases result from PEO-induced depletion attraction. The internal structure of these higher-ordered phases at different Tau coverages was elucidated with in situ SAXS–osmotic pressure measurements. Line shape analysis of azimuthally averaged SAXS data of the samples (Fig. 2) revealed three distinct phases, correlating to the distinct structures seen in DIC microscopy. Fig. 2D shows SAXS profiles with increasing P in mixtures of MTs and 4RS Tau (Fig. 1A) at Φ_4RS = 1/10. At low osmotic pressures (Fig. 2D, bottom profile) (0–0.46 wt% of 20k PEO), where DIC shows the N_MT phase, fits of background-subtracted scattering corresponded to a hollow cylinder form factor, with inner radii (∼8 nm) and cylinder thickness (4.9 nm) consistent with EM data of MTs (42). This behavior is similar to previous reports of bare MTs, where SAXS profiles of the N_MT phase shows no evidence of a correlation peak (5, 32, 40, 41, 43, 44). At intermediate osmotic pressures (∼1–3 wt% of 20k PEO), where DIC shows bundled MTs (Fig. 1D), a scattering structure factor was readily apparent with more than five orders of diffraction peaks indexed to a 2D rectangular lattice (Fig. 2D) (labeled R^B_MT at 1.63 wt% PEO). SAXS studies of bare MTs (40) have shown that the rectangular symmetry results from the buckling of MTs from circular to noncircular in the cross-section, because the larger PEO concentration on the outside compared with the inside lumen of MTs produces an excess pressure on the MT wall (Fig. 2B). The gradient is expected, because the radius of gyration of 20k PEO ∼ 6.9 nm is close to the inner radii of MTs (45), and at these intermediate concentrations, PEO does not readily enter the lumen because of an entropic confinement penalty.

Fig. 2.

MT bundling transitions with increasing osmotic pressure are Tau isoform- and concentration-dependent. (A–C) Schematics of the (A) nematic (N_MT; with orientational order and no positional order), (B) buckled rectangular bundle (R^B_MT; characterized by the rectangular lattice constants a_R and b_R), and (C) hexagonal bundle (H_MT; characterized by the hexagonal lattice constant a_H) phases of Tau MTs, with PEO colored in yellow. (D and E) Azimuthally averaged synchrotron SAXS data of Tau MTs plotted as a function of increasing osmotic pressure induced by 20k PEO, with PEO concentration and corresponding pressure shown next to each profile. (D) A reaction mixture of the short projection domain isoform 4RS at Tau/tubulin-dimer molar ratio Φ_4RS = 1/10, exhibits an osmotic pressure-induced phase transition from nematic (N_MT) to buckled rectangular (R^B_MT; a_R = 17.0 nm and b_R = 30.7 nm) and from buckled rectangular to hexagonal (H_MT; a_H = 30.2 nm), with coexistence regimes between phases. (E) However, another mixture (long projection domain isoform 4RL at Φ_4RL = 1/10) displays a transition from nematic (N_MT) to hexagonal (H_MT; a_H = 29.3 nm) phases, bypassing the buckled rectangular phase entirely. SAXS data were analyzed and presented fit parameters extracted with fitted model scattering curves (red lines) corresponding to the model appropriate structure and form factor as described in the text.

At higher osmotic pressures (∼7–14 wt% of 20k PEO), the Bragg diffraction peaks could now be indexed to a 2D hexagonal bundled phase with lattice parameter a_H (Fig. 2D) (labeled H_MT at 13.9 wt% PEO). The structural transition at higher P from the R^B_MT phase (Fig. 2B) to the H_MT phase (Fig. 2C) results from a transition from buckled (noncircular) to unbuckled (circular) MTs. The unbuckling occurs at concentrations near the chain overlap concentration (c* ∼ 7.5 wt% for 20k PEO), where the external crowding of PEO eventually forces PEO chains to enter the MT lumen (46, 47), thus equalizing the outside/inside pressures on MTs. The absence and presence of 20k PEO in the MT lumen in the R^B_MT and H_MT phases, respectively, have been directly confirmed with labeled PEO in fluorescence microscopy studies of bare MTs with increasing osmotic pressure (40, 41).

For most samples, the scattering from one phase clearly dominated, but samples at certain Tau coverages and osmotic pressures exhibited scattering from coexisting phases (N_MT + R^B_MT and R^B_MT + H_MT phases). Generally, MTs transitioned from N_MT to the R^B_MT and finally, the H_MT phase under increasing osmotic pressure, such as it did for Φ_4RS = 1/10 (Fig. 2D). Strikingly, for Tau isoforms with the longest PDs (3RL and 4RL), R^B_MT phase was entirely bypassed at the highest Tau coverage (i.e., N_MT transitioned directly to the H_MT phase). Fig. 2E shows SAXS profiles for 4RL Tau at Φ_4RL = 1/10, where the N_MT phase remains stable well into the intermediate osmotic pressure range, with MT bundling being suppressed up to P_B = 21,800 Pa (= 4.48 wt% 20k PEO) before transitioning to the bundled H_MT phase. This phase transition behavior is in contrast to SAXS data for Tau isoforms with short PDs, which undergo bundling at nearly an order of magnitude lower P_B (Fig. 2D) (profile at P = 1,900 Pa; 0.93 wt% 20k PEO). To fully elucidate the Tau isoform dependence of MT bundling, we mapped out the phase behavior by systemically altering all relevant variables (Tau isoform, Tau/tubulin-dimer molar ratio, and osmotic pressure).

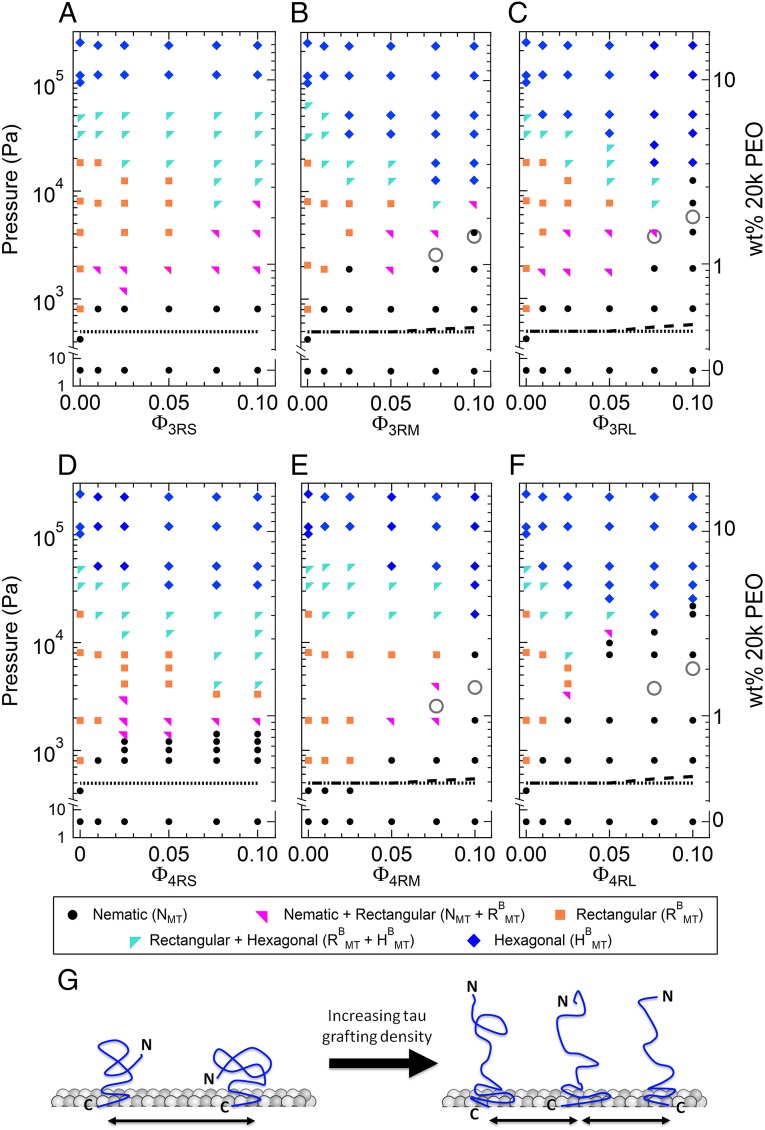
The osmotic pressure–Tau/tubulin composition (P-Φ_Tau) phase diagram of all six WT Tau isoforms is shown in Fig. 3, revealing regions of stability for unbundled N_MT and bundled R^B_MT and H_MT phases. All three structural phases (either singularly or in coexistence) were exhibited at all concentrations for Tau isoforms with the short PD (Fig. 3 A and D). However, Tau isoforms with the longest PDs (3RL and 4RL) suppress the R^B_MT phase at high Φ_Tau (Fig. 3 C for Φ_3RL = 1/10 and F for Φ_4RL = 1/13 and 1/10). Tau isoforms with medium-length PDs (3RM and 4RM) also show a much narrower pressure range for the R^B_MT phase for Φ_3RM,4RM = 1/13 and 1/10 (Fig. 3 B and E).

Fig. 3.

Osmotic pressure against Tau/tubulin concentration-phase diagram for all six Tau isoforms. (A–F) MT/Tau phases, determined by SAXS analysis, plotted as a function of increasing osmotic pressure (left y axis) induced by increasing weight percentage of 20k PEO (right y axis, which has independent log domains to match PEO concentrations) against various Tau/tubulin-dimer molar ratios (Φ_Tau) of (A) 3RS, (B) 3RM, (C) 3RL, (D) 4RS, (E) 4RM, and (F) 4RL isoforms of Tau. The observed phases were nematic (N), buckled rectangular (R^B_MT), or hexagonally bundled (H_MT) phases or regions of phase coexistence. For isoforms with the longer PD (-M and -L), the MT bundling pressure, P_B, increased abruptly at higher Tau coverages (Φ_Tau = 1/10). Notably, increasing Tau coverage of the 3RS and 4RS isoforms of Tau shows little effect in affecting the MT bundling pressure. As described in the text, the lines and open circles in the phase diagram correspond to the expected P_B for the soft cylinder model for bare MTs (dotted line), the charged soft cylinder model for selected Tau isoforms (-M and -L) bound to MTs (dashed line), and the charged brush model for Tau for selected Tau isoforms (-M and -L) at the highest coverages (Φ_Tau = 1/10 and 1/13; gray open circles). (G) Cartoon depicting the (Left) mushroom and (Right) brush states of Tau’s NTT with increasing grafting density.

Remarkably, the phase diagram reveals that, at the highest coverages of Tau with longer PDs (Φ_3RM,4RM = 1/10 and Φ_3RL,4RL = 1/10 and 1/13; both near the physiological regime), significantly higher osmotic pressures are required to stabilize MTs against bundling (P_B ∼ 10,000 Pa and P_B ∼ 20,000 Pa at Φ = 1/10 for -M and -L isoforms, respectively). This behavior is in marked contrast to Tau with short PD, which seems to have little effect on the bundling pressure (P_B ∼ 1,000 Pa) at all measured coverages. The dramatic increase in pressure strongly indicates that the conformations of the medium and long PDs have transitioned from a “mushroom” state (Fig. 3G, Left) to a “brush” state (Fig. 3G, Right). This change in conformation would give rise to an enhanced repulsive force of substantial magnitude between MTs, requiring much higher osmotic pressures to overcome that repulsion and bundle.

Classically, polymers undergo a mushroom to brush transition when the grafting distance between polymers is comparable with the diameter of the tethered polymer. Using SAXS (48), the physical diameters of the medium and long PDs in solution were shown to be ∼10 nm (in similar buffer conditions to those used in our study). This physical diameter was calculated as two times the physical radius, which is proportional to the radius of gyration (49) [D_Phys = 2R_Phys = 2(5/3)^1/2R_g]. The radii of gyration for unstructured proteins were found (50) to fit the Flory equation R_g = 0.1927N^0.588 nm, which for the PDs of -M and -L isoforms (degree of polymerization, N_PD = 121, 150), are 3.30 and 3.75 nm, respectively [in agreement with SAXS measurements of the PD in solution (48)], giving us D_Phys = 8.5 (-M) and 9.6 nm (-L). This scaling behavior follows previous measurements from SAXS (R_g = 6.5 nm) (51), dynamic light scattering (R_g = 6.6 nm) (51), and Monte Carlo simulations (R_g = 6.5 nm) (52) that confirm the R_G of isolated 4RL Tau in solution scales as a random coil conformation protein. However, the grafting distance, d_g^Tau = 4.5 × (Φ_Tau/2)^−1/2 nm (4.5 nm is the average tubulin monomer–monomer distance, and the factor of 2 arises, because Φ is a Tau to tubulin-dimer ratio), at the lowest Φ_Tau where the abrupt increase in bundling pressure is observed (Φ_3RM,4RM = 1/10 and Φ_3RL,4RL = 1/13) corresponds to d_g^Tau = 20.3 and 23.1 nm for -M and -L isoforms of Tau, respectively. Both grafting distances are considerably larger than the physical diameter, indicating that the Tau PD protruding away from the MT surface, at grafting densities before the transition to the brush state, is considerably more extended than the PD in solution.

Modeling the Interaction Potential of MTs with MT-Associated Protein Tau.

To elucidate the distinct contributions of the -M and -L Tau isoforms with longer PDs (Fig. 1B) in suppressing bundling at higher osmotic pressures, we modeled the pairwise potential energy between two MTs in the absence and presence of Tau. The model presented here balances the repulsive interactions (because of the overall anionic MT and the PD of surface-adsorbed Tau) against the depletion attraction resulting from the addition of PEO (i.e., the PEO-induced osmotic pressure, which effectively forces MTs together).

MTs without MT-associated protein Tau (SI Appendix, SI Note S1 and Table S1).

The overall bare charges of α- and β-tubulin (summing over negative and positive charged residues, including CTTs and bound nucleotides/ions) are −21.7e and −22.6e, respectively, at pH 6.8 (National Center for Biotechnology Information Protein Database accession nos. NP_001159977.1 and NP_001040014.1). The α- and β-tubulin CTTs, which contain either neutral or negative residues, have bare charges of −9e and −11e, respectively (Fig. 4A) (53). Because of the high charge of tubulin and its CTT, partial counterion neutralization of tubulin is expected; indeed, previous work (54) measured an effective charge of −23e per dimer (through MT electrophoretic movement in microchannels) against a calculated bare charge of −50e per dimer at pH 6.9. This calculation gave an effective charge renormalization prefactor r = Q_eff/Q_bare = 0.46, which was subsequently used in our calculations. The repulsive electrostatic potential energy between two MTs with wall to wall separation H may then be written in terms of a contribution from the renormalized charge of the CTTs and separately, the remaining renormalized charge of αβ-tubulin dimers:

$$V_{\text{MT}}^{\text{Repulsive}}\left(\mathit{H}\right)=V_{\text{cyl}}^{\text{hard}\hspace{0.17em}\text{MT}}\left(\mathit{H}\right)+V_{\text{cyl}}^{\text{soft}\hspace{0.17em}\text{CTT}}\left(\mathit{H}\right).$$ [1]

The first term in Eq. 1 describes the electrostatic repulsion between MTs modeled as hard cylinders with outer radius R = 12.5 nm and mean surface charge density σ = σ_Tub-CTT = −0.387e nm⁻² because of the renormalized charge of αβ-tubulin dimers minus the charge of the CTTs. Thus, we write (SI Appendix, SI Note S1.2) (55)

$$V_{\text{cyl}}^{\text{hard}}\left(H\right)=\frac{2\sqrt{\text{π}R}{\text{σ}}^2}{{\epsilon }_{\text{r}}{\epsilon }_0{\text{κ}}^{3/2}}L{i}_{1/2}\left({\text{e}}^{-\text{κ}H}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\mathrm{Energy}/\mathrm{Length}\right].$$ [2]

In Eq. 2, κ = 1/λ_D, with λ_D being the Debye–Hückel screening length (0.85 nm in our experiments), ε_rε₀ is the permittivity, and $L{i}_{1/2}\left(z\right)={\displaystyle {\sum }_{k=1}^{\infty }{z}^k/k^{1/2}}$ is the polylogarithm function of order 1/2. The second term in Eq. 1 takes into account the contribution of the CTTs modeled as “soft cylinders” (i.e., where the charge of the CTTs is distributed within a layer of thickness L around the MTs), giving rise to a soft repulsive potential (SI Appendix, SI Note S1.4) (56):

$$V_{\text{cyl}}^{\text{soft}\hspace{0.5em}\text{CTT}}\left(H\right)=\frac{2\sqrt{\text{π}R}{\text{ρ}}^2}{{\epsilon }_{\text{r}}{\epsilon }_0{\text{κ}}^{7/2}}{\sinh }^2\left(\text{κ}L\right)L{i}_{1/2}\left({\text{e}}^{-\text{κ}H}\right)H\mathrm{>}2L\left[\mathrm{Energy}/\mathrm{Length}\right].$$ [3]

ρ = −rfNe/(d_g²L) is the charge density (charge/volume) of the polyelectrolyte layer, where r = 0.46 is the charge renormalization factor (SI Appendix, SI Note S1.2), e is the elementary charge, f ∼ 1/2 is the net ionization fraction of CTTs (53), N = 19.5 is the mean number of residues in the CTTs, d_g = 4.6 nm is the grafting distance between CTTs, and L ∼ 4.0 nm is the mean height of the CTTs (57). For separations H < 2L, where the polyelectrolyte layer is compressed, L is replaced by H/2 in Eq. 3. In Eq. 3, the added salt leads to the presence of a double layer and the exponential screening of the electrostatic interactions between the polyelectrolyte-grafted surfaces.

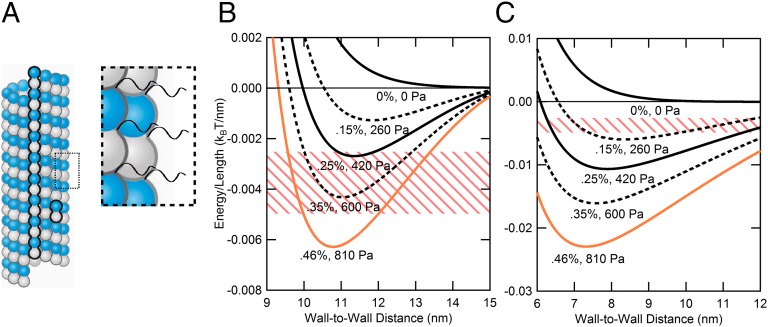
Fig. 4.

Modeling MT–MT interactions requires more than a simple charged cylinder model. (A) Schematic of bare MT and expanded view showing negatively charged C-terminal tails (CTTs) of α- and β-tubulin. The presence of CTTs on the MT surface requires the model to incorporate a soft polyelectrolyte layer above the surface of the MT. (B) Curves derived from the soft cylinder model plotted for actual PEO weight percentage used in experiments (solid lines) and in-between concentrations (dashed lines). Colors (from black to orange) are coordinated with data in Fig. 3 (Φ_Tau = 0). The pink-striped zone corresponds to a potential depth of 5–10 k_BT for 2-µm MTs (SI Appendix, SI Note S1 and Fig. S1.6 show MT length distribution), where one would expect MT bundling. The orange curve, which falls in this zone, corresponds to the lowest pressure where MT bundles are observed in the absence of Tau (Fig. 3). (C) Assuming the same potential depth (pink-striped zone; 5–10 k_BT for 2-µm-length MTs) for MT bundling, the charged hard cylinder model (i.e., all tubulin charge on the surface) predicts bundling at lower PEO concentrations compared with what is observed experimentally (between 0.25 and 0.46 wt% PEO).

The total effective interaction potential between bare MTs in the presence of PEO may be written as (SI Appendix, SI Note S1.5)

$$V_{\text{MT}}^{\text{Total}}\left(\mathit{H}\right)=V_{\text{cyl}}^{\text{hard}\hspace{0.17em}\text{MT}}\left(\mathit{H}\right)+V_{\text{cyl}}^{\text{soft}\hspace{0.17em}\text{CTT}}\left(\mathit{H}\right)+V_{\text{Depletion}}\left(\mathit{H}\right).$$ [4]

The third term is the depletion attraction between cylinders (energy per unit length) because of the presence of noninteracting 20k PEO polymer “depletants” with an effective radius a = 2R_g/(π)^1/2 ∼ 7.8 nm, with R_g = 6.9 nm for 20k PEO (58, 59) (SI Appendix, SI Note S1.1):

$$V_{\text{Depletion}}\left(\mathit{H}\right)=-\mathrm{\Pi }\hspace{0.17em}A\left(H\text{,}R\text{,}a\right)\hspace{1em}\text{0}<H\mathrm{\le }2a.$$ [5]

Here, A(H,R,a) = ${(a+R)}^2(\mathrm{\Theta }-\sin \left(\mathrm{\Theta }\right))$ is the overlap in the excluded area, where $\mathrm{\Theta }=2{\sin }^{-1}\left(\sqrt{\left(2a-H\right)\left(2a+H+4R\right)}/2\left(a+R\right)\right)$, and Π is the osmotic pressure of the depletant, including second- and higher-order virial coefficients to account for deviations from the ideal gas derivation for depletion attraction. For 20k PEO, measurements of Π (Pascals) fit an empirical expression, ${\text{Log}}_{10}(\Pi )=0.57+2.75\times {\left(\text{PEOwt\%}\right)}^{0.21}$, where PEOwt% is the weight percentage of 20k PEO (SI Appendix, Fig. S1.3) (37, 60). For H > 2a, depletion attraction vanishes, because the overlap in the excluded area term A(H,R,a) is zero.

Fig. 4B is a plot of V_MT^Total (H)/length vs. H as a function of increasing weight percentage of 20k PEO. The solid curves in Fig. 4B (color coordinated with data points in Fig. 3) correspond to experimental PEO concentrations studied, and the dashed curves in Fig. 4B correspond to in-between PEO concentrations. We see that, with increasing PEO concentration, the potential curve begins to develop a well-defined minimum with a bound state and depth of 5–10 k_BT (where MT bundles may be expected to be stable) appearing between ∼0.30 and ∼0.5 wt% of 20k PEO. [The pink striped zones in Fig. 4 B and C correspond to a potential depth of 5–10 k_BT for MTs, with average length of 2 µm (SI Appendix, SI Note S1 and Fig. S1.6 show MT length distribution).] We see in Fig. 3 that the onset of MT bundling at Φ_Tau = 0 is between 0.25 and 0.46 wt% 20k PEO concentrations (P between 420 and 810 Pa), which is in reasonable agreement with the MT model that takes into account the added repulsion from the short polyelectrolyte CTTs. [The horizontal dotted lines in Fig. 3 A–F correspond to the pressures where the depth of the potential between MTs (Eq. 4) is 7.5 ± 2.5 k_BT.] Fig. 4C shows that, if one ignores the CTTs and models MTs as charged hard cylinders with mean surface charge density σ = σ_Tub = −0.497e nm⁻², then the potential curve develops a minimum at much lower PEO concentrations and predicts that bundling with a potential depth ∼7.5 k_BT would occur as low as ∼0.15 wt% PEO, significantly lower than the experimentally observed bundling between 0.25 and 0.46 wt% PEO. [The potential energy curves in Fig. 4C are calculated from the first and third terms in Eq. 4, assuming that the renormalized net negative charge of αβ-tubulin dimer (−r44.3e per dimer, including CTTs, where r = 0.46) is located on the surface of the hard cylinder (SI Appendix, SI Notes S1.1 and S1.2).]

MTs coated with MT-associated protein Tau (SI Appendix, SI Note S2 and Table S1).

To model the contribution of Tau isoforms with longer PDs (because the short PD showed no appreciable change in P_B) to the MT–MT interaction potential energy, we considered the overall anionic PD of the NTT (Fig. 1B) to be extended away from the negative MT surface, with the remaining weakly positive PRR of the NTT being very weakly bound in a pancake-like conformation (61) near the surface [consistent with NMR spectroscopy (31)] with a height of ∼1 nm, in agreement with simulation (62, 63) and atomic-force microscopy (64). The PRR, MT binding region, and CTT were taken to contribute to the overall charge of αβ-tubulin dimers.

We first estimated Tau’s contribution (with Tau’s PD in the mushroom conformation) (Fig. 3G, Left) within the soft potential model described above. The total potential considered (V_MT+Tau^soft) used Eq. 4 and added the soft potential term for the PD with r = 1, where charge renormalization is not required because the combination of a low net ionization (f_net ∼ 0.1) of PD and the low Tau coverage results in a low charge density polyelectrolyte layer surrounding the MT. Furthermore, the V_cyl^hardMT (H) term incorporated the modified surface charge density σ = −0.387 + 0.253 × Φ_Tau(e nm⁻²), accounting for the renormalized, reduced negative charge [i.e., the charge of tubulin dimer minus the charge of the CTTs (−0.387e nm⁻²) plus the added charge from Tau without the PD (0.253 × Φ_Taue nm⁻² for 0 ≤ Φ_Tau ≤ 0.1)] (SI Appendix, SI Note S2.2). For the soft potential, Eq. 3 was used with the appropriate substitutions for parameters related to the PD: (f, N_PD, L_TauPD) = (0.120, 121, 20.1 nm) and (0.120, 150, 23.1 nm) for the medium (-M) and (-L) Tau isoforms, respectively. Here, f is the net ionization fraction of the PD, N_PD is the degree of polymerization of the PD, and L_TauPD is the height of the PD. The Φ at which the mushroom to brush transition (Fig. 3G) occurs gives us an estimate for the polyelectrolyte layer height of the longer PDs. As discussed in the previous section, the lowest Φ_Tau, where the transition is observed (Φ_3RM,4RM = 1/10 and Φ_3RL,4RL = 1/13) corresponds to a d_g^Tau = 20.3 and 23.1 nm for -M and -L isoforms of Tau, respectively, which we used for L_TauPD.

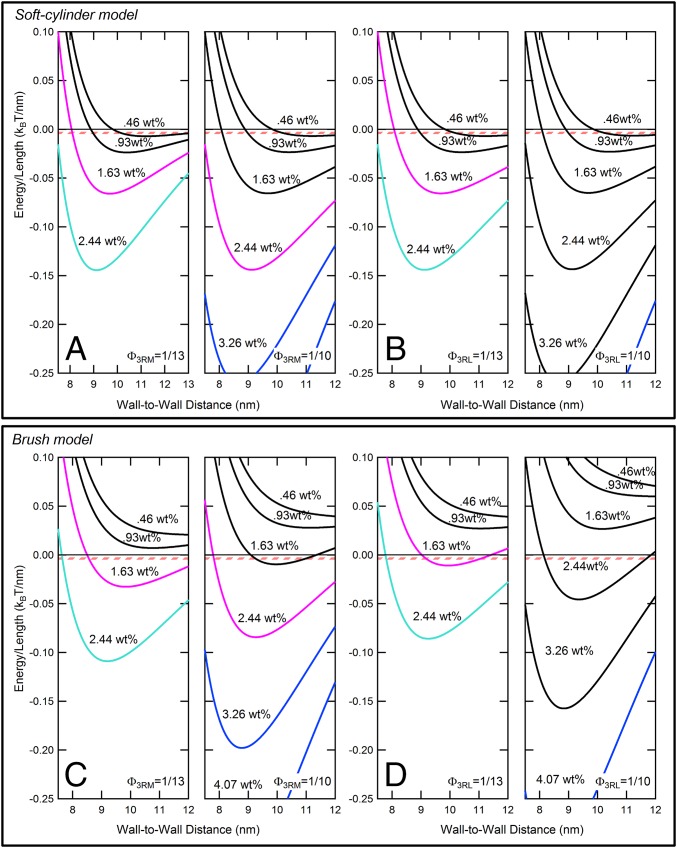
Fig. 5 A and B shows V_MT+Tau^soft/k_BT vs. H for 3RM and 3RL isoforms plotted with increasing weight percentages of 20k PEO (0.46, 0.93, 1.63, 2.44) and (0.46, 0.93, 1.63, 2.44, 3.26, 4.07) for the higher Tau coverages Φ_Tau = 1/13 and 1/10, respectively. These PEO concentrations correspond to the lower range of PEO weight percentage data shown in Fig. 3. The potential curves with depths between 5 and 10 k_BT (where one would expect bundling) are predicted to occur, even for the lowest concentration ∼0.46 wt% PEO, whereas bundling at these higher Tau coverages requires much larger PEO concentrations as seen in Fig. 3 (the pink striped lines in Fig. 5 correspond to a potential depth of 7.5 ± 2.5 k_BT for MTs with average length of 2 µm). Although the soft potential model predicts a slight increase in repulsion from the Tau PD (and subsequent increase in weight percentage of PEO to bundle MTs), the difference is minor compared with MTs without Tau (the dashed lines vs. the dotted lines in Fig. 3 B, C, E, and F) and fails to capture the dramatic increase in osmotic pressure required to bundle MTs assembled with the longer -M and -L isoforms at higher coverages (Φ_Tau = 1/13 and 1/10). For the 3RS isoform, the MT interaction potential within the soft potential model (V_MT+Tau^soft) is dominated by the high-density CTTs, which make a larger contribution than the 3RS PD in this coverage range.

Fig. 5.

The charged brush model for Tau isoforms with longer (-M and -L) PDs better captures the bundling behavior of MT/Tau mixtures at higher Tau coverages (Φ_Tau = 1/13 and 1/10). Potential energy curves plotted for high coverages of Φ_3RM,3RL = 1/13 and Φ_3RM,3RL = 1/10 using (A and B) the soft cylinder model and (C and D) the charged brush model as discussed in the text. The curves are (Left) [0.46, 0.93, 1.63, and 2.44] wt% PEO for Φ_3RM,3RL = 1/13 and (Right) [0.46, 0.93, 1.63, 2.44, 3.26, and 4.07] wt% PEO for Φ_3RM,3RL = 1/10. The concentrations are those used in experiments, and the curves are color-coded as in Fig. 3, where the first colored curves indicates the PEO concentration where bundling is first observed (Fig. 3) (Φ_Tau = 1/13 and 1/10 for -M and -L isoforms, respectively). The pink-striped zone corresponds to a potential depth of 5–10 k_BT for 2-µm MTs (SI Appendix, SI Note S1 and Fig. S1.6 shows MT length distribution), where one would expect MT bundling. Comparison between the model shows that (C and D) the charged brush model for the PD gives better qualitative agreement between theory and experiment compared with (A and B) the soft cylinder model.

Polyelectrolyte brush model at high coverages for the longer -M and -L Tau isoforms (SI Appendix, SI Note S2.3 and Table S1).

The soft potential model (dashed lines in Fig. 3 C–F) is not able to account for the dramatic increase in the bundling pressure, which suggests that a polyelectrolyte brush model would be more appropriate for Tau with the longer PDs at high coverage (Φ_Tau = 1/13 and 1/10). We note that the L_TauPD (20.3 and 23.1 nm for -M and -L isoforms of Tau, respectively) used is, in fact, an underestimate of the brush height, because the applied height is only relevant for Tau coverage up until the point of the mushroom to brush transition, beyond which the brush height should increase as Φ_Tau increases.

Within the polyelectrolyte brush model, the total potential considered (V_MT+Tau^brush) consisted of the terms in Eq. 4 [with V_cyl^hardMT(H) incorporating σ = −0.387 + 0.253 × Φ_Tau(e nm⁻²) to account for the added charge from Tau minus the charge of the PD as described above] plus the interaction potential between cylindrical MTs coated with Tau’s PD in the brush state [V_cyl^brush,Tau-PD(H)]. Following the works by Witten and Pincus (65) and Pincus (66), the interaction potential between polyelectrolyte brushes in a 1:1 salt solution with concentration c_s may be written as (SI Appendix, SI Note S2.3)

$$V_{\text{cyl}}^{\text{brush,TauPD}}\left(\mathit{H}\right)/k_{\text{B}}T=\frac{2\text{π}\sqrt{R_{\text{MT}}}{f}_{\text{TauPD}}^2{N}_{\text{TauPD}}^2}{c_{\text{s}}{\left(d_{\text{g}}^{\text{Tau}}\right)}^4}\left(\frac{1}{\sqrt{H}}-\frac{1}{\sqrt{2L_{\text{TauPD}}}}\right).$$ [6]

In this equation, the counterion distribution is predominantly determined by the local counterions needed to neutralize the polyelectrolyte-grafted surface. The repulsive potential between opposing grafted polyelectrolyte surfaces results from both the counterion pressure and contributions from chain configurational entropy.

Fig. 5 C and D show plots of V_MT+Tau^brush/k_BT vs. H for 3RM and 3RL isoforms with increasing weight percentages of 20k PEO (0.46, 0.93, 1.63, and 2.44 wt% for Φ_Tau = 1/13 and 0.46, 0.93, 1.63, 2.44, 3.26, and 4.07 wt% for Φ_Tau = 1/10). The colored potential curves in Fig. 5 C and D correspond to PEO concentrations, where bundling is observed in experiments as shown in Fig. 3. Compared with the soft cylinder model, we see that the longer Tau PDs modeled as grafted charged brushes now provide a significant increased repulsion at the higher Tau coverages (Fig. 5 C and D compared with Fig. 5 A and B, where the potential curves develop minima at significantly higher PEO concentrations).

Overall, the qualitative agreement with similar trends at high Tau coverage between experimentally observed PEO bundling concentrations (Fig. 3) and the prediction by the charged brush model (open gray circles in Fig. 3 B, C, E, and F for PEO concentrations predicting potential depths at 7.5 k_BT for 2-µm MTs) for the -M and -L Tau isoforms is clear. It is also clear that the use of an estimate for the height of the brush is responsible for the lack of quantitative agreement. Thus, the analysis of the data suggests that the longer Tau PDs (-M and -L) undergo a conformational change and are likely in a more extended state at Φ_Tau = 1/10, conferring steric stabilization up to osmotic pressures of ∼10,000–20,000 Pa, an order of magnitude higher compared with the short Tau isoforms.

Tau Induces Attraction Between MTs at High Osmotic Pressure.

To characterize the P distance curves in the bundled-phase regime, we analyzed the SAXS data in the high P regime (30,000 Pa < P < 120,000 Pa), where the system was in the hexagonal (H_MT) phase with unbuckled MTs with circular cross-section. At low P in the N_MT phase, the SAXS data were fit to the square of the MT form factor |F_MT|², where MTs are modeled as hollow cylinders with inner radius <R_in^MT> ∼ 8.0 nm (a fit parameter) and constant wall thickness w = 4.9 nm, consistent with EM models of MTs (41) (e.g., Fig. 2 D, bottom profile and E, bottom profile). As shown previously (5, 67), the MT wall to wall spacing [D_w-w = a_H − 2 × (<R_in> + w)] in the H_MT phase can be quantitatively determined by measuring the X-ray structure factor (giving the hexagonal lattice parameter a_H) and simultaneously, the MT form factor, yielding <R_in> and w. The structure factor was taken to be the sum of Bragg diffraction peaks at the reciprocal lattice vectors |G_hk| = G₁₀(h² + k² + hk)^1/2 and G₁₀ = 4π/(3^1/2a_H). Each peak was represented as a squared Lorentzian: [A_hk/(W_q² + (q_⊥ − G_hk)²)]², with G_hk, amplitude A_hk, and a single peak width proportional to W_q (where 1/W_q is approximately the bundle size in cross-section) as fitting parameters. The background-subtracted SAXS data for unoriented MT bundles were fit to the MT bundle structure factor multiplied by |F_MT|² and averaged over all orientations in q space (solid lines in Fig. 2 D, top profile and E, top profile).

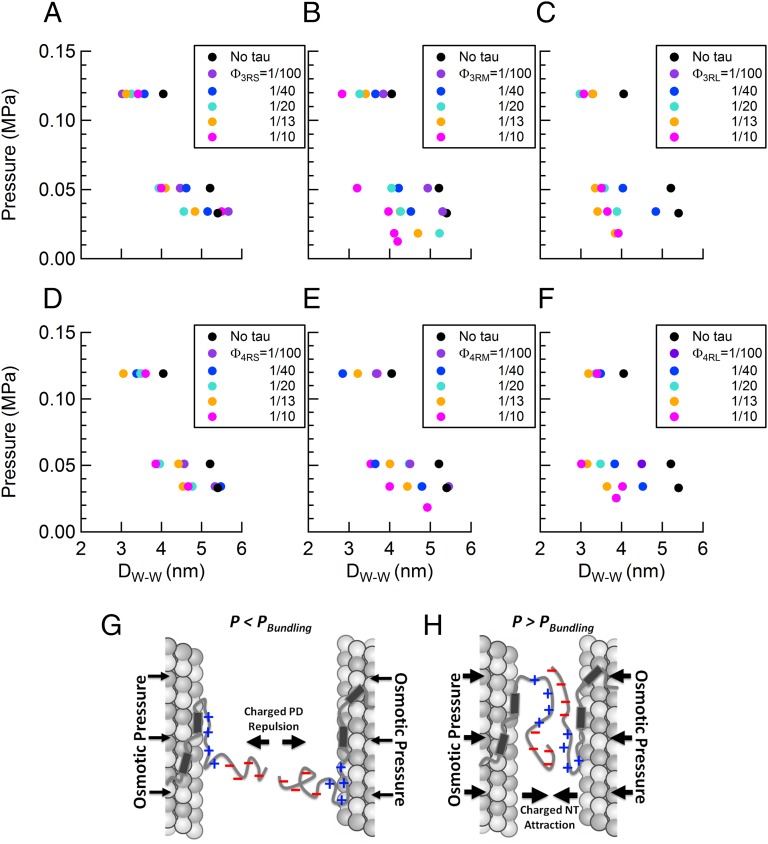
Most interestingly, SAXS analysis showed that, for a majority of given osmotic pressures, not only did the addition of Tau serve to decrease the wall-to-wall distance D_w-w relative to “naked” MTs (black circles in Fig. 6 A–F), but also, increases in concentration of Tau further decreased D_w-w (colored circles in Fig. 6 A–F). Although the decrease due to added Tau was apparent in Tau isoforms with the short PD (ΔD_w-w ∼ 0.7 nm) (Fig. 6 A and D), the effect was noticeably more pronounced for Tau isoforms with the long PD (ΔD_w-w ∼ 1.5 nm) (Fig. 6 C and F). The data are consistent with the onset of Tau-induced short-range attractions arising from the polyampholytic nature of Tau (i.e., with negative and positive amino acid residues) and in particular, the dipolar nature of the NTT of all six isoforms (the PD and overall cationic PRR) (Fig. 1B). With increasing osmotic pressures overcoming longer-ranged repulsions of the overall anionic Tau-PD (Fig. 6G) (discussed above), Tau’s NTTs on neighboring MTs are expected to interpenetrate, leading to the formation of favorable short-range anionic/cationic electrostatic bonds between overlapping chains and effectively reducing the MT wall to wall spacing (Fig. 6H). Similar chain interpenetration behavior has been reported for protruding neurofilament side arms, which are also unstructured polyampholytes, at high osmotic pressures (68–70).

Fig. 6.

At high osmotic pressures, Tau mediates short-range attractions between MTs in the bundled phase. (A–F) The wall to wall distance between MTs in hexagonally packed bundles plotted as a function of increasing osmotic pressure. Increasing concentrations of (A) 3RS, (B) 3RM, (C) 3RL, (D) 4RS, (E) 4RM, and (F) 4RL isoforms decrease the wall to wall distance between MTs, indicative of the onset of Tau-induced short-range attractions (black circles correspond to distances between bare MTs). (G and H) Schematic cartoons show differing MT–MT interactions mediated by Tau. (G) The repulsion of the anionic component of Tau PDs at long distances, where low osmotic pressures do not favor chain interpenetration. (H) The favorable cationic/anionic interaction between overlapping Tau PDs (possibly including sections of the PRR) at short distances, where high osmotic pressures favor chain interpenetration.

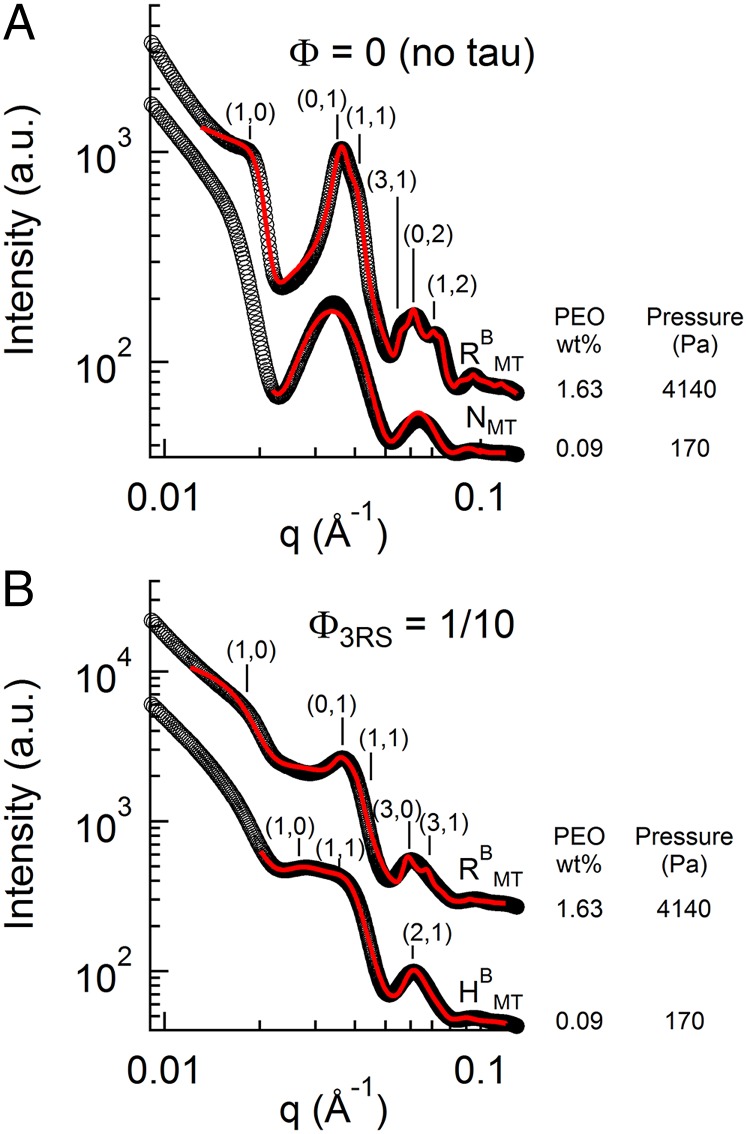
To confirm that the attractive regime was mediated by Tau, we conducted reversibility experiments. When bare MTs were osmotically pressured into the rectangular-buckled phase at 4,100 Pa (Fig. 7A, upper profile at 1.63 wt% PEO), lowering of PEO to below the bundling concentration resulted in a reversible transition back to the unbundled N_MT phase, consistent with the repulsive nature of MTs (Fig. 7A, lower profile at 0.09 wt% PEO). However, bundling of Tau-covered MTs (Φ_3RS = 1/10) into the R^B_MT phase at the same osmotic pressure (Fig. 7B, upper profile at 1.63 wt% PEO) followed by a similar dilution did not lead to the unbundled N_MT phase, but rather, they remained in a bundled phase for up to 60 h after dilution (Fig. 7B, lower profile at 0.09 wt% PEO), indicative of stable Tau-induced short-range attraction. Interestingly, the MT bundles did not retain the original rectangular symmetry of the R^B_MT phase but rather, transitioned to the hexagonal bundled state, H_MT. This change in lattice symmetry was to be expected, because removal of most of the PEO effectively removed the pressure difference between the outside wall of the MT and the inside luminal wall, causing MTs to unbuckle and revert back to their circular cross-section.

Fig. 7.

MT-associated protein Tau-induced irreversible MT bundling. Reversibility experiments confirm that the short-range attractions are because of Tau. (A) With no Tau, SAXS data analysis shows that an osmotic pressure-induced (1.63 wt% 20k PEO) R^B_MT phase (upper profile; a_R = 17.3 nm and b_R = 30.9 nm) relaxes into an N_MT by diluting PEO to 0.09wt% (lower profile). (B) In the presence of Tau (Φ_3RS = 1/10), a similar dilution from 1.63 to 0.09 wt% 20k PEO shows that the bundled state remains (showing the presence of Tau-induced short-range attractions), but the bundled phase now transitions from the buckled R^B_MT phase (upper profile; a_R = 17.5 nm and b_R = 32.7 nm) to the unbuckled H_MT phase (lower profile; a_H = 32.2 nm) because of the large dilution of PEO as described in the text. SAXS data were analyzed, and they presented fit parameters extracted with fitted model scattering curves (red lines) corresponding to the model appropriate structure and form factor as described in text.

Conclusions

We have investigated Tau-mediated forces between MTs over a range of Tau/tubulin-dimer molar ratios (Φ_Tau = 1/100–1/10, which includes the physiological regime) using SAXS on mixtures subjected to osmotic pressure. This study has revealed that MT-associated protein Tau fundamentally alters the repulsive forces between MTs in an isoform-dependent manner. In particular, the jump in osmotic pressure required to bundle MTs coated with -M and -L Tau isoforms at the higher physiological coverages, at the mushroom to brush transition, reveals a gain of function of Tau isoforms with longer NTTs (because of the longer PDs) in imparting steric stabilization to individual MTs against bundling. Significantly, the Φ_Tau at which the jump occurs shows that the conformation of the NTT of Tau bound to the MT surface at low coverages (before the mushroom to brush transition) is substantially more extended (approximately a factor of two) than would be expected from SAXS measurements of the radius of gyration of Tau’s NTT in solution (48).

What is highly significant in this work is the demonstration of the functional property of the charged PD in sterically stabilizing MTs on undergoing a transition to a brush state from a direct force measurement. Previous identification of Tau’s PD was based entirely on its lack of binding affinity to MTs and did not give insight to its biophysical functions (24). Steric stabilization against cellular biomacromolecules is essential in preventing MT loss of function in the crowded axon environment. Furthermore, the conformation of Tau on the MT surface is intrinsically connected to its coverage. The discovery of two distinct conformation states of MT-bound Tau, namely mushroom or brush, further emphasizes the need for future biophysical measurements of MT-bound Tau to be conducted in both regimes.

It is interesting to note that the expression of six different Tau isoforms is developmentally regulated, where fetal brain expresses only the shortest isoform (3RS), whereas the adult brain (with Tau concentration increasing along the length of the axon away from the cell body) expresses an ∼1:1 ratio of 3R and 4R Tau (71). This observation would suggest that the 3RS isoform is likely to be expressed at a higher level in fetal brain (i.e., compared with the adult brain), enabling steric stabilization of fetal MTs at higher coverage, where 3RS Tau would be in a more extended brush conformation. With respect to the adult brain, although the composition of different isoforms is not known at different points along the length of the axon [where the ratio of -S:-M:-L N-terminal configurations in adult brain, averaged over the entire axon, is 4:5:1, respectively (72)], our finding points to a minimum coverage needed by the longer isoforms (either -M or -L) to impart steric stabilization to MTs.

This minimum coverage required for MT steric stabilization by Tau could also shed light on a possible pathway for neurodegeneration. In the diseased state, Tau is often found to be hyperphosphorylated, with a weaker binding affinity to MTs. Should MTs lose sufficient Tau coverage to the degree where PDs transition from brush to mushroom and fail to sterically stabilize MTs, intracellular trafficking on MTs could be significantly hampered by the nonphysiological close-bundled state in the crowded axonal environment.

At high pressures in the MT bundled-phase regime, the polyampholytic nature of Tau resulted in a coverage-dependent electrostatic attraction between MTs. This regime of “tight bundles,” resisted by longer PDs, may conceivably be accessed in vivo in the presence of excess molecular crowding forces. Tight bundles would have negative consequences for organelle trafficking by MTs, where the small MT wall to wall spacing, ranging between 3 and 5 nm, would be expected to interfere with motors carrying cargo (73).

In addition to the biological interest in MT-associated protein Tau as a key component of the axonal cytoskeleton, the directed assembly of MTs by intrinsically disorder protein Tau is also of broad interest from a biomolecular materials and biophysics perspective. The unique manifestation of short-range attraction and long-range repulsion by Tau of MTs gives inspiration for the design of biomaterials with multiple interaction motifs.

Methods

Tubulin Purification.

Tubulin was purified as described (74, 75). Briefly, MT-associated protein-rich tubulin was isolated from bovine brain through successive in vitro polymerization/depolymerization cycles. After suspension in 50 mM PIPES (piperazine-N,N'-bis[2-ethanesulfonic acid]), pH 6.85, 1 mM MgCl₂, 1 mM EGTA, and 0.1 mM GTP, tubulin was purified by running through a P-11 Phosphocellulose Column (GE Healthcare), with nontubulin elements binding to the column. Tubulin (>99% purity) was drop frozen with liquid nitrogen and stored at −70 °C, with protein concentration determined by Bradford assay.

Tau Purification.

Tau was expressed and purified as described (11, 76). Briefly, the human cDNA for all six Tau isoforms was encoded in pRK expression vectors and expressed through BL21(DE3) cells. Bacteria was collected and lysed through sonication and boiling. After isolation by centrifugation, the soluble Tau was bound to a P-11 Phosphocellulose Column and eluted by increasing NaCl concentrations. SDS/PAGE was used to identify fractions where Tau was collected, and fractions were run and bound through a HiTrap Phenyl HP Column (GE Healthcare), whereby Tau was again eluted by decreasing (NH₄)₂SO₄ concentrations. Fractions with Tau were identified as before and suspended in 80 mM PIPES, pH 6.8, 1 mM MgSO₄, 1 mM EGTA, and 0.1% β-mercaptoethanol. Concentration was determined by SDS/PAGE compared with Tau standard, with original concentration determined by amino acid analysis.

Sample Preparation.

MTs were polymerized from 45 µM (5 mg/mL) tubulin, 1 mM GTP, and 5 wt% glycerol mixed in 50 mM PIPES, 1 mM EGTA, and 1 mM MgCl₂, pH 6.8, at 35 °C for 20 min, after which 40 µM taxol, dissolved in DMSO, was added (matching the subsequent final tubulin concentration) to stabilize MTs. Tau was then added to preassembled MTs to desired Φ_Tau with a small amount of 1 M KCl in buffer to bring the solution to a final concentration of 25 mM KCl. Varying concentrations of 20,000 molecular weight poly(ethylene oxide) or 20k PEO dissolved in buffer were then added, with osmotic pressure induced calculated as a function of 20k PEO concentration: log(P) = 1.57 + 2.75 × [PEO wt%]^0.21, where P is the pressure in dynes centimeter⁻² (37).

DIC Microscopy.

A charged-couple device Camera (SensiCam^QE; Cooke) mounted on a Diaphot 300 (Nikon) with Xenon Lamp (Sutter Instrument) was used for optical microscopy measurements, with samples placed between two microscopic slides sealed by wax.

SAXS.

SAXS was carried out at the Stanford Synchrotron Radiation Lightsource Beamline 4–2 at 9 keV with an Si(111) monochromator. Scattering data were taken with a 2D Area Detector (MarUSA), with a sample to detector distance of ∼3.5 m. Prepared samples were spun down at 16,000 × g for 30 min and loaded into 1.5-mm-diameter quartz capillaries (Hilgenberg GmbH) at 3,500 rpm. Data analysis incorporated structure and form factors (as described above) fit with nonlinear least-squared fitting routines, with background subtraction of SAXS data.