Noise in gene expression is coupled to growth rate

Abstract

Genetically identical cells exposed to the same environment display variability in gene expression (noise), with important consequences for the fidelity of cellular regulation and biological function. Although population average gene expression is tightly coupled to growth rate, the effects of changes in environmental conditions on expression variability are not known. Here, we measure the single-cell expression distributions of approximately 900 Saccharomyces cerevisiae promoters across four environmental conditions using flow cytometry, and find that gene expression noise is tightly coupled to the environment and is generally higher at lower growth rates. Nutrient-poor conditions, which support lower growth rates, display elevated levels of noise for most promoters, regardless of their specific expression values. We present a simple model of noise in expression that results from having an asynchronous population, with cells at different cell-cycle stages, and with different partitioning of the cells between the stages at different growth rates. This model predicts non-monotonic global changes in noise at different growth rates as well as overall higher variability in expression for cell-cycle–regulated genes in all conditions. The consistency between this model and our data, as well as with noise measurements of cells growing in a chemostat at well-defined growth rates, suggests that cell-cycle heterogeneity is a major contributor to gene expression noise. Finally, we identify gene and promoter features that play a role in gene expression noise across conditions. Our results show the existence of growth-related global changes in gene expression noise and suggest their potential phenotypic implications.

Proper control of gene expression is critical in nearly all biological processes. However, genetically identical cells exposed to the same environment display heterogeneity in gene expression (noise), with important phenotypic consequences (Grossman 1995; Rao et al. 2002; Blake et al. 2003; Balaban et al. 2004; Colman-Lerner et al. 2005; Kærn et al. 2005; Balázsi et al. 2011; Munsky et al. 2012; Lee et al. 2014). Variability in expression is anti-correlated to population average gene expression, which in turn is tightly coupled to growth rate (Tyson et al. 1979; Ingraham et al. 1983; Bar-Even et al. 2006; Newman et al. 2006; Brauer et al. 2008; Klumpp et al. 2009; Taniguchi et al. 2010; Keren et al. 2013). However, except for isolated examples (Guido et al. 2007), the effects of growth conditions on expression noise have not been systematically investigated.

The expression noise of a gene in a clonal population is determined by intrinsic and extrinsic factors (Elowitz et al. 2002). Intrinsic noise describes the variation at the level of a single gene due to the stochastic nature of the transcriptional process, whereas extrinsic noise relates to the variability in expression shared across different genes due to population dynamics, global differences in cellular environment, and shared upstream components (Thattai and van Oudenaarden 2001; Elowitz et al. 2002; Blake et al. 2003; Raser and O'Shea 2004; Pedraza and van Oudenaarden 2005; Volfson et al. 2006; das Neves et al. 2010; Stewart-Ornstein et al. 2012; Schwabe and Bruggeman 2014). Although research, in particular at the theoretical level, has focused on stochastic, intrinsic noise (for review, see Raj and van Oudenaarden 2008; Balázsi et al. 2011; Sanchez and Golding 2013), in most organisms that have been studied, the majority of the variability in gene expression is extrinsic (Raser and O'Shea 2004; Acar et al. 2005; Colman-Lerner et al. 2005; Newman et al. 2006; Volfson et al. 2006; Raj and van Oudenaarden 2008; Schwabe and Bruggeman 2014). Intrinsic expression noise is tightly coupled to the mean expression of the population and generally decreases as mean expression increases (Bar-Even et al. 2006; Newman et al. 2006; Taniguchi et al. 2010), as depicted schematically in Figure 1A. At high expression levels, there is no longer a dependence on the mean, as global, extrinsic factors set a lower bound (extrinsic limit) for the overall variability (Bar-Even et al. 2006; Newman et al. 2006; Taniguchi et al. 2010). Deviations of genes from this trend are attributed to their specific regulatory architectures, often encoded by their promoter sequence, which may specifically result in either high or low levels of noise (Blake et al. 2003; Raser and O'Shea 2004; Carey et al. 2013; Dadiani et al. 2013; Sanchez and Golding 2013; Jones et al. 2014).

Figure 1.

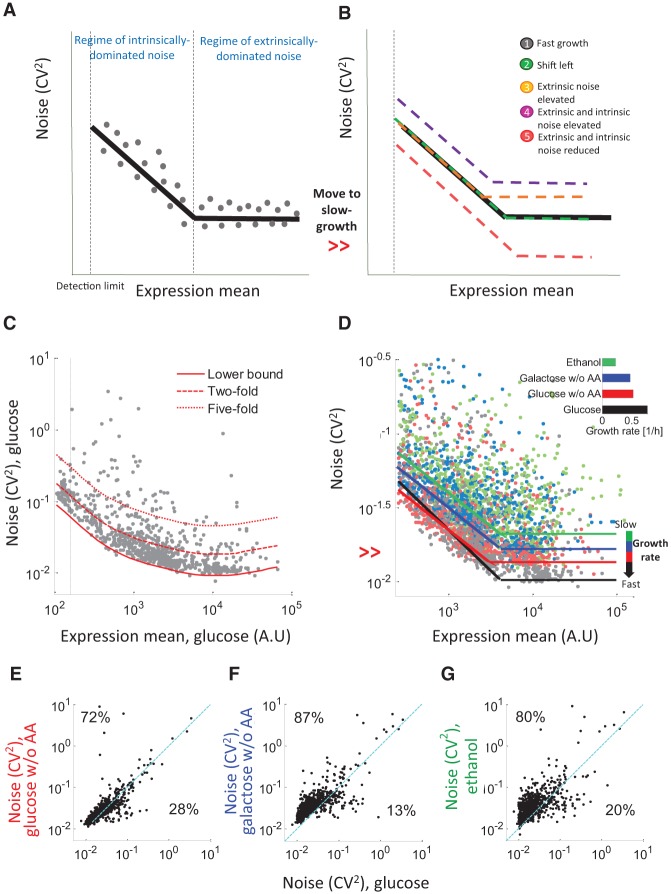
Gene expression noise is higher at lower growth rates. (A) A schematic of the genome-wide relationship between mean expression (x-axis) and noise (CV², y-axis) in a single condition as determined experimentally (Newman et al. 2006; Taniguchi et al. 2010). At low expression levels, the noise is inversely correlated with the mean expression of the gene and is dominated by intrinsic factors. At high expression levels, noise and mean are uncorrelated, presumably since intrinsic noise levels decrease, and extrinsic factors set a lower bound (extrinsic limit) for the CV² (Bar-Even et al. 2006; Newman et al. 2006; Taniguchi et al. 2010). The black line denotes the median of all genes. The dashed line separates the regimes dominated by intrinsic or extrinsic variability. (B) Alternative predictions for global, genome-wide changes in mean and noise when cells are moved to a condition that supports a lower growth rate. The black line is as in A, whereas colored lines denote the behavior in the new condition. (1) Mean-noise curve is unchanged in slow growth. (2) Slower growth is coupled with a global decrease in mean (Brauer et al. 2008; Keren et al. 2013). Promoters shift left along the black curve, such that the noise of each promoter is higher, but globally, the same mean expression is associated with similar noise levels in both conditions. (3) Slow growth causes an increase in extrinsic noise, such that the same mean expression is associated with higher noise levels. This effectively increases the extrinsic limit and shifts the boundary between the regimes. (4) Slow growth causes an increase in both extrinsic and intrinsic noise. (5) Slow growth causes a decrease in both intrinsic and extrinsic noise. Plausible reasons for the different predictions are discussed in Supplemental Note 1. (C) Scatterplot of the YFP mean (x-axis) and CV² (y-axis) for cells grown in glucose plus amino acids. Red lines depict lower noise bound (solid), twofold (dashed), or fivefold (dotted) above the lower bound. (D) Scatterplot of the YFP mean (x-axis) and noise (CV², y-axis) for all promoters in each of the four conditions with linear fits of the data: (black) glucose; (red) glucose w/o AA; (blue) galactose w/o AA; (green) ethanol. The different conditions exhibit different levels of noise for the same mean expression. (Inset) the growth rate (in doublings per hour) in each of the tested conditions. (E–G) Scatter of the noise of all promoters in the fastest growth condition (glucose, x-axis) and each of the other conditions (y-axis): glucose w/o AA (E); galactose w/o AA (F); and ethanol (G). Dashed cyan line indicates y = x. In all comparisons, most of the promoters are above the line (74%, 87%, and 81%, respectively), indicating that they display lower noise values in the fast growth condition.

Parameters affecting gene expression variability change across conditions in a coordinated manner, e.g., growth rate (Tyson et al. 1979; Ingraham et al. 1983), mean expression (Berthoumieux et al. 2013; Gerosa et al. 2013; Keren et al. 2013), and concentration of RNA polymerases and ribosomes (Pedersen et al. 1978; Ingraham et al. 1983; Klumpp and Hwa 2008). Harsher conditions, which support slower growth, also display lower protein abundances for most genes and, specifically, lower abundances of RNA polymerases and ribosomes (Pedersen et al. 1978; Tyson et al. 1979; Ingraham et al. 1983; Klumpp and Hwa 2008, 2014; Klumpp et al. 2009; Berthoumieux et al. 2013; Gerosa et al. 2013; Keren et al. 2013). However, it is not clear whether noise levels are expected to change globally between conditions and in what direction because many of these changes may have opposing effects (Fig. 1B; Supplemental Note 1).

To examine how noise changes across conditions, we measured the single-cell expression distributions of approximately 900 Saccharomyces cerevisiae promoters upstream of a fluorescent reporter across four environmental conditions using flow cytometry. We find a genome-wide increase in gene expression noise at lower growth rates, with most genes displaying elevated noise levels at slow growth. We examine the dependence of noise in expression on growth rate by modeling the noise that results only from changes in the composition of cell-cycle stages in the population at different growth rates. Consistent with our data, we find that this highly simplified model predicts a non-monotonic relationship between growth rate and noise, as well as overall higher variability in expression for cell-cycle–regulated genes in all conditions. Measurements of several strains grown in a chemostat further support our model and suggest that differential partitioning of the population between cell-cycle stages in different growth rates is a major determinant of extrinsic noise.

Our work underscores the importance of growth rate–related effects in noise, showing that some conditions show elevated levels of expression variability genome-wide, with potential phenotypic consequences. Since cell-to-cell variability in gene expression underlies important phenotypic phenomena such as persistence (Balaban et al. 2004), competence (Maamar et al. 2007), latency (Dar et al. 2014), metastasis (Lee et al. 2014), responsiveness to fluctuating environments (Acar et al. 2005, 2008; Blake et al. 2006; Kaufmann et al. 2007; Levy et al. 2012; Vardi et al. 2013), and triggering of meiosis (Nachman et al. 2007), our results suggest that the probability and efficiency of these processes will be tightly coupled to environmental conditions, with potential evolutionary implications.

Results

Measurement of promoter-driven expression distributions across conditions

To systematically examine noise in gene expression across environmental conditions, we utilized a previously described library of yeast strains, in which we genomically integrated 859 different native yeast promoters, spanning a wide variety of cellular functions and processes, upstream of a stable yellow fluorescent protein (YFP) (Keren et al. 2013). These strains also include a second mCherry fluorescent reporter downstream from a constant promoter in all strains, allowing control of the experimental variability of our system (Supplemental Fig. S1). We grew the strains in four environmental conditions, differing in carbon source and availability of amino acids, and measured single-cell expression distributions using flow cytometry at midexponential growth. For each promoter–reporter, we extracted both its mean and noise (σ²/µ², variance divided by the mean squared, known as the squared coefficient of variation [CV²]) (Methods; Supplemental Table S1). We performed several analyses to gauge the integrity and accuracy of the system. We examined our experimental variability using biological replicates and obtained high reproducibility (mean R = 0.99, CV² R = 0.91) (Supplemental Fig. S2). We also assessed the sensitivity of our system and found that 96% of our strains (822/857) were above the detection limit in at least one of the tested conditions (Methods).

We find that in each condition, our measurements largely recapitulate previous flow cytometry measurements of protein abundances (Bar-Even et al. 2006; Newman et al. 2006; Stewart-Ornstein et al. 2012). At low expression levels, the noise decreases with increasing mean expression, whereas at high expression levels it remains constant (Fig. 1C; Supplemental Fig. S3). In all conditions, promoters display a large span in their noise values. Promoters encoding for similar mean expression values may display more than an order-of-magnitude difference in noise values (Fig. 1C; Supplemental Fig. S3), similar to the range reported for proteins (Bar-Even et al. 2006; Newman et al. 2006). Comparing our results in rich media to flow cytometry measurements of protein abundances in rich media (Stewart-Ornstein et al. 2012) yields a positive correlation (mean R = 0.64, noise R = 0.5) (Supplemental Fig. S4), indicating that variability in yeast protein levels is at least partly encoded by their promoter sequence. Taken together, our results suggest that we can accurately capture variability in gene expression, which is encoded within the promoter region, of approximately 900 different genes under four growth conditions.

Variability of promoter-driven expression decreases with increasing growth rate

To examine how promoter-driven expression levels change across conditions, we compared the mean and noise (Fig. 1E–G; Supplemental Fig. S5) of all promoters in every pair of conditions. In agreement with previous reports (Brauer et al. 2008; Keren et al. 2013), we found a global decrease in mean expression for most genes in slow growth conditions. Notably, we found that for most promoters, noise differs across conditions in a manner that correlated with growth rate (Fig. 1D, inset). Nutrient-rich conditions, which support faster growth rates, exhibit lower noise for most promoters (74%–87% of the genes for the conditions examined). We validated that these changes in noise are not a result of experimental artifacts (Methods; Supplemental Fig. S2). This result implies that the cell-to-cell variability in expression levels is a function of the environment, whereby in poor growth conditions an isogenic cell population will generally be more variable than the same population in rich conditions.

There are alternative predictions for the global, genome-wide elevation in noise when cells are moved to a condition that supports slower growth rate. Since slower growth is coupled with a global decrease in mean expression (Brauer et al. 2008; Keren et al. 2013), it could be that each gene will have a lower mean and, consequently, higher noise due to the inverse mean–noise relationship. Overall, this will result in promoters shifting left along the existing mean–noise curve without changing the coupling of a particular value of mean expression to a particular value of noise (Fig. 1B, green). Alternatively, it could result from a global elevation in intrinsic or extrinsic noise, such that the same mean expression is coupled to higher noise levels in slow-growth conditions in either intrinsically dominated or extrinsically dominated regimes or in both (Fig. 1B, orange and purple).

To examine the sources of these global changes in noise across conditions and distinguish between the different predictions in Figure 1B, we plotted the mean and CV² of each promoter in each condition. For each condition, we fitted the dependence of noise on mean expression, extracted the extrinsic variability limit, and defined the regimes of expression dominated by either intrinsic sources (low expression) or extrinsic sources (high expression) as previously done (Fig. 1D; Supplemental Fig. S6; Methods; Bar-Even et al. 2006). Interestingly, we found that slow-growth conditions display a global, genome-wide elevation in noise for the entire range of expression (as predicted by line 4 in Figure 1B). For example, in ethanol, the slowest growth condition that we examined, the extrinsic noise limit is elevated ≈threefold compared to glucose, the fastest growth condition (Fig. 1D). In slow growth rates, the mean expression of all promoters is lower, which in itself contributes to an increase in noise. Here we found that even for the same value of mean expression (associated with different promoters at different growth rates), there is a significant increase in noise in slow growth. Notably, both extrinsically and intrinsically dominated regimes are associated with higher noise, and the observed changes cannot result solely from an increase in extrinsic noise (Supplemental Fig. S7; Supplemental Note 2). These results suggest that in slow-growth conditions, noise is generally higher such that the same mean expression is associated with elevated noise levels.

A model of noise that reflects changes in cell-cycle–stage distributions in the population at different growth rates predicts global changes in noise across conditions

Extrinsic noise has been previously attributed to various factors, primarily population dynamics and variability in shared upstream components, such as the cellular expression machinery and transcription factors (Thattai and van Oudenaarden 2001; Elowitz et al. 2002; Blake et al. 2003; Raser and O'Shea 2004; Pedraza and van Oudenaarden 2005; Volfson et al. 2006; das Neves et al. 2010; Stewart-Ornstein et al. 2012; Jones et al. 2014; Schwabe and Bruggeman 2014). To study the sources for changes in extrinsic noise between conditions, we developed a simple model that explores the variability in gene expression resulting only from having an asynchronous population with cells at different cell-cycle stages (Methods). Our model assumes a growing, asynchronous population of cells, in which cells can be either in G1 or G2, with G2 cells displaying overall higher expression levels due to increased gene copy number (O'Duibhir et al. 2014)—for simplicity, we assume that the average expression of G2 cells is twice that of G1 cells, but this assumption can be relaxed (see Supplemental Note 5; Supplemental Fig. S8). Following previous observations in yeast, we next assume that changes in growth rate are mainly attributed to a change in the time spent in G1, leading to different fractions of cells in G1 at different growth rates (Tyson et al. 1979; Brauer et al. 2008). Using this simplified model in which each cell takes on one of two possible expression states (corresponding to G1 and G2), we find that the variability (CV²) is related to the fraction of cells in G2 (f) by the following relationship:

$${\mathrm{CV}}^2=\frac{f\left(1-f\right)}{{\left(f+1\right)}^2}+C,$$ (1)

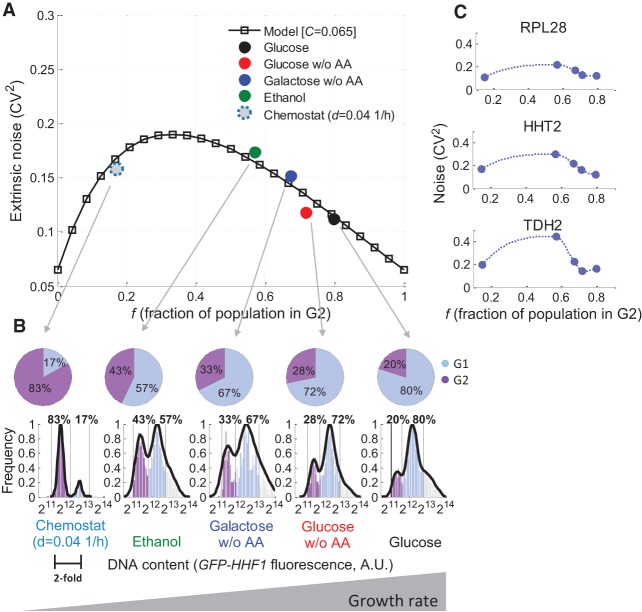
with C representing the extrinsic noise added by all other, non-cell-cycle–related components. This equation yields a non-monotonous relationship between variability and the growth rate of the population, with a peak in variability at growth rates in which one-third of the population is in G2 (Fig. 2A, solid line).

Figure 2.

A model of noise that results from changes in cell-cycle–stage distributions in the population at different growth rates predicts global changes in noise across conditions. (A) Our model prediction of how noise (CV², y-axis) globally changes with the G2 fraction of the population (x-axis), according to Equation 1, with C = 0.065 (black line). Colored points represent experimental data. The fraction of G2 cells in the population at each growth condition was determined by flow cytometry measurements of a histone-GFP reporter construct (GFP-HHF1) (B, x-axis). The extrinsic noise limit for the batch-growth conditions (glucose, glucose w/o AA, galactose w/o AA, and ethanol) was extracted by a linear fit to the ungated promoter–reporter measurements (Supplemental Fig. S9, y-axis). The extrinsic noise limit for the chemostat condition was computed as the average CV² of the three promoter–reporter strains assayed in the chemostat (RPL28, HHT2, and TDH2). (B) The fraction of G2 cells in the population increases with growth rate, as determined by flow cytometry measurements of GFP-HHF1. (C) In addition to the measurements of the entire library in different batch conditions, three high-expressing strains from the library were grown in a His-limited chemostat (dilution rate of 0.04h⁻¹). Shown are their CV² values (y-axis) versus the fraction of the population in G2 (x-axis) in all assayed conditions. Lines are cubic interpolations between measured points and serve as a visual guide.

To identify what fraction of the changes observed experimentally in extrinsic variability are captured by this naïve model, we measured the fraction of cells in G1 and G2 in our growth conditions. We constructed a strain in which green fluorescent protein (GFP) was fused to the N-terminal region of the H4 histone protein (GFP-HHF1) (Methods) and grew it together with our library to obtain the fraction of cells in G1 and G2 in the different growth conditions. We found that the fraction of G2 cells increases with growth rate, ranging from ∼55% for cells grown in ethanol to ∼80% in glucose (Fig. 2B). These values are in excellent agreement with G2 fractions previously reported in the literature for these conditions (Supplemental Table S2; Slater et al. 1977; Johnston et al. 1979; Tyson et al. 1979). We then compared the model predictions at these G2 fractions to the extrinsic noise limit we extracted for each growth condition (Methods; Supplemental Fig. S9). We found that our simplified model quantitatively accounts for >60% of the extrinsic variability for each of the examined growth conditions and recapitulates the decrease of extrinsic variability with growth rate (Fig. 2). These results suggest that the fact that at different growth rates the population of cells is differentially partitioned between the different cell-cycle stages may lead to a higher variability limit (higher “noise floor”) (Volfson et al. 2006; Taniguchi et al. 2010) on gene expression at slow-growth conditions, affecting all genes.

Our model predicts a non-monotonic change in CV² with growth rate (Fig. 2A). To test this prediction, we wished to study the noise at very low G2 fractions, which we could not obtain by batch growth conditions (Supplemental Note 3) nor by measurements of our library in stationary state (Methods; Supplemental Fig. S10; Guido et al. 2007). To this end, we decided to undertake a complementary approach and measure a subset of our high-expressing strains, whose noise is likely dominated by extrinsic factors, using a chemostat (Brauer et al. 2008). We constructed a system of a ministat array as previously described (Miller et al. 2013) and grew four of our strains under conditions of histidine limitation (Levy et al. 2007) at a dilution rate of 0.04 h⁻¹, corresponding to a doubling time of ∼17.5 h (Methods; Supplemental Fig. S11). To find the fraction of G2 cells, we grew HHF1-GFP in the first ministat. In the other three ministats, we grew the promoter–reporter strains for RPL28, HHT2, and TDH2, which had high expression levels in all conditions in our batch growth experiments (Supplemental Table S1). Upon stabilization of the chemostats, cells were measured by flow cytometry. We found that under these conditions, the culture reached a low G2 fraction of 17% (Fig. 2B). Notably, for all three strains, noise was reduced (Fig. 2C), and their average noise value agreed well with the predictions of the model (Fig. 2A). We further validated the non-monotonic relationship between growth rate and expression variability for RPL28 by growing this strain in a large histidine-limited chemostat at dilution rates ranging from 0.3 to 0.05 h⁻¹ (corresponding to doubling times of 2–14 h, respectively) (Supplemental Note 6; Supplemental Fig. S12). These results suggest that for high-expressing genes, whose noise levels are dominated by extrinsic factors, the differential partitioning of the population between the cell-cycle stages at different growth rates is a significant determinant of the final noise levels. They also suggest that although the measurements of the entire promoter library in common laboratory conditions predominantly showed that extrinsic noise is higher at lower growth rates, this relationship may be reversed for some genes at very slow growth rates. This hypothesis requires further exploration on a larger scale.

In addition, for all of our strains, we performed simulations on our measured data in which we generated in silico wells with different compositions of G1 and G2 cells (Methods; Supplemental Fig. S13). We found that our model was highly successful in predicting the outcome of these simulations. Although each strain has its own range of CV² values (derived from its mean expression and intrinsic properties), the overwhelming majority of the strains perform as predicted by our model when subsampling different compositions of G1/G2 cells in the population (Supplemental Fig. S14).

Finally, in addition to a global increase in extrinsic variability in slow-growth conditions, we found that these conditions also exhibit a systematic increase in intrinsic variability (Fig. 1D). We explored whether changes in cell-cycle–stage distributions across conditions could also lead to changes in intrinsic variability by extending our model to incorporate the variability within G1 and G2 populations (Supplemental Note 4). Our model predicts that genes with higher values of intrinsic noise will show a steeper increase in their noise with decreasing growth rate (Supplemental Fig. S15A). That is, for genes with higher levels of intrinsic variability, the decrease in CV² with increasing G2 fraction (i.e., faster growth rate) will be larger. Indeed, we observe experimentally such a trend in our data (K–S P < 1 × 10⁻⁶) (Supplemental Fig. S15B).

Taken together, these results suggest that changes in the population cell-cycle distribution as a function of changing growth rate may significantly contribute to changes in both intrinsic and extrinsic variability. We note that our models provide an underestimation of the noise (C > 0) (Methods) in each condition and other factors probably contribute to the observed coupling between environmental conditions, growth rate and noise.

Cell-cycle–dependent genes have high expression variability

The above model suggests that coupling of gene expression to the cell cycle may result in increased expression variability (Supplemental Note 5; Zopf et al. 2013). We therefore examined the distributions of mean expression and noise in all growth conditions for promoters of genes that were previously shown to be either cycling or noncycling (Spellman et al. 1998). We find that in all our growth conditions, genes whose expression is coupled to the cell cycle exhibit significantly higher levels of variability (13%–37%, K–S P < 10⁻⁵) (Fig. 3; Supplemental Fig. S16). Importantly, this elevation in variability does not result from different mean expression levels between cycling and noncycling genes (0.14 < P < 0.64 for paired K–S test) (Supplemental Fig. S16) and appears to be dominated by an increase in extrinsic noise, as predicted by our model.

Figure 3.

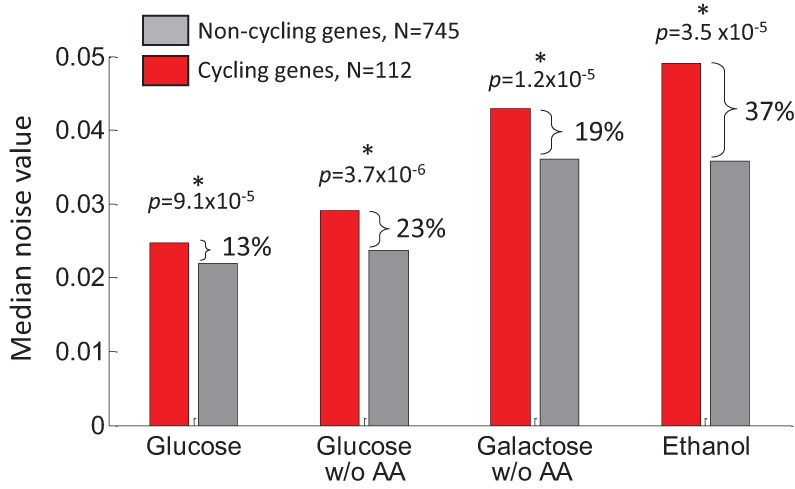
Cell-cycle–regulated genes have higher variability levels. For each condition, the median noise level is shown for genes that cycle with the cell cycle (red bars) or not (gray bars), as previously defined by Spellman et al. (1998). In all conditions, cycling genes display higher variability levels than noncycling genes. P-values are for paired K–S tests (Supplemental Fig. S15).

To test whether this property of cell-cycle–regulated genes is also maintained at the protein level, we analyzed two published data sets of genome-wide protein distributions in two conditions measured by flow cytometry of yeast proteins fused to GFP (Newman et al. 2006; Stewart-Ornstein et al. 2012). We find that in both data sets, cell-cycle–regulated proteins exhibit significantly higher levels of variability (P < 3 × 10⁻⁵ for paired K–S test) (Supplemental Fig. S17). As expected, most of the change is attributed to the extrinsic component (Supplemental Fig. S17E–J). Taken together, these results suggest that in all conditions examined, the coupling of gene expression to cell cycle results in higher expression variability.

Sequence determinants of high promoter variability change between conditions

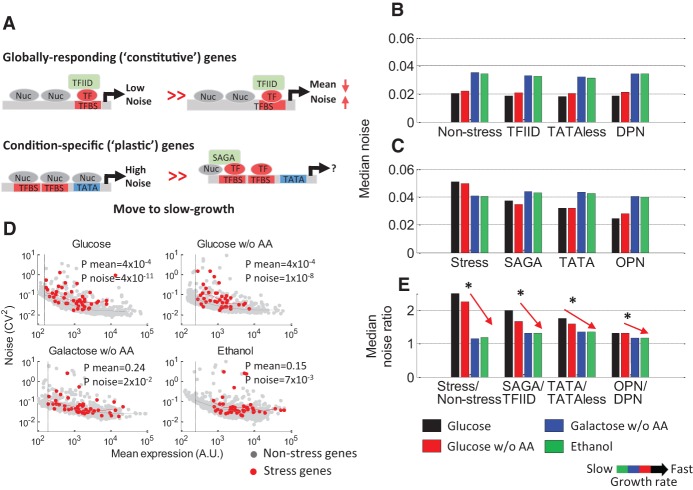
Next, we examined how different promoter features relate to expression variability across conditions. Previous studies, conducted in fast growth conditions, identified that “housekeeping” genes, which are not differentially regulated across conditions, are generally associated with low levels of noise, whereas “plastic,” “condition-specific” genes are often associated with high levels of noise (Bar-Even et al. 2006; Newman et al. 2006). This high variability of the condition-specific genes coincides with their promoter architectures, which are generally highly occupied by nucleosomes, remodeled by the SAGA complex, and contain strong TATA elements (Fig. 4A; Newman et al. 2006; Field et al. 2008; Tirosh and Barkai 2008; Zenklusen et al. 2008; Hornung et al. 2012). As these features are encoded mainly by the promoter sequence, we verified that these features are also strongly correlated with expression variability in our library in fast growth conditions (Supplemental Fig. S18). We also found that nucleosome occupancy, regulation by SAGA or TFIID, and TATA strength are highly correlated with variability in all examined conditions (Fig. 4B,C; Supplemental Fig. S19A). However, in slow-growth conditions, the effect of these features is reduced (e.g., differences in variability between TATA and TATA-less promoters are less significant) (Fig. 4D,E; Supplemental Fig. S19B), primarily due to the global increase in noise (Fig. 4B,D) together with the activation of some of the condition-specific genes, which is coupled to a reduction in noise (Fig. 4C,D). Notably, this result implies that care should be taken when classifying a certain promoter architecture as “noisy,” because this classification depends on the environmental conditions.

Figure 4.

Features associated with high noise decrease in significance with decreasing growth rate. (A) A schematic depiction of two stereotypical promoter architectures in yeast, characteristic of either globally changing genes or condition-specific genes and associated with low or high levels of noise, respectively, in fast growth conditions (Field et al. 2008; Tirosh and Barkai 2008). (B–E) Promoters were classified according to activation in stress (Gasch et al. 2000), regulation by TFIID or SAGA (Huisinga and Pugh 2004), TATA or TATA-less (Basehoar et al. 2004), and high (OPN) or low (DPN) nucleosome occupancy (Tirosh and Barkai 2008). Conditions are colored as in Figure 1. (B) The median noise in each condition of the non-stress, TFIID-regulated, TATA-less, and DPN groups. Median noise of these groups increases in slow-growth conditions. (C) The median noise in each condition of the stress, SAGA-regulated, TATA, and OPN groups. In all growth conditions, these groups exhibit higher noise levels than their counterpart plotted in B. (D) Scatterplot of the YFP mean (x-axis) and CV² (y-axis) for all promoters in each of the four conditions. Stress genes are colored red. In glucose (fast growth), global noise levels are low. Stress genes are repressed and associated with high levels of noise, higher than expected by their low mean. In ethanol (slow growth), global noise levels are high. Stress genes are up-regulated, and their noise levels decrease. (E) For each condition, the median noise of each group was divided by the median noise of its counterpart (e.g., median noise of promoters with TATA divided by the median noise of TATA-less promoters). Values higher than 1 indicate that the features are associated with high and low noise, respectively. For all features examined, values are above 1 but decrease with decreasing growth rate, indicating that their contribution to noise decreases in slow growth conditions. Significance was determined by K–S test and corrected using FDR (Supplemental Fig. S18).

Next, we examined how specific regulation across conditions affects expression variability. To this end, we compared the mean and noise across conditions of coregulated groups of genes known to be differentially regulated under our experimental conditions (Keren et al. 2013), e.g., amino acid biosynthesis genes, which are repressed in rich media and activated in minimal media. We found that all examined groups display high levels of noise when repressed, even higher than expected from their low expression mean. However, these different groups behaved differently when activated. For example, the amino acid biosynthesis genes (e.g., MET2, LEU4, ADE13, ARO3, and LYS20) had higher CV² values than expected from their mean. In contrast, aerobic respiration genes (e.g., ATP1, ATP5, COX4, COX6, QCR7, and QCR9) and galactose assimilation genes (e.g., GAL1, GAL7, GAL10, and GAL80) had noise values comparable to those expected from their mean in media containing either ethanol or galactose as a carbon source, respectively. These unique behaviors may be attributed to variability propagated from shared upstream regulators of these groups (e.g., GCN4 for the amino-acid biosynthesis group; HAP4, CAT8, and ADR1 for the aerobic respiration group; and GAL4 for the galactose assimilation group), which tend to show similar noise levels as their regulated genes (Supplemental Fig. S20). These distinct levels of pathway-specific noise of the different regulators also matches their strength of activation and nucleosome eviction, which is known to be strong for GAL4 (Bryant et al. 2008), but weak for GCN4 (Raveh-Sadka et al. 2012). Taken together, we found that different genes deviate from the mean-noise trend at different conditions. These deviations may be attributed to their specific regulatory architectures, as encoded by their promoter sequence, and to noise propagated from shared upstream regulators.

Discussion

Here, we investigated how cell-to-cell variability in gene expression changes across different growth conditions. By measuring approximately 900 yeast fluorescent reporters in four growth conditions, we found that noise is coupled to the environment and is intimately connected with growth rate. This result adds to previous observations, which have connected population-average expression levels to growth rate (Pedersen et al. 1978; Tyson et al. 1979; Ingraham et al. 1983; Klumpp and Hwa 2008, 2014; Klumpp et al. 2009; Berthoumieux et al. 2013; Gerosa et al. 2013; Keren et al. 2013) and suggests that environmental conditions have a prominent role in cell-to-cell expression variability. An isogenic population of cells will be more variable in their expression pattern in one growth condition than in another.

Increased variability in expression may be both detrimental and beneficial for growth in harsh environments. Cells growing in harsh environments may experience increased difficulty in maintaining the fidelity of gene expression levels. However, increased variability in harsh environments may also have an evolutionary advantage, as bet-hedging may be the preferred strategy in such cases (Acar et al. 2008). Whether advantageous or detrimental, global changes in noise in different environments probably have an important effect on the outcome of processes dependent on noise, such as the probability to sporulate (Grossman 1995; Maamar et al. 2007) or become competent (Balaban et al. 2004).

Global changes in noise with growth rate may be a general phenomenon, not restricted to microorganisms. Although there are currently no data sets that allow proper examination of this question, a preliminary analysis that we performed on a published data set of cancer cells treated by a drug (Cohen et al. 2008; Supplemental Fig. S21) hints in this direction. While drugs reduce growth rate, cell-to-cell variability in protein abundance increases for most genes, regardless of specific activation or repression, with potential consequences for survival after treatment. Following a promising example in HIV treatment with drugs that modulate expression noise (Dar et al. 2014), our results suggest that similar approaches may be meaningful in cancer.

The observed change in expression variability across conditions is not fully determined by changes in mean expression, as we find higher levels of variability in slow-growth conditions for similar mean expression values. Global changes in expression when changing growth conditions are for a significant part determined by changes in population cell-cycle composition (Volfson et al. 2006; Levy et al. 2012; Zopf et al. 2013; Jones et al. 2014; O'Duibhir et al. 2014). Recently, such changes in cell-cycle composition have been suggested to explain expression noise in E. coli grown in a single growth condition (Jones et al. 2014). Here, we propose that differential partitioning of the population across cell-cycle stages may contribute to a global elevation in noise in slow-growth conditions and provide evidence suggesting that it is a major contributor to extrinsic noise. Our understanding of the mechanisms underlying global changes of intrinsic noise with growth rate is still very poor.

However, differential cell-cycle–stage distributions do not entirely account for the higher expression variability in slow growth conditions, even for extrinsic noise, and other factors likely affect our results. One prominent feature that changes with growth rate is the cell size because yeast are smaller at slower growth rates (Tyson et al. 1979). However, at least from a mathematical investigation, we find no support for smaller cells displaying higher extrinsic noise (Supplemental Note 7). Other factors may contribute to the elevation in noise in slow-growth conditions. For example, in slow growth, RNA polymerases are expressed at lower levels, with increased noise. This increase in variability in the expression of the transcriptional machinery is expected to propagate downstream to all genes, globally increasing their noise. It will be interesting to further explore these different mechanisms and quantify how much they contribute to expression variability in different environmental conditions.

In our analysis, we also found gene- and function-specific determinants of noise. Promoter features highly correlated with expression variability in fast growth conditions such as TATA boxes and high nucleosome occupancy exhibit weaker correlations with expression variability in slow-growth conditions. We suggest that this reduction may be the result of the combination of several factors: The rise of extrinsic noise in slow-growth conditions entails that under these conditions the variability of more genes is dominated by extrinsic factors, thus reducing the contribution of intrinsic sequence determinants; many of these features were determined experimentally in fast-growth conditions and thus may be inadequate for slow growth conditions; and changes in trans between the conditions, such as the concentration of TBP (Basehoar et al. 2004), may render that promoter configurations that have high expression variability in one condition will have low variability in another. Taken together, our results suggest that the classification of promoters as “noisy” depends on the environmental conditions.

Previous reports have linked global changes in gene expression to changes in the environment, in synchrony with changes in growth rates and population composition (Regenberg et al. 2006; Brauer et al. 2008; Berthoumieux et al. 2013; Gerosa et al. 2013; Keren et al. 2013; O'Duibhir et al. 2014). Here, we show that variability in expression of all genes is also strongly affected by the environment, as has been shown for a synthetic construct in E.coli (Guido et al. 2007). This effect of the environment on expression may have phenotypic consequences, which may be subject to evolutionary selection. For example, since cell-to-cell variability in gene expression underlies important phenotypic phenomena such as persistence (Balaban et al. 2004), competence (Maamar et al. 2007), latency (Dar et al. 2014), responsiveness to fluctuating environments (Acar et al. 2005, 2008; Blake et al. 2006; Kaufmann et al. 2007; Levy et al. 2012; Vardi et al. 2013), and triggering of meiosis (Nachman et al. 2007), our results suggest that the probability and efficiency of these processes will be tightly coupled to environmental conditions. Demonstrating the relevance of this hypothesis in natural environments remains an ongoing challenge.

Methods

Strains and media

All promoter–reporter strains are haploid MAT-α derivatives of Y8205 and were described previously (Keren et al. 2013). Media were prepared as follows: glucose/ethanol: synthetic complete media (6.7 g/L yeast nitrogen base [YNB], 1.6 g/L amino acids) with 2% glucose or ethanol, respectively; glucose/galactose without AA: YNB 6.7 g/L supplemented with histidine, with 2% glucose/galactose, respectively.

Measurements of promoter noise across conditions

Cells were inoculated from frozen stocks into one of four defined media (150 μL, 96-well plate) and grown for 48 h at 30°C, reaching complete saturation. Cells were then diluted 1:3000–1:9000 in fresh medium to a total volume of 150 μL and were grown at 30°C for at least 8 generations of exponential growth before measurement by flow cytometry. For measurements in early stationary state, cells were grown in glucose and were assayed 2 h after reaching stationary OD. Flow cytometry experiments were conducted using the Becton Dickinson LSRII machine and standard protocols. Four channels were acquired: forward-scatter, side-scatter, YFP (excitation 488 nm BP 525/50), and mCherry (excitation 561 nm BP 610/20).

Flow cytometry analysis

An automatic data analysis pipeline was applied for gating and filtering the data. In each well, cells were discarded from further analysis if they were collected in the first 0.5 sec or over periods that show flow instability (bubbles, etc.), or if they had negative or saturated values in one of the parameters. We gated the data based on the forward scatter (FSC) and the side scatter (SSC) of the cells by using a stringent gate that removed the cells that had the extreme 60% values in either FSC or SSC, leaving at most 40% of the centermost cells for further analysis, as previously done (Bar-Even et al. 2006; Newman et al. 2006). Wells in which this process resulted in less than 500 cells were discarded from further analysis. For each well, we calculated the mean and noise (σ²/µ^2, variance divided by the mean squared) for both YFP and mCherry. For wells with replicate measurements, the replicate with the lowest noise in YFP was taken for further analysis under the assumption that technical noise may elevate observed noise levels, but not decrease them.

Detection level and technical noise

The detection level of the system was assessed by examining the distribution of promoter activity levels for a strain containing a mCherry gene but no YFP gene. For each condition, more than 30 biological replicates of the strain were measured and fitted to a normal distribution. The 95th percentile of the distribution was taken to be the detection level. The technical error of measurements was estimated by replicate measurements. Technical error did not change between conditions in a systematic manner, as we obtained similar correlations for replicates measured in either fast growth (glucose) or slow growth (ethanol) (Supplemental Fig. S2).

CV² as a function of mean

We applied two strategies to find how CV² levels change with mean expression for each condition. In the first strategy, for each condition, we partitioned the data into 20 equally log-spaced bins, computed the median CV² value for each bin, and performed a linear interpolation of the CV² of each bin using the CV²s of four neighboring bins. This strategy does not make any prior assumptions as to how noise should depend on mean expression (Supplemental Fig. S6). The second strategy (Fig. 1) is model driven. For each condition, we fit the data with a mixture model of two linear curves

$$f(x)=\{\begin{array}{cc}ax+b& \mathrm{if}x<T\\ c& \text{if}x>T\end{array}$$

We used the following exponential noise model to ensure that the lower bound of values will be identified:

$$p(\nu )=\{\begin{array}{cc}0.95e^{-\nu }& \text{if}\nu >0\\ 0.05e^{\nu }& \text{if}\nu <0\end{array}$$

We enumerated over the range of mean expression values T = [10³ 10⁴], and selected the best model by minimizing the log-loss, with 10-fold cross validation.

Model for CV² as a function of cell-cycle stage composition of the population

The following assumptions were made:

1. The population of growing cells is asynchronous: At any given time some cells are in G1 and the rest in G2 (we ignore S for simplicity).

2. Differences in growth rate lead to different compositions of the population at different conditions: Growth rate mainly affects the time spent in G1, such that f, the fraction of the population in G2, increases with increasing growth rate (Tyson et al. 1979).

3. Gene expression in G2 is higher (2× DNA content): In Figure 2, we assume that the average expression of G2 cells is 2× that of G1 cells. However, this assumption can be relaxed, with similar qualitative behavior, as shown in Supplemental Figure S8.

To examine how CV² is affected by changes in growth rate, we use the simplest model in which the cells can take on one of two expression states (relating to G1 and G2).

We define: E_g1 is the expression in G1; E_g2 is the expression in G2; µ_E is the mean population expression; and f is the fraction of cells in G2.

Mean expression is:

$${\mu }_E=f\cdot E_{g2}+(1-f)E_{g1}$$

Variance is:

$${\sigma }^2=f{(E_{g2}-{\mu }_E)}^2+(1-f){(E_{g1}-{\mu }_E)}^2$$

Assuming:

$$E_{g2}=2\cdot E_{g1}$$

We get that:

$${\mathrm{CV}}^2=\frac{{\sigma }^2}{{{\mu }_E}^2}=\frac{f(1-f)}{{(f+1)}^2}.$$ (2)

We note that variability in expression resulting from cell-cycle variability is only dependent on f. The actual expression values disappear from the equation.

Measurements of G1/G2 distributions using HHF1-tagged strains

GFP was fused to the N terminus of endogenous HHF1 using homologous recombination. A 27-nt linker was inserted between the GFP and HHF1 coding sequence. The construction of the eGFP-linker-HHF1 cassettes was performed in two sequential PCR reactions. In the first PCR, GFP was amplified from pKT128 plasmid with a flanking sequence to match the upstream sequence of HHF1 in the Fw primer and a 27-nt linker followed by a matching sequence to HHF1 coding sequence in the Rv primer. The termination codon of the GFP and the start codon of HHF1 were removed in the primers design to create a fused protein. In the second PCR reaction, the left and right homologous arms were elongated to 66 and 47 nt, respectively. BY4741 were transformed with the constructed cassettes using heat-shock LiAc transformation protocol. Positive GFP strains were isolated using Fluorescence-activated cell sorting (FACS).

Primers and linker sequences were the following: linker: ggtcgacggatccccgggttaattaac; first PCR (Fw): 5′-aaaaacaagcaacaaatataatatagtaaaatatgtctaaaggtgaagaattattcactg-3′ and (Rv) 5′-tctaccggagtta attaacccggggatccgtcgacctttgtacaattcatccataccatg-3′; second PCR (Fw): 5′-cattattgtactctatagtactaaagcaacaaacaaaaacaagcaacaaatataatatag-3′ and (Rv) 5′-ttggcaccacctttacctagacctttaccacctttacctctaccggagttaattaacccg-3′.

GFP-HHF1 cells were inoculated from frozen stocks, grown in one of four defined media measured by flow cytometry and analyzed as described above. For each condition, the GFP distribution density (f) was estimated using standard software (ksdensity, MATLAB), and the G1/G2 peaks were identified. We verified by eye that the G2 peak was indeed located at twice the G1 peak. We define three points: (A) G1 GFP peak; (B) minimum point between G1 GFP and G2 GFP peaks; and (C) G2 GFP peak. The G1 ratio was defined as

$$\frac{{\int }_A^{B}g(x)dx}{{\int }_A^{B}g(x)dx+{\int }_B^{C}g(x)dx}$$

and the G2 ratio as

$$\frac{{\int }_B^{C}g(x)dx}{{\int }_A^{B}g(x)dx+{\int }_B^{C}g(x)dx}.$$

Extrinsic variability and cell-cycle model

For each condition, we found the expected CV² according to our model, by assigning to f (Equation 1) the G2 ratio experimentally measured using the histone-tagged strains. Additionally, for each condition, we extract the extrinsic CV² limit from the linear fits to the ungated promoter–reporter measurements as described above (Supplemental Fig. S9). We use ungated data for this analysis because gating artificially decreases the extrinsic noise limit and partially masks the contribution of G1-G2 fractions to extrinsic noise. For each condition, we compute the ratio between the model predictions and the actual extrinsic limit to infer how much of the observed extrinsic variability limit is predicted by our model. We find that without adding any other source of extrinsic noise (C = 0), Equation 1 quantitatively accounts for 45%–60% of the extrinsic variability for each of the examined growth conditions.

The cell-cycle model serves as a lower bound for extrinsic noise, to which other extrinsic factors may add. Therefore, we allow a scaling factor to be added to Equation 2, such that

$${\mathrm{CV}}^2=\frac{{\sigma }^2}{{\mu }_E^2}=\frac{f(1-f)}{{(f+1)}^2}+C.$$ (3)

Since the model represents the lower bound, by definition {C > 0}. Fitting Equation 2 to the data results in C = 0.065.

In silico simulation of wells with different G1/G2 compositions

Flow cytometry measurements of the strain GFP-HHF1 were used to define gates on FSC_A/FSC_W and FSC_A/SSC_A that best separate G1 from G2 cells (Supplemental Fig. S12). For each strain, in each condition, the cells in G1 and in G2 were defined according to this gating. Simulated wells were then generated in silico with a predefined fraction of the population in G2, ranging from 0 to 1. The process was repeated 500 times, and the mean and standard deviation of observed CV² values were extracted and plotted (Supplemental Fig. S13).

Ministat array growth and measurements

Ministat array was constructed as previously described (Miller et al. 2013), allowing for growth of four independent samples in parallel (Supplemental Fig. S11A). The histone–reporter strain GFP-HHF1 and the promoter–reporter strains of the highly expressed RPL28, HHT2, and TDH2 strains were streaked to a YPD plate and then grown for 2 d in histidine limited media. Media were prepared as previously described (Brauer et al. 2008). To choose the limiting concentration of histidine, a preliminary experiment was conducted in which GFP-HHF1 and RPL28 were grown to saturation with histidine concentrations ranging from 1 to 20 mg/L (Supplemental Fig. S11B). The final working histidine concentration was 2 mg/L as previously described (Levy et al. 2007). To obtain very low G2 fractions (Brauer et al. 2008), chemostat was set to a dilution rate of 0.04 h⁻¹, corresponding to a doubling time of ∼17.5 h. The four strains were inoculated simultaneously, and after stabilization of OD (∼24 h), they were examined under the microscope and measured by flow cytometry as described above. Under these conditions, we identified a non-negligible population (15% of the cells) of sub-G1 cells: either enlarged or very small and deformed cells, which did not express GFP/YFP (Supplemental Fig. S11C–F). These cells were removed from further analysis by gating on positive GFP/YFP levels (>10³). The same gating was applied to these strains in all conditions to ensure the fair comparison of noise levels reported in Figure 2C.

Analysis of groups

Information regarding cell-cycle regulation (Spellman et al. 1998), stress (Gasch et al. 2000), TATA (Basehoar et al. 2004), TFIID-SAGA (Huisinga and Pugh 2004), OPN-DPN (Tirosh and Barkai 2008), and differential expression (Keren et al. 2013) was obtained for all promoters in the library.

Data access

Data from this study are available in the Supplemental Material.