Two-Variance-Component Model Improves Genetic Prediction in Family Datasets

Abstract

Genetic prediction based on either identity by state (IBS) sharing or pedigree information has been investigated extensively with best linear unbiased prediction (BLUP) methods. Such methods were pioneered in plant and animal-breeding literature and have since been applied to predict human traits, with the aim of eventual clinical utility. However, methods to combine IBS sharing and pedigree information for genetic prediction in humans have not been explored. We introduce a two-variance-component model for genetic prediction: one component for IBS sharing and one for approximate pedigree structure, both estimated with genetic markers. In simulations using real genotypes from the Candidate-gene Association Resource (CARe) and Framingham Heart Study (FHS) family cohorts, we demonstrate that the two-variance-component model achieves gains in prediction $r^2$ over standard BLUP at current sample sizes, and we project, based on simulations, that these gains will continue to hold at larger sample sizes. Accordingly, in analyses of four quantitative phenotypes from CARe and two quantitative phenotypes from FHS, the two-variance-component model significantly improves prediction $r^2$ in each case, with up to a 20% relative improvement. We also find that standard mixed-model association tests can produce inflated test statistics in datasets with related individuals, whereas the two-variance-component model corrects for inflation.

Introduction

Mixed linear models (MLMs) are widely used for genetic prediction and association testing in genome-wide association studies (GWASs). In prediction, MLMs produce best linear unbiased predictions (BLUPs); BLUP and its extensions were first developed in agricultural genetics^{1, 2, 3, 4} and have since been applied to human genetics.^{5, 6, 7, 8, 9, 10} In association testing, MLMs model relatedness and population stratification, correcting for confounding and increasing power over linear regression (essentially by testing association of the residual from BLUP).^{11, 12, 13, 14, 15, 16} Mixed-model methods harness information from either genetic markers (identity by state [IBS] sharing) or known pedigree relationships. Recent work on the estimation of components of heritability¹⁷ has demonstrated the advantages of a model with two variance components: one component for IBS sharing (corresponding to SNP heritability, $h_g^2$ ^{18, 19}) and one for approximate pedigree structure, estimated via IBS sharing above a threshold (corresponding to total narrow-sense heritability, $h^2$ ²⁰). However, the potential advantages of this model for genetic prediction (or mixed-model association) have not been explored.

Through systematic simulations and analyses of quantitative phenotypes in the Candidate-gene Association Resource (CARe)²¹ and Framingham Heart Study (FHS)^{22, 23} cohorts, we show that the two-variance-component model improves prediction $r^2$ over single-variance-component (standard BLUP) methods. Our simulations demonstrate that this improvement is achieved both at current sample sizes and for larger sample sizes, and our analyses of real CARe and FHS phenotypes confirm relative improvements in prediction $r^2$ of up to 20%. We also consider the situation in which phenotypes are available for ungenotyped individuals who are related to the genotyped cohort (e.g., via family history^{24, 25}) and show that leveraging this additional information for genetic prediction within a two-variance-component model achieves similar gains.

Additionally, we investigate the utility of the two-variance-component model for association testing. We evaluate the standard prospective MLM association statistic¹⁵ in the context of familial relatedness and observe inflation of test statistics over a range of simulation parameters, contrary to previous findings.^{11, 13, 14, 15, 26} We show that the two-variance-component model substantially reduces the inflation in simulations and in GWASs of CARe and FHS phenotypes.

Material and Methods

Overview of Methods

We use the two-variance-component model described in previous work on the estimation of components of heritability.¹⁷ The first variance component is the usual genetic relationship matrix (GRM) computed from genetic markers (corresponding to $h_g^2$).¹⁸ The second variance component is a thresholded version of the GRM in which pairwise relationship estimates smaller than a threshold t are set to zero. The idea is to capture strong relatedness structure, similarly to a pedigree relationship matrix. (If full pedigree information is available, the pedigree relationship matrix can also be used directly.) Explicitly modeling relatedness in this way allows the two-variance-component mixed model to capture additional heritability from untyped SNPs (corresponding to $h^2-h_g^2$).¹⁷ We used the two-variance-component model to compute genetic predictions via BLUP and to compute test association statistics via a Wald test.^{1, 11, 27} (We note that best linear unbiased prediction, BLUP, is a general method for prediction that can be applied once a covariance model has been established, whether from one or many variance components. We will therefore use “standard BLUP” to refer to BLUP with the GRM as a single variance component, and we will use “BLUP” to more generally refer to BLUP with any number of variance components.) We further developed methods to treat the situation in which phenotypes for ungenotyped relatives are available; in brief, our approach uses pedigree information to impute the missing information.²⁸ Full mathematical details are provided below and in the Appendix, and we have released an open source Matlab implementation of these methods (FAMBLUP; see Web Resources).

Standard Mixed Model for Prediction

We begin by establishing notation and reviewing standard formulas for mixed-model prediction (i.e., standard BLUP) and association testing with one variance component.^{1, 11, 27} Let N be the number of individuals in the study and M be the number of genotyped SNPs. Denote phenotypes by y, fixed-effect covariates by X, and normalized genotypes by W, all of which are mean-centered. We normalize each genotype by dividing by $\sqrt{2\hat{p}\left(1-\hat{p}\right)}$, where $\hat{p}$ is the empirical minor allele frequency (MAF).¹⁸ We model phenotypes by using the following mixed model:

$$y=Xb+g+\mathit{ϵ},$$ (Equation 1)

where $g\sim N\left(0,{\text{Σ}}_g\right)$ is a random-effect term modeling genetic effects, $\mathit{ϵ}\sim N\left(0,{\sigma }_e^{2}I\right)$ is a random-effect modeling noise, and b is a vector of coefficients for the fixed effects. In the standard marker-based mixed model, we assume $g=W\alpha$ is a linear combination of genotyped SNPs, where α is an M-vector of independent and identically distributed (iid) normal SNP effect sizes (the infinitesimal model), so that

$$y=Xb+W\alpha +\mathit{ϵ}.$$ (Equation 2)

Then the genetic covariance satisfies ${\text{Σ}}_g={\sigma }_g^{2}W{W}^T/M$, where $W{W}^T/M$ is the GRM and ${\sigma }_g^2$ and ${\sigma }_e^2$ are variance parameters typically estimated via restricted maximum likelihood (REML).²⁹ In pedigree-based models that do not use marker information, ${\text{Σ}}_g={\sigma }_h^2\text{Θ}$, where $\text{Θ}$ is the pedigree relationship matrix, ${\sigma }_h^2$ and ${\sigma }_e^2$ are again estimated via REML.

These models naturally yield formulas for standard BLUP prediction.¹ Explicitly, if we denote training individuals (i.e., those with observed phenotypes) with subscript $-i$ and test individuals (i.e., those with phenotypes to be predicted) with subscript $i$, predictions are given by

$${\hat{y}}_i={\sigma }_g^2{W}_i{W}_{-i}^T{\left({\sigma }_g^2{W}_{-i}{W}_{-i}^T+{\sigma }_e^{2}I\right)}^{-1}\left(y_{-i}-X_{-i}b\right)+X_{i}b.$$ (Equation 3)

Standard Mixed-Model Association Test

To test a candidate SNP (w) for association with the phenotype (y), we augment the marker-based model by including w as an additional fixed-effect covariate:

$$y=w\beta +Xb+W\alpha +\mathit{ϵ},$$ (Equation 4)

where β is the coefficient for the SNP (w) and we wish to test whether $\beta \ne 0$. To do so, we estimate the variance parameters (${\sigma }_g^2$, ${\sigma }_e^2$) by using REML and estimate the fixed-effect coefficients $\left(\beta ,b\right)$ by using maximum likelihood.²⁷ We then compute the Wald statistic to test $\beta \ne 0$ as follows. Let

$$V=\widehat{{\sigma }_g^2}W{W}^T/M+\widehat{{\sigma }_e^2}I$$ (Equation 5)

denote the total phenotypic covariance and let $Q=\left[w;X\right]$ denote the combined fixed effects. Then $\hat{\beta }$ is equal to the first entry of ${\left(Q^T{V}^{-1}Q\right)}^{-1}{Q}^T{V}^{-1}y$ and $\text{var}\left(\hat{\beta }\right)$ is equal to the first entry of ${\left(Q^T{V}^{-1}Q\right)}^{-1}$. The Wald chi-square test statistic is given by

$${\chi }_{\text{Wald}}^2=\frac{{\hat{\beta }}^2}{\text{var}\left(\hat{\beta }\right)}$$ (Equation 6)

and is asymptotically ${\chi }^2$ distributed with 1 degree of freedom (df) under the null distribution. (We note that, theoretically, comparing the square root of Equation 6 to a t distribution is more precise, but in practice, the distinction is negligible at sample sizes of many thousands.)

We make one slight modification to the above association test to avoid proximal contamination (i.e., masking of the association signal by SNPs included in the random-effects term that are in linkage disequilibrium [LD] with the SNP being tested). Specifically, we use a leave-one-chromosome-out procedure in which, when testing SNP w, we exclude all SNPs on the same chromosome as w from the genotype matrix W used to model random genetic effects.^{15, 30, 31}

Two-Variance-Component Mixed Model

Our use of a two-variance-component mixed model is motivated by the idea that in a sample containing related individuals, the pedigree relationship matrix (or an approximation thereof) can model additional heritable variance explained by untyped SNPs.¹⁷ More precisely, consider expanding the marker-based model (Equation 2) to

$$y=Xb+W\alpha +U\gamma +\mathit{ϵ},$$ (Equation 7)

where $U\gamma$ is the analog of $W\alpha$ for untyped SNPs, U, so that the total genetic effect is $g=W\alpha +U\gamma$. Ideally, we would use this model for prediction and its augmentation for association testing, but U is unobserved. Because the BLUP and Wald statistic formulas only require $U{U}^T$, however, we can still improve upon the standard model (Equation 2) by using an approximation of $U{U}^T$. If we let $M_h$ denote the number of untyped SNPs, the matrix $U{U}^T/M_h$ is the realized relationship matrix from untyped SNPs. Assuming a fixed pedigree relationship matrix $\left(\text{Θ}\right)$ we have

$$E\left[U{U}^T/M_h\right]=\text{Θ},$$ (Equation 8)

where the expectation is computed over possible realizations of genotypes passed down by descent (e.g., siblings share half of their genomes on average). When the study samples include close relatives, off-diagonal entries of $\text{Θ}$ can be large, in which case these entries are good approximations of the corresponding entries of $U{U}^T/M_h$ and hold additional information not fully harnessed by models that use only the usual GRM from typed SNPs ($W{W}^T/M$). Substituting $\text{Θ}$ for $U{U}^T/M_h$ gives the model

$$y\sim N\left(Xb,{\sigma }_g^{2}W{W}^T/M+{\sigma }_h^2\text{Θ}+{\sigma }_e^{2}I\right).$$ (Equation 9)

In our case, the pedigree relationship matrix $\left(\text{Θ}\right)$ is also unavailable, so we need to make a further approximation in which we replace $\text{Θ}$ with the estimator

$$\text{Θ}\approx {\left(W{W}^T/M\right)}_{>t},$$ (Equation 10)

obtained from the usual GRM by keeping only those entries larger than a threshold t and setting all other entries to zero.¹⁷ This approximation gives the model

$$y\sim N\left(Xb,{\sigma }_g^{2}W{W}^T/M+{\sigma }_h^2{\left(W{W}^T/M\right)}_{>t}+{\sigma }_e^{2}I\right).$$ (Equation 11)

In theory, the optimal threshold (t) depends on $M,N$, and the amount of relatedness in the dataset, but in our genetic prediction analyses using human datasets, we found that the results were robust to the choice of t, so we set $t=0.05$. For association testing, we found $t=0.05$ to generally be robust (and we expect this choice to be appropriate in human genetics settings), but in more extreme simulation scenarios in which we built the GRM from only a few chromosomes, we observed that higher thresholds were required to model relatedness accurately enough to produce well-calibrated statistics. We therefore optimize t in all association analyses (all of which we conduct by using a leave-one-chromosome-out procedure^{15, 30, 31}) by using the following approach. For each chromosome c in turn, we choose t to minimize the deviation between the thresholded GRM, ${\left(W_{-c}{W}_{-c}^T/M_{-c}\right)}_{>t}$, computed with all chromosomes but c, and the GRM, $W_c{W}_c^T/M_c$, computed on the left-out chromosome c. We measure this deviation with the Frobenius norm

$$\Vert W_c{W}_c^T/M_c-{\left(W_{-c}{W}_{-c}^T/M_{-c}\right)}_{>t}{\Vert }_2^2,$$ (Equation 12)

i.e., the sum of squared differences between matrix entries. Prediction and association testing proceed as before, once the threshold (t) has been set: we estimate ${\sigma }_g^2,{\sigma }_h^2,$ and ${\sigma }_e^2$ by REML to enable calculation of BLUP predictions, and for association testing, we again introduce an additional fixed-effect term, $w\beta$, for the SNP being tested and construct a Wald statistic. (Again, for computational efficiency, we apply a leave-one-chromosome-out procedure within which we reuse variance parameters fitted once per left-out chromosome.^{13, 15, 16}) We note that the computation of predictions, $\hat{y}$, can no longer be expressed as a simple matrix-vector product of genotypes with a vector $\left(\hat{\beta }\right)$ of SNP weights, as is the case for standard (one-variance-component) genomic BLUP. Instead, the formula for $\hat{y}$ (given in the Appendix) involves two terms, only one of which has the above form; the other involves combining training and testing genotypes and has substantially greater computational cost $\left(O\left(N^3\right)\right)$. Although performing prediction with the first term alone would be computationally efficient, we found that such an approach yields suboptimal results; see the Appendix for details.

We have released Matlab code that implements these methods in a stand-alone software package, FAMBLUP (see Web Resources). Although our implementation uses standard $O\left(N^3\right)$-time eigendecomposition-based variance components methods, we have taken care to optimize its central processing unit (CPU) and memory use: for example, FAMBLUP association analysis of N = 20,000 samples requires $\approx$ 16 GB RAM and $\approx$ 1 single-threaded CPU day per chromosome. Memory usage scales with $N^2$, and computation time scales with $N^3$, so for N = 30,000 samples, the requirements are $\approx$ 36 GB RAM and $\approx$ 4 CPU days per chromosome. These computations are automatically multithreaded on multi-core machines and can be parallelized across chromosomes.

Extension to Ungenotyped Individuals

In the Appendix, we derive extensions of two-variance-component mixed-model prediction and association testing to make use of data available from additional phenotyped but ungenotyped relatives of genotyped individuals. In this setup, we assume that the full pedigree relationship matrix (containing both typed and untyped individuals) is known, whereas some entries of the SNP GRM—namely, those in rows or columns corresponding to untyped individuals—are unknown. Our procedure amounts to replacing the unobserved GRM with the expected GRM (based on known pedigree),^{32, 33, 34} similar in spirit to regression imputation; mathematical derivations are presented in the Appendix.

CARe and FHS Datasets

We analyzed 8,367 African-American CARe samples from the ARIC, CARDIA, CFS, JHS, and MESA cohorts, comprising high-quality genotypes at 770,390 SNPs from an Affymetrix 6.0 array; the CARe dataset and quality-control procedures used to obtain the sample and SNP sets we analyzed are described in Lettre et al. and Pasaniuc et al.^{21, 35} We analyzed all samples in analyses of simulated phenotypes (for which real genotypes were used); in analyses of real CARe phenotypes—including BMI, height, high density lipoprotein cholesterol (HDL), and low density lipoprotein cholesterol (LDL), each available for 5,000–8,000 samples—we removed outlier individuals with phenotype values in the top or bottom 0.1%, individuals younger than 18 years old, and individuals with missing age or sex, given that regression results can be quite sensitive to outliers; we then applied a Box-Cox transformation to remove skewness. We analyzed 7,476 FHS SHARe samples with high-quality genotypes at 413,943 SNPs from an Affymetrix 500K array and with BMI and height phenotypes available; the FHS dataset and quality-control procedures are described in Dawber et al., Splansky et al., and Chen et al.^{22, 23, 36} Our analyses were performed under the oversight of the Harvard institutional review board.

Genetic Prediction: Simulations with Real Genotypes

To assess the accuracy of genetic prediction methods, we simulated phenotypes based on genotypes from the CARe and FHS datasets; both CARe and FHS are family studies containing many close relatives. Because the CARe individuals are admixed, we projected out the first five principal components (equivalent to including them as fixed-effect covariates²⁹) from genotypes and phenotypes in all analyses of both CARe and FHS data to avoid confounding from population structure.³⁷ We simulated phenotypes by generating causal effects for two subsets of SNPs: a set of M “observed SNPs,” which we used for both phenotype simulation and BLUP prediction, and a set of $M_h$ “untyped SNPs,” which we used for phenotype simulation but did not provide to prediction methods. In this simulation framework, the standard GRM built by MLM methods accurately models variation due to observed SNPs, but direct or inferred pedigree information is necessary to capture variation due to untyped SNPs. We generated effect sizes for observed and untyped SNPs from independent normal distributions $N\left(0,h_g^2/M\right)$ and $N\left(0,\left(h^2-h_g^2\right)/M_h\right)$, respectively, where $h_g^2$ denotes heritability explained by observed SNPs and $h^2$ denotes total narrow-sense heritability. To build phenotypes, we multiplied the simulated effect sizes with the genotypes and added random noise from $N\left(0,\left(1-h^2\right)\right)$. We used SNPs on chromosome 1 as untyped SNPs and SNPs on varying subsets of chromosomes 2–22 as observed SNPs so as to simulate different values of $N/M$ (which is a key quantity affecting performance of mixed-model prediction³⁸ and association¹⁵) and thereby estimate projected performance at larger N. We used $h_g^2=0.25$ and $h^2=0.5$ as typical values of these parameters.³⁹

We note that under the above setup, untyped SNPs are completely untagged by typed SNPs, whereas in real data, untyped SNPs might be partially tagged by typed SNPs. In either case, the phenotype can be written as a sum of “genetic value explained by typed SNPs,” “remaining genetic value,” and “environmental value” (with variance parameters $h_g^2$, $h^2-h_g^2$, and $1-h^2$ corresponding to the same covariance structures in either case), so we expected that our results would be insensitive to this distinction. To verify this expectation, we also performed a set of simulations in which we selected the set of observed SNPs to be the 90% of SNPs with highest MAF and the set of untyped SNPs to be the 10% of SNPs with lowest MAF—similar to the simulation framework of Yang et al.¹⁸—to produce a realistic gap between $h_g^2$ and $h^2$ as a result of untyped rare variants. (The MAF cutoff corresponding to this split was 5.4%.)

Genetic Prediction: Simulations with Simulated Genotypes

To assess the potential performance of genetic prediction methods at extremely large sample sizes, we also simulated genotypes for sets of sib-pairs (relatedness = 0.5) with M = 100 SNPs and $N/M$ = 10,20,…,100. We generated unlinked markers for simplicity by randomly generating MAFs uniformly in the interval $\left[0.05,0.5\right]$ and sampling genotypes of unrelated individuals from a binomial distribution with the generated MAF. For sib-pairs, with probability 0.5, the pair shared an allele drawn randomly; otherwise, the alleles for the pair were drawn independently. (We ran this procedure twice per SNP to create diploid genotypes.) We simulated phenotypes as above.

Genetic Prediction: Assessing Performance on Real Phenotypes

To compare the predictive performance of the two-variance-component model versus standard BLUP on real phenotypes, we performed cross-validation studies in which we repeatedly selected 10% of the phenotyped samples (from either CARe or FHS) as test data and used the remaining 90% of samples to train each predictor. For each training/test split (s) we thus obtained a pair of observed prediction $r^2$ values $\left(r_{2\text{VC},s}^2,r_{\text{BLUP},s}^2\right)$. We then estimated the improvement of the two-variance-component model over standard BLUP as

$$\widehat{r_{2\text{VC}}^2-r_{\text{BLUP}}^2}=\text{mean}\left(r_{2\text{VC},s}^2-r_{\text{BLUP},s}^2\right),$$ (Equation 13)

where the mean is taken over the random splits (s). We estimated the SE of this quantity as:

$$\text{SE}\left(\widehat{r_{2\text{VC}}^2-r_{\text{BLUP}}^2}\right)\approx \text{SD}\left(r_{2\text{VC},s}^2-r_{\text{BLUP},s}^2\right)/\sqrt{10}.$$ (Equation 14)

The numerator is the SD of the per-split differences in $r^2$ (across random 90% training and 10% test set splits [s]), which measures the variability in observed performance differences between the two methods when assessed on 10% of the data. The division by $\sqrt{10}$ accounts for the 10× larger sample size of the full dataset. This estimate is approximate due to the complexities of estimating variance under cross-validation (specifically, the overlap among different test sets and among different training sets); in general, unbiased estimators of variance under cross-validation do not exist.⁴⁰

Finally, in the Results section, we estimate relative improvements and SEs (i.e., we divide Equations (Equation 13), (Equation 14) by the estimated baseline, $\text{mean}\left(r_{\text{BLUP},s}^2\right)$) to put our absolute estimates in context.

Association Testing: Simulations with Simulated Genotypes

We conducted a suite of mixed-model association simulations by using genotypes simulated in a similar manner as above. We systematically varied the number of related individuals, the degree of relatedness, the number of markers (M) in the genome, and the SNP heritability $\left(h_g^2\right)$ and total heritability $\left(h^2\right)$ of the simulated trait. Specifically, we simulated sets of N = 1,000 diploid individuals, in which $N_{\text{rel}}$ = 50, 125, 250, or 500 pairs of individuals who were related (leaving 900, 750, 500, or 0 unrelated individuals, respectively). Each pair of individuals shared a proportion, namely p = 0, 0.1, 0.2, 0.3, 0.4, or 0.5, of their genomes in expectation. Additionally, we varied the number of markers, using M = 1,000, 5,000, 10,000, or 20,000. We generated unlinked markers as above; for pairs of related individuals, with probability equal to the relatedness (p), the pair shared an allele drawn randomly; otherwise, the alleles for the pair were drawn independently. (As above, we ran this procedure twice per SNP to create diploid genotypes.) We also generated 100 additional candidate causal SNPs and 500 candidate null SNPs (at which to compute association test statistics) in the same way. We used an infinitesimal model to generate the phenotype: that is, we generated effect sizes for the observed SNPs from $N\left(0,h_g^2/M\right)$. We also generated effect sizes for the candidate causal SNPs from $N\left(0,\left(h^2-h_g^2\right)/100\right)$. Because these SNPs are distinct from the M SNPs used for model building, they effectively served as untyped causal loci. Finally, we formed the phenotype by multiplying the effect sizes with the genotypes and adding independent noise distributed as $N\left(0,\left(1-h^2\right)I\right)$.

Association Testing: Simulations with Real Genotypes

We also assessed mixed-model association methods in simulation studies by using simulated phenotypes based on genotypes from the CARe and FHS datasets. To avoid proximal contamination,^{15, 30, 31} we tested SNPs on chromosomes 1 and 2 for association and used M observed SNPs on subsets of chromosomes 3–22 to compute GRMs, varying the number of chromosomes used in order to vary $N/M$. We generated quantitative phenotypes in which observed SNPs collectively explained 25% of variance and 250 causal SNPs from chromosome 1 explained another 25% of variance; all SNPs on chromosome 2 were null SNPs.

Results

Genetic Prediction: Simulations

To analyze the predictive power of the two-variance-component model, we simulated phenotypes based on genotypes from the CARe and FHS datasets as described in Material and Methods. In each simulation, we used the following procedure to measure the prediction accuracies of BLUP with the standard GRM as a single variance component, BLUP with the thresholded GRM as a single variance component, and BLUP with the two-variance-component model. First, we simulated phenotypes for all individuals (independently for each simulation replicate). Second, we randomly split the dataset, setting aside 90% of the individuals for training and 10% for testing. We then used each BLUP method to predict held-out test phenotypes by using the training samples to estimate genetic effects, and we calculated $r^2$ between the predicted phenotypes and the true genetic components of the simulated phenotypes (i.e., eliminating the added noise) on the test samples. (We chose to compute $r^2$ because it is a very widely used metric for assessing prediction accuracy;^{2, 3, 4, 6, 7, 9} however, other metrics such as mean square error are also sometimes used.⁵) We call this quantity “prediction $r^2\left(g\right)$”; on average, prediction $r^2\left(g\right)$ is $1/h^2$ times as large as standard prediction $r^2$, i.e., $r^2$ computed to simulated phenotypes that include both genetic and noise components. Relative performance of prediction methods is the same (on average) whether measured with prediction $r^2$ or prediction $r^2\left(g\right)$.

The two-variance-component model provided significant increases in $r^2\left(g\right)$ over both standard BLUP and BLUP using the thresholded GRM alone (Table 1), and the improvements were consistent across simulation replicates (Figure S1). We observed much larger prediction $r^2\left(g\right)$ values (across all methods) for the FHS simulations than for the CARe simulations, as expected given the much greater number of close relatives in the FHS dataset (18,415 pairs of individuals with genetic relatedness $>$ 0.2 among 7,476 FHS individuals versus 4,954 pairs among 8,367 CARe individuals). However, the relative improvements achieved by the two-variance-component model were fairly similar in these two distinct pedigree structures, and importantly, increasing values of $N/M$ (mimicking larger sample sizes) also yielded similar relative improvements (Table 1). We also observed that the heritability parameter estimated by the standard mixed model was intermediate to $h_g^2$ and $h^2$, whereas the two-variance-component model accurately estimated $h_g^2$ and $h^2-h_g^2$ (Table S1), as expected in samples with related individuals.¹⁷ (We note that because the sum of the entries of the thresholded GRM is nonzero, we used the general formula given in Speed et al.⁴¹ to estimate heritability parameters.) We also verified that in simulations with no untyped causal SNPs, the two-variance-component model produced no improvement over standard BLUP, indicating that our cross-validation scheme was immune to differences in model complexity (Table S2). Finally, we verified that simulations involving linkage disequilbrium between typed and untyped SNPs (achieved by setting typed SNPs to be the 90% of SNPs with highest MAF and untyped SNPs to be the 10% of SNPs with lowest MAF) produced similar results (Table S3). In these simulations, we also varied the fraction of heritability explained by typed versus untyped SNPs, and we observed that the two-variance-component model achieved larger gains for $h_g^2\ll h^2$ and smaller gains for $h_g^2$ approaching $h^2$ (Table S3), consistent with our intuition that, if typed SNPs explain most of heritable variance, prediction using only typed SNPs achieves most of the available predictive power.

Table 1.

Prediction Accuracy for Simulations Using CARe and FHS Genotypes

Observed SNPs	Prediction$r^2\left(g\right)$
BLUP	BLUP w/ Thresh.	2VC BLUP
CARe genotypes
chr 2–22	0.062 (0.002)	0.061 (0.002)	0.071 (0.002)
chr 3–6	0.084 (0.002)	0.063 (0.002)	0.094 (0.002)
chr 3–4	0.098 (0.002)	0.059 (0.002)	0.108 (0.002)
FHS genotypes
chr 2–22	0.225 (0.003)	0.225 (0.003)	0.238 (0.003)
chr 3–6	0.246 (0.003)	0.230 (0.003)	0.269 (0.003)
chr 3–4	0.263 (0.003)	0.231 (0.003)	0.291 (0.003)

Phenotypes were simulated to have $h^2=0.5$ and $h_g^2=0.25$, and we measured prediction $r^2\left(g\right)$ by using a random 90% of samples as training data and the remaining 10% as test data. Reported values are mean prediction $r^2\left(g\right)$ and SEM over 100 independent simulations (in which phenotypes were re-simulated and training-test splits resampled). “BLUP w/ Thresh.” denotes BLUP prediction using the thresholded relationship matrix instead of the standard approach of using the GRM (denoted simply as “BLUP”). “2VC BLUP” denotes two-variance-component BLUP. “Prediction $r^2\left(g\right)$” denotes $r^2$ between predicted phenotypes and true genetic components of the simulated phenotypes.

We further assessed the potential performance of the two-variance-component approach at very large values of $N/M$ (up to 100) by simulating both genotypes and phenotypes (Material and Methods). (We note that human genotyping arrays typically contain $\approx$ 60,000 independent SNPs,^{15, 42} so $N/M$ = 8 in this simulation corresponds to a dataset the size of UK Biobank, N = 500,000; see Web Resources.) In these simulations, we continued to observe gains when using the two-variance-component approach; two-variance-component prediction $r^2$ exceeded $h_g^2$ for very large N, whereas standard BLUP prediction $r^2$ was limited to less than $h_g^2$ (Figure S2).

Genetic Prediction: Real Phenotypes

Next, we evaluated the prediction accuracy of each method on CARe phenotypes—BMI, height, LDL, and HDL—and on FHS phenotypes—height and BMI. We adjusted phenotypes for age, sex, study center (for CARe phenotypes), and the top five principal components. (The complexities of the impact of ancestry on genetic prediction are discussed in Chen et al.⁴³) To measure performance, we created 100 independent random 90%/10% splits of the dataset, as before, and calculated $r^2$ between predicted and true phenotypes on the test samples of each split. We observed that, for all phenotypes, the two-variance-component model increased prediction accuracy over both single-variance-component BLUP approaches, with a maximum relative improvement of 20% for height (Table 2); this improvement was consistent across different training/test splits (Figure S4). We observed no significant difference between the performance of the the two single-variance-component BLUP approaches (Table 2). As in our simulations, we observed a larger absolute prediction $r^2$ in FHS than in CARe, due to strong relatedness (consistent with de los Campos et al.⁶), and we observed that the heritability parameter estimated by the standard mixed model was intermediate to the heritability parameters ${\hat{h}}_g^2$ and ${\hat{h}}^2$ estimated by the two-variance-component model (Table S4). We verified in the CARe data that evaluating prediction accuracy by using the mean square error metric produced near-identical results (Table S5).

Table 2.

Prediction Accuracy for CARe and FHS Phenotypes

Phenotype	Prediction$r^2$			Prediction$r^2$Relative to BLUP (SE)
BLUP	BLUP w/ Thresh.	2VC BLUP	BLUP w/ Thresh.	2VC BLUP
CARe prediction
BMI	0.023	0.027	0.029	+14% (9%)	+18% (5%)
height	0.063	0.067	0.079	+5% (5%)	+20% (3%)
LDL	0.017	0.017	0.019	+2% (15%)	+11% (5%)
HDL	0.034	0.032	0.038	−7% (10%)	+11% (4%)
FHS prediction
BMI	0.103	0.104	0.107	+1.0% (2.3%)	+3.5% (1.2%)
height	0.344	0.342	0.354	−0.7% (1.1%)	+2.9% (0.5%)
CARe prediction with genome-wide significant SNPs as fixed-effect covariates
BMI	0.023	0.026	0.028	+14% (9%)	+19% (5%)
height	0.063	0.066	0.078	+5% (5%)	+20% (3%)
LDL	0.038	0.039	0.041	+3% (6%)	+6% (2%)
HDL	0.051	0.049	0.055	−4% (6%)	+7% (3%)
FHS prediction with genome-wide significant SNPs as fixed-effect covariates
BMI	0.105	0.107	0.109	+1.2% (2.3%)	+3.5% (1.2%)
height	0.344	0.341	0.354	−0.8% (1.1%)	+2.8% (0.5%)

Prediction $r^2$ values are means over 100 random 90% training and 10% test data splits. Relative performance values reported are ratios of means minus 1; SEs are estimated as SDs of per-split differences in $r^2$ (over the random 10% test sets) divided by $\sqrt{10}$ (to account for the 10× larger sample size of the full dataset; see Material and Methods). “BLUP w/ Thresh.” denotes BLUP prediction using the thresholded relationship matrix instead of the standard approach of using the GRM (denoted simply as “BLUP”). “2VC BLUP” denotes two-variance-component BLUP.

For phenotypes with a small number of large-effect loci, methods that explicitly model a non-infinitesimal genetic architecture can have substantially better prediction accuracy than standard BLUP.² A two-variance-component approach could be combined with such models, and as an initial exploration of this approach, we examined a non-infinitesimal extension of two-variance-component BLUP in which we included large-effect loci as fixed-effect covariates.⁸ Explicitly, we first identified genome-wide significant SNPs $\left(p<5\times {10}^{-8}\right)$ according to a two-variance-component mixed-model association statistic. (As we show below, the standard MLM statistic is miscalibrated in scenarios with pervasive relatedness, precluding its use.) We then added these SNPs as fixed-effect covariates in all of the models we previously compared and recomputed predictions (Table 2). Including large-effect loci resulted in substantial improvements in prediction $r^2$ achieved by each model for the CARe HDL and LDL phenotypes (Table 2), both of which are known to have several large-effect loci.⁴⁴ As before, for all phenotypes, we observed an increase in $r^2$ when using the two-variance-component model. We expect that the two-variance-component model will provide similar improvements in prediction $r^2$ if incorporated in more sophisticated non-infinitesimal models (e.g., Erbe et al. and Zhou et al. ^{3, 5}).

Additionally, we explored the scenario in which some phenotypes are available for ungenotyped relatives of genotyped individuals. We simulated data with ungenotyped individuals by randomly masking the genotypes of 25% of the training individuals. Results on simulated and real phenotypes when using this masking were broadly consistent with the results reported above in which all individuals were typed (Tables S6–S9).

Association Testing

We next compared mixed-model association testing using the two-variance-component approach to standard MLM association testing^{12, 15} in datasets with related individuals, measuring calibration and power for each method. We began by running a suite of tests using simulated genotypes and phenotypes, systematically varying the number of related individuals, the degree of relatedness, the number of markers in the genome, and the heritability of the simulated trait (see Material and Methods). Each simulation included both causal SNPs and “null SNPs,” i.e., SNPs with no phenotypic effect. For null SNPs, Wald statistics computed by mixed-model association tests follow a 1 df chi-square distribution, under the assumption that the mixed model accurately models the phenotypic covariance. If the mixed model does not accurately model the covariance, as we expect for phenotypes with $h_g^2<h^2$ in datasets containing relatedness, then the distribution of association statistics at null SNPs is miscalibrated, i.e., approximately follows a scaled 1 df chi-square.⁴⁵ We therefore measured calibration of MLM association methods by computing the mean Wald statistic over null SNPs. We measured power by dividing the mean Wald statistic over causal SNPs by the mean Wald statistic over null SNPs. Computing the ratio in the latter benchmark ensured that all methods, including those susceptible to inflation of test statistics, were equally calibrated before we compared power.

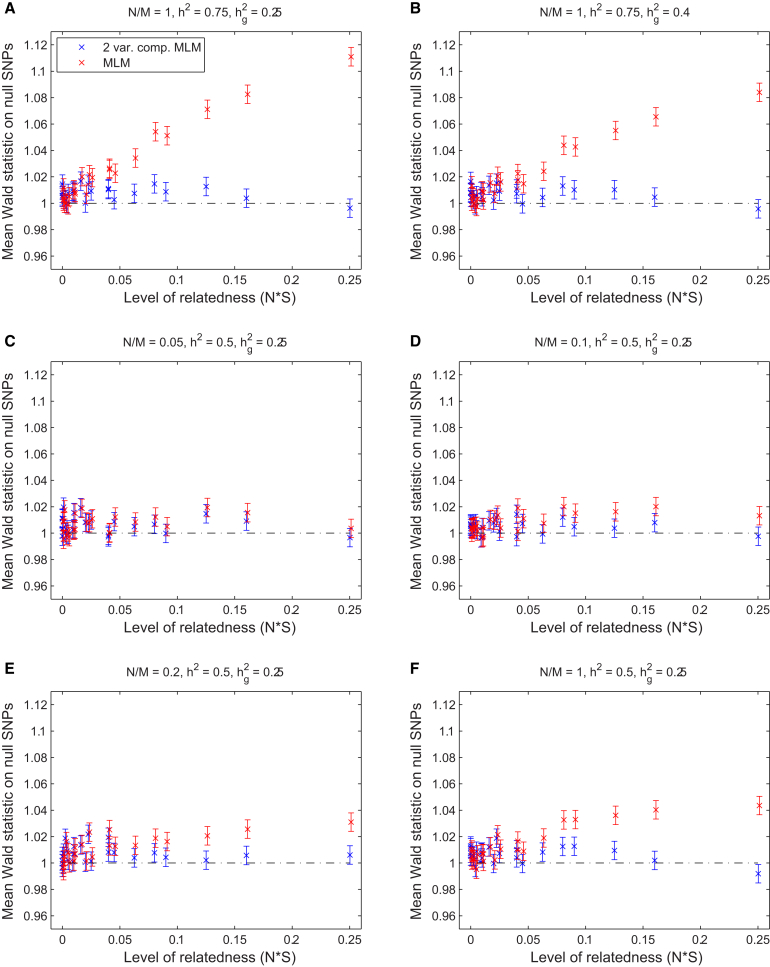
Contrary to previous work suggesting that mixed models fully correct for relatedness,^{11, 13, 14, 15, 26} we found that for many parameter settings, standard MLM association analysis produced significantly inflated test statistics (up to 11% inflation, increasing with trait heritability, sample size, and extent of relatedness; Figure 1). In contrast, introducing a second variance component—either the thresholded GRM (Figure 1) or the true pedigree (Figure S4)—nearly eliminated the inflation. For all parameter settings, we observed that, compared to standard MLM association, the two-variance-component model maintained or slightly increased power (Figure S4).

Figure 1.

Calibration of Standard and Two-Variance-Component Mixed-Model Association Statistics on Simulated Genotypes and Phenotypes

We computed mean Wald statistics over null SNPs by using the standard mixed-model association test (MLM) and a two-variance-component model (2 var. comp. MLM) using GRM and thresholded GRM (i.e., approximate pedigree) components. Each panel shows results from a set of simulations with selected values of the simulation parameters $N/M$, $h^2$, and $h_g^2$. The set of simulations contained within each panel varies one additional parameter, $NS$, which measures the amount of relatedness in the simulated data. (S denotes the average squared off-diagonal entry of the pedigree relationship matrix.) Plotted values are mean Wald statistics and SEM over 100 simulations.

Next, we simulated phenotypes based on genotypes from the CARe and FHS datasets (Material and Methods). Consistent with the previous simulations, standard MLM association produced inflated statistics (as measured in test statistics from chromosome 2, simulated to contain no causal SNPs) whereas the two-variance-component model alleviated inflation (Table 3; also see type I errors in Table S10). Importantly, these results suggest that the levels of relatedness that are required for inflation are present in real datasets.

Table 3.

Calibration of Standard and Two-Variance-Component Mixed-Model Association Statistics in CARe and FHS Simulations

Observed SNPs	No. of SNPs (M)	Standard Mixed Model	Two Variance Components
Mean Wald	Mean Wald	Threshold (t)
CARe genotypes
chr 3–22	615,445	1.013 (0.002)	1.000 (0.002)	0.024
chr 3–6	195,333	1.024 (0.002)	1.002 (0.002)	0.051
chr 3–4	99,690	1.028 (0.002)	1.003 (0.002)	0.081
chr 22	9,713	1.036 (0.002)	1.014 (0.002)	0.387
FHS genotypes
chr 3–22	346,005	1.032 (0.003)	1.003 (0.003)	0.021
chr 3–6	110,203	1.071 (0.003)	1.008 (0.003)	0.040
chr 3–4	55,480	1.097 (0.003)	1.014 (0.003)	0.055
chr 22	5,277	1.189 (0.004)	1.055 (0.003)	0.258

Mean Wald statistics on candidate null SNPs for simulations with CARe or FHS genotypes and a trait with $h^2=0.5,h_g^2=0.25$. Reported values are means and SEM over 100 simulations. The two-variance-component model selected the specified threshold (t) to estimate the relatedness matrix. In simulations using only SNPs on chromosome 22 to compute GRMs, we observed slight inflation when using the two-variance-component model; given the large thresholds $\left(t>0.25\right)$ chosen by the model in these scenarios, we hypothesize that the number of SNPs was too small to distinguish relatedness from noise in the GRM, causing an incomplete correction. For corresponding type I error at different α levels, see Table S10.

Finally, we analyzed MLM association statistics for the CARe and FHS phenotypes (adjusted for covariates as before). Because we do not know the identity of causal and null SNPs in this case, we calculated the average Wald statistic over all SNPs by using leave-one-chromosome-out analysis,^{15, 30} noting that we expected the statistics to be slightly larger than 1 due to polygenicity.^{15, 42} Consistent with simulations, the average Wald statistics were higher for standard MLM association than for the two-variance-component method, suggesting that standard MLM statistics are slightly inflated, with an up to 1.05-fold inflation in FHS data (Table 4). Analysis of genomic inflation factors ${\lambda }_{GC}$⁴⁶ corroborated these results (Table 4). We also compared our test statistics (which involve approximations, as in previous work^{13, 15, 16}; see Material and Methods) to exact likelihood ratio test statistics under the two-variance-component model and verified that the approximate versus exact statistics were near identical ($r^2$ = 0.999997; Figure S5).

Table 4.

Calibration of Standard and Two-Variance-Component Mixed-Model Association Statistics for CARe and FHS Phenotypes

Phenotype	N	Standard Mixed Model			Two Variance Components
Mean Wald	${\lambda }_{\text{GC}}$	${\hat{h}}_g^2$	Mean Wald	${\lambda }_{\text{GC}}$	${\hat{h}}_g^2$	${\hat{h}}^2$
CARe phenotypes
BMI	7,987	1.044	1.044	0.35	1.029	1.027	0.17	0.46
height	7,988	1.110	1.099	0.73	1.080	1.070	0.38	0.95
LDL	4,965	1.030	1.026	0.32	1.021	1.017	0.18	0.44
HDL	5,184	1.054	1.046	0.50	1.037	1.028	0.26	0.66
FHS phenotypes
BMI	7,476	1.060	1.058	0.43	1.032	1.032	0.21	0.47
height	7,476	1.126	1.112	0.81	1.070	1.058	0.39	0.87

We report the number of individuals (N) phenotyped for each trait and the mean Wald statistics and heritability parameters computed by the standard and two-variance-component mixed models (averaged over 22 leave-one-chromosome-out runs).

Discussion

We have shown that a mixed model with two variance components, one modeling genetic effects of typed SNPs and the other modeling phenotypic covariance from close relatives, offers increased prediction accuracy over standard BLUP and corrects miscalibration of standard mixed-model association analysis in human datasets containing strong relatedness. For current sample sizes and levels of relatedness, the absolute increase in prediction accuracy is modest (similar to other recent work on improving prediction accuracy for human complex traits,^{5, 7, 8, 9, 10} in contrast to agricultural traits^{2, 3, 4}) and the inflation of standard mixed-model test statistics is small. However, our simulations suggest that, for larger sample sizes, the effects of relatedness will become more pronounced, so we expect the two-variance-component model to become increasingly relevant as sample sizes increase.

Although we are not aware of prior work in human genetics that involves using two variance components to model effects of typed SNPs as well as additional phenotypic covariance from close relatives, other methods for combining these two sources of information for prediction have been proposed; however, these methods either use only a limited number of genome-wide significant SNPs²⁴ or use only limited information about family history.²⁵ Separately, several studies have applied different multiple-variance-component models to improve mixed-model prediction and association in other ways. Widmer et al.²⁶ recently proposed a two-variance-component model that uses the standard GRM along with a GRM created from selected SNPs (as in FaST-LMM-Select³¹) that improves association power and calibration in family studies. (We note that, although Widmer et al. observe that standard mixed-model association is properly calibrated in their simulated family datasets, their simulations do not include untyped causal SNPs.) In another direction, Speed et al.⁷ recently proposed a multiple variance component model that partitions SNPs into contiguous blocks, each used in a distinct variance component, and showed that this approach improves prediction accuracy. Incorporation of a variance component modeling relatedness—either from pedigree, thresholding the GRM, or other approaches⁴⁷—into these methods or into recently proposed non-infinitesimal models for genetic prediction (e.g., weighted G-BLUP,⁶ BayesR,^{3, 10} or BSLMM⁵) is a possible direction for future research.

A challenge facing all genetic prediction methods is the very large sample sizes that will be required to achieve clinically relevant prediction accuracy.^{25, 48} Indeed, in absolute terms, the prediction accuracy we achieved on real datasets of up to 8,000 samples was low, similar to other methods when applied to traits without large-effect loci.^{5, 6, 10} Our simulations show that the two-variance-component approach we have proposed will maintain its relative improvement over standard BLUP as sample sizes increase; however, both of these methods face computational barriers at large N. (Standard BLUP does have the advantage that $O\left(N^3\right)$-time computation is required only for fitting the model but not for computing predictions on new samples; in contrast, a straightforward implementation of our two-variance-component method for prediction requires $O\left(N^3\right)$ time per REML iteration when estimating variance parameters as well as when computing predictions, a consequence of the need to combine training and target genotypes.) These limitations could potentially be overcome by using a combination of rapid relationship inference,⁴⁹ fast multiple-variance-component analysis (e.g., as implemented in BOLT-REML⁵⁰), and iterative solution of the mixed-model equations.^{51, 52} Similarly, the computational challenge of large-scale two-variance-component association analysis could potentially be addressed by extending fast iterative methods for mixed-model association.¹⁶ An alternative, computationally simple solution to inflation of association-test statistics is LD score regression;⁵³ however, this approach might incur slight deflation as a result of attenuation bias.^{16, 53}

We also note four additional limitations of our two-variance-component approach. First, the method is only applicable to datasets with related individuals for which genotypes are available for analysis; however, large human datasets of this type are now being generated: deCODE Genetics has genotyped >30% of the Icelandic population,⁵⁴ the UK Biobank will soon have genotypes for N = 500,000 individuals (close to 1% of the UK population; see Web Resources), and 23andMe has assembled an even larger cohort.⁵⁵ Second, the improved predictive performance of the two-variance-component approach is a function of the relatedness structure. Our parallel work in cattle has reported improved prediction accuracy when using a two-variance-component model incorporating exact pedigree information⁵⁶ or breed information;⁵⁷ however, the two-variance-component model did not produce an improvement in analyses of Holstein dairy cattle (Table S11), perhaps because of the very small effective population size of this breed.⁵⁸ Third, although the intuition behind the two-variance-component model is to capture effects of rare variants not tagged by SNP arrays, our observed gains in prediction accuracy could also be partially explained by the approximate pedigree component picking up shared environment or epistasis; as such, care is needed in interpreting fitted variance parameters as heritability estimates.¹⁷ Fourth, our approach does not address case-control ascertainment. Although many large family datasets are not ascertained for phenotype, investigating whether techniques employed by methods that do model ascertainment⁸ can be integrated into our two-variance-component approach is a possible avenue for future work.

Published: November 5, 2015

Appendix A

Formulas for Two-Variance-Component Mixed-Model Prediction

Here, we provide explicit formulas for computing best linear unbiased predictions under the two-variance-component model

$$y\sim N\left(0,W{W}^T{\sigma }_g^2/M+{\left(W{W}^T/M\right)}_{>t}{\sigma }_h^2+I{\sigma }_e^2\right),$$

combining Equation 9 with the approximation of pedigree by using thresholded IBS, Equation 10, and leaving out fixed effects for simplicity. We assume that we have a set of training individuals (denoted with subscript − i) for whom we have both genotype and phenotype information and that we have a set of testing individuals (denoted with subscript i) for whom we have only genotype information and wish to predict phenotypes. Thus, under this notation, $W_i$ denotes the submatrix of genotypes from testing individuals and $W_{-i}$ denotes the submatrix of genotypes from training individuals.

Under the assumption that the variance parameters ${\sigma }_g^2,{\sigma }_h^2,$ and ${\sigma }_e^2$ have already been fitted (e.g., by using REML on the training individuals), the BLUP predictions for the test phenotypes are given by

$${\hat{y}}_i=W_i\hat{\beta }+{\sigma }_h^2{\left(W_i{W}_{-i}^T/M\right)}_{>t}{\left(W_{-i}{W}_{-i}^T{\sigma }_g^2/M+{\left(W_{-i}{W}_{-i}^T/M\right)}_{>t}{\sigma }_h^2+I{\sigma }_e^2\right)}^{-1}{y}_{-i},$$

where

$$\hat{\beta }={\sigma }_g^2{W}_i^T{\left(W_{-i}{W}_{-i}^T{\sigma }_g^2/M+{\left(W_{-i}{W}_{-i}^T/M\right)}_{>t}{\sigma }_h^2+I{\sigma }_e^2\right)}^{-1}{y}_{-i}.$$

We note that the first term of the formula for ${\hat{y}}_i$, namely $W_i\hat{\beta }$, has the form of a simple matrix-vector product between genotypes of testing individuals and a vector $\left(\hat{\beta }\right)$ of SNP weights, as is the case for standard (one-variance-component) genomic BLUP. This term is easy to compute on testing individuals once we have estimated $\hat{\beta }$ by using the training data, whereas the second term of the prediction formula requires more computation.

This observation suggests the possibility of performing prediction by using only the first term as a computationally efficient alternative to carrying out the full two-variance-component computation. We tested the performance of this approach on the CARe height phenotype but found no significant difference in its performance versus that of standard BLUP: –1% (SE 3%) change in prediction $r^2$, in contrast to the +20% (SE 3%) change in prediction $r^2$ of the full two-variance-component approach over standard BLUP (Table 2). This observation indicates that the gain in prediction accuracy achieved by the two-variance-component model is largely a result of capturing effects of rare variants and requires the use of both variance components.

Two-Variance-Component Mixed Model with Ungenotyped Individuals

Here, we derive extensions of two-variance-component mixed-model prediction and association testing to make use of data available from additional phenotyped but ungenotyped relatives of genotyped individuals. In this case, we assume that we are given the pedigree relationship matrix $\left(\text{Θ}\right)$ among all individuals, both typed and untyped.

We will use subscripts u and t to denote submatrices of genotype and relationship matrices corresponding to untyped and typed individuals (e.g., $W_u$ is the matrix of [unobserved] genotypes for the ungenotyped individuals, and $W_t$ is the matrix of genotypes for the typed individuals, so that $W_u$ and $W_t$ together comprise the genotype matrix W). Because $W_u$ is unknown, we need a distribution on W to describe the relationship between the genotypes of typed and untyped individuals. For modeling purposes, we assume that normalized SNPs in $W_u$ are independently drawn from a multivariate normal distribution according to the pedigree structure: $N\left(0,\text{Θ}\right)$.

To adapt our pedigree-based two-variance-component model (Equation 9),

$$y\sim N\left(Xb,W{W}^T{\sigma }_g^2/M+\text{Θ}{\sigma }_h^2+I{\sigma }_e^2\right),$$

to deal with the fact that W now has a subset of unknown entries, we would ideally marginalize over the unobserved genotypes, assuming the above distribution on $W_u$. However, this approach leads to an intractable integral. Instead, we assume that y is normally distributed conditional on the observed genotypes, in which case it suffices to compute the mean and covariance of y. It is straightforward to see that the mean of y is $Xb$ (assuming that we observe the covariates for all individuals), and the covariance of y is

$$V:=\text{Cov}\left(y\right)={\sigma }_g^{2}E[W{W}^T/M|W_t]+{\sigma }_h^2\text{Θ}+{\sigma }_e^{2}I.$$

Therefore, this procedure amounts to replacing the unobserved GRM with the expected GRM,

$$E_{W_u}\left[W{W}^T/M|W_t\right],$$

where the expectation is over the unobserved genotypes. By using standard properties of the normal distribution, we can compute the required moments

$$\begin{array}{l}E\left[W_u|W_t\right]={\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{W}_t\\ E\left[W_u{W}_u^T|W_t\right]=M{\text{Θ}}_{uu}-M{\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{\text{Θ}}_{tu}+E\left[W_u|W_t\right]E\left[W_u^T|W_t\right]\\ =M{\text{Θ}}_{uu}+{\text{Θ}}_{ut}\left(W_t{W}_t^T-M{\text{Θ}}_{tt}^{-1}\right){\text{Θ}}_{tu}.\end{array}$$

Thus,

$$E_{W_u}\left[W{W}^T/M|W_t\right]=\left[\begin{array}{cc}{\text{Θ}}_{uu}+{\text{Θ}}_{ut}\left(W_t{W}_t^T/M-{\text{Θ}}_{tt}^{-1}\right){\text{Θ}}_{tu}& {\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{W}_t{W}_t^T/M\\ W_t{W}_t^T{\text{Θ}}_{tt}^{-1}{\text{Θ}}_{tu}/M& W_t{W}_t^T/M\end{array}\right].$$

Legarra, Misztal, and Aguilar developed the same variance component to incorporate genetic marker information with pedigree information in the context of cattle phenotype prediction.³², ³³, ³⁴

The new phenotype model

$$y\sim N\left(Xb,{\sigma }_g^{2}E\left[W{W}^T/M|W_t\right]+{\sigma }_h^2\text{Θ}+{\sigma }_e^{2}I\right)=N\left(Xb,V\right)$$

immediately enables BLUP prediction as before. However, for association testing, the test SNP $w=\left[w_u;w_t\right]$ is not completely specified, so we need a novel association statistic that accounts for the uncertainty in w. Assuming that $w\sim N\left(0,\text{Θ}\right)$, the model for y simplifies to

$$y\sim N\left(\left[\begin{array}{c}{\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{w}_t\\ w_t\end{array}\right]\beta +Xb,\left[\begin{array}{cc}{\text{Θ}}_{uu}-{\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{\text{Θ}}_{tu}& 0\\ 0& 0\end{array}\right]{\beta }^2+V\right).$$

and $\tilde{w}=\left[{\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{w}_t;w_t\right]$ can be interpreted as the BLUP imputation of the missing genotypes.

This distribution for y gives rise to a score statistic as follows. We start from the log likelihood function

$$\text{log}p\left(y|V,X,W,\tilde{w},\text{Θ},\beta \right)=-0.5\left(\text{log}|V+A{\beta }^2|+{\left(y-\tilde{w}\beta -Xb\right)}^T{\left(V+A{\beta }^2\right)}^{-1}\left(y-\tilde{w}\beta -Xb\right)\right)$$

(up to a constant that does not depend on y or β), where

$$A=\left[\begin{array}{cc}{\text{Θ}}_{uu}-{\text{Θ}}_{ut}{\text{Θ}}_{tt}^{-1}{\text{Θ}}_{tu}& 0\\ 0& 0\end{array}\right]$$

is the adjustment to the variance. Expanding around $\beta =0$, the log likelihood simplifies to

$$-2\text{log}p\left(y|V,X,W,\tilde{w},\text{Θ},\beta \right)=\text{log}\left|V\right|+\text{trace}\left(V^{-1}A\right){\beta }^2+{\left(y-\tilde{w}\beta -Xb\right)}^T{V}^{-1}\left(y-\tilde{w}\beta -Xb\right)-{\left(y-Xb\right)}^T\left(V^{-2}A\right)\left(y-Xb\right){\beta }^2+O\left({\beta }^3\right),$$

so the score function is

$$U\left(\beta \right)=\frac{\partial \text{log}p\left(y|V,X,W,\tilde{w},\text{Θ},\beta \right)}{\partial \beta }=-(\text{trace}\left(V^{-1}A\right)\beta +{\left(y-Xb\right)}^T{V}^{-1}\tilde{w}+{\tilde{w}}^T{V}^{-1}\tilde{w}\beta -{\left(y-Xb\right)}^T\left(V^{-2}A\right)\left(y-Xb\right)\beta )+O\left({\beta }^2\right),$$

and

$$\frac{\partial U}{\partial \beta }=-\left(\text{trace}\left(V^{-1}A\right)+{\tilde{w}}^T{V}^{-1}\tilde{w}-{\left(y-Xb\right)}^T\left(V^{-2}A\right)\left(y-Xb\right)\right)+O\left(\beta \right)$$

Hence, the score statistic to test the hypothesis that $\beta =0$ is

$$\frac{U{\left(0\right)}^2}{-\partial U/\partial \beta \left(0\right)}=\frac{{\left({\tilde{w}}^T{V}^{-1}\left(y-Xb\right)\right)}^2}{{\tilde{w}}^T{V}^{-1}\tilde{w}+\text{trace}\left(V^{-1}A\right)-{\left(y-Xb\right)}^T\left(V^{-2}A\right)\left(y-Xb\right)},$$

where the nuisance parameters $\left(b,{\sigma }_g^2,{\sigma }_h^2,{\sigma }_e^2\right)$ are set to their maximum likelihood values when $\beta =0$. The score statistic is asymptotically distributed as ${\chi }^2$ with 1 df. It is possible to adjust the statistic slightly to produce a nearly equivalent statistic that is easier to compute and precisely ${\chi }^2$-distributed under the null distribution. Observe that

$$\begin{array}{l}E\left[{\left(y-Xb\right)}^T\left(V^{-2}A\right)\left(y-Xb\right)\right]=E\left[\text{trace}\left({\left(y-Xb\right)}^T\left(V^{-2}A\right)\left(y-Xb\right)\right)\right]\\ =\text{trace}\left(E\left(y-Xb\right){\left(y-Xb\right)}^T]V^{-2}A\right)\\ =\text{trace}\left(V{V}^{-2}A\right)\\ =\text{trace}\left(V^{-1}A\right),\end{array}$$

resulting in the simplified statistic

$$\frac{{\left({\tilde{w}}^T{V}^{-1}\left(y-Xb\right)\right)}^2}{{\tilde{w}}^T{V}^{-1}\tilde{w}},$$

which is ${\chi }^2$-distributed under the null distribution. Notably, when V only incorporates pedigree information (i.e., $V=\text{Θ}{\sigma }_h^2+I{\sigma }_e^2$), we recover a prospective analog to the retrospective MASTOR statistic.²⁸

Alternatively, in a similar manner, we can compute a retrospective statistic by considering the score statistic produced by $\text{log}p\left(w|y\right)$ instead. Analogous manipulations yield the retrospective statistic

$$\frac{{\left({\tilde{w}}^T{V}^{-1}\left(y-Xb\right)\right)}^2}{{\left(y-Xb\right)}^T{V}^{-1}{\text{Θ}}_{\cdot t}{\text{Θ}}_{tt}^{-1}{\text{Θ}}_{t\cdot }{V}^{-1}\left(y-Xb\right)}.$$

Given that the results from the retrospective model and prospective model are similar (data not shown), we focused on the more commonly used prospective approach.

Web Resources

The URLs for data presented herein are as follows:

• FAMBLUP software (Matlab code), http://github.com/gjtucker/FAMBLUP

• UK Biobank, http://www.ukbiobank.ac.uk/