Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Dec 2;5:17634. doi: 10.1038/srep17634

Hydrogen Impurity Defects in Rutile TiO2

Li-Bin Mo 1, Yu Wang 2, Yang Bai 1, Qing-Yun Xiang 1, Qun Li 1, Wen-Qing Yao 3, Jia-Ou Wang 4, Kurash Ibrahim 4, Huan-Hua Wang 4, Cai-Hua Wan 5, Jiang-Li Cao 1,a
PMCID: PMC4667266  PMID: 26627134

Abstract

Hydrogen-related defects play crucial roles in determining physical properties of their host oxides. In this work, we report our systematic experimental and theoretical (based on density functional theory) studies of the defect states formed in hydrogenated-rutile TiO2 in gaseous H2 and atomic H. In gas-hydrogenated TiO2, the incorporated hydrogen tends to occupy the oxygen vacancy site and negatively charged. The incorporated hydrogen takes the interstitial position in atom-hydrogenated TiO2, forming a weak O-H bond with the closest oxygen ion, and becomes positive. Both states of hydrogen affect the electronic structure of TiO2 mainly through changes of Ti 3d and O 2p states instead of the direct contributions of hydrogen. The resulted electronic structures of the hydrogenated TiO2 are manifested in modifications of the electrical and optical properties that will be useful for the design of new materials capable for green energy economy.

Hydrogen has rather complex chemical states in nature including H+, H0 and H−, which makes its behaviors in the host materials complicated. A fuller understanding of the interactions between oxide materials and hydrogen is crucial for the research and successful applications of such materials in a broad range of scientific and technological fields from green energy techniques to electronics industries. For example, hydrogen ions are positively charged in ZnO, contributing to high conductivity1,2. In BaTiO3, instead, hydrogen ions are negatively charged, occupying the position of oxygen vacancies3. As-doped BaTiO3-xHx is also electronically conductive and stable in air and water at ambient conditions3. It is also proposed that new materials or devices with novel functionalities may be designed through appropriate hydrogen treatment. All these areas are calling for a thorough understanding of the hydrogen behaviors in oxide materials and responses of the hosts to different hydrogen atmospheres.

TiO2 shows promising application prospects in some rapidly growing hydrogen-related technologies such as hydrogen production4,5, and solar cells6, etc7,8,9 because of its excellent properties and ready accessibility. For example, Chen et al.10 reported that hydrogenated anatase TiO2 nanocrystals exhibited significantly improved solar photocatalytic performances, which triggered much research interest in the hydrogen defect engineering of oxide materials. Furthermore, hydrogenated TiO2 nanowire arrays also possess excellent photoelectrochemical-water-splitting performance11 and super capacitive properties12. Interestingly, besides of high-temperature annealing in gaseous H2, treatment by atomic H at room temperatures could also significantly change performances of TiO2. Chester13 first found that the conductivity of TiO2 increased upon atom-hydrogenation through water electrolysis. Chen14 also observed similar effects in TiO2 and other oxides. But the proposed mechanisms for the above behaviors diverge in different researches. Chen10,15 and Naldoni16 regarded surface disorders induced narrowing of bandgap of TiO2 and therefore the enhancement of its absorption ratio in visible light range. Deford17, Herklotz18 and Kilici19 assumed that the interstitial hydrogen was formed in gas-hydrogenated TiO2 and correlated the interstitial hydrogen with the increase in conductivity and light absorption. Besides of the viewpoint that interstitial hydrogen atom was the origin of enhanced conductivity in atom-hydrogenated TiO2, Chester13 and Chen14 also regarded that VO formed in oxide materials in hydrogen atmospheres20,21,22,23. Wang11 and Zhai24, however, regarded that VO was the main reason responsible for the reduction of bandgap. Even more complex, Lu et al.12 thought that the surface hydroxyl groups of hydrogenated TiO2 should be responsible for the change of performances. Filippone et al.25 reported that H behaved as a deep donor in rutile and formed stable H-oxygen vacancies (VO) complexes. Though the defect engineering by hydrogen treatment has attracted much attention over recent years, the defect states and their atomic- and electronic structure in hydrogenated TiO2 are still not clearly understood so far. The above debate is partially induced, we think, by different sample structures (nano-particles, nanowires or bulk materials) and/or by different treatment conditions (high temperature annealing or room temperature electrochemical method) among different research groups. In this research, we focus only on bulk materials with single crystalline to first minimize the influence of surface disorder. Further, we applied the above two methods to treat the same batch of samples to minimize influence of diversity among different samples. The above controlled conditions will make our data more comparative and suggestive to dissolve some basic questions in this field Therefore, the present study aims at exploring the hydrogen impurity-related defect states in bulk rutile TiO2. Oxygen vacancies and H-oxygen vacancies (VO) complexes as main defects in gas-hydrogenated TiO2 were introduced through high-temperature annealing treatment and interstitial hydrogen as main defects in atom-hydrogenated TiO2 were introduced by water electrolysis. Through comparison experiments with bulk TiO2 samples with different defects as well as density functional theory (DFT) calculations, we hope to open up new opportunities in green energy techniques, including water splitting, dye-sensitized solar cells, and photocatalysis etc.

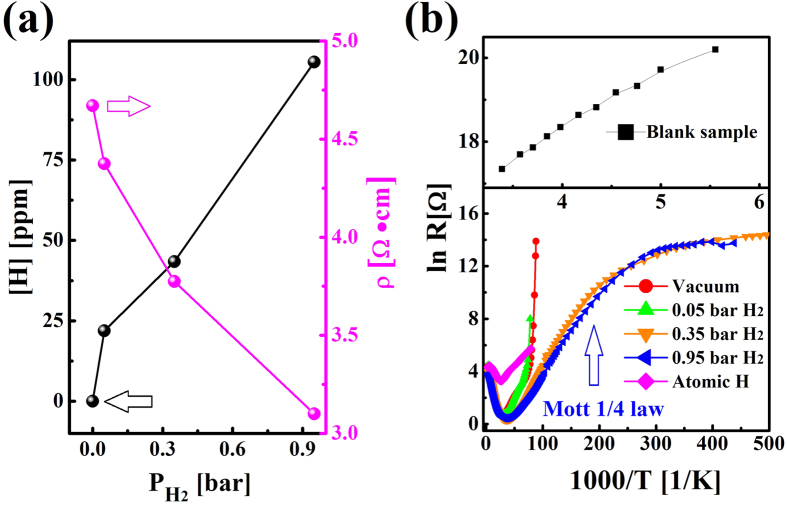
Figure 1 (a) shows hydrogen contents and room temperature (RT) resistivity of gas-hydrogenated rutile TiO2. The samples treated with PH2 = 0 were named as vacuum-annealed samples. Their resistivity decreases by more than seven orders of magnitude to several Ω cm, which could be attributed to the formation of VO22,23. With increasing PH2 the incorporated hydrogen content increases and resistivity decreases monotonically. Hall measurements show that the carriers in these high temperature-annealed samples are all electrons (Supplemental Fig. S1), demonstrating formation of donor defects. Carrier mobility in the 0.95 bar gas-hydrogenated sample is 42.3 cm2 V−1 s−1 at 30 K, lower than 94.5 cm2 V−1 s−1 of the vacuum-annealed sample. Fig. 1(b) plots the temperature-dependence of the resistivity between 2 K and 300 K. Different from the blank sample, the resistivity of the high temperature-annealed samples first decreases with decreasing temperature and then increases sharply after reaching a minimum around 30 K. Here, the temperature dependence of the resistivity above 30 K is proposed to be determined mainly by the carrier mobility. Below 30 K, the donors start to be frozen out from conduction band (CB). The resistivity exhibits an exponential dependence on 1/T, following the equation ρ = ρ0exp(–ΔED/kBT)26. And fittings show that the ionization energy of defects ΔED of all high temperature-annealed samples are 6.5 ± 1.5 meV. It indicates that their dominant defects could be the same, i.e. VO. Similarly, Yagi23 et al. reported a ΔED of ~5 meV for VO in rutile TiO2. The resistivity of the samples annealed in 0.35 and 0.95 bar H2 at high temperature increases with further decreasing temperature, following Mott’s law ρ = ρ1exp(T0/T)1/4. Their conductivity mechanism could be attributed to the variable range hopping conduction26,27. The higher PH2 leads to a higher donor density and finally produces a defect band in the band gap. Consequently, electrons could hop between donors through thermal-assisted tunneling, which answers for the residual conductivity below 4 K in the higher PH2-hydrogenated TiO2.

Figure 1. Molar content of incorporated hydrogen and transport properties of hydrogenated TiO2 single crystals.

Figure 1

Open in a new tab

(a) Changes of the hydrogen content and RT resistivity of TiO2 with PH2 upon gas-hydrogenation. An oxygen loss of about 300 ppm is measured for the 0.95 bar gas-hydrogenated rutile TiO2, which is approximately 3 times of the hydrogen content. (b) temperature-dependences of resistivity from 2 K to 300 K.

TiO2 single crystals with interstitial H (Hi) defects fabricated by atom hydrogenation at RT show a much reduced RT resistivity of 14.5 Ω cm and a similar temperature-dependence with the high temperature-annealed samples (Fig. 1b). The ΔED of atom-hydrogenated TiO2 has not been reported before. Here, a shallow donor level with a ΔED of 3.9 meV is measured, smaller than that in the high temperature-annealed samples. Thus, it is inferred that the defects in atom-hydrogenated TiO2 are different from those in gas-hydrogenated TiO2. Furthermore, carrier mobility of the atom-hydrogenated sample is 7.71 cm2 V−1 s−1 (Supplemental Fig. S1), much smaller than that of vacuum-annealed sample and that of gas-hydrogenated TiO2, which further indicates different scattering defects in samples treated by the different methods.

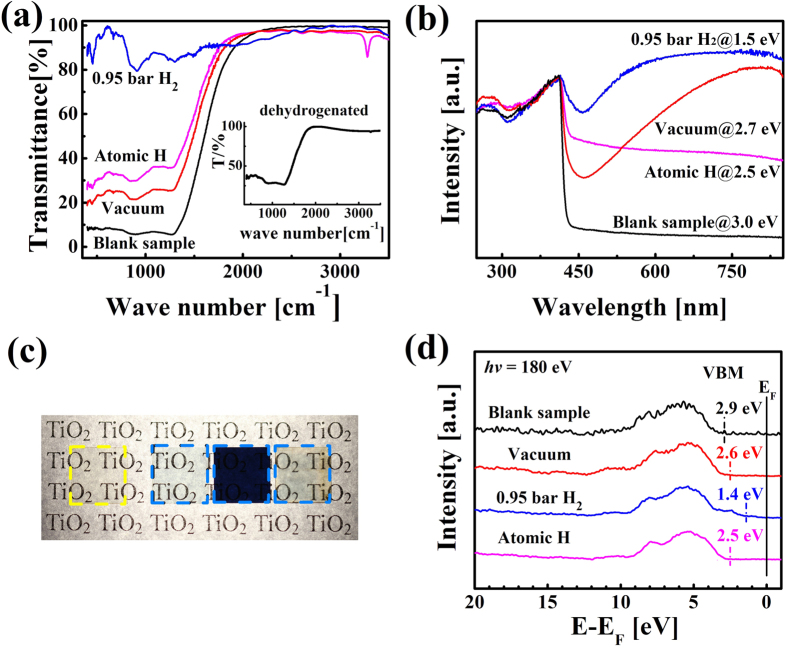
Figure 2a shows the Fourier transform infrared (FTIR) absorption spectra. The blank sample has strong absorption between 400 ~ 1300 cm−1 as normal28,29. In contrast, the transparency of hydrogenated samples increases significantly. Interestingly, the 0.95 bar gas-hydrogenated sample becomes almost completely infrared transparent in the full range of measurement. Note that the gas-hydrogenated TiO2 also has high conductivity and could be potentially used as transparent conductors in the infrared band. A strong absorption peak at 3280 cm−1 is observable for the atom-hydrogenated sample. This peak should be the stretch mode of O-H bonds in rutile TiO218,28. The O-H absorption peak in atom-hydrogenated TiO2 disappears after a 10 min-dehydrogenation in air at 700 ºC, as shown in the inset of Fig. 2a. Furthermore, high resistivity of the atom-hydrogenated TiO2 recovered gradually to the virgin state after a few days aging at RT, similar with previous report30, whereas little changes can be observed in the gas-hydrogenated TiO2 after a five-day aging. Therefore, the incorporated hydrogen in atom-hydrogenated TiO2 is more diffusible and unstable than that in gas-hydrogenated TiO2. By contrast, no such an absorption peak can be observed for the gas-hydrogenated samples.

Figure 2. Characterizations of TiO2 single crystals.

Figure 2

Open in a new tab

(a) FTIR absorption spectra. The inset shows the FTIR spectrum of the atom-hydrogenated TiO2 after a 10 min-dehydrogenation at 700 ºC. (b) Optical absorption spectra. The band gap values are given. (c) Optical images of the blank, vacuum-annealed, gas-hydrogenated and atom-hydrogenated samples (from left to right). (d) Valence-band spectra of synchrotron radiation.

Figure 2b presents optical absorption spectra of the samples. Upon hydrogenation or vacuum-annealing, the absorption edge shifts to the lower energy side and the absorption ratio for photons with lower energy than the absorption edge increases significantly. Meanwhile, colors of vacuum-annealed samples and the atom-hydrogenated TiO2, turn from light yellow of blank sample to light blue (Fig. 2c) and the color of gas-hydrogenated sample becomes even dark blue, similar with the case of gas-hydrogenated anatase TiO2 nanocrystals10. The valence-band (VB) spectra were measured by synchrotron radiation x-ray photoelectron spectroscopy (XPS) (Fig. 2d). For the vacuum-annealed and hydrogenated samples, the VB maximum lies at 2.6 eV and 1.4 eV, respectively, which are closer to the Femi level than blank sample as reported by Chen10. The results suggest a narrowing of the band gap, in agreement with the optical absorption measurements in Fig. 2b. Naldoni16 and Zuo31 regarded that VO contributed energy levels 0.7 ~ 1.0 eV below conduction band. Chen10 and Naldoni16 regarded that surface disorder contributed levels 2.0 eV below conduction band. In our VB spectra, we also observed a band 1.4 eV below Fermi level in samples annealed in 0.95 bar H2 atmospheres. Instead, the VB position of the atom-hydrogenated TiO2 was 2.5 eV. And the VB position of vacuum-annealed samples was also about 2.6 eV. These results made us propose that different hydrogen defects formed in different treatment methods. Furthermore, O-H bonds only formed in atom-hydrogenated TiO2 but not in gas-hydrogenated samples. Instead, a large amount of VO and H defects coexisted in the gas-hydrogenated samples. Therefore we propose oxygen vacancies and hydrogen ions coexist independently or correlatedly in the gas-hydrogenated samples while only interstitial hydrogen atoms exist in the samples treated by electrochemical method. In order to understand different existing forms of hydrogen defects, we have turned to DFT calculations.

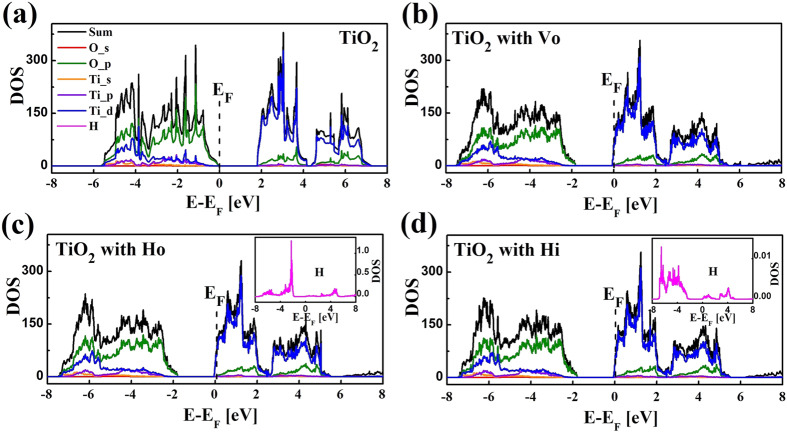
DFT calculations were carried out using the Vienna ab initio Simulation Program (VASP) code with projector-augmented-wave (PAW) pseudopotentials and the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional. The rutile TiO2 structure was described as a 3 × 3 × 3 supercell. First, the density of states (DOS) and the partial density of states (PDOS) of a perfect TiO2 supercell (Fig. 3a) and the supercell with VO were calculated (Fig. 3b). As compared to the perfect TiO2, the introduction of VO in the supercell results in two loosely captured electrons by three Ti dangling bonds. These two electrons can be transferred to Ti 3d states32. Then a H atom was incorporated in the supercell with VO and perfect supercell, respectively. It was found after structure optimization that the H atom added in the supercell with VO tends to reside on the VO’s site as HO and the resulting lattice distortion becomes smaller than that with VO alone. This finding agrees with our synchrotron radiation x-ray diffraction results (Supplemental Fig. S3). The Fermi level for TiO2 with HO also lies in the conduction band (CB) owing to the contribution of Ti 3d electrons (Fig. 3c). The inset shows that the states of HO contribute mainly to the VB. By contrast, H in the perfect TiO2 prefers the interstitial site of oxygen octahedral as Hi, which is consistent with an earlier report33. The distance from Hi to the closest O is found to be 0.991 Å, very similar to the bond length of hydroxyl in H2O. Hi can also affect the Ti 3d band structure and move the Fermi level into the CB. The inset of Fig. 3d shows that some states of Hi appear in the CB. Note that DOS of interstitial H is very small and only as 1% as that of H defects around Oxygen vacancies. In all these configurations, the VB and the CB are still primarily formed by O 2p and empty Ti 3d states, respectively. Hydrogen defects have little direct influence on the structure of VB or CB, contributing few DOS near the bandgap. However, they could modulate the structure of TiO2 indirectly by their hybridization with O 2p and Ti 3d orbits. Chen10 and Naldoni16 proposed this shift was due to surface disorders. Here we tend to ascribe this shift in bulk and single crystalline TiO2 to hybridization of H with O 2p orbits. This result agrees with our previous work34.

Figure 3. DFT calculations.

Figure 3

Open in a new tab

The DOS and PDOS of (a) the perfect rutile TiO2 and (b) TiO2 with VO in simulation of vacuum-annealed TiO2. In our calculations, the intrinsic band gap of rutile TiO2 is 1.7 eV, in agreement with reported values37,38. (c) Gas-hydrogenated TiO2 with H staying at VO which corresponds to the minimum energy state. (d) Atom-hydrogenated TiO2 with Hi. The insets of (c) and (d) show the PDOS of the hydrogen, respectively.

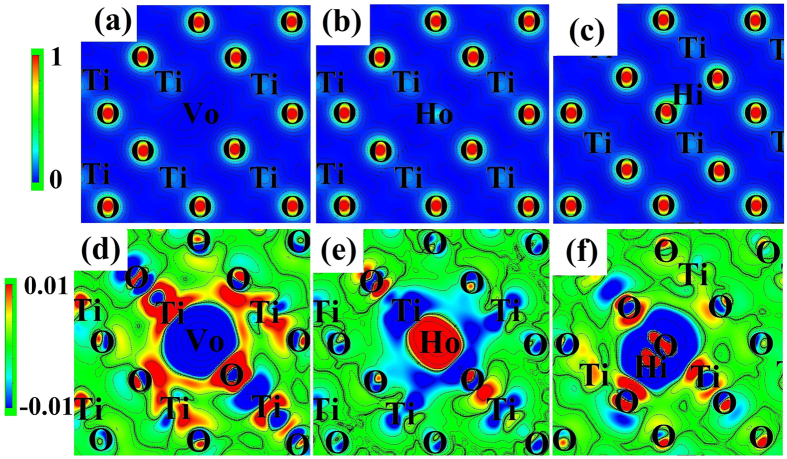
The charge density and differential charge density analyses show that electrons move from VO to the neighboring Ti and O atoms in TiO2 with VO (Fig. 4a,d). When H stays on the site of VO, the neighboring Ti and O atoms give electrons to HO, making HO negatively charged (Fig. 4b,e). Bader analyses also show that HO has 1.50 valence electrons (supplemental Table 1). In TiO2 with Hi, the charge density of Hi and the closest O atoms overlaps (Fig. 4c) and the charge density in between them is high (Fig. 4f), revealing the formation of a covalent bond, or specifically an O-H bond. The valence electron of Hi is 0.35 and similar with that of H atoms in H2O. These DFT calculations coincide well with our experimental observations of the appearance of the 3280 cm−1 IR absorption peak in atom-hydrogenated TiO2, but not in gas-hydrogenated TiO2. Higher hydrogen contents in the supercell do not bring about significant charge density differences. Indeed, no experimental and theoretical evidences were found for the existence of O-H bonds in gas-hydrogenated TiO2.

Figure 4. Charge density and differential charge density for different configurations.

Figure 4

Open in a new tab

(a–c) is the charge density of the perfect TiO2, TiO2 with VO, TiO2 with HO, and TiO2 with Hi, respectively. (d–f) is the differential charge density of TiO2 with VO, TiO2 with HO, and TiO2 with Hi, respectively. The blue color indicates the low electron density and the red color indicates the high electron density.

Annealing in vacuum and gaseous H2 can both introduce a shallow donor state in rutile TiO2 with nearly the same ionization energy of 6.5 ± 1.5 meV. The Hi alone in atom-hydrogenated TiO2 also introduces a shallow donor, however, with lower ionization energy of 3.9 meV. Note that the Hi is weakly bonded to the closest O atom and the resulted O-H bonds could be easily broken by high temperature annealing in air in short time or by several days’ aging at RT14. This hydrogenation-derived O-H bonds behave quite differently from those inherent O-H defects in earlier studies in flame fusion-derived rutile TiO2 crystals28,29 or natural ores35 which contained unavoidably large contents of OH defects, or the deuteration was carried out in D2O through isotope exchange36. Those inherent hydrogen defects were rather stable against high temperature annealing26. The HO defects, or the combination of H atoms with VO could stabilize the hydrogen atoms in TiO2, making it insensitive to RT aging. Our study offers useful insights for studies of the interplay of hydrogen atmospheres and solid state oxide materials. We expect this research could contribute to the property tailoring of TiO2 through appropriate hydrogen-related defect engineering.

Methods

Rutile TiO2 single crystals of (001)-orientation synthesized by floating zone method were used. All the samples were annealed in air at 700 °C for 120 hours to eliminate the native defects and reached a RT equilibrium resistivity of (2.0 ± 0.1) × 108 Ω cm. For high-temperature annealing, the samples were sealed in pre-evacuated quartz ampoules (background pressure <1.0 × 10−9 bar) with 99.999% H2 of a RT pressure of 0, 0.05, 0.35 and 0.95 bar, respectively. Then the samples were annealed at 600 °C for 50 hours to reach their equilibrium state, followed by air quenching to RT. It is worth mentioning that the infrared spectra would be significantly affected by the hydroxyl pollution from quartz ampoules. The FTIR spectra obtained in the samples annealed in vacuum in normal quartz tubes also showed an observable absorption peak at 3280 cm−1 (as shown in Supplemental Fig. S3). In order to avoid possible hydroxyl pollution from quartz ampoules, we have chosen dehydroxylated quartz ampoules. Furthermore, flame fusion-derived rutile TiO2 single crystals unavoidably contained large contents of OH defects28,29, so we chose the rutile single crystals synthesized by floating zone method. Moreover, high pressure hydrogen gas can also help to avoid hydroxyl pollution from quartz ampoules.

For comparison, interstitial hydrogen was introduced by atom-hydrogenation through electrolysis of 0.1 M Na2SO4 water solution at RT22. The TiO2 chips were electroded by firing Ag pastes on parts of the chips. Atomic H was generated on the Ag electrode and then diffused into TiO2 during the hydrogenation. The TiO2 crystals became gradually blue and hydrogen started to form directly on the TiO2 crystals. A surface layer of 50 μm thick was removed in order to keep the surface clean for following analyses.

The resistivity and Hall Effect of the samples were measured from 2 to 300 K by Physical Property Measurement System 9 (PPMS-9) and the current–voltage (I–V) characteristics were measured by Keithley 2400 using a four-electrode method. The oxygen loss was calculated through weight measurement using a micro-balance. The crystal structures were examined by synchrotron radiation x-ray diffraction (XRD) at 1W1A of Beijing Synchrotron Radiation Facility (BSRF). The optical absorption spectra of rutile TiO2 samples were measured by Fourier-transform infrared spectrometer (Nicolet 6700) under transmission mode and Double beam UV-visible spectrophotometer (TU-1901) under reflection mode. The valence band structures were examined by synchrotron radiation XPS at 4B9B of BSRF. Hydrogen contents of samples were determined by diffusible hydrogen analyzer (Bruker-G4 Phoenix) at 700 °C.

The electronic structures of TiO2 with different defects were calculated based on density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional using the Vienna ab initio Simulation Program (VASP) code with projector-augmented-wave (PAW) pseudopotentials. The rutile TiO2 structure was described as a 3 × 3 × 3 supercell with 162 atoms consisting of a twelve-trilayer slab. The cutoff energy for expanding the Kohn-Sham wave functions was 400 eV. We used the experimentally derived lattice constants (a = b = 4.595 Å, c = 2.959 Å). All the atoms were fully relaxed without constraints until the forces were converged to 0.01 eV/Å. The Monkhorst-Pack k-point grid was 5 × 5 × 9 for Brillouin zone integration of the supercell which was tested to be well converged.

Additional Information

How to cite this article: Mo, L.-B. et al. Hydrogen Impurity Defects in Rutile TiO2. Sci. Rep. 5, 17634; doi: 10.1038/srep17634 (2015).

Supplementary Material

Supplementary Information
srep17634-s1.pdf (312KB, pdf)

Acknowledgments

Authors thank the support of Program for Fundamental Research Funds for the Central Universities (FRF-SD-12-027A), New Century Excellent Talents in Universities (NCET-12-0778), Ministry of Science and Technology of China (2012IM030500) and China Scholarship Council. Work at BSRF was supported by the project 1G2009312311750101 of Chinese Academy of Sciences and the project 11375228 of NSFC. This work used the VASP code of Supercomputing Center at CNIC of Chinese Academy of Sciences. J.L.C thanks U. Diebold, M. Schmid, M. Setvín and X.F. Hao for their valuable advice.

Footnotes

Author Contributions L.B.M. conducted the experiments and computations and contributed to writing of the manuscript. Y.W. and C.H.W. contributed to the design of the study and writing of the manuscript. Y.B., Q.Y.X. and Q.L. contributed to the experiments. W.Q.Y. did XPS and AES analyses. J.O.W. and I.K. conducted XPS analyses at BSRF. H.H.W. did XRD measurements at BSRF. J.L.C. designed the study and wrote the manuscript.

References

  1. Walle C. G. & Neugebauer J. Universal alignment of hydrogen levels in semiconductors, insulators and solutions. Nature 423, 626–628 (2003). [DOI] [PubMed] [Google Scholar]
  2. Janotti A. et al. Hybrid functional studies of the oxygen vacancy in TiO2. Phys. Rev. B 81, 085212 (2010). [Google Scholar]
  3. Kobayashi Y. et al. An oxyhydride of BaTiO3 exhibiting hydride exchange and electronic conductivity. Nature Mater. 11, 507–511 (2012). [DOI] [PubMed] [Google Scholar]
  4. Tang J., Durrant J. R. & Klug D. R. Mechanism of Photocatalytic Water Splitting in TiO2. Reaction of Water with Photoholes, Importance of Charge Carrier Dynamics, and Evidence for Four-Hole Chemistry. J. Am. Chem. Soc. 130, 13885–13891 (2008). [DOI] [PubMed] [Google Scholar]
  5. Fujishima A. & Honda K. Electrochemical photolysis of water at a semiconductor electrode. Nature 238, 37–38 (1972). [DOI] [PubMed] [Google Scholar]
  6. Etgar L. et al. Mesoscopic CH3NH3PbI3/TiO2 Heterojunction Solar Cells. J. Am. Chem. Soc. 134, 17396–17399 (2011). [DOI] [PubMed] [Google Scholar]
  7. Kaden W. E., Wu T., Kunkel W. A. & Anderson S. L. Electronic structure controls reactivity of size-selected Pd clusters adsorbed on TiO2 surfaces. Science 326, 826–829 (2009). [DOI] [PubMed] [Google Scholar]
  8. Bavykin D. V., Friedrich J. M. & Walsh F. C. Protonated titanates and TiO2 nanostructured materials: synthesis, properties, and applications. Adv. Mater. 18, 2807–2824 (2006). [Google Scholar]
  9. Lee J., Sorescu D. C. & Deng X. Electron-Induced Dissociation of CO2 on TiO2(110). J. Am. Chem. Soc. 133, 10066–10069 (2011). [DOI] [PubMed] [Google Scholar]
  10. Chen X. B., Liu L., Yu P. Y. & Mao S. S. Increasing solar absorption for photocatalysis with black hydrogenated titanium dioxide nanocrystals. Science 331, 746–750 (2011). [DOI] [PubMed] [Google Scholar]
  11. Wang G. et al. Hydrogen-Treated TiO2 Nanowire Arrays for Photoelectrochemical Water Splitting. Nano Lett. 11, 3026–3033 (2011). [DOI] [PubMed] [Google Scholar]
  12. Lu X. et al. Hydrogenated TiO2 Nanotube Arrays for Supercapacitors. Nano Lett. 12, 1690–1696 (2012). [DOI] [PubMed] [Google Scholar]
  13. Chester P. F. & Bradhurst D. H. Electrolytically Induced Conductivity in Rutile. Nature 199, 1056–1057 (1963). [Google Scholar]
  14. Chen W. P., He K. F., Wang Y., Chan H. L. W. & Yan Z. J. Highly mobile and reactive state of hydrogen in metal oxide semiconductors at room temperature. Sci. Rep. 3, 3149 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Liu L., Yu P. Y., Chen X. B., Mao S. S. & Shen D. Z. Hydrogenation and Disorder in Engineered Black TiO2. Phys. Rev. Lett. 111, 065505 (2013). [DOI] [PubMed] [Google Scholar]
  16. Naldoni A. et al. Effect of Nature and Location of Defects on Bandgap Narrowing in Black TiO2 Nanoparticles. J. Am. Chem. Soc. 134, 7600–7603 (2012). [DOI] [PubMed] [Google Scholar]
  17. DeFord J. W. & Johnson O. W. Electron transport properties in rutile from 6 to 40 K. J. Appl. Phys. 54, 889–897 (1983). [Google Scholar]
  18. Herklotz F., Lavrov E. V. & Weber J. Infrared absorption of the hydrogen donor in rutile TiO2. Phys. Rev. B 83, 235202 (2011). [Google Scholar]
  19. Kilic C. & Zunger A. n-type doping of oxides by hydrogen. Appl. Phys. Lett. 81, 73–75 (2002). [Google Scholar]
  20. Diebold U. The surface science of TiO2. Surf. Sci. Rep. 48, 53–229 (2003). [Google Scholar]
  21. Diebold U., Li S. C. & Schmid M. Oxide surface science. Annu. Rev. Phys. Chem. 61, 129–148 (2010). [DOI] [PubMed] [Google Scholar]
  22. Wang Z. T., Deskins N. A., Henderson M. A. & Lyubinetsky I. Inhibitive influence of oxygen vacancies for photoactivity on TiO2 (110). Phys. Rev. Lett. 109, 266103 (2012). [DOI] [PubMed] [Google Scholar]
  23. Yagi E., Hasiguti R. R. & Aono M. Electronic conduction above 4 K of slightly reduced oxygen-deficient rutile TiO2-x. Phys. Rev. B 54, 7945–7956 (1996). [DOI] [PubMed] [Google Scholar]
  24. Zhai T. et al. Oxygen vacancies enhancing capacitive properties of MnO2 nanorods for wearable asymmetric supercapacitors. Nano Energy 8, 255–263 (2014). [Google Scholar]
  25. Filippone F., Mattioli G., Alippi P. & Bonapasta A. A. Properties of hydrogen and hydrogen-vacancy complexes in the rutile phase of titanium dioxide. Phys. Rev. B 80, 245203 (2009) [Google Scholar]
  26. Sze S. M. & NG K. K. Physic of semiconductor devices Ch. 1 (John Wiley & Sons, Inc. Press, New York, 2006). [Google Scholar]
  27. Shu D. J., Ge S. T., Wang M. & Ming N. B. Interplay between external strain and oxygen vacancies on a Rutile TiO2 (110) surface. Phys. Rev. Lett. 101, 116102 (2008). [DOI] [PubMed] [Google Scholar]
  28. Soffer B. H. Studies of the optical and infrared absorption spectra of rutile single crystals. J. Chem. Phys. 35, 940–945 (1961). [Google Scholar]
  29. Johnson O. W., Ohlsen W. D. & Kingsbury P. I. Defects in rutile. III. Optical and electrical properties of impurities and charge carriers. Phys. Rev. 175, 1102–1109 (1968). [Google Scholar]
  30. Chen W. P. et al. Spontaneous recovery of hydrogen-degraded TiO2 ceramic capacitors. Appl. Phys. Lett. 84, 103–105 (2004). [Google Scholar]
  31. Zuo F. et al. Self-Doped Ti3+ Enhanced Photocatalyst for Hydrogen Production under Visible Light. J. Am. Chem. Soc. 132, 11856–11857 (2010). [DOI] [PubMed] [Google Scholar]
  32. Ganduglia-Pirovano M. V., Hofmann A. & Sauer J. Oxygen vacancies in transition metal and rare earth oxides: Current state of understanding and remaining challenges. Surf. Sci. Rep. 62, 219–270 (2007). [Google Scholar]
  33. Koudriachova M. V., Leeuw S. W. & Harrison N. M. First-principles study of H intercalation in rutile TiO2. Phys. Rev. B 70, 165421 (2004). [Google Scholar]
  34. Mo L. B. et al. Band gap engineering of TiO2 through hydrogenation. Appl. Phys. Lett. 105, 202114 (2014). [Google Scholar]
  35. Maldener J., Rauch F., Gavranic M. & Beran A. OH absorption coefficients of rutile and cassiterite deduced from nuclear reaction analysis and FTIR spectroscopy. Miner. Petrol. 71, 21–29 (2001). [Google Scholar]
  36. Spahr E. J. et al. Giant enhancement of hydrogen transport in rutile TiO2 at low temperatures. Phys. Rev. Lett. 104, 205901 (2010). [DOI] [PubMed] [Google Scholar]
  37. Pan H., Zhang Y. W., Shenoy V. B. & Gao H. J. Effects of H-, N-, and (H, N)-doping on the photocatalytic activity of TiO2. J. Phys. Chem. C 115, 12224 (2011). [Google Scholar]
  38. Shirly R., Kraft M. & Inderwildi O. R. Electronic and optical properties of aluminium-doped anatase and rutile TiO2 from ab initio calculations. Phys. Rev. B 81, 075111 (2010). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep17634-s1.pdf (312KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES