Elucidating Quantitative Stability/Flexibility Relationships Within Thioredoxin and its Fragments Using a Distance Constraint Model

Abstract

Numerous quantitative stability/flexibility relationships, within Escherichia coli thioredoxin (Trx) and its fragments are determined using a minimal distance constraint model (DCM). A one-dimensional free energy landscape as a function of global flexibility reveals Trx to fold in a low-barrier two-state process, with a voluminous transition state. Near the folding transition temperature, the native free energy basin is markedly skewed to allow partial unfolded forms. Under native conditions the skewed shape is lost, and the protein forms a compact structure with some flexibility. Predictions on ten Trx fragments are generally consistent with experimental observations that they are disordered, and that complementary fragments reconstitute. A hierarchical unfolding pathway is uncovered using an exhaustive computational procedure of breaking interfacial cross-linking hydrogen bonds that span over a series of fragment dissociations. The unfolding pathway leads to a stable core structure (residues 22–90), predicted to act as a kinetic trap. Direct connection between degree of rigidity within molecular structure and non-additivity of free energy is demonstrated using a thermodynamic cycle involving fragments and their hierarchical unfolding pathway. Additionally, the model provides insight about molecular cooperativity within Trx in its native state, and about intermediate states populating the folding/unfolding pathways. Native state cooperativity correlation plots highlight several flexibly correlated regions, giving insight into the catalytic mechanism that facilitates access to the active site disulfide bond. Residual native cooperativity correlations are present in the core substructure, suggesting that Trx can function when it is partly unfolded. This natively disordered kinetic trap, interpreted as a molten globule, has a wide temperature range of metastability, and it is identified as the “slow intermediate state” observed in kinetic experiments. These computational results are found to be in overall agreement with a large array of experimental data.

Introduction

Thioredoxin (Trx) is a small, single domain α/β enzyme (about 100 residues) found in all three kingdoms of life. Trx is involved in a wide variety of cellular processes, but most frequently acts as a cofactor for coupled redox reactions.¹ Trx variants also serve as transcription factor regulators, protein binding regulators, protein folding catalysts, growth factors, and in vivo anti-oxidants. Trx redox changes occur through disulfide bond formation/loss within a Cys pair (C-X-Y-C) located on the active site loop. Due to the wealth of experimental data describing its structure and stability,² and that of its fragments,^2–9 Trx is an ideal candidate to test the ability of the minimal distance constraint model (DCM) to accurately assess protein fragment stability, structure, and flexibility.

For some time, properties of molecular fragments have been investigated to elucidate complex structure/stability and structure/function relationships within proteins and enzymes (for a review see Prat-Gay).¹⁰ For example, fragments have been used to probe protein folding pathways,¹¹ molecular recognition events,³ and conformational features.¹² Similarly, computational fragment-based approaches are routinely used by theorists and bioinformaticians to predict the same types of information.^13–16 Here, the relative stability and flexibility of all possible fragment pairs within Trx are evaluated using a recently developed DCM.^17,18 Free energy differences for computer-generated fragments to remain physically separated or to reconstitute are calculated blind to experimental data. Using a similar computational procedure that exhaustively removes cross-linking hydrogen bonds (H-bonds) that bridge a series of unzipping fragments, a hierarchical unfolding pathway is identified. This unfolding pathway leads to a stable structural bottleneck that provides new insight about the intermediate states populating the folding/unfolding pathways. The predictions support interpretations derived from two systematic experimental works,^19,20 which seemed to have conflicting conclusions about the presence of a slow intermediate state. Despite the simplicity of the employed minimal DCM, predicted quantitative stability/flexibility relationships (QSFR) in Trx and its fragments are in good agreement with most experimental conclusions. Taken together, these results give a consistent understanding of experimental observations.

The DCM is a recent²¹ extension of the application of network rigidity to predict protein stability as well as flexibility. Network rigidity properties can be calculated using an efficient graph-algorithm,²² which is implemented in the FIRST software,^† to provide detailed mechanical information about flexible and rigid regions. FIRST provides this information by modeling native protein structure using a specific quenched topological arrangement of constraints. To arrive at protein thermodynamics, the DCM employs a free energy decomposition scheme that assigns an enthalpy and entropy contribution to each constraint. Network rigidity is explicitly regarded as an underlying mechanical interaction, from which independent and redundant constraints can be determined. Non-additivity in conformational entropy components, which is common in free energy decomposition of large biopolymers,²³ is accounted for by adding entropy contributions from only independent constraints. Consequently, free energies, and thus Boltzmann weights, can be assigned to each mechanical framework within an ensemble of constraint topologies. Incorporating a statistical mechanical approach, protein stability and flexibility information is calculated in a harmonious way using network rigidity. Protein stability is derived from the ensemble statistical mechanics, whereas flexibility descriptions are quantified by probabilities and averages of the underlying network rigidity properties. Therefore, QSFR can be calculated²⁴ and used to provide a direct way to assess the give-and-take between stability and flexibility under different thermodynamic conditions.

The employed minimal DCM is based on a simple free energy decomposition scheme that introduces only a few constraint types. In particular, intramolecular H-bonding (where salt-bridges are included as special type of H-bonds), native and disordered torsion constraints, as well as an energy contribution from H-bonds that form between the protein and solvent are explicitly modeled. Without loss of generality, some enthalpy and entropy parameters are arbitrarily set to convenient values to define a reference state free energy. Entropy parameters for disordered torsion constraints and for H-bonds have been optimized in prior work¹⁷ under the assumption they are transferable between all protein structures irrespective of the solvent condition. In addition, the minimal DCM retains three phenomenological parameters related to: (i) an average protein to solvent H-bond energy, u; (ii) the average native-like torsion constraint energy, v; and (iii) a native-like torsion constraint entropy, Rδ_nat, where R is the ideal gas constant. The parameter δ_nat is dimensionless. The three parameters {u, v, δ_nat} must be determined on a case-by-case basis, as they depend on protein sequence, structural architecture and solvent conditions. Hydrophobic effects are implicitly accounted for through adjustment of these parameters.²⁴

By perturbing away from known native structure, an ensemble of constraint topologies (which can be considered analogous to conformations) is generated. In this sense, the minimal DCM is an ensemble-based free energy decomposition approach similar to COREX,²⁵ and other Ising-like models.²⁶ Given the set of parameters, {u, v, δ_nat}, the formal statistical mechanical problem is solved within a novel mean field treatment described in Materials and Methods. Unfortunately, these parameters are not known in advance. Therefore, a simulated annealing procedure has been developed to determine these unknown parameters by fitting to experimental thermodynamic data.¹⁷ Fitting to differential scanning calorimetry (DSC) C_P curves has been our preference because it provides stringent conditions related to microscopic energy fluctuations about equilibrium, although there is no theoretical reason preventing fitting to other types of data, i.e. stability curves, foldedness curves, etc. It has been found^17,18,24 that the free parameters {u, v, δ_nat} provide enough plasticity to fit to a diverse set of proteins¹⁸ whether they fold in a two-state process or not. In addition, multiple good fits from the simulated annealing procedure are found to yield robust thermodynamic and mechanical predictions.²⁴ Details of the simulating annealing protocol are given in Materials and Methods.

Results and Discussion

Global QSFR within intact Trx

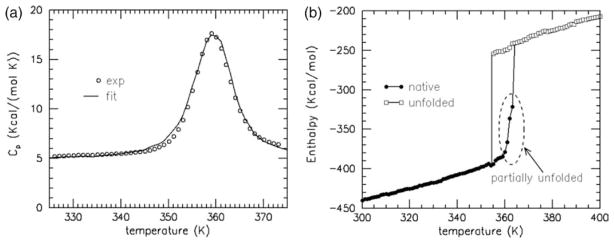
The best C_P fit to experimental data obtained for Trx⁵ is shown in Figure 1(a) using fitting parameters {u=−2.236 kcal/mol, v=−0.893 kcal/mol, δ_nat= 0.965}. All of these values are physically reasonable, and they fall within a range established over previous investigations.^17,18 Fortunately, multiple good fits identified by simulated annealing are found to yield consistent thermodynamic and flexibility conclusions. Previously, insensitivity to parameterization differences between good fitting simulated annealing runs was demonstrated using exhaustive grid searches over parameter space.²⁴ Once parameterization is achieved, a wide variety of robust QSFR descriptors are computed, including thermodynamic properties. The presence of hysteresis in the predicted enthalpy (Figure 1(b)) of Trx indicates two-state behavior, implying native and unfolded populations co-exist within the full thermodynamic ensemble. However, an unusual property, never observed in any previous DCM analyses, is present in Trx. Although hysteresis occurs, the unfolding curve is not as sharp as the folding curve. This result suggests that Trx folding/unfolding processes are not strictly two-state.

Figure 1.

(a) DCM parameterization is achieved by fitting to heat capacity curves. The best-fit (line) and experimental curves (circles) at pH 7.0 are shown. The experimental curves are taken from Georgescu et al.⁵ (b) The enthalpy for the native and unfolded states is shown. Hysteresis indicates that the transition has two-state character. The region outlined by the broken ellipse for the unfolding process is not sharp, suggesting the protein partly unfolds before it completely unfolds.

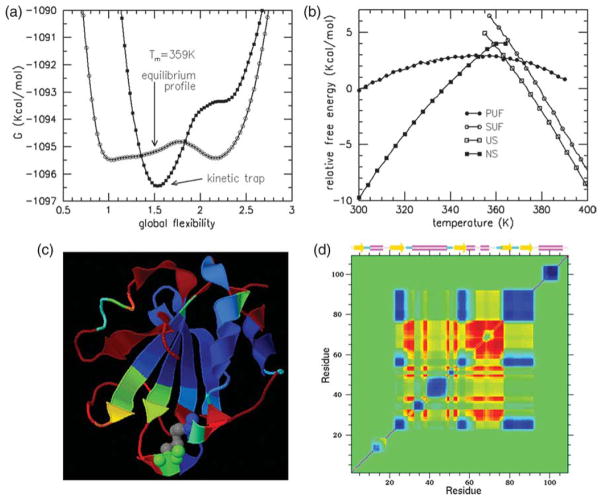
To investigate the nature of the transition in detail, one-dimensional flexibility free energy landscapes are calculated that relate thermal stability to global flexibility at a given temperature. The average number of independent degrees of freedom (dof) establishes this connection. Dividing the latter quantity by the number of residues in the protein defines a flexibility order parameter, θ, which is an intensive measure of global flexibility. This order parameter effectively reduces the high dimensionality required to track the most relevant mechanical dof describing protein conformation to a one-dimensional measure to quantify the amount of freedom available for essential dynamics. We generally assume that the flexibility order parameter serves as a faithful reaction coordinate for folding/unfolding kinetics,^17,18,24 yet this remains to be conclusively confirmed. Under this assumption, the free energy profiles, denoted as G_f(θ,T), over a succession of temperatures (Figure 2) quantifies unfolding in Trx as a quasi first-order phase transition. The depth and width of the native and unfolded basins (stable minima) characterize thermal stability.

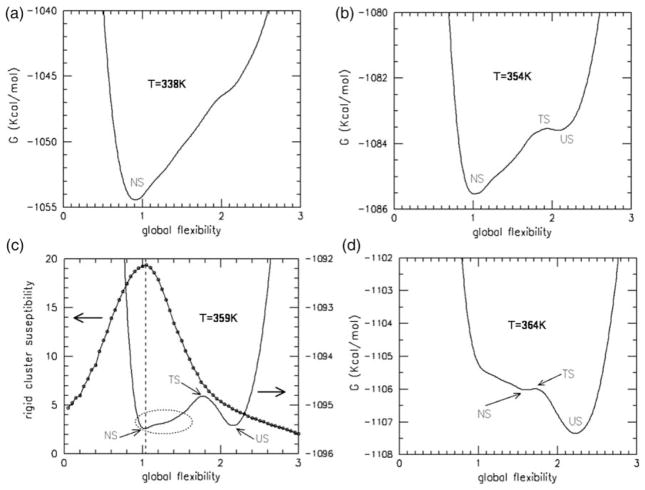
Figure 2.

Flexibility free energy landscapes as a function of global flexibility at temperatures 338 K, 354 K, 359 K and 364 K indicate a first-order (two-state) phase transition. The labels NS, TS and US denote the native, transition and unfolded states, respectively. (a) Only one free energy basin occurs at T=338 K. (b) A metastable unfolded state is present at 5 °C below T_m. (c) The free energy has two stable basins at T_m (359 K), where native and unfolded ensembles are populated. The mechanical transition is also characterized by the rigid cluster susceptibility. The vertical broken line shows how near the minimum in the native free energy basin is to the maximum in the rigid cluster susceptibility. The broken ellipse highlights the skewness within the bottom of the native-state basin showing that the native basin contains many flexible conformations. (d) The native metastable state is nearly vanished at 5 °C above T_m.

On average, the unfolded state has slightly more than one dof per residue than the native state. This release of native constraints (intramolecular contacts) on the protein chain is the source of intense energy fluctuations at the T_m, causing the sharp heat capacity peak. Metastable states are possible up to some minimum and maximum temperatures (i.e. spinodal line) after which point there is only one free energy basin present, exemplified by the native state at T=338 K (Figure 2(a)). As unfolding of the native state takes place, a rigidity transition typically occurs, driven by the change in constraint topology. This rigidity transition is well characterized by the thermodynamic average of rigid cluster fluctuations as a function of global flexibility. This quantity is referred to as the rigid cluster susceptibility, denoted by χ_RC, which is virtually temperature-independent.^17,18,24 The peak in χ_RC at point θ_RP locates the rigidity transition. When θ<θ_RP, a protein is a globally rigid and compact structure, with few disconnected flexible regions (usually in protruding loops). When θ>θ_RP, a protein is globally flexible and voluminous, with many disconnected rigid regions. The protein cannot be classified as rigid or flexible when θ≈θ_RP, because the majority of regions are in a state of flux (rigid⇔flexible).

Characteristics of G_f(θ,T_m) and χ_RC(θ) are shown in Figure 2(c). The T_m (359 K) is defined by the maximum in the DSC C_p curve, which can vary from the temperature for which there are equal populations in the native and unfolded basins. The two wells found in G_f(θ,T_m) are of similar depth, with the native basin slightly (0.06 kcal/mol) more shallow than the unfolded basin. Typically, the unfolded basin has a shallower well depth with greater curvature, thus creating a compensating affect for ensemble populations to be nearly evenly split between basins. However, an unusual skewness is present in the native basin of Trx. Therefore, at T=T_m more than 50% of the equilibrium conformations will be in the native basin. The most stable part of the native basin is located at θ_nat=1.03 close to θ_RP= 1.05, indicating that it is in a state of nearly maximum flux between being rigid and flexible. Accounting for the skewed basin, a large fraction of native conformations will have global flexibilities at least as high as 1.4, indicating that the native state is quite flexible at the transition temperature. The low free energy barrier of ≈0.5 kcal/mol at the transition state (θ_TS=1.77) found in G_f(θ,T_m) predicts Trx folding/unfolding to occur quickly, where the transition state is predicted to be voluminous in character since θ_TS>θ_RP. Based upon global QSFR properties from flexibility free energies (Figure 2), the model clearly predicts that the Trx native state transitions into a partially unfolded form (PUF) before it completely unfolds. At lower temperatures, such as at T=338 K where θ_nat=0.91 in strong native conditions (Figure 2(a)), the fold is predicted to be compact and globally rigid. This result combined with the narrow range for which the native and unfolded states co-exist is consistent with the experimental finding that Trx is resistant to limited proteolysis (unpublished results).

Prediction of kinetic rates is not explicitly part of QSFR. However, θ may serve as a good progress variable for (folding, unfolding), because it tracks the number of dof describing protein motion as constraints are (formed, broken).¹⁷ Constraints easiest to break will provide further gain in conformational flexibility, and by intuition, this process may govern kinetic pathways. These arguments are not unique to the DCM. Using an Ising-like model,²⁷ it has been shown that diffusion on one-dimensional free energy landscapes as a function of native contact order provides good estimates for kinetic folding rates. Perhaps the underlying reason why a simple Ising-like model successfully describes kinetics is because the topological process of folding exhibits minimal frustration due to folding funnels.²⁸ Given the successes uncovered in predicting kinetic rates by minimalist models, it is encouraging to find a low free energy barrier of ≈0.5 kcal/mol in G_f(θ,T_m) at the transition state (θ_TS=1.77). This low barrier height suggests Trx folding/unfolding occurs rapidly, which is consistent with experiment.²⁹ The qualitative correlation found between fast/ slow rates with low/high barrier heights found previously,¹⁸ and now augmented by Trx data, suggests that the flexibility free energy can be used to calculate kinetic rates. Investigation of kinetics using the flexibility order parameter as a reaction coordinate will be published elsewhere.

Fragment stability

For the first time, the DCM is also employed to investigate fragment stability and flexibility. Experimentally, an isolated fragment experiences a different environment than it does as part of the complete protein. Nevertheless, preserving the same conditions is easiest to implement computationally by making two simplifications. First, well-defined structure in fragments is assumed to be the same as the input X-ray crystal structure. Second, all subsequent calculations use the same parameters initially determined by the best fit to C_p data (Figure 1(a)). All predictions thereafter are blind to experimental data. Despite these oversimplifications, predictions for fragment stability may still be in-line with experimental trends. This study serves to test limits of applicability for the minimal DCM. Moreover, the calculations define hypothetical situations, that while not experimentally realizable, aid understanding of the QSFR within intact Trx.

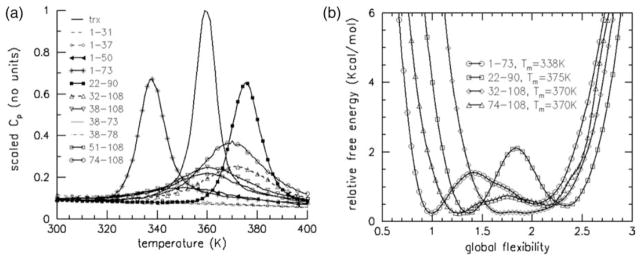
Predicted C_P curves for ten experimentally investigated fragments, and a fragment defined by the predicted folding core, are compared to intact Trx (Figure 3(a)). The procedure to identify the folding core region (residues 22–90) is discussed below in conjunction with unfolding pathways. Since heat capacity is a direct measure of energy fluctuations, a lower C_p,max implies less breaking and forming of constraints (native contacts), which in turn, depends on the number of constraints present. To facilitate comparison between fragments of different size, C_p,max is divided by fragment size (specific heat) and then normalized relative to intact Trx. Not surprisingly, there is a significant reduction in the scaled C_P curves for all fragments. Fragments 1–73 and 22–90 exhibit the highest scaled heat capacity peaks, where they both are reduced to about half the peak value of intact Trx. The next highest peak occurs in fragment 74–108. From the scaled C_p data, it is clear that there are more intrinsic energy fluctuations among the constraints present in fragment 74–108 compared to those present within fragment 51–108. Four of the fragments completely lack a peak, and, as such, do not exhibit a folding transition.

Figure 3.

(a) Scaled C_p predictions (C_p,max×108)/(C_p,max,Trx×N_res) for intact Trx, and ten fragments using the same DCM parameters based upon the best-fit to C_p of intact Trx. The large reduction in the scaled C_p curves for each of the fragments indicates that they are generally disordered. (b) Four fragments are selected to illustrate the diversity found in flexibility free energy curves that describe thermodynamic properties and the characteristic of their structural transitions (if any).

Flexibility free energy curves for individual fragments reveal whether a transition is present, and if so, whether it is two-state or continuous. In Figure 3(b), G_f(θ,T_m) is shown for fragments 1–73, 22–90, 32–108, and 74–108. Fragment 32–108 exhibits a continuous transition, while the other three cases show two-state behavior. In addition, χ_RC(θ) is calculated for all fragments. Relevant data from C_p(T), G_f(θ,T_m) and χ_RC(θ) are summarized in Table 1 for all fragments, intact Trx, and a partly unfolded Trx structure that is called core (defined below). The four fragments not exhibiting a folding transition are always flexible, and thus do not undergo a rigidity transition. This is tangentially explained by their small size, where the largest fragment (38–78) has only 41 residues and 33 native H-bonds. The specific condition is whether there are enough cross-linking H-bonds with well-placed topology to allow a rigid structure to form. In the case of fragment 74–108, it too has 33 native H-bonds, but only 35 residues. This higher density of cross-linking H-bonds allows a rigidity transition to occur, albeit θ_RP is at a low value of global flexibility. Interestingly, fragment 74–108 exhibits clear two-state behavior, yet its native state has a high degree of conformational flexibility, with a global flexibility greater than the rigidity transition threshold value. Clearly, being in a native basin does not strictly impose the condition of a rigid structure. A PUF characterizes this fragment, where its “native” state can be expected to have a “voluminous” or “natively disordered” structure. Because the number of dof is considerably less than the unfolded state, some native-like structure is present (possibly intermittent).

Table 1.

Summary of structure based predictions for thermodynamic properties and global QSFR characteristics in Trx

Sequence range	Tm (K)	Excess Cp,max (kcal/mol K)	Rel. Cp,max (%)	Folding transition	HB No.	θRP	θnat	θTS	θunf	BH
1–108 (WT)	359	17.5	100	Two-state	133	1.05	1.03	1.77	2.16	0.67
Core	370	8.8	79	Two-state	92	0.10	1.57	1.93	2.35	1.66
22–90	375	5.7	51	Two-state	67	1.22	1.36	1.84	2.34	2.40
1–31	–	No peak	–	None	25	Flex	–	–	–	–
32–108	371	2.4	19	Continuous	77	0.35	–	1.80	–	–
1–37	–	No peak	–	None	34	Flex	–	–	–	–
38–108	363	2.2	19	Continuous	68	0.40	–	1.90	–	–
38–73	–	No peak	–	None	32	–	–	–	–	–
38–78	–	No peak	–	None	33	Flex	–	–	–	–
1–50	350	0.9	11	Continuous	61	0.5	–	1.67	–	–
51–108	361	1.6	17	Continuous	44	0.10	–	2.01	–	–
1–73	338	6.0	51	Two-state	92	1.15	0.99	1.41	2.02	1.53
74–108	370	1.6	28	Two-state	33	0.75	1.26	1.75	2.14	0.52
1–83	343	8.4	62	Two-state	97	1.20	1.05	1.56	2.15	1.50

For a variety of structures identified by sequence range, DCM predictions are given here for the T_m based on the maximum in the C_p curve, excess C_p,max that does not include baselines, the percent reduction of the relative scaled C_p,max compared to intact Trx, character of the folding transition, maximum number of H-bonds (HB no.) in the X-ray structure template, locations for the rigidity percolation threshold (θ_RP), native state (θ_nat), transition state (θ_TS) and unfolded state (θ_unf) in terms of global flexibility, and the normalized barrier height (BH). The core defines a structure that has the same number of residues as intact Trx, but all H-bonds (and salt-bridges) are removed that cross-link a residue that is within the range 22–90 to a residue outside this range. Intramolecular H-bonds within or outside the range 22–90 are allowed. The scaled C_p,max is defined as (C_p,max of the fragment times 108 for the number of residues in the intact Trx) all divided by (C_p,max of intact Trx times the number of residues in the fragment). The normalized barrier height is defined by (the free energy difference between the transition state and the average free energies of the native and unfolded states) all divided by RT_m. When Flex is used for the value of θ_RP, this indicates that no peak is observed in the rigid cluster susceptibility because the structure is always flexible. The value of θ_TS represents the minimum in the flexibility free energy at T_m when the transition is continuous.

There are four cases where the fragments undergo a continuous folding transition, meaning only a single free energy basin is present. The location of the minimum increases (from low to high global flexibility) as temperature increases. In a continuous transition, there is no metastable state, and thus no free energy barrier to surmount. All fragments with continuous folding transitions have weak heat capacities with more than 80% reduction in C_p,max relative to intact Trx. Moreover, each possesses an extremely flexible native state. In contrast, fragments 22–90 and 1–73 exhibit strong two-state behavior, with relative G_f(θ,T_m) barrier heights even greater than intact Trx. The folding core, fragment 22–90, maintains a high degree of global flexibility in the native state at its T_m. Unlike fragment 74–108, the flexibility within 22–90 indicates that a substructure rigidity transition is not required for a free energy barrier. Rather, the presence of a barrier requires a large increase in the number of independent dof upon breaking of intramolecular constraints. Typically, the jump in dof will straddle the rigidity percolation threshold,^17,18 but for most of the Trx fragments checked (all but 1–73 and 1–83), they are very flexible within the native basin.

Interestingly, fragment 1–73 has the lowest T_m (338 K), indicating that it is much less resistant to heat denaturation than wild-type Trx (T_m=359 K). All fragments, except for 1–50, 1–73 and 1–83, have a greater T_m than that of intact Trx (see Table 1). This perhaps counter-intuitive result indicates that simply having more intramolecular constraints in the native state is not the only way to increase T_m. Flexibility in the native state indicates a disordered structure (at least in part) with less constraints and higher entropy. Using a two-state model estimate (T_m≈ΔH/ΔS), it is apparent that a smaller change in entropy upon unfolding is another means to increase the T_m. Conventional wisdom states that (increasing, decreasing) the number of native-constraints will generally (increase, decrease) both ΔH and ΔS simultaneously. However, details in constraint placement are the determining factor of ΔH and ΔS contributions, where conformational flexibility and enthalpy-entropy compensation are intimately related.^17,18,24 Accounting for these effects in a general way (beyond a two-state model), DCM predictions show that all fragments in Table 1, except 1–73 and 1–83, have disordered native states. Fragment 1–83, which is called mini-Trx, has been shown by spectroscopic measurements to form a compact native structure that retains function.³⁰

Experimental DSC C_P analyses on all Trx fragments listed in Table 1 except 22–90 and 1–83, for which DSC data is not available, reveal each to be natively disordered.^5,7 Experimental determination of absolute heat capacity uncovers no cooperative transition in any of the isolated fragments.^5,7 Likewise, a drastic reduction in predicted C_p,max (compared to intact Trx) is found (Table 1). Four fragments completely lack a peak within their theoretical C_p curve. Five of the remaining six fragments exhibit at least an 86% reduction of the maximal C_p, with much broader curvature, indicating that they too are predicted to be largely without structure. Nine out of ten C_p predictions are in excellent agreement with the DSC measurements. The DCM predicts that fragment 1–73 possesses a significant C_P peak, contrary to experimental annotation as it being natively disordered. The peak height is 6.0 kcal/(mol K), which constitutes a 65% reduction from intact Trx. Two-state behavior is predicted within the 1–73 fragment with a relative barrier height almost twice as great as that within intact Trx, but with its T_m 21 °C lower. Its T_m of 338 K is the lowest of any fragment investigated, indicating that it is much less resistant to heating.

Hydrophobic interactions are commonly expressed in terms of accessible surface area (ASA) of polar and apolar groups. The minimal DCM does not explicitly account for this effect, but it is indirectly accounted for through its free parameters,²⁴ which in principle can be adjusted based on ASA. Calculation of ASA and H-bond energies depend on conformational geometry. Variation in ASA and H-bond energies are related to geometrical properties of fragment conformation as its structure deviates from native Trx. In light of the observation that H-bond breaking/forming is directly coupled to the gain/loss of hydrophobic interactions,³¹ it is fair to reason that there is a geometrical coupling between ASA and intra-molecular H-bond geometries. In the implementation employed here, the DCM calculation inherits error in its predictions because fragment structure is modeled (for simplicity sake) using atomic coordinates of the native structure. Although ignoring geometrical variation brings about errors, the minimal DCM has been shown to provide much insight into a wide array of phenomena^17,18,24 consistent with experiment. Therefore, it is prudent to apply the minimal DCM, not only to test its limitations, but also to understand the significance played by the H-bond network. Interestingly, the same reason (geometric coupling between H-bonds and hydrophobic interactions) in reverse can be used to justify neglect of H-bonds! Consequently, two opposite theoretical approaches, one focusing only on ASA of polar and apolar groups, and the DCM focusing on the H-bond network, have success in understanding protein stability. The DCM is not intrinsically limited, however, to just H-bond networks. Work to extend the DCM to also explicitly account for hydrophobic interactions and non-native geometries is in progress.

Quantitative flexibility measures calculated by the DCM are found to be markedly robust under strong native conditions.²⁴ Thus, flexibility predictions under strong native conditions are expected to be largely unaffected by slightly modified (u, v, δ_nat) parameters, even when much more accurate stability predictions can be ascertained. The reason why flexibility measures are less sensitive to the precise parameter values is due to reduced constraint fluctuations at low T, where native contacts become quenched in optimal geometries. This explains why FIRST, an athermal rigidity model, obtains good flexibility predictions for the native state of a protein. The degree of flexibility within all fragments, except 1–73 and 1–83, are predicted to be natively disordered or unfolded because θ_nat>θ_RP or θ_nat does not exist, respectively. Mini-Trx (1–83) is known to possess a compact native structure.³⁰ Of the ten cases that were concluded from C_p measurements that the fragments are natively disordered or unfolded, nine predictions are in good agreement. The only exception, is for fragment 1–73, having θ_RP−θ_nat=0.16 that predicts a compact native state. Interestingly, fragment 1–73 deviated from theoretical ASA-based C_p predictions,^5,7 and it was concluded based on this anomaly that some residual native-like structure must be present. It was proposed that the helix containing the active site retains native structure, and a net number of apolar groups are buried within a cluster. Moreover, the structural and dynamic NMR data indicate helicity and rigidity in the region around the active site.³² Although these characteristics lead to distinct geometric features, fragment 1–73 was classified as natively disordered, implying the DCM θ_RP−θ_nat prediction should be negative. This discrepancy may be somewhat reconcilable based on the predicted low T_m of the fragment. A low predicted T_m is consistent with having a greater fraction of unfolded populations probed in contrast to the other fragments with higher predicted T_m. Therefore, a closer look at fragment 1–73 and its complimentary fragment is warranted.

Complementary fragments (1–73, 74–108) are both predicted to unfold in a two-state manner. The melting temperatures for fragment 1–73, wild-type Trx, and fragment 74–108 are 338 K, 359 K, and 370 K, respectively. At T=359 K, the corresponding individual flexibility free energy curves show fragment 1–73 is predicted to be unfolded, whereas fragment 74–108 is predicted to be in the native state. Both barely possess a shallow metastable state. From Table 1, the transition states (at their respective T_m) are (1.41, 1.75) for fragment (1–73, 74–108). What happens when these two fragments associate? It is tempting to view the intact Trx as having its transition state controlled by fragment 74–108, while the skewness in its native state is controlled by fragment 1–73. From a kinetics viewpoint, it appears that fragment 74–108 may serve as a folding nucleation site, which is not a rigid substructure. Nevertheless, a certain degree of molecular cooperativity follows from forming native contacts during association. Therefore, it is necessary to understand the affect that constraint topology has on modifying cooperativity and stability.

Fragment association allows more cross-linking H-bonds to form, thereby lowering enthalpy, and further constraining conformational flexibility (i.e. decreasing entropy). On association, 1–73 becomes less flexible compared to its unfolded state. It is interesting to estimate the relative importance of the fragments in stabilizing intact Trx compared to the intramolecular interactions between the fragments based on the predicted heat capacity contributions. Once relative size is accounted for, a simple, and naïve, estimate (from Table 1) suggests that fragment (1–73, 74–108) constitutes about (51%, 28%) of the thermodynamic response during the unfolding transition. If there were negligible coupling between the fragment pairs, a naïve estimate would be correct. This exercise yields a total contribution of only 79%. The shortcoming is not surprising considering all bridging constraints are ignored. Moreover, this crude estimate does not take into account differences in the transition temperature for each fragment. Two immediate conclusions follow from these results. (i) Fragment 1–73 is stabilized dramatically by its smaller complement, at the expense of a slight destabilizing effect on the smaller fragment. (ii) Neither fragment 1–73 nor 74–108 plays a dominant role in the structural transition upon unfolding. Rather, the bridging interactions between these two fragments play the main role in the thermodynamics of intact Trx. Bridging interactions are central to the understanding of Trx stability via fragment pairs. Therefore, a simpler procedure of simulated proteolysis is employed to look at stability issues between all complementary fragment pairs.

Simulated proteolysis within Trx

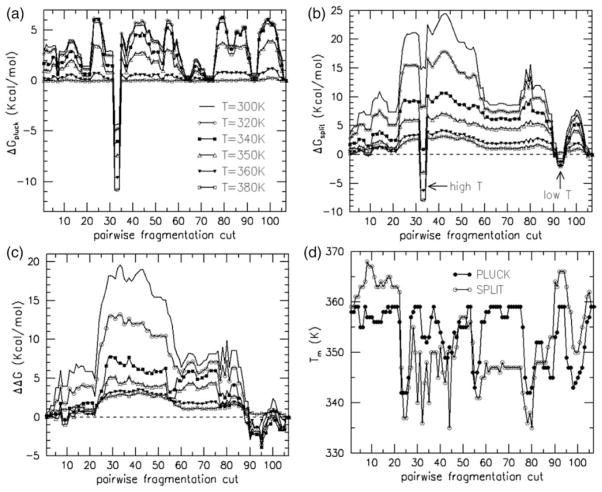
In the analyses above, the fragments were investigated individually. Here, the DCM is used to determine if complementary fragment pairs will reconstitute. Two types of proteolytic cuts are performed (Table 2). The “pluck” method simply removes a peptide bond, meaning that all cross-linking constraints between the two fragments remain. The “split” method removes the peptide bond, and all cross-linking constraints. Plucks can be considered as a reconstituted fragment pair, whereas splits correspond to physically separated fragments. Discounting free energy contributions from peptide bonds themselves, the change in free energy between intact Trx and reconstituted complementary fragment pairs are shown in Figure 4(a) at six different temperatures. Generally, a reconstituted pair is less stable than the intact reference at any temperature, although there are three cut regions (62–65, 71–75, 91–95) that show little temperature sensitivity. The specification of a cut is defined by x (say 62) that removes the peptide bond between residues x and x+1 (i.e. the peptide bond linking 62 and 63). Interestingly, Figure 4(a) indicates that reconstituted structures from cuts at 32 and 34 are more stable than intact Trx, as seen by the large drop in ΔG values regardless of temperature. The reason for this stability gain is because the disulfide bond between residues 32 and 35 provides the required structural support, but does so at the expense of creating strain within the backbone loops between these residues.

Table 2.

Fragment cut definitions used in this work

Type	Computational implementation	Physical analogy
Pluck	Remove peptide bond only	Reconstituted fragment pair
Split	Remove peptide bond and all cross-linking H-bonds	Physical separation of fragments
Track	Remove only cross-linking H-bonds	Hierarchical protein unfolding via H-bond unzipping

Figure 4.

Free energy differences are plotted against simulated proteolysis cut position where a set of symbols is used to denote different temperatures for all ΔG graphs. (a) ΔG_pluck>0 indicates the perturbed structure is less stable relative to intact Trx, and ΔG_pluck<0, shows that the cut stabilizes the structure. (b) ΔG_split shows two locations where the perturbed structure has greater stability than intact Trx, but over different temperature ranges. (c) ΔΔG=ΔG_split−ΔG_pluck is plotted against simulated proteolysis cut position. When ΔΔG>0, two fragments reconstitute. ΔΔG<0 implies the protein will fragment into two pieces. (d) Melting temperatures are plotted against cut positions.

A similar analysis of free energy change between intact Trx and separated fragments (split) is shown in Figure 4(b). Splitting Trx into two separated fragments is thermodynamically unfavorable, compared to intact Trx, at all temperatures except for splits within regions 32–34 and 92–94. Splits at 32–34 are predicted to be stabilizing (see Figure 4(b)) only at high temperatures where the entropy gain overcomes the enthalpy gain. Splitting the protein in the region of 92–94, which is part of a loop region connecting β5 and α5, is found to be more stabilizing at low temperatures. A simple explanation for the observed stability gain is due to the entropy loss associated with tethering α5, which is itself an extremely stable unit, against the rest of the protein. However, based solely on this explanation, one should expect that greater stability would be derived at higher temperatures. This apparent contradiction is resolved because at higher temperatures α5 is able to wiggle around more in the intact Trx structure as well, even though it is tethered. Tethering also lowers enthalpy. As a consequence, the difference in free energy works out to be less at higher temperatures.

In fragmentation studies, the peptide bond is conditionally removed, leaving the relevant question to be whether or not the two complementary fragments will reconstitute. Therefore, ΔΔGs are calculated using an energy cycle, defined as ΔG_split-−ΔG_pluck. As Figure 4(c) shows, fragment reconstitution is generally more favorable everywhere, except in four cut regions (5–6, 8–10, 89–96, 103–106). These trends are in agreement with fragments 10–108, 21–108, 1–93 experimentally determined to be native-like (unpublished results), and as such they are not expected to reconstitute. Interestingly, cut regions 5–6 and 8–10 both prefer to reconstitute at low and high temperatures, but to split at intermediate temperatures. However, region 5–6 has a very narrow temperature range near T=350(±10) K and |ΔΔG|<0.25 kcal/mol. The intermediate temperature range for region 8–10 is broader (T=350(±20) K) and |ΔΔG| can become greater than 1 kcal/mol. Regions 89–96 and 103–106 favor splitting at low temperatures, and reconstituting at higher temperature. It is also noted that at very high temperatures, α5 would prefer splitting away from the rest of the protein. Splitting around Ala93, as discussed above, is favorable at all but very high temperatures, where the difference in stability is small. Fragment pairs derived from cuts within the region 20–60 show a relatively stronger thermodynamic driving force to reconstitute at low and intermediate temperatures. Reconstitutions between fragment pairs from cuts made within region 60–80 are predicted to be thermodynamically favorable, but to a lesser degree at low and intermediate temperatures. At high temperatures, these cut regions merge.

Melting temperatures are also investigated for both types of cuts. Treating both fragments as a single system, whether they reconstitute or split, allows C_p curves to be calculated. T_m is based on the maximum of these curves. When two separate fragments exist, it is not clear which one, or possibly both, melts using this type of analysis. As shown in Figure 4(d), the T_m for the pluck data (reconstituted fragments) is never greater than T_m of intact Trx (359 K) and is more than 70% of the time within 4 K lower. The T_m as calculated for the split data (separating fragments) is most frequently lower than the T_m of intact Trx, but is greater in the cut regions (3–22, 90–95, 104–105). Four cut regions (23–26, 54–57, 77–81, 98–101) are found to have relatively lower T_m in both the pluck and split type of cuts. The significance of these characteristics is not obvious, but intuition suggests that when large deviations are found in T_m, the missing constraints play an important role in maintaining stability in intact Trx. In this vein, it is concluded that these seven identified regions are thermodynamically sensitive. These regions are compared to backbone flexibility characteristics (Figure 5) discussed below. It is found that the second set of cut regions (23–26, 54–57, 77–81, 98–101) all fall in rigid regions that are over-constrained. The other three cut regions break into two parts. Regions 90–95 and 104–105 are found to be flexible, whereas, 3–22 is mixed between flexible and rigid. However, it is also demonstrated in the next section that there is a high propensity for these latter three portions of Trx to be partly unfolded.

Figure 5.

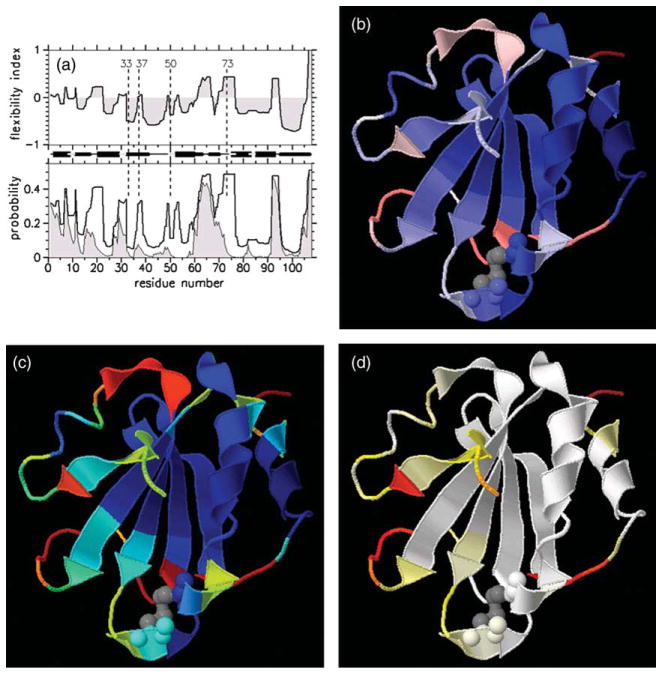
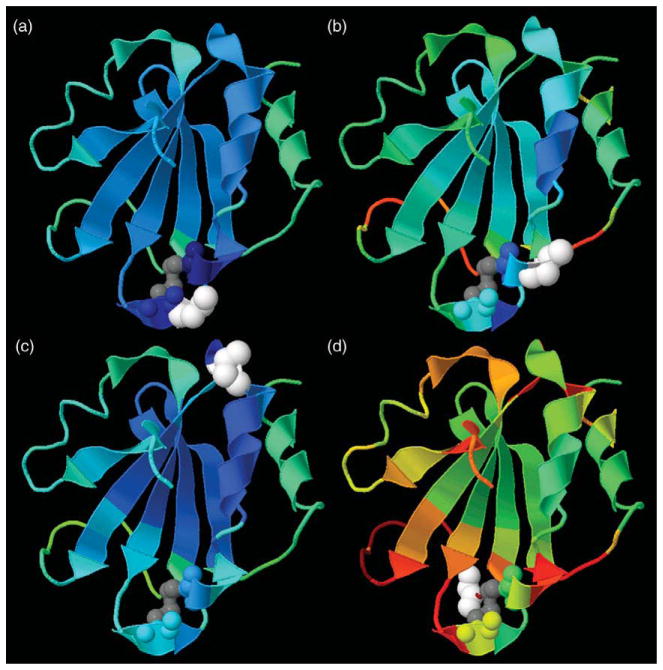
Native state backbone flexibility profiles for T=338 K. (a) Three backbone measures for flexibility are plotted against residue number, where flexibility index, F_index, is in the top panel, the probability to rotate, P_R, and probability to be an independent dof, P_idf, are both shown in the lower panel. Shading is used for P_idf. Between the two panels is a schematic representation of the secondary structure along the sequence. Residues 33, 37, 50 and 73 are highlighted using vertical broken lines to guide the eye between the three graphics. These three quantities are rendered onto a 3D cartoon representation. Gray coloring for the disulfide bond between residues 32–35 highlights the active site region. (b) F_index is colored red when flexible, blue when rigid, and white near marginally rigid. (c) P_R is colored red when very flexible, yellow when flexible, green when marginally rigid, cyan when rigid, and dark blue when very rigid. P_R highlights the regions that maintain being flexible, or rigid consistently. (d) P_idf is colored white when it equals zero, and (yellow, red) for when there are (low, high) density of independent dof.

Elucidating a hierarchical unfolding pathway

The skewness of the native basin (Figure 2(c)) creates a large ensemble of flexible conformations. This leads to the question of whether or not Trx has multiple unfolding pathways. Different unfolding pathways are defined based on the order that native contacts break. Consequently, an astronomical number of test pathways should be considered, and those with the lowest free energy costs along the trial unfolding path are presumed to be the ones the protein will frequently follow. The analysis employed here is similar in spirit to investigations using FIRST,^33,34 where pathways are defined based on the prescription of removing H-bonds one at a time in order from highest to lowest energy. In this report, connection between the fragmentation results and the unfolding process is of interest. Therefore, a prescription for hierarchical unfolding is defined. Using the DCM, the relative stability/ instability of internal protein regions is used to determine the order in which entire groups of bridging H-bonds and salt-bridges break simultaneously in a cooperative manner.

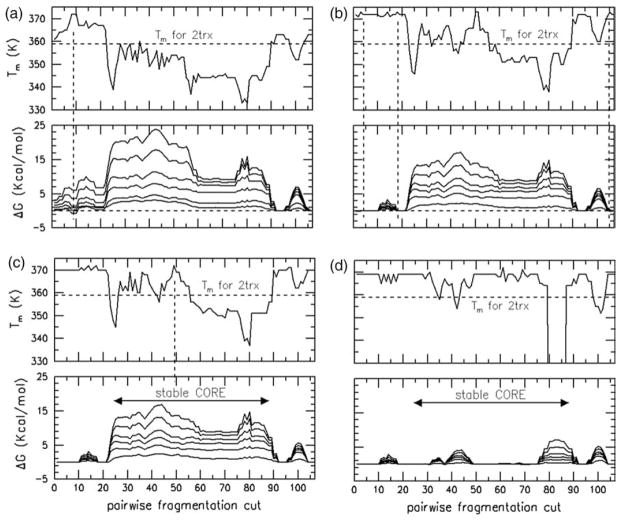
A “track” method is introduced to track a hierarchical unfolding pathway, where the procedure is similar to pluck and split (see Table 2). The track method is used to evaluate the relative stability of a protein when it is cleaved at a specific residue location. Cleaving defines two fragments (like pluck or split), but only cross-linking intra-molecular contacts (i.e. H-bonds and salt-bridges) are removed. All covalent bonds are left intact. The change in free energy between the initial structure and a particular cleave is calculated. The transition temperatures for all final cleaved structures are also calculated. As a primary criterion, cut positions are selected based on those cleavages that lower free energy. As a secondary criterion, cut positions are selected when they increase the T_m the most. These two rules define a series of successive cleavages that form the unfolding pathway. This pathway occurs by way of fragmentation steps ordered sequentially to maintain the greatest stability throughout the process. This exercise defines an unfolding path that is hierarchical in nature, as it is completely controlled by sequence. The uncovered hierarchical path is physically reasonable, though not expected to be unique due to the high degree of flexibility in the native basin.

Starting with intact Trx, it is found that removing bridging H-bonds at track-cuts 92–94 makes the protein more stable, whereas track-cuts at all other sites destabilize the protein. After cleavage, the T_m of the partly unfolded protein increases to 366 K. The graphs showing these data are not shown, because they look similar to Figure 4(c) and (d). All the stabilizing track-cuts at 92 through 94 are made. Then another set of all possible track-cuts is calculated, as shown in Figure 6(a). No track-cut that increases stability is found. The least destabilizing location is at 8, 9 and 10, and it considerably elevates T_m to 372 K. Consequently, a second set of track-cuts in the range 8–10 was made. The next stage of all possible track-cuts is shown in Figure 6(b). There are four regions with elevated T_m, but three of them have no destabilizing effect, while the remaining has a large destabilizing effect. All three of the non-destabilizing regions are therefore cleaved. The protein at this point is partially unfolded. The outcome of the next set of track-cuts shows (Figure 6(c)) that there is no place to cut without a high free energy cost (except in two isolated stable regions). It is found that the remaining region 22–90 is very stable, and any single cut within it completely destroys stability, as illustrated in Figure 6(d). The procedure discussed here is summarized in Table 3. Once the folding core breaks apart, the residual peaks in free energy differences identify two helical structures in the range (11–18) and (95–107) that are predicted to preempt the folding process. Surprisingly, the region 76–89 that has loop structure and a beta-hairpin turn maintains structural stability after disintegration of the folding core. However, the loop region has an extremely low melting temperature (off scale), indicating that the loop will remain flexible, and disordered. The beta-hairpin is expected to form only as a short-lived substructure.

Figure 6.

In all four panels, two graphs (bottom and top) are shown. ΔG of track-cuts with respect to a previously perturbed structure is plotted against cut-locations in the bottom graph. These data depend on temperature, but the curves lack labels for clarity. Although there are some line crossings, generally, the greatest ΔG occur at 300 K, and each line moving downward tends to flatten out, corresponding in turn to 320 K, 340 K, 360 K, 380 K, and 400 K. The top graph shows the melting temperature. All four panels (a)–(d) have the same scale for the abscissa and ordinate. Therefore, axis labels are only provided on the graphs in the left-most and bottom-most panels. Each panel shows the result of a series of fragmentations that is explained in the text.

Table 3.

Hierarchical unfolding pathway by successively cleaving off fragments

Step	ΔG (kcal/mol)	Tm (K)	Fragmentation region
1	−1	366	92–95
2	1.4	372	8–10
3	0	372	1–7, 18, 21, 104–107
4	7	372	49–51

For the purpose of this Table, the quoted ΔG is taken at 340 K.

Based on the hierarchical unfolding pathway, Trx is predicted to have a stable core that must break apart for it to completely unfold. The flexibility free energy for fragment 22–90 (Figure 3(b)), representing the folding core, is very stable, yet flexible. Interestingly, the G_f(θ,T_m) barrier height of intact Trx is actually lower than 22–90. There may exist other unfolding pathways (for example following the global flexibility order parameter as a reaction coordinate) allowing Trx to unfold with a lower barrier. However, conformational flexibility found in the native state of Trx establishes segue to the flexible folding core, which has two disordered flanking sides. Therefore, the folding core can be expected to appear in the equilibrium ensemble of populated conformations, irrespective of the hierarchical pathway used to identify it. When present, this stable conformational state acts as a gatekeeper between the folded and unfolded basins, because of its deep local minimum in free energy, compared to intact Trx. These considerations lead to the prediction that the presence of the folding core will create a kinetic trap. This means that Trx will find itself most frequently in a state that is partly ordered (native-like) and partly disordered. Finding this conformational state is easy, whereas getting out of it is more difficult (i.e. kinetic trap). This prediction is consistent with experiments on unfolding kinetics of Escherichia coli Trx shown to exhibit two-state behavior,¹⁹ whereas refolding kinetics is observed to be multi-phasic.^20,29 The prediction that the core-structure is a kinetic trap, and the interpretation of its role as an intermediate state along the folding/unfolding pathway is compared to experimental results in the next to last section (immediately prior to Conclusions).

Table 1 indicates that the C_p,max of the core fragment is significantly larger than the C_p,max of all investigated natively disordered fragments. In fact, the C_p,max is even greater than that of the 1–83 fragment, which is natively structured and retains function.³⁰ The C_p,max of 1–83 is second largest in Table 1 (not counting wild-type Trx). Nevertheless, θ_nat of the core fragment is 1.57, indicating that it is markedly flexible (and consequently voluminous), whereas wild-type Trx and 1–83 are much more compact (θ_nat=1.03 and 1.05, respectively). Despite this native flexibility, the core fragment is very stable; its T_m is actually 11 K higher than the wild-type T_m. It has already been pointed out above that a rigid⇔flexible transition is not required for a heat capacity barrier; however, the discussion here also illustrates that rigid structures are not necessarily a prerequisite to stable conformations. While protein stability and flexibility are frequently anti-correlated,³⁵ there is no theoretical reason to assume the ubiquity of these observations. The DCM is uniquely suited to test all sorts of paradigm permutations within QSFR. (Note that the stability of the core fragment and associated folding/unfolding consequences are discussed in detail below.)

Characteristics of molecular cooperativity within intact Trx

Many thermodynamic quantities can be estimated using macroscopic two-state thermodynamic models, which typically require fitting three free parameters to DSC profiles. A major advantage of the DCM, besides not being limited by the assumption of a two-state process, is its ability to predict local QSFRs that are consistent with protein thermodynamics. The QSFR measures are functions of temperature, and dependent on the ensemble of conformations that are being probed. In particular, if a protein exhibits two-state behavior, QSFR measures can be calculated for the native, transition, and unfolded states. QSFR in the native and transition states provide the most useful information. These local QSFR measures provide insight into the characteristics of molecular cooperativity.

The DCM quantifies local backbone flexibility in several different ways. One indicator is the probability for the backbone torsion angles to rotate (P_R). A flexibility index, F_index, is used as another indicator to characterize the local density of excess independent degrees of freedom or redundant constraints throughout a protein. F_index and P_R have been shown to correlate well with experimental B-factors and folding cores,^17,18 respectively. In a previous investigation of two RNase H orthologs,²⁴ it was demonstrated that backbone flexibility in the native state is, for the most part, evolutionarily conserved at appropriately shifted temperatures (i.e. the T_m). Differences in enthalpy-entropy compensation mechanisms were also uncovered, which provided intuitive explanations for the cooperativity correlation differences in response to mutation. In this work, deeper connections between flexibility and stability are sought within Trx by using additional QSFR measures. Here, the probability for a dihedral angle to be an independent dof, denoted as P_idf is also calculated, which links F_index and P_R. It should be pointed out that P_idf is not a unique measure, because the location of independent dof within distinct flexible regions is to some degree arbitrary. The rule employed here to remove this arbitrariness, is to preferentially identify independent dof along the backbone, and also preferentially assign them to dihedral angles that are closer to the N terminus.

The three QSFR backbone flexibility measures {F_index, P_R, P_idf} are plotted against backbone residue location (Figure 5(a)), each showing a different aspect of thermal-mechanical response within Trx at T=338 K. At this temperature, Trx processes only a native basin (see Figure 2(a)) with compact structure that maintains flexibility mainly in its loop regions. The three quantities {F_index, P_R, P_idf} are shown as a cartoon rendering of the three-dimensional structure of Trx (Figure 5(b)–(d)). These structural renderings and comparison with secondary structure elements along the sequence (Figure 5(a)), reveal helix α5 (residues 95–107) and the majority of the β-sheet to be rigid. Inspecting all four plots within Figure 5, clearly shows that Trx is predicted to be globally rigid at T=338 K, with intrinsic flexibility within loop regions and on the fringe of some secondary structure elements. This general pattern is not surprising, as it is found to be typically the case for globular proteins under strong native conditions. More importantly, special locations that have been addressed experimentally are of interest to compare with the flexibility predictions.

Curiously, α2 (residues 32–41) is not predicted to be contiguously rigid. Despite its location at the center of the helix, Met37 corresponds to a relatively high P_R value. The flexibility within Met37 derives from its location directly adjacent to a kink within the helix. The helical kink is caused by the evolutionarily conserved Pro40,³⁶ observed within all solved Trx structures. Based on ¹³C NMR relaxation analyses, LeMaster & Kushlan have suggested that the kink caused by Pro40 provides flexibility for the peptide plane of Lys36, widely believed to be critical for a redox change mechanism of the enzyme.³⁷ Flexibility is exhibited within the flanking sides of the active site, which itself forms a rigid substructure between Cys32–Cys35. Both Met37 and Trp31 show approximately the same degree of backbone flexibility. Note that Lys36 is part of the rigid active site structural motif, where it sits at the edge between rigid (Cys35) and flexible (Met37). By hydrogen exchange experiments under strongly native conditions¹⁹ it was concluded that Lys36 and Ala46 have no significant change in their exposed surface area to which the guanidium chloride denaturant can bind. Also Leu24 and Leu79 were found to have relatively slow exchange kinetics. All four of these locations are predicted to be in a local rigid cluster.

On the flanking sides of the active site, the flexibility index characterizing the motion at Trp31 and Met37 is low (Figure 5(a) and (b)). The affect of a few independent dof controlling many dihedral angles implies that correlated motion is propagating. Correlated motions are associated with low |F_index|, regardless of whether P_R is low or high. A low |F_index| implies that the region is near marginally rigid. Regions within a protein generally fluctuate between being rigid or flexible, which is why P_R is usually not zero or one (Figure 5(c)). The P_R measure makes flexible regions appear more flexible than indicated by F_index. This difference is because the number of independent dof within flexible regions, or the number of redundant constraints within rigid regions, is not of any relevance in the P_R measure, whereas it is the key attribute of the F_index. Connection between P_R and F_index is visualized in terms of high/low density of independent dof that are accumulated along the backbone (Figure 5(d)). A high density of independent dof is generally found in loop regions. However, loop regions that are part of correlated motions often will have low density of independent dof.

In this section, the mechanical properties of residues {33, 37, 50, 73} are considered explicitly because cuts were made involving these residues (see Table 1) where the thermodynamics of each complementary fragment pair was investigated separately. Gly33 and Gln50 both occur within over-constrained regions. Met37 is found to be flexible (moderately high P_R) within a correlated region (very low F_index). Based on the high values of P_R and F_index it appears that residue 73 is flexible, but not involved in molecular cooperativity. One source of molecular cooperativity is from flexibility among many dihedral angles that is controlled by few independent dof over extended regions. Another source of cooperativity is through paths of rigidity, controlled by the number of excess redundant constraints within these rigid substructures. How are these mechanical notions of molecular cooperativity related to the thermodynamic notion involving free energies?

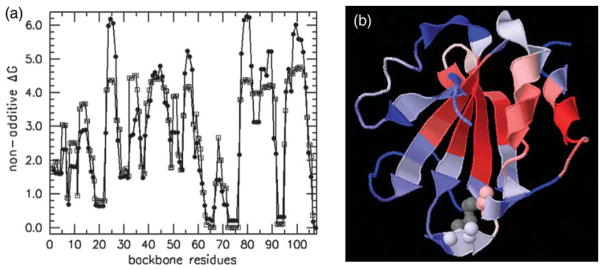
Given the analysis used above on fragment stability and hierarchical unfolding, differences in free energies in perturbing the protein using the pluck, split and track cuts are calculated. This free energy is defined as ΔG_na =G_pluck +G_track −G_split − G_Trx and is used as an indicator of the degree of non-additivity found within different parts of the protein. If the cutting procedure was always between uncoupled subsystems, then it would follow that ΔG_na=0. Larger |ΔG_na| values imply that non-additivity is more prevalent in that particular cut region. Intuition suggests that the presence of non-additivity will be more appreciable in over-constrained regions, and less so in flexible regions. Through network rigidity, the DCM directly links molecular cooperativity to the non-additivity of conformational entropy. Connection between non-additivity in total free energy of a protein and its flexibility is investigated by comparing ΔG_na to backbone flexibility (Figure 7). It is found that ΔG_na linearly correlates best to P_R, having a R=0.87 correlation. These results confirm expectations based upon intuition, and are consistent with conclusions from hydrogen exchange experiments that the central β-strands form a cooperatively folding unit.¹⁹ Moreover, the greatest degree of non-additivity, which imparts molecular cooperativity, is between β2 and β4 that were identified as the initiating nucleation center.² Additionally, there is a relatively high degree of non-additivity in the α-helix at the C terminus, corresponding to an independent process from the β-strands, but reflects cooperativity present within a helix-coil transition. The observation that (rigid, flexible) regions exhibit (more, less) non-additivity in the otherwise sum-zero free energy cycles is expected to be generally true, because the underlying mechanism invoked is network rigidity. It is worth noting that ΔG_na is found to be positive for all temperatures and cut-positions along the backbone. Negative ΔG_na may appear when constraints are added, but this has not been checked.

Figure 7.

(a) ΔG_na is plotted against backbone cut-position, identified using filled circle symbols. In addition, y=A+BP_R (with A=5.054 and B=−10.34) is also plotted against backbone position, identified using open square symbols. The (A and B) constants are obtained by linearly correlating ΔG_na to P_R. (b) ΔG_na is rendered onto a 3D cartoon of Trx using color red for high values, white for intermediate values, and blue for low values. The coloring scale is relative to the input data, with no absolute range defined. Gray coloring highlights the disulfide bond at the active site (residues 32–35).

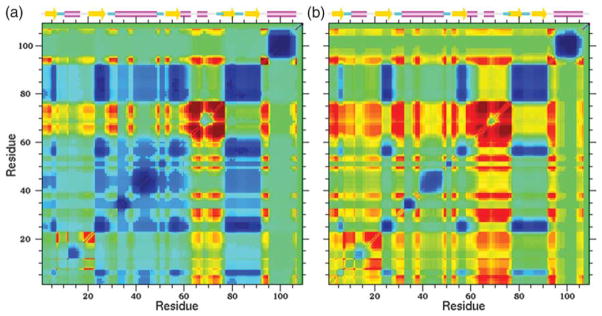
Notwithstanding exceptions, it is reasonable to assume that correlated motions occur on long time-scales, essentially determined by how close a flexible region is to being rigid. Although kinetics is not addressed in the DCM, it is expected that QSFR measures are meaningful on any time scale that is quasi-stationary. With this view, it is prudent to look at correlations between pairs of dihedral angles to quantify molecular cooperativity. A cooperativity correlation plot (Figure 8) for the native state provides insight into the enzymatic functional dynamics of Trx. Cooperativity correlation plots quantify the amount of flexibility/ rigidity correlation between dihedral angle pairs at a given temperature. Two parts of a protein are correlated only if they belong to a single contiguous mechanically linked rigid or flexible region, as determined by network rigidity graph algorithms.^22,38 Two separate localities that are simultaneously rigid or flexible are not correlated. For example, the flexible C-terminal region is not identified as flexibly correlated to the flexible flanking sides of the active site. Cooperativity correlations are calculated as averages over an ensemble of mechanical frameworks, often within a selected basin, via statistical sampling weighted by Boltzmann factors. In Figure 8 only the native ensemble, which is assumed to be most relevant to Trx function, is used in the averaging.

Figure 8.

Native state cooperativity correlation plots with secondary structure schematically shown on top. Red regions are highly correlated via a flexible mechanism, yellow a lesser degree, green there is no correlation, cyan indicates a limited degree that two regions are mutually rigid, and blue regions are highly correlated via a rigid path. Correlations are strongly dependent on temperature. Two cases are shown: (a) T= 338 K, (b) T=359 K, which is the melting temperature of intact Trx.

The degree of correlation depends on temperature. At T=338 K, flexibly correlated regions are identified (Figure 8(a)). Residues (27–31) and (37–39) located on the flanking sides of the active site, and residues (61–75) and (92–95) are not only flexibly correlated to one another, but are members of a previously identified active site groove of Trx.³⁹ Other flexible residues such as (48–54) and (58–60) are not flexibly correlated to either flanking side of the active site. To gain a better understanding of molecular cooperativity, one row (or column) of the symmetric correlation matrix (Figure 8(a)) is selected based on a reference residue, and the correlation along that row (or column) is rendered onto the structure of Trx. For residues 33, 37, 50 and 73 the cooperativity correlation is shown in Figure 9 and summarized in Table 4. Dramatic changes in appearance are a striking feature of viewing molecular cooperativity vis-à-vis different reference sites. Interestingly, the reference residue can be rigidly correlated to one part of the protein, while simultaneously flexibly correlated to another part. Therefore, the color of the reference residue in the structural renderings is selected to be a neutral white. Although, in principle, the cooperativity correlation plots contain complete information (Figure 8), a series of 3D renderings, as illustrated in Figure 9, facilitates analysis.

Figure 9.

The cooperativity correlation plot for T=338 K in Figure 8(a) is mapped onto the 3D Trx structure using residues 33, 37, 50 and 73 as four different reference points. The coloring used for the rendering retains the same meaning as defined in Figure 8. The gray coloring for the disulfide bond between residues 32–35 highlights the active site region. The reference residue is colored white, because it can be flexibly and rigidly correlated to different regions within the protein simultaneously. Renderings for reference residues, 33, 37, 50 and 73 are shown in (a), (b), (c) and (d), respectively.

Table 4.

Summary of molecular cooperativity in Trx characterized by identifying correlated regions for T=338 K

Reference residue(s)	Flexibly correlated	Rigidly correlated	Uncorrelated
Active site Cys32, Gly33, Pro34, Cys35	None, the active site is always a rigid unit	Except for uncorrelated regions, the entire protein is rigidly correlated	7–22, 62–76, 92–108
Side flanks to the active site at residues Trp31 or Met37 giving virtually identical results	61–75, 92–95, 105	None. The flanking sides of the active site are always flexible	7–22, 96–104, 106–108
Gln50	This location is rigid, and therefore is not flexibly correlated with any region	Weakly to 7–18 and more strongly to 33, 35 which are in the active site	19–23, 62–76, 92–108
Arg73	1–22, 26–32, 37–39, 48–54, 58–77, 91–95 Both flanking sides to the active site are included	Virtually none, except weak correlation to the helix between 40–44	Everything else

It may, at first, be surprising that the active site residue Gly33 (Figure 9(a)) is rigidly correlated to the majority of the protein, except three regions (7–22, 62–76, 92–108) for which it is uncorrelated. This result is easily explained. No flexible correlations occur because the active site is a rigid substructure. Due to fluctuations, flexible regions appear and break the propagation of rigidity. On average, rigidity does persist over a large region. Nevertheless, the active site (as a rigid unit) is often flexible with respect to the beta sheet. In contrast, it is clear (Figure 9(b)) that Met37 (result for Trp31 is not shown, but virtually identical) is flexibly correlated to residues 61–75, 92–95 and 105. Gln50 (Figure 9(c)) has similar properties as the active site residue, sharing similar mutually rigid regions. From the perspective of Arg73 (Figure 9(d)), Trx is very flexible with extended flexible correlations. Interestingly, Arg73 is flexibly correlated to residues 37–39 and 48–54, yet Met37 is not flexibly correlated to the residues 48–54. This is not to say that a flexible linkage never occurs between Met37 to residues 48–54, but on average it is more often rigidly linked.

The analysis of molecular cooperativity within Trx implies that the four regions (29–31, 37–38, 61–75, 92–95) are flexibly correlated, presumably moving in concert during substrate binding and/or catalysis to facilitate access to the active site Cys pair. This theoretical prediction is in qualitative agreement with experimentally determined long-timescale (microsecond to millisecond) dynamics inferred from NMR.³⁷ Moreover, H/²H exchange results have determined that significant exchange rate differences at regions structurally proximal to the active site loop occur on changes in the redox state.⁴⁰ The collective nature of the observed changes within the dynamics is strongly consistent with the predicted flexibility correlation.

Intermediate states within Trx

The above cooperativity analysis focused on equilibrium properties of native Trx (T<T_m). From Figure 8(b), it is clear that flexibility increases dramatically at the T_m. However, it is not clear that the equilibrium ensemble is most relevant when making a connection to experiment. If indeed a kinetic trap formed by the folding core appears, then it can be studied in the same way because, by being metastable, it is also quasi-stationary. As described above, the core structure is the same as intact Trx, but with removal of all H-bonds (and salt-bridges) that span residue pairs for which one residue is in the core and the other is out of the core. Thermodynamics and molecular cooperativity of the folding core are analyzed using this conditional ensemble of conformations. The folding core has a free energy profile (Figure 10(a)) that clearly shows it forms a kinetic trap. Interestingly, the T_m of intact Trx (359 K) is lower than the T_m of the folding core (370 K), and surprisingly, at T=359 K, the T_m of wild-type Trx, this kinetic trap has a lower free energy than both the native and unfolding states! This brings about a paradox because it is conventional wisdom that the lowest free energy state represents true equilibrium.

Figure 10.

(a) Under the appropriate conditional ensemble of conformations for the folding core, its flexibility free energy is compared with that of intact Trx in equilibrium at T=359 K. The partially unfolded form (PUF) has lowest free energy. (b) The relative free energies of the native state (NS), unfolded state (US), PUF representing the kinetic trap, and its denatured super unfolded form (SUF) are plotted as a function of temperature. If the actual free energies were plotted, the results would be obscure. Therefore, all data points for all four free energies were plotted and a best linear straight line fit was made. From linear regression, the free energy reference line G_ref=(−2.128T–335.431) kcal/mol was used to define the zero in this plot. Note that T is measured in Kelvin. (c) A color ribbon cartoon for P_R is shown, where red denotes high probability (flexible) and blue is low probability (rigid). Comparison to Figure 5(c) highlights how the PUF is much more flexible compared to the native state. (d) The cooperativity correlation plot within the folding core at T=359 K is similar to that of intact Trx at T=359 K, as shown in Figure 8(b). However, there are no correlations (green) in far off-diagonal terms outside the core region. The flexibly correlated regions that couple to the active site are identical, albeit with higher degree of flexibility.

This apparent paradox is resolved by noting that the folding core is defined from a conditional ensemble, which does not represent a true thermodynamic state. This particular state represents only one type of many partially unfolded states accessible to Trx. Nevertheless, if by chance this conformational state is reached, it will enjoy a lower free energy, which means that it will be well populated for some time period. This time period depends on timescales for which local dynamics destroys the conditional ensemble (when the partially unfolded parts recollect) that leads to this lower free energy. At T=359 K the free energy of this core is not only locally stable, but is, for a time, more stable than either the native or unfolded states, resulting in a deep kinetic trap. This trap allows Trx to be extremely flexible in the core region, and unfolded at its flanks, without unfolding the remainder of the way. The stable core region was identified by hydrogen exchange experiments,^20,29 and core residues were termed class II. The predicted kinetic trap is interpreted as the slow intermediate state previously identified^20,29 from experiments.

This slow intermediate state represents a particular Trx PUF. It is special in that it is easily reached via the identified hierarchal unfolding pathway. The free energy profile of this kinetic trap as a function of temperature (not shown) shows that it exhibits strong two-state behavior (see Table 2). Consequently, there is a PUF free energy basin, and an unfolded version of this PUF, labeled here as super unfolded form (SUF). The unfolding of the core provides the ability for this intermediate to have its own unfolding/folding transition. As the SUF name implies, the unfolded part of the PUF state (the slow intermediate) is more unfolded than it can sustain, as this occurrence represents a fluctuation from equilibrium. The θ_unf of the core, which corresponds to the SUF, is 2.35, whereas the θ_unf of the wild-type Trx is only 2.16 (Table 1). At all temperatures, the free energy of the SUF state is greater than the normal unfolded state. The free energy for the native, unfolded, PUF and SUF states as a function of temperature are shown (Figure 10(b)). At temperatures below the T_m for the PUF⇔SUF transition, there is bias for the SUF state to transition to the PUF state. Conversely, it would be difficult for the PUF to transition to the SUF. Therefore, the SUF state is identified as the medium intermediate state previously identified.^20,29

Kinetic experiments^29,41 have determined that different types of unfolded states exist, related to proline isomerization, which this analysis and implementation of the DCM does not address. The presence of these states does not affect the arguments and discussions made about the PUF and SUF states, which are assumed to have all native proline isomers. It is well recognized that there is both a fast and a slow Trx folding mechanism. Using θ as a reaction coordinate, normal transition state analysis predicts there should be a fast folding mechanism (Figure 2(c)). The finding of the PUF and SUF states, however, complicates this folding process. Instead of going over the barrier from an unfolded state to transition to the native state, a typical unfolded conformation can increase its free energy by ≈1.5 kcal/mol via a fluctuation from equilibrium, and become a super unfolded form. This allows a new pathway to reveal itself, SUF→PUF, which is essentially irreversible because of the steep barrier and difference in free energy that exist between the two states. The PUF state will eventually be lost, but at high temperatures, it is expected to be persistent.

As Figure 10(b) clearly shows, a considerably different situation occurs at lower temperatures. As temperature is lowered, the free energy of the PUF state increases relative to the native state of Trx. This result indicates that, at native conditions, a population of unfolded conformations can follow either the fast or slows paths, as proposed previously from kinetic experiments. However, in the unfolding process (versus the folding process), the kinetic trap is less attractive, and once the PUF state is explored, it cannot get out via the SUF. At low enough temperatures, the PUF becomes a dead-end, and must revert back to the native state. Thus, unfolding in strongly native conditions will look like a normal two-state process. These predictions fit nicely with the experimental results, including the apparent paradox that the slow intermediate was not found in strong native conditions. Furthermore, the existence of a high free energy state beyond the normal unfolded state was concluded to exist, with an estimate of 1.4 kcal/mol for class II residues, which reside in the core substructure. However, in the actual experiments, chemical denaturants are used to shift melting temperatures. Although the DCM can handle solvent properties,⁴² this full analysis is not done here. Nevertheless, the general features of these predictions provide useful insight to help interpret experimental results. Considering the overall qualitative agreement with experimental conclusions about kinetics and intermediate states of Trx, the interpretation of PUF and SUF states as the slow and medium intermediates appears sound.

As just described, the theoretical free energy profiles aid interpretation of the kinetic experiments.^19,20,29 The existence of this stable PUF may play an important role in the function of Trx. What are the flexibility characteristics of the PUF? It is shown in Figure 10(c) that the PUF is much more flexible than the native state. Nevertheless, the PUF preserves the cooperativity correlations found in the native state of wild-type Trx (Figure 10(d) compared to Figure 8(b)). This result suggests that the natively disordered kinetic trap has the same allosteric mechanisms as the native state, and thus, despite being partly disordered, may retain biological function. This result suggests that a molten globule state is well characterized by the PUF, and by having a greater T_m than that of Trx, the unfolded ensemble should exhibit characteristics of a molten globule over a wide range of elevated temperatures near the T_m. As a final remark, in light of the free energy analysis, metastability analysis, and observation that mini-Trx exhibits similar kinetic intermediates as intact Trx,³⁰ it is likely that a hierarchical unfolding pathway analysis on fragment 1–73 will similarly reveal a metastable PUF. If this is the case, the discrepancy between experiment and prediction for the degree of cooperativity found in fragment 1–73 is eliminated.

Conclusions

Flexibility free energy curves are obtained as a function of a global flexibility order parameter, which are central to QSFR. The native state of Trx in strong native conditions is predicted to form a compact structure, which is consistent with experimental results showing that Trx is highly resistant to limited proteolysis. However, near its melting temperature, Trx becomes partly unfolded before it fully unfolds. Obtaining a high degree of flexibility in its native state near T_m, derives from a skewed free-energy barrier, which gives quasi-two-state behavior. Computer-generated proteolysis showed that most peptide cuts are destabilizing, with residues 23–25, 55, 78–80, and 99 being especially so. Only cuts at residues 32–34 or 92–94 are stabilizing. Cuts at residues 32–34 show a strong tendency to form a reconstituted structure over a broad temperature range, but separated fragments are more stable for cuts at residues 92–94. Thermodynamic stability of isolated fragments was investigated. Isolated fragments were generally predicted to be natively disordered, without a cooperative transition, in overall good agreement with experiment.

Investigation of fragment stability clearly shows that bridging interactions between fragment pairs play a key role in the thermodynamics, and non-additivity properties of intact Trx. By focusing on removal of these bridging interactions, presumed to be important for kinetics in terms of Trx stability via fragment dissociation, a hierarchical sequence-directed unfolding pathway is traced, and a folding core is identified. This folding core does not correspond to the transition state. This core structure forms a kinetic trap, which is likely to be the slow intermediate state that is known to exist. Further detailed QSFR analysis on this core structure highlights the fact that a substructure transition (rigid⇔flexible) is not a requirement of free energy barriers. Rather, a large increase in the number of independent degrees of freedom upon release of intramolecular constraints on the poly-peptide chain is sufficient. Consequently, this intermediate state allows Trx to be much more flexible as a partially unfolded form, but it is very stable against complete unfolding. The results of this analysis are fully consistent with kinetic experiments.

The degree of rigid/flexible correlation between residue pairs along the backbone identifies mechanical stability as a function of temperature. Cooperativity correlation plots provide insight into molecular cooperativity by visualizing these data with a coloring schema that is consistent over the entire temperature range. With respect to a reference point, the molecular cooperativity can be visualized over the three-dimensional structure of a protein. Different reference points exhibit very different perspectives about non-local cooperative effects (flexible or rigid). Flexibility predictions are inline with experimental determinations from H/²H exchange. Flexibility characteristics within the kinetic trap are similar to those of intact Trx. In particular, having the same cooperativity correlations with respect to the active site within the structurally well-defined core, suggests that Trx can function as a molten globule, as previously suggested based on early experiments.

Finally, it is found that the widespread predictions from the minimal DCM are in agreement with experimental trends. Specifically, the results aid interpretation of apparent experimental contradictions, and serve as an illustration of the DCM approach to predicting QSFR in general. The DCM captures essential physics through a free energy decomposition that accounts for non-additivity of entropy (or free energy) by regarding network rigidity as an underlying interaction. The DCM allows a host of QSFR predictions to be calculated in practical computational times. Motivated by the resiliency of this minimal DCM as demonstrated here, and other recent works,^17,18,24 a more accurate free energy decomposition scheme that explicitly accounts for free energy contributions from both hydrophobic interactions and residue-dependent conformational states is currently being developed. Methods to explicitly model non-native conformations are also being developed.

Materials and Methods

The DCM applies constraint theory from structural mechanics to the procedure of free energy decomposition that is ubiquitously employed in physical chemistry. Consequently, a coarse-grain scheme that retains atomic level details is defined. The DCM was first introduced using exact transfer matrix methods for investigating helix–coil transitions.^21,42 Subsequently, a mean-field treatment was developed so that protein investigations are computationally tractable, the details of which have been published.^17,18,24 Here, we provide highlights of the theoretical underpinnings of the DCM in general terms. Then the specific free energy decomposition used for the minimal DCM is summarized, followed by a description of the mean field calculation. The most important elements of the simulated annealing procedure that is employed to fit to heat capacity data is provided here (not published previously), which will be of particular importance to those interested in performing DCM calculations efficiently. Finally, methods used for Trx structural manipulations are provided.

The distance constraint model

A free energy decomposition breaks down a system (defining a molecule) into component parts, where each part is assigned a free energy. Decompositions are not unique, and are often constructed in terms of specific molecular interactions, denoted as t. A local free energy is given by G_t=−RT ln Q_t, where Q_t is a microscopic partition function, R is the universal gas constant and T is the absolute temperature. A common assumption is to express the free energy of a particular protein conformation, C, as a linear sum of its components, for example, see Hedwig & Hinz.⁴³ This approach defines a linear decomposition scheme, where the free energy of a conformation takes the form: G(C)= Σ_t N_t(C)G_t(C) and N_t is the number of interactions of type t present in the system. Using the linearity assumption of independent component parts, the partition function takes the form, $Q(C)={\prod }_t{Q}_t^{N_t}$. Unfortunately, this approach overestimates the total conformational entropy because various regions in phase space may be “double counted” due to overlap when different Q_t share the same phase space. Careful analyses^23,44 indicate that, in general, linear decomposition schemes fail because entropy components are non-additive whenever component parts are not independent. Although the assumption of additivity is generally acceptable for small molecules, it is now clearly established that linear decompositions break down when applied to proteins, and other macromolecular systems with highly convoluted non-covalent interaction topologies.^23,44

Constraint theory is explicitly incorporated into the calculations to correct overestimates in the conformational entropy. To achieve this, each interaction is not only assigned a G_t value, but is also represented as a distance constraint (or multiple distance constraints) on the system. These constraints form a network. This network defines a mechanical framework, F, which is analyzed with FIRST.²² FIRST identifies many network rigidity properties, such as rigid clusters, independent/redundant constraints, degrees of freedom and maximally flexible regions. A framework is analogous to a conformation, but is a truly distinct concept because it represents a constraint topology, rather than a protein geometry. Constraints are allowed to form and break, which results in a change in total enthalpy and entropy. An ensemble of all possible frameworks must be considered to calculate protein thermodynamics. Separating G_t into enthalpy (H_t) and entropy (S_t) components yields:

$$G_{\mathrm{\alpha }t}(F)=H_t{\mathrm{\eta }}_{\mathrm{\alpha }t}-RT(S_t/m_t){\mathrm{\sigma }}_{\mathrm{\alpha }t}$$ (1)

where η_αt can be (0 or 1) when the αth local interaction of type t is present or not. When η_αt=0, the interaction is not present so there is no enthalpy contribution, and therefore σ_αt=0, as well, as there is no entropy contribution either. However, when η_αt=1, then σ_αt can be any integer value between 0 and m_t, where m_t gives the maximum number of independent distance constraints that represent type t interaction. Notice that to keep the model simple, only a finite number of interaction types are considered. Therefore, the free energy of a framework is coarse-grained into a function of two discrete variables (η_αt, σ_αt). The value of η_αt (being a 1 or 0) is trivially determined based on the specified framework. More interestingly, σ_αt depends on network rigidity. Consequently, a graph-rigidity algorithm is used to identify network rigidity properties for the framework. The entropy term is categorized in discrete levels of contribution ranging from 0 to S_t, when the constraint is determined to be completely redundant or completely independent, respectively. Rewriting equation (1) with a change of variables then yields:

$$G(F)=\sum _t{\mathrm{\epsilon }}_t{N}_t(F)-\sum _t{\mathrm{\gamma }}_t{I}_t(F)$$ (2)

where ε_t is used in place of H_t, γ_t is defined as S_t/m_t, N_t(F)=Σ_α η_αt and I_t(F)=Σ_α σ_αt. Since pressure dependence is not considered in this work, the enthalpy contributions are treated as energies. G(F) is the total free energy for framework F, which accounts for degeneracy in atomic coordinates consistent with the specified constraint topology.

The estimation for G(F) in equation (2) is not a linear summation over free energy components. The energy contributions are additive, but entropy components of only independent constraints are added. Due to the long-range nature of network rigidity, this procedure is far different than a linear decomposition. Consequently, the estimation for conformational entropy is lower than adding all entropy components (i.e. including those associated with redundant constraints). Unfortunately, sets of independent constraints do not generally provide an orthogonal basis; so double counting of phase space is not completely eliminated. The entropy term in equation (2) provides an upper bound estimate for conformational entropy. This upper bound depends on the identified set of independent constraints, which is not unique. By prioritizing the identification of independent constraints by taking those with lower pure entropy components prior to those with larger entropy components, a unique preferential independent set of constraints is obtained. Preferential sorting provides a rigorous lowest upper bound because it is equivalent to determination of an independent basis set implemented as a greedy algorithm.⁴⁵ This mathematical result is easy to understand using a proof by contradiction. Assume a lower net entropy can be obtained by using one or more high entropy constraints to define an independent set of constraints before lower entropy constraints are checked for linear independence. Since all constraints must be checked, an unchecked lower entropy constraint will likely be found redundant as the network is continued to be built up. If this happens the initial assumption is wrong, because this lower entropy redundant constraint needs to be exchanged with an independent higher entropy constraint at this juncture to get a lower sum. This exchange does not expand the algebraic space covered by the independent set, and therefore has no affect on determination of redundant/independent constraints afterward. Preferential sorting avoids all such possible mistakes by making sure that as the independent set of constraints expands, it is step by step (greedy) a minimum throughout the process.⁴⁵

The partition function is constructed over an ensemble of frameworks and is given by:

$$Q=\sum _F{\mathrm{e}}^{-\mathrm{\beta }G(F)}=\sum _F{\mathrm{e}}^{\mathrm{\tau }(F)}{\mathrm{e}}^{-\mathrm{\beta }E(F)}$$ (3)

where β=1/RT and τ(F)=S(F)/R. In order to calculate Q, one still needs to find computational methods to sample large numbers of frameworks. For each framework, the independent constraints subject to the preferential ordering must be calculated. It turns out that this process can be done not only in a computationally tractable way, but is surprisingly fast. However, to understand the details of the computational method for the minimal DCM, it is prudent to precisely define the free energy decomposition scheme that has been selected to be similar to Ising-like models²⁶ commonly employed in the literature. A fundamental difference is that in the minimal DCM molecular cooperativity is a direct result from network rigidity interactions coupling to the otherwise independent variables. No special nucleation mechanism needs to be invoked because this is automatically taken care of by constraint topology.

Free energy decomposition scheme

In general, a free energy decomposition scheme for the DCM assigns an enthalpy, entropy, and number of bars used to model each constraint. This triplet of numbers is written as (ε_t, γ_t, B_t) using the same notation as in equation (2) for constraint type, t. Note that a constraint can be modeled using one or more bars, specified by B_t, and for simplicity each bar is assigned the same entropy value given as γ_t. By equation (2) the actual entropy contribution could be 0, Rγ_t,2Rγ_t,…,B_tRγ_t, depending on the number of bars found to be independent. In the minimal DCM, the following assignments are made: Covalent bonds: (0,0,5) serves as a reference state. Native torsion constraints: (v, δ_nat, 1) which has only one bar, and both enthalpy and entropy parameters are free to fit to experimental data. Disordered torsion constraints: (0, δ_dis=2.560, 1) where the zero energy value also serves as defining a reference state, and the value of δ_dis is fixed based on previous work.¹⁷ H-bonds to solvent are characterized as: (u, ∞, 5) where the ∞ simply indicates that no entropy penalty is given. Intramolecular H-bond constraints: (E_hb, γ_hb, 5) where five bars are used to represent one H-bond (or salt-bridge treated as special case).

Based on prior work,¹⁷ E_hb gives the local H-bond energy using the function described by Mayo,⁴⁶ which depends on local geometry details. Note that this empirical function gives the lowest possible energy of −8 kcal/mol. The corresponding entropy contribution for one bar is taken as a linear function of this energy, so that γ_hb =γ_max(1+E_hb/8). Without loss of generality, the entropy level of one of the fluctuating constraints (non-covalent bonds) can be set. Exercising this freedom gives γ_hb=0 for the lowest energy H-bond of −8 kcal/mol. The optimal value γ_max=1.986 was also determined in prior work.¹⁷ The transferable parameters were determined based on reproducing experimental C_p data for two diverse proteins (ubiquitin in five different pH conditions and histidine binding protein in one solvent condition). Thus, the disordered torsion and intramolecular H-bond parameters are regarded as transferable parameters (now and when initially optimized). However, there are three remaining parameters {u, v, δ_nat} that need to be determined on a case-by-case basis. The minimal DCM implicitly accounts for hydrophobic interactions and variation in chemical behavior among different amino acids in an effective way by adjusting the three free parameters. Although attempts have been made to fix an additional transferable parameter (i.e. either u, v or δ_dis) it has been found that it takes all three free parameters to provide a simple phenomenological model that can robustly reproduce heat capacity data.¹⁸ It has also been found that proteins sharing the same architecture, but different sequence and/or different solvent condition, can fit to experimental heat capacity data with the same δ_dis by varying only u and v.²⁴

Constraint topology ensembles and free energy landscape in constraint space

Because of the immense number of frameworks within the ensemble, two approximations are made to make the problem tractable. The first approximation is to reduce the number of frameworks sampled by generating a sub-ensemble of constraint topologies that are perturbed away from the input template structure. These frameworks are then partitioned into smaller sub-ensembles, each characterizing a macrostate of a protein in terms of the number of native torsion, N_nt, and H-bond constraints, N_hb, present. The macrostate is represented as a node (N_nt,N_hb) within a two-dimensional grid that defines a free energy landscape in constraint space.

A second approximation is applied to each sub-ensemble of frameworks within a node by expressing the probability for a specific framework, F, to appear within a node as a product function of independent occupation probabilities, p_t, for each constraint type, t. In homogeneous media, this procedure formally defines a mean field approximation where all occupation probabilities of a given type are equivalent. Here, the occupation probabilities are not equivalent, but nevertheless, long-range correlations are truncated via the introduction of the product function, which is the nature of mean field approximations. The product function is given by:

$$P(F)\prod _t{p}_t^{n_t}{(1-p_t)}^{(1-n_t)}$$ (4)

where for simplicity in notation, n_t and t are used in place of n_αt and the double index (α, t). The variational function p_t is selected to have the form:

$$p_t(E_t,E_t^{\prime },\mathrm{\mu },T)={\mathrm{e}}^{-\mathrm{\beta }(E_t-\mathrm{\mu })}/[{\mathrm{e}}^{-\mathrm{\beta }{E}_t^{\prime }}+{\mathrm{e}}^{-\mathrm{\beta }(E_t-\mathrm{\mu })}]$$ (5)

where $E_t^{\prime }$ is the energy that results when the constraint is not present. Although the energy $E_t^{\prime }$ will generally depend on the local environment within the protein, in the minimal DCM all native and disordered torsion constraints and all H-bonds to solvent are treated as independent of their local environment. This simplification is another kind of mean field approximation, because local variations are neglected in favor of a homogeneous description. However, variations in E_t describing intra-molecular H-bond constraints are accounted for by using an energy function⁴⁶ in conjunction with the template native protein structure. The variable μ is a Lagrange multiplier used to control the number of constraints present within the system, and is analogous to a chemical potential. Two types of μ representing native-torsion constraints (μ_nt) or H-bond constraints (μ_hb) are determined using an iterative back-solving method to yield an average number of native-torsion constraints (N_nt) or H-bond constraints (N_hb), respectively. Although occupation probabilities are not treated equivalently, knowing the functional form of the trial function and the global constraint counts allows each p_t to be determined quickly. The occupation probabilities are determined without requiring any network rigidity calculation to be performed. However, network rigidity calculations to identify independent constraints are needed to estimate conformational entropy at a node.

The free energy at a given node has the form:

$$G(N_{\text{hb}},N_{\text{nt}})=U(N_{\text{hb}})-u{N}_{\text{hb}}+v{N}_{\text{nt}}-T(S_{\mathrm{c}}({\mathrm{\delta }}_{\text{nat}})+S_{\text{mix}})$$ (6)

where U(N_hb) gives the average total intramolecular H-bond energy, S_c is the total conformational entropy, and S_mix is a mixing entropy for the number of ways to have N_hb H-bonds and N_nt native-torsion constraints. The mixing entropy is a standard term when applying a mean field approach in terms of a priori assumed independent occupation probabilities. The phenomenological parameters {u,v,δ_nat} directly relate to microscopic enthalpy-entropy mechanisms. When a H-bond (or salt-bridge) breaks, the compensating energetically favorable interaction with solvent is described by u. If a torsion constraint is in a (native, disordered) state it contributes (v,0) energy and is described by v. When a torsion constraint is determined to be independent, δ_nat describes its entropy contribution divided by R. The free energy landscape in two-dimensional constraint space is subsequently determined by calculating equation (6) for each node (N_nt,N_hb). Splitting the problem into separate independent nodes is easy to implement. For a given node, the procedure is to numerically back solve for μ_hb that satisfies the equation N_hb =Σ_t′ η_t′ p_t′ where this sum is only over H-bond constraints, labeled as t′. Due to the simplicity in treating torsion constraints equivalently, the occupation probability for a native-torsion works out to be N_nt/N_nt,max, the ratio of native-torsion constraints present to the maximum possible number. The average H-bond energy is given as U(N_hb) = Σ_t′ E_t′ p_t′, and mixing entropy as S_mix =−R Σ_t[p_t ln(p_t)+q_t ln(q_t)], where q_t= 1−p_t, and index t runs over all constraints. Conformational entropy, S_c, within a node is found by averaging the numbers of independent constraints identified by FIRST such that the estimated conformational entropy within a given node is given by:

$$S_{\mathrm{c}}(\text{node})=R\sum _t{\mathrm{\gamma }}_t\langle I_t(\text{node})\rangle$$ (7)

The average quantities, 〈I_t(node)〉, describe the effect of network rigidity at the mean field level, because mechanical interactions are averaged over a sub-ensemble of frameworks (configurations). In practice, averaging is done using Monte Carlo sampling, where the a priori calculated occupation probabilities for the constraints are used. In this way, the sub-ensemble of frameworks is generated from the probability distribution defined in equation (4). Applying equation (6) at each node combined with Monte Carlo sampling makes this method different than a traditional mean field approach used in homogeneous media of infinite extent. Its major advantage is that long-range correlations due to network rigidity are retained. To go beyond using a mean field approximation, exact calculations would require accounting for each framework in the ensemble directly using equation (3), as was done for describing the helix–coil transition employing transfer matrices.^21,42

Working through the machinery of steps outlined above, a complete two-dimensional free energy landscape can be calculated straightforwardly using equation (6) within each node. In this way, all macrostates within the two-dimensional constraint space are assigned a free energy. However, this approach would lead to a performance that goes as the square in the number of residues. Therefore, an adaptive grid method is implemented where Taylor expansions are used to interpolate between nodes. After all interpolations are finished, the complete free energy landscape is used to provide a more accurate statistical description than a traditional mean field treatment. From the two-dimensional landscape, all thermodynamic properties can be calculated. For example, to calculate heat capacity, first the average enthalpy fluctuation is calculated using the formula:

$$\langle \mathrm{\Delta }{H}^2\rangle =\sum _{\text{node}}[{\langle {(h-\langle h\rangle )}^2\rangle }_{\text{node}}]{\mathrm{e}}^{-\mathrm{\beta }G(\text{node}\mid T,u,v,{\mathrm{\delta }}_{\text{nat}})}$$ (8)

G(node|T,u,v,δ_nat) is the free energy that is numerically determined by equations (6) and (7) in constraint space at each node for a given temperature, T, and the set of parameters {u,v,δ_nat}. The enthalpy part of G, of equation (6), is explicitly given by h(node)= Σ_t,α ε_t,αη_t,α where ε_t,α and η_t,α were introduced above. The non-zero energies that make up the ε_t,α are intramolecular H-bond energies, E_hb, native torsion energies, v, and the protein-solvent H-bond energy, u. Since the mean field approximation provides all the occupation probabilities, p_t,α, within a node, the enthalpy fluctuations within a node, [〈(h−〈h〉)²〉_node are readily calculated. Then the heat capacity, $C_{\mathrm{p}}^{(\text{fel})}$, is given by 〈ΔH²〉/KT² where the superscript is added to denote that the prediction is directly from the model using the free energy landscape (fel). Note that all thermodynamic quantities are calculated directly using the full two-dimensional free energy landscape, not the one-dimensional flexibility free energy function.

To more simply understand QSFR, the two-dimensional landscape is also used to calculate the free energy as a function of global flexibility order parameter. The one-dimensional flexibility free energy curves are obtained by combining all nodes sharing the same degree of flexibility,¹⁷ to provide a direct connection between global flexibility and thermodynamic stability.²⁴ The mathematical formula is G_f(θ)=−RT ln[Q_f(θ)] where the conditional partition function is defined by: Q_f(θ)=Σ_node B(θ−θ′(node))e^−βG(node)where θ′(node) is the average global flexibility of the node, and B(x) is a binning function, such that B(x)=1 for −0.005<x<−0.005 and zero otherwise.

Simulated annealing procedure

Simulated annealing is used to determine the three free parameters, {u,v,δ_nat}, using the criterion that calculated and measured heat capacities match. Normally, only excess heat capacities are reported in the literature. Moreover, absolute numbers are often not reported, but only the relative scale. In other cases, negative values are reported. Here, we had absolute heat capacity data, so these considerations were not an issue. Nevertheless, in general, the objective function tries to minimize the difference between $C_{\mathrm{p}}^{(exp)}-[C_{\mathrm{p}}^{(\text{fel})}+C_{\mathrm{p}}^{(\text{bl})}]$ where $C_{\mathrm{p}}^{(\text{fel})}$ is the calculated heat capacity from the free energy landscape (fel) and $C_{\mathrm{p}}^{(\text{bl})}$ is an added baseline (bl) function of the form:

$$C_{\mathrm{p}}^{(\text{bl})}(T)=a+\frac{b}{2}(1+tanh(c(T-T_{\mathrm{m}})))$$ (9)

The baseline function has three free parameters {a,b,c}, and T_m is taken to be the experimentally determined peak in the heat capacity. For any guess of the three values {u,v,δ_nat} the $C_{\mathrm{p}}^{(\text{fel})}$ is calculated, and for these three parameters fixed, and thus for $C_{\mathrm{p}}^{(\text{fel})}$ fixed, the parameters {a,b,c} are conditionally optimized exactly. In this way, the auxiliary parameters {a,b,c} are not increasing the function space. In this work, a=3.79 kcal/(mol K), b=0.082 kcal/(mol K), and c=0.300 and because the main difference is off by a constant shift of 3.79 kcal/mol the baseline is ignored, except for the initial fitting using simulating annealing. Note that the minimal DCM cannot be expected to get the absolute baseline correct since the C_p contributions that are nearly the same in both native and unfolded states are not modeled. The fact that the fit to absolute heat capacity yields a>0 is reassuring, since anything the DCM neglects must provide a positive contribution. In addition, the amount that is missed in the unfolded state is very small, b= 0.082 kcal/(mol K).

The simulated annealing is constructed as a random walk in a three-dimensional space starting from a semi-arbitrary starting point {u_o,v_o,δ_nat,o}. Semi-arbitrary is claimed because we only consider starting values within factors of 3 from physically reasonable values. The simulated annealing is usually run about ten times with different starting points, and the final values found are generally similar; at least when a good fit is obtained. Occasionally, a not so good fit is found, indicating the search got stuck in a local minimum. These problems come and go depending on the rate of “cooling” in the simulating annealing process. “Cooling” is incorporated by making walk steps {Δu,Δv,Δδ_nat} start at a high value, and gradually decrease. Each random step is drawn from a normal distribution characterized by standard deviations {σ_u,σ_v,σ_δ}. Thus, the average step size is controlled by the standard deviations. Starting from some initial specification, the standard deviations decay like: (new value)= fraction×(current value). However, the decay is not always implemented. At a fixed set level of standard deviations, X-amount of failed moves must occur before the standard deviation is lowered. Success is defined whenever the objective function is improved. The random walker moves on all successes, and never on a failure. Moves on failures can be done, based on some probability, but worse performance is always observed. The random walk process continues with smaller and smaller step sizes until the standard deviations reach a value small enough that controls accuracy in the third digit. The choice of what X is and the rate of decay given by the “fraction” is more art than science. Typically the fraction is 0.98 and X=100. Slower runs produce better results, and we have used 0.999 for the fraction with X=10, etc. At the end, the simulating annealing approach has been very successful in generating robust results with only little fiddling.

Although the simulated annealing procedure defined above will work in principle, it would be very slow because each time δ_nat changes, a new rigidity calculation must be performed. However, it is observed that the determination of which constraints are independent and redundant does not depend on the values of the entropy parameters per se, but only on their sorted order from smallest to largest. If δ_nat is a low value, less number of H-bond constraints will be ranked lower, and more H-bond constraints will be ranked higher, and vice versa. Therefore, in order to avoid recalculating the rigidity information each time a random walk step is made, the simulated annealing is done in a nested loop. The entropy parameter, δ_nat, is varied as explained above with a normal distribution on the outer loop. The u and v parameters (which are energies) are varied simultaneously in an inner loop using normal distributions in a two-dimensional walk for fixed δ_nat. By setting up a double loop structure in this way, the process is approximately 100+ times faster. Another saving of the order of 10 or so is achieved by realizing that all the covalent bonds must be placed before any of the non-covalent bonds. Because covalent bonds are quenched, it makes no sense to start from scratch each time. The starting point can be made after all covalent bonds are initially placed.

With these improvements in the random walk implementation, we provide the following benchmark. Upon the first encounter of a new δ_nat value for the set of {u,v,δ_nat} parameters, a protein with 200 residues requires ≈8 min of CPU time to calculate the free energy landscape, and all thermodynamic properties for one temperature on a 1.4 GHz processor. In practice, this CPU time scales nearly as the square in the number of residues. Upon subsequent calculations where {u,v} are changed, for fixed δ_nat the rigidity calculation can be avoided, and CPU time reduces to only a few seconds. An alternate implementation only works with a random walk in two dimensions using the {u,v} parameters, and the δ_nat parameter is varied sequentially by a fixed step-increment over a predefined range. Once reasonably good fits are obtained, the range is decreased, and so is the step size in direct proportion to the range. In this work, the three parameters {u=−2.236 kcal/mol, v=−0.893 kcal/mol, δ_nat=0.965} are physically reasonable, with values that lie within a range established over previous investigations.^17,18,24 Fortunately, multiple good fits identified by simulated annealing are found to yield consistent thermodynamic and flexibility conclusions. Previously, insensitivity to parameterization differences between good fitting simulated annealing runs was demonstrated using exhaustive grid searches over parameter space.²⁴

Trx structure manipulations

All calculations are performed on the wild-type Trx structure PDB:2trx and substructures thereof. Hydrogen atoms are added using the Molecular Operating Environment (MOE), with no further optimization because the method employed in MOE assumes pH 7.0. The underlying DSC experiments were performed at pH 7.0.⁵ Individual fragments are simply generated by deleting the non-corresponding atoms. No changes to the underlying molecular structure are performed in the fragment pair analyses. Like COREX,²⁵ the DCM creates an ensemble by simply perturbing away from the native structure. All H-bond, salt-bridge, torsion angle, and covalent bond constraints are included within the DCM input, which is used to construct the topological frameworks. All pluck, split, and track cuts are performed by simply removing the corresponding constraints from the DCM input.

Abbreviations used

Trx

thioredoxin

DCM

distance constraint model

QSFR

quantitative stability/flexibility relationships

C_p

heat capacity at constant pressure

T_m

melting temperature

H-bond

hydrogen bond

dof

degrees of freedom

G_f

flexibility free energy

χ_RC

rigid cluster susceptibility

θ

global flexibility order parameter

PUF

partially unfolded form

SUF

super unfolded form

P_R

probability of a backbone torsion angle to rotate

P_idf

probability of an independent dof