Local and macroscopic electrostatic interactions in single α-helices

Abstract

The non-covalent forces that stabilise protein structures are not fully understood. One way to address this is to study equilibria between unfolded states and α-helices in peptides. For these, electrostatic forces are believed to contribute, including interactions between: side chains; the backbone and side chains; and side chains and the helix macrodipole. Here we probe these experimentally using designed peptides. We find that both terminal backbone-side chain and certain side chain-side chain interactions (i.e., local effects between proximal charges, or interatomic contacts) contribute much more to helix stability than side chain-helix macrodipole electrostatics, which are believed to operate at larger distances. This has implications for current descriptions of helix stability, understanding protein folding, and the refinement of force fields for biomolecular modelling and simulations. In addition, it sheds light on the stability of rod-like structures formed by single α-helices that are common in natural proteins including non-muscle myosins.

Folded proteins are stabilised by many weak intramolecular forces between thousands of atoms, including: hydrogen bonds, van der Waals’ contacts, and Coulombic interactions between formal charges (i.e., salt bridges).¹ Because of the interdependence of non-covalent interactions, and the resulting cooperativity of protein folding, it is extremely difficult to disentangle contributions from these various components. For example, in terms of backbone interactions alone, CO_i➔NH_i+4 hydrogen bonds are regarded as the major factor stabilising α-helices.² Whilst this remains unchallenged, recent studies have identified additional contributions from CO_i➔CO_i+1 n➔π* interactions,³ which can “compete” with traditional hydrogen bonding.⁴ Thus, it is important to develop continually, and to challenge our understanding of the fundamental forces underpinning protein folding, and of biomolecular interactions in water more generally. Improved understanding will lead to better modelling, prediction and design of biomolecular structures and assemblies ab initio, and with these many improved applications in the basic and applied biosciences will follow.

One way forward is to establish straightforward experimental models that isolate certain interactions, or reduce the complexity of their contexts. An example is the study of helix⇆coil transitions in short peptides. This began with observations that certain peptide fragments of natural proteins exhibit considerable α-helicity,^5,6 and developed to the de novo design of model peptides that behave systematically with rational changes to sequence.⁷ The latter led to the dissection of various non-covalent interactions, and to sequence-to-structure relationships also apparent in fully folded natural proteins, including: α-helical propensity scales;^8-10 specific backbone-side chain interactions;¹¹ and pairwise and higher-order side-chain interactions.^12-15

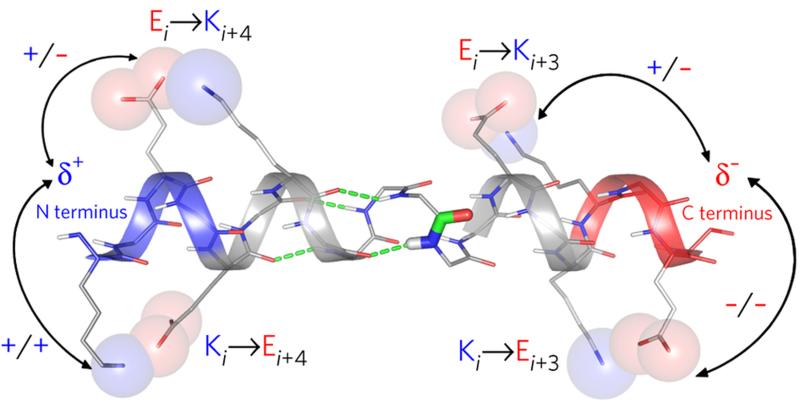
To balance the configurational entropy lost on folding into an α-helix, a number of electrostatic forces probably contribute to favourable enthalpies of helix folding, including: backbone CO_i➔NH_i+4 hydrogen bonds; hydrogen bonds and salt bridges between side chains spaced i➔i+3 and i➔i+4;¹⁶ backbone-side chain interactions at both helical termini;¹⁷ and through-space electrostatic interactions between charged side chains and the so-called helix macrodipole¹⁸ (Fig. 1). The latter is believed to arise from the alignment of individual dipoles of backbone peptide units parallel to the major axis of the α-helix. This has local consequences: it results in partial positive and negative charges at the N- and C-termini, respectively,^19,20 which leads to side-chain preferences and ligand-binding phenomena at these sites.²¹ However, the evidence and roles for the macroscopic effects are less clear, and the energetic contributions to structure and stability by both surface-exposed salt bridges^22-24 and the α-helix macrodipole²⁵ remain unresolved.

Figure 1. Electrostatic interactions in the α-helix.

Cartoon representation of the α-helix showing the following: CO_i➔NH_i+4 hydrogen bonds (green dashes); the peptide-bond dipole (thick sticks, centre), many copies of which align to give the helix macrodipole; clusters of backbone NH and CO groups, which give rise to local δ⁺ and δ⁻ charges at the N- (blue) and C- termini (red), respectively; interactions between charged side chains and the helix terminal charges (arrows); and salt bridges between charged side chains spaced i➔i+3 and i➔i+4 apart (labelled spheres).

Most recently, the field has come full circle with observations of natural long single α-helices that span 30 – 200 residues. These self-stabilising structures do not require tertiary or quaternary interactions to persist. Originally noted in the calmodulin-binding protein caldesmon²⁶ and the non-muscle myosins VI,²⁷ VII,²⁸ and X²⁹, these single α-helices (SAHs) are predicted to occur widely.^30-32 Their hallmark is alternating blocks of four negatively charged glutamic acid (Glu, E) and four positively charged arginine (Arg, R) or lysine (Lys, K) residues.³³ They are also dubbed charged single α-helix (CSAH) domains,³¹ or E-R/K α-helical motifs³⁴ and are proposed to form rigid rods or spacers to separate other protein domains.

Given this revived interest in single α-helices, but the incomplete understanding of the forces that stabilise them, we designed a series of peptides comprising predominantly Glu and Lys to prise apart different contributions to helix stability. Our first designs were consistent with preceding reports. However, further iterations conflicted with current thinking for the contributions from both salt-bridge and macrodipole interactions. Specifically, certain side-chain arrangements between Glu and Lys are favoured over others, and these dominate any manifestation of the macroscopic helix dipole; indeed, for these systems, there is no need to invoke macroscopic effects and local descriptions suffice.

RESULTS

Peptide design – iteration 1

We followed foregoing studies of de novo³⁵ and natural SAHs²⁹ to design two highly helical peptides, (E₄K₄)₃ and (K₄E₄)₃ (Table 1). In these, alternating blocks of four Glu and four Lys, which both have favourable α-helical propensities,¹⁰ were used to match the 3.6-residues per turn of the α-helix. This maximises potentially favourable i➔i+4 E➔K and K➔E inter-side-chain salt bridges (Fig. 1), whilst minimising unfavourable inter-side-chain electrostatic interactions (Supplementary Results, Supplementary Table 1). N.B., in these two designs, both i➔i+4 E➔K and K➔E interactions are possible, but one potentially outnumbers the other by 3:2 in each case. In addition, all four types of side-chain-terminus interaction are represented, e.g. blocks of four Glu or Lys at both the N- and C- termini of the peptides (Fig. 1). We used (E₂K₂)₆ as a control peptide of the same length, which maximises repulsive i➔i+4 E➔E and K➔K pairs (Supplementary Table 1).³⁵

Table 1. Peptide designs.

Names, sequences, mean residue ellipticities at 222 nm (MRE₂₂₂) and 5 °C, corresponding percent helicities, and midpoints of thermal denaturation curves (T_m) for the peptides used in this study. Conditions: phosphate buffered saline (PBS, 137 mM NaCl), pH 7.4, and 100 μM peptide concentration. The purity and identities of the peptides were confirmed by HPLC and MALDI-TOF mass spectrometry (Supplementary Figs. 1 – 27).

Peptide Name	Sequence1	MRE222	Fraction Helix (%)	Tm (°C)
(E2K2)6	Ac–GEEKKEEKKEEKKEEKKEEKKEEKKGYY–NH2	813	−1
(EK)12	AC–GEKEKEKEKEKEKEKEKEKEKEKEKGW–NH2	−8,136	22
(KE)12	AC–GKEKEKEKEKEKEKEKEKEKEKEKEGW–NH2	−4,180	12
(E4K4)4	AC–GEEEEKKKKEEEEKKKKEEEEKKKKEEEEKKKKGW–NH2	−36,454	94
(E4K4)3	AC–GEEEEKKKKEEEEKKKKEEEEKKKKGW–NH2	−27,885	74
(E4K4)2	AC–GEEEEKKKKEEEEKKKKGW–NH2	−23,374	65
(E4K4)	AC–GEEEEKKKKGW–NH2	−4,219	14
(K4E4)4	AC–GKKKKEEEEKKKKEEEEKKKKEEEEKKKKEEEEGW–NH2	−35,479	91	28
(K4E4)3	AC–GKKKKEEEEKKKKEEEEKKKKEEEEGW–NH2	−23,493	62
(K4E4)2	AC–GKKKKEEEEKKKKEEEEGW–NH2	−7,666	22
(K4E4)	AC–GKKKKEEEEGW–NH2	816	−1
A4(E4K4)3A4	AC–GAAAAEEEEKKKKEEEEKKKKEEEEKKKKAAAAGW–NH2	−33,934	87
A4(E4K4)2A4	AC–GAAAAEEEEKKKKEEEEKKKKAAAAGW–NH2	−27,313	72
A4(E4K4)A4	AC–GAAAAEEEEKKKKAAAAGW–NH2	−18,885	53
A4(K4E4)3A4	AC–GAAAAKKKKEEEEKKKKEEEEKKKKEEEEAAAAGW–NH2	−38,166	98	33
A4(K4E4)2A4	AC–GAAAAKKKKEEEEKKKKEEEEAAAAGW–NH2	−29,687	78	21
A4(K4E4)A4	AC–GAAAAKKKKEEEEAAAAGW–NH2	−21,847	61
A4(E4K4)3	AC–GAAAAEEEEKKKKEEEEKKKKEEEEKKKKGW–NH2	−33,288	87
(E4K4)3A4	AC–GEEEEKKKKEEEEKKKKEEEEKKKKAAAAGW–NH2	−32,668	85
A4(K4E4)3	AC–GAAAAKKKKEEEEKKKKEEEEKKKKEEEEGW–NH2	−35,177	91	25
(K4E4)3A4	AC–GKKKKEEEEKKKKEEEEKKKKEEEEAAAAGW–NH2	−32,796	85	22
A4(E4K4)A4(E4K4)A4	AC–GAAAAEEEEKKKKAAAAEEEEKKKKAAAAGW–NH2	−31,779	83	24
A4(K4E4)A4(K4E4)A4	AC–GAAAAKKKKEEEEAAAAKKKKEEEEAAAAGW–NH2	−37,155	97	29
(E3K3)4	AC–GEEEKKKEEEKKKEEEKKKEEEKKKGWW–NH2	−25,428	67
(K3E3)4	AC–GKKKEEEKKKEEEKKKEEEKKKEEEGWW–NH2	−12,229	33
A4(E3K3)4A4	AC–GAAAAEEEKKKEEEKKKEEEKKKEEEKKKAAAAGWW–NH2	−31,869	82	21
A4(K3E3)4A4	AC–GAAAAKKKEEEKKKEEEKKKEEEKKKEEEAAAAGWW–NH2	−30,287	78	14

¹Amino acids are represented by standard one-letter codes: A, alanine; E, glutamic acid; G, glycine; and K, lysine. To remove complicating terminal formal charges, and to ameliorate end effects in the helices, the E/K regions in all of the peptides for this study were flanked by glycine residues, and capped with acetyl (Ac) and amide groups (NH₂) at their N-and C-termini, respectively. C-terminal tryptophan (W) or tyrosine (Y) residues were included for concentration determination.

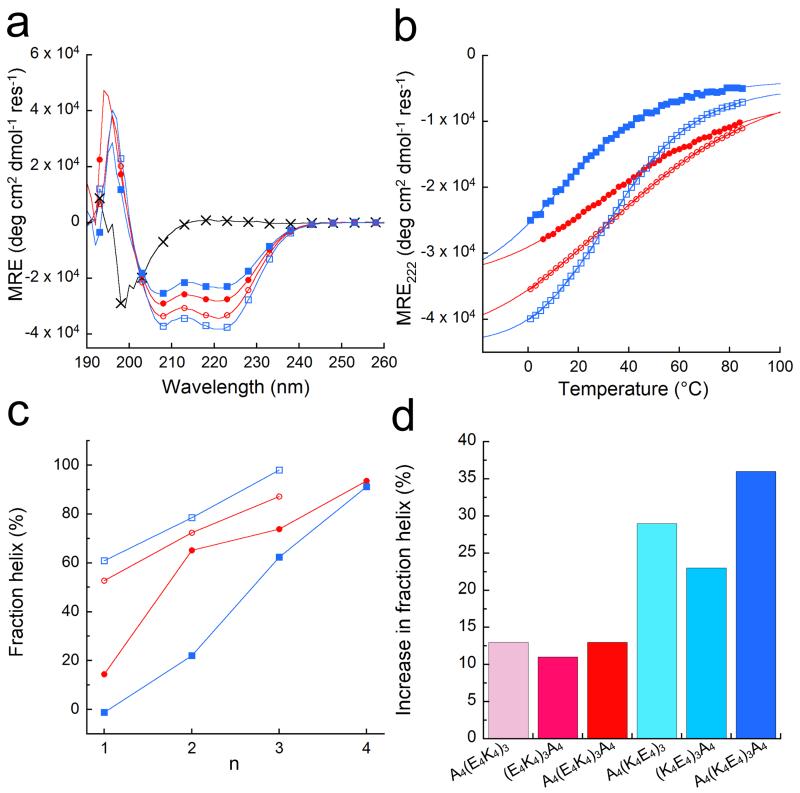
Circular dichroism (CD) spectroscopy showed that (E₂K₂)₆ was largely unfolded; and that both (E₄K₄)₃ and (K₄E₄)₃ had high mean residue ellipticities at 222 nm (MRE₂₂₂), which translated to 74% and 62% helix, respectively (Fig. 2, Supplementary Fig. 28a&b and Table 1). (E₄K₄)₃ was expected to be more helical than (K₄E₄)₃ because: it better matches the formal charges of the side chains and the partial charges of backbone in the N- and C-terminal turns (Fig. 1); and, the E_i➔K_i+4 arrangement counters the helix macrodipole better. This continued over a range of peptide lengths for (E₄K₄)_n and (K₄E₄)_n, where n = 1 – 4, with the former being the more helical in each case (Fig. 2c).

Figure 2. Helicities of the designed peptides in solution.

(a) CD spectra at 5 °C of: (E₂K₂)₆ (black crosses), (E₄K₄)₃ (red circles), (K₄E₄)₃ (blue squares), A₄(E₄K₄)₃A₄ (red open circles), and A₄(K₄E₄)₃A₄ (blue open squares). (b) Thermal unfolding curves followed by the change in MRE₂₂₂ for all except (E₂K₂)₆, with the symbols and colours from (a) preserved. Fits to the Gibbs-Helmholtz equation are shown by solid lines. (c) Fraction helix as a function of peptide length for the (E₄K₄)_n-(red) and (K₄E₄)_n-based (blue) peptides with (open symbols) and without (filled symbols) tetra-alanine flanks (data points are joined by lines to guide the eye). (d) Increase in fraction helicities at 5 °C of the alanine-flanked peptides A₄(E₄K₄)₃, (E₄K₄)₃A₄ and A₄(E₄K₄)₃A₄ (red colours) relative to (E₄K₄)₃; and for A₄(K₄E₄)₃, (K₄E₄)₃A₄ and A₄(K₄E₄)₃A₄ (blue colours) relative to (K₄E₄)₃. Conditions: 100 μM peptide concentration in PBS 137 mM NaCl, pH 7.4.

As secondary structure can be stabilised by peptide association, we used sedimentation equilibrium experiments to determine peptide oligomeric states. These indicated that both (E₄K₄)₃ and (K₄E₄)₃ were monomeric in solution (Supplementary Fig. 30 and Supplementary Table 2).

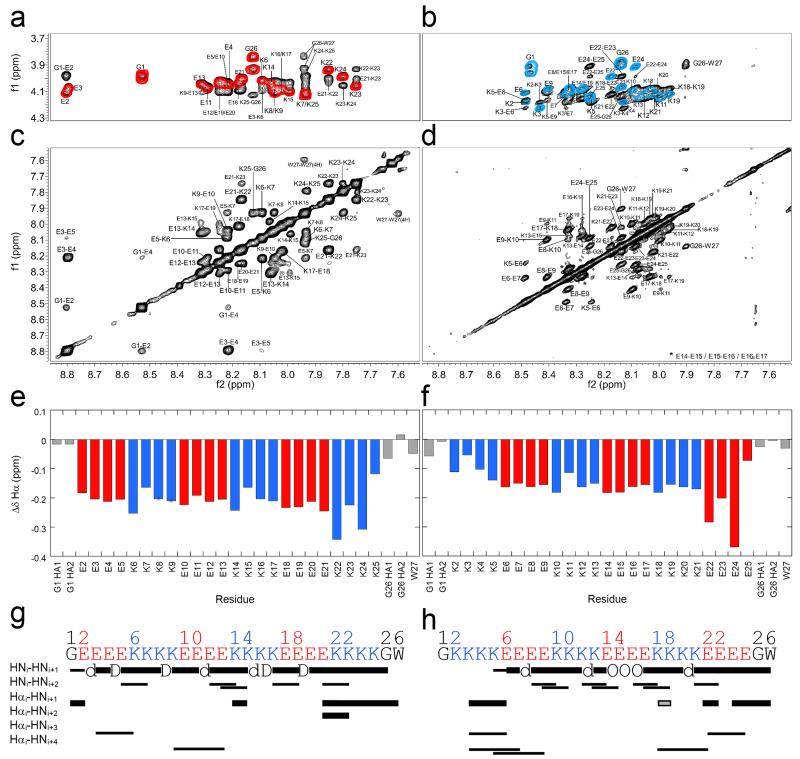
Next, we used high-resolution ¹H-NMR NOESY and TOCSY experiments to probe the structure in (E₄K₄)₃ and (K₄E₄)₃ in detail (Fig. 3 and Supplementary Figs. 31-34). Sequence-specific assignments were made for all backbone HN resonances, and the majority of the Hα resonances for both peptides. From Δδ and NOE measurements, (E₄K₄)₃ was helical throughout with contiguous, sequential HN_i-HN_i+1 NOEs from Gly1 through Trp27 (Fig. 3g). Whereas, for (K₄E₄)₃ the N-terminal residues Lys2 – Lys4 appeared disordered (Fig. 3h); otherwise, the helical structure continued through the sequence from Lys5 to Trp27. This fraying in (K₄E₄)₃ seems best explained by the mismatched charge of the side chains of Lys2, 3 and 4 with the δ⁺ N-terminus; although the C- terminus is folded despite the negatively charged Glu residues at this δ⁻ end.

Figure 3. Locating α-helical structure by NMR spectroscopy.

¹H-NMR spectra for (E₄K₄)₃ (a&c) and (K₄E₄)₃ (b&d). (a&b) Overlaid fingerprint regions of the TOCSY (coloured contours: red for (E₄K₄)₃, and blue for (K₄E₄)₃) and NOESY (black contours) spectra. Note the larger range of HN shifts for (E₄K₄)₃. (b&d) NOESY spectra showing the amide regions and large number of sequential HN_i-HN_i+1 NOEs. Note the first NOE of this type for (K₄E₄)₃ is between Lys-5 and Glu-6 (K5/E6 circled in d). (e&f) Δδ plots for the backbone Hα chemical shifts of (E₄K₄)₃ and (K₄E₄)₃, respectively. Key: Glu, red; Lys, blue; Gly and Trp, grey. Δδ values are the difference in sequence-corrected random coil chemical shifts from those observed. Δδs are greater for (E₄K₄)₃ than (K₄E₄)₃ on average, consistent with a more folded α-helix. (g&h) Connectivity diagrams for (E₄K₄)₃ and (K₄E₄)₃, respectively. Note there are only a few identifiable Hα-HN NOEs due to significant peak overlap in this region (a&b). Key: thick bars, medium intensity NOEs (1.8 – 3.5 Å); thin bars, weak NOEs (1.8 – 5.0 Å); grey, ambiguous; d, NOE hidden by diagonal; D, degenerate; O, overlapped. Conditions: 1 mM peptide concentration in PBS (137 mM NaCl) with 10% D₂O, pH 7.4 at 5 °C; (E₄K₄)₃ 600 MHz, and (K₄E₄)₃ 900 MHz.

Peptide design – iteration 2

To reduce complications from end effects—i.e., local electrostatic interactions between charged side chains and the partially charged termini—we synthesised peptides in which (E₄K₄)₃ and (K₄E₄)₃ were flanked at one or both sides by tetra-alanine (Ala₄, A₄) blocks (Table 1). Alanine was chosen for its high helix propensity,¹⁰ small size and charge neutrality. Although we anticipated some influence of these blocks on overall helicity of the peptides, we reasoned that these properties would best serve the purpose of homogenising end effects. The resulting six peptides, A₄(E₄K₄)₃, (E₄K₄)₃A₄, A₄(E₄K₄)₃A₄, A₄(K₄E₄)₃, (K₄E₄)₃A₄ and A₄(K₄E₄)₃A₄, showed the following responses to the flanks in CD spectroscopy (Fig. 2, and Supplementary Figs. 28c – f and 29c – f).

First, the percent helix in all of the peptides increased compared with the parents (Fig. 2d). This is almost certainly due in part to the increased lengths of the peptides and the choice of Ala as the flanking residues. It is also fully consistent with the Ala₄ flanks limiting the terminal fraying/unfolding of the peptides.^36-38 Second, changes in helicity were more pronounced for the (K₄E₄)₃-based peptides. This seems best explained simply by the removal of fraying due to the block of unfavourable positive charge from the helical N-termini. Consistent with this, within the (K₄E₄)₃ series the favourable impact of the flanks was largest at the N-terminus.

However, a final response was unexpected, and is less readily explained by current thinking. Comparing the overall helicities of the parent and doubly flanked peptides (E₄K₄)₃ > (K₄E₄)₃, but A₄(K₄E₄)₃A₄ > A₄(E₄K₄)₃A₄ (Table 1 and Fig. 2). This runs contrary to most reports of side chain-side chain interactions between Glu and Lys in the context of the helix macrodipole. Current understanding is that E_i➔K_i+4 should be more stabilising than the reverse combination because the side chains align energetically favourably with the helix macrodipole.^7,39 However, we find the opposite: A₄(K₄E₄)₃A₄, which has more potential K_i➔E_i+4 pairings than E_i➔K_i+4, is the more helical.

Further NMR measurements on A₄(K₄E₄)₃A₄ confirmed contiguous sequential HN_i-to-HN_i+1 NOEs from Ala3 through Trp35 (Supplementary Fig. 34). Thus, the entire central (K₄E₄)₃ block is α-helical. Moreover, length-dependence experiments for the flanked peptides revealed that the (K₄E₄)_n blocks were consistently more helical than (E₄K₄)_n blocks (Fig. 2c). N.B., sedimentation-equilibrium studies confirmed that both A₄(E₄K₄)₃A₄ and A₄(K₄E₄)₃A₄ were monomeric in solution (Supplementary Fig. 30 and Supplementary Table 2).

K_i➔E_i+4 salt bridges are enthalpically better

The additional stabilising effect of K_i➔E_i+4 pairings compared with E_i➔K_i+4 was also evident in thermal unfolding followed by CD spectroscopy. The E₄K₄-based peptides showed broad and approximately linear transitions from predominantly helical to gradually less helical states, including the most folded A₄(E₄K₄)₃A₄ (Fig. 2b and Supplementary Figs. 29c&e). This is typical of short de novo α-helical peptides.⁷ By contrast, the K₄E₄-based peptides had sharper more-sigmoidal transitions (Fig. 2b and Supplementary Figs. 29d&f), and some had measurable midpoints (T_M) with A₄(K₄E₄)₃A₄ having the highest. Though there are examples of such behaviour,⁴⁰ it is unusual and suggests cooperativity in the transitions, and that more enthalpically favourable interactions are being made in the folded state of this peptide.

We fitted the thermal unfolding data to the Gibbs-Helmholtz equation (Fig. 2b and Supplementary Fig. 29). This assumed ΔC_p = 0, and that helix⇆coil transitions are two-state processes. The latter is almost certainly incorrect as the “folded states” are likely ensembles of unfolded, folded and partly folded species;⁴⁰ however, we found no evidence for alternative “unfolded” states by CD spectroscopy at least, i.e. no polyproline helices or β-structure. Caveats aside, the analysis is valuable because the gradients of the fits reflect the enthalpy change accompanying unfolding. For our designed peptides, the enthalpies of folding were all exothermic (Supplementary Table 7). Moreover, the enthalpies for the (K₄E₄)_n-based peptides were higher than for the (E₄K₄)_n analogues. This suggests that K_i➔E_i+4 salt bridges are somehow enthalpically better than E_i➔K_i+4 interactions, and cooperate better to induce and maintain structure in A₄(K₄E₄)₃A₄.

Helical propensities and salt-bridges in folded proteins

There have been extensive analyses of residue preferences and pairings in α-helices,^12,41,42 but our results raised issues to be addressed afresh. Therefore, we analysed the conformations and interactions of Glu and Lys side chains in α-helices from the PDB (Fig. 4).⁴³

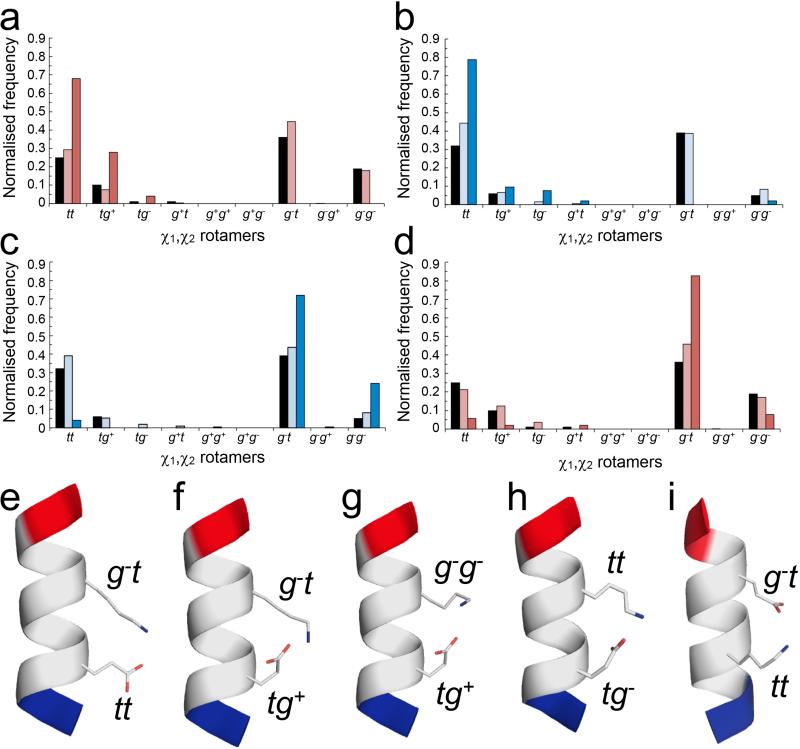
Figure 4. Side-chain interactions observed in α-helices from the Protein Data Bank.

χ₁,χ₂ distributions and conformers for E_i➔K_i+4 and K_i➔E_i+4 pairs in high-resolution X-ray crystal structures. (a – d) Normalised frequencies of preferred χ₁,χ₂ angles for Glu (a&d) and Lys (b&c) residues in E_i➔K_i+4 (a&c) and K_i➔Ei₊₄ (b&d) pairs. Key: red for Glu, blue for Lys; black bars indicate the frequency of each rotamer found in all α-helices; pale bars indicate pairs where no salt bridge is made; and dark bars indicate pairs where a salt bridge is formed. (e – i) Examples of salt-bridging pairs. For the E_i➔K_i+4 pairs, there are two dominant rotamer combinations, with Glu (tt; tg⁺) plus Lys (g⁻t) (e&f, 17 examples (68%) and 6 examples (24%), respectively), and two minor combinations (g&h, 1 example of each (8%)) with Glu;Lys (tg⁺;g⁻g⁻) and Glu;Lys (tg⁻; tt). Whereas for the K_i➔E_i+4 pairs there is one clearly preferred conformation (Glu, g⁻t; Lys, tt) (i, 39 examples (75%)). Only the g⁻t;g⁻t combination would be better, but inspection of molecular models revealed that with χ₁ = g⁻ for Lys takes the ε-amino group too far from the γ-carboxylate of Glu to form a salt bridge. Examples were taken from the PDB as follows: (e) 1kqp A246-A250; (f) 1moq A481-A485; (g) 3n0u A177-A181; (h) 2r75 A141-A145; (i) 1egw A30-A34. Images were generated with PyMol (www.pymol.org).

First, we tested for specific side-chain-backbone interactions at the helical termini. Consistent with previous studies^9,36-38 and our experiments, this analysis gave favourable propensities for Glu at helical N-termini and Lys at the C-termini of 1.24 and 1.26, respectively (Supplementary Table 8). However, using HBPLUS,⁴⁴ we found that only small fractions (9% for Glu at N-termini, and 2.5% for Lys at C-termini) of these made side-chain-backbone hydrogen bonds (Supplementary Fig. 36). In the context of the many potential hydrogen bonds with water, this suggests strongly that the experimental and statistical preferences for Glu at N-termini are best attributed to proximal through-space electrostatic interactions between the γ-carboxylate and the δ⁺ ends of nearby peptide-bond dipoles, rather than by specific atomic contacts; and the preferences for Lys at C-termini by similar interactions between the ε-amino moiety and the δ⁻ charge.

Regarding potential E_i➔K_i+4 and K_i➔E_i+4 salt bridges, we found that more K_i➔E_i+4 pairs (21%) formed salt bridges than E_i➔K_i+4 (11%); and that the salt-bridged K_i➔E_i+4 pairs were more structurally conserved, with a lower RMSD value of 1.08 Å, vs. 1.79 Å for those made by E_i➔K_i+4; calculated over all side-chain atoms, (Supplementary Fig. 37). To understand this, we compared the χ₁,χ₂ distributions for Glu-Lys salt bridges (Fig. 4) and all possible χ₁,χ₂ combinations for Glu and Lys in i➔i+3 and i➔i+4 pairings in α-helices (Supplementary Table 9).

Glu has three dominant χ₁,χ₂ combinations: gauche⁻,trans (g⁻ t, 36%); trans,trans (tt, 25%); and gauche⁻,gauche⁻ (g⁻g⁻, 19%), (Figs. 4a&d). However, when paired with Lys only certain combinations of these led to salt bridges: For E_i➔K_i+4 pairs, salt bridges were only made with Glu in the second-favoured conformer (tt) or a fourth minor conformation (tg⁺, 10%), (Fig. 4a,e&f and Supplementary Table 9). Having to fix the side chain in these less-favoured rotamers incurs an entropic penalty. Nevertheless, the more-flexible side chain of Lys complemented these Glu conformers to account for 92% (23/25) of the E_i➔K_i+4 salt-bridge interactions (Figs. 4c,e&f). By contrast, 75% of the salt-bridged K_i➔E_i+4 pairs had the same paired conformation, with Glu in its preferred χ₁,χ₂ conformation and Lys in its second-favoured conformer (tt, 32%; which was only marginally less preferred than g⁻ t (39%)), (Figs. 4b,d,i). Hence, the entropic penalty of freezing out this conformer is near the minimum possible.

Thus, compared with E_i➔K_i+4 salt bridges, the preferred K_i➔E_i+4 salt bridges appear to sample fewer conformations and use more-favourable χ₁χ₂ pairs for each residue. We posit that this leads to K_i➔E_i+4 interactions that are enthalpically better, because the side chains are predisposed in conformations to facilitate salt bridges. This is not to say that sequences dominated by E_i➔K_i+4 arrangements will necessarily be less helical; from our data and the literature this is patently not the case. However, as discussed below, the mechanism of helix stability is subtly different.

Uncoupling (E₄K₄) and (K₄E₄) blocks

The peptide designs described above can make both E_i➔K_i+4 and K_i➔E_i+4 interactions. Thus, it is not possible to ascribe absolutely either the percent-helix or thermal unfolding properties to one i➔i+4 interaction type. To address this, we designed further sequences with isolated E₄K₄ or K₄E₄ blocks flanked by A₄ blocks; namely, A₄(E₄K₄)A₄, A₄(K₄E₄)A₄, A₄(E₄K₄)A₄(E₄K₄)A₄ and A₄(K₄E₄)A₄(K₄E₄)A₄ (Table 1). In these, only one type of i➔i+4 E➔K or K➔E interaction can be made. The shorter peptides were surprisingly helical (Fig. 2c, Table 1, and Supplementary Fig. 28c&d), with A₄(K₄E₄)A₄ having the higher α-helicity. Moreover, the thermal-unfolding curve for this peptide was sharper and more sigmoidal than for A₄(E₄K₄)A₄ (Supplementary Fig. 29c&d). The longer peptides with the additional, but uncoupled, E₄K₄ or K₄E₄ blocks were highly helical at 83% and 97%, respectively. (N.B., some of the structure is likely due to the central Ala₄ block). Both peptides had sigmoidal thermal-denaturation curves with measurable midpoints, but the K➔E arrangement had the sharper transition and the higher T_M (Table 1 and Supplementary Fig. 29g). This confirms that K_i➔E_i+4 potential salt bridges contribute more to helical stability than E_i➔K_i+4 pairs, despite the apparent misalignment with the helix macrodipole.

Consideration of E/K_i➔K/E_i+3 interactions

Our designs could also make i➔i+3 interactions (Supplementary Table 1). Therefore, we examined such pairs in α-helices of the PDB. Interestingly, more E_i➔K_i+3 pairs (23.4%) made salt bridges than the K_i➔E_i+3 pairs (15.6%) (Supplementary Table 8b). Also, for the E_i➔ K_i+3 pairs there was one dominant rotamer combination that accounted for 77% of E_i➔K_i+3 salt bridges made; whilst, for K_i➔E_i+3 pairs multiple conformers made salt bridges, with two accounting for 60% of the interactions (Supplementary Fig. 38). In addition, we found that E_i➔K_i+3 salt bridges were more structurally conserved, with lower a RMSD (1.09 Å) than for K_i➔E_i+3 salt bridges (2.27 Å) (Supplementary Fig. 37). These trends are the opposite of those observed for the i➔i+4 pairs, which suggest that E_i➔K_i+3 salt bridges might be more helix stabilising than K_i➔E_i+3.

To test this, we synthesised A₄(E₃K₃)₄A₄ and A₄(K₃E₃)₄A₄. Both peptides were highly helical and showed clear thermal unfolding transitions (Table 1 and Supplementary Figs. 39b&d). However, they were less helical than the E₄K₄ and K₄E₄ analogues, A₄(E₄K₄)₃A₄ and A₄(K₄E₄)₃A₄, illustrating that i➔i+3 interactions are less favourable than i➔i+4. In addition, and as predicted above, the trend was switched compared with E₄K₄ and K₄E₄, i.e., A₄(E₃K₃)₄A₄ was more helical and had a higher T_M than A₄(K₃E₃)₄A₄ (Table 1). Nonetheless, and perhaps counter-intuitively, the folding of A₄(K₃E₃)₄A₄ was the more exothermic (Supplementary Table 7). We suggest that this is because A₄(K₃E₃)₄A₄ can make more of the higher-enthalpy K➔E i➔i+4 interactions (Supplementary Table 1).

The role of the helix macrodipole

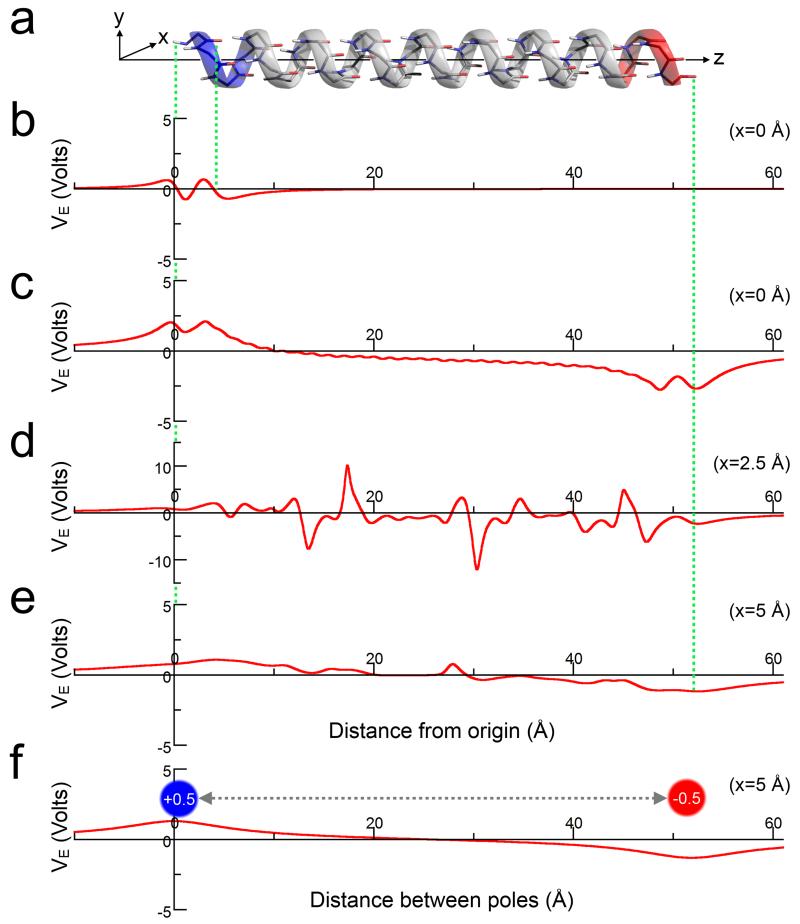
Whilst K_i➔E_i+4 salt bridges make enthalpically better interactions and lead to more-folded α-helical peptides than E_i➔K_i+4, this arrangement of positively charged lysine blocks N-terminal to negatively charged glutamate blocks is predicted to be unfavourable with respect to the helix macrodipole. Therefore, we calculated the electrostatic potential (V_E) of a model α-helix in vacuum, and at varying distances (x) from the central helix axis (z) by approximating partial dipole charges as point charges (Fig. 5a and Supplementary Fig. 40). In this model, the electrostatic potential for an individual peptide dipole was ≈ ± 0.7 V (Fig. 5b). For x = 0 in an extended helix, i.e. directly along its axis, we found that the central peptide-bond dipoles cancelled, leaving a negligible macrodipole at the termini (V_E ≈ ±1.5 V, Fig. 5c). At x = 2.5 Å, i.e. where the majority of backbone atoms lie, the residual macrodipole is overshadowed by local electrostatics from these atoms, with V_E ≈ ±10 V (Fig. 5d). At x = 5 Å, i.e. approximately at the termini of side chains, the effect is similar to x = 0, but with the macrodipole diminished further (V_E ≈ ±0.6 V, Fig. 5e). Indeed, at this distance the macrodipole is approximated by partial point charges at the termini of the helix (Fig. 5f). Thus, and even in the absence of solvation effects, the influence of the macrodipole on the stability of central K➔E interactions is predicted to be minimal.

Figure 5. Electrostatic potential of a model α-helix.

(a) A 32-residue α-helix with its long axis aligned along z. (b) The electrostatic potential (V_E) of a single residue from the helix at x = 0 Å. (c-e) The electrostatic potential along the entire helix at varying distances (x) from the helix axis: (c) x = 0 Å; (d) x = 2.5 Å; and (e) x = 5.0 Å. Note, the increased limits for the V_E-axis in part (d). (f) The electrostatic potential arising from point charges of +0.5 and −0.5 at positions equivalent to the N- and C-terminal helical atoms on the z-axis, respectively. The electrostatic potentials in all parts (b-f) were calculated in vacuum.

Correlation with helix-prediction programs

Considerable effort has gone into capturing the data from helix⇆coil transitions in computational methods to predict helix content from peptide sequence, with AGADIR probably being the most popular.⁴⁵ We made AGADIR predictions for both the percentage helix and thermal unfolding behaviours of our designs, and compared these with our experimental data (Supplementary Figs. 41&42). At first sight, the predictions appeared good. However, there were some deviations from the observed values, particularly for the longer and Ala₄-flanked variants. Moreover, the thermal unfolding data were not modelled well by AGADIR, which tended to over predict stabilities. This paper provides new data that could be modelled to improve these predictions and to aid peptide designs.

Biological context

Our observations that certain side-chain arrangements are more stabilising than others, i.e. K_i➔E_i+4 > E_i➔K_i+4 and E_i➔K_i+3 > K_i➔E_i+3, may help understand the behaviour of SAHs. To examine this in the natural sequences, we counted all of the potential D/E➔K/R and K/R➔D/E pairs spaced i➔i+3/4 in sequences from non-homologous proteins assigned as SAHs from CD spectroscopy and/or electron microscopy; we then normalised the data with expected rates (Supplementary Fig. 43). Firstly, as anticipated,¹⁰ we found that aspartic acid (D) hardly featured in the sequences or pairings. Secondly, the normalised frequencies of oppositely charged pairs were much greater than those for like-charge pairs, by an average factor of 7 for i➔i+4, and 3 for i➔i+3. Third, except for the E➔R combinations, which had similar observed/expected ratios, the propensities of oppositely charged i➔i+4 pairs were greater than those for the corresponding i➔i+3 pairs. Fourthly, and consistent with our model-peptide studies, there were more R/K_i➔E_i+4 pairs than the reverse orientation. Fifthly, the data for i➔i+3 pairings in natural SAHs were less clear-cut, although the pairs with overall highest propensity were E_i➔R_i+3, and K_i➔E_i+3. Finally, there was a consistent slight preference for Arg-based pairings over those involving Lys (apart from K_i➔E_i+3 > R_i➔E_i+3), which may reflect arginine’s potential to participate simultaneously in two salt bridges.¹⁵

DISCUSSION

We have found that: (1) short peptides of ≈20 – 30 residues comprising alternating blocks of Glu₄ and Lys₄ formed highly α–helical structures; (2) flanking these with Ala₄ blocks increased helical content and revealed context-dependent phenomena; for example, (3) Glu residues in the N-terminal turn strongly promoted α–helix formation, and Lys in these positions disrupted it; whereas, (4) similar effects at the C-terminus were less pronounced; (5) central K_i➔E_i+4 arrangements made enthalpically better side-chain salt-bridge interactions than E_i➔K_i+4 pairs; as a result, (6) although central E_i➔K_i+4 and K_i➔E_i+4 arrangements both favoured helix formation, the resulting helical structures were different in nature, particularly in how they responded to temperature; and (7) i➔i+3 potential salt-bridge interactions were weaker than those made by i➔i+4 arrangements. We place these results in context as follows.

1. Local interactions between side-chain and backbone moieties at helical termini

It is well established, in peptides^9,36-38 and proteins,¹¹ that certain side chains interact favourably with polar backbone groups and/or partial charges at the N- and C-termini of α-helices.²⁵ Our first peptide designs confirmed this: peptides with N-terminal blocks of lysine were less folded and more frayed than those with blocks of glutamate at that end. Curiously, however, in protein structures of the PDB, we found very few examples of formal hydrogen-bonded or other atom-atom contacts between side chains and backbone atoms at the termini. This indicates that such interactions are ephemeral, if there at all, and that more-general electrostatic interactions are at play between side chains and the partial charge at the N-terminus. Moreover, for our de novo peptides, these effects were much more pronounced at the N-terminus than at the C-terminus. This is readily understood as side chains emerge from the helical backbone and point towards the N-terminus (Fig. 1).

2. Local interactions between side-chain groups in the central regions of helices

To remove the end effects, we flanked the Glu/Lys-based peptide sequences with tetra-alanine units. This led to a surprising discovery: i➔i+4 K➔E pairs stabilised α-helical structure more than the reversed E➔K orientation. This result was consistent across all of our peptides, and was supported by the analysis of the PDB. The latter revealed that K_i➔E_i+4 pairs make more formal salt-bridges than E_i➔K_i+4 pairs. Moreover, the mechanisms through which such salt bridges are formed appears different in the two cases: whereas, those in K_i➔E_i+4 pairs employ a small number of sterically favoured side-chain conformations, salt-bridges made by E_i➔K_i+4 arrangements use many more and less-favoured conformations. We argue, that this leads to enthalpically better K_i➔E_i+4 salt bridges, and entropically favoured E_i➔K_i+4 interactions. This was manifest in the thermal unfolding transitions of different peptides: those with more K_i➔E_i+4 arrangements had sharper, and in some cases sigmoidal, thermal unfolding curves; whereas, peptides dominated by E_i➔K_i+4 pairs showed broader, less-defined transitions.

These findings are noteworthy as there is disagreement in the literature over which pairing is the more stabilising, with all possible stances being adopted: E_i➔K_i+4 > K_i➔E_i+4,⁷ vice versa,¹² and that the two interactions are equivalent.¹⁶ We believe that our combined experimental and bioinformatics studies help resolve this.

3. Non-local interactions between side chains and the macroscopic helix dipole

Our finding that K_i➔E_i+4 pairs are more stabilising than E_i➔K_i+4 arrangements has a further implication. This result is contrary to that expected from consideration of the macroscopic helix dipole alone.⁷ Organising K_i➔E_i+4 (+ve −ve) pairs in an α-helical conformation should require work against the helix macrodipole, which runs from a partially positively charged N-terminus to a partially negatively charged C-terminus; i.e., it will cost free energy and disfavour the helical state. In contrast, folding of E_i➔K_i+4 pairs should counter the dipole and therefore be favourable. That we do not see this effect—indeed, we observe the opposite—requires explaining.

The most straightforward explanation is that the macrodipole does not operate and is attenuated out where the charged moieties of the side chains reside. That is, even in the absence of solvation and dielectric effects, the charged moieties of side chains such as glutamic acid and lysine are not expected to make significant Coulombic interactions with the macrodipole. That said, they are expected to interact with the terminal partial charges arising from the half-dipoles organised at the N- and C-termini. Thus the local, terminal effects of the helix dipole are not in doubt; indeed, these are well established, and our results and conclusion in point 1 above support this. What we do question, however, is the need to invoke helix-dipole arguments beyond this, i.e., any macrodipole effect of the α-helix; we argue that the local description of the helix dipole, and how this affects side-chain preferences, binding of co-factors in proteins and so on, should be sufficient for explanations of experimental data and theoretical treatments.

In addition to contributing to fundamental understanding of helix stability, we envisage that our systematic set of designed peptides, the inventory of potential interactions within these, and the experimental data that we provide on helix content and thermal stability, will provide a useful resource to computational chemists and biochemists developing empirical and theoretical methods for analysing and predicting helix-forming peptides and protein fragments, and force fields for protein modelling more generally. Finally, in the context of synthetic biology, the fully folded peptides that we present may find use as linkers and spacers of tuneable length and thermal unfolding behaviour to combine protein domains in defined ways.^46,47

METHODS

General methods

Rink amide ChemMatrix^™ resin was purchased from PCAS Biomatrix Inc (St-Jean-sur-Richelieu, Canada). Fmoc protected amino acids, peptide grade DMF and HBTU (2-(1H-benzotriazol-1-yl)-1,1,3,3-tetramethyluronium hexafluorophosphate) were obtained from ACTG Bioproducts (Hessle, UK). All other reagents were acquired from Fisher Scientific (Loughborough, UK). Peptide concentrations were determined by absorbance at 280 nm using a NanoDrop 2000 spectrophotometer (Thermo Scientific) and employing Trp ε₂₈₀ = 5690 M⁻¹ cm⁻¹ and Tyr ε₂₈₀ = 1280 M⁻¹ cm⁻¹.

Peptides synthesis

Peptides were synthesised on a 0.1 mmole scale using a Liberty CEM microwave-assisted automated synthesiser (CEM corporation, Mathews, NC, U.S.A.) with standard Fmoc chemistry (deprotection of Fmoc using 20% piperidine in DMF) and HBTU coupling (0.45 M HBTU as activator, 1M DIPEA in DMF as activator base) on a rink amide ChemMatrix^™ resin. Each coupling and deprotection step was performed twice to minimise amino-acid deletions from the sequence, in addition to extra washings between steps.

Acetylations of N-termini were performed in DMF using 0.25 mL acetic anhydride and 0.5 mL pyridine. The resin was washed with DCM before peptides were cleaved by treatment with TFA (trifluoroacetic acid) / triisopropylsilane / water (90:5:5 vol%) for 3 hours under agitation. The cleavage mixtures were extracted by filtration and the resin rinsed with a further 5 mL of TFA before the total volume obtained was reduced to <5 mL under a flow of nitrogen. Crude peptides were precipitated in cold diethyl ether (~50 mL) and centrifuged to produce a pellet, which was then dissolved in 50:50(vol%) acetonitrile:water and freeze-dried to yield a fine white solid.

Peptide purification

Peptides were purified by reverse phase HPLC using a JASCO chromatography system with a KYA TECH HiQ C18 column (150 μm × 10 cm) and linear gradients of various buffers depending on the peptide sequence. (E₄K₄)₄, (K₄E₄)₄, A₄(E₄K₄)₃A₄, A₄(K₄E₄)₃A₄, A₄(E₄K₄)₃, (E₄K₄)₃A₄, A₄(K₄E₄)₃, (K₄E₄)₃A₄, A₄(E₄K₄)A₄(E₄K₄)A₄, A₄(K₄E₄)A₄(K₄E₄)A₄, A₄(E₃K₄)₃A₄ and A₄(K₃E₃)₄A₄ were purified using linear gradients of water (buffer A, 13 mM ammonium acetate) and 20:80 (vol%) water:acetonitrile (buffer B, 13 mM ammonium acetate). Suitable fractions were freeze-dried and re-purified using linear gradients of water (buffer A, 0.1 vol% TFA) and acetonitrile (buffer B, 0.1 vol% TFA). All other peptides were purified directly using linear gradients of water (buffer A, 0.1 vol% TFA) and acetonitrile (buffer B, 0.1 vol% acetonitrile).

Peptide characterisation

Peptide identities were confirmed by mass spectrometry (matrix: α-cyano-4-hydroxycinnamic acid) using an Applied Biosystems 4700 Proteomics Analyser MALDI-TOF instrument in reflector mode. Linear mode was used for (K₄E₄)₄. Peptide purity was confirmed using a JASCO chromatography system with analytical C18 (Phenomenex Kinetex. 5 μm, 100 × 4.6 mm) or C8 (GraceVydac 5 μm, 250 × 4.6 mm) HPLC columns to >95% purity for all peptides.

Circular dichroism (CD) spectroscopy

CD spectra and thermal denaturation curves were recorded once for each peptide at 100 μM peptide concentration, pH 7.4 in phosphate buffered saline (PBS), comprising Na₂HPO₄ (8.2 mM), KH₂PO₄ (1.8 mM), NaCl (137 mM) and KCl (2.7 mM). Data were recorded using a JASCO-815 spectropolorimeter fitted with a Peltier temperature controller and baseline corrected. Spectra were recorded at 5 °C from 260 – 190 nm, with a data pitch and bandwidth of 1 nm, and a scan speed of 100 nm/min. Fraction helix (%) = 100(([θ]₂₂₂ – [θ]_coil) / (−42,500(1–(3/n) – [θ]_coil)). Where [θ]_coil = 640–45T = 415 deg cm² dmol⁻¹ res⁻¹ at 5 °C, and n is the number of peptide bonds including the N-terminal acetyl.^48,49 Thermal denaturation curves were obtained by heating from 0 – 85 °C at 40 °C/hr and monitoring the absorbance at 222 nm over 1 °C increments (16 sec delay, and 16 sec response times), with CD spectra being taken at 5 °C intervals. The midpoints of thermal transitions (T_M) were taken as the maximum of the first derivative of the thermal denaturation curves. Thermal unfolding curves were also fitted to the Gibbs-Helmholtz equation to give the calculated mid-point (T_M) and enthalpies (ΔH) of folding. These fits assumed ΔC_p = 0: and used the following equations in Sigma Plot to fit the observed MRE (MRE_obs) to the predicted MRE (MRE_pred) as a function of temperature:⁵⁰ (1) T = T_(°C)+273.15 and T_M = T_M(°C)+273.15, to convert temperatures to Kelvin; (2) K = exp((ΔH/(1.987*T))*((T/T_m)-1)), to calculate the equilibrium constant (K) at any temperature; (3) F = K/(1+K), to calculate fractions folded (F) at any temperature; and (4) MRE_pred = ((MRE_hel-MRE_unf)*F)+MRE_unf, where MRE_hel = MRE of 100% helical peptide, and MRE_unf = MRE of unfolded peptide. Starting parameters were as follows: ΔH = −20 kcal mol⁻¹; T_m = 30 °C, MRE_hel = −32,000 deg cm² dmol⁻¹ res⁻¹, and MRE_unf = −5000 deg cm² dmol⁻¹ res⁻¹.

Analytical Ultracentrifugation

AUC sedimentation-equilibrium experiments were conducted once for each of: (E₄K₄)₃, (K₄E₄)₃, A₄(E₄K₄)₃A₄, and A₄(K₄E₄)₃A₄ at 88 μM peptide concentration (110 μL) in PBS at 20 °C in a Beckman Optima XL-A analytical ultracentrifuge using an An-60 Ti rotor, with a cell comprising an aluminium centre piece and sapphire windows. The reference channel contained 120 μL of PBS buffer. The samples were centrifuged at speeds ranging 40 – 60 krpm, and the absorbance recorded across the cell at a radial distance of 5.8 – 7.3 cm. The absorbance was recorded after 8 hrs at each speed, followed by another scan after 1 hr to check the sample had reached equilibrium before moving onto the next speed. Data were fitted to single-ideal species using Ultrascan⁵¹ and 99% confidence limits obtained by Monte Carlo analysis of the fits.

NMR spectroscopy

Each of (E₄K₄)₃, (K₄E₄)₃, (K₄E₄)₄ and A₄(K₄E₄)₃A₄ were prepared at 1 mM peptide concentration in PBS, and the pH adjusted to pH 7.4 using 10 mM NaOH. Samples were then lyophilised and reconstituted in the appropriate volume of water/D₂O (90:10 vol%) to give 1 mM of peptide at pH 7.4. 330 μL of each sample was measured in a D₂O-matched Shigemi tube. High-resolution 2D NOESY and TOCSY spectra were recorded once for (E₄K₄)₃, (K₄E₄)₃, (K₄E₄)₄ and A₄(E₄K₄)₃A₄, with 250 ms mixing times at 600 MHz on a Varian VNMRS or INOVA spectrometer (University of Bristol) equipped with a triple resonance cryogenically cooled probe-head and room-temperature probe, respectively. Spectral widths of 7000 Hz, 8192 complex points in f₂ and 800 complex points in f₁ were used for both the NOESY and TOSCY spectra. Due to signal overlap at 600 MHz data for (K₄E₄)₃, (K₄E₄)₄ and A₄(K₄E₄)₃A₄, spectra were also recorded once at 900 MHz on a Varian INOVA spectrometer (University of Birmingham) equipped with a triple-resonance cryogenically cooled probe-head. Spectral widths of 8000 Hz, 8192 complex points in f₂ and 1024 complex points in f₁ were used for both the NOESY and TOCSY spectra.

Δδ values were calculated as the difference in the observed chemical shifts and the sequence-corrected random-coil chemical shifts. The latter were generated using the chemical shifts for intrinsically disordered proteins javascript (http://www1.bio.ku.dk/english/research/pv/sbin_lab/staff/MAK/randomcoil/script/).^52,53

Bioinformatics

Bioinformatics analyses were performed using in-house Perl scripts on α-helices from a non-redundant set (≤30% pairwise sequence identity) of 2775 sub-1.6 Å resolution X-ray crystal structures collated from the RCSB Protein Data Bank (PDB)⁴³ using PISCES.⁵⁴ Only helices of 12 amino acids or longer and as identified by Promotif,⁵⁵ which uses a modified algorithm⁵⁶ for protein secondary structure assignment, were considered.

The distribution of hydrogen bonds made by Glu, Lys and Asn, were identified using Promotif⁵⁵ at various positions within the α-helices. Hydrogen bonds were identified using HBPlus⁴⁴ and categorised according to hydrogen bond donor type as follows: no hydrogen bond; ≥1 hydrogen bond to water; ≥1 hydrogen bond to a side chain atom; and ≥1 hydrogen bond to a main-chain atom.

Identification of interacting residue pairs within helices were identified as follows: The first four residues of each helix were classed as N-terminal; residues at least 4 positions in sequence away from the N- and C-termini were considered ‘central’; and the last four residues were classed as C-terminal. Numbers of attractive E_i➔K_i+4, K_i➔E_i+4, E_i➔K_i+3, and K_i➔E_i+3 and repulsive E_i➔E_i+4, K_i➔K_i+4, E_i➔E_i+3, and K_i➔K_i+3 pairs were identified. Expected numbers of pairs were estimated using the occurrence of each residue in the whole dataset. Salt bridges were considered to be formed if the distance between Lys Nζ and the centroid of (Glu Oε1, Oε2) was ≤ 4 Å. For the repulsive pairs, the mean shortest distance between side-chain atoms was recorded, along with the percentage of repulsive residue pairs with sub-4 Å distances between them.

χ₁χ₂ Side-chain rotamer distributions of for both salt-bridging and non-salt-bridged central E/K_i➔E/K_i+3/4 pairs were categorised as follows: t, χ > 120° or χ < −120°; g⁺, 0° < χ < 120°; g⁻, −120° < χ < 0° for Glu and Lys residues in all α-helices. Theoretical rotamer combinations were modelled in PyMOL (www.pymol.org) and salt-bridge potential assigned if Glu Oε1/Oε2…Lys Nζ < 4 Å. Rotamer combinations were identified using Promotif.⁵⁵

Calculating electrostatic potentials

A 32 residue polyalanine α-helix was aligned along its long axis, z, (x,y = 0,0), so that the N-terminal atom was at z = 0 (all distances are in Angstroms). The relative partial charges of each dipole were approximated by single point charges on atoms as follows: HN, −0.307; N, −0.621; C, +0.582; O, −0.574.⁵⁷ Overall charge neutrality was preserved with the following point charges for side chain atoms: Cα, +0.250; Hα, +0.085; Cβ, −0.416; and Hβ, +0.129. The electrostatic potential in vacuum V_E(x,0,z), (i.e. Coulomb’s potential) at a distance (x) from the helix axis (y = 0) was calculated in volts using Mathematica scripts to sum the electrostatic potentials arising from all of the atomically centred point charges.