Nonmonotonic diffusion in crowded environments

Abstract

We study the diffusive motion of particles among fixed spherical crowders. The diffusers interact with the crowders through a combination of a hard-core repulsion and a short-range attraction. The long-time effective diffusion coefficient of the diffusers is found to depend non-monotonically on the strength of their attraction to the crowders. That is, for a given concentration of crowders, a weak attraction to the crowders enhances diffusion. We show that this counterintuitive fact can be understood in terms of the mesoscopic excess chemical potential landscape experienced by the diffuser. The roughness of this excess chemical potential landscape quantitatively captures the nonmonotonic dependence of the diffusion rate on the strength of crowder-diffuser attraction; thus it is a purely static predictor of dynamic behavior. The mesoscopic view given here provides a unified explanation for enhanced diffusion effects that have been found in various systems of technological and biological interest.

The physical crowdedness occurring within living cells is now known to play a key role in intracellular biological processes [1]. This understanding has inspired studies of macromolecular crowding effects on protein-protein binding [2–4], transcriptional regulation [5], chromatin compaction [6], and enzyme-catalyzed reactions [7]. A key aspect of these effects is the fact that molecules diffuse more slowly in the crowded interior of a living cell than in a dilute solution [8]. This reduction in diffusion rate has been studied experimentally in vivo [9] and in vitro [10], as well by computer simulation [11], with an increasing emphasis on how the diffusion of molecules might depend on numerous properties of the crowding agents, such as their size and mobility [12].

Here we focus on the effects of a diffusing particle's interactions with the crowding obstacles. For instance, a transcription factor protein diffusing in the cell nucleus has nonspecific interactions with the surrounding chromatin; these interactions are known to play an important role in the kinetics of protein-DNA binding [13]. Furthermore, since chromatin is a large complex of DNA and proteins, the timescale of its own motion must be slower than that of the diffusing protein. If this separation of timescales is extreme, the protein diffuses in an effectively fixed environment. Diffusion among fixed obstacles arises in many other contexts as well, ranging from gel electrophoresis to the functioning of fuel cells; in all of these contexts we must understand the effects of the diffusing particle's interactions with its surroundings.

In this letter we study the diffusive motion of a particle among fixed “crowders.” The diffuser has an attractive interaction with the crowders as well as excluded volume interactions. We use Brownian Dynamics simulations to calculate the long-time effective diffusion coefficient of the diffuser as a function of the strength of its attraction to the crowders. Because the crowders impede the motion of the diffuser, one might expect any crowder-diffuser attraction to slow down diffusion. Counterintuitively, however, the effective diffusion coefficient is larger among slightly attractive crowders than among purely repulsive ones; that is, the effective rate of diffusion depends non-monotonically on the attraction strength. An enhanced rate of diffusion due to weak attractive interactions has been found previously in several different systems [14-16] and explained in terms appropriate to each system. Here we argue that the non-monotonic dependence of the diffusion coefficient on the attraction strength is a general feature of diffusion in a crowded environment, and show that it can be understood quantitatively in terms of the effective excess chemical potential landscape experienced by the diffuser. The roughness of this landscape is decreased when a small attractive interaction is added, resulting in faster diffusion. This mechanism for enhanced diffusion holds even at low densities of crowders, where previous explanations of the non-monotonic behavior in terms of “caging” do not apply.

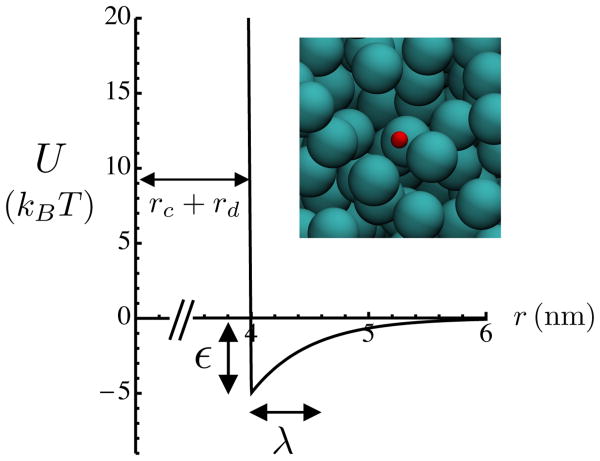
We study the motion of a spherical “diffuser” of radius r_d = 1 nm in a space containing a number N_crowd of fixed spherical “crowders” of radius r_c = 3 nm; see the inset of Fig. 1. The diffusing particle interacts with the crowders via the pairwise potential

Fig. 1.

Plot of interaction potential between crowders (radius 3 nm) and diffusers (radius 1 nm) as a function of the distance r between particle centers. The potential is given by Eq. 1. Inset: BD simulation snapshot showing crowders (blue) and a single diffuser (red). Crowder volume fraction ϕ = 0.24. Snapshot made using VMD [18].

$$U(r)=\{\begin{array}{cc}{U}_{\text{large}}-\frac{U_{\text{large}}+\epsilon }{\delta }\cdot (r-r_t+\delta )& \text{if}r\le r_t\\ -\epsilon \cdot exp[-(r-r_t)/\lambda ]& \text{if}r\ge r_t,\end{array}$$ (1)

where r_t = r_c + r_d is the sum of the hard-core radii of the crowder and diffuser. This function is plotted in Fig. 1. The first part of this potential closely approximates a hard-core interaction, using a large but finite force approximately equal to U_large/δ; here we have used U_large = 40k_BT and δ = 0.1 nm. The second part of the potential gives rise to an attractive interaction of strength ε and characteristic range λ between the diffuser and the crowders. We have used a value λ = 0.5 nm throughout this work. The diffuser moves under the influence of thermal fluctuations as well as its interactions with crowders; its motion is described by the over-damped Langevin equation. The overall time scale of the problem can be described in terms of the diffusion coefficient D₀ of the diffuser in the absence of any crowders. We define the elementary time $\tau =r_d^2/6D_0$.

We study the motion of the diffuser among the fixed crowders by performing Brownian Dynamics (BD) simulations using the GROMACS package [17], solving the over-damped Langevin equation numerically. A time step of dt = 4.5 × 10⁻⁴ τ is used, and the attractive interaction is ignored for r − r_t > 6 λ. In the Supplementary Materials we show that this time step is sufficiently small to accurately simulate the system. The fixed positions of the crowders are chosen by performing short simulations with only mobile crowders. In several cases we have verified that our results to not depend on the specific random choice of crowder positions. The simulations used to determine the effective diffusion coefficient of the diffuser are performed with different numbers N_crowd of crowders in a cubic simulation box of side L = 70 nm with periodic boundary conditions. This gives rise to different volume fractions $\varphi =4\pi r_c^3{N}_{\text{crowd}}/3L^3$ of crowders. We note that because of the nonzero size of the diffuser, the crowder volume fraction ϕ is distinct from the fraction of the volume excluded to the diffuser. In order to obtain good statistics on diffuser motion, each simulation is performed with 500 diffusers moving independently of each other (without diffuser-diffuser interactions). This would not be possible in simulations with mobile crowders, since crowder-diffuser interactions would give rise to effective diffuser-diffuser interactions.

The mean-squared displacement (MSD) of the diffuser, 〈r²(t)〉, is calculated from simulations lasting from 3 × 10⁵ τ to 2 × 10⁶ τ. By averaging the MSD over 500 independent diffusers, we obtain meaningful statistics even for time intervals comparable to the simulation length. Raw MSD data are shown in the Supplementary Materials. The long-time effective diffusion coefficient D_eff of the diffuser is equal to one-sixth of the slope of the MSD curve at long times. To calculate D_eff we use the average slope of the MSD curve between t = 1 × 10⁴ τ and t = 2 × 10⁴ τ. At these times, the MSD is almost linear with time, except for high volume fractions near ϕ = 0.5.

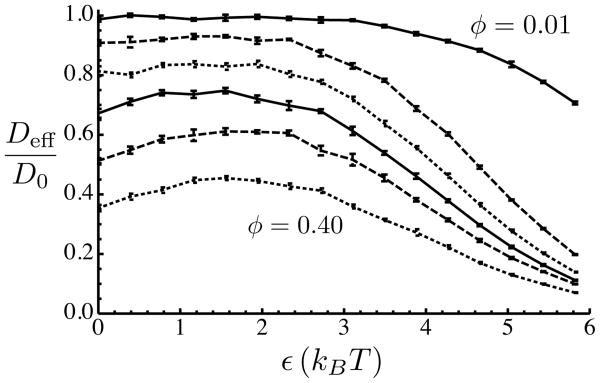
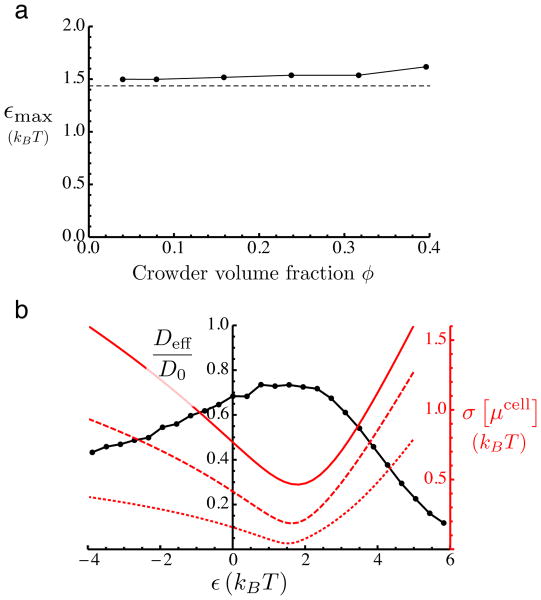
With increasing volume fraction of crowders, the resulting obstruction causes the effective diffusion coefficient of the diffuser to decrease (Fig. 2). It might be expected that by turning on the attractive interaction between the diffuser and the crowders, the effective diffusion coefficient would be further decreased, since the diffuser would on average spend more time near the crowders. Instead we find that, counterintuitively, a small attractive interaction with the crowders leads to a higher effective diffusion coefficient (see Fig. 2). At a fixed crowding level ϕ, the effective diffusion coefficient of the diffuser depends non-monotonically on the strength ε of its attraction to the crowders. The extent of the initial increase in D_eff becomes larger with increasing density of crowders, and so does the value of ε at which the maximum D_eff occurs (Fig. 3a). This value, ε_max, was estimated by fitting a sixth-order polynomial to the estimated diffusion coefficients as a function of ε and then maximizing the resulting polynomial.

Fig. 2.

Diffusion coefficient of the diffuser as a function of the strength ε of the crowder-diffuser attractive interaction. The diffusion coefficient is normalized by its value in the absence of crowding, and is shown for six different values of the crowder volume fraction ϕ. Top to bottom: ϕ = 0.01, ϕ = 0.08, ϕ = 0.16, ϕ = 0.24, ϕ = 0.32, and ϕ = 0.40. Error bars are from the standard error of the means of five subgroups of diffusers (100 in each group).

Fig. 3.

a: The value of the crowder-diffuser attraction strength, ε, at which the maximum in the diffusion coefficient occurs (see Fig. 2), as a function of the volume fraction ϕ of crowders. Solid line: simulation results. Dashed line: approximate value given by Eq. 4. b: Black curve, left y axis: Diffusion coefficient of diffuser as a function of the strength ε of the crowder-diffuser attractive interaction. The volume fraction of crowders is fixed at ϕ = 0.24. The diffusion coefficient is normalized by its value in the absence of crowding. Red curves, right y axis: Standard deviation of cell free energies calculated using Eqs. 2 and 3 over the simulation box of size 70 × 70 × 70 nm. Solid red curve: 5 nm cubic cells. Dashed red curve: 7 nm cubic cells. Dotted red curve: 14 nm cubic cells. Note that in this figure we show data for negative values of ε, corresponding to crowder-diffuser repulsion.

A particle diffusing in a rugged potential energy landscape must overcome energy barriers, and will always diffuse more slowly than in a flat potential landscape [19]. It is tempting to reason that in the absence of any crowder-diffuser attractions, the diffuser experiences a flat potential energy in between its collisions with crowders, and that any attractive interactions will only slow down diffusion. However, we have just seen that this is not the case. Next we will see that the enhanced diffusion due to the attractive interactions may be understood from a mesoscopic perspective that relates the effective diffusion rate to the roughness or flatness of a coarse-grained effective potential.

We partition space into cubic “cells” intermediate in size between the crowders and the simulation box. Viewed on this scale, the diffuser moves from cell to cell, feeling an effective potential equal to the excess or non-ideal contribution to the diffuser's chemical potential:

$${\mu }_i^{\text{cell}}=-k_{B}T\cdot ln{V}_{\text{cell}}^{-1}{\int }_{\text{cell}i}{e}^{-\beta U_{\text{tot}}(\overrightarrow{r})}d\overrightarrow{r},$$ (2)

where U_tot(r⃗) is the total potential energy of a diffuser at position r⃗. Using the same crowder positions as in the BD simulations, we calculate the effective potential for each cell numerically by discretizing the integral in Eq. 2. A measure of the roughness of the effective potential landscape is the standard deviation of the cell potentials:

$$\sigma \left[{\mu }^{\text{cell}}\right]=\sqrt{\frac{1}{N_{\text{cells}}}\sum _i{({\mu }_i^{\text{cell}}-\overline{{\mu }^{\text{cell}}})}^2}$$ (3)

This standard deviation is plotted in Fig. 3b as a function of the attraction strength ε (right vertical axis) for the case where the crowder volume fraction is ϕ = 0.24. The three curves show this quantity for different cell sizes (5, 7, and 14 nm in length). In all three cases, the roughness of the effective potential landscape depends non-monotonically on ε, reaching a minimum near the value at which D_eff is maximized. This suggests the idea of a random walk on the lattice of cells, with maximum diffusion when the landscape of cell excess chemical potentials is flattest. This picture is valid when the cells are large enough that the effective steps taking the diffuser from one cell to another are statistically uncorrelated. The correlation of successive displacements on short time scales is reflected by the changing slope of the MSD as a function of time. The time scale of crossover to the asymptotic regime corresponds to a length-scale, weakly dependent on ϕ, of about 6 nm (data not shown). The variance shown in Fig. 3b for cell size 14 nm (dotted curve) or 7 nm (dashed curve) should therefore provide a good measure of the roughness of the effective excess chemical potential landscape.

Equation 2 for a cell's effective potential suggests the following way to estimate the value of ε at which D_eff is maximized. In the limit of dilute crowders, some cells will contain a crowder, while others will not. In the absence of any attractive interactions, cells with crowders will have a higher effective potential due to the volume excluded to the diffuser. These are precisely the cells whose effective potentials will be decreased when ε is increased from zero; the statistical spread in cell effective potentials will decrease as a result, leading to a flatter potential landscape and faster diffusion. The fastest diffusion should occur when the attractive interactions compensate, in the integral of Eq. 2, for the excluded volume of a crowder. Thus diffusion will be maximized when ε is chosen such that

$${\int }_0^{\infty }4\pi r^2(e^{-\beta U(r)}-1)dr=0.$$ (4)

This results in the estimate of ε_max ≈ 1.4 k_BT, in good agreement with the values of ε_max from the BD simulations (Fig. 3a). The integral in Eq. 4 above is proportional to the second virial coefficient for crowder-diffuser interaction. In the Supplementary Materials we analyze Eq. 4 for the simple case of a square-well crowder-diffuser potential.

The accelerated diffusion in the presence of small attractive interactions is reminiscent of the phenomenon of facilitated diffusion [13, 20], in which non-specific protein-DNA attractions allow a transcription factor to find its binding site on DNA faster than is possible simply by diffusion in the three-dimensional bulk. Our results may indeed be relevant to diffusion in chromatin; however, existing theories of facilitated diffusion predict an effective three-dimensional diffusion coefficient that is strictly decreasing as a function of protein-DNA attraction strength [21]. The reduction in search time in facilitated diffusion is not due to any increase in overall diffusion rate, but rather to the geometric fact that the target is on the quasi-one-dimensional DNA. For similar reasons, the time necessary for a molecule to diffuse through a pore [22] or out of a spherical cavity [23] may be a non-monotonic function of its attraction to the confining walls.

Several authors have found non-monotonic dependences in effective diffusion coefficients with increasing strengths of attraction between molecules. Huang et al. [24] performed simulations of polymers diffusing amongst fixed attractive nanoparticles and noted that as the attraction is turned on, the effective diffusion coefficient of the polymers initially remains constant before decreasing. In one case (see Fig. 1 of ref. [24]) their data show a non-monotonic dependence on attraction strength, but they did not appear to consider this statistically significant. The small excluded volume of their nanoparticles implies via Eq.4 that the maximum of the diffusion coefficient should occur at very small values of the attraction strength, making it difficult to resolve. In another work, Lee et al. [25] showed that polymers diffusing among fixed spherical obstacles could diffuse faster if they were slightly attracted to those obstacles. However, they attributed this effect to a mechanism involving the decreased configurational entropy as polymers squeeze through constrictions between cages formed by the obstacles. Here we have shown not only that the same non-monotonic dependence occurs with monomers rather than polymers, but also that it occurs even when the crowders are dilute and the cage picture does not apply.

Holmes [14] has used an effective medium theory to calculate the effective diffusion coefficient of ions moving in a charged polymeric gel, finding it to be a non-monotonic function of the charge of the ion, with a maximum near zero charge. Similarly, Yamamoto and Schweitzer [15] used mode coupling theory to study the diffusion of nanoparticles in polymer melts and found the effective diffusion coefficient to depend non-monotonically on the strength of the polymer-nanoparticle attraction. Finally, Pham et al. [16] simulated systems of sticky hard spheres at very high densities near the glass transition, revealing a pronounced non-monotonic dependence of the diffusion rate on the attractions between molecules. Our results show that the same non-monotonic behavior occurs even at low crowder densities, where caging does not occur. Instead we have shown that the non-monotonicity of the effective diffusion coefficient is attributable to changes in roughness of the effective excess chemical potential landscape as a function of the attraction strength. This explanation makes no reference to the particular details of the system; therefore we expect that enhanced diffusion due to weak attraction interactions is a general phenomenon. Indeed, in the Supplementary Materials (SM) we show that the non-monotonic dependence of the effective diffusion coefficient on the attraction strength is almost completely independent of the details of the arrangement of the crowders; these can be arranged in a periodic array or in gel-like structures, for example. The non-monotonicity persists as well (although weakly) when the diffuser moves among mobile crowders. Finally, we show in the SM that the diffusion rate of a small polymer among fixed crowders has a very pronounced nonmonotonic dependence on ε The intuitive picture that emerges is that maximal diffusion is obtained when the diffusing particle sees a relatively flat effective potential at the long length scale relevant for diffusion. This potential is measured, to first order, by the second virial coefficient between the crowders and the diffusing particle and it is a generic feature that does not depend on the details of the interaction potential.

In summary, we performed BD simulations of particles diffusing among fixed spherical crowders. As the strength of the attractive diffuser-crowder interaction was varied, the long-time effective diffusion coefficient of the diffusers changed non-monotonically (Fig. 2). The enhancement of diffusion due to attractive interactions has been noted previously in several system, but was attributed to aspects of these systems such as the polymeric nature of the diffuser [25] or the caging effect that occurs at high densities [16]. Here we have given a generic analysis of this counterintuitive effect in terms of the coarse-grained excess chemical potential landscape in which the diffuser moves. The roughness or flatness of this landscape is a purely static quantity that correlates very well with the effective diffusion coefficient of the diffuser (Fig. 3b). Our results suggest that quite generally, the diffusion rate of molecules moving in crowded environments will depend non-monotonically on the strength of attractions between the diffusers and crowding agents, and provides a way of predicting the conditions that will maximize the diffusion rate.