Combined Néel and Brown rotational Langevin dynamics in magnetic particle imaging, sensing, and therapy

Abstract

Magnetic nanoparticles have been studied intensely because of their possible uses in biomedical applications. Biosensing using the rotational freedom of particles has been used to detect biomarkers for cancer, hyperthermia therapy has been used to treat tumors, and magnetic particle imaging is a promising new imaging modality that can spatially resolve the concentration of nanoparticles. There are two mechanisms by which the magnetization of a nanoparticle can rotate, a fact that poses a challenge for applications that rely on precisely one mechanism. The challenge is exacerbated by the high sensitivity of the dominant mechanism to applied fields. Here, we demonstrate stochastic Langevin equation simulations for the combined rotation in magnetic nanoparticles exposed to oscillating applied fields typical to these applications to both highlight the existing relevant theory and quantify which mechanism should occur in various parameter ranges.

Nanotechnology's relevance to medicine is only increasing as we learn to manipulate the human body with objects of size equivalent to cells and molecules. State of the art techniques from materials science allow the creation of nanoscopic magnetic particles with moments substantial enough for remote control and detection. Exposure to lower (audio) frequency magnetic fields is not harmful to the human body and thus magnetic particles can in principle be controlled and monitored by magnetic fields in vivo. Biosensing for cancer biomarkers,¹ hyperthermia therapy for cancer cell destruction,² and magnetic particle imaging (MPI) for local quantification of particle concentrations in vivo³ are exciting applications of nanotechnology in medicine.

It has long been understood that for a magnetic particle suspended in liquid, two mechanisms exist to rotate the direction of the particle's magnetic moment. The solid state mechanism first described by Néel involves the restructuring of electronic states allowing the magnetic moment to rotate internally.⁴ The so-called “Néel rotation” is influenced by magnetic anisotropy arising from the crystal structure or the shape of the particle.⁵ Simultaneously, the entire particle can rotate in the fluid, undergoing “Brownian rotation.”⁶ The direction of the magnetic moment of the nanoparticle is written $\mathbf{m}$ and the direction of a uniaxial anisotropy or “easy axis” is $\mathbf{n}$.

A common property for imaging, sensing, and therapy applications is the use of oscillating magnetic fields to activate rotations in the particles. However, these technologies can differ in the necessary rotation mechanism and ensuring a specific rotation mechanism in diverse magnetic field conditions can be paramount for successful application. For example, biosensing requires Brownian rotation to couple the nanoparticle rotations to environmental variables (like viscosity).^1,7 Alternatively, MPI requires Néel rotation, and any Brownian relaxation necessitates signal corrections to estimate the nanoparticle concentration quantitatively.^3,8 Hyperthermia treatment has been proposed using both mechanisms, and great effort has been put into deciphering which mechanism is occurring, and how to optimize heating accordingly.^9,10 Moreover, because both MPI and hyperthermia have some competing requirements (e.g., particle size or anisotropy), preemptive theoretical advice for the optimal size or anisotropy is valuable.

It has become typical to use the theory of Rosensweig to decouple the mechanisms based on their relaxation times.¹¹ However, in each application, experimental work has demonstrated that both effects are present.^9,12,13 Though we are not the first to say, it,¹⁴ we are explicit in our statement: using Rosensweig's expression for the dominant relaxation time using the zero-field relaxation times can result in seriously flawed analyses in cases of strong applied magnetic fields. It is necessary to study the simultaneous stochastic rotation equations to accurately predict the dynamics in diverse fields for different applications.

A review of the combined differential equation approach is found in the excellent work of Coffey, Cregg, and Kalmykov.⁶ While the theory has existed, first use of the coupled formalism in the applied literature is more recent. The equations can be formulated from first principles with a generalized torque¹⁵ or in a slightly more transparent approximate form.^16,17 The complete, coupled equations of motion track both the direction of the easy axis of the particle $\mathbf{n}$ and the direction of the magnetization $\mathbf{m}$ simultaneously. The dynamics depends on the relevant viscosity of the fluid η in [Ns/m²] and hydrodynamic volume of the particle $V_{\mathrm{h}}$ in [m³]. As typically done, accelerations can be neglected because nanoparticle motions are dominated by viscous forces, i.e., they have vanishingly small Reynolds numbers. The internal magnetization direction $\mathbf{m}$ rotates within the nanoparticle's magnetic core following the Landau-Lifshitz-Gilbert (LLG) equation in terms of the generalized total field H in [T/μ₀], the electron gyromagnetic ratio γ (typically 176 GHz/T), and the LLG damping parameter α = 1.

The combined differential equations are

$$\begin{array}{c}\frac{d\mathbf{n}}{\mathit{d}\mathit{t}}=\frac{\mathit{\theta }}{6\eta V_{\mathrm{h}}}\times \mathbf{n}\\ \frac{d\mathbf{m}}{\mathit{d}\mathit{t}}=\frac{\gamma }{1+{\alpha }^2}\left(\mathbf{H}+\alpha \mathbf{m}\times \mathbf{H}\right)\times \mathbf{m}\end{array}$$ (1)

with generalized torque $\mathit{\theta }$¹⁵ and total field H that arise from partial derivatives of the Helmholtz free energy $F=U-TS$. We are not considering the clustering of particles, and so, the entropic contribution is ignored. We express the internal energy of the particle in the typical Stoner-Wolhfarth prescription¹⁸ and thus

$$U=-\mu \mathbf{m}·{\mathbf{H}}_{\mathrm{a}}-K{V}_{\mathrm{c}}{(\mathbf{m}·\mathbf{n})}^2$$ (2)

in terms of an applied field ${\mathbf{H}}_{\mathrm{a}}$ and the magnetic moment $\mu =M_{\mathrm{s}}{V}_{\mathrm{c}}$ in [J/T] as related to the saturation magnetization $M_{\mathrm{s}}$ in [J/Tm³] and the magnetic core volume of the particle $V_{\mathrm{c}}$ in [m³]. This leads to the generalized torque and field

$$\mathit{\theta }=\frac{\partial U}{\partial \mathbf{n}}\times \mathbf{n}=2K{V}_{\mathrm{c}}\left(\mathbf{m}·\mathbf{n}\right)\left(\mathbf{m}\times \mathbf{n}\right)+{\mathit{\theta }}_{\text{th}},$$ (3)

$$\mathbf{H}=-\frac{1}{\mu }\frac{\partial U}{\partial \mathbf{m}}={\mathbf{H}}_{\mathrm{a}}+\frac{2K{V}_{\mathrm{c}}}{\mu }\left(\mathbf{m}·\mathbf{n}\right)\mathbf{n}+{\mathbf{H}}_{\text{th}},$$ (4)

where we include thermally generated fields ${\mathbf{H}}_{\text{th}}$ and torques ${\mathit{\theta }}_{\text{th}}$ that are normal- or Gaussian-distributed and arise from many microscopic random fields or torques. The frequency distribution of the noise terms are assumed to be approximately flat (in the fashion of white noise) with mean magnitude zero and with no correlations in time or space. The magnitudes of the fluctuations include nanoparticle and fluid parameters as well as the Boltzmann constant $k_{\mathrm{B}}$ in [J/K] and the temperature T in [K]. Thus, the mean is zero $⟨{\mathit{\theta }}_{\text{th}}^i(t)⟩=0$, and the correlation function is Dirac-delta correlated in time and Kronecker-delta correlated in space (with i, j representing Cartesian direction) $⟨{\mathit{\theta }}_{\text{th}}^i(t){\mathit{\theta }}_{\text{th}}^j(t\prime )⟩=12k_{\mathrm{B}}T\eta V_{\mathrm{h}}{\delta }_{\mathit{i}\mathit{j}}\delta (t-t\prime )$. The thermal fields are similarly defined as having zero mean value $⟨{\mathbf{H}}_{\text{th}}^i(t)⟩=0$ with correlations $⟨{\mathbf{H}}_{\text{th}}^i(t){\mathbf{H}}_{\text{th}}^j(t\prime )⟩=\frac{2k_{\mathrm{B}}T}{\gamma \mu }\frac{1+{\alpha }^2}{\alpha }{\delta }_{\mathit{i}\mathit{j}}\delta (t-t\prime )$.

The unitless anisotropy σ, Brownian relaxation time ${\tau }_{\mathrm{B}}$, and the Néel event time ${\tau }_0$ are defined

$$\sigma =\frac{K{V}_{\mathrm{c}}}{k_{\mathrm{B}}T}\hspace{1em}{\tau }_{\mathrm{B}}=\frac{3\eta V_{\mathrm{h}}}{k_{\mathrm{B}}T}\hspace{1em}{\tau }_0=\frac{\mu }{2k_{\mathrm{B}}T\gamma }\frac{1+{\alpha }^2}{\alpha }.$$ (5)

Note that as in Chantrell's work,¹⁹ α is found in the numerator and the denominator of ${\tau }_0$, because in the limit of small and large damping constant, the relaxation time should approach infinity. There is sometimes confusion over the expressions listed for the formulation of τ_N. The most general zero-field relaxation times are²⁰

$${\tau }_N=\{\begin{array}{cc}{\tau }_0{(1-\frac{2}{5}\sigma +\frac{48}{875}{\sigma }^2)}^{-1}\hfill & \text{if}\hspace{0.17em}\sigma <1\hfill \\ \frac{{\tau }_0}{2}\sqrt{\frac{\pi }{{\sigma }^3}}\hspace{0.17em}\text{exp}(\sigma )\hfill & \text{if}\hspace{0.17em}\sigma \ge 1.\hfill \end{array}$$ (6)

The combined rotation can be simulated numerically using typical prescriptions.²¹ Physics commonly uses the Stratonovich interpretation because white noise is a limit approximation of colored noise with a correlation time much faster than the timescales of the nanoparticle dynamics.²² To achieve convergent solutions, the magnitude of each numerical step must be below unity (e.g., $\Delta \mathbf{n},\Delta \mathbf{m}<1$). Following Refs. 22 and 23, for example, we used an integration time-step 1/100th of the smallest timescale for each simulation. We also found that using a normalization step as suggested in Ref. 24 enhanced the convergence, though numerical artifacts were still common when the time-step was too large.

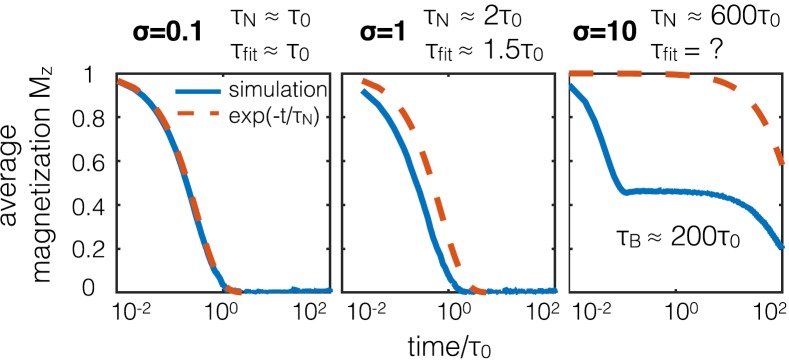
In Fig. 1, we have used Eq. (1) to simulate a possible measurement of the perpendicular relaxation time by polarizing the magnetizations and then allowing them to decay to equilibrium. For Brownian particles, the easy axis directions decay exponentially as $\text{exp}(-t/{\tau }_{\mathrm{B}})$. However, this experiment is not well posed to measure the Néel relaxation time ${\tau }_{\mathrm{N}}$. Imagine that the magnetizations begin polarized in the positive z-direction while each nanoparticle easy axis points in a random direction; perhaps, a static field has been applied to particles in a highly viscous liquid. When the magnetic field is released, the nanoparticle magnetizations will snap to align either with or against their nearest easy axis (in this case uniaxial anisotropy implies one nearest direction in the upper half plane), resulting in a short-lived asymmetric and non-zero net magnetization. Only then does the magnetization decay to a randomized equilibrium state.

FIG. 1.

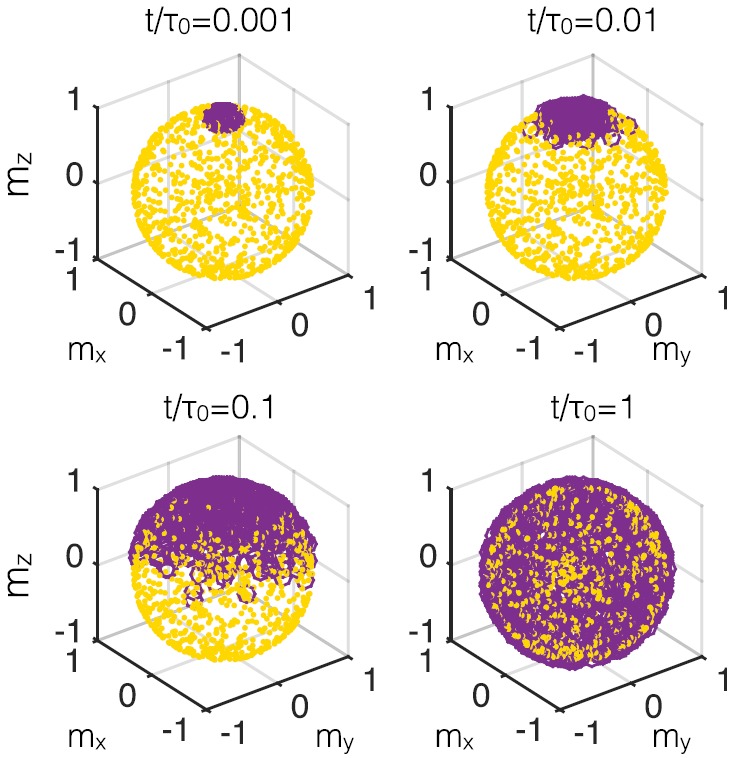
Visualization of a relaxation decay experiment of 100 nanoparticles. With each easy axis in a random direction (${\mathbf{n}}_i$ yellow dots), the initially polarized magnetization directions (${\mathbf{m}}_i$ purple circles) spread to align with their respective easy axes. Comparing this simulation with exponential decay will not in general determine the perpendicular ${\tau }_{\mathrm{N}}$ for larger anisotropy.

This gedanken experiment presents multiple stages of relaxation of the magnetization direction. The first is a driven process dependent on the magnitude of the anisotropy. The next is a free relaxation to randomized equilibrium where the magnetization directions are randomized by Brownian and Néel relaxation. The timescale of this two stage process cannot be precisely described by an exponential decay using Eq. (6). We can however derive the evolution equation for the magnetization in the frame of reference of the easy axis. We examine the early Néel dynamics of the fast snapping process (when $\frac{d\mathbf{n}}{\mathit{d}\mathit{t}}=0$) assuming as in Usov and Liubimov's work¹⁵ that the stochastic field ${\mathbf{H}}_{\text{th}}$ is ignorable. Rewriting the second of Eq. (1) in a dimensionless form results in

$$2{\tau }_0\frac{d\mathbf{m}}{\mathit{d}\mathit{t}}=\left(\frac{\mathit{\xi }}{\alpha }+\mathbf{m}\times \mathit{\xi }\right)\times \mathbf{m}.$$ (7)

Then, external magnetic field is zero so that the total unitless field strength is only given by the internal field $\mathit{\xi }=\frac{\mu \mathbf{H}}{k_{\mathrm{B}}T}=2\sigma (\mathbf{m}·\mathbf{n})\mathbf{n}$, where $\mathbf{n}$ is fixed in time and randomized on the unit sphere for each particle. Now because we have assumed very high viscosity, $\frac{d\mathbf{n}}{\mathit{d}\mathit{t}}=0$ and we can study the dynamics projected into the direction of the easy axis. Letting $a=\mathbf{m}·\mathbf{n}$ and taking the dot product of both sides of Eq. (7) with $\mathbf{n}$ leaves

$$2{\tau }_0\frac{\mathit{d}\mathit{a}}{\mathit{d}\mathit{t}}=2\sigma a\left[1-a^2\right],$$ (8)

where we have used $|\mathbf{m}{|}^2=|{\mathbf{n}}^2|=1$ and $(\mathbf{n}\times \mathbf{m})·\mathbf{n}=0$. Separating variables and integrating, the evolution of the magnitude of the dot product, a surrogate for the angle between the vectors, is

$$a\left(t\right)=\sqrt{\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}\frac{t}{{\tau }_a}}{1+\text{exp}\hspace{0.17em}\frac{t}{{\tau }_a}}},$$ (9)

where we identify the alignment timescale as ${\tau }_a={\tau }_0/2\sigma$. By the time the argument $t/{\tau }_a\to 10$, the alignment is complete. The alignment occurs extremely quickly, on the order of the Néel event time, and the alignment rate only increases with increasing anisotropy.

Inconsistencies with the exponential decay for different anisotropies are visualized in Fig. 2. Even here, we have extended the previous decay experiment now allowing the easy axes to rotate. The evolution of the average magnetization direction (written M_z) is plotted in comparison to the expected exponential decays of form $M_z=\text{exp}(-t/{\tau }_N)$ in each panel of Fig. 2. On the left panel, the anisotropy is small $\sigma =0.1$, and the relaxation process occurs freely, matching the exponential decay formula with equilibrium perpendicular Néel relaxation time. On the middle panel, σ = 1 and the anisotropy is large enough to distort the exponential decay with the typical perpendicular relaxation time. On the rightmost panel, σ = 10 and the Néel time constant is larger than the Brownian relaxation time (${\tau }_B=50$ μs). The fast relaxation process dominates such that the relaxation cannot even be fit with an exponential decay and the second relaxation stage is then Brownian thermalization.

FIG. 2.

Three regimes of magnetization decay to disorder with randomized easy axes. At higher anisotropy, the magnetization decay does not fit an exponential of the form $M_z=\text{exp}(-t/{\tau }_{\mathrm{N}})$.

We also model applications that use oscillating applied fields, with $\mathit{\xi }=\xi \hspace{0.17em}\text{cos}\hspace{0.17em}2\pi ft\hspace{0.17em}\widehat{z}$ and f = 10 kHz. The combined simulations concur with previous works that show the high sensitivity to applied field amplitude in deciding which mechanism will occur.¹⁴ In Fig. 3, we examine the realistic scales of anisotropy constant σ ranging from $3\to 30$. In the case of a lower applied field ξ = 4 shown on the left panels, minimal steady-state Brownian responses occur even as the anisotropy (and Néel relaxation time) increases (see the bottom 4th and 5th plots), and the external polarization (direction of the easy axis N_z) still lags behind the internal polarization (magnetization M_z). On the right panels when ξ = 20, an even larger anisotropy is needed to observe Brownian rotations because the larger applied field is able to force Néel rotations. Purely changing the zero-field Néel relaxation time by changing σ in Eq. (6) does not block the Néel oscillations because the equilibrium timescale is no longer valid. With that logic, the ratio of $\sigma /\xi$, the anisotropy relative to dimensionless field, is important to consider in predicting which mechanism dominates.

FIG. 3.

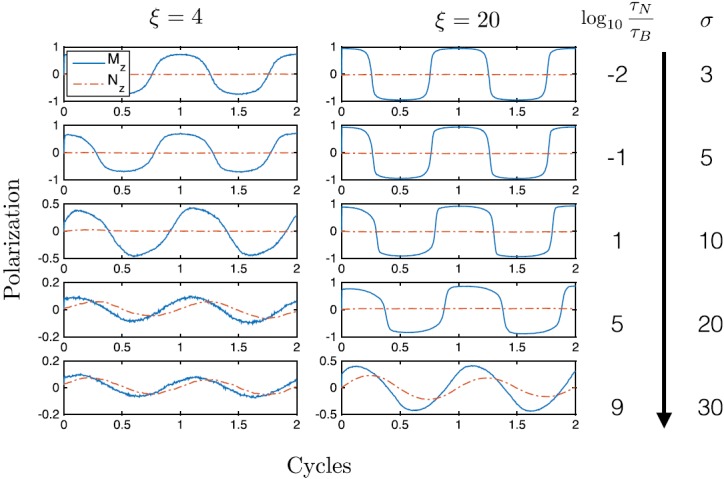
Simulations of combined stochastic rotation with 10³ averages. The average magnetization direction M_z and average anisotropy axis direction N_z are plotted over parameter ranges demonstrating the inability to determine the mechanism purely based on zero-field equilibrium relaxation times.

Though the formalism is quite general, we quickly comment on the amount of Brownian and Néel rotation expected in specific examples. The saturation magnetization and anisotropy constants for typical magnetite particles are on the order of 100 kA/m and 10 kJ/m³, respectively. Thus, the sizes of the particles and the field amplitudes applied can be used to classify their probable behavior in comparison to Fig. 3. For example, hyperthermia typically uses particles with 5 nm core radius and 15 nm hydrodynamic radius and fields and frequencies up to 100 mT/μ₀ and above 100 kHz.²⁵ Using Eq. (5) leads to ${\tau }_0\sim {10}^{-10},\hspace{0.17em}\sigma \sim 1,\hspace{0.17em}{\xi }_0\sim 3$, and $\hspace{0.17em}{\text{log}}_{10}({\tau }_{\mathrm{N}}/{\tau }_{\mathrm{B}})\sim -4$, well within the range for expected Néel rotations. Magnetic particle imaging uses particles with roughly 15 nm core and 25 nm hydrodynamic radii in 25 kHz, 20 mT/μ₀ applied fields.²⁶ This leads to ${\tau }_0\sim {10}^{-9},\hspace{0.17em}\sigma \sim 20,\hspace{0.17em}{\xi }_0\sim 20$, and $\hspace{0.17em}{\text{log}}_{10}({\tau }_{\mathrm{N}}/{\tau }_{\mathrm{B}})\sim 2$, likely leading to predominantly Néel rotations but as has been shown recently, may include some Brownian rotation especially when a size distribution is present.¹² In biosensing applications with 10 mT/μ₀ fields, 20 nm core and 50 nm hydrodynamic radii particles,¹ ${\tau }_0\sim {10}^{-8},\sigma \sim 80,\hspace{0.17em}{\xi }_0\sim 10$, and $\hspace{0.17em}{\text{log}}_{10}({\tau }_{\mathrm{N}}/{\tau }_{\mathrm{B}})\sim 12$ and we expect Brownian rotation. These calculations are nicely accordant checks on the theory as these technologies are proven.

For the success of technology, understanding the nanoparticle rotation mechanism is necessary. Our conclusion is that purely by comparing the equilibrium relaxation times that arise from the average size of the nanoparticles, it is unlikely that the mechanisms will be accurately predicted. Moreover, in cases including polydisperse size- and anisotropy-distributions, there will be a mixture of effects and the formalism provided here allows exploration with specific and detailed simulations given the application or nanoparticles of interest.