NonCartesian MR image reconstruction with integrated gradient nonlinearity correction

Abstract

Purpose:

To derive a noniterative gridding-type reconstruction framework for nonCartesian magnetic resonance imaging (MRI) that prospectively accounts for gradient nonlinearity (GNL)-induced image geometrical distortion during MR image reconstruction, as opposed to the standard, image-domain based GNL correction that is applied after reconstruction; to demonstrate that such framework is able to reduce the image blurring introduced by the conventional GNL correction, while still offering effective correction of GNL-induced geometrical distortion and compatibility with off-resonance correction.

Methods:

After introducing the nonCartesian MRI signal model that explicitly accounts for the effects of GNL and off-resonance, a noniterative gridding-type reconstruction framework with integrated GNL correction based on the type-III nonuniform fast Fourier transform (NUFFT) is derived. A novel type-III NUFFT implementation is then proposed as a numerically efficient solution to the proposed framework. The incorporation of simultaneous B₀ off-resonance correction to the proposed framework is then discussed. Several phantom and in vivo data acquired via various 2D and 3D nonCartesian acquisitions, including 2D Archimedean spiral, 3D shells with integrated radial and spiral, and 3D radial sampling, are used to compare the results of the proposed and the standard GNL correction methods.

Results:

Various phantom and in vivo data demonstrate that both the proposed and the standard GNL correction methods are able to correct the coarse-scale geometric distortion and blurring induced by GNL and off-resonance. However, the standard GNL correction method also introduces blurring effects to corrected images, causing blurring of resolution inserts in the phantom images and loss of small vessel clarity in the angiography examples. On the other hand, the results after the proposed GNL correction show better depiction of resolution inserts and higher clarity of small vessel.

Conclusions:

The proposed GNL-integrated nonCartesian reconstruction method can mitigate the resolution loss that occurs during standard image-domain GNL correction, while still providing effective correction of coarse-scale geometric distortion and blurring induced by GNL and off-resonance.

1. INTRODUCTION

In conventional magnetic resonance imaging (MRI), the spatial encoding gradient fields are usually assumed to vary linearly across the entire imaging field-of-view (FOV). Due to engineering limitations, perfect gradient linearity can never be exactly achieved in practice, and may even be intentionally compromised to alleviate peripheral nerve stimulation, relax technical requirements on system hardware, and/or to enable high gradient amplitudes and slew rates.^1–3 Gradient nonlinearity (GNL), if not compensated, manifests as geometric distortion in reconstructed images.^4–6 Many MRI applications rely on high geometric accuracy, such as radiation therapy pretreatment planning or multicenter, longitudinal studies of neurodegenerative diseases, and attenuation correction for MR/PET. In such scenarios, correction of GNL-induced geometric distortion has been reported to be beneficial by increasing imaging anatomical accuracy, improving image reproducibility, and reducing cross-site variability.^7–11

Conventionally, the geometric distortion induced by GNL is corrected after MRI reconstruction via image-domain interpolation based on a presumed a priori known spatial distortion field.¹ Such techniques are widely available on commercial MR scanners (e.g., “GradWarp” on General Electric’s scanners). Despite being able to accurately correct coarse-scale geometric distortion, standard GNL correction methods introduce additional, unnecessary image blurring and resolution loss to the corrected images due to the intrinsic smoothing effect of image interpolation.^12–14 In the case of nonCartesian MRI, the image blurring effect is further complicated by the presence of main magnetic field (B₀) inhomogeneity and susceptibility.^15,16

Recently, a model-based reconstruction framework for Cartesian MRI that performed GNL correction during—rather than after—image reconstruction was developed.¹³ This integrated GNL correction method was shown to be able to alleviate the image blurring and resolution loss introduced by the standard GNL correction. In this work, we discuss the generalization of this GNL-aware reconstruction framework for nonCartesian acquisitions. The signal model is modified to account for the effect of GNL during nonCartesian data acquisition, from which we derive a noniterative, gridding-type reconstruction framework that also prospectively corrects for the GNL-induced spatial distortion during image reconstruction. A numerically efficient implementation of this framework is then proposed. The incorporation of simultaneous B₀ off-resonance correction (ORC) to the proposed framework is also discussed. Finally, representative reconstruction results for several 2D and 3D nonCartesian acquisition methods are presented to compare the proposed and the standard GNL correction methods.

2. THEORY

2.A. NonCartesian signal model with GNL

In the presence of both GNL and B₀ inhomogeneity, the κth k-space signal measurement, g[κ], obtained during a nonCartesian MRI acquisition can be modeled as¹⁷

$${\displaystyle \mathbf{g}\left[\kappa \right]={\int }_{\mathrm{\Omega }}f\left(\mathbf{x}\right)e^{-j{\omega }_0\left(\mathbf{x}\right)t\left[\kappa \right]}{e}^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{x}\right)}d\mathbf{x}+\mathbf{n}\left[\kappa \right],}$$ (1)

where f(x) is a continuous image-domain function denoting the object of interest, with x denoting the (true) physical coordinates; Ω is the field of excitation; and Δ(x) is the distortion field mapping from physical to distorted coordinates due to GNL. In the context of GNL correction, Δ(x) is assumed to be bijective and invertible. In practice, the distortion mapping can be obtained from electromagnetic field simulation, or measured with phantoms designed for distortion tracking,^18–20 and is therefore assumed to be a priori known; ω₀(x) indicates the spatial off-resonance map; t[κ] is the readout time of the κth signal measurement; $\omega \left[\kappa \right]$ denotes the k-space coordinates of the κth signal sample for a certain nonCartesian k-space sampling trajectory. Finally, n[κ] is zero-mean proper complex Gaussian noise in the κth measurement.

Given a finite measurement vector, g, the goal of image reconstruction is to estimate the continuous image function f; however, auxiliary assumptions must be made for this problem to be well-posed. Hence, a finite series representation of f is usually pursued instead, i.e., $f\left(\mathbf{x}\right)\approx \sum _{i\in \mathrm{\Theta }}\mathbf{u}\left[i\right]b(\mathbf{x}-\mathbf{r}\left[i\right])$, where b(⋅) is the continuous pixel model function, r[i] is the physical position of the ith pixel, and u[i] is its corresponding display coefficient.²¹ Assuming a Dirac delta pixel model, i.e., b(x) = δ(x), Eq. (1) reduces to

$${\displaystyle \mathbf{g}\left[\kappa \right]=\sum _{i\in \mathrm{\Theta }}\mathbf{u}\left[i\right]e^{-j{\omega }_0\left(\mathbf{r}\left[i\right]\right)t\left[\kappa \right]}{e}^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{r}\left[i\right]\right)}+\mathbf{n}\left[\kappa \right],}$$ (2)

which has the following affine algebraic form:

$${\displaystyle \mathbf{g}=\mathbf{Au}+\mathbf{n},}$$ (3)

with $\mathbf{A}(\kappa ,i)=e^{-j{\omega }_0\left(\mathbf{r}\left[i\right]\right)t\left[\kappa \right]}{e}^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{r}\left[i\right]\right)}$ denoting the forward encoding matrix that accounts for the effects of nonCartesian sampling, off-resonance effects, and GNL-based distortion.

2.B. Proposed implementation of type-III nonuniform fast Fourier transform (NUFFT)

In the absence of B₀ inhomogeneity, i.e., ω₀(x) = 0, Eq. (3) reduces to

$${\displaystyle \mathbf{g}=\hat{\mathbf{A}}\mathbf{u}+\mathbf{n}.}$$ (4)

In nonCartesian imaging, k-space data are sampled on a nonuniform grid. In the absence of GNL, Δ(r) = r, and the true pixel positions are located on a uniform grid in the image space. In this case, Eq. (4) reduces to the standard nonCartesian MRI signal model, while $\hat{\mathbf{A}}$ denotes a discrete-space Fourier transform (DSFT) mapping from a uniform image grid onto a nonuniform k-space grid. In conventional gridding nonCartesian MRI reconstructions, the adjoint operator, ${\hat{\mathbf{A}}}^{*}$, is applied to the (density-compensated) k-space data to reconstruct the image vector. This process can be efficiently implemented by a type-II NUFFT.^22,23

With GNL, Δ(r)≠r, and the pixel positions deviate from uniform image-domain grids due to GNL-induced distortion. The forward operator, $\hat{\mathbf{A}}$, then represents a mapping from nonuniform image space grids to nonuniform k-space grids for nonCartesian MRI, which can be implemented via a type-III NUFFT.²⁴ Note that for Cartesian imaging with GNL, the forward operator $\hat{\mathbf{A}}$ can be realized as a type-I NUFFT (Ref. 13) operation.

Whereas the algebraic structure of type-I and type-II NUFFTs is well-defined, type-III NUFFTs were initially introduced only abstractly.²⁴ As such, attempts at efficiently realizing nonuniform-to-nonuniform mappings have been proposed. One implementation of the type-III NUFFT has been described and used in reconstruction of parallel acquisition with localized gradient (PATLOC) with radial k-space sampling.²⁵ In PATLOC, nonlinear, nonbijective spatial encoding magnetic fields are intentionally introduced to increase the efficiency of gradient usage.²⁶ In Ref. 25, the forward type-III NUFFT is implemented by combining one forward type-I and one adjoint type-II NUFFT operator, which requires two oversampled FFTs and one regular-sized FFT per execution. In the rest of this section, we will describe an integrated type-III NUFFT operator that provides improved numerical efficiency by requiring only a single Fourier transform operation per execution.

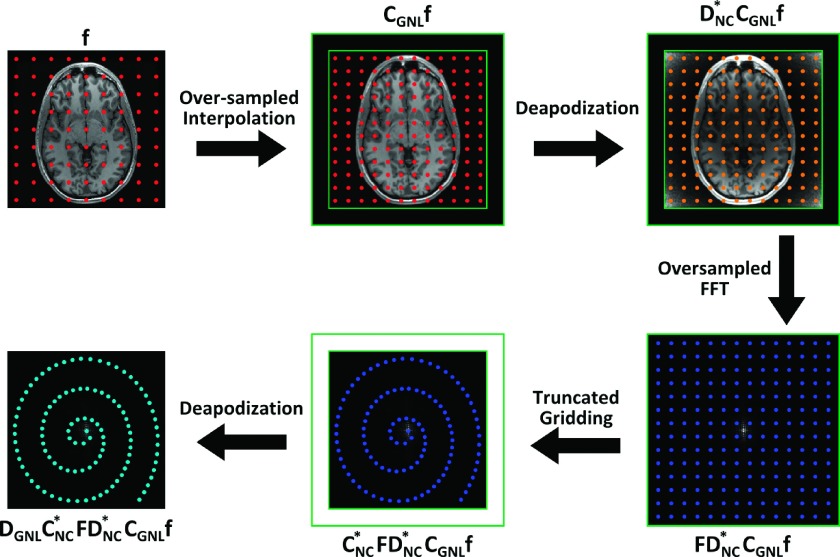
Various NUFFT operators use interpolation either before or after an oversampled FFT operator to account for distortion in image space (type-I NUFFT), or nonuniform sampling in k-space (type-II NUFFT), or both (type-III NUFFT). Such an interpolation is typically performed using a convolutional kernel of finite supports, such as a Kaiser–Bessel kernel used in this work as well as other nonCartesian reconstruction methods.^22,23 Since the Kaiser–Bessel kernel itself is not interpolating and can potentially introduce blurring, an explicit deapodization/deconvolution step is usually integrated into NUFFT operator to modify the kernel into interpolating and account for these blurring. Therefore, implementations of NUFFT operators typically involve data interpolation, oversampled FFT, and deapodization.^22–25 In the case of nonuniform-to-nonuniform mappings, interpolation and deapodization operations must be performed both spatially and spectrally. For example, the distortion in image domain caused by GNL is implemented using the convolutional interpolation, while a deapodization kernel is applied in k-space to account for the blurring that may happen. These operators mirror the function of gridding kernel and deconvolution kernel used in gridding reconstruction of nonCartesian acquisition. In this work, we utilize the following type-III NUFFT form, which is also illustrated in the flow chart in Fig. 1,

$${\displaystyle \hat{\mathbf{A}}\approx {\mathbf{D}}_{\text{GNL}}{\mathbf{C}}_{\text{NC}}^{*}{\mathbf{FD}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{GNL}},}$$ (5)

where C_GNL denotes an oversampled interpolation that maps the regular image grids onto oversampled uniform image grids in an extended field of view with zeros values at the edges. Note that the convolution accounts for the distortion induced by GNL, and the purpose of interpolating into extended field of view is to account for the later oversampling in k-space and to prevent aliasing due to GNL distortion and circulant boundary condition setting. D_GNL indicates a deapodization operation that accounts for the blurring introduced by C_GNL; F is an oversampled FFT operator; ${\mathbf{C}}_{\text{NC}}^{*}$ denotes a truncated gridding operator that maps from oversampled uniform k-space grids onto nonuniform k-space grids (corresponding to a certain nonCartesian k-space sampling pattern) within the k-space sampling range specified by this nonCartesian acquisition; and finally, ${\mathbf{D}}_{\text{NC}}^{*}$ defines a deapodization operation that accounts for the blurring introduced by ${\mathbf{C}}_{\text{NC}}^{*}$.

FIG. 1.

Schematic representation of work flow demonstrating the structure of the forward operator of the proposed type-III NUFFT operator. f: regular-sized image vector; F: oversampled forward FFT operator; C_GNL: image-domain oversampled interpolation operator; ${\mathbf{C}}_{\text{NC}}^{*}$: k-space gridding operator; D_GNL and ${\mathbf{D}}_{\text{NC}}^{*}$: deapodization operators accounting for the blurring introduced by C_GNL and ${\mathbf{C}}_{\text{NC}}^{*}$, respectively.

The effects of each operator in Eq. (5) are illustrated in Fig. 1. Regular-sized image matrix (denoted as f) is first interpolated/distorted onto an oversampled grid in an extended FOV with zero values on the edges. The obtained image matrix $\left({\mathbf{C}}_{\text{GNL}}\mathbf{f}\right)$ is then weighted/deapodized at each pixel $\left({\mathbf{D}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{GNL}}\mathbf{f}\right)$, and Fourier transformed into k-space $\left({\mathbf{FD}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{GNL}}\mathbf{f}\right)$. The obtained oversampled k-space samples are then gridded onto a nonCartesian sampling trajectory within a predefined k-space range $\left({\mathbf{C}}_{\text{NC}}^{*}{\mathbf{FD}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{GNL}}\mathbf{f}\right)$. Since this k-space sampling range is by definition smaller than the range of the oversampled k-space, matrix truncation is implied. Finally, each sample is weighted/deapodized according to its position in k-space $\left({\mathbf{D}}_{\text{GNL}}{\mathbf{C}}_{\text{NC}}^{*}{\mathbf{FD}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{GNL}}\mathbf{f}\right)$.

The adjoint operator, ${\hat{\mathbf{A}}}^{*}$, has the similar structure as Eq. (5),

$${\displaystyle {\hat{\mathbf{A}}}^{*}\approx {\mathbf{C}}_{\text{GNL}}^{*}{\mathbf{D}}_{\text{NC}}{\mathbf{F}}^{*}{\mathbf{C}}_{\text{NC}}{\mathbf{D}}_{\text{GNL}}^{*},}$$ (6)

where ${\mathbf{C}}_{\text{GNL}}^{*}$ and ${\mathbf{D}}_{\text{GNL}}^{*}$ are the adjoint operators of C_GNL and D_GNL, respectively; C_NC and D_NC are the adjoint operators of ${\mathbf{C}}_{\text{NC}}^{*}$ and ${\mathbf{D}}_{\text{NC}}^{*}$, respectively. Note that, different from the implementation in Ref. 25, Eqs. (5) and (6) only require one oversampled FFT. A detailed computational complexity analysis based on floating point operation (FLOP) number is demonstrated later.

2.C. Reconstruction with modified gridding algorithm

In the absence of off-resonance, the display coefficient vector u in Eq. (4) can be reconstructed using the method-of-moments estimator, similar to the conventional gridding reconstruction. Take the expected value [E(⋅)] on both sides of Eq. (4) and substitute Eq. (5) into Eq. (4), it gives $E\left(\mathbf{g}\right)=E\left(\hat{\mathbf{A}}\mathbf{u}+\mathbf{n}\right)=\hat{\mathbf{A}}\mathbf{u}\approx {\mathbf{D}}_{\text{GNL}}{\mathbf{C}}_{\text{NC}}^{*}{\mathbf{FD}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{GNL}}\mathbf{u}$. The method-of-moments estimator replaces the ensemble average [E(⋅)] with the sample average, or, in this case, the observation vector itself, i.e., $E\left(\mathbf{g}\right)=\mathbf{g}$. Consequently, the display coefficient vector u can be reconstructed by sequentially inverting each operator of $\hat{\mathbf{A}}$ in Eq. (5), which leads to

$${\displaystyle \mathbf{u}\approx {\left({\mathbf{C}}_{\text{GNL}}^{*}{\mathbf{C}}_{\text{GNL}}\right)}^{-1}{\mathbf{C}}_{\text{GNL}}^{*}{\left({\mathbf{D}}_{\text{NC}}{\mathbf{D}}_{\text{NC}}^{*}\right)}^{-1}\times {\mathbf{D}}_{\text{NC}}{\mathbf{F}}^{*}{\mathbf{C}}_{\text{NC}}{\left({\mathbf{C}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{NC}}\right)}^{-1}{\left({\mathbf{D}}_{\text{GNL}}^{*}{\mathbf{D}}_{\text{GNL}}\right)}^{-1}{\mathbf{D}}_{\text{GNL}}^{*}\mathbf{g}.}$$ (7)

In conventional gridding nonCartesian image reconstruction, the ${\left({\mathbf{C}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{NC}}\right)}^{-1}$ term is approximated as a diagonal matrix representing a density compensation function, Φ_NC.²⁷ Furthermore, previous work has shown that the ${\left({\mathbf{C}}_{\text{GNL}}^{*}{\mathbf{C}}_{\text{GNL}}\right)}^{-1}$ term can be approximated by a diagonal matrix denoting the Jacobian determinant of the distortion field, J_GNL.¹³ The diagonal matrix approximations of ${\left({\mathbf{C}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{NC}}\right)}^{-1}\approx {\mathbf{\Phi }}_{\text{NC}}$ and ${\left({\mathbf{C}}_{\text{GNL}}^{*}{\mathbf{C}}_{\text{GNL}}\right)}^{-1}\approx {\mathbf{J}}_{\text{GNL}}$ imply that each row of C_NC and C_GNL contains relatively few nonzero elements (due to the finite extent of the convolution kernel). Therefore, energy in the Gram matrix ${\mathbf{C}}_{\text{NC}}^{*}{\mathbf{C}}_{\text{NC}}$ and ${\mathbf{C}}_{\text{GNL}}^{*}{\mathbf{C}}_{\text{GNL}}$ is concentrated about the main diagonal and the diagonal approximation is efficient. For consistency, following the migration of C_NC and C_GNL from a convolution operator to a simple pointwise scaling (i.e., diagonal matrix), its corresponding “inverse” operator, D_NC and D_GNL, must be similarly translated. It then follows that D_NC and D_GNL as well as ${\left({\mathbf{D}}_{\text{NC}}{\mathbf{D}}_{\text{NC}}^{*}\right)}^{-1}$ and ${\left({\mathbf{D}}_{\text{GNL}}^{*}{\mathbf{D}}_{\text{GNL}}\right)}^{-1}$ can be practically approximated by a simple scaling, i.e., ${\left({\mathbf{D}}_{\text{NC}}{\mathbf{D}}_{\text{NC}}^{*}\right)}^{-1}\approx \alpha \mathbf{I}$ and ${\left({\mathbf{D}}_{\text{GNL}}^{*}{\mathbf{D}}_{\text{GNL}}\right)}^{-1}\approx \beta \mathbf{I}$. Hence, Eq. (7) reduces to

$${\displaystyle \mathbf{u}\propto {\mathbf{J}}_{\text{GNL}}{\mathbf{C}}_{\text{GNL}}^{*}{\mathbf{D}}_{\text{NC}}{\mathbf{F}}^{*}{\mathbf{C}}_{\text{NC}}{\mathbf{D}}_{\text{GNL}}^{*}{\mathbf{\Phi }}_{\text{NC}}\mathbf{g}={\mathbf{J}}_{\text{GNL}}{\hat{\mathbf{A}}}^{*}{\mathbf{\Phi }}_{\text{NC}}\mathbf{g}.}$$ (8)

From Eq. (8), the image vector u can be reconstructed by applying the adjoint operator ${\hat{\mathbf{A}}}^{*}$ to the density compensated k-space signal, Φ_NCg, followed by an image intensity correction indicated by J_GNL. Note that, without GNL, ${\hat{\mathbf{A}}}^{*}$ represents the adjoint operator of a type-II NUFFT, and J_GNL = I. In such case, the above expression reduces to the conventional nonCartesian gridding reconstruction.

2.D. Time-segmented signal approximation

The spatiotemporal dependence of the off-resonance components of the forward operator, A, in Eq. (3) impedes the direct use of computational efficient algorithm like standard or nonuniform fast Fourier transforms (NUFFT) for its application. To enable efficient application, a low-rank approximation of this operator is typically adopted. This approximation of A may be obtained by temporally segmenting the presumed a priori known off-resonance phasor,²⁸ i.e.,

$${\displaystyle \mathbf{A}(\kappa ,i)=e^{-j{\omega }_0\left(\mathbf{r}\left[i\right]\right)t\left[\kappa \right]}{e}^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{r}\left[i\right]\right)}\approx \left(\sum _{l=1}^L{w}_l\left(\kappa \right)e^{-j{\omega }_0\left(\mathbf{r}\left[i\right]\right)t_l}\right)e^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{r}\left[i\right]\right)}=\left(\sum _{l=1}^L{w}_l\left(\kappa \right)v_l\left(i\right)\right)e^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{r}\left[i\right]\right)},}$$ (9)

where L is the number of segments; t_l denotes the center of the time window corresponding to the lth k-space segment; w_l(κ) is a k-space window function that weights each data sample based on the difference between its measurement time, t[κ], and the window center, t_l, i.e., |t[κ] − t_l|; and v_l(i) = e^{−jω₀(r[i]) t_l} is pixelwise weighting function in the image domain associated with the lth time segment. In general, using a smooth spectral windowing function, w_l, like a Hanning window will result in superior approximation performance.²⁸ The time-segmented approximation model in Eq. (9) can be summarized in the following affine algebraic form:

$${\displaystyle \mathbf{A}\approx \sum _{l=1}^L{\mathbf{W}}_l\hat{\mathbf{A}}{\mathbf{V}}_l,}$$ (10)

and Eq. (3) then resorts to

$${\displaystyle \mathbf{g}\approx \left(\sum _{l=1}^L{\mathbf{W}}_l\hat{\mathbf{A}}{\mathbf{V}}_l\right)\mathbf{u}+\mathbf{n},}$$ (11)

where K and N are the numbers of signal measurements and pixels, respectively; W_l is a K × K diagonal matrix $\left[{\mathbf{W}}_l(\kappa ,\kappa )=w_l\left(\kappa \right)\right]$; V_l denotes an N × N diagonal matrix $\left[{\mathbf{V}}_l(i,i)=v_l\left(i\right)\right]$; and $\hat{\mathbf{A}}(\kappa ,i)=e^{-j\omega \left[\kappa \right]\mathrm{\Delta }\left(\mathbf{r}\left[i\right]\right)}$ denotes the forward spatial encoding operator (K × N matrix) that accounts for the effect of GNL.

2.E. Off-resonance correction

For nonCartesian imaging, B₀ inhomogeneity can cause image blurring and spatial distortion, especially for long readout acquisitions or when at high field strength. Similar to conventional gridding, off-resonance correction can be incorporated into the proposed reconstruction framework in Eq. (8) by replacing the adjoint operator ${\hat{\mathbf{A}}}^{*}$ with A^*, which accounts for off-resonance effects, i.e.,

$${\displaystyle {\mathbf{A}}^{*}\approx \sum _{l=1}^L\underset{l}{\overset{*}{\mathbf{V}}}{\hat{\mathbf{A}}}^{*}{\mathbf{W}}_l^{*}.}$$ (12)

Hence, the reconstruction framework accounting for both GNL and off-resonance can be expressed as

$${\displaystyle \mathbf{u}\propto {\mathbf{J}}_{\text{GNL}}{\mathbf{A}}^{*}{\mathbf{\Phi }}_{\text{NC}}\mathbf{g}\approx {\mathbf{J}}_{\text{GNL}}\left(\sum _{l=1}^L\underset{l}{\overset{*}{\mathbf{V}}}{\hat{\mathbf{A}}}^{*}{\mathbf{W}}_l^{*}\right){\mathbf{\Phi }}_{\text{NC}}\mathbf{g}.}$$ (13)

Mirroring the base case above, without GNL, the above expression reduces to the conventional time-segmented nonCartesian gridding reconstruction with integrated off-resonance correction.²⁸

2.F. Iterative SENSE reconstruction

The proposed signal model in Eq. (1) can be utilized into various model-based iterative reconstruction frameworks, such as nonCartesian SENSE-type reconstruction with Tikhonov regularization, by replacing the forward and adjoint DFT operator with their type-III NUFFT counterparts. Denoting S (N by C matrix) as the sensitivity profile for the C channels of the phased array receiver coil, the objective image vector, u (N × 1 vector) can be reconstructed by solving the following least-squares optimization problem:

$${\displaystyle arg\underset{\mathbf{u}}{min}{‖\mathbf{\Phi }\mathbf{A}\text{diag}\left\{\mathbf{u}\right\}\mathbf{S}-\mathbf{G}‖}_F^2+\lambda {‖\mathbf{u}‖}_2^2,}$$ (14)

where G indicates the multicoil k-space measurement matrix (K by C); Φ is a binary undersampling matrix; $\text{diag}\left\{\mathbf{u}\right\}$ denotes a diagonal matrix with the ith diagonal element $\text{diag}{\left\{\mathbf{u}\right\}}_{\left(i,i\right)}={\mathbf{u}}_i$; ${‖\cdot ‖}_F^2$ represents the Frobenius norm of matrix; and λ > 0 is a regularization parameter. Such an optimization problem can be solved iteratively using conjugate gradient (CG) method.²⁹ Note that the off-resonance effect can be accounted for using the time-segmentation approximation shown in Eq. (10).

3. MATERIALS AND METHODS

3.A. Computational complexity analysis

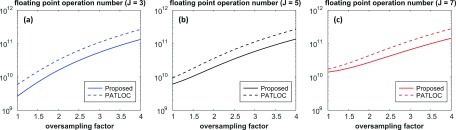
The proposed type-III NUFFT operators as in Eqs. (5) and (6) consist of five successive operations, including two oversampled interpolations $\left({\mathbf{C}}_{\text{GNL}}\text{and}{\mathbf{C}}_{\text{NC}}^{*}\right)$, two deapodization operations $\left({\mathbf{D}}_{\text{GNL}}\text{and}{\mathbf{D}}_{\text{NC}}^{*}\right)$, and one oversampled FFT (F). Since two oversampled interpolations are involved, the overall oversampling factor (OF) is the product of the oversampling factor in each. Define the interpolation kernel size as J and the overall oversampling factor as OF. Then, the oversampling factor for each of the interpolation can be assigned as $\sqrt{OF}$. The overall computational load of the proposed NUFFT operator is the sum of the five individual operators. For the purpose of demonstration, assume a N^D × 1 display coefficient vector to be reconstructed from a K × 1 measurement data vector, where D is the dimension of the reconstructed matrix size. Then, the five operations in Eq. (5), from right to left, require 2N^D × J^D, ${\left(N\times OF\right)}^D$, $5D{\left(N\times OF\right)}^D{log}_2(N\times OF)$, 2K × J^D, and K FLOPs, respectively. Thus, the total FLOP number of the proposed type-III NUFFT operator is ${(N\times OF)}^D\left(5D{log}_2(N\times OF)+1\right)+2J^D\left(N^D+K\right)+K$. For a certain reconstruction matrix size $\left(N^D\right)$ and data size $\left(K\right)$, the FLOP number is a function of oversampling factor, OF, and interpolation kernel size, J.

The type-III NUFFT operator proposed in PATLOC reconstruction²⁵ consists of one forward operator of type-I NUFFT, one regular-sized FFT, followed by one adjoint operator of type-II NUFFT. Assuming the same oversampling factor and kernel size is used, the number of floating point operations required for these three operators is $2N^D\times J^D+5D{\left(N\times OF\right)}^D{log}_2(N\times OF)+N^D$, 5D × N^Dlog₂(N), and $2K\times J^D+5D{\left(N\times OF\right)}^D{log}_2(N\times OF)+N^D$, respectively, which add up to a total of $10D{\left(N\times OF\right)}^D{log}_2(N\times OF)+5D\times N^D{log}_2\left(N\right)+2J^D\left(N^D+K\right)+2N^D$ FLOPs.

3.B. Experiments

Several 2D and 3D nonCartesian protocols were used to compare the standard and the proposed GNL correction methods. A static cylindrical phantom with resolution bars¹⁵ was scanned on a 3 T scanner (General Electric, Signa HDxt, v16.0) using the zoom mode gradient [maximum gradient amplitude 40 mT/m; slew rate 200 (T/m)/s] and a single-channel T/R head coil. The phantom was translated to 84 mm in gradient inferior direction to observe a relatively strong GNL effect, and scanned with a 2D Archimedean spiral sequence (FOV = 22 cm, slice thickness = 3 mm, acquisition plane = axial, TR = 100 ms, BW = ± 62.5 kHz, FA = 30°, 16 interleaves, 4096 readout points per interleave).¹⁶ A separate 2D Cartesian B₀ mapping sequence that uses two different TEs was then performed at the same location (FOV = 22 cm, slice thickness = 3 mm, acquisition plane = axial, TR = 100 ms, $\mathrm{matrix}=256\times 256$, receive BW = ± 31.25 kHz, FA = 30°, echo spacing = 1.0 ms).

The same phantom was additionally scanned on a 1.5 T (General Electric, Signa HDxt, v16.0) scanner with an 8-channel receive-only head coil and zoom mode gradient using the same 2D Archimedean spiral sequence and B₀ mapping sequence. The phantom was translated to 75 mm in gradient inferior direction. A separate calibration scan was performed to obtain coil sensitivity information.

The brain of a healthy volunteer subject was also scanned on a 3 T scanner (General Electric, DVMR, v22.0) with a 8-channel receive-only head coil under an IRB-approved protocol using an accelerated 3D contrast enhanced (CE) shells with integrated radial and spiral (SWIRLS) with acquisition setting as FOV =24³ cm³, TR = 80 ms, BW = ± 62.5 kHz, FA = 35°, 8047 shots, 512 sample per shot.¹⁵ A test bolus of 1 ml was first used for bolus arrival timing. Then, a bolus of 18 ml gadobenate dimeglumine contrast agent (Multihance, Bracco Diagnostics, Princeton, NJ, USA) was injected into the right antecubital vein at 3 ml/s, followed by 25 ml of saline flush with a power injector. Then, a 3D Cartesian B₀ mapping sequence based on two different TEs was performed separately with the same spatial coverage (FOV =24³ cm³, matrix =256 × 128 × 60, TR = 95 ms, BW = ± 31.25 kHz, FA = 10°, echo spacing = 2.3 ms).

Finally, the American College of Radiology (ACR) quality control MR phantom was scanned on a 1.5 T scanner (General Electric, Signa Hdx; v23.0) with a cardiac MR gradient [maximum gradient amplitude 33 mT/m; slew rate 120 (T/m)/s] using a center-out, fully 3D radial protocol^30,31 (FOV = 24³ cm³, BW = ± 31.25 kHz, FA = 15°, number of readouts = 30 000, readout length = 258). An 8-channel cardiac coil was used (GE HD Cardiac, Waukesha, WI). A high bandwidth dual-echo 3D radial GRE protocol with the same spatial coverage and matrix size (TR = 4.2 ms, first TE = 120 μs, BW = ± 160 kHz, FA = 15°, echo spacing = 3.0 ms) was also performed and subsequently used for off-resonance map estimation. For all the experiments, raw complex k-space data were retained.

3.C. Reconstruction analysis

All computational experiments in this work were implemented in c/c + + with FFTW and OpenMP parallelization and executed on a dual 8-core 2.6 GHz machine with 128 GB memory. The standard GNL corrections were implemented with cubic spline interpolation.¹ The cubic spline interpolation is used in this work since vendor’s GNL correction is based on the same technique.¹ We have previously compared cubic spline interpolation with other interpolation techniques like Kaiser–Bessel interpolator, which is used in the NUFFT operator itself.^22,23 The results showed that the cubic spline interpolation, when used for GNL correction in image domain, offered superior performance. All types of NUFFT operators were implemented with a 1.25 × oversampled FFT, and a five point Kaiser–Bessel interpolator.^22,23 Phase unwrapped B₀ maps for all data sets were estimated using a graph cut based optimization procedure.³² For all the experiments in this work, the vendor-provided gradient field parameterization was used to obtain GNL distortion field.

For each data set, four separate reconstructions were performed. To separately investigate the blurring effect caused by off-resonance and GNL, the standard gridding reconstruction without and with off-resonance correction was first performed with no GNL correction based on Eqs. (8) and (13), but with ${\hat{\mathbf{A}}}^{*}$ denoting the adjoint operator of type-II NUFFT. Then, the standard GNL correction was applied to the image with off-resonance correction, followed by image intensity correction based on Jacobian determinant of the distortion field. Finally, the same data were directly reconstructed with the proposed reconstruction strategy with integrated GNL and off-resonance correction [Eq. (13)], where ${\hat{\mathbf{A}}}^{*}$ denotes the adjoint NUFFT operator of type-III implemented based on Eq. (6).

The reconstruction matrix size of 2D spiral data was set as 256² for all four reconstruction experiments, and off-resonance correction was performed with L = 64 time segments. The reconstructed images were 4× sinc interpolated for display. For the in vivo 3D SWIRLS scan, the reconstruction matrix size was set as 240³, and off-resonance correction was performed with L = 8 segments. Then, each 2D slice in coronal plane was sinc interpolated to 512 × 512 points slice by slice, and the maximum intensity projection (MIP) was then applied to a coronal thin slab of 20 mm centered at 50 mm in the anterior direction. Finally, the 3D center out radial scan data were reconstructed onto a 256³ image grid, and a total of L = 16 time segments are used for off-resonance correction. The images were then sinc interpolated (4 ×) for display.

To examine the compatibility of the proposed method with iterative nonCartesian reconstruction framework, the multicoil 2D spiral data set was retrospectively undersampled (2 ×) by discarding every other readout to simulate a 2D SENSE-type nonCartesian reconstruction scenario. The coil sensitivity profiles were estimated from a separate calibration scan using ESPIRiT.³³ Two reconstruction experiments were performed on the same data set based on the SENSE-type reconstruction scheme shown in Eq. (14). In the first experiment, the conventional SENSE reconstruction was performed, with A denoting a conventional type-II NUFFT operator. The reconstructed image was then corrected with the standard GNL correction method. Next, the proposed iterative reconstruction scheme was performed with A denoting the proposed type-III NUFFT operator. In both cases, the effect of off-resonance was accounted for using time-segmented approximation (L = 64). All the images were sinc interpolated (4 ×) and Fermi windowed for display. Our previous study has investigated the effect of performing sinc interpolation before standard GNL correction.¹³ As a comparison, the standard GNL correction was also applied to the sinc interpolated (4 ×) image obtained from the standard reconstruction scheme.

4. RESULTS

4.A. Computational complexity analysis

Figure 2 shows the FLOP numbers (at three different interpolation kernel sizes J) versus oversampling factor (OF) for the proposed implementation of type-III NUFFT (proposed) and that used in radial PATLOC reconstruction (PATLOC). A 3D reconstruction scenario based on the SWIRLS acquisition indicated in Sec. 3 is assumed. For each kernel size, the proposed implementation is more efficient in terms of FLOP number at the same oversampling factor. The FLOP number ratio between the implementation used in Ref. 25 and the proposed is 1.6 under the numerical setting in this study (OF = 1.25, J = 5) and gradually increases to 2.0 when OF increases to 4 (as used in Ref. 25).

FIG. 2.

FLOP numbers of the proposed type-III NUFFT operator (solid lines) and that used in reconstruction of PATLOC with radial k-space sampling (dash lines) at different oversampling factors and interpolation kernel sizes (J = 3, 5, 7).

4.B. 2D spiral

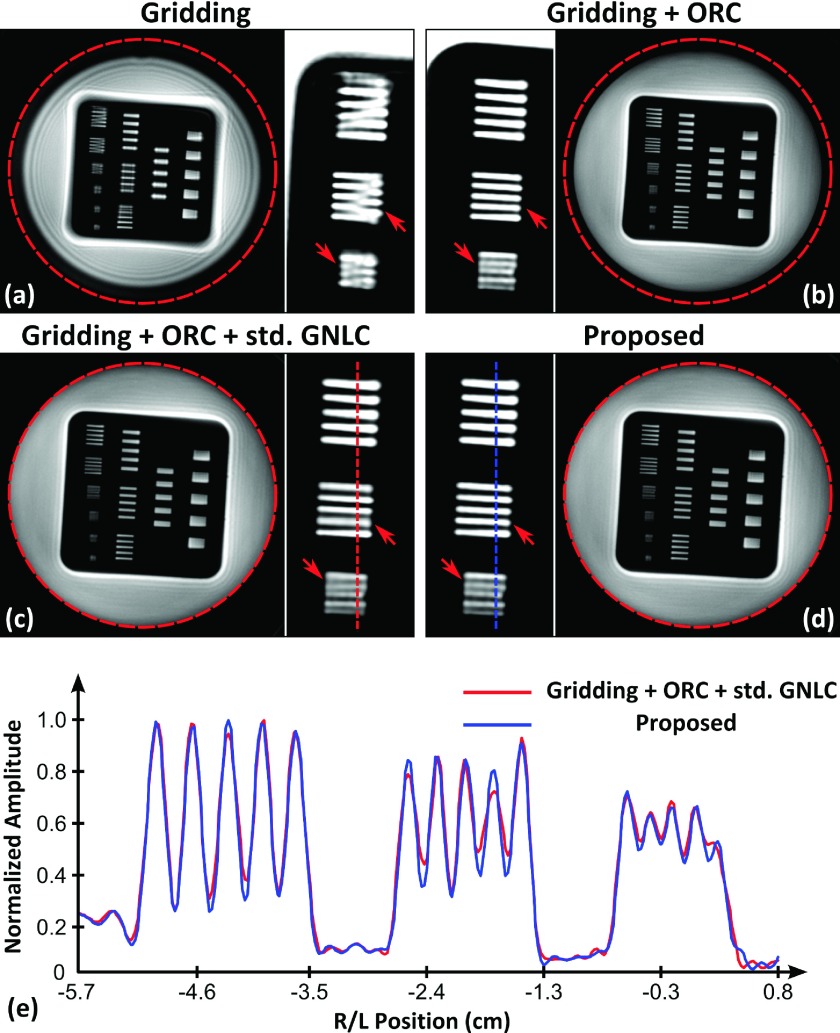
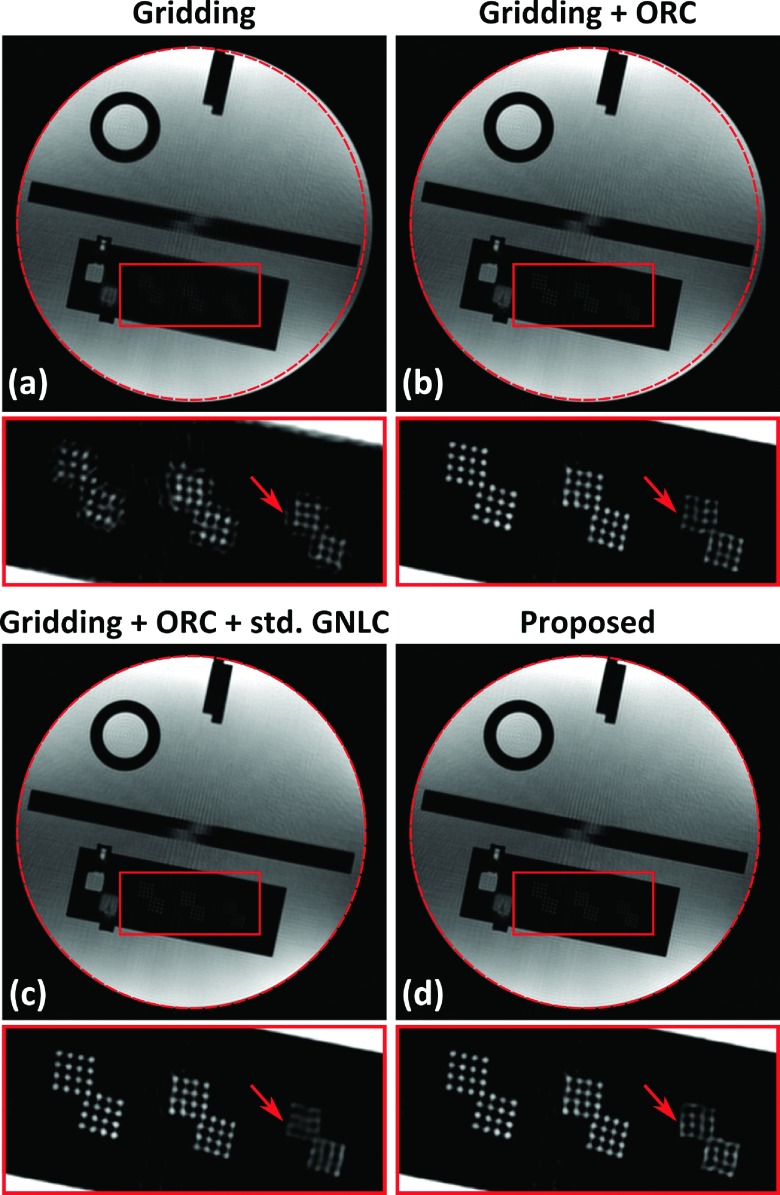
Figure 3 shows the images reconstructed from 2D spiral scan data by (a) standard gridding algorithm without off-resonance correction or GNL correction, (b) standard gridding algorithm with off-resonance correction, (c) applying the standard GNL correction to the gridding reconstruction result in (b), and (d) the proposed NUFFT-based correction with simultaneous off-resonance correction and GNL correction. The enlargements of the resolution bars are also shown. The outer contours of the cylindrical phantom were tracked from images after GNL corrections and are indicated as the red circles overlapping onto each panel of Fig. 3. Comparison between Figs. 3(a) and 3(b) highlights that the majority of blurring in Fig. 3(a) is caused by off-resonance effect. Both the standard and the proposed GNL correction methods are able to correct the geometric distortion caused by GNL and off-resonance correction [Figs. 3(c) and 3(d)], but the standard GNL correction also introduces image blurring as shown around the resolution bars (see arrows), similar to that observed in Cartesian imaging.¹³ On the other hand, the resolution bars are better depicted in the image corrected with the proposed strategy [Fig. 3(d)]. Figure 3(e) shows the line profiles across three groups of resolution bars in the images after the standard and the proposed GNL correction in Figs. 3(c) and 3(d) (positions marked in zoom-in panels). The standard GNL correction decreases the contrast of the resolution bars as reflected by the decreased bar prominence. Note that the rightmost resolution bar in the image corrected with the standard method (red curve) is hardly identifiable. The line profile is better preserved in the image reconstructed with the proposed NUFFT-based correction (blue curve).

FIG. 3.

Images reconstructed from 2D spiral acquisition data. [(a) and (b)] Image obtained by conventional gridding reconstruction without (a) and with (b) ORC; (c) image obtained after applying standard GNL correction (std. GNLC) to (b); (d) result of the proposed reconstruction method with integrated GNL correction and simultaneous ORC; (e) line profiles across three groups of resolution bars in the images after the standard (c) and the proposed GNL correction (d). The red circles indicate the outer contours of the phantom tracked from the images after GNL correction.

4.C. 3D contrast enhanced SWIRLS

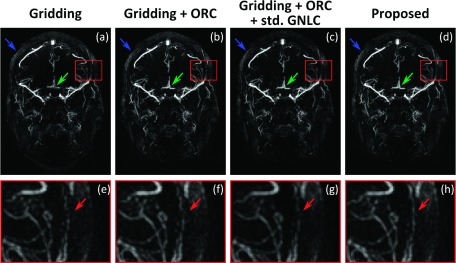
Figure 4 shows the 20 mm coronal thin slab MIP (full scale and magnified insets) for the in vivo 3D-SWIRLS data set. Figures 4(a) and 4(b) show the full scale MIP images of the results of direct, standard gridding reconstruction without and with off-resonance correction, respectively. Figure 4(c) shows the MIP image obtained after applying standard GNL correction to the gridding reconstruction results with off-resonance correction. Figure 4(d) is the MIP image reconstructed by the proposed NUFFT-based framework with integrated GNL correction and off-resonance correction. Again, the GNL-induced image distortion is corrected by both the standard and the proposed GNL method. Note the change of vessel contour in MIP images before [Fig. 4(b)] and after [Figs. 4(c) and 4(d)] GNL correction, as indicated by the blue arrows in Figs. 4(a)–4(d). The green arrows in Figs. 4(a)–4(d) demonstrate the effect of off-resonance correction of the standard and proposed reconstruction methods. As shown, the proposed method [Fig. 4(d)] provides effective off-resonance correction similar to that of the standard gridding reconstruction with off-resonance correction [Figs. 4(b) and 4(c)]. The effect of GNL correction is highlighted in Figs. 4(e)–4(h). Although the GNL induced distortion is relatively small in this example, the standard GNL correction causes loss of small vessel clarity, which is better preserved by the proposed NUFFT-based correction, as revealed in Figs. 4(g) and 4(h) (see red arrows). Note that the image intensity change due to GNL-induced distortion was corrected in both standard GNL correction and the proposed reconstruction method using the Jacobian determinant of the distortion field. Therefore, the clearer vessel definition shown in Fig. 4(h) is due to the benefit of proposed reconstruction method, rather than image intensity shift.

FIG. 4.

Coronal thin slab MIP of images (full scale and magnified insets) reconstructed from the in vivo 3D-SWIRLS data set. [(a) and (e)] and [(b) and (f)] MIP of images (full scale and magnified insets) reconstructed by conventional gridding reconstruction without [(a) and (e)] and with [(b) and (f)] ORC; [(c) and (g)] MIP of images (full scale and magnified insets) obtained after applying standard GNL correction (std. GNLC) to the gridding reconstruction results with ORC; [(d) and (h)] MIP of images (full scale and magnified insets) reconstructed by the proposed method with integrated GNL correction and simultaneous ORC. The blue arrows in (a)–(d) demonstrate the change of vessel contour in MIP images caused by correction of GNL-induced distortion. The green arrows in (a)–(d) show that the proposed method (d) provides effective off-resonance correction as the standard gridding reconstruction [(b) and (c)]. The red arrows in [(e)–(h)] highlight that the proposed method with integrated GNL correction (h) prevents the blurring caused by standard GNL correction (g) and improves the vessel clarity in corrected image.

4.D. 3D radial

The axial resolution inserts slices of the ACR phantom images reconstructed from 3D radial data are shown in Fig. 5. Figures 5(a) and 5(b) are the conventional gridding reconstruction results without and with off-resonance correction. Figure 5(c) is the image corrected with the standard GNL correction. Figure 5(d) shows the image reconstructed with the proposed method. The red circles in Fig. 5 indicate the outer contours of the ACR phantom tracked from the images after GNL correction. Off-resonance induced image blurring and distortion are corrected in results of both the conventional gridding [Fig. 5(b)] and the proposed reconstruction [Fig. 5(d)]. As shown in Fig. 5(c), the conventional GNL correction method introduces blurring to images especially around the smallest resolution insert group (see arrows). On the other hand, the image corrected with the proposed method [Fig. 5(d)] shows better depiction of resolution inserts, while providing equivalent distortion correction as the conventional method.

FIG. 5.

Images reconstructed from 3D radial acquisition data. [(a) and (b)] Image obtained by conventional gridding reconstruction without (a) and with (b) ORC; (c) image obtained after applying standard GNL correction (std. GNLC) to (b); (d) result of the proposed reconstruction method with integrated GNL correction and simultaneous ORC. The dashed circles indicate the outer contours of the phantom tracked from the images after GNL correction.

4.E. 2D SENSE

Figure 6 depicts the results (full scale images and magnified inserts) of the conventional and the proposed iterative SENSE reconstruction schemes. Figure 6(a) shows the conventional SENSE reconstruction results with off-resonance correction but before GNL correction. Figure 6(b) is obtained after applying the standard GNL correction to Fig. 6(a). As a comparison, Fig. 6(a) is sinc interpolated (4 × zero-padding in k-space) and GNL-corrected using the standard method to obtain Fig. 6(c). Figure 6(d) shows the image reconstructed using the proposed method based on type-III NUFFT. The blurring around the resolution inserts can be observed in the images before GNL correction [Fig. 6(a)], corrected with the standard GNL correction either before [Fig. 6(b)] or after sinc interpolation [Fig. 6(c)] but is reduced in the image obtained using the proposed reconstruction with integrated GNL correction [Fig. 6(d)].

FIG. 6.

Images reconstructed using the conventional and the proposed iterative SENSE reconstruction schemes. [(a) and (b)] Image obtained by conventional iterative SENSE-type reconstruction with ORC before and after standard GNL correction (std. GNLC), respectively; (a) is first sinc interpolated (k-space zero-padding, ZP) and then GNL-corrected using the standard method to obtain (c); (d) result of the proposed iterative SENSE reconstruction method with integrated GNL correction and simultaneous ORC.

5. DISCUSSION

In this work, we have described a GNL-aware nonCartesian MR image reconstruction and derived a noniterative gridding-type framework for this application. The proposed signal processing framework prospectively accounts for the effect of GNL, as opposed to the standard image-domain based GNL correction method that is applied after image reconstruction is performed. Due to the smoothing effect of strict image-domain interpolation operations, the conventional GNL correction method introduces unnecessary image blurring and resolution loss to the GNL-corrected images, as previously reported for Cartesian MRI acquisitions. This blurring can be prevented by the proposed type-III NUFFT-based correction, as demonstrated with various nonCartesian protocols. As shown in Figs. 3 and 5, the blurring around the resolution inserts in phantom images after the conventional GNL correction was eliminated by the proposed correction. Figure 4 shows that the vessel continuity and clarity in MIP image are better preserved by the proposed method. In nonCartesian MR protocols, off-resonance effects can cause significant blurring and distortion especially for long-readout acquisitions or when at high field strengths. Similar to the conventional gridding algorithm for nonCartesian reconstruction, off-resonance correction can be incorporated into the proposed integrated GNL reconstruction framework without limiting computational burden. Figures 3–5 show that the geometric distortion and blurring effect caused by GNL and off-resonance can be simultaneously corrected by the proposed method. The proposed signal model as in Eq. (11) can also be integrated into iterative model-based reconstruction frameworks by replacing the forward and adjoint type-II NUFFT operators with the type-III NUFFT operators, as demonstrated in Eq. (14) using an iterative SENSE type reconstruction scenario. The results in Fig. 6 show that image details are better preserved by the proposed method. The proposed method can also be incorporated into other advanced reconstruction schemes assuming more sophisticated data undersampling strategies and constraints, such as compressed sensing.

As shown by our previous work,¹³ performing sinc interpolation can only partly reduce the blurring observed after conventional GNL correction but not fully eliminate the problem. Consistent with these previous results, the comparison between Figs. 6(c) and 6(d) shows that the proposed NUFFT-based reconstruction method is able to better reserve image details and can retain image information that is not recoverable merely using image-domain based GNL correction.

The framework described in this work is quite general and can be readily extended to other nonCartesian data acquisitions where noniterative gridding-based reconstruction is applied. This includes hybrid Cartesian acquisitions, such as ramp-sampled echo planar imaging (EPI).

The resolution preserving effect of the proposed method is expected to be more pronounced for regions where strong GNL presents, as reported in Cartesian MRI cases.¹³ It may especially benefit nonCartesian applications with a large FOV and high resolution requirement, e.g., 3D MR angiography with full-brain coverage or 3D MR peripheral angiography of the lower limbs,³⁴ since GNL is usually stronger in regions far away from gradient isocenter. The proposed reconstruction method is also expected to provide benefit even in regions with moderate GNL distortion. As shown in our previous work,¹³ the standard image-domain GNL correction removes the high frequency component in the noise power spectra of the reconstructed images and causes image blurring—similar to a low pass filtering effect. On the other hand, the NUFFT operator used in the proposed reconstruction scheme is able to retain these high frequency components and reduce image blurring observed after conventional GNL correction. The forward and adjoint operators of type-III NUFFT described in Eqs. (5) and (6) are also compatible with the reconstruction framework for radial PATLOC (Ref. 25) or other MRI applications where nonlinear spatial encoding gradients are intentionally employed. These include single-shot MR acquisition technique with higher-dimensional encoding³⁵ and alternative spatial encoding schemes where dynamic, higher-order spatial encoding field was performed together with conventional linear gradient fields.³⁶ The proposed type-III NUFFT implementation is more numerically efficient than the implementation used in Ref. 25 in terms of float point operation per operator. Detailed comparison between different implementations of type-III NUFFT in terms of numerical accuracy at various configurations is beyond the scope of this work. If necessary, the B₀ inhomogeneity and susceptibility effects in PATLOC reconstruction can be corrected based on the same framework described here by adopting the type-III NUFFT operators with integrated off-resonance correction as in Eqs. (10) and (12). Note that in the context of nonlinear spatial encoding schemes, the forward spatial encoding operator A is usually rank deficient, and one may have to resort to advanced iterative reconstruction methods making use of coil sensitivity information and further auxiliary assumption on imaging object.

Gradient delays and eddy currents can lead to deviations between the nominal and actual k-space trajectories utilized by the scanner, causing blurring, ghosting, or distortion in reconstructed images if unaccounted for. For conventional nonCartesian acquisitions, these trajectory errors can be estimated via a gradient system characterization procedure assuming a linear time invariant (LTI) system model³⁷ or a combination of anisotropic gradient delay model and convolution eddy current model.³⁸ The k-space trajectories presumed during image reconstruction are then updated based on this information. In a similar fashion, the effects of gradient delay and eddy current can be integrated into the proposed reconstruction framework by updating the signal model in Eq. (1) according to the actual k-space trajectory obtained from the same characterization procedures for conventional nonCartesian acquisition. We expect the resolution preserving effect of the proposed method to be consistent.

6. CONCLUSIONS

In this work, we have developed a gridding-based reconstruction framework with integrated GNL and off-resonance correction for nonCartesian MRI. The proposed method is able to mitigate the resolution loss that occurs during standard image-domain GNL correction, while still providing effective correction of coarse-scale geometric distortion and blurring induced by GNL and off-resonance.