How fast-growing bacteria robustly tune their ribosome concentration to approximate growth-rate maximization

Abstract

Maximization of growth rate is an important fitness strategy for bacteria. Bacteria can achieve this by expressing proteins at optimal concentrations, such that resources are not wasted. This is exemplified for Escherichia coli by the increase of its ribosomal protein-fraction with growth rate, which precisely matches the increased protein synthesis demand. These findings and others have led to the hypothesis that E. coli aims to maximize its growth rate in environments that support growth. However, what kind of regulatory strategy is required for a robust, optimal adjustment of the ribosome concentration to the prevailing condition is still an open question. In the present study, we analyze the ppGpp-controlled mechanism of ribosome expression used by E. coli and show that this mechanism maintains the ribosomes saturated with its substrates. In this manner, overexpression of the highly abundant ribosomal proteins is prevented, and limited resources can be redirected to the synthesis of other growth-promoting enzymes. It turns out that the kinetic conditions for robust, optimal protein-partitioning, which are required for growth rate maximization across conditions, can be achieved with basic biochemical interactions. We show that inactive ribosomes are the most suitable ‘signal’ for tracking the intracellular nutritional state and for adjusting gene expression accordingly, as small deviations from optimal ribosome concentration cause a huge fractional change in ribosome inactivity. We expect to find this control logic implemented across fast-growing microbial species because growth rate maximization is a common selective pressure, ribosomes are typically highly abundant and thus costly, and the required control can be implemented by a small, simple network.

Introduction

Bacterial growth rates vary greatly with conditions. Doubling times in Escherichia coli range from tens of minutes to tens of hours. Evolutionary reasoning indicates the importance of the maximization of bacterial growth rate. In environments that support growth, the growth rate of a bacterium equates directly to fitness ¹ because it allows for outgrowth of competitors. Even during irregular feast–famine fluctuations, growth rate remains important, because it gives rise to more offspring and spread of genetic diversity.

Bacteria adjust their growth rate by adapting their metabolism. Recent experimental ^2–5 and theoretical work ^6–8, inspired by studies carried out decades ago ^9–11, indicate the importance of the covariation of the bacterial protein composition with growth rate. It turns out that reasoning about the ‘protein economy’ of a bacterial cell ^6,12 provides an intuitive framework that relates growth rate changes to the regulation and kinetics of metabolic reactions. Yet, it remains poorly understood how bacteria perceive their growth rate and adjust it via the regulation of gene activity and metabolic enzymes.

At steady-state exponential growth, the macromolecular content (mass) and volume of a bacterial cell increase exponentially with time at an equal rate, (i.e. the exponential growth rate, which is inversely proportional to the doubling time). The growth rate depends on the rate at which the cell is able to synthesize new proteins ^6,12. This, in turn, depends on the cellular ribosome concentration, but also on how efficient each ribosome is used. For ribosomes to be used efficiently, they need to be supplied with enough amino acids. Because the total protein concentration of a bacterial cell (defined as protein mass per cell mass) hardly changes across conditions ¹³, synthesizing more of certain proteins goes at the expense of others. This implies that synthesis of more ribosomal proteins reduces the concentration of metabolic proteins, which produce amino acids, such that the ribosomes are used less efficiently. This indicates that an optimal ribosome concentration exists, matching the supply of amino acids by metabolism to the demand of protein synthesis, and maximizing the growth rate. This argument applies more generally to metabolic proteins; the rate of all metabolic reactions increases with both the concentration of the catalyzing enzyme and that of its substrates. From an economic perspective, it is thus advantageous to saturate enzymes with their substrates, because this means that less protein is needed to attain the same rate. Consequently, more resources are available for other proteins; for example, for those that supply the substrate. Management of the protein economy by bacteria is thus central to understanding strategies for growth rate regulation.

The importance of protein economy for growth rate maximization is supported by three types of experimental findings. Firstly, the growth rate ‘cost’ of enzyme excess is illustrated by observations that the growth rate decreases upon non-functional protein synthesis. This decrease is often observed to be linear with the non-functional protein fraction ^14,7,15, which is predicted by theory ^7,16. However, non-linear protein costs have also been reported ¹⁷, possibly as a result of effects related to protein activity rather than production ¹⁸. Secondly, the concentration of each protein should be precisely tuned ^16,19. This has been found for several enzymes in E. coli, ^20,21,17,22, Lactococcus lactis ^23–25 and Saccharomyces cerevisiae ²⁶. These latter studies report that the relationship between the growth rate and a metabolic enzyme concentration displays a maximum and that the wild-type growth rate is close to this maximal value. Thirdly, evolutionary experiments show the prevention of the synthesis of unneeded costly protein for the general stress response of E. coli ²⁷ and the loss of excess protein in yeast glycolysis ²⁸.

However, chemostat studies indicate a remarkable degree of protein excess of glycolysis at low growth rates in Bacillus subtilis ²⁹, L. lactis (A. Goel, T.H. Eckhardt, P. Puri, A. de Jong, F. Branco dos Santos, M. Giera, F. Fusetti, W.M. de Vos, J. Kok, B. Poolman, D. Molenaar, O.P. Kuipers and B. Teusink, unpublished data), and S. cerevisiae ³⁰. This could be because microorganisms hardly encounter chemostat-like growth conditions in the wild and that they tend to be optimized more for feast and famine conditions rather than for sub-saturating nutrient conditions. Alternatively, efficient regulation of glycolysis during glucose dynamics may require enzyme excess. This is supported by evolution of S. cerevisiae in glucose-limited chemostats where enzyme overexpression in glycolysis is reduced ²⁸. In any case, trade offs can occur in metabolism that prevent the optimal tuning of all metabolic enzyme levels.

One can imagine that the control task to precisely tune the concentrations of all proteins may be too hard to solve for the cell. It turns out that this is also not required. What is intuitively clear is that near-maximal growth rates can be achieved by carefully tuning only the most abundant proteins. Compare a protein that is 5% of total cellular protein and 10% in excess with another protein that is 0.5% of total and also 10% in excess. Thus, the former protein should be 4.5% and therefore 0.5% of total protein is wasted, whereas, in the latter case, this amounts to only 0.05%. Thus, tuning abundant proteins liberates most resources for acceleration of other reactions.

Evolution of regulatory systems that achieve tuning of abundant protein concentration is therefore strongly selected for. This intuition is supported by recent theoretical work, which indicates that abundant proteins have the highest influence on growth rate ¹⁶. The translation machinery, including the ribosome and elongation factors, is the functional class with the largest protein fraction in E. coli at maximal growth rate ²² (between 20–40% depending on growth conditions). A visualisation of the E. coli proteome is provided elsewhere ³¹. We expect that a high abundance of translation machinery applies to fast-growing bacteria in general ^32,33,4.

The ribosome concentration is thus likely tightly regulated. Indeed, the well established linear relationship between ribosomal concentration and growth rate in E. coli ^2,4,9,11,34 is considered to be the result of growth rate optimization. Decades ago, Maaløe and Kjeldgaard ³⁴ and, more recently, Scott et al. ¹², reasoned about optimality, explaining the high degree of substrate-saturation of ribosomes and the linear relationship between ribosome fraction and growth rate ^34,12. Ehrenberg and Kurland ³⁵ analyzed what the consequences of optimality are for the error rate of translation and deduced the linear relation from this perspective.

So, given both experimental and theoretical work, growth rate maximization by E. coli has turned into a decades old persistent hypothesis for which (circumstantial) evidence continues to pile up. Yet, how bacteria can optimise their growth rate is unclear: (a) Which internal variables should they sense?, (b) Which feedback designs are required?, and (c) How rapidly would we expect those to evolve? It is becoming clear that the molecular circuitry underlying such seemingly complex regulatory tasks can be remarkably simple ^36–42. In this spirit and to answers these questions, we will use a model of E. coli growth and its regulation of ribosome synthesis that captures the essential dynamics but is otherwise as simple as possible. The benefit of using simple models is that they are more tractable and therefore the underlying logic is more transparent. We will first show that our model reproduces the well known linear relationship between growth rate and the optimal ribosomal concentration. We explain how deviations from the optimal ribosome concentration are sensed, how this signal is translated into ppGpp dynamics and subsequent compensatory gene regulation, and how this ensures that the optimal ribosomal protein concentration is attained. We derive the minimal kinetic requirements at the level of metabolism and gene regulation for growth-rate maximization across a wide range of conditions, show that E. coli implements these, and ask whether those are likely implemented by other fast-growing bacteria. We use parameter values obtained from literature for our model, and we show that the qualitative behaviour of the model is extremely insensitive to the actual parameter values.

Results

Model description

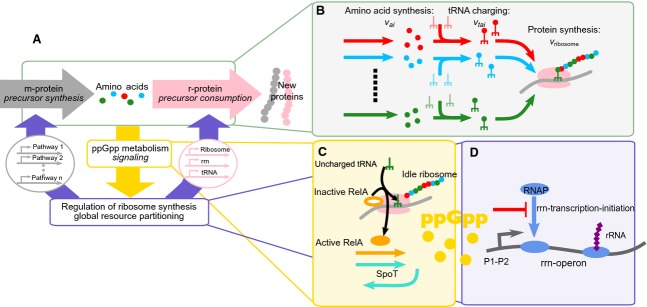
Here, we will give a general outline of our model of E. coli growth and its regulation. A detailed derivation and mathematical description of the model, including the justification of many details that we left out of our model, is provided in Doc. S1 and Tables S1 and S2. We only take metabolic proteins (m-proteins), ribosomal proteins (r-proteins; this also includes all other proteins involved in translation, such as elongation factors) and rRNA into account. Our model can be conceptually divided in three modules (Fig.  1A).

Figure 1.

Model of E. coli growth and regulation of its ribosome concentration. (A) Coarse-grained perspective on the coupling of amino acid synthesis, protein synthesis and the ppGpp-mediated control of ribosome concentrations. (B) Model of Escherichia coli growth. Amino acids are synthesised by m-proteins at a rate v_ai which depends on the environmental condition and the m-protein concentration. These amino acids are used to charge their conjugate tRNAs. Charged tRNAs subsequently bind to the ribosome that links the amino acids to the growing peptide chain which eventually becomes the new protein. The growth rate is proportional to the total protein synthesis rate. (C) Model of ppGpp metabolism. When the concentration of an amino acid is low, the concentration of its cognate uncharged tRNA is high. When this uncharged tRNA binds to the ribosome, RelA produces ppGpp. Alternatively, ppGpp can be produced by SpoT. (D) Model of the regulation of ribosome synthesis. ppGpp diverts RNA polymerase from ribosomal operons to catabolic operons. This reduces the transcription of rRNA and translation of ribosomal proteins, which increases catabolism and so restores the synthesis of the limiting amino acid.

Amino acid metabolism and protein synthesis

First, we consider amino acid metabolism and protein synthesis (Fig.  1B). Twenty different amino acid species are synthesized by the m-proteins, each at a rate

1

where a_i is the concentration of amino acid species i, K_I is the product inhibition constant, m_i the concentration of m-proteins in the biosynthetic pathway of amino acid i, all in μm. is the effective turnover number of the pathway, i.e. 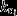is the maximal rate of synthesis of a_i per second per unit m_i-protein. Changes in environmental conditions are modelled by changing the average k_n, which reflects the assumption that in high quality nutrient media, less metabolic proteins are required to attain the same amino acid synthesis flux.

The amino acids are added to their conjugate tRNAs to form aminoacyl-tRNA complexes (‘charged’ tRNAs). These serve as the substrate for biomass synthesis, catalyzed by ribosomes, consisting of r-protein and rRNA. The system is in (metabolic) steady state when the production rate of each amino acid equals its consumption rate in protein synthesis.

When new biomass is being synthesized, it is also diluted out due to (cell volume) growth. By definition, this dilution rate is the specific growth rate μ, and it is equal to the rate of biomass synthesis per unit biomass. During balanced growth, the fraction of proteins in total biomass is constant, from which it follows that μ is equal to the rate of protein synthesis (v_ribosome, in μm amino acids per second) per unit protein ⁴³, (see Equations S2, S7 of Doc. S1):

2

where k_rib is the maximal specific peptide elongation rate of the ribosomes (in other words, the ‘k_cat’ of the ribosome, in units amino acids per ribosome per second), t_a={t_a1,…,t_a20} is the vector containing the concentrations of charged tRNAs (in μm), and f(t_a) gives the degree to which ribosomes are saturated with charged tRNAs, i.e.  0 ≤ f(t_a) ≤1. Note that [total protein] and [r-protein] are expressed in μm-amino acids, such that μ is per second. Increasing the r-protein fraction 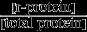, has two effects on μ: a positive one because it increases the total capacity to synthesized new proteins and a negative one because it reduces the m-protein fraction, which leads to a lower amino acid supply, lower tRNA charging, and thus a lower saturation degree of the ribosome, f(t_a). A lower saturation degree of the ribosome is disadvantageous, because it indicates protein excess, which is at the expense of other proteins, of which some are limiting the growth rate and those should therefore increase in concentration.

ppGpp metabolism

Second, we consider the signalling of the ribosome saturation state to the translational machinery by the signalling molecule ppGpp (Fig.  1C). In E. coli, ppGpp is synthesized from GTP by two synthetases, SpoT and RelA ^44,45. RelA binds to ribosomes and converts GTP into ppGpp (via the intermediate pppGpp) when the ribosome has an uncharged tRNA bound to its A-site ⁴⁴ and as such signals the shortage of the cognate amino acid ⁴³. We model the rate of ppGpp synthesis by RelA proportional to the concentration of uncharged tRNA bound to the ribosomes (Eqn S9a). SpoT has a dual activity. It synthesizes ppGpp in response to stresses and nutrient limitations (but not amino acid limitations), and it also hydrolyses ppGpp to GDP ^44,46. We are interested in amino acid deprivation related ppGpp-synthesis, and so we simply model ppGpp synthesis by SpoT as a low constant background rate, and ppGpp hydrolysis by SpoT with mass-action kinetics.

Regulation of r-protein synthesis

Third, we consider the ppGpp-mediated regulation of the partitioning of transcription proteins, RNA polymerase and sigma factor 70, over operons encoding the r-proteins and m-proteins (Fig.  1D). In our model, the relative concentrations of m-proteins and r-proteins at steady state depend on the ribosome fractions dedicated to their synthesis. Because we only model protein dilution and not degradation, at steady state, the concentration r-protein (m-protein) is set by the fraction of ribosomes synthezising r-proteins (m-proteins). In other words, if 20% of the ribosomal capacity is allocated to the synthesis of r-proteins (m-proteins), [r-protein]/[total protein] = 0.2.

Although there are many factors influencing the cell’s physiology, ppGpp can account for the majority of E. coli growth rate control ⁴⁷. Therefore, in our model, we only incorporate the regulation of ribosome synthesis by ppGpp. Synthesis of r-proteins is tightly matched to the synthesis of rRNA ⁴⁸, and concentrations of elongation factors and tRNA are maintained at a constant ratio with the concentration of ribosomes ^49,50. Synthesis of rRNA is inhibited by ppGpp, most likely by inhibition of rRNA transcription initiation [48,49,51,52]. ppGpp interacts with the protein DskA ⁴⁵, and factors such as Fis and NTPs are also involved ⁵³. However, the precise mechanism does not affect the model results. In Doc. S1, we offer a more detailed discussion on how ppGpp inhibits rRNA synthesis. So, ppGpp indirectly inhibits r-protein synthesis and frees up ribosomes for the synthesis of m-proteins. In our model, the rate of r-protein synthesis, v_r-protein is related to the ppGpp concentration in the following manner:

3

K_i,ppGpp is the inhibition constant of rRNA operon transcription initiation by ppGpp, and ppGpp and K_i,ppGpp both have unit μm. Because the total protein concentration is fixed, the r-protein fraction and the ribosome concentration are directly proportional. Since ribosomes that are not synthezising r-proteins synthesize m-proteins instead, ppGpp redirects biosynthetic resources from r-protein synthesis to m-protein synthesis.

The dynamics of this system are described by a system of ordinary differential equations. Together, these three modules form a coupled system. Given a certain environment, the system will autonomously evolve to a steady state, where the time derivative of the concentration of all species in the model (including those of r-and m-protein) are equal to zero. The steady state growth rate depends on the nutrient quality (quantified by k_n) and the fraction of r-proteins.

In silico, numerical optimization of the ribosome protein fraction reproduces its linear relationship with growth rate

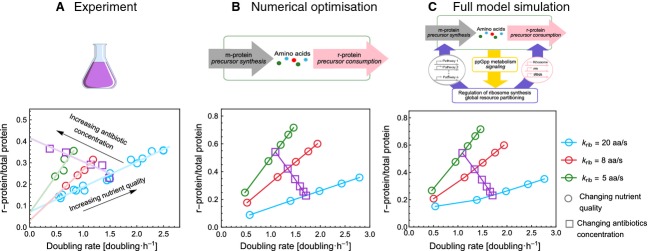
A study by Scott et al. ⁴ showed that the r-protein fraction increases linearly with growth rate when the nutrient quality is increased, and that the slope of this increase is steeper for mutants with a lower ribosome elongation rate, k_rib. Furthermore, when the k_rib is reduced by the addition of translation inhibiting antibiotics, the r-protein fraction increases linearly with decreasing growth rate. The data are reproduced in Fig.  2A.

Figure 2.

ppGpp regulation of the r-protein fraction maximizes growth rate and reproduces the experimentally observed linear relationship between r-protein fraction and growth rate. All panels plot the r-protein fraction against the growth rate. (A) Experimental data adapted from Scott et al. ⁴. (B) Results obtained from numerically optimising the r-protein fraction in a model without ppGpp-regulation. (C) ‘Self-optimization’ model, where the r-protein fraction is set by the ppGpp regulation mechanism. The growth rate was varied by changing the nutrient quality of the medium in which the cells were grown (circles) or by changing the concentration of a translation-inhibiting antibiotic (squares). The blue circles represent wild-type cells; the red and green circles indicate mutants with a decreased maximal specific elongation rate, k_rib. Clearly, all results are similar. With increasing nutrient quality, they show the linear increase of r-protein fraction with growth rate, and this increase is steeper for mutants with a lower k_rib (blue, red and green circles). If the k_rib is reduced by addition of antibiotics, the r-protein fraction increases linearly with decreasing growth rate (purple symbols). These observations imply that the saturation of ribosomes with charged tRNA is kept constant.

To test whether growth rate optimization in our model is consistent with these findings, we first study our model without regulation of r-protein synthesis. We numerically calculated which r-protein fraction maximizes the growth rate for different nutrient qualities, k_n. The results are shown in Fig.  2B and S1A. We find that indeed the optimal r-protein fraction increases linearly with growth rate and this increase is steeper when k_rib is lower. When we reduce k_rib while keeping the nutrient quality constant, which simulates addition of translation inhibiting antibiotics to the growth medium, we also reproduce the linear increase in r-protein fraction with decreasing growth rate.

From Eqn 2, we can see that these observations are expected only when the degree of saturation of the ribosome, f(t_a), is kept constant. As noted above, from an economic perspective we also expect f(t_a) to be close to 1. Indeed, in our model, for a large range of growth conditions, the optimal r-protein fraction is such that ribosomes are operating close to their maximal capacity (Fig.  S1B). This is also consistent with the experimental observation that E. coli maintains its level of tRNA charging high ⁵⁴ and thus its functioning ribosomes active at over 80% of their maximal activity ¹³. Approximately 80% of total ribosomes are functioning, the remainder are presumably maturating ⁷. In our model, there is some deviation from this behaviour at low growth rates, which might be because we model tRNA concentrations to be proportional to that of r-proteins. As a consequence, at low r-protein fractions, the ribosomes are not saturated with charged tRNAs, even when all tRNA are charged, simply because there is not insufficient tRNA around. This deviation might be a model artefact.

From these model optimizations, we conclude that the observed relationship between growth rate and r-protein fraction are consistent with growth rate optimization. This brings us to the next question: is the ppGpp regulatory mechanism of E. coli capable of optimizing the r-protein fraction?

ppGpp-mediated regulation optimizes ribosome protein fraction equally well as in silico, numerical optimization

We tested whether our model, including regulation of r-protein synthesis by ppGpp, is capable of reproducing the above mentioned observations. Figs 2C and S1A indicate that this is the case. So, ppGpp regulation functions in a similar manner as the numerical optimization algorithm used to obtain Fig.  2B. Across conditions, ppGpp regulation of r-protein synthesis maximizes the growth rate by maintaining the ribosomes saturated with amino acids (Fig. S1), giving rise to the known linear relationship between growth rate and r-protein fraction (Fig.  2C). To test how sensitive these finding are to the model parameters, we changed all parameters involved in the regulation of r-protein synthesis and calculated how much the new growth rate deviated from its theoretical maximum. Without exception, all of the parameters can be changed by five- to 10-fold in either direction without a noteworthy decrease in growth rate (Fig. S1). This can be considered as an experimentally testable prediction of our model: moderate changes in, for example the RelA concentration should not affect the (steady state) growth rate and ribosome concentration. This regulatory mechanism is, therefore, extremely robust. We consider the ability of the ppGpp mediated system to attain optimal ribosomes concentrations, regardless of the exact values of the parameters, as one of the main findings of the present study and below, we further determine the origin of this robustness.

In Fig. 3, we compare several other model predictions with experimental data reported in the literature. Figure 3A shows that our model predicts that upon a downshift from a rich medium to a less favourable one, there will be a large transient increase in ppGpp synthesis. We modelled this downshift as a stepwise decrease in the catalytic efficiency of amino acid synthesis, k_n. Upon such a downshift, amino acids will become limiting and ppGpp synthesis is activated. This results in a decrease in the r-protein concentration and an increase in m-proteins, leading to increased amino acid synthesis, an increase in tRNA charging and a decrease in ppGpp levels. So, upon a downshift, we expect a large transient increase in the ppGpp level after which it will decrease, as the r-protein concentration is adjusted to the new environment, finally reaching a concentration close to the one before the downshift (Fig.  3A, solid line). Indeed, such transient increases in the ppGpp level, followed by a slower decrease, have been observed in experiments (Fig.  3A, grey circles) ⁵¹; similar data are also reported elsewhere ⁵⁵). Similarly, upon a nutritional upshift, there is a strong repression of ppGpp synthesis, causing a drop in the ppGpp concentration (Fig.  3B,⁵¹). In our model, this drop causes a near maximal ribosome synthesis rate until the ribosome concentration settles on its new, higher steady state concentration (not shown) and the ppGpp concentration returns to a value close to its pre-shift value. The (nearly) immediate increase in the rate of ribosome synthesis upon a nutritional upshift has also been experimentally observed by Shepherd et al. ⁵⁶ (see also Langeler et al. ⁵⁷.) Note that the magnitude of the transient increase or drop in the ppGpp concentration depends on the magnitude of the nutrient shift. We used shifts from k_n=0.275 to k_n=0.15, and back again. Our model also predicts a decrease of the steady state ppGpp concentration with increasing growth rate, because higher ribosome concentrations require a higher rate of ribosome synthesis (Fig.  3C). This is, yet again, consistent with an experimental observation on the relationship between growth rate and ribosome concentration as reported by Bremer & Dennis ¹³. The ppGpp-feedback mechanism partially compensates for rrn-operon deletion; however, abolishing the regulation of ribosome synthesis by knocking out RelA and SpoT reduces the growth rate. This can be seen from Fig.  3D, which compares the effect in our model of reducing the maximal ribosome synthesis rate (to simulate rrn-operon deletion) and of uninhibited ribosome synthesis (to simulate RelA and SpoT knockout) to experiments performed by Bollenbach et al. ⁵⁸. Finally, we note that these model results are also consistent with the observation that increased rRNA gene-dosage does not significantly increase rRNA transcription ⁵⁹.

Figure 3.

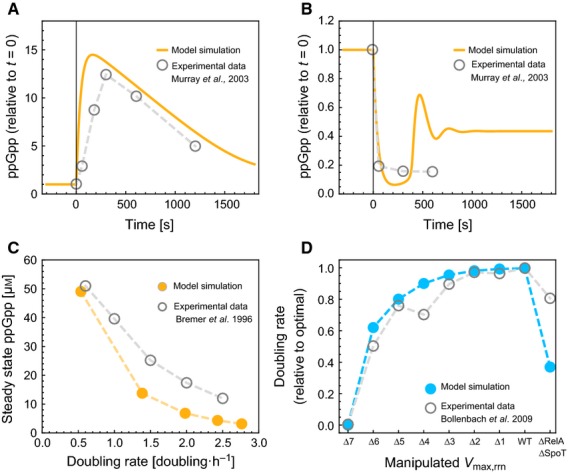
The self-regulation model of protein synthesis incorporating ppGpp control reproduces experimental data. Model predictions (coloured lines or discs) are compared with experimental data from the literature (grey circles). (A) Dynamic response of ppGpp to a nutritional downshift at t = 0. Experimental data is reproduced form Murray et al. ⁵¹. Lazzarani & Cashel ⁵⁵ report similar dynamics (not shown). (B) Dynamic response of ppGpp to a nutritional upshift at t=0. Experimental data is reproduced form Murray et al. ⁵¹. (C) Dependence of the steady state ppGpp concentration on growth rate. Data reproduced from Bremer & Dennis ¹³. The steady state ppGpp concentration decreases with increasing growth rate because higher ribosome concentrations require a higher rate of ribosome synthesis. (D) The effect of rRNA operon number or SpoT and RelA knockout on growth rate. Δx indicates that x out of 7 rrn-operons were knocked out. Data are reproduced from Bollenbach et al. ⁵⁸.

Summarizing, we conclude that the likely control objective of the ppGpp system is to maintain the ribosomes saturated by matching the ribosome concentration to its demand. The resulting dynamics are consistent with a number of experimental observations. The next questions are: How is this achieved? What are the essential kinetic requirements for this optimizing behaviour?

The essence of the ppGpp-regulatory mechanism

To extrapolate the previous results to fast-growing bacteria in general, we need to determine the requirements for optimal regulation. First, we analyze the mechanism of the full model and then we simplify this model to its essential behaviour. It is the biochemical complexity of this latter model that will allow us to speculate on the evolvability and prevalence of this optimal network motif across fast-growing bacteria. If it is simple, then we expect this regulatory motif to occur across fast-growing bacteria, likely by way of parallel evolution.

In Fig.  4, we illustrate the compensatory response of the ppGpp regulatory system to deviations of the r-protein fraction from its optimal value. Figure  4A shows the dependence of the doubling rate, proportional to the growth rate, on the ribosomal protein fraction. These relationships were calculated by only considering the metabolic subnetwork; thus, the ppGpp-controlled activities of catabolic and anabolic protein synthesis were removed. The grey lines indicate the steady state that the full model reaches. In poor media near-optimal behaviour is reached, with a minor deviation of a few percent, which improves with an increased quality of the medium. In Fig.  4B, we consider the model without transcriptional regulation and with ppGpp and the metabolic subnetwork. Calculation of its steady state indicates ultrasensitivity of the steady-state concentration of ppGpp to changes in the ribosomal protein fraction. Small deviations from the optimal r-protein fraction cause large changes in ppGpp concentration, making it a potent signal for deviations from optimality. In Fig.4C, we show that the relationship of the r-protein synthesis and degradation rate with the r-protein fraction leads to the optimal r-protein fraction. At the steady state that the system finally reaches, the synthesis and degradation rates are equal, and the r-protein synthesis rate depends on the r-protein fraction through its regulation by ppGpp.

Figure 4.

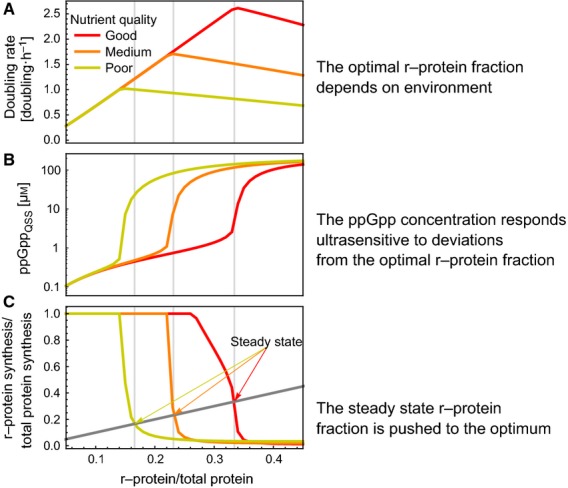
The ultrasensitive response of the ppGpp concentration to deviations from the optimal r-protein fraction lead to optimality across conditions. We computed the response of the system to deviations from optimal r-protein fractions for three different nutrient conditions (indicated by the different colours). (A) Doubling rate. (B) the ppGpp concentration. (C) the r-protein synthesis and degradation rate (relative to the total protein synthesis rate), as a function of the r-protein fraction. (A) The optimal growth rate and ribosome protein fraction together form the linear relationship, as discussed in the main text. (B) The quasi steady state ppGpp concentration changes strongly from around 1 μm when the r-protein fraction is just below its optimum to 100 μm when it is just above it. This is a consequence of the strong response in the levels of uncharged tRNA bound to the ribosome (see Fig. S3). (C) The system is in steady state when r-protein synthesis and dilution (dark grey line) rates are equal. This is indicated by the vertical grey lines. Note that these lines almost coincide with the optimal r-protein fractions. Regulation of ribosome synthesis always pushes the system back to optimal levels: if the ribosome concentration is too low, ppGpp is low as well and so synthesis exceeds degradation, and vice versa.

The ultrasensitivity of ppGpp to deviations from optimality is the origin of the robustness of the ppGpp-regulatory mechanism (Fig.  4C). When the r-protein fraction is slightly less than optimal, ppGpp is very low and thus the r-protein synthesis rate is very high. Similarly, when the r-protein fraction is slightly higher than optimal, ppGpp overshoots and r-protein synthesis is almost completely shut down. Because the dependence of ppGpp on the deviation from optimality is so steep, simple first-order inhibition of rRNA synthesis, and thus indirectly of r-protein synthesis, suffices. The strength of ribosome synthesis inhibition by ppGpp (quantified by K_IppGpp) therefore, does not need to be precisely tuned to attain optimal regulation, which makes the system very robust. In addition, the steep dependency of the r-protein synthesis rate on the r-protein fraction (Fig.  4C), as a result of the ultrasensitivity of the ppGpp concentration, indicates that the steady-state r-protein fraction always lies close to the maximum.

The origin of the ultrasensitivity of ppGpp is that the signal controlling its synthesis, uncharged tRNA bound to the ribosome, also responds ultrasensitively around the optimum (Fig. S3). Other quantities that could have been candidates for signalling the deviation from optimality, such as the total amino acid pool or the concentration of charged tRNA, do not show this ultrasensitive behaviour. The uncharged tRNA bound to the ribosome therefore appears as the best signal for detecting deviations from the optimal ribosome concentration. The question that now remains is the origin of the ultrasensitivity of the concentration of the complex of uncharged tRNA bound to the ribosome. This is addressed below.

Figure  4 also explains the response of the system to a change in nutrient quality that leads to a growth rate change (as shown in Fig.  3A,B). Consider the nutrient upshift from medium (orange lines) to good (red line) nutrient quality. As soon as the nutrient is changed, the ppGpp concentration will drop; the time that this takes will be in the order of seconds to minutes (Fig.3A ). This causes an increase in ribosome synthesis, the uncharged-tRNA/ribosome complex increases, and ppGpp rises until the ribosome transcript level has achieved steady state. At this steady state, the ppGpp and uncharged-tRNA/ribosome complex concentration have increased slightly and the growth rate has increased to its new maximal value.

A reduced model that captures the kinetic requirements for optimal protein levels

We use two reduced models to highlight key features of the ppGpp regulatory system in E. coli, required for robust and optimal regulation of ribosome synthesis. The first model explains the general requirements for the occurrence of ultrasensitivity in metabolic pathways. The second model explains why the concentration of the complex of uncharged-tRNA bound to the ribosome is the best signal to measure deviations from optimality. A full mathematical description of these models is provided in Doc. S2.

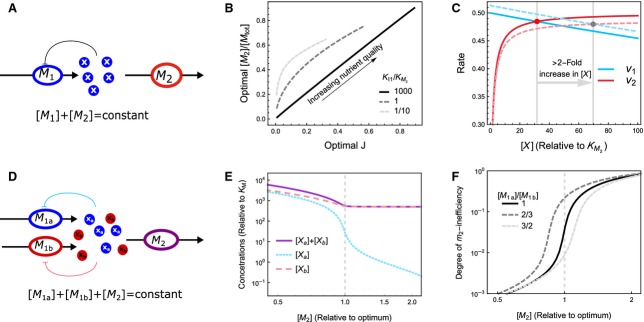
The first model (Fig.5A) considers two enzymes, M₁ and M₂, in sequence. The rate, v₁, at which the metabolic intermediate X is produced by M₁, depends on the nutrient availability, and we include product inhibition by X with inhibition constant K_I1. The rate of X consumption, v₂, is described by simple Michaelis–Menten kinetics, with Michaelis–Menten constant 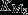. The aim is to maximize the steady state flux, J, by optimization of the concentrations [M₁] and [M₂] under the constraint of a maximal enzyme concentration ([M₁]+[M₂]=[M_tot]). Clearly, the highest flux is attained if the inhibition of M₁ is negligible, and M₂ is saturated with substrate, because then both enzymes are operating close to their maximal rate. This can only be attained if product inhibition is weak (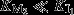), in which case the optimum is characterized by the condition:

4

We note that there exists an approximately 100-fold difference between the product inhibition constant for amino acid synthesis and the K_M for the ternary complex ⁶⁰, indicating that the condition, Eqn 4, is met by E. coli.

Figure 5.

Minimal models that achieve optimal protein concentrations to maximize metabolic pathway flux per total invested protein. (A) The metabolite X is synthesized by metabolic enzyme M₁ and consumed by M₂, whereas the total amount of protein resources is fixed: [M₁]+[M₂]=[M_tot]. A mathematical description of the model is provided in Doc. S2. (B) The relationship between optimal [M₂] and the maximal flux. The maximal flux is increased by increasing the nutrient availability. At large values of the ratio of the product inhibition constant (K_I1) over the Michaelis constant (K_M2) the optimal [M₂] increases linearly with the optimal flux J (black solid line). This linear relationship breaks down when K_I1 is not much larger than K_M2. (C) The rates v₁ and v₂ as a function of [X]. Solid lines indicate the optimum where [M₂]=0.5·[M_tot] and dashed lines indicate a slight deviation from optimality, [M₂]=0.49·[M_tot]. The steady states are indicated by a red and grey dot, respectively. Clearly, a small change in [M₂] brings about a large change in steady state [X]. (D) A model of two converging pathways. Both metabolites X_a and X_b are required as a substrate for M₂, and have weak feedback inhibition (i.e. K_1a and K_1b are much larger than K_M2a and K_M2b, respectively). (E) Because consumption of X_a and X_b are stoichiometrically coupled, the concentration of the non-limiting metabolite (here [X_b]) remains high, even when [M₂] is higher than optimal. Hence, the metabolites are not a reliable signal for deviations from optimality. (F) The degree of inefficiency of M₂, defined as 1−v₂/V_{max, 2}, responds ultrasensitively to deviations from optimality. This behaviour does not depend on the relative rate of X_a and X_b synthesis. Hence, this is a suitable regulatory signal.

This condition has two important consequences: (a) the optimal J and [M₂] are linearly related because in the optimum M₂ is saturated with X (Fig.5B, solid line), this linear relationship agrees with the linear relationship between E. coli’s growth rate and its ribosome fraction. If 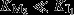does not hold, the linear relationship between optimal flux and [M₂] breaks down (Fig.5B, dashed lines), because it is no longer optimal to keep M₂ fully saturated. (b) A small deviation from optimality in [M₂] causes a large change in steady state [X]. This is illustrated in Fig.5C, which shows v₁ and v₂ as a function of [X] for the optimal [M₂] (solid curves) and when [M₂] is slightly reduced (dashed curves). We decreased [M₂] from 0.5[M_tot] (its optimal value) to 0.49[M_tot], which decreases the flux J by 1%, but increases the steady state [X] by more than 200%. As a result of Eqn 4, the sensitivity of both v₁ and v₂ to changes in [X] is low, which can be seen from the flatness of the curves. Thus, around the optimum, small changes in flux are accompanied by large changes in the steady state [X], which explains the ultrasensitivity of [X] with respect to deviations from optimality. Conversely, it also implies that a large range of [X] corresponds to close to optimal conditions. Any regulatory systems that assures that [X] returns to approximately the same level upon a perturbation therefore keeps the flux very close to optimal. Simple repression of synthesis of M₁ proteins, or activation of synthesis of M₂ proteins, by X, therefore suffices and the exact parameters of the regulatory system are of little importance, indicating robustness (Fig. S4).

Given the discussion above, one might hypothezise that the amino acid or charged-tRNA pool, which correspond to the pool of the intermediate X in the minimal model, could be a good signal for the regulation of r-protein synthesis. However, this is not the case. The reason is that multiple, independent amino acid biosynthesis pathways converge in this pool. Instead, the concentration of the uncharged-tRNA (bound to the ribosome) is a much better signal for deviations of the ribosome concentration from its optimum. We illustrate this assertion with a second model that has one synthesis reaction more than the first model: two metabolites, X_a and X_b, are now produced by M_1a and M_1b, respectively, and consumed by M₂ (Fig.5D). We again consider weak product inhibition, such that K_Ia≫K_2Ma and K_Ib≫K_2Mb. In the optimum, M₂ will operate close to its maximal rate and M_1a and M_1b close to their uninhibited rates. If M₂ is limiting, all intermediate levels will be very high. However, if one of the intermediate-producing pathways is limiting, only the concentration of the product of that pathway will be low. Because the consumption of all metabolites is stoichiometrically coupled (for proteins the stoichiometric coefficients equal the average amino acid composition), all non-limiting metabolite levels will be high (Fig.5E; also see Elf & Ehrenberg ⁶⁰ for a detailed discussion on the accumulation of non-limiting amino acids). Hence, neither X_a nor X_b are reliable signals for the regulation of M₂ synthesis because a high level of either intermediate does not necessarily imply that M₂ is limiting. Furthermore, the total intermediate pool is also not a suitable signal because, when the concentration of M₂ is above optimal, this pool will not be depleted.

The degree of inefficiency of M₂, defined as 1−v₂/V_max,2, is a good signal. Fig.5F shows that this measure changes strongly around the optimum. Also, it is not very sensitive to sub-optimality of relative abundances of supply pathways (dashed lines). The reason for ultrasensitivity is that, in the optimum, the degree of inefficiency is very small, and small absolute deviations from optimality result in large relative changes of this signal. For example, assume that in the optimum, M₂ is 95% saturated (i.e. the degree of inefficiency equals 0.05 and the degree of efficiency equals 0.95). If the system is perturbed such that [M₂] decreases and the saturation increases to 99%, this would lead to an 0.04/0.95 × 100% ≈ 4% change in the degree of efficiency, but an 0.04/0.05 × 100% ≈ 80% change in the degree of inefficiency.

Translating this to E. coli, uncharged tRNA bound to the ribosome is a measure for ribosome inefficiency, and hence the most suitable signal to detect deviations from optimality. However, there is an additional effect relevant for E. coli, which is absent in the reduced model, further amplifying the ultrasensitivity of the uncharged-tRNA ribosome complex. When a particular amino acid becomes limiting, ribosomes will tend to stall at the conjugate codon. As a result, there are more sites for the uncharged tRNA to bind to and the ultrasensitivity is further enhanced (Fig. S5). When these mechanisms are combined, they explain the robustness with respect to changes in kinetic parameter values (Fig. S2) and environmental conditions (Figs2D and 4) of the full growth model.

Discussion

We used a coarse-grained, kinetic model of the regulation mechanism that E. coli uses to balance its catabolic and anabolic protein synthesis rates to show that the (famous) linear relationship between the ribosome fraction and the growth rate is in agreement with growth-rate maximization. E. coli exploits the binding of uncharged tRNA to the ribosome as a signal of ribosome excess and subsequently synthesizes ppGpp. Because this signal responds ultrasensitive to deviations from optimality, an adjustment in the ribosome concentration that restores optimality can be made in a robust manner. An unexpectedly simple view emerges on the relationship between the global protein economy - [i.e. the partitioning of resources between catabolic (m-proteins) and anabolic (r-proteins) processes] and growth rate. When nutrients are scarce, nutrient uptake and assimilation are substrate-concentration limited and high catabolic protein concentrations are required to attain high rates of these processes. This occurs at the expense of protein investment in anabolic processes. As a consequence, the rate of protein synthesis decreases, it takes longer to double the cellular protein content, and the growth rate decreases. When nutrients are in excess, nutrient uptake and assimilation reaction are saturated and require less protein to attain the same rate, a larger fraction of total protein synthesis can be diverted to anabolism, the protein synthesis rate increases, and an increased growth rate follows. This view is consistent with experimental findings ⁴ and is supported by mathematical models ^6,7,12. However, direct experimental illustrations of optimality of the ribosomal concentration are regrettably scarce, partially because such experiments are not straightforward. The most direct evidence that we are aware of is by Bollenbach et al. ⁵⁸. They manipulated ribosome concentrations by deleting either various numbers of ribosomal operons or the genes coding for RelA and SpoT, and found that, in one particular growth condition, the wild-type ribosome concentration maximizes growth rate.

Because we focused on the regulation of ribosome synthesis, we only modelled how the optimal control of the synthesis of ribosomes liberates resources to invest in amino acid synthesis, but not how these resources are subsequently distributed over metabolic processes. Interestingly, most amino acid biosynthesis pathways are either under repressor control of their own product, or are activated by high levels of uncharged tRNA conjugate to their product, both of which respond ultrasensitively to deficiencies in that particular amino acid ⁶¹. As a result, when one amino acid becomes limiting, resources are likely redirected from ribosome synthesis to synthesis of proteins in the biosynthetic pathway of that particular amino acid. In our model, we took this into account by making the amino acid supply well balanced, i.e. the relative synthesis rate of all amino acids are approximately equal to their relative consumption rate. More generally, within metabolism there are other key regulators, transcription factors and associated metabolic signals, such as cAMP and fructose 1,6-bisphosphatase, that redistribute resources according to metabolic demands ³. Another source of growth rate related regulation of major classes of metabolic proteins is via growth rate-dependent, but selective, adaptation of mRNA stability ⁶². We emphasize that, for tuning of the ribosome concentration whether, and how, the concentrations of metabolic proteins are optimised is not relevant, because these effects are all absorbed in the catalytic efficiency of amino acid synthesis. Ribosome concentrations are tuned to the available amino acid supply, regardless of what is happening ‘inside’ upstream metabolism.

We did not consider protein degradation, which might explain why we find an (approximate) proportional relationship between growth rate and r-protein, where as experimental studies suggest a linear but not proportional relationship ⁴. The reason for this is that protein degradation implies the need for a certain baseline rate of protein production to compensate for the proteins that are degraded. Technically, the in corporation of a constant rate of protein degradation in our model would mean that the steady state growth condition [Eqn 2] changes to μ = (v_ribosome−v_{protein degradation})/total protein. This implies the curves in Fig. 2B and C are shifted to the left by an amount v_{proteindegradation}/total protein, which would make the relationship between r-protein and growth rate linear but not proportional. Alternatively, a pool of catalytically inactive ribosomes could explain the linear rather than proportional relationship.

Degradation of specific proteins can also play a role in adaptation to stresses. For example, in response to amino acid starvation, ribosomal proteins are degraded by the protease Lon, in a manner involving ppGpp ⁶³. Degradation of r-proteins by Lon requires inorganic polyphosphate (polyP) ⁶⁴, and polyP degradation is inhibited by ppGpp and pppGpp ⁶⁵. So, polyP accumulates in response to ppGpp accumulation as a result of amino acid starvation. The inhibition constant of polyP degradation by ppGpp is 200 μm ⁶⁵, which is much higher than K_i,ppGpp (see eqn 3 and Table S1) and than the ppGpp concentrations in growing cells (Up to 50μm, Fig.3C). Thus, r-protein degradation by Lon is repressed in growing cells, when amino acids levels are sufficient. Furthermore, Lon does not degrade intact ribosomes, but only free ribosomal proteins ⁶⁴. As a result, Lon dependent, ppGpp triggered, r-protein degradation does not affect the steady state ribosome concentration, although it presumably speeds up adaptation to nutrient stress by liberating amino acids to be used for synthesis of nutrient stress related proteins.

In our model, all parameter values except two (the strength of binding of uncharged tRNA to the ribosome, κ_rt, and the constant rate of ppGpp synthesis by SpoT, v_{SpoT,synthesis}) are based on literature. Because of the extreme robustness of the system, we can use practically any arbitrary value for most parameters without qualitatively affecting the model behaviour. For example changing κ_rt by an order of magnitude in either direction still leads to a growth rate of more than 95% of the theoretically maximal one, and for v_{SpoT, synthesis} this is even 99%. This independence of the (qualitative) model behaviour form the parameter values not only makes the conclusions derived in the present study more robust, but also more likely to apply to other micro-organisms.

Extrapolation of the strategy used by E. coli for growth rate maximization to other fast growing bacteria suggests that three closely-related conditions are met by this class of bacteria: (a) they are expected to have high ribosome concentration, (b) since overexpression of abundant proteins has a high fitness penalty, ribosomes are expected to be highly saturated with substrate; and (c) to achieve the last feature robustly across conditions, a regulatory system is active that regulates the ribosome concentration and keeps the ribosome saturation degree high across conditions. This is likely attained by using the inefficiency of translation as a signal for the regulation of ribosome synthesis. Because of the simplicity of this regulatory system, we expect it to occur across fast-growing bacteria.

Scott et al. ⁴ collected literature data of growth rate and ribosome concentration for the fast- growing bacteria Aerobacter aerogenes ⁶⁶, Candida utilis ⁶⁷ and Neurospora crassa ⁶⁸, which all showed a linear relationship (see Fig. S1). The linearity occurs when two conditions are met across conditions: (a) the total cellular protein concentration is fixed and (b) the specific elongation rate (i.e. the rate of protein formation per ribosome) is fixed, which implies that the saturation of the ribosome with substrate is maintained at a fixed degree. Scott et al. ⁴ also report the ribosome growth rate relationship for Euglena gracilis ⁶⁹, which has a maximal growth rate that is over 20-fold lower than E. coli, whereas its ribosome concentration is only approximately 2 fold lower. Cox ³³ reports similar data for the slow-growing bacteria Streptomyces coelicolor. Slow growing bacteria require more ribosomes to attain the same growth rate (or, equivalently, grow slower at the same ribosome concentration), which can be explained by a lower maximal specific elongation rate of the ribosomes ^4,32,33.

Also, for bacteria that grow slow at high ribosome concentrations, it is expected that they actively prevent higher than optimal ribosome concentrations, to reduce the fitness reduction associated with protein overexpression of an abundant protein. The linear relationship between the growth rate and ribosome concentration of these bacteria indicate that they likely control the saturation degree of ribosomes as E. coli does.

Little is known about how other bacteria regulate their ribosome levels. The best understood example is most likely Bacillus subtilis. It exploits a similar mechanism as that employed by E. coli. Also, in this organism, ppGpp is produced in response to uncharged tRNA that is bound to the ribosome ⁷⁰. However, in B. subtilis, transcription regulation of ribosomal promoters is ppGpp independent and is achieved by regulation by the GTP concentration ⁷⁰. When this concentration is high, transcription initiation occurs. Synthesis of ppGpp during ribosome excess causes GTP to drop, which inhibits ribosomal gene expression. Conversely, degradation of ppGpp during ribosome shortage causes GTP to rise and activate ribosomal gene expression ⁷⁰. In E. coli, transcription initiation of ribosomal genes is also dependent on the energy status of the cell via the dependency of the transcription initiation rate on the concentrations of ATP, GTP, FIS and H-NS ⁵³. However, at nutrient changes during exponential growth, ATP and GTP concentrations remain homeostatic in E. coli, and this possibly explains why ppGpp-mediated control is dominant in E. coli ⁷¹. It appears that B. subtilis and E. coli share the same growth rate control strategy and both aim to match their ribosome concentration to the growth demand. Even though both use different molecular mechanisms, they effectively monitor the same signal: uncharged tRNA bound to the ribosome, and thus, ribosome inefficiency. We also note that, for Thermus thermophilus, a similar control mechanism has been proposed ⁷². Also, in Mycobacterium tuberculosis, ppGpp synthesis is activated by uncharged tRNA bound to the ribosomes ⁷³.

In the eukaryote Saccharomyces cerevisiae, the molecular players leading to the adjustments in growth rate are very different from those in E. coli and B. subtilis ⁷⁴. Yet, at a coarse-grained level, the general control strategy appears to be very similar. The transcription factor GCN4p plays in many ways a similar role as ppGpp. At high concentrations, GCN4p induces transcription responses to nutrient and amino acid starvation. The initiation of the translation of GCN4 transcripts is regulated by Gcn2p, a kinase, which is either activated by direct sensing of amino acid limitation at the ribosome or via other kinases, such as protein kinase A, involved in nutrient-limitation or stresses ^74,75. Gcn2p binds to the ribosome and is activated through phosphorylation by a ribosome-bound protein complex Gcn1p/Gcn20p that becomes active when an uncharged tRNA binds to the A-site of the ribosome. Again, activation of a stringent response depends on a drop in the saturation degree of the ribosome.

Materials and methods

All models were analysed using mathematica, version 10.0 (Wolfram Research, Champaign, IL, USA). For the E. coli growth model, steady states were first approximated by integrating the ordinary differential equations forward in time using the NDSolve function, and then FindRoot to determine the actual steady state. For the minimal models, steady states were calculated by setting the time derivatives equal to zero and (numerically) solving the obtained system of equalities using the mathematica (N)Solve function. Because the dynamics of the metabolic part of all models is much faster than that at which the biomass concentration changes, a quasi steady state (QSS) can be defined as the steady state of metabolism for fixed r and m_i values. Optimal states were calculated by maximizing the growth rate/flux under the constraint that the system is in QSS, using the mathematica Maximize or FindMaximum function. A notebook containing the E. coli growth model is provided in (Doc. S3).

Glossary

polyP

polyphosphate

QSS

quasi steady state

Author contributions

EB, FJB and DM designed the research and developed the mathematical models. EB performed numerical simulations and theoretical analysis. EB, FJB, DM and BT wrote the manuscript.