Transient-State Kinetic Analysis of the RNA Polymerase I Nucleotide Incorporation Mechanism

Abstract

Eukaryotes express three or more multisubunit nuclear RNA polymerases (Pols) referred to as Pols I, II, and III, each of which synthesizes a specific subset of RNAs. Consistent with the diversity of their target genes, eukaryotic cells have evolved divergent cohorts of transcription factors and enzymatic properties for each RNA polymerase system. Over the years, many trans-acting factors that orchestrate transcription by the individual Pols have been described; however, little effort has been devoted to characterizing the molecular mechanisms of Pol I activity. To begin to address this gap in our understanding of eukaryotic gene expression, here we establish transient-state kinetic approaches to characterize the nucleotide incorporation mechanism of Pol I. We collected time courses for single turnover nucleotide incorporation reactions over a range of substrate ATP concentrations that provide information on both Pol I’s nucleotide addition and nuclease activities. The data were analyzed by model-independent and model-dependent approaches, resulting in, to our knowledge, the first minimal model for the nucleotide addition pathway for Pol I. Using a grid searching approach we provide rigorous bounds on estimated values of the individual elementary rate constants within the proposed model. This work reports the most detailed analysis of Pol I mechanism to date. Furthermore, in addition to their use in transient state kinetic analyses, the computational approaches applied here are broadly applicable to global optimization problems.

Introduction

Eukaryotic cells express at least three multisubunit nuclear RNA polymerases referred to as Pols I, II, and III. These enzymes are composed of 14, 12, and 17 subunits, respectively. Nuclear RNA synthesis is divided between the Pols with Pol I being responsible for production of the majority of the ribosomal RNA, Pol II being responsible for the production of messenger RNA and many small RNAs, and Pol III being responsible for production of transfer RNAs and the smallest ribosomal RNA.

RNA expression is the first critical step in gene expression, thus understanding the enzymatic features and regulatory pathways that control polymerase function is critical for establishing a thorough understanding of cell biology. Although the three nuclear RNA polymerases share considerable homology, we and others have recently demonstrated critical structural and/or functional differences between Pols I and II (1, 2). Thus, to develop a detailed understanding of eukaryotic gene expression, genetic, biochemical, and biophysical studies focused on each of the three Pols must be conducted. To date, mechanistic studies of multisubunit RNA polymerase transcription have focused on prokaryotic RNA polymerases or eukaryotic RNA polymerase II. This study uses transient-state kinetic approaches to probe the mechanism of transcription by Pol I.

Although Pol I transcribes a single target gene, it is responsible for the majority of RNA synthesis in the nucleus (3). Ribosome biosynthesis, and by association Pol I transcription, are tightly linked to cell proliferation and this link has recently gained attention from the chemotherapeutic field (4). Indeed, a small number of inhibitors that potentially target Pol I activity have been identified (5). However, the molecular mechanisms of inhibition by any of these compounds are unknown.

Due to its central role in cell growth and its potential as a chemotherapeutic target, there is a need to understand mechanistic details of transcription by Pol I. The aim of this study was to determine a minimal kinetic model that describes the nucleotide addition cycle of Pol I. Such a model provides quantitative estimates of elementary rate constants governing the nucleotide addition cycle, ultimately yielding insight into the evolutionary forces that have given rise to the partitioning of eukaryotic transcriptional responsibilities among three or more polymerases.

To develop this kinetic model, we used a transient state kinetic approach to monitor single nucleotide addition and nuclease reactions catalyzed by Pol I. We developed and applied, to our knowledge, a novel optimization method that enabled us to fit our data to a single model describing the Pol I nucleotide addition and nuclease cycles. Confidence intervals for each estimated elementary rate constant were calculated using a rigorous grid search-based approach. To our knowledge, this is the first study of its kind for Pol I and represents the first set of quantitative mechanistic data concerning this important enzyme. In addition, the computational strategies developed in this work can be broadly applied to diverse transient-state kinetic data sets, and more generally, to global optimization problems in which many parameters are being simultaneously determined.

Materials and Methods

Buffers

Buffers were prepared using water that was twice deionized and filtered using a Millipore ultrafiltration system (Billerica, MA) (R ≥ 18 MΩ) and reagent grade chemicals. A list of all buffers is available in the Supporting Materials and Methods.

Proteins

Pol I was purified according to Appling and Schneider (6). Pol I is stored in a storage buffer at −20°C.

Heparin and bovine serum albumin preparation

Heparin and BSA were dialyzed extensively before use. A detailed description of heparin and BSA preparation is available in the Supporting Materials and Methods.

Nucleic acids

All nucleic acids were commercially synthesized by Integrated DNA Technologies (Coralville, IA). All nucleic acids were purified and dialyzed before use. A detailed description of nucleic acid preparation is available in the Supporting Materials and Methods.

All data presented here were collected using elongation complexes (ECs) assembled with the following nucleic acid sequences:

• RNA(5′-AUCGAGAGG)

• DNA template strand (DNA-t) (5′ ACCAGCAGGCCGATTGGGATGGGTATTCCCTCCTGCCTCTCGATGGCTGTAAGTATCCTATAGG)

• DNA nontemplate strand (DNA-nt) (5′ CCTATAGGATACTTACAGCCATCGAGAGGCAGGAGGGAATACCCATCCCAATCGGCCTGCTGGT).

EC assembly

ECs were assembled in a stepwise manner from purified protein and nucleic acid components. The EC assembly protocol can be found in the Supporting Materials and Methods.

ATP substrates

ATP substrates were dialyzed before use. Preparation of ATP substrates is described in the Supporting Materials and Methods.

Quenched flow time courses

Nucleotide incorporation time courses were collected using a chemical quenched flow instrument. The chemical quenched flow conditions and protocol are described in the main text and in the Supporting Material.

Nucleotide addition reaction electrophoresis

Reactant and product RNAs were separated by high resolution denaturing polyacrylamide gel electrophoresis (PAGE). A description of PAGE conditions is available in the Supporting Materials and Methods.

Data analysis

Data analysis was performed using MATLAB (The MathWorks, Natick, MA) and KaleidaGraph (Synergy Software, Reading, PA). Matrix manipulations were performed in MATLAB. Optimization of the parameters shown in Schemes 1 and 2 was accomplished using a custom-built genetic algorithm. A detailed description of all data analyses is available in the Supporting Materials and Methods.

Results

Single turnover nucleotide addition reactions

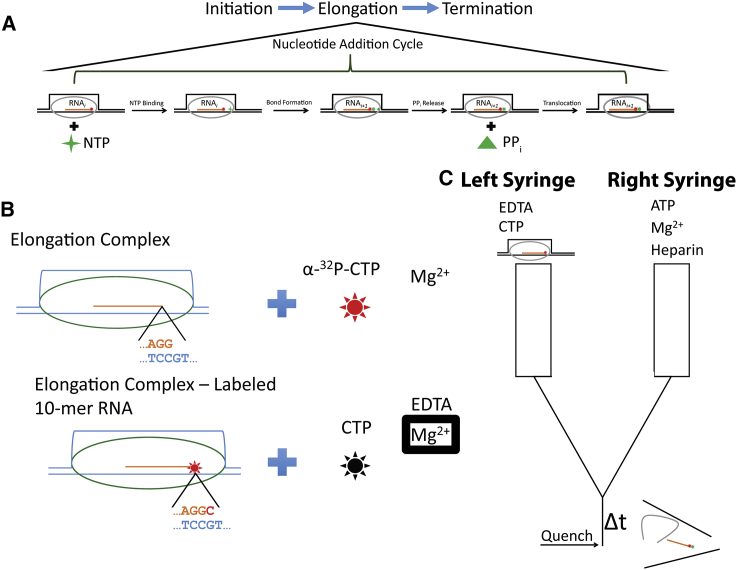
The transcription cycle can be divided into three phases: initiation, elongation, and termination (Fig. 1 A). The elongation phase is composed of a repetition of the nucleotide addition cycle. At a minimum the nucleotide addition cycle must consist of nucleotide binding, phosphodiester bond formation, pyrophosphate release, and translocation as schematized in Fig. 1 A. The goal of this work is to establish a minimal kinetic mechanism describing a single round of the Pol I nucleotide addition cycle.

Figure 1.

Schematic representations of the Pol I nucleotide addition cycle, EC-catalyzed RNA labeling and the quenched flow setup used to collect nucleotide addition time courses. (A) The transcription cycle is composed of three distinct phases corresponding to initiation, elongation, and termination. The elongation phase is composed of a repetition of the nucleotide addition cycle. The expanded schematic represents the minimal steps that must occur during the nucleotide addition cycle. These steps include substrate NTP binding, phosphodiester bond formation, pyrophosphate release, and translocation. (Stars) NMPs; (diamond) NTPs; (triangle) pyrophosphate. (B) ECs are formed using the scaffold template approach. DNA template and nontemplate strands and hybridized RNA bound by oval Pol I are illustrated. The expansion underneath the schematized EC displays the sequence of the 3′-end of the RNA and its cognate DNA template sequence. To visualize RNA, the polymerase is forced to incorporate a single labeled CMP into the 3′-end of the RNA. This labeling reaction is accomplished by adding labeled CTP and Mg²⁺. (Stars) Labeled CTP and CMP; (black star) unlabeled CTP. Mg²⁺ inside a box below “EDTA” denotes that solution Mg²⁺ has been chelated by EDTA. (C) Chemical quenched flow setup used to collect nucleotide incorporation time courses. To initiate each reaction the contents of the left and right syringes are rapidly mixed. (Δt) Line indicates that the reaction is allowed to proceed for a specified amount of time. After this specified reaction time the reaction mixture is rapidly mixed with 1 M HCl (as indicated by the arrow labeled quench). (Disordered lines to the right of the quench arrow) Quenching reaction inactivates and denatures the EC. The left syringe contains the EC mixture depicted at the bottom of (B). The right syringe contains ATP, Mg²⁺, and heparin. To see this figure in color, go online.

The functional form of Pol I during the elongation phase of transcription is referred to as the EC. The minimal components of an EC are polymerase, template and nontemplate DNA, and RNA. In this work we have reconstituted Pol I ECs using the scaffold template approach, which involves directly building ECs from purified protein and nucleic acid components (7, 8). To label RNA for visualization, once the EC was assembled, we used the polymerase to incorporate a single ³²P-labeled CMP (cytosine monophosphate) into the 3′-end of a 9 nucleotide RNA as depicted in Fig. 1 B. This was accomplished by mixing the assembled EC with Mg²⁺ and α-³²P-CTP (cytosine triphosphate) (see Fig. 1 B and the Supporting Materials and Methods). After 10 min, reactions were stopped by mixing ECs with EDTA and an excess (over radiolabeled CTP) of unlabeled CTP (Fig. 1 B). Chelation of solution divalent cation by EDTA leaves Pol I reversibly inactivated because divalent cation is required for both Pol I nucleotide addition and nuclease activities (9, 10).

A chemical quenched flow instrument was used, as schematized, in Fig. 1 C to acquire time courses for single nucleotide extension from the radiolabeled RNA. Reactions were initiated by rapidly mixing the radiolabeled Pol I ECs illustrated in Fig. 1 B with a solution containing ATP (adenosine triphosphate), Mg²⁺, and heparin. After rapid mixing of the two reagents and a delay time, the reaction was stopped by mixing with 1 M HCl. Nucleotide addition time courses were reconstructed by varying the quenched flow delay time between 0.005 and 10 s (see the Supporting Materials and Methods).

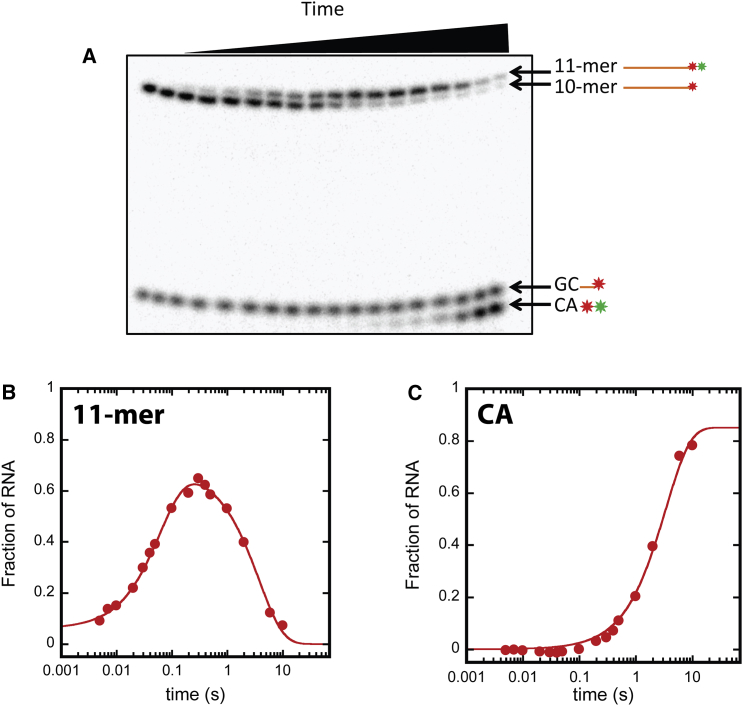
Reactions collected in the quenched flow were subjected to high resolution denaturing PAGE to separate reactants and products. ³²P-labeled RNA was visualized by phosphorimaging; a representative gel is shown in Fig. 2 A. Five distinguishable ³²P-labeled species corresponding to 10- and 11-mer RNA, CA, and GC dinucleotide RNA, and unincorporated cytosine nucleotide were observed on imaged gels (Fig. 2 A—unincorporated nucleotide was cut off). The identities of these individual species were confirmed by comparison to commercial standards and control reactions (see Fig. S1). Upon quantification we found that [GC] does not exhibit time dependence during nucleotide incorporation time courses (see Fig. S2). Visualization of these RNA species enabled analysis of nucleotide addition and nuclease activities of Pol I.

Figure 2.

AMP incorporation time course collected at 10 μM substrate ATP. Representative gel and quantifications of the gel. (A) Denaturing PAGE separation of reactants and products from a nucleotide addition time course. (Leftmost two lanes) t = 0 points. Quenched flow delay time increases from left to right. The species in the gel are labeled to the right of the gel. (B) Quantified 11-mer time course. (Circles) Fraction of RNA in the 11-mer state as a function of time quantified according to Eq. S1. (Solid traces) NLLS fit of the data to Eq. S2 (j = 2). (C) Quantified CA time course. (Circles) Fraction of RNA in the CA state as a function of time quantified according to Eq. S1. (Solid traces) NLLS fit of the data to Eq. S2 (j = 1). To see this figure in color, go online.

Model-independent analysis of nucleotide addition and nuclease reactions

Fig. 2, B and C, displays 11-mer and CA time courses, respectively. The time courses were reconstructed from quantification of the 11-mer and CA bands on the gel displayed in Fig. 2 A using Eq. S1 in the Supporting Materials and Methods. The nucleotide addition reaction analyzed in Fig. 2 was collected at 10 μM ATP.

Fig. 2 B shows that the fraction of RNA in the 11-mer state increases between ∼0 and 200 ms before decaying slowly for the remainder of the time course (note log timescale). In contrast, Fig. 2 C shows that the fraction of CA RNA rises in a single phase throughout the time course. The quantifications in Fig. 2, B and C, indicate that the fall of [11-mer] and the rise of [CA] occur over approximately the same timescale. The time courses in Fig. 2, B and C, suggest that 11-mer is directly converted to labeled CA and unlabeled 9-mer.

To quantify the time courses, we applied nonlinear least-squares (NLLS) analysis. The time courses appear to be exponential, thus the data were fit to a sum of exponential terms (see Eq. S2). The experiments were performed three times and each time course was subjected to NLLS analysis. The three determinations of the parameters obtained from this approach were averaged and the standard deviation was determined.

The CA time course was adequately described by a single exponential function while the 11-mer data required two exponentials (solid red lines in Fig. 2, B and C, display representative fits). The 11-mer time course yielded a fast and a slow observed rate constant with values of (15 ± 1) s⁻¹ and (0.29 ± 0.07) s⁻¹, respectively, whereas CA accumulated with a rate constant of (0.35 ± 0.05) s⁻¹.

If CA production is the result of cleavage of the 11-mer then the rate constant for formation of CA would be expected to be the same as the rate constant for disappearance of the 11-mer. Consistently, the rate constant for the disappearance of the 11-mer, (0.29 ± 0.07) s⁻¹, is within error of the observed rate constant for CA formation (0.35 ± 0.05) s⁻¹. This observation indicates that these two rate constants directly report on Pol I’s nuclease activity.

To obtain additional information about the nucleotide addition mechanism and further probe the linkage between 11-mer decay and CA accumulation, the system must be perturbed and the kinetic response(s) measured. Taking into account the minimal steps that must occur during the nucleotide addition cycle, Fig. 1 A, a simple way to perturb the system is to vary the [ATP]. At sufficiently low ATP concentrations the ATP binding step will become rate limiting. In contrast, at sufficiently high ATP concentrations, the time courses will be independent of ATP concentration. Thus, the behavior of the 11-mer and CA time courses as a function of [ATP] will contain information about the nucleotide addition mechanism.

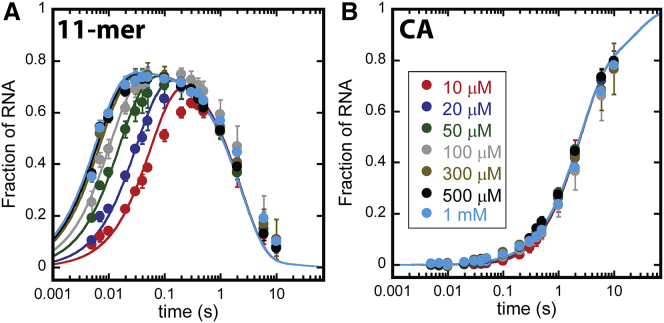
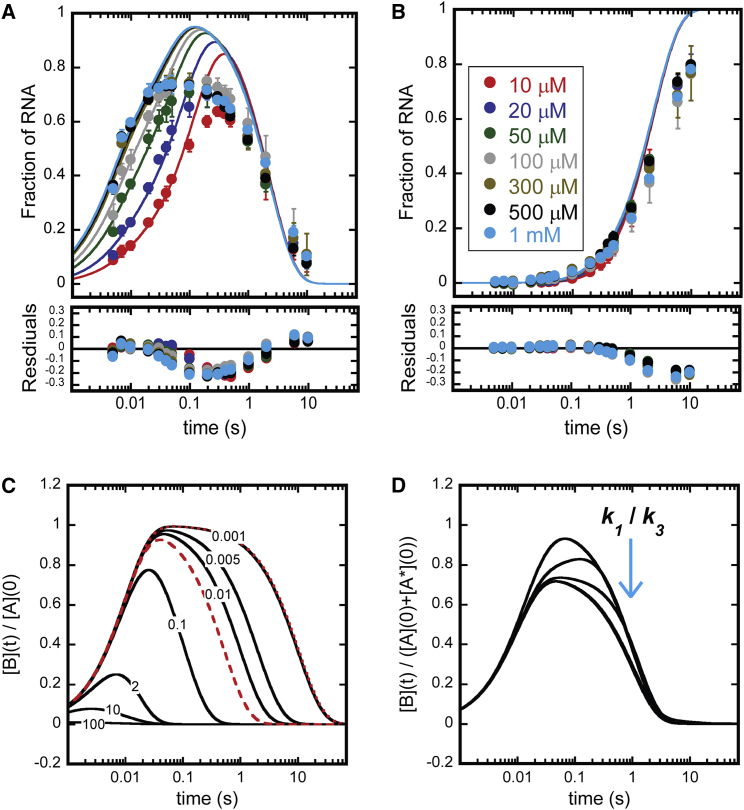
Fig. 3 A shows 11-mer time courses collected between 10 μM and 1 mM ATP. As described above and observed in Fig. 2 B, all of the 11-mer time courses are biphasic. As seen in Fig. 3 A, the two phases clearly respond differently to changing [ATP]. The rising phases of the 11-mer time courses (first ≈100 ms) appear to accelerate as [ATP] is increased (traces shift left in Fig. 3 A). In sharp contrast, the decay phases of the 11-mer time courses virtually overlay indicating no dependence on [ATP].

Figure 3.

Nucleotide addition time courses collected as a function of [ATP] (A) 11-mer time courses collected as a function of [ATP]. (Circles) Average value of three independent measurements quantified according to Eq. S2. Uncertainty bars represent standard deviation about the average. (Solid traces) Global WNLLS fit of the data to Scheme 2. Colors denoting [ATP] are the same as those displayed in the legend shown in (B). (B) CA time courses collected as a function of [ATP]. (Circles) Average value of three independent measurements quantified according to Eq. S2. (Uncertainty bars) Standard deviation about the average. (Solid traces) Global WNLLS fit of the data to Scheme 2. (Inset legend) Experimental substrate [ATP].

Fig. 3 B shows the corresponding CA time courses collected between 10 μM and 1 mM ATP. As described above and observed in Fig. 2 C, [CA] rises continuously throughout the time course. In contrast to the time courses for 11-mer, the time courses for CA are invariant across the experimental [ATP]. This observation indicates that this reaction is independent of [ATP].

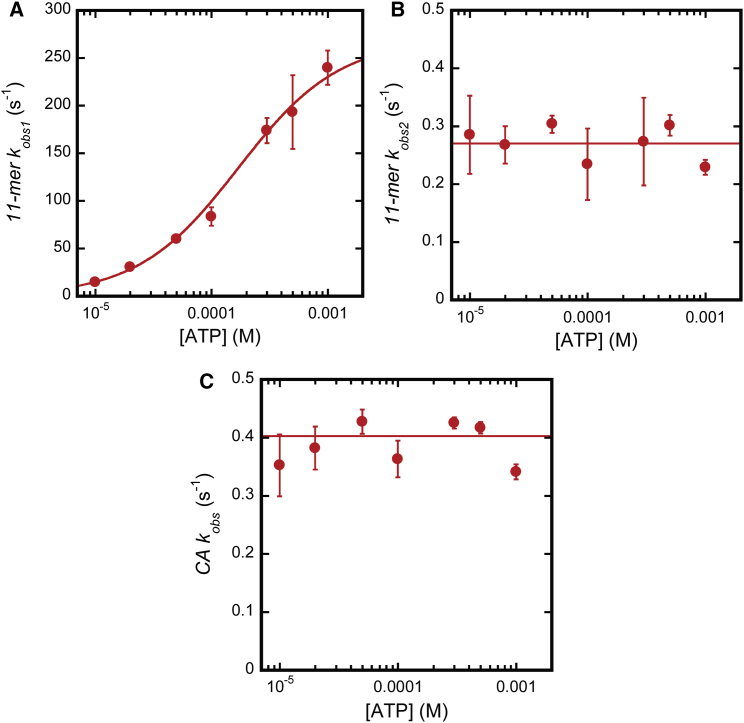
To quantify the effects of [ATP] on the 11-mer and CA time courses, each time course was subjected to NLLS-weighted nonlinear least-squares (WNLLS) analysis using a sum of exponential terms as described above for the 10 μM ATP data (Fig. 2, B and C) (see Eq. S2). WNLLS analysis of the 11-mer time courses yielded two observed rate constants which are plotted as a function of [ATP] in Fig. 4, A and B (circles). It is clear from Fig. 4, A and B, that the two 11-mer observed rate constants (11-mer k_obs1 and 11-mer k_obs2, respectively) differ in both magnitude and response to [ATP]. Specifically, 11-mer k_obs1 (Fig. 4 A) exhibits a hyperbolic dependence on [ATP] whereas the 11-mer k_obs2 (Fig. 4 B) appears to be independent of [ATP].

Figure 4.

k_obs versus [ATP]. (A) 11-mer k_obs1 plotted as a function of [ATP]. (Circles) Average k_obs value determined from analysis of three independent time courses according to Eq. S2 (j = 2). (Uncertainty bars) Standard deviation about the average. (Solid traces) WNLLS fit of the data to Eq. S3. (B) 11-mer k_obs2 plotted as a function of [ATP]. (Circles) Average k_obs value determined from analysis of three independent time courses according to Eq. S1 (j = 2). Uncertainty bars represent standard deviation about the average. (Solid traces) WNLLS fit of the data to Eq. S4. (C) CA k_obs plotted as a function of [ATP]. (Circles) Average k_obs value determined from analysis of three independent time courses according to Eq. S2 (j = 1). Uncertainty bars represent standard deviation about the average. (Solid traces) WNLLS fit of the data to Eq. S4. To see this figure in color, go online.

The 11-mer k_obs1 versus [ATP] data were subjected to weighted nonlinear least-squares (WNLLS) analysis using the equation for a rectangular hyperbola given by Eq. S3. The analysis yielded k_max = (270 ± 30) s⁻¹, and K_1/2 = (170 ± 30) μM. The 11-mer k_obs2 versus [ATP] data in Fig. 4 B were also subjected to WNLLS analysis to a constant (see Eq. S4). From this analysis a constant corresponding to 11-mer k_obs2 = (0.27 ± 0.02) s⁻¹ was determined.

CA time courses collected at each [ATP] were similarly subjected to WNLLS analysis. As observed for the 10 μM ATP data set (Fig. 2 C), CA time courses at each [ATP] were adequately described by a single exponential function (see Eq. S2 ). In Fig. 4 C, CA observed rate constants (CA k_obs) are plotted against [ATP]. As described above for 11-mer k_obs2, CA k_obs versus [ATP] data were fit to a constant (see Eq. S4) to yield a value of (0.40 ± 0.02) s⁻¹.

The analysis described above leads to three conclusions: 1) The hyperbolic dependence of 11-mer k_obs1 on [ATP] indicates that ATP binding is best described as a rapid equilibrium process with respect to the step following ATP binding. 2) The lack of a lag in the 11-mer time courses at any [ATP] along with the hyperbolic dependence of 11-mer k_obs1 on [ATP] indicate that the step reported on by 11-mer k_obs1 is directly linked to ATP binding (11). 3) The correspondence between 11-mer k_obs2 and CA k_obs values and [ATP] independence indicates that these two rate constants are reporting on the same process, most likely the nuclease activity of Pol I.

Model-dependent analysis of single turnover nucleotide addition and nuclease reactions

Scheme 1 of Fig. 5 shows the minimal steps that must be present in the nucleotide addition reaction. In this scheme EC_n refers to EC with RNA of length n, PP_i refers to pyrophosphate, and $CA$ refers to the dinucleotide fragment liberated from the 3′-end of the RNA. The system of coupled ordinary differential equations (ODEs) defined by Scheme 1 was numerically integrated to globally fit 11-mer and CA time courses collected at each [ATP] by WNLLS analysis using a custom built genetic algorithm (see the Supporting Materials and Methods). Fig. 6, A and B, displays the 11-mer and CA time courses, respectively, collected at each [ATP] (circles) overlaid with simulations produced from the best fit parameter values using Scheme 1 (solid lines).

Figure 5.

Reaction schemes. (Scheme 1, top) EC_n, EC with RNA of length n; PP_i, pyrophosphate; CA, dinucleotide fragment removed from 3′-terminus of RNA. (Scheme 2, bottom) All species are the same as in Scheme 1, with the exception of EC^°₁₀, which corresponds to a subset of the EC₁₀ population that is reversibly inactivated.

Figure 6.

Global fit of Scheme 1. Simulations of Eqs. 2 and 4. (A) Global WNLLS fit of 11-mer time course to Scheme 1. (Circles) Experimental data as described in Fig. 3A. (Solid lines) Scheme 1 simulated at best-fit parameter values. k₁ = 1 × 10⁸ s⁻¹, k₂ = 5534 s⁻¹, k₃ = 142.8 s⁻¹, k₄ = 84.6 s⁻¹, k₅ = 52.3 s⁻¹, and k₆ = 0.43 s⁻¹. (B) Global WNLLS fit of CA time courses to Scheme 1. (Circles) Experimental data as described in Fig. 3B. (Solid lines) Scheme 1 simulated at best-fit parameter values listed in the description in (A). (C) Evaluation of Eq. 2 at a range of k₂/k₁. Each trace is labeled with its respective k₂/k₁ ratio. For each evaluation, k₁ = 100 s⁻¹. To generate solid lines, k₂ was set to the values {10,000, 1000, 200, 10, 1, 0.5, 0.1} s⁻¹, to result in the k₂/k₁ ratio {100, 10, 2, 0.1, 0.01, 0.005, 0.001}, respectively. To generate broken and dashed red lines, k₂ was set to the values {0.0955, 1.92} s⁻¹ to result in the k₁/k₂ ratios {0.00096, 0.019}, respectively. (D) Evaluation of Eq. 4 at a range of k₁/k₃ ratios. For each evaluation, k₂ = 100 s⁻¹, k₃ = 1 s⁻¹, A(0) = 0.75, A^∗(0) = 0.25. To generate solid lines, k₁ was set to the values {50, 10, 2, 0.1, 0.01, 0.005, 0.001} s⁻¹, to result in the k₁/k₃ ratios {50, 10, 2, 0.1, 0.01, 0.005, 0.001}, respectively. Note that below a k₁/k₃ ratio of 0.1, all curves overlay.

From inspection of Fig. 6, A and B, it is clear that there are systematic deviations between the fit (solid lines) and data (circles). The largest deviation occurs in the 11-mer time courses between ∼0.1 and 1 s (see Fig. 6 A). The best-fit lines according to Scheme 1 predict 11-mer peak heights that are consistently greater than those observed in the experimental data (see Fig. 6 A residuals between 0.1 and 1 s). Specifically, Scheme 1 predicts 11-mer peak heights ≈1 whereas the experimental data do not exhibit peak heights above ≈0.75 (see light-blue solid line and circles for comparison of fit and data at 1 mM ATP). The inability of Scheme 1 to describe the data indicates that a step or steps in addition to the minimal number of steps included in Scheme 1 must be present in the Pol I nucleotide addition mechanism. Furthermore, this step(s) must regulate the peak height of the 11-mer.

In the nucleotide addition time courses that we have collected, the 11-mer RNA species can be considered an intermediate and CA can be considered the reaction product. The relative rates of influx and efflux through an intermediate in a reaction pathway regulates the peak height of the intermediate. As an example a generic three state system of the form given by

$$A\stackrel{k_1}{\to }B\stackrel{k_2}{\to }C$$ (1)

can be used to explore how the relative magnitudes of flux through an intermediate can regulate the peak height of the intermediate. According to Eq. 1, [B](t) normalized to the initial concentration of reactant ([A](0)) is given by

$$\frac{\left[B\right]\left(t\right)}{\left[A\right]\left(0\right)}=\left(\frac{1}{1-\frac{k_2}{k_1}}\right)\left(e^{-k_{2}t}-e^{-k_{1}t}\right).$$ (2)

Inspection of Eq. 2 indicates that [B](t) is scaled by a factor that is a function of the ratio of rate constants governing the formation and decay of B. In addition to this scaling factor, two time–dependent exponential terms of opposite sign modulate both the height of the [B] peak and its position with respect to the time axis.

Due to the time dependence of Eq. 2, simple inferences involving the k₂/k₁ ratio regarding the peak height of B are difficult to draw. However, Eq. 2 can be evaluated at a range of k₂/k₁ ratios and the behavior of [B] peak heights monitored. Fig. 6 C displays time courses simulated from Eq. 2 at seven k₂/k₁ ratios (100, 10, 2, 0.1, 0.01, 0.005, and 0.001, solid black lines) and plotted over the experimental time range. In addition, Fig. 6 C displays Eq. 2 evaluated at the k₂/k₁ ratios obtained from 11-mer time courses collected at 1 mM and 10 μM ATP (11-mer k_obs1/11-mer k_obs2 ratios) plotted as dotted and broken red lines, respectively. From these simulations, it is clear that there is no combination of experimental 11-mer influx and efflux rates (11-mer k_obs1 and 11-mer k_obs2 values) that result in an 11-mer peak height below ≈1. In fact, an analysis of Fig. 6 C indicates that a k₂/k₁ ratio ≈ 0.1 is required to result in a peak height ≈ 0.8. According to the 11-mer k_obs2 values plotted in Fig. 4 B, this ratio would correspond to an 11-mer k_obs1 value of ≈2–3 s⁻¹. This value is much smaller than any experimentally observed 11-mer k_obs1 value (Fig. 4 A). In terms of the nucleotide addition mechanism these analyses indicate that there is not a step that can follow ATP binding that could modulate the 11-mer peak heights while preserving the 11-mer influx and efflux rates (see Fig. 4, A and B, for 11-mer flux rates reported as 11-mer k_obs1 and 11-mer k_obs2).

The simplest model that preserves the 11-mer k_obs1 and 11-mer k_obs2 values while reducing the 11-mer peak heights is one that includes an EC subpopulation that undergoes an inactive to active transition. If this inactive to active transition were governed by a rate constant less than that governing CA production, the 11-mer peak heights would respond to the fraction of the EC population in the active form when the reaction begins. A model of this form can be approximated by the generic four state system given by

$$A^{\ast }\stackrel{k_1}{\to }A\stackrel{k_2}{\to }B\stackrel{k_3}{\to }C$$ (3)

where A^∗ denotes the subpopulation that must undergo an inactive to active transition. B[B](t) normalized to the initial total [A] ([A^∗](0)+[A](0)) can be obtained and takes the form of Eq. 4, where A(0) and A^∗(0) denote the initial concentrations of active and inactive species, respectively:

$$\frac{B\left(t\right)}{A^{\ast }\left(0\right)+A\left(0\right)}=k_2\left(\frac{A^{\ast }\left(0\right){\text{e}}^{-k_{1}t}{k}_1}{\left(k_1-k_2\right)\left(k_1-k_3\right)}+\frac{e^{-k_{2}t}\left(\left(A\left(0\right)+A^{\ast }\left(0\right)\right)k_1-A\left(0\right)k_2\right)}{\left(-k_1+k_2\right)\left(k_2-k_3\right)}+\frac{e^{-k_{3}t}\left(\left(A\left(0\right)+A^{\ast }\left(0\right)\right)k_1-A\left(0\right)k_3\right)}{\left(-k_1+k_3\right)\left(-k_2+k_3\right)}\right).$$ (4)

Equation 4 demonstrates that the interplay of rate constants that governs an intermediate’s peak height quickly grows in complexity as a function of the number of steps in a reaction pathway. In the limit that k₁ approaches zero, Eq. 4 becomes

$$\underset{k_1\to 0}{\text{lim}}\frac{B\left(t\right)}{A^{\ast }\left(0\right)+A\left(0\right)}=\left(\frac{A\left(0\right)}{A\left(0\right)+A^{\ast }\left(0\right)}\right)\frac{\left(-e^{-k_{2}t}+e^{-k_{3}t}\right)k_2}{\left(k_2-k_3\right)}.$$ (5)

Although this is the trivial case in which Eq. 3 collapses to Eq. 1 with an inactive reactant population, this limit demonstrates that as k₁ becomes very small the entire function is scaled by the fraction of reactant A in the active form. In fact, inspection and rearrangement of Eq. 5 yields Eq. 6, where frac_active is given by Eq. 7, below:

$$\underset{k_1\to 0}{\text{lim}}\frac{B\left(t\right)}{A^{\ast }\left(0\right)+A\left(0\right)}=\mathit{fra}{\mathit{c}}_{\text{active}}\left(\frac{1}{1-\frac{k_3}{k_2}}\right)\left(-e^{-k_{2}t}+e^{-k_{3}t}\right),$$ (6)

$$fra{c}_{\text{active}}=\frac{A\left(0\right)}{A\left(0\right)+A^{\ast }\left(0\right)}.$$ (7)

Comparison between Eqs. 6 and 2 reveals that Eq. 6 is simply Eq. 2 scaled by a constant. This constant scaling factor is the fraction of total reactant population in the active state at t = 0.

Fig. 6 D displays Eq. 4 evaluated at seven k₁/k₃ ratios (50, 10, 2, 0.1, 0.01, 0.005, and 0.001) and plotted over the experimental time range. Importantly, the scaling factor given by Eq. 15 was fixed to 0.75 in all evaluations plotted in Fig. 6 D. It is clear from Fig. 6 D that as the k₁/k₃ ratio decreases, the peak height quickly approaches that given by Eq. 7 (note that below a k₁/k₃ ratio of 0.1 the curves overlay giving the appearance that only four curves are plotted). Fig. 6 D indicates that Eq. 4 approaches Eq. 6 before the limit in Eq. 5 is achieved.

Scheme 2 places the inactive to active transition model into the context of the nucleotide addition cycle. In Scheme 2 there are initially two EC₁₀ populations before rapid mixing with ATP to initiate single nucleotide addition; only one of which is initially active. As described above for Scheme 1, the ODEs derived from Scheme 2 were numerically integrated to globally fit all time course data. Fig. 3, A and B, display 11-mer and CA time course data, respectively (circles) overlaid with simulations of Scheme 2 evaluated at the parameter values obtained from the global fit (solid lines, Table 1). There is clear agreement between the time courses predicted by Scheme 2 and the experimental data.

Table 1.

Scheme 2 fitted parameter values and parameter value limits

Parameter	Fitted Valuea	Lower Bound	Upper Bound
k1	l × 108 M−1 s−1	—	—
k2	9800 s−1	8100 s−1	12,100 s−1
k3	180 s−1	160 s−1	220 s−1
k4	≈0 s1	—	—
k5	>300 s−1	300 s−1	—
k6	0.42 s−1	0.40 s−1	0.44 s−1
k7	0.04 s−1	0.01 s−1	0.07 s−1
[EC10]/[ECtotal]	0.77	0.74	0.79

^ak₁ and k₄ values were not optimized in the fitting routine.

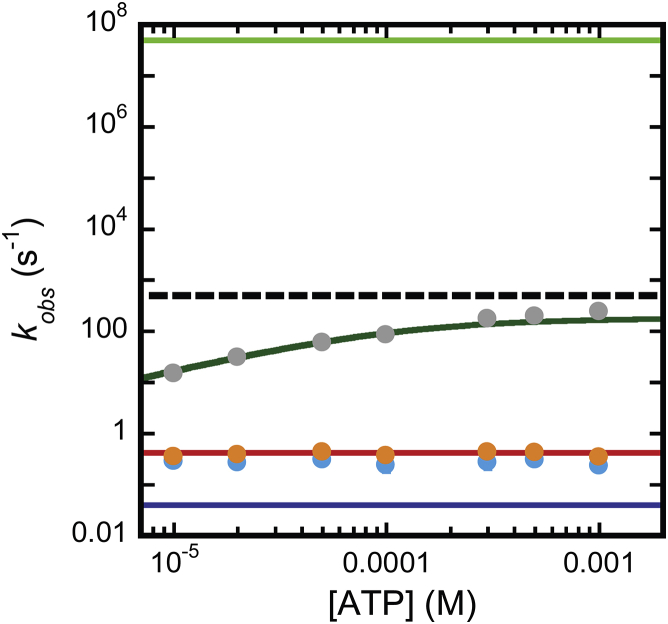
To further test Scheme 2’s ability to describe our experimental data we obtained the eigenvalues from the coefficient matrix of the system of ODEs describing Scheme 2. These eigenvalues are functions describing the negative observable rate constants that Scheme 2 would produce. Scheme 2 gives rise to four unique nonzero observable rate constant functions. These functions were evaluated at the parameter values obtained from globally fitting 11-mer and CA time courses at each [ATP] to Scheme 2 and are plotted (solid lines) along with experimental k_obs versus [ATP] data (circles) in Fig. 7. Two of these observable rate constants are functions of [ATP] whereas two are constants. It is clear from Fig. 7 (see comparison to the reciprocal of a 2 ms quenched-flow dead time, broken line) that only one of the [ATP]-dependent observable rate constants would actually be observed under our experimental conditions. This leaves three observable rate constant functions that give rise to values detectable under our experimental conditions. Two of these three observable rate constants correspond well to experimental k_obs versus [ATP] data (Fig. 7).

Figure 7.

Eigenvalue decomposition of the ODEs describing Scheme 2. (Solid lines) Negative eigenvalues evaluated at the best-fit parameter values obtained from global WNLLS analysis of the 11-mer and CA time courses according to Scheme 2 (red, −λ₁; blue, −λ₂; dark green, −λ₃; light green, −λ₄). (Circles) Experimental k_obs values (gray, 11-mer k_obs1; blue, 11-mer k_obs2; orange, CA k_obs). (Broken line) Upper limit of a rate constant detectable in our quenched flow instrument according to a dead time of 0.002 s. To see this figure in color, go online.

Scheme 2 is clearly capable of describing both time course data (Fig. 3, A and B) and k_obs versus [ATP] data (Fig. 7). Thus, we used Scheme 2 to provide estimates of elementary rate constant values describing the nucleotide addition cycle.

Assignment of parameter uncertainties

It is well established that χ² functions resulting from systems of equations derived from models such as Scheme 2 display correlated parameters (12, 13). These correlations make optimization of the parameter values and calculation of uncertainties on parameter values challenging. For example, the on and off rate constants of a bimolecular reaction are highly correlated. Taking this correlation into account, k₁ was fixed in all global fits performed in this work.

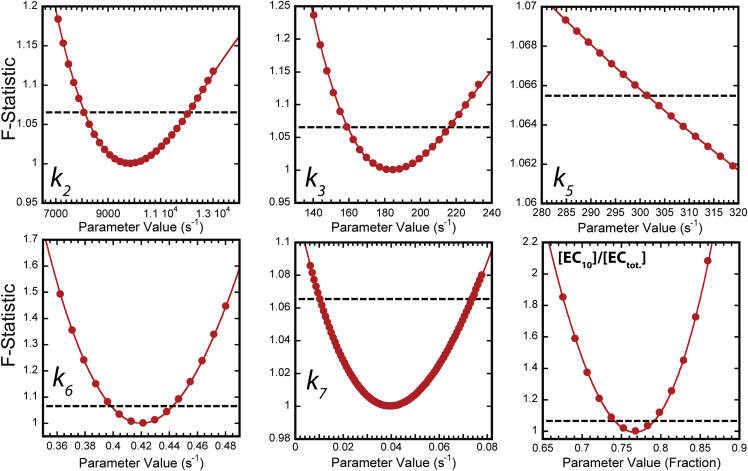
To provide bounds on the elementary rate constants we obtained by globally fitting time course data to Scheme 2, we employed a grid searching strategy. In this approach one parameter at a time was chosen and its value scanned across a specified range (13). At each value the scanned parameter was held constant while all other parameters were optimized to minimize χ². This procedure enabled calculation of a parameter value versus F-statistic data set. This data set was analyzed in the context of an F-critical value and parameter bounds were calculated (see the Supporting Materials and Methods for a detailed description) (14). Parameter value versus F-statistic data sets for each parameter that floated during global fitting of Scheme 2 are presented in Fig. 8.

Figure 8.

Calculation of parameter uncertainties. Each panel represents the resultant F-statistic versus parameter value data set from a grid search performed as described in Materials and Methods. Each panel is labeled with the specific fixed parameter. (Circles) Individual F-statistic values; (solid lines) fits to a third-order polynomial (with the exception of the k₅ data set, which was fit to a second-order polynomial). (Broken line in each panel) F-critical value calculated as described in Materials and Methods. To see this figure in color, go online.

Grid searching revealed that not all parameters in Scheme 2 were equally constrained (see relative width of each data set at the F-critical value (broken lines) in Fig. 8). Importantly, we found that k₃, k₄, and k₅ values could not be simultaneously determined. This observation required that we constrain the fit by fixing one of the parameters and determining bounds for the remaining parameter values. Our 11-mer k_obs1 versus [ATP] data indicate that the reverse rate of bond formation is very near zero (see Eq. 8). For this reason we chose to constrain k₄ to a value of zero and optimize the remainder of the parameters to yield the values shown in Table 1. The grid searches displayed in Fig. 8 were performed based on the parameter values optimized in the global fit and the calculated uncertainties are reported in Table 1. Global fitting of time course data combined with grid searching provides rigorous determination of parameter values and bounds on each parameter value.

Discussion

Information content of nucleotide addition time courses

The minimal steps that must occur in the Pol I nucleotide addition cycle are displayed in Fig. 1 A. Using the methods described above, we have generated the first model describing the Pol I single nucleotide addition mechanism. It is important to note that our experimental approach may or may not be sensitive to all the steps in the nucleotide addition cycle. There are two simple scenarios that could each render a step invisible to our measurements. First, an event governed by a very large rate constant would reach completion in the dead time of the quenched flow instrument. Furthermore, an internal step governed by a relatively large rate constant (in comparison to flanking steps) will not contribute to the shape of the observed time course. Second, our experimental approach may leave our measurements insensitive to a specific step. A noteworthy example of a step that may fall into both categories is translocation of the polymerase along the nucleic acid. Translocation could either be relatively fast (with respect to other steps in the nucleotide addition cycle) or not be required before nucleotide addition. We do not know the translocation state of the EC with respect to the 3′-terminus of the RNA following our EC assembly protocol. Therefore, before nucleotide addition Pol I may or may not have to take a translocation step. Taking this uncertainty into account, we have not assigned any of the kinetic steps proposed in Scheme 2 to translocation.

In addition to the minimal steps depicted in Fig. 1 A, our experimental setup may render our measurements sensitive to steps that do not occur frequently during processive elongation. Upon conducting single nucleotide addition reactions we observed robust nuclease activity (Figs. 1 D and 2 B) that liberated a dinucleotide fragment from the 3′-end of the RNA. This observation required that we include a dinucleotide production step in any model describing the Pol I nucleotide addition pathway. With these information content considerations in mind we proceed with a synopsis of the Pol I single nucleotide addition mechanism.

ATP binding

Our data indicate that ATP binding is best described as a rapid equilibrium process with respect to the rest of the pathway. There are two key pieces of evidence that support this interpretation. First, the model-independent analyses of the time courses displayed in Fig. 3 C reveal that there is a step leading to 11-mer formation that is governed by an [ATP]-dependent rate constant that saturates at k_max = (270 ± 30) s⁻¹ and is characterized by a half-maximal [ATP] of K_1/2 = (170 ± 30) μM. Second, the time courses shown in Fig. 3 A do not display a lag at any [ATP]. The lack of a lag in the time courses and the hyperbolic dependence of 11-mer k_obs1 on [ATP] indicate that the step that is being reported on by 11-mer k_obs1 is directly linked to ATP binding and occurs immediately after ATP binding. Assuming that ATP binding is a diffusion-limited process occurring with a rate constant of ≈1 × 10⁸ M⁻¹ s⁻¹ and that K_1/2 is approximating the ATP dissociation equilibrium constant, ATP release must be governed by a rate constant ≈2 × 10⁴ s⁻¹. A rate constant of this magnitude places the ATP binding step well within the rapid equilibrium regime with respect to the subsequent step in the pathway (i.e., k_reverse >> k_forward). Rapid equilibrium ATP binding governed by a dissociation equilibrium constant ≈100 μM (obtained from global fit; see Table 1, k₂/k₁) are consistent with other RNA polymerases and ATPase motor enzymes (15, 16).

Work from the Erie group has indicated that Escherichia coli RNA polymerase possesses an allosteric NTP binding site (15, 17). They observed that occupation of this site leads to alterations in nucleotide incorporation rates. Our data contain no indications of such allostery. Specifically, 11-mer k_obs1 versus [ATP] data are described well by a rectangular hyperbola (see Fig. 4 A). The difference between our results and those from the Erie group highlights the need to carefully investigate each RNA polymerase system, rather than assuming conservation of mechanism. As discussed in the introduction, eukaryotes have evolved to require at least three nuclear RNA polymerases. It is unlikely that each of these enzymes is governed by the same molecular mechanisms.

Phosphodiester bond formation

We have interpreted the step immediately after ATP binding as phosphodiester bond formation or a conformational change immediately preceding rapid bond formation. In Scheme 2, k₃ is similar to k_max but not identical. Taking into account Scheme 2 and the fitted parameter values, k₃ should equal k_max. To probe this discrepancy we attempted to fit individual 11-mer time courses collected at 1 mM ATP (roughly saturating [ATP]) to a sum of two exponential terms in which one of the rate constants was constrained to equal k₃. The fits with or without this constraint were virtually indistinguishable (data not shown). In time courses collected at 1 mM ATP there are very few data points that fall in the region of the curve defining the faster of the two rate constants. This region of low data density leads to increased uncertainty in this parameter’s fitted value. The observation of this discrepancy highlights the strengths of simultaneously fitting a data set collected as a function of two or more variables (in our case time and [ATP]) to constrain parameter values. Together, these analyses indicate that k_max is reporting on k₃.

Considering the analyses discussed in the above two paragraphs and the relative values of the fitted parameters from Table 1, 11-mer k_obs1 can be approximated by Eq. 8 (11) in which k_n are defined in Scheme 2 and K_1/2 refers to the [ATP] at k₃/2,

$$11-mer{k}_{obs1}\approx \frac{k_3\left[ATP\right]}{K_{1/2}+\left[ATP\right]}+k_4.$$ (8)

In the limit that [ATP] in Eq. 8 goes to zero, 11-mer k_obs1 would equal k₄. Inspection of Fig. 4 A indicates that in this [ATP] limit, 11-mer k_obs1 ≈ 0. Satisfying the simple relationship described by Eq. 8 requires that the remaining steps of the pathway leading to signal change be rapid with respect to k₃ and k₄ (11). Although our data do not contain direct information on k₄ or k₅, the above discussion and the k₅ grid search results presented in Fig. 8 and table 1 indicate that k₄ must be very small and/or k₅ must be very large. Constraint on k₄ and k₅ will require a direct measure of one of these steps.

The Belogurov group has recently reported direct measurements of pyrophosphate release kinetics for E. coli RNA polymerase (18). Each nucleotide incorporation was monitored (AMP, CMP, GMP, UMP) at a single [NTP]. The Belogurov group reported rate constant values ≈ 100 s⁻¹ for pyrophosphate release following each incorporation event. Considering the difference in enzyme and analytical approaches between our study and theirs, this value is in reasonable agreement with the lower limit of 300 s⁻¹ we have placed on Pol I pyrophosphate release following an AMP incorporation (see Table 1, k₅). Further refinement of the Pol I pyrophosphate release rate constant value will require direct measurement of this step.

Nuclease activity of Pol I as a possible fidelity mechanism

Pol I-catalyzed dinucleotide production is governed by a rate constant much slower than all other steps in the pathway with the exception of the active-inactive transition (Table 1). This observation indicates that a nucleolytic event would be rare during processive elongation. It has been reported that polymerase elongation rate decreases immediately following a misincorporation event (19). Under these conditions, the probability of a nucleolytic event by Pol I would greatly increase. Thus, Pol I’s nuclease activity would serve a role in increasing transcriptional fidelity. This hypothesis is the subject of ongoing investigation.

Both Pols I and III possess robust nuclease activities, whereas purified Pol II and E. coli RNAP require additional trans-acting factors to stimulate cleavage of the nascent RNA (TFIIS and GreA/B, respectively (10)). There are two potential explanations for this disparity. First, it is possible that the cleavage assisting factors saturate elongating Pol II and RNAP in vivo. If these polymerases are continuously occupied by their cognate cleavage assisting factor in vivo the argument is an artifact of enzyme purification. Alternatively, eukaryotic evolution may have selected for enhanced fidelity of synthesis for the stable RNAs involved in translation (ribosomal RNA and transfer RNA), resulting in the observed nuclease activities in Pols I and III.

Inactive to active EC interconversion

The physical origins of a pre-ATP binding step and the observation of two polymerase populations are unclear (see EC^∗ and EC₁₀ in Scheme 2). Heterogeneity in motor enzyme systems is not uncommon. Data obtained both at the single molecule level as well as in the ensemble point to the presence of both static (distinct enzyme populations) and dynamic (single enzymes converting between distinct conformers) heterogeneity (18, 20, 21, 22). In the past decade there has been significant interest in the mechanisms governing RNA polymerase pausing (23, 24, 25, 26). Pausing is often discussed as an on-pathway or off-pathway event in which the entire polymerase population experiences the pause or only a subset, respectively (25, 26). The off-pathway events could be due to either static (only a subset of the polymerase molecules are sensitive to the conditions leading to a pause) or dynamic (stochastic recognition of the conditions leading to a pause by a given polymerase molecule) heterogeneity. As of this writing, we are monitoring multi-NTP incorporation reactions to better understand the inactive to active conversion we have observed (see EC^∗ and EC₁₀ in Scheme 2). Specifically, we are working to determine if the polymerase population repartitions after each incorporation event or if once the inactive population has entered the active polymerase pool it remains there during a processive elongation event.

Measuring the time dependence of each intermediate RNA length in a processive elongation reaction will reveal whether or not a transiently inactivated population is generated after each incorporation event. Although these ensemble measurements will not be able to distinguish between static and dynamic heterogeneity, they will be able to distinguish between on-pathway and off-pathway events. An off-pathway event will be experienced by only a subset of the polymerase population and will be reported on as a fraction of the polymerase population entering an inactivated state after the nucleotide incorporation event. Experimentally, these events will give rise to multiphasic decays of the paused RNA intermediate. It is important to recognize that an on-pathway pause observed in the ensemble is a bit of a misnomer. Instead, this event should be viewed as a difference in relative nucleotide incorporation rates between the paused base and the flanking incorporations. An on-pathway event would be characterized by monophasic decay of the paused RNA intermediate. For now, we can say that under our conditions there is a Pol I population that must undergo a slow transition to achieve catalytic competency during a single nucleotide incorporation event.

Conclusion

We have developed a minimal kinetic model describing Pol I-catalyzed nucleotide addition and nuclease reactions. Using reconstituted ECs we monitored single nucleotide addition and nuclease reactions under single turnover conditions. Using global fitting techniques and a novel fitting algorithm, we provide quantitative estimates and rigorous limits of the elementary rate constants governing Pol I-catalyzed nucleotide addition and phosphodiester bond hydrolysis. Using the experimental and analytical methods described herein, a deeper understanding of the mechanistic consequences of inhibitory compounds, trans-acting factors, and mutations in Pol I is within reach.

Author Contributions

F.D.A. designed research, performed research, contributed analytical tools, analyzed data, and wrote the article; A.L.L. designed research, contributed analytical tools, analyzed data, and wrote the article; and D.A.S. designed research, analyzed data, and wrote the article.

Editor: Timothy Lohman.