Transbilayer Colocalization of Lipid Domains Explained via Measurement of Strong Coupling Parameters

Abstract

When micron-scale compositional heterogeneity develops in membranes, the distribution of lipids on one face of the membrane strongly affects the distribution on the other. Specifically, when lipid membranes phase separate into coexisting liquid phases, domains in each monolayer leaflet of the membrane are colocalized with domains in the opposite leaflet. Colocalized domains have never been observed to spontaneously move out of registry. This result indicates that the lipid compositions in one leaflet are strongly coupled to compositions in the opposing leaflet. Predictions of the interleaflet coupling parameter, Λ, vary by a factor of 50. We measure the value of Λ by applying high shear forces to supported lipid bilayers. This causes the upper leaflet to slide over the lower leaflet, moving domains out of registry. We find that the threshold shear stress required to deregister domains in the upper and lower leaflets increases with the inverse length of domains. We derive a simple, closed-form expression relating the threshold shear to Λ, and find Λ = 0.016 ± 0.004 k_BT/nm².

Introduction

Lipid bilayers are the primary structural component of cell membranes, and are increasingly recognized to play an active role in regulating cell function (1). One such function is signaling, which requires colocalization of proteins. The mechanism by which peripheral proteins on opposite faces of a cell membrane colocalize is unknown. One proposed mechanism is based on the coupling of lipid compositions in one leaflet to compositions in the opposite leaflet (2, 3, 4, 5, 6, 7, 8).

The surface of a cell membrane is heterogeneous and the overall lipid compositions of the cytoplasmic and extracellular leaflets differ (1, 9). A wide variety of model membrane systems exhibit lipid compositional heterogeneity and are accessible to biophysical experiments. Within giant unilamellar vesicles (GUVs), demixing of lipids in the plane of the membrane occurs over a broad range of compositions and temperatures (Fig. 1 A) (10, 11). The resulting two coexisting liquid phases are termed liquid-ordered (Lo) and liquid-disordered (Ld).

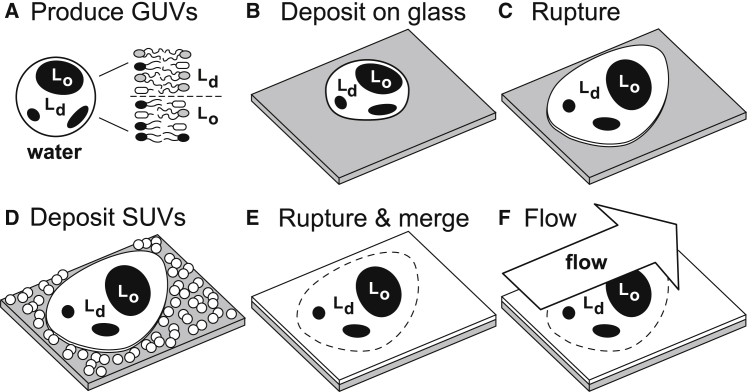
Figure 1.

Supported lipid bilayer containing micron-scale Lo domains. Giant unilamellar vesicles, GUVs, in water (A) are deposited on a glass substrate (B), where they rupture (C). Next, small unilamellar vesicles, SUVs, are deposited (D). The SUVs rupture and merge with the ruptured GUVs to form a single layer (E). Flow of the solution above the lipids imparts shear (F).

Coupling between liquid domains that lie in each of the two leaflets of a membrane is strong even in the absence of transbilayer proteins. Micron-scale Lo and Ld domains in one leaflet of a freestanding membrane have always been observed to be directly opposite (i.e., in registration with) domains of the same type in the opposite leaflet (12, 13). Moreover, phase separation in one leaflet can induce phase separation in an opposing leaflet that would not otherwise demix into Lo and Ld phases (14). Translating these qualitative descriptions into a quantitative explanation requires measurement of the transbilayer coupling parameter, Λ. This parameter is defined as the free energetic cost per unit area of misregistered domains in the two leaflets. We know of no previous measurements of Λ. The absence of thermally driven, optically observable (micron-scale) misregistration of domains gives a weak constraint of Λ > 10⁻⁸ k_BT/nm² (15).

Theoretical predictions for the transbilayer coupling parameter vary widely, from 0.01 k_BT/nm² to 0.5 k_BT/nm² (15, 16, 17), and molecular dynamics simulations yield values of 0.1 k_BT/nm² in lipid bilayers and 2 k_BT/nm² in polymer bilayers (18, 19, 20). Further theoretical work has explored how the value of Λ determines the degree of colocalization between lateral heterogeneity in leaflets with different compositions (15, 21, 22, 23, 24).

Here, we measure Λ by applying hydrodynamic shear stress, referred to here as “shear”. We determine how much shear we must apply to membranes on a solid support to move domains in one leaflet out of registry with domains in the other (Figs. 1 and 2). To controllably apply shear, we modify the method of Jönsson et al. (25) of introducing hydrodynamic flow over a supported bilayer in a microfluidic channel, as in Fig. 2. When exposed to shear above a cutoff value, the upper monolayer leaflet moves over the lower leaflet, which has velocity ∼0 (Fig. 2 B) (25), in agreement with previous reports (12, 13).

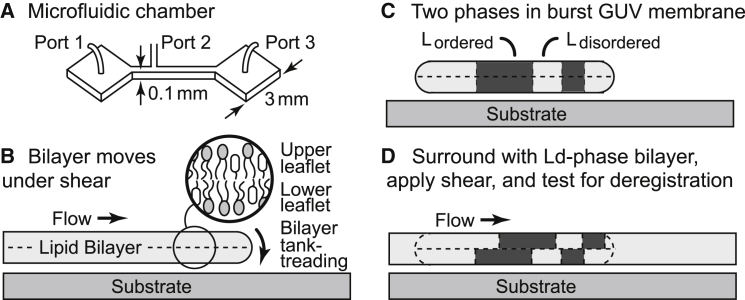
Figure 2.

Experimental system. (A) Hydrodynamic flow is achieved by pumping fluid through a microfluidic channel. (B) A supported bilayer under flow moves in a tank-treading motion (25, 26). (C) Lo and Ld phases from a GUV are retained when the GUV is ruptured to form a supported bilayer. (D) All remaining bare substrate is covered with a bilayer of the same Ld phase, and shear is applied.

In this article, we show that when we apply low shear to supported bilayers containing Lo domains within a background Ld phase, the domains remain stationary while the Ld phase moves around them. We find that when we increase shear to a value above a threshold, Lo domains in the upper leaflet move (Fig. 2 D and Fig. S1 in the Supporting Material). Next, we develop a model that relates the interleaflet domain coupling parameter to the threshold shear. Applying this model to our data yields Λ = 0.016 ± 0.004 k_BT/nm², consistent with a prediction of Λ of 0.01–0.03 k_BT/nm² by Putzel et al. (15).

The use of supported bilayers is necessary in this measurement because the magnitude of coupling between domains in the two leaflets is high. Strong interactions between the substrate and the lower leaflet are required to hold the lower leaflet stationary while the upper leaflet is displaced by shear. Geometries in which the bilayer is not strongly attached to a surface fail in tests to deregister leaflet domains via shear. In all of these previous experiments, domains in both leaflets move in registry for all values of shear that have been applied. The previous experimental systems include giant unilamellar vesicles (27), stacked bilayers (28), and black lipid membranes supported across a circular hole in a thin partition (our laboratory). For the system of supported bilayers used here, theoretical arguments convincingly describe how a hydrodynamic coupling between the lower leaflet and the substrate hinders collective motion of lipids (29). For a 10 μm domain in a supported bilayer 1 nm from the substrate (30, 31), the effective friction due to this coupling is ∼10³ times stronger than the frictional coupling between the lower leaflet and the top leaflet, implying that domains in the lower leaflet remain effectively stationary.

Because the domains that we seek to decouple are micron-scale, a distinction must be made between the movement of individual, nanometer-scale lipids and the collective motion of all lipids that constitute a micron-scale domain. Individual lipids are free to move. Diffusion coefficients for individual lipids moving in the upper and lower leaflets of the membrane have been measured to be the same within experimental uncertainty (32), or at least within a factor of 2 (33, 34). In contrast, large-scale movement is hindered (29). For example, on experimental timescales, large domains within single-layer supported bilayers in direct contact with a substrate not observed to diffuse (12, 13, 35). In our system of supported bilayers under shear, the lower leaflet has a velocity of zero even when the top leaflet is flowing (25). In both of these examples, the collective motion of lipids is hindered even when fluorescence recovery after photobleaching of dye-labeled lipids demonstrates that individual lipids diffuse freely in the plane of the bilayer (12, 35, 36).

Materials and Methods

Chemicals

DiPhyPC (1,2-diphytanoyl-sn-glycero-3-phosphocholine), DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine), POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine), and DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) were obtained from Avanti Polar Lipids (Alabaster, AL). Cholesterol was obtained from Sigma-Aldrich (St. Louis, MO). All lipids were used without further purification and were stored in chloroform at 20°C until use. TR-DPPE (Texas Red 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine) from Invitrogen (Eugene, OR) was included at 0.8 mol % as a dye for contrast between phases in fluorescence experiments. All water was filtered by a Barnstead filtration system (Barnstead Lab Water Products, http://www.barnstead-water.com) to a final conductivity of 18 MΩ cm. All other chemicals were obtained from Sigma-Aldrich.

Producing vesicles

We produced GUVs by electroformation as in Blosser et al. (37). Briefly, 0.25 mg of lipids, in a mixture of 29.2/32.4/28.4 DiPhyPC/DPPC/chol in chloroform, was spread on to a clean, ITO-coated glass slide (Delta Technologies, Loveland, CO) at 60°C, which is above the gel-liquid melting transition of all lipids used here. Slides were dried under vacuum for >30 min, then assembled face-to-face to form a capacitor. The interior of the capacitor was hydrated with ∼300 μL of aqueous 200 mM sucrose and the edges were sealed with vacuum grease. A square wave potential was applied with an amplitude of 1.5 V and a frequency of 10 Hz. The resulting solution of GUVs was transferred from the capacitor to a glass test tube, sealed, and stored at 60°C until use. GUV solutions were not filtered or purified in any way. Vesicles were used and imaged within 4 h of production, which entailed diluting GUV solutions into a solution of 200 mM glucose and 5 mM CaCl₂ to induce sedimentation to the solid support and subsequent rupture. All transfers of GUV solutions were performed by slow, gentle manipulation of a syringe with a wide-bore, 22-gauge needle. The variation in lipid composition from vesicle-to-vesicle has been estimated to be <2 mol % (11).

We produced small unilamellar vesicles (SUVs) by bath sonication as in Pitcher and Huestis (38). Briefly, 0.5 mg of lipids in chloroform were dried under nitrogen in a clean glass test tube, and further dried under vacuum for >30 min. The dried lipid film was hydrated in 1 mL of a buffer of 150 mM NaCl, 10 mM HEPES, and 1 mM EDTA at pH 8.0. This buffer was used for all further steps, including the application of hydrodynamic shear. The lipid solution was briefly vortexed and placed in a bath sonicator (SharperTek, Detroit, MI) for 2 h to create SUVs. The vesicle solution was then centrifuged for 5 min and decanted to leave behind any remaining large aggregates. For experiments involving phase-separated supported membranes, SUVs were produced from a mixture of 68/16.4/15.6/0.8 DiPhyPC/DPPC/chol/Texas Red DPPE. This composition was chosen because it is the mole ratio of lipids in the majority phase of the GUVs. In other words, within a Gibbs ternary phase diagram, this composition is the end-point of the tie line that passes through the point representing the overall lipid composition of which GUVs were produced (39). By choosing the composition of SUVs to lie at a tie-line endpoint, we ensure that the composition of the Lo and Ld phases in the ruptured GUVs will not change when we introduce SUVs, no matter what fraction of the final, merged supported bilayer originated in SUVs. For experiments that did not involve phase-separated membranes, SUVs were made from a mixture of 99.2:0.8 bulk phospholipid/Texas Red DPPE.

Fabricating channels

We produced PDMS (polydimethylsiloxane) microfluidic channels with rectangular cross sections. The channels were arranged in a T-shape using replica molding as in Jönsson et al. (25). Briefly, the master mold was made from SU8 2075 (MicroChem, Newton, MA), which was spun to a thickness of ∼100 μm, and was exposed to ultraviolet light through a high-resolution mask. PDMS replicas were made with a 10:1 mixture of Sylgard 184 to curing agent (Dow Corning, Midland, MI), and were cured at 60–75°C for at least 1 h. Access holes were made with a 0.75 mm Uni-Core punch (Ted Pella, Redding, CA).

Immediately before each experiment, glass slides (Menzel-Gläser, Braunschweig, Germany) were cleaned by boiling in a 2:1 mixture of water to 7× detergent (ICN Biomedical, Aurora, OH), thoroughly rinsing in water, and drying under nitrogen. The surface of the cured PDMS was cleaned with Magic Tape (3M, St. Paul, MN). Then, to create a more hydrophilic surface, the PDMS was plasma-cleaned (Harrick Plasma, Ithaca, NY) for 45 s. The PDMS was then immediately sealed to a clean glass slide to create a channel. To prevent leakage of fluid at high flow rates, the channel assembly was gently compressed in a home-built clamp consisting of parallel aluminum plates with optical and fluidic access. The interior volume of the channel was connected to Tygon tubing (Saint-Gobain Performance Plastics, Puyallup, WA) via 22-gauge dispensing needles inserted into access ports with no adhesive. The tubing was connected to a syringe in a syringe pump (Harvard Apparatus, Cambridge, MA). Each channel was used immediately after fabrication.

Forming supported lipid bilayers

Supported lipid bilayers without phase-separated domains were formed from SUVs. SUVs were flowed through Port 1 of the channel (as defined in Fig. 2 A) at a rate of 12 μL/min for 15 min. The resulting supported lipid bilayer was rinsed with buffer at a rate of 120 μL/min for 10 min to remove excess SUVs. To create a sharp edge of the supported lipid bilayer (Fig. S2), buffer without vesicles was flowed through the opposing arm (Port 3) of the channel, with the vesicle and buffer solutions both exiting from a channel perpendicular to the others (Port 2). To form bilayers with micron-scale domains, GUVs were added to the chamber and allowed to sediment and rupture over a period of ∼10 min. SUVs were then added and rinsed as above, except that no sharp bilayer edge was formed.

Imaging

Epifluorescence microscopy was performed with a 40× objective on a microscope (Nikon, Melville, NY) with a Coolsnap HQ charge-coupled device camera (Photometrics, Tucson, AZ). All image analysis was performed using ImageJ (public domain http://rsbweb.nih.gov/ij/). The areas of domains were determined by using ImageJ’s threshold function within a user-defined boundary around each individual domain. Area fractions were determined by measuring the area of all domains in 10 ruptured vesicles of the same composition.

Measuring interleaflet friction

To measure the interleaflet friction, we tracked the movement of the edge of a supported lipid bilayer formed from ruptured SUVs. The supported lipid bilayer tanktreads under shear (25). The leading edge was determined using ImageJ’s edge finding algorithm, as in Fig. S2. Movement at a given shear was tracked for at least 5 min, and the linear, late time behavior was fit with a line (see later in Fig. 4). To verify that the history of the bilayer (namely the time elapsed and the total distance moved) did not affect our results, we exposed a bilayer to a sequence of low shear, then high shear, then low shear. We found that the movement at low shear was unchanged by the intervening high shear. At long times, on the order of hours, defects appeared in the bilayer as the interface became unstable and the rate of movement changed. Consequently, data after the appearance of defects were discarded.

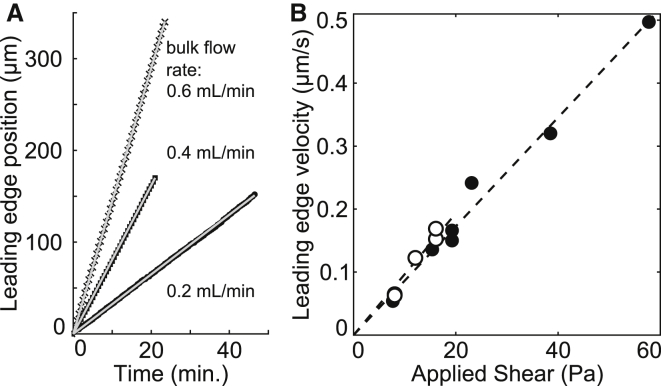
Figure 4.

Smooth flow achieved at the leading edge of tank-treading unilamellar supported bilayers subjected to shear as in Fig. 2B. (A) Position of the leading edge of a POPC bilayer through time for three bulk flow rates. Linear fits are overlaid on experimental data points. (B) Velocity of the bilayer’s leading edge as a function of shear. The velocity was determined from the slope of tracks as in (A), and the shear was calculated as outlined in the Supporting Material). Uncertainty due to the fit alone is less than the size of the symbols. (Solid circles) POPC bilayers and (open circles) DOPC bilayers, delaminated at applied shears of ∼20 Pa, limiting the range of data. Below an applied shear of ∼3 Pa, DOPC bilayers do not display tank-treading motion, indicating the presence of static friction.

Measuring threshold shear

To measure the threshold shear at which domains move out of registry, supported lipid bilayers containing micron-scale domains were formed as described above. Shear was applied for at least 7 min. After the first 2 min, the bilayer was imaged every 30 s. Domains were classified as either moving or stationary. Domains were considered stationary if the front edge moved <1 μm over 5 min. The shear was then increased in a stepwise fashion (typically ∼10 Pa/step) and the process repeated until all domains were observed to move. For each domain, we recorded the highest domain shear at which the domain remained stationary and the lowest shear at which the domain moved. All domains that were completely contained in the field of view, remained intact before moving, and moved at an experimentally obtainable shear, were analyzed.

Results

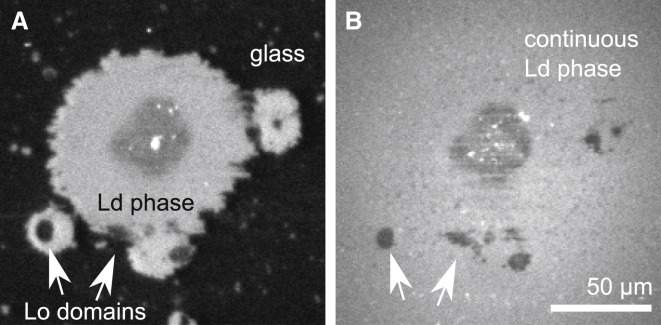
To create a single supported bilayer containing micron-scale domains, we introduced a method of rupturing GUVs containing micron-scale domains of the Lo and the Ld phases onto glass and then covering the remaining glass substrate with ruptured SUVs as in Fig. 1. This method modifies previous protocols of backfilling bilayers formed by microcontact printing (26, 40), and avoids pinning artifacts at bilayer edges as in Fig. S3. The controls shown in Figs. 3 and S4 demonstrate that lipids freely diffuse between supported bilayer regions formed from ruptured GUVs and neighboring regions formed from ruptured SUVs. This result confirms that the entire bilayer is continuous.

Figure 3.

Formation of a single continuous supported bilayer. (A) Labeled GUVs ruptured on a glass substrate. The rupturing process distorts domains into noncircular shapes that are prevented from relaxing by substrate interactions (29). Unlabeled SUVs were then introduced, which ruptured to cover all remaining bare areas of the substrate. (B) After 15 min, the fluorescently labeled lipids that were originally associated with only the GUVs have diffused throughout the entire field of view of the newly formed bilayers. This process is explicitly documented in Fig. S4.

As a control for our ability to apply a shear of known value, we sheared a uniform supported bilayer in a glass-bottomed microfluidic channel of PDMS (Figs. S2 and S5). We verified the value of the applied shear by measuring the interleaflet friction as previously reported in Jönsson et al. (36). In the absence of obstacles and above a cutoff value due to static friction, an applied shear τ results in a constant, uniform velocity of the upper leaflet, ν₀. Above the cutoff, the dominant term influencing the velocity is interleaflet friction (25). The coefficient of dynamic friction, b_d, is defined by τ = b_dν₀. We determined v₀ by measuring the trajectory of the front edge of the bilayer, which moves at half the average velocity of the top leaflet. The data in Fig. 4 give b_d = (5.8 ± 0.8)·10⁷ Pa s/m for bilayers of POPC (palmitoyloleoyl-phosphatidylcholine) lipids and b_d = (5.2 ± 0.4)·10⁷ Pa s/m for bilayers of DOPC (dioleoyl-phosphatidylcholine). These values agree with reported values of b_d = 2.4·10⁷ Pa s/m in a similar measurement of egg-phosphatidylcholine (36), and with values between 10⁷ and 10⁹ Pa s/m obtained using different methods (41, 42, 43, 44, 45). To test that the bilayer motion is independent of specific interactions between the bottom leaflet and the substrate, we repeated the experiments in Fig. 4 using POPC bilayers on two new substrates of different surface roughness: silicon wafers and PDMS. As expected, bilayer velocities on all three substrates were indistinguishable.

We find that at shears below a cutoff of ∼3 Pa, the single-component supported bilayers in Fig. 4 do not move. This implies the existence of a static friction that is independent of velocity at low shears. Above 3 Pa, the motion of tanktreading membranes is described solely by the dynamic friction, i.e., the data in Fig. 4 B are well fit by a straight line with an x-intercept of zero. In the next section, the presence of static friction is readily accounted for in the derivation of the threshold shear required to deregister domains of a particular size. This derivation enables the measurement of the interleaflet domain coupling parameter Λ using supported bilayers.

Our central experimental result is that domains in the upper leaflet of supported lipid bilayers move out of registry with domains in the lower leaflet when subjected to shear above a threshold that is linearly related to domain inverse length (Figs. 5 and 6). At the lowest values of shear, all Lo domains are stationary while the surrounding Ld phase bilayer advances in the direction of the shear (Fig. S1). At intermediate values of shear, a single membrane contains both large, mobile domains and small, immobile domains. We directly observe misregistered domains, characterized by three distinct fluorescence levels, infrequently (Fig. S6). In most experiments, only two fluorescence levels are observed (as in Fig. 5) because the membrane is labeled with charged and bulky fluorophores that likely partition predominantly to the upper leaflet, as has been previously reported for charged lipids on glass substrates (45) and for fluorescently labeled lipids in microfluidic devices (25, 46). In these cases, we infer domain deregistration from domain movement, and our resulting data are consistent with data from systems in which we observe three distinct fluorescence levels. Slight variations in substrate preparation likely account for variations in labeling of the lower leaflet.

Figure 5.

Movement of membrane domains from left to right under solvent flow rates of 0.44 mL/min (top row, corresponding to 17 Pa shear at the center of the image), and 0.66 mL/min (middle row, corresponding to 25 Pa). The large starred domain moves at both flow rates. The bottom row shows a domain in the upper leaflet moving out of registry with a stationary domain in the unlabeled lower leaflet, under a flow of 0.66 mL/min. The same domain was stationary at 0.44 mL/min.

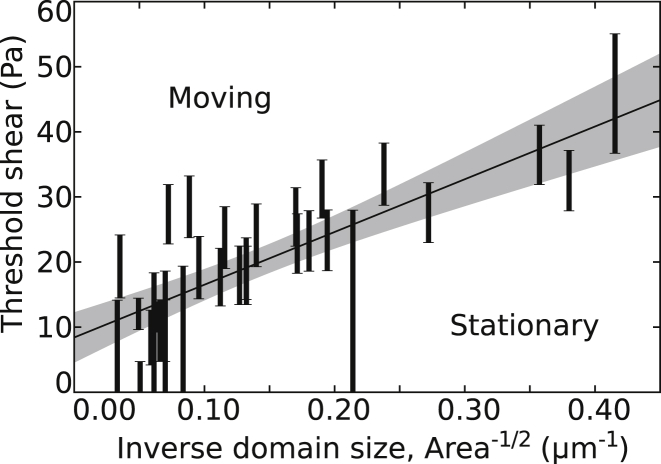
Figure 6.

Threshold shear required to move Lo domains in the upper leaflet of a supported bilayer as a function of the inverse domain length scale, $1/\sqrt{\text{Area}}$. Each bar demarks the entire range of data consistent with observations of a single domain. The bottom of a bar corresponds to the highest shear at which the domain was observed to be stationary, and the top of the bar corresponds to the lowest shear at which the domain was observed to move. Shear was increased in steps of typically ∼10 Pa and was calculated as outlined in the Supporting Material. (Solid line) Best linear fit; (shaded area) 2σ confidence interval.

Fig. 6 quantifies threshold shears required to deregister domains versus the inverse length $=1/\sqrt{\text{Area}}$. A linear fit yields a slope of 81 ± 22 Pa μm (47). We use this result in the next section to obtain a value of the interleaflet domain coupling parameter Λ. We measured threshold shears at which domains first began to move, rather than extended trajectories of domains, for several reasons: 1) Shapes and overlap areas of moving domains change through time. 2) Domain movement is accompanied by the development of membrane defects, identified as small-scale speckles. 3) Domains displaced under shear do not return to their original positions when shear ceases (Fig. S7); this observation is consistent with reports that micron-scale domains in opposing monolayers fail to register when in close proximity to a substrate (12, 13), and is further evidence for the presence of static friction. 4) Occasionally, domains disappear under shear (Fig. S8). One possible reason for this behavior is that misregistered domains constitute asymmetric bilayers in which a single membrane phase is a lower energy state than coexisting membrane phases (14, 15, 16, 17). Another possible reason is that the lipid composition of a moving domain changes through advection of lipids, until the composition is no longer in a two-phase region of the phase diagram. One more possibility is that a hole in the membrane is misidentified as a domain, and that this hole fills as the membrane is sheared. All data from domains that disappeared were discarded. In several cases, domains were irregularly shaped (meaning that they contained smaller domains of the majority phase, their boundaries were not smooth, and/or their overall shapes were nonconvex). The starred domain in Fig. 5 is an extreme example. To avoid bias due to subjective determinations of which domains were excluded, all domains were included in the analysis. The data points corresponding to domains with the most irregular shapes, chosen by eye, are highlighted in Fig. S9. Excluding these data from the analysis has a statistically insignificant effect on the measured slope, changing it from 81 ± 22 to 79 ± 23 Pa μm. This implies that domain shape does not significantly affect our measurement of Λ.

Derivation of threshold shear

Here we derive analytical formulas to predict the threshold applied shear τ at which circular Lo domains deregister as a function of Λ and domain length scale. We use these formulas to extract a value of Λ. We consider only the forces acting directly on a single circular domain in the upper leaflet, and only when that domain remains stationary, with the surrounding Ld membrane flowing around it. The presence of other domains is accounted for within an effective medium approach, yielding a small correction to the force acting on an isolated domain; that correction depends on the area fraction of Lo domains.

Given these conditions, four forces act on a stationary domain in the upper leaflet of a membrane under shear. 1) F_shear arises from the externally applied shear, 2) F_drag arises from hydrodynamic drag due to perturbation of the upper leaflet flow field, 3) F_frict arises from static friction between leaflets, and 4) F_reg arises from transbilayer coupling favoring domain registration. The two driving terms (F_shear and F_drag, explained schematically in Fig. S1) are proportional to τ, whereas the two restoring terms (F_frict and F_reg) are independent of τ. Hence, for sufficiently large τ, the driving forces overcome the restoring forces and domain registry can no longer be sustained.

The four forces on a circular domain of radius R in the upper leaflet are written in closed form as follows. When the upper leaflet is moving at velocity ν₀, the domain experiences a direct shear force from the solvent of

$$F_{\text{shear}}=\pi R^2\tau .$$ (1)

The forces due to drag within a leaflet and due to static friction between leaflets are

$$F_{\text{drag}}={\lambda }_T{\nu }_0=\pi R^2\tau /\left(1-\varphi \right)$$ (2)

$$F_{\text{frict}}=-b_s\pi R^2,$$ (3)

where the drag coefficient λ_T = πR²b_d/(1−ϕ) is derived in the Supporting Material, b_s is the static friction coefficient, and ϕ denotes the area fraction of the Lo phase. The friction experienced by the domain is determined by the static friction because the domain is stationary, whereas the drag force is determined by the dynamic friction of the surrounding, mobile phase. If domains in the upper and lower leaflets are offset by a distance a ≤ 2R, then the area of domain overlap, A_overlap, is

$$A_{\text{overlap}}=2R^2{\text{cos}}^{-1}\left(a/2R\right)-aR\sqrt{1-{\left(\frac{a}{2R}\right)}^2}.$$ (4)

The force due to interleaflet coupling, F_reg, is derived from the registration energy

$$E_{\text{reg}}=2\Lambda \left(\pi R^2-A_{\text{overlap}}\right)$$ (5)

as

$$F_{\text{reg}}=-\frac{\partial E_{\text{reg}}}{\partial a}=-4\Lambda R\sqrt{1-{\left(\frac{a}{2R}\right)}^2}\Theta \left(\left|a\right|/d_0\right),$$ (6)

where d₀ is the capillary length (i.e., the compositional interface width, d₀ << R) and Θ(u) denotes a smooth step function with Θ(0) = 0 and Θ(u) → 1 for u ≳ 1. The step function ensures that F_reg vanishes at perfect overlap.

Balancing these four forces yields the threshold applied shear at which domains deregister. This result holds in the absence of diffusive fluxes, as would apply to gel-phase domains. The net force on a domain in the upper leaflet is

$$F_{\text{net}}=F_{\text{shear}}+F_{\text{drag}}+F_{\text{frict}}+F_{\text{reg}}$$ (7)

$$=\pi R^2\tau \left(2+\frac{\varphi }{1-\varphi }\right)-b_s\pi R^2-4\Lambda R\sqrt{1-{\left(\frac{a}{2R}\right)}^2}\Theta \left(\left|a\right|/d_0\right).$$ (8)

When the driving force $F_{\text{shear}}+F_{\text{drag}}=\pi R^2\tau \left(2+\left(\varphi /1-\varphi \right)\right)$ exceeds the maximum restoring force F_frict + F_reg, gel domains deregister. This condition is met when the applied shear τ is >τ_gel, where $\pi R^2{\tau }_{\text{gel}}\left(2+\left(\varphi /1-\varphi \right)\right)-b_s\pi R^2-4\Lambda R=0$, or

$${\tau }_{\text{gel}}=\frac{b_s}{\left(2+\frac{\varphi }{1-\varphi }\right)}+\frac{4\Lambda }{\pi R\left(2+\frac{\varphi }{1-\varphi }\right)}.$$ (9)

Equation 9 is the first result of this analysis. The 1/R behavior of τ_gel implies that large domains deregister under lower shear than small domains do. This counterintuitive result arises because the registration force scales as R, whereas all other forces scale as R².

To calculate the threshold shear required to deregister liquid domains (as opposed to gel-phase domains), we recast the force balance argument above as a velocity condition to account for diffusive terms. Analogous to a person walking on a treadmill, who appears stationary in the lab frame, domain registration is sustained when the velocity of domain relative to the substrate vanishes; that is

$${\nu }_0+{\nu }_{\text{rel}}=0,$$ (10)

where ν_rel denotes the velocity of the mobile domain with respect of the immobile one. The value ν_rel, which quantifies the rate at which two partially overlapping domains in the absence of external shear achieve perfect overlap (48), contains terms due to advective and diffusive fluxes such that ν_rel = ν_adv + ν_diff. In the absence of diffusion, combining the force balance argument of Eq. 7 with F_drag = λ_Tν₀ yields

$${\nu }_0+\frac{1}{{\lambda }_T}\left(F_{\text{shear}}+F_{\text{reg}}+F_{\text{frict}}\right)=0$$ (11)

such that ${\nu }_{\text{adv}}\equiv \left(1/{\lambda }_T\right)\left(F_{\text{shear}}+F_{\text{reg}}+F_{\text{frict}}\right)$.

Nonzero diffusive lipid fluxes emerge when domains partially deregister due to chemical potential gradients acting across the domain. To account for these fluxes, we extend our previous calculation of the relative velocity of two monolayer domains approaching from opposite directions due to diffusive transport alone (49, 50). When only the upper monolayer domain is mobile, ν_diff = (2d₀DF_reg)/(πR²σ), where D is the lipid diffusivity and σ is the interfacial line tension. Using this diffusive part of ν_rel in Eq. 10 together with the advective velocity from Eq. 11 gives the condition for sustained registry of liquid domains as

$${\nu }_0+\frac{1}{{\lambda }_T}\left(F_{\text{shear}}+F_{\text{reg}}+F_{\text{frict}}\right)+\frac{2d_{0}D{F}_{\text{reg}}}{\pi R^2\sigma }=0.$$ (12)

Applying ${\lambda }_T=\pi R^2{b}_d\left(1+\left(\varphi /1-\varphi \right)\right)$, F_frict = −b_sπR², and F_shear = πR²τ = πR²b_dν₀ yields

$$\left(2+\frac{\varphi }{1-\varphi }\right){\nu }_0-\frac{b_s}{b_d}+\frac{F_{\text{reg}}}{\pi R^2}\left[\frac{1}{b_d}+\frac{2d_{0}D}{\sigma }\left(1+\frac{\varphi }{1-\varphi }\right)\right]=0.$$ (13)

Given that τ = b_dν₀ and |F_reg| reaches a maximum value of −4ΛR when d₀ ≲ a ≪ R, the threshold shear for deregistering liquid domains in the upper and lower leaflets becomes

$${\tau }_{\text{liquid}}=\frac{b_s}{\left(2+\frac{\varphi }{1-\varphi }\right)}+\frac{4\Lambda }{\pi R\left(2+\frac{\varphi }{1-\varphi }\right)}\left[1+\frac{2d_{0}D{b}_d}{\sigma }\left(1+\frac{\varphi }{1-\varphi }\right)\right].$$ (14)

Equation 14 presents a closed-form expression for the threshold membrane shear required to deregister liquid domains in a bilayer. An earlier form of this derivation appears in Han (50). As in Eq. 9 for τ_gel, τ_liquid displays a 1/R domain length dependence. The expressions for τ_gel and τ_liquid coincide when the dimensionless diffusive transport term 2d₀Db_d/σ is eliminated by setting D = 0. Characteristic values of d₀ = 10⁻⁹ m, D = 10⁻¹² m² s⁻¹, b_d = 10⁸ Pa s/m, and σ = 10⁻¹² N (48), yield a value of 2d₀Db_d/σ ∼ 0.2.

Recasting Eq. 14 in the form of τ = slope 1/R + intercept for comparison with the fit in Fig. 6 yields Λ = 0.016 ± 0.004 k_BT/nm² and highlights that liquid bilayers on solid surfaces experience a nonzero static coefficient of friction of b_s = 22 ± 11 Pa. This value of Λ is robust; even if the true value of 2d₀Db_d/σ is an order-of-magnitude higher, our value of Λ would change only by order 1, and if the true value is an order-of-magnitude lower, our result would change by no more than 20%. For details of the preceding derivation, see Han (50). Our estimate of Λ includes a correction for the area fraction ϕ, measured to be 0.28 ± 0.05. This density of domains increases Λ by ∼10%, less than the statistical uncertainty in Λ.

Discussion

Our measured value of Λ = 0.016 ± 0.004 k_BT/nm² is consistent with the prediction of Λ = 0.01–0.03 k_BT/nm² by Putzel et al. (15), and is inconsistent with predictions of ∼0.1 k_BT/nm², 0.15 k_BT/nm², and 0.5 k_BT/nm² (16, 17, 18). To avoid confusion by a well-read audience, we note that the symbol Λ has been defined here and in other works in the literature as the compositional interleaflet coupling parameter in units of k_BT/nm², whereas some other authors define Λ as the interleaflet friction with units of Pa s/m (51), which we denote here as b_d. Our measured value of Λ is in agreement with previous qualitative reports of strong interleaflet coupling. For example, demixing of one leaflet of an asymmetric unsupported bilayer into coexisting Lo and Ld phases can induce demixing in an opposing leaflet that would not otherwise phase-separate (14).

Scatter that appears within the data in Fig. 6 could arise from multiple sources, including the spatial distribution and shape of domains. Our model assumes isolated domains for simplicity. In contrast, our experiments investigate a field of domains that may experience changes in intraleaflet drag as neighboring domains alter the flow field. Regarding the shape of domains, our choice of $\sqrt{\text{Area}}$ as the domain length scale does not significantly affect our results. An alternate length scale, namely area divided by the length perpendicular to the direction of flow, yields Λ = 0.013 ± 0.008 k_BT/nm², which is within uncertainty of our reported value. The ability of a domain to change shape is predicted to have only a weak effect on domain registration ((49, 50) and M. Haataja and H. A. Stone, unpublished data).

As noted in the Introduction, we know of no bilayer geometry other than a supported bilayer in which measurement of Λ is possible. Therefore, it is important to consider how Λ measured in a supported bilayer may differ from Λ measured in the canonical system of a membrane of a taut GUV far from a surface. We consider five effects: 1) lipid mobility, 2) membrane average shape, 3) membrane fluctuations, 4) lipid headgroup alignment, and 5) shifts in membrane composition. We expect that none of these effects will alter the value of Λ significantly, and we discuss each in turn below.

On experimental timescales, large, noncircular domains within supported bilayers did not diffuse and did not become round, in agreement with previous results (12, 13, 35). The long timescale in this system arises from two effects. The first is that collective motion of lipids within supported bilayers is hindered by hydrodynamic interactions (29). These hydrodynamic interactions should not affect the molecular-scale interleaflet interactions that give rise to Λ. It is clear that hydrodynamic effects are not the only impediment to lipid mobility in our supported bilayers because the timescale over which diffusion of individual lipids should lead to relaxation of a noncircular domain is ∼R³/(d₀D) ∼ 10³ s (17 min), which is roughly our experimental timescale. Here, R ∼ 5 × 10⁻⁶ m is the typical linear dimension of a domain in our experiments, d₀ ∼ 10⁻⁸ m is the capillary length, and D ∼ 10⁻¹² m²/s is the lipid diffusivity (52).

The second effect arises from strong local interactions between the membrane and the substrate, for example from pinning. Similar interactions have been documented even when bilayers are deposited on mica (which is ideally atomically flat), and were observed to increase with the roughness of the mica (53). In a system like ours, it has been estimated that pinning renders ∼0.1–1% of all lipids immobile (36, 54). We deposit vesicles on glass surfaces, and each surface may present a different local density of membrane pinning sites. Nevertheless, changes in the overall, average density of pinning sites do not affect our measured value of Λ because the pinning force would scale with domain area, as applied shear does. We speculate that pinning, even by a very small fraction of lipids, is the source of the static friction term observed at low values of shear. In the section on the derivation of threshold shear, the presence of static friction was accounted for, enabling the measurement of Λ. Noncircular domain shapes can be handled perturbatively (M. Haataja and H. A. Stone, unpublished data).

We expect no significant difference in Λ between supported bilayers and taut GUVs due to average membrane shape, because in both systems the average radius of curvature is large. In our system of a supported bilayer, it is infinite. For free-floating, taut GUVs, the membrane’s average radius of curvature is typically >10 μm, orders of magnitude larger than the nanometer-scale thickness of the bilayer.

Next, we discuss why consideration of membrane shape in the context of bending energy and domain size is unnecessary in our system. First, a typical value for the total bending energy of a GUV is ∼10⁻⁸ k_BT/nm² (55), orders of magnitude less than our measured value of the interleaflet coupling. Second, we observe micron-scale domains. Together, these attributes of our membranes mean that we can disregard how membrane bending properties have been proposed to affect miscibility phase separation, particularly the composition in apposing leaflets, favoring antiregistration (56, 57, 58). We may also disregard predictions by molecular dynamics simulations that nanometer-scale domains (as opposed to the micron-scale domains we observe) antiregister, implying a negative value of Λ (59). Bending may also occur within each monolayer leaflet of the membrane. The membrane deforms at the nanoscopic interface between Lo and Ld phases to accommodate the height mismatch, and this deformation contributes to the line tension (60). According to a recent model (61), this line tension is minimized when domains are in registry. This interaction would give rise to a registration force that maintains domain registration with the same dependence on R as Eq. 6. This new model differs from the one that we present in that the registration force vanishes when domains are displaced by only ∼20 nm. In contrast, in our model, the registration force is nonzero under this condition; domains would return to registry in the absence of static friction. Our experimental results do not distinguish between the two models, and may reflect contributions from both mechanisms.

Membrane height fluctuations exist in even taut GUVs. These fluctuations are suppressed as tension is applied to the membrane (62). Deposition of a membrane on a surface eliminates membrane height fluctuations. We expect this phenomenon to have a minor effect on the lipid interactions at the midplane because the application of tension to membranes has a minor effect on the membrane’s miscibility transition temperature, ∼1°C m/mN (63). It has been suggested that in addition to direct interactions between leaflets, the entropic favorability of height fluctuations causes stiffer regions to move into registry (64). This effect does not occur in membranes in which height fluctuations are suppressed, such as membranes under tension or in contact with a substrate. Existing theoretical work that predicts values of Λ focuses on interleaflet coupling in membranes that do not exhibit height fluctuations (15, 17), and our results are most appropriate for comparison to such theories. In fluctuating membranes, we would expect the value of Λ to be higher. An advantage of our system is that the entire supported membrane experiences a suppression of height and curvature fluctuations. Previous studies on both intact GUVs and giant vesicles derived from plasma membranes resting on a substrate have found that the region of the membrane in contact with the substrate can experience phase separation, presumably due to adhesion and the suppression of fluctuations in that region (65, 66).

The issue of headgroup alignment arises because it is assumed that lipids in a free-floating, taut GUV are symmetrically distributed about the membrane midplane, so that any thickness mismatch between Lo and Ld phases is equally distributed on both leaflets of the bilayer. The alignment in supported bilayers is less clear. On one hand, Jensen et al. (28) and Nielsen and Simonsen (67) reported that the total thickness mismatch between Lo and Ld phases measured by ellipsometry on supported bilayers of 40:40:20 DOPC/DPPC/chol is at least twice the mismatch of only the upper leaflet of a supported bilayer measured by AFM (1.69 nm vs. 0.65 ± 0.02 nm). They concluded that the thickness mismatch of a supported bilayer is equally distributed on both membrane leaflets. On the other hand, Chen et al. (68) reported that the total thickness mismatch measured by x-ray diffraction of free-floating vesicles of the same composition (0.56 ± 0.2 nm) agrees with the mismatch found by AFM. This result leads to the opposite conclusion, that the thickness mismatch of a supported bilayer is accommodated only in the upper monolayer.

To minimize any shift in Λ due to a potential difference in the alignment of lipid headgroups, we chose phospholipids likely to produce approximately equal thicknesses of Lo and Ld phases. These lipids, DiPhyPC and DPPC, have equal numbers of carbons in the backbones of their acyl chains. We are unaware of any published thickness values for the Lo and Ld phases of the membranes we use. Thicknesses for pure and binary membranes are available (bilayers of pure DiPhyPC bilayers are 3.6 nm thick (69) and bilayers of primarily DPPC and cholesterol are 4.6 nm thick (68)), but these thicknesses are difficult to compare because cholesterol thickens phospholipid membranes (70). Another reason we chose lipids with the same length of acyl chains is that height mismatch between coexisting phases has been predicted to promote antiregistered phases (24).

We expect that the association of the entire membrane with the solid substrate results in only minor changes in lipid compositions of the Lo and Ld phases. For the lipid system used here, we measured a shift in miscibility temperature in free floating GUV membranes versus supported bilayers of <5°C, in line with other measurements of a shift in the main chain transition temperature of ≲2°C (71, 72). Additional evidence that the GUV’s composition does not significantly change when it is ruptured on the substrate is that the area fraction occupied by each phase is the same in GUVs and in the resulting supported bilayers (73). Changes in phase composition have been modeled as affecting interleaflet coupling only quadratically (17), meaning that small changes in membrane composition would only minimally alter interleaflet coupling.

Determining the mechanism of interleaflet coupling is beyond the scope of this work. Possible mechanisms include electrostatic interactions, cholesterol flip-flop, and/or lipid chain interdigitation. Estimates by May (17) conclude that the most significant energetic cost imposed by misregistration is due to a loss of acyl-chain entropy when chains interdigitate. In our study, we used lipids with equal chain lengths, which would minimize interdigitation. If interdigitation is a primary determinant of interleaflet coupling, we would expect that higher values of Λ would be found if our experiment were repeated using lipids with highly asymmetric acyl chains (74).

Our results are consistent with the theoretical work of Putzel et al. (15), who used a molecular model of a ternary system containing DPPC, DOPC, and cholesterol. Their model explicitly considers the configurational states of the hydrocarbon chains and mixing entropies of the lipids and cholesterol, and phenomenologically treats solvent and headgroup interactions. Based on their analysis, they argue that “…interleaflet coupling is not driven by a single property, such as configurational entropy or gauche bond energy, but rather by the complex interplay between these properties” (15). Thus, one might not expect simple order-of-magnitude arguments proposed earlier (16, 17) to yield quantitatively accurate estimates for Λ, and it is not clear whether interleaflet interactions between Lo domains, between Ld domains, or between Lo and Ld domains will dominate. In addition, Putzel et al. (15) have identified difficulties in extracting Λ from analysis of domain overlap area probability distributions obtained from molecular dynamics (or other particle-based) simulations (18, 19) due to the rather small system sizes that can be simulated at present and due to diffuse compositional interfaces.

Conclusions

We show that domains in the upper and lower leaflets of a supported lipid bilayer deregister under shear, and we measure the interleaflet coupling parameter Λ = 0.016 ± 0.004 k_BT/nm². This value is consistent with one theoretical model of registration, rules out others, and limits the parameter space for models of asymmetric bilayers. By systematically varying conditions, the method developed here can be used to further explore the physical mechanism and biological role of interleaflet coupling. We speculate that Λ is substantially larger in biological membranes containing lipids with different acyl-chain lengths and transmembrane proteins.

Author Contributions

M.C.B., A.R.H.-S., and S.L.K. designed the experiments; M.C.B. and A.R.H.-S. performed the experiments; T.H. and M.H. developed the theoretical framework; M.C.B. analyzed the results; and M.C.B. and S.L.K. wrote the article. All authors edited the article.

Editor: Heiko Heerklotz.

Supporting Citations

The references (75, 76, 77, 78) appear in the Supporting Material.