Intrinsic Stepwise Translocation of Stretched ssDNA in Graphene Nanopores

Abstract

We investigate by means of molecular dynamics simulations stretch-induced stepwise translocation of single-stranded DNA (ssDNA) through graphene nanopores. The intrinsic stepwise DNA motion, found to be largely independent of size and shape of the graphene nanopore, is brought about through alternating conformational changes between spontaneous adhesion of DNA bases to the rim of the graphene nanopore and unbinding due to mechanical force or electric field. The adhesion reduces the DNA bases’ vertical conformational fluctuations, facilitating base detection and recognition. A graphene membrane shaped as a quantum point contact permits, by means of transverse electronic conductance measurement, detection of the stepwise translocation of the DNA as predicted through quantum mechanical Green’s function-based transport calculations. The measurement scheme described opens a route to enhance the signal-to-noise ratio not only by slowing down DNA translocation to provide sufficient time for base recognition but also by stabilizing single DNA bases and, thereby, reducing thermal noise.

Nanopores hold great promise as next-generation sequencing devices to revolutionize conventional sequencing technology by eliminating the need for chemical labeling or sample amplification.¹⁻⁵ Although biological nanopores such as α-hemolysin^6,7 and MspA⁸⁻¹⁰ exhibit already great potential for DNA sequencing, there are drawbacks to biological pores, including fixed pore size and weak mechanical strength. Such drawbacks can be overcome by the use of solid-state nanopores.¹¹⁻¹⁴ Among various synthetic substrates for solid-state nanopores, layered materials such as graphene¹⁵⁻¹⁷ and MoS₂^18,19 have attracted particular attention because of their atomically thin layer that predisposes them to offer single-base resolution recognition. In typical nanopore sequencing experiments, DNA molecules are threaded through a nanopore under an applied voltage; an ionic current flowing through the nanopore alongside the DNA is observed and different transient dips due to different DNA nucleotides (ionic current blockade) are measured. Resolving the magnitude and duration of each dip permits one, in principle, to identify individual bases and, in turn, the sequence of DNA.

Experiments on DNA translocation through graphene nanopores have been successfully performed in 2010 by three independent groups.¹⁵⁻¹⁷ In parallel, molecular dynamics (MD) simulations, widely used in cell biology research,^20,21 were also adopted to characterize the ability of graphene nanopores to identify DNA sequences through ionic current measurement.²²⁻²⁵ MD simulations are capable of capturing atomic-scale details of the translocation dynamics of DNA as well as of DNA–nanopore interactions. For example, Liang et al.²⁶ addressed key factors in DNA sensing using graphene nanopores and quantified the relationship between ionic current blockade and occupied nanopore area during DNA translocation.

In the ionic current measurements discussed above, graphene merely serves as a passive membrane. However, first-principles calculations suggest another opportunity for graphene to detect DNA, namely through the transverse sheet current across graphene nanoribbons (GNRs) that can be directly measured.²⁷⁻²⁹ We showed previously that the sensitivity of GNR to translocating DNA can be drastically enhanced by tailoring the edge of the GNR into a quantum point contact geometry (QPC) or by tuning the carrier concentration in the GNR.³⁰ The GNR devices were found in simulations to be able to sensitively probe the helical geometry of double-stranded DNA (dsDNA),³⁰ the conformational transitions from helical to zipper form of dsDNA³¹ as well as the number of nucleotides in stretched ssDNA.³² A further advancement encouraging the use of graphene nanopores for DNA sequencing are actual experiments that have detected DNA permeation through a nanopore in GNRs by means of sheet current measurements³³ but have not yet resolved DNA nucleotide identity.

Despite intense research efforts, the identification of individual bases could not be achieved yet by means of graphene nanopores, mainly because DNA translocation through the pore is too fast and thermal motion of bases is too strong to permit individual bases to be resolved. Besides, the stochastic conformational fluctuations of DNA inside the pore also introduce significant noise on top of the measured signal.³⁴ Similar problems also arise for conventional solid-state nanopores. In an attempt to overcome these problems, a number of experimental and computational studies were carried out seeking reduction in nanopore size,³⁵ enhancement in solvent viscosity,³⁶⁻³⁸ and adjustment of surface charge density of the graphene membrane.³⁹

In the present study, we suggest an intrinsic stepwise translocation of ssDNA through graphene nanopores to improve the signal characteristics for DNA sequencing. We show that stepwise translocation can be achieved by mechanically stretching ssDNA to a straight ribbon as it passes through the nanopore. All-atom MD simulations capable of capturing the details of ssDNA translocation dynamics are combined with quantum mechanical nonequilibrium Green’s function-based transport calculations. The results show that a stepwise motion of ssDNA can be achieved and accurately probed by the sheet current, promising a strategy for resolving nucleotide identity.

Results and Discussion

We performed MD simulations as outlined in Methods to investigate translocation of stretched ssDNA through graphene nanopores. For this purpose, we carried out simulations for ssDNA with different DNA sequences as well as different pore sizes, pore shapes, membrane materials and DNA driving strategies. On the basis of the resulting MD trajectories, nonequilibrium transport calculations based on Green’s function were carried out to determine the associated electronic sheet current in the graphene layer during DNA translocation.

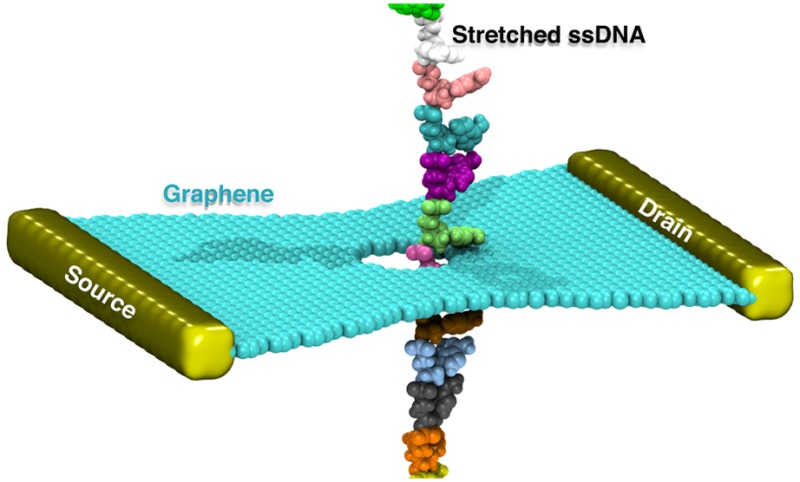
Figure 1a illustrates the simulation setup designed for the purpose of nanopore DNA sensing. A stretched ssDNA molecule, poly(dA), containing 14 adenine nucleotides with interbase spacing of 0.77 nm is seen to be threaded through a 1.6 nm diameter graphene nanopore. For the purpose of the simulations that require periodic boundary conditions for efficient calculation of electrostatic forces (see Methods), the ssDNA, at its two ends, was covalently bonded to it is periodic copies above and below to form an infinitely long periodic DNA strand.

Figure 1.

Molecular dynamics simulation of stretched poly(dA) ssDNA being threaded through a graphene nanopore. (a) Schematic of the system being simulated in this study. The system consists of a graphene monolayer and stretched ssDNA immersed in an electrolyte solution. ssDNA is here graphically represented through van der Waals (vdW) spheres, with each nucleotide colored differently; ions are represented as colored dots and aqueous solvent as a transparent medium. The system shown is periodically repeated along x, y, and z axes for the purpose of evaluating Coulomb interactions efficiently and for avoiding surface effects. ssDNA is made periodic not only by copying it periodically as the rest of the system but also by covalently linking the two ends of each ssDNA segment to its above and below copy, thereby generating an infinite periodic ssDNA strand. (b) Initial (top) and relaxed (bottom) conformations of ssDNA interacting with the fixed graphene sheet.

At the start of our simulations, ssDNA was placed with its backbone at the center of the graphene nanopore, as shown in Figure 1a. In the subsequent 120 ns equilibrium simulation, in which neither stretching force nor electrical biases were added, DNA was observed to move away from the pore center and adhere, within 1 ns, to the pore rim. Eventually, the pore rim was seen to become sandwiched by two DNA bases (bottom panel in Figure 1b) that originally occupied the pore (top panel in Figure 1b). The spontaneous adhesion of DNA bases to the pore rim originates from hydrophobic interaction between the bases and the graphene surface. DNA bases were not found to escape away from the pore rim at any moment within our 120 ns MD trajectory, showing the robustness of the adhesion, though the bases can still diffuse freely along the pore edge as shown in Figure 2.

Figure 2.

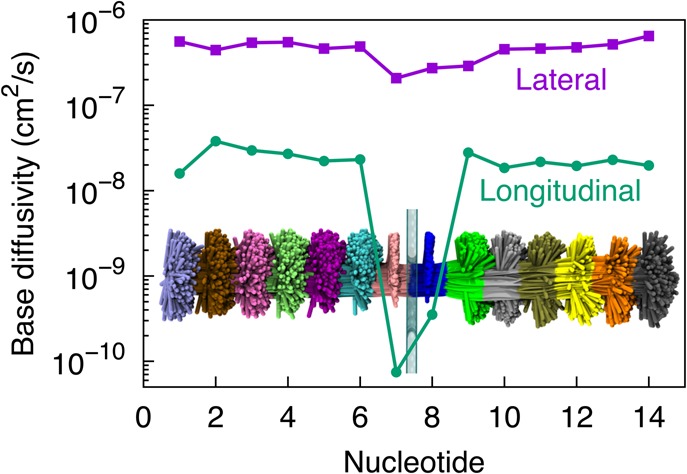
Fluctuations of ssDNA nucleotides. The lateral (parallel to graphene) and longitudinal (normal to graphene) diffusivities (defined in Methods) for nucleotides of poly(dA) ssDNA shown were evaluated from the last 100 ns of a 120 ns equilibration simulation. Nucleotides numbered 7 and 8 with lower longitudinal fluctuations are those that adhere to the graphene layer as shown in Figure 1b (bottom); nucleotides 1–6 and 9–14 that are not in direct contact with the graphene layer exhibit extensive fluctuations. The inset shows overlapped conformations of ssDNA in a 100 ns MD trajectory at 100 ps intervals; in comparison to Figure 1, where ssDNA is oriented along the vertical axis, in the inset here, ssDNA is shown oriented along the horizontal to better fit into the graph.

Figure 2 displays the diffusivity of each DNA base during the equilibrium simulation, determined separately along lateral (parallel with the graphene plane) and longitudinal (normal to the graphene plane) directions, as defined in Methods. The nucleotides are numbered 1 to 14 from the 3′ end to the 5′ end. In general, the lateral diffusivities for all bases are at least 10 times higher than the longitudinal diffusivities. For the lateral direction only, we found that all DNA bases have a comparable diffusivity of about 10^–7 cm²/s, though the two bases that adhere to graphene (nucleotides 7 and 8 at the moment depicted in Figure 2) exhibit relatively lower diffusivities. In the case of the longitudinal direction, on the other hand, these two bases exhibit an approximately 100 times lower diffusivity than other bases in the DNA strand, indicating that the base fluctuations normal to the graphene plane are significantly reduced due to base–graphene adhesion (see also Figure 2). The reduction in conformational fluctuations of the DNA molecule plays a major role in achieving a high signal-to-noise ratio for measurements as we document below.

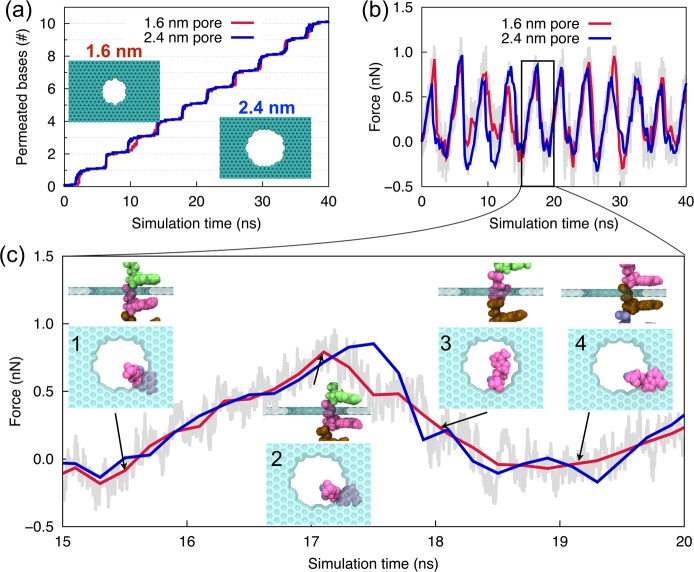
In order to investigate the translocation process, a series of so-called steered molecular dynamics (SMD) simulations, in which ssDNA was pulled upward (pulling in the direction of the ssDNA 5′ end) with a harmonic spring, were performed after the equilibrium simulations. One end of the spring was moved at a constant velocity of 2 Å/ns, whereas the other end was attached to the center of mass of all phosphorus atoms of DNA. This type of force application, namely distributed over all phosphorus atoms, prevents the introduction of tension between neighboring nucleotides that would arise if only the first of the phosphorus atoms were pulled; a similar driving strategy had been employed successfully in previous simulation studies.^36,40Figure 3a shows the number of nucleotides moving through the nanopore during ssDNA translocation. One can recognize a regular stepwise motion, each step representing the permeation of a single nucleotide.

Figure 3.

Translocation of poly(dA) ssDNA through graphene nanopores. Number of permeated nucleotides (a) and the associated pulling force (b) during 40 ns simulation, as well as the pulling force during a single base permeation step (15–20 ns) (c) when ssDNA is pulled through 1.6 nm (red line) and 2.4 nm (blue line) diameter graphene nanopores at a constant velocity of 2 Å/ns. Insets in (c) show side and top views of the ssDNA–graphene nanopore complex at different stages of a single base permeation step.

As stated, the translocation of the ssDNA shown in Figure 3a is brought about by a spring exerting a force. This force, presented in Figure 3b, varies characteristically during each of the translocation steps. The variation in force is due to overcoming the adhesive interactions between graphene and DNA bases that slows down the translocation as the spring pulls the ssDNA. Periodic peaks and valleys seen in the force signal correspond to translocations of single nucleotide. Figure 3c resolves a single force peak in Figure 3b illustrating the force change during a typical DNA base permeation, in which “uphill” and “downhill” motions are attributed to the adhesive trapping and forced release of nucleotide, respectively. The conformations of the nucleotide–graphene nanopore complex in the stepwise translocation are shown in the insets of Figure 3c. Typically, a permeation event (see also Supporting Information (SI) Movie M1) involves the approach and adhesion of the base to the lower graphene surface (insets 1 and 2), a sudden flip of the base about the backbone to move through the pore (inset 3), and the rebinding and adhesion of the base to the upper graphene surface (inset 4). A slight movement of the DNA backbone accompanies the motion of the DNA base, and occasionally, such backbone movement can become extensive, leading to an overall position change of DNA inside the pore.

For the 1.6 nm pore, we also examined translocation of homopolymers consisting of the other three base types, that is, poly(dT), poly(dC), and poly(dG), and found that the recorded force signals shown in Figure 3 are rather insensitive to base type (SI Figure S1).

We investigated then how pulling speed and pulling direction affect ssDNA translocation. With a decrease of the pulling velocity to 0.2 Å/ns, the duration of each permeation event becomes approximately 10 times longer. Nevertheless, we found base permeation (SI Figure S2a) and pulling force (SI Figure S2b) profiles similar to those of the 2 Å/ns pulling velocity case. In particular, the peak values of the pulling force arising are largely unaffected by the pulling speed.

However, change of the pulling direction has a drastic effect on the DNA motion; with the direction reversal, such that 3′ permeates the pore first, the stepwise DNA translocation changes to a steady sliding requiring much lower pulling force (SI Figures S2c and S2d). A previous study had shown that DNA bases tend to tilt collectively toward the 5′ end when ssDNA is confined or stretched.⁴¹ As a result, if one reverses the pulling direction to translocate ssDNA’s 3′ end first through the nanopore, the DNA bases form a large angle with the pulling direction and, accordingly, glide easily through the nanopore; pulling in the original direction, namely 5′ first, makes the DNA bases form a small angle with the pulling direction such that they get stuck in the nanopore, giving rise to the stepwise translocation. The former scenario is sketched in the inset of SI Figure S2c. The difference in ssDNA translocation behavior for the two opposite pulling directions arises only when the translocating ssDNA is kept stretched.

In experiments, it is difficult to precisely control the pore geometry when fabricating nanopores in solid-state membranes, affecting the effectiveness and reproducibility for single-molecule studies. Thus, a test of the robustness of the reported stepwise DNA motion in regard to the pore dimension is necessary. The pore diameters considered here are 1.6 nm (red curve in Figure 3) and 2.4 nm (blue curve in Figure 3). We note that the 2.4 nm pore allows the permeation of even double stranded DNA. Interestingly, the permeation and pulling force curves for the 2.4 nm pore are nearly identical to those for a 1.6 nm pore. In addition to circular pores, we also examined DNA permeation through an elliptical pore and found a similar permeation behavior (see SI Figures S3a and S3b), in contrast to a previous study where unstretched DNA was found to jam when translocating through an elliptical pore.²³ The independence of DNA translocation to size and shape of the nanopore makes the present findings useful for experimental applications.

We have related above the stepwise motion of ssDNA, shown in Figure 3, to the stretch-induced tilting and hydrophobic adhesion between graphene and DNA bases. To further confirm the relationship to hydrophobic adhesion, we replaced the graphene membrane by a two-dimensional monolayer material with less surface hydrophobicity, namely MoS₂. In this case, the trajectory again exibits a stepwise translocation (SI Figure S3c) but with lower associated pulling forces (SI Figure S3d). In addition, the translocation does not always occur in single-nucleotide steps, but rather contains “skips”, that is, two or more nucleotides translocate simultaneously (see arrow in SI Figure S3c). Despite being unlikely to produce a perfect stepwise translocation of stretched ssDNA, MoS₂ nanopore has advantages over graphene, namely, improved signal-noise-ratio¹⁸ and controllable nanopore fabrication,¹⁹ suggesting MoS₂ as another promising candidate for DNA sequencing next to graphene. Further skipping events are observed when the average spacing between neighboring bases in the ssDNA is reduced to 6.8 Å by weakening the mechanical stretching (SI Figures S3e and S3f).

Instead of applying a pulling force induced by a mechanical spring, we also performed MD simulations of up to 80 ns with a bias voltage applied to drive the stretched (continued to be induced by a mechanical stretching force) ssDNA through the pore. At a voltage of 1.5 V, ssDNA translocates, similar to the prior cases with mechanical pulling forces, in a stepwise fashion. In contrast, at a voltage of 4 V, a big skip over five nucleotides was observed during the DNA translocation (see Figure S4 in the Supporting Information). Here, high voltages (≥1.5 V) were used, but only over the brief simulation time of <80 ns, in order to induce a sufficient number of translocation events of DNA bases within the short time scale of the MD simulation. In experiments, the transmembrane voltages are usually less than 200 mV to avoid damage due to dielectric breakdown. Under such low driving voltages, DNA may move instantaneously backward when the induced driving forces on DNA are weak and comparable to the stochastic forces induced by thermal fluctuations.^42,43 Such a backward motion may lead to a double reading of an individual base and, in turn, an inaccurately read DNA sequence. Mechanical manipulation of translocating DNA, through application of nonelectric stretching and shifting forces, can prevent spontaneous backward movement without the limitation that needs to be placed on voltage biases. One might also apply both weak mechanical manipulation and weak voltage bias that together lead to low noise and unidirectional DNA translocation. Another solution to deal with the spontaneous backward movement might be use of multilayer devices containing two or more layers of graphene separated by dielectric materials that can recognize backward motion by comparing signals from adjacent layers.

As suggested above, stepwise translocation comes about via alternate binding and unbinding of DNA bases to the rim of a graphene nanopore. The process can be further illustrated by monitoring the change of graphene–DNA contact through the contact areas, S, defined through S = (SASA_graphene + SASA_DNA – SASA_graphene+DNA)/2. Here, SASA_graphene, SASA_DNA, SASA_graphene+DNA designate the solvent-accessible surface area of graphene only, DNA only, and the graphene–DNA complex, respectively. Figure 4a shows the contact area between ssDNA and graphene membrane during translocation through a 1.6 nm graphene nanopore for a pulling velocity of 2 Å/ns. One can recognize that the DNA–graphene contact area oscillates periodically between two values (purple and green dotted lines in Figure 4a) during the stepwise translocation. The higher surface value corresponds to an “adhesion” conformation in which a DNA base is trapped and steadily adheres to the graphene pore rims (Figure 4a, top inset), whereas the lower value represents a “permeating” conformation, in which the base is being rotated to facilitate its translocation through the narrow pore (Figure 4a, bottom inset).

Figure 4.

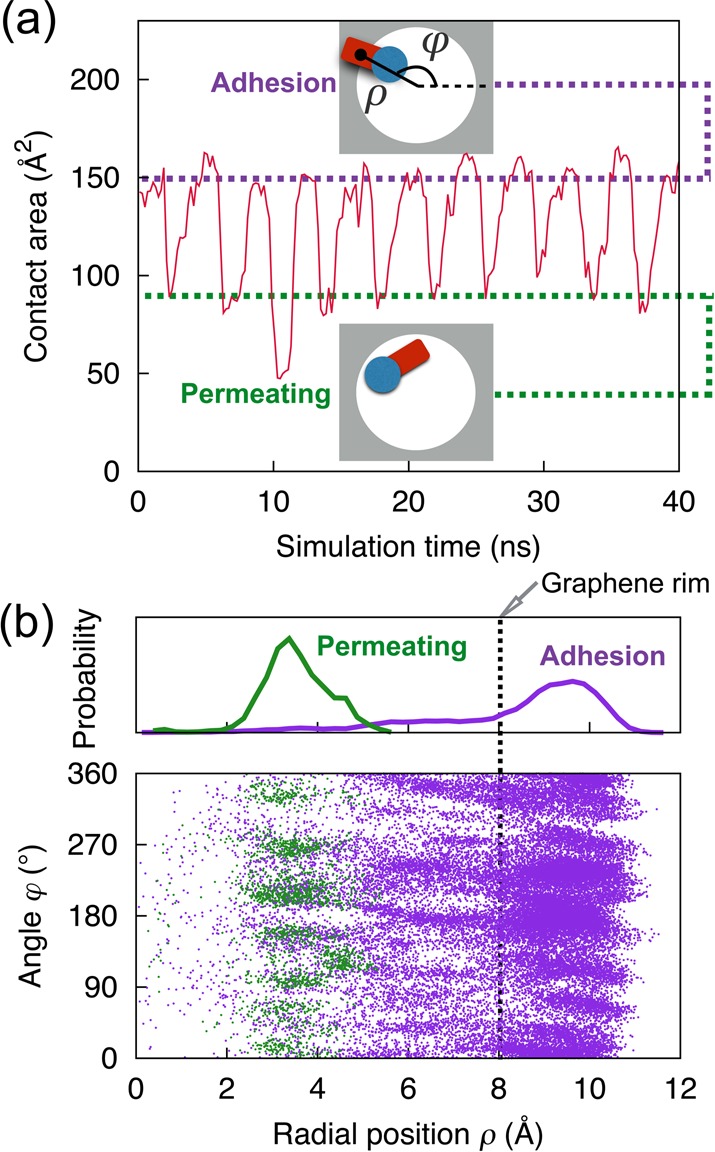
Alternate binding and unbinding of ssDNA to the graphene rim as ssDNA is pulled through a graphene nanopore. (a) Contact area between ssDNA and graphene versus simulation time. Insets show the conformations of the nucleobase adhering to the graphene membrane (top) and permeating through the pore (bottom). (b) Scatter diagram showing center of mass positions of DNA nucleobases during permeating or adhesion. The orientation of the nucleobase is specified by radial coordinate ρ and angular coordinate φ, as shown schematically in the top inset of (a). The top panel shows the normalized distribution of ρ. The vertical dotted line indicates the position of the graphene rim.

Figure 4b shows in polar coordinates the orientation of the DNA bases in the adhesion or permeating conformation. Here, the base orientation is specified by radial coordinate ρ and angular coordinate φ of the center of mass of DNA bases, as shown schematically in the top inset of Figure 4a. A base is considered in the permeating conformation if the z coordinate of its Cl′ atoms, z_Cl′, obeys |z_Cl′| < 5.5 Å and the z coordinate of the center of mass of DNA bases, z_base, obeys |z_base| < 1.674 Å. Otherwise, if only the former condition is satisfied and the latter is not, the DNA base is considered in the adhesion conformation. For the adhesion conformation, the single peak at ρ = 9.5 Å, as observed in the distribution profile of radial base position shown in the top panel of Figure 4b, is seen to locate beyond the pore rim (ρ = 8 Å), indicating that DNA bases overlap with some fraction of graphene around and slightly beyond the pore rim. For the permeating conformation, the single peak is located inside the pore at ρ = 3.3 Å. We note that the number of data points corresponding to the permeating conformations are much fewer than the number corresponding to the adhesion conformations, as DNA bases inside the pore are relatively short-lived.

We have previously shown that a GNR with QPC edges is capable of detecting, by means of transport measurement, individual bases in a stretched ssDNA.³² However, in the prior study, we had to translocate the ssDNA rigidly through nanopores, as we noted that DNA permeation with realistic thermal fluctuations would introduce significant noise to the measured signal, making individual bases impossible to be identified. In the present study, we have shown that fluctuations of DNA bases, especially in the longitudinal direction (normal to the graphene plane), can be considerably reduced due to adhesion to the graphene surface. We suggest that such stabilization effect is beneficial for the fidelity of a measured transverse sheet current signal.

To explore this suggestion, we simulated a GNR device with QPC edges and a 1.6 nm nanopore connected to source and drain leads, as shown in Figure 5a. We adopt a back gate parallel to the GNR layer (not shown here) as such a gate can control the charge carrier concentration in graphene and, hence, its detection sensitivity.⁴⁴ In order to determine the effect of ssDNA translocation on the sheet current around the pore, we followed the approach described in Methods and extracted the coordinates of the translocating DNA segment from our DNA translocation simulation through a 1.6 nm pore at 2 Å/ns pulling speed. Thereby, realistic motions of DNA atoms were fully taken into account in the subsequent transverse sheet current calculations. After mapping the charge distribution of DNA corresponding to the trajectory to a Poisson−Boltzmann solver, the on-site electrostatic potential on the graphene membrane was calculated for each trajectory frame.

Figure 5.

Electronic detection of stepwise motion of ssDNA through a graphene nanopore. (a) Schematic model consisting of ssDNA and a QPC-edge graphene nanopore of 1.6 nm diameter. The current is measured between source and drain leads, V_S and V_D. (b) Electrostatic potential in graphene plane corresponding to four snapshots in Figure 3c during a typical event of nucleotide permeation. Dotted lines mark the rims of graphene nanopores. (c) Calculated transverse sheet current through graphene at 0.03 eV Fermi energy shown together with the number of permeated nucleotides during the corresponding simulated ssDNA translocation.

Electric potential maps corresponding to four successive frames (Figure 3c, insets) during a typical permeation of a DNA base are presented in Figure 5b. In general, the results establish a clear relationship between electric potential and DNA positions inside the pore. Typically, the localized potential can only be observed around the DNA backbone in the adhesion conformation (i.e., 1, 2, and 4), whereas in the case of a permeating conformation (3), the potential spreads around the whole nucleotide. The strong features due to the DNA backbone in the electric potential map is reasonable as the backbone is highly charged and always occupies the pore. A lack of features from the DNA bases in most frames of the electric potential maps is due to the strong screening effect by ions and water near the graphene sheet; due to this effect, the electric potential at the electronic orbital positions in the graphene sheet is mainly affected by the charges within a narrow slice coplanar with the graphene membrane layer and directly within the pore. As a result, the electric potentials in the graphene sheet, shown in Figure 5b for four ssDNA snapshots (1, 2, 3, and 4 as shown in Figure 3c), are dominated by nucleotides in the immediate vicinity of the graphene nanopore, namely, nucleotides 7 and 8 as depicted in Figure 2; nucleotides 1–6 and 9–14 hardly contribute. Indeed, in case of snapshots 1, 2, 4, one can readily recognize that all electrostatically visible nucleotides, as expected according to Figure 3c, adhere to the nanopore rim.

The electrostatic potentials determined on the basis of trajectories were then included in the quantum mechanical description of electrons in the graphene layer to calculate the transverse sheet current across the graphene layer.³⁰ Shown in Figure 5c is the calculated sheet current (red line) during the stepwise motion of stretched DNA together with the base permeation profile (blue line). In general, the transverse sheet current in the graphene layer oscillates with a variation of 2–3%, the oscillation originating from the change in DNA base occupation of the pore. Specifically, in each base translocation event, a distinct current minimum (e.g, at the moment depicted by arrow 3 in Figure 5c) is detected for the permeating conformation (see the bottom inset in Figure 4a), whereas current maxima always arise for the relatively long-lived adhesion conformation (see the top inset in Figure 4a). As a result, the present GNR device is able to count nucleotides in the ssDNA molecule, namely through counting the current minima. We expect that further studies focusing on the design of pore or edge geometries of the GNR device, as well as on the adjustment of carrier concentration in the GNR by a biased back gate, will enhance the sensitivity of the device to individual DNA bases and, in turn, will hopefully unveil not only the number but also the identity of the bases and, thereby, unveil the sequence of the DNA.

A critical element of the suggested mechanism of stepwise ssDNA translocation is maintenance of ssDNA inside an actual nanosensor in a stretched conformation as the molecule passes through the graphene nanopore. Previous studies reported several means for stretching (elongating) DNA molecules inside solid-state nanopores.⁴⁵⁻⁴⁷In particular, DNA stretching can be accomplished by threading ssDNA through a solid-state nanopore under electric fields.⁴⁵ Accordingly, we suggest for future nanosensors to realize stretched DNA translocation through the use of a multilayer arrangement consisting of a monolayer graphene sandwiched between two layers of a thicker solid-state material such as SiO₂ and SiN (see SI Figure S5). The nanopore in graphene should adopt, in this case, a diameter smaller than that of the narrowest part of the two solid-state pores such that graphene surface around and slightly beyond the pore rim is exposed to the pore volume to interact with interior DNA molecules being threaded into the leading solid layer nanopore. ssDNA stretching can be further enhanced by employing, instead of a nanopore in a SiO₂ or SiN membrane, actually a semiconductor membrane of a p–n junction.⁴⁶ Additionally, in order to further facilitate the inside-pore stretching, ssDNA could be prestretched by being confined to a very narrow nanochannel before being threaded through the nanopore.^48,49 Employing a combination of the strategies, ssDNA molecules should be made to translocate through the nanopore with the DNA part crossing the pore adopting a fully stretched conformation, resembling the DNA conformation simulated here (see SI section I for details).

Another key element to the proposed measurement scheme is the availability of instrument bandwidth, namely frequency of signal recording.⁵⁰⁻⁵² Under the high driving voltages (≥1.5 V) used in our simulations, a frequency of recording up to the order of gigahertz would be required in order to count nucleotides during the fast DNA translocation (assuming that ten measurements are needed to detect the permeation of a single base). However, in real experiments, the transmembrane voltages for driving DNA translocation through the pore are usually less than 200 mV. For example, an experimental study by Radenovic et al.³³ showed that a 2713-bp-long double-stranded DNA was translocated through a 10 nm diameter graphene nanopore within about 1 ms under a driving voltage of 200 mV. Assuming again that each base pair is measured ten times, the required frequency of recording is ∼27 MHz. Previous experimental studies showed that ionic current through solid-state nanopores can be measured at a bandwidth of 1 MHz.^51,52 In the case of transverse sheet current, the measurement bandwidth could be larger, possibly tens of megahertz, as discussed previously.⁵⁰ Actually, in the experiments by Radenovic et al., DNA translocation is relatively fast because DNA passes through the 10 nm diameter graphene nanopore without much interaction at the rim due to the wide opening. For narrower pores, it is found that the adhesion of stretched ssDNA to the pore rim slows down DNA translocation, as discussed above, thereby lowering the required bandwidth. Other strategies such as increasing solvent viscosity and modifying charge density of a pore surface can also be used to slow down DNA translocation, as reviewed previously.^37,53

In summary, our extensive molecular dynamics simulations have demonstrated that DNA bases can spontaneously bind to the graphene pore rim due to hydrophobic interactions between base and graphene, resulting in the graphene pore rim becoming sandwiched by two adjacent nucleotides. In this conformation, the fluctuations of nucleotides that adhere to the graphene surface are greatly reduced, especially in the direction normal to the graphene plane, suppressing the noise of the measured signal for the nucleotide. When applying a pulling force to DNA backbones or an electric field normal to the graphene membrane, the ssDNA, moving 5′ end first through the pore, engages in a step-by-step transport through alternate nucleotide unbinding from and binding to the graphene pore rim. The stepwise translocation holds promise in enhancing the signal quality by not only slowing down DNA translocation providing sufficient time to ensure high fidelity sensing, but also by stabilizing single DNA bases and, thereby, reducing thermal noise. Our further simulations have shown that the stepwise translocation is independent of size and shape of graphene nanopores, making our finding useful for practical applications as it is difficult to precisely control the geometry of fabricated nanopores. Our quantum transport calculations show that GNRs with QPC edges are capable of detecting the stepwise translocation of DNA through graphene pores by means of a transverse current in the graphene sheet.

Methods

Our methodological approach outlined below combined classical MD simulations of stretched ssDNA translocating through a graphene nanopore as depicted in Figure 1 with quantum mechanical calculations for the graphene electronic sheet current. We extracted the charge distribution ρ_DNA(r) of the ssDNA from each frame of the MD trajectory at 100 ps intervals. This distribution was employed in a Poisson−Boltzmann equation to determine, with a continuum description of the aqueous solvent, the electrical potential φ(r) that contributes to the local energy of graphene sheet electrons. Accordingly, the potential was included in the calculation of the transverse sheet conductance and associated sheet current, the latter constituting the measured signal that is expected to reveal the sequence of nucleotides of ssDNA when translocated through the graphene nanopore.

Molecular Dynamics Simulations

To induce DNA stretching, we fixed the 3′ end of a ssDNA molecule and moved the 5′ end at a constant velocity of 10 Å/ns to reach a straight ribbon with an average spacing of 0.77 nm between neighboring bases. The stretched DNA–graphene system was solvated in a 65 × 65 × 110 ų water box with 1 M KCl using the solvate Plugin of VMD,⁵⁴ resulting in a simulation system of ∼45 000 atoms (Figure 1a). In the simulations of DNA translocation through graphene nanopores, two ends of ssDNA were covalently bonded to each other to form an infinitely long DNA strand under the periodic boundary conditions adopted for the simulations. The long axis of ssDNA was aligned along the z direction and the nanopore center was set to be the origin of the coordinate system. After a 5000-step energy minimization, the system was equilibrated as an NPT ensemble at 300 K and 1 atm for 1 ns, during which time the lateral size of the simulation box was fixed while the longitudinal one was allowed to freely change to accommodate the constant pressure. Subsequently, a 120 ns NVT ensemble simulation was carried out to further equilibrate the system and to sample the conformation of the graphene–DNA complex. The graphene monolayer was fixed during all MD simulations. A test simulation with only two lines of graphene sheet atoms fixed along the lateral edges of the periodic cell yielded similar results, though with a weaker associated pulling force. Through steered molecular dynamics (SMD) simulations,⁵⁵ an external force was applied to all phosphorus atoms of the stretched ssDNA, as described in SI Figure S6, to induce a constant-velocity movement of the ssDNA.

All MD simulations were performed using NAMD 2.9,⁵⁶ with the CHARMM27 force field⁵⁷ for DNA and graphene and the TIP3P model⁵⁸ for water. Carbon atoms in graphene were treated as CA carbon in the CHARMM27 force field. A 2 fs integration time step and a 2–2–4 multiple timestepping scheme were employed. van der Waals energies were calculated with a 12 Å cutoff. The particle-mesh-Ewald (PME) method was adopted to treat long-range electrostatics.⁵⁹ NPT ensemble simulations were carried out with a Nosé–Hoover Langevin piston⁶⁰ for pressure control and Langevin dynamics for temperature control.

Calculation of Lateral and Longitudinal Diffusivities

The mean squared displacement (MSD) for DNA base atoms was calculated according to the expression

1

where ⟨...⟩ represents the average over all base atoms of a single nucleotide and r defines the atom position at time t or t + Δt. MSD was calculated for all bases separately along lateral (x and y; parallel with the graphene plane) and longitudinal (z; normal to the graphene plane) directions. MSD was averaged over snapshots of the whole MD trajectory extending over a time Δt.

The diffusivity D was evaluated using the Einstein relation

2

where d is the dimensionality of the monitored motion (2 for the lateral direction and 1 for the longitudinal direction). The lateral or longitudinal diffusivity of a DNA base was determined from a linear fit to the calculated MSD(Δt) plot within the time interval 0.2 < Δt < 1 ns. The Einstein relation employed applies strictly only to freely diffusing systems, not bound systems; since the present purpose is a qualitative characterization of diffusivities and the chosen sampling time is brief (1 ns), the resulting D values are meaningful.

Quantum Transport Calculations

In order to evaluate the effect of ssDNA translocation through a graphene nanopore on the sheet current in the graphene surrounding the pore, we extracted snapshots from the ssDNA translocation trajectory at 100 ps intervals. For each snapshot, the electric potential induced by the charge distribution of ssDNA was determined by means of the self-consistent Poisson−Boltzmann equation.^30,31 Then the transverse conductance across the graphene sheet was calculated employing for the relevant electronic degrees of freedom a tight binding Hamiltonian and evaluating the current through the associated nonequilibrium Green’s function.^30,31

Given the MD trajectory snapshots of translocating ssDNA defining the charge density ρ_DNA(r) through the coordinates of all atoms and their partial charges, the electric potential φ(r) was calculated using the Poisson−Boltzmann equation^30,31

3

In this calculation, the charges due to solute ions were described assuming a Boltzmann equilibrium, namely through

4

5

Here, C_K⁺(r) and C_Cl^–(r) are the local ion concentrations of K⁺ and Cl^–, and C₀ is the molar concentration in the solution which we have set to 1 M. Equations 3–5 were solved iteratively until convergence. The system was discretized into a 129 × 129 × 129 point grid, spanning a box of dimension 10 × 10 × 13 nm³. The potential at the top and bottom plane of the box was set to Dirichlet boundary conditions V_top = V_bottom = 0. The sides of the box were subjected to von Neumann boundary conditions. The dielectric constants of graphene (ϵ_g) and water (ϵ_w) were set to 6 and 78, respectively.

To describe the electronic transport in graphene, we assume a single orbital tight binding Hamiltonian given by^30,44

6

where E is the on-site energy at each carbon atom in the graphene layer and φ(r_n) is the electric potential at the on-site positions calculated by means of (eqs 3–5). The index n runs over all carbon atoms in the GNR; here, the second term describes the nearest neighbor interactions. The index j runs over all nearest neighbor carbon atoms of site i, with t_ij being the single-electron coupling between site i and site j. In our calculations, we adopted a single nearest neighbor and three orbital interaction Hamiltonian.³⁰ The GNR edges were assumed to be passivated with hydrogen.

Given the Hamiltonian (eq 6), we employed the nonequilibrium Green’s function method^30,31 to calculate the transmission function T(E). The conductance for a given source-drain bias across the graphene ribbon is given by

7

where h is the Planck constant, and f₁(E) and f₂(E) are the Fermi–Dirac distributions at source and drain, respectively. In the present study, we used a source-drain voltage V_DS = 5 mV at a system temperature of 300 K. The resulting conductance may be altered by nonideal boundaries of the GNR as they arise in real systems. Further details of the calculation of the sheet conductivity/current can be found in our prior studies.^30,31

Supporting Information Available

This material is available free of charge via the Internet at http://pubs.acs.org/. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b03963.

• Additional simulation results for ssDNA with different DNA sequences (S1), different DNA driving strategies (S2, S4), as well as different pore shapes, membrane materials and ssDNA stretching lengths (S3), followed by experimental realization of the present findings (S5) and additional details of steered molecular dynamics simulations (S6). (PDF)

• A movie representing a molecular dynamics trajectory and showing stepwise translocation of stretched ssDNA through a graphene nanopore. (MOV)

The authors declare no competing financial interest.