Conserved Quantitative Stability/Flexibility Relationships (QSFR) in an Orthologous RNase H Pair

Abstract

Many reports qualitatively describe conserved stability and flexibility profiles across protein families, but biophysical modeling schemes have not been available to robustly quantify both. Here we investigate an orthologous RNase H pair by using a minimal distance constraint model (DCM). The DCM is an all atom microscopic model that accurately reproduces heat capacity measurements, and is unique in its ability to harmoniously calculate thermodynamic stability and flexibility in practical computing times. Consequently, quantified stability/flexibility relationships (QSFR) can be determined using the DCM. For the first time, a comparative QSFR analysis is performed, serving as a paradigm study to illustrate the utility of a QSFR analysis for elucidating evolutionarily conserved stability and flexibility profiles. Despite global conservation of QSFR profiles, distinct enthalpy-entropy compensation mechanisms are identified between the RNase H pair. In both cases, local flexibility metrics parallel H/D exchange experiments by correctly identifying the folding core and several flexible regions. Remarkably, at appropriately shifted temperatures (e.g., melting temperature), these differences lead to a global conservation in Landau free energy landscapes, which directly relate thermodynamic stability to global flexibility. Using ensemble-based sampling within free energy basins, rigidly, and flexibly correlated regions are quantified through cooperativity correlation plots. Five conserved flexible regions are identified within the structures of the orthologous pair. Evolutionary conservation of these flexibly correlated regions is strongly suggestive of their catalytic importance. Conclusions made herein are demonstrated to be robust with respect to the DCM parameterization.

INTRODUCTION

Throughout evolution, Nature must delicately balance protein flexibility with thermodynamic stability. A functioning enzyme must be flexible enough to mediate the reaction pathway, rigid enough to support reproducibility in molecular recognition, and do both in a thermodynamically stable state.¹ Consequently, similar stabilities and flexible motions have been identified across entire protein families.^2,3 Balance between flexibility and thermodynamic stability is best exemplified by evolutionary adaptation to environmental condition. Cooling a thermophilic protein will generally result in a marked stability increase.⁴ However, the stability gain frequently comes at the expense of functional efficiency, presumably by over-rigidifying catalytic motions.⁵ As such, quantitative descriptions of flexibility and stability are required for a more complete understanding of protein function.

Many recent investigations of orthologous mesophilic/thermophilic pairs have attempted to decipher these complex relationships; for a review see Kumar and Nussinov.⁶ Such comparisons provide a framework to explore functionally conserved proteins with acute stability differences. One important conclusion from this body of work is that orthologous protein pairs have similar stabilities at the optimal growth temperature of their respective organisms.² This result confirms the evolutionary importance of conserved stability/flexibility relationships. Unfortunately, beyond qualitative conclusions, very little quantitative information is available describing the give-and-take between stability and flexibility. Furthermore, evidence supporting familial conservation in stability/flexibility relationships is sparse. To mainstream such investigations, computationally efficient biophysical models that calculate both flexibility and stability are required.^7,8

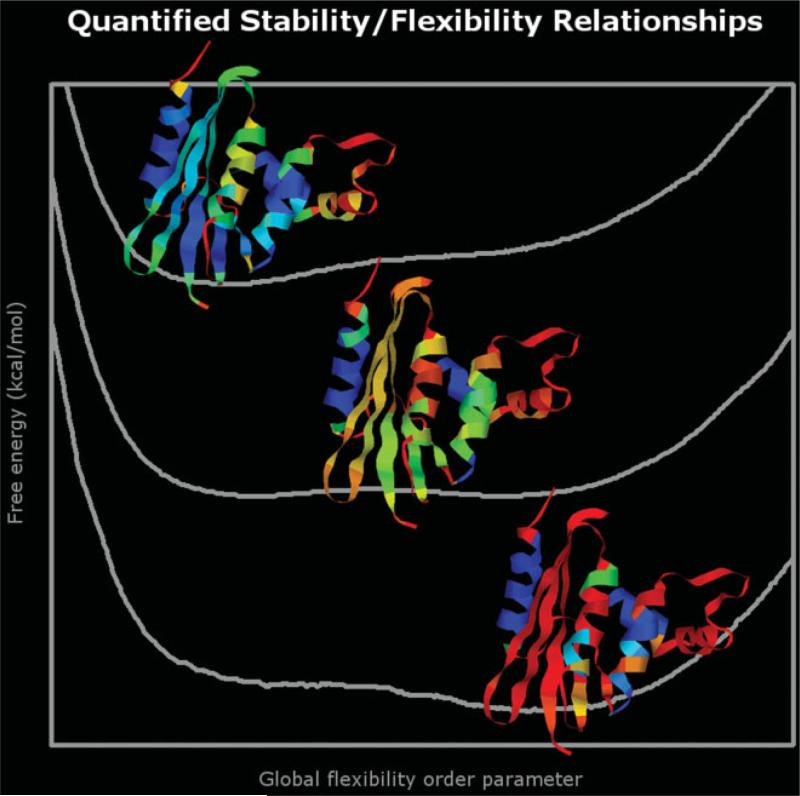
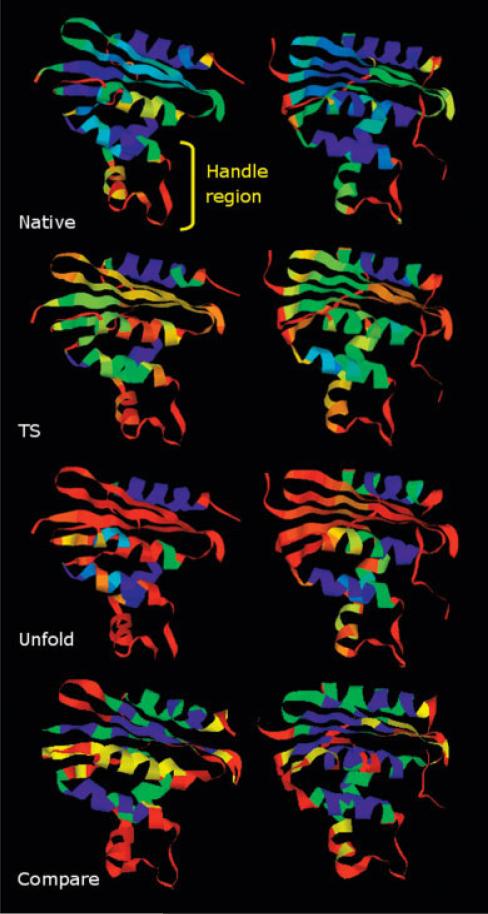
In this report, the notion of protein quantitative stability/flexibility relationships (QSFR) is introduced for the first time (see Fig. 1). By quantitatively assessing the give-and-take between stability and flexibility, QSFR provide a means to understand how functional efficiency is affected by thermodynamic condition. A variety of QSFR descriptors are presented here, including: (a) stability as a function of a flexibility order parameter, (b) local flexibility profiles, and (c) cooperativity correlation plots. When taken together, the QSFR descriptors provide key insight concerning the physical mechanisms leading to protein function. QSFR quantities are calculated by a recently introduced^9,10 distance constraint model (DCM). Here, a minimal DCM is used to identify stability/flexibility similarities and differences within a well-characterized mesophilic and thermophilic RNase H pair.

Fig. 1.

QSFR are used to precisely describe the give-and-take between protein stability and global flexibility. Local flexibility characteristics of RNase H are shown as cartoon ribbon diagrams (red = very flexible, yellow = slightly flexible, green = marginal, cyan = slightly rigid, blue = very rigid) for three different thermodynamic states (native, transition, and unfolded).

RNase H is a small (~165 residues) microbial endonuclease that selectively digests RNA from RNA/DNA hybrids.¹¹ Crystal structures are currently available for the Escherichia coli¹² and Thermus thermophilus¹³ orthologs. Despite remarkably similar structures and 53% sequence identity, there are significant thermodynamic differences between the two.² At neutral pH, the most obvious difference is melting temperature (T_m) where E. coli melts at 66°C, whereas T. thermophilus melts at 86°C. The T_m difference arises from a significantly lower ΔC_p in the thermophilic ortholog, which has been ascribed to residual hydrophobic structure within the denatured ensemble.^14,15 Better hydrophobic packing in the thermophilic native structure has also been shown to contribute to its stability.¹³ At their respective optimal functioning temperature, conservation of stability,² structural distribution of stability,¹⁶ and folding mechanisms¹⁷ have been observed.

A key result of this investigation shows that the DCM provides a robust QSFR analysis consistent with experimental observations, which is computationally tractable in practical computing times. Whereas the minimal DCM cannot unambiguously identify residual structure within the denatured ensemble, a greater dependence on hydrophobic interactions within the native state is observed. Nontrivial differences in the enthalpy-entropy compensation mechanisms are determined and found to provide globally similar stability and flexibility profiles between the pair at their respective T_m. Flexibly correlated loop regions coupling to the binding site are found conserved. Evolutionary conservation of the flexibly correlated regions strongly suggests an important catalytic role, thus providing new insight into experimentally available functional efficiency data. Accurately identifying subtle, yet meaningful, QSFR differences in realistic computing time-scales, suggests this approach will become an important tool in the structural genomics era for comparative investigations of evolutionarily related proteins.

METHODS

A DCM, minimally implemented as a phenomenological theory requiring three free parameters, is used to describe protein thermodynamics and a variety of mechanical properties. Whereas experimentalists routinely use a two-state thermodynamic model to accurately fit C_p curves requiring five free parameters (e.g., see Refs. 14 and 15), no assumption about a two-state process is required using the DCM. Instead, structural topology of a protein governs local microscopic free energy contributions. Total free energies are calculated through explicit modeling of competing atomic-scale enthalpy-entropy compensation mechanisms that are linked (coupled) mechanically through constraint topology. This is made possible because the DCM uses efficient network rigidity graph-algorithms¹⁸ to identify flexible and rigid regions within a protein structure under a specified set of constraints. Applying statistical mechanics to an ensemble of constraint topologies, the DCM explicitly accounts for network rigidity as an underlying mechanical interaction.¹⁹

Free energy decomposition schemes have been introduced and frequently used for some time (see discussions within Refs. 20–22). The most sought-after property is linearity, where the addition of all local microscopic free energy contributions within a protein yields a complete and accurate description of protein thermodynamics. Linear decomposition schemes have proved useful in providing accurate predicted heat capacities of unfolded proteins,²³ and in estimating ΔC_p based on differences in solvent exposed surface area.²¹ Accurate predictions of ΔC_p imply that both the native and unfolded states are well represented. To our knowledge, additive free energy decomposition schemes remain unable to reproduce entire experimental C_p curves—implying that energy fluctuations about equilibrium are not being addressed correctly. Conversely, successful fitting of C_p implies that energy fluctuations are accurately represented. Through energy fluctuations, dynamic simulations (MD, Go-like models, etc.) routinely calculate heat capacity curves (e.g., see Ref. 24). However, we are unaware of any results demonstrating that MD-generated C_p curves quantitatively reproduce experimental values, which must be attributed to the substantial computational cost involved in phase space exploration and/or inaccurate parameterization of the force field.

A distinct advantage of the DCM is that it provides a robust all atom microscopic free energy decomposition scheme that accurately reproduces entire protein unfolding heat capacity curves.^9,10 We argue^9,10 that the inability of additive free energy decomposition schemes to quantitatively reproduce C_p curves is a consequence of overestimating conformational entropy due to intrinsic nonadditivity property of component entropies.²² The DCM accounts for nonadditivity in conformational entropy through network rigidity.^9,10 Detailed descriptions of the DCM have been published elsewhere,^9,10,19,25 but for completeness, a cursorily overview is provided here. The implemented minimal three free parameter DCM calculates protein stability within a two-dimensional constraint space.^9,10 The number of native-like torsion constraints, N_nt, and number of H-bond constraints, N_hb, specifies the macrostate of a protein. A Landau free energy functional is constructed to be dependent on constraint topology at atomic level of detail. For each node (N_hb, N_nt) specifying the topological macrostate of a protein, the Landau functional has the form:

$$\mathrm{G}({\mathrm{N}}_{\mathrm{hb}},{\mathrm{N}}_{\mathrm{nt}})=\mathrm{U}\left({\mathrm{N}}_{\mathrm{hb}}\right)-\mathrm{u}{\mathrm{N}}_{\mathrm{hb}}+\mathrm{v}{\mathrm{N}}_{\mathrm{nt}}-\mathrm{T}({\mathrm{S}}_{\mathrm{c}}\left({\delta }_{\mathrm{nat}}\right)+{\mathrm{S}}_{\mathrm{mix}})$$ (1)

where U(N_hb) is the average total intramolecular H-bond energy, S_c is a conformational entropy, S_mix is a mixing entropy for the number of ways to have N_hb H-bonds, and N_nt native-torsion constraints, and {u, v, δ_nat} are treated as phenomenological parameters. The three phenomenological parameters (u, v, δ_nat) effectively account for hydrophobic interactions, structural diversity, and differences in solvent conditions. Hydrogen bond energies are calculated from an empirical potential.²⁶ Salt bridges are considered a special hydrogen bond case. When a hydrogen bond breaks, the compensating (energetically favorable) interaction with solvent is described by u. If a torsion constraint is in a (native, disordered) state it contributes (v, 0) energy, and when the constraint is independent, it contributes Rδ_nat entropy, where R is the ideal gas constant. For each node (N_nt, N_hb), the Landau free energy [Eq. (1)] is calculated by Monte Carlo sampling over an ensemble of constraint topologies. Each constraint topology requires a network rigidity calculation¹⁸ to determine conformational entropy. Conformational entropy is directly related to a preferentially determined set of independent constraints within the protein structure, and it strongly depends on constraint topology and the locations of rigid substructures that form within.

Heat capacity curves from differential scanning calorimetry (DSC) for the thermophilic RNase H at pH 2.5, 3.5, and 5.5 have recently been published.¹⁵ Because of problems with aggregation, the only heat capacity curve available for the mesophilic protein¹⁵ is at pH 3.5. DCM parameterization is achieved by fitting to these experimental heat capacity curves in conjunction with an X-ray crystal structure as input. As described previously,⁹ energy minimization and continuum electrostatic pK_a calculations are performed to ensure proper ionization before fitting to the C_p curves. Alternatively, fitting to stability curves, unfolding curves, or other thermodynamic data can parameterize the DCM. Once parameterization is achieved, Eq. (1) is used to assign free energies, and thus Boltzmann weights, to each topological framework (i.e., conformation) within the ensemble.

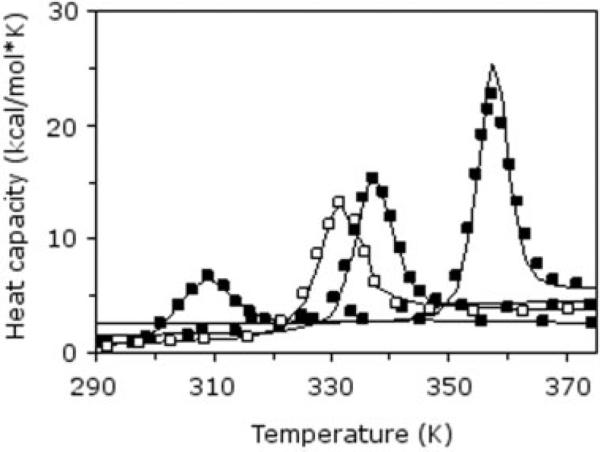
With δ_nat simultaneously fit across all C_p curves, nine phenomenological parameters provide excellent fits for the four different curves (Fig. 2). All best-fit parameters are physically reasonable (Table I), but the discussion in this report focuses on the shared (pH 3.5) thermodynamic condition. Because of the structural similarity within the pair¹³ and identical conditions within the DSC experiments,¹⁵ parameter differences are ascribed to hydrophobic interaction differences. Despite not modeling hydrophobic interactions explicitly, it will be seen that the minimal DCM captures essential differences between the pair. This point is addressed further below in the Results and Discussion section.

Fig. 2.

DCM parameterization is achieved by fitting to heat capacity curves. Best fits to T. thermophilus (filled symbols) RNase H heat capacity curves at pH 2.5, 3.5, and 5.5 (left to right, respectively). Only the pH 3.5 E. coli (open symbols) RNase H heat capacity curve is available. All experimental curves are from Ref. 15.

TABLE I.

RNase H DCM Model Parameters and QSFR Values

Organism	pH	Tma	#HB	AHBEb	THBE	u	v	BHc	θ nat d	θ TS	θ unf	θ RP
E. coli	3.5	59	203	–3.01	–611.0	–1.86	–0.37	1.41	1.50	1.91	2.42	1.65
T. thermophilus	2.5	36	199	–2.72	–541.3	–1.63	–0.34	1.07	1.68	1.98	2.31	1.22
T. thermophilus	3.5	64	200	–2.70	–540.0	–1.56	–0.44	2.58	1.45	1.89	2.40	1.15
T. thermophilus	5.5	84	200	–2.70	–540.0	–1.54	–0.54	4.85	1.25	1.79	2.44	1.16

^aT_m = melting temperature (°C).

^bAHBE = average hydrogen bond energy (kcal/mol); THBE = total hydrogen bond energy (#HB multiplied by AHBE).

^cBH = barrier height at T_m normalized by RT_m.

^dθ_nat, θ_TS, θ_unf, and θ_RP = global flexibility order parameter values corresponding to the native state, transition state, unfolded state, and rigidity percolation threshold at T_m.

A common criticism of the DCM (personal communications) is that the experimental C_p curves are over fit, which if true, implies that parameter values have no physical basis. This belief is attributable to a misunderstanding of the DCM. Whereas there are multiple acceptable parameterizations, all acceptable parameters are similar and physically intuitive. Parameters that go against physical intuition (e.g., the average H-bond between solvent and protein being enthalpically unfavorable) have never been observed within anything approaching a reasonable fit. Moreover, flexibility descriptions for the native ensemble of protein structures are demonstrated [in Supplementary Material and discussions below] to be insensitive to parameterization differences. The main result of parameter differences is simply a shifting of T_m. In this investigation, four C_p curves are reproduced with nine phenomenological parameters (2.25 parameters per curve). The free parameters within the minimal DCM largely account for solvent (ionic strength, pH, cosolutes, etc.) and hydrophobic effects. Previous investigations have shown that a two free parameter minimal DCM is unable to robustly reproduce C_p curves,^9,10 indicating that all three phenomenological parameters are required to describe the essential physics. Improvements within the free energy decomposition scheme to explicitly account for hydrophobic interactions, hydration effects, etc., are currently being incorporated and should decrease the number of necessary free parameters. However, in the spirit of the review by Lazaridis and Karplus,⁸ maintaining a limited number of free parameters provides a natural and computationally efficient mechanism to account for differences in solvent conditions.

Another common criticism of the DCM arises from the use of different energy functions for different proteins. However, this is the essence of Landau theory, where different physical effects are contained in phenomenological parameters that retain physical meaning. As a consequence, this apparent weakness is actually its strength for practical applications, because it provides a computationally tractable manner to exhaustively investigate effects (i.e., solvent conditions) that are prohibitive to traditional simulation techniques. In no way is the current DCM being used to investigate ab initio protein folding. Nor is the objective of fitting to C_p simply a way to estimate ΔH and ΔS, as in thermodynamic fits. The objective is to provide a realistic representation of the native ensemble to make sound predictions involving mechanisms important to protein function. The DCM highlights QSFR as detailed information involving quantified flexibility and rigidity characteristics that are consistent with thermal fluctuations about equilibrium. Through modeling of atomic scale enthalpy-entropy mechanisms, the DCM provides a stepping-stone between general descriptions using thermodynamic models without any microscopic correspondence and the detailed atomic dynamic simulations that obscure the essential emergent properties governing QSFR. DCM ensemble averaged long timescale flexibility predictions¹⁰ are as good as other state-of-the-art methods (i.e., FIRST¹⁸ and the Gaussian network model²⁷). With these objectives and tools at hand, it is possible to calculate pair correlations to quantify molecular cooperativity.

Molecular cooperativity between different regions of a protein is identified using ensemble sampling, similar to COREX.²⁸ In an elegant study, Pan et al.²⁹ used COREX to explore how mutations in dihydrofolate reductase affect energetic connections between various structural elements to reveal functional connectivity between binding sites. Functional connectivity is present when pairwise folded/unfolded designations are linked by mutation. Unlike COREX, functional connectivity is revealed in QSFR through rigidly and flexibly coupled regions. In this regard, DCM is most similar to FIRST,¹⁸ which also uses network rigidity to identify rigid and flexible regions within a protein. However, FIRST is strictly an athermal (T = 0) analysis of mechanical stability of the native structure. The DCM accounts for entropic effects by ensemble averaging over constraint topologies consistent with thermodynamic stability. The degree of rigidity or flexibility within a protein and the degree of correlation linking these regions are characterized using probability measures and various moments thereof. Here, we focus on the probability that a dihedral angle can rotate, P_R, which provides a robust local flexibility measure. In addition, a cooperativity correlation plot identifies the statistical pairwise couplings in P_R. Cooperativity correlation plots can be used to identify allosteric effects present in a protein. As will be seen, application of a constraint at one location can produce a dramatic effect on conformational flexibility far removed from that location. These and many more QSFR descriptors are calculated in a matter of hours on a desktop computer because the DCM samples conformations as constraint topologies, not atomic geometries.

Electrostatics Stability Model

Electrostatic free energies are calculated using the University of Houston Brownian Dynamics (UHBD) suite of programs.³⁰ UHBD calculates electrostatic free energies using the multiple-site titration method described in Gilson³¹ and Antosiewicz et al.³² The protonation state of acids and bases is calculated versus pH, allowing calculation of the ideal charge state at a particular pH. The linearized Poisson-Boltzmann equation is solved using the Choleski preconditioned conjugate gradient method. The protein is centered on a 65 × 65 × 65 grid with each grid unit equaling 1.5 Å. A solvent dielectric constant of 80 and a protein dielectric constant of 20 are used for all stability calculations. Using an interior protein dielectric of 20 has been shown to reproduce experimental pK_a results much better than lower values.^33,34 Protein partial charges are taken from the CHARMM parameter set³⁵ and radii from the Optimized Potentials for Liquid Systems (OPLS).³⁶ The temperature is 298 K, and the ionic strength equals 0.15 M.

Protein stabilities are calculated as the difference of the native and denatured electrostatic free energies. Denatured structures are generated using the molecular mechanics protocol of Elcock.³⁷ The method is based on the premise that the denatured ensemble retains characteristics of the native structure.³⁸ The method works by “exploding” a native protein by systematically increasing (up to 6 Å in 1 Å increments) the location of the energy minima within the Lennard-Jones portion of the CHARMM³⁵ force field. Although seemingly arbitrary, the model is more accurate than fully extended representations because it better approximates the average electrostatic profile of the denatured ensemble. This approach was previously used³⁹ to characterize stability differences in cold shock protein mutants,⁴⁰ where the method was found to agree well with 27 experimentally tested mutants with better than 0.87 correlation coefficient. The method used here is general, and it compares favorably over alternative methods^41–43 because it produces reasonably robust results.

RESULTS AND DISCUSSION

Globally Conserved Stability/Flexibility Relationships

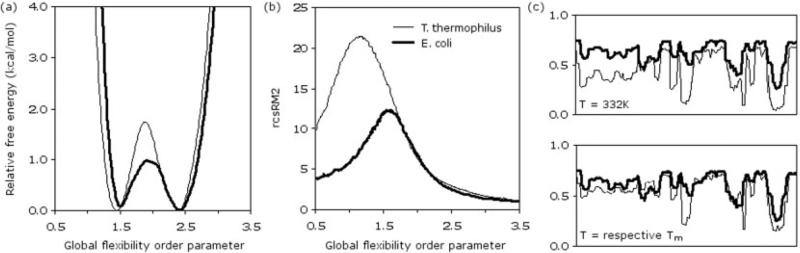
An important QSFR descriptor is the Landau free energy landscape, which describes the free energy, G(T,θ), as a function of temperature and a global flexibility order parameter. Landau theory is a generic phenomenological mean field approach that expresses a free energy function in terms of some global order parameter. Plotting the free energy as a function of the order parameter generally results in a phase transition [e.g., see Fig. 3(a)]. In this work, the global flexibility order parameter θ is defined as the average number of independent disordered torsion constraints divided by the number of protein residues, and the transition describes protein unfolding. At pH 3.5, the T_m's of the mesophilic and thermophilic protein are 59° and 64°C, respectively. In agreement with experiment,² the thermophilic protein is more stable than its mesophilic counterpart at any given temperature. However, the stability profiles for the two proteins are markedly similar at appropriately shifted temperatures. For example, Figure 3(a) compares G(T,θ) of each at their respective T_m. Each free energy landscape has two minima of near equal depth separated by a small energy barrier of <2 kcal/mol, but indicative of first-order phase transitions. In both cases, the scale of G(T,θ) is 9.35 ± 0.15 kcal/(mol • residue), which translates to ~1425 kcal/mol for the E. coli ortholog. At (lower, higher) temperatures, the relative amount of (native, denatured) protein is increased. In addition to observed similarity over the entire range of θ, global flexibility at key points describing characteristic G(T,θ) features (i.e., locations of the native, transition, and unfolded states) are virtually identical. These results strongly support the claim of Hollien and Marqusee² that a balance between thermodynamic stability and flexibility in this RNase H pair is critical to conservation of function.

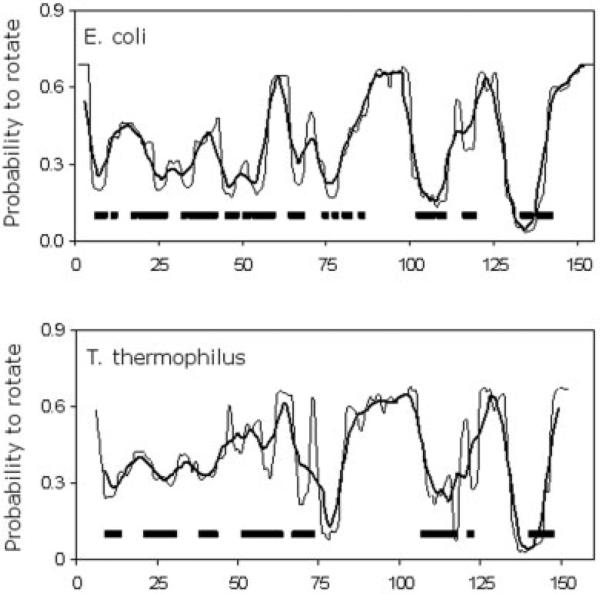
Fig. 3.

Landau free energies for the mesophilic E. coli (T_m = 59°C) and thermophilic T. thermophilus (T_m = 64°C) RHase H orthologs at pH 3.5. b: The rigid cluster size susceptibility, denoted by rcsRM₂, is defined as the second moment of rigid cluster size with the biggest cluster size excluded.⁵³ c: Backbone flexibility quantified by the probability that a PHI or PSI dihedral angle can rotate (P_R) versus residue number. At common temperatures, the thermophilic protein is predicted to be more rigid than its mesophilic counterpart. At respective T_m, flexibility information is conserved. The values here are thermodynamically averaged over the full ensemble of all accessible conformations.

Distinct Enthalpic/Entropic Compensation Mechanisms

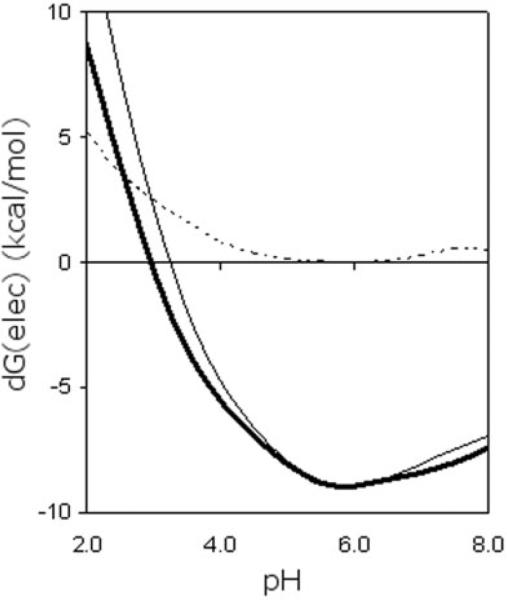
Global conservation within the Landau free energy landscapes is a nontrivial result because the stability of each occurs through distinct enthalpy-entropy compensation mechanisms. For example, the mesophilic protein not only has three extra hydrogen bonds, but their average stability is increased as well (Table I). As a consequence, the total hydrogen bond energy of the mesophilic protein is 71.0 kcal/mol more stabilizing than its thermophilic ortholog. Moreover, our Poisson-Boltzmann continuum electrostatic free energy model³⁹ actually predicts the electrostatic contribution of the mesophilic protein to be more stable at pH 3.5 (Fig. 4). These mentioned specific attributes are counter to the previously described stability conservation. The DCM parameterization differences (Table I) provide the necessary compensating factors, which imply improved hydrophobic interactions within the T. thermophilus structure. This result is exactly consistent with the earlier results of Ishikawa et al.¹³

Fig. 4.

E. coli (bold solid line) and T. thermophilus (light solid line) RNase H stabilities (ΔG_elec) calculated from a simple Poisson-Boltzmann continuum electrostatics model.³⁹ The difference between the calculated stabilities (ΔΔG_elec) of the two orthologs is indicated by the dashed line. The electrostatics-only model incorrectly predicts the E. coli ortholog to be 1.59 kcal/mol more stable at pH 3.5.

The phenomenological parameters (u and v) relatively stabilize the thermophilic protein. Ostensibly, u and v are enthalpic parameters, dealing with protein–solvent interactions and native torsion angle energies, respectively. However, in reality, phenomenological parameters serve as effective catch-all parameters. It has previously been demonstrated that v is a structurally dependent parameter.^9,10 The best-fit v parameters differ by 17%; however, other good fits were found to yield differences as little as 5%. In the latter cases, more dramatic differences within u compensate for the reduced variability within v. These details typify how u and v act in concert with each other. Nevertheless, arbitrarily locking v as a transferable variable across all proteins and solvent conditions has been found to be overly restrictive, thus leading us^9,10 to use a three-parameter minimal DCM (not two parameters). As foreshadowed in the Methods section, differences in u and v are largely a result of an added cohesive force relatively stabilizing the thermophilic ortholog. In the context of Landau theory, parameterization differences provide physical insight. Through a process of elimination, the cohesive force is interpreted to be primarily hydrophobic. Differences arising from varying solvent conditions are moot because of common experimental conditions. Because of the high degree of structural similarity between the pair, structural differences are unlikely to be a contributing factor for causing differences in parameters. Furthermore, it has been suggested based on supporting evidence that hydrophobic contacts track H-bond formation well.⁴⁴

Rigid cluster susceptibility characterizes fluctuations in the size of rigid clusters that form and break within the protein as a function of θ. The peak, denoted by θ_RP, defines a rigidity percolation threshold where the protein is transitioning from predominantly one large rigid cluster to many smaller ones. Differences between the transition state location, θ_TS, and θ_RP have previously been used to correctly infer transition state compactness.¹⁰ For example, when θ_RP > θ_TS, the transition state consists of predominately one large rigid cluster, presumed to be native-like. In both cases here, θ_TS > θ_RP [Fig. 3(b)], meaning the transition state of each protein is expected to consist of many small rigid clusters.

The rigid cluster susceptibility is primarily determined by constraint topology details, which encompasses the specification of the type, strength, and distribution of constraints within the protein structure. The intrinsic network rigidity properties of each RNase ortholog are found to be largely insensitive to temperature—further supporting a prior claim⁹ that this quantity characterizes mechanical response to changes in global flexibility. Surprisingly, in view of their structural similarities, significant differences are observed in the rigidity percolation susceptibility curves between the RNase H pair. The mesophilic protein has θ_nat < θ_RP < θ_TS (see Fig. 3 and Table I). The thermophilic susceptibility curve is broader, has a higher maximum value, and interestingly has θ_RP < θ_nat. These attributes indicate that the native ensemble of conformations of the thermophilic protein is in a state of flux, much different than its mesophilic counterpart. This result further supports the increased importance of hydrophobic interactions within the thermophilic protein. The fluctuation content in rigid substructures is possible because of the fluid nature of hydrophobic cores.⁴⁵

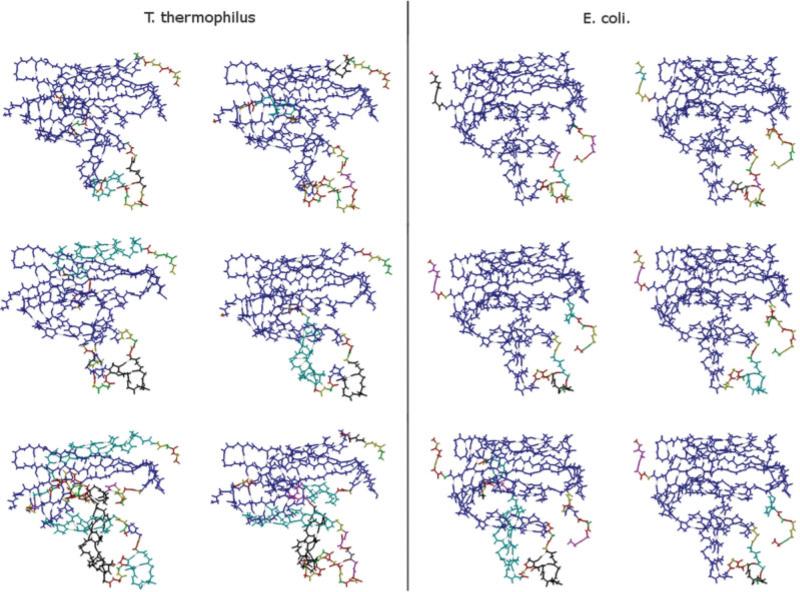
Typical samples of rigid cluster decompositions taken from the thermophilic and mesophilic native-state ensembles are shown in Figure 5. In nearly all samples, the mesophilic protein is primarily composed of one large rigid cluster, with a few flanking flexible coil and turn regions mostly corresponding to the substrate orienting “handle region.”⁴⁶ Similarly, the folding core¹⁶ of the thermophilic protein is frequently intact. However, consistent with rigid cluster susceptibility results, the entire thermophilic structures are not always composed of a single cluster. The most common differences occur in helices C and E, which are consistent with previous experimental conclusions describing their role in catalysis.¹⁶ For example, helix C makes up a large portion of the flexible handle region. Correspondingly, a mutant E. coli RNase H without helix E has been shown to be slightly active,⁴⁷ which indicates that its exclusion from the rigid core is not expected to be deleterious.

Fig. 5.

E. coli and T. thermophilus RNase H example rigid substructure decompositions. Color variations indicate unique rigid substructures. The native structure of the T. thermophilus is less likely to be primarily composed of a single rigid substructure, yet the folding core generally remains intact.

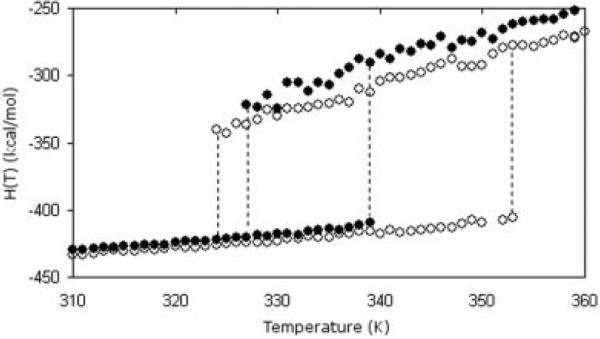
Dramatic differences in metastability are also observed. Simultaneous occurrence of the native and unfolded states is shown as hysteresis curves for both orthologs in Figure 6. Hysteresis is a consequence of two metastable free energy basins in G(T,θ), as seen in Figures 1 and 3(a), resulting in two state behavior. A hysteresis temperature range of 12° and 29°C is found for E. coli and T. thermophilus orthologs, respectively. Hysteresis occurs slightly sooner in the T. thermophilus ortholog, and also extends to significantly higher temperatures. At respective T_m's, ΔH_fold = (−419.4 + 311.5) = −107.9 kcal/mol and −T_mΔS_fold = (−1,005.7 + 1,113.8) = 108.1 kcal/mol for the mesophilic protein, and ΔH_fold = (−420.4 + 308.3) = −112.1 kcal/mol and −T_mΔS_fold = (−975.3 + 1,087.3) = 112.0 kcal/mol for the thermophilic protein. Interestingly, the native states of both orthologs are energetically similar (−419.4 vs. −420.4 kcal/mol), but the E. coli ortholog has comparatively greater conformational entropy (−1,005.7 vs. −975.3 kcal/mol). Based on these global thermodynamic properties of the native state and the electrostatic stabilization analysis described above, it naively appears that E. coli should be more resistant to thermal denaturation. The only explanation found for the observed differences in thermodynamic response is a direct manifestation of the subtle differences in constraint topology. The essential topological deterministic is the compactness of the folding core at the transition state, which is responsible for the distinct enthalpy-entropy compensation mechanisms in the unfolding/folding process.

Fig. 6.

The coexistence of folded (bottom) and unfolded states (top) implies a first-order phase transition. The extent of the hysteresis range corresponds to the vanishing of the unstable minimum in the Landau free energy. That is, at a temperature where a local metastable minimum ceases to exist, one of the above lines ends. The hysteresis range is much greater in the T. thermophilus structure (open symbols) than its E. coli counterpart (filled symbols). Vertical lines were added to guide the eye.

As temperature increases, the compact native folding core of the E. coli ortholog will comparatively break apart more readily because the conformational entropy cost within this folding core (not the entire protein) is greater than the thermophilic protein. The predominate rigid cluster in the native state becomes thermodynamically unstable, thus it spontaneously breaks apart in order to exchange a large gain in enthalpy for a compensating gain in conformational entropy. This process disintegrates the folding core into many different rigid clusters making up the unfolded protein. In contrast, breaking up the folding core in the T. thermophilus ortholog will yield less conformational entropy gain because of the “slippery” nature of the hydrophobic interactions⁴⁵ within the native free energy basin. The DCM captures this effect through a less favorable value of the u parameter. As temperature increases, the number of crosslinking H-bonds is reduced similarly as the mesophilic protein. However, the driving force to disintegrate the folding core is absent because of the fluid nature of the hydrophobic contacts, which is reflected in the rigid cluster susceptibility curves [Fig. 3(b)]. Therefore, the native T. thermophilus structure is better able to withstand temperature increases.

An appropriate analogy is the difference between brittle and elastic mechanical structures. Although it may initially appear that brittle structures are more resistant to applied forces, the elastic structure is able to give way to these forces, thus retaining its integrity longer. The analysis presented here implies that the E. coli ortholog localizes thermal fluctuations into the compact folding core to such a degree that structural integrity at higher temperatures is compromised. The T. thermophilus ortholog, in contrast, more evenly distributes thermal fluctuations into conformational changes. Presumably, its increased barrier height is related to the greater amount of thermal energy that can be absorbed before a large-scale change in constraint topology (i.e., unfolding) is necessary to maintain a thermodynamically stable ensemble of conformations. Taken together, this analysis illustrates the intimate connection between thermodynamic and mechanical response, both of which are directly quantified in the DCM.

Locally Conserved Flexibility Profiles

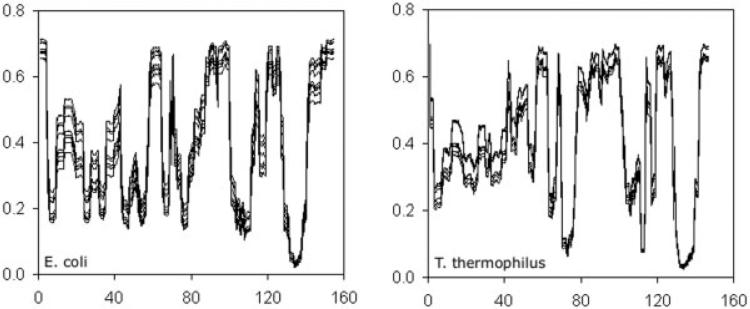
In Figure 3(c), the probability that a backbone dihedral angle can rotate, P_R, for each protein is compared. It is found that the backbone flexibility is less in the thermophilic protein than its mesophilic counterpart when compared at the same temperature. The measure of P_R was obtained by averaging over all accessible conformations. This result is found to extend into predicted thermodynamic properties as quantified by comparing −TS_c, where it is found (results not shown) that, over the entire temperature range, conformational entropy is lower in the thermophilic protein. The backbone flexibility profile is conserved at respective T_m when averaging over the full ensemble of accessible conformations. The only prominent difference occurs within helix A. Consistent with H/D exchange results,¹⁶ helix A is predicted to be rigid within the mesophilic structure. However, helix A of the thermophilic protein is incorrectly predicted to be flexible because of a crystal contact artifact in the input structure. Nonnative crystal contacts within the thermophilic unit cell cause a kink at the N-terminal end of the helix. Except for this one difference, the local distribution of flexibility is similar throughout the remainder of the protein structure. In the restricted native structure sub-ensemble basin (Fig. 7), both proteins share common rigid regions consisting of the β-sheet and helices B, D, and E, whereas the handle region is flexible. A complete lack of slowly H/D exchanging amides within the handle regions of the native structures experimentally confirm their floppiness.¹⁶ Furthermore, the overall flexibility profiles of the transition state and unfolded structures are also qualitatively conserved, confirming the previously described unfolding pathway conservation.¹⁷

Fig. 7.

T. thermophilus (left) and E. coli (right) RNase H probability to rotate (P_R) for the native, transition, and unfolded sub-ensembles are shown (vs. the full ensemble shown in Figure 3(c). From the free energy basin governing accessible native conformations, the flexible (red) and rigid (blue) regions agree well with H/D exchange results that explicitly characterize only the native sub-ensemble.¹⁶ In the bottom pair: red, blue, green, and yellow indicate simultaneous occurrence of flexible/no slowly exchanging amides, rigid/slowly exchanging amides, rigid/no slowly exchanging amides, and flexibly/slowly exchanging amides, respectively. Red and blue coarsely indicate similarity between theory and experiment. Green may or may not indicate agreement depending on solvent accessibility (see text), and yellow indicates disagreement.

As described within refs. 9 and 10, the biggest problem in comparing two flexibility quantities is to ensure that the physical content of both is the same. It is unreasonable to expect that P_R should correlate exactly with B-factors, S2-order parameters, and H/D exchange data when these quantities do not linearly correlate with each other better than 65%. At this crude level of correlation, it has previously been demonstrated that DCM flexibility measures are in agreement with all three of these experimental measures.¹⁰ Here, a qualitative comparison of P_R with H/D exchange data¹⁶ is made (Fig. 7, bottom comparison). Red indicates regions where flexible P_R > 0.35 values and a lack of slowly exchanging amides simultaneously occur, whereas blue indicates the reverse scenario. These situations, roughly corresponding to agreement between theory and experiment, occur 64% of the time. Green highlights regions where the DCM predicts rigidity, yet no slowly exchanging amides are observed. Most of these situations are a result of solvent accessibility—a region might be rigid, but if it is exposed, exchange with solvent will still occur. Not considering green sites that are solvent accessible raises the agreement to 80% and 72% for the E. coli and T. thermophilus orthologs, respectively. The larger discrepancy in the thermophilic structure is the result of unrealistic flexibility (colored yellow) predicted in helix A (center of structure). As discussed above, flexibility in helix A is an artifact of a kink introduced by a nonnative unit cell crystal contact. As a function of sequence, P_R is compared with the experimentally identified folding core in Figure 8.

Fig. 8.

Backbone flexibility quantified by the probability that a PHI or PSI dihedral angle can rotate (P_R) versus residue number (thin line). The values reported are for the native structure sub-ensembles, contrast to Fig. 3(c), which is the full thermodynamic average. The bold black squares at the bottom of each plot indicate experimentally determined slowly exchanging amides,¹⁶ which are also determined solely from the native structure. Smoothed values (bold line) are provided to facilitate comparisons. The theoretical predictions are consistent with the experimental results; however, there are some subtle differences. The differences can largely be attributed to solvent exposure and the crystal contact artifact within the T. thermophilus unit-cell.

Conserved Correlated Catalytic Motions

Several experimental investigations^46,48,49 have identified sites in RNase H critical to function. The three most important sites, which are related to Mg²⁺ binding, are Asp10, Glu48, and Asp70.¹³ Furthermore, the conserved His124 is also critical to function. Davies et al.⁴⁸ have concluded from a comparison of several crystal structures from RNase H-like proteins that the loop centered on His124 is universally flexible. Functional efficiency is further affected by the orientation of the handle region,⁵⁰ which is sensitive to alignment position 80. Gly80 occurs in the thermophilic protein, whereas a gap occurs in the mesophilic. The crystal structure of a mutant mesophilic protein with an inserted Gly at position 80 induces a local reorientation of the handle region, resulting in a drastic loss of enzymatic activity.⁴⁹

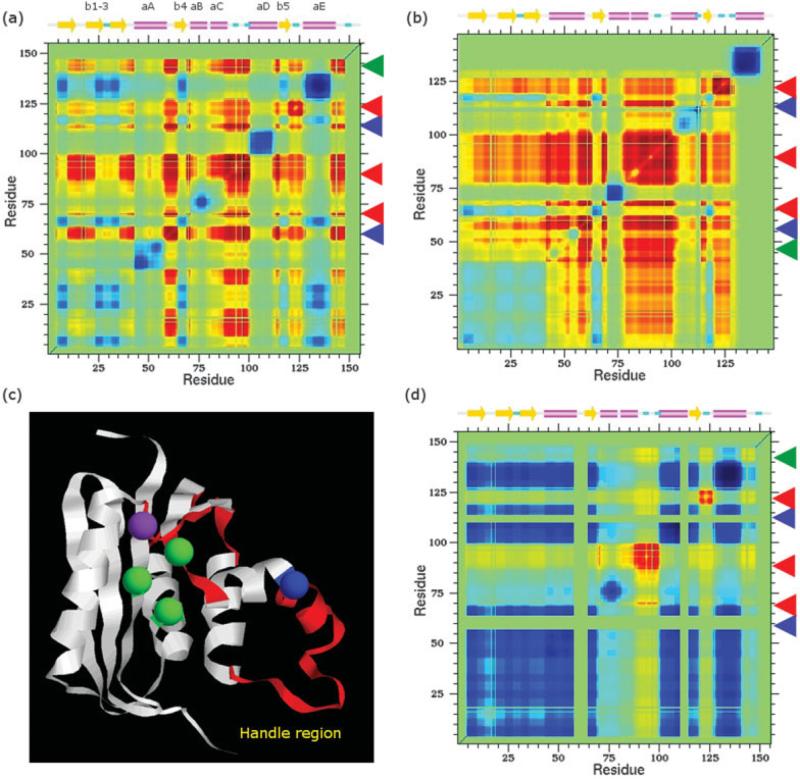
The cooperativity correlation plots shown in Figure 9(a, b) are used to identify correlated (allosteric) motions. The cooperativity correlation plots do not simply highlight flexible and rigid regions. For example, the N- and C-terminal coil segments, which are the most flexible portions of the protein, do not participate in any concerted motion. Cooperativity plots identify regions that are correlated across the entire ensemble of realizations (see Fig. 5), and therefore they provide entropic information as well as mechanical. Information about which regions are flexibly and rigidly correlated is strongly dependent on temperature.

Fig. 9.

Cooperativity correlation plots identify rigidly or flexibly correlated regions. Regions colored red are flexibly correlated, blue regions are rigidly correlated, and green regions are without correlation. The E. coli and T. thermophilus structures are shown in (a) and (b), respectively. The thermophilic protein has a more extended flexibly correlated region, which is consistent with a greater degree of hydrophobicity in its folding core. Arrows highlight the five identified flexibly correlated regions. The blue arrows indicate the two flexibly correlated “connection loops.” The green arrows highlight flexibly correlated regions that are not evolutionarily conserved between the two orthologs. c: The flexibly correlated regions (colored red) are mapped onto the mesophilic structure. Asp10, Glu48, and Asp70 (shown in green) are evolutionarily invariant and known to be involved in Mg²⁺ binding.¹³ His124 and Gly80 are colored purple and blue, respectively. The allosteric loops are obscured (they occur on the polar opposite face of the protein). Note: the structural orientation has been changed from Fig. 7 to highlight the active site. d: Cooperativity correlation plot of the mesophilic RNase H with an allosteric loop rigidified. This result demonstrates that the connection loops are necessary for the concerted motions within the three remaining flexibly correlated loops.

Barring the exception of helix A, the two cooperativity correlation plots are found to be similar at their respective T_m. In both cases, the surface loops connecting helix A/strand IV, strand IV/helix B, helix D/strand V, and strand V/helix E are flexibly correlated. Additionally, the handle region is flexibly correlated with the above secondary structure connection. However, the flexibility correlation with the handle of the T. thermophilus structure is greater than its E. coli counterpart. Figure 9(c) highlights the conserved flexibly correlated regions and the five discussed functional sites. Asp70 and His124 are located within flexibly correlated loops. Furthermore, Gly80 occurs at the N-terminal edge of the flexibly correlated handle region. Based on their recognized functional importance, it is not surprising that allosterism is observed within these regions. All three regions are located on the active site face of the enzyme surface. However, the functional role of the two remaining flexibly correlated loops, termed here “connection loops” is not immediately clear. The connection loops are not particularly notable because they are located on the opposite side of the active site (at residues 59–64 and 110–113). Furthermore, their functional importance is unexpected because of little sequence conservation across the complete RNase H family (unpublished results). However, the connection loops identified in both orthologs provide a mechanistic connection that couples to the other conserved flexibly correlated regions known to be important for function.^13,48–51

Whereas there is no known evidence confirming the functional role of the correlated motions, evolutionary conservation of the calculated QSFR within the two orthologs is strongly suggestive. In both cases, a single nonconserved flexibly correlated region is identified (highlighted in Fig. 9 by green arrows). In the thermophilic case, the additional flexibly correlated region is simply an artifact of the crystal contact in helix A. In the mesophilic case, the additional flexibly correlated region occurs within a stretch of coil after helix E. It is difficult to predict whether this particular region is critical to functional efficiency, but lack of a corresponding flexibly correlated region in the thermophilic ortholog suggests it is not. The degree to which these nonlocal connecting loops have a governing role on function is now addressed using the DCM and predicted QSFR upon perturbation.

The sum total of the cooperativity correlation analysis on both structures suggests that correlated conformational changes are necessary for functional efficiency. To confirm their functional importance, a DCM analysis was repeated with the backbone dihedral angle pairs of five residues externally locked within the connection loops (three on one loop and two on the other). Thereafter, only very weak flexible correlation between the handle region and the Asp70 loop remains [Fig. 9(d)] within the E. coli structure. All other flexibility correlations are destroyed, suggesting that the predicted concerted motion is functionally important. Besides making for a direct experimental test, functional efficiency might be controlled by engineering a locally rigidifying structure, such as incorporation of a cysteine bridge redox switch⁵² spanning the connection loops. The reduction in the flexibility correlation within the T. thermophilus structure is far less. In fact, externally locking all 14 connection loop dihedral angle pairs results in a structure in which the flexibility correlation is still greater than that shown in Figure 9(d). The predicted difference is likely a consequence of the geometrically confined mechanical tethers (hydrogen bonds and salt bridges) of the E. coli structure, whereas the hydrophobic interactions within the T. thermophilus structure are more accommodating.

Model Sensitivity to Parameterization Differences

To test the sensitivity of the flexibility predictions on parameterization, a thorough three-dimensional grid search over different parameter sets (u, v, δ_nat) is provided. Not surprisingly, as reported earlier,^9,10 there are multiple good fits to the experimental C_p curves that do reasonably well. Upon close inspection, we find a line of good fits, which we view as a function of δ_nat. That is, for a given δ_nat, there is a u,v pair that allows a good fit. If this line were to extend indefinitely, one of the parameters (say v) could be fixed for all proteins to reduce the minimal DCM to have only two free parameters. However, a two free parameter DCM was attempted (unpublished data) early in its development, but to robustly cover protein diversity, three fitting parameters (u, v, δ_nat) are required. Examination of these alternative parameter sets, as detailed within the supplementary data, demonstrates that the analysis and conclusions based only on best-fit parameters (Table I) are robust. The analysis of parameter sensitivity is summarized through both statistical analysis and a series of exemplar comparisons that were selected at random involving nine alternative good fits plus one bad fit. The exact values of all exemplar parameter sets are provided in Supplementary Table I.

Good fits are defined as having a root mean square-least squares error of <0.03 where the error function is normalized the same way as in Livesay et al.¹⁰ and defined in Supplemental Material. The best good-fit u,v pairs (as a function of δ_nat) robustly indicate that an added cohesive force is present within the thermophilic ortholog (Supplementary Fig. 1). Furthermore, as discussed within refs. 9 and 10, flexibility profiles are mainly a manifestation of constraint topology and are rather insensitive to parameter differences (Fig. 10). The range of variation found in the quantities C_p,max, T_m, and θ_nat,TS,unf over the collection of multiple good fits, are respectively: ±5 kcal/(mol K), ±3 K, and at worst ±0.28 for θ_nat, as shown in scatter plots (Supplementary Fig. 2). Although variability increases drastically in poorer fits, no drastic differences are found in QSFR descriptors or any thermodynamic properties for either of the mesophilic and thermophilic orthologs when restricting parameter sensitivity to the set of good-fit parameters. At very high errors of 0.12, none of the fits can predict T_m within ±6 K, and moreover, this deviation monotonically increases as the error increases. This result indicates that parameters simply cannot compensate enough to achieve arbitrary targets. Despite a good-fit degeneracy in the form of a line in parameter space, these results give assurance that any good fit to heat capacity curves obtained by simulated annealing will almost surely provide robust QSFR predictions. Also important to test is whether parameter variation within a good-fit tolerance level retains robust physical insight.

Fig. 10.

Backbone flexibility quantified by the probability that a PHI or PSI dihedral angle can rotate (P_R) versus residue number for nine E. coli and nine T. thermophilus exemplar parameter sets, each with an overall error ≤0.03. In all cases, flexibility information is conserved. The values here are thermodynamically averaged over the native structure sub-ensemble only. Values averaged over the full thermodynamic ensemble of all accessible conformations are provided in Supplementary Figure 6. Exact values of all exemplar parameter sets are provided in Supplementary Table I.

The entropic parameter δ_nat quantifies the entropic cost of being within a native torsion angle. Consequently, δ_nat is presumed to be fold-dependent. As described above, δ_nat is simultaneously fit over the two similar structures, resulting in differences only within the u,v pair. Supplementary Figure 3 correlates these parameter differences within the best u,v pair as a function of δ_nat, demonstrating how all three phenomenological parameters work in concert. Not surprisingly, a strong correlation (R = 0.89) is observed between δ_nat and v, the enthalpic cost of transitioning from a native to unfolded torsion angle, meaning that v can compensate for δ_nat, and vice versa. Weaker correlations exist between the other two combinations with trends that follow physical expectation. Supplementary Table II correlates all parameter pairs between themselves and several other model predictions. Most noteworthy is that δ_nat,TS,unf have greatest sensitivity to parameterization. Interesting, because of the initial assumption that both orthologs share the same δ_nat parameter value (because of similar fold characteristics), the trends in θ_nat,TS,unf for the mesophilic and thermophilic orthologs are locked together in concert (Supplementary Fig. 4). Consequently, the conservation of QSFR relating global stability to flexibility (Fig. 1) based on key θ-values is a robust conclusion, insensitive to parameterization.

Perhaps the most important QSFR descriptor is the cooperativity plots that help identify nonlocal influences within the protein. As illustrated using the E. coli ortholog, the cooperativity correlation plots for all nine good-fit cases provide very similar visual information (Supplementary Fig. 5). Excellent visual correspondence is also observed in the T. thermophilus ortholog. The only outliers are from the bad-fit cases. In E. coli ortholog, the bad case is considerably more rigidified. It is found that the full thermodynamic ensemble average (in contrast to the native ensemble) results in greater differences in backbone flexibility predictions between the bad fit and good fits (Supplementary Fig. 6). Nevertheless, parameter variation over the good fits produces robust predictions. Interestingly, this particular bad case happens to be over-rigidified (other bad cases can be too flexible), yet the corresponding T_m is greater than the actual T_m. Because the results are being shown for T = T_m, naively one would think at higher temperatures the structure will be more flexible. This latter nonintuitive result indicates that the rank ordering in the degree of rigidity and flexibility is nontrivially dependent on thermodynamic condition governed by the specifics in constraint topologies.

Clearly, a proper quantification consisting of a meaningful rank ordering depends on the DCM parameterization of constraints, which bridges thermodynamics to mechanical properties. The consistency found in the good-fit predictions supports the idea that successfully fitting to C_p curves ensures that microscopic energy fluctuations are being represented properly. As a further check on the influence of fluctuations (constraints breaking and forming), the rank ordering in cooperativity correlation values should be preserved in addition to local rigidity and flexibility. Of most concern is in the native state, where the rank ordering of predicted local flexibility and rigidity along the backbone is well preserved (Fig. 10). The corresponding rank ordering in degree of cooperative correlation is also well preserved for all good fits (Supplementary Fig. 7). Therefore, the above analysis involving allosteric effects on addition of constraints are robust against DCM parameterization. Given the wide degree of overall qualitative agreement with experimental findings, the quantitative comparative investigation performed with the minimal DCM seems to have intrinsic precision (at the least) and is reasonably accurate, considering the simplicity of the model.

CONCLUSIONS

A minimal DCM predicts substantial differences in the underlying enthalpy-entropy compensation mechanisms of an orthologous RNase H pair. Despite these differences, overall conservation within several QSFR descriptors at their respective melting temperatures is found. Both predictions are consistent with earlier experimental conclusions. Furthermore, the DCM also identifies several functionally important flexibly correlated regions that help explain the rich biochemical literature surrounding RNase H-like proteins. Identification of connection loops highlights the importance of stability and flexibility considerations when describing protein function. We predict locally rigidifying the connection loops located far from the binding site will dramatically reduce functional efficiency in the E. coli structure, but have little effect in the T. thermophilus protein. Furthermore, the conclusions herein are demonstrated to be robust with respect to DCM parameterization. This work serves as a paradigm study to demonstrate the utility of a QSFR analysis in lending itself to computational protein design applications that have never before been possible in biophysical modeling.