Leveraging Distant Relatedness to Quantify Human Mutation and Gene-Conversion Rates

Abstract

The rate at which human genomes mutate is a central biological parameter that has many implications for our ability to understand demographic and evolutionary phenomena. We present a method for inferring mutation and gene-conversion rates by using the number of sequence differences observed in identical-by-descent (IBD) segments together with a reconstructed model of recent population-size history. This approach is robust to, and can quantify, the presence of substantial genotyping error, as validated in coalescent simulations. We applied the method to 498 trio-phased sequenced Dutch individuals and inferred a point mutation rate of 1.66 × 10⁻⁸ per base per generation and a rate of 1.26 × 10⁻⁹ for <20 bp indels. By quantifying how estimates varied as a function of allele frequency, we inferred the probability that a site is involved in non-crossover gene conversion as 5.99 × 10⁻⁶. We found that recombination does not have observable mutagenic effects after gene conversion is accounted for and that local gene-conversion rates reflect recombination rates. We detected a strong enrichment of recent deleterious variation among mismatching variants found within IBD regions and observed summary statistics of local sharing of IBD segments to closely match previously proposed metrics of background selection; however, we found no significant effects of selection on our mutation-rate estimates. We detected no evidence of strong variation of mutation rates in a number of genomic annotations obtained from several recent studies. Our analysis suggests that a mutation-rate estimate higher than that reported by recent pedigree-based studies should be adopted in the context of DNA-based demographic reconstruction.

Introduction

Germline mutations represent a fundamental evolutionary force that shapes phenotypic variation and has a profound impact on heritable diversity. Precise estimation of mutation rates has several applications, including the interpretation of mutations implicated in diseases,^{1, 2, 3} studies of natural selection,^{4, 5} the timing of demographic events inferred from genetic analysis,^{6, 7, 8} and the study of several aspects of human mutagenesis.⁹ High-throughput sequencing technologies have recently enabled the quantification of germline mutation rates, but the estimates obtained by these methods are inconsistent with those of previous studies. The source of these inconsistencies, whether biological or due to methodological biases, is at the center of recent debate,^{7, 10, 11} and gaining additional insight into germline mutation rates will require new methods.

In this work, we propose a method for estimating mutation rates by using mutations occurring within identical-by-descent (IBD) haplotype blocks^{12, 13, 14, 15, 16, 17} transmitted through recent common ancestors who lived ∼100 generations (∼3,000 years) before the present. These IBD segments can be detected by several available methods^{13, 18, 19} and reflect genetic relationships that are typically not known to the affected individuals but are found to be ubiquitous even in outbred populations.^{15, 20} IBD segments are defined in our work as contiguous chromosomal regions in which the most recent common ancestor (MRCA) for two sampled chromosomes is unchanged. Occasional mutations segregating along the lineages connecting a pair of IBD haplotypes to their MRCA will create mismatched sites on the shared haplotypes, and these sites can be used for inferring the rate at which new germline mutations appear. If the exact number of generations separating the IBD segments (via their MRCA) is known, one can infer the mutation rate by dividing the number of observed sequence mismatches by the number of generations and the physical length for all segments. A special case of this approach is used in trio-based analyses, where transmitted parental haplotypes and IBD offspring haplotypes are separated by a single generation. In this work, we instead use a reconstructed demographic model to infer the age of IBD segments.

The IBD-based approach we propose for inferring mutation rates is robust to, and can quantify, the presence of substantial amounts of genotyping error in the analyzed sequences and can be used for inferring the rate of non-crossover gene conversion. We applied the developed methodology to analyze 250 trio families from the Netherlands and infer mutation and gene-conversion rates. We further studied the rate of short indels and analyzed the relationship between recombination rates and mutation rates. We studied the enrichment of deleterious variation in mismatching variants within IBD regions, showed that the length of shared IBD segments along the genome closely reflects summary statistics of background selection, and explored enrichment or depletion of mutation rates in several specific genomic annotations.

Material and Methods

Overview of Methods

The method we propose is aimed at estimating the sex-averaged, genome-averaged, and time-averaged mutation and gene-conversion rates per base per generation by using mismatching genotype sites found on IBD haplotypes for a sample of individuals from a population of known demographic history. Note that these quantities are affected by several aspects of the study population, such as the length of the generation for males and females along the ancestral lineages in the past several generations (∼100 generations in our analysis; see Discussion). We briefly describe solutions to three challenges. First, to estimate the number of generations separating two IBD segments (twice the time to the MRCA [tMRCA]), we use a recently developed method¹⁴ that relies on the spectrum of observed IBD-segment lengths to infer demographic history. We then use this method to obtain a posterior mean estimate of the average tMRCA for pools of IBD segments of different lengths, as detailed in the real-data description (see GoNL Dataset) and Appendix A. Second, to deal with the presence of genotyping errors rather than rely on stringent filtering criteria (as in trio-based analyses^{21, 22, 23, 24, 25}), we regress the observed sequence mismatches for several IBD-segment length thresholds on the estimated tMRCA; the slope of this regression reflects the rate at which new mutations accumulate per generation time unit, whereas the genotyping error rate is captured by the intercept. We refer to this procedure as tMRCA regression (illustrated in Figure 1). Finally, we correct for the occurrence of non-crossover gene-conversion events along the lineages leading to the MRCA by exploiting the relationship between an allele’s frequency and the probability that it is involved in a gene-conversion event (see Controlling for Gene Conversion via MaAF-Threshold Regression below). This also allows us to estimate the rate at which a genomic locus is involved in a non-crossover gene-conversion event; this rate is proportional to the difference between corrected and uncorrected estimates for mutation rates. We have released open-source software (IBDMUT) implementing these methods (see Web Resources).

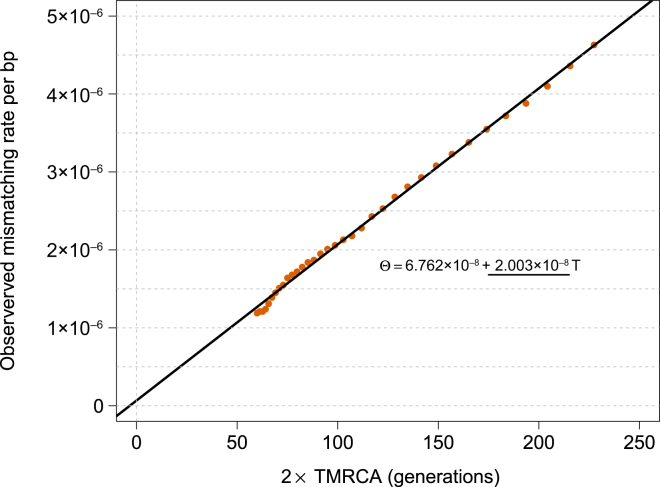
Figure 1.

tMRCA Regression

We simulated a chromosome of 50 cM for 250 diploid samples by using μ = 2 × 10⁻⁸ for the mutation rate and no genotyping error. We matched the allele-frequency spectrum of the simulated samples to the spectrum found in real data for IBD-segment detection with GERMLINE, and we used the IBD-segment detection parameters used in real data. The slope of this regression captures the simulated mutation rate; the intercept is proportional to genotyping error rate.

Estimating the Mutation Rate via tMRCA Regression

The proposed methodology for the inference of mutation rates requires the availability of haploid genotype data, a list of IBD segments that exist between pairs of haploid individuals and that are longer than a specified Morgan length threshold (including start and end positions), and a demographic model, which can be inferred from the spectrum of shared IBD segments as described in Palamara et al.¹⁴ For each IBD segment i, we obtain an observed mismatch rate by counting the number of sequence differences m_i in the haploid genotypes within the region and dividing by the region size s_i in base pairs: θ_i = m_i/s_i. We then obtain the observed mismatch rate by averaging all observations ${\hat{\theta }}_u=n_u^{-1}{\sum }_{i=1}^{n_u}{\theta }_i$ for n_u segments longer than u Morgans. We repeat this measurement for several thresholds u to obtain a vector of observed mismatch rates $\hat{\mathit{\theta }}$. Because of the lack of detailed pedigree structures at deep time scales, the exact number of meiotic events separating two individuals who share IBD segments is generally unknown. Using the reconstructed demographic model, we therefore infer the posterior mean age t_u of pooled IBD segments longer than a known genetic length threshold u by using recently developed coalescent theory^{14, 15} (details are summarized in Appendix A). Finally, we regress the observed mismatch rates ${\hat{\theta }}_u$ on twice the posterior mean age (in generations) to the MRCA of the IBD segments: ${\theta }_u=\alpha +2\mu t_u+\mathit{ϵ}$. We refer to this regression as the tMRCA regression. Older segments will tend to harbor a larger number of sequence differences because mutation events have a higher chance of occurring along the lineages connecting extant individuals to their MRCA. The slope μ of this regression will capture the rate at which mutations arise per unit of time. Note that we are neglecting the uncertainty on the measurement in the regressor t_u, i.e., the inferred age of the pooled IBD segments. As shown in simulations, however, this only results in negligible biases for the estimated slope coefficient because of the large number of pooled segments.

If we assume a genotyping error model for which false-positive or -negative genotype calls are independent of the average coalescent time of pairs of individuals at a locus, the intercept α of this regression is expected to capture the rate at which genotyping errors occur on the considered range of IBD segments. Note that when performing the tMRCA regression, we rely on non-independent observations of mismatch rates (because we use overlapping ranges for the length of the IBD segments), which corresponds to attributing larger weights to measurements obtained from long, more-reliable IBD segments. Although this violates independence assumptions in the regression, the reweighting of the data is not expected to result in biases for the estimated slope and intercept (Table S1), but it decreases heteroscedasticity. In order to estimate SEs of the resulting slope and intercept, which are expected to be biased because of non-independence, we rely in all cases on a block-weighted jackknife procedure,²⁶ which uses independent regions as resampling units.

Controlling for Gene Conversion via MaAF-Threshold Regression

Non-crossover gene-conversion events occur at a rate that is correlated to the recombination rate and have been observed to be more frequent than crossover recombination events.²⁷ In the coalescent process, gene conversion can be modeled as two consecutive recombination events that occur very close to each other,²⁸ at an average distance of ∼300 bp.²⁹ These events introduce the possibility that polymorphisms segregating in the population might be assimilated into haplotypes within IBD regions. These polymorphisms can create sequence differences between individuals who share IBD segments. These sequence differences, however, are not due to newly arising mutations. Note that whereas gene-conversion events change the MRCA of the ∼300 bp converted segment, here we do not consider this to break an IBD block. Furthermore, because the number of gene-conversion events is related to the number of meiotic events, short IBD regions will tend to exhibit more gene-conversion-driven mismatches than longer, more-recent IBD segments, therefore resulting in an upward bias when the mutation rate is estimated via the slope of tMRCA regression. The mismatching variants observed on IBD segments, therefore, will be due to at least two distinct sources of heterozygosity. The first, θ_p, which we hereafter call population heterozygosity, represents the effect of gene-conversion events, which introduce standing genetic variation onto IBD blocks. The second source of heterozygosity is due to newly arising point mutations on IBD blocks and will be referred to as θ_μ. For IBD segments of a chosen length, we can express the total observed mismatch rate as θ = θ_μ + θ_p. To estimate the mutation rate due to point mutations only, we need to exclude the effects of θ_p from our calculations. We make the following two observations:

• 1.The frequency of mutations that arise on long (e.g., ≥1 cM) IBD segments is typically low in the population (Figure S1), so that θ_μ is mostly due to rare variants.
• 2.If we divide the allele-frequency spectrum into bins of equal width, we find an approximately uniform contribution to θ_p for each frequency. This implies that if we compute the frequency-bounded population heterozygosity θ_p,f by using only variants of frequency up to f, we observe an approximately linear relationship between θ_p,f and f (Figure S2; see additional calculations in Appendix A).

Observation 1 implies that if we exclude high-frequency variants when we compute μ by using the proposed regression approach, the contribution of θ_μ to the observed mismatch rate on IBD segments will be largely unaffected. Furthermore, observation 2 suggests that if we estimate a frequency-bounded value of μ_f by ignoring variants of frequency higher than a threshold f, the contribution of population heterozygosity due to gene-conversion events, θ_p,f, will be decreased to an extent that is approximately linear in f. Assuming that the contribution of θ_μ to μ_f is unaffected for values of f in the range F = [F_min, F_max], we can therefore regress μ_f on F and observe a linear relationship. We refer to this regression as the MaAF-threshold regression (Figure 2). The intercept of this regression will then reflect an estimate of μ without the confounding effects of θ_p, whereas the contribution of θ_μ is left unchanged. We avoid computing values of μ_f corresponding to $F\in \left[0,F_{\text{min}}\right)$, for a sufficiently large F_min (e.g., >0.1), given that this might result in removing variants that are due to new point-mutation events on the IBD segments, which we use to estimate μ. Because this approach relies on the stochastic relationship among allele frequency, population heterozygosity, and gene conversion, it is not possible to fully determine whether the sequence mismatches that are found on IBD segments are due to a recent mutation event or a site involved in gene conversion, although those resulting from the latter are expected to have a substantially higher allele frequency. Finally, note that we neglect the possibility that point mutations arising on IBD segments are removed via gene conversion because this does not substantially affect the estimates. As in the tMRCA, the use of nested frequency bins in the MaAF regression results in non-independent observations in the performed regression. The use of nested frequency bins might improve the correction in cases where the relationship between MaAF cutoffs and population heterozygosity deviates from linearity as a result of recent demographic events. Simulations showed that his approach has no significant impact on the quality of the estimated mutation rates (Table S2). As in the case of tMRCA regression, we obtained reported SEs with the block-weighted jackknife method to avoid biases induced by the non-independent observations.

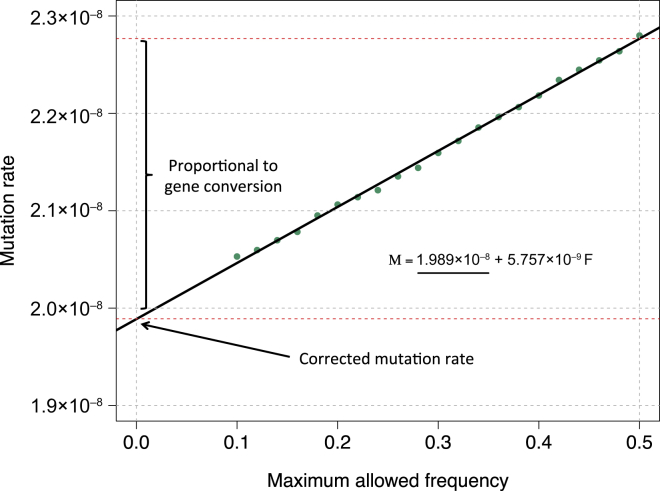
Figure 2.

MaAF-Threshold Regression

We simulated 250 diploid samples as described in Figure 1 and a probability of 6 × 10⁻⁶ for a base pair to be involved in a non-crossover gene-conversion event. We performed the MaAF-threshold regression to correct for the occurrence of gene conversion. The regression intercept is used for estimating the corrected mutation rate, whereas the difference between the corrected and uncorrected mutation rates captures the effects of gene conversion, whose magnitude can be estimated with the observed population heterozygosity.

Estimating the Gene-Conversion Rate

The difference between the mutation rate computed without correction for gene-conversion events and the estimate obtained after removal of the effects of gene conversion can be used for quantifying the probability that a base pair within IBD segments is involved in a gene-conversion event during meiosis. This difference, which we indicate as μ_GC, represents the probability of observing a heterozygous site as a result of existing polymorphisms introduced via gene conversion in a single generation. This rate can be expressed as μ_GC = p(GC) × p(θ_p | GC), i.e., the probability that a base pair is involved in a gene-conversion event can be multiplied by the probability of assimilating a heterozygous site given that the gene-conversion occurs at the locus. The quantity p(θ_p | GC) can be estimated with the genome-wide heterozygosity of the analyzed sample, and the value of μ_GC can be estimated with the previously described correction method. An estimate of p(GC) is therefore obtained as $\hat{p}\left(\text{GC}\right)={\hat{\mu }}_{\text{GC}}\times \hat{p}{\left({\theta }_p|\text{GC}\right)}^{-1}$, and a confidence interval is obtained via block-weighted jackknife.²⁶

Coalescent Simulations

We used extensive coalescent simulation to evaluate the proposed methodology. To this end, we used a publicly available coalescent simulator, COSI2³⁰ (which allows simulation of gene-conversion events), and our implementation of a coalescent simulator, inspired by the existing GENOME algorithm³¹ (which enables simulation of a large number of samples and efficient extraction of information on IBD segments). The algorithm proceeds backward in time and, for each individual at generation g, samples a parent at the discrete time g + 1 in the past, occasionally resulting in coalescent events and sampling a new parent when a recombination event occurs. To speed up computation, the GENOME approach divides the simulated region into relatively large chunks that are not allowed to recombine, discretizing the recombination process and resulting in approximate linkage-disequilibrium (LD) structure at short genomic intervals. The version we developed enables substantial improvements of memory and run-time requirements while circumventing the original GENOME algorithm’s simplifying assumption of non-recombining LD blocks. In brief, we sped up the original algorithm by sampling recombination breakpoints from an exponential distribution and by only storing chromosomal regions and individuals relevant for calculating the ancestral recombination graph (ARG) at each simulated generation. In addition, we applied several improvements to data structures and other algorithmic details. To evaluate our methodology, we further extended the program to allow efficient extraction of IBD segments from the ancestral recombination graph without requiring testing of differences in shared common ancestors for each marginal tree in the ARG, as done in previous works.^{14, 16, 32} We have released open-source software (ARGON) implementing the simulator (see Web Resources).

To assess the impact of demographic history on our estimates, we simulated three plausible demographic scenarios, in addition to the reconstructed GoNL (Genome of the Netherlands; see GoNL Dataset below) demographic history. The simulated populations comprised an expanding population that experienced a severe founding event 30 generations before the present and a population that undergoes severe exponential contraction (referred to as Ashkenazi and Maasai, respectively, because they resemble recently studied groups¹⁴) and an exponentially expanding population (referred to as Europeans; see Figure S3). We used two types of recombination maps to simulate non-uniform recombination rates along the genome (Figure S4). To assess the impact of genotyping errors on our methodology, we simulated errors for which a previously unobserved variant is created (“de novo” errors) or false-positive or -negative calls on existing variants. To model frequency-dependent genotyping error rates, we used a beta distribution as a prior for sampling the frequency of planted genotyping errors³³ (Figure S5). For all simulations, we obtained posterior mean estimates for the age of IBD segments by using the coalescent distributions of the simulated models.

GoNL Dataset

We analyzed sequence data from a recent study of 250 trio families from the Netherlands (GoNL project,³⁴ release 4). The dataset consists of 748 individuals who passed quality control and were sequenced at an average of ∼13× (details are provided in the analysis described elsewhere³⁴). Combining the output of several detection algorithms detected indels (GoNL Release 5). In addition to using the quality-control filters applied in the original analysis of the data, we further excluded regions that did not meet several quality criteria derived from the 1000 Genomes Project phase 1, as described in Genovese et al.³⁵

Trio phasing is expected to result in accurate estimation of haploid sequences in the GoNL data. Low-frequency variants, in particular, are unlikely to result in doubly heterozygous parents, so phasing of rare polymorphisms is generally trivial.

IBD segments and an inferred demographic model were obtained from the analysis described elsewhere³⁴ with the use of genetic maps from in the 1000 Genomes Project.³⁶ 26 regions were selected for the analysis reported in this paper; each was longer than 45 cM, which gave a total of 2,160 cM and an IBD density of 3.07 × 10⁻³ per site per pair. The B statistic of background selection⁴ in these regions is slightly lower than the genome-wide average (0.78 versus 0.79; p < 0.01 based on 10,000 permutations). The B statistic, however, was not found to have a significant impact on our mutation-rate estimates (see Results). The recombination rate was not found to be significantly lower than the genome-wide average (p = 0.37). Informed by the density of de novo mutation events along the genome, a recent study⁹ estimated a map of local variation in substitution rates. Out of the 14 types of substitutions reported in this map, four (C>T and G>A [p < 0.01]; A>T and T>A [p = 0.032]) were found to be depleted in these regions, although the differences were found to be minimal (−1.3% for C>T and G>A; −1.0% for A>T and T>A). This effect is probably mediated by the reduced B statistic in the regions, which is related to the substitution rates computed for primate sequences in Duret and Arndt,³⁷ on which the substitution map is based. Consistent with this hypothesis, we observed a small but significant correlation between these annotations and B statistic in these regions (r = 0.014 for C>T and G>A; r = 0.017 for A>T and T>A; p < 10⁻⁶). The density of IBD-segment sharing along the analyzed regions is depicted in Figure S10 and is occasionally non-uniform, as expected given the deviations from neutrality along the genome.^{20, 38} No significant correlation was observed between our mutation-rate estimates and the density of IBD-segment sharing (see Results). To cope with imperfect detection of the IBD-segment boundaries, we excluded 0.5 cM on either side of the IBD segments from the analysis of mutations and gene-conversion rates, because we observed that inflation due to noisy boundary estimation plateaued for values larger than this threshold (Figure S11).

Demographic inference was performed with the software tool DoRIS.^{14, 32} The resulting demographic history is one of exponential expansion starting with an ancestral population size of 11,500 haploid individuals 150 generations in the past. Two periods of exponential expansion were inferred. The expansion rate between generations 150 and 10 was inferred to be 0.0146 and was followed by a strong expansion in the recent generations at a rate of 0.479 per generation. Because of the scarcity of extremely recent coalescent events, the magnitude of the latter expansion period was inferred with a high degree of uncertainty; however, this was observed to not have appreciable effects on the analysis described in the remainder of the paper (see Results).

Enrichment of Deleterious Variation in IBD Regions

We tested whether mutations arising between the present generation and the MRCA of IBD segments are enriched with deleterious variation. To this end, we ran the software tool ANNOVAR (version “2015Mar22”³⁹) on the GoNL variants and obtained numeric scores for the PolyPhen-2 (“ljb23_pp2hvar”⁴⁰) and Gerp++ (“gerp++gt2”⁴¹) annotations; we restricted the analysis to scores > 2 for the latter. To test for enrichment, we compared the average score of genome-wide variants to the average score of variants found to mismatch within IBD regions; we treated all variants as independent and reported Z test p values.

Analysis of Annotated Genomic Regions

Several sites along the genome were excluded from the analysis after application of the filtering criteria previously described. In addition, we analyzed mutation rates in specific regions described in several annotations (e.g., DNase I hypersensitive sites⁴² and several others, as detailed in Table S3). It is sufficient to neglect regions that fall outside the genomic annotation at hand when computing the observed mismatch rate in the tMRCA regression. Annotations that are too small or too clustered in specific regions of the genome might result in downward biases of the estimated mutation rate because of the “inspection paradox” of the Poisson process underlying the model of IBD-segment sharing¹⁴ (Figure S12). For this reason, our method cannot be used for inferring local mutation rates. Annotation-specific bias due to localization was computed and corrected with a permutation procedure (Table S3). Sequence context was accounted for with the trinucleotide context-specific mutation-rate matrix of Kryukov⁴³ (details in Table S3).

To derive mutation rates for different mutation categories (CpG or non-CpG and transition or transversion), we downloaded the ancestral alignment used in the 1000 Genomes Project³⁶ (see Web Resources). The ancestral allele for loci that were not present in this sequence (545,279 out of 12,181,714) was set to the major allele found in the 1000 Genomes dataset (n = 300,503) or set to the allele found in the human reference genome (UCSC Genome Browser hg19; see Web Resources) if monomorphic in the 1000 Genomes dataset (n = 244,776). We then computed mutation rates by using MaAF-threshold regression and excluding variants that did not match the analyzed mutation type (e.g., CpG transition) and scaled the resulting rate by the genomic fraction that might harbor the specific kind of mutation (e.g., CpG or non-CpG).

Results

Simulations

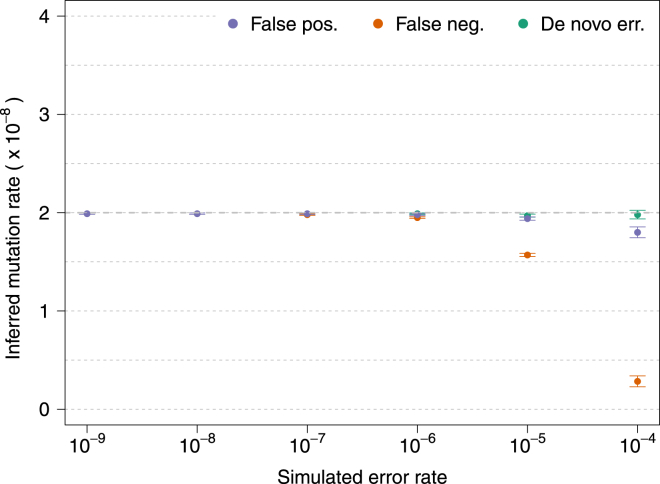
We evaluated the accuracy and robustness of the method via extensive coalescent simulation (see Material and Methods). To assess the impact of demographic history on our estimates, we simulated several plausible demographic scenarios and modeled genotyping errors by using a beta distribution with different parameters and specifying error rate at different allele frequencies (Figure S5). We extracted ground-truth shared IBD segments from the synthetic ancestral recombination graph and simulated three types of errors, referred to as de novo, false-positive, and false-negative errors (see Material and Methods; Figure 3). We observed that tMRCA regression is robust to the presence of substantial levels of de novo genotyping errors, consistent with the fact that IBD segments of different lengths are equally affected by the spurious sequence mismatches that result from errors of this kind. When we simulated false-positive genotyping errors, we observed our approach to be robust to errors up to a rate of ∼10⁻⁵ per base pair. False negatives were tolerated up to a frequency of ∼10⁻⁶. Very large values of false-positive or -negative genotyping error rates resulted in a downward bias of the estimates, which is due to the fact that IBD segments of different lengths harbor a slightly different spectrum of mismatching sites and are therefore not equally likely to be affected by spurious genotype calls (see Figure S1). Similar results were observed for several kinds of genotyping-error distributions, demographic models, and recombination maps, although the approach proved more robust for error distributions that are less concentrated on very rare variants (Figures S3–S5 and S13). The intercept of the tMRCA was observed to reflect genotyping error; average values were between 1× and 2× the simulated error rate (Figure S14), depending on the type of error and the parameters of the distribution used for selecting the frequency of affected alleles.

Figure 3.

Inferred Mutation Rates under Several Values of Simulated Genotyping Error Rate for Three Types of Genotyping Errors

The simulated true underlying mutation rate was μ = 2 × 10⁻⁸. All simulations involved a single chromosome of 250 cM for 200 haploid individuals from a GoNL-like population and used beta(α = 0.5, β = 1) as a prior for the allele frequency of erroneous variants. True IBD segments were extracted from the simulated ancestral recombination graph. Additional simulation results are shown in Figure S13. Error bars represent SE.

We note that the proposed procedure estimates a historical sex-averaged mutation rate per base per generation, a quantity that might be affected by potential differences between the mutation and recombination rates of males and females over several generations in the past. We performed additional simulations to test whether sex-specific mutation and recombination rates and effective population sizes could bias our estimates. We determined that sex-specific variability of these parameters did not produce a bias (Table S4), given that the recovered estimate reflected a flat average of male and female mutation and recombination rates.

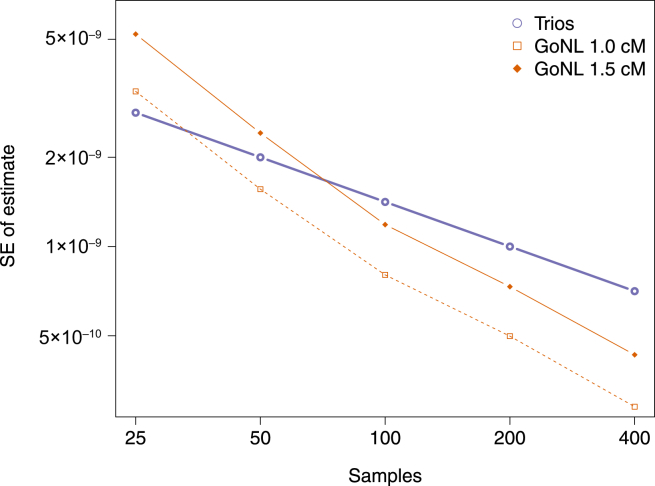
To compare the power of the proposed method to the power of trio-based mutation-rate inference, we simulated data at various sample sizes by using the GoNL demographic model. Because pairs sharing IBD segments increase quadratically as sample size increases, the proposed method results in smaller SEs than the trio-based approach, except at very small sample sizes (Figure 4). However, for demographic models that result in substantial IBD-segment sharing as a result of a small recent effective population size, higher sample size did not substantially decrease the SE (Figure S15). This is due to the fact that as new samples are added, early coalescent events result in overlapping ancestral lineages across pairs of individuals, so that limited new information is obtained from increasing the sample size.

Figure 4.

Comparison of the Estimated SE for Trios and tMRCA under Different Demographic Models and Minimum Cutoffs for IBD-Segment Length

We report the estimated SD from the analysis of several simulations of a single 100 Mb chromosome. For illustrative purposes, we show results of analyses using IBD-length cutoffs of 1.0 and 1.5 cM. Analysis of the GoNL data used a length cutoff of 1.6 cM.

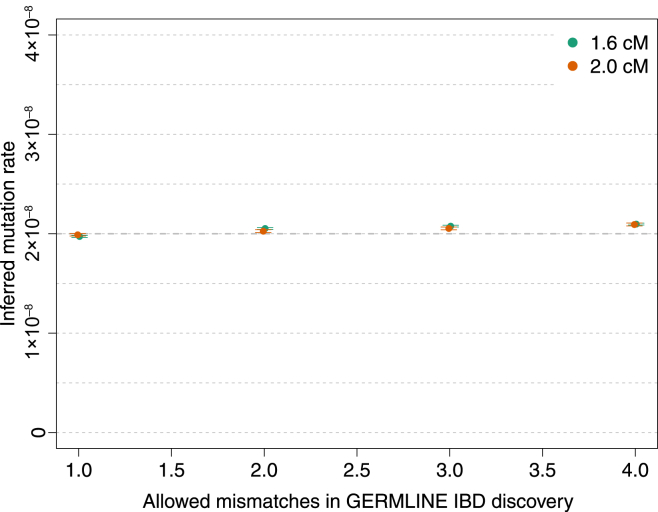
We finally tested the MaAF-threshold-regression approach to correct biases introduced by non-crossover gene-conversion events and estimate the probability that a base pair is involved in gene conversion. We simulated realistic mutation and gene-conversion rates and used GERMLINE to detect IBD-segment sharing after subsampling synthetic SNPs in order to match the allele frequencies observed in the GoNL data. We observed good performance of the MaAF-threshold regression in recovering the simulated mutation-rate value (Figure 5) and observed a small downward bias when we recovered the gene-conversion rate by using the GERMLINE IBD-segment discovery parameters used in the real-data analysis (Figure S16).

Figure 5.

Inference of Gene-Conversion-Corrected Mutation Rate in Simulated Data

We simulated a chromosome of 50 cM for 250 diploid samples by using μ = 2 × 10⁻⁸ for the mutation rate and a probability of 6 × 10⁻⁶ for a base pair to be involved in a non-crossover gene-conversion event. We matched the allele-frequency spectrum of the simulated samples to the spectrum found in real data for IBD-segment detection with GERMLINE. We used several values of the GERMLINE allowed mismatching sites (“-het”) to assess the impact of this parameter in the results. Negligible biases were observed for the recovered mutation rate. Error bars represent SE.

Average Genome-wide Mutation Rate and Gene-Conversion Rate in the GoNL Dataset

We analyzed 498 founders that passed quality control in 250 trio families sequenced within the GoNL project (see Material and Methods). Because of the trio design of the GoNL study, the average ∼13× sequencing depth is effectively doubled to ∼26× for the transmitted haplotypes in the 498 analyzed founders. 248 trios and 2 duos passed sequencing quality control. In the remainder of the paper, we report results for the analysis of transmitted haplotypes only.

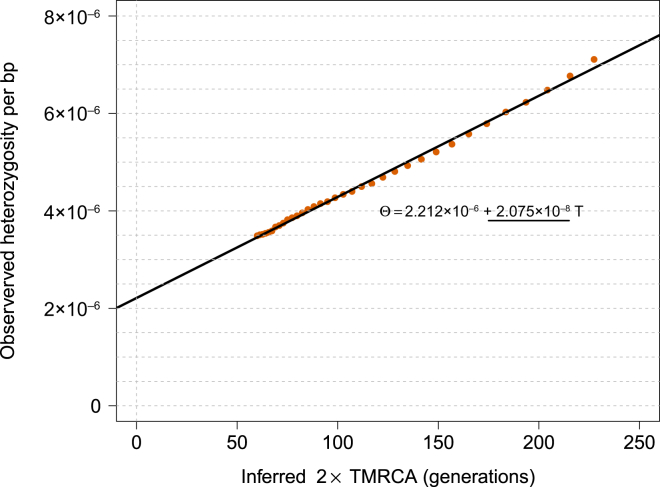
We estimated a mutation rate of (2.08 ± 0.06) × 10⁻⁸ (Figure 6) by using IBD segments between 1.6 and 5.0 cM of length before correcting for gene-conversion events (hereafter, ± introduces a SE). For all analyses of mutation and gene-conversion rates, we discarded 0.5 cM on either edge of the segments and ignored variants with a trio-phasing and genotyping posterior value less than 1.0. Choosing more-conservative values for the minimum-length and edge-exclusion cutoffs resulted in compatible estimates (Figures S11, S17, and S18). As expected, including variants with lower trio-phasing and genotyping posterior values resulted in higher estimates of genotyping error, but negligible effects were observed on the estimates of mutation rate (Figures S6–S9). The tMRCA-regression intercept, which reflects genotyping and phasing error rate (see Material and Methods), was estimated to be (2.21 ± 0.09) × 10⁻⁶, within a range that is not expected to result in biases in the tMRCA-regression slope according to simulations (Figures 3, S6, S9, S13, and S14).

Figure 6.

tMRCA Regression for Segments of Length ≥ 1.6 cM in the GoNL Dataset

The obtained slope is used for estimating mutation rate per generation per base pair before the effects of gene conversion are accounted for.

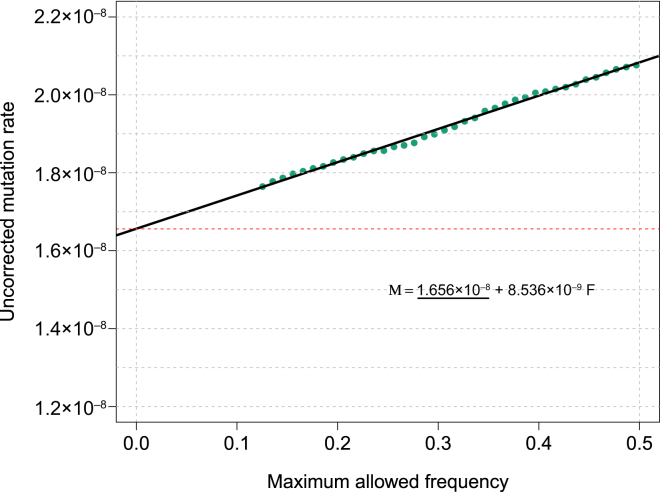
We then performed MaAF-threshold regression to correct for gene-conversion events (see Material and Methods; Figure 7). Using this approach, we estimated a genome-wide average mutation rate of (1.66 ± 0.04) × 10⁻⁸ per base per generation. Note that this represents a historical mutation rate, which includes effects such as average paternal age (see Discussion). Using segments up to 10 cM in length did not result in appreciable changes in our estimate: (1.66 ± 0.04) × 10⁻⁸ per base per generation (tMRCA regression is shown in Figure S19). Analysis performed with only the range of long IBD segments between 5.0 and 10.0 cM resulted in a compatible estimate (but a substantially larger SE). As expected given the simulated data (Tables S1 and S2), a concordant estimate was also obtained when the analysis was repeated with non-overlapping IBD-segment length bins in the tMRCA regression (and inverse-variance weighting of the observations) or with non-overlapping MaAF frequency bins. We truncated the MaAF regression to a conservative lower maximum allele frequency of 12.5% (see Material and Methods), given that including low MaAF values can result in downward biases as a result of the exclusion of recent mutation events (Figure S20). The mutation-rate estimates for each region and for regions of ∼20 cM are shown in Tables S5 and S6. The difference between the corrected and uncorrected genome-wide estimates, (4.18 ± 0.48) × 10⁻⁹, and the observed population heterozygosity of ∼6.98 × 10⁻⁴ can be used for estimating the chance that a base pair is involved in a gene-conversion tract (see Material and Methods). We estimated that a base pair is involved in a gene-conversion event at a rate of (5.99 ± 0.69) × 10⁻⁶ per meiotic event. This rate is in good agreement with a recently published estimate of (5.9 ± 0.71) × 10⁻⁶.²⁷

Figure 7.

MaAF-Threshold Regression for Segments of Length ≥ 1.6 cM in the GoNL Dataset

We computed mutation rates for several allowed maximum-allele-frequency thresholds between 0.125 and 0.5 (green dots) and regressed the observed heterozygosity on the maximum allele frequency. The intercept of the resulting linear model reflects the corrected mutation-rate estimate.

We estimated the effects of uncertainty in the inferred model of demographic history on our estimates. When a genome-wide average mutation rate was inferred for a demographic model with ancestral population size perturbed by 10%, we observed a ∼1.8% difference in the inferred average mutation rate. Larger variation in the ancestral population size was observed to have an approximately linear effect on our estimate (Table S8). We observed very limited effects on the mutation-rate estimate when we perturbed the present-day population size, which is inferred with uncertainty because of the scarcity of very recent coalescent events (Table S8).

Average Genome-wide Indel Rate

We applied the same procedure used for inferring mutation rates to infer the rate of <20 bp indels, which we estimated to be (1.26 ± 0.06) × 10⁻⁹. This rate is higher than a recent estimate of 0.68 × 10⁻⁹, reported in Kloosterman et al.,⁴⁴ but compatible with a second recent estimate of (1.5 ± 0.18) × 10⁻⁹,²⁵ both obtained via observation of de novo events in trios. We further divided the indels into insertions and deletions and estimated the rate of different classes as a function of their maximum length (Figure S21). We observed deletions to be about 50%–100% more frequent than insertions, depending on the length range. We additionally used our method to estimate the gene-conversion rate on the basis of indels and obtained a rate of (9.02 ± 2.91) × 10⁻⁶ per meiotic event, compatible with the rate obtained from point mutations.

Recombination Does Not Strongly Affect Mutation Rate

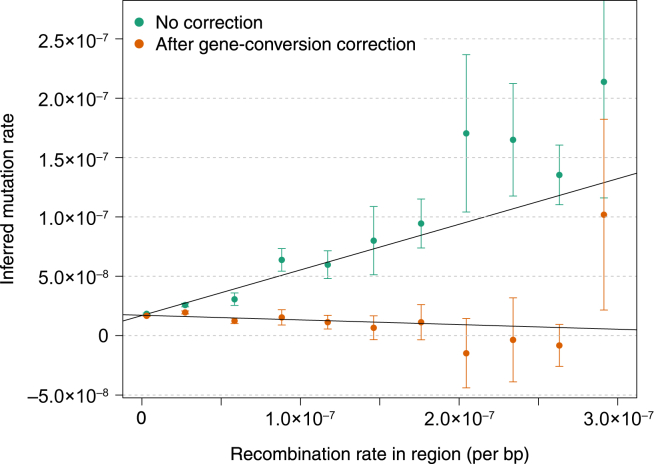
We used our approach to analyze annotation-specific mutation rates (see Material and Methods). We looked for association between recombination rates and mutation rates, a relationship that has been previously detected and attributed to mutagenic properties of recombination.⁴⁵ Indeed, we found our tMRCA-regression estimates of mutation rate to be strongly associated with recombination rate (β = 0.38 ± 0.04 mutations/recombination, F-test p = 5.27 × 10⁻⁶, R² = 0.9; Figure 8). As previously mentioned, however, an increased sequence-mismatch rate at loci that undergo frequent recombination might be a result of polymorphic variants introduced by gene-conversion events, which might increase the slope of the tMRCA regression. Consistently, after controlling for gene conversion, we observed no significant association between recombination rate and mutation rate (β = −0.04 ± 0.03, F-test p = 0.17), suggesting a lack of observable mutagenic effects associated with recombination hotspots (Figures 8 and S22). A recent study reached similar conclusions.⁵ Repeating the same analysis with indels, we detected no significant association between indel rate and recombination rate for either tMRCA-regression slope or MaAF-threshold-regression intercept (β = −0.003 ± 0.003, F-test p = 0.37 after gene-conversion correction).

Figure 8.

Association between Recombination Rate and Mutation Rate

We annotated the genome on the basis of uniform bins of recombination rate and estimated mutation rates for each obtained annotation. We observed a strong association between mutation and recombination rate before correcting for the occurrence of gene-conversion events. After applying the correction, we detected no significant association, which suggests that the linear relationship observed for the uncorrected estimates is induced by gene conversion (see Figure S22). Error bars represent SE.

Effects of Background Selection

Natural selection affecting new mutations can reduce genomic variation, leading to downward bias in our mutation-rate estimates. Because our analysis is limited to mutation events that occurred in the past ∼100 generations, given the length of IBD segments, we expect the effects of natural selection on our genome-wide average mutation rate estimate to be small. Genomic regions with functional or regulatory roles, however, might be under selective pressures that might result in a measurable impact even at these short time scales.

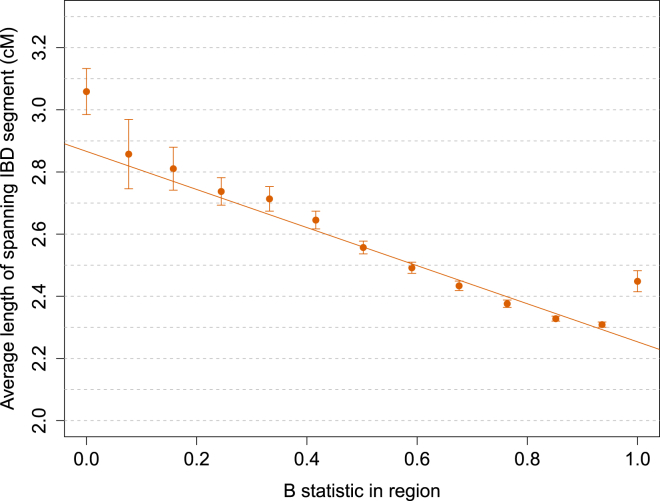
To estimate the impact of selective pressures on our estimates, we divided the genome on the basis of the B statistic proposed in McVicker et al.⁴ The B statistic measures the impact of background selection on a genomic region by estimating the ratio between local effective population size and the effective population size expected under neutrality, such that small values of the B statistic correspond to higher selective pressures (see page 11 in McVicker et al.⁴ for details on the computation of the B statistic). Similarly, a local reduction in effective population size affects the spectrum of shared IBD segments, which are expected to be longer on average, as a result of early coalescent events in populations of smaller effective size.^{20, 38} Indeed, we observed a strong correspondence between small values of the B statistic and the average length of IBD segments (F-test p = 8.43 × 10⁻⁷; Figure 9). As expected, the effect is such that smaller values of the B statistic correspond to longer average shared IBD segments as a result of reduced local effective population size. This effect is remarkably strong up to the measured genome-wide average value of the B statistic. We observed longer average IBD segments for large values of the B statistic, a result that might be explained by biases in either of the two measures or by the fact that additional evolutionary forces, such as selection acting on standing genetic variation,³⁸ are being captured by IBD-segment lengths. When we measured the impact of different values of the B statistic on our estimates of mutation rate, however, we found the effect to not be significant (β = [2.17 ± 1.55] × 10⁻⁹ mutations per generation per unit of B statistic, F-test p = 0.19; Figure S23). The genome-wide average B statistic was estimated to be 0.78. If we were to correct the estimated average genome-wide mutation rate to account for this, we would obtain an updated average mutation rate of (1.7 ± 0.05) × 10⁻⁸, which is not significantly different from the uncorrected estimate. In addition to these analyses, we tested for significant correlation with the mutation rate inferred for each region or for sub-regions of size 10, 20, 30, or 40 cM. The correlation was found to not be significant for the average value of the B statistic in the region, the recombination rate, or the average density of IBD sharing.

Figure 9.

Relationship between Region-Specific Values of the B Statistic and the Average Length of ≥1.6 cM IBD Segments Spanning the Regions

Equally spaced bins of the B statistic were used. Reduced local effective population size has similar effects on the B statistic and the length of IBD haplotypes, which are longer in regions of strong background selection as a result of earlier average coalescent times between pairs of individuals. Error bars represent SE.

Sequence Differences in IBD Segments Are Enriched with Deleterious Variation

Mutation events occurring within the analyzed IBD regions are expected to have arisen within the past ∼100 generations and are therefore on average substantially younger than variants randomly sampled along the genome. Several recent studies have outlined the recent origin of a large fraction of functionally relevant variants.^{46, 47, 48} We therefore tested whether the presence of recent mutations on IBD segments results in more deleterious variants than in the average genome-wide locus by contrasting average scores obtained from PolyPhen-2⁴⁰ and Gerp++⁴¹ annotations (see Material and Methods). Of the analyzed GoNL variants, 54,960 were annotated with PolyPhen-2, and 948,782 were annotated with Gerp++; of these, 1,843 and 27,900, respectively, were found to be mismatched on IBD segments of 1 cM or longer. When we compared average scores, we found that mismatching sites within IBD regions were strongly enriched with higher scores in both annotations (PolyPhen-2 Z-test p = 2.8 × 10⁻⁵; Gerp++ Z-test p = 9.03 × 10⁻¹⁰; Table 1). We further found a marginal association between PolyPhen-2 scores and the B statistic of background selection (β = −0.074 ± 0.025, p = 0.014, R² = 0.39) and a strong association between Gerp++ scores and regional B statistics (β = −0.734 ± 0.068, p = 3.55 × 10⁻⁷, R² = 0.91; Figure S24), which is expected because both measures rely on metrics related to sequence conservation.

Table 1.

Analyses of PolyPhen-2 and Gerp++ Annotated Variants: Genome-wide versus Mismatching within IBD Segments

	Genome-wide	Mismatching in IBD Segments
PolyPhen-2 Results
Annotated variants	54,960	1,843
Mean score	0.41 ± 0.0018	0.45 ± 0.0099
Gerp++ (>2) Results
Annotated variants	948,782	27,900
Mean score	3.08 ± 0.00098	3.11 ± 0.0059

We finally tested for enrichment or depletion of the mutation rate in several genomic annotations that have recently been extracted from several studies (Material and Methods; Table S3). None of the annotations were significantly enriched with or depleted of mutation rates after we controlled for trinucleotide context and multiple hypothesis testing. A recent paper⁴⁹ found that cell-specific chromatin features are a strong determinant of cancer mutations. On the other hand, our estimated mutation rate of (1.66 ± 0.05) × 10⁻⁸ in DNase I hypersensitive regions suggests that the germline mutation rate is not substantially different from the genome-wide average in these regions, in line with recent analyses.⁹ We further computed estimates of the rate of mutations at CpG and non-CpG sites (Table S7) and found them to be higher than in previous reports according to trio analysis, consistent with a higher genome-wide rate (see Table 2 in Kong et al.²⁴).

Discussion

We propose a method for estimating mutation and gene-conversion rates from genealogical relationships across the past tens to few hundreds of generations. This approach is robust to substantial amounts of genotyping error, which is an important confounder for many recent mutation-rate estimators based on trio data. Using this method, we inferred a genome-wide average point mutation rate of (1.66 ± 0.04) × 10⁻⁸ per base per generation, which is significantly higher than several recent family-based estimates ranging from 1.0 × 10⁻⁸ to 1.2 × 10⁻⁸ per base per generation.^{7, 10, 11} Family-based methods have the advantage of relying on direct observation of de novo mutation events while making minimal modeling assumptions but are currently affected by the need to rely on strict filtering criteria to deal with false-positive and -negative genotype calls, and this could in part or entirely explain the discrepancy with our results. We note that the approach of Campbell et al.²³ is similar in spirit to ours, because it uses de novo mutations on long stretches of recently arisen autozygosity within individuals from a known pedigree. However, the autozygosity reflects identity by descent at a more recent time scale, and the authors still mainly rely on stringent filtering criteria to avoid false-positive genotype calls, thereby incurring the same potential biases as other trio-based studies. Phylogenetic methods, on the other hand, fall within the range of 2.0 × 10⁻⁸ to 2.5 × 10⁻⁸ per base per generation.^{50, 51} These estimates rely on several underlying modeling assumptions, which provide a possible explanation for the higher inferred rates, although some have suggested the possibility that these analyses might capture the results of evolutionary changes of the mutation rate across populations or the effects of a varying length of generation times.^{7, 10, 52} Converting between per-year and per-generation estimates requires making assumptions on the sex-averaged generation length.¹⁰ This is generally done with indirect evidence, which complicates the comparison of different estimates. If we assume a sex-averaged long-term generation length of 29 years,⁵³ we can convert our inferred sex-averaged per-generation rate to (5.71 ± 0.14) × 10⁻¹⁰ per base per year. Fu et al.⁵⁴ used ancient DNA to estimate a range of 0.4 × 10⁻⁹ to 0.6 × 10⁻⁹ per year, which is slightly lower than our result, but the reported confidence intervals are compatible. Similarly, Sun et al.⁵⁵ computed a rate of 1.4 × 10⁻⁸ to 2.3 × 10⁻⁸ per base per generation on the basis of point mutations near microsatellites, which is also compatible with our estimate. A contemporary study⁵⁶ related in spirit to ours used simulation-based calibration of the decay of heterozygosity along the genome to infer an average genome-wide mutation rate of (1.61 ± 0.13) × 10⁻⁸, which matches our estimated value. The authors discuss several implications of this mutation rate on the ability to reconcile demographic events inferred with DNA analysis and fossil records, which apply to our analysis as well.

Because conversion between sequence divergence and phylogenetic split times across different primate species relies on an estimate of the per-year mutation rate, different values of this rate have a direct impact on our ability to reconstruct the timing of these events.^{7, 10} If we assume no significant effects of generation time and no changes in mutation rates, our estimate (in conjunction with additional data from Table S5 of Prado-Martinez et al.⁵⁷) implies that the split between humans and chimpanzees occurred ∼6.6 million years ago and that the split between humans and orangutans occurred about ∼19.5 million years ago. When we used our estimate of mutation rate to interpret recently reported split times across human populations,⁸ we found dates that are compatible with what has been inferred by methods other than DNA-based reconstruction. The split of African and non-African populations is estimated to have occurred 46,000–61,000 years ago, whereas a split time of 15,000 years ago is inferred for the separation of East Asians and Native American populations. These estimates are lower than those obtained under the assumption of a smaller mutation rate, but they do not contradict current fossil evidence.

Note that the several different available estimates might disagree not only because of statistical uncertainty and possible biases induced by violations of modeling assumptions but also as a result of differences in the underlying quantity being estimated. Our approach aims at measuring the sex-averaged, genome-averaged, and time-averaged mutation and gene-conversion rates per base per generation. As pointed out in several recent studies,^{10, 23, 24, 55, 58} paternal age at conception is an important determinant of sex-averaged mutation rates, and it is interesting to ask whether variation in historical paternal age might at least partially explain the discrepancy between our estimate and that obtained in recent pedigree studies. In Kong et al.,²⁴ the authors reported that the paternal age in Iceland between 1650 and 1900 was ∼36 years, significantly higher than the average paternal age of ∼30 years for the contemporary samples they analyzed. We found that even if we conservatively assume the per-year paternal-age effect β_y from Kong et al.²⁴—which is higher than the β_y value from other studies^{10, 23, 55, 58}—and a drop from the historical paternal age of 36 years to the contemporary paternal age of 30 years, then our extrapolated estimate decreases to 1.43 × 10⁻⁸ (Table S9). Thus, in the absence of additional evidence for historical average age variation in the analyzed samples, this observation alone might not fully explain the difference between our estimate and those reported in recent pedigree studies, although it outlines the importance of taking this additional source of variation into account in a comparison of estimates obtained from different methods. We note that paternal-age-related differences in per-generation estimates of the mutation rate might also affect the previously described conversion between the per-generation and per-year scales.

In addition to estimating the rate of point mutations, we report a gene-conversion rate of (5.99 ± 0.69) × 10⁻⁶ per base per generation, in close agreement with a recent report,²⁷ and have found that recombination is not associated with mutation rates, supporting recent findings.⁵ A recent sperm-typing study further dissected the relationship among mutation, recombination, and gene conversion and found evidence of both higher mutational load in regions of high recombination and repairing mechanisms associated with gene conversion.⁵⁹ These lead to a higher prevalence of GC alleles than of AT alleles. Overall, these effects might be counteracting each other in a way that results in minimal differences in the total number of observed mutations in recombination-rich regions while affecting sequence composition. Interestingly, a recent study has reported that recombination rate affects the distribution of putatively deleterious variants along the genome but found no evidence suggesting a role of biased gene conversion in this observation.⁶⁰

Finally, we applied our method to estimate the rate of short (<20 bp) indels, which have not thus far been extensively characterized. We inferred a rate of (1.26 ± 0.06) × 10⁻⁹, compatible with two previous estimates of (1.5 ± 0.18) × 10⁻⁹ from Besenbacher et al.²⁵ and (1.06 ± 0.1) × 10⁻⁹ from Ramu et al.⁶¹ but higher than the estimate of 0.68 × 10⁻⁹ reported in Kloosterman et al.⁴⁴ Although these analyses are most likely affected by difficulties related to detection of short indels, collectively they suggest that insertions and deletions occur at a significantly lower rate than do single point mutations.

In addition to analyzing genome-wide average rates, we looked for enrichment or depletion of mutation rates in a number of genomic annotations that were recently derived from several studies. Although we cannot exclude significant deviations from genome-wide averages, we found no evidence of changes in overall mutation rates for the analyzed regions. Notably, although the distribution of shared IBD haplotypes closely reflects the effects of background selection along the genome, we observed a negligible effect on our estimated mutation rates, suggesting that estimating mutation rates by using mutation events under the effects of ∼100 generations of natural selection does not significantly bias local mutation-rate estimates in European populations. Consistent with the idea that mutations on IBD segments are recent and under the effects of selective forces,^{46, 47, 48} we found a strong enrichment of deleterious variants within IBD regions.

Our method provides a way of studying mutation and gene-conversion events in large samples of unrelated individuals because it is robust to substantial amounts of genotyping error, which limits other approaches. A main limitation is the need to rely on two fundamental components—namely, detecting shared IBD segments and inferring the recent demographic history for the analyzed population—that are potential sources of bias. Our analysis of mutation rates in the GoNL dataset relies on IBD detection and demographic inference performed in a previous study,³⁴ but it is possible that additional sources of uncertainty in these two components affect our results. Our conservative exclusion of substantial portions of IBD segments, together with our sensitivity analysis for changes in the demographic model, however, suggests that these biases, if present, should not be substantial.

Several potential directions for improvement of the proposed methodology and analysis can be outlined. First, additional developments of the coalescent calculations used in this work can remove the requirement of estimating a demographic model for the analyzed samples.⁶² Second, it might be possible to devise more-sophisticated weighting schemes for dealing with heteroscedasticity in the regressions and develop additional modeling for dealing with any small deviations from linearity that demographic variation might induce in the MaAF regression. Third, alternative genotype-calling strategies (e.g., individual-based calling) can be employed for reducing these effects of the relationship between allele frequency and genotyping error rates. Finally, applying the tMRCA regression approach proposed in this paper might make it possible to analyze multi-generation pedigrees (e.g., Campbell et al.²³) while controlling for substantial genotyping error. In this scenario, in fact, IBD calling and the inference of tMRCA for IBD segments are substantially simplified.

Future improvements of sequencing technologies and methods for downstream analysis will lead to accurate and direct characterization of biological properties of the processes leading to mutation and gene-conversion events. These advances will also shed light on the discrepancy between previous pedigree-based mutation-rate estimates and those obtained by our methods and will enable testing whether cross-population differences exist. In particular, it will be possible to test whether false-negative de novo genotype calls due to stringent filtering criteria lead to systematically lower mutation-rate estimates in pedigree-based studies (we currently believe this to be the most plausible explanation for the observed discrepancy). Accordingly, we expect that improved sequence quality and analysis will lead trio-based studies to detect a higher number of de novo mutations. Because our methodology relies on evidence from several generations in the past, it is sensitive to additional historical parameters, such as variation in the average paternal age or changes of the mutation rate itself. Although we cannot exclude that historical variation in these quantities might play a role in the higher mutation-rate estimate we obtained, our method relies on evidence from a relatively small number of generations, and it seems less plausible that substantial variation might be observed in such a short time span. Future methodological developments, however, might enable testing of these hypotheses. On the basis of the analysis we described, we believe that several pedigree-based estimates available to date might not accurately reflect the historical mutation rate, particularly in the context of demographic reconstruction, where a higher rate should be assumed.

Consortia

The members of the Genome of the Netherlands Consortium are Laurent C. Francioli, Androniki Menelaou, Sara L. Pulit, Freerk van Dijk, Pier Francesco Palamara, Clara C. Elbers, Pieter B.T. Neerincx, Kai Ye, Victor Guryev, Wigard P. Kloosterman, Patrick Deelen, Abdel Abdellaoui, Elisabeth M. van Leeuwen, Mannis van Oven, Martijn Vermaat, Mingkun Li, Jeroen F.J. Laros, Lennart C. Karssen, Alexandros Kanterakis, Najaf Amin, Jouke Jan Hottenga, Eric-Wubbo Lameijer, Mathijs Kattenberg, Martijn Dijkstra, Heorhiy Byelas, Jessica van Setten, Barbera D.C. van Schaik, Jan Bot, Isac J. Nijman, Ivo Renkens, Tobias Marschall, Alexander Schnhuth, Jayne Y. Hehir-Kwa, Robert E Handsaker, Paz Polak, Mashaal Sohail, Dana Vuzman, Fereydoun Hormozdiari, David van Enckevort, Hailiang Mei, Vyacheslav Koval, Matthijs H. Moed, K. Joeri van der Velde, Fernando Rivadeneira, Karol Estrada, Carolina Medina-Gomez, Aaron Isaacs, Steven A. McCarroll, Marian Beekman, Anton J.M. de Craen, H. Eka D. Suchiman, Albert Hofman, Ben Oostra, Andr G. Uitterlinden, Gonneke Willemsen, LifeLines Cohort Study, Mathieu Platteel, Jan H. Veldink, Leonard H. van den Berg, Steven J. Pitts, Shobha Potluri, Purnima Sundar, David R. Cox, Shamil R. Sunyaev, Johan T. den Dunnen, Mark Stoneking, Peter de Knijff, Manfred Kayser, Qibin Li, Yingrui Li, Yuanping Du, Ruoyan Chen, Hongzhi Cao, Ning Li, Sujie Cao, Jun Wang, Jasper A. Bovenberg, Itsik Pe’er, P. Eline Slagboom, Cornelia M. van Duijn, Dorret I. Boomsma, Gert-Jan B van Ommen, Paul I.W. de Bakker, Morris A. Swertz, and Cisca Wijmenga.

Published: November 12, 2015

Appendix A

The Age of IBD Segments

If a pair of chromosomes share a common ancestor at time t generations before present, the probability that a single site is spanned by an IBD segment of length l at least u Morgans can be expressed as

$$\begin{array}{c}\sigma \left(t\right)={\int }_u^{\infty }l{\left(2t\right)}^2{e}^{-2tl}dl\\ =e^{-2tu}\left(2tu+1\right).\end{array}$$ (Equation A1)

The distribution $l{\left(2t\right)}^2{e}^{-2tl}$ represents the sum of two exponential random variables with parameter 2t, which is the rate at which a recombination occurs on either side of the chosen site. Note that this assumes that an IBD segment is delimited by the occurrence of recombination events, which is equivalent to assuming an underlying sequentially Markovian coalescent (SMC) model. For very short IBD segments (e.g., <0.3 cM) and in populations that experience substantial and long-lasting isolation (e.g., N_e < 1,000), the slightly more-complex SMC′ model⁶³ provides more-accurate calculations.⁸, ⁶⁴ This is, however, unnecessary given the demographic history and length ranges here considered. It follows from the linearity of the expectation operator that the expected genomic fraction f(t) shared identically by descent by a pair of individuals whose ancestral lineages coalesce at time t can be obtained from the probability that a single site is spanned by an IBD segment of length at least u Morgans, which we write f(t) = σ(t). The expected length of an IBD segment transmitted from a common ancestor living at time t is therefore

$$\begin{array}{c}\ell \left(t\right)={\int }_u^{\infty }l\times 2t{e}^{2t\left(u-l\right)}dl=1/\left(2t\right)+u\end{array}.$$ (Equation A2)

To determine the expected number of IBD segments obtained if the lineages of two individuals coalesce at time t, we therefore divide the expected total amount of genome shared identically by descent by the expected length of an IBD segment co-inherited from an ancestor living at time t. This yields

$$\begin{array}{c}{n}_u\left(t\right)=L{f}_u\left(t\right)/\ell \left(t\right)\\ =\frac{L{e}^{-2tu}\left(2tu+1\right)}{1/\left(2t\right)+u}\\ =L2e^{-2tu}t,\end{array}$$ (Equation A3)

where L is the size, in Morgans, of the considered genomic region. To obtain the expected number of IBD segments longer than u Morgans for the average pair of individuals in the population, we marginalize over the distribution of pairwise coalescence times, c(t), which depends on the demographic history,

$$\begin{array}{c}{n}_u={\int }_0^{\infty }c\left(t\right)n_u\left(t\right)dt.\end{array}$$ (Equation A4)

This quantity has a closed-form expression if we assume that the population size becomes constant at an arbitrarily remote point in time, and we can use it to obtain the posterior age distribution of IBD-segment ages,

$$\begin{array}{c}{p}_u\left(t\right)=\frac{c\left(t\right)n_u\left(t\right)}{n_u}.\end{array}$$ (Equation A5)

Contribution of Individual Variants to Heterozygosity

For a sample of K homologous sequences from a population, the heterozygosity per site can be estimated by

$$\begin{array}{c}\hat{\theta }=\frac{1}{s}\sum _{i=1}^s\frac{K}{K-1}2\frac{x_i}{K}\left(1-\frac{x_i}{K}\right)\end{array},$$ (Equation A6)

(see Nei⁶⁵), where s is the number of sites in each sequence, x_i is the number of samples carrying a derived allele at site i, and K/(K − 1) is a bias-correction factor. Defining M(x) as the total number of sites in the sample for which exactly x sequences carry a derived allele, we can rewrite this equation as a sum over x:

$$\begin{array}{c}\hat{\theta }=\sum _{x=1}^{K-1}\frac{M\left(x\right)}{s}\frac{2x\left(K-x\right)}{K\left(K-1\right)}.\end{array}$$ (Equation A7)

The term M(x)/s is the proportion of sites at which x of the K sequences carry a derived allele, and the term

$$\begin{array}{c}\frac{2x\left(K-x\right)}{K\left(K-1\right)}\end{array}$$ (Equation A8)

is the probability of discovering such a polymorphic site when just two sequences are sampled without replacement from the K sequences. Note that this probability is the same for sites with x copies of a derived allele as it is for sites with K − x copies. Thus, we can also write

$$\begin{array}{c}\hat{\theta }=\sum _{x=1}^{\left[K/2\right]}\frac{M\left(x\right)+M\left(K-x\right)}{s}\frac{2x\left(K-x\right)}{K\left(K-1\right)},\end{array}$$ (Equation A9)

where [K/2] is the largest integer that is less than or equal to K/2, and x is now the count of the minor allele.

This allows us to consider the average contribution of different kinds of polymorphic sites to overall heterozygosity. Under the model of constant population size and neutral evolution of Watterson,⁶⁶

$$\begin{array}{c}E\left[M\left(x\right)\right]=\frac{s\theta }{x}\end{array}$$ (Equation A10)

(see Fu⁶⁷), in which θ = 4Nμ is the diploid population-scaled mutation rate per site, or the expected per-site heterozygosity of the population. Using Equation A10 together with Equation A9 and simplifying gives

$$E\left[\hat{\theta }\right]=\stackrel{\left(K-1\right)/2}{\sum _{x=1}}\theta \frac{2}{K-1},$$ (Equation A11)

in which we assume that K is odd for simplicity. The sum in Equation A11 evaluates to θ, as expected for an unbiased estimator.

Equation A11 shows that, on average, the different kinds of polymorphic sites, categorized by minor allele frequency, contribute uniformly to heterozygosity, as noted previously by Kruglyak and Nickerson.⁶⁸ Another way of stating this is that polymorphisms discovered by screening in samples of size two will be uniformly distributed among classes of minor allele frequencies. This depends on genotype-calling criteria and a constant population size over time and is also not true for derived allele-frequency classes. Figure S2 shows that contributions to heterozygosity are close to uniform for the GoNL site-frequency spectrum.

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes ancestral alignments, ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase1/analysis_results/supporting/ancestral_alignments/

• ARGON, https://github.com/pierpal/ARGON

• IBDMUT, https://github.com/pierpal/IBDMUT

• UCSC Genome Browser hg19 assembly, http://hgdownload.cse.ucsc.edu/goldenPath/hg19/chromosomes/