An extended Tajima’s D neutrality test incorporating SNP calling and imputation uncertainties

Abstract

To identify evolutionary events from the footprints left in the patterns of genetic variation in a population, people use many statistical frameworks, including neutrality tests. In datasets from current high throughput sequencing and genotyping platforms, it is common to have missing data and low-confidence SNP calls at many segregating sites. However, the traditional statistical framework for neutrality tests does not allow for these possibilities; therefore the usual way of treating missing data is to ignore segregating sites with missing/low confidence calls, regardless of the good SNP calls at these sites in other individuals. In this work, we propose a modified neutrality test, Extended Tajima’s D, which incorporates missing data and SNP-calling uncertainties. Because we do not specify any particular error-generating mechanism, this approach is robust and widely applicable. Simulations show that in most cases the power of the new test is better than the original Tajima’s D, given the same type I error. Applications to real data show that it detects fewer outliers associated with low quality data.

1. INTRODUCTION

Empowered by modern high-throughout sequencing technologies, more and more evolutionary insights are revealed and it was predicted that a golden age is coming (Hernandez et al. 2011; Przeworski 2011). However, some of the most important statistical frameworks to detect evolutionary events within a population, traditional frequency-based neutrality tests, e.g. Tajima’s D (Tajima 1989), Fu & Li’s D (Fu and Li 1993) and Fay & Wu’s H (Fay and Wu 2000), all assume that the sample size is the same for different segregating sites. That is, if we find a total of S segregating sites in n chromosomes, then for any given site we must observe one of its alleles in all the chromosomes. (Actually, in standard analytical tools, e.g., DnaSP (Rozas et al. 2003), SNPs with even one missing call in the input file will be discarded.) However, for the current high-throughput sequencing platforms, e.g. Illumina (Bentley et al. 2008), where low-coverage data are often used, this precondition is rarely fulfilled. There is often a large number of missing calls. For instance, in the SNP calls from 51 low-coverage individuals in the 1000 Genomes Project (1000-Genomes-Project-Consortium 2010) (http://www.1000genomes.org/page.php) freeze 3 data, only about 1% of SNPs have calls in all individuals. The reason is that if we resequence a large number of individuals at millions of sites with relatively low coverage, it is likely that the sample sizes will not be equal at different sites even if the success rate of sequencing is very high. Actually, the variable sample size problem is not a new problem observed only in high-throughput resequencing projects; it is also seen in high-throughput genotyping data. An example is that, in the HapMap III dataset (International-HapMap-Consortium et al. 2010) (http://www.hapmap.org/), after QC, only half of the SNPs have a full list of genotyping calls in all individuals. To either discard these sites, or do extra experiments (usually using non-high-throughput instruments) is a poor use of resources. Sometimes, people allow PHASE (Stephens et al. 2001) or other programs (Stephens and Scheet 2005; Marchini et al. 2007) to fill in the missing data by imputation. But there are also uncertainties in the imputation results that may distort traditional neutrality test results, particularly for low-frequency variants.

Besides missing data, another important feature is that SNPs are often called from a small number of reads within a statistical model. Therefore, when the coverage is low, we may have substantial uncertainties in the SNP calls; but, fortunately, this uncertainty can be expressed quantitatively by confidence scores calculated as a posterior probability. If we could incorporate these uncertainties when carrying out neutrality tests, the robustness of the results might be significantly increased. Incorporating uncertainties of SNP calling could also be used in other scenarios as well. For example, as mentioned above, both resequencing-based and genotyping-based genotypes may be improved by imputation (Stephens and Scheet 2005; Marchini et al. 2007; Delaneau et al. 2013). Due to the stochastic nature of the original data, the confidence of imputed alleles at different segregating sites may be different, and this variation should therefore be incorporated when carrying out neutrality tests.

In this article we revise Tajima’s D, which is the first and most widely-used neutrality test, by incorporating SNP uncertainties into the calculation without specifying any particular scenario of error mechanism. The first section serves as an introduction to the general background. After that, we detail the intuitions and mathematics of our new statistic in the second section. In the third section, we present the critical value calculation and power evaluation from simulated data. Applications to real data from the pilot phase of the 1000 Genomes Project (1000-Genomes-Project-Consortium 2010) and comparisons with SeattleSNP (http://pga.gs.washington.edu/new.html) regions are presented in the fourth section. Finally, a section of discussion and comparisons with existing work is provided. To keep the main text suitable for general readers, we have placed most of the mathematical and simulation details in Appendices.

2. GENERAL BACKGROUND

High-throughput resequencing

In current high-throughput sequencing experiments, e.g., Illumina/454, resequencing instruments generate very short reads. For a genome the size of the human genome, these cannot be reliably assembled de novo, but have to be mapped onto a reference sequence (e.g. using MAQ (Li et al. 2008), BWA (Li and Durbin 2009) or SSAHA (Ning et al. 2001)). Afterwards, we can call SNPs from the consensus heterozygous or homozygous calls in the assembly. Given the analysis of single molecules, the relatively short length of the reads and the complexity of mammalian genomes, the “SNP calling” process contains more uncertainties than in traditional Sanger capillary resequencing. One obvious consequence is that low confidence SNPs will inflate the variance and therefore leads to more false positives in the selection scan. At the same time, based on the base qualities and mapping qualities of the reads supporting a SNP call, most mapping tools provide SNP scores which could be utilized to calculate the probabilities that the SNP calls are wrong. This enables us to incorporate these uncertainties quantitatively into neutrality tests.

Tajima’s D

Let us assume we have n individuals with S segregating sites, effective population size N (unknown), and a mutation rate per generation of μ (also unknown). The traditional Tajima’s D is defined as the difference between two estimators of the scaled mutation rate θ = 4N μ divided by its standard deviation. The first estimator is Tajima’s estimator θ_π (Tajima 1983) which is the average number of pairwise differences. The second is Watterson’s estimator θ_W (Watterson 1975) which reflects the number of segregating sites. Thus, we have:

$$\mathit{\text{Tajima\_D}}=\frac{{\theta }_{\pi }-{\theta }_W}{\sqrt{\mathit{Var}({\theta }_{\pi }-{\theta }_W)}}$$

Where,

$$\begin{array}{cc}\hfill & {\theta }_W=\frac{S}{a_1},a_1=\sum _{i=1}^{n-1}\frac{1}{i},\hfill \\ \hfill & {\theta }_{\pi }=\frac{{\sum i}_{<j}{k}_{ij}}{\left(\frac{n}{2}\right)},\hfill \end{array}$$

k_ij is the difference between sequence i and j.

Since both statistics are estimators of θ under the neutral model, the mean of Tajima’s D is zero when the null hypothesis holds. Assuming that selection or a population event changes allele frequencies, these in turn change the pairwise difference measure, but leave the total number of segregating sites unchanged. Thus observing a Tajima’s D value with significant derivation from zero can be taken as a sign of a non-neutral event such as selection or a demographic change.

3. CONSTRUCTING THE STATISTICAL TEST

We assume the dataset contains missing genotype calls and each of the known calls is assigned a confidence score. (In an extreme case, the score could be 1.0, indicating that there is no uncertainty in this call, or 0.0 indicating no confidence at all.) We will describe the intuition behind our approach in this section, leaving detailed mathematics to Appendix A. In this work, we adopt the framework of the original Tajima’s D, but calculate the denominator in a different way.

A hypothesis is that the total number of segregating sites observed is not sensitive to missing genotypes in a subset of individuals. (But in the case of a singleton-segregating site, this does not hold: see Discussion.) Therefore we keep the Watterson estimator the same. That is:

$${\theta }_W=\frac{S}{a_1},\text{where}{a}_1=\sum _{i=1}^{n-1}\frac{1}{i}.$$

On the other hand, we use ${\theta }_{\pi }^e$ to denote the estimated θ_π for Tajima’s estimator, calculated as below:

1. Calculate the allele frequencies x_ij of different segregating sites in the individuals in whom we can call the genotype, where i is the site index and j is the allele index.

2. Estimate the sample heterozygosity ${\widehat{h}}_i$ using the allele frequencies calculated from known sites:

   $${\widehat{h}}_i=\frac{n(1-{\sum }_j{x}_{ij}^2)}{n-1}.$$

3. Sum up all ${\widehat{h}}_i$ and get ${\theta }_{\pi }^e={\sum }_{i=1}^S{\widehat{h}}_i$.

If we do not have missing data, it has already been pointed out that ${\theta }_{\pi }^e$ is identical to θ_π (Tajima 1989), (Fay and Wu 2000). When we have missing data, ${\widehat{h}}_i$ is an unbiased estimator of h_i. Therefore the mean of ${\theta }_{\pi }^e$ equals θ_π, implying that ${\theta }_{\pi }^e$ is still a useful estimator of θ.

In the standard framework of designing these statistics, the remaining task is to calculate the variance of (${\theta }_{\pi }^e$ − θ_W), i.e. Var(${\theta }_{\pi }^e$ − θ_W). We have not derived the closed form of this variance. Instead, with the underlying motivation of capturing the inflated variance due to the missing/uncertain data, we use the approximation below.

As mentioned above, it is proven that the calculation of the scaled mutation rate by means of pairwise difference and by means of heterozygosity are identical when calculating Tajima’s D (Tajima 1989), (Fay and Wu 2000). However, in the presence of missing/uncertain data, the calculation based on heterozygosity is only an estimate of the pairwise difference. Essentially, when calculating ${\theta }_{\pi }^e$, we are using a subset of the sample (the individuals who have genotype calls at this particular site) to calculate the heterozygosity, and we then assume this is the heterozygosity of the full sample, which in turn evaluates the heterozygosity of the population. If fewer known genotypes (and hence more “guessed” genotypes) contribute to the calculation, the variance will be inflated. The same idea applies to uncertain genotypes – the more uncertain the calls, the larger the variance. Actually, the total variance of (θ − θ_W) can be decomposed into many terms in which each term depends on two pairs of sequences (See Appendix A for mathematical details). Making use of this, we assign a weight to the contribution from each pair of sequences. The value of this weight is decided by the number of missing calls and the confidence levels of the calls that are present. More missing calls (or less confidence in the present calls) will result in a larger weight. (To detail how the weighting system works and the flexibility offered to users, see Appendix A.) In this sense, although the denominator in our D is not the standard deviation of the nominator, (${\theta }_{\pi }^e$ − θ_W), it captures the fact that the variance is inflated and precisely captures where and to what extent it is inflated. Therefore we expect it to be a good approximation of the extent of variation of (${\theta }_{\pi }^e$ − θ_W). In the extreme case, if there is no missing data and all the genotype calls have confidence 1.0, the extended D is identical to the original Tajima’s D.

In practice, the confidence score from different statistical frameworks can vary in absolute value, even though more confident calls have higher scores and less confident calls have lower scores. Some people use a mapping based tool, e.g. (Li et al. 2008), which adopts a binomial model; others may use an imputation algorithm using a hidden Markov model (Scheet and Stephens 2006). Given this variability, it would be useful for users to be able to decide to what extent they want the uncertainties to influence the calculation. We therefore provide a user-specified parameter c in the calculation. It ranges from 0.0 to 1.0. In the extreme case, if the user sets c = 0, the extended D is identical to the original Tajima’s D (See Appendix A for details).

4. POWER OF THE TEST

In this section we estimate the power of the new test and compare it with the existing Tajima’s D (Tajima 1989) by simulations. In most comparisons of this kind, researchers compare the power of newly invented and existing tests under a range of selection/demographic models. However, the key point of the test presented in this work is not any special insight into evolutionary/demographic scenarios. Instead, using the same framework as the original Tajima’s D, it focuses on how to handle uncertainties in the data. Therefore we use only two representative scenarios and focus more on simulating data with variable data error models.

SFS_CODE (Hernandez 2008) is a generalized Wright-Fisher population forward genetic simulation program for finite-site mutation models with selection, recombination, and demography. It enables us to incorporate many kinds of evolutionary/demographic events. In this section, besides the neutral sequences, we simulate sequences under two scenarios: one includes selection, and the other population growth. Based on the “genomic” sequences simulated by SFS_CODE under these scenarios, we then simulate “sequenced” data under different error distributions and calculate the extended Tajima’s D with different c settings. In this section, we focus more on the data error distribution model, rather than the evolutionary/demographic model used in SFS_CODE. The detailed SFS_CODE commands used are listed in Appendix B.

Following the standard process of power calculation, in all the simulations, for a given data error model, uncertainty weight c, sample size n, and scaled mutation rate θ, we generate 10,000 samples under the null hypothesis, i.e., the neutral model, to get the one-tailed 0.01 critical values for both the original and extended Tajima’s D. Using those critical values, we generate another 10,000 samples under a selective/demographic model and calculate the power. All the critical values we use are listed in Appendix B. Actually, we generate these critical values only for the purpose of the comparison in this study; we do not suggest that users should use them in practice. Instead, because of the complexity of different error model and the investigators’ different insights into the extent to which they want the uncertainty to affect the calculation, we do not provide a set of critical values in advance. We suggest that users do simulations themselves to find the most suitable critical value(s) for their applications.

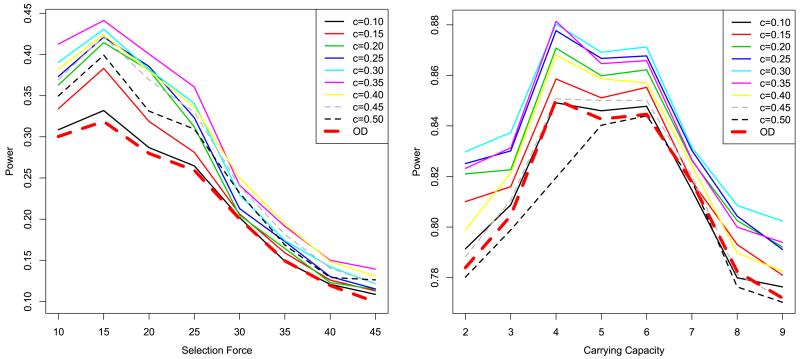
Firstly, we use an error-generating model based on the empirical distribution. More specifically, we summarize the empirical error distribution in the real data from the 1000 Genomes Project and simulate confidence scores of each SNP according to this empirical distribution independently. The power results are depicted in Figure 1. One can see that the powers of extended Tajima’s Ds are generally higher than the power of the original Tajima’s D. When small c values are taken, the power is slightly higher but close to the original Tajima’s D. Reasonably larger c can increase power significantly; however, when it is greater than 0.4, the power goes down to even lower than the original Tajima’s D.

Figure 1.

Power comparison for independent error models. The left panel shows the selection model, and the right panel the demographic model. OD (dashed thick line) stands for the original Tajima’s D. The other lines stand for the extended Tajima’s D with different c settings. The x axis shows the SFS_CODE parameter of selection or demographic force, respectively

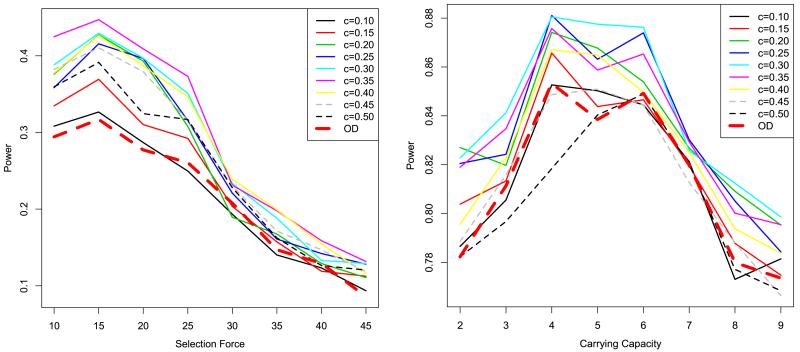
We note that, in the above settings, the confidence scores of different SNPs are independent, which is not realistic. In practice, the error rates of SNPs in adjacent regions are dependent for various reasons. The most common of these are library preparation or sequencing artifacts. For example, a poor PCR product, or a low-quality or mismapped read can make the error distribution blocky. What is more, if we use an imputation algorithm, the low confidences of SNPs in a particular region will be propagated to the other SNPs in the same region. It would be good if we could find a model capturing all the above-mentioned factors and simulate data accordingly. However, due to the complexity of the factors affecting the blocky structure, it is not easy to do such more realistic simulations. Therefore, we adopted a relatively simple simulation scheme. That is, we keep the total error rate the same as in the empirical distribution in the independent model, but make the SNPs in the same region correlated to each other. The result of this simulation is shown in Figure 2, which shows similar trends to the random error models.

Figure 2.

Power comparison for blocky error models. The left panel shows the selection model, and the right panel the demographic model. OD (dashed thick line) stands for the original Tajima’s D. The other lines stand for the extended Tajima’s D with different c settings. The x axis shows the SFS_CODE parameter of selection or demographic force, respectively

The power simulations presented above show that the extended Tajima’s D is in general more powerful than the original Tajima’s D given the same false positive rate. In practice, the parameter c is an important factor that influences the power of the test.

5. APPLICATION TO REAL DATA

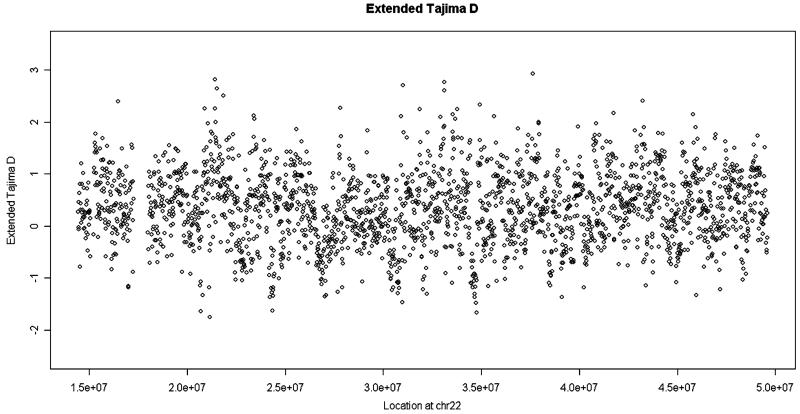
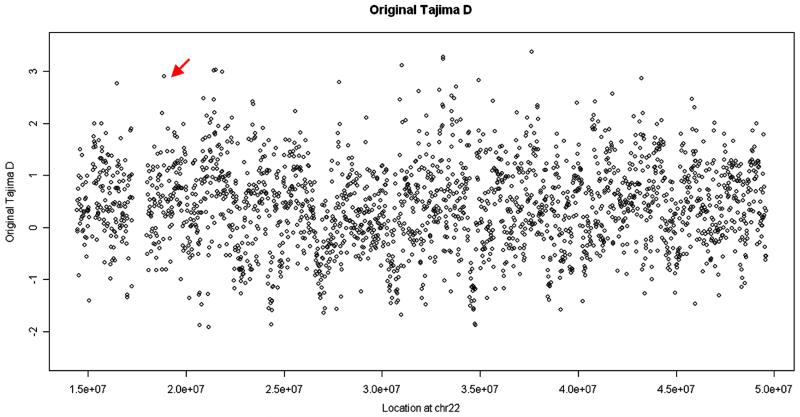
We next apply our analysis to real data from the 1000 Genomes Project. The coverage of each individual is around 4× and the data were generated by different sequencing platforms. (1000-Genomes-Project-Consortium 2010) Although the 1000 Genomes Project has subsequently updated its datasets, these early data illustrate the power of the extended Tajima’s D particularly clearly. A small portion (chromosome 22 from the 36 CEU sample with European ancestry) of the analysis is depicted in Figures 3 and 4. In these figures, each point shows the extended/original Tajima’s D value for a 15 kb window along the chromosome. These values are highly correlated and the patterns have striking similarities, as expected. But there are also significant differences. For example, there is an outstandingly high value in the original Tajima’s D (indicated by the red arrow), which does not show up in the extended Tajima’s D. On checking the raw data from this region, we find that the confidence values of SNPs there are quite low, suggesting that this high value is likely to represent a false positive.

Figure 3.

Extended Tajima’s D values in 15 kb windows along chromosome 22 using data from the 1000 Genomes Project freeze 3 CEU samples

Figure 4.

The original Tajima’s D values in 15 kb windows along chromosome 22 using data from the 1000 Genomes Project freeze 3 CEU samples

The top 1% of negative and positive values from these calculations are of interest as empirical outliers and are listed in Tables 1 and 2 (The coordinates are based on NCBI Build 36).

Table 1.

Top 1% of significant negative values

location	ED	OD	location	ED	OD
21151870	−1.83664	−1.91643	21151870	−1.83664	−1.91643
20709004	−1.77186	−1.87306	34777312	−1.7665	−1.87811
34777312	−1.7665	−1.87811	20709004	−1.77186	−1.87306
24352535	−1.74789	−1.86262	24352535	−1.74789	−1.86262
34724879	−1.72383	−1.84616	34724879	−1.72383	−1.84616
30977332	−1.5423	−1.68049	30977332	−1.5423	−1.68049
39098072	−1.50474	−1.57443	27019460	−1.43642	−1.64345
27019460	−1.43642	−1.64345	24386697	−1.41989	−1.58939
34651216	−1.42319	−1.58113	34651216	−1.42319	−1.58113
24386697	−1.41989	−1.58939	39098072	−1.50474	−1.57443
24217783	−1.41195	−1.55516	27666372	−1.3688	−1.56211
34493620	−1.3999	−1.50594	27079043	−1.38865	−1.55645
45967255	−1.39275	−1.46628	34667372	−1.36135	−1.5557
27079043	−1.38865	−1.55645	24217783	−1.41195	−1.55516
32214456	−1.37372	−1.47708	34493620	−1.3999	−1.50594
27666372	−1.3688	−1.56211	20787369	−1.33111	−1.48388
34667372	−1.36135	−1.5557	32214456	−1.37372	−1.47708
24325574	−1.35516	−1.45527	45967255	−1.39275	−1.46628
15076629	−1.33518	−1.40567	24325574	−1.35516	−1.45527
20787369	−1.33111	−1.48388	30435841	−1.26914	−1.44788
30744501	−1.30964	−1.44008	30744501	−1.30964	−1.44008

The left panel is sorted by extended Tajima’s D (c = 0.25) and the right panel by the original Tajima’s D

Table 2.

Top 1% of significant positive values

location	ED	OD	location	ED	OD
21515571	2.846391	3.028526	37625562	2.691356	3.369293
21426012	2.816427	3.01648	33116938	2.479885	3.274953
37625562	2.691356	3.369293	33103566	2.297268	3.23722
31020083	2.514281	3.111772	21515571	2.846391	3.028526
33116938	2.479885	3.274953	21426012	2.816427	3.01648
21836759	2.318392	2.984994	21836759	2.318392	2.984994
21412052	2.297929	2.454759	18888594	1.628212	2.899158
33103566	2.297268	3.23722	43219974	2.194745	2.869068
16472649	2.225322	2.762314	34915188	2.113339	2.821092
43219974	2.194745	2.869068	27808831	2.060364	2.785883
20888310	2.184635	2.483804	16472649	2.225322	2.762314
34915188	2.113339	2.821092	33790522	2.004768	2.699624
31862932	2.094596	2.6124	32932188	1.881843	2.643153
21470159	2.078124	2.20137	31862932	2.094596	2.6124
41734964	2.076077	2.562095	41734964	2.076077	2.562095
27808831	2.060364	2.785883	33561762	1.999181	2.523429
23406938	2.031665	2.416551	20888310	2.184635	2.483804
33790522	2.004768	2.699624	33667758	1.848925	2.475666
45816855	2.003667	2.461891	45816855	2.003667	2.461891
33561762	1.999181	2.523429	21412052	2.297929	2.454759
23424794	1.980101	2.366971	30914501	1.947837	2.450824

The left panel is sorted by extended Tajima’s D (c = 0.25) and the right panel by the original Tajima’s D

Despite the similarities between the overall patterns, among the extreme outliers, which are of particular biological interest, 39 of the 44 locations are shared. These regions are therefore candidates for further biological investigation.

We also compared our original and extended Tajima’s D values with empirical data from the six chromosome 22 regions investigated by the SeattleSNPs Project (http://pga.gs.washington.edu/) in independent samples of European origin. This project re-sequenced genes of interest by standard capillary sequencing and identified SNPs with high reliability. The results are shown in Table 3, where the high correlation between the SeattleSNPs values and both the original and extended Tajima’s D values (both r² = 0.92) is notable.

Table 3.

Comparison of gene regions analyzed by the SeattleSNPs and 1000 Genomes Projects

Gene	Start	End	#Seqs Seattle	#Seqs 1000g	#SNPs Seattle	#SNPs 1000g	OD Seattle	ED 1000g	OD 1000g
A4GALT	41416394	41447672	46	72	80	208	0.924	1.142	1.346
APOBEC3F	37766357	37781373	46	72	40	56	2.140	1.425	1.683
APOBEC3G	37801497	37814271	46	72	51	58	−0.690	0.112	0.126
HMOX1	34103954	34122171	46	72	45	91	0.243	0.356	0.403
IL2RB	35850703	35876286	46	72	97	130	0.718	0.875	1.025
PPARA	44926043	45010351	46	72	79	256	−0.787	−0.249	−0.281

#Seqs = number of sequences. OD = Original Tajima D, ED = Extended Tajima D (at ED column, c = 0.25)

6. DISCUSSION

We designed an extended Tajima’s D statistic especially for whole genome scans based on low coverage sequencing data. If data are complete and accurate, it returns the same value as the original Tajima’s D and thus, as expected, extended D values are generally similar to the original D values calculated from either 1000 Genomes or SeattleSNPs data (Figures 3, 4; Table 3). Its novel advantages are seen when data are incomplete or of low quality. When applying our statistic, if a particular region was under selection, but does not have enough SNPs or we fail to call the SNPs with high confidence, we may see a small D value and therefore have less opportunity to identify this selection. So at the first glance, our extended D serves as a kind of filter to guarantee that most signals we find are based on high quality data. However, if the selection signal is strong enough, we can still identify it even if the data quality is not very good. In this sense, it is not a simple filter on data quality. Instead, it strikes a balance between true selective signals and the false positives caused by low quality data. We believe that, compared with our statistic, simply applying traditional Tajima’s D analysis will generate more false positives, but simply filtering in advance will cause more false negatives.

Power calculations following standard procedures are presented in this paper. In practice, the complexities of evolutionary histories and DNA sequences mean that researchers cannot precisely specify critical values for significance levels. Therefore, sometimes investigators still rely on manual review of the values of the test statistic across the genome, and report significant events based on a combination of the empirical distribution and modeling. In this case, our extended Tajima D has a substantial advantage because it prevents us from being misled by false positives arising from poor data.

An important feature of re-sequencing, compared with genotyping at known sites, is its ability to detect novel rare SNPs. In an extreme case we could see many singleton SNPs (Nelson et al. 2012; Tennessen et al. 2012). In such a case, the uncertainty of calling singleton SNPs will influence the precision of Watterson’s estimator. We have not dealt with this situation in this study. In particular, to calculate Fu & Li’s D, the precision of singletons is more important than in Tajima’s D. This problem needs to be addressed in future work. Another interesting extension is to incorporate the uncertainties into the calculation of the numerator too, which needs another extension to the present statistical framework that models the variance.

Other researchers have also considered the uncertainties introduced by sequencing errors. Johnson and Slatkin (Johnson and Slatkin 2008) and Achaz (Achaz 2008) have incorporated the bias from sequencing error into population-genetic estimates by calculating the mean of the observed estimator using the closed form of the probability of the observed variation as a function of true variation. Hellmann et al. (Hellmann et al. 2008) proposed an extended Watterson estimator as a CLE (composite likelihood estimator) in the presence of variable read lengths and coverage at different segregating sites and potential sequencing errors. Compared with the framework adopted in our extended Tajima’s D, both of their approaches can provide more precise estimators when their assumptions hold because of the use of the closed form. However, at the same time, assuming the specific distributions/probabilities of the source of the error may also decrease the flexibility of the method and therefore restrict the scope of its applications. For example, in Johnson and Slatkin’s work, they assume that the distribution of the number of pairs of sites that are in fact the same but mismatched due to sequencing errors, Y_k, follows a Bernoulli distribution and can be estimated from the overall error probability. Therefore it does not address the different error rates found in different regions. In contrast, Hellmann et al.’s work addresses this aspect very well, but veers towards another extreme: it specifies a very detailed model for shotgun assemblies which might not be appropriate if the error source is, for example, imputation software. Another factor is that, for both known and unknown reasons, the confidence score may not faithfully tell us the probability that the SNP call is correct. If this is the case, in most applications our framework is more appropriate. Although we also hope that the quality score of a SNP call is the probability of the call being correct, our calculation does not depend on the absolute value of the score very much. As long as the order of the scores is right, i.e. the call with higher score has higher reliability, our approach works robustly. In a sense, the trade-offs between our approach and the existing approaches are similar to the trade-offs between model-free approaches and model-based approaches. This is a controversial topic in statistics, but one that it is useful to explore in the context of neutrality tests based on new technology sequence data, and we have provided a novel alternative: a robust statistic in a model-free context.

In conclusion, we have developed an extended version of the most widely-used neutrality statistic, Tajima’s D, suitable for whole-genome re-sequence data such as that produced by the 1000 Genomes Project. This statistic will improve the detection of non-neutral regions of the genome and thus promises novel genome wide insights into human evolutionary history.

APPENDIX A. MATHEMATICAL DETAILS

Let us say we have n chromosomes (i.e., n/2 individuals) and in total S segregating sites, and ${\theta }_{\pi }^e$ and θ_W are calculated as described in the main text. Now we are going to discuss the variance:

$$\mathit{Var}({\theta }_{\pi }^e-{\theta }_W)=\mathit{Var}\left({\theta }_{\pi }^e\right)-2\mathit{Cov}({\theta }_{\pi }^e,{\theta }_W)+\mathit{Var}\left({\theta }_W\right)$$

As described in the section Approach, by adding weights to Var(θ_π) and Cov(θ_π, θ_W), we can approximately replace Var(${\theta }_{\pi }^e$) and Cov(${\theta }_{\pi }^e$, θ_W). Formally, we would like to derive

$${\mathit{Var}}^{\ast }({\theta }_{\pi }^e-{\theta }_W)={\mathit{Var}}^{\ast }\left({\theta }_{\pi }^e\right)-2{\mathit{Cov}}^{\ast }({\theta }_{\pi }^e,{\theta }_W)+\mathit{Var}\left({\theta }_W\right)$$ (0)

We use k_ij to denote the random variable of the pairwise difference between chromosome i and j. We have:

$$\begin{array}{cc}\hfill \mathit{Var}\left({\theta }_{\pi }\right)=& E\left({\theta }_{\pi }^2\right)-E{\left({\theta }_{\pi }\right)}^2\hfill \\ \hfill =& E\left({\left(\sum _{i<j}{k}_{ij}\right)}^2\right)∕C^2-{\theta }^2\hfill \\ \hfill & \text{where}C=\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)=\frac{n(n-1)}{2}\hfill \\ \hfill =& E\left(\sum _{i<j}{k}_{ij}^2+\sum _{i\ne j\ne r}{k}_{ij}{k}_{ir}+\sum _{i\ne j\ne r\ne s,i<j,r<s}{k}_{ij}{k}_{rs}\right)∕C^2-{\theta }^2\hfill \end{array}$$

Following (Tajima 1983) (A7) we define

$$\begin{array}{cc}\hfill U_2=& E\left(k_{ij}^2\right)-{\theta }^2\hfill \\ \hfill U_3=& E\left(k_{ij}{k}_{ir}\right)-{\theta }^2\hfill \\ \hfill U_4=& E\left(k_{ij}{k}_{rs}\right)-{\theta }^2\hfill \end{array}$$

Intuitively, U₂, U₃, U₄ are variance contributed by two pair of chromosomes. The only difference between those formulas is the overlapping chromosomes between the pairs that result in a different way of counting.

The solutions to the above equations are given by (Tajima 1983) (A12):

$$\begin{array}{cc}\hfill U_2=& \theta +{\theta }^2\hfill \\ \hfill U_3=& \frac{1}{2}\theta +\frac{1}{3}{\theta }^2\hfill \\ \hfill U_4=& \frac{1}{3}\theta +\frac{2}{9}{\theta }^2\hfill \end{array}$$

It is obvious that ∀i, j, we have E(k_ij) = θ, thus we have

$$\mathit{Var}\left({\theta }_{\pi }\right)=\left(\sum _{i<j}{U}_2+\sum _{i\ne j\ne r}{U}_3+\sum _{i\ne j\ne r\ne s,i<j,r<s}{U}_4\right)∕C^2$$

Let us define W_ijrs = Π_m=i,j,r,s Π_l=1…S u(m_l) as the weight added to each U in the above equation, where u(m_l) is the uncertainty factor calculated by the SNP calling confidence of the l th site of chromosome m. More precisely, it is defined as follows:

If the allele of m_l is decided in SNP calling with confidence p, u(m_l) = e^(1−p)c where c is a constant coefficient that allows tuning by users. If the confidence is 1, then the weight is 1, which means no weight. On the other hand, if m_l is an uncertain call, then $u\left(m_l\right)=e^{(1-\overline{p})\mathit{nc}∕n_l}$, where $\overline{p}$ is the average confidence of all the known SNPs called at this site, n is the total number of chromosomes, and n_l is the total number of known SNPs at site l. The intuition behind this setting is that the confidence of the unknown SNP depends on the average of the known SNP, and the number of known SNPs.

With this weighting system defined, we can define an approximate variance of ${\theta }_{\pi }^e$ as the weighted variance:

$$\mathit{Var}\ast \left({\theta }_{\pi }^e\right)=\left(\sum _{i,j,r,s}\mathit{Cov}\left(k_{ij}{k}_{rs}\right)W_{ijrs}\right)∕C^2,$$ (1)

where each Cov(k_ijk_rs) is given by the corresponding U_α (α = 2, 3, 4).

Next let us derive the approximate covariance Cov * (${\theta }_{\pi }^e$, θ_W).

From (Tajima 1989), we have

$$\begin{array}{cc}\hfill \mathit{Cov}({\theta }_{\pi },S)=& \frac{(n+1)(n-2)}{n(n-1)}\mathit{Cov}({\theta }_{\pi }^{\ast },S^{\ast })\hfill \\ \hfill & +\frac{2\theta }{n(n-1)}+\frac{2{\theta }^2}{n{(n-1)}^2},\hfill \end{array}$$

where Cov(${\theta }_{\pi }^{\ast }$, S*) is the corresponding covariance of (n−1) chromosomes and $\frac{2\theta }{n(n-1)}+\frac{2{\theta }^2}{n{(n-1)}^2}$ is the variance at any terminal branch of the genealogical tree.

We add the average weight $\overline{W}=\frac{1}{C^2}{\sum }_{i,j,r,s}{W}_{ijrs}$ to above term, and therefore yield:

$$\begin{array}{cc}\hfill {\mathit{Cov}}^{\ast }({\theta }_{\pi }^e,S)=& \frac{(n+1)(n-2)}{n(n-1)}{\mathit{Cov}}^{\ast }({\theta }_{\pi }^{\ast },S^{\ast })\hfill \\ \hfill & +\left(\frac{2\theta }{n(n-1)}+\frac{2{\theta }^2}{n{(n-1)}^2}\right)\overline{W}\hfill \end{array}$$

Because when n = 2, we have

$$\mathit{Cov}({\theta }_{\pi },S)=\theta +{\theta }^2.$$

We could define when n = 2,

$$\mathit{Cov}\ast ({\theta }_{\pi }^e,S)=(\theta +{\theta }^2)\overline{W}.$$

We could expend this iterative equation and finally derive that

$$\mathit{Cov}\ast ({\theta }_{\pi }^e,S)=\left(\theta +\left(\frac{1}{2}+\frac{1}{n}\right){\theta }^2\right)\overline{W}$$

Therefore,

$$\mathit{Cov}\ast ({\theta }_{\pi }^e,{\theta }_W)=\frac{1}{a_1}\left(\theta +\left(\frac{1}{2}+\frac{1}{n}\right){\theta }^2\right)\overline{W}\text{where}{a}_1=\sum _{i=1}^{n-1}\frac{1}{i}$$ (2)

Also, from (Watterson 1975) we have

$$\mathit{Var}\left(S\right)=a_1\theta +a_2{\theta }^2,\text{where}{a}_1=\sum _{i=1}^{n-1}\frac{1}{i},a_2=\sum _{i=1}^{n-1}\frac{1}{i^2}$$

Therefore,

$$\mathit{Var}\left({\theta }_W\right)=\frac{1}{a_1}\theta +\frac{a_2}{a_1^2}{\theta }^2$$ (3)

Substitute (1), (2), and (3) into (0), we get Var*(${\theta }_{\pi }^e$ − θ_W).

In summary, our statistic is defined as

$$D=\frac{({\theta }_{\pi }^e-{\theta }_W)}{\sqrt{{\mathit{Var}}^{\ast }({\theta }_{\pi }^e-{\theta }_W)}}$$

Where Var*(${\theta }_{\pi }^e$ − θ_W) is given by (0)–(3).

APPENDIX B. SFS_CODE COMMANDS AND CRITICAL VALUES USED

Firstly, we use the basic SFS_CODE command, “sfs_code 1 1 -n 36”, to generate data under a neutral model in which there is no selection or demographic events. The sample size is fixed at 36, identical to the real data used in this paper. We simulate data under this setting 10,000 times for each different uncertainty weight c. Please note that, in the case of extended Tajima’s D, for different c, the critical values of the same significance level are different. A larger c should yield a smaller critical value. On the other hand, for the original Tajima’s D, the critical values should be the same regardless of the c parameter.

Here are the detailed SFS_CODE commands we used:

• (1)
  For demographic models:

  • sfs_code 1 1 -n 36 -Tk 0 2.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 3.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 4.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 5.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 6.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 7.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 8.0 1.2 -TE 1 -a N
  • sfs_code 1 1 -n 36 -Tk 0 9.0 1.2 -TE 1 -a N.
• (2)
  For selective models:

  • sfs_code 1 1 -n 36 -W 1 10.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 15.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 20.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 25.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 35.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 40.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 45.0 0.5 1.0 -a N
  • sfs_code 1 1 -n 36 -W 1 50.0 0.5 1.0 -a N

Here are the critical values used:

• (1)For the independent error model (ED stands for extended Tajima’s D, whereas OD stands for the original Tajima’s D) (Table 4).
• (2)For blocky error model (ED stands for extended Tajima’s D, whereas OD stands for the original Tajima’s D) (Table 5).

Table 4.

c	ED negative	ED positive	OD negative	OD positive
0.10	−1.781	2.171	−1.845	2.231
0.15	−1.721	2.065	−1.845	2.231
0.20	−1.672	2.021	−1.845	2.231
0.25	−1.553	1.948	−1.845	2.231
0.30	−1.545	1.896	−1.845	2.231
0.35	−1.512	1.875	−1.845	2.231
0.40	−1.441	1.823	−1.845	2.231
0.45	−1.394	1.782	−1.845	2.231
0.50	−1.371	1.724	−1.845	2.231

Table 5.

c	ED negative	ED positive	OD negative	OD positive
0.10	−1.801	2.178	−1.870	2.234
0.15	−1.785	2.172	−1.870	2.234
0.20	−1.770	2.144	−1.870	2.234
0.25	−1.760	2.087	−1.870	2.234
0.30	−1.721	2.080	−1.870	2.234
0.35	−1.678	2.079	−1.870	2.234
0.40	−1.674	2.075	−1.870	2.234
0.45	−1.668	1.991	−1.870	2.234
0.50	−1.615	1.990	−1.870	2.234