Abstract
We discuss the evaluation of subsets of variables for the discriminative evidence they provide in multivariate mixture modeling for classification. The novel development of Bayesian classification analysis presented is partly motivated by problems of design and selection of variables in biomolecular studies, particularly involving widely used assays of large-scale single-cell data generated using flow cytometry technology. For such studies and for mixture modeling generally, we define discriminative analysis that overlays fitted mixture models using a natural measure of concordance between mixture component densities, and define an effective and computationally feasible method for assessing and prioritizing subsets of variables according to their roles in discrimination of one or more mixture components. We relate the new discriminative information measures to Bayesian classification probabilities and error rates, and exemplify their use in Bayesian analysis of Dirichlet process mixture models fitted via Markov chain Monte Carlo methods as well as using a novel Bayesian expectation–maximization algorithm. We present a series of theoretical and simulated data examples to fix concepts and exhibit the utility of the approach, and compare with prior approaches. We demonstrate application in the context of automatic classification and discriminative variable selection in high-throughput systems biology using large flow cytometry datasets.
Keywords: Bayesian expectation–maximization, Bayesian mixture models, Classification error rates, Concordance of densities, Dirichlet process mixtures, Discriminative information measure, Discriminative threshold probabilities, Flow cytometry data, Non-Gaussian component mixtures, Variable subset selection
1. Introduction
We are interested in the general question of identifying subsets of variables that play roles in discrimination of subpopulations in the context of multivariate mixture modeling. We are particularly concerned with applications of mixture models to increasingly large samples such as arise in single-cell biomolecular studies typified by current, very widely used flow cytometry technology. In such studies, the samples sizes are large (hundreds of thousands to several millions) and the numbers of mixture components representing meaningful subpopulations can run into the several hundreds. Typified by studies of vaccine design and immune response in multiple areas involving clinical studies of infectious diseases, there is a need for formal statistical methods to guide identification and prioritization of molecular markers both as end-points to variable selection studies and for follow-on confirmatory experiments. The challenge to statistical methodology is that of creating valid, effective, and computationally accessible approaches to variable subset assessment and prioritization with regard to the ability of each subset to discriminate one or more subpopulations from the rest.
Routinely applied biological cell assays using flow cytometry generate multiple data sets with sample sizes (numbers of cells) in the hundreds of thousands or millions and involving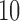 
–
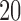variables (cell surface markers) allowing interrogation of cell population heterogeneity. Mixture modeling approaches (e.g., Boedigheimer and Ferbas, 2008; Lo and others, 2008; Chan and others, 2008; Finak and others, 2009; Pyne and others, 2009) are now central in studies to automatically identify different cell populations, a necessary step before applying flow cytometric data to design of new studies, e.g., correlation with possible clinical outcomes of interest. Automated mixture model fitting overlaid with an effective approach to discriminative analysis to prioritize subsets of variables can be expected to have a major impact on advancing statistical work in this area, among others.
This is our setting and challenge: Given a mixture model previously fitted (in our cases, using Bayesian methods via Bayesian EM and/or Markov chain Monte Carlo methods), formalize and implement an effective Bayesian/decision analytic approach to prioritizing variables in their ability to discriminate each practically relevant mixture component from the rest.
Notationally, we consider a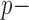 
dimensional, 
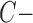component mixture distribution with density function
 |
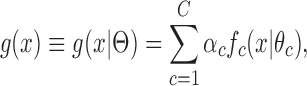(1.1) |
where each subpopulation density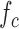 
has its own parameters 
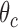and component probability 
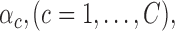and 
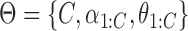is the full set of parameters. Based on fitting the model to an observed data set, we address the following questions. For each component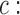 
Which subsets of the
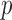variables, if any, contribute in meaningful ways to discrimination of 
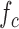from the other components?Are there variables that are irrelevant to discrimination of
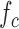?Are there single or small subsets of variables that characterize
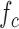alone and play no roles in discriminating other components?Can we rank subsets of variables by their discriminative ability with respect to
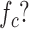
The general questions relate to variable selection in mixtures. We address the discriminative analysis following model fitting: we assume that the model is available with either plug-in parameter estimates or Markov chain Monte Carlo based posterior samples, e.g., Lavine and West (1992), West (1992, 1997), Dellaportas and Papageorgiou (2006), Frühwirth-Schnatter and Pyne (2010) and aim to then interrogate the model to evaluate the discriminative roles of different subsets of variables. As part of this, we directly address the issue that very different subsets of variables may play roles in differentiating different mixture components. Also, we are keen to define computationally effective approaches so as to enable access and routine use, and an ability to scale to larger models.
We provide theoretical development and then examples in Bayesian mixture models using standard truncated Dirichlet process mixtures. The analysis is quite general, but this Bayesian normal mixture framework, e.g., Escobar and West (1995), MacEachern and Müller (1998), Ishwaran and James (2001), and Müller and Quintana (2004) will be familiar to many readers; among other things, it offers an approach to handling uncertainty about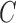 
subject to a specified large upper bound.
Our examples and much applied interest lies in mixture models where each component density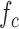 
may have a non-Gaussian form. One effective approach is to fit an encompassing mixture of Gaussians and then aggregate subsets of the fitted densities; that is, each 
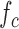is itself represented as a mixture of, typically, a small number of Gaussians, e.g., Chan and others (2008) and Finak and others (2009). Supplementary material available at Biostatistics online summarizes Bayesian computational methods for Gaussian mixtures and technical details of the subsequent construction of non-Gaussian subpopulation densities, as well as other technical details. Our computational work also introduces a new Bayesian expectation–maximization algorithm for truncated Dirichlet process mixtures, while the MCMC analysis exploits the most effective component relabeling approach Cron and West (2011). Both optimization and simulation analyses utilize efficient parallel implementations of Bayesian computations for these mixture models Suchard and others (2010).
2. Discriminative information
2.1. Classification
In the mixture model of equation (1.1), focus on one of the component distributions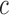 
. For notational clarity here write 
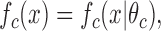the dependence on parameters being implicit. The mixture pdf is then
 |
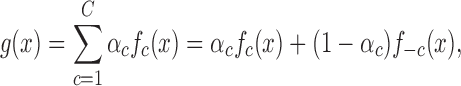(2.1) |
where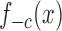 
is the conditional mixture
 |
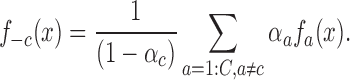(2.2) |
We will also interpret this notation as extending to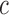 
being a set of components, for contexts when we want to compare discrimination of a set/collection of clusters—or subpopulations-from the others; the notation obviously encompasses this.
Now suppose we record an observation at the point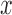 
in the sample space with no additional information about its genesis. The classification probability for component 
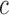—the probability that this case in fact arose from that component (or set of components) — is then simply the posterior probability 
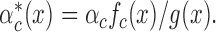Any hard classification rule chooses to classify 
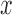as coming from component (group or cluster) 
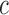if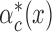 
is large enough, i.e., if 
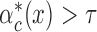for some chosen threshold 
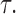Now note that 
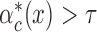if any only if, 
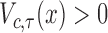where
 |
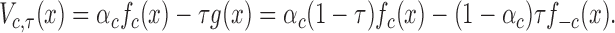(2.3) |
Definition 1 —
As a function of
for given component
and classification probability threshold
in (2.3) is the classifier for component
determining classification boundaries/regions in the sample space.
2.2. Discriminative information measures of evidence
Cases when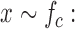 
Assume we know that a specific observation 
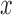actually arises from component 
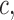i.e.,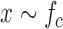 
. In such a case, larger values of 
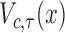are desirable to generate high rates of true-positive classifications. We see that
 |
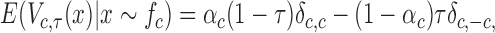(2.4) |
where
 |
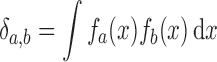(2.5) |
for any two distributions with pdfs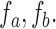 
Note that 
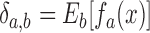where the expectation is over 
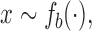and the measure is symmetric in 
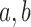. The number 
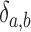is a natural measure of agreement, overlap or concordance between the two distributions. This measure of concordance takes higher values when 
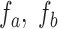are closely similar, is maximized when the densities agree exactly, and otherwise decays towards zero as the densities become more separated. Concordance was discussed as the basis of a similarity distance between densities by Scott and Szewczyk (2001), for example. In the mixture context, assessing how different component 
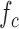is to the set of remaining components of the mixture, it is therefore intuitively natural that the concordance 
arises as in (2.4).
Continuing under the true-positive assumption that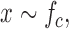 
we see that 
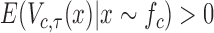implies and is implied from (2.4) by
 |
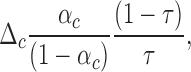(2.6) |
where
 |
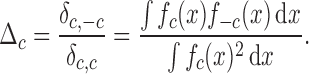(2.7) |
Cases when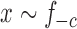 
: In the complementary case when 
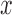actually generated from 
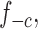then for any specified classification probability threshold 
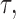small values of 
below zero are desirable in order to appropriately classify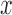 
with a high success rate. In other words, 
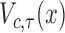should be large in terms of its absolute value. A similar argument to that above then yields 
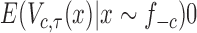if, and only if,
 |
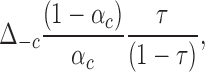(2.8) |
where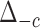 
is the analogous discriminative information measure of evidence (DIME) for components 
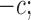that is,
 |
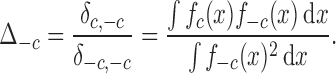(2.9) |
Definition 2 —
For any component
the number
defined in (2.7) is the true-positive discriminative information measure of evidence
DIME
for component
The number
of (2.9) is the corresponding true-negative DIME value for component
In comparing discrimination based on different subsets of variables, we will modify the notation to make explicit which variables are used. For any subset of variables
when restricting to the mixture distribution on only the
margin, we denote the DIME values by
The two DIME values for any component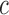 
are standardized, directional versions of the basic concordance measure 
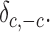Small values imply good discrimination. Note also that they are measures on a likelihood ratio scale, and so are easily interpretable measures of pure discrimination. Specifically for positive discrimination, (2.6) shows that the DIME value 
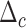is in fact a likelihood ratio, i.e., a Bayes’ factor, that maps prior odds 
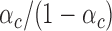on component 
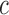to an implied posterior odds ratio of at least 
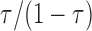based on a Bayes’ factor of 
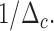Similar comments apply to the role and interpretation of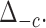 
2.3. DIME and classification performance
Given a mixture, we can directly and simply compute the DIME values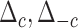 
as numerical summaries of discrimination of component 
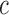from the rest, with their interpretations as Bayes’ factors (likelihood ratios). They nicely quantify discrimination between mixture components decoupled completely from prior probabilities of mixture components and hence from classification rates. Further development now relates them to classification performance in the context of the overall mixture model now involving the prior probabilities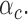 
Note that classifying any future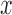 
value as coming from component 
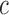based on 
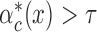induces a classifier 
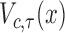whose expectation under 
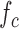is positive when, from equations (2.6) and (2.7),
 |
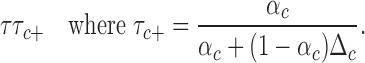(2.10) |
Similarly, the expected classifier is negative under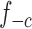 
when, from equations (2.8) and (2.9),
 |
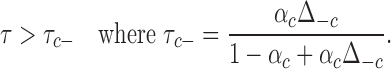(2.11) |
The key equations (2.10) and (2.11) map the DIME measures and prior probabilities to easily computable classification thresholds on the interpretable probability scale. It turns out that we can further interpret these thresholds in connection with classification performance measured by the theoretical expected posterior classification probabilities, namely
 |
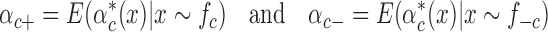where, for all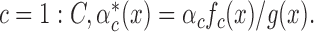 
Refer to 
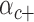as the expected true-positive classification rate, and 
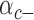as the expected false-positive rate1. In simple examples, these rates can be approximately computed by simulation, e.g., by simple importance sampling. However, computing their values exactly is impossible and estimating them a standing issue in classification with mixtures.
It turns out that the trivially computed classification probability bounds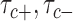 
are simple, direct first-order approximations to 
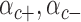, respectively, as follows. For the former, simply note that 
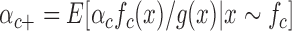, the expectation of the ratio of 
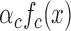to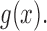 
Using the first-order approximation given by the ratio of the two corresponding expectations yields
 |
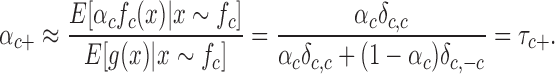We similarly deduce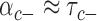 
, with details left to the reader. Section 5 of Supplementary material available at Biostatistics online shows high accuracy of the approximation works across practically relevant contexts.
Definition 3 —
The quantities
and
are referred to as the true- and false-positive discriminative threshold probabilities for classification into component
of the mixture. As with DIME values in Definition 2, when comparing discrimination based on different subsets of variables, we will make explicit in the notation which variables are used. For any subset of variables
when restricting to the mixture distribution on only the
margin, we denote the discriminative threshold probabilities by
This represents an advance in practical evaluation of classification performance using mixtures; direct evaluation of expected classification rates is simply infeasible, while these trivially computed discriminative threshold probabilities are easy to compute based on DIME measures and prior probabilities. In addition to the bounds they provide for classification, they are seen to also define estimates of expected classification rates.
3. Practical discrimination
3.1. Overview
The above theoretical and conceptual developments generate advances in terms of efficient computation of bounds related to classification rates. Our main interest here is in the practical use of this to evaluate the discriminative information provided by different subsets of variable in connection with one or any of the mixture components. We can now do this in both relative and absolute senses; DIME measures are likelihood ratios that provide relative assessments across variable subsets, while the derived discriminative threshold probabilities provide absolute comparisons on the probability scale. Practically, small values of 
are desirable as they will lead to higher sensitivity and specificity in classification of cases as coming from component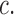 
Correspondingly, high values of 
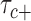and low values of 
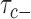indicate good discrimination of component 
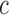from the rest concerning true-positive and false-positive rates, respectively. These easily computed bounds that depend naturally on concordance between densities can therefore compare and absolutely quantify discriminative abilities of differing subsets of variables within the same overall joint mixture model.
Given a specified mixture on the full set of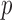 
-variables in 
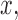we will just directly marginalize to the variable subset 
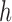to compute DIME values and discrimination probabilities for each component 
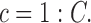This way the issue of evaluating discriminative subsets can be carried out for all components and any selected subsets of variables based on the fitted model, without refitting. By exploring subsets 
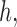we can automatically generate ranked sets of variables for each component and address the questions above. Notice that, at an extreme, if one or a subset of variables 
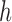is independent of the rest and has the same distribution over all components, then 
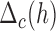will take the same values when computed in the mixture model analysis with or without those variables, showing their irrelevance.
3.2. Evaluations on variable subsets
For each component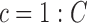 
and a given subset of variables 
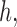consider the quantity
 |
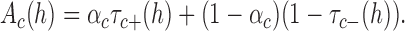(3.1) |
This is the natural prior/base-rate weighted average of discriminative threshold probabilities for classification into component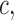 
an overall classification rate summary. Note that it is on the absolute probability scale so differences across different subsets 
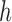can be easily interpreted.
Definition 4 —
For each component
the quantity
in (3.1) is referred to as the aggregate discriminative accuracy measure for component
in the marginal mixture distribution for variable subset
Given the mixture of (1.1) on the full set of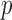 
variables, we can directly extract the implied marginal mixture on any subset of variables 
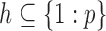for discriminative evaluation of components based on only that subset (
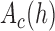). When 
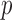is small, we can directly evaluate all possible 
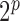variable subsets. For moderate and larger 
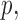this is of course infeasible and some form of guided search over variable subsets is needed. Forward (Section 7 of Supplementary material available at Biostatistics online) and/or backward selection methods are obvious first steps. Our examples and application below utilize a first, direct forward search method as follows. In higher-dimensional problems, it would be natural to utilize ideas of stochastic search methods as used for exploring variable subsets in regression and for graphical model search (e.g., Jones and others, 2005; Hans and others, 2007), but this is beyond our scope here.
3.3. Model fitting and estimation of discriminative measures
All of the above theoretical development has assumed a given mixture model—that is, a given set of values of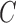 
and full knowledge of the 
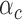and all model densities 
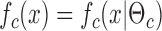in (1.1). In practice, we perform inference on all model parameters and this translates to estimation of the DIME, discriminative threshold probabilities and discriminative accuracy measures. Our Bayesian analysis in examples here uses standard truncated Dirichlet process mixtures of multivariate normal distributions. This context involves fixing a (large) upper bound on the number of normal components in the mixture, and then developing the posterior over all model parameters, including the effective number of components, based on any given data set. Summary details and references are given in Supplementary material available at Biostatistics online.
4. Synthetic data example
Two proof-of-principle examples to demonstrate the DIME-based analysis are in Section 8 of Supplementary material available at Biostatistics online. Here, we show one example that strongly illustrates the ability of DIME-based analysis to dissect component-specific discriminatory variables from the rest, comparing the analysis with the ridgeline-based separability measure (RSM) of Lee and Li (2012), which appears to be the most directly related approach to discriminative assessment. RSM, which measures the pairwise separability between the modes of any two clusters, has been shown to be superior to earlier methods including the scatter separability criterion (SSC) (Dy and Brodley, 2004). RSM is a global measure that selects one subset of variables for all components, and it has an explicit analytic expression only in cases of two component normal mixtures with identity covariance matrices. Logistically, we follow the forward selected strategy and recommendations in Lee and Li (2012), evaluating variables to add to a current discriminatory subset if the increase in RSM exceeds 0.01 at each step, and stopping otherwise. MCMC analyses were initialized at the Bayesian EM-based posterior modes, and we generated posterior simulations of size 10,000 following additional burn-in iterates. For most direct comparison, RSM measures were evaluated using mixture model parameters estimated by MCMC-based posterior means.
We generated a synthetic sample of 6000 from an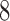 
-dimensional mixture of normals. The mixture has four components of proportions 
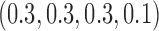and with mean vectors 
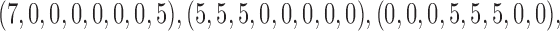and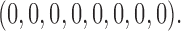 
The covariance matrix of component 1 is 
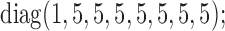for components 2 and 3, the covariance matrix entries for the subsets of variables having non-zero means are
 |
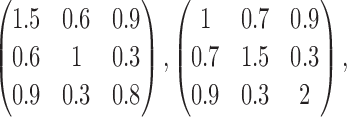respectively, the remaining dimensions have zero covariances with any other variables and variances 5. The covariance matrix for component 4 is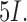 
Figure 1 displays standardized data.
Fig. 1.
Pairwise scatter plots of a randomly selected subset of the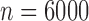 
observations in the synthetic example.
The MCMC-based posterior from analysis with a mixture of at most 16 multivariate normals strongly identifies four effective components; discriminative summaries for the dominant first 3 appear in Table 1. For each of the first 3 components, these summaries identify a single but component-specific variable as being relevant and sufficient to achieve an overall average classification probability at 95% accuracy; they also indicate the extent to which—on this interpretable scale—additional variables can be expected to improve this, reaching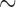 
99% with two variable subsets that are again different across components. In contrast, RSM selects all the variables except 
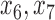(a union of the DIME selected variables), with no insights into relative discriminative information of variable subsets across components.
Table 1.
Accuracy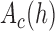 
, 
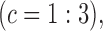in the synthetic example, variables are ordered according to the forward search based on discriminative accuracy 
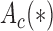or RSM
 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Variable |  |
1 |  |
2 | 6 | 5 | 4 | 7 |
 |
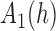0.956 | 0.986 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
 |
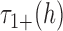0.897 | 0.973 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
 |
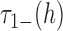0.021 | 0.009 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
 |
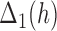0.049 | 0.012 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
 |
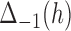0.050 | 0.022 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Variable |  |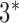
 |
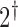1 | 4 | 6 | 8 | 5 | 7 |
 |
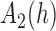0.985 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
 |
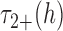0.970 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
 |
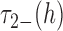0.010 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
 |
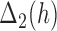0.013 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
 |
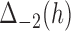0.022 | 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| Variable |  |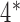
 |
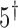6 | 1 | 3 | 2 | 8 | 7 |
 |
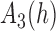0.980 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
 |
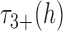0.958 | 0.997 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
 |
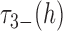0.012 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
 |
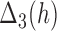0.019 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
 |
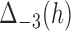0.027 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| Variable | 1 | 2 | 4 | 8 | 5 | 3 | 6 | 7 |
 |
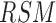0.312 | 0.580 | 0.618 | 0.646 | 0.669 | 0.681 | 0.682 | 0.681 |
Note. For the former, variables indicated by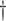 
would terminate the forward search for discriminatory variables if we choose to do so based on a minimal change of 0.01 in accuracy. We now also indicate by 
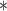the last variable identified to define a minimal set with absolute accuracy (average classification probability) 
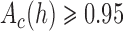, if this is achieved. We underline the index of the last variable entered using RSM.
5. Discriminatory markers in flow cytometry analysis
Multi-parameter flow cytometry can measure 15 or more variables—biological phenotypic or functional markers—on thousands of cells per second; it is a routine biological assay used in basic and clinical research laboratories worldwide. The primary use of flow cytometry data is in identifying subpopulations within large data sets that represent different regions of the multivariate marker space that relate to differentiation of cells and their biological function. Multivariate mixture models are increasingly used (Chan and others, 2008; Lin and others, 2013) and the interest in identifying relevant subsets of markers, addressing the general questions of discriminative subsets posed in Section 1, is fundamental to both analysis of experimental results and to the design and selection of marker variables for future studies.
We give an example in which a subset of variables is biologically known to define a scientifically interesting subpopulation. The study is an applied proof-of-concept, but also turns out to be more interesting biologically as we identify somewhat different marker subsets that have been commonly believed to be key. In this study, we are interested in regulatory T cells (Tregs), a specialized subtype of T cells that are critical to the maintenance of immune cell homeostasis and tolerance to self-antigens. We analyzed data from three replicate samples of peripheral blood mononuclear cells from the same donor to identify the minimal marker subset needed to discriminate Tregs from all other cellular subtypes. Each data set comprises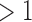 
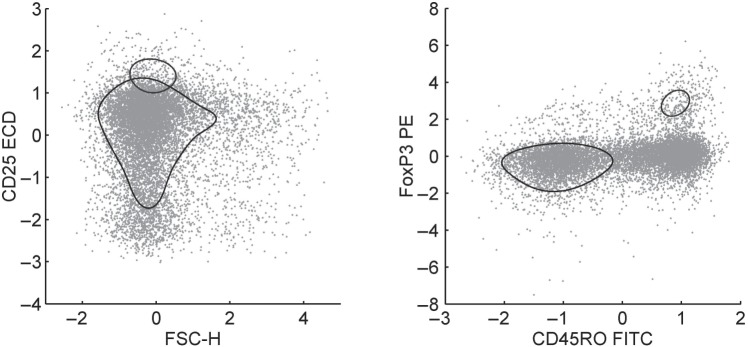
million observations coming from multiple cellular subtypes of which Treqs are just one subpopulation, and the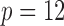 
scatter and fluorescent markers used in the analysis were FSC-A, FSC-H, SSC-A, vAmine (viability dye), CD3 V500, CD4 PerCP-Cy55, CD45R0 FITC, CD25 ECD, CD127 PE-Cy5, FoxP3 PE, Helios A647, and CD39 PE-Cy7. While FoxP3 is a master regulator in the development and function of Tregs and the most specific single Treg marker, it requires intra-nuclear staining to detect and the use of FoxP3 is not compatible with obtaining viable Tregs for functional studies using fluorescent activated cell sorting (FACS). Therefore, one major interest is to evaluate the extent to which FoxP3 is indispensable in identifying Tregs. Aspects of the data in four important marker variable dimensions, in displays that also illustrate—dimensional projections of some particular non-Gaussian cellular subtypes, appear in Figure 2.
Fig. 2.
Scatter plots of standardized flow cytometry levels for 4 of the 12 marker variables, showing a randomly selected subsample of 10,000 cells. To highlight basic aspects of the mixture model analysis, the scatters are overlaid with contours of the corresponding two-dimensional margins of the two mixture components with highest estimated probabilities. Purely for display here, the specific estimate of the pdf is based on the mixture model with plug-in parameters defined by the posterior mode computed using the Bayesian EM algorithm, followed by component aggregation to identify the non-Gaussian subtypes displayed. The area of each contour displayed is approximately proportional to the corresponding posterior modal estimate of the resulting component probabilities.
Analysis used an upper bound of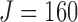 
on the number of Gaussian components with the strategy of identifying subtypes by aggregating components around modes of attraction; see Supplementary material available at Biostatistics online. We remark that this aggregation strategy is now becoming standard in mixture model analysis in this application area. Repeat posterior mode search via the Bayesian EM algorithm of Supplementary material available at Biostatistics online identified a highest posterior mode used to initialize the MCMC, followed by component relabeling and aggregation to define possibly non-normal components (
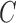= 88, 86, and 123 for the three samples, respectively). From the posterior summaries resulting, we first identified a component corresponding to the Tregs cellular subtype based on biological knowledge; Tregs are defined as having high values in FoxP3, CD25, CD3 and CD4, and low values in vAmine and CD127. We use 
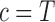to denote the Treg subpopulation and evaluate markers for their ability to discriminate Treg cells from the remaining components– some of which are identifiable cellular subtypes– represented by the posterior. We computed MCMC-based posterior means of the probabilistic classification accuracy measures 
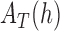for all possible subsets
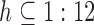; Figure 3 reports a summary selection, including the most discriminative subset of 
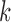markers for each 
.
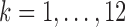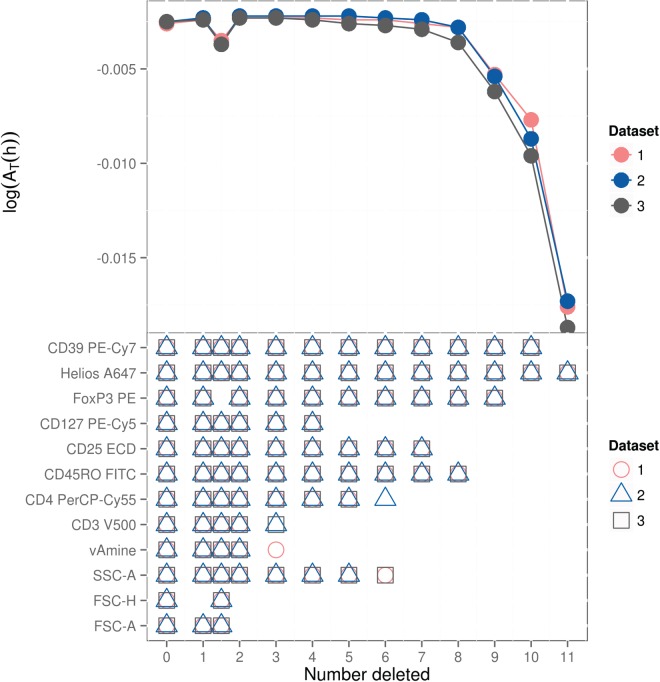
Fig. 3.
Summary discriminative measures for selected marker variable subsets in the analysis of Tregs flow cytometry data. The number of markers is decreased one at a time from left to right, with the best discriminative subsets indicated by different colors/symbols for each of the three data sets. The corresponding accuracy measures—plotted on the log scale—are shown at the top. The loss in accuracy when deleting FoxP3 is also shown—plotted, simply for convenience, at 1.5 on the horizontal axis.
Very good discrimination of Tregs is obtained using as few as four markers, with only modest increases in accuracy as markers are added; this is relevant for future studies to isolate only Treg cells with a reduced set of markers. The smallest subset of markers to identify Tregs in the absence of FoxP3 is CD39 and Helios with an accuracy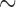 
0.99. CD39 and Helios markers are known to characterize functionally active and thymic-derived Tregs, respectively (Borsellino and others, 2007; Thornton and others, 2010), and so constitute the dominant Treg population in these samples. However, as shown in Figure 3, dropping FOXP3 results in a small but significant decrease in accuracy, confirming that FOXP3 is an important marker characterizing Tregs.
6. Additional comments
The utility and effectiveness of the discriminative information and probabilistic classification measures introduced here are clear in both the synthetic and real data examples. Based on discrimination of mixture components via measures of concordance, the approach is intuitive and natural; the ties to misclassification rates provides additional theoretical insights and a map to the intuitive probability scale for evaluating and comparing variable subsets.
Coupled with existing approaches and software tools for posterior mode search and posterior simulation in multivariate mixtures, the approach extends the toolbox of statistical discrimination and classification for studies aiming to dissect the roles played by variables, both individually and in association with other variables, in the determination of discrimination of mixture subpopulations. In contrast to variable selection approaches (e.g., Raftery and Dean, 2006; Kim and others, 2006), this new method overlays an existing mixture model analysis to explore and quantify the roles of subsets of variables, and so can be applied easily and routinely across analysis. Our examples show how it relates to and improves upon existing approaches. Further in comparison, the current approach is computationally accessible and scalable. The dissection of roles of variables cuts deeper than other methods in evaluating local discriminative roles of variables; that is, assessing subsets of variables for their roles on each subpopulation, rather than aiming to select one set of variables for all components. This is key in applications such as the flow cytometry study illustrated here, where different, generally small subsets of variables can characterize subpopulations, with some variables being irrelevant for discrimination of many components but critically relevant for others.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
This research was partially supported by grants from the U.S. National Institutes of Health (RC1-AI086032, P30-AI06451) and the National Science Foundation (DMS-1106516). Any opinions, findings, and conclusions or recommendations expressed in this work are those of the authors and do not necessarily reflect the views of the NIH or NSF.
Supplementary Material
Acknowledgements
The authors are grateful to David Murdoch, Janet Staats, and Kent Weinhold for providing the flow cytometry dataset and for discussions of the biological context of that motivating study (Section 5). Conflict of Interest: None declared.
Footnotes
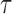, i.e.,
 |
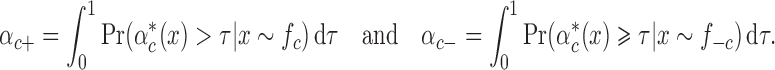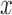—is seen to be apt.References
- Boedigheimer M. J., Ferbas J. (2008). Mixture modeling approach to flow cytometry data. Cytometry Part A 73A(5), 421–429. [DOI] [PubMed] [Google Scholar]
- Borsellino G., Kleinewietfeld M., Di, Mitri, Diamantini A., Giometto R., Höpner S., Centonze D., Bernardi G., Dell’Acqua M. L.. and others (2007). Expression of ectonucleotidase CD39 by Foxp3+ Treg cells: hydrolysis of extracellular ATP and immune suppression. Blood 110(4), 1225–1232. [DOI] [PubMed] [Google Scholar]
- Chan C., Feng F., West M., Kepler T. B. (2008). Statistical mixture modelling for cell subtype identification in flow cytometry. Cytometry, A 73, 693–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cron A. J., West M. (2011). Efficient classification-based relabeling in mixture models. The American Statistician 65, 16–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellaportas P., Papageorgiou I. (2006). Multivariate mixtures of normals with unknown number of components. Statistics and Computing 16(1), 57–68. [Google Scholar]
- Dy J. G., Brodley C. E. (2004). Feature selection for unsupervised learning. Journal of Machine Learning Research 5, 845–889. [Google Scholar]
- Escobar M. D., West M. (1995). Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association 90, 577–588. [Google Scholar]
- Finak G., Bashashati A., Brinkman R., Gottardo R. (2009). Merging mixture components for cell population identification in flow cytometry. Advances in Bioinformatics Article ID 247646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frühwirth-Schnatter S., Pyne S. (2010). Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 11(2), 317–336. [DOI] [PubMed] [Google Scholar]
- Hans C., Wang Q., Dobra A., West M. (2007). SSS: high-dimensional Bayesian regression model search. Bulletin of the International Society for Bayesian Analysis 24, 8–9. [Google Scholar]
- Ishwaran H., James L. F. (2001). Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association 96, 161–C173. [Google Scholar]
- Jones B., Dobra A., Carvalho C. M., Hans C., Carter C., West M. (2005). Experiments in stochastic computation for high-dimensional graphical models. Statistical Science 20, 388–400. [Google Scholar]
- Kim S., Tadesse M. G., Vannucci M. (2006). Variable selection in clustering via Dirichlet process mixture models. Biometrika 93, 877–893. [Google Scholar]
- Lavine M., West M. (1992). A Bayesian method for classification and discrimination. Canadian Journal of Statistics 20, 451–461. [Google Scholar]
- Lee H., Li J. (2012). Variable selection for clustering by ridgeline-based separability. Journal of Computational and Graphical Statistics 21, 315—337. [Google Scholar]
- Lin L., Chan C., Hadrup S. R., Froesig T. M., Wang Q., West M. (2013). Hierarchical Bayesian mixture modelling for antigen-specific T-cell subtyping in combinatorially encoded flow cytometry studies. Statistical Applications in Genetics and Molecular Biology 12, 309—331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo K., Brinkman R. R., Gottardo R. (2008). Automated gating of flow cytometry data via robust model-based clustering. Cytometry Part A 73A(4), 321–332. [DOI] [PubMed] [Google Scholar]
- MacEachern S. N., Müller P. (1998). Estimating mixture of Dirichlet process models. Journal of Computational and Graphical Statistics 7, 223—238. [Google Scholar]
- Müller P., Quintana F. A. (2004). Nonparametric Bayesian data analysis. Statistical Science 19, 95–110. [Google Scholar]
- Pyne S., Hu X., Wang K., Rossin E., Lin T.-I., Maier L. M., Baecher-Allan C., McLachlan G. J., Tamayo P., Hafler D. A., De Jager P. L.. and others (2009). Automated high-dimensional flow cytometric data analysis. The Proceedings of the National Academy of Sciences of the United States of America 106(21), 8519–8524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery A. E., Dean N. (2006). Variable selection for model-based clustering. Journal of the American Statistical Association 101, 168–178. [Google Scholar]
- Scott D. W., Szewczyk W. F. (2001). From kernels to mixtures. Technometrics 3, 323–335. [Google Scholar]
- Suchard M. A., Wang Q., Chan C., Frelinger J., Cron A. J., West M. (2010). Understanding GPU programming for statistical computation: studies in massively parallel massive mixtures. Journal of Computational and Graphical Statistics 19, 419—438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton A. M., Korty P. E., Tran D. Q., Wohlfert E. A., Murray P. E., Belkaid Y., Shevach E. M. (2010). Expression of Helios, an Ikaros transcription factor family member, differentiates thymic-derived from peripherally induced Foxp3+ T regulatory cells. The Journal of Immunology 184(7), 3433–3441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West M. (1992). Modelling with mixtures (with discussion). In: Bernardo J. M., Berger J. O., Dawid A. P., Smith A. F. M. (editors), Bayesian Statistics 4 Oxford University Press, pp. 503–524. [Google Scholar]
- West M. (1997). Hierarchical mixture models in neurological transmission analysis. Journal of the American Statistical Association 92, 587–606. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.