Modeling Intensive Longitudinal Data With Mixtures of Nonparametric Trajectories and Time-Varying Effects

Abstract

Behavioral scientists increasingly collect intensive longitudinal data (ILD), in which phenomena are measured at high frequency and in real time. In many such studies, it is of interest to describe the pattern of change over time in important variables as well as the changing nature of the relationship between variables. Individuals' trajectories on variables of interest may be far from linear, and the predictive relationship between variables of interest and related covariates may also change over time in a nonlinear way. Time-varying effect models (TVEMs; see Tan, Shiyko, Li, Li, & Dierker, 2012) address these needs by allowing regression coefficients to be smooth, nonlinear functions of time rather than constants. However, it is possible that not only observed covariates but also unknown, latent variables may be related to the outcome. That is, regression coefficients may change over time and also vary for different kinds of individuals. Therefore, we describe a finite mixture version of TVEM for situations in which the population is heterogeneous and in which a single trajectory would conceal important, inter-individual differences. This extended approach, MixTVEM, combines finite mixture modeling with non- or semi-parametric regression modeling, in order to describe a complex pattern of change over time for distinct latent classes of individuals. The usefulness of the method is demonstrated in an empirical example from a smoking cessation study. We provide a versatile SAS macro and R function for fitting MixTVEMs.

Intensive longitudinal data (ILD) are increasingly prevalent in the behavioral sciences, because of improved data-collection techniques and dynamic theories of human functioning. Collection of ILD is encouraged by reduced cost of technology and by benefits of ILD such as improved ecological validity and minimized recall bias. ILD are collected in studies under different names, including ecological momentary assessments (EMA; Stone & Shiffman, 1994; Shiffman, Stone, & Hufford, 2008), experience sampling (Larson & Csikszentmihalyi, 1983), ambulatory assessment (Fahrenberg, Myrtek, Pawlik, & Perrez, 2007), and diary studies (Bolger, Davis, & Rafaeli, 2003). ILD are generally characterized by a large number of repeated assessments designed to capture personal experiences and environmental conditions at or near the time of their occurrence. Applications of ILD are diverse and growing, and a few examples include studies of addictive behaviors (Shiffman, 2009), eating disorders (Munsch et al., 2009), and physical activity (Sternfeld et al., 2012). While rich and detailed, ILD pose numerous analytical challenges in order to make fuller use of the information available (Walls & Schafer 2006). Two important challenges are heterogeneity (important differences exist between study participants that are not fully captured by measured covariates) and nonlinearity (trajectories of variables cannot always be modeled as simply linear or quadratic). In this paper we describe a modeling approach, MixTVEM (mixture of time-varying effect models), which address both of these issues and offers a framework for investigating novel research questions.

The goals of this paper are threefold. The first is to introduce MixTVEM to behavioral scientists. Similar models were proposed before in the statistical literature (Lu and Song, 2012) but have not been put to use in the psychological literature. The second goal is to provide convenient software to fit MixTVEMs; no such software has previously been available. The third goal is to provide an example data analysis using MixTVEM, with recommendations for model selection and for using the results of the fitted model to investigate important scientific questions.

MixTVEM is an extension of the time-varying effect model (TVEM) described by Tan, Shiyko, Li, Li, and Dierker (2012). As in TVEM, MixTVEM addresses nonlinearity by modeling regression coefficients as smooth functions of time rather than as constants. Additionally, MixTVEM allows for direct modeling of interpersonal heterogeneity by assuming that each participant belongs to one of multiple latent classes (analogously to the group-based trajectory modeling of Nagin, 1999) with class-specific regression functions.

In the sections that follow, we discuss issues of nonlinearity and participant heterogeneity, introduce MixTVEM as a possible solution, and briefly review the literature and reasoning underlying MixTVEM. An empirical examination of smoking withdrawal symptoms during a quit attempt serves as a practical demonstration. A SAS macro and R function for fitting these models and a discussion on practical issues related to model fitting and interpretation are provided to promote a broader application of the method.

Motivation for MixTVEM

To illustrate the motivation for MixTVEM, we first review some existing methods and some of their limitations. Suppose that for each individual i = 1,…, N, an outcome variable y (e.g., self-rated urge to smoke) is measured at each of n_i measurement times t_ij, j=1,…,n_i. Suppose an investigator wishes to fit a model to predict the change in the average value of y as a function of time t. As a starting point, the simplest possible way to model change would be a linear model,

$$y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+e_{ij},$$ (1)

where the residuals e_ij are assumed to be independent and normally distributed with mean 0 and variance σ². This model represents the mean growth curve over time by a straight line β₀ + β₁t. It also assumes that each individual follows the same underlying growth pattern. This very restrictive model would not allow the investigation of important questions about (a) how the relationship between variables differs over time as a process evolves, or (b) how the relationship differs between individuals due to differing personal characteristics. These restrictions are overcome by nonparametric regression on one hand, and mixture modeling on the other hand. We review two specific approaches in the literature, TVEM (a kind of nonparametric regression) and group-based trajectory modeling (a kind of mixture modeling), which generalize model (1) in different ways. We then describe how to combine them in an extended approach, which we call MixTVEM. MixTVEM is suitable for exploring more nuanced questions about ILD, specifically about the heterogeneity of nonlinear, time-varying relationships between variables.

Modeling Nonlinearity

For traditional longitudinal data, the linearity assumption can be relaxed in several ways (see the review by Aunola & Nurmi, 2004). For example, if there are only a few measurement time points t_ij shared by all individuals, then the mean observed y can be estimated separately within each time point j, with no a priori restrictions on the shape or pattern of change. Similarly, in a latent basis or free-slope-loading model (e.g., Meredith & Tisak, 1990; Muthén & Khoo, 1998), the values of y at each measurement time are estimated in terms of factor loadings. These approaches are not very practical for ILD, in which observations can vary in frequency and timing across participants and are not arranged in regular waves (hence cannot easily be organized as a single N × n matrix).

Another way of relaxing linearity is to allow the growth curve to be some polynomial of order greater than one, such as quadratic or cubic. This approach often works quite well (recent examples of the use of quadratic trajectories include Cofta-Woerpel et al., 2011, and Javitz, Lerman & Swan, 2012) but still has some limitations. It limits modeling to only a few basic shapes (e.g., flat, rising, falling, rising and then falling, or falling and then rising, in the case of quadratic trajectories). Higher-order polynomials are possible, but involve very high sampling variability and an unnecessarily complex appearance with potential for spurious peaks and valleys; therefore they can be impractical to interpret (Weisberg, 2005). If there is a theoretical reason to expect a parametric curve with a specific nonlinear shape, such as a logistic curve (see, e.g., Kelley, 2008), then this could be a better, more interpretable option than a high-order polynomial. However, in other settings there is no specific family of parametric curves to propose.

Another approach to estimating nonlinear growth is to allow different linear or quadratic trajectories for theoretically distinct time periods (e.g., middle versus high school, Crawford, Pentz, Chou, Li, & Dwyer 2003; prequit versus postquit, McCarthy, Piasecki, Fiore & Baker, 2006). In smoking cessation, for example, one could study how prequit and postquit slopes are related. This piece-wise approach is versatile and interpretable, but still imposes a linear (or other simple and known) form of growth during each time period. It also requires a priori knowledge of these distinct time periods.

In order to estimate growth more flexibly, consider replacing model (1) with

$$y_{ij}=\beta (t_{ij})+e_{ij},$$ (2)

where β(t) is a smooth function of t, unknown beforehand but estimated nonparametrically from the data, and e_ij∼N(0, σ²) independently for each measurement time. Model (2) generalizes Model (1) by removing the assumption that the underlying trajectory is linear. The shape of β can be flexibly and smoothly modeled using splines (see Eilers & Marx, 1996), as described later (other estimation approaches are also available; see Tan et al., 2012). Model (2) can easily be extended to include covariates. The values of the covariates may be either constant over time (e.g., gender or treatment group) or time-varying (e.g., like stress level, time of day). In addition, their relationship with the response (their effects in a regression sense) can also be time-varying:

$$y_{ij}={\beta }_0(t_{ij})+{\beta }_1(t_{ij})x_{ij1}+\cdots +{\beta }_P(t_{ij})x_{ijP}+e_{ij}.$$ (3)

Tan, Shiyko, Li, Li and Dierker (2012) called Equation (3) the time-varying effect model (TVEM), to emphasize that covariates may have substantively different relationships with y at different time points. For example, a covariate might be a more important predictor near the beginning of a process than near the end. Because TVEM allows the coefficients to be functions of time, a rich description of the changes in processes over time is possible. TVEM can be described as an application of varying-coefficients regression (Hastie & Tibshirani, 1993) to longitudinal data. Alternatively, if the predictors are considered to be functions of time, it is essentially equivalent to what Ramsay and Silverman (2005) call the concurrent functional dependent variable form of the functional linear model. Model (2) is a very simple case of model (3), containing only a time-varying intercept.

In the TVEM framework, there are several possibilities for the relationship between y and a given covariate x_k,; these progress from the simplest to the most general.

• If β_k(t) is 0 for all t, then x_k is always unrelated to y after conditioning upon other covariates (i.e., x_k is excluded from the model).

• If β_k(t) is a nonzero constant (i.e., β_k(t) = β_k for some number β_k) then the regression effect of x_k on predicted y at any given measurement time is the same regardless of the time of assessment. A unit difference in x_k between subjects at a given time predicts a difference of β_k in y at that time, and this difference is assumed to be the same regardless of the measurement time. A covariate cannot be more important at the beginning of the study than at the end, nor vice versa.

• If β_k(t) is equal to a linear function of t, then x_k can be said to have an interaction with time in the usual multiple linear regression sense (i.e., both x_ijk and x_ijkt_ij are included in the regression model). This could be extended to a quadratic or other nonlinear parametric shape.

• Most generally, if β_k(t) is a nonparametric function, then x_k interacts with time in a nonlinear way. Thus, it is possible for differences between subjects in x_k to be positively related, negatively related, or unrelated, to differences between subjects in y, at different times during the study.

Nonparametric β_k(t) functions can be estimated in a straightforward way using splines, and their basic form (zero, constant, linear, quadratic, cubic, or general) can be selected by using graphical or model-based fit criteria.

Modeling Heterogeneity

The TVEM approach as described above will provide a flexible curve for the regression functions. However, it does not capture interindividual differences in trajectories over time. Such an aggregate model may not be a good representation of all, or even any, of the observed individuals (Hertzog & Nesselroade, 2003). There are three common ways to generalize a parametric regression model to allow different growth curves for different subjects (see Muthén, 2004; Muthén & Asparouhov, 2009; Reinecke, 2006; Erosheva, Matsueda, & Telesca, 2014). Multilevel models (see overview in Singer & Willett, 2003) incorporate random effects (i.e., different regression parameters for each subject, assumed to come from continuous latent distributions). Latent class growth analysis, also called group-based trajectory modeling (Nagin, 1999, 2005), assumes that subjects come from different latent classes with different regression coefficient values for each class (Nagin, 1999). Growth mixture modeling (see Muthén & Shedden, 1999; Muthén & Muthén, 2000) assumes not only different classes but also random effects within each class.

In latent class growth analysis or growth mixture modeling, individuals come from distinct latent classes with different growth parameter values for each class. Each class has its own underlying linear or quadratic trajectory and may also have its own regression coefficients for substantive covariates. This can be extended to allow each class to have its own TVEM; we call the resulting approach MixTVEM. This marriage has important advantages. Users of latent class growth analysis or growth mixture modeling often assume that the regression effects of covariates are constant over time. At best, they assume that the effect changes in a linear way (such as allowing a baseline covariate to affect the linear slope of the growth curve, effectively specifying a linear interaction between covariate and time). TVEM allows regression coefficients to change flexibly over time, but the same TVEM is often assumed to apply to all participants. In MixTVEM it is possible to ask how people differ in terms of the patterns of change in the relationships of multiple variables over time. This may not only facilitate exploratory empirical research but also may ultimately help psychologists formulate and test theories and hypotheses in a richer and more precise way.

A conceptually identical approach to what we call MixTVEM was previously proposed by Lu and Song (2012) as “finite mixture varying coefficient models” and implemented by them in a Bayesian context. Related works include Pleydell and Chrétien (2010), who worked with data arranged in space rather than time, and who used a nonlinear but still somewhat restrictive specification of the coefficient functions. Lu and Song (2012) focused on Bayesian inference, and estimated the model parameters using the Metropolis-Hastings algorithm, a kind of Monte Carlo Markov chain (MCMC) algorithm. In this paper we take a frequentist approach instead and estimate the model parameters using the expectation-maximization (EM) algorithm. More importantly, although they provided a conceptual framework, Lu and Song (2012) did not provide software for routine use of their algorithm. Here we provide SAS and R software for conveniently implementing our approach. As studied by Celeux, Hurn, and Robert (2000) and Frühwirth-Schnatter (2001), the MCMC method for mixture models needs to be used carefully because of potential label switching during the course of the MCMC procedure, which could cause bias. Lu and Song (2012) recommend imposing appropriate constraints to keep the class order identified during the procedure. However, it may be difficult to find the right constraints because of the complex and unknown nature of the true model in nonparametric mixture regression models. This may be a relative advantage of EM in this situation.

We also handle serial correlation differently from Lu and Song (2012), and in a way which we argue to be more realistic, at least for some examples. However, both approaches share some common advantages and limitations. The assumptions of each approach are described in the following section.

The Model: MixTVEM

The previous section described the motivations for MixTVEM as an extension both of TVEM and of latent class growth analysis. In this section we explain the Lu and Song implementation of MixTVEM and our implementation of MixTVEM in more detail.

Definition of the Model

A MixTVEM analysis (or equivalently a finite mixture varying coefficient model) consists of two parts: a multinomial logistic model to predict class membership c for each individual, and a linear model to predict measured responses y₁,…, y_ni within each individual conditional upon class membership c. While c is a categorical variable, the responses y₁, …, y_ni are assumed multivariate normal conditional on the latent c. Non-normally distributed responses (in particular binary y) are possible, but for simplicity we consider only the normal case here.

Model for c

We follow the common approach of allowing latent class membership to be the outcome of a multiple-category logistic regression model. This has been done before with categorical latent class analysis (Dayton & Macready, 1988; Lanza, Collins, Lemmon, & Schafer, 2007) and with analyses of trajectories on a numerical variable (e.g., Shi & Wang, 2008; Lu & Song, 2012). Conditional upon time-invariant subject-level covariates s₁,…, s_Q, individual i has a probability π_ic of belonging to a given class c, where

$${\pi }_{ic}=P(c_i=c)=\frac{exp({\gamma }_{0,c}+\sum _{q=1}^Q{\gamma }_{1qc}{S}_q)}{\sum _{c^{\prime }=1}^{C}exp({\gamma }_{0,c^{\prime }}+\sum _{q=1}^Q{\gamma }_{1q{c}^{\prime }}{S}_q)}.$$ (4)

For model identifiability in this case, one of the classes has its γ parameters constrained to 0 and is treated as a baseline or comparison group. If there are no time-invariant covariates of interest (Q=0), then Model (4) simplifies to assuming that there is simply an unknown population proportion π_c for each class.

Model for mean of y

Within each class, the mean model is essentially the same as the TVEM in Tan et al. (2012). Specifically, conditional upon time t_ij, upon the individual's class membership c_i, and upon the observation-level covariates x₁, …, x_p, the response y_ij is modeled as normal with true expected value

$${\mu }_{ij}=\mathrm{E}(y_{ij}|(c_i=c))={\beta }_{0c}(t_{ij})+{\beta }_{1c}(t_{ij})x_{ij1}+\cdots +{\beta }_{Pc}(t_{ij})x_{ijP}.$$ (5)

The investigator can allow all of the coefficients to be time-varying or can optionally restrict some coefficients to be constant over time. Model (5) generalizes Model (3), but allows the regression parameters to be class-specific (i.e., to depend on c_i). Note that the values of time t_ij may be individual-specific (as in the random electronic assessments used in many ILD applications), but the form of the function β_kc(t) is assumed constant for each class.

Models for variance of y

While Model (5) provides the conditional expected value of the response, it does not specify the covariance structure. The simplest option would be to assume that all responses are independent, conditional on class. That is, all differences between individuals are accounted for by class. This would generally not be a realistic model for longitudinal data, unless the number of observations per subject is small compared to the number of classes. Ignoring within-subject correlation will tend to require more classes to adequately account for the observed data, relative to an approach that considers within-subject correlation (see Bauer & Curran, 2003; Lubke & Neale, 2006; Muthén, 2004; Petras & Masyn, 2010).

In contrast, the richest possible approach would be to have a truly multilevel regression within each class. For example, each β_kc(t) in (5) could be replaced by a mean function β_kc0(t) plus some random Gaussian process b_ik(t) with mean zero. This general idea might be implemented by adding a random effect to each column of the spline expansion. James and Sugar (2003) followed this approach for a model closely similar to (2). However, it might be difficult to get such a model to converge in the case of multiple covariates such as in Model (5).

A reasonable compromise approach, taken by Lu and Song (2012), is to add a parametric random effects structure within each class. Thus, for example,

$$y_{ij}={\mu }_{ij}+a_i+b_i{t}_{ij}+e_{ij},$$ (6)

where μ_ij is given by Model (5), a_i and b_i are independently normally distributed at the subject level, and e_ij are independently normally distributed at the observation level. There may also be random effects of $t_{ij}^2$ or even $t_{ij}^3$. The number of random effects presents another tradeoff. It is not clear why subject-specific effects should be linear when mean trajectories are nonlinear. However, the more random effects are added, especially to a model that already contains a latent categorical variable, the harder it will be to find the global optimum of the likelihood function. Thus, keeping the random effects structure reasonably simple is wise.

A disadvantage of a random effects model such as Model (6) is that it forces a particular kind of heteroskedasticity over time. Model (6) suggests that the marginal within-class variance at time t_ij is ${\sigma }_a^2+{\sigma }_b^2{t}_{ij}^2+{\sigma }_e^2$, where ${\sigma }_a^2$, ${\sigma }_b^2$, and ${\sigma }_e^2$ are the variances of the three random terms. Thus, whichever time is designated as time zero must have the lowest marginal error variance, and the variance must increase monotonically thereafter in each class. In the substantive example we provide below, which involves smoking urges during a cessation attempt, it is not clear whether the variance should necessarily be increasing in this way, especially if latent class membership has already been taken into account. Therefore, we wished to use a parametric covariance structure such as AR-1 (autoregressive of order one) instead of using random effects. In studies with equally spaced measurements, AR-1 specifies that the overall variance is constant and that the correlation between two measurements depends on the number of measurement intervals between them: ρ (say, .1) for a lag of one unit, ρ² (say, .01) for two units, and so on, for some parameter ρ (see, e.g., Liang & Zeger, 1986). In many ILD studies, especially those involving EMA, this seems unreasonable because measurements are not taken in evenly spaced waves; one lag might involve an hour, while another involves a day. That problem can be addressed by generalizing the AR-1 definition so that the correlation is Corr(y_ij, y_ij′) = ρ^{|t_ij−t_ij′|}, allowing t to be a continuous rather than integer-valued variable (see Diggle, 1988; Schwartz & Stone, 1998). Shi and Wang (2008) followed a somewhat similar approach in their work with longitudinal mixture modeling.

However, even with this extension, AR-1 has some limitations. We were not able to fit it to our sample data, even after extending it to allow unequal lags. This was because an AR-1 structure would specify that either distant observations are essentially uncorrelated (if ρ is low), or else adjacent observations (for which the time lag is very small) must be essentially identical (if ρ is high). Examination of the data showed that for many subjects the urge trajectories had a chaotic appearance, with very low values sometimes followed by very high ones or vice versa. This led to numerical instability in estimating ρ, and thus failure to converge, if we assumed a simple autoregressive error process. Therefore, it is necessary to allow for a measurement error or “nugget” effect (see Banerjee, Carlin, & Gelfand, 2015) that is specific to a particular time, in addition to the smooth autoregressive process. Adding a nugget to AR-1 structure leads to

$$Cov(y_{ij},y_{i{j}^{\prime }})={\sigma }_a^2{\rho }^{|t_{ij}-t_{i{j}^{\prime }}|}+{\sigma }_e^2.$$ (7)

This structure implies that the total variance at any time period is ${\sigma }_{\mathit{\text{total}}}^2={\sigma }_a^2+{\sigma }_e^2$, and the within-subject covariance is Corr(y_ij, y_ij′) = (1 − p_e)ρ^{|t_ij−t_ij′|}, where we denote $p_e={\sigma }_e^2/{\sigma }_{\mathit{\text{total}}}^2$ as the proportion nugget. We allow different values of the overall noise level ${\sigma }_{\mathit{\text{total}}}^2$ for each class. However, to improve convergence, we assume a shared value of p_e.

The autocorrelation structure with nugget is intuitively plausible. It posits that variations in observations are partly due to a smooth, subject-specific process, and partly due to observation-specific noise. It also does not require variance to increase monotonically, as would be required by adding random coefficients of time, time squared, and so on to the model. However, it is not as computationally burdensome as making each spline coefficient random. Thus, it appears to be a very satisfactory covariance model, and we consequently implemented it in our software and empirical example. As an aside, in the special case of equally spaced data the AR(1) structure with nugget is equivalent to the ARMA(1,1) structure, a simple autoregressive moving average covariance structure (see SAS Institute, 2008, pp. 2192, 2203).

Summary

MixTVEM accomodates heterogeneity and nonlinearity by allowing different nonparametric regression function shapes for each of multiple latent classes of subjects. We write Model (5) as a normal linear model, although generalized linear models (such as a binary logistic response) are also possible. Although the model for the mean of y is nonparametric (i.e., its exact form is not specified by the model), we still use a parametric normal probability distribution for the errors to enable computation of posterior probabilities. We also use a parametric autoregressive moving average structure for the correlation of observations within subjects. An entirely nonparametric mixture regression model would be very difficult to identify or estimate. Thus MixTVEM might better be considered semiparametric than nonparametric.

Estimation of Model Parameters

The two main challenges in estimating the coefficients for MixTVEM are the fact that the class memberships c are latent rather than observed and the fact that the β coefficients are functions rather than single numbers. Both of these technical challenges, however, have relatively straightforward technical solutions: the EM algorithm (Dempster, Laird, & Rubin, 1977) and spline-basis expansion (Schoenberg, 1946; Eilers & Marx, 1996), respectively.

EM Algorithm

As in other finite mixture models (see McLachlan & Peel, 2000), the EM algorithm is very useful in estimating the coefficients for each latent class. It involves iterating between estimating individuals' posterior probabilities of belonging to each class (E step) and using these probabilities as weights for estimating the parameters of each class (M step). To begin this iterative process, starting values are randomly generated (in our MixTVEM software we do this by randomly generating initial posterior probabilities). It is important to use multiple random starts to increase the probability of finding the best available solution. This algorithm is implemented for MixTVEM in our SAS macro and R function, included in the online appendix.

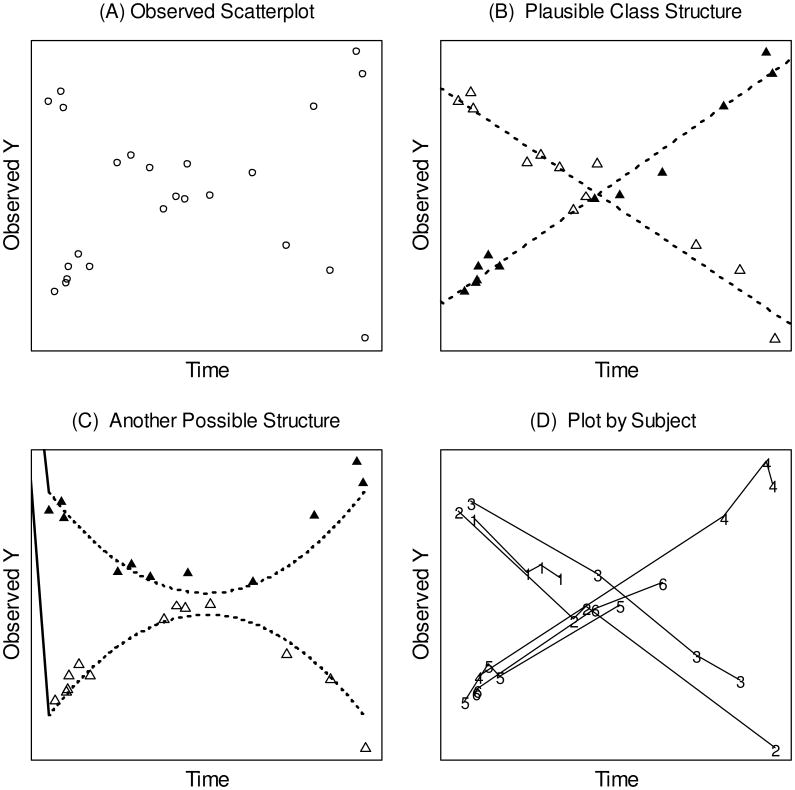
The EM algorithm as we implement it for MixTVEM takes into account the fact that that the observations are clustered within individuals. That is, it assigns posterior probabilities to individuals as a whole rather than to particular observations. This is especially important because the identifiability of a mixture of nonparametric trajectories depends upon at least some individuals having multiple measurements and upon the assumption that each individual belongs to one and only one latent class without switching classes. As a hypothetical example, consider panel A in Figure 1. The hypothetical data could be fit just as well by at least two different two-class structures: one with a rising trajectory and another with a falling trajectory (panel B), or one with a concave trajectory and another with a convex trajectory (panel C). However, once individual-level information is available as in panel D, it becomes clearer which model is more appropriate: the one in panel B, in this case. Huang, Li, and Wang (2013) provide more specific information on identifiability conditions for nonparametric trajectories.

Figure 1.

Distinguishing between two possible fits for a hypothetical sample of longitudinal data. Panel A shows a hypothetical dataset of repeated measurements, ignoring subject identity. Panels B and C show two possible models to fit the data. Panel D shows that connecting the dots for each subject (i.e., taking into account the fact that all measurements on a subject have the same class membership) helps identify the model.

Spline Basis Expansion

There are various ways to estimate a nonparametric function β(t). In this paper we use the penalized B-spline approach of Eilers and Marx (1996). As in polynomial regression, we approximate β(t) by a linear combination of several functions of t. However, instead of a simple polynomial basis, we use a spline basis, constructed using several “knots” at τ₁,…, τ_K, which are prespecified time points at which the shape of the trajectory function changes. This method is described further in the Appendix.

Spline models resemble piecewise models in that both allow the slope or curve of the growth trajectory to change at specific times. Piecewise models have only one or a few knots, each corresponding to a theoretically important change point caused by a known event or transition. However, in the spline approach, there may be many knots, and the knots are primarily a mathematical device for allowing a smooth function estimate without specifying a shape in advance. Between any two knots of the spline, the trajectory may be assumed to be linear, quadratic, or cubic. Each time a knot is passed, the model effectively allows the parameters that describe the shape to change, and therefore any smooth function can be approximated reasonably well if there are enough knots.

To keep the resulting fit from being too “wiggly,” (i.e., too prone to spuriously recognizing small-scale sampling variability as replicable features; Eilers & Marx, 1996, p. 98) we adjust the log-likelihood with a second-order difference penalty function on the regression coefficients for the knots, in order to reduce the size of the changes occurring at each knot (see Eilers & Marx, 1996, for details). It is necessary to choose the strength of the penalty using some data-driven criterion.

One option is to use a weighted form of the generalized cross validation (GCV) statistic (see Craven & Wahba, 1979; Eilers & Marx, 1996), adjusted for the presence of multiple classes (replacing the residual sum of squares in the numerator of the usual GCV formula with a weighted residual sum of squares, and summing the effective number of parameters across classes). Eilers and Marx (1996) used a simple AIC-like criterion, consisting of the deviance (or -2 log-likelihood) plus twice the effective number of parameters. AIC performs similarly to GCV and both have favorable properties for estimating nonparametric functions (Shao, 1997; Hastie, Tibshirani, & Friedman, 2001). However, we found that in the mixture context, this criterion seemed to be overfitting. We therefore implemented a more parsimonious version; specifically, we used a penalty multiplier of log(N) instead of 2, where N is the number of subjects, basing this on the form of the BIC statistic. This is likely to lead to a smooth function, because BIC tends to be quite resistant to overfitting (see, e.g., Dziak, Coffman, Lanza & Li, 2012). In addition, Wang, Li, and Tsai (2007) used a similar BIC-based function to choose a penalty tuning parameter in a different context (that of high-dimensional variable selection). To summarize, in our R and SAS functions, we choose the size of the penalty function automatically using a BIC-like criterion in order to provide a smooth and parsimonious shape.

Choosing the Number of Classes

Theory to provide the number or nature of classes a priori will often be unavailable (Petras & Masyn, 2010), so some data-driven approach is desirable. Likelihood-based fit criteria such as AIC (Akaike, 1973) or BIC (Schwarz, 1978) seem to beobvious candidates, but they face some limitations in the context of MixTVEM. First, assumptions about the asymptotic behavior of the information criteria are not necessarily met in a mixture context (see McLachlan & Peel, 2000, pp. 202-212; Steele & Raftery, 2010, p. 118). Second, because of the large number of observations per subject available in ILD and the complicated and unknown nature of the true within-subject covariance structure, the model may have a statistically significant lack of fit for any interpretable number of classes. Hence, the information criteria will sometimes indicate that an impractically large number of classes should be fit. Lu and Song (2012), despite using a relatively richand realistic model for the within-subject covariance structure, found in their empirical example that their fit criterion suggested the largest available model; therefore they had to choose a model size based largely on substantive interpretability.

Thus, in addition to AIC and BIC, in this paper we consider a heuristic approach similar to the “elbow plot” or “scree plot”frequently used in factor analysis. Petras and Masyn (2010) used elbow plots to help in choosing the number of classes in a parametric growth mixture analysis. A measure of in-sample prediction inaccuracy (such as sum of squared errors or a log-likelihood-based criterion) is plotted against a measure of model size (such as number of classes). Because the model is being fit and evaluated with the same data, the fit of the model to the observed data improves as model size increases (one gets closer and closer to merely “connecting the dots”). Thus, a plot of inaccuracy against model size will tend to be a decreasing function, but not necessarily linearly decreasing. One should examine the plot for the “elbow”: a model size that, if decreased, gives dramatically worse performance, but if increased, does not give dramatically better performance. While a subjective determination, this approach has the advantage of being straightforward and easily interpretable. In order to create an elbow plot, a measure of model fit is required. A common measure of regression model fit is the residual sum of squared errors $\mathit{\text{RSS}}={\sum }_{i=1}^N{\sum }_{j=1}^{n_i}{(y_{ij}-{\widehat{y}}_{ij})}^2$, where ŷ_ij is a predicted value for Y_ij from the fitted model. However, this formula cannot be used directly in MixTVEM because the model provides several different predictions for y_ij, one for each class to which individual i might belong. If individual i were known to belong to class c, one could use Model (5) to calculate a class-specific prediction ŷ_ij|c for each observed t_ij. However, because class membership is latent rather than observed, all that is available here is the posterior probability of class membership, ω_ic, for each individual i and class c (see McLachlan & Peel, 2000). Therefore, one could examine an elbow plot of a weighted measure of predictive accuracy such as weighted residual sum of squares:

$$\mathit{\text{WRSS}}=\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{c=1}^{n_{\text{classes}}}{\omega }_{ic}\left(\sum _{j=1}^{n_i}{(y_{ij}-{\widehat{y}}_{ij|c})}^2\right),$$ (8)

where N is the number of individuals and n_i is the number of observations for the ith individual. Using this measure, the importance of a particular class's model fitting an individual's observed trajectory well (in terms of low sum of squared errors, $\sum _{j=1}^{n_i}{(y_{ij}-{\widehat{y}}_{ij|c})}^2$) is determined by the estimated posterior probability ω_ic of the individual belonging to that class. Another option would be to examine an elbow plot of the log-likelihood itself. The WRSS approach would treat all classes equally, but the log-likelihood approach would weight errors according to the estimated error variance in each class.

A final consideration for model selection is the degree of confidence in the identification of the global maximum likelihood solution. This can be assessed in terms of the dependence of the solution on the random starting value. If many random starts are used, and most of them lead to essentially the same fitted model (after permutation of the class labels if necessary), then it is reasonable to suppose that this fitted model is the best available given the model and data. If they lead to many different solutions, so that the best-fitting estimate available is reached by only one or a few of the starting values, then it is not clear that even this estimate is truly the global maximum. We assess this by comparing several starting values, with the level of the penalty tuning parameter held constant, and recording the proportion of starting values that lead to a log-likelihood agreeing (to within, say, .1 units) with the best log-likelihood available.

Standard Errors

As in any kind of regression model, standard errors are of interest for summarizing uncertainty about the coefficient estimates. In our implementation of MixTVEM we calculate standard error estimates by combining the mixture regression information approach (used because of the uncertainty about true class membership) of Louis (1982) and Turner (2000), with the “sandwich” or “robust” formula (used because of the unknown true covariance of the observations within subject, and analogous to working-independence GEE; see Liang & Zeger, 1986). We also treat the covariance parameters as known when calculating confidence intervals for the regression parameters, which is a common practice in multivariate regression and would be difficult to avoid given the rather complicated covariance structure. Some further research would be useful here, especially in light of concerns about possible undercoverage with the sandwich approach (Kauermann & Carroll, 2001); as Ma and Zhong (2008) pointed out, construction of frequentist standard errors and confidence intervals for nonparametric models is challenging. The standard error formulas do not account for bias which can occur if an overly high penalty parameter is selected and the functions are oversmoothed; however, this bias should generally operate in a conservative way (against the spurious discovery of new features). The current approach appears to be the most plausible available method without using resampling.

Bootstrap methods would be computationally quite costly because of the requirement for running an EM algorithm for each of many starting values within each of many bootstrap replications. However, they might provide more accurate standard errors. We do not investigate bootstrap standard errors in the current paper. Note that bootstrapping in a finite mixture context such as MixTVEM would require considerable care and modification in order to deal with label switching (i.e., the meaning of “Class 2” changing from one bootstrap replication to the next) without introducing new bias through inappropriate constraints on the true parameters. Therefore, more study on its advantages and disadvantages is required.

Summary

In summary, MixTVEM provides a solution for describing complex within-person changes, identifying clusters of individuals with similar change patterns, and characterizing clusters based on covariates, thus satisfying essential goals of longitudinal data analysis (see Bollen & Curran, 2006). In the following section, empirical data from a smoking-cessation study is analyzed with MixTVEM for demonstration.

Smoking Cessation Example

In this section, we describe two applications of MixTVEM to data from an EMA study (Shiffman, Hickcox et al., 1996; Shiffman, 1997) that investigated personal and contextual factors related to smoking cessation. Urge to smoke, as well as other self-reported variables, were repeatedly assessed in a sample of highly motivated quitters for about two weeks before, and up to about four weeks after, a planned quit date. Participants were prompted at random times by an electronic device, typically multiple times per day, to answer questions about their current mood and smoking urge intensity. (Participants were also given event-driven prompts in certain situations, but we consider only the random prompts in the current paper, in order to treat the observation times as non-informative.)

Heterogeneity and nonlinearity are both very relevant to the study of smoking cessation because of the dynamic and personal nature of smoking behavior. Shiffman and colleagues (1997) found that craving declined over time for this sample as a whole, but this could mask substantial heterogeneity. Conceptually, some individuals may have rapidly improving withdrawal symptoms, some might not improve at all, and some might improve and then plateau or perhaps even rebound (a phenomenon that could not be modeled by simply allowing linear slopes). Indeed, past research has suggested important between-person heterogeneity in withdrawal trajectories (e.g., Piasecki, Fiore, & Baker, 1998, McCarthy et al., 2006).

Not only negative affect and urge, but also the relationship between them, may differ among people. This may be because people have qualitatively different reasons for smoking in the first place or because they have different underlying levels of physiological addiction. Past research suggests that smokers report diverse motivations and triggers for smoking, but negative affect or desire to relieve it is often among the most prominent (see Brandon, 1994; Baker, Piper, McCarthy, Majeski & Fiore, 2004; Leung, Gartner, Dobson, Lucke & Hall, 2011; UW Center for Tobacco Research and Intervention, 2002). In addition to differing among people, the relationship between negative affect and urge for a given person may change over time during the quitting process. For example, Zinser, Baker, Sherman, & Cannon (1992) suggested that urge to smoke may be associated with positive affect when smoking ad libitum, but with negative affect after quitting. The dataset of interest has been previously analyzed using TVEM (although not MixTVEM), and it was found that the marginal relationship between negative affect and urge to smoke indeed tended to weaken over time for the sample in general, although it might temporarily peak in the few days immediately following quit date (see Li, Root, & Shiffman, 2006; Shiyko, Lanza, Tan, Li & Shiffman, 2012). Nicotine withdrawal should fade over time, which would cause the association between smoking and nicotine withdrawal (which is marked by negative affect) to decrease, with external cues perhaps becoming more important over time. This would suggest a weakening or change in the relationship between negative affect and craving.

If the classes found in a MixTVEM analysis are valid constructs, one would expect that they should predict other constructs. Craving or urge has been shown to be a powerful predictor of lapse and relapse during smoking attempts (Piper et al., 2008; also see review in Bagot, Heishman & Moolchan, 2007). As a symptom of withdrawal, it should presumably also be higher in those who were more severely addicted prior to the quit attempt. These relationships would be expected to be maintained even if urge is expressed in terms of classes or trajectories rather than a single numerical value. In light of these considerations, we consider the following questions:

1. Diversity of trajectories. How does the urge to smoke change over time, and do change trajectories differ across latent classes of participants?

2. Diversity of covariate-adjusted trajectories. How does the relationship of negative affect (see Brandon, 1994; Shiffman & Waters, 2004) to urge to smoke change over time, and do these changes differ across latent classes of participants?

3. Relationship of trajectory to subject-level predictors. Are the latent class variables identified in questions 1 and 2 related to subject characteristics, especially prior measures of addiction severity?

4. Relationship of trajectory to subject-level outcome. Do the latent class variables identified in questions 1 and 2 predict later relapse?

We explored these questions using our R MixTVEM software. We also verified the most important analyses using our SAS MixTVEM software.

Sample

We study a subsample of 200 participants from a smoking cessation study (Shiffman, Hickcox, et al., 1996; Shiffman, Paty, et al., 1996; Shiffman et al., 1997). This subsample consisted of those who had at least one week of postquit data, who abstained successfully for at least a day, and who did not experience full relapses during the first week. Relapse was defined as smoking at least 5 cigarettes for 3 consecutive days. Participants received behavioral counseling, but were not using pharmacological therapy such as nicotine replacement. We consider the first seven days after the designated quit date, and consider observations having full data for the emotion questions and the urge to smoke question described below. This period provides a total of 4,975 observations, with each individual contributing a total of 2 to 53 observations (mean=24.9, SD=11.0), averaging about 3 observations per person per day.

Measures

Urge to Smoke

Participants rated their urge to smoke on a 0 (no urge) to 10 (the strongest urge) scale on each measurement occasion.

Negative Affect

Participants responded to questions about their mood on a scale of 1 (strongly no) to 4 (strongly yes). A negative affect (NegAff) scale was created by averaging responses to items on miserable, irritable, tense, frustrated/angry, sad, happy, and contented (with the last two states reverse-coded). This was roughly based on the first factor in the factor analysis reported by Shiffman and colleagues (Shiffman, Hickcox, et al, 1996). The item set had a Cronbach alpha of .84 (95% confidence interval .83 to .85), suggesting a fairly cohesive measure of negative affect.

As a caveat, the confidence interval for alpha above is calculated for the dataset as a whole and treating all observations as independent. Considering only the first observation from each individual in order to force independence would give a Cronbach alpha of .79 (95% confidence interval of .74 to .83). The Cronbach's alpha should still be considered only a heuristic description here, because the items are not normally distributed: first, they are limited to values of 1, 2, 3, and 4, and second, some of them (particularly miserable, frustrated/angry, and sad) are heavily right-skewed. The confidence intervals for alpha were calculated using the psychometric R package (Fletcher, 2010) using the formulas of Feldt, Woodruff, and Salih (1987), which assume normal distributions, although Feldt, Woodruff, and Salih (1987) provided some evidence to suggest that their results were fairly robust to violations of this assumption.

Relapse Status

Relapse status was considered to be a dichotomous variable expressing whether the subject was recorded as relapsing to regular smoking during a follow-up period of four weeks following quit date (i.e., three weeks following the week of data used in the model; recall that to be included in the analysis at all, participants had to quit for at least 24 hours and then avoid relapse for at least one week).

Results: Question 1

We first sought a descriptive picture of how average urge changes over time for different groups of participants. This involves an intercept-only MixTVEM in which, for measurement occasion j on member i belonging to latent class c, the predicted value of urge is

$${\text{Urge}}_{ij}|(c_i=c)={\beta }_{0|c}(t_{ij})+e_{ij},$$ (9)

where t_ij denotes time since quit (expressed in units of days for convenience, but allowing fractional values). The error term e_ij is assumed N(0, ${\sigma }_c^2$) with class-specific ${\sigma }_c^2$.

Spline model details

In Model (9), we estimated the function β_0|c for each class as a penalized B-spline (Eilers & Marx, 1996). Several choices must be made when implementing a penalized B-spline, especially the degree d_s of the spline, the degree d_p of the penalty, and the number of internal knots used to partition the interval of interest. The literature offers general advice for these choices, but no specific rules. These choices could be made by trying many alternative values and choosing the best AIC or BIC. Engel and Kneip (1996) support this approach, suggesting that both the tuning parameter (penalty strength) and the number of knots be chosen using AIC. For this illustrative example, however, we simply chose a reasonable value for each, as described below.

It is common practice to use a quadratic or cubic spline (d_s=2 or d_s=3), and often not much difference is observed between them. We recommend a cubic spline (d_s=3). A higher d_s is possible in principle, but in practice researchers who are seeking a more flexible function can simply add more knots or reduce the strength of the penalty function. A linear spline (d_s=1) will look very different, and we do not recommend it because it will look jagged instead of smooth (that is, it will not have a continuous first derivative at the knots).

Eilers and Marx (1996, p. 116) recommend d_s = 3 and d_p = 3 as a rule of thumb, although they note d_p = 2 is consistent with past literature. We use a slightly more parsimonious d_p = 2, which means, heuristically, that the penalty function will bias the estimated function in the direction of a straight line (Eilers & Marx, 1996, p. 91). This does not mean that the estimated function will be linear, only that it will be close to linear wherever the data does not clearly indicate otherwise. Eilers and Marx (1996) observe that a d_p = 1 would lead to a jagged-looking piecewise linear fit, while a higher d_p (biasing the result towards a quadratic or higher-order polynomial instead of a line) could make computation more complicated.

In the absence of a penalty function, using too many knots would cause the model to severely overfit the data, leading to a highly unstable, uninterpretable estimate with spurious features (rises and falls which are actually just the result of sampling error or noise). However, the penalty function is used to help prevent this from happening. Thus, in the presence of a penalty, it is generally advised that while using too few knots may reduce the accuracy of the estimate, using too many knots simply slows down computation without appreciably changing the final estimated function (see Ruppert, Wand, and Carroll, 2003). From this perspective, a prudent researcher should err on the side of more knots. However, there is some evidence that even when a penalty is being used, too many knots can lead to too high sampling variability, although there is not a clear rule for the correct number of knots for a given sample size (Claeskens, Krivobokova, and Opsomer, 2009). From this perspective, the number of knots presents a bias-variance tradeoff, where using too few knots make it impossible to fit a complicated nonlinear function adequately, while using too many adds noise.

There is little specific guidance on choosing the number of knots for splines in a mixture model context. Lu and Song (2012) used 10 internal knots. In a non-mixture context, Eilers and Marx (1996, p. 93) stated that generally 10-20 basis functions are used, which suggests about 6-16 internal knots for a cubic B-spline (see the Appendix for an explanation of the additional four basis functions). Ruppert, Wand, and Carroll (2003, pp. 125-6) suggest a rule of thumb of either 35 internal knots, or one fourth as many knots as there are unique measurement time values, whichever is lower. In the empirical example used in this paper, time is measured on a continuous scale so there are essentially hundreds of unique measurement times, and so this rule of thumb would suggest 35 knots.

However, in a mixture context it may be wise to use fewer knots than one would use for estimating just a single function, because the larger number of functions being estimated may pose more risk for overfitting at least some of them. In the current example, there are good reasons to believe that the underlying mean function, although not linear, will have a fairly simple shape. First, we are not trying to model effects related to diurnal rhythms in this analysis, and we have only a few observations per person per day, so changes on a scale much smaller than a day may be of less interest here. Second, participants are not all necessarily following the same daily schedule. Thus, although individual participants will experience sudden rises and falls in urge caused by internal or external stressors, there is no particular reason why these should be synchronized among large numbers of subjects. In other words, mean trajectories should be expected to be much smoother than individual trajectories. For example, if we were to find a class with a small number of members which was characterized by a spike in urge on the second half of day 3 and an inexplicable dip on day 5 and 6, it would probably more reasonable to treat this as random than to report it as a substantive new clinical finding. Thus, it seems parsimonious to use rather fewer knots.

With these considerations in mind, we allowed six knots per spline, that is, one between each day, and allowed the function to have a cubic shape between any pair of knots, allowing the third derivative of the function to change at each knot. This was thought to be enough to describe the trend over the week. If there had been more observations per day for each participant, more knots could have be included to describe the changes within each day. However, this would have made the model more complicated and would also not be the best way to handle within-day changes, which might be better viewed as a periodic function. Thus, we used only six knots, an adequate complexity for this illustrative example. Fortunately, the exact choice of number of knots is often not crucial, and a sensitivity analysis can be performed. To check the robustness of the solution to our choice of knots, we repeated the three-class analysis for this example using quadratic or cubic B-splines and using 2, 5, or 30 knots. The resulting estimated trajectories were all visually indistinguishable, and the class proportions were also the same to two significant digits. This occurs because the penalty function prevents overfitting and forces a reasonably parsimonious shape.

Number of classes

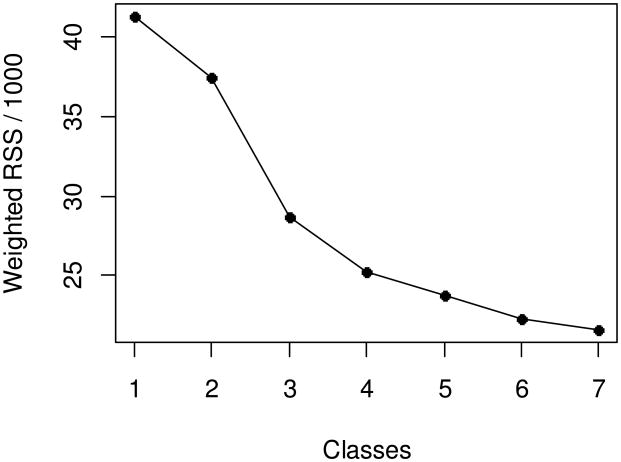
Similarly to other kinds of mixture models, we performed model selection by sequentially fitting the simplest model (one-class) through more complex models, comparing models with one through seven classes. For each candidate number of classes, we used 50 random starting values and then refitted the model using the starting value that led to the best fit (highest fitted penalized log-likelihood). We used a very high penalty strength (thus temporarily forcing an effectively parametric solution) when selecting the best starting value, in order to make the log-likelihood surface being searched more regular; we then estimated the optimal level of the tuning parameter using a BIC-like statistic, treating the starting value and the initial estimates of ρ and proportion nugget as fixed. Finally, we re-fit the model to find the regression coefficients, assuming these estimates of the tuning parameter, of ρ, and of proportion nugget. Fit statistics for models with one through seven classes are shown in Table 1.

Table 1. Model Fit Statistics for Model (9) Given Different Numbers of Classes.

Num. of Classes	Effective Number of Parameters	Log-Likelihood	AIC	BIC	Weighted RSS	Agreement With Best Fit Seed
1	5.42	-10544.9	21100.7	21118.6	41298.4	49/49
2	14.24	-10513.1	21054.6	21101.6	37473.4	49/49
3	16.80	-10226.6	20486.8	20542.2	28673.7	49/49
4	23.35	-10026.6	20099.9	20176.9	25277.3	4/49
5	29.11	-9864.6	19787.4	19883.4	23715.7	5/49
6	33.79	-9896.2	19860.0	19971.5	22300.8	0/49
7	38.50	-9840.3	19757.5	19884.5	21629.7	1/49

An elbow plot of the weighted RSS statistic as given in Model (8) was rather inconclusive, except for making it clear that at least three or four classes were needed (the plot is shown in Figure 2). The three-class model also had a well-identified estimate (all of the starting values agreed on approximately the best solution). The optimum solution for larger model sizes was less clear; it is doubtful that the global maximum likelihood was identified for the 4, 6, or 7-class models. The AIC progressively improved from the one-class through the seven-class models, and the BIC improved until at least the five-class model, but models with so many classes would be difficult to use and interpret in this context, especially because they seem to be rather poorly identified. Furthermore, with only 200 subjects total, a model with many classes would necessarily have some classes with very few members, perhaps too few for a good estimate of the coefficient functions. Therefore, we choose the three-class model for further analysis. Lu and Song (2012) followed a similar reasoning in their empirical example, emphasizing identifiability and interpretability over fit statistics.

Figure 2. Elbow plot of weighted residual sum of squared errors (weighted RSS), divided by 1000 for convenience of scale, for Model (9) with 1 through 7 classes.

Coefficient estimates

Estimated trajectories for the three-class model are presented in Figure 3. The mean urge trajectories that characterize the classes can be described as follows:

• Rapidly Declining Urge (62% of the sample)

• Gradually Declining Urge (19% of the sample)

• Persistently High Urge (19% of the sample).

Figure 3.

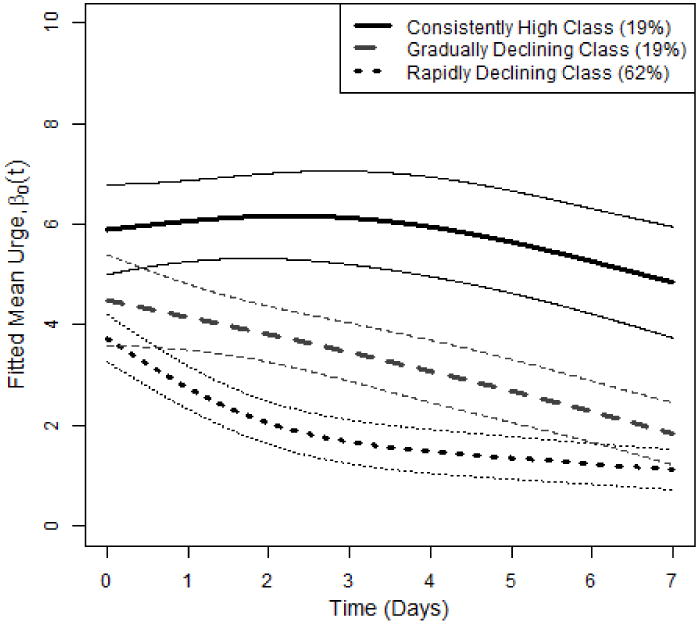
Fitted coefficients for MixTVEM of urge in Model (9) using a cubic spline with six interior knots and a second-order penalty. The upper panel represents the 3-class model, and the lower panel represents the 5-class model. The heavy curves represent estimated mean trajectories (β₀ in Model (9)). The light dotted curves above and below each curve represent estimated 95% pointwise confidence intervals.

Approximate 95% confidence intervals for class proportions were estimated using Cramer's delta method (Taylor linearization) as follows: 40% to 83% for the rapidly declining class and 13% to 25% for each of the two other classes.

The figure suggests that initial level of urge was related to the rate of decline. Individuals in the Rapidly Declining Urge class started with a relatively smaller level of mean urge, then had a rapid decline in urge over the first two days, after which the trajectory levels off and the participants generally report minimal urges. Individuals in the Gradually Declining Urge class began at an intermediate level and also had an intermediate rate of decline. Individuals in the Persistently High Urge class reported the highest urges immediately after the quit attempt and showed relatively little decline in urge over time, perhaps even increasing slightly for a few days. Thus, the three classes could be roughly interpreted as characterized by low, medium and high urge, both in terms of initial level and in terms of rate of decline.

As the figure shows, individuals in the Rapidly Declining class or Persistently High class had a rather nonlinear trajectory of change. Individuals in the medium-urge class appear to experience a relatively linear decline. The nonlinearity of the Rapidly Declining trajectory may simply have been caused by the truncated scale (because urge cannot be negative). The nonlinearity of the Persistently High trajectory may be more substantively interesting as a steady or gradually increasing level followed by a gradual decrease, although the differences over time are for this class not clearly statistically significant because the confidence intervals for different times overlap. These confidence intervals are pointwise; joint intervals (which might be computed using bootstrapping) would be even wider. The wide intervals are a result of the relatively small number of individuals in the high class (total N=200, estimated 19% prevalence, suggesting an effective sample size less than 40) and the highly volatile response variable (see Figure 4, described below). If parametric shapes (such as straight lines) were assumed for the trajectories, the standard errors might have been smaller, but at a cost of increased bias; this is a basic tradeoff between parametric approaches and nonparametric or semiparametric approaches.

Figure 4.

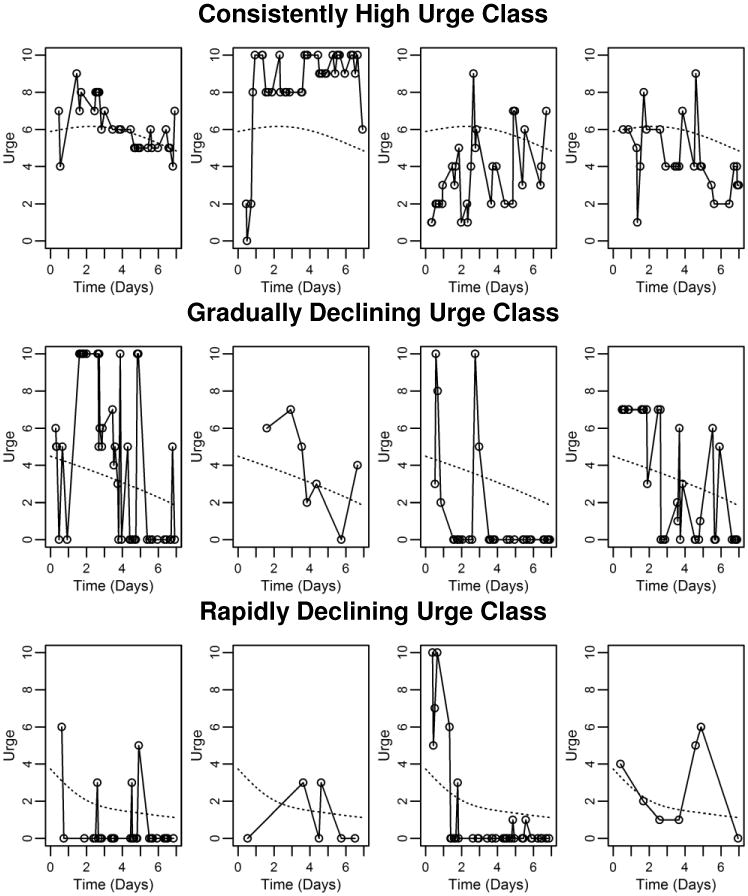
Observed data for twelve participants. All data on the outcome variable is plotted for four randomly selected participants from each of the three latent classes in Model (9). For comparison, the fitted mean trajectory in each class is shown as a dotted line. In each plot, the y-axis represents self-rated urge and the x-axis represents time in days.

Standard deviations and covariance structure

Subjects were assumed independent from each other, with the dependence within subject assumed to follow an AR-1 variance structure with nugget as given in Model (7). To make computation and identification more feasible, we assume that the nugget proportion $p_e={\sigma }_e^2/({\sigma }_a^2+{\sigma }_e^2)$ and the autoregressive parameter ρ are constant across classes, and we estimate them before choosing the final tuning parameter. We allow the total variance ${\sigma }_t^2={\sigma }_a^2+{\sigma }_e^2$ to vary across classes.

In the three-class model, the estimated p_e was .592, and the estimated ρ was .577, with time measured in units of days. Using (7), this suggests that the residuals for two urge measurements taken a few hours apart (|t_ij−t_ij′| ≈.1) would be moderately correlated (r ≈.39); those taken a day apart (|t_ij − t_ij′| ≈ 1) would be more weakly correlated (r ≈.24). However, because these residuals are deviations from class-specific means, the interpretation of the error correlations is conditional on the model; if more (or fewer) classes had been specified, there would have been less (or more) leftover correlation to be accounted for by the autoregressive model. In particular, if all participants were forced to share a single mean trajectory, then one would expect a higher estimated autocorrelation parameter and/or smaller nugget proportion, because the autocorrelation would have to account for the between-subjects variability that class differences were no longer able to account for.

The Gradually Declining Urge class had a higher estimated total standard deviation (σ̂_total =3.40) than the Rapidly Declining Urge class ((σ̂_total =1.93) or the Consistently High Urge class (σ̂_total =2.54). This is partly due to floor and ceiling effects. Many members of this class were not consistently giving medium responses, but alternately giving low and high responses. Indeed, plots of raw data from individual participants demonstrate that observed urge trajectories often consist of sharp peaks and valleys. In past literature, the experience of cravings during cessation has been described as often being episodic or phasic (Ferguson & Shiffman, 2009), with important implication for theory (suggesting the urges may derive as much or more from exposure to situational stimuli and/or stressors, than from nicotine withdrawal). The episodic nature of cravings also has implications for treatment (suggesting a need to provide smokers with strategies to cope with these episodic peaks in urge intensity). Data from four randomly selected individuals classified into each of the three classes are plotted in Figure 4. While some individuals report gradual changes, others seem to oscillate between periods of very high and very low urge.

Conclusions

In general, individuals with higher initial urge seem to have a slower decline in urge and more volatility in urge. The model could easily be made richer in order to provide more accurate predictions, such as by including indicator variables for times of day and for weekends. However, we have left these out for simplicity because our main goal is to demonstrate MixTVEM. Similarly, a more thorough analysis should test the relationship of class membership to baseline characteristics such as the assessed degree of addiction severity, the prequit mean urge, or the prequit mean negative affect. It would be reasonable to conjecture in this case that the Persistently High Urge class may consist of more addicted individuals and/or individuals who are more sensitive to distress related to withdrawal. We explore this hypothesis later as Question 3.

This simple example shows the usefulness of MixTVEM in describing trajectories of change. Note that Piasecki et al. (1998, 2000) fit a model something like Model (9) with a smoking cessation data set: namely, they performed a cluster analysis of nonlinear trajectories for describing the self-reported affective states of participants. However, their approach was limited in that it involved considering a small, regularly timed set of measurements for each individual, treating each as a single multivariate vector. This approach is not ideal for ecological momentary assessment datasets having many unevenly spaced measurements per individual, unless the researcher is willing to considerably compress the data (e.g., to an average for each day in order to create a regular grid). In contrast, MixTVEM allows information to be pooled across many irregular measurement times without coarsening time to an integer grid, and MixTVEM similarly allows coefficients to be smooth nonparametric functions of time rather than treating days as separate discrete units.

Results: Question 2

To evaluate the time-varying relationship between smoking urges (Urge) and negative affect (NegAff) across time in the different latent classes of study participants, a MixTVEM was constructed as follows:

$${\text{Urge}}_{ij}|(c_i)={\beta }_{0|c}(t_{ij})+{\beta }_{1|c}(t_{ij}){\text{NegAff}}_{ij}+e_{ij}.$$ (10)

The time-varying covariate NegAff_ij was centered at the overall mean of approximately 1.74. The residuals, e_ij, are assumed to be correlated according to the structure in Expression (7). The β_1|c function represents the strength of the association between NegAff and Urge for each latent class at each time point across the week of observations.

Number of classes

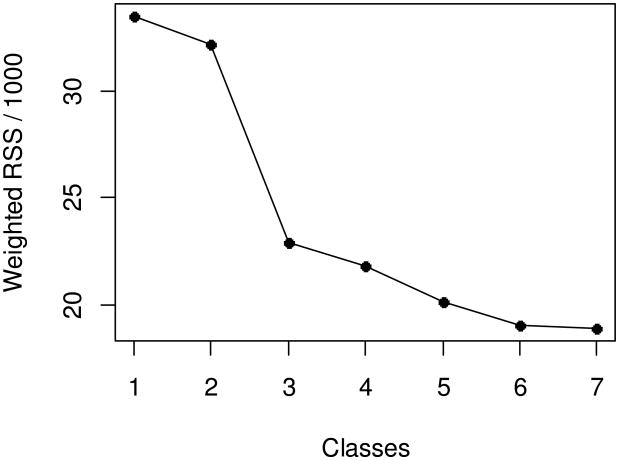
Based on a model-selection process similar to the first example, a three-class model was chosen again. The three-class solution was well identified (40 of 50 starting values arrived at the best obtained log-likelihood) and strongly favored by an elbow plot of WRSS (as shown in Figure 5).

Figure 5. Elbow plot of weighted residual sum of squared errors (weighted RSS), divided by 1000 for convenience of scale, for Model (10) with 1 through 7 classes.

Coefficient estimates

The coefficient functions for the three latent classes are summarized in Figure 6, with β_0|c(t) trajectories shown in the upper panel and β_1|c(t) trajectories in the lower. In all three classes, β₀ was either always gently declining or else first declining and then leveling off, and β₁ was either always gently increasing or increasing and then leveling off. However, while the changes of the trajectories over time were roughly similar, the overall levels of the trajectories differed greatly. The three classes can be characterized as follows:

• Low β₀ Low β₁ (49% of the sample)

• Medium β₀ High β₁ (20% of the sample)

• High β₀ High β₁ (31% of the sample).

Figure 6.

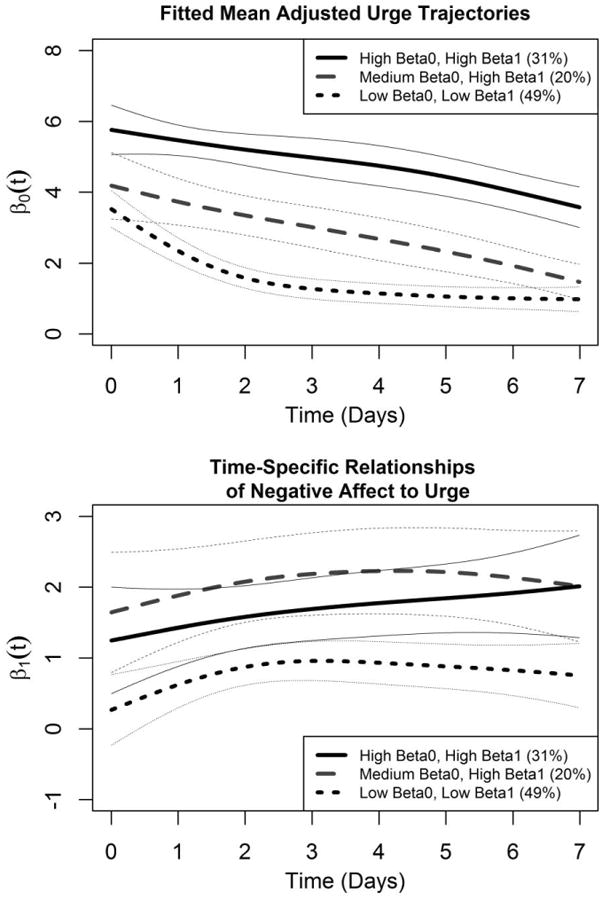
Fitted coefficients for MixTVEM of urge adjusted for negative affect. The heavy curves represent estimated coefficient functions for β₀ (intercept) and β₁ (coefficient for negative affect) in Model (10) for each class. The light dotted curves above and below each curve represent estimated 95% pointwise confidence intervals. The β₀ function could be considered, roughly, to show the expected course of urge over time if negative affect were held constant. The β₁ function measures the strength of relationship between negative affect and urge. The upper panel shows the β₀ functions and the lower panel shows the β₁ functions.

Confidence intervals for the class proportions are 42% to 57%, 10% to 30%, and 26% to 36% respectively.

Unlike in Model (9), the exact shapes of the β_0|c trajectories in Model (10) are not of much intrinsic interest. The β_0|c trajectories in Model (10) would be equivalent to the predicted mean trajectories of Urge only if NegAff were imagined to be held constant, which is not very realistic. Recall that even in classic linear regression, the meaning of the intercept can sometimes be unclear if the predictor variable is not centered to have mean zero;and it is infeasible to center ILD within all time points and all latent classes at once. Therefore, the main focus of interest is on the class-specific β_1|c functions presented in the lower panel.

Individuals in the Low β₀, Low β₁ class have only a relatively weak relationship between negative affect and urge at any given time. Figure 6 suggests that this may be largely a consequence of truncated range, as urge cannot take on negative values, and members of the low class do not often report very high-urge episodes. Interestingly, however, individuals in the medium-intercept class have as strong a relationship between negative affect and urge, or perhaps stronger, relative to those in the high-intercept class. For all classes, the relationship between negative affect and urge seems to strengthen over the first few days, even though the intercept for urge lessens. This is further discussed below. The estimated trajectories seem to suggest that the Medium β₀, High β₁ class has a roughly linear increase in β_1|c (t) over the week, while the High β₀, High β₁ class has a sharp increase followed by a leveling off and the beginning of a decrease. However, the significance of the apparent difference in shapes is unclear, especially because the confidence intervals for the β_1|c(t) trajectories are quite wide.

Membership in classes

The vast majority of participants (84%) were classified in analogous classes under Models (9) and (10). That is, low-level (Rapidly Declining Urge) class members in Model (9) were typically in the low-level (Low β₀, Low β₁) class in Model (10). Medium (Gradually Declining Urge) class members in Model (9) were typically in the medium (Medium β₀, High β₁) class in Model (10). High (Persistently High Urge) class members in Model (9) were typically in the high (High β₀ High β₁) class in Model (10). Another 4% of individuals were in neighboring classes (low and medium, or medium and high).

However, 12% of participants were somewhat anomalous. They were classified as Rapidly Declining Urge when negative affect was not accounted for, but High β₀, High β₁ when negative affect was accounted for. The reverse situation was not observed. That is, certain individuals are “low” for Figure 3 but “high” for Figure 6. We call these 23 individuals “discrepant” on class membership. This suggests high covariate-adjusted urge is not the same as high urge. Closer examination revealed that the discrepant participants had typically very low self-assessed negative affect, which made their urge to smoke relatively high in comparison to what might be expected. This could perhaps be an issue of measurement; this subset of individuals may have felt that it was socially desirable to report being in a good mood almost all the time, even if they were suffering from withdrawal symptoms, but they were able to report their urge to smoke more candidly. It is not known whether such individuals might have been engaging in something like repressive coping (see Mund & Mitte, 2012) in dealing with their withdrawal symptoms.

Alternatively, these individuals may actually have been experiencing urge in the absence of negative emotions. That is, they may really have been feeling well, but still experiencing some appetitive desire to smoke despite not being much bothered by either aversive withdrawal symptoms or external stress. They may even have tended to associate the desire to smoke with positive emotional events such as social celebrations. However, for reasons described in the Univariate Descriptive Statistics subsection below, these do not seem to be the main reasons for the discrepancy.

Covariance parameters

The estimate for the nugget proportion was .644 for this analysis. The estimate for the autoregressive parameter ρ was .48, suggesting modest correlation of urge over time after controlling for negative affect. The total variability was strikingly different for the three classes, with σ̂_total estimates of 1.59 for the Low β₀, High β₁ class, 3.04 for the Medium β₀, High β₁ class, and 2.19 for the High β₀, High β₁ class. As in Model 9, the medium class is the most variable.

Univariate trajectories

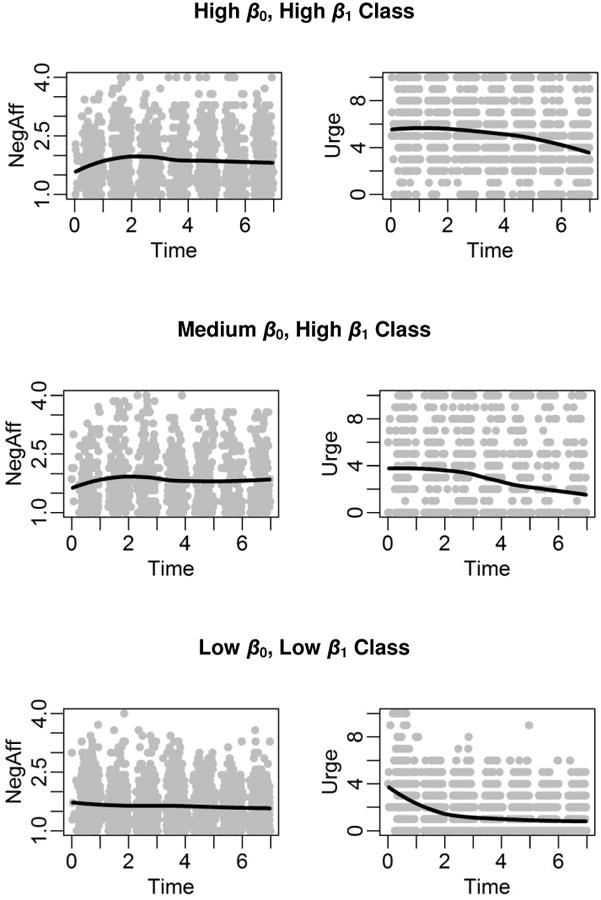
For each class, the observed data points and smoothed trajectories for negative affect and urge are plotted in Figure 7. This figure shows that members of the classes with typically medium and high adjusted urge (i.e., the Medium β₀, High β₁ class and the High β₀, High β₁ class) had about the same mean trajectory of negative affect, ignoring urge; but different trajectories of urge, ignoring negative affect. This supports the interpretability of the difference in adjusted urge.

Figure 7. Observed values, with smoothed means (using the loess function in R; Cleveland, Grosse, & Shyu, 1992) for negative affect and urge among all members of the three class defined in Model (10).

Univariate descriptive statistics

Ignoring measurement time, class membership uncertainty, and within-subject correlation, the sample means and standard deviations of reported negative affect were 1.62 (SD=0.50) for the low-β₀ individuals, 1.83 (SD=0.72) for the medium-β₀ individuals, 2.03 (SD 0.66) for the nondiscrepant high-β₀ individuals, and 1.56 (SD=0.51) for the discrepant high-β₀ individuals. The sample means and standard deviations for reported urge were 1.31 (SD=1.79), 2.82 (SD=3.49), 5.83 (SD=2.60), and 3.51(SD=2.04) for these four groups, respectively. Finally, the sample correlation between negative affect and urge, still ignoring time, class uncertainty, and within-person correlation, was 0.29, 0.40, 0.51, and 0.35 for the low, medium, high nondiscrepant, and high discrepant individuals, respectively. This is obviously a rather crude analysis but does provide some information. Negative affect was positively related to urge to smoke for everyone, but the relationship was weaker for people who had either very low reported urge (the low-β₀ group) or very low reported negative affect (the discrepant high-β₀ group).

Conclusions

Within each class, time and negative affect apparently interact in predicting urge. That is, negative effect has a time-varying relationship with urge, and is a stronger predictor after a few days into the quitting attempt. While these participants were regularly smoking, they managed their urge by smoking regularly, and may also have stabilized affect by this mechanism (Baker et al., 2004). However, after quitting, urges may have become less regular and more triggered by external stress than habit.

An alternative interpretation could be that participants usually felt well, but occasionally had brief but intense episodes of withdrawal causing both high negative affect and high urge. Indeed, previous analyses of data from this study (Shiffman et al., 1997) have shown that although the participants' average urge did decline, they continued to have occasional “temptation” episodes (more than one per day on average during the first week), which were associated with much higher urges. Both interpretations are plausible (i.e., stress causes negative affect which causes urge, or withdrawal causes episodes of urge and negative affect), and they are are not mutually exclusive. Either way, as urge became less prominent as a routine part of daily life, the remaining high-urge episodes became statistically more related to negative affect.

Results: Question 3

When comparing the three trajectories found in Questions 1 and 2, we conjectured that the classes whose members were experiencing higher urge were also those whose members were more addicted before beginning the quit attempt. To explore this question, we consider two objective measures of prequit smoking severity: mean number of cigarettes smoked per day and mean minutes between awakening in the morning and smoking one's first cigarette.

The baseline average numbers of cigarettes per day for each class in Question 1 (using hard assignment) were essentially equal, namely 25, 27, and 27 for the low, medium and high classes, respectively. However, this is not surprising, because the number of cigarettes smoked per day has been found (Donny, Griffin, Shiffman, and Sayette, 2008) to be only a weak indicator of dependence. In contrast, the baseline average minutes to first cigarette for each class were 22.1, 10.8, and 12.4, suggesting that (at least by this measure) the Rapidly Declining urge class tended to represent individuals who were less addicted.

To provide a significance test for minutes to first use as a predictor, Model (9) was refit using baseline minutes to first cigarette as a class membership predictor. This predictor was not statistically significant for the contrast between the rapidly declining and gradually declining class, persistently high and gradually declining class, or rapidly declining and persistently high class. However, the distribution of time to first cigarette was noted to have a large positive skew; within each class, the mean was over twice the median and the observed maximum was over ten times the median. The log-transformed minutes to first cigarette did almost significantly predict membership in the low versus medium class. Specifically, there was a logistic regression coefficient of 0.31 for the effect of log-transformed covariate on membership in the low class, (SE=0.16, z=1.96, p=.0505), treating medium as the reference or baseline class. This does lend some evidence to the reasonable conjecture that less addicted individuals are in the lower urge class.

A similar analysis was also done with the classes in Model (10), with broadly similar results. The mean minutes to first cigarette were 23, 10 and 15.45 for the low β₀/high β₁, medium β₀/high β₁, and high β₀/high β₁ classes, respectively. The mean cigarettes per day were 25, 26, and 27, respectively. However, these differences were not statistically significant at the .05 level. Perhaps adjusting for negative affect attenuated the relationship with prior addiction. This could quite plausibly occur if withdrawal-related negative affect mediates the relationship between prior addiction and current urge to smoke.

Results: Question 4

It is of interest to investigate whether defined latent classes are associated with the ultimate outcome of the smoking cessation attempt. If so, this would provide not only some construct validation for the classes, but also a possible way to predict participants' success from their experiences very early in the attempt. One approach for handling this latent predictor variable is “modal assignment” (using terminology from Bolck, Croon & Hagenaars, 2004) to assign each individual to a latent class based on highest posterior probability, and then to treat this as if it were an observed variable. This is convenient and intuitive, but it has the disadvantage of ignoring uncertainty about class membership. A second approach is “random assignment” (see Bolck, Croon & Hagenaars, 2004). This involves doing a multiple imputation class memberships from the distribution defined by the posterior probabilities, then analyzing each imputed sample separately, and finally combining the results. This approach is intended to take class membership uncertainty into account when testing whether the classes differ on a covariate. A third approach (“one-step” in the terminology of Bolck, Croon & Hagenaars, 2004) is to include the distal outcome as a covariate, even though its occurence in time is after the process being measured. This is not illogical, even though time seems to be reversed, because MixTVEM is a regression model rather than a causal model.

The proportions of individuals experiencing a relapse within the rapidly declining, gradually declining, and consistently high trajectory classes in Model (9) were 9%, 19%, and 20%, respectively. This was not statistically significant even under modal assignment (χ²=4.89, df=2, p=0.09) and therefore would not be statistically significant using the more conservative random assignment approach. It did, however, significantly predict membership in the persistently high versus rapidly declining class when included as a covariate (logistic regression coefficient 1.23, SE=.52, z=-2.35, p=.019).

Statistical power is a problem for this kind of analysis. Piasecki, Jorenby, Smith, Fiore, & Baker (2003) pointed to power as a possible disadvantage of a class-based approach versus an approach based on a continuous latent variable. That is, when there are several classes treated as levels of a nominal variable, rather than a single dimension of low to high, it may become more difficult to distinguish between the levels on a distal outcome.

An Alternative Analysis Using Individually Recentered Data

In addition to modeling within-subject correlations, it might be advantageous to better distinguish between-subjects from within-subjects effects. In Model (10) as presented here, the regression equations within each class are presented in the form of marginal models relating time and negative affect to urge for class members, and therefore do not distinguish between the effect of having an unusually high-negative-affect day and the effect of being an unusually high-negative-affect person. Because these effects are unlikely to be truly the same, it might be better to include both the person's mean value of negative affect and the momentary value centered around the person's mean. This is analogous to the “frog pond” approach in multilevel models of educational attainment within schools (see Kreft, de Leeuw, & Aiken, 1994), except that the cluster here is the person rather than a school. For example, mean negative affect (whether from baseline data, postquit data, or both) could be included as a predictor of class membership in (4), and momentary deviations from this level could be included as a predictor of momentary response in (5).

We explored this approach in an alternative analysis for Model (10), using a subject-specific baseline mean calculated during the most recent week of random assessment data prior to the designated quit date (i.e., days negative seven through zero). We proceeded as described in the section for Question 2 above, except that we centered each participant's data by the participant's own prequit mean, rather than the sample-wide postquit mean, and additionally we included the subject-level prequit mean negative affect as a class membership covariate. The fitted coefficient functions were similar to the grand-mean-centered version shown in Figure 6, although the medium β₀/high β₁ class now had an even higher β₁ in the early part of the interval, and the high β₀/high β₁ class now had a somewhat lower β₁ in the early part of the interval. The estimated class proportions were somewhat different, with 29% in the high β₀/high β₁ class, 18% in the medium β₀/high β₁ class, and 53% in the low β₀/low β₁ class. Higher prequit mean negative affect was significantly related to odds of being in the high β₀/high β₁ class versus the low β₀/low β₁ class (logistic regression coefficient 1.88, SE=0.45, z=4.08, p<.001), although it was not significantly related to the odds of being in the high versus the medium-urge trajectory. In other words, the low urge trajectory class appears to consist of people who either are somewhat less prone to negative affect over the long term, or who are at least somewhat less willing to admit to unpleasant emotions. The other classes may tend to have higher trait negative affectivity.

Note that the prequit mean was calculated using the last week of observations prior to the designated quit date, although these data were not included in the coefficient function trajectories being modeled. We did not try individually centering the postquit data on the subject-specific postquit mean, as this would make it quite difficult to interpret the coefficient functions for early time points. That is, if we had centered by the subject-specific postquit means, then a high value of the predictor variable could indicate either that the individual has especially high negative affect now, or that the individual is going to have especially low negative affect at a later time. It would be difficult to interpret a model in which the past is effectively changed by the future, so we did not implement it. This interpretational problem does not occur in the analyses we presented earlier in this paper, because we either center only by the grand mean, or only by prequit (i.e., baseline) subject-level means.

Discussion

In this paper we introduce the MixTVEM approach for modeling ILD in the social and behavioral sciences. MixTVEM addresses the important challenges of modeling subject heterogeneity and modeling nonlinear trajectories of change. We emphasize that different individuals follow markedly different processes of change and that these changes are not necessarily well described by linear or quadratic models. To handle this, MixTVEM considers the population to be a mixture of latent classes, in which each latent class has a different shape for its mean trajectory and a different relationship between time-varying covariates and the outcome. MixTVEM combines ideas from latent class growth analysis with TVEM. We provide a SAS macro and an R function to assist in fitting MixTVEM in these commonly used environments.

Related Approaches

The MixTVEM approach as presented here is related in several ways to previously introduced models for longitudinal data. The simplest possible MixTVEM, in which only β_0c is time-varying as in Model (9), could be seen as a latent class growth model (Nagin, 2005) with nonparametric shapes for the trajectories. Of course, nonlinear growth mixtures have been fit before. For example, Galatzer-Levy, Bonanno, and Mancini (2010) used a growth mixture model to describe subjective well-being in unemployed persons, following a piecewise linear approach with four phases. This could be seen as a linear spline, although with only three knots. Similarly, mixtures of classes with quadratic or cubic trajectories have been fit in many studies (e.g., Gaffney & Smith, 2003; Jones, Nagin & Roeder, 2001; Nagin, 1999; Swartout, Swartout & White, 2011). However, these models restrict the shape of the mean trajectory more than MixTVEM does. Mixtures of growth trajectories modeled by splines have recently been proposed in the statistics literature (James & Sugar, 2003; Shi & Wang, 2008), but have not yet been extensively used in social and behavioral sciences. Furthermore, some of the past work on finite mixtures of growth trajectories often either omits covariates or treats the effects of covariates as time-invariant even when the covariate itself is time-varying. In contrast, MixTVEM allows both the intercept and the substantive regression coefficients to have nonparametric shapes.

To the best of our knowledge, the basic approach of MixTVEM with covariates (i.e., models of the form of (4) and (5)) was first proposed, although in a Bayesian form, by Lu and Song (2012). They used a rich Bayesian framework that added informative priors and also multiple parametric random effects, and which required some special care to ensure identifiability. It is possible that for many datasets, their model might be too rich to converge easily in a frequentist context. Earlier, Ma and Zhong (2008) had used a model similar to (5), although without the subject-level Model (4). The Ma and Zhong (2008) model was parameterized in a somewhat different way, which potentially allowed nonparametric interactions between covariates; for simplicity we do not explore that specification here. Lastly, the very general R package flexmix (Grün & Leisch, 2008) is able to fit longitudinal mixtures of many kinds of models, including some semi-parametric models such as spline growth curves and generalized additive models, which are similar to MixTVEM. However, we suspect that for many researchers our specialized SAS macro or R function may be considerably easier to use and interpret for MixTVEM analyses specifically. Our paper is intended as a practical introduction, and accordingly we use a relatively simple approach.

TVEM and MixTVEM as described here describe the changes in momentary association between variables. For example, they can describe how the regression relationship between negative affect at time t and urge to smoke at time t changes as a function of t. A related question would be how the regression relationship between negative affect at time t₀ and urge to smoke at time t₀+t changes as a function of t. TVEM and MixTVEM as described here do not address this second question. Approaches to the second question are described in detail by Selig, Preacher, and Little (2012), who also emphasize the importance of considering nonlinear shapes (at least quadratic or exponential) for the changes in relationship over time. The approaches described in Selig et al. are focused on situations in which the variable is measured at only a very small number of times (often twice) per participant, although they could be extended to more general settings. In contrast, TVEM and MixTVEM are intended for studies with several or many observations per participant (Tan et al., 2012).

Simplifying MixTVEMs

A disadvantage of both TVEM and MixTVEM is that the regression coefficients of interest cannot be described as concisely or parsimoniously as the parameters of a linear or quadratic model, because they are now functions instead of single numbers. However, after fitting a MixTVEM, a researcher could move on to a more parsimonious model if desired. Tan et al. (2012) suggested that investigators who prefer a simpler parametric description might still wish to use TVEM first for exploratory or diagnostic purposes (i.e., to choose a parametric form). In Model (9) in this paper, the sample was classified into low-urge, medium-urge and high-urge classes, perhaps suggesting an underlying continuum. This suggests that instead of a finite mixture, one might use a model with a normally distributed random effect incorporated into a common nonlinear but parametric form (see Lindstrom & Bates, 1990; Blozis, 2004; Cudeck & Harring, 2007). The model could be simplified by doing away with the nonparametric coefficients, the differing latent classes, or both. Thus, one could try linear or quadratic trajectories with random effects, a parametric finite mixture distribution, or both; this might be especially effective if the lower truncation of the scale were taken into account (as in Grün & Hornik, 2012). Yet another possibility would be a mixture of curves sharing a prespecified parametric family of nonlinear shapes such as logistic curves (see Kelley, 2008; Grün & Hornik, 2012) or an ordinal TVEM (see Dziak, Li, Zimmerman, & Buu, 2014). There are many possibilities, but MixTVEM is relatively general and interpretable and therefore provides a good place to start. In summary, MixTVEM is not always needed to describe a given dataset, but even in situations in which a more parsimonious model is later selected, MixTVEM can be useful as a tool for exploratory description, diagnostics, and data visualization.

Sample Size

The sample size requirements of MixTVEM are not yet known but can be investigated using simulations in the future. As with other mixture models, the question is complex and the answer is likely to depend on the number of classes and covariates in the model, the marginal distributions of the response and covariates, and especially the goal of analysis. The goal might involve attaining a particular width for the confidence interval for some quantity, a particular power for the successful detection of some hypothesized feature of a specified size, or the correct choice of number of classes according to some given selection method. Different goals and assumptions would require different sample sizes. However, Tan et al. (2012) tentatively suggested that 100 participants with 10-25 observations per participant seemed sufficient for getting reasonable results from TVEM with a normally distributed outcome. Following this heuristic, in the context of MixTVEM one would hope to see at least 100 participants per class, and preferably more in order to better inform the model for distinguishing between the classes. This implies that a larger sample size will be needed if there are many classes or if some classes are very small. In our empirical example with a three-class model, there were 200 participants and the smallest class proportion was about 20%, so the smallest class had only about 40 subjects. The limited sample size per class partially explains why the confidence intervals in the figures are rather wide and the significance tests for relationships with other constructs were inconclusive or nonsignificant. However, despite the limited sample size, MixTVEM provided promising exploratory insights into the data.

Limitations of the Current Approach and Topics for Future Research

As with other mixture models, the different classes in MixTVEM may be considered either as representing actual distinct subpopulations, such as different alleles on an unknown gene; or else simply as convenient points used in summarizing a continuum, such as the “low,” “medium,” and “high” levels of some construct. There is an important and continuing debate in the literature about the implications of this distinction (see, e.g., Bauer & Curran, 2003, with discussions; Muthén, 2004; Erosheva, Matsueda, & Telesca, 2014). In the former interpretation, assumptions about normality and about random effects structures become extremely important in order to avoid choosing the wrong number of classes or misrepresenting the relationship between class membership and covariates. For example, it appears in Figure 4 that the data in the empirical example are not actually normally distributed, due to the constraints above and below, as well as the seemingly chaotic spikes reported by some participants.

In the latter interpretation, there may not be an unequivocal true answer to the number of classes. For example, either a division into “low,” “medium,” and “high” or into “very low,” “low,” “medium,” “medium high,” and “veryhigh” might lead to similar substantive interpretations. In such a case, the question of the true meaning of the classes would seem less urgent, and the emphasis would simply be to provide a rich but interpretable picture of the data.

Researchers differ in views about whether it is feasible to distinguish between categorical and continuous latent variables (see Cudeck & Henly, 2003; Lubke & Neale, 2006), and hence to tell whether different classes are conceptually distinct entities or merely regions on an underlying continuum. In the nonparametric regression case, as in MixTVEM, the situation might be even more complicated. We cannot attempt to resolve these questions here. It is important that predicted class memberships not be treated as exact diagnoses or complete descriptions of people (Nagin & Tremblay, 2005; Walters, 2011). However, a latent-class-based approach can be a useful tool for describing data in practice, regardless of whether the classes can be reified in a particular field of study (Nagin, 2005; Petras & Masyn, 2010). Thus, the question of whether the classes are really distinct entities might not be as much a limitation as it first seems.

A more practical limitation is that both TVEM and MixTVEM assume that time is measured on a common scale, with a zero point that is meaningful for all participants. Otherwise, it would not be clear how to interpret systematic changes over time. In practice, this means that TVEM and MixTVEM are most suitable for studying processes that lead up to and/or follow from a definable event. In developmental research spanning years, the time variable is likely to be age, which provides milestones that can be at least approximately aligned (such as birth or puberty). In research involving an intervention, the time variable may be the number of hours or days since the beginning of the intervention. Observations before the beginning of the intervention can also be included (i.e., time can be negative), and the role of the beginning of the intervention may be played by a natural or social event rather than one imposed by the investigators. However, there still must be some meaningful event by which to align the data of disparate participants. In the absence of such a shared event, the interpretation of a mean trajectory would be unclear. Calendar date by itself is unlikely to be useful except for studies specifically addressing historical change. Growth curve models and growth mixture models can be extended to allow different people to have different starting points or rates of change but the same underlying shape (e.g., curve registration; see Ramsay & Silverman, 2005; Erosheva, Matsueda, & Telesca, 2014). This could probably be done with TVEM and MixTVEM, although it could further complicate the estimation process. However, in order to make the TVEM coefficient functions meaningful, the process being studied would still need to have one or more shared starting or anchoring points, with the same meaning or characteristics for all participants even if the exact timing were different.

Thus, in situations in which variables are being sampled from different participants over some length of time, but no systematic change is being hypothesized to occur over that time, TVEM and MixTVEM would not be very useful. Other methods that conceive of change in terms of cycles or even random walks (see review in Chow, Hamaker, Fujita, & Boker, 2009) rather than trajectories, might be more useful in such settings. As a caveat, some of these latter methods may be more difficult to apply to unevenly timed measurements such as those found in our empirical example. It is also possible to do something like TVEM using sines and cosines instead of splines as a basis for the coefficient functions, in order to measure cyclical functions rather than processes with beginnings in time (see Fok & Ramsay, 2006), or to study ILD as a pattern of changes from an equilibrium by using parametric differential equations (see Hu, Boker, Neale, & Klump, 2014; Trail et al., 2014), but these are beyond the scope of this paper.

Finally, a MixTVEM such as (5) focuses on modeling the distribution of Y conditioning on the X variables, not the multivariate joint distribution of X and Y together. This may occasionally cause complications, such the “discrepant” individuals in the empirical analysis who had only modest levels on the response variable, but high covariate-adjusted levels, because of unusually low values on the covariate. This difficulty is not unique to MixTVEM, but is a special case of a general caution for regression models with many parameters. The relationship of the distribution of Y|X to a variable such as class membership or time is not necessarily the same as the relationship of Y itself to X, because X itself may also be related to the other variable.

Summary

Despite its limitations, MixTVEM is a promising new way of modeling change over time without making strong assumptions about the shape of change processes and without assuming that this shape is the same for all participants. MixTVEM belongs to an emerging class of new methods that combine both variable-centered and group- or pattern-centered theory into a single model (Kelley, 2008; Muthén Muthén, 2000; Nagin, 1999). The flexibility of MixTVEM to allow not only the values but also the effects of covariates to change over time, and to do so differently for different latent groups, offers new possibilities for research and theory.

Table 2. Model Fit Statistics for Model (10) Given Different Numbers of Classes.

Num. of Classes	Effective Number of Parameters	Log-Likelihood	AIC	BIC	Weighted RSS	Agreement With Best Fit Seed
1	13.84	-10299.8	20627.3	20672.9	33493.8	49/49
2	19.47	-10307.2	20653.2	20717.4	32206.3	49/49
3	26.66	-9938.4	19930.1	20018.0	22897.5	40/49
4	34.64	-9764.7	19598.7	19712.9	21823.0	0/49
5	44.29	-9629.5	19347.5	19493.6	20122.9	1/49
6	94.54	-9538.9	19267.0	19578.8	18999.7	0/49
7	53.84	-9646.8	19401.4	19578.9	18897.9	0/49

Appendix: Resources for Fitting MixTVEM

In this appendix we briefly review the properties of penalized B-splines. We then briefly explain how to use our SAS macro and R function for MixTVEM estimation. Copies of the SAS and R files are included in the online supplemental material for this article. They are also freely downloadable from the Methodology Center website at http://methodology.psu.edu/downloads/mixtvem.

Penalized B-Splines

B-splines, or “basis splines” were introduced by Schoenberg (1946), and are further described in de Boor (1972, 1993) and Eilers and Marx (1996). Like polynomial regression, they are used to approximate a function with unknown shape as a linear combination (weighted sum) of several “basis functions” with known shape. When modeling the growth of a variable with polynomial regression over time t, the basis functions are 1, t, t², t³, etc. The basis becomes richer as more terms become available, which means that more complex functions can be expressed. The well-known flaw of polynomial regression is that its basis functions are highly intercorrelated, leading to computational and inferential problems. B-splines are an alternative system of functions, constructed so that most of the functions in the basis will be independent or nearly independent from one another. The polynomial basis functions are each monotone functions of time from some starting point, and are never zero except at t=0. However, the B-spline basis functions each have a “hump” or “hill” shape (de Boor, 1972, p. 51) instead. Each hill is nonzero only over a limited interval, which begins or ends at special points called knots. The knots are usually either equally spaced through the interval of interest, or at equal quantiles of the data. However, neither the knots nor the data points need to be equally spaced.

Importantly, as Eilers and Marx (1996) point out, the regression coefficient for each basis function has no interpretation by itself; the basis functions are used together to estimate the function of interest, somewhat like pixels in an image or primary colors in a compound color. Thus, there are no “significant” or “non-significant” knots or basis functions. The exact shape of each hill depends on the degree d of the B-spline basis. In general, each hill is a function B(t) composed of d+1 pieces, each a polynomial of degree d, and is nonzero over d+1 of the intervals marked off by the knots. Thus, for a linear B-spline, the hill is triangular with one line segment rising from the time of one knot until the time of the next knot, and then one line segment falling from the time of this second knot to a third. Several such hills are included in a basis: one for each knot, sometimes with extra knots and hills placed automatically just beyond the ends of the interval, in order to specify the behavior of the function at the edges. The actual shape and placement of the functions in the basis is not easy to describe intuitively. Their span (the range of functions that can be created by weighting and summing them) consists of functions that are polynomial of degree d between the knots, and continuous in the (d-1)th derivative at each knot. Thus, for functions estimated by linear B-splines, the estimate will be made of linear pieces connected at the knots. Given an adequate number of knots, a d of 2 or 3 is adequate to estimate a reasonably good portrayal of practically any smooth and bounded function; in our examples we use d=3 (cubic).

Eilers and Marx (1996) have recommended about 10 to 20 basis functions (apparently including the d-1 basis functions at both the lower and upper bound of the interval, and hence apparently suggesting a total of 6 to 16 interior knots) as a reasonable number. However, that was in a non-mixture context; it may be reasonable, as we argued in the empirical example, to have fewer knots than this because of the additional complexity of having to fit the model on each of several latent classes. To avoid overfitting, AIC or BIC can be used to choose the number of knots. However, it is sometimes easier to simply choose a fairly large number of knots and then enforce parsimony by adding a regularization penalty to the model, somewhat as in ridge regression. Such a penalty is essentially a zero-mean, finite-variance prior on the size of the change which occurs in the function at each knot. Thus, as the penalty weight (or the inverse prior variance) approaches infinity, the estimated function becomes a polynomial of degree d over the whole interval, no matter how many knots there are (in other words, the knots will have no effect, so that the overall curve is a simple polynomial). In our application, we use a BIC-like criterion to choose the weight of the penalty. One can penalize either the difference between consecutive knots or a higher-order difference (e.g., difference between consecutive differences). We use here a spline of degree 3 and difference penalty of degree 2. Thus, instead of an ordinary maximum-likelihood solution, we are actually finding a matrix-weighted penalized maximum likelihood with a weighted quadratic penalty on the coefficients. Equivalently, we are finding a prior mode, with a multivariate normal prior on the coefficients. The process by which the weighting matrix of the penalty (precision matrix of the prior) is determined is described further in Eilers and Marx (1996). In the case of our Model (9), there are ten hills, as shown in Figure 8. Six of them correspond to the six internal knots; the others essentially handle the edges. Thus, a time of t=1 is represented as B₁(t)=0, B₂(t)=0.167, B₃(t)=0.667, B₄(t)=0.167, B₅(t)=B₆(t)=B₇(t)=B₈(t)=B₉(t)=B₁₀(t)=0. Given estimates of posterior probabilities from the E step of the EM algorithm, the best weights for combining these functions to estimate the coefficient function within a class are determined by doing a penalized linear regression of y within each class on the ten B functions, weighting by each individual's posterior probability of class membership. The resulting estimates for Model (9) are shown in Table 3. To fit Model (10), the response (urge) in each class is regressed on B₁(t), B₂(t), …, B₁₀(t), B₁(t) ×X, B₂(t)×X, …, B₁₀(t) ×X where X is the negative affect measure. In order to save space, we omit the equivalent of Table 3 for Model (10).

Figure 8. The B-spline basis functions used as building blocks for the coefficient function estimates in Figures 3 and 6.

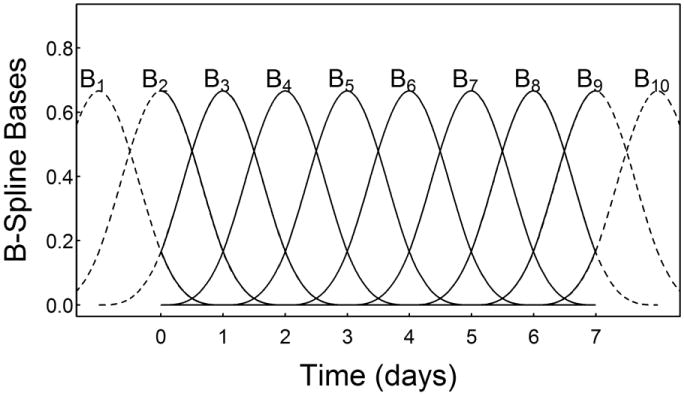
Table 3. Basis Function Coefficient Estimates for Model (9).

	Rapidly Declining Class	Gradually Declining Class	Consistently High Class
B1(t)	4.787	4.836	5.716
B2(t)	3.727	4.493	5.895
B3(t)	2.699	4.151	6.073
B4(t)	1.986	3.818	6.188
B5(t)	1.649	3.462	6.151
B6(t)	1.476	3.077	5.971
B7(t)	1.358	2.695	5.664
B8(t)	1.234	2.281	5.266
B9(t)	1.123	1.838	4.846
B10(t)	1.017	1.390	4.426

Notes. The basis functions are illustrated in Figure 8. The resulting combined curves are the ones plotted in Figure 3.

Tan et al. (2012) and Shiyko et al. (2012) also used penalized splines when fitting non-mixture TVEMs. However, they used different basis functions:truncated power functions, which have some similarities to polynomial regression and some to B-splines. They also used a simpler penalty function (a penalty on the sum of squared coefficients for the knots, treating them somewhat like random effects as described in Ruppert, Wand, & Carroll, 2003). The software for non-mixture TVEM by Yang, Tan, Li, and Wagner (2012) allows either a penalized truncated power spline approach or an unpenalized B-spline approach; both are explained in the user's guide for this software. Because of the extra computational demands in the mixture context, it was decided for the MixTVEM macro that B-splines were more desirable than truncated power splines (due to their low intercorrelation) but that a penalty was also desirable. In practice, penalized truncated power splines are sometimes called P-splines, but the term P-spline was originally coined by Eilers and Marx (1996) for penalized B-splines rather than truncated power splines; this is a potential source of confusion when reading the literature.

TVEM_Mix_Normal R Function

Example

The MixTVEM example in the paper, with relapse as a subject-level covariate and centered negative affect as a time-varying effects covariate, could be fit using the following code.

answer <- TVEMMixNormal(id=firstWeekCessationData$id,

time=firstWeekCessationData$timeDays,

dep=firstWeekCessationData$urge,

doPlot=TRUE,

numInteriorKnots=6,

numClasses=3,

scov=firstWeekCessationData$relapse3WeeksPost,

tcov=cbind(1,

firstWeekCessationData$centeredNegAff),

numStarts=100,

useRoughnessPenalty=TRUE,

getSEs=TRUE);

This assumes that the data of interest are stored in a dataset called “FirstWeekCessationData,” including the variable “timeDays” (time in fractional days), “urge” (self-rated urge, which is here used as the dependent or response variable), “id” (subject ID), “relapse3WeeksPost” (whether the subject relapsed), and “centeredNegAff” (for centered negative affect). The dependent variable is specified by “dep=”, the assessment time by “time=”, the subject-level covariates by “scov=”, and the time-varying effects covariates by “tcov=”. Additional time-varying covariates with non-time-varying effects could be specified using the optional “xcov=” argument. The dataset is assumed to be have one row per observation (hence multiple rows per person), but the subject-level covariates (here, Relapse3WeeksPost) must be the same for all rows within a given person (this can be accomplished using R's merge() function). Three latent classes are fit (numClasses=3). The two time-varying coefficients are modeled as splines with 6 interior knots each. “numStarts” specifies how many random starts should be used to try to find the maximum of the penalized likelihood function.

Inputs

The function takes many inputs, but most of them can be omitted, and sensible defaults will be used. R is case-sensitive, so case (lower or upper) matters. The following represent the input data and should have one row per assessment (multiple rows per subject):

• dep is the dependent variable vector.

• id is the subject ID vector.

• scov (optional) is the matrix of time-invariant covariates for predicting class membership.

• tcov is the matrix of time-varying or time-invariant covariates assumed to have time-varying effects.

• time is the assessment time.

• xcov (optional) is the matrix of time-varying or time-invariant covariates assumed to have time-invariant effects.

Other options tell how to fit the model, and include these among others:

• getSEs tells whether to compute standard errors. Setting it to FALSE saves time for an initial exploration.

• numInteriorKnots is the number of knots for the splines.

• numClasses is the number of distinct classes assumed to exist.

• numStarts tells the number of starting values to use.

Comments in the R function code file describe further optional inputs that are available.

Outputs

Results about the estimated model are shown on the screen, and output is also returned as an R list structure. The components of the list are documented inside the R file. The most important ones are listed below. Suppose that the answer is stored in the R object “answer” as in the R code above. Then

• answer$bestFit$converged tells whether the EM algorithm converged.

• answer$bestFit$enp tells the effective number of parameters (see Eilers & Marx, 1996) for the best-fitting model.

• answer$bestFit$weightedRSS tells the weighted RSS fit statistic for the best-fitting model.

• answer$bestFit$proportionNugget, answer$bestFit$rho, answer$bestFit$sigsq.total tell the estimated variance parameters for each class.

• answer$beta is a list. Each element of the list corresponds to one of the time-varying coefficients in the model and is a matrix with one column per class. Each column tells, for that class, the fitted value of the coefficient at each observed time point. There are as many rows as observations in the input dataset (not counting observations that were excluded because of missingness).

• answer$betaByGrid is similar to answer$beta except that it provides fitted values of the coefficients on a regular grid of time points (by default 1000 points).

• answer$betaSE and answer$betaSEByGrid provide pointwise standard error estimates corresponding to each entry in answer$beta and answer$betaByGrid.

• answer$fittedValues is a matrix with one row for each non-excluded observation in the dataset and one column for each class. It tells the predicted value of the response variable for each subject, assuming that the subject belongs to that class.

• answer$knotLocations tells the locations of the knots used for the spline fit.

• answer$logisticRegOutput provides the output for the logistic regression of predicting class membership from the subject-level covariates. There is always at least one subject-level covariate, the intercept (which we denote as “S1” meaning the first column of subject-level data).

Cautions

Evenly spaced observations or equal numbers of observations per subject are not required. However, observations (dataset rows) with any missing data in the response, in the time variable, or in any of the predictors and covariates in the model, are excluded from the analysis. They are also excluded from counts of the number of observations. Exclusion is done by row (i.e., observation), rather than by subject, so a whole subject is not necessarily excluded just because one of his or her observation times is excluded. To avoid possible confusion in interpreting fitted values, it is recommended to either delete or impute assessments with some variables missing before calling the function. Also, if informative dropout occurs (e.g., participants missing appointments or dropping out of the study for reasons related to the response variable) then the results may be biased by it, because trajectories at a given time point can reflect only the subjects with data available near that time point.

TVEM_Mix_Normal SAS Macro

Example

The MixTVEM example in the paper, with relapse as a subject-level covariate and centered negative affect as a time-varying effects covariate, could be fit using the following code. The variable “Intercept” was defined in an earlier DATA step as simply Intercept=1 for all rows.

%TVEM_Mix_Normal(mydata = FirstWeekCessationData,

time = TimeDays,

dep = urge,

id = id,

deg = 2,

scov = Relapse3WeeksPost,

tcov = Intercept CenteredNegAff,

latent_classes = 3,

ref = 1,

knots = 6 6,

use_roughness_penalty = yes,

num_starts = 100,

std_err_option= yes);

This assumes that the data of interest are stored in a dataset called “FirstWeekCessationData,” including the variable “TimeDays” (time in fractional days), “urge” (self-rated urge), “id” (subject ID), “Relapse3WeeksPost” (whether the subject relapsed), “Intercept” (previously defined as a column of all 1's in the dataset) and “CenteredNA” (for negative affect). The dataset is assumed to be have one row per observation (hence multiple rows per person), but the subject-level covariate “Relapse3WeeksPost” must be the same for all rows within a given person. Three latent classes are fit; the first is the reference class against which the others are compared. The two time-varying coefficients are modeled as splines with 6 interior knots each.

Inputs

The following inputs are required. Case (upper or lower) does not matter.

• MyData gives the name of the dataset containing the variables to be analyzed.

• Time gives the name of the variable for time t_ij in MyData.

• Dep gives the name of the variable for response y_ij in MyData.

• ID gives the name of the variable for subject ID.

• Latent_Classes gives the number of classes to be fit (1 or more, but no more than 9 is recommended).

• TCov gives the names of covariates assumed to have time-varying effects (their values may be time-varying or not). The first TCov variable should usually be defined to have a value of 1 in each row (it could be named Intercept).

• Knots gives the number of knots for each TCov variable (0 or more), not counting the endpoints of the interval.

The following two inputs are only needed for certain models.

• Cov gives the names, if any, of covariates assumed to have non-time-varying effects (their values may be time-varying or not)

• SCov gives the names, if any, of covariates used to predict class membership (these must be the same for all measurements on a single individual). A column of 1s should not be provided for SCov because, unlike in the case of TCov, an intercept column is included automatically by the code.

Finally, the inputs below are more technical and can be left at default values if desired.

• Ref is the number of the class to be used as a reference class (this is only important if there are SCov covariates). The default is one.

• Deg is the degree of the polynomial assumed to exist between any two knots. It should be 1, 2, or 3, where 1 is linear, 2 is quadratic and 3 is cubic. The default is 3.

• Std_Err_Option is yes if standard errors are to be calculated, and no if they are to be omitted. Standard errors can be omitted if several different models are being tried (e.g., different numbers of classes) just to compare their fit statistics; this will save much computational time.

• Roughness_Penalty is yes to use a second-order difference penalty as in Eilers and Marx (1996) to reduce overfitting and estimate smoother-looking coefficient curves, and no otherwise.

• Initial_Seed is the initial random number seed. The default is arbitrarily set at 100000. This seed is used to generate further random seeds, one for each starting value.

• Num_Starts is the number of different starting values to try. The default is 5 in order to provide a quick initial estimate, but a higher number such as 100 or 500 is recommended.

Some other, more technical options are omitted in this appendix. They can be left at their defaults.

Outputs

Results about the estimated model are shown on the screen. The macro also automatically generates many output datasets, each with a name prefixed by “MixTVEM.” The most important are called MixTVEMGridBeta#, where # is a number ranging from 1 to the number of variables specified as TCov. Each dataset contains estimates, as well as estimated pointwise confidence intervals, for the corresponding time-varying regression coefficient over a series of points in time. For instance, in our example, there is MixTVEMGridBeta1 for the Intercept variable and MixTVEMGridBeta2 for Centered NegAff. To avoid confusion, notice that MixTVEMGridBeta1 is actually β_0t in the notation of our article, since it represents the intercept term. However, it is automatically labeled with the number 1 because it is the first time-varying covariate.

To plot the three trajectories, one can use SAS code such as the following.

PROC GPLOT DATA=MixTVEMGridFittedBeta1;

PLOT Class1*TimeDays Class2*TimeDays

Class3*TimeDays/OVERLAY;

RUN;

To plot one of the trajectories with confidence intervals, one can use code like the following.

PROC GPLOT DATA=MixTVEMGridFittedBeta1;

PLOT Class1*TimeDays Upper_Class1*TimeDays

Lower_Class1*TimeDays/OVERLAY;

RUN;

In case it is of interest to know the underlying spline basis terms and the estimated coefficients for each term, they are in datasets called MixTVEMTimeBasis# and MixTVEMTheta. However, rather than trying to interpret each of these coefficients, it is better to interpret the plots of the resulting β coefficients as described above.

BesidesMixTVEMGridFittedBeta#, the macro automatically generates many other SAS datasets, some of which contain very technical information. Some of the most useful datasets are these:

• MixTVEMFitStatistics contains the fit statistics such as the log-likelihood, the weighted RSS, and hard-classified RSS.

• MixTVEMFittedValues contains fitted values for each observation

• MixTVEMPostProbs contains the estimated posterior probabilities for each subject of belonging to each class under the assumed model.

• MixTVEMRandomSeeds contains the different random seeds that were used in trying to find the best likelihood, and the fit statistics obtained for each.

There are several ways in which this macro could be expanded in the future. The current version of the macro, while allowing error variance to depend on class, does not allow error variance to depend on time. Thus, it would be desirable to allow for heteroskedastic data (e.g., variance increasing with time) in future versions. It would also be desirable to allow binary, Poisson, truncated or other non-normal data. Nagin's PROC TRAJ (Jones, Nagin, & Roeder, 2001) handled non-normal outcomes in the case of a mixture of parametric (e.g., linear) growth curves. Non-normal outcomes with non-mixture TVEM are handled in existing software from The Methodology Center (see Yang, Tan, Li,& Wagner, 2012; Dziak, Li, Zimmerman, & Buu, 2014).

Lastly, it would be desirable to be able to model the dropout process somehow to reduce the risk of bias caused by nonignorable dropout. This might be done using a joint modeling approach or a latent frailty parameter (see Albert & Follman, 2009; Muthén, Asparouhov, Hunter, & Leuchter, 2011). However, it would make estimation more complicated and therefore might require a large dataset.

Both the R function and SAS macro assume an autoregression parameter ρ greater than zero in expression (7). However, we also make available a simpler version of the R and SAS software, which handles the rarer case in which errors are assumed to be independent. We do not discuss this simpler version further here, because it does not seem likely to be widely applicable except perhaps in simulations.

The R and SAS files, along with tutorials for using them, are available at the Pennsylvania State University Methodology Center website (http://methodology.psu.edu/downloads/mixtvem) as well as the GitHub repository (https://github.com/dziakj1/MixTVEM) and the archival site ScholarSphere (https://scholarsphere.psu.edu/collections/x346dv602).