A Common Spatial Factor Analysis Model for Measured Neighborhood-Level Characteristics: The Multi-Ethnic Study of Atherosclerosis

Abstract

The purpose of this study was to reduce the dimensionality of a set of neighborhood-level variables collected on participants in the Multi-Ethnic Study of Atherosclerosis (MESA) while appropriately accounting for the spatial structure of the data. A common spatial factor analysis model in the Bayesian setting was utilized in order to properly characterize dependencies in the data. Results suggest that use of the spatial factor model can result in more precise estimation of factor scores, improved insight into the spatial patterns in the data, and the ability to more accurately assess associations between the neighborhood environment and health outcomes.

1 Introduction

Observational studies typically collect large quantities of detailed information on participants in order to identify risk factors for adverse health related outcomes. Researchers working with these data often encounter the need to reduce the dimensionality, a measure of data size, of a dataset in order to facilitate inference in modeling or to generally better understand the underlying structure of a large set of highly correlated measured variables. Factor analysis, a procedure that identifies and estimates a relatively small number of latent variables that capture variability in a larger set of observed variables, can be used to both reduce dimensionality and explore the data structure (Rowe, 1998).

The growing interest in the effects of spatial context on health and the growing availability of large amounts of spatially-referenced data have led to an explosion of spatial variables in observational studies. Because these spatial variables are often interrelated, the development of techniques that allow for the exploration of relationships and reduction of dimensionality in the presence of spatial correlation is critical. In this study, we analyze data from the Multi-Ethnic Study of Atherosclerosis (MESA). MESA collects information on over 45 spatial (neighborhood) variables characterizing built and social environments, and researchers stand to gain great insights from the reduction and summarization of these data. However, in the case of neighborhood environment measures, spatial correlation in the variables may be present, and assumptions of independence may be invalid as a result. When working with such spatially-referenced data, a common factor analysis may be inadequate because it neglects the potential spatial dependencies in the responses, resulting in violated model assumptions, incorrect and misleading standard error estimates for key model parameters such as the factor scores, and, as a result, the potential for incorrect inference (Rowe, 1998). Spatial factor models are needed to circumvent these issues.

Previous applications of spatial factor models have varied considerably in their methods and purposes, including both multiple and single latent factors, utilizing both continuous and discrete outcome data, adding temporal components, and using the models for prediction (Hogan and Tchernis, 2004; Liu et al., 2005; Lopes et al., 2008; Mezzetti, 2012; Stakhovych et al., 2012; Wang and Wall, 2003). See Table 1 of Stakhovych et al. (2012) for a summary of the spatial factor analysis literature. Building on these prior studies, our analysis combines and applies elements of Bayesian spatial factor analysis methodology in order to properly analyze the neighborhood measurements from the MESA study. While Lopes et al. (2008) used their model to predict the outcome variables at new time points and unobserved spatial locations and Wang and Wall (2003) predicted the values of the latent factors at previously observed locations, to our knowledge, ours is the first study to predict the values of the latent factors at unobserved spatial locations. Furthermore, our model is the first to assume a common spatial structure for each of the latent factors without the inclusion of an independent source of variability unique to each location, referred to as the nugget effect in spatial modeling. Finally, our model is introduced and implemented in the point-referenced spatial data setting. Previous studies have introduced these point-referenced models but often work with areal data in the application (Hogan and Tchernis, 2004; Wang and Wall, 2003).

Our analysis begins with the standard non-spatial Bayesian factor analysis model to reduce the dimensionality of a set of MESA neighborhood environment variables. In order to take into account the presumed correlation between the factor scores based on spatial proximity, a second factor analysis model is implemented that allows for the possibility of spatial correlation between the factor scores. The two models are compared to determine if considerable correlation across space exists in the factor scores and to decide whether the added complexity of the spatial model improves the model fit and interpretation of the factors. Because the goal of factor analysis is often the reduction of data to be used as covariates in a health outcome model, an analysis is presented to compare the precision and accuracy of the results of two regression models using body mass index (BMI) as the outcome and the spatially and non-spatially correlated factors, respectively, as covariates.

Working in the Bayesian setting offers a flexible framework for introducing correlation between the latent factor scores. Bayesian estimation is implemented using Markov chain Monte Carlo (MCMC) sampling algorithms which provide samples from the posterior distribution of the parameters. An analysis of these posterior distributions, when correlations in the data are appropriately accounted for, results in correct characterizations of uncertainties in parameter estimates. Bayesian factor models have been previously discussed in the literature (Ghosh and Dunson, 2009; Lopes and West, 2004; West, 2003), and Rowe (1998) provides a comparison between frequentist and Bayesian versions of the factor model.

Given the importance of spatially-referenced data in the health research community, our analysis has the potential to lend insight to a multitude of other analyses and research projects. In general, an expanded understanding of the spatial nature of a set of measurements, which can be achieved by applying this methodology, will lead to more accurate analyses, due to improved parameter estimation and correct standard errors for the factor score estimates. This model also allows for the prediction of factor scores at new locations, without the need to collect the full set of original covariates at these new locations. For researchers using cohort data, this ability to predict will be useful when participants move during follow-up. In addition, researchers with an interest in associations between neighborhood environment and health outcomes will benefit from the ability to properly reduce neighborhood data dimensionality, potentially enabling more efficient computation and more concise inference in assessing such associations without substantial loss of information.

2 Materials and Methods

2.1 Data Description

MESA is an ongoing population-based, longitudinal study designed to explore subclinical cardiovascular disease prevalence and progression in the United States (US), as well as to investigate its association with other health and lifestyle factors (Bild et al., 2002). Approval for MESA participant enrollment and data collection was obtained from the Institutional Review Board at each study site and the coordinating center. From 2000–2002, study sites in six US cities recruited 6,814 men and women, aged 45–84 years. The sample is 38% white, 28% African American, 23% Hispanic, and 11% Asian. Participants completed questionnaires and participated in a physical examination. For participants in the MESA Neighborhood Study, researchers geocoded the latitude and longitude of each participant’s home residence and collected information about the surrounding neighborhood, such as the density of many varieties of restaurants and stores and the crime rates within buffers of various sizes, centered at the residence and workplace. In total, participant information has been collected at five clinic exams as well as through a number of follow-up phone calls (Bild et al., 2002; MESA Coordinating Center, 2014).

The presented analyses utilize data from the Chicago study site (n=1,161) at Exam 2 (n=1,053), which occurred between July 2002 and February 2004, and the analyses are restricted to participants who completed Exam 2 in 2003 (n=815). Chicago was selected due to the availability of crime data while Exam 2 is chosen to maximize the sample size for a single year. In order to attain the necessary spatial accuracy, only data from locations that are geocoded at the street or zip+4 levels are included (n=804). Furthermore, locations are included in the analysis only if their one-mile buffers are contained entirely within the Chicago city limits (n=603). Participants with the same spatial coordinates (which indicate participants living in the same house or building) have the same neighborhood measurements. Given that our interest lies exclusively in these neighborhood measurements, only the unique locations are included in the spatial analysis (n=376). An additional participant was removed due to inconsistent spatial information, resulting in a final sample of 375 unique locations across Chicago and all with complete data for each of the measurements included in the analysis. The study includes participants that moved within Chicago between baseline and Exam 2, providing greater spatial coverage across Chicago than was originally present in the baseline sample.

In a factor analysis, a fixed set of variables is compiled at the outset to be the subject of reduction and summarization. The following 21 mutually exclusive buffer level variables are included in the presented factor analysis: the kernel density of grocers, supermarket chains, supermarket non-chains, deli/meat/fish/dairy stand-alone stores, liquor stores, drinking places (alcohol), fast food chains, fast food non-chains, other eating places, and total recreational facilities, as well as the percent of land devoted to residential use, the percent of land devoted to commercial use, population density per square kilometer (km), yearly average outdoor murders (per 1000 persons), yearly average indoor murders (per 1000 persons), yearly average outdoor criminal offenses (per 1000 persons), yearly average indoor criminal offenses (per 1000 persons), yearly average outdoor incivilities (per 1000 persons), yearly average indoor incivilities (per 1000 persons), yearly average outdoor assault and battery (per 1000 persons), and yearly average indoor assault and battery (per 1000 persons). A buffer level of one mile is chosen for data completeness purposes and because it represents a common choice in past MESA analyses (Moore et al., 2008, 2009). Numeric summaries of these included variables are displayed in Table 1. In Figure 1 of the Online Supplementary Materials Section, we present a correlation heat map for the 21 variables.

Table 1.

Numeric Summaries of the 21 Mutually Exclusive Neighborhood-Level MESA Analysis Variables.

	Mean	SD	Minimum	Median	Maximum
Food Stores†
Grocery Stores	8.33	5.16	0.23	7.09	23.62
Supermarket Chains	0.85	0.77	0.00	0.72	2.98
Supermarket Non-Chains	0.87	0.89	0.00	0.69	3.82
Deli/Meat/Fish/Dairy	1.20	1.20	0.00	0.87	9.70
Liquor Stores	2.34	2.33	0.00	1.62	10.17
Alcohol Establishments	7.42	11.46	0.00	2.15	45.62
Fast Food Chains	4.22	5.49	0.00	2.32	61.34
Fast Food Non-Chains	3.43	3.58	0.00	2.56	39.23
Restaurants	33.93	41.65	0.60	17.78	210.90
Recreational Facilities†	6.94	8.60	0.36	3.58	41.04
Land Use
Residential Land Use (%)	0.39	0.17	0.08	0.36	0.80
Commercial Land Use (%)	0.09	0.05	0.02	0.08	0.37
Population Density (1,000 per km2)	5.70	1.73	1.73	5.36	10.93
Crime‡
Outdoor Murders	0.14	0.12	0.00	0.11	0.45
Indoor Murders	0.07	0.05	0.00	0.06	0.28
Outdoor Criminal Offenses	6.33	2.50	1.56	5.98	19.79
Indoor Criminal Offenses	11.22	3.60	4.88	10.10	28.76
Outdoor Incivilities	22.56	8.91	7.09	22.14	61.98
Indoor Incivilities	12.00	4.97	3.93	11.78	25.48
Outdoor Assault and Battery	18.21	7.06	5.02	17.41	45.58
Indoor Assault and Battery	27.64	12.85	6.06	23.31	57.43

^†measured in units per mile²

^‡measured in rates per 1,000 persons

Kernel density estimation (Silverman, 1986) is utilized to measure the food stores and recreational facilities in a participant’s buffer. It is a weighted density estimation method based on distance from the centroid of interest. In the generation of the MESA data, kernel density estimation is applied by giving higher weights to establishments nearer to the participant’s home residence and lower weights to those further away (Kesavan, 2013). The densities in the MESA dataset are measured in units per square mile using ArcGIS software (ESRI, Redlands, CA, USA).

Data on food stores were purchased from the National Establishment Time Series (NETS) dataset from Walls and Associates, which included 156 Standard Industrial Classification (SIC) codes (Walls and Associates, 2010). The following nine categories of food stores are included in our analysis: grocers, supermarket chains, supermarket non-chains, deli/meat/fish/dairy stand-alone stores, liquor stores, drinking places (alcohol), fast food chains, fast food non-chains, and other eating places mainly based on SIC code. Grocers are defined as any food stores that are smaller than supermarkets but are not classified as convenience stores. A supermarket chain is a food store that has eight or more locations within the study area (Auchincloss et al., 2012). A supermarket non-chain is a food store that is not categorized as a supermarket chain with more than 25 employees and/or more than $2 million of sales per year. A deli, meat, fish, dairy stand-alone store sells primarily meat, eggs, fish, and/or non-ice cream dairy products. Liquor stores sell alcohol to be consumed elsewhere. Alcohol drinking places are bars and other establishments that mainly sell alcohol to be consumed on the property. An eatery is considered to be a fast food chain if it was listed in the 75 top revenue fast food restaurants in the top 400 Chain Restaurants ranking in Restaurants and Institutions magazine in 2005 (Hume, 2005). Fast food chains specialize in quick food preparation, have no table service, and exclude coffee, donut, and ice cream shops. Fast food non-chains are defined equivalently but are those fast food restaurants not on the aforementioned list. The classification ‘other eating places’ includes any restaurant not included in either of the fast food categories, and this variable will be referred to as simply “Restaurants”.

As with food stores, recreational facilities were purchased from NETS. A total of 133 SIC codes were selected based on existing lists (Gordon-Larsen et al., 2006; Powell et al., 2007), which were then grouped into 12 categories based on SIC code. Our analysis only includes one broad category of recreational facilities which sums together the subsets into total recreational facilities. This includes indoor conditioning (e.g., gyms, dance), recreational (e.g., bowling, horseback riding), team sports (e.g., soccer clubs), water activities (e.g., swimming pool, boating), racquet sports (e.g., tennis, racquetball), and instructional in each (Kesavan, 2013).

Three built environment variables (commercial land use percentage, residential land use percentage, and population density per square km) are included in the analysis. Land use data for the Chicago study site originate primarily from the Chicago, IL city government. Two investigators independently classified parcels of land as residential or commercial based on provided land use codes and any discrepancies were adjudicated by a third investigator. A parcel of land is classified as residential if it is primarily devoted to places where people live, whereas it is classified as commercial if its primary purpose is to house businesses where people can purchase goods and/or services or commercial office space. Finally, investigators compute the percentage of each subject’s buffer that lies in residential and commercial areas by dividing the number of meters squared of land falling into each category by the total number of meters squared of land in the buffer. Data on population density per square km for the year 2003 in each subject’s buffer are taken from the 2000 census. First, a population density is computed for each census block. A weighted average of the percentage of each block that falls within a participant’s buffer is then calculated (Rodriguez et al., 2009).

Crime data are collected by the Chicago Police Department and published on the City of Chicago Data Portal (Chicago Police Department, 2011). Crimes in the Data Portal are excluded if they are missing any of the following: location geocoded to 100th block centerlines, date, time, and type of crime. Crimes perpetrated in airports or airplanes are also excluded. Incidents were coded into categories based on the Illinois Uniform Crime Reporting code system. The categories murder, criminal offenses, incivilities, and assault and battery are included in the analysis and all broken down into their indoor and outdoor components. Indoor and outdoor components are included separately because indoor and outdoor crime rates may relate in differing ways to how an individual interacts with the environment. The category murder includes first and second degree manslaughter and excludes involuntary or reckless incidents resulting in death. Criminal offenses encompass the following crimes: robbery, pocket-picking, purse-snatching, criminal sexual assault, burglary, stalking, arson, and kidnapping. Incivilities include possession and sale of narcotics, prostitution, criminal damage, weapons violations, public indecency, probation/parole violation, gambling with cards/dice, and peeping tom. Finally, assault and battery is a harmful and/or offensive physical attack (Kerr et al., 2015).

A normalized one-year crime rate is then calculated (McGinn et al., 2008). The numerator of the normalized rate is the count of incidents for a given category within the participant’s buffer during the one year time period prior to the participant’s exam. The denominator is the total population within the buffer, which is calculated based on the block-level 2000 census population. Each block is weighted by the percent of the block area that falls within the participant buffer. The total population within that block is then multiplied by this weight and the weighted populations are summed together for the total population within the buffer. The rates are multiplied by 1,000 for a rate of crime per 1,000 persons (Kerr et al., 2015).

To compare the results of the spatial and non-spatial factor analysis models, an additional analysis is performed which utilizes BMI as the outcome of interest. Height and weight were measured at Exam 2, and BMI was calculated as weight in kilograms divided by height in meters squared. The following individual-level covariates are also adjusted for in the sub-analysis: age, gender, race/ethnicity (White/Caucasian, Chinese-American, Black/African-American, or Hispanic), highest level of education completed (high school/G.E.D or less, some college, or B.A. or above), and total gross family income in the previous 12 months (<$40,000, $40,000–$74,999, or $75,000+).

2.2 Statistical Model

Factor analysis is a multivariate statistical tool that can be used to describe relationships between variables. Often times, there may be a relatively small number of latent variables controlling a larger set of continuous, observed variables, and identifying these underlying “factors” may improve understanding of the data and simplify subsequent analyses. Using factor analysis, we can analyze the relationship between each of the latent factors and each of the observed variables in order to understand the nature of the factors. Moreover, through estimation of the latent factor scores, we can reduce the dimensionality of the dataset while retaining a majority of the information contained in the original variables.

The common factor analysis model assumes that the latent factor scores are independent across all spatial locations; however, when the data being collected at each location is related to the neighborhood environment, the assumption of independence is likely incorrect. Instead, the latent factor scores may be spatially correlated, with nearby locations having similar neighborhood environments. Updates to the common factor model are needed in order to properly account for this spatial correlation. By introducing a spatially-referenced prior distribution for the latent factor scores, we can account for the spatial correlation and ensure accurate inference for the model parameters.

We first introduce the standard non-spatial factor analysis model in the Bayesian setting and then extend it to include the possibility of spatial correlation between the factor scores. The common factor analysis model for the 21 observed variables from each unique spatial location (see Table 1) is given as Y(s_i) = Λη(s_i) + ε (s_i); i = 1, …, n, where Y (s_i) is the vector of p continuous, centered and scaled (by standard deviation) neighborhood-level measurements at location s_i (p = 21), Λ represents the p by m matrix of factor loadings (m ≪ p), η (s_i) is the m by 1 vector of latent factor scores at location s_i, ε (s_i) represents the vector of errors unique to location s_i, and n represents the total number of unique locations included in the analysis (n = 375) (Banerjee et al., 2003; Ghosh and Dunson, 2009). It is assumed that the ε (s_i) vectors have independent and identically distributed multivariate normal distributions such that $\mathit{\epsilon }({\mathit{s}}_i)\stackrel{\text{iid}}{\sim }\text{MVN}(\mathbf{0},\mathbf{\sum })$, where Σ is a diagonal matrix with (i, i)^th entry equal to ${\sigma }_i^2$. Λ is constrained to be lower triangular with diagonal entries λ_ii > 0 for identifiability purposes (Bollen, 1989). In the standard non-spatial factor analysis model, the factor scores, η(s_i), are assumed to be independent among locations. The spatial model relaxes this assumption of independent factor scores, and instead allows for the possibility that the factors are spatially correlated. Additional details on the likelihood of the data can be found in Section A.1 of the Appendix.

To complete the Bayesian model specification, prior distributions are chosen for the parameters, Λ, η, and Σ. Prior distributions are chosen to be vague yet proper in order to allow the data to drive the inference rather than our prior beliefs and to ensure that the posterior distribution is proper. Section A.2 of the Appendix provides a detailed description of the specific prior distributions selected for each parameter.

In the spatial model, we introduce a prior distribution that allows for the possibility of spatial correlation between the factor score parameters, η(s_i). This prior distribution accounts for distances between the locations, resulting in increased correlation between factor scores separated by short distances and decreased correlation between factor scores separated by long distances. The rate at which this correlation decays as a function of distance is controlled by an additional parameter in the model, ϕ. We assign ϕ a prior distribution that allows the data to determine the rate of decay, ranging from high spatial correlation to essentially no spatial correlation. Therefore, estimation of ϕ can provide insight into the level of spatial correlation present in the data and the need for the spatial factor analysis model. Full details of the spatially-referenced prior distribution can be found in Section A.2 of the Appendix. MCMC sampling techniques are used to obtain samples from the posterior distribution of all model parameters. Full details on the sampling alorithms for the non-spatial and fully spatial models can be found in Section A.3 of the Appendix.

Another advantage of spatial modeling is the ability to predict the latent factor scores at locations across Chicago where the original set of 21 variables wasn’t directly observed. We do this by using the method of Bayesian kriging (Handcock and Stein, 1993) which allows us to obtain samples from the posterior predictive distribution of the latent factor scores. These samples are summarized in the usual manner leading to posterior predictive means and standard deviations at each prediction location. The summarized predicted latent factors can be mapped across the spatial range of the observed data in order to illustrate the spatial patterns in the factors. Full derivations for the prediction process are described in Section A.4 of the Appendix.

An additional analysis is presented to illustrate how results from the spatial and non-spatial models would compare when being used to analyze the association between neighborhood environments and a health outcome. In this analysis, BMI is used as the health outcome, and the estimated latent factor scores are included as covariates in a regression model (n=586). The analysis accounts for the uncertainties in the estimated factor scores, mimicking a joint model of the factor analysis and the health outcome regression and allowing for a comparison of the precision with which regression parameters could be estimated in the joint spatial and non-spatial models.

3 Results

3.1 Exploratory Analyses

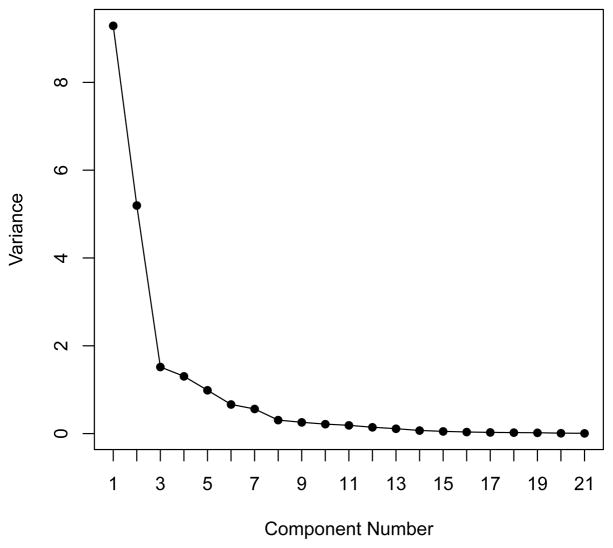
A scree plot of the eigenvalues (Cattell, 1966), shown in Figure 1, suggests that a model with three latent factors (m = 3) is appropriate to describe the underlying structure of the data. The non-spatial and spatial versions of the factor model have equivalent first stage forms. They differ only in the prior distribution for the factor scores. Therefore, we expect the structure of the underlying factors to be similar for both models, with estimation of the factor scores possibly differing if spatial correlation is present. As a result, we rely on the scree plot findings to determine the number of factors for the spatial model as well. This small number of factors is ideal given that interpretability of the factors is a primary goal of the analysis.

Figure 1.

Scree Plot Used to Determine the Appropriate Number of Latent Factors.

All analyses are carried out using R statistical software (R Core Team, 2013). We attempt to determine if the spatial modeling assumptions are justified through the analysis of the estimated factor scores (η (s_i), i = 1, …, n) from the fitting of the non-spatial Bayesian factor analysis model. Empirical semivariogram analyses (Ecker and Gelfand, 1997) for the estimated factor scores suggest that all three factors have a similar spatial structure. Figure 2 in the Online Supplementary Materials Section displays the empirical semivariogram plots from the analyses. These plots suggest that including a nugget effect is not necessary in this setting since at very small distances the semivariance is near zero. In order to investigate this further, we fit univariate Bayesian spatial models with a constant mean and specified covariance structure separately to each set of estimated factor scores. We aim to determine which covariance structure is appropriate for each factor and to estimate the value of the spatial correlation parameter, ϕ, for each selected model. We fit the models using the exponential structure, Gaussian structure, and with no spatial structure. The non-spatial model is used to determine if accounting for space is necessary for each of the factors.

The model comparison results from each of the model and factor combinations are displayed in Table 1 of the Online Supplementary Materials Section. The Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002) is the most common way of comparing models in the Bayesian setting and is particularly preferred over other methods in the case of hierarchical models where the number of parameters is difficult to specify (Wang and Wall, 2003). DIC is penalized for model complexity using the effective number of parameters (Spiegelhalter et al., 2002), a measure of dimensionality that does not require specification of the number of parameters as most other model complexity penalties do (Wang and Wall, 2003). DIC cannot be used as a stand-alone goodness of fit measure for a model, only as a basis for comparison of two models, with preference being given to the model with the smaller value.

It is clear from the results that the exponential structure is preferred for each of the factors. In Table 2 of the Online Supplementary Materials Section, we also display the posterior distribution summaries for ϕ from each of the factors fit using the exponential covariance structure. These results suggest that a common spatial correlation parameter ϕ is an appropriate assumption as the posterior means are very similar and 95% credible intervals overlap significantly. The presented results suggest that our assumptions of a common spatial covariance structure and a common ϕ parameter are valid.

3.2 Spatial Factor Model

Before applying the model to the MESA data, we choose the variables for which some factor loadings will be constrained to zero for identifiability purposes. This choice should not ultimately impact the ability of the model to uncover the latent factor structure, but a wise choice may improve the convergence of our MCMC sampling algorithm. In our application of the model with three latent factors, we must select which three variables will be the leading variable in each of three columns of the Λ matrix. We choose the three least correlated variables (closest to zero), Grocery Stores, Outdoor Criminal Offenses, and Supermarket Non-Chains, since they are less likely to group together in the underlying latent factors.

The sampler for the spatial model was run for 250,000 iterations with the first 50,000 iterations discarded as burn-in. Tables 2 and 3 contain the posterior means for the factor loadings and variance parameters, respectively, for the three-factor spatial model. As in a typical factor model, factor loadings from the spatial factor model can be interpreted as weights or measures of association between the corresponding variable and latent factor. As illustrated by Table 2, the weights of the highest magnitudes for the first factor in the spatial model appear on the following variables: outdoor criminal offenses, fast food non-chains, recreational facilities, population density, and bars/alcohol establishments. Therefore, a possible interpretation of this latent factor is as an indicator of highly populated city blocks with high rates of outdoor criminal offenses. In a recent study of Chicago crime, Bernasco and Block (2011) give the name “crime attractors” to areas with many bars, liquor stores, fast food restaurants, and similar businesses, because the large number of cash transactions taking place in these establishments creates a favorable environment for outdoor criminal activities such as robberies. The results of their study revealed that blocks in Chicago that contain these types of businesses have higher outdoor robbery events than those that do not (Bernasco and Block, 2011). Factor 1 may represent these areas.

Table 2.

Posterior Means of the Factor Loadings for the Spatial and Non-Spatial Factor Models. The Posterior Standard Deviations for the Parameters from the Spatial Model Range from 0.01 to 0.09 with an Average Value of 0.06 ((0.04, 0.11) and 0.07 respectively for the Non-Spatial Model).

	Spatial Model			Non-Spatial Model
	Loading 1	Loading 2	Loading 3	Loading 1	Loading 2	Loading 3
Food Stores†
Grocery Stores	0.25	0.00*	0.00*	0.44	0.00*	0.00*
Supermarket Chains	0.55	0.09	0.69	0.78	−0.20	−0.08
Supermarket Non-Chains	0.47	0.59	0.13	0.45	−0.43	0.08
Deli/Meat/Fish/Dairy	0.53	0.37	0.45	0.54	−0.10	0.35
Liquor Stores	0.61	0.53	0.67	0.77	−0.40	0.36
Alcohol Establishments	0.67	0.44	0.77	0.89	−0.43	0.19
Fast Food Chains	0.60	0.33	0.76	0.70	−0.01	0.69
Fast Food Non-Chains	0.73	0.46	0.66	0.71	0.02	0.69
Restaurants	0.67	0.53	0.76	0.80	−0.34	0.47
Recreational Facilities†	0.78	0.59	0.72	0.82	−0.31	0.46
Land Use
Residential Land Use (%)	−0.14	−0.40	−0.35	−0.25	0.37	−0.46
Commercial Land Use (%)	0.51	−0.13	0.99	0.80	0.04	0.22
Population Density (per km2)	0.71	0.60	0.28	0.64	−0.40	−0.01
Crime‡
Outdoor Murders	0.18	−0.74	−0.00	−0.01	0.67	−0.57
Indoor Murders	−0.05	−0.93	0.36	0.16	0.49	−0.56
Outdoor Criminal Offenses	0.73	0.01	0.00*	0.28	0.78	0.00*
Indoor Criminal Offenses	0.37	−0.68	0.18	0.11	0.85	−0.22
Outdoor Incivilities	−0.20	−1.39	0.76	0.22	0.60	−0.53
Indoor Incivilities	−0.04	−1.21	0.31	0.03	0.81	−0.62
Outdoor Assault and Battery	0.10	−1.33	0.77	0.31	0.81	−0.48
Indoor Assault and Battery	0.30	−0.91	0.19	0.09	0.83	−0.51

^†measured in units per mile²

^‡measured in rates per 1,000 persons

^*constrained to take value 0 for identifiability purposes

Table 3.

Posterior Means of Variance Parameters for the Spatial and Non-Spatial Factor Models. The Posterior Standard Deviations for the Parameters from the Spatial Model Range from 0.0003 to 0.0700 with an Average Value of 0.0255 ((0.0034, 0.0612) and 0.0233 respectively for the Non-Spatial Model).

	Spatial Model	Non-Spatial Model
	Variance	Variance
Food Stores†
Grocery Stores	0.94	0.82
Supermarket Chains	0.54	0.37
Supermarket Non-Chains	0.72	0.64
Deli/Meat/Fish/Dairy	0.62	0.60
Liquor Stores	0.18	0.14
Alcohol Establishments	0.13	0.03
Fast Food Chains	0.27	0.08
Fast Food Non-Chains	0.26	0.07
Restaurants	0.04	0.06
Recreational Facilities†	0.02	0.06
Land Use
Residential Land Use (%)	0.62	0.62
Commercial Land Use (%)	0.32	0.34
Population Density (per km2)	0.56	0.46
Crime‡
Outdoor Murders	0.26	0.27
Indoor Murders	0.54	0.45
Outdoor Criminal Offenses	0.48	0.34
Indoor Criminal Offenses	0.28	0.26
Outdoor Incivilities	0.20	0.34
Indoor Incivilities	0.04	0.02
Outdoor Assault and Battery	0.00	0.06
Indoor Assault and Battery	0.00	0.08

^†measured in units per mile²

^‡measured in rates per 1,000 persons

The second latent factor reflects lower crime rates, as evidenced by the large negative loadings on nearly all of the crime variables. This indicates that factor two may be a measure of neighborhood safety, which takes higher values for neighborhoods with lower crime rates. Finally, factor three is most heavily weighted on the commercial land use variable, with other high magnitude weights on the food and alcohol-related variables, outdoor incivilities, and outdoor assault and battery. Thus, the third factor could be interpreted to be a measure of commercialization of an area, as heavily commercialized areas, such as downtown, typically have high densities of restaurants and bars and generally also have high rates of outdoor crimes like assault (Wikstrom, 1995).

Although the factor interpretations provide insight into the underlying structure of these data, the primary interest of this analysis is in the presence or absence of spatial correlation in the factors. The spatial correlation can be assessed through a variety of measures, the most obvious of which is the parameter ϕ. The posterior mean of the spatial correlation parameter ϕ is 0.13 with 95% credible interval (0.11, 0.15). The convergence of ϕ to a relatively small value indicates that there is considerable spatial dependence in the factor scores, as smaller values imply a stronger correlation between scores at any given pair of distances. A common means of evaluating spatial correlation is through the use of effective range, the distance at which the correlation between two locations becomes negligible (less than or equal to 0.05). The effective range is estimated to be 23 km with 95% credible interval (20 km, 26 km), meaning that the factor scores for locations up to 23 km apart demonstrate non-negligible spatial correlation.

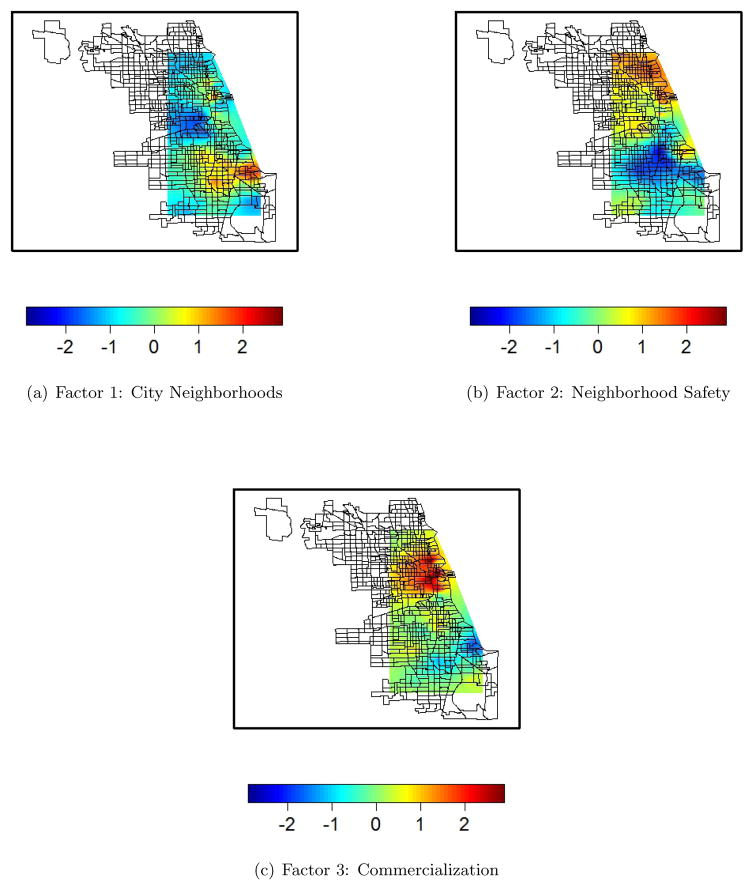
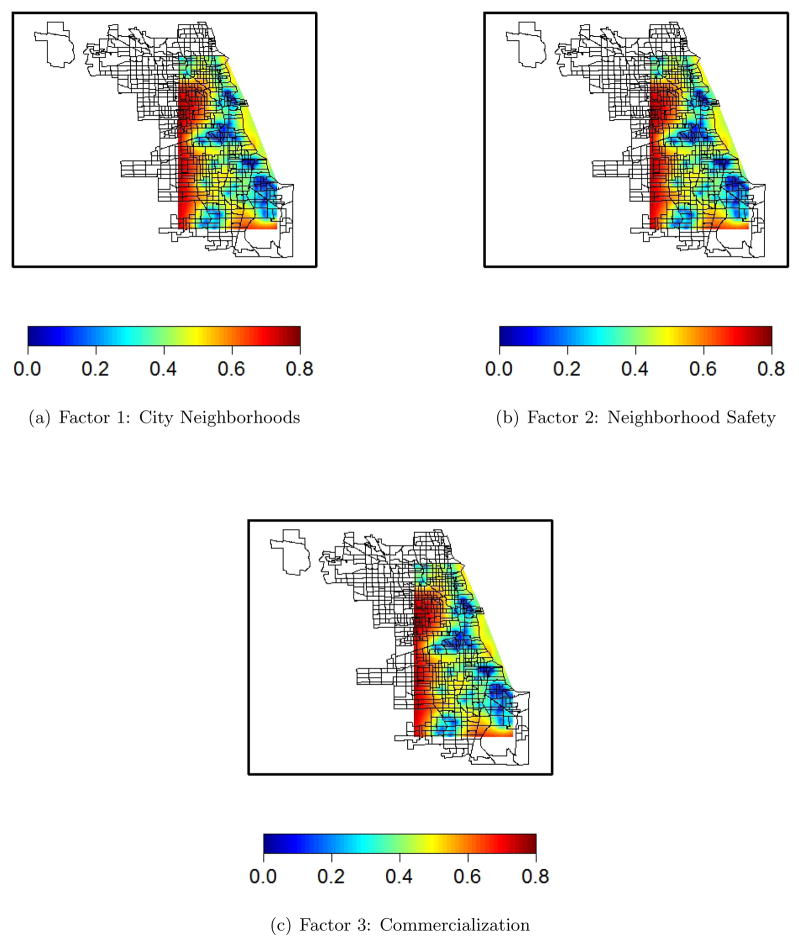
The ability of the model to predict factor scores at new locations where the values of the 21 original variables are unknown is demonstrated in Figures 2 and 3, and these maps also serve as another measure of assessing spatial correlation. These figures display the posterior predictive means and standard deviations, respectively, of the three latent factors across the spatial domain of our data.

Figure 2.

Posterior Predictive Means of Factor Scores over Chicago, Illinois. The Displayed Boundaries Represent Census Tracts from the 2010 Census.

Figure 3.

Posterior Predictive Standard Deviations of Factor Scores over Chicago, Illinois. The Displayed Boundaries Represent Census Tracts from the 2010 Census.

Figure 2 further demonstrates the presence of spatial patterns in the data. The clustering of the extreme values of the factors in different areas of the city is illustrated by the dark red and blue centers, and the spatial correlation can be seen in the way that the colors gradually lighten as one moves away from these dark centers. This implies that certain areas of the city are associated with higher or lower values of the factors and that more proximate locations are more likely to have similar values than more distant locations. The posterior predictive standard deviations, shown in Figure 3, are smallest in the areas where we observe data and increase as we extrapolate outside of these regions.

When the spatial predictions in Figure 2 are paired with an understanding of the nature of different areas of the city of Chicago, further insight is provided into the interpretations of the latent factors, in addition to illustrating the spatial patterns in the factor scores. According to the Chicago Police Department (2014), the north side of the city has relatively low crime rates, while the south side demonstrates higher crime rates. This, along with the knowledge of the location of downtown and commercial versus residential areas can be applied to the prediction maps to guide factor interpretations.

Factor one was earlier interpreted as a variable related to highly populated city neighborhoods with high outdoor criminal activity and this is supported by the heat map of factor one, which demonstrates high predicted values over much of the south side of Chicago. In the heat map of factor two, there is an even more distinct division between the north and south of the city, with moderate to high predicted values in the north and low predicted values in the south. This suggests that the interpretation of factor two as a measure of neighborhood safety could be appropriate, given the discrepancy in crime rates between the north and south sides. Factor three was earlier interpreted as an indicator of commercial areas, such as downtown. Again, this appears to be a reasonable interpretation, given that the heat map demonstrates high values around the commercial downtown area of Chicago and lower values elsewhere.

3.3 Model Comparison

The posterior means of the factor loadings and posterior means of the variance parameters for the spatial and non-spatial factor models are shown in Tables 2 and 3. Note that the columns of factor loadings for the non-spatial model follow a pattern similar to that of the factor loadings in the spatial model, with factors one and three reversed, indicating that both models are detecting and fitting the same three underlying factors. The similarity between the factors uncovered by the two models suggests that a three-factor model is appropriate in both the spatial and non-spatial settings.

Given that neglecting existing spatial correlation impacts the posterior standard deviations, and therefore statistical inference, an important measure of comparison of the two models is the magnitude of the posterior standard deviations for the factor scores. The average and range values of the estimated posterior standard deviations for the factor scores in the spatial model are 0.08 and (0.03, 0.21), respectively. In the non-spatial model, the average and range values are 0.23 and (0.13, 1.10). The overall considerably smaller posterior standard deviations for the spatial model reveal that the factor score estimates in the spatial model are much more precise than in the non-spatial model. Thus, the spatial model leads to more reliable estimates due to increased precision. This discrepancy in posterior standard deviations between the two models in itself indicates that there is substantial spatial correlation in the factors, because, if the factor scores were independent, the posterior standard deviations in the models should be very similar.

Although the graphical results and increased precision of the spatial model clearly demonstrate the spatial dependence in the factors and need to account for it in the model, a more formal comparison of the non-spatial and spatial models is needed to establish the improved fit of the spatial model. The DIC for the spatial model is 8,375.74, with the effective number of parameters at 903.76. For the non-spatial model, these measures are 9,901.77 and 1,080.98, respectively. The spatial model yields a considerably lower DIC value than the non-spatial model, indicating improved fit.

3.4 Association with Body Mass Index

Finally, an analysis is performed to demonstrate the benefits of accounting for spatial correlation in the factor scores when modeling the factor analysis jointly with a regression model that includes a health-related outcome and the estimated latent factors as covariates. In our analysis, we work with BMI as the health outcome of interest.

In order to assess the potential benefits of using spatially-derived factors in a regression analysis, we assess the uncertainty associated with the factor scores through a two-step procedure. In the first step, we obtain samples from the posterior distribution of the factor scores from both the spatial and non-spatial factor analysis models as described in Section 2.2. In the second step, each of the samples from the posterior distribution of the spatially correlated factor scores is used as a set of predictors in a linear regression model with BMI as the outcome. The same procedure is applied to each posterior sample of non-spatially correlated factor scores. Age, gender, race, highest level of education completed, and total gross family income in the previous year are also adjusted for in each model, as was done in the minimal model for BMI by Moore et al. (2013). This procedure results in a set of estimated regression parameters corresponding to each posterior sample from each of the factor analysis models.

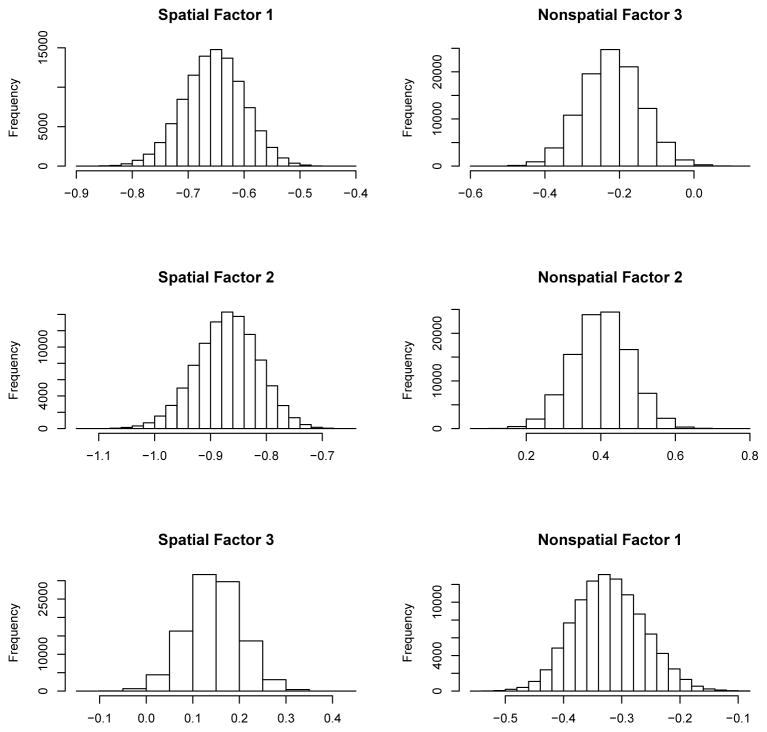
Histograms of the estimated regression coefficients for each of the three latent factors are constructed for both models. The spread of the estimated coefficients for each factor across all the samples should reflect the size of the uncertainties for each parameter resulting from a joint model. Comparing measures of spread for the coefficients of corresponding factors in the spatial and non-spatial models indicates which model would produce more precise estimates. The histograms of the regression coefficients for both models are provided in Figure 4, and Table 4 contains the standard deviations for these coefficient estimates. These measures clearly demonstrate the superior precision of the spatial model, with posterior standard deviations substantially smaller for the coefficients on two of the factors and equivalent for the remaining one. This suggests that the smaller posterior uncertainties for the factor scores in the spatial model would result in improved estimation when modeling a health outcome using the estimated factors as covariates and properly accounting for their uncertainty.

Figure 4.

Histograms of Estimated Regression Coefficients Based on Samples from the Posterior Distribution of the Latent Factor Scores. The Regression Coefficients are Describing the Association Between Each Factor and Body Mass Index.

Table 4.

Standard Deviation of Estimated Coefficients from Body Mass Index Analysis.

	Spatial Model	Non-Spatial Model
	Standard Deviation	Standard Deviation
City Neighborhoods	0.05	0.08
Neighborhood Safety	0.06	0.08
Commercialization	0.06	0.06

Based on the estimates from the spatial BMI analysis, factors one and two are negatively associated with BMI while factor three shows a small positive association with BMI after adjusting for age, gender, race, education, and income. Applying the interpretations of the factors proposed in Section 3.2, this analysis suggests that living in safer neighborhoods and/or heavily populated city neighborhoods is associated with lower BMI, and living in highly commercialized areas is associated with higher BMI after adjusting for all other covariates. The strong association between neighborhood safety and BMI agrees with the findings of previous research using the MESA Chicago data in which Evenson et al. (2012) report that time spent performing various types of physical activity is positively associated with perceived neighborhood safety and negatively associated with measures of criminal activity in the neighborhood.

4 Conclusions

Our results indicate that for the present data, spatial correlation exists and ignoring it could lead to inaccurate estimates of measures of uncertainty, such as posterior standard deviations for the factor scores, as well as incorrect inference when these factor scores are used as predictors in a model of a health outcome. The presented spatial factor model not only provides improved fit according to DIC but also leads to factor score estimates with smaller posterior standard deviations. The factor scores were used as covariates in a model of BMI which demonstrated that the increased precision in the factor score estimates would result in improved estimation when including them as covariates in a health outcome model and appropriately accounting for their uncertainties.

Although the spatial and non-spatial models demonstrate similar factor loading patterns (Table 2), the factor score estimates from the non-spatial model often do not agree with those from the spatial model due to increased levels of uncertainty. Future analyses utilizing these factor scores should therefore include the spatial estimates due to the increased precision. Subsequent statistical analyses should also account for the uncertainty in these factor score estimates by incorporating their posterior uncertainties into the modeling framework in order to correctly characterize the association between the factors and a considered health outcome. Increased uncertainty in the factor scores should lead to increased uncertainty in the associations of interest, as evidenced by the analysis in Section 3.4.

Our analyses shed light on the ability of the spatial factor analysis methodology to reduce the dimensionality of any spatially correlated dataset (using point-referenced spatial data) by estimating latent factor scores at observed locations and, moreover, to predict latent factor scores at unobserved locations. This capacity for prediction at unobserved locations could simplify tremendously the process of collecting and analyzing data at new locations for a new set of individuals (possibly in a different study) or participants that change location during follow-up, since only their spatial coordinates and not the values of the original variables is necessary.

A final benefit of our model is the potential interpretability of the underlying factors. The variables we selected for analyses were not based on any theoretical considerations (we simply included all mutually exclusive variables available for identical buffers for illustrative purposes). As in classic factor analysis, the factors identified and their interpretation can be highly influenced by the set of variables included. The factors identified could therefore be quite different if a different set of neighborhood variables were included. Nevertheless, the patterns in the factor loadings can be very informative and help investigators understand key patterns in the data. A thorough understanding of the nature of these factors aids in the interpretation of results in analyses which employ them. Future work could consider jointly modeling a selected health outcome and the spatial factors in order to determine if these latent factors are associated with the outcome and if incorporating spatial information improves the modeling of the outcome. Future research could also extend the spatial model to the spatiotemporal setting and expand the methodology to make possible the incorporation of multiple exams and multiple years of data.

In conclusion, our analysis confirms the presence of spatial correlation in the factors underlying the neighborhood-level measurements in our data, suggesting that a non-spatial factor model may not be appropriate. Using a spatial factor analysis model, we estimated the factor scores for each participant, predicted the values of the factor scores at new locations, and provided insight into the nature of the latent factors through the interpretation of the factor loadings, all of which will assist researchers in more precisely determining the relationship between neighborhood environments and cardiovascular health. Moreover, the methodology will benefit researchers in all fields who wish to summarize or reduce the dimensionality of a spatially-referenced dataset.

A Appendix

A.1 Data Likelihood

The location-specific vectors of data, conditional on the introduced model parameters, are independently distributed as $\mathit{Y}({\mathit{s}}_i)\mid \mathbf{\Lambda },\mathit{\eta }({\mathit{s}}_i),\mathbf{\sum }\stackrel{\text{ind}}{\sim }\text{MVN}\{\mathbf{\Lambda }\mathit{\eta }({\mathit{s}}_i),\mathbf{\sum }\}$; i = 1, …, n which can also be written jointly as Y |Λ, η, Σ ~ MVN(Λ^*η, Σ^*) where Y = {Y(s₁)^T, …, Y (s_n)^T}^T, Λ^* is an np by nm block diagonal matrix with Λ on the diagonal, Σ^* is an np by np block diagonal matrix with Σ on the diagonal, and η = {η(s₁)^T, …, η(s_n)^T}^T.

A.2 Prior Specification

The diagonal elements of the factor loadings matrix, Λ, are given independent truncated normal prior distributions (truncated below by 0) with a common variance such that ${\lambda }_{jj}\stackrel{\text{iid}}{\sim }\text{TN}(0,{\tau }_1^2;\ge 0)$, j = 1, …, p. The off-diagonal entries (below the diagonal) are given independent normally distributed prior distributions with a common variance such that ${\lambda }_{jk}\stackrel{\text{iid}}{\sim }\mathrm{N}(0,{\tau }_2^2)$, j > k. The variance parameters which control the ε(s_i) vectors are assigned independent and identically distributed inverse gamma prior distributions such that ${\sigma }_j^2\stackrel{\text{iid}}{\sim }\text{IG}(\alpha ,\beta )$, j = 1, …, p. For the non-spatial factor analysis, we assign independent and identically distributed multivariate normal prior distributions to the factor score vectors such that $\mathit{\eta }({\mathit{s}}_i)\stackrel{\text{iid}}{\sim }\text{MVN}(\mathbf{0},{\mathit{I}}_m)$ where I_m is the m by m identity matrix. We assume that the factor scores are independent both within and among locations as is standard in a common factor model. The introduced prior distributions lead to semi-conjugacy in the model. The fixed values of the hyperparameters are chosen to be ${\tau }_1^2={10}^{10},{\tau }_2^2={10}^{10}$, α = 0.0005, and β = 0.0005. These initial values are selected to produce vague yet proper prior distributions so that the inference is data-driven.

For the fully spatial factor model, the same distributions described above are used for Λ and ${\sigma }_j^2$, but without the assumption of independent factors between locations, an exchangeable prior distribution can no longer be assigned to each location’s vector of factor scores. We now specify a spatially referenced prior distribution to the complete η vector that still assumes independence within a location such that η ~ MVN(0, Σ_S ⊗ I_k) where ⊗ represents the Kronecker product. The inter-location spatial dependence is taken into account by the Σ_S matrix. Because point-referenced spatial data are available (latitude and longitude of each location), the structure of Σ_S is determined based on the distances between locations. The specified prior distribution implies that each factor has the same spatial structure and a common level of spatial correlation at each distance. These assumptions are fully investigated and discussed in Section 3.1.

Based on results from the exploratory analyses, we select the exponential covariance matrix which results in Σ_S(i, j) = exp{−ϕ ||s_i − s_j||} where Σ_S (i, j) is the (i, j)^th entry of Σ_S and ||s_i − s_j|| is the Euclidean distance between locations s_i and s_j. The parameter ϕ controls the level of spatial correlation in the data and is assumed to be common among the m factor scores with a prior distribution such that ϕ ~ Uniform(a, b) where the fixed values of a and b are chosen so that, a priori, the level of spatial correlation is allowed to vary between 0.05 and 0.95 for the smallest and largest observed distances respectively (a = 0.001, b = 1116.141). This allows the data to determine the appropriate level of spatial correlation rather than our prior beliefs.

A.3 Posterior Sampling Algorithm

The non-spatial and spatial factor analysis models both employ a Gibbs sampler (Gelfand and Smith, 1990; Geman and Geman, 1984) to obtain draws from the posterior distribution of interest, although the spatial model requires the addition of a Metropolis step (Gilks et al., 1995). The steps for sampling Λ and Σ are identical for the two models. For the non-spatial factor analysis model, sampling η (s_i) entails another Gibbs step. The steps include

1. Sample λ_jj|Σ, η, Y, Λ(−j, −j) from $\text{TN}\left(\frac{{\tau }_1^2{\sum }_{h=1}^n{\gamma }_{h_j}{\eta }_j({\mathit{s}}_h)}{{\tau }_1^2{\sum }_{h=1}^n{\eta }_j{({\mathit{s}}_h)}^2+{\sigma }_j^2},\frac{{\sigma }_j^2{\tau }_1^2}{{\tau }_1^2{\sum }_{h=1}^n{\eta }_j{({\mathit{s}}_h)}^2+{\sigma }_j^2};\ge 0\right)$ for j = 1, …, p where Λ(−j, −j) is the Λ matrix with the (j, j) element removed, γ_hj = Y_j (s_h) − Λ_j(−j)^T η_−j (s_h), Λ_j(−j) is the j^th row of Λ with the j^th component removed, and η_−j (s_h) is the set of factor scores for location s_h with the j^th component removed.

2. Sample λ_jk|Σ, η, Y, Λ (−j, −k) from $\mathrm{N}\left(\frac{{\tau }_2^2{\sum }_{h=1}^n{\gamma }_{h_{jk}}{\eta }_k({\mathit{s}}_h)}{{\tau }_2^2{\sum }_{h=1}^n{\eta }_k{({\mathit{s}}_h)}^2+{\sigma }_j^2},\frac{{\sigma }_j^2{\tau }_2^2}{{\tau }_2^2{\sum }_{h=1}^n{\eta }_k{({\mathit{s}}_h)}^2+{\sigma }_j^2}\right)$ for j > k, k = 1, …, p−1 where Λ (−j, −k) is the Λ matrix with the (j, k) element removed, γ_hjk = Y_j (s_h) − Λ_j(−k)^T η_−k (s_h), Λ_j(−k) is the j^th row of Λ with the k^th component removed, and η_−k (s_h) is the set of factor scores from location s_h with the k^th component removed.

3. Sample ${\sigma }_j^2\mid \mathbf{\Lambda }$, η, Y, Σ (−j, −j) from $\text{IG}\left(\frac{n}{2}+\alpha ,\left(\frac{1}{2}\right){\sum }_{h=1}^n{\{Y_j({\mathit{s}}_h)-{\mathbf{\Lambda }}_j^T\mathit{\eta }({\mathit{s}}_h)\}}^2+\beta \right)$ for j = 1, …, p where Σ (−j, −j) is the Σ matrix with the (j, j) element removed and Λ_j is the j^th row of Λ.

4. Sample η(s_i)|Σ, Λ, Y, η (−s_i) from MVN({Λ^T Σ⁻¹ Λ+ I}⁻¹{Λ^TΣ⁻¹Y (s_i),{Λ^TΣ⁻¹ Λ + I}⁻¹) where η (−s_i) is the complete vector of factor scores with those from location s_i removed.

   In the spatial model, the change in the prior structure of the covariance matrix for η leads to a more complicated posterior, involving the complete data likelihood given in Section A.1 of the Appendix. Furthermore, the full conditional distribution for ϕ, the spatial correlation parameter, has no closed form; thus, a Metropolis step is necessary for sampling.

5. Sample η from

   $$\text{MVN}\left({\left\{{\mathbf{\Lambda }}^{\ast T}{\mathbf{\sum }}^{\ast -1}{\mathbf{\Lambda }}^{\ast }+{\mathbf{\Psi }}^{-1}\right\}}^{-1}\left\{{\mathbf{\Lambda }}^{\ast T}{\mathbf{\sum }}^{\ast -1}\mathit{Y}\right\},{\left\{{\mathbf{\Lambda }}^{\ast T}{\mathbf{\sum }}^{\ast -1}{\mathbf{\Lambda }}^{\ast }+{\mathbf{\Psi }}^{-1}\right\}}^{-1}\right).$$

   where Ψ = Σ_S ⊗ I_m.

6. Sample $\psi =log\left(\frac{\varphi -a}{b-\varphi }\right)\in ℝ$ using a Metropolis sampler with a Normal proposal distribution. ϕ is obtained by transformation such that $\varphi =\frac{exp\{\psi \}b+a}{1+exp\{\psi \}}$.

In order to facilitate model convergence, η (s_i) is standardized during each iteration of the sampler.

A.4 Spatial Prediction of Factor Scores

The prediction locations are selected on a grid over Chicago which provides full spatial coverage within areas where we observe data. We define η₀ = {η (s_0,1)^T, …, η (s_0,r)^T}^T as the vector of latent factor scores at unobserved locations s_0,1, …, s_0,r where r is the number of included prediction locations. The posterior predictive distribution (ppd) of interest is given as

$$f({\mathit{\eta }}_0\mid \mathit{Y})=\int \int \int \int f({\mathit{\eta }}_0\mid \mathit{Y},\mathit{\eta },\mathbf{\Lambda },\mathbf{\sum },\varphi )f(\mathit{\eta },\mathbf{\Lambda },\mathbf{\sum },\varphi \mid \mathit{Y})d\mathit{\eta }d\mathbf{\Lambda }d\mathbf{\sum }d\varphi .$$

In order to obtain samples from this ppd, we rely on the properties of the multivariate normal distribution and the conditional independence of our model formulation such that f (η₀|Y, η, Λ, Σ, ϕ) = f (η₀|η, Λ, Σ, ϕ) where ${\mathit{\eta }}_0\mid \mathit{\eta },\mathbf{\Lambda },\mathbf{\sum },\varphi ~\text{MVN}({\mathrm{\sum }}_{12}{\mathrm{\sum }}_{22}^{-1}\mathit{\eta },{\mathrm{\sum }}_{11}-{\mathrm{\sum }}_{12}{\mathrm{\sum }}_{22}^{-1}{\mathrm{\sum }}_{21})$ and ${\mathbf{\sum }}_{S\ast }(\varphi )\otimes I_m=\left(\begin{array}{cc}{\mathrm{\sum }}_{{11}_{rm\times rm}}& {\mathrm{\sum }}_{{12}_{rm\times nm}}\\ {\mathrm{\sum }}_{{21}_{nm\times rm}}& {\mathrm{\sum }}_{{22}_{nm\times nm}}\end{array}\right)$ with Σ_S^*(ϕ) representing the full spatial covariance matrix of all prediction and observed locations. For each sample from the posterior distribution, we can draw a sample from the ppd of interest using composition sampling (Banerjee et al., 2003).