Spatial Variance in Resting fMRI Networks of Schizophrenia Patients: An Independent Vector Analysis

Abstract

Spatial variability in resting functional MRI (fMRI) brain networks has not been well studied in schizophrenia, a disease known for both neurodevelopmental and widespread anatomic changes. Motivated by abundant evidence of neuroanatomical variability from previous studies of schizophrenia, we draw upon a relatively new approach called independent vector analysis (IVA) to assess this variability in resting fMRI networks. IVA is a blind-source separation algorithm, which segregates fMRI data into temporally coherent but spatially independent networks and has been shown to be especially good at capturing spatial variability among subjects in the extracted networks. We introduce several new ways to quantify differences in variability of IVA-derived networks between schizophrenia patients (SZs = 82) and healthy controls (HCs = 89). Voxelwise amplitude analyses showed significant group differences in the spatial maps of auditory cortex, the basal ganglia, the sensorimotor network, and visual cortex. Tests for differences (HC-SZ) in the spatial variability maps suggest, that at rest, SZs exhibit more activity within externally focused sensory and integrative network and less activity in the default mode network thought to be related to internal reflection. Additionally, tests for difference of variance between groups further emphasize that SZs exhibit greater network variability. These results, consistent with our prediction of increased spatial variability within SZs, enhance our understanding of the disease and suggest that it is not just the amplitude of connectivity that is different in schizophrenia, but also the consistency in spatial connectivity patterns across subjects.

Introduction

Schizophrenia has been widely viewed as a neurodevelopmental disorder substantially affecting the brain structure and function during tasks and at rest.¹ Despite being extensively studied, its etiology remains unknown.^{2 ,[a]} Existing studies support the notion that schizophrenia is a heterogeneous disorder arising from a myriad of causes any of which can lead to similar brain disturbance. There exist many known causes for schizophrenia including environmental, genetic factors, as well as trauma, each possibly having different neuropsychiatric effects with no clear common pathology. Bleuler’s earliest concept of schizophrenia was also based on an assumption that the manifold external clinical manifestation masked an underlying unique neural pathology.^[b] Each case according to Bleuler revealed some significant residual symptoms that were common to all which lead to a similar diagnosis. This complex nature of the disease makes it challenging to characterize using a single model. This leads to variability within the population characterized as schizophrenia based not only on the etiology but also on, several neuropsychiatric factors.

Structural studies of schizophrenia evince a reduced cortical gray matter, amygdala-hippocampal and thalamic volume, and enlarged lateral ventricles.^3,4 These studies suggest that there exists a neural basis for behavioral or cognitive differences within the population.^{5 ,[c]} Additionally, functionally defined regions are inconsistent relative to anatomical landmarks on the cerebral cortex, thereby amplifying this heterogeneity issue. Literature strongly supports this functional variability with respect to anatomical landmarks in healthy population, as well as in schizophrenia with equal conviction.^{6 ,[d]} Many studies have also focused on improving spatial coregistration and thus functional localization or vice versa.^7–9 These structural and functional variations are clearly widespread and likely have a complex impact on the resulting functional patterns, motivating a multivariate whole-brain approach.

Multivariate analysis techniques such as independent component analysis (ICA), of functional MRI (fMRI) data, have been widely established as an approach to study the functional changes across the whole brain for both task and resting fMRI data. The goal of these models is to estimate sources (ie, networks) so that each source can be compared across subjects while maintaining independence between the different sources.¹⁰ To our knowledge, there have been few studies focused on the spatial variability of resting networks¹¹ and none among schizophrenia subjects. Given that we do expect considerable spatial variability, there is a need for approaches that can effectively incorporate this variability in conjunction with studies assessing this variability.

Independent vector analysis (IVA) is one such approach^{12,13 ,[e]} that, like Group ICA (GICA), extends ICA to multiple datasets while retaining subject variability. IVA, however, minimizes mutual information jointly across multiple datasets and hence takes the statistical dependence across multiple datasets (multisubject data in our case) into account. This dependence across subjects with the statistical properties of the ICA model helps with the decomposition into spatially independent components. IVA furthermore keeps each subject dataset separate instead of defining a common group subspace as in GICA, allowing for preservation of individually distinctive features in the estimated sources persuading us to its use. The dependence across multisubject data also enables the matching of sources across the datasets, hence eliminating the permutation ambiguity if ICA were performed separately on each subject’s data.

Anderson and colleagues¹⁴ presented IVA-GL where IVA using the Gaussian density model (IVA-G) is combined with IVA using the Laplace density model (IVA-L) to take both second-order and higher-order statistical dependence among multiple data sets (subjects) into account, denoted as IVA-GL. This model assumes super-Gaussian distribution for the sources providing a good match for fMRI spatial components. IVA-GL has been incorporated into the GIFT toolbox (http://mialab.mrn.org/software/gift), and this version of IVA was used in this study. The performance of IVA has been evaluated in simulations^15–17 and for a small number of fMRI data sets in healthy individuals and those who suffered a stroke¹⁸ to provide initial evidence that IVA captures individual subject variability in spatial patterns. A recent study¹⁷ compared the performance of GICA and IVA-GL spatial maps and timecourses in the presence of spatial variability on simulated data revealing that IVA-GL performs better at higher levels of spatial variability. These initial results and studies show that IVA is an effective approach for source separation and especially promising for preserving spatial variability across subjects.

This study focuses on evaluating spatial variation in IVA-based resting networks across subjects and changes in spatial patterns that occurred in schizophrenia patients (SZs) vs healthy controls (HCs). We predicted that multiple intrinsic brain networks would show increased spatial variance in the schizophrenia patients. To test this hypothesis, we utilized a multifold analyses approach presenting many ways to quantify and compare this variability between groups while also identifying amplitude differences between groups. This includes computing the differences between groups in the global mean of cross-subject variance over the brain voxels and measuring variance across subjects in the amplitude of each voxel.

Methods

Subject Characteristics

We analyzed anonymized data collected on 171 individuals (89 HCs and 82 SZs) who underwent rest fMRI acquisition as part of a center of biomedical research excellence project (https://cobre.mrn.org). Informed consent was obtained according to the University of New Mexico Human Research Protections Office. Patient selection was based on diagnosis of schizophrenia or schizoaffective disorder between 18 and 65 years of age. Diagnostic confirmation and evaluation of comorbidities was done with the Structured Clinical Interview for Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition (DSM-IV) axis I disorders.¹⁹ Exclusion criteria included a history of mental retardation, neurological disorders including head trauma, or of active substance dependence or abuse within the past year (except nicotine). A negative toxicology screen was a prerequisite for scanning. HCs were required to complete the Structured Clinical Interview for DSM-IV axis I disorders—nonpatient edition²⁰ to rule out axis I conditions and were recruited from the same geographical location. The 82 SZs had an average age of 38.07±14.03; 65 males and 17 females. The 89 HCs had an average age of 37.51±11.47, with 63 males and 26 females. There were no significant differences between groups in age (P = .2038) and gender (P = .7761). Additional information regarding demographics, patient recruitement, and summary of symptom and cognitive scores is provided in the supplementary material.

MR Data Acquisition

All participants were scanned at a single site at rest and instructed to keep their eyes open during the scan and stare passively at a central fixation cross. Resting state scans with 151 volumes were collected on a single 3-Tesla Siemens Trio scanner with a 12-channel radio frequency coil for each participant. Each volume consisted of T₂ ^* weighted functional images acquired using a gradient-echo EPI sequence with TR/TE = 2000/29ms, flip angle of 75 degree, 3.5mm slice thickness and 1.05mm slice gap, a field of view 240mm, a matrix size of 64×64, and a voxel size of 3.75×3.75×4.55mm.

Preprocessing

Data were preprocessed using an automated statistical parametric mapping (SPM)-based preprocessing pipeline within a neuroinformatics system developed at The Mind Research Network^{21 ,[f]} (https://coins.mrn.org). Images were realigned using INRIalign which is an extension to SPM’s realignment toolbox. Slice-time correction was applied using the middle slice as the reference frame. Data were then spatially normalized to standard MNI space and resampled to 3×3 × 3mm voxels using the nonlinear registration implemented in the SPM toolbox. Finally, data were smoothed using 10mm full width half maximum Gaussian kernel.

Data Analysis

The IVA models the measured BOLD fMRI signal as a linear combination of mixing matrix A_i and the independent activation sources S_i similar to that in GICA.^{22 ,[g]}

$$X_i=A_i*S_i$$ (1)

The main difference between the 2 algorithms lies in the fact that the mixing matrix A is shared by all the subjects in GICA while each subject i has an individual mixing matrix A_i in IVA. IVA starts with the same assumption that the individual sources S_i are spatially independent within each data set (each subject’s data) and additionally considers statistical dependence of the corresponding sources across other subjects. The demixing matrices W_i are estimated by minimizing mutual information among source component vectors.^{13 ,[h]} We can then form the source estimates U_i of the original sources S_i as

$$U_i=W_i*X_i$$ (2)

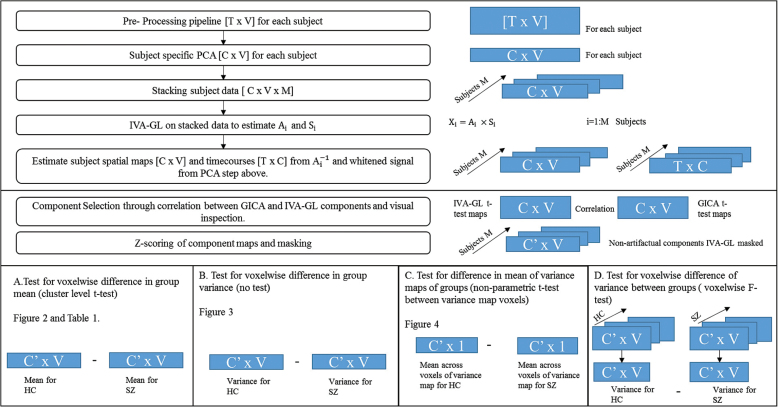
The GIFT toolbox (http://mialab.mrn.org/software/gift/) was used to perform IVA-GL and GICA on the preprocessed fMRI data that are of the form (T [time] × V [voxels]; figure 1). A relatively high model order (C = 75) was used for analysis since this order has previously been shown²³ to yield a preferable decomposition into functional components.

Fig. 1.

Flowchart representing the main steps in the independent vector analysis (IVA)-GL algorithm implementation and an illustration of the statistical tests performed.

Nonartifactual group components were identified using the ratio of the integral of spectral power below 0.10 Hz to the integral of power between 0.15 and 0.25 Hz as a factor for component selection²³ (higher the ratio larger the noise in the component) along with visual inspection and were the only components used for all other analyses. The presence of meaningful components in IVA-GL sources was done through correlation. Vectorized voxel values of the z-scored t-test-based statistical maps of IVA-GL and GICA were used for this. This post hoc comparison was done since GICA of fMRI data for evaluation of clinical populations has been extensively applied by our group and many others.^10,24–27 Further statistical analyses were done using individual subject spatial maps (which were normalized via z-scoring for each subject).²² Each subject’s component map was masked using a union mask between the IVA-GL and GICA t-test-based statistical maps at a z-threshold of 2. Additional description of the masking process is presented in the supplementary material.

Statistical Tests

A detailed description of all the statistical tests for evaluating spatial variability is as follows (figure 1).

• (1) Test for voxelwise difference in group mean (cluster level t test): Voxelwise cluster-level 2 sample t tests were performed on IVA-GL components to evaluate, between group, weighted amplitude differences in the z-scaled maps (HCs–SZs) which were corrected for multiple comparisons across voxels using family wise error (FWE) correction. We speculate that there will be functional networks with significant differences in the mean of the weighted amplitudes between HCs and SZs. At the voxel of maximum difference, a histogram of the amplitude values across subjects (separate for each group SZs and HCs) was plotted for each component with statistically significant differences with at least one cluster surviving correction. This was done predominantly to exhibit variance differences in a case where there are meaningful mean differences.

• (2) Voxelwise difference in variance of groups (no test): Voxelwise variance maps were calculated for each group (HCs and SZs) for each component maps for both IVA-GL and GICA to visually estimate the variance captured at each voxel across each group. Further ANOVA measures was computed only on IVA-GL components.

• (3) Test for difference in mean of variance maps (nonparametric t test between variance map voxels of each group): A nonparametric test to identify global differences between the variance maps of SZs and HCs (calculated in B) was done for each component. A nonparametric test was performed since the distribution of variance among subjects was found to be nonnormal across voxels. We predict that the SZs variance maps will have a significantly greater mean as compared with that of the HCs variance map. This would strengthen our premise that there exists a greater intersubject variability spatially in SZs than in HCs.

• (4) Test for voxelwise difference of variance between groups (voxelwise F test): We performed the difference of variance F test (voxelwise) on each component to distinctly identify the group encompassing greater variability across subjects. The F test assumes a normal distribution of the 2 sample population being compared. The sample populations submitted to the F test here are the weighted (z-scored) amplitude values at a given voxel across all subjects specific to either schizophrenia group or healthy controls. The amplitude of a random sample of voxels should thus have a normal distribution, and the voxels identified in statistical test A are also random. These F-test P values were corrected for multiple comparisons using false discovery rate (FDR) correction. Based on our theories put forward henceforth, we expect that the variance of the weighted (z-scored) amplitudes at any given voxel would favor the SZs.

• (5) Simulations: A simple simulation was implemented to test the effect of smoothing 2 groups of data (one with small and one with large variability in the x-axis translation of the sources) with different kernel sizes. Post hoc analysis on the IVA component sources to check for across subject variability was done. A detailed description of the simulated data is presented in the supplementary material.

Results

Based on the correlation between vectorized group-level GICA components and group-averaged IVA components (|r| ≥ 0.6), our results showed that source separation in IVA was similar to GICA and mostly consistent across subjects, which was visually corroborated.²⁸ Twenty-seven component spatial maps were ascertained to be nonartifactual. A few IVA-GL components had multiple GICA component correlations of which only the first instance of correlations was accepted. A detailed description of the component selection process through correlations is presented in the supplementary material along with spatial maps of the 27 components.

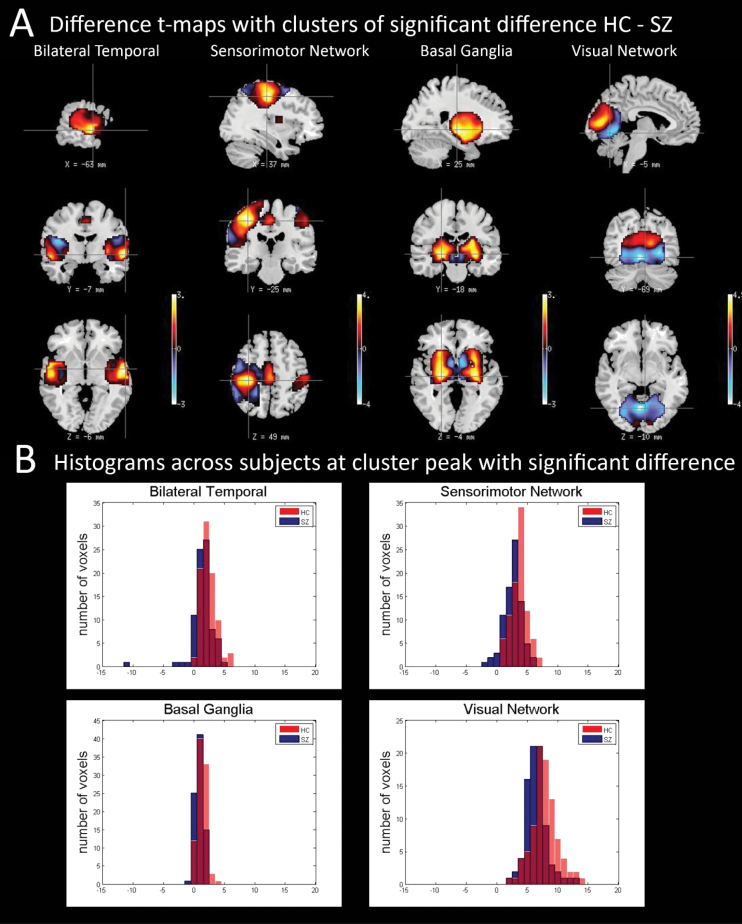
• (1) Test for voxelwise difference in group mean (cluster level t test): Four of the IVA-GL components showed statistically significant cluster-level group differences (P < .01 significance, corrected for multiple comparisons using FWE, HCs > SZs) after masking. The t-scored maps for 2 sample t test of these 4 components, shown in figure 2A, included networks in bilateral temporal (auditory; component number [CN] 19), sensorimotor regions (CN 69), basal ganglia (CN 15), and visual regions (CN 26). Table 1 shows the P values of 2 sample t test on these 4 components for IVA-GL after FWE correction along with the Brodmann areas encompassed by each component. The differences in weighted amplitudes of these components substantiate findings from previous studies and further strengthen an implication of these neuroanatomical areas in schizophrenia.^29–31 We also plotted the amplitude at the voxel of maximum difference for each group for each of these 4 components to ascertain that there existed differences in the observed variance of the groups at these voxels. Figure 2B shows histograms of voxel amplitudes for each group (SZs and HCs) and clearly shows that there exist variance differences even at voxels with mean differences.

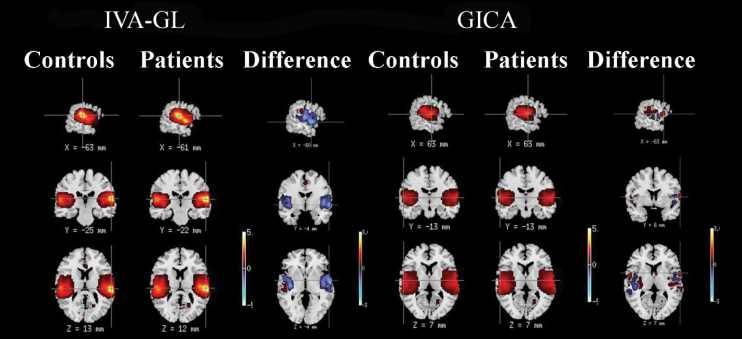
• (2) Test for voxelwise difference in variance (no test): Figure 3 presents the voxelwise variance maps for one representative component, the bilateral temporal component for HCs and SZs along with the difference map between HCs and SZs for IVA-GL and GICA. Simple visual inspection of figure 3 points to evidently larger cross-subject voxelwise variance in component maps estimated by IVA-GL vs. those estimated by GICA. Also, for this component (as it is in most the other components), the SZs have greater variance than the HCs. As expected, IVA-GL captured more variability in the spatial maps than did GICA.

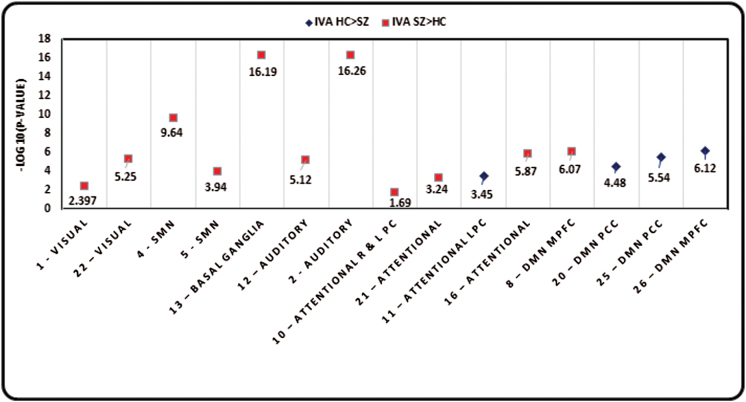
• (3) Test for difference in mean of variance maps of groups (nonparametric t test): Nonparametric tests for difference in the mean of the variance maps for HCs and SZs showed that most of the 27 IVA-GL components show a significant global difference in the mean of variance maps of HCs and SZs. Figure 4 shows negative logarithm of P values for components with a significant difference. Components with HCs > SZs are represented as blue dots and those with SZs > HCs as red dots. A greater variability exists in SZs in sensory networks, whereas there is greater variability in HCs primarily in default mode network (DMN) specifically including the precuneus, posterior cingulate and parts of the parietal cortex and the medial temporal lobe along with some parts of the frontal lobe. However, it is interesting to note that the results also illustrate that different parts of the same network behave somewhat differently from one another. For example, components 8 and 26 represent part of DMN in the medial prefrontal cortex, but the directionality of difference in both is different.

• (4) Test for voxelwise difference of variance between groups (voxelwise F test): Our results validate the hypothesis that SZs have significantly greater variability than HCs in 19 components with at least 30 of the within-mask voxels surviving FDR correction. The direction was found to be SZs > HCs by looking at the variance values for each group in these voxels. These results however provide us with a different facet of understanding variance differences between groups compared with the results presented in C above. In conjunction with other results presented, the interaction of groups in measures of spatial variance seems to provide significant insight into a unique dimension of understanding the disorder.

• (5) Simulations: It was observed through simulations that a basic translation can result in variability in the spatial maps of groups. The group differences in intersubject variability were relatively well preserved in the range of smoothing parameters tested for different types of sources. We also confirmed expectations that a smaller smoothing kernel increases in the variance captured in the dataset.

Fig. 2.

(A) t maps of IVA components with statistically significant difference and corresponding mask used. (B) Histogram of amplitude values at the voxel of maximum difference (between groups) for each group both IVA-GL and group independent-component analysis (GICA) for each of the 4 components with significant difference between groups as featured in figure 2A and table 1. In the histograms, the red-colored plots represent histograms for healthy controls (HCs), and the blue-colored plots represent histograms for schizophrenia patients (SZs). The 2 sample t-test P values and the F-test P values for each of the 4 components at the voxel of maximum difference, respectively, are as follows: Bilateral temporal: t-test P value = .00022 (HC > SZ), F-test P value = .00009 (SZ > HC); Sensorimotor: t-test P value = 3.85×10⁻⁶ (HC > SZ), F-test P value = .457; Basal Ganglia: t-test P value = .00059 (HC > SZ), F-test P value = .3015; and Visual: t-test P value = 1.105×10⁻⁵ (HC > SZ), F-test P value = .1322.

Table 1.

FWE-Corrected P values for IVA-GL Voxelwise Group Differences in the Mean

Component	Brodmann Areas	P values (FWE- Corrected) IVA-GL	Coordinates of Peak Foci	Size of Cluster (No. of Voxels)
Bilateral Temporal Component 19	Superior temporal gyrus (BA: 13, 22, 41)	.042	(63, −6, −6)	542
	Transverse temporal gyrus (BA: 41, 42)
	Insula (BA: 13, 40)
Sensorimotor Network Component 69	Postcentral gyrus (BA: 1, 2, 3, 5, 40)	.016	(−36, −24, 48)	724
	Inferior parietal lobule (BA: 40)
	Precentral gyrus (BA: 4, 6)
Basal Ganglia Component 15	Lentiform nucleus	.000	(−24, −18, −6)	1329
	Caudate
	Claustrum
Visual Network Component 26	Cuneus (BA: 17, 18, 23, 30)	.004	(0, −84, 6)	936
	Lingual gyrus (BA: 17, 18, 19)

Note: FEW, family wise error; IVA-GL, independent vector analysis Gaussian/Laplace density model.

Fig. 3.

Variance maps for patients and controls as well as the difference in the variance maps (HCs − SZs) for the bilateral temporal component for both IVA-GL and GICA.

Fig. 4.

P values for nonparametric test for difference in variance maps of HCs and SZs for all components that have a significant difference P < .05 which is the same as −log10 (P) > 1.301.

Discussion

Networks extracted from resting fMRI data by blind-source separation techniques such as GICA present spatial and temporal sources representing brain areas that are shown to correlate with the presence of schizophrenia and other brain disorders.³² In this study, we used the IVA-GL as an approach to estimate subject-level functional network spatial maps (similar to the ones from GICA) that enable us to focus on predictions regarding subject-level spatial variability. We were able to examine differences in identified functional networks in SZs compared to HCs and our detection of significant voxelwise differences in weighted amplitude (see figure 2, table 1, and test A) in components representing basal ganglia, bilateral temporal, sensorimotor, and visual networks provides a new perspective on the implication of these regions in schizophrenia from earlier studies.^29–31,33 It is noteworthy that no significant voxelwise weighting differences were found in the highly implicated DMN, which is potentially related to the subtle spatial but significant temporal/spectral changes reported in previous work.³⁴ The histograms in figure 2B corroborate our intuitive supposition that SZ functional network maps would be more internally variable than those of HCs spatial maps, contributing to differences between groups. We were also able to identify significant group differences in spatial variability of SZs and HCs in most of the nonartifactual components (test B, C, and D). It is interesting that using a test for difference in the mean of the across-subject variance values; test C exhibits that the components representing the DMN with a few frontal areas show greater variance in HCs whereas the sensory components including auditory, sensorimotor, basal ganglia, and the visual network show greater variance in SZs based on a global measure of variance difference between the groups (figure 4; test C). Concurrently, it has been shown that different parts of the same network may behave differently while considering mean differences in the variance maps between groups. This highlights that variance measures present us with previously unidentified differences within a given network. On the other hand, test D presents that at a voxel level, the SZs encompass a greater variability at the group level than the HCs. These tests quantify different measures of variance differences between groups and thus present results that are diverse but complementary to one another.

Schizophrenia is known to be a complex disorder that is expressed heterogeneously within the population.^35,36 Although many theories exist on the pathological and molecular processes underlying the disease, no single theory has yet emerged as the consensus explanation. Based on empirical evidence from previous fMRI studies, some have proposed a disruption in cognitive circuitry between the prefrontal regions, the thalamic nuclei, and the cerebellum.^35,37 It is essential to acknowledge that this disruption in brain circuitry however does not manifest consistently in the diseased population, which may be a factor introducing variability within the population. Furthermore, one might expect that the reported variability in disease etiology, when combined with spatial variability in the functional activation patterns in the brain, results in increased variability in networks. This extensive symptomatic and behavioral variability among schizophrenic patients makes identifying loci of variability in brain imaging data both interesting and important.^5,38,39

The results obtained using different measures of spatial variance are consistent with the above described theories, which predict cognitive dysregulation that might be expressed variably within the population. The results motivate us to look deeper into these divergent effects. Nevertheless, we would be remiss to not consider the limitations the field is dealing with while presenting such analyses that include but are not limited to the smoothing kernel size. A change in the size of the smoothing kernel will affect the variance captured in the data and in turn the statistical significance of the differences observed, which was verified through the simulations presented. Given that a larger smoothing kernel results in less resolution, decreasing the smoothing kernel would in general tend to increase the variance captured in the data. The particular smoothing kernel size used for this study had been used previously in GICA-based analysis of this data⁴⁰ where it provided robust results,^{41 ,[i–k]} and this consistency with previous studies allowed us to make reasonable comparisons with the GICA spatial maps.

It is also noteworthy that, until now, the established multivariate analysis techniques (including IVA) have not been extensively applied to evaluating the group effects on spatial variability in network spatial maps. It is also important to consider that the factors permitting greater variance retention in IVA-GL compared with GICA are methodological. IVA-GL requires a single PCA reduction compared with 2 PCA steps in GICA. Combined with the fact that IVA-GL computes components separately for each subject, the retained variability is compounded. In spite of the evident advantages of spatial variability to bringing out differences between groups, it is also important to continue to study the relationship between the amount of spatial and temporal variability captured, as well as the implications of the algorithm use on the specific questions of interest. Currently, it appears that IVA has strength in capturing spatial variability in a group model, whereas it is known that GICA has strength in capturing temporal variability.²⁸ It is possible that additional approaches will be developed, which combine these strengths (eg, the use of spatially constrained ICA as a back-reconstruction step for GICA is quite promising in this regard^{42 ,[l]}). In this work, our primary focus was the spatial variability of these networks. The temporal aspects are of obvious interest and will be investigated in the future work.

In summary, our analyses focused on the within- and across-population spatial stability of estimated functional networks in SZs and HCs, shedding new light on how schizophrenia, a disease with widespread effects on cognitive and emotional functioning, maps onto the spatial features of brain function. The networks exhibiting the greatest differences in spatial variability, such as the sensorimotor network, bilateral temporal network, and so on, interestingly, have been previously implicated in other ways in schizophrenia, though not specifically with respect to spatial variation in resting fMRI spatial maps.^{29 ,[m,n]} These results are consistent with but at the same time significantly extend results of previous studies of schizophrenia using multivariate analyses techniques.^{33 ,[o]} In this case, the retention of individually distinctive features appears to sharpen our ability to detect group differences in most of the implicated networks. When pooled with our observation of a division between the DMN and the rest of the networks involved in the subject-level variance as presented in test C and figure 4, this is a novel finding. It points us to additional studies of these specific networks in order to better understand the underlying neurobiological cause of the spatial variability in the patients.

Moreover, in terms of patient selection, this study only incorporated a small subset of the population with schizophrenia diagnoses. This points us to further and more rigorous evaluations of the effect of heterogeneous manifestations of the condition on network spatial variability. Quantifying the spatial distribution of intersubject variability offers potentially novel insights into functional loci of influencing differential symptomatic presentations of schizophrenia. A more detailed understanding of spatial differences in patient functional networks may ultimately lead to a better understanding of schizophrenia itself by means of pointing us to an improved model of the disease, as well as likely identifying areas possibly related to variability in behavior.

Supplementary Material

Supplementary material is available at http://schizophreniabulletin.oxfordjournals.org. The references “[a]--[o]”, cited in the text refers to the bibliography data provided in the supplementary material.

Funding

National Institutes of Health’s Center of Biomedical Research Excellence (5P20GM103472); National Science Foundation’s Information and Intelligent Systems (1017718); Computing and Communication Foundations (1117056).