CLAMMS: a scalable algorithm for calling common and rare copy number variants from exome sequencing data

Abstract

Motivation: Several algorithms exist for detecting copy number variants (CNVs) from human exome sequencing read depth, but previous tools have not been well suited for large population studies on the order of tens or hundreds of thousands of exomes. Their limitations include being difficult to integrate into automated variant-calling pipelines and being ill-suited for detecting common variants. To address these issues, we developed a new algorithm—Copy number estimation using Lattice-Aligned Mixture Models (CLAMMS)—which is highly scalable and suitable for detecting CNVs across the whole allele frequency spectrum.

Results: In this note, we summarize the methods and intended use-case of CLAMMS, compare it to previous algorithms and briefly describe results of validation experiments. We evaluate the adherence of CNV calls from CLAMMS and four other algorithms to Mendelian inheritance patterns on a pedigree; we compare calls from CLAMMS and other algorithms to calls from SNP genotyping arrays for a set of 3164 samples; and we use TaqMan quantitative polymerase chain reaction to validate CNVs predicted by CLAMMS at 39 loci (95% of rare variants validate; across 19 common variant loci, the mean precision and recall are 99% and 94%, respectively). In the Supplementary Materials (available at the CLAMMS Github repository), we present our methods and validation results in greater detail.

Availability and implementation: https://github.com/rgcgithub/clamms (implemented in C).

Contact: jeffrey.reid@regeneron.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Detecting copy number variants (CNVs) with whole exome sequencing data is challenging because CNV breakpoints are likely to fall outside of the exome. Almost all CNV-calling algorithms for whole exome sequencing base their calls on read depths within the CNV, which are linearly correlated to copy number state. Previously published algorithms include CoNIFER (Krumm et al., 2012), XHMM (Fromer et al., 2012), ExomeDepth (Plagnol et al., 2012) and CANOES (Backenroth et al., 2014).

Depth-of-coverage is subject to both systematic biases (often related to sequence GC-content) and stochastic volatility (which is exacerbated by variation in input DNA quality). CNV callers must normalize coverage data to correct for systematic biases and characterize the expected coverage profile given diploid copy number, so that true CNVs can be distinguished from noise. Variability in sample preparation and sequencing procedures result in additional coverage biases, often referred to as ‘batch effects’.

CoNIFER and XHMM use principal components analysis to identify and remove systematic biases, while ExomeDepth and CANOES handle bias by normalizing each sample’s coverage against the average in a small, ‘custom’ reference panel of samples with coverage profiles that are highly correlated to the individual sample in question. Both strategies have quadratic time complexity and large RAM requirements.

Each of these algorithms assumes that reference panel samples are always diploid (presenting a unimodal coverage distribution at each exon), resulting in inaccurate genotypes at common CNV loci. They can also mistake population stratification of common CNVs for batch effects if true batch effects are minimal.

2 Algorithm

The CLAMMS algorithm has three steps, outlined in Figure 1.

1. Coverage values for individual samples are normalized independently to correct for GC-amplification bias and overall average depth-of-coverage. Low-mappability regions are filtered altogether, as the read depths in these regions do not accurately represent the sequence dosage in the genome.

2. Given a reference panel of samples, a finite mixture model is fit for each exome capture region. Each mixture component models the expected distribution of coverage across samples for a particular integer copy number state. Model parameters will vary from exon to exon, correcting for additional non-GC-related coverage biases. Exome-wide, copy numbers 0–3 are considered; in known duplication regions, copy numbers 4–6 are considered as well (see Supplement Section S1.3).

3. CNVs are called for individual samples using a hidden Markov model (HMM). The input sequence to the HMM is the sample’s normalized coverage values for each region. Emission probabilities are based on the trained mixture models and transition probabilities are similar to those used by XHMM.

Fig. 1.

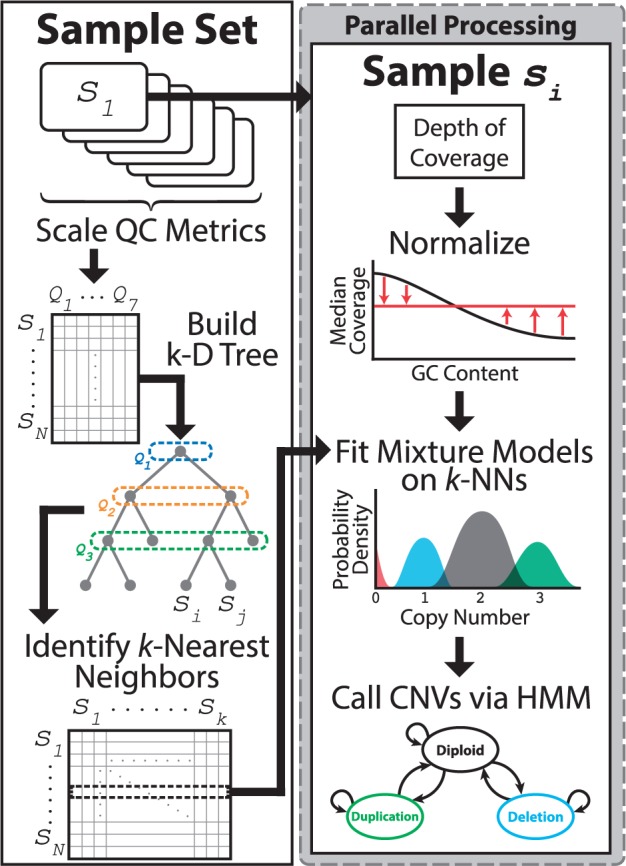
Overview of the CLAMMS CNV-calling pipeline. A reference panel is selected for each sample based on seven sequencing QC metrics using an efficient k-d tree data structure. After selecting reference panels, each sample and its corresponding reference panel may be processed in parallel across processes and/or servers, requiring only ∼50 MB of RAM per process

The details of each step are described in the Supplementary Material. Mixture models allow for copy number polymorphic loci to be handled naturally, while the HMM incorporates the prior expectation that nearby anomalous signals are more likely to be part of a single CNV than multiple small CNVs. Mixture models have previously been used by Genome STRiP (a CNV caller for whole-genome data, Handsaker et al., 2015), and XHMM, ExomeDepth and CANOES use HMMs; but to our knowledge, no previous CNV-calling algorithm has integrated both in a single probabilistic model.

Similar to CANOES and ExomeDepth, we handle data heterogeneity by selecting a ‘custom’ reference panel for each sample. Our CNV calling pipeline (discussed further in the Supplementary Material) works as follows:

1. We define a distance metric between samples based on seven sequencing quality control metrics from Picard (http://broadinstitute.github.io/picard).

2. Each newly sequenced sample is added to a k-d tree in this metric space. CNVs are called using a reference panel consisting of the sample’s 100 nearest neighbors, which are found efficiently using the k-d tree.

Indexing n samples and finding the k nearest-neighbors for each sample takes O(kn log n) time. Once the nearest neighbors have been found, calling CNVs for the n samples takes O(kn) time, so the complexity of the whole pipeline is O(kn log n). This improves on the O(n²) complexity of previous algorithms, which all compare the coverage profile of each sample to every other sample.

3 Validation

We performed computational and biological validations to compare the performance of CLAMMS and previous algorithms. We summarize our results here; details are provided in the Supplementary Material.

First, we used CLAMMS, XHMM, CoNIFER, CANOES and ExomeDepth to call CNVs for an eight-member pedigree, sequenced in three technical replicates. Ninety-two additional samples were provided as a reference panel. By definition, most CNVs in the pedigree are common variants. CLAMMS called a mean of 13.5 CNV/sample. Ninety-five percent of its calls in children were inherited and 92% of calls were consistent across all technical replicates. XHMM, CoNIFER and CANOES were insensitive to common variants; ExomeDepth is sensitive, but $<2/3$ of its calls were inherited.

Second, we compared CNV calls from each algorithm (except CANOES, which ran out of memory on a server with 30 GB RAM) against ‘gold-standard’ calls from microarrays (PennCNV, Wang et al., 2007) for 3164 samples. We limited this analysis to rare variants (AF $\le$ 0.1%) to avoid false positives related to batch effects in the array data. Using high-quality array-based rare-variant calls as the ground-truth, CLAMMS had the best performance (F-score 6.6% higher than ExomeDepth, 9.3% higher than XHMM and over double that of CoNIFER).

Finally, we used TaqMan quantitative polymerase chain reaction to validate a random subset of CNVs predicted by CLAMMS at 20 rare variant loci and 19 common variant loci that overlap disease-associated genes in the Human Gene Mutation Database (not limited to genes associated with CNVs; 7 430 disease genes in total; Stenson et al., 2012); 19/20 (95%) rare variants were validated. At the common variant loci, CLAMMS genotypes achieved mean precision/recall values of 99.0% and 94.0%, respectively. ExomeDepth also had near-perfect performance for mid-frequency CNVs but had inaccurate genotypes at highly polymorphic loci (see Supplementary Table S5).

Funding

This research was supported by the Regeneron Genetics Center.

Conflict of Interest: none declared.