Abstract
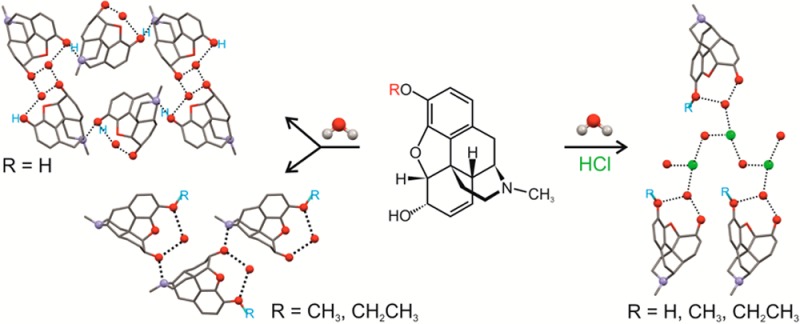
Morphine, codeine, and ethylmorphine are important drug compounds whose free bases and hydrochloride salts form stable hydrates. These compounds were used to systematically investigate the influence of the type of functional groups, the role of water molecules, and the Cl– counterion on molecular aggregation and solid state properties. Five new crystal structures have been determined. Additionally, structure models for anhydrous ethylmorphine and morphine hydrochloride dihydrate, two phases existing only in a very limited humidity range, are proposed on the basis of computational dehydration modeling. These match the experimental powder X-ray diffraction patterns and the structural information derived from infrared spectroscopy. All 12 structurally characterized morphinane forms (including structures from the Cambridge Structural Database) crystallize in the orthorhombic space group P212121. Hydrate formation results in higher dimensional hydrogen bond networks. The salt structures of the different compounds exhibit only little structural variation. Anhydrous polymorphs were detected for all compounds except ethylmorphine (one anhydrate) and its hydrochloride salt (no anhydrate). Morphine HCl forms a trihydrate and dihydrate. Differential scanning and isothermal calorimetry were employed to estimate the heat of the hydrate ↔ anhydrate phase transformations, indicating an enthalpic stabilization of the respective hydrate of 5.7 to 25.6 kJ mol–1 relative to the most stable anhydrate. These results are in qualitative agreement with static 0 K lattice energy calculations for all systems except morphine hydrochloride, showing the need for further improvements in quantitative thermodynamic prediction of hydrates having water···water interactions. Thus, the combination of a variety of experimental techniques, covering temperature- and moisture-dependent stability, and computational modeling allowed us to generate sufficient kinetic, thermodynamic and structural information to understand the principles of hydrate formation of the model compounds. This approach also led to the detection of several new crystal forms of the investigated morphinanes.
Keywords: morphine, codeine, ethylmorphine, dionine, hydrate, crystal polymorphism, crystal structure, lattice energy calculations, thermal analysis, differential scanning calorimetry, isothermal calorimetry, moisture sorption/desorption, X-ray diffraction, IR spectroscopy
1. Introduction
Hydrate formation in molecular compounds is an important phenomenon encountered in many applications, which has also implications for our fundamental understanding of the assembly of molecules in the solid state. Hydrates are often unavoidable when materials are prepared, processed, stored, or used, and therefore they impact the economy of many fine-chemical processes. Water adducts (hydrates) are of high practical importance in drug manufacturing since many processing steps are carried out in the presence of water or moisture (e.g., crystallization, lyophilization, wet granulation, aqueous film-coating, storage, etc.).1 The incorporation of water usually changes the properties of a substance significantly.2−4 Two of the most important aspects are the lower water solubility and dissolution rate of a hydrate compared to the corresponding anhydrous form(s). Moreover, the chemical stability of a hydrate can be different from that of the corresponding water-free form(s). Therefore, the search for potential hydrates and the determination of possible transformation pathways5−7 between the different forms is a crucial part in the development of a drug product.8−10 The presence of water (moisture) in a system alone is not sufficient to trigger hydrate formation, as the activity of water in the crystallizing medium determines whether or not a hydrate will form.11 The occurrence of organic hydrates as well as their stability still remains unpredictable. Statistical surveys indicate that the tendency toward hydrate formation is particularly high when charged groups (salts) or polar functional groups are present.12−14 However, even for types of molecules prone to form hydrates it is not certain whether a hydrate will exist, let alone its stoichiometry,15 i.e., the compound/water ratio. Because of its small size, water can fill structural voids, and it is also an agent with multidirectional hydrogen-bonding capabilities that links molecules into stable crystal structures.1 Indeed, water molecules often stabilize crystal structures when there is an imbalance between the numbers of acceptor and donor groups,16 and a hydrate can be the preferred crystal form of an active pharmaceutical ingredient (API).17
To obtain a better understanding of hydrate formation phenomena in organic (drug) compounds we are expanding our previous studies on phenols18,19 and hydroxycarboxylic acids20,21 with a systematic study of the free bases morphine (M), codeine (C), ethylmorphine (dionine, D), and their hydrochloride salts (Figure 1). The common structural characteristic of these compounds is the rigid morphinan skeleton. All of these six model compounds are important drug substances, which are officinal in the European22 and/or the United States Pharmacopeia23,24 (except for M). By relating the structural, thermodynamic, and kinetic properties of the observed hydrates and water-free forms with the results from theoretical calculations, we expect to obtain a deeper insight into the phenomenon of hydrate formation.
Figure 1.
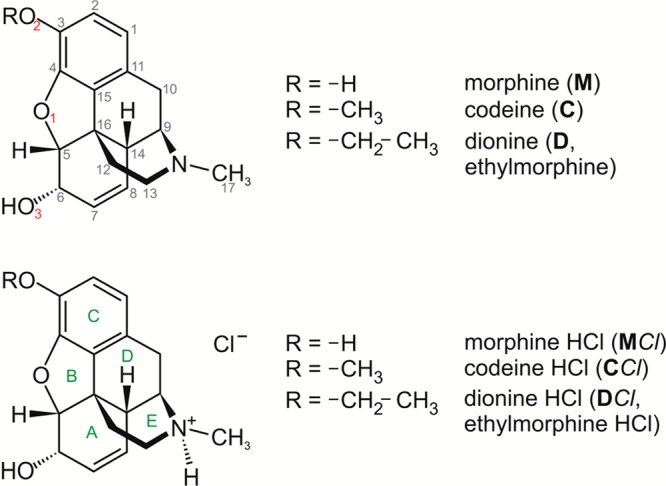
Molecular structures of morphine, codeine, ethylmorphine (dionine), and their HCl salts.
The medical usage of opioids dates back thousands of years to the use of opium, the dried latex of the opium poppy (Papaver somniferum).25M ((5α,6α)-7,8-didehydro-4,5-epoxy-17-methylmorphinan-3,6-diol), the principal alkaloid of opium, is a highly potent analgesic drug. C ((5α,6α)-7,8-didehydro-4,5-epoxy-3-methoxy-17-methylmorphinan-6-ol) is used as a narcotic analgesic for various indications, such as cough, diarrhea, mild to moderate pain, and irritable bowel syndrome.26D ((5α,6α)-7,8-didehydro-4,5-epoxy-3-ethoxy-17-methylmorphinan-6-ol) acts as a narcotic analgesic and antitussive. In 2011, the global manufacture of morphine was 440 tons, 90% of which was converted into other opiates such as codeine and ethylmorphine (in 2011 the world production was 281 tons and 1 ton, respectively).27
Previous solid state characterization studies28−33 of the compounds of our study were mainly based on thermomicroscopical techniques or differential scanning calorimetry (DSC), and the literature contains structural information for a number of crystal forms (Table 1).
Table 1. Overview of Thermochemical and Structural Investigations of M, C, D and Their HCl Saltsa.
| compd | anhydrates | hydrates | |
|---|---|---|---|
| Morphine (M) | M-I° | M-II | M-1H |
| Kofler and Kofler28−30 | mp 240 °Cb (dec.c) | mp 197 °C | existence of a hydrate |
| Kuhnert-Brandstaetter31 | mp 245–255 °C | mp 197 °C | dehy.d 115–140 °C |
| CSD Refcode family34 | Guguta et al.35,e | MORPHM37,38 | |
| MORPIN0136 | MORPIN39,f | ||
| Codeine (C) | C-I° | C-1H | |
| Kofler and Kofler29,30 | mp 155 °C | mp 62–68 °C | |
| Kuhnert-Brandstaetter31 | mp 156 °C | dehy.d | |
| CSD Refcode family34 | ZZZTSE40−43 | ZZZTZQ (unit cell)40 | |
| ZZZTZQ 01(without H)42 | |||
| Ethylmorphine (D) | D-I° | D-1H | |
| Kuhnert-Brandstaetter31 | Sluggish melting, softening | ||
| Morphine HCl (MCl) | MCl-I° | MCl-II | MCl-3H |
| Kofler and Kofler29,30 | mp > 300 °C (dec.c) | trihydrate | |
| Lindpainter32 | mp 295–300 °C | mp 280–284 °C | |
| Kuhnert-Brandstaetter31 | mp 285–320 °C | dehy.d at 80 °C | |
| CSD Refcode family34 | Guguta et al.35,e | MORPHC45 | |
| EFASAH44 | |||
| Codeine HCl (CCl) | CCl-I° | CCl-2H | |
| Kuhnert-Brandstaetter31 | 280–292 °C (dec.c) | partial melting at 165–170 °C | |
| inhom. melting 140–160 °Cg | |||
| Kuhnert-Brandstaetter33 | 290 °C (N2 purge) | mp 140–150 °C (hom.i) | |
| CSD Refcode family34 | ZZZRFQ46,h | ||
| Ethylmorphine HCl (DCl) | DCl-I | DCl-2H | |
| Kuhnert-Brandstaetter31 | 170–174 °C | 148–155 °C (viscous melt) | |
| Kuhnert-Brandstaetter33 | mp 122–125 °C | ||
Anhydrate forms are denoted with roman numerals and hydrates according to stoichiometry, e.g., 2H indicates a dihydrate (see also section 1 of the Supporting Information).
The same phase exhibits different morphologies.
dec: decomposition.
dehy: dehydration.
Structure solved from PXRD data, not in the Cambridge Structural Database (CSD34).
Unit cell parameters reported for anhydrous morphine correspond to those of the monohydrate, as previously noted by Guguta et al.35
inhom: inhomogeneous, the authors have corrected the dihdyrate melting point to 140–160 °C.33 In earlier publications, liquefication of the compound was incorrectly described as the melting event of the hydrate31,47
No atomic coordinates.
hom: homogeneous.
To connect structural features with relevant properties, in particular stability, we investigated the (de)hydration mechanisms of the compounds using a range of multidisciplinary experimental and computational techniques, i.e., hot-stage microscopy, differential scanning calorimetry, isothermal calorimetry (RH perfusion), thermogravimetric analysis, X-ray diffractometry (powder and single crystal), infrared spectroscopy, and moisture sorption/desorption analysis. Single crystal structures of codeine monohydrate (C-1H), ethylmorphine monohydrate (D-1H), codeine HCl anhydrate I° (CCl-I°), codeine HCl dihydrate (CCl-2H), and ethylmorphine HCl dihydrate (DCl-2H) are reported. Furthermore, potential crystal structures of a morphine HCl dihydrate (MCl-2Hcalc) and an ethylmorphine anhydrate (D-Icalc) were derived from computational dehydration modeling. For all six compounds, the temperature- and moisture-dependent relationships between anhydrous and hydrated forms have been established (section 9 of the Supporting Information). The experimental results were complemented by computational modeling, i.e., interaction energy and lattice energy calculations. Only the combination of all these techniques allowed us to comprehend the complexity of the different (de)hydration mechanisms of the model compounds.
2. Experimental Section
2.1. Materials and Preparation of the Solid Forms
M and MCl were obtained from Heilmittelwerke Wien (A); codeine phosphate from Siegfried (CH) and was used for preparing C by adding 1 N NaOH to a saturated aq. codeine phosphate solution; CCl, D, and DCl from Merck, Darmstadt (D).
The hydrate phases were prepared (i) by slowly cooling a saturated solution (at 100 °C) of each compound in water to room temperature and (ii) liquid assisted grinding experiments of the compounds with a few drops of water in a grinding mill (Retsch Schwingmuehle MM301, Retsch, D).
The stable anhydrates (thermodynamic room temperature forms), denoted with superscript ″o″, were obtained by drying the hydrates at 130 °C (M and C) or 200 °C (MCl and CCl) for 30 min. MCl-III, CCl-II, and D-I° were produced by drying the respective hydrate over P2O5 (0% RH). M-II and MCl-II were only obtained concomitantly in sublimation experiments and C-II by quench cooling the melt of codeine.
2.2. Single Crystal X-ray Diffraction
Single crystals of C-1H and D-1H were obtained from cooling crystallization experiments from water, CCl-I° by crystallization from acetonitrile, CCl-2H from an EtOH/water (1:1) mixture, and DCl-2H by solvent evaporation from 2-propanol. Essential crystal data are collected in Table 2 and Table S14 of the Supporting Information. The data for C-1H and DCl-2H (Cu radiation; λ = 1.5418 Å) and D-1H and CCl-I° (Mo radiation; λ = 0.7107 Å) were collected on an Oxford Diffraction Gemini-R Ultra diffractometer operated by CrysAlis software.48 Data for CCl-2H were recorded on a Rigaku AFC12 goniometer driven by the CrystalClear-SM Expert 3.1 b27 software (Rigaku, 2012) and equipped with an enhanced sensitivity (HG) Saturn724+ detector mounted at the window of an FR-E+ Super Bright Mo rotating anode generator with HFVarimax optics.49 The structures were solved by direct methods (SIR201150 or SHELXL201351) and refined by full-matrix least-squares on F2 using SHELXL2013 and the program package WinGX.52 The treatment of the H atoms is reported in section 4.2 of the Supporting Information.
Table 2. Crystallographic Data and Details of Crystal Structure Determinations.
| phase designator | C-1H | D-1H | CCl-I° | CCl-2H | DCl-2H |
|---|---|---|---|---|---|
| compound | C18H21NO3·H2O | C19H23NO3·H2O | C18H22NO3+·Cl– | C18H22NO3+·Cl–·2H2O | C19H24NO3+·Cl–·2H2O |
| formula weight | 317.37 | 331.40 | 335.82 | 371.85 | 385.87 |
| crystal system | orthorhombic | orthorhombic | orthorhombic | orthorhombic | orthorhombic |
| space group | P212121 | P212121 | P212121 | P212121 | P212121 |
| Z/Z′ | 4/1 | 4/1 | 4/1 | 4/1 | 4/1 |
| a (Å) | 10.3994(2) | 7.08246(18) | 7.14435(17) | 6.7621(5) | 6.8715(2) |
| b (Å) | 12.5671(2) | 13.1493(3) | 13.2304(3) | 12.9315(9) | 13.3924(4) |
| c (Å) | 12.0640(2) | 18.0581(5) | 16.5408(4) | 20.3080(14) | 20.4176(5) |
| unit cell volume (Å3) | 1576.65(5) | 1681.74(7) | 1563.48(6) | 1775.8(2) | 1878.95(9) |
| temperature (K) | 173(2) | 173(2) | 173(2) | 123(2) | 123(2) |
| data/parameters | 2833/223 | 3295/232 | 3062/218 | 3492/272 | 3360/259 |
| final R1 value [I > 2σ(I)] | 0.0300 | 0.0308 | 0.0298 | 0.0257 | 0.0397 |
| final wR(F2) value (all data) | 0.0789 | 0.0738 | 0.0739 | 0.0647 | 0.1085 |
| CCDC no. | 1001238 | 1001241 | 1001240 | 1001239 | 1001242 |
2.3. Powder X-ray Diffraction (PXRD)
PXRD patterns were recorded in transmission geometry on an X’Pert PRO diffractometer (PANalytical, Almelo, NL) equipped with a theta/theta coupled goniometer, programmable XYZ stage with well plate holder, Cu–Kα1,2 radiation source with a focusing mirror, 0.5° divergence slit and 0.02° Soller slit collimator on the incident beam side, 2 mm antiscattering slit and 0.02° Soller slit collimator on the diffracted beam side, and solid state PIXcel detector (tube voltage 40 kV, tube current 40 mA, 2θ step size 0.013°, 40 or 80 s per step, 2θ range 2° to 40°). For nonambient RH measurements a VGI stage (VGI 2000M, Middlesex, U.K.) was used.
2.4. Gravimetric Moisture Sorption/Desorption Analysis (GMS)
Moisture sorption and desorption studies were performed with the automatic multisample gravimetric moisture sorption analyzer SPS23-10 μ (Proumid, Ulm, D). Approximately 50–150 mg of the compounds were used for the investigations. The measurement cycles were started either at 40% or 0% relative humidity (RH), applying different sorption/desorption programs as detailed in the Supporting Information (Table S13). The equilibrium condition for each step was set to a mass constancy of ±0.001% over 60 min.
2.5. Hot-Stage Microscopy (HSM)
A Reichert Thermovar polarization microscope equipped with a Kofler hot-stage (Reichert, A) was used for hot-stage thermomicroscopic investigations. Photographs were taken with an Olympus DP71 digital camera (Olympus, D).
2.6. Differential Scanning Calorimetry (DSC)
DSC thermograms were recorded on a DSC 7 or Diamond DSC equipped with a Controlled Cooling Accessory (Intracooler 1P), controlled by the Pyris 7.0 software (PerkinElmer, Norwalk, CT, USA). A few milligrams of accurately weighed (Mettler UM3 ultramicrobalance) sample were heated in perforated or sealed Al-pans (30 μL) or sealed gold plated stainless steel high-pressure capsules. Heating rates from 1.5 to 100 °C min–1 were applied. The instruments were calibrated for temperature with pure benzophenone (mp 48.0 °C) and caffeine (mp 236.2 °C), and the energy calibration was performed with pure indium (mp 156.6 °C, heat of fusion 28.45 J g–1). The quoted error on temperature (extrapolated onset temperature) and enthalpy values correspond to 95% confidence intervals (derived from at least three measurements).
2.7. Thermogravimetric Analysis (TGA)
Thermogravimetric analysis (TGA) was carried out with a TGA7 system (PerkinElmer, USA) using the Pyris 2.0 software. Approximately 3–5 mg of sample was weighed into a platinum pan. A two-point calibration of the temperature was performed with ferromagnetic materials (Alumel and Ni, Curie-point standards, PerkinElmer). Heating rates ranging from 2 to 20 °C min–1 were applied, and dry nitrogen was used as a purge gas (sample purge, 20 mL min–1; balance purge, 40 mL min–1).
2.8. Isothermal Calorimetry (IC, RH-Perfusion Cell)
RH perfusion calorimetry experiments were performed with the TAM III nanocalorimeter unit in a 4 mL stainless steel RH perfusion ampule. The relative humidity was controlled with two mass flow controllers, and dry N2 was used as carrier gas at a constant flow rate of 100 mL h–1. Approximately 10–25 mg of sample was used. The humidity profiles (% RH vs time) were executed as follows: 0 to 90% RH in one step (M-I°), 60 to 95% RH in one step (M-I° and CCl-I°), 40 to 0% and 0 to 40% RH in one step each (D-1H), and 95 to 5% RH in one step (MCl-3H). The RH perfusion cell was calibrated with saturated solutions of NaCl (75.3% RH), Mg(NO3)2 (52.8% RH), and LiCl (11.3% RH). The heat flow of the empty RH perfusion ampule (baseline runs with the same humidity steps) was subtracted from the heat flow of the sample measurement. The errors on the stated (de)hydration enthalpy values are calculated at the 95% confidence intervals (CI) based on three measurements.
2.9. Infrared Spectroscopy (IR) and Principal Component Analysis (PCA)
FT-IR spectra were recorded with a Bruker IFS 25 spectrometer connected to a Bruker IR microscope I with a 15×-Cassegrain-objective (Bruker Analytische Messtechnik GmbH, Ettlingen, Germany). The samples were prepared on ZnSe discs. Nonambient temperature spectra were heated with a Bruker heatable accessory holder, and the following measurement conditions were applied: spectral range 4000 to 600 cm–1, resolution 4 cm–1, and 32 or 64 interferograms per spectrum.
PCA was used to interpret the changes in the IR spectra during heating (dehydration) experiments. Data were processed using Simca-P53 (version 11.0, Umetrics AB, Umea, Sweden). The spectral data were preprocessed using min–max normalization (Opus version 5.5,54 Bruker Optics, Ettlingen, Germany), and first derivatives were calculated using Simca-P. The spectral regions of 3700 to 2400 and 1680 to 600 cm–1 were used for constructing the PCA models.
2.10. XPac Studies
Crystal packing comparisons were carried out using the program XPac,55 and quantitative dissimilarity parameters were generated as described in ref (56). The pairwise comparisons of crystal structures were based on geometrical parameters generated from the positions of 20 atoms of the morphinane moiety (all non-H atoms except for C17 and R, see Figure 1). Water molecules and chloride anions have not been considered in this analysis. Detailed information on corresponding lattice parameters and dissimilarity indices associated with the identified supramolecular constructs55 (SCs) are given in Tables S16–S20 of the Supporting Information.
2.11. Computer Model for Relative Energy Differences (Lattice Energies)
Periodic electronic structure calculations were carried out with the CASTEP plane wave code57 using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) exchange-correlation density functional58 and ultrasoft pseudopotentials,59 with the addition of a semiempirical dispersion correction (Tkatchenko and Scheffler,60 TS). For further details, see section 11 of the Supporting Information.
Conformational energy differences were calculated at the MP2/6-31G(d,p) level using the polarizable continuum model61 (PCM, dielectric constant ε = 3, a value typical of organic crystals62), as implemented in Gaussian09.63
The computationally generated structures were compared using the Molecular Similarity Module in Mercury64 to determine the root-mean-square deviation of the non-hydrogen atoms in a cluster of n molecules (rmsdn).
3. Results and Analysis
3.1. Crystal Structures
3.1.1. Hydrogen Bond Structures
In this section, the crystal structures of C-1H, D-1H, CCl-I°, CCl-2H, and DCl-2H, which have been determined in this study and will be discussed together with the previously reported experimental structures of M-I°,36M-1H,38C-I°,40−43MCl-I°,44 and MCl-3H45 (hydrogen positions have been optimized, see section 3.4.4) and the computationally generated structures of dionine (D-Icalc, see section 3.4.2) and morphinium hydrochloride dihydrate (MCl-2Hcalc, see section 3.4.4). All these crystal structures have the space group P212121, and their asymmetric units consist of one formula unit. The molecules of M, C, and D are geometrically very similar, each consisting of the same rigid skeleton of five fused rings, with minor differences arising from their different −OR substituents on the phenyl ring (Figure 1). Each of the investigated 12 phases is characterized by a specific combination of available functionalities that may be employed as hydrogen bond donor (D) or acceptor (A) sites. An overview of the theoretically possible as well as the utilized D/A combinations in each crystal structure is given in Table 3.
Table 3. Matrix of the Observed and Theoretically Possible Connections between H-Bond Donor (D; Rows) and H-Bond Acceptor (A; Columns) Functions in Crystal Structures of Morphinanes.
| possible H-bond acceptor sitesa | ||||||||
|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | N | Cl | w1 | w2 | w3 | |
| Structure: M-I° | ||||||||
| O3–H | S | X | • | • | ||||
| O2–H | • | • | X | • | ||||
| Structure: M-1H | ||||||||
| O3–H | • | • | • | • | X | |||
| O2–H | • | • | • | X | • | |||
| w1 | • | X | X′ | • | • | |||
| Structure: C-I° | ||||||||
| O3–H | S | • | • | • | ||||
| Structure: Dcalc | ||||||||
| O3–H | • | • | • | X | ||||
| Structures: C-1H and D-1H | ||||||||
| O3–H | • | • | • | X | • | |||
| w1 | • | X | X | • | • | |||
| Structure: MCl-I° | ||||||||
| O3–H | • | • | • | X | ||||
| O2–H | • | • | • | X | ||||
| N–H | • | • | • | X | ||||
| Structure: CCl-I | ||||||||
| O3–H | • | • | • | X | ||||
| N–H | • | • | • | X | ||||
| Structures: CCl-2H and DCl-2H | ||||||||
| O3–H | • | • | • | • | X | • | ||
| N–H | • | • | X | • | • | • | ||
| w1 | • | X | • | X′ | • | • | ||
| w2 | • | • | • | XX′ | • | • | ||
| Structure: MCl-2Hcalc | ||||||||
| O3–H | • | • | • | • | X | • | ||
| O2–H | • | • | • | • | X | • | ||
| N–H | • | • | X | • | • | • | ||
| w1 | • | • | • | X | • | • | ||
| w2 | • | • | • | XX′ | • | • | ||
| Structure: MCl-3H | ||||||||
| O3–H | • | • | • | • | X | • | • | |
| O2–H | • | • | • | • | X | • | • | |
| N–H | • | • | X | • | • | • | • | |
| w1 | • | • | • | X | • | • | • | |
| w2 | • | • | • | X | • | X′ | • | |
| w3 | • | X | • | X′ | • | • | • | |
X = observed intermolecular D–H···A interaction; S = observed intramolecular D–H···A interaction; dot (•) = theoretically possible but unobserved D/A combination; wn = nth water molecule.
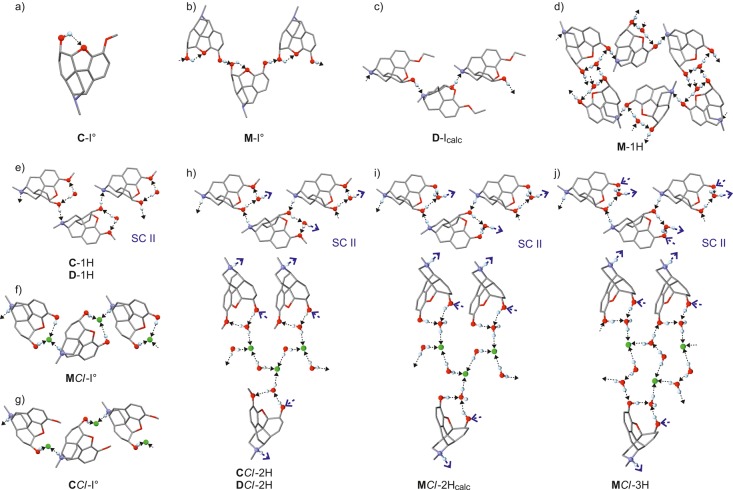
In both C-I° and D-Icalc, the OH group is the only available D function, which in the case of C is engaged in an intramolecular O3–H···O1 interaction (Figure 2a). By contrast, D-Icalc displays intermolecular O3–H···N bonds that result in helical chains along [010] (Figure 2c). The intramolecular O3–H···O1 bond is also formed in the crystal structure of M-I° in which the second OH group is engaged in additional O2–H···O3 interaction, thus generating helical chains of connected molecules parallel to [010] (Figure 2b). In the corresponding monohydrate M-1H, the water (w) molecule serves as an O2···H–Ow–H···O3 bridge between the two OH groups of the morphine molecule, while the intermolecular O2–H···N and O3–H···Ow interactions yield the H-bonded framework depicted in Figure 2d.
Figure 2.
Hydrogen bonded structures in solid forms of morphinanes. O, H, Cl, and N atoms engaged in D–H···A interactions are drawn as balls and D–H···A interactions as dotted lines, with an arrow indicating the direction H → A. The complex frameworks of the three isostructural hydrochloride structures (h–j) are divided into two parts, with the upper diagram showing the common morphinane/H2O helical structure (SC II) and lower diagram depicting the linkage between three such helices by bridging anions and H2O molecules. Connecting points between the two network fragments are indicated by the large blue arrows.
In the anhydrous hydrochloride MCl-I°, the Cl– anion serves as a bridge between the two OH groups of a given morphinium cation, O2–H···Cl–···H–O3. Additionally, it accepts a hydrogen bond from the ammonium group of another cation, N–H···Cl– so that adjacent morphinium units are linked by an N–H···Cl–···H–O3 bridge (Figure 2f). This interaction results in a chain structure parallel to [010]. The same type of bridge is also present in the codeine analogue CCl-I°, but an O2–H···Cl– interaction cannot be formed in this structure because of the ether substituent on the phenyl ring (Figure 2g). The geometry of the resulting chain is, however, very similar to that of MCl-I°, even in the absence of a second set of H-bonds, and the two crystals are isostructural with respect to the packing of morphine and codeine molecules (see section 3.1.2).
The monohydrates C-1H and D-1H exhibit the same H-bond connectivity features. These involve a water molecule acting as an O3···H–O–H···O2 bridge between two O atoms of a single morphinane molecule and chains of O3–H···N linked molecules (Figure 2d,e), which propagate along [001] in C-1H and along [010] in D-1H. Analogous bridge and chain motifs, with modifications regarding the character of O2 and O3 as either a D or an A site, are also present in the H-bonded frameworks of these four hydrogen chloride hydrates: CCl-2H and DCl-2H (O3–H···Ow1–H···O2 and N–H···O3); MCl-2Hcalc and MCl-3H (O3–H···Ow1···H–O2 and N–H···O3) (Figure 2h–j; upper part). Moreover, the first water molecule of each of these structures is Ow1–H···Cl connected to the chloride ion. In the dihydrates, CCl-2H, DCl-2H, and MCl-2Hcalc, the second water molecule serves as a Cl···H–Ow2–H···Cl′ bridge so that the chloride ion accepts three hydrogen bonds altogether (Figure 2i,j; lower part). By contrast, the second water molecule of MCl-3H acts as a Cl···H–Ow2–H···Ow3 bridge between a chloride ion and the third water molecule. Additionally, the third water molecule connects the morphinium ion, via an O2···H–Ow3–H···Cl bridge, to the chloride ion, resulting in large rings, which may be described65,66 as R86(16).
3.1.2. Comparison of Crystal Structures
The packing relationships between the experimental structures of this set, established with XPac, are illustrated in Figure 3. The analysis was based on pairwise comparisons of the morphinane substructures in which neither water molecules nor chloride anions were included. Detailed information on the lattice parameters and dissimilarity indices associated with the identified supramolecular constructs55 (SCs) are given in Tables S16–S20 of the Supporting Information.
Figure 3.
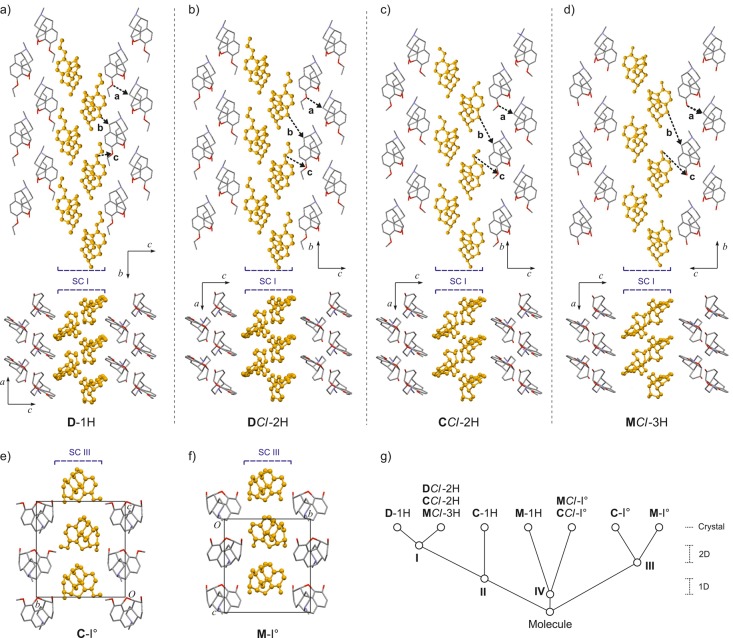
Packing similarities of morphinane moieties in experimental crystal structures as identified with XPac (a)–d): D1-H and the isostructures DCl-2H, CCl-2H, and MCl-3H, all based on the 2D SC I (corresponding sets of three intermolecular vectors, denoted a, b, and c, are drawn for each structure to highlight geometrical differences); (e–f) the crystal structures of C-I° and M-I° are based on the 2D SC III. Instances of SC I and III are highlighted (orange, ball and stick style); H atoms, water molecules, and chloride ions are not shown for clarity. (g) Tree diagram according to ref (68), illustrating the packing relationships between morphinane substructures in the investigated set.
The hydrogen chloride hydrates DCl-2H, CCl-2H, and MCl-3H are isostructural (Figure 2b–d) with respect to their complete morphinane substructures, even though the H-bond structure of the trihydrate is somewhat different from that found in the two dihydrates (see above; Figure 2h,j). The corresponding XPac dissimilarity indices x lie between 4.8 and 9.9 (for the definition of x and additional reference examples, see refs (56) and (67)), with the largest differences occurring for the pairing MCl-3H/DCl-2H(R = H vs −CH2–CH3). The theoretical structure of MCl-2Hcalc, generated from the experimental data of MCl-3H (see section 3.4.4), belongs to the same series of isostructures. Moreover, the structures of DCl-2H, CCl-2H, and MCl-3H agree with those of C-1H and D-1H with regard to the packing geometry of those morphinane moieties, which are linked via water molecules into an H-bonded helical chain. Again, these 1D similarity relationships (denoted SC II; Figure 3b–d) are observed despite differences in the H-bond connectivity modes of the individual H-bonded helices (Figure 2e,h–j; discussed above).
The H-bonded helices running along the respective b-axis of D-1H and the three isostructural hydrochloride hydrates have very similar geometries. Additionally these crystals show the same packing of such helices in the direction of their respective a-axis. The resulting common layer structure of D-1H and the isostructural hydrochloride hydrates is denoted SC I (Figure 3a–d). However, D-1H differs from DCl-2H, CCl-2H, and MCl-3H in the packing of adjacent SC I layers in that interlayer space is increased in the latter three structures to accommodate chloride anions and additional water molecules, accompanied by a significant shift offset between neighboring SC I layers. This situation is illustrated in the packing diagrams of Figure 3a–d where three types of corresponding intermolecular vectors have been drawn. The first of these (denoted a) links two molecules belonging to the same instance of SC I, and therefore, its length and orientation remain largely unchanged over the entire series. By contrast, the length and relative orientation of b and c, each connecting two molecules belonging to neighboring SC I units, differ considerably between D-1H, on the one hand, and the three hydrogen chlorides, on the other. These differences indicate an offset shift of approximately one-third of a translation period along [010] between D-1H and MCl-3H. For the set of isostructures (DCl-2H, CCl-2H, and MCl-3H), subtle variations in the orientation and length of both b and c are observed. These correspond to adjustments in interlayer packing, which are correlated to the specific R substituent and to the number of water molecules in a given crystal. The dissimilarity indices for the match of the smaller SC I and SC II substructures in this series do not differ substantially from those computed for the complete morphinane packing (see Table S17 of the Supporting Information), suggesting that the impact of such adjustments on the packing geometry is fairly isotropic. This is in contrast to a situation where the geometry of the SC II layer would be particularly rigid and adjustments largely limited to the packing mode of these rigid layers.
The crystal structures of C-I° and M-I° exhibit a common layer structure, which lies parallel to (010) in each case (SC III). It is composed of rows of morphinane molecules related to one another by translation symmetry. Neighboring rows of this kind are related to one another by a 21 axis, and the SC III does not contain any classic hydrogen bonds.
MCl-I° and CCl-I° are also isostructural (x = 8.0). Their morphinane substructures are 1D isostructural with that of M-1H (for a discussion of the relationship between MCl-I° and M-1H, see ref (5)). The corresponding SC IV is a stack of morphinane moieties in which the latter are related to one another by translation symmetry. SC IV is associated with a unit cell axis length of between 7.14 and 7.43 Å (see Table S18 of the Supporting Information).
3.2. Moisture-Dependent Phase Transformations
3.2.1. Automated Gravimetric Moisture Sorption/Desorption Experiments (GMS)
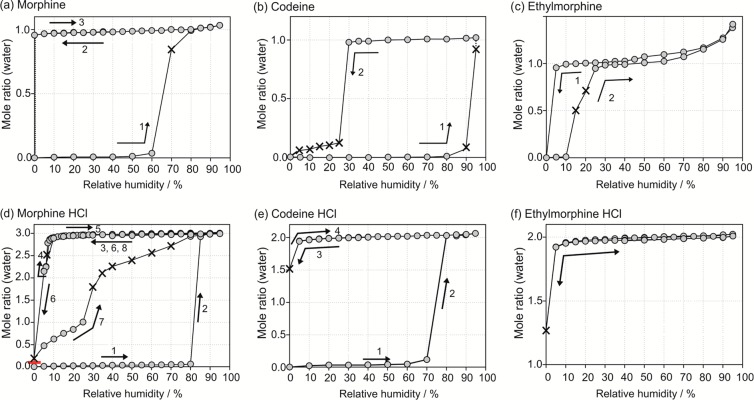
The hydration and dehydration pathways for the six compounds were monitored as a function of relative humidity (RH). The three free bases (M, C, and D) each show the typical sorption/desorption behavior of a “stoichiometric” hydrate,69 with differences in the stability ranging between the corresponding anhydrous and monohydrate forms (Figure 4a–c). M-I° (Figure 4a, curve 1) and C-I° (Figure 4b, 1) transform to the corresponding monohydrate at RH levels of ≥70% and ≥90%, respectively. Desorption of C-1H to C-I° occurs at RH ≤ 25% (Figure 4b, 2). The M-1H phase remains stable even if RH is decreased to the driest moisture conditions (Figure 4a, 2 + 3). However, partial dehydration to M-I° occurs upon storage of M-1H over P2O5 (0% RH) for a longer time period (three months). The desorption isotherm of D-1H (Figure 4c, 1) shows that D-1H is stable down to 5% RH (no water loss). Water was released, at the lowest moisture condition, resulting in D-I°. Water absorption by D-I° and the reverse transformation to D-1H occurs at RH levels above 10% (Figure 4c, 2). At higher RH conditions, D-1H absorbs an additional amount of water (Figure 4c), which is readily released in the subsequent desorption cycle.
Figure 4.
Gravimetric moisture sorption/desorption isotherms of morphinanes and their hydrates at 25 °C: (a) M, (b) C, (c) D, (d) MCl, (e) CCl, and (f) DCl. The gray circles represent data points recorded at equilibrium conditions (see experimental section), and × indicates measurements where equilibrium conditions have not been reached within the set time limit (48 h). The order and direction of the sorption (increasing RH) and desorption (decreasing RH) cycles are indicated by the numbers and arrows, respectively.
MCl-I° (Figure 4d, 1 and Figure S1a of the Supporting Information) and CCl-I° (Figure 4e, 1) adsorb water at RH values >80% RH for MCl and >70% for CCl. Both transform to MCl-3H and CCl-2H, respectively, in a single step. A CCl-I° sample containing amorphous material showed an initial water uptake (Figures S2 of the Supporting Information), followed by a decrease in mass between 50 and 70% RH. The latter indicates a moisture-induced transformation of the amorphous part of the sample, yielding the crystalline anhydrate (CCl-I°). The hydrates MCl-3H, CCl-2H, and DCl-2H are very stable and release water only at the very driest conditions (5% RH or below, Figure 4d–f). None of the salt hydrates had lost its water content completely after 7 days at 0% RH. Moreover, no hysteresis between sorption and desorption was observed for CCl (Figure 4e, curves 3 + 4) and DCl (Figure 4f) after increasing the humidity. The desorption curve for MCl-3H indicated the formation of an intermediate phase, MCl-2H, at 5% RH (Figure 4d, 4 and Figure S1b of the Supporting Information). Similar to CCl and DCl, the isotherm of MCl lacks a clear hysteresis between the desorption and sorption curves if the lower limit of the cycle is 5% RH (Figure 4d, 4). However, exposition of the hydrate to very dry humidity conditions (<5% RH) results in a new anhydrous polymorph (MCl-III) of low crystallinity. This new phase has a continuous sorption profile, up to 25% RH, which is a typical characteristic of an amorphous phase that adsorbs water easily (Figure 4d, 7 and Figure S1c of the Supporting Information). The sorption curve exhibits a step at ≥30% RH, which is followed by a steady increase in the amount of absorbed water until the molar ratio of MCl-3H is reached. This second section of the sorption curve between 30 and 70% RH is out of equilibrium (labeled × in Figure 4d, 7), indicating that the formation of MCl-3H is a sluggish process.
From the sorption/desorption isotherms we deduce that the hydrate phases of M, MCl, CCl, D, and DCl as well as the stable anhydrate phases (labeled I°) of M, C, MCl, and CCl can be handled and stored at ambient moisture conditions (40 to 60% RH) without the risk of a phase transformation. The corresponding phase changes will, however, occur at extremely low and high moisture conditions as well as at higher temperatures. C-1H is the least stable hydrate of this set of compounds and dehydrates below 30% RH, which is a critical aspect for the preservation of hydrate stability during processing and storage.
3.2.2. Morphine HCl: Moisture Controlled PXRD Experiments
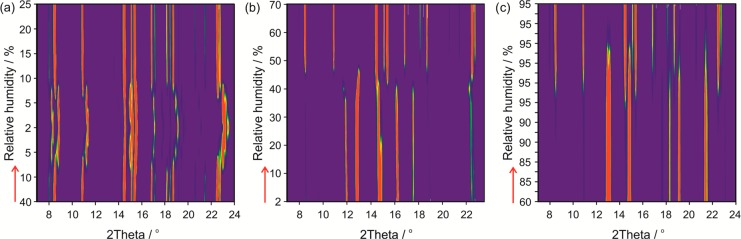
Moisture-controlled PXRD measurements were carried out to monitor the structural changes associated with the complex moisture sorption/desorption behavior (Figure 4d) of MCl (Figure 5 and Figure S7 of the Supporting Information). Starting with MCl-3H (Figure 5a), the RH was decreased from 40% to 5%, which confirmed the occurrence of a phase change between 10% and 5% RH, evidenced by the disappearance of MCl-3H diffraction peaks and appearance of new reflections at higher 2θ values. The high similarity of the PXRD patterns of the two phases (Figures S6 and S7a of the Supporting Information) suggests that minor structural changes take place during dehydration. The space group symmetry of MCl-3H is preserved, as confirmed by indexing70,71 and Pawley fitting72 of the PXRD patterns (section 3.4.4). Notable changes are observed for the lattice parameters a and b, but not for the “stacking” axis c of the morphinium cations. Further lowering of the RH to 2% induces only small changes in the lattice parameters (due to the slightly decreased water content, which is still near to the stoichiometry of the dihydrate). This process is highly reversible (no hysteresis between the sorption and desorption cycles; see Figure S1b of the Supporting Information), which is also consistent with a high degree of similarity between the two structures (section 3.4.4). The different time intervals chosen for the moisture-dependent PXRD measurements (between 12 and 48 h for the lowest RH values) and the GMS isotherms (7 days at the lowest RH value) result in different products. For instance, the dehydration to MCl-III was not observed in the PXRD experiment due to its shorter duration compared to the GMS studies.
Figure 5.
Guinier plots of the moisture-dependent PXRD measurements of morphine HCl: starting with (a) MCl-3H, (b) MCl-III, and (c) MCl-I°. Red arrows mark the starting point.
With MCl-III (high energy, “low crystallinity” form) as the starting material and after increasing the RH from 0% to 40%, anisotropic changes of the crystal lattice are observed, which are due to the absorption of water. According to Figure 4d (curve 7), a considerable amount of water is absorbed before the transformation to the MCl-3H occurs. This behavior is clearly different to that of MCl-I° (Figure 5c) where there is almost no water uptake (<0.06 mol equivalent) prior to the phase transformation to the trihydrate. The transition from MCl-I° to MCl-3H involves major structural changes, which is evident by the disappearance of high-intensity reflections of MCl-I° (e.g., 2θ = 12.97°, 13.13°, and 14.84°) and the emergence of characteristic MCl-3H peaks (e.g., 2θ = 10.90°, 14.50°, and 15.40°). Because of the shorter time intervals used for the moisture-controlled PXRD experiments, the transition to MCl-3H starts at a higher humidity level (95% RH) than in the GMS experiments (Figure 4d, 1).
3.2.3. Dehydration Experiments over Desiccants
The moisture sorption/desorption studies were complemented by long-term storage experiments of the stable hydrate phases over P2O5 (0% RH). The stable anhydrates M-I° and C-I° were obtained for M and C, while D-1H transformed to the new phase D-I°. The latter exists only at extremely dry conditions and readily rehydrates on exposure to moisture conditions that exceed a few percent RH. After six months, M-1H still had not transformed completely to M-I°. By contrast, it was possible to dehydrate the hydrates of MCl and CCl over a desiccant, which resulted in new anhydrous polymorphs (MCl-III and CCl-II, see Figure S6 of the Supporting Information). Both new forms are of lower crystallinity than the dehydration products of the free bases and are not stable at ambient conditions (40% RH, 25 °C), i.e., they quickly transform back to the original hydrates. The removal of water from the DCl-2H structure yields an amorphous phase (see Figure S6 of the Supporting Information).
3.3. Thermal Behavior of the Hydrates
3.3.1. Hot-Stage Microscopy, Differential Scanning Calorimetry, and Thermogravimetric Analysis
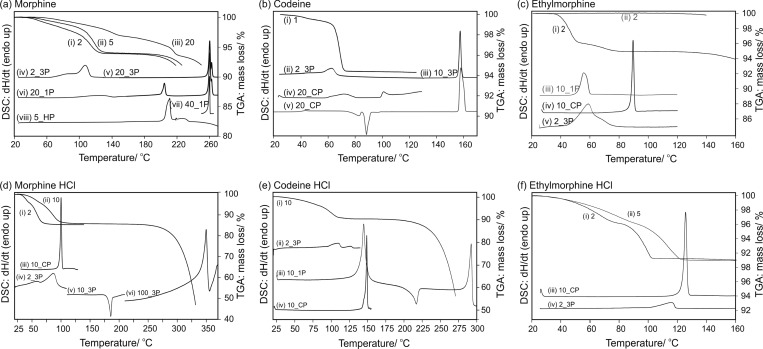
The dehydration process of the six investigated compounds was monitored with HSM (Figure 6, selected photomicrographs shown), DSC, and TGA (Figure 7). To investigate the impact of the atmospheric conditions on the dehydration behavior and associated processes, different experimental conditions were applied: dry and silicon oil preparations (HSM), heating of the sample in a perforated or sealed DSC pan, and different heating rates. The obtained thermodynamic data are collected in Table 4.
Figure 6.

Photomicrographs of morphinanes: (a–c) dehydration of M-1H between 70 and 190 °C, showing a “pseudomorphosis” (dry preparation); (d–f) congruent melting of DCl-2H between 110 and 123 °C. (g) Crystals of MCl-3H, (h,i) and “grainy transformation” of MCl-III to MCl-I°.
Figure 7.
DSC and TGA thermograms of (a) M-1H (i–iii) TGA, (iv–viii) DSC; (b) C, (i) TGA C-1H, (ii–iv) DSC C-1H, (v) amorphous C; (c) D, (i) TGA D-1H, (ii) TGA D-I°, (iii) DSC D-I°, (iv–v) DSC D-1H; (d) MCl-3H, (i–ii) TGA, (iii–vi) DSC; (e) CCl-2H, (i) TGA, (ii–vi) DSC; (f) DCl-2H, (i–ii) TGA, (iii–vi) DSC. The label of each curve corresponds to the applied heating rate in °C min–1. 3P, three pin-holed DSC pan; 1P, one pin-holed DSC pan; CP, closed DSC pan; and HP, high pressure DSC capsule.
Table 4. Thermodynamic Data for M, C, D, and HCl Salts Thereof.
| stable
anhydrate (A) |
hydrate (H) |
transformation (H ↔ A) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| compd | Tfusa (°C) | ΔfusHb (kJ mol–1) | Tdissc (°C) | ΔdissHd (kJ mol–1) | ΔdehyHe (kJ mol–1) | Tdehyf (°C) | ΔtrsHH→Ag (kJ mol–1) | ΔhyHh (kJ mol–1) | ΔtrsHA→Hi (kJ mol–1) |
| M | 258.6 ± 0.3 | 37.6 ± 0.2 | 201.3 ± 0.5 | 63.1 ± 0.5 | 110 | 22.9 ± 0.5 | –66.3 ± 0.1 | –22.3 ± 0.1 | |
| C | 156.3 ± 0.3 | 27.0 ± 0.1 | 99.0 ± 0.2 | 47.9 ± 0.4 | 65 | 5.7 ± 0.4 | |||
| D | 51.4 ± 0.1 | 16.4 ± 0.3 | 88.4 ± 0.5 | 33.1 ± 0.3 | 73.5 ± 2.4j | 60 | 9.0 ± 0.6k | –53.0 ± 0.5 | –9.0 ± 0.5 |
| MCl | 344.2 ± 0.3l | 97.8 ± 0.9 | 170.1 ± 0.8 (−20.3 ± 0.5)m | 90 | 27.7 ± 1.3 | –157.6 ± 0.2 | –25.6 ± 0.2 | ||
| CCl | 288.0 ± 0.5 | 35.0 ± 2.2 | 147.1 ± 1.2 | 41.9 ± 1.0 | 109.0 ± 2.9 (−12.8 ± 1.8)m | 110 | 15.9 ± 4.7 | –104.0 ± 0.9 | –16.0 ± 0.9 |
| DCl | 123.2 ± 0.7 | 45.0 ± 0.2 | 122.0 ± 2.0j | 110 | |||||
Melting point.
Enthalpy of fusion.
Peritectic dissociation.
Enthalpy of dissociation.
Enthalpy of dehydration.
Temperature of dehydration (peak maximum).
Enthalpy of transition (from hydrate to the stable anhydrate).
Enthalpy of hydration at 25 °C.
Enthalpy of transition (from stable anhydrate to hydrate).
Dehydration to amorphous phase.
Determined at 25 °C with isothermal calorimetry.
Determined at a heating rate of 100 °C min–1.
Transformation of high energy anhydrate to stable anhydrate.
On slow heating, the crystals of M-1H turn opaque (Figure 6a–c, dry preparation). The dehydration of smaller crystals (>5 μm) already starts at 60 °C, with the maximum dehydration rate occurring at 110 to 115 °C. For bigger crystals (>100 μm) dehydration is observed between 115 and 140 °C. The dehydration process is indicated by the appearance of “dark” spots on the crystal surface, which correspond to nucleation centers of M-I°. The number of nucleation centers increases with temperature. At the end of the dehydration process the particles are completely opaque due to the formation of numerous small crystallites, but the shape of the original hydrate crystals is maintained. This “pseudomorphosis” is typical for stoichiometric hydrates. The formation of bubbles is observed in silicon oil preparations (Figure S8 of the Supporting Information). The microscopic observations indicate that the dehydration process is controlled by a nucleation and growth mechanism with a high nucleation rate and a low growth rate. In DSC experiments (slow heating rate, 3-pinholed pans) the dehydration process is a broad endothermic event (Figure 7a, curve iv), with a maximum at approximately 110 °C. Upon further heating the sublimation of grainy, prismatic, and needle-like crystals is observed with HSM at 175 °C. A few of the sublimed crystals melt at 197 °C (Kofler form II,28M-II). M-I° melts with decomposition (thermolysis) at 258.6 ± 0.3 °C (Figure 7a, vii, heating rate 40 °C min–1). The decomposition causes a peak splitting of the M-I° melting endotherm if slower heating rates are applied (Figure 7a, curves v/vi, and Figure S10 of the Supporting Information). Peritectic melting of M-1H was detected at 201.3 ± 0.5 °C when faster heating rates (≥20 °C min–1) were applied and the evaporation of water was impeded, i.e., by embedding the sample in high viscosity silicon oil or by using sealed DSC pans (Figure 7a, vi/viii). The mass loss of 6.02 ± 0.06% derived from TGA experiments (Figure 7a, i–iii) corresponds to 1.02 mol of water per mol of M. The TGA curves (Figure 7a, i/ii, slower heating rates) have a two-step profile. The slower dehydration process at the beginning indicates a diffusional loss of water, whereas at higher temperatures (>100 °C) the mechanism becomes faster due to nucleation control. A third distinct step may arise in the TGA curve when fast heating rates (or bigger crystals) are used. This process occurs close to the melting temperature of M-1H (Figure 7a, iii) when the remaining water escapes rapidly during the collapse (peritectic melting) of the hydrate structure.
The thermal dehydration of C-1H begins at 40 °C (Figure 7b, curve i/ii) and yields C-I°. This process has the optical characteristics of a stoichiometric hydrate (“pseudomorphosis”) described above, and the release of water vapor is confirmd by the formation of bubbles. Upon heating above 80 °C the dehydrated crystals (C-I°) sublimate and are deposited on the coverslip as grains and prisms of C-I°, which melt at 156.3 ± 0.3 °C without decomposition. The quench cooled melt of C undergoes a glass transformation at approximately 45 °C (Figure 7b, v) and the crystallization of C-I° ensues at approximately 80 °C. Annealing the supercooled melt below 50 °C gave evidence of a second anhydrous polymorph of codeine (C-II). The latter phase is highly unstable and transforms quickly due to fast arising nuclei of C-I°. Peritectic melting of C-1H occurs at 99.0 ± 0.2 °C (Figure 7b iv, second endotherm). The TGA curve (Figure 7b, i) shows the slow release of water below 65 °C, suggesting that some diffusional loss of water occurs before the anhydrate starts to nucleate. The dehydration is very fast above 65 °C. The observed mass loss of 5.65 ± 0.05% (0.99 mol of water per mol of C) is consistent with the presence of a monohydrate.
D-1H dehydrates to an amorphous phase (Figure 7c, iii), indicated by the loss of birefringence starting above 45 °C. The mass loss of 5.36 ± 0.06% inferred from TGA (Figure 7c, i) corresponds to 0.98 mol of water per mol of D. The melting point of the hydrate was 88.4 ± 0.5 (for a sample in high viscosity silicon oil or in a sealed DSC pan and with a faster heating rate, Figure 7c, iv). D-I° has a lower melting point (51.4 ± 0.1 °C, Figure 7c, iii) than D-1H, which explains why the thermal dehydration reaction produces the amorphous phase rather than the crystalline anhydrate. The melting of D-I° and dehydration of D-1H occur in the same temperature range. The TGA curve (Figure 7c, ii) of D-I° does not show any mass change, which confirms that the endothermic event in the DSC curve of D-I° (Figure 7c, iii) is a pure melting process. Lower stoichiometry hydrates were excluded for all three compounds by stopping the TGA experiments after the first step and analyzing the partially dehydrated samples. The latter consisted exclusively of a mixture of the known monohydrate with a water-free form.
The dehydration of MCl-3H starts above 75 °C (HSM), and under N2 purge (TGA), the dehydration starts at 40 °C (Figure 7d, iv). At the initial dehydration stage (≤60 °C, slow heating rates), the MCl-3H crystals remain largely intact and show no cracks or any of the alterations that are typical for the dehydration of a stoichiometric hydrate, even though bubble formation in silicon oil preparations indicates the release of water. This suggests that a fraction of the water molecules can escape from the hydrate without a fundamental change of the structure. However, significant alterations (turbidity) of the hydrate crystals occur at a later stage of the dehydration process, and finally a new anhydrate (MCl-III) with low crystallinity is formed. Further heating to approximately 160 °C (Figure 6h) triggers a “grainy transformation” (Figure 6h,i) and yields highly crystalline MCl-I° at 190 °C (Figure 6i). In DSC experiments (Figure 7d, v) the phase transformation MCl-III to MCl-I° generates a large exothermic peak around 175 °C. The measured transformation enthalpy ΔtrsHIII–I of −20.3 ± 0.5 kJ mol–1 is rather high but consistent with a transformation from a low crystallinity (high energy) phase to a high crystallinity phase. Above 200 °C the sublimation of grainy and prismatic crystals of MCl-I° is observed, while unstable stems (MCl-II) are deposited on the coverslip between 220 and 230 °C. The unstable stems transform to stable MCl-I° at approximately 250 °C. Lindpainter observed the melting/decomposition of MCl-I° at 295–300 °C and that of MCl-II at 280–284 °C, using HSM and fast heating rates.32 In our study we determined the MCl-I° melting point to be 344.2 ± 0.3 °C with DSC (heating rate: 100 °C min–1). TGA experiments showed a total mass loss of 14.21 ± 0.25%, which corresponds to 2.96 ± 0.06 mol of water per mol of MCl.
The dehydration of CCl-2H occurs between 100 and 135 °C (Figrue 7e, ii/iii). HSM investigations (dry preparation) showed a loss of birefringence on dehydration to a low-crystallinity form CCl-II (as confirmed with PXRD) between 120 and 140 °C. The original shape of the crystals is preserved. A transformation to CCl-I° is observed at 170 °C, and the occurrence of melt droplets, which recrystallize to CCl-I°, indicated that this process is partially incongruent. This process is completed at approximately 220 °C. In the DSC curve (Figure 7e, iii) this transformation is an exothermic event, comprising (a) the transformation of CCl-II to CCl-I°, (b) the liquefaction of CCl-II, and (c) the recrystallization of CCl-I°. The measured heat (ΔtrsH = −12.8 ± 1.8 kJ mol–1) would be rather high for a classic polymorphic phase transformation, but fits well with a transition process from a high energy form to a stable polymorph.73 The melting point of the CCl-I° is 288.0 ± 0.5 °C, and melting point of the hydrate is 147.1 ± 1.2 °C (Figure 7e, iv), which is in good agreement with previous studies.33
DCl-2H dehydrates to an amorphous phase, indicated by a loss of birefringence between 110 and 120 °C. At approximately 150 °C, liquefaction to a viscous melt is observed, and congruent melting of the hydrate occurs at 123.2 ± 0.7 °C (Figure 6d–f and Figure 7f, iii). The mass loss of 9.22 ± 0.10% derived from TGA experiments (Figure 7f, i + ii) confirms the dihydrate composition (1.97 ± 0.02 mol of water per mole of DCl). The observed thermal behavior of this hydrate is in agreement with a report by Kuhnert-Brandstaetter et al.,33 but we did not observe the growth of grains from the melt at 170 °C, which these authors have described in another report.31
3.3.2. Temperature-Dependent IR Spectroscopy
The structural changes during thermal dehydration of the hydrates were monitored with IR spectroscopy (Figure 8a–c, for selected compounds). The spectra were recorded at ambient RH within the temperature interval where dehydration had been observed with HSM and DSC. The measured IR intensities in the spectral ranges 3700 to 2400 and 1680 to 600 cm–1 were used as input variables for PCA, a multivariate data treatment to reduce the number of variables (scores) and the representation of a multivariate data table in a low dimensional space.74 The PCA scores and loadings75 allowed monitoring of the solid state transformations. Three different dehydration mechanisms, i.e., dehydration of a stoichiometric hydrate to a crystalline phase (Figure 8a, M), dehydration of a stoichiometric hydrate to an amorphous phase (Figure 8b, D), and dehydration via a lower hydrate stoichiometry to a high energy form (Figure 8c, MCl), were considered.
Figure 8.
Principal component analysis (PCA) plots based on FT-IR spectra for (a) M (spectra recorded at 2 °C intervals), (b) D (spectra recorded at 1 °C intervals), and (c) MCl (three spectra per 1 °C intervals). Each triangle corresponds to one IR spectrum. Arrows indicate the transformation pathway; numbers correspond to the temperature at which the spectrum was recorded; the big ellipse corresponds to the 95% Hotelling T2. (d) IR spectra of MCl solid forms.
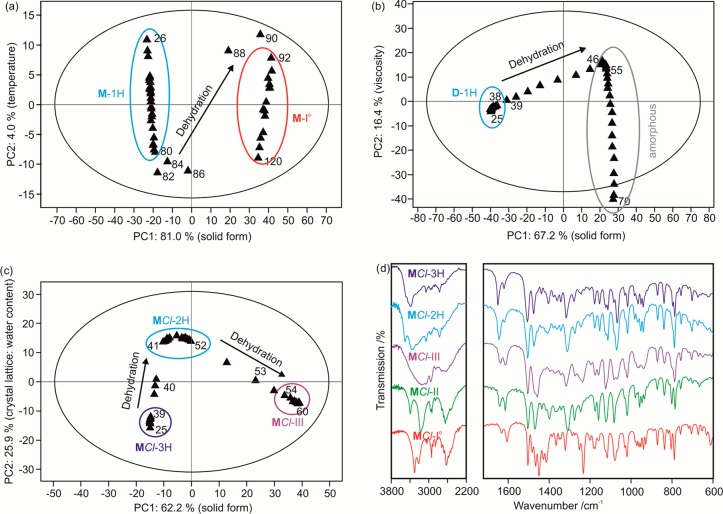
For the dehydration of M-1H, three principal components (PCs) were required to explain the variance in the data–the first PC (PC1) explained 81.0%, the second (PC2) 6.1%, and the third (PC3) 4.0% of the variation in the data. PC1 accounts for the different solid forms, i.e., M-1H versus M-I°, while PC2 and PC3 account for the influence of temperature on the IR spectra. The scores plot (Figure 8a) shows two distinct clusters, corresponding to two distinct crystal forms (M-1H, 26 to 80 °C; M-I°, 92 to 120 °C). Spectra recorded in the range from 82 to 86 °C are mixed phases with M-1H as the dominant phase, whereas in spectra 88 and 90 M-I° is the main phase.
The dehydration process of D-1H can be described with three PCs (PC1 67.1%, PC2 16.4%, and PC3 1.55%): PC1 accounts for the crystal form, while PC2 and PC3 account for the loss of crystallinity of the resulting amorphous phase/melt. The score plot exhibits a continuous course with clusters in the ranges of 25 to 38 °C and 46 to 55 °C (Figure 8b). The first cluster corresponds to the D-1H phase (25 to 38 °C), which dehydrates to the amorphous phase (46 to 55 °C). At higher temperatures (55 to 70 °C) the viscosity of the melt changes (well observable by HSM), as described by PC2.
A slower heating rate (three spectra per degree) was applied for monitoring the MCl-3H dehydration process (Figure 8c) with the aim to isolate the dihydrate phase. MCl-I° spectra were excluded from the model, as the MCl-I° spectrum is very distinct from the spectra of the other MCl solid forms (Figure 8d). Four PCs were required: 66.2% of the variance is explained by PC1 (which describes the solid form and distinguishes between MCl-III and hydrates), 25.9% by PC2 (ratio compound/water), 1.1% by PC3 (crystallinity), and 1.0% by PC4 (solid form). Three clusters were identified: the first corresponds to MCl-3H (25 to 39 °C), the second to MCl-2H (41 to 52 °C) and the third to MCl-III (54 to 60 °C). The first two clusters (MCl-3H and MCl-2H) have almost the same PC1, indicating similar crystal structures, but they are well separated in PC2 (Figure 8c). Thus, MCl-3H and MCl-2H can be classified as two individual hydrate phases rather than a single phase having variable water content. MCl-III differs from the hydrates in PC1 and PC2. It should be noted that the clusters exhibit differences beyond those caused by the influence of temperature. The multivariate analysis of the spectral data allowed us to establish a clear picture of mechanistic details and the pathway of the dehydration process. The dehydration temperatures derived with DSC and IR vary slightly as a result of the different preparation techniques, i.e. on a ZnSe disc or embedding in a pin-holed pan.
3.4. Dehydration: Insights from Lattice Energy Calculations
Computational dehydration calculations were performed to obtain a better structural insight into the dehydration of the hydrate systems and to generate possible D-Icalc and MCl-2Hcalc structures. The hydrate structures were optimized using the method described in section 2.11. The water molecule(s) were removed, and single point (FWfix) and geometry optimization (FWopt) calculations in the hydrate space group P212121 were performed (Supporting Information sections 12 and 13). The lattice energy calculations were complemented with structural void space analyses (Supporting Information section 14),76 which indicate that all structures pack efficiently.
3.4.1. Morphine, Codeine, and Ethylmorphine
The computational model was successful in reproducing the experimental structures, giving rmsd15 values of less than 0.12 Å (Table S23 of the Supporting Information). Intermolecular interactions involving water molecules in the three hydrate structures were calculated to contribute approximately 44% (−123 kJ mol–1), 36% (−88 kJ mol–1), and 33% (−89 kJ mol–1) to the lattice energy of M-1H, C-1H, and D-1H, respectively, and water molecules occupy 2.8% (M-1H), 7.0% (C-1H), and 5.3% (D-1H) of the crystal volume (Tables S24 and S26 of the Supporting Information). The hypothetical M and C frameworks77 (FWopt) are 20.6 and 20.4 kJ mol–1, respectively, less stable than the experimental forms and therefore represent high energy structures in comparison to the known stable anhydrates (I°). These large differences are consistent with the notion that M-1H and C-1H are stoichiometric hydrates.69
3.4.2. Computational Modeling of Ethylmorphine Anhydrate
Indexing70,78 of the diffraction pattern of D-I° using the first 20 peaks indicated an orthorhombic unit cell (P212121, a = 7.417 Å, b = 13.271 Å, c = 16.273 Å; at RT) whose dimensions are in good agreement with those of the computed 0 K FWopt structure (P212121, a = 7.344 Å, b = 13.183 Å, c = 15.868 Å). The largest deviation of 2.5%, ascribed to anisotropic thermal effects, is observed in the length of the c axis. The experimental PXRD pattern of D-I° matches that simulated from the FWopt structure. Likewise, the experimental data for D-1H match those simulated for the corresponding computed monohydrate (Figure 9). The facile and fast dehydration mechanism derived from moisture sorption/desorption studies is in agreement with the structural characteristics of D-1H. It suggests the release of the water molecules through channels extending parallel to the crystallographic c axis (Figure S4f of the Supporting Information). The calculated lattice energy difference (ΔElatt = −ΔU) between D-1H and D-FWopt = D-Icalc of −71.3 kJ mol–1 is similar to the analogous values for the experimental M and C structures (ΔElatt(Hy-AH) = −79.8 and −64.6 kJ mol–1, respectively). Furthermore, the similarity of the IR spectra of D-1H and D-I° (Figure S12 of the Supporting Information) suggests that D-Icalc is identical with the experimental D-I°.
Figure 9.
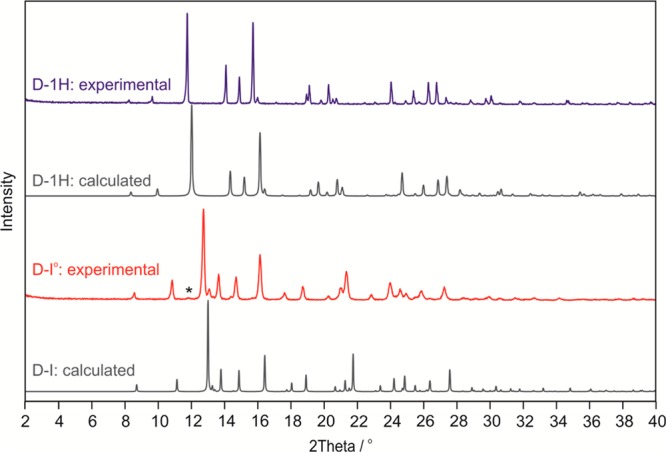
Experimental powder X-ray diffraction patterns (D-1H and D-I°) recorded at room temperature and simulated patterns (λ = 1.5418 Å) for calculated D structures. The peak position in the D-I° pattern marked with an asterisk (*) corresponds to a minor D-1H impurity.
3.4.3. Morphine, Codeine, and Ethylmorphine HCl Salts
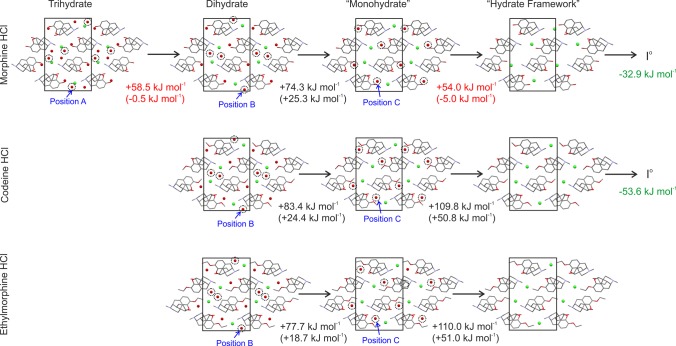
Excellent agreement (rmsd15 ≤ 0.08 Å) between experimental and calculated structures was achieved for the hydrochloride salts, except for MCl-3H (rmsd15 = 0.35 Å; Table S23 of the Supporting Information). Intermolecular interactions involving water are very important for the stability and account for approximately 31%, 23%, and 22% of the lattice energy of the hydrates MCl-3H, CCl-2H, and DCl-2H, respectively, even in the presence of strong ionic intermolecular interactions. Water molecules in positions A (MCl-3H only) and B (MCl-3H, CCl-2H, and DCl-2H; Figure 10) contribute less to the lattice energy (−86 to −94 kJ mol–1) than the water molecules of type C, which bridge between the atomic positions O2 and O3 of the cation (−114 to −127 kJ mol–1). This suggests that the dehydration reaction starts with the removal of the water molecules A and/or B (Figure 10). For MCl-3H the removal of water molecule A and subsequent structure minimization lead to a dihydrate structure that is energetically competitive with MCl-3H. The computed lattice energy difference between MCl-3H and MCl-2Hcalc (Figure 10) is of the same magnitude as the lattice energy of ice (−59 kJ mol–179,80).15 This assumes that hydrate formation is thermodynamically driven, which may be estimated from static lattice energy differences. The removal of the water molecule B does not lead to any stable monohydrate. The removal of water molecule C at any stage would consume even more energy. These results are in agreement with the moisture sorption/desorption studies where the only intermediate phase found was a dihydrate of MCl. By contrast, there was no indication for the existence of a monohydrate of any of the three HCl salts. Thus, these calculations show conclusively that the removal of water beyond the stoichiometry of the dihydrate results in the collapse of each of the three HCl salt structures. There is a large energy difference between the hypothetical water-free frameworks (FWopt) and the experimental anhydrates, which indicates that these frameworks are well outside the energy range that can be expected for any alternative polymorphs.81
Figure 10.
Hypothetical dehydration mechanism for the investigated HCl salts, which results in framework structures. Potential energy differences (and computed heat of transitions, red and black) between experimental structures and (hypothetical) hydrate structures of lower stoichiometry and ice (−59 kJ mol–179,80). Potential energy differences between computed water-free frameworks and experimental anhydrate structures (green numbers). The transformations indicated by red are nearly equi-energetic, and those indicated by black and green are endothermic and exothermic, respectively.
3.4.4. Computational Modeling of the Morphine HCl Dihydrate Structure
The experimental PXRD of MCl-2H, recorded at 5% RH, matches that simulated from the computationally generated MCl-2Hcalc structure (Figure 10). Likewise, the experimental MCl-3H powder pattern matches the data of the corresponding calculated trihydrate (Figure 11). The unit cell volume of MCl-2H is 7.88% (based on the indexed powder pattern, 25 °C: P212121, a = 6.937 Å, b = 12.452 Å, c = 19.819 Å) lower than that of MCl-2H (25 °C: P212121, a = 6.905 Å, b = 13.018 Å, c = 20.704 Å), corresponding to the loss of approximately one mol of water per mol of MCl-3H.
Figure 11.
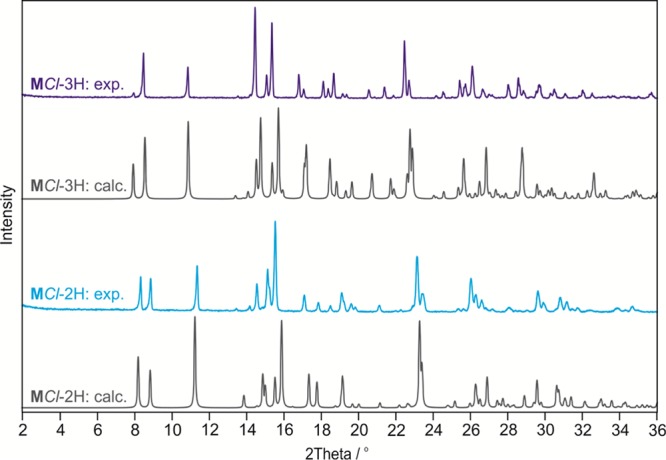
Experimental (exp.) powder X-ray diffraction patterns (MCl-3H and MCl-2H) recorded at room temperature and simulated patterns (λ = 1.5418 Å) for the calculated (calc.) MCl hydrate structures.
The PXRD experiments (Figure 5a) suggest that only minor changes in the packing of the MCl-3H structure occur upon dehydration to MCl-2H. From the IR spectra (Figure 8d) it is evident that the hydrogen bond pattern changes (spectral range: 3600–3100 cm–1), while other spectral regions remain largely unchanged for the two hydrates. In this case the modeling (Figure 10) can be used to derive the most likely (most stable) water orientations. The minimization of the previously reported experimental MCl-3H structure45 (MORPHC) resolved geometric abnormalities (C–O3–H = 87.76° and H–O–H = 135.72° for the water molecule C). The hydrogen bond connectivity was preserved during structure optimization, but the directionality of one of the O2–H···Ow bonds was reversed (Figure 12a,b, red dotted boxes). The removal of water molecule A from the crystal (Figure 12b) results in a reorientation of the adjacent water molecule B (Figure 12c) and substitution of its Ow–H···O2(cation) bond by a new Ow–H···Cl– interaction. This reversible process can take place without changes in the positions and orientations of the morphinium, Cl–, and water A moieties and can proceed continuously. This type of rearrangement of water molecules is in concert with the observed moisture sorption/desorption behavior of MCl-2H.
Figure 12.
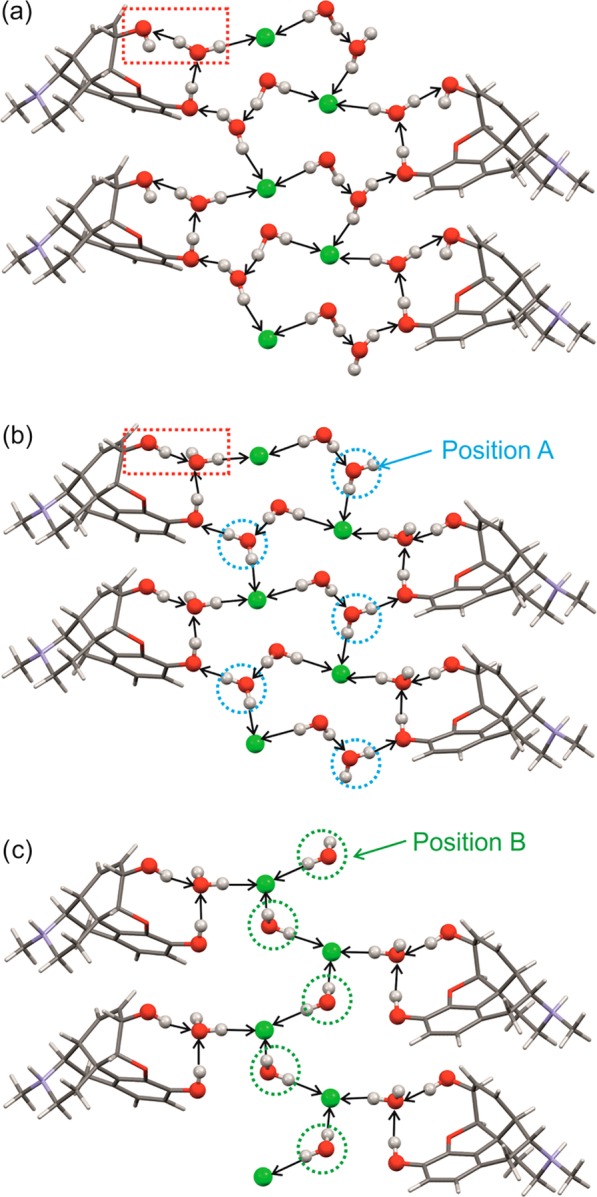
Model for the rearrangement of water molecules in morphine HCl hydrate after the computational removal of water molecule A: (a) experimental MCl-3H, (b) MCl-3Hcalc differing from (a) in the directionality of one hydrogen bond (red dotted box), and (c) MCl-2Hcalc.
3.5. Enthalpy of Hydrate/Anhydrate Transformation
3.5.1. Differential Scanning (DSC) and Isothermal Calorimetry (IC)
Using DSC (section 3.3.1) or IC,18,82 the enthalpy of the hydrate/anhydrate phase transformation was determined for all investigated compounds apart from DCl, for which no crystalline anhydrous form was found. According to eq 1, the dehydration enthalpy, ΔdehyHHy-AH, measured in open DSC pans, can be divided (applying Hess’s law) into a contribution from the vaporization of n water molecules and a contribution from the transition (ΔtrsHHy-AH) of the hydrate (Hy) to the anhydrate (AH):
| 1 |
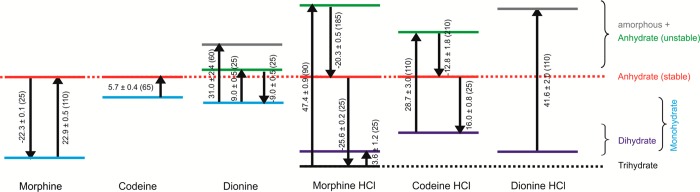
ΔtrsHHy-AH is estimated to be 22.9 ± 0.5 kJ mol–1 for M (Table 4 and Figure 13) and 5.7 ± 0.4 kJ mol–1 for C after the known enthalpy values of water83 at dehydration temperature are subtracted from the measured enthalpy of dehydration. MCl and CCl each dehydrate to a high energy form. The energy of the transformation from the hydrate to I°, obtained by the addition of the transition energies ΔtrsHHy-AH(unstable) and ΔtrsHAH(unstable)-I°, was 27.7 ± 1.3 kJ mol–1 for MCl and 15.9 ± 4.7 kJ mol–1 for CCl. ΔtrsHHy-AH values on the basis of DSC results could not be derived for D and its HCl salt as their respective dehydrations resulted in amorphous phases.
Figure 13.
Relative differences in the thermodynamic stability (enthalpy of transformation in kJ mol–1, temperature range 25 to 110 °C) between the solid forms of M, C, D, and their salts. Each solid form is denoted with a solid line. High energy forms are drawn at the top, low energy forms (more stable) at the bottom. The temperature of each measurement is given in parentheses (°C).
With IC, the enthalpy of dehydration (ΔdehyHHy-AH) and hydration (ΔhyHHy-AH) can be determined. Since the magnitude of the heat of condensation of water (ΔcondHH2O) is equal to the heat of vaporization of water, the transition energy of the AH to Hy (ΔtrsHAH-Hy) can be estimated according to eq 2:
| 2 |
Using a value of ΔvapH°H2O (25 °C) of 43.99 kJ mol–1 for −ΔcondH°H2O (25 °C)83 gives the ΔhyHHy-AH energies listed in Table 4 and Figure 13 for M, C, MCl, and CCl. Additionally it was possible to measure ΔdehyHHy-AH and ΔhyHAH-Hy for D. The enthalpy values derived from the two methods are in good agreement, despite the fact of the different temperature ranges of the measurements (DSC, 60 to 110 °C; IC, 25 °C). Furthermore, the heat of the transformation of MCl-3H to MCl-2H was estimated to be 3.6 ± 1.2 kJ mol–1 on the basis of IC experiments.
The thermodynamic stability order of the stable hydrates, calculated relative to the most stable anhydrate and independent of hydrate stoichiometry, is as follows: MCl-3H > M-1H > CCl-2H > D-1H > C-1H. The lower thermodynamic stability of D-1H and C-1H is in agreement with the lower dehydration temperatures of D-1H and C-1H (60–65 °C in contrast to 90–110 °C, section 3.3.1) and the RH-dependent dehydration of the hydrates (section 3.2.1).
3.5.2. Computed Energy Differences
According to eqs 3 and 4, a simple estimation of ΔdehyUHy-AH and ΔtrsUHy-AH can be made by comparing the lattice energy, Elatt, of the hydrate (the energy required to separate the static lattice into infinitely separated molecules in their lowest-energy conformation) to those of the anhydrate and ice:
| 3 |
| 4 |
Using the lattice energies of the experimental hydrate and anhydrate structures (Tables S24 and S25 of the Supporting Information) and a value of −59 kJ mol–179,80 for ice (the used functional is known to overbind the ice crystal structures84,85), a reasonable agreement with the experimental data is achieved for the three neutral hydrate/anhydrate systems. ΔtrsUHy-AH was calculated to be 20.83 kJ mol–1 for M, 5.57 kJ mol–1 for C, and 12.30 kJ mol–1 for D. These results not only confirm that hydrate formation is driven by a greater potential energy of the hydrates but also reproduce the experimentally derived thermodynamic stability order, despite the fact that the model neglects temperature effects.
Modeling salt structures and especially the energies thereof is a bigger challenge than for neutral structures.86−88 Applying the eqs 3 and 4 to the salts would give a ΔtrsUHy-AH of −23.11 kJ mol–1 for MCl (predicting that the hydrate is thermodynamically unfavored) and 21.57 kJ mol–1 for CCl. The CCl value is in reasonable agreement with the experimental value of 16.0 kJ mol–1, considering the modeling errors and temperature differences between calculated 0 K and experimental data (≥298 K). The only difference between the structures of MCl-3H and CCl-2H are water···water interactions, which are present only in MCl-3H. For the MCl-3H structure the energy estimate of the chosen methodology might not be appropriate, as has been seen in the energy calculations for ice polymorphs.84,85 For the transition of DCl-2H (no water···water interactions) to a computationally generated anhydrate structure (Figure S5e of the Supporting Information), which is isostructural with MCl-I° and CCl-I°, an ΔtrsUHy-AH value close to 80 kJ mol–1 was calculated. This clearly rules out this hypothetical structure as a possible experimental form. Similarly, the optimized hydrate framework structure is too high in energy (ΔtrsUHy-AH = 51 kJ mol–1) to be expected to be observed experimentally.
4. Discussion
4.1. Influence of Salt and Hydrate Formation on Molecular Conformation, Crystal Packing, and Stability
The systematic investigation of chemical analogues differing only in the substituents R = H, −CH3, or −CH2–CH3 (Figure 1) and their HCl salts has enabled us to study the influence of substitution and the presence of the counterion (Cl–) and water molecules on the crystal packing and stability of selected morphinanes, which extends a previous comparison study.35 The rigid geometry of morphinan units and limitation of possible symmetry elements (no inversion, glide/mirror symmetry) template the packing of the compounds. Nevertheless, for the three anhydrates (M- I°, C- I°, and D-I°) three distinct crystal structures are observed, which differ in packing and hydrogen bonding (inter- vs intramolecular). Substitution calculations by placing a “smaller” molecule into the unit cell of a “larger” molecule (M for C and M; C for D) and varying between inter- and intramolecular hydrogen bonding of O2–H gave only high energy structures for M (≥23 kJ mol–1). This suggests that the O2–H···N C11 (9) hydrogen bond is important for the stability of M-I°. For C a hypothetic energetically competitive structure was calculated. There seems to be only one preferred water position in the free base monohydrate structures. The water protons exclusively interact with the O2 and O3 atoms so that the morphine and codeine anhydrate conformations change due to the break of the intramolecular O3–H···O1 bond. The M and C hydrate conformations were calculated (MP2/6-31G(d,p), PCM ε = 3 level of theory) to be 17.0 kJ mol–1 (M) and 22.7 kJ mol–1 (C) less stable than the corresponding experimental I° conformations. (For potential energy surface scans, see Section 10 of the Supporting Information.) D-I° is the only anhydrate of the three free bases exhibiting intermolecular hydrogen-bonding. The calculated conformational energy differences of the forms of D base are smaller than for the other morphinanes, with the monohydrate conformation being only 4.6 kJ mol–1 less stable than the anhydrate conformation. This explains the facile anhydrate/hydrate phase transformation of D in contrast to M and C. Similar to the anhydrates, the monohydrates of the three free bases differ in their packing.
Salt formation eliminates the influence of the substituents of the morphinane molecules on crystal packing of the stable forms and leads to two sets of isostructures: stable anhydrates (MCl-I° and CCl-I°; Figure S5a,c of the Supporting Information) and the hydrates (MCl-3H, MCl-2H, CCl-2H, and DCl-2H; Figures 3b–d and S5b,d,f of the Supporting Information). The morphinanes in MCl-3H and MCl-2H/CCl-2H/DCl-2H are isostructural but show distinct modes of hydrogen-bond connectivity. The Cl– ion takes over the role of the water molecule of the monohydrates in the salt AH-I° structures and forms N–H···Cl– interactions in addition to the Ow–H···Cl– hydrogen bonds. The steric hindrance of the bigger −CH2–CH3 group (R, Figure 1) does not allow DCl to pack as densely as MCl and CCl (packing index of the computationally generated structures: MCl-I°calc = 73.7%, CCl-I°calc = 75.9%, and CCl-Icalc= 69.7%). The latter (calculated) structure is not sufficiently stable to be observed experimentally. When water molecules are present in the salt structures, the Cl– prefers to link to the water molecules instead of the N+–H group, and again, one of the water molecules adopts the corresponding water position of the free base monohydrate structures. The MCl hydrate framework can accommodate up to three moles of water per formula unit. By contrast, the isostructural CCl and DCl frameworks can accommodate only two moles of water per formula unit as the water position A of MCl-3H (Figure 10) is here occupied by the substituent R (−CH3 and −CH2–CH3). Only the first of the three MCl-3H water molecules can be released easily. Isostructural dehydration beyond the dihydrate stoichiometry was computed to be thermodynamically not feasible. The anhydrate and hydrate conformations can be related to the same minima, although there is a considerable energy difference of 11.8 kJ mol–1 for MCl and 19.0 for DCl, with the hydrate conformation being more stable. The inclusion of water molecules leads to a change in the hydrogen-bond network dimensionality, which increases from 1D in I° to 3D in the hydrates. This increase may account for the high stability of the HCl hydrates.
In all cases, with the exception of D, the dehydration leads to a new structure (not only an anisotropic shrinkage as earlier stated for M and MCl(35)), differing in the packing of the morphinane entity, despite maintaining the space group symmetry and similarities in the lattice parameters. Consequently, the physical properties of the hydrated and water free forms differ from each other.3,89
4.2. Comparison of Experimental and Computed Stability Differences
The applied experimental techniques give an insight into the thermodynamic and kinetic stability of the hydrate/anhydrate systems at temperatures ≥25 °C, covering the key variables temperature and RH for the investigation and screening of hydrate systems.90,91 Lattice energy calculations enable the estimation of potential energy differences at 0 K but do not provide information about temperature- and moisture-dependent effects. For the free bases, the calorimetric measurements (DSC and IC) gave the same qualitative result (thermodynamic stability order) as the computational approach (ΔtrsHHy-AH/ΔtrsUHy-AH: M > D > C). For the salt systems CCl and DCl, the calculations qualitatively predicted the experimental results. The energy difference of ΔtrsUHy-AH of approximately 80 kJ mol–1 explains convincingly why the DCl-Icalc (Supporting Information Figure S5e) is not observed experimentally. Our study also shows the limitation of the chosen method in calculating the energy of a salt structure exhibiting water···water interactions, MCl-3H. The calculated lattice energies indicate that MCl-I° should be more stable than MCl-3H, which contradicts the experimental findings. Recalculating the energies using the Grimme0692 dispersion correction instead of the TS gave the same qualitative result.
The use of the heat of vaporization/condensation at the respective dehydration temperature in calculations based on experimental enthalpies and the use of the lattice energy of ice in theoretical calculations gave adequate approximations, which allowed the estimation of ΔtrsHHy-AH and ΔtrsUHy-AH. Using different energy terms, i.e., vaporization and lattice energies, can be justified by the fact that experimentally we are separating the hydrate into the anhydrate and water vapor at temperatures above the melting point of ice (assuming that water evaporates from the liquid state), whereas computationally we “separate” the hydrate into infinitely separated anhydrate and water molecules (ideal gas) at absolute zero. This has already been addressed in one of our previous studies on phloroglucinol dihydrate.18
4.3. Insights From Lattice Energy Calculations into the (De)Hydration
The computational dehydration of an experimental hydrate structure, i.e., the removal of water molecules and subsequent relaxation (energy minimization) of the hypothetical lower stoichiometric hydrate or water-free structure can be a powerful tool to gain an insight into the dehydration at the molecular level.18,19 From structural and lattice energy differences between AH and the hypothetical lower stoichiometric hydrate or water-free structure, one can explain why a hydrate shows a stoichiometric (involving a phase change to a distinct crystalline or amorphous phase) or nonstoichiometic (hydrate with a range of continuously variable compositions that are not associated with significant changes in the crystal lattice, except for a minor anisotropic expansion to accommodate water) behavior.93 For nonstoichiometric hydrates, ΔtrsUHy-AH or ΔtrsUHy-Hy(lower water content) is expected to be in the energy range for polymorphic transformations and not accompanied by structural changes, cf. change in hydrogen bonding motif of MCl-3H/MCl-2H. Furthermore, with this technique, it may also be possible to derive models for experimental solid forms, which are not accessible to conventional determination by single crystal methods, e.g. for forms that exist only in a very narrow RH range. Thus, these computational tools can greatly enhance the characterization of solid forms and study of dehydration pathways.
5. Conclusions
The range of structures and solid forms for morphinanes has been considerably extended in this study. The structures of C-1H, D-1H, CCl-I°, CCl-2H, and DCl-2H were determined. Moreover, structure models were proposed for D-I° and morphine MCl-2H, two forms existing only in a very narrow RH range, based on the combined results of powder X-ray diffraction, IR spectroscopy, and lattice energy minimization techniques. High-energy anhydrates of MCl (III) and CCl (II), D-I°, C-II, and MCl-2H, an intermediate, have been reported for the first time.
The investigated hydrate systems differ considerably in the relative stability of their hydrated and anhydrous forms. The study of this phenomenon required the application of a range of different experimental techniques (X-ray diffraction, IR spectroscopy, differential scanning and isothermal calorimetry, and moisture sorption/desorption experiments) complemented with energy calculations (i.e., conformational, lattice, and interaction energies). Together they provided the basis for the understanding and interpretation of structural differences. In the free bases the substituents influence intermolecular interactions and crystal packing and therefore the stability, because they define the number of hydrogen bond donor groups and the steric characteristics around polar groups. However, such substituent effects are much less pronounced in the salts of the three analogues because their strongest intermolecular interactions involve the counterion Cl–. In each case the introduction of water molecules generates a hydrogen bonding network of higher dimension as there is a better match between the numbers of hydrogen bond donor and acceptor groups than in the anhydrates. This also explains the high propensity of morphinane homologues for the formation of hydrates. Practically all of the investigated hydrate phases (except MCl-2H and C-1H) can be classified as highly stable. As no transformation occurs at ambient conditions (40 to 60% RH at RT), no phase changes to anhydrous forms are expected during storage and handling. Also the anhydrate phases I° of M, MCl, C, and CCl are kinetically well stabilized and are not expected to transform to a hydrate at typical room climates. The fact that both, the hydrate and the anhydrous form of a drug substance, can exist within in a wide humidity range, makes the use of both species in solid dosage formulations possible. This may offer additional options for tuning the release characteristics of an active ingredient from a certain drug product.
The present study highlights that the understanding of the complex behavior of hydrates requires a thorough investigation of the structural and thermodynamic features of all involved hydrate and anhydrate phases. The combination of spectroscopic data with multivariate data analysis (IR and PCA) was found to be a very valuable tool to follow and elucidate structural dehydration mechanisms on the molecular level. The study also sets a benchmark for the computational modeling of hydrates and salt structures and for the quantitative prediction of energy differences of hydrate/anhydrate systems. The ability to accurately model hydrates, in particular the energy of water···water interactions in organic crystals, still needs improvement. However, the computational methods have rapidly advanced in the past few years94−98 and can now be seen as a complementary tool to experimental techniques.
Acknowledgments
We thank Judith Ulmer for experimental assistance and Dr. Simon Coles for the use of the SXRD instruments at Southampton. D.E.B. gratefully acknowledges funding by the Hertha Firnberg (FWF, project T593-N19) program of the Austrian Science Fund. The DFT-D calculations were supported by the Austrian Ministry of Science BMWF as part of the UniInfrastrukturprogramm of the Research Platform Scientific Computing at the University of Innsbruck.
Supporting Information Available
Crystallization experiments, gravimetric moisture sorption/desorption experiments, determination and analysis of crystal structures, powder X-ray diffraction, additional IR spectra, DSC thermograms and HSM photographs, transformation schemes, conformational analysis, representation of the experimental structures with DFT-TS, computational dehydration calculations, void space analysis, and .res files for D–Icalc and MCl–2Hcalc. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Byrn S. R.; Pfeiffer R. R.; Stowell J. G.. Hydrates and Solvates. In Solid-State Chemistry of Drugs, 2nd ed.; Byrn S. R., Pfeiffer R. R., Stowell J. G., Eds.; SSCI Inc.: West Lafayette, IN, 1999; pp 233–248. [Google Scholar]
- Haleblian J. K. Characterization of Habits and Crystalline Modification of Solids and Their Pharmaceutical Applications. J. Pharm. Sci. 1975, 64, 1269–1288. [DOI] [PubMed] [Google Scholar]
- Khankari R. K.; Grant D. J. W. Pharmaceutical Hydrates. Thermochim. Acta 1995, 248, 61–79. [Google Scholar]
- Malaj L.; Censi R.; Gashi Z.; Di M. P. Compression Behaviour of Anhydrous and Hydrate Forms of Sodium Naproxen. Int. J. Pharm. 2010, 390, 142–149. [DOI] [PubMed] [Google Scholar]
- Zhang G. G. Z.; Law D.; Schmitt E. A.; Qiu Y. Phase Transformation Considerations during Process Development and Manufacture of Solid Oral Dosage Forms. Adv. Drug Delivery Rev. 2004, 56, 371–390. [DOI] [PubMed] [Google Scholar]
- Raijada D.; Bond A. D.; Larsen F. H.; Cornett C.; Qu H.; Rantanen J. Exploring the Solid-Form Landscape of Pharmaceutical Hydrates: Transformation Pathways of the Sodium Naproxen Anhydrate-Hydrate System. Pharm. Res. 2013, 30, 280–289. [DOI] [PubMed] [Google Scholar]
- Koradia V.; Fontelonga de Lemos A. F.; Alleso M.; Lopez de Diego H.; Ringkjobing-Elema M.; Muellertz A.; Rantanen J. Phase Transformations of Amlodipine Besylate Solid Forms. J. Pharm. Sci. 2011, 100, 2896–2910. [DOI] [PubMed] [Google Scholar]
- Hilfiker R.Polymorphism in the Pharmaceutical Industry; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Brittain H. G.Polymorphism in Pharmaceutical Solids; Informa Healthcare: New York, 2009; Vol. 192. [Google Scholar]
- Storey R. A.; Ymén I.. Solid State Characterization of Pharmaceuticals; Wiley: Chichester, U.K., 2012. [Google Scholar]
- Vippagunta S. R.; Brittain H. G.; Grant D. J. W. Crystalline solids. Adv. Drug Delivery Rev. 2001, 48, 3–26. [DOI] [PubMed] [Google Scholar]
- Infantes L.; Chisholm J.; Motherwell S. Extended Motifs from Water and Chemical Functional Groups in Organic Molecular Crystals. CrystEngComm 2003, 5, 480–486. [Google Scholar]
- Braun D. E.Crystal Polymorphism of Drug Compounds: Statistical Aspects, Analytical Strategies and Case Studies. PhD Thesis, University of Innsbruck, 2008. [Google Scholar]
- Stahly G. P. Diversity in Single- and Multiple-component Crystals. The Search for and Prevalence of Polymorphs and Cocrystals. Cryst. Growth Des. 2007, 7, 1007–1026. [Google Scholar]
- Braun D. E.; Karamertzanis P. G.; Price S. L. Which, if Any, Hydrates will Crystallise? Predicting Hydrate Formation of Two Dihydroxybenzoic Acids. Chem. Commun. 2011, 47, 5443–5445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desiraju G. R. Hydration in Organic Crystals: Prediction from Molecular Structure. Chem. Commun. 1991, 6, 426–428. [Google Scholar]
- Stahl H. P.The Problems of Drug Interactions with Excipients. In Towards Better Safety of Drugs and Pharmaceutical Products; Braimar D. D., Ed.; Elsevier, North-Holland Biomedical Press: Amsterdam, The Netherlands, 1980; pp 265–280. [Google Scholar]
- Braun D. E.; Tocher D. A.; Price S. L.; Griesser U. J. The Complexity of Hydration of Phloroglucinol: A Comprehensive Structural and Thermodynamic Characterization. J. Phys. Chem. B 2012, 116, 3961–3972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun D. E.; Bhardwaj R. M.; Arlin J. B.; Florence A. J.; Kahlenberg V.; Griesser U. J.; Tocher D. A.; Price S. L. Absorbing a Little Water: The Structural, Thermodynamic, and Kinetic Relationship between Pyrogallol and Its Tetarto-Hydrate. Cryst. Growth Des. 2013, 13, 4071–4083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun D. E.; Karamertzanis P. G.; Arlin J. B.; Florence A. J.; Kahlenberg V.; Tocher D. A.; Griesser U. J.; Price S. L. Solid-State Forms of beta-Resorcylic Acid: How Exhaustive Should a Polymorph Screen Be?. Cryst. Growth Des. 2011, 11, 210–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun D. E.; Bhardwaj R. M.; Florence A. J.; Tocher D. A.; Price S. L. Complex Polymorphic System of Gallic Acid-Five Monohydrates, Three Anhydrates, and over 20 Solvates. Cryst. Growth Des. 2013, 13, 19–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- European Pharmacopoeia, 8th ed.; Council of Europe: Strasbourg, France, 2014. [Google Scholar]
- United States Pharmacopoeia, 36th ed.; United States Pharmacopoeial Convention, Inc.: Rockville, MD, 2013. [Google Scholar]
- In the current version of the European Pharmacopeia, morphine hydrochloride trihydrate, morphine sulfate (pentahydrate), codeine monohydrate, codeine hydrochloride dihdyrate, codeine phosphate hemihydrate and sesquihydrate, and ethylmorphine HCl dihydrate are listed in specific monographs. The United State Pharamcopeia specifies codeine, codeine phosphate, codeine sulfate, and morphine sulfate.
- Brownstein M. J. A. Brief History of Opiates, Opioid Peptides, and Opioid Receptors. Proc. Natl. Acad. Sci. U.S.A. 1993, 90, 5391–5393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrusevski G.; Ugarkovic S.; Makreski P. Solid-State Transformation of the Pseudopolymorphic Forms of Codeine Phosphate Hemihydrate and Codeine Phosphate Sesquihydrate Monitored by Vibrational Spectroscopy and Thermal Analysis. J. Mol. Struct. 2011, 993, 328–335. [Google Scholar]
- Narcotic Drugs: Estimated World Requirements for 2013 (Statistics for 2011); E/INCB/2012/2; International Narcotics Control Board: New York, 2012. [Google Scholar]
- Kofler L.; Kofler A. Melting Points and Crystal Forms of Morphine. Arch. Pharm. Ber. Dtsch. Pharm. Ges. 1933, 271, 387–392. [Google Scholar]
- Kofler L. Microchemistry of the Opium Alkaloids. Pharm. Monatsh. 1933, 14, 220–222. [Google Scholar]
- Kofler L.; Kofler A. Crystal Forms and Melting Points of Opium Alkaloids. Arch. Pharm. Ber. Dtsch. Pharm. Ges. 1934, 272, 537–545. [Google Scholar]
- Kuhnert-Brandstatter M.; Kofler A.; Heindl W. Thermomicroscopic Identification of Additive Drugs. Pharm. Acta Helv. 1975, 50, 360–372. [PubMed] [Google Scholar]
- Lindpaintner E. Microscopic Study of Polymorphic Substances. II. Mikrochemie 1939, 27, 21–41. [Google Scholar]
- Kuhnert-Brandstaetter M.; Proell F. Thermal Analysis of Hydrates of Organic Compounds. II. Mikrochim. Acta 1983, 3, 287–300. [Google Scholar]
- Allen F. H. The Cambridge Structural Database: A quarter of a Million Crystal Structures and Rising. Acta Crystallogr., Sect. B: Struct. Sci. 2002, 58, 380–388. [DOI] [PubMed] [Google Scholar]
- Guguta C.; Peters T.; de Gelder R. Structural Investigations of Hydrate, Anhydrate, Free Base, and Hydrochloride Forms of Morphine and Naloxone. Cryst. Growth Des. 2008, 8, 4150–4158. [Google Scholar]
- Gelbrich T.; Braun D. E.; Griesser U. J. Stable Polymorph of Morphine. Acta Crystallogr., Sect. E: Struct. Rep. Online 2013, 69, o2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bye E. The Crystal Structure of Morphine Hydrate. Acta Chem. Scand., Ser. B 1976, B30, 549–554. [Google Scholar]
- Scheins S.; Messerschmidt M.; Luger P. Submolecular Partitioning of Morphine Hydrate Based on its Experimental Charge Density at 25 K. Acta Crystallogr., Sect. B: Struct. Sci. 2005, 61, 443–448. [DOI] [PubMed] [Google Scholar]
- Duchamp D. J.; Olson E. C.; Chidester C. G. Morphine. ACA, Ser. 2 1977, 5, 83. [Google Scholar]
- Barnes F. Codeine. Can. J. Chem. 1954, 32, 984. [Google Scholar]
- Canfield D. V.; Barrick J.; Giessen B. C. Structure of Codeine. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1987, C43, 977–979. [Google Scholar]
- Bel’skii V. K.; Babilev F. V.; Arzamastsev A. P.; Simonova L. L. Structure of Two Codeine Crystalline Modifications. Khim.-Farm. Zh. 1988, 22, 506–509. [Google Scholar]
- Scheins S.; Messerschmidt M.; Morgenroth W.; Paulmann C.; Luger P. Electron Density Analyses of Opioids: A Comparative Study. J. Phys. Chem. A 2007, 111, 5499–5508. [DOI] [PubMed] [Google Scholar]
- Gelbrich T.; Braun D. E.; Griesser U. J. Morphine Hydrochloride Anhydrate. Acta Crystallogr., Sect. E: Struct. Rep. Online 2012, E68, o3358–o3359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gylbert L. Crystal and Molecular Structure of Morphine Hydrochloride Trihydrate. Acta Crystallogr., Sect. B: Struct. Sci. 1973, 29, 1630–1635. [Google Scholar]
- Barnes L. Codeine Hydrochloride Dihydrate. Can. J. Chem. 1955, 33, 565. [Google Scholar]
- Kofler L.; Kofler A.. Mikromethoden; Universitaetsverlag Wagner: Innsbruck, Austria, 1954. [Google Scholar]
- Oxford Diffraction; Oxford Diffraction Ltd.: Abingdon, Oxford, England, 2003. [Google Scholar]
- Coles S. J.; Gale P. A. Changing and Challenging Times for Service Crystallography. Chem. Sci. 2012, 3, 683–689. [Google Scholar]
- Burla M. C.; Caliandro R.; Camalli M.; Carrozzini B.; Cascarano G. L.; Giacovazzo C.; Mallamo M.; Mazzone A.; Polidori G.; Spagna R. SIR2011: a New Package for Crystal Structure Determination and Refinement. J. Appl. Crystallogr. 2012, 45, 357–361. [Google Scholar]
- Sheldrick G. M. A Short History of SHELX. Acta Crystallogr., Sect. A: Found. Crystallogr. 2008, 64, 112–122. [DOI] [PubMed] [Google Scholar]
- Farrugia L. J. WinGX and ORTEP for Windows: an Update. J. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar]
- SIMCA-P, v. 11.0; Umetrics AB: Umea, Sweden, 2007. [Google Scholar]
- Opus, v. 5.5; Bruker Optics: Ettlingen, Germany, 2005.
- Gelbrich T.; Hursthouse M. B. A Versatile Procedure for the Identification, Description and Quantification of Structural Similarity in Molecular Crystals. CrystEngComm 2005, 7, 324–336. [Google Scholar]
- Gelbrich T.; Threlfall T. L.; Hursthouse M. B. XPac Dissimilarity Parameters as Quantitative Descriptors of Isostructurality: the Case of Fourteen 4,5′-Substituted Benzenesulfonamido-2-pyridines Obtained by Substituent Interchange Involving CF3/I/Br/Cl/F/Me/H. CrystEngComm 2012, 14, 5454–5464. [Google Scholar]
- Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. J.; Refson K.; Payne M. C. First Principles Methods Using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
- Vanderbilt D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B 1990, 41, 7892–7895. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005–1–073005/4. [DOI] [PubMed] [Google Scholar]
- Cossi M.; Scalmani G.; Rega N.; Barone V. New Developments in the Polarizable Continuum Model for Quantum Mechanical and Classical Calculations on Molecules in Solution. J. Chem. Phys. 2002, 117, 43–45. [Google Scholar]
- Cooper T. G.; Hejczyk K. E.; Jones W.; Day G. M. Molecular Polarization Effects on the Relative Energies of the Real and Putative Crystal Structures of Valine. J. Chem. Theory Comput. 2008, 4, 1795–1805. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
- Macrae C. F.; Bruno I. J.; Chisholm J. A.; Edgington P. R.; McCabe P.; Pidcock E.; Rodriguez-Monge L.; Taylor R.; van de Streek J.; Wood P. A. Mercury CSD 2.0: New Features for the Visualization and Investigation of Crystal Structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar]
- Etter M. C.; MacDonald J. C.; Bernstein J. Graph-Set Analysis of Hydrogen-Bond Patterns in Organic-Crystals. Acta Crystallogr., Sect. B: Struct. Sci. 1990, 46, 256–262. [DOI] [PubMed] [Google Scholar]
- Bernstein J.; Davies R. E.; Shimoni L.; Chang N. Patterns in Hydrogen Bonding: Functionality and Graph Set Analysis in Crystals. Angew. Chem., Int. Ed. 1995, 34, 1555–1573. [Google Scholar]
- Gelbrich T.; Threlfall T. L.; Hursthouse M. B. Eight Isostructural 4,4′-Disubstituted N-phenylbenzenesulfonamides. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 2012, 68, o421–o426. [DOI] [PubMed] [Google Scholar]
- Gelbrich T.; Hursthouse M. B. Systematic Investigation of the Relationships between 25 Crystal Structures Containing the Carbamazepine Molecule or a Close Analogue: a Case Study of the XPac Method. CrystEngComm 2006, 8, 448–460. [Google Scholar]
- Griesser U. J.The Importance of Solvates. In Polymorphism: In the Pharmaceutical Industry; Hilfiker R., Ed.; Wiley-VCH: Weinheim, Germany, 2006; pp 211–233. [Google Scholar]
- Markvardsen A. J.; David W. I. F.; Johnson J. C.; Shankland K. A Probabilistic Approach to Space-Group Determination from Powder Diffraction data. Acta Crystallogr., Sect. A: Found. Crystallogr. 2001, 57, 47–54. [DOI] [PubMed] [Google Scholar]
- David W. I. F.; Shankland K.; van de Streek J.; Pidcock E.; Motherwell W. D. S.; Cole J. C. DASH: A Program for Crystal Structure Determination from Powder Diffraction Data. J. Appl. Crystallogr. 2006, 39, 910–915. [Google Scholar]
- Pawley G. S. Unit-Cell Refinement from Powder Diffraction Scans. J. Appl. Crystallogr. 1981, 14, 357–361. [Google Scholar]
- Braun D. E.; McMahon J. A.; Koztecki L. H.; Price S. L.; Reutzel-Edens S. M. Contrasting Polymorphism of Related Small Molecule Drugs Correlated and Guided by the Computed Crystal Energy Landscape. Cryst. Growth Des. 2014, 14, 2056–2072. [Google Scholar]
- Martens H.; Naes T.. Multivariate Calibration; Wiley VCH: Chichester, U.K., 1991. [Google Scholar]
- Jorgensen A. C.; Miroshnyk I.; Karjalainen M.; Jouppila K.; Siiria S.; Antikainen O.; Rantanen J. Multivariate Data Analysis as a Fast Tool in Evaluation of Solid State Phenomena. J. Pharm. Sci. 2006, 95, 906–916. [DOI] [PubMed] [Google Scholar]
- Cruz-Cabeza A. J.; Day G. M.; Jones W. Predicting Inclusion Behaviour and Framework Structures in Organic Crystals. Chem.—Eur. J. 2009, 15, 13033–13040. [DOI] [PubMed] [Google Scholar]
- Hydrate structures with water molecules removed.
- Shankland K.; David W. I. F.; Sivia D. S. Routine Ab Initio Structure Determination of Chlorothiazide by X-ray Powder Diffraction Using Optimized Data Collection and Analysis Strategies. J. Mater. Chem. 1997, 7, 569–572. [Google Scholar]
- Whalley E. The Difference in the Intermolecular Forces on H2O and D2O. Trans. Faraday Soc. 1957, 53, 1578–1585. [Google Scholar]
- Whalley E. The Hydrogen Bond in Ice. Hydrogen Bond 1976, 3, 1425–1470. [Google Scholar]
- Price S. L. Predicting Crystal Strucuture of Organic Compounds. Chem. Soc. Rev. 2014, 43, 2098–2111. [DOI] [PubMed] [Google Scholar]
- Zencirci N.; Gstrein E.; Langes C.; Griesser U. J. Temperature- and Moisture-Dependent Phase Changes in Crystal Forms of Barbituric Acid. Thermochim. Acta 2009, 485, 33–42. [Google Scholar]
- Riddick J. A.; Bunger W. B.. Techniques of Chemistry, Vol. 2: Organic Solvents: Physical Properties and Methods of Purification, 4th ed; Wiley-Interscience: New York, 1986; p 1072. [Google Scholar]
- Thierfelder C.; Hermann A.; Schwerdtfeger P.; Schmidt W. G. Strongly Bonded Water Monomers on the Ice Ih Basal Plane: Density-functional Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 045422–1–045422/5. [Google Scholar]
- Beran G. J. O.; Nanda K. Predicting Organic Crystal Lattice Energies with Chemical Accuracy. J. Phys. Chem. Lett. 2010, 1, 3480–3487. [Google Scholar]
- Karamertzanis P. G.; Anandamanoharan P. R.; Fernandes P.; Cains P. W.; Vickers M.; Tocher D. A.; Florence A. J.; Price S. L. Toward the Computational Design of Diastereomeric Resolving Agents: An Experimental and Computational Study of 1-Phenylethylammonium-2-phenylacetate Derivatives. J. Phys. Chem. B 2007, 111, 5326–5336. [DOI] [PubMed] [Google Scholar]
- Bardwell D. A.; Adjiman C. S.; Arnautova Y. A.; Bartashevich E.; Boerrigter S. X.; Braun D. E.; Cruz-Cabeza A. J.; Day G. M.; la Valle R. G.; Desiraju G. R.; van Eijck B. P.; Facelli J. C.; Ferraro M. B.; Grillo D.; Habgood M.; Hofmann D. W.; Hofmann F.; Jose K. V.; Karamertzanis P. G.; Kazantsev A. V.; Kendrick J.; Kuleshova L. N.; Leusen F. J.; Maleev A. V.; Misquitta A. J.; Mohamed S.; Needs R. J.; Neumann M. A.; Nikylov D.; Orendt A. M.; Pal R.; Pantelides C. C.; Pickard C. J.; Price L. S.; Price S. L.; Scheraga H. A.; van de Streek J.; Thakur T. S.; Tiwari S.; Venuti E.; Zhitkov I. K. Towards Crystal Structure Prediction of Complex Organic Compounds: A Report on the Fifth Blind Test. Acta Crystallogr., Sect. B: Struct. Sci. 2011, 67, 535–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohamed S.; Tocher D. A.; Price S. L. Computational Prediction of Salt and Cocrystal Structures: Does a Proton Position Matter?. Int. J. Pharm. 2011, 418, 187–198. [DOI] [PubMed] [Google Scholar]
- Sun C.; Grant D. J. W. Improved Tableting Properties of p-Hydroxybenzoic Acid by Water of Crystallization: A Molecular Insight. Pharm. Res. 2004, 21, 382–386. [DOI] [PubMed] [Google Scholar]
- Aaltonen J.; Alleso M.; Mirza S.; Koradia V.; Gordon K. C.; Rantanen J. Solid Form Screening: A Review. Eur. J. Pharm. Biopharm. 2009, 71, 23–37. [DOI] [PubMed] [Google Scholar]
- Cui Y.; Yao E. Evaluation of Hydrate-Screening Methods. J. Pharm. Sci. 2008, 97, 2730–2744. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-type Density Functional Constructed with a Long-range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [DOI] [PubMed] [Google Scholar]
- Brittain H. G.; Morris K. R.; Boerrigter S. X. M.. Structural Aspects of Solvatomorphic Systems. In Polymorphism in Pharmaceutical Solids, 2nd ed.; Brittain H. G., Ed.; Informa Healthcare: New York, 2009; Vol. 192, pp 233–281. [Google Scholar]
- Kazantsev A. V.; Karamertzanis P. G.; Adjiman C. S.; Pantelides C. C.; Price S. L.; Galek P. T.; Day G. M.; Cruz-Cabeza A. J. Successful Prediction of a Model Pharmaceutical in the Fifth Blind Test of Crystal Structure Prediction. Int. J. Pharm. 2011, 418, 168–178. [DOI] [PubMed] [Google Scholar]
- Bhardwaj R. M.; Price L. S.; Price S. L.; Reutzel-Edens S. M.; Miller G. J.; Oswald I. D. H.; Johnston B.; Florence A. J. Exploring the Experimental and Computed Crystal Energy Landscape of Olanzapine. Cryst. Growth Des. 2013, 13, 1602–1617. [Google Scholar]
- Ismail S. Z.; Anderton C. L.; Copley R. C.; Price L. S.; Price S. L. Evaluating a Crystal Energy Landscape in the Context of Industrial Polymorph Screening. Cryst. Growth Des. 2013, 13, 2396–2406. [Google Scholar]
- Kendrick J.; Stephenson G. A.; Neumann M. A.; Leusen F. J. Crystal Structure Prediction of a Flexible Molecule of Pharmaceutical Interest with Unusual Polymorphic Behavior. Cryst. Growth Des. 2013, 13, 581–589. [Google Scholar]
- Baias M.; Dumez J. N.; Svensson P. H.; Schantz S.; Day G. M.; Emsley L. De Novo Determination of the Crystal Structure of a Large Drug Molecule by Crystal Structure Prediction-Based Powder NMR Crystallography. J. Am. Chem. Soc. 2013, 135, 17501–17507. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.