Temperature and population density determine reservoir regions of seasonal persistence in highland malaria

Abstract

A better understanding of malaria persistence in highly seasonal environments such as highlands and desert fringes requires identifying the factors behind the spatial reservoir of the pathogen in the low season. In these ‘unstable’ malaria regions, such reservoirs play a critical role by allowing persistence during the low transmission season and therefore, between seasonal outbreaks. In the highlands of East Africa, the most populated epidemic regions in Africa, temperature is expected to be intimately connected to where in space the disease is able to persist because of pronounced altitudinal gradients. Here, we explore other environmental and demographic factors that may contribute to malaria's highland reservoir. We use an extensive spatio-temporal dataset of confirmed monthly Plasmodium falciparum cases from 1995 to 2005 that finely resolves space in an Ethiopian highland. With a Bayesian approach for parameter estimation and a generalized linear mixed model that includes a spatially structured random effect, we demonstrate that population density is important to disease persistence during the low transmission season. This population effect is not accounted for in typical models for the transmission dynamics of the disease, but is consistent in part with a more complex functional form of the force of infection proposed by theory for vector-borne infections, only during the low season as we discuss. As malaria risk usually decreases in more urban environments with increased human densities, the opposite counterintuitive finding identifies novel control targets during the low transmission season in African highlands.

1. Introduction

Highland regions in East Africa are located at the edge of malaria's transmission range due to seasonal rainfall patterns and low average temperatures, which limit the development of the parasite and the abundance of the mosquito vector [1,2]. In these regions of epidemiological transition, disease transmission is generally low, but exhibits intermittent seasonal outbreaks with high mortality and morbidity among large populations with low herd-immunity. Given that climate variables set the limits to the spatial distribution of the disease, changes in temperature and rainfall are expected to have direct effects on malaria transmission in these regions [3]. In particular, it has recently been shown that inter-annual variation in average temperatures can significantly expand and contract the spatial distribution of the disease, with implications for the impact of decadal warming trends [4].

Spatial variation in incidence is also important at the seasonal scale in relation to the persistence of the disease during inter-epidemic periods when transmission is at its lowest. Elevation, through its well-known relation with temperature, is expected to influence the distribution of areas where malaria transmission persists. A better understanding of persistence would require, however, additional consideration of spatial variation in demographic and environmental factors at sufficiently high spatial and temporal resolution. Although among demographic factors, human mobility has recently attracted attention [5–9], the role of population density remains poorly understood in the population dynamics of malaria and other vector-transmitted diseases. In particular, larger numbers of hosts in mathematical models generally dilute the number of vector bites and in so doing also decrease transmission rates [10]. In only a few zoonotic pathogens, namely hantavirus and lymphocytic choriomeningitis virus, have positive associations been reported between host population density and infection prevalence [11,12]. A more complex, non-monotonic, relationship has been proposed for vector-borne infections based on a theoretical framework that incorporates behaviour and encompasses different kinds of transmission [13]. Despite the large spatial variations in population density and associated socio-economic conditions, the question of whether and how these factors interact with temperature to maintain disease transmission remains open.

By combining an extensive 11-year-long record of monthly cases of exceptional spatial resolution and a spatially explicit statistical approach, we examine here the effects of demographic factors in concert with temperature. We specifically consider the influence of population density and access to roads (as a measure of human mobility) on the variability of malaria incidence during the low transmission season. We also consider other environmental factors that could confound our results by affecting soil water content and moisture retention of relevance to the availability of breeding habitats for mosquitoes [14,15]. Our analyses identify population density, in addition to temperature, as having a significant role in the spatial distribution of disease incidence during seasonal troughs. This adds a new dimension to dynamic malaria models during the low season that could guide more effective control as we discuss.

2. Material and methods

(a). Data

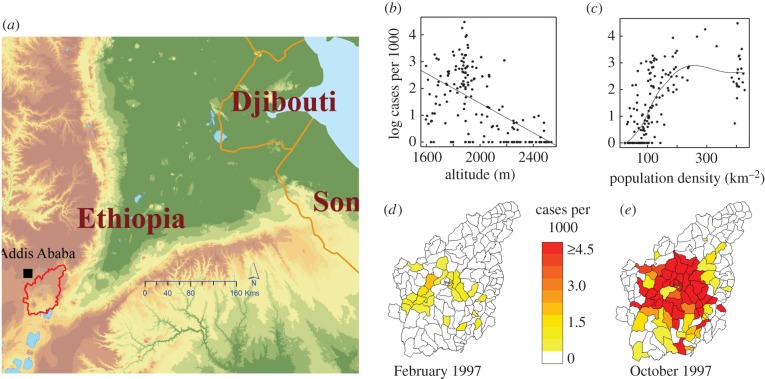
The malaria data consist of an 11 year (1994 through to 2005) time series of monthly Plasmodium falciparum cases, confirmed through microscopy examination of blood slides from clinical (febrile) individuals self-presenting at the health facilities of the Debre Zeit sector of Ethiopia (figure 1a). A total of 159 administrative units (known as kebeles each having an average area size of 23 sq. km) from this sector are comprised in these records (electronic supplementary material, Methods). In order to consider the seasonal dynamics, we aggregated the monthly data for each kebele into four-month blocks—January–April (JFMA), May–August (MJJA), September–December (SOND)—representing, respectively, the low, intermediate and high transmission seasons.

Figure 1.

Location of study area (a), log of number of P. falciparum cases per 1000 population in the low transmission season by altitude of kebele (b), and by population density of kebele (c). Illustration comparing the number of cases per 1000 population in two contrasting seasons—for the low (d) and high season (e), respectively (see also animation of monthly maps for the whole study period in the electronic supplementary material, video S1).

Each kebele further encompasses up to four smaller administrative subunits for which population data were obtained from the Central Statistical Agency of Ethiopia for 1994 and 2007 (CSA 1996, 2008). We interpolated these population data temporally based on growth rates between two censuses in 1994 and 2007 available at the level of four districts that contain the 159 kebeles, by separately considering changes in urban and rural populations. Spatial coordinates obtained from the Oromia Regional Bureau of Health, along with the population data, were used to weight all spatially explicit variables and obtain population weighted estimates for the kebeles.

Two estimates of population density were calculated by drawing circles with respective radii of 5 and 10 km around each kebele. The sum of the population that fell within each of these circles was divided by the circle's area. These values were then averaged at the kebele level. In addition, as a measure of human mobility, we considered distance to roads adjusted for the type of roads, based on the notion that some surfaces are more difficult and costly to traverse than others (electronic supplementary material, Methods).

Monthly mean temperature data were estimated for each location unit based on a temperature lapse rate developed from a combination of elevations and temperature readings at four meteorological stations (electronic supplementary material, Methods). Similarly, monthly rainfall data were obtained by interpolating readings from a maximum of 13 stations using ordinary Kriging (electronic supplementary material, Methods). All climate data were then aggregated at the kebele level, by taking a weighted average, using subunit population as the weight. Other climate-related variables considered include Sea Surface Temperature (SST) anomalies for the Niño 3.4 region and monthly average normalized difference vegetation index (NDVI) at a resolution of 0.1 degrees (electronic supplementary material, Methods).

In order to examine the role of other possible sources of mosquito breeding sites, we considered distances from subunits to perennial water bodies. In addition, we examined the ability of local soils to retain rain and flood water—water holding capacity, as well as landscape slopes (electronic supplementary material, Methods). Land-use change through deforestation was not considered here due to its small area impact, although it has been proposed to increase incidence in other regions [16–18].

Our intervention data consist of indoor residual spraying (IRS) operations at the kebele level during the 11 years spanned by the case data, obtained from the Oromia Regional Bureau of Health. A categorical binary value of 1 was assigned monthly to indicate presence of ‘effective’ IRS intervention whose duration corresponds to the residual effect of the insecticide sprayed (six months for DDT, three months for Malathion) [19].

(b). Selection of explanatory variables

We started our analysis by defining a suite of explanatory variables to be assessed for their association with malaria incidence during the low transmission season from January to April (JFMA), following the main transmission season from September to December (SOND). The low transmission season typically follows the coldest period of the year and receives the lowest rainfall (electronic supplementary material, figure S1). Because we expect the inter-annual variation in the cases for this season to be associated with inter-annual climate variability, we included mean temperature and total rainfall at different temporal aggregation windows, as well as NDVI and the Niño 3.4 SST anomalies, all at different lag periods for each kebele.

Because malaria represents a transmission system, the number of cases in one season should depend, in part, on the number of cases in prior seasons (e.g. [20,21]). We used here a lagged relative risk computed as the log-standardized ratio of observed SOND cases to the global expected seasonal malaria cases. The latter is the population in a kebele multiplied by a global estimate of the average seasonal malaria rate, a value estimated by dividing the total number of cases by the total population across all kebeles [20,21].

Owing to the large number of independent variables (n = 12), it was desirable to reduce this set before consideration of random effects which becomes computationally more demanding. To select among possible explanatory variables of the low season (JFMA) malaria cases, we used a generalized linear model framework. Because observed count data, such as reported cases in infectious diseases, often exhibit significant overdispersion [22], and our exploratory analysis confirmed this pattern for our data, we used a negative binomial distribution of cases. We used (backwards) stepwise model selection by the Akaike information criterion (AIC), implemented with the stepAIC function in the MASS package.

The negative binomial model used to select variables has the following general form:

2.1

and

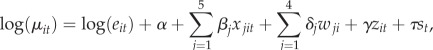2.2

where y_it is the number of JFMA cases for kebele i and year t, μ is the mean count of JFMA malaria cases, θ is a scale parameter (dispersion factor), e_it is the expected number of cases (the corresponding population multiplied by the global malaria rate), α is the intercept, β_j are coefficients of regression for x_j, the time and space varying factors including mean temperature and rainfall (with different lag periods), effective IRS status, population density and NDVI; δ_j are coefficients of regression for the w_j, non-time varying factors including slope, soil water capacity, water bodies and distance to roads; γ is the coefficient of regression for z_it, the prior season's log ratio of cases to the expected cases; and τ is the coefficient of regression for s_t, SST anomalies from the Niño 3.4 region.

(c) Generalized linear mixed model

After identifying the variables that are significantly associated with the JFMA count of cases, we tested these variables for their significance in a generalized linear mixed model (GLMM) framework that includes: (i) a spatially unstructured random effect and (ii) a spatially structured random effect. Spatially structured random effects explicitly account for spatial autocorrelations and weight relative risks in regions according to the relative risks in their neighbourhood. This is consistent with the latent effect of increased infectious disease risks from neighbouring regions of high transmission used in both mathematical [23–25] and statistical models [26,27].

We tested three different neighbourhood structures to represent the spatially structured random effect (electronic supplementary material, Methods). A normal conditional autoregressive (CAR) prior distribution is assumed for these structured spatial effects [28]:

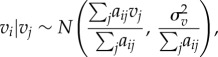2.3

where σ² controls the strength of local spatial dependence, and a_ij are neighbourhood weights for each kebele as defined above, with simple binary values of 1 when kebele i is a neighbour of kebele j, and 0 otherwise. Since the CAR distribution is improper, we applied a ‘sum to zero’ constraint on each v_i.

We chose a Bayesian Markov Chain Monte Carlo (MCMC) parameter sampling implementation in WINBUGS to estimate model parameters and their distributions [29]. We generated a sample of 10 000 parameters sets to generate our posterior distributions. The general form of the GLMM is as follows:

2.4

and

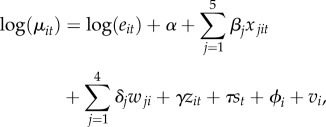2.5

where ϕ and ν are the unstructured and structured random effects, respectively. All other parameters are similar to those described in equation (2.2), as well as covariates (standardized here to zero mean and unit variance to aid convergence in the MCMC sampling). Model selection was based on the deviance information criterion (DIC), a goodness of fit measure for Bayesian models that penalizes for increasing model complexity [30].

3. Results

A temporal pattern of spatial expansion and contraction through the seasons is typically observed (figure 1d,e). This pattern can be followed in time in the form of an animated map (electronic supplementary material, movie S1). The documented changes suggest that a horseshoe-shaped area in the centre of the study region accounts for the majority of cases during the low transmission season and is associated with elevation differences (figure 1b). This contraction area would serve as the reservoir of the pathogen from which disease transmission spatially expands in the main season. Besides elevation (temperature), we are especially interested in the role played by human density because of the apparent increasing relationship observed for malaria cases (figure 1c). (Hereafter, ‘the reservoir’ and the ‘spatial reservoir’ of disease transmission refer to the spatial areas where cases are reported during the low season, and persistence specifically refers to this season. We do not consider here the particular usage of the term reservoir for the subpopulation that carries asymptomatic infections.)

The initial selection of significant explanatory variables revealed that rainfall and mean temperatures in December–February (DJF) are significantly associated with JFMA cases, as was the lagged malaria relative risk. Furthermore, population density obtained from circles of 5 km radius was the most significant non-climatic factor associated with JFMA cases. Neither proximity to roads nor other environmental factors were significant. The Niño 3.4 anomaly lagged by six months was dropped from further consideration despite being significantly associated with JFMA cases, as it was highly collinear with DJF rainfall.

Inclusion of the random effects (both structured and unstructured) resulted in the best model. Moreover, neighbourhood structure based on 10 km least-cost distance proximity (equivalent to 10 km paved roads and 5 km trail distance) proved to be best in capturing the random effects. Population density also contributed significantly when considered together with structured and unstructured random effects (table 1). During the low malaria season, the residual effect of IRS was not significant in all three models, despite a slight improvement of DIC over the models with non-structured random effect.

Table 1.

Comparison of goodness of fit for the different models tested based on the DIC. (Smaller DIC values signify better fit.)

model	DIC
(I) fixed effect only
(A) climate factors only	4346
(B) climate factors and population density	4333
(C) climate factors, population density and IRS status	4324
(II) fixed effect and unstructured random effect
(A) climate factors only	4277
(B) climate factors and population density	4275
(C) climate factors, population density and IRS status	4272
(III) fixed effect, unstructured and structured random effect
(A) climate factors only	4256
(B) climate factors and population density	4256
(C) climate factors, population density and IRS status	4258

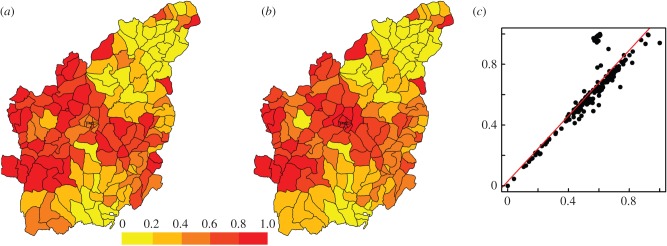
Importantly, population density and the spatial random effect seem to explain similar variation in JFMA cases, where the spatial random effect would compensate for population density when the latter is not included. Consistent with this observation, the spatial random effect alone in model III-A (with no population density) has high partial correlation with the sum of the spatial random effect and population density in model III-B (with population density) (figure 2 and table 1). This pattern is largely due to the fact that population density and the neighbourhood structure, which is defined through proximity measures, are closely related (figure 2c). Indeed, kebeles that have several population centres in their neighbourhood are also likely to fall in a region with high population density. The inclusion of population density in our model helps to explicitly define part of what would have been otherwise incorporated as structured random effects.

Figure 2.

Median structured random effect from model III-A (with no population density) (a), and the sum of median structured random effect and population density from model III-B (with population density) (b), both normalized to range between 0 and 1. The two random variables (respectively, in the x- and y-axes of plot (c) exhibit high association (r² = 0.76), indicating the importance of population density in explicitly defining the spatial structure in the malaria cases during the low season. The red line in plot (c) represents a linear regression line between the two effects.

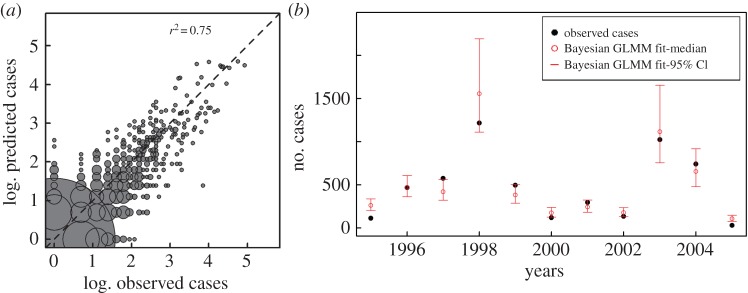
All parameters in the best model (with population density and both unstructured and structured random effects) are significantly different from zero, with posterior distributions from the two chains well mixed and converged (table 2). Comparisons of predictions and observations are illustrated in figure 3 and electronic supplementary material, figure S4. In general, their values for individual kebele-seasons (figure 3a; electronic supplementary material, figure S4), as well as for the aggregated kebeles for a given season (figure 3b), are in good agreement, with a slight tendency to under-predict at the high end of incidence values. Because we are considering the low season, the vast majority of kebeles exhibit no reported cases (62% of kebele-seasons) and our model correctly predicted 89% of these instances (figure 3a).

Table 2.

Coefficients of the best model for the low transmission season (JFMA) cases.

covariate		median	95% CIa
total DJF rainfall	β1	0.2001	[0.117, 0.280]	1.005
mean DJF temperature	β2	0.5299	[0.345, 0.723]	1.008
population density	β3	0.1055	[0.003, 0.204]	1.001
lagged malaria relative risk	γ	1.4270	[1.340, 1.518]	1.002
spatial unstructured hyper-parameter	σ2ϕ	0.3257	[0.134, 0.632]	1.001
spatial structured hyper-parameter	σ2ν	0.0026	[0.000, 0.042]	1.001
overdispersion parameter	θ−1	2.5190	[2.062, 3.098]	1.001

^aCI obtained from the 2.5% and 97.5% quantiles of each parameter's distribution.

Figure 3.

Comparison of predictions and observations for the GLMM model that includes structured and unstructured random effects. In (a), kebele-season predictions are plotted against observations in the log scale, with the identity line in the diagonal (dotted line). Predictions are generated by sampling from the posterior distribution of fitted parameters 10 000 times for 159 × 11 kebeles-seasons and computing the median cases from the simulations. Because the number of prediction–observation pairs at a given point can be (much) higher than 1 (e.g. 963 at the origin), we represent this number by the size of each circle centred at that pair. (Size is specifically scaled by the square root of the frequency.) Thus, although some predictions depart from observations for the kebeles and seasons with no cases, the instances of these discrepancies are very few compared to the bulk of correct predictions. Similarly, for observed non-zero cases, the majority of the predictions fall along the diagonal. See the electronic supplementary material, figure S4, for a version of this graph that includes another representation of the uncertainty around predictions. In (b), predictions of JFMA cases are aggregated for all kebeles and shown in time for the different years. From the 10 000 parameter combinations, the medians of the aggregated cases for a given season are shown together with the 95% credible intervals (CI) (the 2.5% and 97.5% quantiles of the simulated JFMA cases). The GLMM 95% CI include the observed cases 64% of the time (and 82% of the predictions within 7% of the CI intervals).

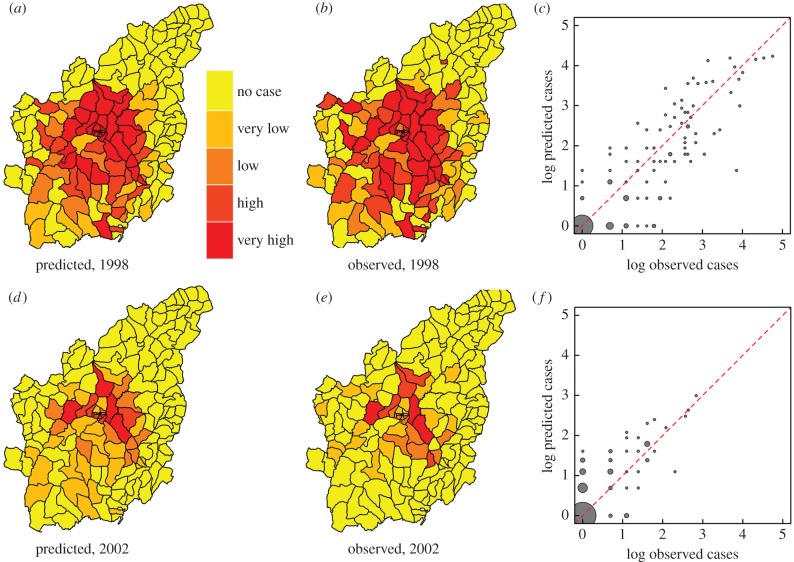
At the level of individual kebeles, figure 4 shows maps comparing observed and predicted cases on a quantile scale for both a high incidence year (1998, panels (a) and (b)) and a low incidence year (2002, panels (d) and (e)). We observe correct quantile predictions for 67% and 89% of kebeles, respectively (figure 4c,f). Similar results are obtained for other years (electronic supplementary material, figure S3). In general, quantiles of JFMA cases are correctly predicted for 70% of all kebele-seasons (electronic supplementary material, table S1).

Figure 4.

Comparison of observed and predicted JFMA cases for 1998 (a–c) and 2002 (d–f). The maps' colour progresses from yellow to red based on quantiles generated by considering all zero cases in one class and by subdividing all remaining non-zero JFMA cases into four equal-sized intervals. The resulting categories correspond to no cases, very low, low, high and very high cases. Comparisons of the quantiles in the maps reveal 67% and 89% of their values correctly match in the years 1998 and 2002, respectively. The scatter plots (c,f) show predicted against observed cases (in logarithmic scale) and include the identity line (in red) for comparison. The sizes of the circles correspond to the number of prediction–observation pairs at a given point (see caption of figure 3 for details). The point, with the highest number (n = 67 for 1998 and n = 107 for 2002) is obtained for (0, 0).The linear association between the observations and predictions is high with respective R² values of 0.79 and 0.63 for 1998 and 2002.

By contrast with the low season, malaria cases in the main season (SOND) were neither significantly associated with rainfall nor with population density, while the effect of IRS status became significant. Mean temperature however remained significant in both seasons (see the electronic supplementary material, table S2).

We confirmed the robustness of our results for the low season, by fitting a model only to the data for the first 6 years (1995–2000). Apart from rainfall, all identified parameters remained significant at 0.05 significance level (electronic supplementary material, table S3), and the model predicted post-2000 data reliably (electronic supplementary material, figures S5 and S6).

4. Discussion

As clearly visible in the animated malaria maps (electronic supplementary material, movie S1), and exemplified in figure 1d,e for the trough and following large peak of 1997, the spatial distribution of malaria expands and contracts as we transition from high to low seasons in a way that at first sight might appear simply related to elevation (or equivalently, to temperature). Our results indicate however that while climate factors play an important role, it is their combined effect with population density that maintains a reservoir of disease transmission and explains the spatial heterogeneity of persistence during the troughs between transmission seasons. Population density helps explicitly define the spatial effects identified in the statistical models. In particular, areas of persistence, where malaria transmission continues in the low season, are largely confined to interconnected population centres forming a horseshoe-shaped stretch of land with population densities ranging from 150 to 700 persons (or 30–80 households) per square km (cf. figure 1c and electronic supplementary material, figure S2a). Population density does not appear to play a role during the main transmission, suggesting a role during inter-epidemic persistence of the disease rather than in the epidemics themselves.

Our study area, which is located at average elevation of 2000 m.a.s.l., has marginal temperatures both for the vector (breeding) and the parasite's development within the vector (sporogony). As suitable vector breeding sites generally decline from rural to urban settlements in Africa [31–34], the finding of higher malaria incidence in suburban rather than in more rural areas during the low transmission season is therefore surprising. Higher population densities may provide not only indoor microclimates with higher ambient temperatures but also higher concentrations of attractants such as carbon dioxide and human odours that guide host seeking by the vector [35]. Higher house occupancy rates could contribute to higher temperatures that permit prolonged sporogony and transmission during the low malaria season. Moreover, (semi)-hibernating mosquitoes continue to feed indoors without the requirement to leave the dwelling for oviposition. Higher occupancy rates will therefore also increase the contact rate between infectives and susceptibles and the probability that an infected vector transmits the parasite. Clustering of malaria cases within households was indeed a common observation in the early 1900s in the Netherlands, where ‘winter transmission’ was not uncommon [36]. Today, people who settle in densely populated, peri-urban areas in East African highlands are often met with inadequate health facilities, a situation exacerbated by poverty, low levels of education and poor infrastructure [32]. They are also involved in economic activities (agriculture, in our case) that demand higher mobility, which together with the higher population density elevate the risk of infection. Higher population numbers in a given area may also alter the agricultural landscape in ways that create additional recruitment sites for the vector [37].

Areas of higher density might also coincide with those of higher immigration from lower, more endemic regions, which would import asymptomatic cases that contribute to persistent transmission. Our results however indicate that human mobility as represented by a simple proximity to roads is not significantly associated with the distribution of cases in the low season. There are only a few roads in the region, and trails rather than roads tend to have wider use, especially in the dry season. Using weighted proximity (as opposed to geographical adjacency) as a basis for neighbourhoods appears effective in capturing human movement patterns that influence disease incidence. This observation is consistent with other studies that used proximity measures as opposed to adjacency measures [23–25]. Moreover, our results confirm significant spatial autocorrelation as expected for vector-borne infections from similar studies [26,27].

In addition to human mobility, vector mobility can also affect low season transmission. The seasonal migration of vectors to microclimates (to warmer or less arid environments) more conducive to bridging periods unfavourable for reproduction has been reported for various Anopheline species [38], and a retreat of vectors to lower elevations during colder months is conceivable. Suburban settlements in highlands with higher population densities may attract larger fractions of migrating vectors than rural areas. During unfavourable climatic conditions, adult survival takes preference over breeding in many Anopheline vector species. Semi-hibernating (or aestivating in arid climates) females [39] continue to feed (and transmit malaria) without breeding. The associated increased lifespan of this condition would turn the vector into a more important reservoir for malaria during the low season.

Increases in mean temperature during the period between December and February have a delayed prompting effect on transmission in the low transmission season (January to April). Since this period includes the coldest months of the year, our results imply that higher DJF temperatures can limit the seasonal inhibition on the development of parasites, the population growth of vectors and their biting frequency [2,40,41]. This finding is consistent with the demonstrated temperature effects on malaria transmission in highland regions, where warmer years contribute to increases in the intensity of the disease [4,20,42].

Higher DJF rainfall may also aid malaria transmission during the low season, a period of low precipitation. The significance of higher DJF rainfall may also operate though increasing humidity (and longevity), rather than through increased breeding. Regardless of mechanism, evidence for a rainfall effect is weak in our model, in the sense that it is not robust to consideration of fewer years. For the main transmission season (SOND), we observe a reverse effect of inter-annual rainfall, where higher levels in the preceding wet months of JJA decrease malaria incidence in SOND, most likely due to a wash out effect on mosquito habitats. Earlier studies have not identified relative humidity as a relevant factor in the Debre Zeit area for this period [43].

Although IRS was not identified here as significant for the low season, it is found to be a major factor in the main transmission season (electronic supplementary material, table S2). IRS operations in our study area exclusively target the main season 90% of the time and thus provide no protection in the low transmission season.

The use of host population size as the only demographic factor in malaria transmission models may be insufficient for low intensity regions (and seasons) with high spatial heterogeneity in incidence levels. A spatially resolved dynamical model would require a more explicit characterization of differences in demographic factors, especially population density to capture its heterogeneity. Along these lines, a recent study on the spatial heterogeneity of malaria risk in a region of low transmission with similar seasonal patterns suggests the importance of considering risk ‘hot spots’ at different spatial scales [44].

The results presented here specifically make a case for revising the functional form of the force of infection (rate of infection of a susceptible individual) used in dynamical process-based models for the population dynamics of malaria. These models are typically variations of the original formulation in the Ross–MacDonald equations and assume that transmission is ‘frequency-dependent’ and its rates depend on the ‘mosquito per human’ ratio [1,45]. As such, they introduce an inverse relationship between the force of infection and the host population numbers (or density). A theoretical argument that explicitly incorporates behavioural considerations proposes a more complex function with an increase at low host numbers (densities), and saturation followed by a decrease at higher values. Our model results are consistent with this pattern at low densities and our observations in figure 1c support a nonlinear form possibly saturating at high densities, if not decreasing, although multiple mechanisms outlined above are possibly at play that go beyond the specific assumptions in [13]. In particular, the additional complexities introduced by explicit space and the violation of well-mixed systems [46] have been ignored in this discussion; they make host density and host numbers no longer interchangeable.

The results presented here also make a case to strengthen control during the low transmission season in rural areas with higher population densities. Such control measures would consist of targeting the spatial reservoir of the pathogen in humans (finding and treating symptomatic and non-symptomatic carriers) and/or the vector (additional rounds of IRS). These measures would improve cost effectiveness and aid existing initiatives to eliminate malaria from African highlands. Our findings could be relevant to other locations with seasonal malaria.

Data accessibility

The data used in this study are available at Dryad (http://dx.doi.org/10.5061/dryad.kc20m).

Authors' contributions

A.S.S., M.S.-V., M.J.B. and M.P. conceived and designed the study. A.S.S. and M.S.-V. performed the analysis with input from D.S.R., M.J.B. and M.P. All authors wrote the manuscript. A.S.S., A.K.Y. and D.Y. participated in the data collection.

Competing interests

We declare we do not have any competing interest.

Funding

Malaria data entry and GPS data collection were funded by a grant from the WHO (RBM/WHO).