Dynamic sensitivity and nonlinear interactions influence the system-level evolutionary patterns of phototransduction proteins

Abstract

Determining the influence of complex, molecular-system dynamics on the evolution of proteins is hindered by the significant challenge of quantifying the control exerted by the proteins on system output. We have employed a combination of systems biology and molecular evolution analyses in a first attempt to unravel this relationship. We employed a comprehensive mathematical model of mammalian phototransduction to predict the degree of influence that each protein in the system exerts on the high-level dynamic behaviour. We found that the genes encoding the most dynamically sensitive proteins exhibit relatively relaxed evolutionary constraint. We also investigated the evolutionary and epistatic influences of the many nonlinear interactions between proteins in the system and found several pairs to have coevolved, including those whose interactions are purely dynamical with respect to system output. This evidence points to a key role played by nonlinear system dynamics in influencing patterns of molecular evolution.

1. Introduction

The flood of genomic and molecular data that has become available in recent years has permitted the investigation of high-level trends in molecular evolution, particularly in the context of whole biochemical systems, with an aim of unravelling the diverse selective pressures acting on proteins. To date, studies on the patterns of molecular evolution within systems have largely focused on representing the systems as networks, in which proteins are represented as nodes and their interactions as the edges that connect them. Graph-topological properties of the proteins are then calculated, and correlations between these properties and the evolutionary histories of the genes are measured [1–12]. While correlations between network topology and molecular evolutionary histories (e.g. between node centrality and evolutionary rates) were found by all, the observed relationships varied from system to system. Thus, there is still no general principle relating the structure of biomolecular networks to molecular evolutionary patterns.

A shortcoming of the network approach is that it treats molecular systems as static entities, defined solely by the existence or absence of interactions between them. That is, it does not consider important dynamic relationships between proteins. Recent studies on molecular evolution in metabolic pathways have begun to consider the influence of system dynamics on natural selection via estimates of the metabolic flux or flux control distributions of the pathways. These are a means of quantifying the flow of metabolites through the pathway and the degree of control that each enzyme has on this flow. In an early study, Vitkup et al. [13] found that yeast proteins carrying high metabolic flux evolved under exponentially stronger selective constraints. More recently, Colombo et al. [14] compared the metabolic fluxes of the erythrocyte core metabolic reaction network with molecular evolutionary rates and found, like Vitkup et al. [13], that enzymes that carry high fluxes have been more constrained in their evolution. Meanwhile, Olson-Manning et al. [15] found that the first upstream enzyme in the alipathic glucosinolate pathway of Arabidopsis thaliana has higher flux control, and that this protein is the only one to show evidence of selection. Though these studies have highlighted some of the processes underlying molecular evolution within metabolic pathways, their methodologies cannot be easily applied to other molecular systems, such as signalling networks. While these methodologies certainly present a more dynamic view of the system than network-based methods would, the steady-state assumption in calculating a metabolic flux distribution or flux control coefficients precludes any assessment of the adaptive influence of non-equilibrium dynamic behaviour. Thus, it is difficult to draw a connection between flux coefficients and the phenotype, which creates a challenge in interpreting flux-based, system-level evolutionary analyses of metabolic pathways.

In order to gain insight into the selective significance of the non-equilibrium system dynamics in molecular evolution, a non-trivial but well-characterized pathway is necessary. Perhaps one of the most well-understood signalling pathways is visual phototransduction, an archetypal G-protein signalling cascade. Phototransduction is the process by which a visual stimulus is converted to a neuronal response. In vertebrates, a light stimulus is absorbed by a visual pigment associated with the receptor, rhodopsin, triggering a conformational change. A heterotrimeric G protein, transducin, binds the activated rhodopsin, which catalyses the exchange of GDP for GTP on the G_tα subunit of transducin, leading to the dissociation of the G protein. G_tα is then free to activate the signal effector, a phosphodiesterase (PDE6), resulting in the hydrolysis of cyclic GMP (cGMP). Falling cGMP concentrations lead to the closure of cGMP-gated ion channels, causing a drop in the cytoplasmic Ca²⁺ concentration and a subsequent hyper-polarization of the cell, which initiates the neuronal signal. Several parallel processes then act to recover from the signal, via deactivating the receptor and the effector and re-opening the ion channels, in order to prepare the cell to respond to further stimuli. Falling Ca²⁺ concentrations activate multiple feedback mechanisms, which tightly regulate the deactivation of the receptor, the re-synthesis of cGMP and the affinity of the ion channels for cGMP. For a detailed overview of the molecular mechanisms of phototransduction, see Pugh Jr & Lamb [16] or Yau & Hardie [17].

Recently, a comprehensive model of phototransduction has been developed to simulate the murine phototransduction response [18]. Following ideas proposed by Gutenkunst [19], by applying a parameter sensitivity analysis to this model, we could make an estimate of the impact of functional variations in the system's proteins on the dynamics of the photoresponse. The system-level phenotype was quantified through four electrophysiological characteristics of the photoresponse, which are in common usage for capturing important functional characteristics of phototransduction. They represent high-level, salient features of the system dynamics that conceivably have been evolutionarily relevant during mammalian divergence. We then investigated whether there exists any relationship between the evolutionary histories of the proteins and the sensitivity of the system to their functional variation in order to gain insight into how genetic variants influence function and thus are filtered by natural selection. Finally, we perturbed pairs of parameters together in order to predict whether any potential nonlinear interactions exist between genes of the phototransduction system and we compared this with evidence for coevolution between the proteins of the system.

2. Results

(a). Parameter sensitivity

We first investigated the local sensitivities of the model parameters in order to determine the degree of influence each parameter has over the response. Parameter sensitivity was estimated for four electrophysiological properties of the photoresponse which characterize high-level features of the system dynamics under different light stimulus regimes. Under dim light conditions, we measured the peak amplitude and the time constant of signal recovery (τ_rec); under bright light conditions, we measured the duration of signal saturation before recovery and the rate at which this time increases with greater stimulus intensities (τ_D). For an illustration of the four electrophysiological features, see electronic supplementary material, figure S1.

Parameter sensitivity values spanned several orders of magnitude, and even after log-transformation their distribution remained skewed towards higher sensitivity values (electronic supplementary material, figure S2). Because we measure parameter sensitivity empirically, based on an arbitrarily chosen perturbation size of 1%, we checked for extreme changes in the empirical measurement functions over a large range of perturbation sizes. Such extremes might indicate less reliable initial parameter values or that a smaller perturbation size would be needed. For each parameter, we generated 39 models in which the parameter value was set between 5% and 195% of its default value. We then simulated flash responses to dim and bright stimuli with each model, and measured the peak amplitudes, τ_rec values, saturation times and τ_D values for each one (for two examples, see electronic supplementary material, figures S3 and S4). In all cases, the magnitude of change in the electrophysiological measurements was relatively small for minimal perturbation sizes. For some parameters, such as kRGS1 (electronic supplementary material, figure S3), significant effects could be seen for large perturbations (less than 50% of the original value).

(b). Gene dynamic sensitivity

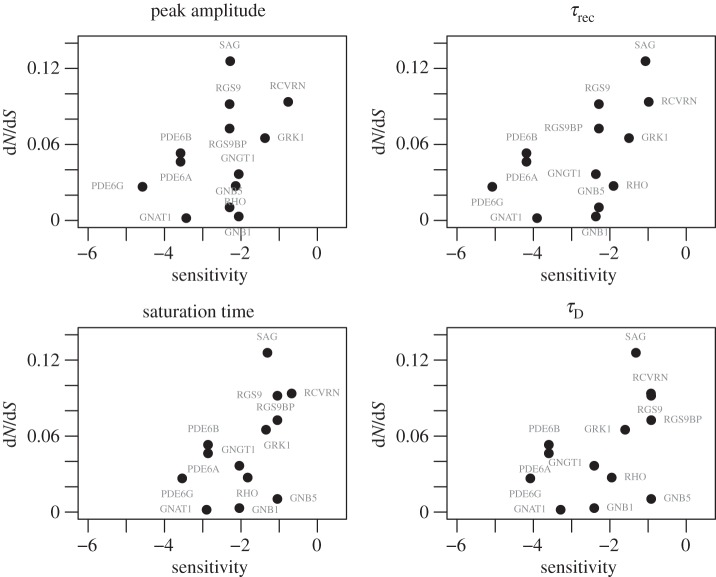
Plotting the ratio of the rates of non-synonymous nucleotide substitutions to synonymous substitutions during species divergence, dN/dS, against gene sensitivities shows similar positive trends for the four electrophysiological measurements (figure 1); however, the sensitivities of individual genes varied for the different measurements. We performed Spearman's rank correlation test to determine the significance of these relationships. Of these, two tests were significant: τ_rec (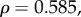 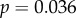) and saturation time (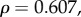 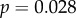). Peak amplitude (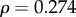, ) and τ_D (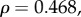 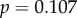) showed no significant relationship with dN/dS. The correlation between dN/dS and the mean sensitivity for each gene was also found to be significant (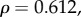 ; figure 2).

Figure 1.

dN/dS plotted as a function of gene dynamic sensitivities for the four electrophysiological measurements.

Figure 2.

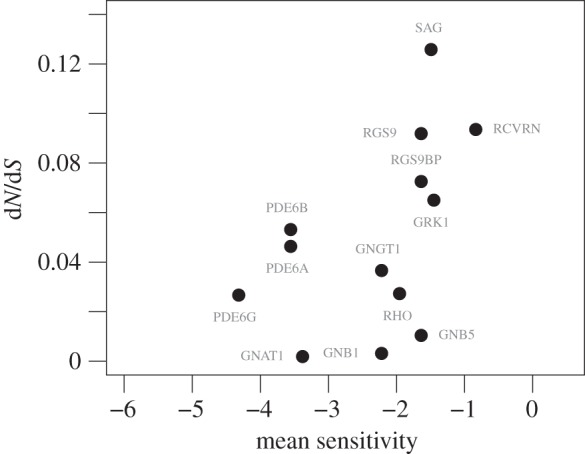
dN/dS plotted as a function of the average sensitivity for each gene.

Because a strongly negative correlation between expression levels and evolutionary rates has previously been identified in yeast [20,21], expression may be a confounding factor in our analysis. We checked the baseline expression patterns of the genes in a panel of RNA-seq data from 53 different human tissues [22], as provided by the Expression Atlas service (https://www.ebi.ac.uk/gxa/experiments/E-MTAB-2919) [23]. The retina was not included in this dataset. Of the phototransduction genes that we studied, only GNB1 showed high expression across many tissues, with a mean of 47.21 fragments per kilobase of transcript per million mapped reads (FPKM) and standard error (s.e.) of 2.51; GNB5 (mean 2.93 FPKM, s.e. 0.343) and RGS9 (mean 2.57 FPKM, s.e. 0.687) also showed moderate expression levels. The other genes, if present, only showed low expression (PDE6B: mean 1.84; others: mean of less than 1 FPKM). We found no significant correlation between dN/dS and mean expression levels, nor were significant correlations found between our sensitivity measurements and mean expression levels (peak amplitude: 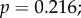τ_rec: 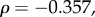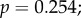saturation time: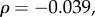 τ_D: 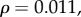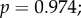average sensitivity: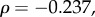 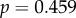). While transcript levels for these genes are not available for the retina, protein quantities for the genes were found in the literature to be in the range of 1 × 10⁵ to 1 × 10⁸ copies per rod photoreceptor outer segment during construction of the phototransduction model [18]. These protein quantities also do not correlate with dN/dS ( 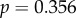). This lack of a correlation between expression and dN/dS agrees with recent data that show that in mammals this relationship is weaker than expected [24].

While mean expression levels showed no correlation with dN/dS, broad expression patterns should cause proteins to evolve under a larger range of selective pressures. Thus, constraint on GNB1, for example, is not exclusively the result of selection on the phototransduction system. When we removed the three proteins showing the highest mean expression levels outside the retina (GNB1, GNB5 and RGS9), the previously found correlations between dN/dS and the gene sensitivity measurements became more significant: τ_rec (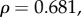 ), saturation time (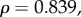 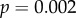) and mean sensitivity (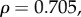 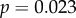). Additionally, the correlation between dN/dS and τ_D became significant with the removal of these genes ( 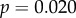). The relationship with peak amplitude remained insignificant ( ).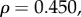

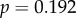(c). Non-additive phenotypic effects

We next used the model to determine whether any non-additive interactions exist in the dynamics. Such nonlinearity would indicate functional interdependence between the proteins' activities, which would have strong implications for their evolution. We tested for non-additive interactions between parameters by checking for equality between the effect of simultaneously perturbing two parameters and the sum of the effects of perturbing each of these two parameters individually. Deviance from equality of these two measurements would indicate a nonlinear interaction between the parameters. For each of the four empirical measurements of phototransduction, every pair of parameters showed a difference in effect size between the ‘double mutant’ and the sum of the ‘single mutants’. Thus, all parameter pairs show at least some degree of nonlinearity in their interactions. The magnitudes of these differences from linearity were small, concomitant with the small, 1% parameter perturbations (ranges in terms of absolute base-2 logarithms of the fold-change—peak amplitude: 2.31 × 10⁻¹² to 7.76 × 10⁻⁵; τ_rec: 5.06 × 10⁻¹⁴ to 1.79 × 10⁻⁴; saturation time: 6.16 × 10⁻¹¹ to 3.55 × 10⁻⁵; τ_D: 2.23 × 10⁻¹⁰ to 5.27 × 10⁻⁵). While the smallest effects are arguably negligible, the larger nonlinear effects point to potentially significant interactions across the network that could have selective relevance, particularly with mutations of larger effect. The parameter pairs showing the highest magnitude of differences from linearity for each empirical measurement are listed in electronic supplementary material, table S5, and are discussed further below.

(d). Coevolution

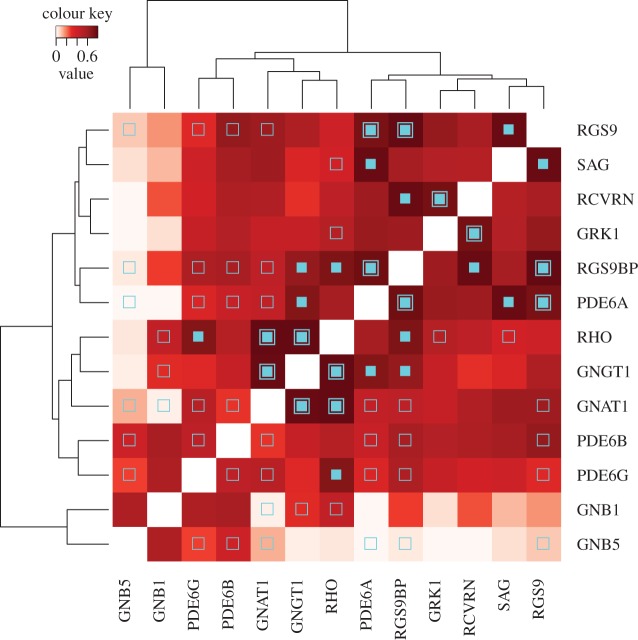
Nonlinear dynamic interactions between proteins can result in epistasis and subsequent coevolution between genes. Thus, we measured the degree of coevolution between the phototransduction genes by calculating the correlation of their phylogenetic trees using the MirrorTree method [25] (see electronic supplementary material, figures S5–S17 for the phylogenetic trees and table S4 for the MirrorTree correlation coefficients). The gene pair GNAT1–RHO (α-transducin–rhodopsin) showed the highest phylogenetic correlation coefficient, consistent with previous assertions of coevolution between G proteins and their receptors [26]. Using this pair as a reference, we tested the other gene pairs for significant evidence of coevolution. Pairs of genes with correlation coefficients that do not differ significantly from that of the reference (with a confidence of 0.05) were then taken to show evidence of coevolution themselves. Thirteen additional gene pairs were found in this way to have coevolved (figure 3).

Figure 3.

Hierarchically clustered phylogenetic tree correlations between phototransduction genes. High correlation values (dark red) indicate evidence of coevolution between the pair. Open square symbols indicate pairs that physically interact (directly or via a molecular complex), closed squares indicate pairs that show statistically significant evidence of coevolution and closed squares nested within open squares indicate physically interacting pairs that show significant evidence of coevolution.

Several of the coevolved protein pairs correspond neatly to the strongest nonlinear parameter interactions (electronic supplementary material, table S5). Some cases involve proteins that physically interact and correspond to parameter pairs whose interaction is readily understood. For example, the rate of binding of activated, α-transducin-bound PDE6 with its regulatory protein RGS9-1 (kRGS1) and rates of cGMP hydrolysis by PDE6 (β_dark, β_sub) have strong nonlinear interaction effects on peak amplitude, τ_rec and saturation time. Of the proteins involved in these processes, a PDE6 catalytic subunit (PDE6A) shows significant evidence of coevolution with RGS9-1 (RGS9) and with RGS9-1's anchor protein (RGS9BP). Similarly, the parameters for the interaction between rhodopsin kinase and its regulatory protein recoverin (kRec3, kRec4) show strong nonlinear interactions with the parameters governing a conformational change of recoverin that modulates in its regulation of the kinase, affecting peak amplitude and saturation time. This is potentially reflected in the significant evidence of coevolution between the genes encoding the kinase (GRK1) and recoverin (RCVRN). However, in these cases, because the proteins physically interact, one would more typically ascribe the coevolution simply to maintaining the proteins' ability to bind each other.

More interesting are the cases where proteins that do not physically interact were found to show evidence of coevolution. Two regulatory proteins, RGS9-1 (RGS9) and arrestin (SAG), appear to have coevolved despite regulating two different proteins (the activated PDE6 complex and activated rhodopsin, respectively). In the model, we find parameter pairs associated with these two proteins among the parameter pairs showing the strongest divergences from linearity (the interactions between kA3 and kA4 with kRGS1 for τ_rec). Specifically, the former parameter pair regulates arrestin's propensity to form homo-dimers and homo-tetramers, while the latter regulates the rate of binding of RGS9-1 and the activated PDE6 complex. We also see coevolution between the RGS9-1 anchor protein (RGS9BP) and another regulatory protein, recoverin (RCVRN), reflected in a nonlinear interaction for kRec1 and kRec2 with kRGS1. Finally, we found evidence of coevolution between γ-transducin (GNGT1) and a catalytic PDE6 subunit (PDE6A), as well as RGS9BP, which is interesting in that only the α-subunit of transducin physically interacts with PDE6. However, we find strong nonlinear interactions between the parameter governing the initial binding of transducin with rhodopsin (kG1₀) and both the cGMP hydrolysis rates (β_sub and β_dark) and RGS9-1 activity (kRGS1). In the case of the rhodopsin–transducin interaction, βγ-transducin is known to be directly involved in the initial docking [27], so it is feasible that evolution of GNGT1 could affect this process.

There are some cases where coevolution is expected but not seen. Most notably, parameters related to arrestin's activity show a tendency towards nonlinear interaction with parameters related to rhodopsin kinases's activity or that of its regulating protein recoverin. This is not surprising, because the binding affinity of arrestin for rhodopsin, and therefore the rate of arrestin's regulatory activity, is modulated by phosphorylation of rhodopsin by rhodopsin kinase. Nevertheless, no coevolution was found between rhodopsin, recoverin/rhodopsin kinase or arrestin.

Importantly, not all protein pairs within the system showed evidence of having coevolved. This indicates that it is not sufficient to attribute the coevolution to simply being active in the same system. Likewise, most of the physically interacting pairs did not show evidence of having coevolved (figure 3), implying that physical interaction is also not a sufficient condition for coevolution. Most interestingly, clustering of the coevolutionary patterns confirms the separation of the broadly expressed genes GNB5 and GNB1 as having evolved under largely unrelated selective pressures, given that their phylogenetic patterns show little to no correlation with those of most of the other genes of the system (figure 3). On the other hand, the strong coevolutionary signal found for RGS9 and other phototransduction proteins suggests that its evolutionary history may have been strongly shaped by its role in this system, despite its broad expression in other tissues.

3. Discussion

In order to truly understand how natural selection on the phenotype gives rise to evolutionary patterns at the genetic level, it is critical to understand how proteins contribute to the phenotype. While each protein taken independently has functionality that contributes to the survival of the organism, it is clear that the nature of that protein's interactions with others should also influence fitness. Nevertheless, probing the influence of genetic variation on high-level system properties in vitro or in vivo, by testing the effects of functional changes in many interacting proteins, is a significant undertaking. To date, advances have been made in this direction only in the use of unicellular organisms [28]. For more complex organisms, it would be necessary to use in silico techniques to predict how functional changes will affect the phenotype. However, until a robust method of predicting a complex phenotype from a genotype is available, we must presently seek correlations between system-level traits and evolutionary patterns at the sequence level.

Given the potential influence of system dynamics on survival, the question arises of how selective constraint varies between proteins with different degrees of influence on a system's output. One would expect that these sensitive parts of the system would be strongly constrained in their evolution, due to their potential to greatly disrupt the normal dynamics. In order to investigate this, we employed a comprehensive model of mammalian visual phototransduction that mathematically captures the main physiological features of the system. We found that, in fact, the more sensitive proteins (those associated with the parameters that most strongly define the photoresponse) have shown less evolutionary constraint during mammalian divergence. Furthermore, we found that concurrent mutations in several pairs of proteins of this system should often result in multiplicative phenotypic effects, which would result in tightly intertwined functionality between the proteins. This may have manifested in the patterns of protein coevolution during species divergence that we identified.

(a). Gene dynamic sensitivity is a determinant of evolutionary constraint

While the dN/dS ratios of the genes in this system are relatively low, indicating that strong purifying selection has been the dominant evolutionary force acting on the genes, it is clear that the more dynamically sensitive proteins have accumulated amino acid substitutions at a faster rate during mammalian divergence. This is an interesting observation as it shows an unexpected behaviour in the strength of conservation in the genome: the genes that have a strong effect on the phenotype are not necessarily those under the strongest purifying selection and thus are not the most conserved. This could be linked to evolvability of the system during adaptation to new visual environments. While we cannot make predictions regarding the specific impact, if any, of those substitutions in such sensitive genes, we show that they would have more potential to alter the system dynamics to a greater degree than functional substitutions in other genes.

Previously, we have shown that proteins that are topologically central in a network representation of the phototransduction pathway have been under stronger purifying selection [12]. Interestingly, we found no correlation between our gene sensitivity measurements and the topological network measurements described in that publication. Nevertheless, the contrast between the two results is striking. This difference is likely to be due to the distinct attributes of the system captured by the two approaches, the static network and the dynamic model. The network was constructed according to the known physical interactions between the proteins. The central proteins may thus be seen as being important in the overall communication of the signal throughout the system. Because they tend to have many interacting partners, their loss would lead to a catastrophic failure to transduce the signal. The way in which we used the dynamic model does not capture this behaviour; slightly modifying one of the parameters associated with such a protein may not, in fact, disrupt the system dynamics to any significant degree. However, if one were to disable that protein in the model altogether, the dynamics would be greatly affected. For example, the proteins comprised by the PDE heterotrimer have relatively high centralities in the network, while the model parameters associated with them were found to be extremely insensitive in this study. Nevertheless, removing PDE from the model would result in cGMP not being hydrolysed and a subsequent lack of any photoresponse. Thus, a network representation is appropriate for capturing the essentiality of the proteins of this system, while a dynamic model can give information on their kinetic fine-tuning. We argue that the use of dynamic models, in fact, may be the key to understanding the evolvability of biochemical systems.

(b). Non-additive interactions and coevolution

When considering the evolution of proteins that interact in a system, it is important to know whether any epistatic interactions exist between them. Epistasis will cause the functional effect of a mutation to be dependent upon the genetic background in which it occurs. Typically, this should manifest as non-additive mutational effects, which are greater or smaller than what is expected [29], and it may implicate coevolution between some of the genes [30]. More importantly, the identification and characterization of epistasis is an important challenge in understanding the nature of the genotype-to-phenotype map [31]. Here, we have proposed a novel approach that employs an accurate, detailed model to predict non-additive functional effects. It proved to be a promising means to quickly assay for the potential for epistatic interactions in a given biological system. We found all parameter interactions in the system to be nonlinear to some degree. This indicates a high probability of finding true epistatic interactions between the genes of the phototransduction pathway.

We tested our predictions of epistasis by looking for evidence of coevolution between pairs of genes. We could identify several such pairs that corroborate the evidence for potential epistasis. For example, the genes RGS9 and SAG, which encode the proteins RGS9-1 and arrestin, respectively, are responsible for deactivating two distinct parts of the pathway: RGS9-1 accelerates the dissociation of α-transducin from PDE6 and halts further hydrolysis of cGMP; arrestin, on the other hand, caps rhodopsin and prevents further activation of the G protein, transducin. Despite interacting with different proteins, they help to shape the recovery of the photoresponse together in a nonlinear manner (electronic supplementary material, table S5). We hypothesize that the indirect dynamic relationship of these proteins is the cause of the significant evidence of coevolution found between their genes (figure 3). We believe that the use of a mathematical model of biochemical systems can in this way provide a quantitative basis on which to quickly and easily form hypotheses about coevolution between proteins that do not physically interact.

It is also interesting to observe that clustering the pairwise correlation coefficients shown in figure 3 can effectively discriminate between genes whose encoded proteins are primarily responsible for the activation of the phototransduction cascade (RHO, GNGT1, GNAT1, PDE6B and PDE6G) from those that encode proteins that work to deactivate the system (RGS9, SAG, RCVRN, GRK1 and RGS9BP). Only the gene PDE6A did not cluster with its expected group (activation). Overall, this reveals broad coevolution within the two modules, as would be expected. Notably, however, we could also identify statistically significant coevolutionary relationships that bridge the activation and deactivation modules. This points to the adaptive need to harmonize the dynamics of activation and deactivation of the system.

(c). Future directions

Similar analyses of other molecular systems are necessary to further unravel the influence of signalling dynamics on natural selection. The present work depended on the availability of a high-quality mathematical model of the phototransduction system. Critically, the model gives focus to the proteins, rather than second messengers, and it consists primarily of low-level descriptions of the reactions rather than mathematically convenient, albeit more abstract, empirical formulae. Future studies will require models of a similar scale and detail to help to elucidate any general trends in the influence of system dynamics on molecular evolution.

While this phototransduction model was constructed from the most up-to-date information available on the system, future research may serve to fine-tune the parameter estimates or to reveal currently unknown mechanisms. However, the core network of this system is widely agreed upon and, to this end, the model has already proved to accurately simulate a large range of experimental conditions, indicating that it is largely correct [18]. Therefore, we believe that subsequent iterations of the model will not greatly disrupt our results. Rather, they will allow the addition of other proteins to the analysis (e.g. phosducin or the guanylate cyclases) and a more accurate assignment of model parameters to specific proteins, especially in the cases of protein complexes.

While we believe the model to be largely accurate, it nevertheless remains a model. Its primary utility in this case was to rapidly assay the effects of many functional perturbations across the whole system. Such tests of functional importance of molecular dynamics and nonlinear interactions on the scale of entire systems remains challenging in a laboratory environment, and thus such simulation-based approaches provide a convenient means to make meaningful predictions on which to base targeted experiments. In particular, it is hoped that the insights gained in the present study will help to guide future investigations into the evolution of phototransduction proteins. For example, biochemical assaying of the dynamically sensitive proteins from diverse mammalian species may reveal functional differences.

(d). Conclusion

This investigation has offered an intriguing insight into molecular evolution in the context of biochemical systems. It is intuitive that the complex dynamics of protein interactions will influence their evolution. However, until now, it has been difficult to show this. With modern advances in computational power along with an ever-increasing depth of knowledge of biochemical pathways, we can begin to assess the role of system dynamics in natural selection by in silico means. In this study, we have found that the dynamic sensitivities of proteins of the phototransduction pathway show a relationship with their rates of molecular evolution. Surprisingly, we found that the relationship was the inverse of our expectations: genes encoding proteins with stronger control over high-level system properties have higher rates of evolution. Furthermore, we found evidence for epistatic interactions arising from these dynamics that highlight the tight functional coupling between proteins of the system.

An implication of this finding is that adaptive tuning of signalling pathways can be rapidly affected by few mutations in dynamically sensitive proteins. Nevertheless, it is likely that most such mutations would be detrimental. The presence of epistatic interactions in the system would promote the fixation of compensatory mutations in other proteins in the system, resulting in coevolution of these proteins during species divergence. In the present study of the phototransduction system, we found that there are indeed many pairs of proteins showing evidence of having coevolved, including pairs that do not physically interact, supporting the notion of system-level epistasis. A model can then provide quantitative insight into the cause of this protein coevolution by offering the means to assay the effects of simultaneous functional changes in associated kinetic rates.

In the case of highly dynamic and nonlinear biochemical systems such as signalling pathways, it is insufficient to consider the evolution of proteins as static, isolated units. We have shown that the concerted activity of proteins in shaping the phenotype may have a notable influence on natural selection. This broadens our understanding of the multitudinous determinants of molecular evolutionary patterns, while opening new methods for investigating evolution on a systems level.

4. Material and methods

(a). Model implementation and simulations

A previously developed model of mammalian phototransduction was used for all simulations [18] (BioModels: MODEL1501210000). The model comprises a system of ordinary differential equations that deterministically track the time evolution of 72 molecular species in 96 reactions and using 62 parameters. It was implemented using SBTOOLBOX2 for MATLAB (http://www.sbtoolbox2.org) [32]. Simulations were run from automatically generated and compiled C-code models, based on the CVODE integrator from SUNDIALS [33]. The primary output of the model is the suppression of the energy induced by the dark-circulating electrical current (measured in change in joules, ΔJ) across the membrane of the photoreceptor outer segment after a stimulus.

(b). Simulated electrophysiological measurements

In order to measure changes in the photoresponse upon perturbation of the system, we required means of quantifiably characterizing the model output. We chose four high-level properties, two each for measuring non-saturating and saturating photoresponses. For the former case, we measured signal amplification via the peak amplitude (maximum change in current from the dark-adapted level) after a dim stimulus; and we quantified the recovery from this peak via the time constant (τ_rec) of a single exponential fit to the second half of the recovery phase of the response to a dim stimulus. For the saturating paradigm, we measured the saturation time (T_sat), the total time the current spends at more than 90% of its peak amplitude after a bright stimulus; and we quantified recovery from saturation via τ_D, measured as the change in T_sat with logarithmically increasing stimulus intensities [34]. All four metrics are commonly used in experimental research to assess phototransduction performance.

Dim-light responses were generated from a simulated stimulus causing 6.536 photoisomerizations per second (R^* s⁻¹). T_sat was determined for simulated responses to a flash generating 1808 R^* s⁻¹. τ_D was computed as the slope of a least-squares fit of the T_sat values measured for responses to stimuli resulting in 403.43 to 1808 R^* s⁻¹, increasing by half-log units. All flash stimuli had a duration of 0.02 s.

(c). Parameter sensitivity analysis

Local parameter sensitivity analysis was performed empirically for each parameter at its default, ‘wild-type’ value by measuring the effect of a small ‘mutation’ of the parameter value on each of the four electrophysiological properties. Lists of parameters associated with each of the proteins of the system were then compiled (electronic supplementary material, table S1). For each gene encoding these proteins, sensitivity values were calculated as the means of the log-transformed sensitivities of the associated parameters, for each of the four electrophysiological properties. Additionally, an average sensitivity across the four properties was computed for each gene. For a full mathematical description, see the electronic supplementary material.

(d). Evolutionary constraint

The evolutionary constraints acting on each gene were estimated according to the ratio of the rates of non-synonymous (dN) to synonymous (dS) substitution. dN/dS values for the genes in this study were retrieved from a previous publication [12]. These values were computed for a phylogenetic tree of nine mammalian species: human, chimpanzee, gorilla, orangutan, macaque, marmoset, mouse, rat and dog. Sequences had been retrieved from the Ensembl database (release 60) or from DNA resequencing. Rates were computed using CODEML model M0 of the PAML package v. 4.4c [35]. This model computes a single dN/dS ratio for the entire tree, treating all sites in the alignment as having evolved at the same rate. While the model is simple, it is relatively conservative and can be used to capture general trends in the evolutionary rates during a phylogenetic divergence. This ratio, in the common case of values less than one, can be taken as an overall measure of the strength of purifying selection [8,36].

(e). Non-additive phenotypic effects

Non-additive dynamic effects were measured by comparing the output of simulations in which a pair of parameters was perturbed to the expected output given independent effects of the perturbations. Specifically, for each pair of parameters, we generated a model with both parameter values increased by 1% as well as models with each of the two parameter values individually increased by 1%. The measurements of the electrophysiological properties of the photoresponses generated from these ‘mutant’ models were then computed. The effect sizes of both of the ‘single-mutant’ models were computed as the difference between the measurement for that ‘mutant’ model and the corresponding measurement for the ‘wild-type’ model. The two ‘single-mutant’ effect sizes were added to the ‘wild-type’ measurement to form the expected measurement value given strictly linear interaction. The magnitude of deviation from linearity for each parameter pair and empirical phototransduction measurement was then computed as the base-2 logarithm of the ratio of the ‘double-mutant’ measurement to the expected measurement given a linear interaction.

(f). Coevolution

Coevolution between the genes was estimated by comparing the similarity of their phylogenetic trees using the MirrorTree algorithm [25]. The amino acid sequences of all one-to-one orthologues within the mammalian clade of the human genes were fetched from Ensembl (v. 77). Sequences containing chains of five ambiguous residues or more were discarded. Multiple sequence alignments were created using MAFFT v. 7.205 [37] and then filtered and used to produce phylogenetic trees using TreeBeST v. 1.9.2 with the default species tree (http://treesoft.sourceforge.net/treebest.shtml).

MirrorTree correlation values were then computed for each pair of genes. These correlations were converted to z-scores using Fisher's r-to-z transformation, following Edgar et al. [38]. For a full mathematical description, see the electronic supplementary material. Because a general trend of coevolution between G proteins and their receptors has been described previously, we chose the MirrorTree correlation between the reference pair RHO–GNAT1 for the basis of comparison in the r-to-z transformation [26]. Protein pairs with MirrorTree correlation coefficients that are significantly less than this reference value, as determined by a significant z-score with a confidence of 0.05, should then be considered to have not coevolved.

(g). Statistical analyses

Correlations were tested by computing Spearman's ρ. All statistical calculations were performed using R v. 3.2.1.

Authors' contributions

B.M.I., L.M. and J.B. conceived of the study and contributed to the manuscript. B.M.I. implemented and performed the simulations and analyses. All authors gave approval for the final publication.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by the Ministerio de Economia y Competitividad, Spain (grant no. BFU2013-43726-P, subprogram BMC) and the María de Maez to Program for Units of Excellence in R&D (MDM-2014-0370); the Departament d'Economia i Coneixement de la Generalitat de Catalunya (Grup de Recerca Consolidat GRC 2014 SGR 866); AGAUR, Generalitat de Catalunya (2011 FI BI 00275 to B.M.I.); and the Spanish Ministry of Science and Innovation (MICINN) (Juan de la Cierva Program to L.M.).