How Tolerant are Membrane Simulations with Mismatch in Area per Lipid between Leaflets?

Abstract

Difficulties in estimating the correct number of lipids in each leaflet of complex bilayer membrane simulation systems make it inevitable to introduce a mismatch in lipid packing (i.e., area per lipid) and thus alter the lateral pressure of each leaflet. To investigate potential impacts of such mismatch on simulation results, we performed molecular dynamics simulations of saturated and monounsaturated lipid bilayers with and without gramicidin A or WALP23 at various mismatches by adjusting the number of lipids in the lower leaflet from no mismatch to a 25% reduction compared to that in the upper leaflet. All simulations were stable under the constant pressure barostat, but the mismatch induces asymmetric lipid packing between the leaflets, so that the upper leaflet becomes more ordered, and the lower leaflet becomes less ordered. The mismatch impacts on various bilayer properties are mild up to 5–10% mismatch, and bilayers with fully saturated chains appear to be more prone to these impacts than those with unsaturated tails. The nonvanishing leaflet surface tensions and the free energy derivatives with respect to the bilayer curvature indicate that the bilayer would be energetically unstable in the presence of mismatch. We propose a quantitative criterion for allowable mismatch based on the energetics derived from a continuum elastic model, which grows as a square root of the number of the lipids in the system. On the basis of this criterion, we infer that the area per lipid mismatch up to 5% would be tolerable in various membrane simulations of reasonable all-atom system sizes (40–160 lipids per leaflet).

Introduction

Cell membranes are made up of a wide variety of lipids that act as a matrix to host integral membrane proteins, to recruit peripheral membrane proteins, and thus to actively participate in cellular membrane functions together with these proteins. Complexity of biological membrane systems arises from a considerable heterogeneity in the spatial distribution of lipids and proteins in the cell membrane and between the bilayer leaflets.¹ The outer membrane of gram-negative bacteria provides an extreme example of this situation, where the lipid component of the outer leaflet is predominantly lipopolysaccharides, and those of the inner leaflet are typical phospholipids.^2,3 To a lesser extent, the outer leaflet of the plasma membrane contains more lipids with the phosphatidylcholine headgroup and sphingolipids (e.g., sphingomyelin) than the inner leaflet, and glycosphingolipids (e.g., gangliosides) exist only in the outer leaflet.

In this context, the use of molecular dynamics (MD) simulations to study asymmetric membranes requires that lipid packing (i.e., lateral pressure) of each leaflet be very similar to prevent strain on the bilayer by having too few lipids in one of the leaflets. The surface area per lipid (SA/lipid) of each lipid type in these asymmetric membranes can be used to build the membranes, but such information is usually not known a priori. Therefore, most simulations with asymmetric membranes assume lipid packing based on the SA/lipid information estimated from simulations of symmetric bilayers with a single lipid type or multiple lipid types.⁴⁻⁸ This issue of leaflet lipid packing is not limited to building asymmetric bilayers but also is of considerable concern when introducing an integral membrane protein or a membrane surface-bound protein (or peptide) into the bilayer. Most integral membrane proteins contain some degree of asymmetry in their lateral (cross-sectional) surface area along the membrane normal; that is, the surface area of the protein in contact with one leaflet is not equal to that exposed to the other leaflet.

Several approaches are used to build bilayers around membrane proteins. For example, in CHARMM-GUI Membrane Builder,⁹⁻¹² lipid-like pseudo atoms are first distributed and packed around a protein and then replaced by lipid molecules one at a time starting from the ones nearest to the protein. This so-called “replacement” method^13,14 allows one to easily control the lipid types and the number of each lipid type based on the protein surface area and the SA/lipid of each lipid type (estimated from pure bilayer simulations) in a complex membrane system. Even after these careful building procedures, there may still be a mismatch in lipid packing (SA/lipid) and thus a lateral pressure between the leaflets, which could affect the structure and dynamics of the membrane-associated protein or peptide. This could especially be an issue with mechanosensitive channel proteins that are sensitive to the mechanical properties of the membrane.¹⁵ One approach to avoid such mismatch between the leaflets is to use P2₁ boundary conditions that allow for direct lipid flip/flop between the leaflets.¹⁶ Although this has been used for membrane proteins and peptides,¹⁷⁻²¹ it is not reasonable to use this technique for bilayers with asymmetry in lipid components in each leaflet, such as the bacterial outer membrane. In addition, its extra computation time and its availability only in the CHARMM²² simulation package preclude it from widespread use. Recently, a protocol for building asymmetric bilayers with minimal SA mismatch between leaflets was proposed in an all-atom simulation study of asymmetric bacterial outer membranes as well as in a coarse-grained simulation study of a plasma membrane, where each leaflet was prepared from its corresponding symmetric bilayers.^8,23 Yet, this protocol is computationally expensive (especially for all-atom membrane simulations), so that it has been applied only to a few simulation studies.^8,23,24 Therefore, it is still difficult to avoid a certain extent of SA/lipid mismatch between two leaflets in MD simulations of complex asymmetrical membranes or those with proteins.

In this context, understanding the influence of the mismatch on bilayer properties as well as protein–lipid interactions can provide insight if the simulations of large complex bilayers are physically meaningful or realistic. There have been only a few studies that address the impacts of SA mismatch between leaflets, but these studies considered model bilayers composed of a single lipid type without energetic considerations of bilayer stability.^25,26 Therefore, it is still necessary to better understand the mismatch influence depending on lipid saturation, mismatch’s impacts on the protein–lipid interactions, and energetic quantification of bilayer stability due to such mismatch.

This work focuses on addressing the impacts of mismatched leaflets on lipid bilayer properties and stability with and without proteins in MD simulations. Simple pure lipid bilayers were simulated to probe the impacts of bilayer mismatch. Specifically, 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) serve as models for how leaflet mismatch influences bilayers that have fully saturated chains and those with chain unsaturation. The number of lipids in the lower leaflet was adjusted from no mismatch to a 25% reduction compared to the upper leaflet. Gramicidin A (gA) channel and WALP23 peptide were also simulated in bilayers with the same SA/lipid leaflet mismatch. The gA channel is fairly rigid, and its orientation in the bilayer is known to be less dependent on hydrophobic mismatch, so that it is used as a model membrane protein causing bilayer adaptation.²⁷ WALP23 is used as a model for peptides and membrane proteins whose orientation and conformation depend strongly on hydrophobic mismatch.²⁸⁻³⁰ Chain order parameters, hydrophobic thickness, SA/lipid, lateral diffusion coefficient, lateral pressure profile, surface tension, spontaneous curvature, structure and orientation of gA and WALP23, and their interactions with lipids are used as the metrics to determine tolerable levels of leaflet mismatch in membrane simulations. Finally, the energetics derived from a continuum elastic model is used as a quantitative measure for allowable mismatch in various membrane simulations of reasonable system sizes.

Methods

System Setup and Simulation Details

Using the general input scripts from CHARMM-GUI Membrane Builder,⁹⁻¹² we set up bilayer membrane simulations for two lipid types (DMPC and POPC) with and without gA or WALP23 at various mismatches between the numbers of lipids in the upper and lower leaflets (N_T and N_B, respectively). For each bilayer system, six different mismatches were made by decreasing N_B from 0 to 25% of N_T with a 5% interval. For each mismatch, two sets of simulations were set up with different sizes (N_T = 40 or 80) to take into account the finite size effect. For the pure POPC bilayer simulations, we set up an additional system with N_T = 160. The membrane simulation systems considered in this study is summarized in Table 1.

Table 1. Simulation System Information.

	Number of lipids in the upper leafleta
protein	DMPC		POPC
no	40	80	40	80	160
gA	40	80	40	80
WALP23	40	80	40	80

^aFor each number of lipids in the upper leaflet, six different mismatched systems were made by decreasing the number of lipids in the lower leaflet from 0 to 25% with a 5% interval (gA = Gramicidin A).

For each bilayer system, the initial configuration was built with bulk water and ions (150 mM KCl) and equilibrated by following the Membrane Builder’s six-step protocol⁹ using CHARMM;²² the restraints on the components (lipids, water, and gA/WALP23) were gradually relaxed during the equilibration. Then, a 135-ns NAMD³¹ production run was performed for the systems with N_T = 40 and 80. For the pure POPC systems with N_T = 160, we performed 70-ns NAMD production runs. All production runs were performed without any restraints under the constant temperature and pressure condition (NPT) at 303.15 K and 1 bar, where the temperature and pressure were maintained using the Langevin thermostat³² with a coupling coefficient of 1 ps^–1 and the Langevin piston barostat³³ with a piston period of 50 fs and a decay of 25 fs. The CHARMM all-atom protein force field³⁴ including CMAP³⁵ and dCMAP³⁶ was used together with the C36 lipid force field³⁷ and a TIP3P water model.³⁸ The van der Waals interactions were smoothly switched off over 10–12 Å by a force-switching function.³⁹ For the long-range electrostatic interactions, we used the particle mesh Ewald method⁴⁰ with a mesh size ∼1 Å for fast Fourier transformation and the sixth order B-spline interpolation. We used the integration time step of 2 fs with SHAKE algorithm.⁴¹

Analysis

The trajectories were saved at every 2 ps, whose last 120 ns were used for the analysis, and the error bars were obtained from the three 40-ns block averages except the systems with N_T = 160, for which the last 60-ns trajectories and 20-ns block averages were used. 100 uniform slabs (width <1 Å) along the z-direction (i.e., the membrane normal) were used to save the lateral pressure profiles at every 2 ps. The impacts of the mismatch on the bilayer properties and stability were analyzed by calculating various properties described below.

Order Parameter and Area per Lipid

The extent of lipid packing in a leaflet of a bilayer can be described by the deuterium order parameter of the lipid tail (S_CD) and the SA/lipid for each leaflet. The S_CD is defined as S_CD = ⟨3 × cos²(θ_CH) – 1⟩/2, where θ_CH is the angle between a C–H bond vector and the z-axis, and the bracket represents the time and ensemble average (reported here is the absolute value of the S_CD). When S_CD = 1/2, the C–H bond is perpendicular to the membrane normal, whereas, when S_CD = 0, the bond has random orientation with respect to the bilayer normal. The S_CD is a common metric to characterize bilayer fluidity (i.e., liquid ordered, where the S_CD is closer to 0.5, versus liquid disordered, where the S_CD is <0.25).

For the pure bilayer systems, the individual leaflet SA/lipid is obtained by dividing the xy system area by N_T and N_B. Under the conditions that there is only one lipid type in a bilayer, the SA of each leaflet is the same, and the system is in mechanical equilibrium (i.e., zero bilayer surface tension), we obtained an expression for the SA (A_ϕ) and SA/lipid of each leaflet at a given fractional mismatch, ϕ = 1 – N_B/N_T, (see Appendix for details)

1

where A̅_T and A̅_B are the SA/lipid for the upper and lower leaflets, respectively.

Hydrophobic Thickness and Lateral Diffusion Coefficient

The hydrophobic thickness is one of the most important bilayer properties, which is inversely proportional to the SA/lipid. As lipids are more tightly packed (i.e., the chain order increases and the SA/lipid decreases), the bilayer thickness increases, whereas the mobility of each lipid diminishes. Therefore, the thickness of the bilayer and the diffusivity of the lipids are correlated to the lipid packing (S_CD and SA/lipid). The hydrophobic thickness of each leaflet was measured as the distance between the average z-coordinates of C22 and C32 atoms (i.e., carbon atoms adjacent and below the carbonyl C atoms) of each lipid in a given leaflet and the bilayer center. The bilayer hydrophobic thickness is the sum of the leaflet hydrophobic thicknesses. For the membrane systems with gA or WALP23, a two-dimensional (2D) hydrophobic thickness map on the xy plane was calculated using the x and y center of mass (COM) of each lipid including its images. To obtain the 2D hydrophobic thickness map, we aligned each frame as described below. For the membranes with gA, the origin was set to the COM of gA heavy atoms, and a vector from the COM of gA to the COM of Trp15 in the upper leaflet was aligned along the positive x-direction. For those with WALP23, the origin was set to the COM of WALP23 C_α atoms, and the helix principal axis vector of WALP23 was aligned to the positive x-direction.

Self-diffusion coefficients of lipids (D_L) were calculated from the slope of the lateral mean-square displacement (MSD)

2

where t₀ is the time origin for MSD calculations ranging from t_max – t to t_max, and t_max is the total simulation time. In this work, the MSD was calculated for the COM of each lipid and averaged over time and over all lipid molecules in each leaflet. Before calculating the MSD, a correction was introduced to the positions of lipid molecules to unfold the trajectory and thus to eliminate the effect of periodic boundary conditions and remove the drift of the entire leaflet. We used a linear region (10–30 ns) of the MSD obtained from each 40 ns block for D_L calculations, and a linear region from 7.5 to 12.5 ns for the POPC systems with N_T = 160. Note that the current method may underestimate D_L if the system size is not sufficiently large due to possible dampening of long-ranged motions⁴² or correlated motions arising from the periodic boundary conditions.⁴³

Lateral Pressure Profile and the Derived Quantities

The bilayer stability can be described by the surface tension and the free energy derivative at planar curvature, which can be calculated from the lateral pressure profile, p(z) = p_L(z) – p_N(z), where p_L(z) and p_N(z) are the lateral and normal components of the pressure tensor; that is, p_L(z) = [p_xx(z) + p_yy(z)]/2 and p_N(z) = p_zz(z). Because the distribution of water, lipid head groups, and tails are heterogeneous along the z-axis; p(z) is nonuniform in general. The integral of p(z) over the thickness of the membrane (i.e., the sum of all the interactions along the z-axis) equals the surface tension with the opposite sign; that is, γ = −∫dz p(z). By noting that p(z) vanishes in the bulk water region, the surface tension can be written as

3

where L_z is the box size along the z-direction. The first moment of the pressure profile provides the free energy derivative at planar curvature,^44,45

4

where the bar means that the free energy is expressed per unit lipid area. Nonvanishing F̅′(0) implies that a bilayer is not energetically stable, so it would bend toward a preferred curvature (without the constraints of periodic boundary conditions).

The lateral pressure profile in NAMD output is calculated using Harasima contour,⁴⁶ whose normal component p_N(z) cannot be simply obtained.⁴⁷ By noting that the bilayer systems were equilibrated (i.e., vanishing γ) and were in mechanical equilibrium (uniform p_N), we estimated p_N as

5

and the standard errors were found to be less than 0.1 bar. Because the bilayer generally drifted during the simulations and its center (Z_CEN) is not positioned at z = 0 in the NAMD trajectories, the pressure profiles needed to be recentered at z = 0 by estimating the Z_CEN. While it would be a trivial task for a symmetric bilayer, care must be taken to properly estimate the Z_CEN for mismatched or asymmetric bilayers, as the quality of the pressure profile and thus the derived quantities [γ and F̅′(0)] are sensitive to the accuracy of the estimated Z_CEN.

Estimation of the Bilayer Center

The Z_CEN is typically assigned as the geometric COM of the entire membrane, Z_MCOM. For symmetric membrane systems, this estimate is accurate enough. However, when there exist significant mismatch in the SA/lipid between the leaflets, such estimates may yield blurry (i.e., low accuracy) z-axis-related profiles. For example, a simple assignment of Z_CEN as Z_MCOM becomes less accurate at larger mismatch, and the central peak of the pressure profile shifts to the lower leaflet side (Figure 1A). We find that the peak position (Z_NMAX) along the z-profile of the number of lipids⁴⁸ provides a better estimate of Z_CEN. As shown in Figure 1B, the shift of the central peak in Figure 1A is corrected with Z_NMAX, which results in a higher resolution (accurate) pressure profile. Note that throughout this work, Z_NMAX was used to estimate Z_CEN for the analysis of density, hydrophobic thickness, and pressure profiles.

Figure 1.

Influence of the estimated bilayer center, Z_CEN, on the lateral pressure profiles. The pressure profiles were calculated for the pure DMPC bilayers with N_T = 80 at various mismatches between N_T and N_B: 0% (black), 5% (red), 10% (green), 15% (blue), 20% (magenta), and 25% (cyan). The left panels show the pressure profiles calculated using the Z_CEN based on (A) the bilayer geometric center of mass, Z_MCOM, and (B) the peak position, Z_NMAX, of the number of lipid profile. The dashed boxes are enlarged in the right panels.

Having this estimate of Z_CEN, the leaflet surface tension can be accurately calculated as

6

where 0 stands for the bilayer center, and γ_T and γ_B are the surface tension for the upper and lower leaflets, respectively. The bilayer surface tension is the sum of leaflet tensions, γ = γ_T + γ_B. In addition, we define the leaflet free energy derivative as

7

and their interpretation is given as follows. A leaflet (L = T or B) would prefer more positive curvature (bending toward tail side) if F̅_L′(0) < 0, whereas it would be curved toward the headgroup direction if F̅_L′(0) > 0. The bilayer free energy derivative is given by F̅′(0) = F̅_T′(0) – F̅_B′(0), which should vanish for membranes that have symmetric lipid packing.

Structure and Orientation of Peptides and Their Interactions with the Environment

For the gA-bilayer and WALP23-bilayer systems, the mismatch impacts on the structure and the orientation of gA and WALP23 in bilayer membranes were monitored by calculating the root mean squared deviation (RMSD) of gA and WALP23 with respect to their initial structure, their z-COM (Z_COM), and tilt angle with respect to the membrane normal. In addition, the interactions between gA/WALP23 and environments (water, lipid head groups, and tails) were characterized by the interaction patterns. We define that gA/WALP23 and environment are in contact (i.e., interacting), when any heavy atoms between a given residue and the environment are within a distance of 4.5 Å. To precisely monitor the gA/WALP23 and lipid interactions, we counted the contact between gA/WALP23 and the lipids in the upper and lower leaflets separately.

Results and Discussion

In this section, we will show the simulation results for the bilayer systems with N_T = 80. All the simulations were stable during the entire simulation consistent with previous work,²⁵ and the complete results from all simulations are given in the Supporting Information. This section is organized as follows. We start from pure bilayers and discuss the impacts of the mismatch on bilayer properties. Then, the mismatch impacts on the gA-bilayer and WALP23-bilayer systems are presented and discussed. Finally, a discussion about the stability of bilayers in the presence of mismatch follows.

Pure Lipid Bilayers

To characterize the impacts of mismatch on the distribution of bilayer components, we calculated the density profiles of water, lipid head groups and tails, and phosphate groups along the membrane normal (i.e., the z-axis). Overall, the upper leaflet is stretched, while the lower leaflet is contracted with increasing fractional mismatch, although the impacts are mild up to 5–10% mismatch (see density profiles in Supporting Information, Figures S1 and S2). The deuterium order parameters are consistent with the density profiles in that the upper leaflet is more ordered, and the lower leaflet is less ordered with increasing mismatch (Supporting Information, Figure S3).

In Figure 2A, the density profiles for pure bilayers at 25% mismatch are shown. For DMPC bilayers, the upper leaflet is more affected than the lower leaflet, which is clearly shown as asymmetric broadening and shifts in the headgroup and phosphate density profiles at z > 0. On the other hand, for POPC bilayers, the lower leaflet is more affected than the upper leaflet, shown as shifts in the phosphate and headgroup density profiles at z < 0. The different behavior between DMPC and POPC bilayers due to the mismatch can be explained by nature of their lipid packing. DMPC has shorter fully saturated lipid tails, whereas POPC has longer lipid tails and a double bond in its sn-2 tail. Thus, a POPC bilayer is less tightly packed than a DMPC bilayer, which allows better adaptation to mismatch. The inferior adaptability of DMPC bilayers is shown as wider and more asymmetric broadening of density profiles of bilayer components (in upper leaflet side), whereas those for POPC bilayers are mostly shifted without significant broadening.

Figure 2.

(A) Density profiles of water (blue), head groups (cyan), lipid tails (orange), and P atoms in phosphate groups (red) along the membrane normal (z-axis) at 25% mismatch between N_T and N_B. Shown together are those at 0% mismatch (gray). Note that the density of phosphate group is multiplied by five. (B–D) The average properties of lipid bilayers at various mismatches between N_T and N_B, where the leaflet properties are shown in red (upper) and blue (lower), and bilayer properties are shown in black: (B) hydrophobic thickness (symbols) with the upper limit of the upper leaflet thickness (orange dashed line). In each panel, the leaflet (upper) or bilayer (lower) hydrophobic thickness at 0% mismatch (black dashed line) is shown together for visual guide; (C) SA/lipid (symbols) and the predicted one from eq 1 (lines). Shown together is SA/lipid at 0% mismatch (black dashed line); (D) lateral diffusion coefficient (D_L). In all the panels, the error bars are the standard errors calculated from three block averages.

The mismatch impacts on the bilayer hydrophobic thickness are shown in Figure 2B (and Supporting Information, Figure S4). Consistent with the density profiles (crossing point between headgroup and tail density), the leaflet thickness of POPC bilayers is more affected by the mismatch than that of DMPC bilayers, whose lower leaflet is more affected than the upper leaflet. The POPC bilayer thickness, on the other hand, does not change up to 10% mismatch and then decreases slightly with increasing mismatch due to partial cancelation of thickening and thinning effects of the upper and lower leaflets, respectively. Both leaflet and bilayer thicknesses of DMPC bilayers are less dependent on the mismatch than POPC bilayers because of its shorter lipid tails. If a leaflet behaves elastically, its SA/lipid would change inversely proportional to its thickness, which is qualitatively shown in Figure 2C (and Supporting Information, Figure S5). For DMPC bilayers, the changes in the SA/lipid for both leaflets are comparable, whereas for POPC bilayers, the lower leaflet SA/lipid grows faster beyond 15% mismatch.

This seemingly different adaptation to the mismatch between DMPC and POPC bilayers is further analyzed by using an elastic model, where the deformation preserves the volume of each leaflet. Up to 15% of the fractional mismatch, we find that the SA and SA/lipid of leaflets agree well with eq 1 (Figure 2C and Supporting Information, Figure S5). However, the leaflet hydrophobic thickness changes less than the expected one from the elastic model (data not shown) and the upper leaflet thickness for both DMPC and POPC bilayers in MD simulations seems to reach a limiting value for ϕ ≥ 0.1 (Figure 2B and Supporting Information, Figure S4). This suggests that mismatch larger than 10% would be problematic due to highly stressed lipids in the crowded (upper) leaflet.

The overall effects of the mismatch on the leaflet D_L of DMPC and POPC bilayers agree with the other bilayer properties, in that the mobility of lipids decreases when the lipids are more tightly packed (i.e., increased chain order and hydrophobic thickness and decreased SA/lipid). However, consistent with the previously reported system size dependence of diffusion coefficient,⁴³D_L at 0% mismatch shows system size dependence (Supporting Information, Figure S6). This fact makes it hard to get a statistically clear trend with increasing mismatch, although D_L appears to be affected by mismatches larger than 10% (Figure 2D).

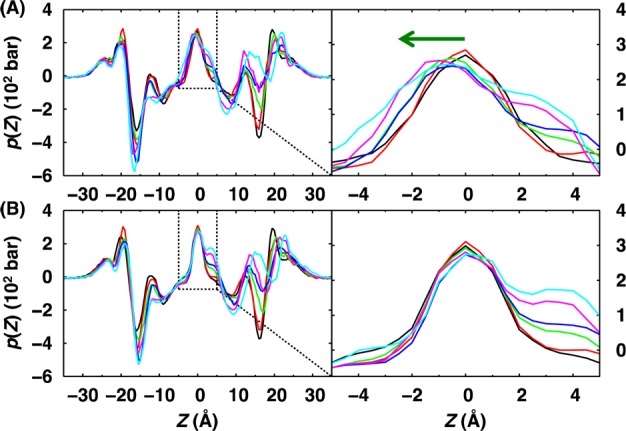
Resulting from the asymmetric lipid packing, the lateral pressure along the membrane normal becomes more asymmetric with increasing mismatch as shown in Figure 3 (and Supporting Information, Figure S7). For symmetric bilayers, the positions of characteristic peaks and dips in p(z) from water-headgroup interfaces, head groups, and bilayer center can be clearly assigned. The impacts of the mismatch on p(z) are mild up to 5% and 10% mismatch for DMPC and POPC bilayers, respectively. At larger mismatch, p(z) becomes more repulsive in the upper leaflet, whereas it gets more attractive in the lower leaflet. The peaks and dips are also shifted along the membrane normal, consistent with the density profiles; that is, the shift is larger at the upper leaflet for DMPC bilayers and at the lower leaflet for POPC bilayers. Note that there is a system size dependence in the pressure profile (Supporting Information, Figure S7), which seems to originate from the fluctuation of the bilayer along the membrane normal.⁴⁹

Figure 3.

Lateral pressure profiles for (A) DMPC and (B) POPC bilayers at various mismatches between N_T and N_B: 0% (black), 5% (red), 10% (green), 15% (blue), 20% (magenta), and 25% (cyan). The error bars are omitted for clarity.

Peptide-Bilayer Systems

So far, the mismatch in N_T and N_B is shown to induce asymmetric lipid packing between the leaflets, to which DMPC bilayers have inferior adaptability when compared to POPC bilayers. Such SA/lipid mismatch may influence protein–lipid interactions, which are regulated to minimize the hydrophobic mismatch between the hydrophobic length of the protein’s transmembrane domain and that of the lipid bilayer. These aspects naturally lead to the following questions: how protein–lipid interactions are influenced by SA/lipid mismatch, and how the protein and bilayer adapt to hydrophobic and SA/lipid mismatch. These questions are addressed below by characterizing the structure and orientation of gA and WALP23 (both of which are peptides frequently used to mimic larger, more complex proteins), interaction patterns between gA (or WALP23) and DMPC (or POPC) bilayers, and two-dimensional hydrophobic thickness maps for DMPC and POPC bilayers. The overall bilayer properties are examined by density and lateral pressure profiles along the bilayer normal.

Gramicidin A Inserted in Mismatched Lipid Bilayers

Consistent with the known behavior of gA, its structure and orientation in both DMPC and POPC bilayers are not sensitive to SA/lipid mismatch except gA in DMPC bilayers at 25% mismatch (Figure 4 and Supporting Information, Figure S8). Compared to the no-mismatch case, the peak of the gA tilt angle distribution is shifted to ∼15° at 25% mismatch, and its COM z-coordinate (Z_COM) is shifted to ca. −2 Å. Interestingly, as shown in Figure 5 (and Supporting Information, Figure S9), the interaction patterns between gA and environments are not dependent on the mismatch, indicating that the lipids around gA adapt to the protein even at 25% mismatch. Indeed, as shown in Figure 6 (and Supporting Information, Figures S10–13), there is no major change in the 2D hydrophobic thickness maps of both DMPC and POPC bilayers near gA at different mismatch conditions. Nonetheless, each leaflet behaves differently depending on the lipid type. With increasing mismatch in DMPC bilayers, away from the protein–lipid interfaces, the upper leaflet hydrophobic thickness map becomes more asymmetric, whereas that for the lower leaflet shows opposite behavior in a lesser extent; that is, areas with a thinner leaflet thickness at the lower leaflet has a thicker leaflet thickness at the upper leaflet. On the contrary, for POPC bilayers, the thickness maps for both leaflets remain rather uniform even at 25% mismatch and agree well with those for the pure POPC bilayer at the same mismatch, which is consistent with the better adaptability of POPC bilayers to SA/lipid mismatch. The density and pressure profiles behave more or less the same as those from the pure bilayer membranes (Supporting Information, Figures S14 and S15).

Figure 4.

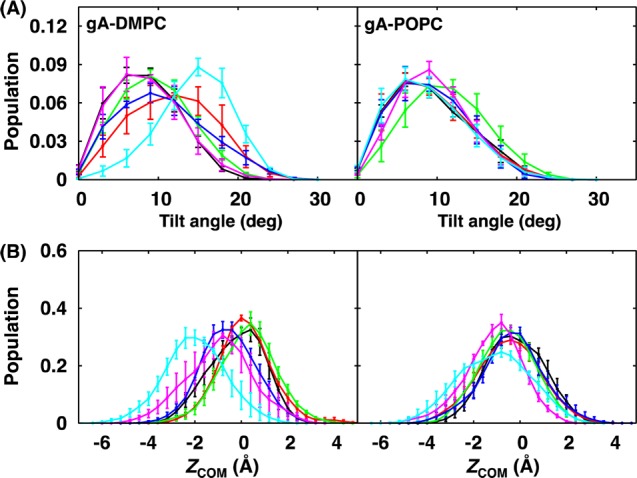
(A) Tilt angle and (B) Z_COM distributions of gA in DMPC and POPC bilayers at various mismatches between N_T and N_B: 0% (black), 5% (red), 10% (green), 15% (blue), 20% (magenta), and 25% (cyan). The error bars are the standard errors calculated from three block averages.

Figure 5.

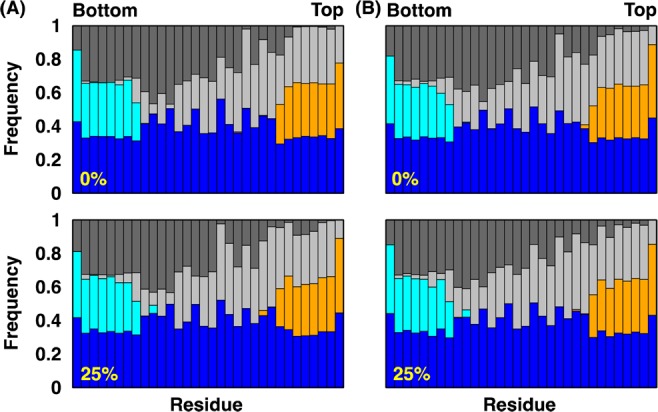
Interaction patterns of gA residues and their environment in (A) gA-DMPC and (B) gA-POPC bilayers at 0% (upper panels) and 25% (lower panels) mismatches. The graph shows, for each residue, the frequency of occurrence within 4.5 Å of water (blue), headgroup (cyan) and tail (dark gray) in the lower leaflet, and headgroup (orange) and tail (light gray) in the upper leaflet.

Figure 6.

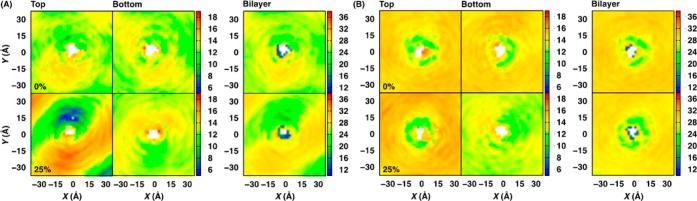
Two dimensional hydrophobic thickness maps for (A) gA-DMPC and (B) gA-POPC bilayer systems at 0% (upper panels) and 25% (lower panels) mismatch. The profiles were calculated from 120-ns trajectories with a bin size of 2 Å in both x- and y-dimensions.

WALP23 Inserted in Mismatched Lipid Bilayers

Similar to gA, the SA/lipid mismatch does not affect the helical structure of WALP23 in DMPC and POPC bilayers within the current simulation time scale (Supporting Information, Figure S16A). However, its orientation is sensitive to SA/lipid mismatch, and it is more affected in DMPC bilayers, as shown in Figure 7 (and Supporting Information, Figures S16B and S16C). Similar to the gA-DMPC bilayer system, WALP23 is shifted to the lower leaflet at 25% mismatch in DMPC bilayer, and the interaction patterns between WALP23 and environments are insensitive to mismatch for both DMPC and POPC bilayers (Supporting Information, Figure S17). The 2D hydrophobic thickness maps show the same trend as in the gA-bilayer systems; that is, the upper leaflet of DMPC bilayer is affected more than the lower leaflet, and the POPC bilayers adapt better to the hydrophobic and SA/lipid mismatches compared to DMPC bilayers (Supporting Information, Figures S18–21). The density and pressure profiles show the same trend as those from the pure bilayers (Supporting Information, Figures S22 and S23).

Figure 7.

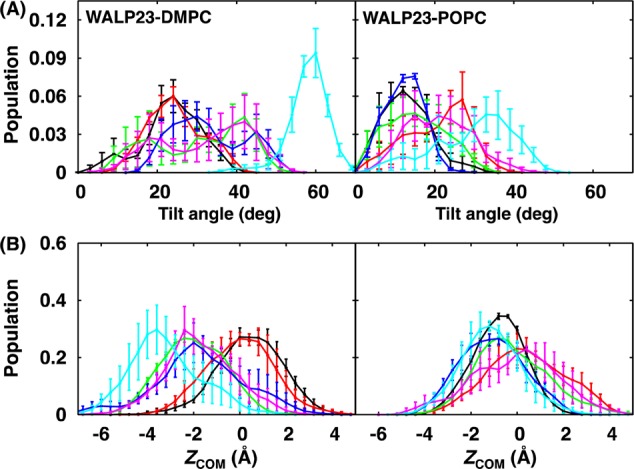
(A) Tilt angle and (B) Z_COM distributions of WALP23 in DMPC and POPC bilayers at various mismatches between N_T and N_B: 0% (black), 5% (red), 10% (green), 15% (blue), 20% (magenta), and 25% (cyan). The error bars are the standard errors calculated from three block averages.

Figure 8 shows representative snapshots of gA and WALP23 in DMPC and POPC bilayers at 25% mismatch. The lipid tails of DMPC bilayers at the upper leaflet are highly stretched (i.e., ordered), which imposes repulsive forces on gA and WALP23 to relieve the strain while maintaining the interfaces between gA/WALP23 and DMPC bilayers. Thus, gA and WALP23 are shifted to the lower leaflet side together with interfacing lipids, which has room to accommodate gA and WALP23. On the other hand, the lipid tails in the upper leaflet of POPC bilayers are less ordered compared to those in DMPC bilayers. Therefore, there are less repulsive forces imposed on gA and WALP23 toward the lower leaflet side, resulting in much weaker dependence of the Z_COM shift on the SA/lipid mismatch and more uniform 2D thickness map for both leaflets.

Figure 8.

(A, B) Snapshots of gA in (A) DMPC and (B) POPC bilayers at 25% mismatch between N_T and N_B. (C, D) Snapshots of WALP23 in (C) DMPC and (D) POPC bilayers at 25% mismatch. The gA/WALP23 is shown in green cartoon representation, C21 and C31 atoms in upper and lower leaflets are shown in orange and cyan spheres (to clarify adaptation to hydrophobic mismatch), and lipid tails at the upper and lower leaflets are shown in light and dark gray lines. For clarity, water and other components are omitted.

Energetic Penalty from SA/Lipid Mismatch

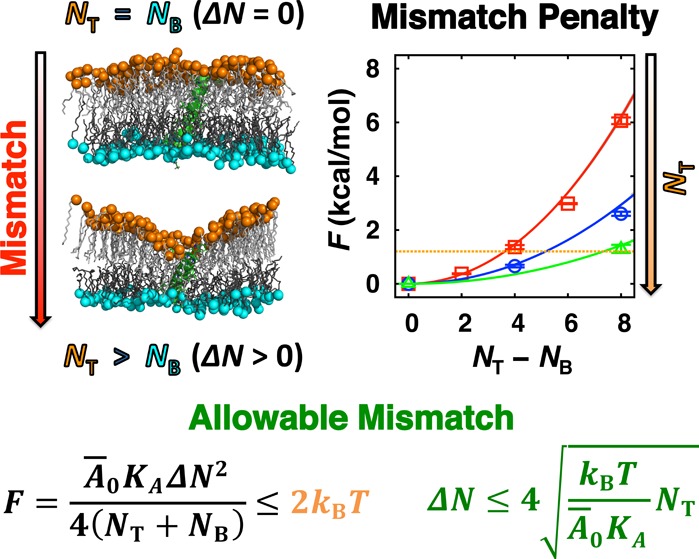
Although the simulations were stable at least within the current simulation time scale, observed behaviors of DMPC and POPC bilayers imply that the presence of SA/lipid mismatch results in strain on the bilayers. To characterize the energetic penalty to bilayer systems due to the SA/lipid mismatch, we calculated the surface tensions (Figure 9A and Supporting Information, Figure S24) and free energy derivatives with respect to curvature (Figure 9B and Supporting Information, Figure S25) from the pressure profiles. As shown in Figure 9A, the bilayer surface tension (black) remains zero, which is expected from the mechanical equilibrium under the constant pressure (zero surface tension) barostat. However, there is a clear linear dependence of the leaflet surface tensions on the mismatch, which is consistent with the decrease in the bilayer free energy derivative with respect to the curvature of membrane (Figure 9B). Both leaflet surface tensions and F̅′(0) imply that the bilayers become more stressed with increasing mismatch; that is, the upper leaflet would prefer larger surface area (γ_T < 0), whereas the lower leaflet would prefer more compact packing (γ_B > 0). These surface tensions would induce more positive curvature to relax such asymmetric stress applied to the bilayer membrane (F̅′(0) < 0; i.e., the upper leaflet is bending toward tail side, and the lower leaflet is curved toward the headgroup direction).

Figure 9.

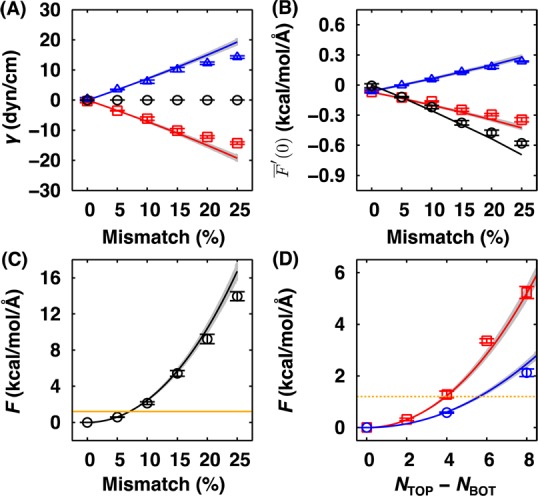
(A, B) The surface tension and the free energy derivative at planar curvature at various mismatches for pure DMPC bilayer with N_T = 80, where the leaflet properties are shown in red (upper) and blue (lower), and bilayer properties are shown in black: (A) The surface tensions, γ (circle), γ_T (square), γ_B (triangle), and the estimates calculated from eq 8 (lines); (B) The free energy derivatives at planar curvature, F̅′(0) (circle), F̅_T′(0) (square), and F̅_B′(0) (triangle) and the estimate of these derivatives calculated from eq 9 (lines). (C, D) The energetic penalty due to SA/lipid mismatch estimated from eq 11 (symbol), the prediction from eq 10 (line), and an energy level, 2k_BT (orange line):⁵⁰ (C) the energetic penalty for pure DMPC bilayer with N_T = 80 and (D) the energetic penalty for pure DMPC bilayers with different sizes, N_T = 40 (red square) and 80 (blue circle). In all the panels (A–D), the error bars are standard errors from three block averages, and the gray area represents the region within one standard error of the predicted line.

The above observations and speculation can be characterized quantitatively by using a continuum elastic model (see Appendix for details).^44,51−53 For pure bilayers, from the definition of the surface tension and the energetic cost during the lateral stretch of the leaflets that changes SA from A₀ (without tension) to A_ϕ, we obtained an expression for the leaflet surface tension

8

where ΔN = N_T – N_B and K_A is the area compressibility modulus for a bilayer. To estimate K_A, we numerically fitted the surface tension data from the pure bilayer simulations up to 15% mismatch (Figure 9A), in which the SA/lipid is well-described by the prediction, as shown in Figure 2C. For DMPC bilayers, the estimated K_A is 270 ± 17 dyn/cm, which is reasonably close to the previously reported values, 234⁵⁴ and 257 dyn/cm.⁵⁵ For POPC bilayer, we obtained an estimate of K_A = 299 ± 6 dyn/cm, which also agrees reasonably well with the reported values, 278⁵⁵ and 282 dyn/cm.⁵⁶ Then, we obtained an expression for the free energy derivative at the planar bilayer curvature that can be interpreted as a mechanical torque applied to the leaflet and the bilayer

9

where l_BL = l_T + l_B is the hydrophobic thickness of the bilayer as a sum of those for the upper (l_T) and lower (l_B) leaflets. As shown in Figure 9B, the predicted free energy derivatives, eq 9, show remarkable agreement with those calculated from the pressure profiles.

In addition, we obtained an expression for the energetic penalty arising from the SA/lipid mismatch

10

As shown in Figure 9C, eq 10 agrees well with the estimate calculated from the following equation using F̅′(0) calculated from pressure profiles,

11

where the spontaneous curvature R₀^–1 is estimated as

12

It is interesting to note that at R₀^–1 the SA/lipid restores its tension free value A̅₀ (see eq 28). Most importantly, by comparing the accessible thermal fluctuation of the bilayer energy (≤2k_BT)⁵⁰ and eq 10, we are able to obtain a quantitative criterion for an allowable mismatch in the number of lipids between leaflets as

13

It should be stressed that the maximum allowable mismatch ΔN_MAX grows as a function of N_T^1/2, from which we infer that the simulations for bigger bilayer membranes would suffer less from the effects of the SA/lipid mismatch. In Figure 9D, we show the estimate of an energetic penalty due to the SA/lipid mismatch for DMPC bilayers with N_T = 40 (red square) and 80 (blue circle), where the energetic penalty at the same ΔN becomes less severe for the bigger systems; that is, the bigger systems are more tolerant from the SA/lipid mismatch. For reasonable sizes of simple bilayers (N_T = 40–160) composed of DMPC and POPC, we find that up to 5% mismatch in SA/lipid between leaflets is allowable (Supporting Information, Figure S26).

However, as the complexity and system size increase, it becomes more and more challenging to calculate the lateral pressure profile due to undulations. Large undulations are problematic because these prevent accurate estimation of bilayer center, which in turn makes the calculations of the pressure profile difficult. Thus, such technical difficulties make it challenging to prove if the aforementioned criterion could be applicable to more complex and larger systems. In practice, such large undulations can be suppressed by applying weak restraints to hold bilayer relatively flat, which is reasonable (realistic) considering that the cytoskeleton network supports the cell’s shape. In fact, such restraints were used in a recent study of the plasma membrane,²³ where the bilayer was forced to remain flat. Therefore, even for complex and large bilayers, one can still estimate a meaningful free energy derivative at planar bilayer curvature, which could allow the application of the stability criterion, eq 13, to these bilayers. For example, let us consider a large bilayer whose system size is 10 000 lipids per leaflet, with mean bilayer area compressibility modulus and mean tension-free SA/lipid are 200 dyn/cm and 60 Ų, respectively. For this system, a mismatch below 75 lipids would not cause energetic penalty greater than 2k_BT.

Conclusion

This work aims to quantitatively characterize the impacts of the mismatch in the SA/lipid between leaflets on bilayer membrane simulations. Under constant pressure and periodic boundary conditions, the MD simulations of DMPC and POPC bilayers with and without gA or WALP23 at various mismatches ranging from 0 to 25% show that increasing SA/lipid mismatch induces more asymmetric lipid packing, so that the upper leaflet becomes more ordered, whereas the lower leaflet is less tightly packed (disordered). The mismatch impacts on the bilayer properties are mild up to 5–10% mismatch, and the peptide-bilayer interfaces are not generally sensitive to SA/lipid mismatch. The poor adaptability of saturated DMPC bilayers results in highly asymmetric 2D-thickness distribution of upper leaflet at larger SA/lipid mismatch, whereas monounsaturated POPC bilayers show better adaptability to both hydrophobic and SA/lipid mismatches. All the analyses imply that bilayers with fully saturated chains are more prone to SA/lipid mismatch than those with unsaturation in lipid tails. Although all present simulations were stable within the simulation time scale of hundred nanoseconds, the leaflet surface tension and the free energy derivative with respect to bilayer curvature do not vanish, indicating that the mismatched bilayers are not energetically stable. Estimation of the energetic penalty due to the SA/lipid mismatch based on a continuum elastic model and its comparison with the thermal energy make it possible for us to propose a criterion for allowable mismatch in membrane simulations. On the basis of this criterion, we infer that the SA/lipid mismatch up to 5% would be tolerant in membrane simulations of reasonable sizes (a total of 40–160 lipids in one leaflet).

Appendix: A Continuum Model Description of Energetic Penalty from SA/Lipid Mismatch

In this appendix, we first estimate the energetic penalty from the SA/lipid mismatch between leaflets by considering the lateral stretch of monolayers in the framework of the Helfrich model,⁵¹ where we consider a bilayer consisting of a single lipid type and each leaflet of the bilayer as a thin continuum elastic body. Then, for completeness, we rederive the contribution from the SA/lipid imbalance to the free energy derivative (per unit area) with respect to the bilayer curvature, which was originally given in the work of Sodt and Pastor (in Supporting Material of ref 53). The connection to the bilayer bending follows by equating the energetic penalty and the bending free energy given by

14

where k_c is the bending modulus, and R^–1 and R₀^–1 are the curvature and the spontaneous curvature of the bilayer, respectively. Comparing the energetic penalty with the thermal fluctuation of the bilayer energy, we provide a quantitative criterion for an allowable mismatch in membrane simulations. This appendix then concludes with an estimate of the energetic penalty for bilayers with an inserted protein whose size is sufficiently small compared to the lipid bilayer.

Energetic Penalty from SA/Lipid Mismatch

Let us start by considering an energetic penalty due to the lateral stretch of a bilayer. The free energy contribution from the lateral stretch of a planar leaflet that changes its surface area from A₀^M to A can be phenomenologically described by

15

whose derivative with respect to the area is given by

16

Here, A₀^M = N_MA̅₀ is the entire leaflet SA without tension (N_M is the number of lipid in a leaflet and A̅₀ is the tension-free SA/lipid) and K_A is the area compressibility modulus of the monolayer. At a given fractional mismatch, ϕ = 1 – N_B/N_T, the SA of each leaflet is identical to that of the bilayer (A_ϕ). By defining a surface density for a leaflet, x_L ≡ A̅₀/A̅_L, and noting that the surface tension vanishes (γ = γ_T + γ_B ≡ 0), from eq 16, the surface densities can be expressed as

17

Thus, A_ϕ and SA/lipid of each leaflet at ϕ can be derived as eq 1, and an expression for the leaflet surface tension is immediately given by eq 8, which are equivalent to

18

19

In the present study, we estimate K_A from the surface tensions, which can be related to the area compressibility modulus of monolayer, K_A = 2K_A^M.⁵² By inserting eq 18 into eq 15, the energetic penalty for the bilayer due to ϕ is given by eq 10 or its equivalent form

20

If the restraints (periodic boundary conditions) holding the planar bilayer were relaxed, the upper and lower leaflets would adjust their surface area to minimize the energetic penalty, which would induce a total bilayer curvature. In order words, the bilayer would deform to its spontaneous curvature (dependent on leaflet mismatch), R₀^–1.

Free Energy Derivative with Respect to Bilayer Curvature

Now, let us consider bending of a planar leaflet with surface area A_ϕ around an arbitrary pivotal plane, z = z_p, which preserves the area of the plane and the volume of the leaflet.⁴⁴ For simplicity, we will consider bending that does not perturb the y degree of freedom, that is, cylindrical bending. Before bending, the volume of the leaflet is given by V = A_ϕ|δz|, where δz = z_ns – z_p. Here, z_ns is the location of the neutral surface (plane) of a leaflet, where the lateral stretch is decoupled from the bending degrees of freedom in the framework of the Helfrich model.⁵⁷ After bending, this volume can be written as V = A_ϕ|δR|(1 + R^–1δR/2), where δR = R_ns – R, and R^–1 and R_ns^–1 are the curvatures of the pivotal and neutral planes, respectively. In the small curvature limit (|R^–1δz| ≪ 1), one can find δR ≈ δz(1 – R^–1δz/2), from which the area A(z_ns) can be expressed as

21

In their study of the lipid inverse hexagonal phase,⁴⁴ Sodt and Pastor reported that the neutral surface is near the C22 atom, the first carbon of the hydrophobic chain of the lipids. Thus, the neutral surface of each leaflet is located at z_ns,T = l_T and z_ns,B = −l_B, where l_L is the hydrophobic thickness of each leaflet of a bilayer centered at z = 0. We note that the above equation can be also obtained for more general bending that is described by two principal curvatures.⁵²

From eqs 16 and 21, the energetic penalty from the lateral stretch can be connected to the free energy derivative (per unit area) with respect to the curvature for a leaflet as

22

Note that, for bilayer bending, the pivotal plane is at the bilayer center (z_p = 0), where both upper and lower leaflets have the same SA. Thus, the free energy derivative of each leaflet becomes

23

which has a slightly different form compared to eq S22 in ref 53. The estimated free energy derivatives indicate that both the upper (dF̅_T/dR^–1 < 0) and lower (dF̅_B/dR^–1 > 0) leaflets would bend toward the lower leaflet side for ΔN > 0. From eq 23, the bilayer free energy derivative can be written as

24

where l_BL = l_T + l_B is the hydrophobic thickness of the bilayer. Note that eqs 23 and 24 are the estimations only considering the SA imbalance. These can be written in a compact form as eq 9.

Depending on the lipid type, the leaflet free energy derivatives may not vanish even for symmetric bilayers. To take into account such situations, we assume that the intrinsic lipid-specific contribution is insensitive to the mismatch, that is,

25

where dF̅_M/dR^–1 is the contribution from mismatch given by eq 24, and dF̅₀/dR^–1 is the free energy derivative calculated for the symmetric bilayer. For the bilayer free energy derivative, we again obtain eq 24 because the second term of the right hand side of eq 25 is canceled out. The estimated free energy derivatives by eqs 24 and 25 agree excellently with those calculated from the pressure profiles (see Figure 9B and Supporting Information, Figure S25).

Spontaneous Curvature and Criterion for Allowable SA/Lipid Mismatch

From eqs 14 and 20, and the relation F̅′(0) = dF̅/dR^–1|_R^–1 = 0 = −k_cR₀^–1, an expression for the spontaneous curvature of the bilayer can be derived as eq 12 or its equivalent form

26

and that for the bending modulus k_c = K_A(l_BL⁰/2)² (via a coupled shell model),⁵² where l_BL is the hydrophobic thickness of a symmetric bilayer. The implications of the obtained R₀^–1 can be better understood by geometric consideration, where the SA of the neutral surface of both upper and lower leaflets at R₀ is given by

27

By inserting eqs 18 and 26 into eq 27, we obtain

28

where A̅_L,R0^–1 is the SA/lipid of a leaflet at R₀^–1. Because eq 28 holds for any given ϕ, the SA/lipid of the neutral surface of each leaflet becomes A̅₀ (i.e., tension-free SA/lipid).

The energetic penalty given by eq 20 can be rewritten in a form of bending free as eq 11 or its equivalent form

29

By considering that the fluctuation of the bilayer energy is bounded by the thermally accessible range, 2k_BT,⁵⁰ we claim that a free energy penalty due to an allowable SA/lipid mismatch needs to be less than 2k_BT (i.e., F ≤ 2k_BT). From eq 20, this leads to a criterion for the allowable SA/lipid mismatch

30

For a typical bilayer with A̅₀ = 60 Ų and K_A = 250 dyn/cm, A̅₀K_A ≈ 360k_BT at room temperature, so that eq 30 can be simplified to eq 13.

Energetic Penalty for Bilayers with Inserted Protein

To estimate the energetic penalty due to the SA/lipid mismatch for bilayers with an inserted protein, we assume that (1) the system is sufficiently large; that is, the protein–lipid adaptation is a local behavior, so that the average lipid properties are similar to those for the pure bilayer, for example, A_ϕ ≈ 2A̅₀/(N_T^–1 + N_B), and the SA/lipid is given by eq 18, and that (2) the contributions from the SA/lipid mismatch and the protein–lipid interactions to the spontaneous bilayer curvature are additive. Under these assumptions, the bending free energy can be approximately described by

31

where R_M^–1 and R_P are the contributions from the SA/lipid and protein–lipid interactions to the spontaneous curvature of a bilayer; that is, R₀^–1 = R_M + R_P^–1. Here, we assume that R_M is given by eq 26 and R_P^–1 = −F̅_P′(0)/k_c, where F̅_P′(0) is the free energy derivative at the planar bilayer curvature calculated from the symmetric bilayer with inserted protein and k_c = K_A(l_BL/2)² in our model. It is expected to be small, but for proteins with highly asymmetric cross sectional area along the membrane normal, it may be substantial. Note that this model does not take into account the detailed protein–lipid interactions but just considers the overall effects on the bilayer curvature.

Before estimating the energetic penalty, we obtained expressions for the leaflet surface tension and the free energy derivative at planar bilayer curvature as follows. For the leaflet surface tension, based on assumption (1), we obtained the identical expression to eq 19, where γ is replaced by γ – γ₀ and γ₀ is the leaflet surface tension calculated for the symmetric bilayer with inserted protein. The free energy derivative at the planar bilayer curvature is obtained by differentiating eq 31 with respect to the curvature, which has identical form to eq 25. The second term in the right hand side of this equation may not vanish depending on the specific protein–lipid interactions. Using the same K_A for the pure lipid bilayers, we estimated surface tensions and the free energy derivatives, which show good agreement with those calculated from the pressure profiles up to 15% of mismatch (see Supporting Information, Figures S24 and S25), justifying our assumptions.

Now let us consider the energetic penalty in a form of bending free energy. From eq 31, the energetic penalty from the SA/lipid mismatch can be written as

32

where F_P is the estimate of an energetic penalty due to the inserted protein

33

Note that eq 33 does not take into account the local adaptation of protein–lipid interactions at the monolayer level, which may be substantial, for example, when there is a large hydrophobic mismatch between protein and bilayer. For a small membrane protein or peptides, its contribution to the bilayer bending is expected to be fairly small. In fact, the estimated energetic penalty (with respect to the bilayer bending) due to gA and WALP23 is much smaller than k_BT (data not shown). Equation 32 can be rewritten as

34

where the first term is the contribution solely from the SA/lipid mismatch, which is given by eq 20, and the second term is the contribution from the coupling between mismatch and the protein–lipid interactions

35

Similarly to F_P, F_M–P is expected to be small for bilayers with small membrane proteins. Although the contribution from eq 35 is small in the total energetic penalty, the direct estimate calculated from eq 32 shows better agreement with that from eq 34 than that from eq 20 as shown in Supporting Information, Figure S26. These results again support our assumptions. The allowable mismatch can be estimated either analytically or graphically from F ≤ 2k_BT. However, note again that the above estimations do not apply for bilayers whose size is not sufficiently large compared to the inserted proteins.

Supporting Information Available

The complete results from all simulations: Density and pressure profiles, order parameter, hydrophobic thickness, SA/lipid, lateral diffusion coefficients; Distributions of root mean square deviation, tilt angle, and z center of mass of peptides; Interaction patterns of peptide's residues with their environment; Two-dimensional hydrophobic thickness maps; Surface tension, free energy derivative, and the estimate of an energetic penalty due to SA/lipid mismatch. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.5b00232.

The authors declare no competing financial interest.