Tension tests on mammalian collagen fibrils

Abstract

A brief overview of isolated collagen fibril mechanics testing is followed by presentation of the first results testing fibrils isolated from load-bearing mammalian tendons using a microelectromechanical systems platform. The in vitro modulus (326 ± 112 MPa) and fracture stress (71 ± 23 MPa) are shown to be lower than previously measured on fibrils extracted from sea cucumber dermis and tested with the same technique. Scanning electron microscope images show the fibrils can fail with a mechanism that involves circumferential rupture, whereas the core of the fibril stays at least partially intact.

1. Introduction

One of the best examples of the interface between biology and engineering can be found in the quest to relate extracellular matrix structure with its mechanical function. These studies have applications as varied as understanding mechanotransduction and fracture in tissues, such as bone [1], tendon [2], cartilage [3], skin [4] and cornea [5]. The structures of such collagen-based extracellular matrices have been studied extensively dating back to the earliest works of Leeuwenhoek [6]. It is generally accepted that these tissues are hierarchical assemblies [7,8], of which the bulk consists of cylindrical structures, the so-called collagen fibrils, well described as ordered arrays of collagen molecules. Substantial work in the last century was devoted to describing the details of this structure referred to as a D-staggered array [9,10]. More recently, the three-dimensional molecular scale details of these arrays have been described using high-resolution X-ray diffraction and modelling [11,12]. Description of the location and energetics of water molecules existing between collagen molecules within the fibrils has also been achieved [13]. The specific location and energetics of individual fluid ions interacting with collagen molecules within the fibrils is likely to also play a role in their mechanical behaviour, but this area is not completely understood.

While knowledge of the structural details has been accumulated over the past 300 years, it is only in the last few decades that this information has been applied towards improved understanding of mechanical function. A severe limitation of the earlier mathematical models is that their creators lacked knowledge of the constitutive equations (the stress–strain laws) of the substructures within the hierarchical assembly of tissue, including the collagen molecules and fibrils. As a result, even though the models contained topological features meant to approximate each of these components, they assigned to the sub-elements constitutive parameters and strength values that had been inferred from measurements at the macro scale using whole tissues [8,14,15]. This serious limitation inspired, as summarized next, significant interest and progress in the development and application of clever experimental techniques for probing the mechanical properties of the smallest constituents of biological tissues.

Advances in probing the mechanical properties of the substructures of collagenous tissues began in the 1980s when the stiffness of collagen molecules was indirectly determined using polymer mechanics techniques such as light scattering and viscosity measurements [16,17]. Scanned force microscopes [18] and laser tweezers [19,20], in turn, made the structural stiffness (force divided by displacement) of single molecules directly measureable. It is important to note that the common continuum notion of modulus for an assembly of molecules cannot be applied unless it is made of a minimum number of molecules. This was demonstrated through molecular dynamics simulations of collagen fibrils [21] that showed an assembly of collagen molecules becomes a representative volume element (the stress–strain curve becomes insensitive to volumes larger than the representative volume) only if it contains at least 10–20 molecules along its length and a similar number across its diameter.

Techniques similar to those used at the molecular scale have also been applied at the sub-micrometre scale to measure the stiffness of fibrils. Testing isolated single fibrils is a daunting task. For example, while X-ray-based stress measurements were used to measure fibril stiffness, these experiments were performed on large assemblies of fibrils [22]. This complicated the analysis by requiring inter-fibril interactions to be included in the mechanics analysis of the experimental data. The ability to isolate and test single fibrils, as described subsequently, eliminated the problem of inferring inter-fibril interactions.

Indentation tests on fibrils using scanned force microscopy provided substantial insight into the qualitative and to a lesser extent the quantitative mechanical behaviour of individual fibrils [23–25]. Any attempt at quantitative interpretation of the measurements requires, in addition to knowledge of the size and shape of the tip of the indenter, determination of the contact area throughout the loading. The most accurate methods for such quantification including multidimensional thresholding [26] have typically not been used in previous studies. Perhaps more importantly the indentation test as applied to biological tissues which are associated with nonlinear and time-dependent inelastic behaviour, spatial inhomogeneity and inherent anisotropy is difficult to interpret. Applying the solution to the axisymmetric Boussinesq problem [27], which neglects these realities, may appear to bring significantly more rigour into the analysis, but it does not. What does offer promise for improved understanding of the data obtained from indentation experiments is the ever-increasing use of theoretical and computational methods for solving the ill-posed inverse problem [28] of determining constitutive parameters from a finite number of surface deformation measurements.

In the past 10 years, measurements obtained from isolated fibrils loaded in tension using scanned force techniques have provided valuable data in the low strain regime. Originally, limits on displacement of the piezo-actuated devices used to perform the tests did not allow excursion into the large strain region of the stress–strain curve [29], and therefore the ultimate strength of the fibrils was not determined. More recently, by using stiffer cantilevers, a greater range of strain was achieved and fracture tensile tests were performed [30,31].

A significant advance in structural testing of individual collagen fibrils was made possible by the advent of custom designed microelectromechanical systems (MEMS) platforms [32]. These mechanical laboratories on a chip allow individual fibrils to be tested in a text-book tension configuration involving well-defined boundary conditions at the end of the specimen, an easily visualized gauge region and practically perfectly aligned static [33] or time-dependent [34] loading. In addition, the actuation that generates force could be accomplished both in air and in fluid [35]. Experiments performed on fibrils isolated from the dermis of sea cucumbers provided valuable lessons about the mechanical behaviour of unmineralized fibrils. First, fibrils are complex heterogeneous materials with mechanical behaviour that likely involves uncertainties in their geometry and in the mechanical properties of their constituents [33,35]. The large variations in the small-strain limit elastic modulus, strain to failure and tensile strength of dozens of tested fibrils attest to this fact. Second, fibrils from sea cucumber dermis fail at much higher stresses and strains than whole tendons [35]. (As reported in this paper, this holds true for mammalian fibrils, and therefore the stiffness and strength of tissues must be understood within the context of stress concentrators and the roles played by their non-collagenous components.) Third, the degree of hydration is very important with respect to fibril mechanics [33,35]. Going from water to humid air to vacuum, the modulus, strength and strain to failure all change dramatically. And, fourth, single fibrils show time-dependent behaviour whose characterization requires at least two relaxation times [34]. This suggests the existence of complex viscous mechanisms involving transport of water and ions between collagen molecules within a fibril.

While sea cucumber dermis fibrils have provided many interesting results, a robust treatment of more evolutionarily advanced tissues like tendon, ligament and bone requires making similar tests on fibrils extracted from these tissues. This brings up a new set of experimental problems. Sea cucumber dermis fibrils can be extracted with mild exposure to ethylenediaminetetraacetic acid (EDTA) followed by a gentle rocking in water [36]. This leaves the investigator with high confidence that extraction has not altered the mechanical properties of the fibrils. Such gentle treatments produce few if any isolated fibrils from mammalian tendon. Investigators have used several methods to overcome this including vortexing [37], hard drying [30,38] and tissue homogenization [29,31,39].

An effective way to determine whether a treatment has the ability to alter fibril mechanics involves comparing against water extraction using sea cucumber dermis. Prior to the mechanical tensile tests reported in the current paper, we performed a preliminary experiment where we looked at end-to-end distance of the isolated fibrils measured using dark-field contrast optical microscopy. We found that tissue homogenization alters the end-to-end distance compared to water extraction. In particular, the average distance decreased by 45% and histograms of over 100 fibrils each showed that water extraction resulted in a single symmetric peak while homogenized tissue extraction resulted in two peaks [40]. This suggests that tissue homogenization is able to fracture fibrils into smaller pieces placing mechanical patency of fibrils extracted with tissue homogenization in question.

This paper uses a gentler method to extract single fibrils from the load-bearing patellar tendon of rats. We show the first stress–strain curves and scanning electron microscopy (SEM) images of fibrils extracted using this new technique. The initial elastic modulus and fracture stress and strain are within a factor of two of what was previously measured using fibrils from sea cucumber dermis. There appear to be qualitative differences in the shape of the stress–strain curves between the two tissues. Based on post-loaded fibril imaging, it appears that single fibril rupture can occur without frank fracture (complete separation of the fracture surfaces) of an individual fibril. These results are primarily descriptive in nature and are presented in the spirit of opening the door to new questions that might be answered using MEMS platforms to test such gently isolated fibrils.

2. Methods

2.1. Collagen fibril sample preparation

Collagen fibrils were isolated from the rat patellar tendon using an isolation protocol developed previously [40]. In brief, patellar tendons were harvested from euthanized rats from the control groups of unrelated studies. The tendons were rinsed with deionized (DI) water followed by phosphate-buffered saline (PBS). Several cuts were made on the surface of the tendon using razor blades, which broke the fascicular membrane of the tendons. The tendons were then shaken gently in an extraction solution containing 4 mM EDTA and more than 1000 BAEE unit trypsin, buffered with Tris-hydrochloric acid at pH = 7.8. The tissue swelled in a few minutes. The swollen tissue was then soaked in approximately 2 ml of PBS, and pulled gently with two pairs of tweezers. Collagen fibrils from the tendons were released into the solution in this process. The solution was collected and the fibrils in the solution imaged using dark-field optical microscopy. Individual fibrils in the solution were isolated using micropipettes and a hydraulic micromanipulator. The isolated fibrils were loaded on top of the MEMS device and fixed with epoxy droplets delivered by another micromanipulator and micropipette. Twelve specimens were mounted this way and subsequently mechanically tested on a MEMS platform then imaged with a scanning electron microscope.

2.2. Microelectromechanical system device

The MEMS platforms used to perform tension tests on individual collagen fibrils have been described in detail previously [33–35]. Two generations of devices were developed. The first generation used electrostatic actuation to apply force to the specimen, and the displacements were measured using a Vernier scale. The second-generation devices rely on piezoelectric displacement transducers capable of applying displacement-controlled motions with nanometre-scale resolution. Digital-image-correlation software in conjunction with in situ microscopy enabled displacement measurements with 40 nm precision. Accurate determination of force from measured displacement was accomplished using standard MEMS technology. The basic idea of the MEMS paradigm is that if displacements of an elastic test structure with known dimensions and elastic moduli can be measured accurately, the forces can be determined using a structural analysis.

An image of the second-generation device used to test individual collagen fibrils is shown together with its schematic in figure 1. Multiple devices were fabricated with standard MEMS processing techniques, using 100 mm diameter silicon wafers as substrates. The wafers were SOI prime silicon with 4.5 µm overlayers and a 2 µm sacrificial oxide layer (Ultrasil Corp., Hawyard, CA, USA). The wafers were diced into 3 mm × 3 mm pieces each containing nine devices. After dicing and just prior to use, the photoresist on the diced silicon chips was removed in acetone, and devices were released by immersion in 49% hydrofluoric acid, followed by rinsing in methanol and critical point drying. The release etch dissolved all the sacrificial oxide beneath the portions of the device that were designed to be movable. Oxide left beneath areas of the device designed as anchors kept those portions of the device attached to the silicon handle. Because the device is less than 1 mm² in size, thousands of devices were fabricated simultaneously on a single silicon wafer. In the device shown in figure 1c, the black areas labelled A are anchored to the substrate, while the white areas are free to move. The device is designed for one end of the collagen fibril to be attached to the pad labelled 1 and the other end to be attached to the pad labelled 2. The device contains a window, a close-up view of which is shown in figure 1d, which allows measurement of the nominal diameter of the unloaded fibril. Uniaxial loading of the fibril was achieved by mounting the 3 mm × 3 mm MEMS piece on a single axis piezoelectric stage (Nano H100, Mad City Labs, Madison, WI, USA), and then placing a needle tip into the square pinhole shown in the schematic. When the base of the device is displaced to the upper left using the piezo stage, as oriented in figure 1c, the device applies a tensile stretch to the attached fibril specimen in the direction shown with the arrow. This makes the tensile test displacement controlled rather than load controlled, and the movement of all three positions, labelled 1, 2 and 3, are recorded simultaneously.

Figure 1.

(a) Bright field optical microscopy image of a MEMS device for testing collagen fibrils. (b) Higher magnification optical microscopy image of the sample loading area of a MEMS device (indicated with the box in (a)), showing a single collagen fibril loaded and fixed with three micro epoxy droplets. (c) Schematic of a MEMS device. The grey part indicates the base of the device. The black parts are connected to the base. The white part (movable pad) is suspended above the base with four tether beams connected to the anchor pad. Collagen fibrils samples are loaded across the fixed pad and the strain gauge pad. Upon testing, the movable pad is pulled towards the direction indicated with the arrow labelled ‘tensile displacement’, with a needle inserted to the pinhole, applying a tensile force to the specimen. The force is reflected by the deformation of the force gauge beams. The diameter of the specimen is measured above the window on the fixed pad using SEM. Contraction of the fibril is accounted for as described previously [35]. (d) SEM image of the window region of a MEMS device (indicated by the box in (b)), showing a region of the collagen fibril in the same state of load as the gauge region prior to application of any tensile stress. (Online version in colour.)

Since pad 1 is anchored to the substrate, the elongation of the collagen fibril specimen will be equal to the increase in separation between pads 1 and 2. The force applied to move pad 2 to the lower right is equal to the force applied to move pad 3 to the lower right. Therefore, the force applied to the specimen can be determined by measuring the elastic deformation involved in the increase in separation between pads 2 and 3. That separation is controlled by the elastic response of the silicon force gauge beams labelled in figure 1c. The dimensions of the force gauge beams are measured accurately using scanning electron microscopy, and the elastic modulus of silicon is known. This information is used as input into a finite-element model of the device to infer the forces necessary to achieve the observed displacements. In this manner, both the force and elongation of the fibril are determined simultaneously.

Before the tensile test, each MEMS piece was inserted into a thermally machined socket in a 35 mm petri dish, and the petri dish was then mounted on top of the piezo stage using double sided tape. During the test, the MEMS pieces were immersed in PBS, and all of the experiments were carried out at room temperature. In the tensile test reported in this manuscript, a constant 400 nm s⁻¹ elongation rate generated by the piezo stage was used to drive the MEMS devices, pulling the attached collagen fibrils. After mechanical testing, PBS was gently replaced with DI water and then the samples were allowed to air dry. In total, 40 nm of palladium was sputter coated on the samples which were then imaged using scanning electron microscopy (Helios Nanolab 650, FEI, Hillsboro, OR, USA).

3. Results and discussion

3.1. Collagen fibril morphology

Scanning electron microscope images showed D-banding patterns in all of the specimens (figure 2). This is important evidence consistent with the tested specimens being collagen fibrils and not some other biological fibrous tissue component. We were particularly interested in the diameters and the gauge lengths of the fibrils, because these data allow estimation of the engineering stress and strain. To avoid artefactual broadening of fibril diameters due to surface tension spreading, all fibril diameters were obtained using regions imaged over a window designed in the MEMS device (box in figure 1b, full view in figure 1d). Taking into account the palladium coating used to facilitate SEM imaging as well as the known reduction in diameter due to dehydration, [35] the diameters of 12 fibrils during testing ranged from 174 to 463 nm with a mean of 305 nm and an s.d. of 79 nm.

Figure 2.

SEM images of two fibrils at the locations of tensile fracture (scale bars represent 1 µm in a,b and 200 nm in c,d). (a) In this particular fibril, tensile fracture occurs in the middle of the strain gauge region. (b) In this particular fibril, tensile fracture occurs close to the surface of the MEMS device. (c) A higher magnification image of the fibril in the box in (a). (d) A higher magnification image of the fibril in the box in (b). (e) In both fibrils, fracture occurs at angles of about 45° to the axial direction of the fibrils. (f) In both fibrils, one of the fracture edges appears to be sharp, while the other edge appears to be blunt and irregularly shaped. (Online version in colour.)

The gauge lengths ranged from 4.6 to 20.8 µm, measured as the end-to-end distance between the fibril-epoxy interfaces on each side of the gauge region. Some fibrils fractured near their fixed ends while others fractured nearer the middle of the gauge region. In previous work, we vigorously exchanged the PBS medium after testing to remove any salts and then critically point dried the samples. In the current experiment, we more gently exchanged the PBS for DI water and then allowed for simple air drying. This modified SEM preparation procedure resulted in several fibrils still being suspended in the gauge region showing obvious damage from the previously applied tensile loading. Figure 2 shows SEM images of two fibrils near the locations of fracture. Some similar features are seen in both cases. The fractures occur at an angle of about 45° to the axial directions of the fibrils. One side of the break appears sharp while the other edge is smooth. D-banding features are clear near the sharp edge but disappear near the smooth edge. To our knowledge, these are the first images of rat patellar tendon fibrils fractured in isolation. It would be quite interesting to design an experiment in which the polarity of the collagen molecules within the fibril could be assessed near a break like the one shown in figure 2. It is known that both unipolar and bipolar arrangements can exist in fibrils [41]. In a bipolar fibril, the symmetry point at which the collagen molecules flip their carboxy/amino orientation may provide the stress concentrator that results in fractures like the one shown in figure 2.

3.2. Mechanical properties

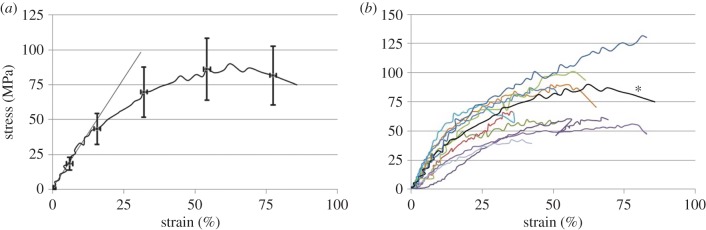
The representative stress–strain curve shown in figure 3a indicates that at low strains the stress is a linear function of strain. Above approximately 12% strain, the curve begins to bend over. This general softening effect appeared in all the tested fibrils between 10% and 20% strain (figure 3b). The stress–strain ratio associated with the initial linear region ranged from 160 to 520 MPa with a mean of 326 MPa and an s.d. 112 MPa. This is about 30% lower than the results previously reported for sea cucumber fibrils tested with an MEMS platform. In addition, the standard deviation is only 30% of the mean value here while it was approximately 100% of the mean value with the sea cucumber fibrils. This is consistent with the fact that the current fibrils were tested relatively quickly after harvesting from the animal while the sea cucumber fibrils were stored for many months before testing. The ageing of the sea cucumber fibrils may have allowed for more cross-linking to take place and more variability to evolve among the population of tested fibrils.

Figure 3.

(a) Stress–strain curve of a typical collagen fibril tested in this study. The stress–strain ratio at the low strain linear region (less than 12%) is 315 MPa, maximum tensile strength is 90 MPa and fracture stress is 75 MPa with associated fracture strain of 86%. Fracture toughness is 47 × 10⁶ J m⁻³. (b) Stress–strain curves for all 12 fibrils tested are shown. For reference, the particular curve in (a) is indicated with an asterisk. (Online version in colour.)

The general shape of these curves differs from what we previously found using fibrils extracted from sea cucumber dermis [35]. Those earlier tests showed relatively linear portions throughout the stress–strain curves with kinks between portions of differing slope. The current fibrils extracted from mammalian tendon show a more graceful softening with increasing strain. While we had previously shown that the sea cucumber fibrils displayed what appeared to be well-defined points where the stress ceases to be a linear function of strain [33], the fact that the rat patellar tendon fibrils display a qualitatively different curve prevents us from drawing conclusions regarding at what level of stress the fibril initiates irreversible deformation. Further work will have to be done in which the patellar tendon fibrils are unloaded during the test to explore the possibility of inelastic strains before statements regarding elastic and yield properties can be made. Qualitatively, the data clearly show that, in most cases, the specimens failed at a nominal stress lower than the peak stress. The true stress was most likely a monotonically increasing function of strain.

Fracture strength, on the other hand, can be assessed quantitatively with the current data. Fracture was defined as the point at which the strain gauge clearly relaxed. The device was continuously moved in a direction that induced tensile strain in the fibril. For most of the test, the force gauge beams moved away from the movable pad (figure 1). At the fracture point, the force gauge beams quickly relaxed back to their starting positions and piezo motion was stopped. The stress at which the fibrils ruptured ranged from 39 to 130 MPa, with a mean value of 71 MPa and an s.d. of 23 MPa. The average strain to failure was 63%, with an s.d. 21%. Like the stiffness, these strength numbers are considerably less than what was found using sea cucumber fibrils (mean fracture strength of 230 MPa [35]). The toughness of the fibrils, quantified as the area under the stress–strain curve, ranged from 12 to 71 MJ m⁻³, with a mean of 34 MJ m⁻³ and an s.d. of 17 MJ m⁻³. Worth noting here is that these measurements were taken at room temperature. Before strong quantitative statements can be made about the physiologically relevant strength and toughness of mammalian collagen fibrils, the experiments will have to be repeated at elevated temperatures.

For more detailed information about the individual collagen fibrils tested in this study, the mechanical properties of each fibril are listed in table 1. There is no evident relationship between the dimensions of the fibrils and their mechanical properties.

Table 1.

Mechanical properties of the collagen fibrils tested in this study.

fibril no.	wet diameter (nm)	initial σ/ɛ ratio (MPa)	maximum strain (%)	fracture stress (MPa)	toughness (×106 J m−3)
1	134.68	391	51.84	58.66	23.33
2	207.29	185	66.71	58.65	25.57
3	161.94	160	106.55	54.37	44.88
4	173.93	459	57.07	85.23	37.14
5	188.00	520	51.20	83.19	31.66
6	159.51	266	35.77	66.19	13.20
7	119.26	287	61.33	93.59	39.93
8	250.26	329	81.44	50.60	33.44
9	184.22	467	36.03	65.54	19.24
10	190.55	315	85.74	74.97	56.67
11	216.03	190	42.39	39.26	11.97
12	159.64	341	82.83	130.29	71.32
mean	178.78	325.83	63.24	71.71	34.03
s.d.	34.27	112.12	21.13	23.17	16.82

3.3. Comparison with previous results

Previously, investigators have tested the mechanical strength of mammalian patellar tendon components at different length scales using various micro tensile systems. Most of the measurements were conducted on animal models different from ours. Miyazaki & Hayashi [42] measured the tensile strength of approximately 1 µm diameter bundles of collagen fibrils from rabbit patellar tendon. At this slightly greater length scale than the one presented in the current paper, the measured fracture tensile stress was 8.5 ± 2.6 MPa, with a strain to failure 21.6 ± 3.0%. At the fascicle scale, the fracture tensile stress of approximately 300 µm diameter rabbit patellar tendon fascicles measured by Yamamoto et al. [43] was 17.2 ± 4.1 MPa, with a strain to failure 10.9 ± 1.6%. In the same study, Yamamoto also tested the fracture mechanical properties of entire rabbit patellar tendons with diameter approximately 3000 µm. In this case, the measured fracture stress was 40.5 ± 4.3 MPa at 6.1 ± 1.0% strain. Incorporating our fracture mechanical properties of single collagen fibrils, it is found that strain to failure is inversely proportional to the size of the test piece. Conversely, the fracture strength of individual collagen fibrils does not follow the general trend of the larger tested structures. Above the level of a single fibril, fracture strength increases with the size of the test piece. Instead, a single fibril is measured to be almost twice as strong as a whole tendon. We reported a similar finding in previous tests using fibrils from sea cucumber dermis [35]. The current paper shows this finding persists when using patellar tendon as the fibril source. This indicates that the mechanical strength of patellar tendon is not limited by the strength of individual collagen fibrils. A reasonable place to look for the strength limiting structure in this tissue would be the proteoglycan-rich cement substance between the fibrils or the interface between the fibrils and the cement.

More recently, fracture mechanical properties of collagen fibrils have also been measured with scanning force microscopy techniques. The maximum tensile strength of bovine Achilles tendon collagen fibrils measured by Yang et al. [39] is 60 ± 10 MPa, with strain to failure 13 ± 2%, while the maximum tensile strength of human patellar collagen fibrils measured by Svensson et al. [30] is 540 ± 140 MPa assuming dry cross-sectional area, with strain to failure of 20 ± 1%. Our measured fracture strength, 71 ± 23 MPa, overlaps with Yang's results, while the shape of the stress–strain curve looks more similar to Svensson's results. Our measured strain to failure, 63.24 ± 21.13%, is greater than the results from either of the other two groups. The difference in the fracture mechanical properties could be caused by variations in tissue type, sample preparation techniques and measurement techniques.

4. Summary

We have shown the first MEMS platform mechanical tests of fibrils isolated from a load-bearing mammalian tendon. Quantitatively, the data for modulus and fracture stress and strain are easily within a factor of two of what was previously measured with this technique using fibrils from sea cucumber dermis. However, additional data are required before statistically significant statements can be made about the differences in constitutive parameters between fibrils extracted from these different tissues. There appear to be qualitative differences in the shape of the stress–strain curves between the two tissues. However, it would be necessary to use the same mechano-chemical extraction protocol to obtain fibrils from both tissues before any strong conclusions can be drawn. Finally, it appears that single fibril rupture can occur without frank fracture (complete separation of the fracture surfaces) of an individual fibril. It will be very interesting to try to duplicate this phenomenon with a multiscale model. Such an exercise may produce new mechanisms relating to tissue damage as a consequence of combining nanoscale experimental mechanics with detailed multiscale modelling.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.